
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Built Environ. , 03 November 2022
Sec. Earthquake Engineering
Volume 8 - 2022 | https://doi.org/10.3389/fbuil.2022.1037832
This article is part of the Research Topic Energy dissipation devices and vibration-control systems for structures and infrastructures to mitigate damages under different hazards View all 6 articles
 Yutaka Nakamura*
Yutaka Nakamura* Ryota Matsumura
Ryota MatsumuraTimber frame structures are commonly used in housing construction that use squared-off timber beams, columns, and walls as lateral load-bearing members. A small-size viscous damper can be applied to timber frame houses to reduce damage caused by major earthquakes. Dampers are normally installed inter-story (between adjacent floors) to absorb vibration energy and reduce seismic response. Another method is the cross-story installation wherein a damper is installed between the rooftop and base of the structure across intermediate floors. This study investigated the effectiveness of cross-story installation of a viscous damper by conducting eigenvalue analyses of 2DOF models and earthquake response analyses of a two-story timber frame house subjected to the 2016 Kumamoto earthquake and other major earthquakes. We compared the damping factors and response reduction effects of the cross-story installation with those of conventional inter-story installations. The results showed that the cross-story installation of dampers was more effective than the inter-story installation in terms of reducing story drift. Furthermore, the cross-story installation reduced the number of dampers required for preventing severe damage by half. Finally, the cross-story installation allowed the viscous damper in the first story to absorb vibration energy nearly twice as much as that of the inter-story installation. Therefore, while the cross-story damper is typically installed on an outer frame fixed to the house, our results conclude that it can be applied to an existing house as a seismic retrofitting measure.
The passive control method has been widely used in buildings where various dampers have been installed inter-story onto structural frames to dissipate seismic energy and reduce earthquake damage to buildings. In Japan, the application of dampers to structures has increased considerably since the 1995 Kobe earthquake (Kasai et al., 2008; Kasai et al., 2009). According to the Japan Society of Seismic Isolation (JSSI), as of 2020, the total number of buildings with dampers was 1,600 in Japan. Metallic hysteretic, fluid viscous (oil), and viscous liquid dampers accounted for 36%, 21%, and 18% of all dampers, respectively (Manual for Design and Construction, 2013; Design of Seismic Isolation and Response Control, 2016; MENSHIN, 2022). Design manuals for passive building control have been published in Japan in 2013 and 2016.
Since the 1990s, viscous dampers have been studied for building applications, mainly based on mechanical engineering (Constantinou and Symans, 1992; Constantinou and Symans, 1993; Taylor and Constantinou, 1995; Seleemah and Constantinou, 1997; Soong and Dargush, 1997; Fu and Kasai, 1998). In the last 2 decades, several studies have been conducted on device development, seismic performances, applications in tall buildings, response analyses, and experiments (Lee and Taylor, 2001; Lin and Chopra, 2002; Soong and Spencer, 2002; McNamara and Taylor, 2003; Sorace and Terenzi, 2008; Liang et al., 2012; Seo et al., 2014; Tubaldi et al., 2014; Dong et al., 2016). Viscous dampers have been installed inter-story (between adjacent floors) in the same manner as other dampers to absorb vibration energy.
Furthermore, viscous dampers have been used for seismic enhancement and retrofitting (Uriz and Whittaker, 2001; Martinez-Rodrigo and Romero, 2003; Sorace and Terenzi, 2009; Rama Raju et al., 2014; Lavan, 2015; Pollini et al., 2016, 2017; Impollonia and Palmeri, 2018; Aydin et al., 2019; Tabar et al., 2021). Design procedures and optimum design methods have been studied for use of supplemental dampers in structures (Tsuji and Nakamura T, 1996; Uetani et al., 2003; Lavan and Levy, 2005; Lavan and Levy, 2006; Silvestri and Trombetti, 2007; Hwang et al., 2008; Takewaki, 2009; Hao and Zhang, 2016; Kawamoto et al., 2016; Parcianello et al., 2017; Wang and Mahin, 2018; De Domenico et al., 2019; De Domenico and Ricciardi, 2019; Idels and Lavan, 2020; De Domenico and Hajirasouliha, 2021; Wani et al., 2022). While previous studies have investigated high-rise buildings, slender towers, and long-span bridges that may suffer severe damage due to seismic excitations or wind loads, no research had been conducted on low-story houses until small-size viscous dampers were developed and applied to housing structures.
Various studies have investigated the effectiveness of a small-size viscous damper installed in a timber frame house to reduce damage caused by earthquakes. Conventionally, timber frame structures are used in housing construction in Japan, and their seismic performance can be secured by the load-bearing capacity of erected braces and walls. However, major earthquakes of the past, such as the 2016 Kumamoto earthquake, have caused severe damage to earthquake-resistant timber frame houses (Yamada et al., 2017). Previous studies on small-size viscous dampers (Matsuno et al., 1999; Matsuno et al., 2000) have conducted shaking table tests and simulation analyses on a one-story timber test structure subjected to the 1995 Kobe earthquake. In addition, earthquake response analyses of a full-scale two-story timber frame house with small-size viscous dampers against the 2016 Kumamoto earthquake have been conducted (Nakamura and Fujii, 2021). These studies showed that the small-size viscous dampers effectively reduced the story drift and prevented severe damage.
Cross-story installation is another method wherein a damper is installed between the roof top and base of the structure across intermediate floors to enhance the response reduction effects. Recent studies on the cross-story installation of dampers conducted earthquake response analyses on super high-rise reinforced-concrete buildings installed with cross-story buckling restrained braces (Maida et al., 2015; Ueno and Ikenaga, 2018) and on steel buildings installed with cross-story viscous dampers (Ueno et al., 2020). The effects of tuned viscous mass dampers installed across multiple stories have been investigated through earthquake response analyses of tall buildings (Ogino et al., 2014; Fujise and Ikenaga, 2021; Lim and Ikenaga, 2021). These studies concluded that the cross-story installation of dampers effectively reduced the earthquake response of buildings. However, no research has been conducted on the cross-story installation of dampers in timber frame houses.
This study investigates the cross-story installation of a small-size viscous damper in a two-story timber frame house to demonstrate its advantage over the conventional inter-story installation, where a damper is installed between adjacent floors. Eigenvalue analyses of 2DOF mass-spring-dashpot models and earthquake response analyses of a two-story timber frame house installed with small-size viscous dampers are performed to investigate the effectiveness of the cross-story installation of a damper. Compared to inter-story installation, the cross-story installation of dampers effectively reduced the story drift and the number of dampers required for preventing severe damage by half. The results of the study demonstrated that a cross-story damper can effectively enhance the seismic resistance of timber frame houses.
The small-size viscous damper shown in Figure 1 was developed based on a general-type viscous damper, which is used mainly in timber frame houses in Japan to reduce damage caused by earthquakes (Matsuno et al., 1999; Matsuno et al., 2000). Similarly, the small-size viscous damper is installed inter-story, which induces a damping force proportional to the relative velocity of the piston rod.
We considered 2DOF mass-spring-dashpot models, where a dashpot was installed between floors as a damping element. Figures 2A, B show the conventional inter-story and cross-story dashpot installation where each dashpot was installed between adjacent floors and between the roof top and base of the building, respectively. No structural damping was assumed, and the dashpots represented the installed dampers. The connection member was assumed to be rigid. The free vibration of a two-story shear building can be expressed as
where m1 and m2 are the first and second story masses, respectively; k1 and k2 are the first and second story shear stiffnesses, respectively; c1 and c2 are the damping coefficients of the first and second inter-story dashpots, respectively; and cs is the damping coefficient of the cross-story dashpot.
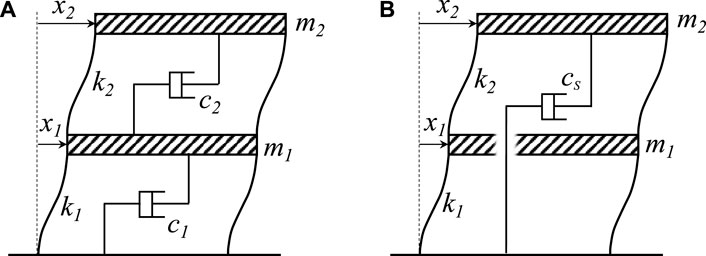
FIGURE 2. 2DOF mass-spring-dashpot models. (A) Inter-story dashpot installation (B) Cross-story dashpot installation.
The damping matrix, CD in Eq. 3 represents non-proportional damping, and the eigenvalue problem of Eq. 1 can be solved using Foss’s method (Foss, 1958) as
Equation 7 yields two pairs of complex conjugate eigenvalues, {λ}, and their corresponding eigenvectors, {u}, for damped vibration; {λ} can be expressed as
The natural circular frequencies, ω1 and ω2, and the damping factors, h1 and h2, of the first and second modes, respectively, are expressed as
When m1 = m2 = m, k1 = k2 = k, and c1 = c2 = cs = c, the characteristic equation of the eigenvalue problem of Eq. 7 can be expressed as a quartic equation of λ, given as for inter-story installation,
for cross-story installation,
By solving Eqs 13, 14 numerically for a specified set of {m, k, c}, two pairs of complex conjugate eigenvalues, {λ}, can be obtained, and the modal circular frequencies, ω1 and ω2, as well as the damping factors, h1 and h2, can be obtained by Eq. 12. Figure 3 shows the relationship between the damping coefficient, c, and the damping factors, h1 and h2, for m = 10
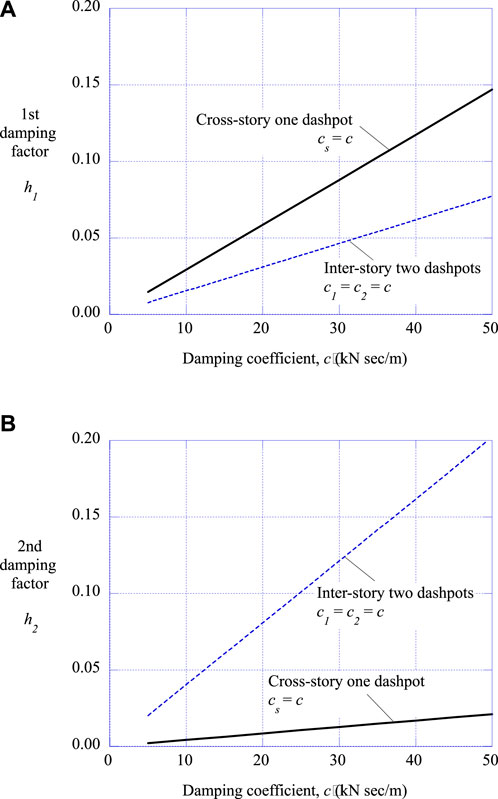
FIGURE 3. Damping factors of 2DOF mass-spring-dashpot models. (A) Relationship between the first damping factor and the damping coefficient (B) Relationship between the second damping factor and the damping coefficient.
The framework of an actual timber frame house, designed and built for sustaining seismic grade 3 (the highest grade) using the latest Japanese standards, used in this study is shown in Figure 4. The columns were made of Japanese cedar, each having dimensions of 12 cm × 12 cm; the beams were made of Douglas Fir. Young’s modulus and bending yield stress of the columns and beams were 7,500 N/mm2 and 24 N/mm2, respectively. The weights of the second story and rooftop were 198 kN and 158 kN, respectively.
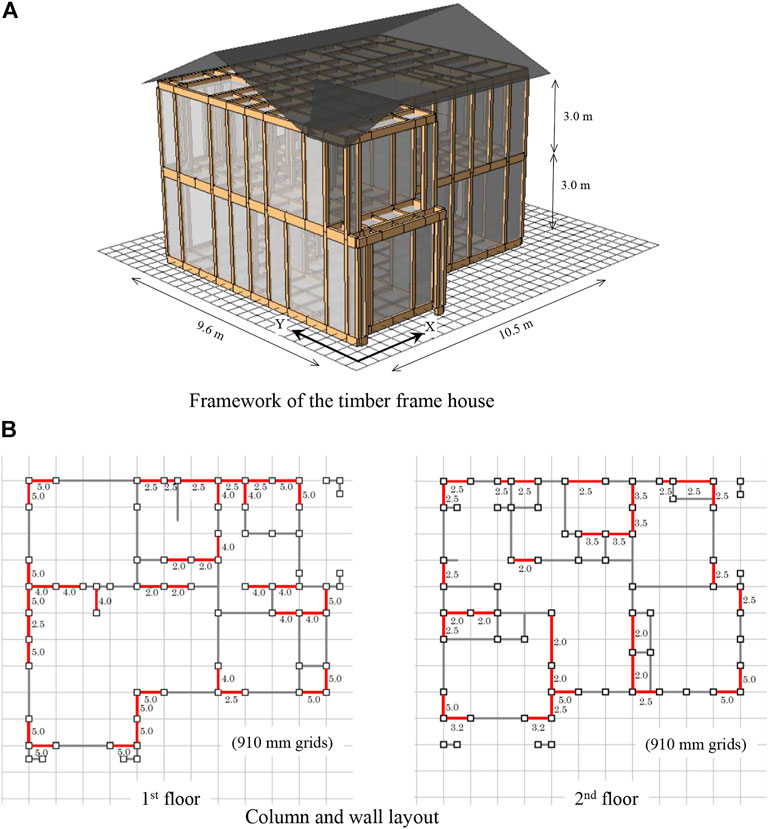
FIGURE 4. Timber frame house for earthquake analyses (A) Framework of the timber frame house (B) Column and wall layout.
Figure 4B shows the wall layout and ratio (Supplementary Appendix S1) of each wall of the timber frame house. The walls were spaced uniformly on each floor. Table 1 shows the existing wall length LE and necessary wall length LN for seismic grade 3 for each floor and direction. Every LE/LN ratio was greater than one, indicating that the timber frame house was suitable for seismic grade 3.
A beam and column were connected by a tenon joint or joint metals, such as “CP-T″ and “Hold-Down (HD)” joints, as shown in Figure 5A. Figure 5B shows the joint layout of the timber frame house. For conducting the earthquake response analyses, each beam-column joint was represented as an axial spring and a rotational spring with trilinear elastoplastic properties (Supplementary Appendix S2). Each timber beam or column was represented as an elastic bar element with rotational springs at both ends (Supplementary Appendix S3).
The 2016 Kumamoto earthquake occurred beneath Kumamoto City of Kumamoto Prefecture in the Kyushu region of Japan. It comprised a series of earthquakes: a foreshock earthquake on April 14, and a main earthquake on 16 April 2016. Earthquakes exceeding the JMA seismic intensity of seven occurred twice with a maximum magnitude of 7.3. The earthquake resulted in 273 deaths, and 2,809 people were injured. Numerous structures had either collapsed or suffered severe damage (Yamada et al., 2017), including the Great Aso Bridge, Kumamoto Castle, and Aso Shrine. Over 8,500 houses collapsed, and 35,000 houses were partly destroyed. Even timber frame houses that were designed according to the latest quake-proof standards and built after the year 2000 were destroyed.
The records of the foreshock earthquake observed in Mashiki Town in Kumamoto Prefecture, as shown in Figure 6A, were used for the response analyses. The displacement and acceleration response spectra of the observed records are shown in Figures 6B, C, respectively.
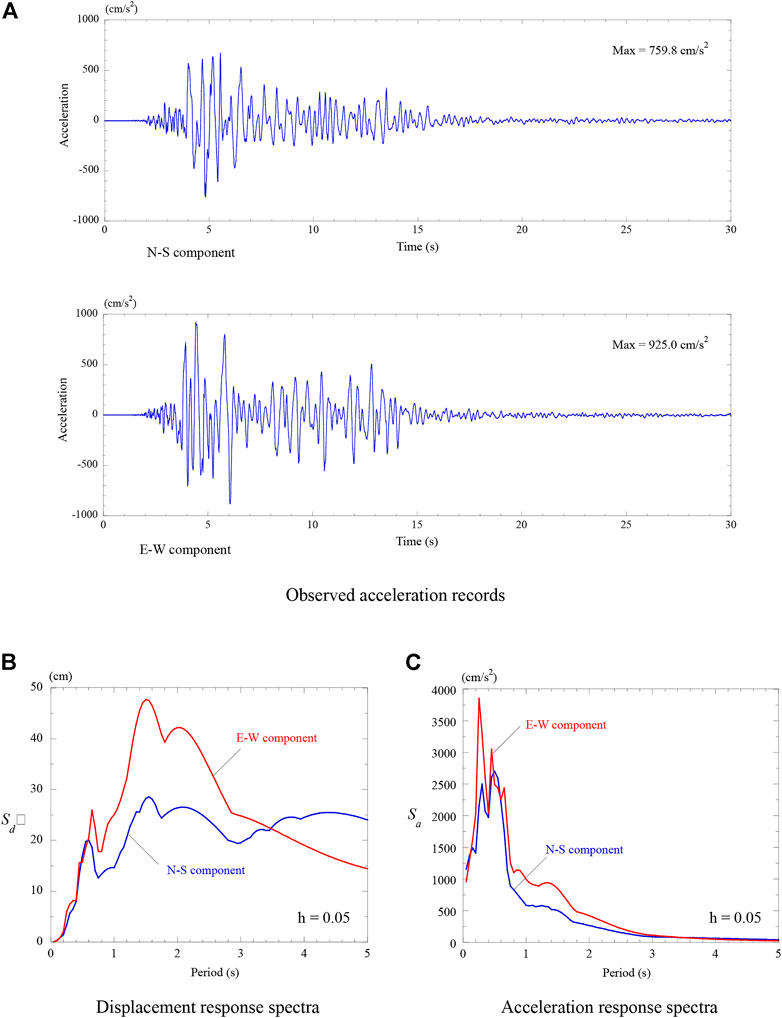
FIGURE 6. Foreshock of the 2016 Kumamoto earthquake (14 April 2016) (A) Observed acceleration records (B) Displacement response spectra (C) Acceleration response spectra.
In this study, a collapse analysis program for timber structures, “wallstat”, was used for the earthquake response analyses. The “wallstat” program was developed to assess the damage status and likelihood of collapse of a timber structure when subjected to an earthquake motion (Nakagawa et al., 2010; Suzuki and Nakagawa, 2020). It is now widely used by housing makers to demonstrate the earthquake-proofing performance of timber frame houses at high seismic grades. The program utilizes the distinct element method, which is a non-continuum analysis method that can be applied to large deformation and collapse analyses.
The validity of the “wallstat” program was verified by comparing the simulation results and shaking table tests of full-size housing models (Nakagawa et al., 2006; Nakagawa et al., 2007; Fukumoto et al., 2008). Destructive damage of timber frame houses due to the 2016 Kumamoto earthquake was also analyzed using the “wallstat” program (Nakagawa, 2017; Namba et al., 2020).
A viscous damper can be represented by either the Maxwell model that connects a dashpot and spring in series or the Voigt model, which connects a dashpot and spring in parallel. The Maxwell model was used in this study.
Figures 7A, B shows the 3D pictures of the response analysis and loci of the first-story drift angles, respectively, of the house model without dampers when subjected to 100% of the foreshock of the 2016 Kumamoto earthquake: The Y- and X-directions represent the N-S and the EW components, respectively. The first-story drift angle in the X-direction was dominant and exceeded 1/10, causing the house model without dampers to break down in the X-direction. Therefore, the dampers were placed in that direction to reduce the earthquake response and prevent severe damage.
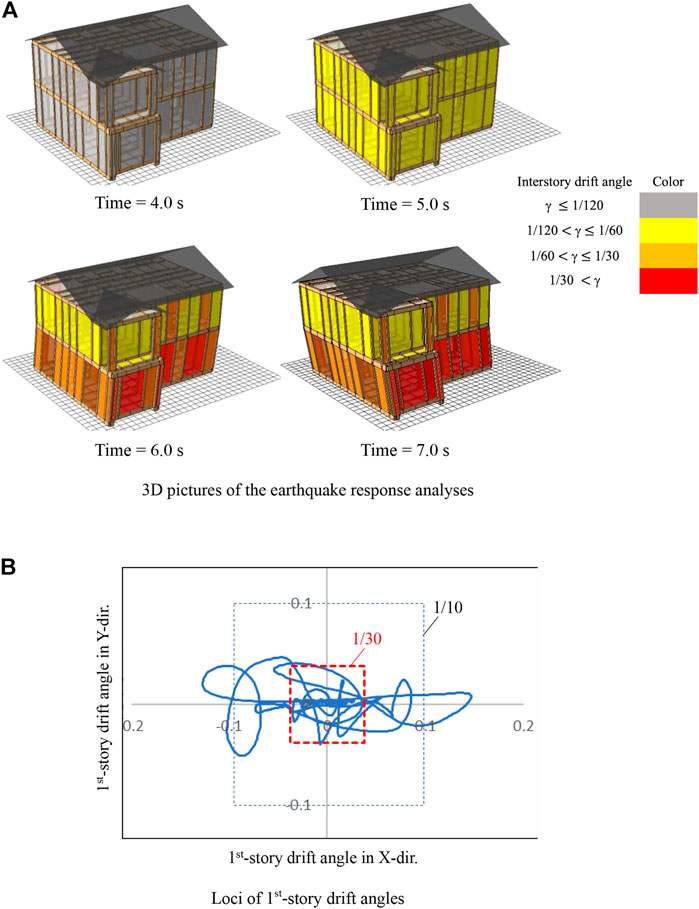
FIGURE 7. Results of the earthquake response analyses of the timber frame house without dampers (100% of the foreshock of the 2016 Kumamoto earthquake) (A) 3D pictures of the earthquake response analyses (B) Loci of first-story drift angles.
Figures 8A, B show the inter-story and cross-story installation of the viscous dampers (Figure 1) in the timber frame house (Figure 4), respectively. Whether inter- or cross-story, viscous dampers are typically installed onto an outer frame fixed to the timber frame house so as not to block visibility and are placed uniformly in the X-direction at four, five, or six locations so as not to induce torsional oscillations (Figure 9). In the Maxwell model that was used to depict the viscous damper, the spring represented the stiffness of the connection member. For the dashpot, the relationship between the damping force and relative velocity was given by a bilinear model. The properties of the damper shown in Figure 9 were based on the performance tests of the manufactured small-size viscous damper (Figure 1).
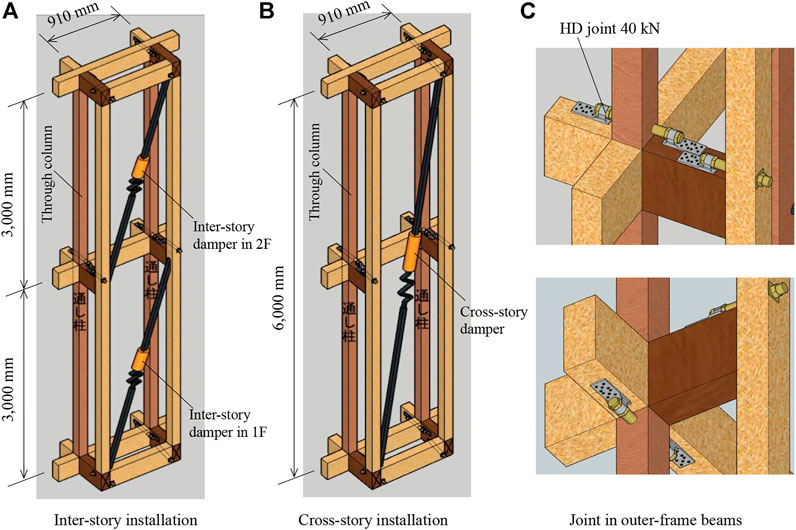
FIGURE 8. Installation of viscous dampers in the timber frame house (A) Inter-story installation (B) Cross-story installation (C) Joint in outer-frame beams.
The target maximum story drift angle was specified as 1/30 given that a timber frame house would most likely be severely damaged or broken. Because the foreshock (Figure 6) was quite severe and the first-story drift angle in the X-direction was dominant, the timber house model with dampers was subjected to 70% of the E-W component of the foreshock in the X-direction. Figure 10A compares the resulting maximum first-story drift angles, γ1max, in the X-direction between the house model without dampers and that installed with cross-story or inter-story dampers. Figure 10B shows the time histories of the first-story drift angles in the X-direction for the three cases: no dampers, 12 inter-story dampers (six in each story), and six cross-story dampers. For the model without dampers, γ1max exceeded 1/26, and the structure was on the verge of collapse. Four cross-story and eight inter-story (four in each story) dampers reduced γ1max to 1/30. The six cross-story dampers reduced γ1max to 1/80, and the structure exhibited almost no damage. Therefore, the cross-story installation of dampers reduced the story drift more effectively than the inter-story installation while using half as many dampers.
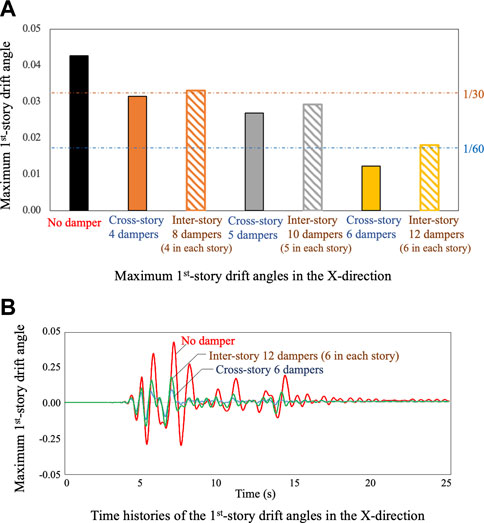
FIGURE 10. Results of the earthquake response analyses of the timber frame house models with and without dampers (70% of the E-W component of the foreshock of the 2016 Kumamoto earthquake in X-dir.). (A) Maximum first-story drift angles in the X-direction (B) Time histories of the first-story drift angles in the X-direction.
Figure 11 compares γ1max’s between the house model without dampers and that with six cross-story dampers or 12 inter-story dampers (six in each story) after being subjected to other major earthquakes in the X-direction. The peak velocity or input level of each earthquake was adjusted such that γ1max of the house model without dampers was close to that of the model subjected to 70% of the E-W component of the foreshock of the 2016 Kumamoto earthquake. The mean and standard deviation of γ1max’s for the three cases were also shown in the figure. The results showed that the reduction effects of the installed dampers differed among the earthquakes and that the six cross-story and 12 inter-story dampers (six in each story) reduced the story drift by almost equal amounts. Additionally, neither the cross-story nor inter-story dampers were able to reduce the γ1max of the house model subjected to 70% of the N-S component of the 1995 Hyogo-ken Nanbu Earthquake (JMA Kobe). This may be because the JMA Kobe included an impulsive wave, and the peak response occurred before the dampers exhibited a damping effect.
Note that the effects of installed dampers differed among the applied earthquake excitations and cannot be generalized from the results by small number of earthquake excitations. When the models installed with cross- or inter-story dampers in the X-direction were subjected to bilateral earthquake excitations, the first-story drift angles in the X-direction were reduced by the dampers in a similar manner as above. This is because the model had little eccentricities, and almost no torsional or rotational vibration occurred.
The relationship between the damping force (induced by the viscous damper) and relative velocity was given by a bilinear model, where the gradient (i.e., the damping coefficient) changed when the velocity reached the relief velocity (Figure 9). Figure 12A shows the hysteresis loop of a cross-story viscous damper of the house model installed with six cross-story dampers subjected to 70% of the E-W component of the foreshock of the 2016 Kumamoto earthquake. Figure 12B shows the hysteresis loops of two inter-story viscous dampers in the first and second stories of the house model installed with 12 inter-story dampers (six in each story) for the same input. The induced damping force of every hysteresis loop in Figure 12 reached the same limit value of 4 kN (= C1
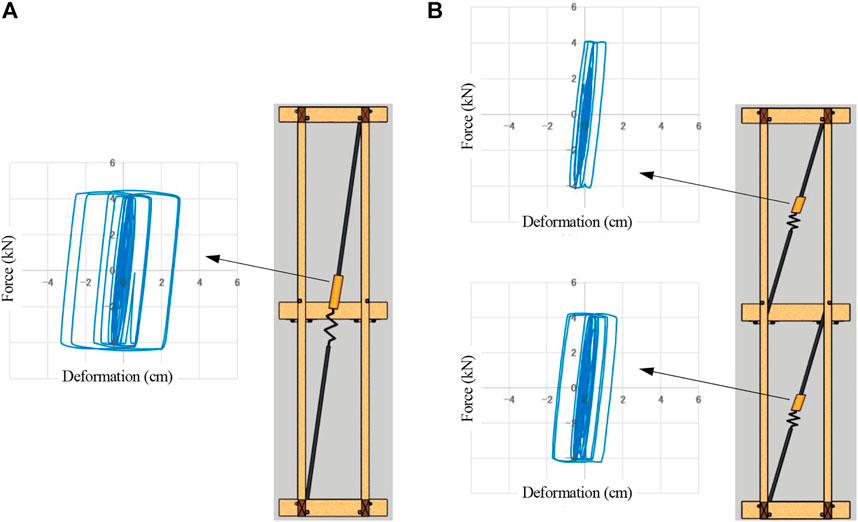
FIGURE 12. Hysteresis loops of viscous dampers (A) Hysteresis loop of a cross-story viscous damper (B) Hysteresis loops of inter-story viscous dampers.
The energy dissipated by the viscous dampers was obtained by integrating the damping force along the deformation of the hysteresis loop. Figure 13 shows the dissipated energy of the cross-story damper of the house model installed with six cross-story dampers and those of two inter-story dampers in the first and second stories of the house model installed with 12 inter-story dampers (six in each story) when subjected to major earthquakes in the X-direction. The results showed that the energy dissipated by a single cross-story damper was larger than the sum of the dissipated energies of two inter-story dampers for all applied earthquake inputs. Therefore, the cross-story installation allowed the viscous damper in the first story to absorb vibration energy nearly twice as much as that of the inter-story installation. The volumes of dissipated energy differed among the earthquakes and were irrelevant to the response reduction effects of the dampers (Figure 11).
In this study, we investigated the effectiveness of the cross-story installation of a damper by performing eigenvalue analyses of 2DOF mass-spring-dashpot models and earthquake response analyses of a two-story timber frame house installed with small-size viscous dampers. The damping factors and response reduction effects of the cross-story installation of a damping device were compared with those of the conventional inter-story installation. The results showed that the single cross-story dashpot multiplied the first damping factor twice as much as the two inter-story dashpots. Moreover, although the cross-story dashpot effectively increased the first damping factor, it had little effect on the second damping factor.
The house models were subjected to 70% of the E-W component of the foreshock of the 2016 Kumamoto earthquake in the X-direction. The earthquake response analyses revealed that, without the dampers, the first-story drift angle exceeded 1/25, and the structure was on the verge of collapse. Four cross-story and eight inter-story (four in each story) dampers reduced the first-story drift angle to 1/30. The six cross-story dampers reduced the first-story drift angle to 1/80, and the structure experienced almost no damage. The cross-story installation of dampers was quite effective in reducing the story drift and also reduced the necessary number of dampers by half compared to the inter-story installation.
Earthquake response analyses of the house model subjected to other major earthquakes showed that the response reduction effects of the installed dampers differed among the earthquakes. The six cross-story and 12 inter-story (six in each story) dampers had almost equal effects on the story drift. However, owing to its impulsive wave, neither the cross-story nor inter-story dampers reduced the story drift of the house model subjected to the 1995 Hyogo-ken Nanbu Earthquake (JMA Kobe).
The hysteresis loop and dissipated energy of a cross-story viscous damper of the house model installed with six cross-story dampers were compared with those of the inter-story viscous dampers in the first and second stories of the house model installed with 12 inter-story dampers (six in each story). The energy dissipated by a single cross-story damper was larger than the sum of the dissipated energies of two inter-story dampers for all applied earthquake inputs. Furthermore, the cross-story installation allowed the viscous damper in the first story to absorb vibration energy nearly twice as much as that of the inter-story installation. The volumes of dissipated energy differed among earthquakes and were irrelevant to the response reduction effects of dampers.
Therefore, compared to the conventional inter-story installation, the cross-story installation of a viscous damper could upgrade the response reduction effects of the installed dampers and reduced the number of dampers necessary for preventing severe damage by half, although the effects varied with earthquake excitations and cannot be generalized. As a cross-story damper can be installed onto an outer frame fixed to the house, it can be used as a seismic retrofitting measure in an existing house. Further research will focus on the application of cross-story dampers to low-rise structures made of laminated wood members.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
YN: eigenvalue analyses of the two-story shear building installed with dashpots. RM: time-history response analyses of the timber frame house models installed with viscous dampers.
This study has been supported by JSPS KAKENHI (grant number JP20K04792).
The authors would like to express their appreciation to Ichijo Co. Ltd. for providing the design documents of the timber frame house and to Edogawa Mokuzai Co. Ltd. for providing permission to use the pictures of the small-size viscous damper.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2022.1037832/full#supplementary-material
Aydin, E., Noroozinejad Farsangi, E., Öztürk, B., Bogdanovic, A., and Dutkiewicz, M. (2019). “Improvement of building resilience by viscous dampers,” in Resilient structures and infrastructure (Singapore: Springer), 105–127. doi:10.1007/978-981-13-7446-3_4
Constantinou, M. C., and Symans, M. D. (1992). Experimental and analytical investigation of seismic response of structures with supplemental viscous viscous dampers. Buffalo, NY: National Center for Earthquake Engineering Research. Technical Report NCEER-92-0032.
Constantinou, M. C., and Symans, M. D. (1993). Experimental study of seismic response of buildings with supplemental fluid dampers. Struct. Des. Tall Build. 2 (2), 93–132. doi:10.1002/tal.4320020203
De Domenico, D., and Hajirasouliha, I. (2021). Multi-level performance-based design optimisation of steel frames with nonlinear viscous dampers. Bull. Earthq. Eng. 19, 5015–5049. doi:10.1007/s10518-021-01152-7
De Domenico, D., and Ricciardi, G. (2019). Earthquake protection of structures with nonlinear viscous dampers optimized through an energy-based stochastic approach. Eng. Struct. 179, 523–539. doi:10.1016/j.engstruct.2018.09.076
De Domenico, D., Ricciardi, G., and Takewaki, I. (2019). Design strategies of viscous dampers for seismic protection of building structures: A review. Soil Dyn. Earthq. Eng. 118, 144–165. doi:10.1016/j.soildyn.2018.12.024
Design of Seismic Isolation and Response Control (2016). Design of seismic isolation and response control methods of buildings in Japan. Japan: Kanto Branch of the Architectural Institute of Japan.
Dong, B., Sause, R., and Ricles, J. M. (2016). Seismic response and performance of a steel MRF building with nonlinear viscous dampers under DBE and MCE. J. Struct. Eng. 142, 6. doi:10.1061/(asce)st.1943-541x.0001482
Foss, K. A. (1958). Co-ordinates which uncouple the equations of motion of damped linear ynamic systems. J. Appl. Mech. 25, 361–364. doi:10.1115/1.4011828
Fu, Y., and Kasai, K. (1998). Comparative study of frames using viscoelastic and viscous dampers. J. Struct. Eng. 124 (5), 513–522. doi:10.1061/(asce)0733-9445(1998)124:5(513)
Fujise, W., and Ikenaga, M. (2021). “Modal response characteristics and maximum response characteristics of seismic controlled buildings incorporated with tuned viscous mass dampers across multiple layers
Hao, L., and Zhang, R. (2016). Structural safety redundancy-based design method for structure with viscous dampers. Struct. Eng. Mech. 59 (5), 821–840. doi:10.12989/sem.2016.59.5.821
Hwang, J.-S., Huang, Y.-N., Yi, S.-L., and Ho, S.-Y. (2008). Design formulations for supplemental viscous dampers to building structures. J. Struct. Eng. 134 (1), 22–31. doi:10.1061/(asce)0733-9445(2008)134:1(22)
Idels, O., and Lavan, O. (2020). Optimization-based seismic design of steel moment-resisting frames with nonlinear viscous dampers. Struct. Control Health Monit. 28, 1e2655. doi:10.1002/stc.2655
Impollonia, N., and Palmeri, A. (2018). Seismic performance of buildings retrofitted with nonlinear viscous dampers and adjacent reaction towers. Earthq. Eng. Struct. Dyn. 47 (5), 1329–1351. doi:10.1002/eqe.3020
Kasai, K., Nakai, M., Nakamura, Y., Asai, H., Suzuki, Y., and Ishii, M. (2008). “Current status of building passive control in Japan,” in Proceedings of the 14th World on Earthquake Engineering, 12-17 October 2008, Beijing, China.
Kasai, K., Nakai, M., Nakai, M., Nakamura, Y., Asai, H., Suzuki, Y., et al. (2009). Building passive control in Japan. J. Disaster Res. 4 (3), 261–269. doi:10.20965/jdr.2009.p0261
Kawamoto, T., Fujita, K., Tsuji, M., and Takewaki, I. (2016). Robust optimal placement of dampers in structures with set-back and eccentricity using sensitivity analysis for integrated transfer function. Ijeie 1 (4), 377–394. doi:10.1504/IJEIE.2016.083252
Lavan, O., and Levy, R. (2005). Optimal design of supplemental viscous dampers for irregular shear-frames in the presence of yielding. Earthq. Eng. Struct. Dyn. 34 (8), 889–907. doi:10.1002/eqe.458
Lavan, O., and Levy, R. (2006). Optimal design of supplemental viscous dampers for linear framed structures. Earthq. Eng. Struct. Dyn. 35 (3), 337–356. doi:10.1002/eqe.524
Lavan, O. (2015). Optimal design of viscous dampers and their supporting members for the seismic retrofitting of 3D irregular frame structures. J. Struct. Eng. 141, 04015026–4015111. doi:10.1061/(ASCE)ST.1943-541X.0001261
Lee, D., and Taylor, D. P. (2001). Viscous damper development and future trends. Struct. Des. Tall Build. 10 (5), 311–320. doi:10.1002/tal.188
Liang, Z., Lee, G. C., Dargush, G. F., and Song, J. (2012). Structural damping: Application in seismic response modification. Boca Raton, Florida, United States: CRC Press, Taylor & Francis Group.
Lim, K., and Ikenaga, M. (2021). “Effectiveness of arranging tuned viscous mass dampers across multiple layers in deformation concentration to lower stories,” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 723–724.
Lin, W. H., and Chopra, A. K. (2002). Earthquake response of elastic SDF systems with non-linear fluid viscous dampers. Earthq. Eng. Struct. Dyn. 31 (9), 1623–1642. doi:10.1002/eqe.179
Maida, Y., Maegawa, T., Demizu, T., Qu, Z., Kishiki, S., Sakata, H., et al. (2015). Seismic response control of super high-rise RC buildings utilizing buckling restrained braces and the design of brace connections. J. Struct. Constr. Eng. 80 (710), 647–657. doi:10.3130/aijs.80.647
Manual for Design and Construction (2013). Manual for design and construction of passively-controlled buildings. 3rd Edition. Tokyo, Japan: The Japan Society of Seismic Isolation.
Martinez-Rodrigo, M., and Romero, M. L. (2003). An optimum retrofit strategy for moment resisting frames with nonlinear viscous dampers for seismic applications. Eng. Struct. 25 (7), 913–925. doi:10.1016/s0141-0296(03)00025-7
Matsuno, A., Hashimoto, J., Katayama, Y., and Fukui, K. (1999). “Application of the oil damper to wooden house by conventional construction method (Part 1: Verification of damping effect by experiment and simulation),” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 179–180.
Matsuno, A., Hashimoto, J., and Katayama, Y. (2000). Vibration test of wooden house with oil Damper.Summaries of technical papers of annual meeting. Tokyo, Japan: Architectural Institute of Japan, 1113–1114.
McNamara, R. J., and Taylor, D. P. (2003). Fluid viscous dampers for high-rise buildings. Struct. Des. Tall Spec. Build. 12 (2), 145–154. doi:10.1002/tal.218
Nakagawa, T., Kawai, N., Tsuchimoto, T., and Okabe, M. (2006). “Verification for seismic performance of existing wood houses by shaking table test (Part 15: Structural performance of wooden frame walls in the building by shaking table tests),” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 395–396.
Nakagawa, T., Kawai, N., Tsuchimoto, T., and Ohta, M. (2007). “Verification for seismic performance of existing wood houses by shaking table test (Part 26: Collapsing process simulations by the extended distinct element method),” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 489–490.
Nakagawa, T., Ohta, M., Tsuchimoto, T., and Kawai, N. (2010). Collapsing process simulations of timber structures under Dynamic loading III: Numerical simulations of real-size wooden houses. J. Wood Sci. 56 (4), 284–292. doi:10.1007/s10086-009-1101-x
Nakagawa, T. (2017). “Seismic response analysis of wooden houses using ground motion observed at 2016 Kumamoto earthquakes,” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 489–490.
Nakamura, Y., and Fujii, H. (2021). Earthquake damage reduction in timber frame houses using small-size fluid damper. Front. Built Environ. 7, 767741. doi:10.3389/fbuil.2021.767741
Namba, T., Sumida, K., Nakagawa, T., and Isoda, H. (2020). “Seismic response analysis of a collapsed wooden house in 2016 Kumamoto earthquake,” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 433–434. (in Japanese).
Ogino, M., Sumiyama, T., and Takei, H. (2014). “Structural design of a high-rise building using tuned viscous mass dampers installed across each three consecutive stories (Part 1 – 3),” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 771–776.
Parcianello, E., Chisari, C., and Amadio, C. (2017). Optimal design of nonlinear viscous dampers for frame structures. Soil Dyn. Earthq. Eng. 100, 257–260. doi:10.1016/j.soildyn.2017.06.006
Pollini, N., Lavan, O., and Amir, O. (2016). Towards realistic minimum-cost optimization of viscous fluid dampers for seismic retrofitting. Bull. Earthq. Eng. 14 (3), 971–998. doi:10.1007/s10518-015-9844-9
Pollini, N., Lavan, O., and Amir, O. (2017). Minimum-cost optimization of nonlinear fluid viscous dampers and their supporting members for seismic retrofitting. Earthq. Eng. Struct. Dyn. 46 (12), 1941–1961. doi:10.1002/eqe.2888
Rama Raju, K., Ansu, M., and Iyer, N. R. (2014). A methodology of design for seismic performance enhancement of buildings using viscous fluid dampers. Struct. Control Health Monit. 21 (3), 342–355. doi:10.1002/stc.1568
Seleemah, A. A., and Constantinou, M. C. (1997). Investigation of seismic response of buildings with linear and nonlinear viscous viscous dampers. Buffalo, NY: National Center for Earthquake Engineering Research. Technical Report NCEER-97- 0004.
Seo, C.-Y., Karavasilis, T. L., Ricles, J. M., and Sause, R. (2014). Seismic performance and probabilistic collapse resistance assessment of steel moment resisting frames with fluid viscous dampers. Earthq. Eng. Struct. Dyn. 43 (14), 2135–2154. doi:10.1002/eqe.2440
Silvestri, S., and Trombetti, T. (2007). Physical and numerical approaches for the optimal insertion of seismic viscous dampers in shear-type structures. J. Earthq. Eng. 11 (5), 787–828. doi:10.1080/13632460601034155
Soong, T. T., and Dargush, G. F. (1997). Passive energy dissipation systems in structural engineering. Chichester: John Wiley & Sons.
Soong, T. T., and Spencer, B. F. (2002). Supplemental energy dissipation: State-of- the-art and state-of-the-practice. Eng. Struct. 24 (3), 243–259. doi:10.1016/s0141-0296(01)00092-x
Sorace, S., and Terenzi, G. (2008). Seismic protection of frame structures by fluid viscous damped braces. J. Struct. Eng. 134 (1), 45–55. doi:10.1061/(asce)0733-9445(2008)134:1(45)
Sorace, S., and Terenzi, G. (2009). Viscous damper-based seismic retrofit strategies of steel structures: General concepts and design applications. Adv. Steel Constr. 5 (3), 325–342. doi:10.18057/ijasc.2009.5.3.7
Suzuki, T., and Nakagawa, T. (2020). Seismic simulation wallstat guide. Japan: Gakugei Shuppan Publishing Co. Ltd.
Tabar, A. M., De Domenico, D., and Dindari, H. (2021). Seismic rehabilitation of steel arch bridges using nonlinear viscous dampers: Application to a case study. Pract. Period. Struct. Des. Constr. 26 (3), 04021012. doi:10.1061/(ASCE)SC.1943-5576.0000576
Takewaki, I. (2009). Building control with passive dampers: Optimal performance- based design for earthquakes. Singapore: John Wiley & Sons (Asia) Pte Ltd.
Taylor, D. P., and Constantinou, M. C. (1995). Testing procedures for high output fluid viscous dampers used in building and bridge structures to dissipate seismic energy. Shock Vib. 2 (5), 373–381. doi:10.1155/1995/676035
Tsuchimoto, T. (2008). “Verification for seismic performance of existing wood houses by shaking table test (Part 29: Response analysis of 2-DOF system for the test),” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 137–138.
Tsuji, M., and Nakamura, T. (1996). Optimum viscous dampers for stiffness design of shear buildings. Struct. Des. Tall Build. 5 (3), 217–234. doi:10.1002/(sici)1099-1794(199609)5:3<217::aid-tal70>3.0.co;2-r
Tubaldi, E., Barbato, M., and Dall’Asta, A. (2014). Performance-based seismic risk assessment for buildings equipped with linear and nonlinear viscous dampers. Eng. Struct. 78, 90–99. doi:10.1016/j.engstruct.2014.04.052
Ueno, F., and Ikenaga, M. (2018). “A study on reduction effects of dampers across multiple layers against deformation concentration to lower-stories in a high-rise building,” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 395–396.CRC:
Ueno, F., Watai, K., Sato, D., Kasai, K., Saburi, K., Maeda, T., et al. (2020). “Passive control design using oil dampers arranged in multi-story Double layer (Part 1: Proposal of design method, Part 2: Application to member-to-member model),” in Summaries of technical papers of annual meeting (Tokyo, Japan: Architectural Institute of Japan), 881–884.
Uetani, K., Tsuji, M., and Takewaki, I. (2003). Application of an optimum design method to practical building frames with viscous dampers and hysteretic dampers. Eng. Struct. 25, 579–592. doi:10.1016/S0141-0296(02)00168-2
Uriz, P., and Whittaker, A. S. (2001). Retrofit of pre-Northridge steel moment-resisting frames using fluid viscous dampers. Struct. Des. Tall Build. 10 (5), 371–390. doi:10.1002/tal.199
Wang, S., and Mahin, S. A. (2018). High-performance computer-aided optimization of viscous dampers for improving the seismic performance of a tall building. Soil Dyn. Earthq. Eng. 113, 454–461. doi:10.1016/j.soildyn.2018.06.008
Wani, Z. R., Tantray, M., Farsangi, E. N., Nikitas, N., Noori, M., Samali, B., et al. (2022). A critical review on control strategies for structural vibration control. Annu. Rev. Control, 25, 1–22. doi:10.1016/j.arcontrol.2022.09.002
Keywords: seismic response, timber frame house, viscous damper, cross-story installation, 2016 kumamoto earthquake, inter-story drift
Citation: Nakamura Y and Matsumura R (2022) Cross-story installation of viscous dampers in timber frame houses for earthquake damage reduction. Front. Built Environ. 8:1037832. doi: 10.3389/fbuil.2022.1037832
Received: 06 September 2022; Accepted: 17 October 2022;
Published: 03 November 2022.
Edited by:
Izuru Takewaki, Kyoto University, JapanReviewed by:
Ehsan Noroozinejad Farsangi, University of British Columbia, CanadaCopyright © 2022 Nakamura and Matsumura. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yutaka Nakamura, eXV0YWthLm5ha2FtdXJhQHJpa28uc2hpbWFuZS11LmFjLmpw
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.