Taylor Made Landscapes: Using Taylor's Law to Scale Between Metapopulations and Source-Sinks in Urban Garden Space

The structure of terrestrial landscapes is commonly viewed as a problem of statistical description defined by the number, size and distance between habitat patches. Yet, for organisms living in that landscape, structure may be perceived very differently depending on the dispersal capacity of the organism of concern—large animals may perceive a highly fragmented forest as a single patch if adjacent forest patches are sufficiently close, while small animals may be less likely to disperse across degraded habitat and therefore experience a much different patch structure. This is particularly relevant for fragmented landscapes like cities. Urban gardens are reputed to support a diversity of native and non-native urban species found in urban landscapes. Yet we know little about the long-term persistence of organisms associated with urban gardens. Here we utilize Taylor's law, a universal scaling law denoting a power law relationship between population size and variance to indicate the synchrony of arthropod populations sampled across time in a fragmented urban landscape. Our results indicate that the utility of urban gardens as habitat is strongly dependent on sampling month, spatial scale and taxon. Constrained dispersal across the landscape may limit the potential of urban gardens to conserve natural enemies including ladybird beetles and parasitoid wasps. In contrast, aphid pests are moving much more freely in the landscape as exhibited through synchrony in abundances sampled across local and landscape scales. We find that regardless of the fragmentation pattern existing in the landscape, short-ranged arthropods are isolated to small, independent garden habitat patches (metapopulation-like) with abundances that oscillate out of sync, while long-ranged species traverse greater distances, synchronizing abundances across large, shared spaces (source sink-like). These results suggest an inherent link between Taylor's temporal law and metapopulation theory, providing a potential mechanism to explain species-specific slopes of Taylor's law as arising from the ability of organisms to differentially experience fragmented space along the continuum between metapopulation and source-sink.

Introduction

With more than 54% of the human population residing in urban areas, urban agriculture is emerging as an alternative food movement that proposes to eliminate the rural-urban divide between food production and consumption, improve food security, build community and provide green space for people and biodiversity in urban areas (Brown and Jameton, 2000; Goddard et al., 2010; McClintock, 2010; Barthel et al., 2014; Lin et al., 2015; World Health Organization, 2016). Though many studies indicate that urban gardens can provide substantial resources to support a diversity of ecosystem service-providing organisms, the long-term viability of biodiversity in urban gardens is still in question (MacDougall et al., 2013; Beninde et al., 2015). Since urban agriculture is often small-scale, plots can be carefully managed to support a surprising amount of biodiversity in terms of crops, ornamentals and their associated wildlife (pollinators, natural enemies, birds, etc.) (Akinnifesi et al., 2009; Lin et al., 2015). These results suggest that urban gardens could represent high-quality habitat, akin to the source habitats of classic ecological theory. According to this theory, habitat patches differ in quality; source patches are capable of supporting positive population growth of a species, while sink patches incur population declines. Though gardens may be a clear improvement to cement in cities, when comparing urban gardens to rural sites on city outskirts, relative quality becomes unclear. Management for pest control, crop diversity, soil nutrition, and water conservation can significantly impact habitat quality of both urban and rural sites. In addition, metrics of habitat suitability are not necessarily universal across species. In a recent paper comparing ladybird beetles inhabiting urban gardens in Michigan and California, Egerer et al. found that beetles decreased in abundance and diversity with urbanization in Michigan but were positively associated with metrics of urbanization (% impervious surface) in California (Egerer et al., 2018). The authors suggest that drought conditions may serve to enhance the importance of source-like urban gardens in California, while the excess of wet and verdant habitat surrounding sites in Michigan make urban gardens more of a sink habitat. These results suggest that for some species and locations, urban gardens may represent higher quality habitat than rural sites, whereas for other locations or species, urban gardens may represent lower quality sink habitats with correspondingly lower conservation potential. However, there remains no simple way of assessing whether urban gardens are perceived of as sink or source habitat to different organisms.

The permeability of urban landscapes for dispersing organisms is another issue when considering the conservation potential of urban gardens. Many species of conservation concern are known to survive in small pockets of habitat in fragmented landscapes through a mechanism known as the rescue effect (Gotelli, 1991). According to this theory, if each urban garden represents a sink habitat that is at risk of extinction, random dispersal events between multiple sink patches can nonetheless allow for the collection of populations, known as the metapopulation, to persist long-term. However, lack of dispersal between isolated subpopulations can significantly increase extinction risks (Perfecto et al., 2009; Vandermeer, 2010). For example, fragmentation in landscapes may prevent species from dispersing and colonizing more appropriate habitats as climate change shifts species' ranges northward (Sæther et al., 2000). Thus, improving the matrix between habitat fragments is considered key for increasing the resilience of threatened populations to environmental perturbations (Goddard et al., 2010; McClintock, 2010; Gardiner et al., 2013; Lin et al., 2015).

In cities, impervious surface, heat island effects, human-wildlife conflict, and pollution present critical obstacles for the dispersal and maintenance of populations persisting in putative urban garden refuges (Goddard et al., 2010; Beninde et al., 2015). We can envision each garden as representing a habitat patch interspersed within a matrix of urban space. However, the degree to which organisms perceive urban gardens as quality habitat and the urban environment between gardens as an obstacle for dispersal is difficult to assess, especially for small organisms where mark and recapture techniques are largely unreliable (Nathan, 2001). This is particularly problematic since a large number of urban garden biodiversity studies focus on pest control and pollination service-providing arthropods (Goddard et al., 2010; Guitart et al., 2012; Lin et al., 2015). If urban gardens represent poor quality habitat for inhabiting organisms or if there is insufficient dispersal between garden patches, populations existing in urban gardens may not be viable in the long-term.

In this paper we use a universal scaling law known as Taylor's law to assess the permeability of an urban landscape to dispersing arthropods. The law has been described as one of the few unifying laws in ecology, with many case studies in support of its claims (Taylor, 1961; Kilpatrick and Ives, 2003; Eisler et al., 2008). It arises from the seemingly ubiquitous power law relationship between group sizes and their variances, a relationship that remains consistent across a great diversity of systems ranging from physics to economics (Eisler et al., 2008). There are two forms of the law, one spatial and one temporal. We focus on the temporal form of Taylor's law because it can measure synchrony of temporal oscillations in groups sampled across space (Ballantyne and Kerkhoff, 2005, 2007; Eisler et al., 2008). Since synchrony across subgroups is often induced by high dispersal rates in metapopulation models (Hanski and Woiwod, 1993; Ranta et al., 1995; Ruxton and Rohani, 1999), Taylor's law may provide a simple tool for assessing the permeability of urban landscapes to dispersing organisms.

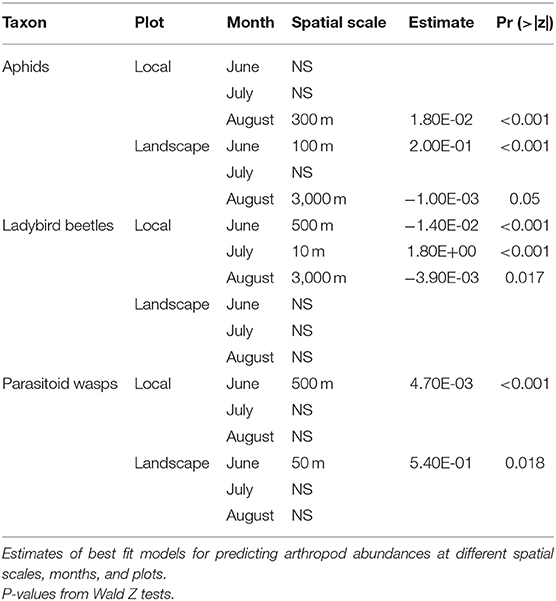
The temporal form of the law states that the variance (V) of abundances over time will follow a power function relationship to the mean (M) of abundances over the same time frame, i.e., V = aM^b(Taylor, 1961). The exponent b, the slope of the linear regression on the log-scale, indicates whether temporal fluctuations are invariant to group size (slope = 2), or whether groups are more (slope > 2) or less (slope < 2) variable than expected by chance. Theoretical and empirical studies have demonstrated that the slope of Taylor's temporal law switches from 1 to 2 exactly at the point of synchrony where trees begin to exhibit masting behavior (Satake and Iwasa, 2000; Ballantyne and Kerkhoff, 2005, 2007; Eisler et al., 2008). This is because variance over time becomes independent of group identity when groups across a landscape grow and decline in complete synchrony (Eisler et al., 2008). Much of the literature on Taylor's Law is directed toward providing mechanisms that explain Taylor's Law slopes below 2 because they imply unusually high levels of stability (defined here as low variance) of large populations, an oft-sought goal for conservation (Anderson et al., 1982; Titmus, 1983; Kilpatrick and Ives, 2003). However, we note that slopes below 2 could just as easily imply that small populations are more variable than expected by chance (Figure 1). This observation links the temporal form of Taylor's law to metapopulation theory. When the permeability of a landscape is high, or the dispersal range of an organism is long, large amounts of habitat space in a landscape are shared, in other words, sampled populations are no longer independent. Since all samples in such a landscape are actually part of a single larger population, they are by default expected to grow and decline in synchrony, producing a Taylor's law slope near 2. However, when the dispersal range of an organism is short or the permeability of a landscape is constrained, sampled sites are actually isolated populations. Since individuals cannot move easily between isolated sites, rare and random dispersal events between sites should cause asynchrony across the metapopulation as a whole. This allows us to derive the potentially practical conclusion that populations closer to metapopulations will have slopes of Taylor's temporal law near 1, whereas populations in landscapes that are highly connected should have Taylor's law slopes near 2.

FIGURE 1

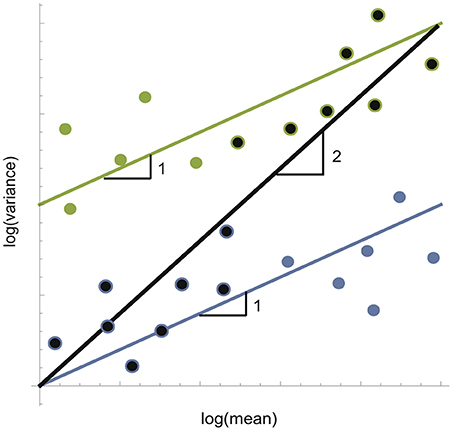
Figure 1. Conceptual figure of how lower variance of large groups or higher variance of small groups can reduce Taylor's law slopes from the null of 2 to 1. Color of points match regression lines they belong to. Bicolor points belong to two regression lines.

Few ecological studies have the resources or capability to directly assess landscape permeability with high-resolution tracking of organisms through space and time, though some recent advances have been made for larger organisms (Dell et al., 2014; Graving et al., 2019). Here we suggest that by leveraging the statistical relationship between group sizes and variances, we may be able to substitute time for space and reduce the temporal scale necessary to measure permeability across a given space. Since the time series used to calculate Taylor's temporal law are inevitably sampled from different spatial locations, Taylor's temporal law can be useful in short ecological studies where spatial samples are more easily obtained than temporal sequences. Rather than having to track the specific movements of organisms across large areas at many time points, we can assume that populations that are temporally synchronous across large spatial scales are moving relatively freely through that space, while those that are asynchronous are constrained. When organisms can move freely through space, high quality source patches are likely to be colonized first. These source patches then produce migrants that disperse to lower quality sink patches, defined as less suitable patches, in the landscape (Pulliam, 1988). Directed dispersal events in contiguous space can cause populations within that space to synchronize (Ruxton and Rohani, 1999). We can then use the slope of Taylor's law as a simple means for assessing how groups of organisms experience a fragmented urban landscape as a whole; is it split into many asynchronous metapopulations or does it function as a source-sink landscape where clear migratory pathways lead to synchrony?

We apply this theory to assess the permeability of an urban landscape to three specific groups of urban garden-inhabiting arthropods: aphids, ladybird beetles and parasitoid wasps. A variety of organisms inhabit urban gardens, but those of particular ease to study are also those of most concern to gardeners, agricultural pests. Aphids are important agricultural pests because of their propensity for spreading viral diseases combined with their incredibly fast rates of growth (Sylvester, 1980). Aphids are also long-distance dispersers known to be sensitive to broad scale changes in percentage of non-crop habitat within agricultural landscapes (Werling and Gratton, 2010). This makes them an ideal study organism to address questions regarding landscape permeability and habitat suitability. In addition, urban gardens are known to harbor an abundant and diverse suite of natural enemies that attack aphids and other agricultural pests (Goddard et al., 2010; Speak et al., 2015). Here we examine two of these groups, ladybird beetles and parasitoid wasps, excluding predator wasps, specifically those from the family Vespidae. Though Vespid wasps are important for controlling garden pests, we were more interested in parasitoid wasps due to their reliance on floral resources and potential to be natural enemies of aphids (Brodeur and Rosenheim, 2000; Donovan, 2003). Studies addressing how natural enemy communities respond to urbanization find that local level factors including garden management (% flowering plants, pesticide use) tend to be more important than landscape level factors such as the % impervious surface or agricultural land (Bennett and Gratton, 2012; Otoshi et al., 2015; Egerer et al., 2017; Philpott and Bichier, 2017). This sensitivity to local-scale conditions could potentially constrain the movement of natural enemies in urban landscapes. However, ladybird beetles are known to migrate long distances to wintering sites, and several invasive species have spread quickly throughout the globe (Bahlai et al., 2014). Less is known about the movement patterns of parasitoid wasps, which may depend and map onto specific parasitoid-host relationships. However, these three specific groups of winged arthropods are all commonly found in urban gardens and have the potential to disperse long-distances, making them ideal for assessing whether the quality of urban gardens as habitat or the permeability of a single urban landscape changes from taxon to taxon.

We expect differences in dispersal amongst organisms to change the perceived landscape structure of an urban landscape. If organisms are unable to easily move through the landscape, urban gardens are likely to represent very patchy, isolated sink habitats common of metapopulations. We expect this to increase the variation of small populations. However, if the urban landscape is highly permeable, gardens could form clusters and create source-sink dynamics in the landscape. We anticipate a heightened sensitivity to local conditions to constrain dispersal in wasps, translating to more asynchronous abundances and Taylor's law slopes nearer to 1. In contrast, we predict beetles and aphids to have more synchronous abundances with Taylor's law slopes nearer to 2 because of their capacity for long-distance dispersal.

Materials and Methods

Arthropod Census

Glue-based, yellow sticky card traps were used to monitor aphid, ladybird beetle, and parasitoid wasp abundances in Ann Arbor, MI during the months of June, July and August 2013.

In order to determine how arthropods responded to gardens at different spatial scales, we placed sticky traps at mapped grid points spaced regularly across the landscape in one local and one landscape plot (Figure 2). The landscape plot corresponded to a regular grid over the total area of the city of Ann Arbor and the local plot covered just the area of downtown Ann Arbor and adjacent neighborhoods. The finer, local-level plot had 100 points spread an average of 128 m apart. The coarser, landscape-level plot had 28 points, spread an average of 1,470 m apart. We constructed these two plots in order to assess how spatial synchrony may change as a function of habitat overlap. If dispersal range is constrained at landscape scales but not at local scales, we would expect spatial synchrony to be higher in our local plot. Each sticky trap location represents an individual point in a regression of log mean abundances and variances taken over the three time points for each sampled site, the slope of which is the exponent of Taylor's law. At each site, a sticky trap was either taped to a metal street pole or stapled to a tree or wooden post at breast height. Every 5 weeks for 15 weeks (3-months), the sticky traps were collected and sampled for abundance of each arthropod group.

FIGURE 2

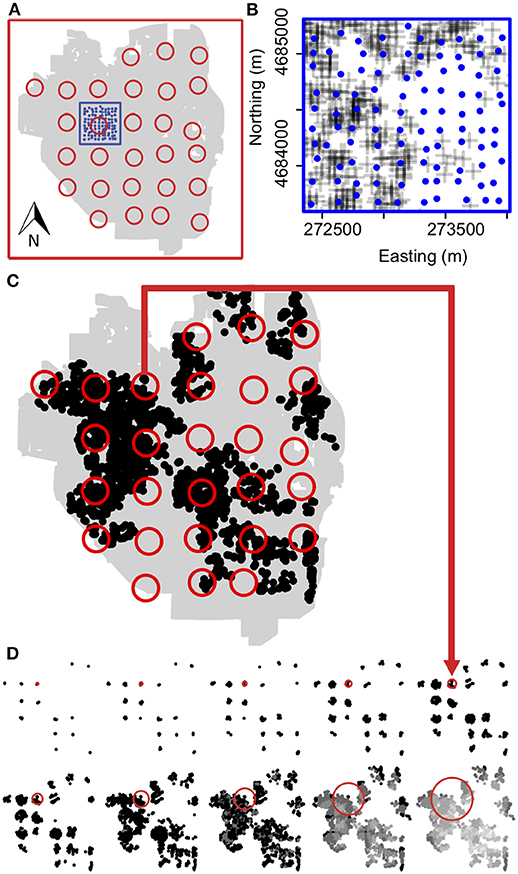
Figure 2. Sampling scheme and scale-dependent landscape structure. (A) Sampling scheme of gardens in the area of Ann Arbor, MI (grey background). Sampling of arthropods was conducted regularly across the entire landscape in two plots (red box: landscape and blue box: local) and three time points (June, July, and August 2013). A total of 28 samples were collected at the landscape (open red circles), and 100 at the local plots (blue circles) per month. (B) Close-up of sampling locations (blue dots) and easement gardens (plus signs) in local plot. Landscape-plot samples are drawn in (C) at a radius of 400 m on top of actual distribution of urban gardens (closed black circles). Patch size was equal to number of gardens falling within the radius of a single sampling circle, visualized in (D) by plotting only the gardens (black/gray points) falling within radii of 100, 150, 200, 300, 400 m (top row), and 500, 750, 1,000, 1,500, 2,000 m (bottom row) for the 28 landscape-level sampling points only. One patch is highlighted for each radius (open red circles) to show scale, with a red arrow connecting this point to its location among all landscape-level sample points plotted at the same 400 m radius in (C). At a radius of 1,000 m and beyond, neighboring landscape-level samples begin to overlap; degree of overlap is indicated by the darkness of garden points with lightest points having the greatest overlap. The same patch size analysis was done for local plot samples, but not visualized here.

We used a 20–80 X magnification stereo microscope and characteristic morphological features to identify each aphid, ladybird beetle, and parasitoid wasp individual using field guides (Borror and White, 1970; Goulet et al., 1993). Aphids (superfamily Aphidoidea) were identified as soft bodied insects with sucking mouth parts and cornicles, a pair of tubes on the 5th abdominal segment that are present in most aphids (Borror and White, 1970). Ladybird beetles (family Coccinellidae) were identified as beetles with dome-shaped bodies, four wings including a pair of hard wings known as elytra and club shaped antennae (Borror and White, 1970). Parasitoid wasps (group of superfamilies) were identified as insects with 2 pairs of clear or smoky membranous wings, long antennae, a thin waist and the presence of an ovipositor. While we did not identify individuals into families or assign them into morpho-species (due to degraded sticky trap samples), we did exclude predatory wasps, specifically those from the family Vespidae using (Goulet et al., 1993) field guide (1993).

Urban Garden Census

In order to assess how sampled arthropods were using urban gardens as habitat, we mapped our spatio-temporal arthropod data onto an existing spatial dataset of urban gardens in the same area. Gardens were surveyed 1 year before the arthropod census. Though gardens were sampled 1 year prior to arthropods, we expect little change in home ownership and the spatial distribution of easement gardens within a 1 year span. Garden census data was taken from Hunter and Brown (2012), in which all private properties within the entire Ann Arbor, MI municipal region (N > 20,000) were surveyed in person, recording the location and presence of easement gardens (municipally owned green space that falls between the sidewalk and the road) (Lin et al., 2015). In Ann Arbor, homeowners are required to care and manage these city-owned parcels. The universal tranverse mercator (UTM) coordinates of any parcel showing signs of horticulture (other than mowed lawn) was recorded as an easement garden. Both primarily aesthetic and food-related gardens were recorded since both are important for insect communities. Urban gardens are very broadly defined in the literature and include any horticulture (both ornamental and edible) occurring in urban areas, including easement gardens (Mougeot, 1999; Lin et al., 2017). The majority of easement gardens in this study were dominated by flowering herbaceous perennials (91%), followed by shrubs (6%), ornamental grass (2%), and edible plants (1%). Further details on the specific easement gardens in this study are available from the original source (Hunter and Brown, 2012). Although the use of easement gardens in this study excludes other examples of urban gardens in Ann Arbor (public gardens, community gardens, backyard gardens, etc.), it is a consistent census tool that has been extensively ground-truthed in the study area. Results from the original mapping study showed that easement gardens are significantly clustered in space, which the authors argued is a result of a spatial-contagion effect (Hunter and Brown, 2012). Visual access to the nearest neighbor's easement garden increased the intensity of garden clustering so that homeowners were more than twice as likely to have an easement garden if one existed within 30 m. Due to this spatial-contagion effect, we expect areas with many easement gardens to contain other kinds of urban gardens in the region as well. To confirm this we calculated the bivariate Ripley's K clustering statistic known as the Cross K-function (Ripley, 1976; Juhász and Hochmair, 2017):

$\begin{array}{ll}{K}_{ij}(r)={\lambda }^{-1}E\left[f(r)\right]& (1)\end{array}$

K_ij (r) describes clustering of j type events within r distance of an i event with f(r) representing the number of j events and λ representing the density of j events within the circular area defined by r. We compared the spatial distribution of the easement gardens to the full set of Project Grow (PG) community gardens that were present within the city limits of Ann Arbor in 2012 and 2013. No PG gardens changed within this time frame. PG gardens is the largest and oldest community garden organization in Ann Arbor, first established in 1972 as part of the USA's victory garden wartime effort. The gardens are managed organically and split into allotments that are rented by community members who primarily grow annual edible crops but also perennial crops and ornamentals. We calculated the Cross K-function (1) for the observed distribution of PG and easement gardens as well as for n = 999 Monte-Carlo simulations where PG and easement garden labels were randomly assigned (Ripley, 1976; Juhász and Hochmair, 2017). We found that easement gardens were significantly more clustered to PG community gardens than expected by chance for radii from 300 to 2,500 m (Figure 3) suggesting a strong spatial relationship between easement gardens and PG community gardens in Ann Arbor. Thus, in this study we use easement gardens as a proxy for urban gardens, generally.

FIGURE 3

Figure 3. Easement gardens cluster around community gardens. (A) Spatial distribution of easement gardens (black dots) and Project Grow (PG) community gardens in the city limits of Ann Arbor (gray polygon). (B) The observed Cross-K function (black line), which calculates the number of easement gardens within a radius r of every community garden compared to the mean (red dashed line) for n = 999 Monte Carlo simulations where easement and community garden labels are randomly assigned along with the upper and lower simulation envelope (gray band), which signifies a significance level of alpha = 0.002 for the Monte Carlo test.

Urban Gardens as Habitat

To assess the habitat quality of urban gardens at each sampling point where arthropod data was taken, we calculated garden patch size by summing the number of gardens falling within a radius of 100, 150, 200, 300, 400, 500, 750, 1,000, 1,500, and 2,000 m from the sampling location. This range of radii was chosen so that sampled sites go from independent to overlapping as the sampling radius increases (Figure 2). Low quality sites had few gardens and high-quality sites had more gardens. We tracked how garden habitat size distributions changed with spatial scale by calculating skewness, kurtosis and Gini coefficients (a measure of inequality) for each sampling radius in both local and landscape plots (Gini, 1912). Though we acknowledge that other more specific indicators of habitat quality including local features like floral resources or landscape features including impervious surface could and should be used to assess quality in future studies, we feel that our patch size approach is universally applicable to all study organisms and the most useful metric considering our questions regarding habitat overlap and dispersal range.

In order to determine whether and at what spatial scale urban gardens were perceived as habitat by each taxon, we compared several linear models predicting the abundance of each group of arthropods as a function of patch size for the radii specified above. Sets of models at these radii were created to predict monthly abundances for each organism at each plot in the months of June, July and August 2013. The Akaike Information Criterion (AIC) for each radius was compared to a null model to determine whether and if so, at which radius, garden patch size best predicts organism abundance. If the null model was the best fit model, we concluded that gardens did not represent significant habitat. In cases where the null model was not the best fit, we concluded that gardens significantly influenced arthropod abundances. In these cases, we used the radius of the model with the lowest AIC to indicate the dispersal range of the taxon and from there, calculated the perceived distribution of garden patch size in the landscape. The magnitude of garden effects on abundances were quantified by calculating the estimate of the generalized linear model predicting arthropod abundance for the spatial scale and month appropriate. We assumed Poisson error distributions for count data and tested for significant garden effects using Wald Z-tests (Bolker et al., 2009).

Landscape Permeability

We used synchrony in taxon abundances to measure the permeability of the urban landscape for each of our sampled arthropods. Synchrony of each arthropod group was measured directly using cross-correlation coefficients and indirectly using the slope of Taylor's law. Mean cross-correlations were calculated for each arthropod type by taking the mean of Pearson's correlation coefficient for all 3-pt time series in the lower half of the orthogonal N x N matrix in all unique taxon crosses, excluding the identity line for local (N = 100) and landscape (N = 28) plots. We averaged the absolute values for all cross-correlation coefficients and calculated the 95% quantiles for each arthropod group and sample plot to determine the average level of temporal synchrony (Hanski, 1987). The variance and means of arthropod group abundances over time were also calculated for each sampled site and regressed on a log scale. The slope of these regressions are the exponents of Taylor's temporal law (Eisler et al., 2008). The slope, R² and P-values (calculated using T-tests) of regressions were determined for each arthropod group and plot.

Results

Habitat Patch Quality

We found that the distribution of urban garden habitat quality in our sampled arthropod groups depended strongly on the radius of influence of gardens from each sampled site. Patch quality, measured in terms of the number of gardens within a specified radius, moves from right, even, to left skewed distributions as sampling radius increases. This was indicated by decreases in skewness with sampling radius (Figure 4). Kurtosis, a measure of the tails of the distribution, also declines as sampling radius increases but is higher at smaller and larger radii where captured gardens in plots are more evenly distributed (all very small or large patches) (Figure 4). The gardens in each site become more similar as sampling radius increases and the Gini coefficient approaches 0. Note that the radius of influence determines whether sites represent independent or dependent samples. When sampling radius is small, most sampled locations represent low quality habitat patches with very few urban gardens. However, as sampling radius increases, quality becomes more even across samples as gardens in samples begin to overlap until eventually, all sample locations include the full set of gardens in the landscape (Figure 4). Thus, when sampling radius is large, most samples include the majority of urban gardens, with only a few isolated sites that capture few gardens. The rate at which the distribution changes, depends on how far apart sampled sites are from one another, as demonstrated by slower rates of change in the Gini coefficient for local vs. landscape plot samples (Figure 4).

FIGURE 4

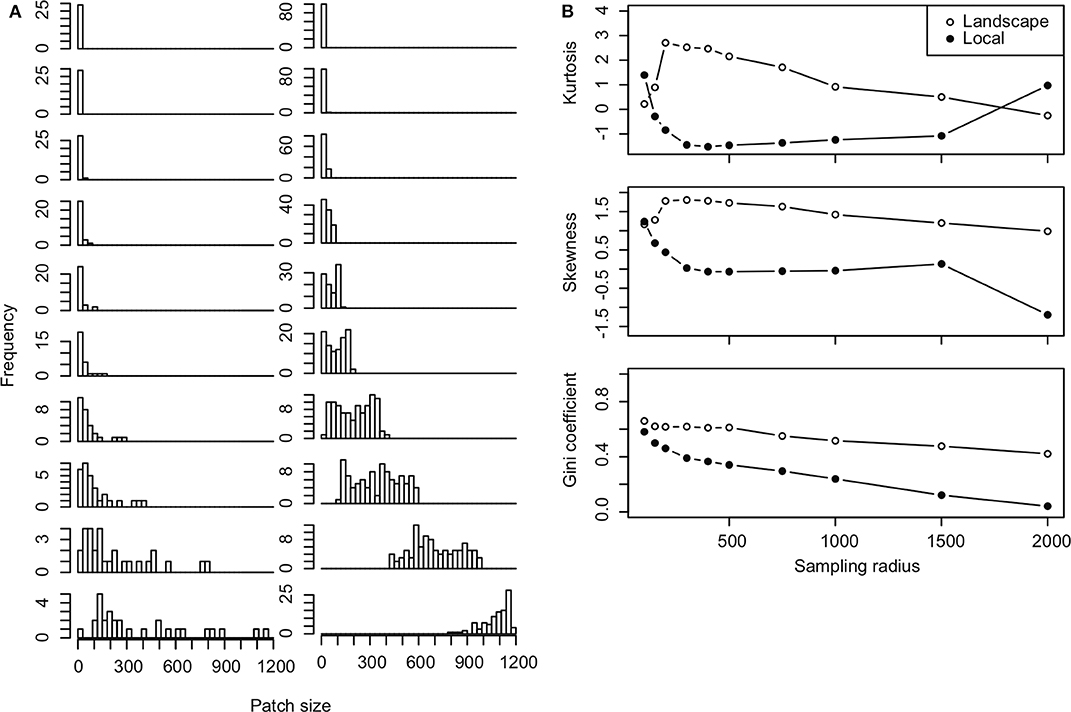
Figure 4. Shifting patch size distributions. (A) Histograms of patch size at each sampling radius of 100, 150, 200, 300, 400, 500, 750, 1,000, 1,500, 2,000 m (from top to bottom rows) are plotted for local (left column) and landscape-plot samples (right column). (B) Kurtosis, skewness and Gini coefficients calculated for patch size distributions at each sampling radius in landscape (open circles) and local-plot samples (solid points).

Arthropod Responses to Gardens

We collected a total of 5,842 invertebrates with the aphids being the most abundant group. A total of 3,667 aphids were sampled between June and August. The highest numbers of aphids were collected in June (1,688 aphids) and July (1,850 aphids) and we surveyed far less aphids in August with only 129 aphids accounted for Figure 5. All aphids surveyed were winged alates. The second most abundant group was the parasitoid wasps with 1,686 wasps. The number of parasitoids surveyed was relatively constant for the 3 months with 549 wasps collected in June, 645 wasps collected in July and 492 collected in August (Figure 5). Finally, we collected a total of 492 ladybird beetles from June to August. Similar to the parasitoid wasps, the number of beetles collected from June to August remained relatively constant. A total of 119 ladybird beetles were collected in June, 254 in July and 119 in August (Figure 5).

FIGURE 5

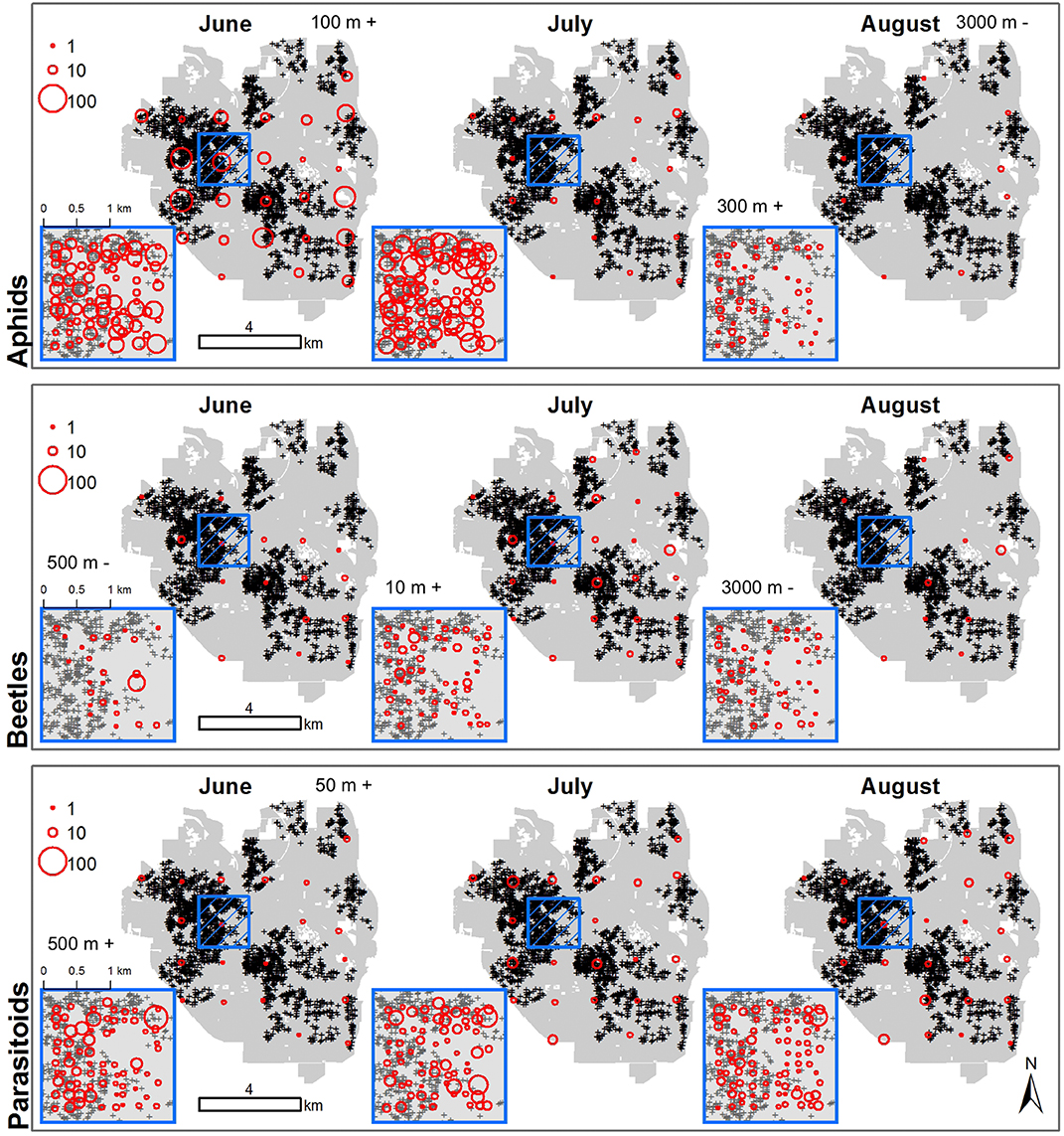
Figure 5. Arthropods are sensitive to urban gardens at different spatio-temporal scales. The sizes of red, open circles indicate the abundance of aphids (top row), ladybird beetles (middle row), and parasitoid wasps (bottom row) in June (first column), July (second column) and August (third column) 2013. Small blue box indicates position of the local plot, which covers downtown Ann Arbor, MI and adjacent neighborhoods with 100 sampled points placed an average of 128 m apart. Larger blue box is an enlarged view of the local plot. The landscape plot covers the entire city landscape with 28 points placed an average of 1,470 m apart. Easement gardens are indicated by black and grey plus signs. Local and landscape plots in each month are labeled above plots with the spatial scale for which gardens had a significant positive (+) or negative (–) effect on abundances.

The spatial scale in which abundances of arthropods best responded to urban gardens varied by arthropod group, sampling month and plot. Aphid abundances were positively driven by gardens at a scale of 100 m in June for the landscape plot, but this relationship did not hold for other months or in the local plot (Figure 5, Table 1). In August, more aphids were found where there were more gardens within a 300 m radius of local plot sites, but samples of aphids in the landscape plot were negatively associated with gardens at 3,000 m. Ladybird beetle abundances only responded to gardens when sampled at the local plot, moving from negative associations at 500 m in June to positive associations at 10 m in July and negative associations at 3,000 m in August (Figure 5, Table 1). Parasitoid wasp abundance responded positively to gardens at a 50 m radius for landscape and 500 m radius for local plots taken in June only. However, these relationships did not hold across the months of July and August (Figure 5, Table 1).

TABLE 1

Table 1. Summary of garden effects on arthropods.

Spatial Synchrony

For aphids, the mean correlation was 0.71 (0.13–0.99, 95% quantiles) in the local plot and 0.91 (0.5–1.0, 95% quantiles) in the landscape plot. The slope of Taylor's law was 1.98 in the local plot (R² = 0.88, P < 0.001) and 2.15 in the landscape plot (R² = 0.92, P < 0.001) (Figure 6). Temporal synchrony for beetles and parasitoids was consistently lower; for beetles the mean correlation was 0.65 (0.00–1.00, 95% quantiles) in the local plot and 0.66 (0.18–1.00, 95% quantiles) in the landscape plot. Ladybird beetles had Taylor's law slopes of 1.42 for local (R² = 0.68, P < 0.001) and 1.40 for landscape plots (R² = 0.65, P < 0.001) (Figure 6). For parasitoids, the mean correlation was 0.63 (0.068–0.99, 95% quantiles) for the local plot and 0.61 (0.082–1.00, 95% quantiles) for the landscape plot. Parasitoid wasps had slopes equal to 1.46 for local (R² = 0.45, P < 0.001) and 0.92 for landscape plots (R² = 0.20, P = 0.013) (Figure 6). We found that declines in Taylor's law were driven by greater variance in smaller abundances of ladybird beetles and parasitoid wasps as compared to equivalently small abundances of aphids (Figure 6).

FIGURE 6

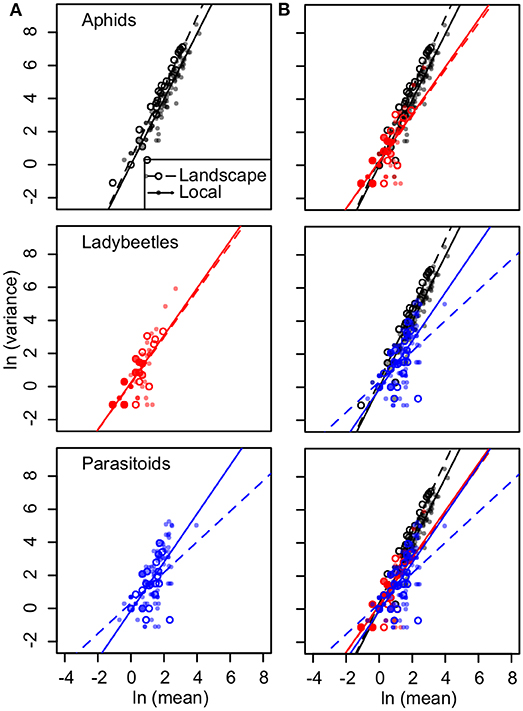
Figure 6. (A) Linear regressions to calculate Taylor's temporal law for abundances of aphids (black), ladybird beetles (red), and parasitoid wasps (blue) at landscape (open circles) and local plots (solid points). For aphids, slopes = 2.14, 1.98, R² = 0.92, 0.88, P < 0.001 for both; ladybird beetles, slopes = 1.40, 1.42, R² = 0.65, 0.68, P < 0.001 for both; and parasitoid wasps, slopes = 0.92, 1.46, R² = 0.20, 0.45, P = 0.13 and P < 0.001 for landscape and local plot sample points, respectively. (B) Plots are repeated and overlaid in different combinations to visually compare arthropod groups.

Discussion

Our results link Taylor's temporal law slopes to perceptions of habitat quality on a continuum between metapopulation and source-sink. We find that aphids had a slope approaching 2 and larger mean cross-correlations, while ladybird beetles and parasitoid wasps had lower slopes and mean cross-correlations (Figure 6). These results are consistent with previous studies that link higher Taylor's law slopes with greater synchrony in temporal oscillations sampled across landscapes (Satake and Iwasa, 2000; Ballantyne and Kerkhoff, 2005, 2007; Eisler et al., 2008).

We conclude that the permeability of Ann Arbor for aphids is relatively high, while dispersal for beetles and wasps may be more constrained. Constrained movement in the landscape not only increases the chance of random extinction events but also fundamentally changes the habitat distribution of sampled sites so that they consist of smaller, right skewed distributions of gardens patches (Figure 4). The greater variance of small ladybird beetle and parasitoid abundances in comparison to small aphid abundances supports the hypothesis that these natural enemies are more isolated and prone to random dispersal and extinction events like in the sink patches of a metapopulation (Figures 1, 6).

The sensitivity of organism abundances to gardens at various spatial scales in local and landscape plots also support this conclusion, although there was significant variation in individual responses. As expected from the relatively high levels of synchrony observed across the landscape, aphid abundances responded to gardens primarily in the landscape plot (Figure 5). These observations support our predictions that permeability of the urban landscape is high for aphids. Since landscape plot samples were synchronized, dispersal must be sufficient to connect the visible clusters of urban garden habitats across the landscape (Figures 2, 5). In a source-sink landscape, we would expect populations to have positive relationships with habitat quality at a larger scale, which we do find in our landscape plot aphid samples. However, aphids did also become sensitive to gardens in the local plot in August. During this last sampling month, gardens had a negative effect on aphid abundances at large spatial scales (3,000 m) in the landscape plot and a positive effect at smaller scales (300 m) in the local plot (Figure 5, Table 1). This may indicate a source-sink relationship between large source patches at the landscape scale early in the season to smaller sink patches at the local scale later in the season. At the end of the summer, aphids produce winged aphids that disperse for the purpose of sexual reproduction (Kring, 1972; Le Trionnaire et al., 2008). Because we placed sticky traps at breast height on telephone or other metal poles not necessarily in garden habitats, we only collected dispersing winged aphid alates. Dispersal across the landscape toward specific local nesting sites at the end of the growing season could explain the shift in spatial sensitivities for this final sampling month. We did observe a sharp decline in aphid abundances during August that we take to indicate that overwintering had already begun during this final sampling period and suggests that we were able to capture the seasonal dynamics in the system by accumulating abundances over 5 week periods across the season (Figure 5). Aphid dispersal can be passive through wind, though they move directionally when attracted to plants and in our case, yellow sticky cards (Kring, 1972). Our results indicate that winged aphid alates are moving through the landscape at large spatial scales and that they have a strong affinity to locations with more urban gardens (Figures 5, 6, Table 1). This would suggest that their movement in Ann Arbor is more directed than passive. They do also appear in locations without gardens as indicated by sample sites where there are aphids and no gardens, however abundances at these sites are consistently lower (Figure 5). Aphids that are found in areas with few gardens are likely moving through that area passively by wind, but the presence of some individuals in these areas indicate that they do indeed move through them. Large clusters of urban gardens may encourage passively dispersing aphids to increase directed movement to traps in search of host plants.

In contrast, ladybird beetle abundances only responded to gardens in our local plot, which we take to indicate strong dispersal limitation and a metapopulation like landscape structure (Figures 2, 5). Though beetles were consistently associated with local plot gardens, the specific effects were various. For example, garden effects on beetle abundance changed from negative to positive depending on the sampling month (Figure 5, Table 1). The tendency of many ladybird beetles to rely on urban resources including built infrastructure as nesting sites in the winter may explain these shifts (Evans and Dixon, 1986; Koch and Galvan, 2008; Bahlai et al., 2014). Researchers have reported divergent responses to urbanization by ladybird beetles (Egerer et al., 2017, 2018). We suggest that these varied responses may be driven by seasonal trends. The negative effects of gardens on beetle abundance occurred toward the beginning and end of the growing season, which could indicate beetles leaving and returning to urban nesting sites during these periods. Random dispersal between isolated patches could therefore explain the beetle's inconsistent spatial responses to gardens and asynchronous abundances, as indicated by low cross-correlation coefficients and slopes for Taylor's law. We note that since metapopulations are characterized by random migration between small sink patches, the inconsistency in our beetle abundance patterns generally supports the hypothesis that beetles are dispersal limited in Ann Arbor.

In contrast, parasitoid abundances appear much more sensitive to sampling month than spatial scale. These insects responded positively to gardens in both the local and landscape plots at various spatial scales but in June only. Gardens may be a particularly important habitat for parasitoid wasps early in the season when aphid hosts first emerge and establish clonal colonies (Kring, 1972). Aphids do also have a positive association with gardens in June but this relationship disapears in July and then reappears in August (Table 1). Though we cannot distinguish parasitoid species in this study or confirm whether their host species were predominantely aphids, if parasitoids were able to closely track aphid abundances, we would expect sensitivity to gardens to closely follow these aphid patterns, which we have no evidence for in August. We hypothesize that constrained dispersal may prevent parasitoids from tracking aphid hosts later in the season. However, since we did not classify parasitoid wasps by species, our results could also indicate a shift in wasp or host community compositions, which may not use urban gardens as habitat, during the later growing season months of July and August. Future research that can identify species compositions shifts along with abundance and distribution are needed to clarify such effects.

Despite these limitations, our empirical results do satisfy theoretical predictions and are biologically reasonable. Aphids are known to have long dispersal ranges and large, synchronized population booms and busts are typical for agricultural pests (Wallner, 1987; Hanski and Woiwod, 1993). We found evidence that aphid abundances are synchronized across the landscape, regardless of the fragmented distribution of urban gardens found in the landscape. In contrast, natural enemies like ladybird beetles and parasitoid wasps are known to be highly sensitive to local conditions, including flower density and diversity. Our results do indicate much more constrained movement of natural enemies. Navigating through highly disturbed urban landscapes is known to be difficult for some arthropod predators and parasitoids (Langellotto and Denno, 2004; O'Rourke et al., 2011; Bennett and Gratton, 2012; Jha and Kremen, 2013). Since Ann Arbor is not particularly urban, the asynchrony of the natural enemies observed in this study suggests that even suburban landscapes can pose significant barriers to dispersal.

Our study focused on group rather than species-level abundance patterns across time and space and their relationship to Taylor's law. Taylor's law is applied to many non-species-specific groups from traffic on Internet routers to transactions on the Stock Exchange (Eisler et al., 2008). The theory similarly applies to the three arthropod groups in this study. Though we did not identify arthropods to species and are not be able to interpret whether specific natural enemy species were responding to trends in their host or prey species, understanding how these groups of arthropods collectively respond to fragmentation patterns is still of interest and are of applied interest to urban garden practitioners who are concerned with overarching pest and natural enemy dynamics. Large-scale synchrony and dependence on urban gardens in aphid abundances suggest that species within the larger aphid group are responding similarly or are driven primarily by a dominant species we could not identify. Regardless of whether the results are general or species-specific, recent work indicates that trophic position may strongly influence how dispersal effects the persistence of metacommunities. In a study of tropical terrestrial leaf litter communities, higher rates of dispersal in non-predators caused higher rates of extinction for predator species (Hajian-Forooshani et al., 2019). Our study could indicate that such a pattern exists since aphid prey were observed to have much greater levels of dispersal than natural enemies. Examining levels of synchrony across trophic levels in other ecological communities where we can separate species from community-level effects may help determine whether greater rates of dispersal are generally more common amongst lower trophic levels and are somehow subject to multi-level selection pressures (Nowak et al., 2010).

We expected synchrony in abundances to decrease when moving from local to landscape plots if dispersal across the landscape is constrained. Taylor's law slopes were very consistent across plots for ladybird beetles and aphids (Figure 6). However, we did find that parasitoid wasps had much lower Taylor's law slopes in our landscape plot, confirming our prediction that synchrony of arthropod groups sampled far from one another should decrease. The greatest differences in cross-correlations across plots was in aphids, with lower cross-correlation coefficients in local samples (0.71) than landscape samples (0.91) but the large 95% quantile confidence intervals of this and other cross-correlation coefficients suggest that these values may not be very useful metrics of synchrony. In our study, Taylor's law may provide a more accurate measure of spatial synchrony since our time series were short, 3 time point samples (Figure 6). We had only one plot of each type in a single fragmented landscape, limiting our ability to generalize the results of our work too broadly. Future work comparing the same arthropod groups distributed across many landscapes that vary in degrees of fragmentation may better elucidate how fragmentation can differentially influence spatial synchrony and Taylor's law generally.

In this paper we focused on investigating how Taylor's law maps onto spatial synchrony and the permeability of fragmented landscapes for three different arthropod groups. Our study is unique in having an expansive survey of urban gardens in the entire city of Ann Arbor to test the relationship between gardens and arthropod abundances. However, if other studies did not have the underlying information on the habitat distribution or if the habitat was unknown, a simple calculation of Taylor's law may still be sufficient to assess how a group of organisms is filtering a fragmented space like the peri-urban city of Ann Arbor, MI. We predict that future work utilizing Taylor's law in other cities or fragmented landscapes like agriculture may reveal divergent trends in the slope of Taylor's law, even for the same species in different landscapes. This would suggest that this slope depends not only on species identity as previously suggested (Taylor, 1961), but also on the permeability of a given landscape to that species. As such, we believe that Taylor's law will be a particularly useful tool for studying how the role of urban gardens to urban biodiversity changes across cities.

Here we show that different organisms can perceive the same fragmented landscape very differently depending on their dispersal capacities and the slope of Taylor's temporal law may be intricately linked to these perceptions and the fundamental structure of communities. Not only may organisms respond to landscapes forming a continuum from metapopulation to source-sink, but a single landscape may fall anywhere along this continuum simultaneously and differentially for each organism that exists within it.

In the context of trophic interactions, other questions arise. Is biological control best achieved when organisms experience the landscape similarly, or does a disjunction between perceptions keep the system in a state of persistence that may be impossible to maintain otherwise? Is there a way of maximizing long-distance dispersal events in organisms of conservation concern while maintaining asynchrony of their populations across the landscape? The answers to such questions require further study, but the results of this work imply that we may no longer be able to simplify landscapes to their obvious physical features such as size and distance between habitat patches. Here we demonstrate one example where aphid pests are less constrained than their natural enemies in a fragmented, sub-urban landscape. Future studies testing the effects of fragmentation patterns on Taylor's temporal law across multiple landscapes and organisms may help untangle the complex relationship between population, community and landscape structures. Practical applications including the design of urban garden landscapes that can maximize natural enemy persistence, while reducing synchronous dynamics in long-range pest species is just one example.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

TO and JV conceived and developed the study. TO, LH, and AL jointly designed and carried out the field surveys. DP and LH identified the field specimens. TO, KL, DP, and AL analyzed the field data. MH provided the original garden data. TO and JV drafted the manuscript. All authors contributed the revisions.

Funding

The University of Michigan Rackham Graduate School and Program in Environmental Studies at Dartmouth College provided financial support.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Thank you to Ivette Perfecto and Stacy Philpott for comments on an early version of this manuscript.

References

Akinnifesi, F. K., Sileshi, G. W., Ajayi, O. C., Akinnifesi, A. I., Moura, E. G., de Linhares, J. F. P., et al. (2009). Biodiversity of the urban homegardens of São Luís city, Northeastern Brazil. Urban Ecosyst. 13, 129–146. doi: 10.1007/s11252-009-0108-9

CrossRef Full Text | Google Scholar

Anderson, R. M., Gordon, D. M., Crawley, M. J., and Hassell, M. P. (1982). Variability in the abundance of animal and plant species. Nature 296, 245–248. doi: 10.1038/296245a0

CrossRef Full Text | Google Scholar

Bahlai, C. A., Colunga-Garcia, M., Gage, S. H., and Landis, D. A. (2014). The role of exotic ladybeetles in the decline of native ladybeetle populations: evidence from long-term monitoring. Biol. Invasions 17, 1005–1024. doi: 10.1007/s10530-014-0772-4

CrossRef Full Text | Google Scholar

Ballantyne, I. J., and Kerkhoff, A. (2007). The observed range for temporal mean-variance scaling exponents can be explained by reproductive correlation. Oikos 116, 174–180. doi: 10.1111/j.2006.0030-1299.15383.x

CrossRef Full Text | Google Scholar

Ballantyne, I. V., and F. Kerkhoff, A. J. (2005). Reproductive correlation and mean–variance scaling of reproductive output for a forest model. J. Theor. Biol. 235, 373–380. doi: 10.1016/j.jtbi.2005.01.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Barthel, S., Parker, J., Folke, C., and Colding, J. (2014). “Urban gardens: pockets of social-ecological memory,” in Greening in the Red Zone, eds K. G. Tidball and M. E. Krasny (Springer Netherlands), 145–158. Available online at: http://link.springer.com/chapter/10.1007/978-90-481-9947-1_11 (accessed September 1, 2015).

Google Scholar

Beninde, J., Veith, M., and Hochkirch, A. (2015). Biodiversity in cities needs space: a meta-analysis of factors determining intra-urban biodiversity variation. Ecol. Lett. 18, 581–592. doi: 10.1111/ele.12427

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, A. B., and Gratton, C. (2012). Local and landscape scale variables impact parasitoid assemblages across an urbanization gradient. Landsc. Urban Plan. 104, 26–33. doi: 10.1016/j.landurbplan.2011.09.007

CrossRef Full Text | Google Scholar

Bolker, B. M., Brooks, M. E., Clark, C. J., Geange, S. W., Poulsen, J. R., Stevens, M. H. H., et al. (2009). Generalized linear mixed models: a practical guide for ecology and evolution. Trends Ecol. Evol. 24, 127–135. doi: 10.1016/j.tree.2008.10.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Borror, D. J., and White, R. E. (1970). A Field Guide to Insects: America North of Mexico. Boston, MA: Houghton Mifflin Harcourt.

Google Scholar

Brodeur, J., and Rosenheim, J. A. (2000). Intraguild interactions in aphid parasitoids. Entomol. Exp. Appl. 97, 93–108. doi: 10.1046/j.1570-7458.2000.00720.x

CrossRef Full Text | Google Scholar

Brown, K. H., and Jameton, A. L. (2000). Public health implications of urban agriculture. J. Public Health Policy 21, 20–39. doi: 10.2307/3343472

PubMed Abstract | CrossRef Full Text | Google Scholar

Dell, A. I., Bender, J. A., Branson, K., Couzin, I. D., de Polavieja, G. G., Noldus, L. P. J. J., et al. (2014). Automated image-based tracking and its application in ecology. Trends Ecol. Evol. 29, 417–428. doi: 10.1016/j.tree.2014.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Donovan, B. J. (2003). Potential manageable exploitation of social wasps, Vespula spp. (Hymenoptera: Vespidae), as generalist predators of insect pests. Int. J. Pest Manag. 49, 281–285. doi: 10.1080/0967087031000123698

CrossRef Full Text | Google Scholar

Egerer, M. H., Bichier, P., and Philpott, S. M. (2017). Landscape and local habitat correlates of lady beetle abundance and species richness in urban agriculture. Ann. Entomol. Soc. Am. 110, 97–103. doi: 10.1093/aesa/saw063

CrossRef Full Text | Google Scholar

Egerer, M. H., Li, K., and Ong, T. W. (2018). Context matters: contrasting ladybird beetle responses to urban environments across two US regions. Sustainability 10:1829. doi: 10.3390/su10061829

CrossRef Full Text | Google Scholar

Eisler, Z., Bartos, I., and Kertesz, J. (2008). Fluctuation scaling in complex systems: Taylor's law and beyond 1. Adv. Phys. 57, 89–142. doi: 10.1080/00018730801893043

CrossRef Full Text | Google Scholar

Evans, E. W., and Dixon, A. F. G. (1986). Cues for oviposition by ladybird beetles (Coccinellidae): response to aphids. J. Anim. Ecol. 55:1027. doi: 10.2307/4431

CrossRef Full Text | Google Scholar

Gardiner, M. M., Burkman, C. E., and Prajzner, S. P. (2013). The value of urban vacant land to support arthropod biodiversity and ecosystem services. Environ. Entomol. 42, 1123–1136. doi: 10.1603/EN12275

PubMed Abstract | CrossRef Full Text | Google Scholar

Gini, C. (1912). Variabilita Emutability. Vol. 3. Studi Economico-Giuridici dell'Universita di Cagliari, 1–158.

Google Scholar

Goddard, M. A., Dougill, A. J., and Benton, T. G. (2010). Scaling up from gardens: biodiversity conservation in urban environments. Trends Ecol. Evol. 25, 90–98. doi: 10.1016/j.tree.2009.07.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Gotelli, N. J. (1991). Metapopulation models: the rescue effect, the propagule rain, and the core-satellite hypothesis. Am. Natural. 138, 768–776. doi: 10.1086/285249

CrossRef Full Text | Google Scholar

Goulet, H., (ed.), Agriculture Canada, O., and Huber, J. T., (ed.). (1993). Hymenoptera of the World: An Identification Guide to Families. Available online at: http://agris.fao.org/agris-search/search.do?recordID=XF2015036851 (accessed March 19, 2020).

Google Scholar

Graving, J. M., Chae, D., Naik, H., Li, L., Koger, B., Costelloe, B. R., et al. (2019). DeepPoseKit, a software toolkit for fast and robust animal pose estimation using deep learning. Elife 8:e47994. doi: 10.7554/eLife.47994.sa2

PubMed Abstract | CrossRef Full Text | Google Scholar

Guitart, D., Pickering, C., and Byrne, J. (2012). Past results and future directions in urban community gardens research. Urban For. Urban Greening 11, 364–373. doi: 10.1016/j.ufug.2012.06.007

CrossRef Full Text | Google Scholar

Hajian-Forooshani, Z., Schmitt, L., Medina, N., and Vandermeer, J. (2019). Trophic-specific responses to migration in empirical metacommunities. Oikos 129, 413–419. doi: 10.1111/oik.06342

CrossRef Full Text | Google Scholar

Hanski, I. (1987). Cross-correlation in population dynamics and the slope of spatial variance: mean regressions. Oikos 50, 148–151. doi: 10.2307/3565413

CrossRef Full Text | Google Scholar

Hanski, I., and Woiwod, I. P. (1993). Spatial synchrony in the dynamics of moth and aphid populations. J. Anim. Ecol. 62, 656–668. doi: 10.2307/5386

CrossRef Full Text | Google Scholar

Hunter, M. C. R., and Brown, D. G. (2012). Spatial contagion: gardening along the street in residential neighborhoods. Landsc. Urban Plan. 105, 407–416. doi: 10.1016/j.landurbplan.2012.01.013

CrossRef Full Text | Google Scholar

Jha, S., and Kremen, C. (2013). Resource diversity and landscape-level homogeneity drive native bee foraging. PNAS 110, 555–558. doi: 10.1073/pnas.1208682110

PubMed Abstract | CrossRef Full Text | Google Scholar

Juhász, L., and Hochmair, H. H. (2017). Where to catch ‘em all? – a geographic analysis of Pokémon Go locations. Geo Spatial Inform. Sci. 20, 241–251. doi: 10.1080/10095020.2017.1368200

CrossRef Full Text | Google Scholar

Kilpatrick, A. M., and Ives, A. R. (2003). Species interactions can explain Taylor's power law for ecological time series. Nature 422, 65–68. doi: 10.1038/nature01471

PubMed Abstract | CrossRef Full Text | Google Scholar

Koch, R. L., and Galvan, T. L. (2008). “Bad side of a good beetle: the North American experience with Harmonia axyridis,” in From Biological Control to Invasion: the Ladybird Harmonia axyridis as a Model Species, eds H. E. Roy and E. Wajnberg (Dordrecht: Springer Netherlands), 23–35.

Google Scholar

Kring, J. B. (1972). Flight behavior of aphids. Annu. Rev. Entomol. 17, 461–492. doi: 10.1146/annurev.en.17.010172.002333

CrossRef Full Text | Google Scholar

Langellotto, G. A., and Denno, R. F. (2004). Responses of invertebrate natural enemies to complex-structured habitats: a meta-analytical synthesis. Oecologia 139, 1–10. doi: 10.1007/s00442-004-1497-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Le Trionnaire, G., Hardie, J., Jaubert-Possamai, S., Simon, J.-C., and Tagu, D. (2008). Shifting from clonal to sexual reproduction in aphids: physiological and developmental aspects. Biol. Cell 100, 441–451. doi: 10.1042/BC20070135

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, B. B., Philpott, S. M., and Jha, S. (2015). The future of urban agriculture and biodiversity-ecosystem services: Challenges and next steps. Basic Appl. Ecol. 16, 189–201. doi: 10.1016/j.baae.2015.01.005

CrossRef Full Text | Google Scholar

Lin, B. B., Philpott, S. M., Jha, S., and Liere, H. (2017). “Urban agriculture as a productive green infrastructure for environmental and social well-being,” in Greening Cities: Forms and Functions Advances in 21st Century Human Settlements, eds P. Y. Tan and C. Y. Jim (Singapore: Springer Singapore), 155–179.

Google Scholar

MacDougall, A. S., McCann, K. S., Gellner, G., and Turkington, R. (2013). Diversity loss with persistent human disturbance increases vulnerability to ecosystem collapse. Nature 494, 86–89. doi: 10.1038/nature11869

PubMed Abstract | CrossRef Full Text | Google Scholar

McClintock, N. (2010). Why farm the city? Theorizing urban agriculture through a lens of metabolic rift. Cambridge J Regions Econ Soc. 3, 191–207. doi: 10.1093/cjres/rsq005

CrossRef Full Text | Google Scholar

Mougeot, L. J. A. (1999). Urban Agriculture: Definition, Presence, Potentials and Risks. Available online at: http://agris.fao.org/agris-search/search.do?recordID=NL2001003053 (Accessed July 31, 2019).

Google Scholar

Nathan, R. (2001). The challenges of studying dispersal. Trends Ecol. Evol. 16, 481–483. doi: 10.1016/S0169-5347(01)02272-8

CrossRef Full Text | Google Scholar

Nowak, M. A., Tarnita, C. E., and Wilson, E. O. (2010). The evolution of eusociality. Nature 466, 1057–1062. doi: 10.1038/nature09205

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Rourke, M. E., Rienzo-Stack, K., and Power, A. G. (2011). A multi-scale, landscape approach to predicting insect populations in agroecosystems. Ecol. Appl. 21, 1782–1791. doi: 10.1890/10-0241.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Otoshi, M. D., Bichier, P., and Philpott, S. M. (2015). Local and landscape correlates of spider activity density and species richness in urban gardens. Environ. Entomol. 44, 1043–1051. doi: 10.1093/ee/nvv098

PubMed Abstract | CrossRef Full Text | Google Scholar

Perfecto, I., Vandermeer, J. H., and Wright, A. L. (2009). Nature's Matrix: Linking Agriculture, Conservation and Food Sovereignty. New York, NY: Earthscan.

Google Scholar

Philpott, S. M., and Bichier, P. (2017). Local and landscape drivers of predation services in urban gardens. Ecol. Appl. 27, 966–976. doi: 10.1002/eap.1500

PubMed Abstract | CrossRef Full Text | Google Scholar

Pulliam, H. R. (1988). Sources, sinks, and population regulation. Am. Nat. 132, 652–661. doi: 10.1086/284880

CrossRef Full Text | Google Scholar

Ranta, E., Kaitala, V., Lindstrom, J., and Linden, H. (1995). Synchrony in population dynamics. Proc. R. Soc. Lond. B Biol. Sci. 262, 113–118.

Google Scholar

Ripley, B. D. (1976). The second-order analysis of stationary point processes. J. Appl. Probab. 13, 255–266. doi: 10.2307/3212829

CrossRef Full Text | Google Scholar

Ruxton, G. D., and Rohani, P. (1999). Fitness-dependent dispersal in metapopulations and its consequences for persistence and synchrony. J. Anim. Ecol. 68, 530–539. doi: 10.1046/j.1365-2656.1999.00300.x

CrossRef Full Text | Google Scholar

Sæther, B.-E., Tufto, J., Engen, S., Jerstad, K., Røstad, O. W., and Skåtan, J. E. (2000). Population dynamical consequences of climate change for a small temperate songbird. Science 287, 854–856. doi: 10.1126/science.287.5454.854

PubMed Abstract | CrossRef Full Text | Google Scholar

Satake, A., and Iwasa, Y. (2000). Pollen coupling of forest trees: forming synchronized and periodic reproduction out of chaos. J. Theor. Biol. 203, 63–84. doi: 10.1006/jtbi.1999.1066

PubMed Abstract | CrossRef Full Text | Google Scholar

Speak, A. F., Mizgajski, A., and Borysiak, J. (2015). Allotment gardens and parks: provision of ecosystem services with an emphasis on biodiversity. Urban For. Urban Greening 14, 772–781. doi: 10.1016/j.ufug.2015.07.007

CrossRef Full Text | Google Scholar

Sylvester, E. S. (1980). Circulative and propagative virus transmission by aphids. Annu. Rev. Entomol. 25, 257–286. doi: 10.1146/annurev.en.25.010180.001353

CrossRef Full Text | Google Scholar

Taylor, L. (1961). Aggregation, variance and the mean. Nature 189, 732–735. doi: 10.1038/189732a0

CrossRef Full Text | Google Scholar

Titmus, G. (1983). Are animal populations really aggregated. Oikos 40, 64–68. doi: 10.2307/3544199

CrossRef Full Text | Google Scholar

Vandermeer, J. H. (2010). The Ecology of Agroecosystems. Sudbury, MA: Jones and Bartlett Publishers.

Google Scholar

Wallner, W. E. (1987). Factors affecting insect population dynamics: differences between outbreak and non-outbreak species. Annu. Rev. Entomol. 32, 317–340. doi: 10.1146/annurev.en.32.010187.001533

CrossRef Full Text | Google Scholar

Werling, B. P., and Gratton, C. (2010). Local and broadscale landscape structure differentially impact predation of two potato pests. Ecol. Appl. 20, 1114–1125. doi: 10.1890/09-0597.1

PubMed Abstract | CrossRef Full Text | Google Scholar

World Health Organization (2016). Global Report on Urban Health. Available online at: http://www.who.int/kobe_centre/publications/urban-global-report/en/ (accessed August 31, 2016).

Google Scholar