Seasonal prediction of rainfall variability for the West African Sudan-Sahel

The Sudan-Sahel region in West Africa is highly vulnerable to rainfall variability, which poses significant challenges to agriculture and water resource management. This study provides an assessment of seasonal rainfall prediction models in the region, focusing on the West African Regional Climate Outlook Forum (WARCOF, 1998–2023), the latest generation of the seasonal forecasting system from the European Centre for Medium-Range Weather Forecasts (ECMWF SEAS5, 1981-2023), and a novel atmospheric circulation-pattern-based logistic regression model (1981–2023). The circulation-pattern-based model, which integrates key atmospheric dynamics like near-surface wind anomalies, outperforms both WARCOF and SEAS5 in predicting interannual rainfall variability. While WARCOF and SEAS5 demonstrate some predictive skill, both models exhibit biases: WARCOF has a dry bias, and SEAS5 displays both dry and wet biases. The circulation-pattern-based model, despite a slight wet bias, delivers more accurate categorical predictions and offers greater reliability. An economic value analysis reveals that the circulation-pattern-based model provides a broader range of positive economic outcomes, making it more suitable for decision-making across various cost-loss scenarios. By introducing this novel model and evaluating traditional forecasting techniques, this study lays the groundwork for more accurate and reliable seasonal rainfall predictions.

1 Introduction

The Sudan-Sahel region has experienced significant interannual variability in seasonal rainfall over recent decades (Nouaceur and Murarescu, 2020; Rauch et al., 2024), presenting a major challenge due to the high dependence on rain-fed agriculture and pastoralism (Zampaligré et al., 2014; Coly et al., 2024). Livelihoods are highly vulnerable to changes in seasonal rainfall patterns (Mertz et al., 2012). Accurate seasonal rainfall forecasts are therefore critical for reducing vulnerability and enhancing resilience in sectors such as agriculture and water resource management (Yengoh, 2012). Inaccurate or limited predictions of droughts, for instance, can have far-reaching effects on food security, economic stability, and water availability (Wilhite et al., 2007; Hao et al., 2018). Thus, improving seasonal rainfall predictions would enable stakeholders to better prepare for such events, mitigating their adverse effects and enhancing disaster preparedness (Portele et al., 2021).

In many parts of the world, seasonal predictions are generated by Regional Climate Outlook Forums (RCOFs), which bring together climate experts from national, regional, and international institutions (Semazzi, 2011). These forums aim to develop and disseminate seasonal climate outlooks, typically once or multiple times a year, tailored to specific geographic regions. The forum currently serving the Sudan-Sahel region in West Africa is known as Prévisions Climatiques Saisonnières en Afrique Soudano-Sahélienne (PRESASS). This forum is organized by the African Centre of Meteorological Application for Development (ACMAD) and the Centre Regional de Formation et d'Application en Agrométéorologie et Hydrologie Opérationelle (AGRYMET), which regularly convene in April or May to produce forecasts for the rainy season (Bliefernicht et al., 2019). These forecasts focus on June, July, August or July, August, September (JAS) periods and are disseminated to stakeholders in the form of maps and advisory documents, which serve as critical tools for decision-making across various sectors. The forecasting process categorizes seasonal rainfall into terciles (below-average, near-average, and above-average), where each tercile represents one-third of the long-term climatological data (typically 1981-2010). These categories are communicated through maps that indicate the likelihood of each category occurring across different regions. This approach helps simplify complex climate data into actionable insights for local decision-makers (Figure 1). For a more detailed discussion of this forecasting methodology, see Bliefernicht et al. (2019) and Pirret et al. (2020).

Figure 1

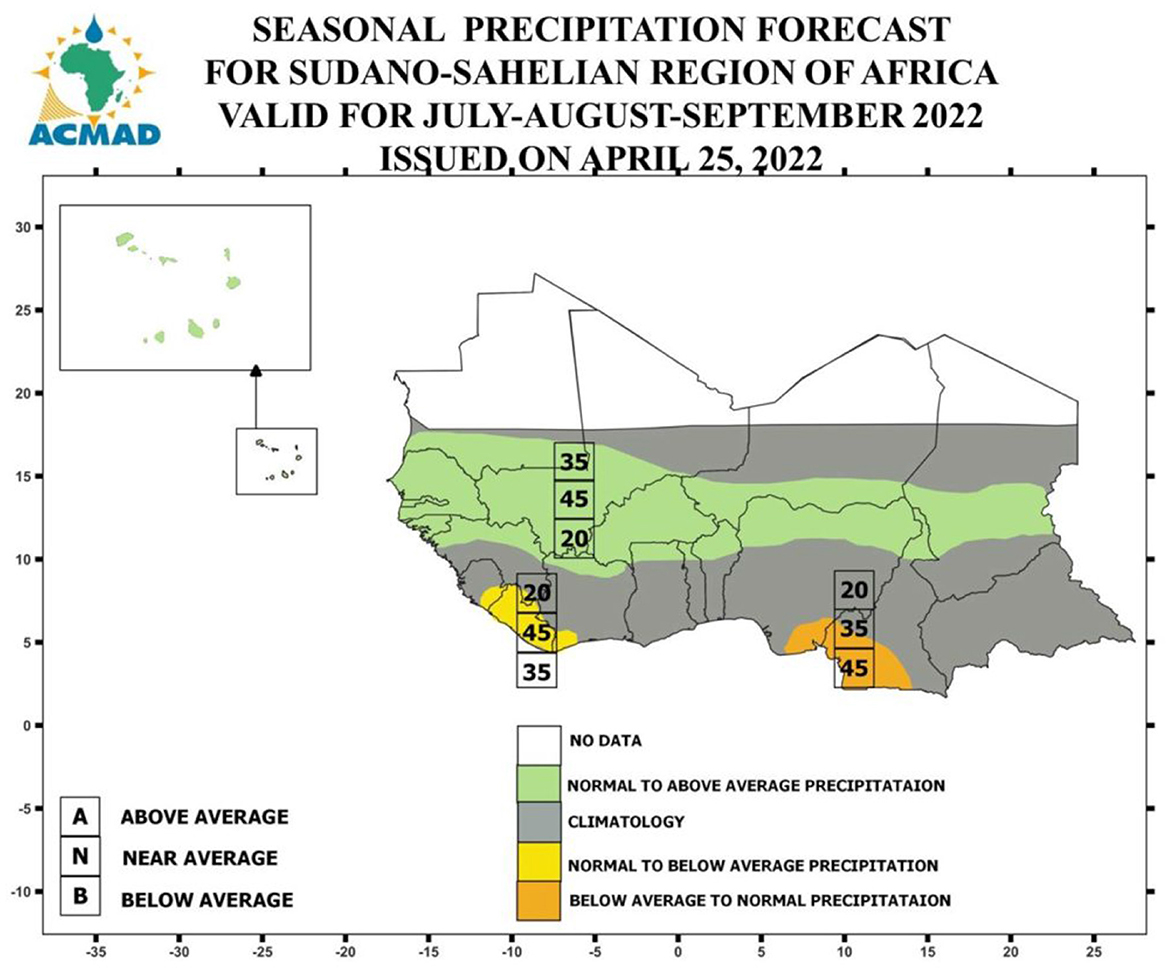
Figure 1. An example of the West African Regional Climate Outlook Forum rainfall outlook for JAS 2022 (ACMAD, 2022).

Mason and Chidzambwa (2009) conducted the first assessment of seasonal precipitation forecasts produced by the West African RCOF (WARCOF) for the period 1998–2007, identifying both positive skill in predicting below-normal and above-normal precipitation, as well as several limitations, particularly a lack of sharpness. Extending this analysis to 2013, Bliefernicht et al. (2019) confirmed these findings but also highlighted issues such as overforecasting near-normal conditions, which were attributed to forecasters' risk aversion. Similarly, Pirret et al. (2020) observed a bias in the WARCOF forecasts (1998–2017) toward underestimating probabilities for the below-normal category, linked to similar hedging behaviors identified in previous studies. Houngnibo et al. (2023) identified the temporal aggregation of forecasts as a significant limitation and proposed a temporal disaggregation method to address this issue. These forecasting limitations, including biases and temporal aggregation, hinder optimal decision-making, particularly in agriculture and water resource management, where accurate forecasts are critical. Therefore, further evaluation and development of more advanced forecasting methods within the WARCOF process are essential.

Operational seasonal forecasting models that support the WARCOF are relatively rare in West Africa. Many downscaling studies have primarily focused on developing and evaluating dynamical approaches (e.g., Siegmund et al., 2015; Klein et al., 2015; Paeth et al., 2017), which are computationally expensive, or providing regional climate projections (e.g., Lorenz et al., 2018; Siabi et al., 2021; Polasky et al., 2024). In contrast, statistical downscaling frameworks have shown significant promise, offering a more accessible and efficient alternative. For example, Ndiaye et al. (2011) used a linear least squares regression based on the time series of the first empirical orthogonal function from tropical Atlantic low-level winds as the predictor and the Sahel rainfall index as the predictand for seasonal rainfall forecasting. Manzanas (2017) applied the analog method for downscaling temperature and rainfall in Senegal, while Rauch et al. (2019) employed a simple bias correction (quantile-quantile mapping) to refine rainfall data for forecasting the onset of the rainy season. A further overview and examples of downscaling techniques for rainfall in West Africa is given in Paeth et al. (2011). Moreover, the reconstruction based on atmospheric circulation patterns (CPs) in combination with a logistic regression model of the interannual rainfall variability in West Africa as detailed in Rauch et al. (2024) shows promise in improving the predictive skill of seasonal rainfall forecasts.

To address these challenges, the present study applies the CP-based logistic regression downscaling method developed by Rauch et al. (2024) to seasonal rainfall predictions for the first time. This approach integrates physically meaningful atmospheric processes to enhance forecast reliability and reduce errors. By employing advanced verification tool like the ranked probability skill score (e.g., Weigel et al., 2007), the multicategory reliability diagram (Hamill, 1997), and an economic value framework (e.g., Bliefernicht et al., 2019), the study provides deeper insights into the models' reliability, accuracy, and practical decision-making value. Furthermore, by incorporating atmospheric circulation patterns into the logistic regression model, this work offers an objective, and more physically grounded method.

In addition, it presents a more comprehensive and current evaluation of the WARCOF performance compared to previous studies like Mason and Chidzambwa (2009), Bliefernicht et al. (2019), and Pirret et al. (2020). Within this extended context, the study provides a comprehensive assessment of forecasting capabilities by comparing three approaches over their respective validation periods: the CP-based logistic regression forecasts from Rauch et al. (2024) (1981-2023), WARCOF's regional forecasts (1998-2023), and the global seasonal forecast system SEAS5 from ECMWF (1981-2023).

2 Material and methods

This section outlines the target region, materials and methods used for the preprocessing, development, and evaluation of the selected seasonal rainfall prediction models for the Sudan-Sahel region. An overview of the workflow is provided in Figure 3.

2.1 Target region

For this evaluation, we focus on the Sudan-Sahel region (5.5°W 11°N to 2.4°E 13.5°N, Figure 2) as the target area, following a similar domain as Bliefernicht et al. (2019). This region was chosen due to its relatively high density of in-situ rainfall stations (see Figure 3 in Bliefernicht et al., 2019), which likely improves the reliability of the remote sensing precipitation products. This region experiences a single, short rainy season spanning from June to September with a peak in August (Bliefernicht et al., 2022; Rauch et al., 2024).

Figure 2

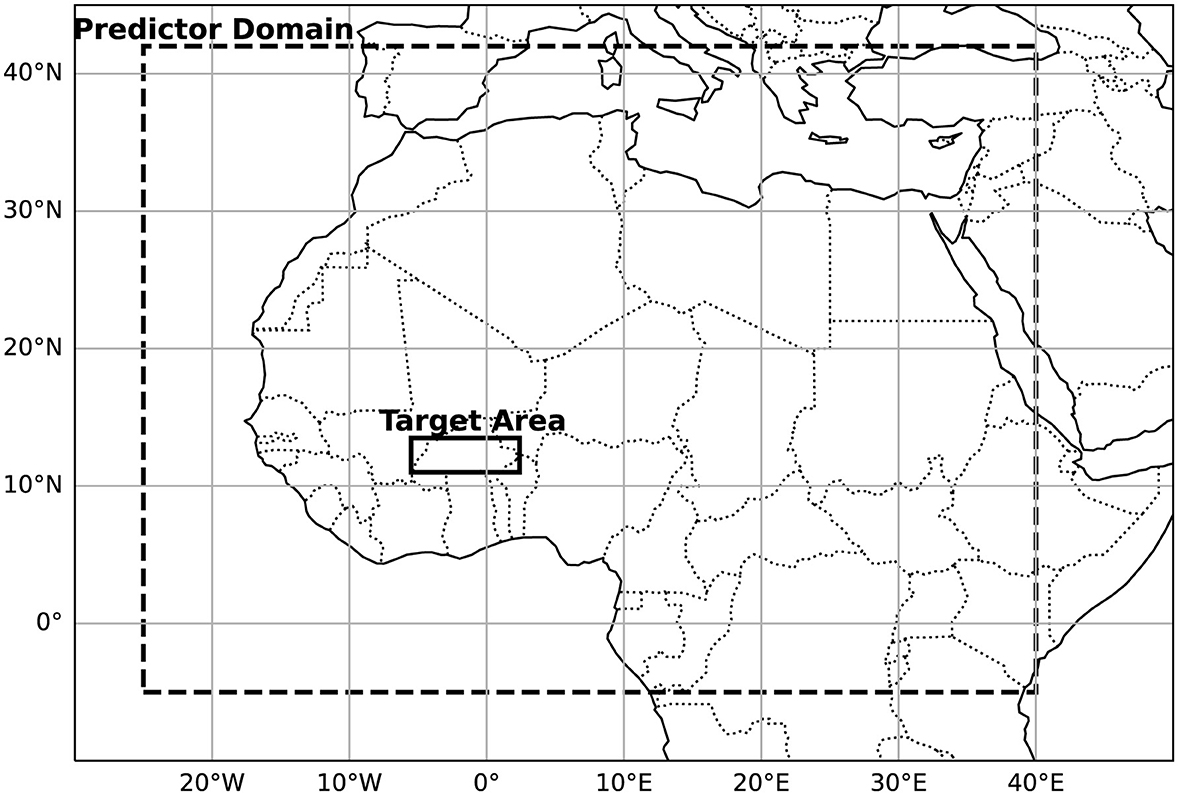
Figure 2. The dashed domain indicates the predictor domain (30°W 5°S to 40°E 40°N), the smaller domain (solid) highlights the target area (5.5°W 11°N to 2.4°E 13.5°N).

2.2 CHIRPS

Due to the lack of access to recent observational data and the goal of developing an operational framework, we use the Climate Hazards Group Infrared Precipitation with Stations (CHIRPS) product (Funk et al., 2015). CHIRPS combines satellite rainfall estimates with gauge and station data corrections, providing a relatively reliable dataset that balances the wide coverage of satellite data with the accuracy of ground-based measurements. This product offers rainfall data on a 0.05° grid, covering the period from 1981 to the present. Furthermore, CHIRPS is selected for its proven performance, long-term availability, and frequent use in West Africa for studies on rainfall variability and its impacts (Dembélé and Zwart, 2016; Rauch et al., 2019; Pirret et al., 2020; Kouakou et al., 2023).

We select all grid points within the target area of Figure 2, average them spatially to extract a single daily time series, and then aggregate this to standardized annual JAS sums (denoted hereafter as R_A). R_A is then discretized into ordinal classes using two quantile thresholds (q₁ and q₂), where q₁ represents the first and q₂ the second tercile. This classification results in three categories: R_A ≤ q₁ (Class 1, below-average condition), q₁ < R_A < q₂ (Class 2, near-average condition), and R_A ≥ q₂ (Class 3, above-average condition). These categorizations serve as the target variables in a multi-class logistic regression model (similar to Rauch et al., 2024), ensuring consistency with the regional nature of WARCOF outputs through spatial aggregation and the categorical probabilistic forecast method.

As illustrated in Figure 4, the standardized JAS annual rainfall amounts from 1981 to 2023 capture the severe droughts of the 1980s, followed by a recovery in rainfall extending into the early 2020s (Hagos and Cook, 2008; Descroix et al., 2018). This figure not only highlights these climatic trends but also delineates the target evaluation categories used in our analysis.

Figure 3

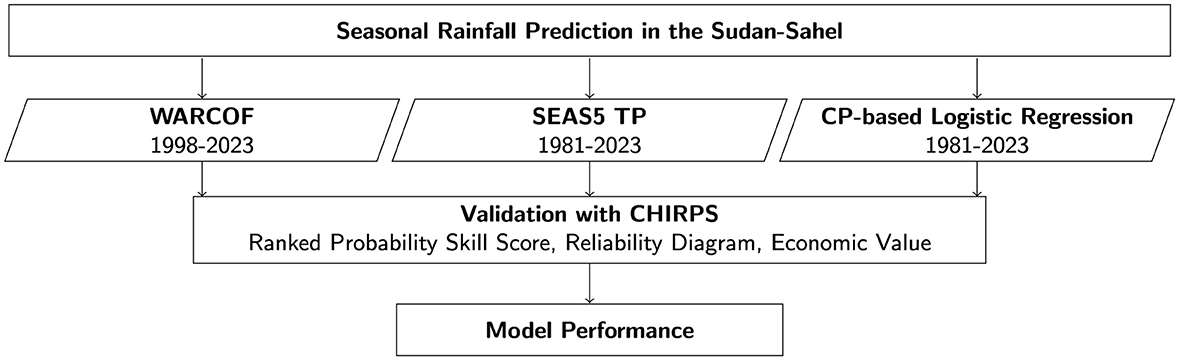
Figure 3. Workflow for seasonal rainfall prediction model evaluation in the Sudan-Sahel region. The process involves three prediction models: WARCOF (West African Regional Climate Outlook Forum), SEAS5 TP (“raw” total precipitation output from SEAS5), and CP-based logistic regression (Rauch et al., 2024). Each model is validated against observed CHIRPS (Climate Hazards Group InfraRed Precipitation with Stations) data using the ranked probability skill score, multicategory reliability diagram, and economic value.

Figure 4

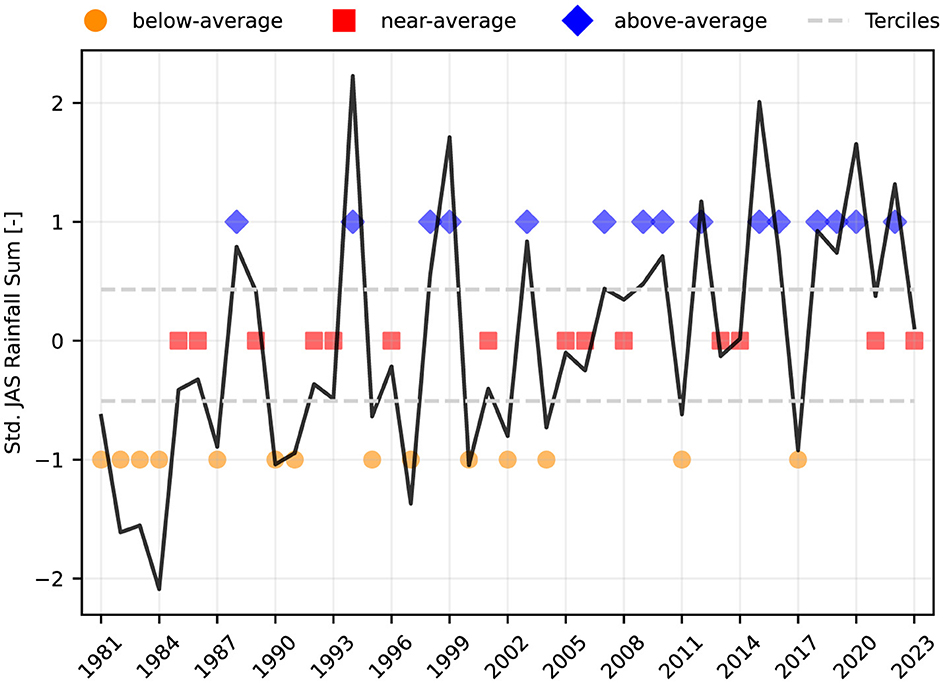
Figure 4. The standardized interannual rainfall variability for the target region ($\overline{x}=552.38\mathrm{\text{mm}}$, σ = 78.01mm) and the period from 1981 to 2023 based on CHIRPS. The solid black line indicates the actual values of standardized annual rainfall sums (JAS). The two dashed lines mark the first and second tercile, dividing the data into three categories: below-average (yellow circle, below the first dashed line), near-average (red square, between the two dashed lines), and above-average (blue diamond, above the second dashed line).

2.3 West African Regional Climate Outlook Forum

WARCOF provides seasonal rainfall forecasts tailored for the main rainy season (JAS). The forecasts use tercile-based probabilities to categorize rainfall as below-average, near-average, or above-average (Figure 1). We use the WARCOF forecast maps from 1998 to 2017 archived by Pirret et al. (2020) and manually archived maps from 2018 to 2024 (see Supplementary Figures S1–S7). For each year, we digitized these tercile-based probabilities to create a consistent benchmark dataset for model comparison. Although WARCOF does not have a defined spatial resolution like gridded datasets, its outputs are represented as regional forecasts that can be interpreted spatially, reflecting variability across broader areas rather than specific grid cells. This dataset represents the initial standard against which the predictive skill is evaluated.

2.4 Seasonal prediction system from ECMWF

The fifth version of ECMWF's seasonal prediction system (SEAS5) is based on a medium-range atmospheric model integrated with ocean, sea ice, land, and wave models (Johnson et al., 2019). SEAS5, operational since November 2017, generates a 51-member ensemble, with hindcasts available from 1981 to 2016, consisting of 25 ensemble members initialized on the first of each month. The model data can be downloaded from the Climate Data Store of the Copernicus Climate Change Service in a horizontal resolution of 1° x 1°.

As a second benchmark, we use the total precipitation (TP) variable from the forecast system initialized from 1 May. We select all available grid points within the target domain (Figure 2) to obtain an areal average of the JAS rainfall sums. This average is then categorized into ordinal classes: below-average, near-average, and above-average conditions, similar to the CHIRPS preprocessing (Section 2.2) but using mean and standard deviation of the system itself. However, each ensemble member is categorized individually to create probabilities for each tercile-based category. The results can be found in Supplementary Table S2.

2.5 The CP-based logistic regression model

The CP-based logistic regression model employed here closely aligns with that outlined in Rauch et al. (2024) for reconstructing interannual rainfall anomalies in West Africa. The pre-selection of predictor variables (Table 1) in this study is based on existing literature, aligning with the studies by Moron et al. (2008), Guèye et al. (2011), Guèye et al. (2012), and Bliefernicht et al. (2022). To capture dominant regional-scale features of the West African Monsoon we use a domain spanning from 30°W to 40°E and 5°S to 40°N (see Figure 2). This domain covers most regions in Africa north of the equator, consistent with the domain size used by Bliefernicht et al. (2022). To maintain consistency with WARCOF, the forecast runs are initialized from 1 May from ECMWF SEAS5, and the JAS period is selected. For data preparation, standardized daily anomalies, denoted as z(i, t, e), were derived from the predictor data x(i, t, e) according to:

$\begin{array}{ll}z(i,t,e)=\frac{x(i,t,e)-\overline{x}(i)}{s(i)}& (1)\end{array}$

In this equation, i = 1, ..., L represents the grid points, t = 1, ..., T denotes the time steps in days, e = 1, ..., E indicates the ensemble members, $\overline{x}(i)$ signifies the long-term mean over time and all ensemble members, and s(i) indicates the standard deviation of the time series over time and all ensemble members. This standardized unfiltered daily anomalies are then used to generate daily CPs with cluster counts ranging from 5 to 15 using k-means, and the respective clusters' annual occurrence frequencies are computed for each ensemble individually. These frequencies serve as predictor variables in a multi-class logistic regression model. The predictants in this regression are the classes: below-average, near-average, and above-average conditions (as described in Section 2.2 and shown in Figure 4). The logistic regression model predicts the category of each rainfall condition for every ensemble, generating probabilistic forecasts similar to those used in WARCOF by assigning probabilities to each tercile-based category. Methodological details about the different components (e.g., k-means or logistic regression) and the general workflow can be found in Rauch et al. (2024).

Table 1

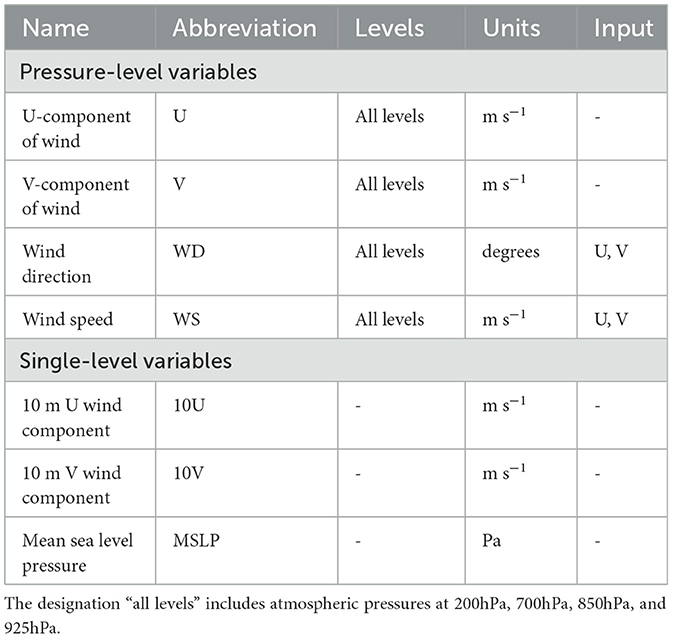
Table 1. Atmospheric variables from SEAS5, ECMWF: Listing of abbreviations, associated atmospheric pressures, units, and input variables for computation.

2.6 Validation and performance measures

The models are trained on the SEAS5 hindcast period (1981 to 2016) and validated using the operational forecast period (2017–2023). The RPSS is calculated separately for the training (t) and validation (v) periods using this split-sampling approach, with further analysis performed using multicategory reliability diagrams, and the economic value and comparisons made to WARCOF and the raw TP output from SEAS5. The evaluation measures are further explained in the subsequent sections.

2.6.1 Ranked probability skill score

To evaluate the performance of our proposed model, one key metric is the Ranked Probability Score (RPS), which is widely used for probabilistic forecast verification (Kumar et al., 2001; Christensen et al., 2015). The RPS evaluates the accuracy of probabilistic predictions by measuring the cumulative squared differences between the predicted and actual cumulative probabilities across all categories, as implemented by Wilks (2006). The formula for the RPS is given by:

$\begin{array}{ll}\text{RPS}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{k=1}^K}{\left(F_{i,k}-O_{i,k}\right)}^2& (2)\end{array}$

where N is the total number of forecasts, K is the number of cumulative categories (e.g., below, near-average, above), F_{i, k} represents the cumulative forecast probability for the i-th event up to and including category k, and O_{i, k} represents the cumulative observed outcome for the i-th event up to and including category k (1 if the event is in or below category k; 0 otherwise). A lower RPS indicates better forecast accuracy, reflecting a closer alignment between predicted probabilities and observed events.

To further assess the forecast skill, we calculate the Ranked Probability Skill Score (RPSS), which measures the performance of our forecasts relative to reference forecasts. The RPSS is computed as follows:

$\begin{array}{ll}\text{RPSS}=1-\frac{\text{RPS}}{{\text{RPS}}_{\text{ref}}}& (3)\end{array}$

where RPS_ref is the RPS of the reference forecast. An RPSS value greater than 0 indicates that the model outperforms the reference forecast, while a value of 1 indicates a perfect forecast.

In this study, we first calculate the RPS for two types of reference forecasts: a persistence forecast, which assumes that decadal variability strongly influences interannual rainfall variability, and a uniform distribution forecast, which assigns equal probabilities to each category (0.33, 0.33, 0.33) for each year. Given that the uniform distribution forecast has a lower RPS value (0.45 compared to 0.93 for the persistence forecast), indicating better baseline performance, we use it as the reference forecast for calculating the skill score.

While the RPSS provides a single metric of improvement over a reference forecast, additional diagnostic tools are required to understand the nature of the forecast errors. In the literature, reliability diagrams are often used to assess quality for seasonal forecast products to determine conditional biases in the forecast product (Mason and Chidzambwa, 2009; Bliefernicht et al., 2019; Pirret et al., 2020).

2.6.2 Multicategory reliability diagram

In this chapter, we extend the traditional reliability diagram to evaluate probabilistic forecasts using the Multicategory Reliability Diagram (MCRD; Hamill, 1997). This approach is particularly well-suited for multicategory forecasts and has been chosen for the following reasons: a conventional reliability diagram is typically applied to binary events (e.g., rain or no rain). However, seasonal rainfall forecasting often involves multiple categories. For this type of multicategory forecast, three separate diagrams would be needed to capture each class. If we focus solely on one specific class, the sample size may be too small to generate meaningful insights (potentially N/3 due to the tercile-based approach). Furthermore, WARCOF has already been extensively evaluated using traditional methods like reliability diagrams or receiver operating characteristics (Mason and Chidzambwa, 2009; Bliefernicht et al., 2019; Pirret et al., 2020). For the purpose of thoroughness, the traditional reliability diagrams have also been included in Supplementary Figures S8–S10.

The following explanations are strongly based on Hamill (1997) adapted to the tercile-based seasonal forecasting process. For each forecast season, the forecaster provides a probability vector predicting the likelihood that the seasonal rainfall will fall into one of three categories: below-average, near-average, or above-average rainfall. Let y_i = [y_i1, y_i2, y_i3] represent the forecasted probabilities for year i. For example, a forecast for a given year might look like y_i = [0.4, 0.4, 0.2], indicating a 40% probability of below-average rainfall, a 40% probability of near-average rainfall, and a 20% probability of above-average rainfall. To perform reliability analysis with a MCRD, we discretize the forecast probabilities into quantiles. Specifically, we divide the forecast probability space into preset quantiles: q ∈ {0.10, 0.20, 0.30, …, 0.90}. For each forecast y_i, the probability vector is transformed into a category vector z_i, which assigns forecast categories to each quantile. For example, for the forecast y_i = [0.4, 0.4, 0.2], the corresponding category vector would be z_i = [1, 1, 1, 1, 2, 2, 2, 2, 3, 3].

The calibration (or reliability) at a given quantile q, denoted as C_q, is defined as the probability that the observed rainfall category o_i is less than the forecast category $z_i^q$. This metric allows us to quantify how well the forecasted categories align with the actual observations across different quantiles. Formally, the calibration for a given quantile q is computed by averaging over all N forecast years as follows:

$\begin{array}{ll}{C}_q=\frac{1}{N}{\displaystyle \sum _{i=1}^N}P(o_i<z_i^q),& (4)\end{array}$

For any given year, one of three calibration scenarios will occur:

1. Observed category is less than the forecast category ($o_i<z_i^q$): The observed category is lower than the forecast category, so $P(o_i<z_i^q)=1$.

2. Observed category equals the forecast category ($o_i=z_i^q$): In this case, we interpolate between the minimum and maximum quantiles where the forecast and observed categories match. The calibration is determined using the following formula:

$\begin{array}{ll}P(o_i<z_i^q)=\frac{q-q_{\text{min}}}{q_{\text{max}}-q_{\text{min}}},& (5)\end{array}$

where q_min and q_max are the lowest and highest quantiles where $o_i=z_i^q$.

3. Observed category is greater than the forecast category ($o_i>z_i^q$): The observed category exceeds the forecast category, so $P(o_i<z_i^q)=0$.

For perfect calibration, C_q should equal the quantile q, meaning that, for example, 25% of observations should fall below the 25th percentile of the forecast distribution. The MCRD is generated by plotting C_q against q, with an uncertainty range representing the 95% confidence interval derived from bootstrap resampling, repeated 1,000 times.

In addition to the calibration plot, the MCRD includes a checkerboard plot that visualizes the mean absolute category error across quantiles. This helps identify systematic biases or inconsistencies in forecast performance. The checkerboard plot complements the calibration diagram by revealing sharpness and skill across the full range of potential outcomes. For instance, significant deviations between forecast and observed categories at certain quantiles could indicate overconfidence or underprediction in the probabilistic forecasts.

2.6.3 Economic value

Besides to forecast skill and quality, it is crucial to address the economic value of a forecast. Consider a decision maker who is concerned about a specific weather event, such as the forecast of rainfall falling into one of the defined tercile categories. For instance, the event A might be defined as “above-average” or “below-average” categories in a seasonal forecast. These forecasts are particularly significant for various sectors, where the amount of rainfall can have substantial economic and safety implications. If this unfavorable weather event occurs and no preventative measures are taken, the decision maker is expected to incur a loss L. The forecast is valuable only if it enables the decision maker to take action to reduce or avoid the potential loss. In this simplified scenario, the decision maker has two options: either continue with normal activities or take protective measures to mitigate the loss. Implementing such measures would incur an additional cost C beyond the usual expenses.

A deterministic binary forecasting system provides a straightforward yes/no prediction regarding the occurrence of a specific weather event A. The decision maker opts to take protective measures if the forecast indicates that event A will occur and takes no action if the forecast suggests otherwise. The usefulness of such forecasts for a series of past events can be evaluated by analyzing a contingency table compiled from those previous events (see Richardson, 2000; Wilks, 2001; Richardson, 2011; Bliefernicht et al., 2019; Portele et al., 2021 for further explanation and examples).

To compute the economic value V of the forecast, we first established the cost-loss ratio α = C/L, which represents the cost of taking preventive action divided by the potential loss incurred if the event occurs without any action. This ratio is critical as it quantifies the decision-maker's trade-off between the cost of action and the potential loss, influencing whether protective measures should be taken based on the forecast.

In probabilistic forecasts, for each probability threshold p_t, the hit rate H and false alarm rate F can be derived from a contingency table, reflecting the system's ability to correctly predict events. Here, a represents the number of correct predictions of the event occurring, b the false alarms, c the missed events, and d the correct predictions of the event not occurring. The total number of events observed, n, is n = a + b + c + d (Wilks, 2006).

The economic value V was then calculated using the following formula:

$\begin{array}{ll}V=\frac{min(\alpha ,s)-F·(1-s)·\alpha +H·s·(1-\alpha )-s}{min(\alpha ,s)-s·\alpha }& (6)\end{array}$

where $s=\frac{a+c}{n}$ represents the baseline probability (Richardson, 2011). The numerator reflects the difference between the benefits of the forecast (correct predictions adjusted for the cost-loss ratio) and the baseline probability, while the denominator normalizes this value by the baseline scenario without the forecast.

The value score ranges from −∞ to 1, where a score of 1 indicates perfect forecast performance and a score of 0 represents no added value over climatology. Negative values suggest that the forecast system is less effective than the climatological baseline, i.e., increase the decision-maker's costs compared to simply ignoring the forecast and using historical climatology.

3 Results

3.1 Ranked probability skill score

Table 2 presents the top three performing configurations of the CP-based logistic regression model based on the combined (RPSS_{t, v}) for both training and validation periods. The table also includes the RPSS for the training (RPSS_t, 1981-2016) and validation (RPSS_v, 2017-2023) periods, along with the number of CPs used. Benchmark results for WARCOF and the TP variable from SEAS5 are also shown. The WS925-based model, using 13 CPs, outperformed the other configurations with an RPSS_{t, v} of 0.233. It showed a good training performance (RPSS_t = 0.218) and reasonable validation skill (RPSS_v = 0.310). The WARCOF and SEAS5 TP benchmarks performed worse, with RPSS_{t, v} values of 0.070 and 0.039, respectively. These three solutions are further discussed and evaluated in the subsequent sections of this results section. It should be noted here that the WARCOF period is from 1998 to 2023, while the SEAS5 period is from 1981 to 2023, and thus they are not directly comparable.

Table 2

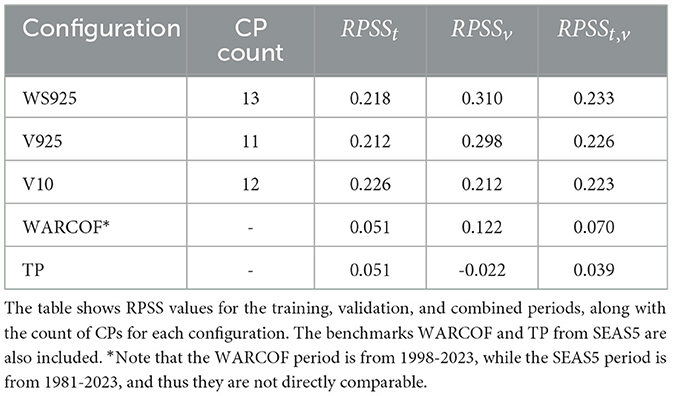
Table 2. Top three performing configurations of the CP-based logistic regression according to RPSS_t,v.

3.2 Multicategory reliability diagram

The performance of the probabilistic seasonal rainfall forecasts is further evaluated using a MCRD which is presented on the left-hand side of each row, with the corresponding checkerboard plots on the right-hand side (Figure 5). Each row represents the performance of one forecasting model: WARCOF model (top row, 1998–2023), SEAS5 TP dynamical model (middle row, 1981–2023), and CP-based logistic regression model (bottom row, 1981–2023).

Figure 5

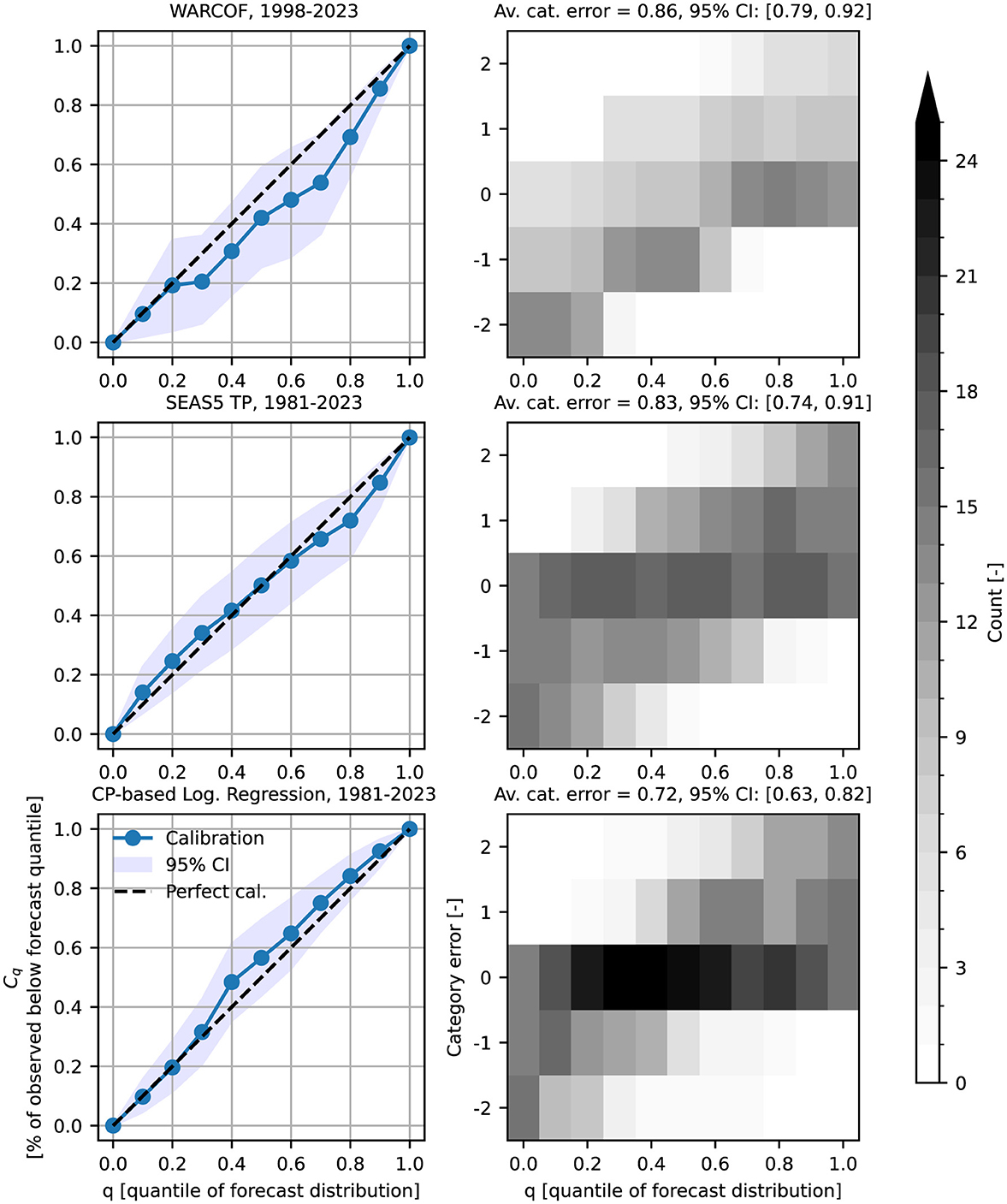
Figure 5. Multicategory reliability diagrams for WARCOF (1998-2023), SEAS5 TP (1981–2023), and CP-based logistic regression (1981–2023). The left column shows the observed frequency vs. forecast quantiles, with perfect calibration as the diagonal dashed line and 95% confidence interval (CI) shaded. The right column displays checkerboard plots of forecast errors, where darker shades indicate more accurate predictions (zero error).

The WARCOF forecasts exhibit good calibration at lower quantiles (below 0.20), where the predicted probabilities align closely with the observed frequencies. However, there is notable under-prediction between quantiles 0.20 and 0.90 (dry bias). This may be because forecasters often assign a higher probability to near-normal conditions to minimize the risk of incorrectly predicting one of the other two categories. This is also shown by Mason and Chidzambwa (2009), Bliefernicht et al. (2019), and Pirret et al. (2020). At higher quantiles (above 0.90), the forecasts again align well with observed frequencies. Overall, the calibration is low, with relatively narrow 95% confidence intervals in the lower and upper quantiles, though they widen slightly in the middle quantile range. The benchmark model exhibits a relatively broad spread of errors, particularly in the mid-quantiles (e.g., 0.30–0.70). A significant portion of forecasts remain near zero error (dark regions), though light shading at the top and bottom of the plot indicates that WARCOF sometimes predicts two categories away from the observed values, particularly for extreme quantiles. The average category error for WARCOF is 0.86 (95% CI: [0.79, 0.92]).

The SEAS5 TP model exhibits the best overall calibration, with a slight over-prediction in the lower quantiles (0.10–0.40) and under-prediction in the higher quantiles (above 0.60). The 95% confidence intervals are narrower than those for WARCOF, particularly in the mid-range quantiles, suggesting higher certainty. This may be attributed to the larger sample size, which provides more reliable estimates across the forecast distribution. SEAS5 TP shows slightly better performance in terms of categorical error compared to WARCOF. There is a larger concentration of darker shading near zero error, particularly in the mid-quantiles, indicating more frequent correct predictions in these ranges or just an error of one category. However, in the low and high quantiles, there is some spread, with errors of one or two categories being more frequent. The average category error for SEAS5 TP is 0.83 (95% CI: [0.74, 0.91]), representing a modest improvement over WARCOF.

The CP-based logistic regression model shows good calibration, particularly in the lower quantiles (up to 0.40), with slight over-prediction beyond this point. The confidence intervals are the narrowest of the three models, especially for mid-range quantiles (0.40–0.70). The CP-based logistic regression model shows the best performance in the category error, with the darkest regions concentrated around zero category error, especially in the mid-quantiles (0.20–0.60), where this model consistently performs well. Errors of two categories are rare, particularly in the mid-quantiles. The average category error for this model is the lowest, at 0.72 (95% CI: [0.63, 0.82]), indicating fewer category mismatches than the other models.

All three models show generally moderate to good calibration, with the SEAS5 TP model performing the best overall, followed by CP-based logistic regression, and then WARCOF. However, the CP-based model consistently provides more accurate category predictions, as indicated by the lower mean category error and clustered errors around zero. SEAS5 TP shows modest improvement over WARCOF which suffers from slightly larger deviations from perfect calibration and more frequent category mismatches, particularly in the mid-quantile range (0.20–0.80).

3.3 Value of the forecast system

Figure 6 presents a comparison of the economic values (V) for the three models across two rainfall categories: below-average and above-average. V is plotted against the cost-loss ratio, representing the trade-off faced by decision-makers between the cost of preventive measures and the potential loss incurred if no action is taken. On the vertical axis, economic value ranges from 0 to 1, with 1 indicating perfect forecast performance and 0 indicating no added value over climatology. The horizontal axis denotes the cost-loss ratio (α), where lower values suggest a relatively small cost of action compared to potential loss, and higher values indicate a higher relative cost.

Figure 6

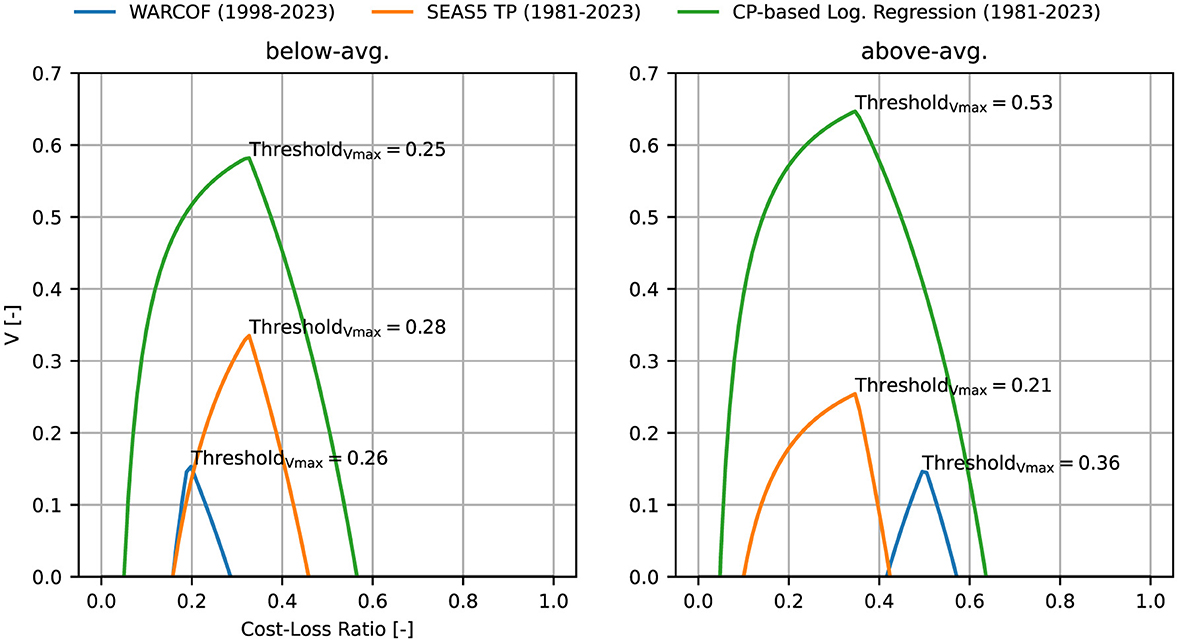
Figure 6. Economic value V as a function of the cost-loss ratio is shown for two rainfall categories below-average and above-average using the CP-based logistic regression, SEAS5 TP, and WARCOF at the threshold maximizing VV. The left panels correspond to “below-average” rainfall, while the right panels correspond to “above-average” rainfall.

Notably, V displayed for each model represent the maximum value obtained using the optimal forecast threshold. This optimal threshold is determined by evaluating a range of probability thresholds from 0.1 to 0.9 in increments of 0.01 (similar to Bliefernicht et al., 2019). This threshold optimization allows each model to be assessed under conditions most favorable for decision-making, ensuring the highest possible economic value. The following sections analyzes the performance at their respective optimal thresholds for each model.

The left panel of Figure 6 shows the results for below-average rainfall. The CP-based logistic regression model (green curve) achieves its maximum economic value at a probability threshold of 0.25, suggesting that preventive measures should be taken when the forecasted probability of below-average rainfall exceeds 25%. This model provides a broad range of positive economic values across the cost-loss ratio spectrum, indicating its usability in various decision-making contexts. In contrast, the SEAS5 TP model (orange curve) reaches its maximum economic value at a slightly higher threshold of 0.28, but its economic value declines rapidly as the cost-loss ratio increases, indicating limited applicability to specific scenarios. Similarly, the WARCOF model (blue curve) peaks at a threshold of 0.26, showing a narrow range of utility with diminishing economic value at higher cost-loss ratios.

The right panel of Figure 6 presents the results for above-average rainfall. Here, the CP-based logistic regression model outperforms the other models, with a maximum economic value at a threshold of 0.53. This higher threshold suggests that preventive actions are recommended only when there is greater confidence in the forecast (i.e., when the probability exceeds 53%). The model demonstrates robust performance, maintaining positive economic values across a wide range of cost-loss ratios, making it particularly suitable for high-cost scenarios. SEAS5 TP peaks at a threshold of 0.21, but, similar to its performance in the below-average category, its economic value declines sharply beyond this point, indicating effectiveness only within narrowly defined conditions. WARCOF performs best at a threshold of 0.36, yet exhibits a similarly narrow range of utility, especially at higher cost-loss ratios.

One key takeaway from this analysis is the crucial role of selecting the appropriate probability threshold to maximize the economic value of each forecasting model. The CP-based logistic regression model proves to be the most robust across both rainfall categories, maintaining positive economic values over a wider range of cost-loss ratios due to its higher optimal thresholds. This adaptability makes it suitable for various decision-making scenarios. In contrast, SEAS5 TP and WARCOF, while effective under specific conditions, show rapid declines in economic value as the cost-loss ratio increases. SEAS5 TP shows a sharp peak in economic value when the cost of action is low but diminishes quickly beyond its optimal threshold. Similarly, WARCOF offers utility primarily at lower thresholds and cost-loss ratios.

Furthermore, this analysis provides insights for decision-makers, where rainfall forecasts play a critical role. Understanding the relationship between probability thresholds, cost-loss ratios, and economic value helps optimize strategies for taking preventive action. The threshold selection process is crucial in guiding when action should be taken. For instance, using the CP-based logistic regression model, preventive measures are advisable if the forecasted probability of below-average rainfall exceeds 25%. This threshold reflects the point at which the benefits of action outweigh the costs. Lower thresholds, such as 0.25, support a more conservative approach, appropriate for risk-averse sectors like flood management or critical infrastructure. Higher thresholds, like 0.53 for above-average rainfall, suggest action should be taken only when there is greater confidence in the forecast, which may be more suitable for high-cost industries like large-scale agriculture, where unnecessary actions are expensive. Additionally, the cost-loss ratio provides another layer of decision-making support. A lower cost-loss ratio indicates that taking action is relatively inexpensive compared to potential losses, encouraging more frequent responses to forecasted events. Conversely, a higher cost-loss ratio suggests that preventive actions are more costly, necessitating selective decisions that rely on higher forecast confidence levels.

This section highlights the value of optimizing probability thresholds in rainfall forecasting models to maximize their economic usage. While the CP-based logistic regression model demonstrates robust performance across various scenarios, SEAS5 TP and WARCOF have more limited applications. These findings underscore the importance of context-specific decision-making in sectors reliant on accurate rainfall forecasting.

3.4 Summary of performance results

To provide an overview of each performance, we compared key evaluation metrics across the three prediction models (WARCOF, SEAS5 TP, and CP-based logistic regression) in Table 3 as a summary of RPSS, calibration, category error, and economic value (V_max) for below-average and above-average rainfall conditions. The CP-based logistic regression model demonstrated the highest RPSS, suggesting superior predictive accuracy over the other models. SEAS5 TP showed the best calibration overall, with a lower category error compared to WARCOF, but higher than the CP-based logistic regression model. In economic value analysis, the CP-based logistic regression model provided substantial advantages under conditions of below- and above-average rainfall, highlighting its effectiveness for decision-making applications.

Table 3

Table 3. Comparison of the three seasonal rainfall prediction models (WARCOF, SEAS5 TP, and CP-based logistic regression) across key performance metrics: Ranked Probability Skill Score (RPSS), calibration quality, category error, and maximum economic value (V_max) for below-average and above-average rainfall scenarios.

3.5 The CP-based logistic regression model

Given the necessity of not only achieving strong forecast evaluation scores but also ensuring a model's reliability and meaningfulness in terms of statistical downscaling, it is crucial to establish a robust connection between large-scale atmospheric patterns and the target variable, in this case, the rainfall categories derived through the logistic regression model. Therefore, Figure 7 shows the composites of the spatial CPs derived from WS925 anomalies (the best model, Table 2), which signify changes in wind speed in the lower troposphere, around an altitude of 700–800 m. These changes are often associated with variations in the upper-air wind patterns. The monsoon winds at 925 hPa are generally southwesterly during the monsoon season (approximately June to September) (see Figure 1.19 from Fink et al., 2017), bringing moisture-laden air from the Gulf of Guinea into the interior of West Africa (Lélé et al., 2015). This low-level flow is a key component of the monsoon system and is strongly correlated with rainfall (Janicot and Sultan, 2001; Thorncroft et al., 2011).

Figure 7

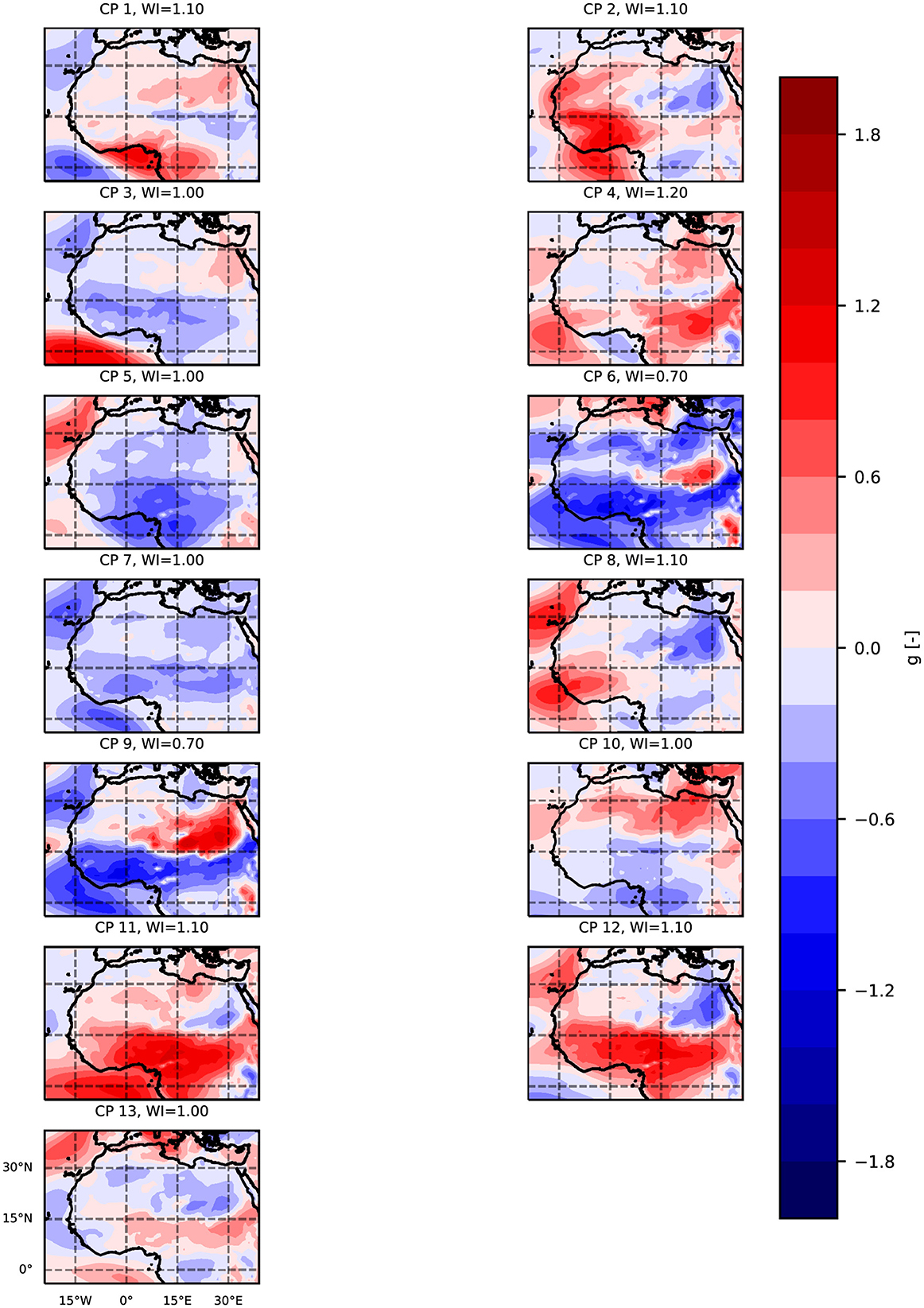
Figure 7. Atmospheric CPs for the WS925 variable as the chosen solution for the CP-based logistic regression model. The color scale signifies the mean intensity of the measured variable, where red and blue shades represent positive and negative anomalies, respectively. The Wetness Index (WI) [-] is defined as the ratio of the conditional rainfall amount of a CP to the unconditional rainfall amount for the studied period.

This relationship is also reflected in our analysis of CPs. Specifically, CPs exhibiting strong positive anomalies in the region from 0° to 15°N, where southwesterly winds typically occur, are associated with wetter-than-average conditions (WI > 1),¹ as seen in CP11 and CP12. This suggests an increase in wind speeds, which in turn enhances the southwesterly flow. Conversely, CPs characterized by strong negative anomalies in this region, such as CP6 and CP9, are associated with drier-than-average conditions (WI < 1). This indicates a decrease in wind speeds, leading to a slowdown of the southwesterlies. The association between these wind patterns and rainfall outcomes may explains these CPs as reasonable predictors for categorizing rainfall as below or above average in the context of seasonal forecasting.

The findings from the logistic regression model further support this hypothesis (Figure 8). The purpose of these coefficients is to measure the likelihood of each CP occurring under specific categories, thereby providing a foundation for understanding their sensitivity in terms of seasonal rainfall forecasting. For CP11 and CP12, the coefficients are positive during wet years (0.15 and 0.20, respectively) but negative during dry years (-0.15 for CP12), aligning with the observed occurrence of these CPs. This suggests that these patterns play a role in enhancing rainfall when they indicate an increase in the southwesterly flow. In contrast, for CP6 and CP9, the model indicates positive coefficients during dry years (0.23 for CP6 and 0.11 for CP9) and negative coefficients during wet years (-0.20 for CP6 and -0.15 for CP9). This behavior underscores their role in the suppression of rainfall, indicating how reduced wind speeds in these patterns correlate with drier conditions. CP4 and CP8 present more neutral roles, with CP4 showing a slightly positive coefficient in wet years (0.06) and negative in dry years (-0.19), while CP8 has relatively small coefficients in both categories (-0.10 for dry and 0.07 for wet). This suggests a context-dependent influence, potentially modulated by other atmospheric factors not directly captured in this model.

Figure 8

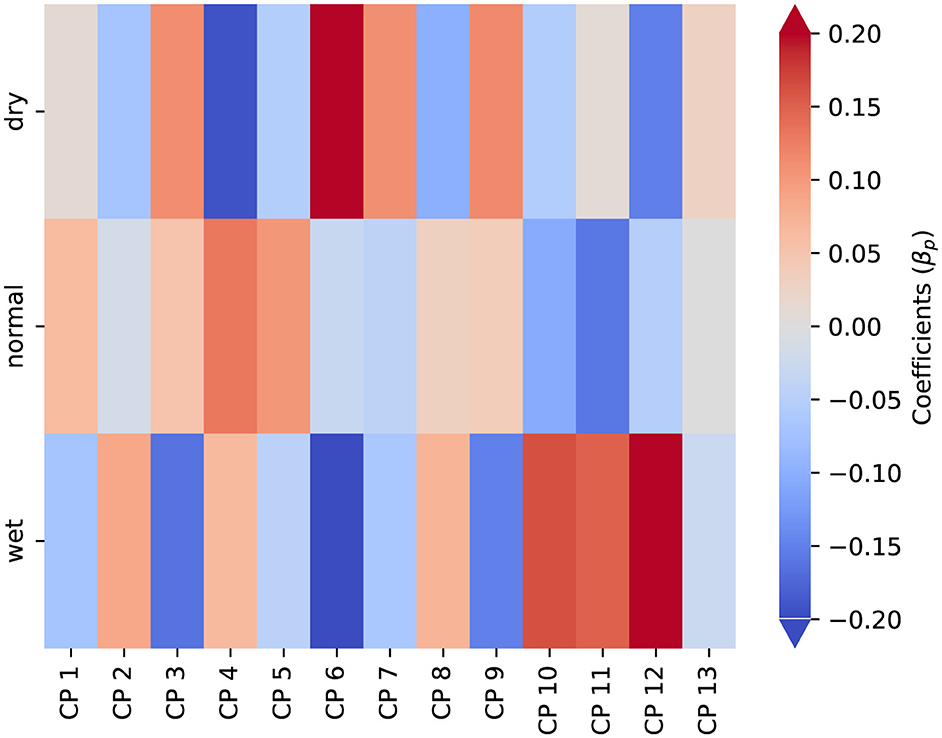
Figure 8. Heat map of coefficients from the multi-class logistic regression model. The color coding indicates the importance of each CP for dry, normal, or wet years.

These results underline the importance of incorporating atmospheric dynamics into the statistical downscaling process. The associations between near-surface wind patterns, and rainfall outcomes validate the use of the logistic regression model, emphasizing its ability to capture the physical mechanisms underlying rainfall variability in the region. This insight enhances the predictive capability of the model, making it not only statistically reliable but also meaningful in a meteorological context.

4 Discussion

This study presents an evaluation of probabilistic seasonal rainfall forecasts for the Sudan-Sahel region using three models: WARCOF, SEAS5 TP, and a CP-based logistic regression model. As highlighted, seasonal rainfall variability poses significant risks to agriculture and water resource management in the Sudan-Sahel region, making accurate predictions critical for mitigating adverse impacts. The results from this study provide valuable insights into the performance of these models, showcasing their potential for improving forecast accuracy and decision-making in vulnerable sectors.

The CP-based logistic regression model demonstrated the best overall performance, particularly in terms of category error and economic value. This model is based on WS925 anomalies, which are strongly associated with southwesterly monsoon winds that influence moisture transport from the Gulf of Guinea, a key atmospheric process driving rainfall variability in the region (Janicot and Sultan, 2001; Thorncroft et al., 2011; Lélé et al., 2015). By integrating these physically meaningful predictors, the CP-based logistic regression model captures essential large-scale CPs, allowing it to provide more accurate and reliable rainfall forecasts. This aligns with the aim to develop models that improve forecast reliability through the integration of robust atmospheric processes.

The calibration evaluation with the MCRD analysis further underscores the usability of all three forecasting products for seasonal rainfall forecasting. However, the lower average category error and stronger performance in the economic value analysis of the CP-based logistic regression model indicate that it provides more accurate predictions than the other models. This improvement in category error aligns with the goals mentioned in previous studies (e.g., Pirret et al., 2020), which stressed the need for enhancing the sharpness and reliability of seasonal forecasts in West Africa. The economic value analysis reveals that the CP-based model maintains a broader range of positive economic value across different cost-loss ratios, making it adaptable to a variety of decision-making contexts. This adaptability is crucial for sectors dependent on rainfall, where the ability to tailor forecasts to different risk thresholds can reduce economic losses.

One key aspect affecting model performance is the difference in temporal coverage between the models. The CP-based logistic regression model and SEAS5 TP cover the period 1981-2023, whereas WARCOF covers the shorter period of 1998–2023. This difference in dataset length makes direct comparisons between these models more challenging, as the longer time period likely contributes to the narrower confidence intervals in SEAS5 TP and the CP-based model, given that a larger sample size typically enhances forecast reliability. Nevertheless, this study builds upon and extends previous analyses of WARCOF, incorporating additional evaluation tools such as the MCRD for recent time periods (Mason and Chidzambwa, 2009; Bliefernicht et al., 2019; Pirret et al., 2020). The detection of a dry bias in WARCOF is consistent with prior studies and may also be attributed to forecasters' risk aversion and biases toward near-normal conditions.

Despite the strengths of the CP-based logistic regression model, it is important to acknowledge certain limitations. One key limitation is the model's wet bias, which may reduce its ability to accurately predict droughts and lead to an overestimation of wetter-than-average years. Given the vulnerability of the Sudan-Sahel region to both drought and excess rainfall, a bias toward wet conditions could negatively impact drought management strategies. This bias might reduce the model's effectiveness for sectors like agriculture, where underestimating dry conditions could result in insufficient preparation for crop failures or water shortages. Addressing this wet bias is crucial for building resilience in the region (Mertz et al., 2012; Wilhite et al., 2007).

To mitigate the wet bias and further improve the model's accuracy, additional predictors could be incorporated. For instance, integrating sea surface temperatures (Fontaine and Bigot, 1993; Losada et al., 2010) or higher-level wind fields, such as the 200 hPa wind fields as an indicator of the tropical easterly jet (Nicholson and Klotter, 2021) and the 700 hPa wind fields as indicators of African easterly waves or the African easterly jet (Bliefernicht et al., 2022), could enhance the model's ability to forecast both extremes of rainfall variability. These additional predictors would likely improve the model's representation of atmospheric processes that drive both drought and excessive rainfall in the region, thereby reducing prediction errors.

One limitation of this study is the use of CHIRPS rainfall data as a reference dataset instead of relying directly on ground-based observations. Although CHIRPS has been validated in numerous studies and generally shows good performance compared to ground-based observations (e.g., Garba et al., 2023; Didi et al., 2020), it is known to underestimate or overestimate rainfall extremes in certain regions (e.g., Diedhiou et al., 2024). By treating CHIRPS as directly observed data, this study inherits biases that could affect the accuracy of model performance evaluations. Despite these limitations, CHIRPS remains an invaluable resource for regional-scale analyses due to its consistency, spatiotemporal coverage, and suitability for operational frameworks in data-scarce regions like the Sudan-Sahel.

While the CP-based logistic regression model shows promise, further research is needed to test its applicability in other regions, such as the Sahel or Guinea zones. Expanding the model to different geographic contexts would allow for a better understanding of how effective it is in regions with different climatic drivers. Moreover, this statistical downscaling approach could benefit from the application of more advanced techniques like deep learning, which have shown potential in capturing non-linear relationships between atmospheric predictors and rainfall variability (Pan et al., 2022; Patil et al., 2023; Dotse, 2024). For instance, Glawion et al. (2023) presents a promising spatio-temporal downscaling approach using a cGAN method, which could enhance the predictive skill of seasonal rainfall forecasts. Furthermore, additional aspects of rainfall variability beyond seasonal totals should also be addressed. Parameters such as the onset and offset of the rainy season, dry spells during critical growth stages, and extreme events like heatwaves are equally important for stakeholders, especially in agricultural planning and disaster preparedness. Including these parameters would make the model more comprehensive and better suited to the needs of end users.

However, the simplicity of statistical downscaling methods like CP classification in combination with logistic regression makes them accessible and computationally efficient, particularly for operational use in developing countries. These advantages should not be overlooked when considering model improvements, but integrating more complex techniques may further enhance model performance and accuracy.

5 Conclusion

This study advances seasonal rainfall prediction for West Africa by applying the statistical downscaling method developed by Rauch et al. (2024), using a logistic regression model based on atmospheric CPs. Building on the findings of Mason and Chidzambwa (2009), Bliefernicht et al. (2019), and Pirret et al. (2020), this research offers an updated assessment of WARCOF and SEAS5 from ECMWF, providing new insights into the strengths and limitations of these models in predicting rainfall variability in the Sudan-Sahel region.

The results demonstrate that, while each of the models evaluated (WARCOF, SEAS5 TP, and the CP-based logistic regression model) has distinct strengths, the CP-based model shows the greatest potential for interannual rainfall prediction. This novel approach effectively links southwesterly monsoon winds to rainfall variability, providing a robust statistical downscaling framework that captures the key physical mechanisms driving precipitation variability in the region.

Calibration analysis based on a multicategory reliability diagram (Hamill, 1997) revealed that although all models perform moderately well, the SEAS5 TP model showed the best overall calibration, followed by the CP-based model and then WARCOF. However, each model suffers from biases: WARCOF demonstrates a dry bias, SEAS5 TP exhibits both dry and wet biases, and the CP-based model also has also a wet bias. Notably, the CP-based model consistently delivers more accurate category predictions, with lower mean category errors and tighter error distributions around zero. This makes it a more robust option compared to WARCOF, which exhibits larger deviations from perfect calibration, especially in the mid-quantile range. The economic value analysis further supports the potential of the CP-based model, particularly across a broader range of cost-loss ratios and optimal thresholds. While SEAS5 TP and WARCOF may be suitable for more narrowly defined decision-making contexts, the CP-based model offers greater versatility, providing decision-makers with a more reliable tool for balancing cost and risk.

Furthermore, the CP-based model provides significant potential to enhance existing forecasting frameworks like WARCOF. While WARCOF has traditionally relied on subjective expert judgment and reinterpretation of statistical and global forecasts (Bliefernicht et al., 2019), the CP-based logistic regression model offers an objective, physically-grounded alternative. By integrating this model into the WARCOF framework, stakeholders like farmers and policymakers could benefit from more actionable and reliable forecasts. Farmers, for instance, could use these enhanced forecasts for improved planning of planting schedules and irrigation strategies, while policymakers could leverage the outputs for disaster preparedness and resource allocation. This integration represents a key step toward addressing the need for more objective methodologies in seasonal forecasting (Pirret et al., 2020).

In conclusion, this study lays a strong foundation for further enhancing seasonal forecasting in West Africa. The improved accuracy and economic value demonstrated by the CP-based logistic regression model highlight its potential as a reliable forecasting tool, capable of supporting more informed and impactful decision-making. As forecasting tools continue to evolve, the development of adaptable, region-specific models will be key to improving resilience against climate variability in the region.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MR: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Visualization, Writing – original draft, Writing – review & editing. JB: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Writing – original draft, Writing – review & editing. WS: Writing – original draft, Writing – review & editing. SS: Writing – original draft, Writing – review & editing. MW: Writing – original draft, Writing – review & editing. HK: Funding acquisition, Project administration, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was part of the FURIFLOOD (Current and future risks of urban and rural flooding in West Africa) project, which was funded by the Federal Ministry of Education and Research in Germany (grant number: 01LG2086A).

Acknowledgments

We would like to thank our partners involved in the FURIFLOOD project for their invaluable support over the past three years. We also thank the editor and the two reviewers for their helpful comments that improved the quality of the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. Chat-GPT was used for grammar and spell checking.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2024.1523898/full#supplementary-material

Footnotes

1. ^Wetness Index (WI): Ratio of CP-specified rainfall to the long-term average.

References

ACMAD (2022). Regional Climate Outlook Forum for Sudano-Sahelian Region (Presass 9). Available at: https://acmad.org/index.php/regional-climate-outlook-forum-for-sudano-sahelian-regionpresass-9/

Google Scholar

Bliefernicht, J., Rauch, M., Laux, P., and Kunstmann, H. (2022). Atmospheric circulation patterns that trigger heavy rainfall in West Africa. Int. J. Climatol. 42, 6515–6536. doi: 10.1002/joc.7613

Crossref Full Text | Google Scholar

Bliefernicht, J., Waongo, M., Salack, S., Seidel, J., Laux, P., and Kunstmann, H. (2019). Quality and value of seasonal precipitation forecasts issued by the West African Regional Climate Outlook Forum. J. Appl. Meteorol. Climatol. 58, 621–642. doi: 10.1175/JAMC-D-18-0066.1

PubMed Abstract | Crossref Full Text | Google Scholar

Christensen, H. M., Moroz, I. M., and Palmer, T. N. (2015). Evaluation of ensemble forecast uncertainty using a new proper score: application to medium–range and seasonal forecasts. Q. J. R. Meteorol. Soc. 141, 538–549. doi: 10.1002/qj.2375

Crossref Full Text | Google Scholar

Coly, S. M., Zorom, M., Leye, B., Guiro, A., and Karambiri, H. (2024). Assessing climate change vulnerability and livelihood strategies in Burkina Faso including insecurity paradigm: a focus on rain-fed agriculture households. Environ Dev Sustain (2024). doi: 10.1007/s10668-024-05442-3

Crossref Full Text | Google Scholar

Dembélé, M., and Zwart, S. J. (2016). Evaluation and comparison of satellite-based rainfall products in Burkina Faso, West Africa. Int. J. Remote Sens. 37, 3995–4014. doi: 10.1080/01431161.2016.1207258

Crossref Full Text | Google Scholar

Descroix, L., Guichard, F., Grippa, M., Lambert, L., Panthou, G., Mahé, G., et al. (2018). Evolution of surface hydrology in the sahelo-sudanian strip: an updated review. Water 10:748. doi: 10.3390/w10060748

Crossref Full Text | Google Scholar

Didi, S. R. M., Mouhamed, L., Kouakou, K., Adeline, B., Arona, D., Houebagnon Saint, J., et al. (2020). Using the CHIRPS dataset to investigate historical changes in precipitation extremes in West Africa. Climate 8:84. doi: 10.3390/cli8070084

Crossref Full Text | Google Scholar

Diedhiou, S., Rauch, M., Dieng, A. L., Bliefernicht, J., Sy, S., Sall, S. M., et al. (2024). Extreme rainfall in Dakar (Senegal): a case study for September 5, 2020. Front. Water 6:1439404. doi: 10.3389/frwa.2024.1439404

Crossref Full Text | Google Scholar

Dotse, S.-Q. (2024). Deep learning-based long short-term memory recurrent neural networks for monthly rainfall forecasting in Ghana, West Africa. Theoret. Appl. Climatol. 155, 3033–3045. doi: 10.1007/s00704-023-04773-x

Crossref Full Text | Google Scholar

Fink, A. H., Engel, T., Ermert, V., van der Linden, R., Schneidewind, M., Redl, R., et al. (2017). “Mean climate and seasonal cycle,” in Meteorology of Tropical West Africa (Hoboken, NJ: Wiley), 1–39.

Google Scholar

Fontaine, B., and Bigot, S. (1993). West African rainfall deficits and sea surface temperatures. Int. J. Climatol. 13, 271–285. doi: 10.1002/joc.3370130304

PubMed Abstract | Crossref Full Text | Google Scholar

Funk, C., Peterson, P., Landsfeld, M., Pedreros, D., Verdin, J., Shukla, S., et al. (2015). The climate hazards infrared precipitation with stations-a new environmental record for monitoring extremes. Scientific Data 2, 1–21. doi: 10.1038/sdata.2015.66

PubMed Abstract | Crossref Full Text | Google Scholar

Garba, J. N., Diasso, U. J., Waongo, M., Sawadogo, W., and Daho, T. (2023). Performance evaluation of satellite-based rainfall estimation across climatic zones in Burkina Faso. Theor Appl Climatol. 154, 1051–1073. doi: 10.1007/s00704-023-04593-z

Crossref Full Text | Google Scholar

Glawion, L., Polz, J., Kunstmann, H., Fersch, B., and Chwala, C. (2023). spateGAN: spatio-temporal downscaling of rainfall fields using a cGAN approach. Earth Space Sci. 10:10. doi: 10.1029/2023EA002906

Crossref Full Text | Google Scholar

Guèye, A. K., Janicot, S., Niang, A., Sawadogo, S., Sultan, B., Diongue-Niang, A., et al. (2011). Weather regimes over Senegal during the summer monsoon season using self-organizing maps and hierarchical ascendant classification. Part I: synoptic time scale. Clim. Dynam. 36, 1–18. doi: 10.1007/s00382-010-0782-6

Crossref Full Text | Google Scholar

Guèye, A. K., Janicot, S., Niang, A., Sawadogo, S., Sultan, B., Diongue-Niang, A., et al. (2012). Weather regimes over Senegal during the summer monsoon season using self-organizing maps and hierarchical ascendant classification. Part II: Interannual time scale. Clim. Dynam. 39, 2251–2272. doi: 10.1007/s00382-012-1346-8

Crossref Full Text | Google Scholar

Hagos, S. M., and Cook, K. H. (2008). Ocean warming and late-twentieth-century sahel drought and recovery. J. Clim. 21, 3797–3814. doi: 10.1175/2008JCLI2055.1

PubMed Abstract | Crossref Full Text | Google Scholar

Hamill, T. M. (1997). Reliability diagrams for multicategory probabilistic forecasts. Weather Forecast. 12, 736–741.

Google Scholar

Hao, Z., Singh, V. P., and Xia, Y. (2018). Seasonal drought prediction: advances, challenges, and future prospects. Rev. Geophys. 56, 108–141. doi: 10.1002/2016RG000549

Crossref Full Text | Google Scholar

Houngnibo, M. C. M., Minoungou, B., Traore, S. B., Maidment, R. I., Alhassane, A., and Ali, A. (2023). Validation of high-resolution satellite precipitation products over West Africa for rainfall monitoring and early warning. Front. Clim. 5:1185754. doi: 10.3389/fclim.2023.1185754

Crossref Full Text | Google Scholar

Janicot, S., and Sultan, B. (2001). Intra-seasonal modulation of convection in the West African Monsoon. Geophys. Res. Lett. 28, 523–526. doi: 10.1029/2000GL012424

Crossref Full Text | Google Scholar

Johnson, S. J., Stockdale, T. N., Ferranti, L., Balmaseda, M. A., Molteni, F., Magnusson, L., et al. (2019). SEAS5: the new ECMWF seasonal forecast system. Geosci. Model Dev. 12, 1087–1117. doi: 10.5194/gmd-12-1087-2019

Crossref Full Text | Google Scholar

Klein, C., Heinzeller, D., Bliefernicht, J., and Kunstmann, H. (2015). Variability of West African monsoon patterns generated by a WRF multi-physics ensemble. Clim. Dynam. 45, 2733–2755. doi: 10.1007/s00382-015-2505-5

Crossref Full Text | Google Scholar

Kouakou, C., Paturel, J. E., Satgé, F., Tramblay, Y., Defrance, D., and Rouché, N. (2023). Comparison of gridded precipitation estimates for regional hydrological modeling in West and Central Africa. J. Hydrol. 47:101409. doi: 10.1016/j.ejrh.2023.101409

Crossref Full Text | Google Scholar

Kumar, A., Barnston, A. G., and Hoerling, M. P. (2001). Seasonal predictions, probabilistic verifications, and ensemble size. J. Clim. 14, 1671–1676. doi: 10.1175/1520-0442(2001)014%3C1671:SPPVAE%3E2.0.CO;2

Crossref Full Text | Google Scholar

Lélé, M. I., Leslie, L. M., and Lamb, P. J. (2015). Analysis of low-level atmospheric moisture transport associated with the West African Monsoon. J. Clim. 28, 4414–4430. doi: 10.1175/JCLI-D-14-00746.1

PubMed Abstract | Crossref Full Text | Google Scholar

Lorenz, M., Bliefernicht, J., Haese, B., and Kunstmann, H. (2018). Copula-based downscaling of daily precipitation fields. Hydrol. Process. 32, 3479–3494. doi: 10.1002/hyp.13271

Crossref Full Text | Google Scholar

Losada, T., Rodríguez-Fonseca, B., Janicot, S., Gervois, S., Chauvin, F., and Ruti, P. (2010). A multi-model approach to the Atlantic Equatorial mode: impact on the West African monsoon. Clim. Dynam. 35, 29–43. doi: 10.1007/s00382-009-0625-5

Crossref Full Text | Google Scholar

Manzanas, R. (2017). Assessing the suitability of statistical downscaling approaches for seasonal forecasting in Senegal. Atmosph. Sci. Lett. 18, 381–386. doi: 10.1002/asl.767

Crossref Full Text | Google Scholar

Mason, S., and Chidzambwa, S. (2009). “Position paper: verification of African RCOF forecasts,” in IRI Technical Report (International Research Institute for Climate and Society).

Google Scholar

Mertz, O., D'haen, S., Maiga, A., Moussa, I. B., Barbier, B., Diouf, A., et al. (2012). Climate variability and environmental stress in the Sudan-Sahel Zone of West Africa. Ambio 41, 380–392. doi: 10.1007/s13280-011-0231-8

PubMed Abstract | Crossref Full Text | Google Scholar

Moron, V., Robertson, A. W., Ward, M. N., and Ndiaye, O. (2008). Weather types and rainfall over Senegal. Part I: observational analysis. J. Clim. 21, 266–287. doi: 10.1175/2007JCLI1601.1

PubMed Abstract | Crossref Full Text | Google Scholar

Ndiaye, O., Ward, M. N., and Thiaw, W. M. (2011). Predictability of seasonal sahel rainfall using GCMs and lead-time improvements through the use of a coupled model. J. Clim. 24, 1931–1949. doi: 10.1175/2010JCLI3557.1

PubMed Abstract | Crossref Full Text | Google Scholar

Nicholson, S. E., and Klotter, D. (2021). The Tropical Easterly Jet over Africa, its representation in six reanalysis products, and its association with Sahel rainfall. Int. J. Climatol. 41, 328–347. doi: 10.1002/joc.6623

Crossref Full Text | Google Scholar

Nouaceur, Z., and Murarescu, O. (2020). Rainfall variability and trend analysis of rainfall in West Africa (Senegal, Mauritania, Burkina Faso). Water 12:1754. doi: 10.3390/w12061754

Crossref Full Text | Google Scholar

Paeth, H., Fink, A. H., Pohle, S., Keis, F., Mächel, H., and Samimi, C. (2011). Meteorological characteristics and potential causes of the 2007 flood in sub-Saharan Africa. Int. J. Climatol. 31, 1908–1926. doi: 10.1002/joc.2199

PubMed Abstract | Crossref Full Text | Google Scholar

Paeth, H., Paxian, A., Sein, D. V., Jacob, D., Panitz, H.-J., Warscher, M., et al. (2017). Decadal and multi-year predictability of the West African monsoon and the role of dynamical downscaling. Meteorologische Zeitschrift 26, 363–377. doi: 10.1127/metz/2017/0811

PubMed Abstract | Crossref Full Text | Google Scholar

Pan, B., Anderson, G. J., Goncalves, A., Lucas, D. D., Bonfils, C. J. W., and Lee, J. (2022). Improving seasonal forecast using probabilistic deep learning. J. Adv. Model. Earth Syst. 14:2766. doi: 10.1029/2021MS002766

Crossref Full Text | Google Scholar

Patil, K. R., Doi, T., and Behera, S. K. (2023). Predicting extreme floods and droughts in East Africa using a deep learning approach. NPJ Clim. Atmosph. Sci. 6:108. doi: 10.1038/s41612-023-00435-x

Crossref Full Text | Google Scholar

Pirret, J. S. R., Daron, J. D., Bett, P. E., Fournier, N., and Foamouhoue, A. K. (2020). Assessing the skill and reliability of seasonal climate forecasts in Sahelian West Africa. Weather Forecast. 35, 1035–1050. doi: 10.1175/WAF-D-19-0168.1

PubMed Abstract | Crossref Full Text | Google Scholar

Polasky, A., Evans, J. L., and Fuentes, J. D. (2024). Statistical downscaling for precipitation projections in West Africa. Theoret. Appl. Climatol. 155, 327–347. doi: 10.1007/s00704-023-04637-4

Crossref Full Text | Google Scholar

Portele, T. C., Lorenz, C., Dibrani, B., Laux, P., Bliefernicht, J., and Kunstmann, H. (2021). Seasonal forecasts offer economic benefit for hydrological decision making in semi-arid regions. Sci. Rep. 11:10581. doi: 10.1038/s41598-021-89564-y

PubMed Abstract | Crossref Full Text | Google Scholar

Rauch, M., Bliefernicht, J., Laux, P., Salack, S., Waongo, M., and Kunstmann, H. (2019). Seasonal forecasting of the onset of the rainy season in West Africa. Atmosphere 10:528. doi: 10.3390/atmos10090528

Crossref Full Text | Google Scholar

Rauch, M., Bliefernicht, J., Maranan, M., Fink, A. H., and Kunstmann, H. (2024). Interannual rainfall variability in west africa: reconstruction based on atmospheric circulation patterns. Int. J. Climatol. doi: 10.5281/zenodo.14046484

Crossref Full Text | Google Scholar

Richardson, D. S. (2000). Skill and relative economic value of the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 126, 649–667. doi: 10.1256/smsqj.56312

Crossref Full Text | Google Scholar

Richardson, D. S. (2011). “Economic value and skill,” in Forecast Verification (Hoboken, NJ: Wiley), 167–184.

Google Scholar

Semazzi, F. (2011). Framework for climate services in developing countries. Clim. Res. 47, 145–150. doi: 10.3354/cr00955

Crossref Full Text | Google Scholar

Siabi, E. K., Kabobah, A. T., Akpoti, K., Anornu, G. K., Amo-Boateng, M., and Nyantakyi, E. K. (2021). Statistical downscaling of global circulation models to assess future climate changes in the Black Volta basin of Ghana. Environm. Challen. 5:100299. doi: 10.1016/j.envc.2021.100299

Crossref Full Text | Google Scholar

Siegmund, J., Bliefernicht, J., Laux, P., and Kunstmann, H. (2015). Toward a seasonal precipitation prediction system for West Africa: Performance of CFSv2 and high–resolution dynamical downscaling. J. Geophys. Res.: Atmosph. 120, 7316–7339. doi: 10.1002/2014JD022692

Crossref Full Text | Google Scholar

Thorncroft, C. D., Nguyen, H., Zhang, C., and Peyrillé, P. (2011). Annual cycle of the West African monsoon: regional circulations and associated water vapour transport. Q. J. R. Meteorol. Soc. 137, 129–147. doi: 10.1002/qj.728

Crossref Full Text | Google Scholar

Weigel, A. P., Liniger, M. A., and Appenzeller, C. (2007). The discrete brier and ranked probability skill scores. Monthly Weather Rev. 135, 118–124. doi: 10.1175/MWR3280.1

PubMed Abstract | Crossref Full Text | Google Scholar

Wilhite, D. A., Svoboda, M. D., and Hayes, M. J. (2007). Understanding the complex impacts of drought: A key to enhancing drought mitigation and preparedness. Water Resour. Managem. 21, 763–774. doi: 10.1007/s11269-006-9076-5

Crossref Full Text | Google Scholar

Wilks, D. (2006). Statistical Methods in the Atmospheric Sciences. Amsterdam: Elsevier.

Google Scholar

Wilks, D. S. (2001). A skill score based on economic value for probability forecasts. Meteorol. Appl. 8, 209–219. doi: 10.1017/S1350482701002092

Crossref Full Text | Google Scholar

Yengoh, G. (2012). Climate and food production: understanding vulnerability from past trends in Africa's Sudan-Sahel. Sustainability 5:52–71. doi: 10.3390/su5010052

Crossref Full Text | Google Scholar

Zampaligré, N., Dossa, L. H., and Schlecht, E. (2014). Climate change and variability: perception and adaptation strategies of pastoralists and agro-pastoralists across different zones of Burkina Faso. Regional Environm. Change 14, 769–783. doi: 10.1007/s10113-013-0532-5

Crossref Full Text | Google Scholar