An effect of a snow cover on solar heating and melting of lake or sea ice

Solar radiative heating and melting of lake and sea ice is a geophysical problem that has attracted the attention of researchers for many years. This problem is important in connection with the current global change of the climate. Physical and computational models of the process are suggested in the paper. Analytical solutions for the transfer of solar radiation in light-scattering snow cover and ice are combined with numerical calculations of heat transfer in a multilayer system. The thermal boundary conditions take into account convective heat losses to the ambient air and radiative cooling in the mid-infrared window of transparency of the cloudless atmosphere. The study begins with an anomalous spring melting of ice on the large high-mountain lakes of Tibet. It was found that a thick ice layer not covered with snow starts to melt at the ice-water interface due to volumetric solar heating of ice. The results of the calculations are in good agreement with the field observations. The computational analysis showed a dramatic change in the process when the ice is covered with snow. A qualitative change in the physical picture of the process occurs when the snow cover thickness increases to 20–30 cm. In this case, the snow melting precedes ice melting and water ponds are formed on the ice surface. This is typical for the Arctic Sea in polar summer. Known experimental data are used to estimate the melting of sea ice under the melt pond. Positive or negative feedback related to the specific optical and thermal properties of snow, ice, and water are discussed.

Introduction

This paper presents a general approach to solving geophysical problems related to solar heating and the melting of ice on the water surface. The spring melting of lake ice is a relatively simple problem and this will be considered in more detail. After that, a general view of the more complex problem of melting of sea ice during the polar summer will be discussed. Ice melting on the Arctic Sea surface is really important for global climate change. What is less well known is that the opening from the ice of high-mountain lakes in Tibet, sometimes referred to as the Earth’s third pole, significantly affects the climate of not only central Asia. Recall that the Tibetan Plateau is home to about a thousand large lakes with a total area of about 15,000 km² (Su et al., 2020; Zhang and Duan, 2021). Interestingly, the early opening time of these lakes is an indicator of global warming (Su et al., 2019; Zhang and Duan, 2021).

It should be noted that the physical picture of heating and melting of the ice on the lake surface turns out to be quite different for the case when the ice is not covered with snow and in the case when a snow cover is present. However, the approach to solving problems of radiative transfer in snow and ice layers has a common methodological basis, and this can be used in theoretical studies of both lake and sea ice melting. In the spectral range of semitransparency of snow and ice, one should take into account the scattering of radiation either by ice grains in snow or by gas bubbles, which are usually contained in the ice. This means that one should focus on choosing a simple and sufficiently accurate method for solving the radiative transfer equation (RTE) (Dombrovsky and Baillis, 2010; Howell et al., 2021; Modest and Mazumder, 2021).

The main difficulties in radiative transfer modeling are caused by the RTE’s integral term, which takes into account the anisotropic scattering of radiation by particles or bubbles in the medium and contains a scattering phase function. Fortunately, we deal with multiple scattering of radiation in an optically thick medium when the transport approximation is quite sufficient. According to this approach, the scattering function is replaced by a sum of the isotropic and forward components. The resulting transport RTE looks like that for the hypothetic isotropic scattering but with the transport scattering coefficient (Dombrovsky, 2012; Dombrovsky, 2019). It should be recalled that the transport approximation has been successfully employed in diverse problems of radiative transfer in thermal engineering (Dombrovsky et al., 2017; Dombrovsky et al., 2020), biomedicine (Tuchin, 2007; Sandell and Zhu, 2011; Dombrovsky et al., 2012; Jacques, 2013; Eisel et al., 2018; Dombrovsky, 2022), and geophysics (Dombrovsky and Kokhanovsky, 2022; Dombrovsky and Kokhanovsky, 2023; Dombrovsky et al., 2019; Dombrovsky et al., 2022).

The linearity of the RTE makes possible another significant simplification of the problem. In the case of direct solar irradiation of a scattering medium, the radiation intensity can be represented in the form of two additive components: direct radiation and a diffuse component formed due to the scattering. In highly scattering media, the diffuse component of radiation intensity can be calculated using one of the simplest differential approximations: either the known P₁ approximation of the spherical harmonics method or the two-flux approximation. These approximations make it sufficient to solve a boundary-value problem for a second-order ordinary differential equation instead of the RTE. The choice between these approximations is determined by the problem statement. Comparison with exact numerical solutions (Dombrovsky and Baillis, 2010) has shown that the two-flux method is preferable when solving one-dimensional problems typical of solar heating. In this case, the error of P₁ is larger because this method does not take into account the discontinuity in the angular dependence of the radiation intensity on the illuminated surface of the medium.

Transient heat transfer model

Generally speaking, there are various thermal processes in a snowpack or scattering ice sheet and these processes should be involved in a complete heat transfer model. As an example, one can recall the ice sublimation and diffusion of water vapor through a snow layer. This may be important for the snow microstructure but the related effects are insignificant in our problem.

The 1D transient energy equation for temperature $T\left(t,z\right)$ in a layer of snow or ice and the accompanying initial and boundary conditions can be written as follows:

$\rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+P,t>0,0<z<d_{\text{th}},(\mathrm{1a})$

$T\left(0,z\right)=T_{\text{init}}\left(z\right),(\mathrm{1b})$

$z=0,k\frac{\partial T}{\partial z}=h\left(T_{\text{air}}-T\right)-q_{\text{rc}},z=d_{\text{th}},\frac{\partial T}{\partial z}=0,(\mathrm{1c})$

where $z$ is the is the coordinate measured from the illuminated surface, $\rho$, $c$, and $k$ are the density, the specific heat capacity, and the thermal conductivity of the medium, $T_{\text{air}}\left(t\right)$ and $h\left(t\right)$ are the temperature of ambient air and convective heat transfer coefficient which depends on the wind velocity. The adiabatic condition at $z=d_{\text{th}}$ should be replaced by the condition of the first kind when the temperature of the lower interface is known (as in the case of the ice-water interface). The heat flux $q_{\text{rc}}$ is the mid-infrared cooling due to thermal radiation of the snow or ice surface in the atmospheric transparency window of ${\lambda }_{\mathrm{w}1}<\lambda <{\lambda }_{\mathrm{w}2}$ (${\lambda }_{\mathrm{w}1}=8$ µm, ${\lambda }_{\mathrm{w}2}=13$ µm) (Raman et al., 2014; Chen et al., 2016; Hossain and Gu, 2016). Of course, the latent heat of ice melting, $L=0.34$ MJ/kg, should be taken into account in the calculations. This can be done using an equivalent additional heat capacity in a narrow temperature interval near the melting temperature as it was done by Dombrovsky et al. (2019). This simple technique is not new and was successfully used by the author in the numerical solution of other problems to account for the latent heat of phase change of the first kind, including the general case when the so-called mushy zone is formed between solidus and liquidus (Dombrovsky et al., 2015; Roy et al., 2023).

It is usually difficult to choose a realistic initial profile of temperature, $T_{\text{init}}\left(z\right)$, for the heat transfer calculations. Fortunately, the effect of this temperature profile decreases with time. As an example, it was shown by Dombrovsky et al. (2019) that the choice of this temperature profile makes no difference for the snow layer after about 4 h from the initial time moment.

Solution for ice-covered lake

In the case of ice not covered by snow, sunlight penetrates through the ice layer and leads to water heating. In limnology, the transfer of solar radiation in ice and water is described using the exponential Bouguer law, which is applicable only in the case of direct incident radiation and single scattering of light in the medium. This methodological drawback remained even in recent papers (Kirillin et al., 2012; Leppäranta, 2015; Kirillin et al., 2021). The error of this simplified model for the radiative transfer was partially compensated for by the selection of an extinction coefficient, which provided a satisfactory agreement between the calculations and the field measurements. This semiempirical approach to radiative transfer is incorrect. The multiple scattering of short-wave solar radiation by microcracks and gas bubbles leads to stronger solar heating of ice. In addition, the radiation transmitted through the ice layer contains both direct and diffuse components.

According to (Hale and Querry, 1973), the absorption index of water increases with the wavelength from ${\kappa }_{\mathrm{w}}={10}^{-9}-2\times {10}^{-9}$ at $\lambda =0.4-0.5$ µm to ${\kappa }_{\mathrm{w}}={10}^{-5}$ at $\lambda =1.2$ µm. The corresponding water absorption coefficient, defined as ${\alpha }_{\mathrm{\lambda }}^{\mathrm{w}}=4\pi {\kappa }_{\mathrm{w}}/\lambda$, changes from ${\alpha }_{\mathrm{\lambda }}^{\mathrm{w}}=0.025-0.063$ m⁻¹ to ${\alpha }_{\mathrm{\lambda }}^{\mathrm{w}}=100$ m⁻¹. The latter means that visible radiation penetrates water to a depth of tens of meters, while infrared radiation with wavelength $\lambda =1.2$ µm penetrates to a depth of less than 1 cm. In the wavelength range $0.6<\lambda <1.2$ µm, the absorption index of ice differs slightly from that of water (Warren and Brandt, 2008), and a similar situation occurs for ice. The radiation with wavelength $\lambda >{\lambda }_{*}=1.2$ µm is absorbed in a relatively thin surface layer of ice. That is why the threshold value of ${\lambda }_{*}$ is considered as a conventional boundary of the range of semitransparency.

The influence of uncertainty in the experimental values of the ice absorption index on the computational data for solar heating of snow and ice has been analyzed by Dombrovsky and Kokhanovsky (2022), Dombrovsky and Kokhanovsky (2023). It was shown that the discrepancy between the data of (Warren and Brandt, 2008; Picard et al., 2016) in the $\lambda <0.6$ μm range does not significantly affect the results of calculations. Therefore, the more complete spectral data of Warren and Brandt (2008) are used in the present work.

The gas bubbles in ice are assumed to be spherical and the radii of these bubbles, $a$, are much greater than the wavelength. The corresponding diffraction parameter $x=2\pi a/\lambda$ is very large, and therefore the geometrical optics approximation can be used instead of the rigorous Mie theory (Bohren and Huffman, 1998). As a result, the absorption coefficient of ice containing bubbles can be calculated as follows (Dombrovsky, 2004):

${\alpha }_{\mathrm{\lambda }}=\left(1-f_{\mathrm{v}}\right){\alpha }_{\mathrm{\lambda }}^0,(2)$

where $f_{\mathrm{v}}$ is the volume fraction of bubbles, ${\alpha }_{\mathrm{\lambda }}^0=4\pi {\kappa }_{\text{ice}}/\lambda$ is the absorption coefficient of ice without bubbles, and ${\kappa }_{\text{ice}}$ is the index of absorption of ice. In most real cases, $f_{\mathrm{v}}\ll 1$ and ${\alpha }_{\mathrm{\lambda }}\approx {\alpha }_{\mathrm{\lambda }}^0$. Not only the gas bubbles but also the average distance between them is very large compared to the wavelength of the radiation. Therefore, the hypothesis of independent scattering by single bubbles is true (Mishchenko, 2014; 2018).

According to (Kirillin et al., 2012), the gas bubbles are usually not uniformly distributed in the ice layer: there are more of them in the lower part of the layer. This can be taken into account in the calculations. However, the simplest model including only two bubble parameters is chosen in the present study: the average values of volume fraction and radius of bubbles. According to (Dombrovsky and Kokhanovsky, 2020b), the scattering parameter $S=f_{\mathrm{v}}/a_{32}$, where $a_{32}$ is the Sauter’s mean radius of bubbles, is sufficient to describe light scattering by polydisperse bubbles. The transport scattering coefficient of ice with gas bubbles can be calculated as follows (Dombrovsky, 2004):

${\sigma }_{\mathrm{\lambda }}^{\text{tr}}=0.675\left(n_{\text{ice}}\left(\lambda \right)-1\right)S,(3)$

where $n_{\text{ice}}$ is the refraction index of ice. The value ${\sigma }_{\mathrm{\lambda }}^{\text{tr}}$ is usually greater than the absorption coefficient in the entire spectral range under consideration. As a result, the extinction of sunlight in an ice layer is determined by the light scattering.

Following the recent study by Dombrovsky and Kokhanovsky (2023), the present paper is focused primarily on modeling the thermal regime of mountain lakes like those of the Qinghai–Tibet Plateau, located at a height of more than 4 km above sea level, for which the problem is somewhat easier: it can be assumed that the sky is clear and only a small part of the solar light is scattered in the atmosphere. As a result, it is sufficient to consider the transfer of direct solar radiation, the intensity and spectral composition of which change with the zenith angle of the Sun. Minor atmospheric precipitation and strong winds (Wang et al., 2022) result in the absence of snow cover on the ice surface. This leads to a significant solar heating of the ice and water in the lake.

The problem can be simplified because the refractive indices of water and ice differ only slightly in the wavelength range of ${\lambda }_{\text{uv}-\text{vis}}<\lambda <{\lambda }_{*}$ (${\lambda }_{\text{uv}-\text{vis}}\approx 0.4$ µm). As a result, the reflection and refraction of light at the ice-water interface are small and can be neglected. The effect of solar light reflection at the ice-water interface is even smaller. It can be estimated from the Fresnel formulas for the reflection coefficient at the interface of transparent media with different refractive index values. At wavelength $\lambda =0.6$ µm the refractive indices of ice and water are 1.31 and 1.33, respectively, and the reflection coefficient of light incident at an angle of 45^o is equal to 1.2%, and when illuminated along the normal–0.06%. The refraction of light at the ice-water interface is also negligibly small.

It is assumed that optical properties of ice do not change along the horizontal ice surface and the radiative transfer along the surface of an ice-covered lake may not be considered. The 1D model for the propagation of obliquely incident radiation in an ice layer containing gas bubbles has been described recently by Dombrovsky and Kokhanovsky (2022). It is assumed that there are no any bubbles in water, and scattering by a small amount of plankton is insignificant. In this case, the problem of radiative transfer in the ice layer can be solved independently of the propagation of light in water. It is convenient to write the transport RTE and the boundary conditions at an oblique illumination of the ice layer with thickness $d$ in dimensionless variables (Dombrovsky and Kokhanovsky, 2023):

$\mu \frac{\partial {\overline{I}}_{\mathrm{\lambda }}}{\partial {\tau }_{\mathrm{\lambda }}^{\text{tr}}}+{\overline{I}}_{\mathrm{\lambda }}=\frac{{\omega }_{\lambda }^{\text{tr}}}{2}{\overline{G}}_{\mathrm{\lambda }},{\overline{G}}_{\mathrm{\lambda }}\left({\tau }_{\mathrm{\lambda }}^{\text{tr}}\right)={\displaystyle \underset{-1}{\overset{1}{\int }}}{\overline{I}}_{\mathrm{\lambda }}\left({\tau }_{\mathrm{\lambda }}^{\text{tr}},\mu \right)\mathrm{d}\mu ,(\mathrm{4a})$

${\overline{I}}_{\mathrm{\lambda }}\left(0,\mu \right)=r_{\mathrm{\lambda }}{\overline{I}}_{\mathrm{\lambda }}\left(0,-\mu \right)+\left(1-r_{\mathrm{\lambda }}\right)\delta \left({\mu }_{\mathrm{j}}-\mu \right),{\overline{I}}_{\mathrm{\lambda }}\left({\tau }_{\mathrm{\lambda },0}^{\text{tr}},-\mu \right)=0,\mu ,{\mu }_{\mathrm{j}}>0,(\mathrm{4b})$

where ${\overline{I}}_{\mathrm{\lambda }}=I_{\mathrm{\lambda }}/I_{\mathrm{\lambda }}^{\text{inc}}$, ${\overline{G}}_{\mathrm{\lambda }}=G_{\mathrm{\lambda }}/I_{\mathrm{\lambda }}^{\text{inc}}$, $I_{\mathrm{\lambda }}^{\text{inc}}$ is the spectral intensity of incident radiation in direction ${\mu }_{\mathrm{i}}=\cos {\theta }_{\mathrm{i}}$ (${\theta }_{\mathrm{i}}$ is measured from the external normal), $r_{\mathrm{\lambda }}=r_{\mathrm{\lambda }}\left(n_{\text{ice}},{\mu }_{\mathrm{i}}\right)$ is the Fresnel reflection coefficient, ${\mu }_{\mathrm{j}}=\sqrt{1-\left(1-{\mu }_{\mathrm{i}}^2\right)/n_{\text{ice}}^2}$ is the cosine of the refraction angle, ${\tau }_{\mathrm{\lambda }}^{\text{tr}}\left(z\right)={\displaystyle \underset{0}{\overset{z}{\int }}}{\beta }_{\mathrm{\lambda }}^{\text{tr}}\left(z\right)\mathrm{d}z$ is the optical depth and ${\tau }_{\mathrm{\lambda },0}^{\text{tr}}={\tau }_{\mathrm{\lambda }}^{\text{tr}}\left(d\right)$.

The intensity of radiation and the spectral irradiation are presented as follows:

${\overline{I}}_{\mathrm{\lambda }}={\overline{J}}_{\mathrm{\lambda }}+\left(1-r_{\mathrm{\lambda }}\right)E_{\mathrm{\lambda }}^{\mathrm{j}}\delta \left({\mu }_{\mathrm{j}}-\mu \right),E_{\mathrm{\lambda }}^{\mathrm{j}}=\exp \left(-{\tau }_{\mathrm{\lambda }}^{\text{tr}}/{\mu }_{\mathrm{j}}\right),(\mathrm{5a})$

${\overline{G}}_{\mathrm{\lambda }}={\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}+\left(1-r_{\mathrm{\lambda }}\right)E_{\mathrm{\lambda }}^{\mathrm{j}},{\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}={\displaystyle \underset{-1}{\overset{1}{\int }}}{\overline{J}}_{\lambda }\mathrm{d}\mu .(\mathrm{5b})$

The resulting equations for the diffuse component ${\overline{J}}_{\mathrm{\lambda }}$ are:

$\mu \frac{\partial {\overline{J}}_{\mathrm{\lambda }}}{\partial {\tau }_{\mathrm{\lambda }}^{\text{tr}}}+{\overline{J}}_{\mathrm{\lambda }}=\frac{{\omega }_{\mathrm{\lambda }}^{\text{tr}}}{2}{\overline{G}}_{\mathrm{\lambda }},(\mathrm{6a})$

${\overline{J}}_{\mathrm{\lambda }}\left(0,\mu \right)=r_{\mathrm{\lambda }}{\overline{J}}_{\mathrm{\lambda }}\left(0,-\mu \right),{\overline{J}}_{\mathrm{\lambda }}\left(d,-\mu \right)=0,\mu >0.(\mathrm{6b})$

The two-flux method gives the following boundary-value problem for the irradiation ${\overline{G}}_{\mathrm{\lambda },\mathrm{i}}^{\text{dif}}\left({\tau }_{\lambda }^{\text{tr}}\right)$:

$-{\left({\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}\right)}^{″}+{\xi }_{\mathrm{\lambda }}^2{\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}=4{\omega }_{\mathrm{\lambda }}^{\text{tr}}\left(1-r_{\mathrm{\lambda },\mathrm{i}}\right)E_{\mathrm{\lambda }}^{\mathrm{j}},{\xi }_{\mathrm{\lambda }}=\sqrt{1-{\omega }_{\mathrm{\lambda }}^{\text{tr}}},(\mathrm{7a})$

${\tau }_{\mathrm{\lambda }}^{\text{tr}}=0,{\left({\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}\right)}^{\prime }=2\gamma {\overline{G}}_{\mathrm{\lambda }}^{\text{dif}},{\tau }_{\mathrm{\lambda }}^{\text{tr}}={\tau }_{\mathrm{\lambda },0}^{\text{tr}},{\left({\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}\right)}^{\prime }=-2{\overline{G}}_{\mathrm{\lambda }}^{\text{dif}},(\mathrm{7b})$

where ${\overline{r}}_{\mathrm{\lambda }}$ is the angle-averaged reflection coefficient of the ice layer surface and $\gamma =\left(1-{\overline{r}}_{\mathrm{\lambda }}\right)/\left(1+{\overline{r}}_{\mathrm{\lambda }}\right)$. This problem statement is correct for any variation of the optical properties across the ice layer and can be solved numerically (Dombrovsky and Baillis, 2010). In the case of uniform optical properties of ice, one can obtain an analytical solution to the problem.

The calculations made after publication of paper by Dombrovsky and Kokhanovsky (2023) showed that the reflection of sunlight from the illuminated ice surface is negligible and can be disregarded without any significant loss of calculation accuracy. At the same time, the refraction of light at an oblique illumination of ice should be taken into account and ${\mu }_{\mathrm{j}}>{\mu }_{\mathrm{i}}$. Therefore, below is the solution of the problem at ${\overline{r}}_{\mathrm{\lambda }}=0$ ($\gamma =1$). This simplified analytical solution at ${\xi }_{\lambda }\ne {\nu }_{\mathrm{j}}=1/{\mu }_{\mathrm{j}}$ is as follows:

${\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}=\frac{4{\omega }_{\mathrm{\lambda }}^{\text{tr}}}{{\xi }_{\mathrm{\lambda }}^2-{\nu }_{\mathrm{j}}^2}\left(E_{\mathrm{\lambda }}^{\mathrm{j}}+\frac{2-{\nu }_{\mathrm{j}}}{2-{\xi }_{\mathrm{\lambda }}}\frac{A{E}_{\mathrm{\lambda }}^{\text{dif}}+B/E_{\mathrm{\lambda }}^{\text{dif}}}{{\left(E_{\mathrm{\lambda },0}^{\text{dif}}\right)}^2-{\zeta }_{\lambda }^2}\right),{\zeta }_{\mathrm{\lambda }}=\frac{2+{\xi }_{\mathrm{\lambda }}}{2-{\xi }_{\mathrm{\lambda }}},(\mathrm{8a})$

$A=\psi {\zeta }_{\mathrm{\lambda }}-E_{\mathrm{\lambda },0}^{\mathrm{j}}{E}_{\mathrm{\lambda },0}^{\text{dif}},B=E_{\mathrm{\lambda },0}^{\text{dif}}\left({\zeta }_{\mathrm{\lambda }}{E}_{\mathrm{\lambda },0}^{\mathrm{j}}-\psi E_{\mathrm{\lambda },0}^{\text{dif}}\right),\psi =\frac{2+{\nu }_{\mathrm{j}}}{2-{\nu }_{\mathrm{j}}},(\mathrm{8b})$

$E_{\mathrm{\lambda },0}^{\mathrm{j}}=\exp \left(-{\nu }_{\mathrm{j}}{\tau }_{\mathrm{\lambda },0}^{\text{tr}}\right){,E}_{\mathrm{\lambda }}^{\text{dif}}=\exp \left(-{\xi }_{\mathrm{\lambda }}{\tau }_{\mathrm{\lambda }}^{\text{tr}}\right),E_{\mathrm{\lambda },0}^{\text{dif}}=\exp \left(-{\xi }_{\mathrm{\lambda }}{\tau }_{\mathrm{\lambda },0}^{\text{tr}}\right).(\mathrm{8c})$

The relation between ${\overline{G}}_{\mathrm{\lambda }}$ and ${\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}$ also simplifies when $r_{\mathrm{\lambda }}=0$: ${\overline{G}}_{\mathrm{\lambda }}={\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}+E_{\mathrm{\lambda }}^{\mathrm{j}}$.

The radiative transfer problem in water is as follows:

$\mu \frac{\partial {\overline{I}}_{\mathrm{\lambda }}^w}{\partial {\tau }_{\mathrm{\lambda }}^{\mathrm{w}}}+{\overline{I}}_{\mathrm{\lambda }}^{\mathrm{w}}=0,{\tau }_{\mathrm{\lambda }}^{\mathrm{w}}={\alpha }_{\mathrm{\lambda }}^{\mathrm{w}}\times \left(z-d\right),z>d,(\mathrm{9a})$

${\overline{I}}_{\mathrm{\lambda }}^{\mathrm{w}}\left(d,\mu \right)={\overline{I}}_{\mathrm{\lambda }}\left(d,\mu \right),{\overline{I}}_{\mathrm{\lambda }}^{\mathrm{w}}\left(\infty ,\mu \right)={\overline{I}}_{\mathrm{\lambda }}^{\mathrm{w}}\left(\infty ,-\mu \right)=0,\mu >0.(\mathrm{9b})$

where ${\alpha }_{\mathrm{\lambda }}^{\mathrm{w}}=4\pi {\kappa }_{\mathrm{w}}/\lambda$ is the absorption coefficient of water. The solution to this problem is:

${\overline{I}}_{\mathrm{\lambda }}^{\mathrm{w}}\left(z,\mu \right)=\left\{\begin{array}{c}{\overline{I}}_{\mathrm{\lambda }}\left(d,\mu \right)\exp \left(-{\tau }_{\mathrm{\lambda }}^{\mathrm{w}}/\mu \right)\text{\hspace{0.5em}when\hspace{0.5em}}\mu >0\\ 0\text{\hspace{0.5em}when\hspace{0.5em}}\mu <0.\end{array}\right.(10)$

According to Eq. 10, the intensity of light in water at $\mu =1$ decreases most slowly. As a result, with increasing depth the light becomes less diffuse and closer to directed vertically downward.

The solar radiation power absorbed in ice and water can be calculated as follows:

$P\left(z\right)={\int }_{{\lambda }_{\text{uv}-\text{vis}}}^{{\lambda }_{*}}p\left(\lambda ,z\right)\mathrm{d}\lambda ,p\left(\lambda ,z\right)=\left\{\begin{array}{c}{\alpha }_{\mathrm{\lambda }}{G}_{\mathrm{\lambda }}\left(z\right)\text{\hspace{0.5em}when\hspace{0.5em}}z\le d\\ {\alpha }_{\mathrm{\lambda }}^{\mathrm{w}}{G}_{\mathrm{\lambda }}^{\mathrm{w}}\left(z\right)\text{\hspace{0.5em}when\hspace{0.5em}}z>d.\end{array}\right.(11)$

The functions in the right-hand side of the second of these equations are defined as:

$G_{\mathrm{\lambda }}\left(z\right)=I_{\mathrm{\lambda },\mathrm{i}}^{\text{inc}}\times \left\{{\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}\left(z\right)+\exp \left(-{\nu }_{\mathrm{j}}{\beta }_{\mathrm{\lambda }}^{\text{tr}}z\right)\}\right.,(\mathrm{12a})$

$G_{\mathrm{\lambda }}^{\mathrm{w}}\left(z\right)=I_{\mathrm{\lambda },\mathrm{i}}^{\text{inc}}\times \left\{{\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}\left(d\right)\exp \left({-2\tau }_{\mathrm{\lambda }}^{\mathrm{w}}\right)+\exp \left[-{\nu }_{\mathrm{j}}\left({\beta }_{\mathrm{\lambda }}^{\text{tr}}d+{\tau }_{\mathrm{\lambda }}^{\mathrm{w}}\right)\right]\right\}.(\mathrm{12b})$

Obviously, $G_{\mathrm{\lambda }}^{\mathrm{w}}\left(d\right)$ = $G_{\mathrm{\lambda }}\left(d\right)$, whereas the function $p\left(\lambda ,z\right)$ is not continuous at $z=d$. The diffuse irradiation component in water (the first term in Eq. 12b) decreases with depth twice as fast as the directional one. It is clear that Bouguer’s law with a constant extinction coefficient in the exponent, which was applied for the light propagation in water under an ice layer in limnology studies, is not correct.

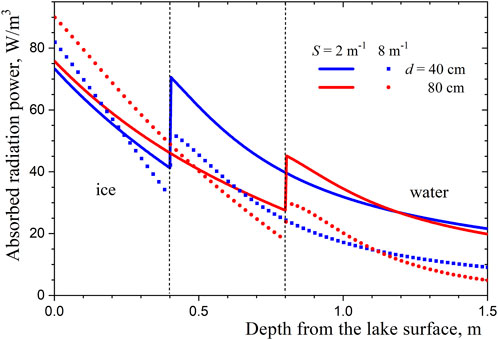
Profiles of absorbed radiation power in ice and water

The spectral radiative flux at the surface of Ngoring Lake at the end of March (the time of the beginning of ice melting) at different values of the Sun’s zenith angle has been calculated in (Dombrovsky and Kokhanovsky, 2023). The results obtained are used below in calculating profiles of absorbed radiation power in ice and water. Typical profiles of this radiation power at the zenith angle 60^o for two values of the scattering parameter and different thicknesses of the ice layer are shown in Figure 1. A significant attenuation of light in the ice layer draws attention. Increasing the scattering parameter leads to an increase in the absorption of solar radiation in the upper part of the ice layer and a significant decrease in the absorption in the lake water. When ice melts and the thickness of the ice becomes smaller, the radiation absorption in ice decreases considerably and the absorption in water increases very strongly. The latter is the physical cause of an observation by Lazhu et al. (2021) for several lakes in the Tibetan Plateau where the water temperature at some distance from the ice-water interface increased rapidly during ice melting.

Figure 1

Figure 1. Absorbed radiation power in ice and water.

Temperature stratification of water in a deep lake

The temperature field in the lake water is largely determined by the non-monotonic dependence of the water density on temperature with a maximum density ${\rho }_{\mathrm{w}}^{*}=1000$ kg/m³ at temperature $T_{*}=4℃$. At the beginning of ice formation, the water temperature at the ice-water interface becomes equal to $T_0=0℃$, while the water at depth may remain warmer. However, even at the bottom of a deep lake, the water temperature cannot be higher than $T_{*}$. In a severe winter, even a deep lake can freeze to the bottom (as in the case of Ngoring Lake), but this paper considers early spring, when the ice thickness does not exceed 1 m.

Field observations of Ngoring Lake and some other lakes in the Qinghai–Tibet Plateau have shown an interesting thermal regime, named “anomalous winter” by Kirillin et al. (2021), when at a depth of 1.5–3 m under the ice layer the water is heated by solar radiation to a temperature $T_{\max }>T_{*}$. Solar radiation absorbed in the upper water layer leads to an increase in $T_{\max }$, and this effect was measured by Kirillin et al. (2021) in March and early April. An estimate of the heat flux from relatively warm water to the ice layer in (Dombrovsky and Kokhanovsky, 2023) gave the value $q_{\mathrm{w}-\text{ice}}\approx 1.2$ kW/m². The effect of this heat flux is much smaller than ice heating by solar radiation.

Averaging thermal boundary conditions for thick ice layers

The heat transfer on the illuminated ice surface changes significantly during the day but this does not affect the temperature of ice at some distance from the surface because of the large heat capacity of the ice layer. A simple estimate based on the Fourier criterion confirms that a thermal relaxation time for the 0.5 m thick ice is about 10 days. This allows using a steady-state model with constant heat transfer parameters, varying according to weather changes from week to week.

The ice melting at Ngoring Lake in March is very slow, and only in April does ice melting accelerate, completed by April 16 (Kirillin et al., 2021). This result is clear from the observations by Zhou et al. (2022): the air temperature in March is almost constant and does not exceed $-10℃$, while it increases up to $-3℃$ in the middle of April at the lake. Therefore, the analysis of ice melting on the lake surface should refer to the conditions of the first half of April, when the day-averaged solar illumination of the lake practically does not change and the air temperature is the only changing parameter of the problem. According to (Wang et al., 2022), the wind speed in the first 2 weeks of April is equal to 4 m/s and not changed during the day. The corresponding value of the heat transfer coefficient is about $h=20$ W/(m²K) (Defraeye et al., 2011; Mirsadeghi et al., 2013).

The boundary-value problem for the quasi-steady temperature profile in the ice layer is as follows:

$k_{\text{ice}}{T}^{″}+\overline{P}\left(z\right)=0,0<z<d,(\mathrm{13a})$

$-k_{\text{ice}}{T}^{\prime }\left(0\right)={\overline{q}}_{\inf }^{\text{sol}}-q_{\text{conv}}-q_{\text{rc}},T\left(d\right)=T_0,(\mathrm{13b})$

where

$\overline{P}\left(z\right)=\frac{1}{t_{\text{day}}}{\int }_0^{t_{\text{day}}}P\left(z,t\right)\mathrm{d}t,{\overline{q}}_{\inf }^{\text{sol}}=\frac{1}{t_{\text{day}}}{\int }_0^{t_{\text{day}}}{q}_{\inf }^{\text{sol}}\left(t\right)\mathrm{d}t,q_{\text{conv}}=h\left({T\left(0\right)-T}_{\text{air}}\right)(\mathrm{14a})$

$q_{\inf }^{\text{sol}}\left(t\right)={\int }_{{\lambda }_{*}}^{\infty }{q}_{\mathrm{i},\mathrm{\lambda }}^{\text{inc}}\left(\lambda ,t\right)\mathrm{d}\lambda ,q_{\text{rc}}=\pi {\int }_{{\lambda }_{\mathrm{w}1}}^{{\lambda }_{\mathrm{w}2}}{I}_{\mathrm{\lambda },\mathrm{b}}\left(T\left(0\right)\right)\mathrm{d}\lambda .(\mathrm{14b})$

Here $q_{\mathrm{i},\mathrm{\lambda }}^{\text{inc}}$ is the incident radiative flux at the solar zenith angle ${\theta }_{\mathrm{i}}$. To determine the function $\overline{P}\left(z\right)=P\left(z\right)\times t_{\text{dl}}/t_{\text{day}}=P\left(z\right)/2$ one can use the average profiles of $P\left(z\right)$ for daylight hours. The same relation is true for the solar infrared radiation flux, taking into account its contribution to the integral radiative flux. The value ${\overline{q}}_{\inf }^{\text{sol}}=37$ W/m² is used in the calculations. It is also convenient to use the following approximation for the temperature dependence of $q_{\text{rc}}$:

$q_{\text{rc}}=q_0+\eta \times \left(T\left(0\right)-T_0\right),q_0=93\mathrm{W}/{\mathrm{m}}^2,\eta =1.6\mathrm{W}/\left({\mathrm{m}}^2\mathrm{K}\right).(15)$

The radiative cooling of ice compensates the radiative flux to the ice surface in the opacity range and the infrared solar heating cannot lead to the surface ice melting.

The condition for the beginning of ice melting can be obtained using the analytical solution to the problem (13a)–(13b):

$T\left(z\right)=T_0+\frac{f_2\left(d\right)-f_2\left(z\right)}{k_{\text{ice}}}-\frac{Q}{k_{\text{ice}}}\left(d-z\right),(\mathrm{16a})$

$f_1\left(z\right)=\frac{1}{2}{\int }_0^{z}P\left(z\right)\mathrm{d}z,f_2\left(z\right)={\int }_0^z{f}_1\left(z\right)\mathrm{d}z,Q=q_{\text{conv}}+q_{\inf }^{\text{ice}}-{\overline{q}}_{\inf }^{\text{sol}}.(\mathrm{16b})$

The ice melting on its lower surface begins when $T^{\prime }\left(d\right)=0$. This enables us to obtain the threshold temperature profile in the ice layer:

$T\left(z\right)=T_0+\frac{f_2\left(d\right)-f_2\left(z\right)}{k_{\text{ice}}}-\frac{f_1\left(d\right)}{k_{\text{ice}}}\left(d-z\right).(17)$

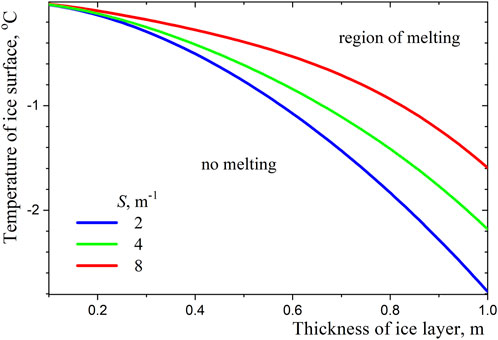
The calculated temperature profiles are shown in Figure 2. As one might expect, scattering plays a significant role in the case of a thick ice layer and the assumption of uniform distribution of gas bubbles in the ice is acceptable only for ice layers less than 0.5 m thick. One can also determine the temperature of the illuminated ice surface, at which melting begins at the ice-water interface:

$T_{\text{surf}}^{*}=T_0+\frac{f_2\left(d\right)-f_1\left(d\right)d}{k_{\text{ice}}}.(18)$

Figure 2

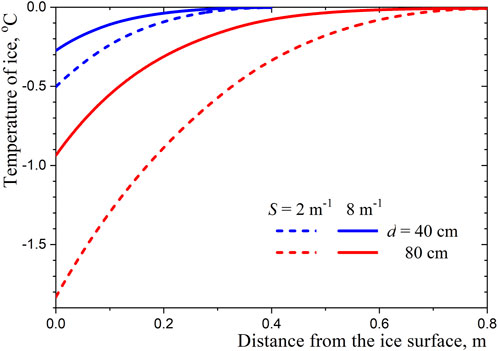
Figure 2. Temperature profiles in ice layers of different thicknesses at the onset of melting on the ice-water interface.

Typical dependences of $T_{\text{surf}}^{*}\left(d\right)$ are plotted in Figure 3. As one might expect, the effect of light scattering by gas bubbles is more significant for thick ice layers.

Figure 3

Figure 3. Dependences of the surface temperature threshold value on the ice thickness.

Effect of a snow layer on lake ice melting

In the absence of snow cover on the lake ice surface, solar radiation penetrates through the semitransparent ice and already in the beginning of spring significantly heats up the water under the ice. Interestingly, the lake ice, even with a thickness of about 1 m, begins to melt from the lower surface. Calculations have shown that this is not due to heating of the ice by the warmer water, but almost exclusively due to solar heating of the ice. This is so because the upper layer of ice is continuously cooled by the colder air, as well as by the thermal radiation in the middle-infrared window of transparency of the cloudless atmosphere. This cooling is not compensated by the daytime heating of the ice surface by the infrared radiation of the Sun but does not prevent heating of the lower part of the ice layer and the beginning of spring ice melting.

The discussed peculiarity of the thermal regime of ice on the lake surface and its melting under the action of spring solar heating changes radically in the presence of even a thin layer of snow on the ice surface. The effect of snow is due to two main factors: firstly, snow significantly reduces the solar radiative flux on the ice surface due to strong scattering of radiation and, secondly, the thermal conductivity of snow is so small that even a thin layer of snow protects the ice surface from convective and radiative cooling. The physical model of snow’s effect on ice melting should include not only the transfer of solar radiation in the snow and ice layer but also the heat conduction process. If we do not take into account changes in the structure and optical properties of snow during its heating (before the melting), the above physical problems can be solved sequentially: first to calculate radiative transfer, and then to solve the heat transfer problem taking into account the absorption of solar radiation both on the snow surface and in the volume of snow and ice. Of course, in the thermal part of the computational model, it is necessary to consider the convective heat transfer with the surrounding air, as well as the mid-infrared radiative cooling of the snow surface.

Let us first consider the propagation of direct solar radiation through the snow layer. In order not to complicate the solution, we will not take into account the scattered radiation from a cloudless sky. Nor will we take into account that there is ice under the snow, which also scatters sunlight. The ice with air bubbles scatters light much more weakly than snow, and only a small fraction of the light transmitted through the snow is scattered by the ice in the direction of the snow. In the case of a very thin snow layer, the scattering of radiation in the ice layer has some influence on the radiative transfer in the snow layer, but this does not affect the main results of the calculations presented below.

As usual, when calculating radiative transfer in a medium with multiple scattering, the transport approximation is used. In addition, the radiation intensity is represented in the form of two additive components: direct radiation and a diffuse component formed due to the scattering of radiation in the medium. The irradiation is also additive:

${\overline{G}}_{\mathrm{\lambda }}=E_{\mathrm{\lambda }}^{\mathrm{i}}+{\overline{G}}_{\mathrm{\lambda }}^{\text{dif}},E_{\mathrm{\lambda }}^{\mathrm{i}}=\exp \left(-{\nu }_{\mathrm{i}}{\tau }_{\mathrm{\lambda }}^{\text{tr}}\right),{\nu }_{\mathrm{i}}=1/{\mu }_{\mathrm{i}}.(19)$

Here ${\tau }_{\mathrm{\lambda }}^{\text{tr}}$ is the optical coordinate measured from the illuminated surface and ${\mu }_{\mathrm{i}}$ is the cosine of the Sun’s zenith angle measured from the normal to the horizontal snow surface. The use of the two-flux method leads to the boundary-value problem for the normalized diffuse irradiation:

$-{\left({\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}\right)}^{″}+{\xi }_{\mathrm{\lambda }}^2{\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}=4{\omega }_{\mathrm{\lambda }}^{\text{tr}}{E}_{\mathrm{\lambda }}^{\mathrm{j}},{\xi }_{\mathrm{\lambda }}=2\sqrt{1-{\omega }_{\mathrm{\lambda }}^{\text{tr}}}(\mathrm{20a})$

${\tau }_{\mathrm{\lambda }}^{\text{tr}}=0,{\left({\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}\right)}^{\prime }=2{\overline{G}}_{\mathrm{\lambda }}^{\text{dif}},{\tau }_{\mathrm{\lambda }}^{\text{tr}}={\tau }_{\mathrm{\lambda },0}^{\text{tr}},{\left({\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}\right)}^{\prime }=-2{\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}.(\mathrm{20b})$

This problem is a little simpler than that for the ice layer since the sunlight is not reflected and refracted on the snow surface. For a snow layer with constant values of ${\alpha }_{\mathrm{\lambda }}$ and ${\beta }_{\mathrm{\lambda }}^{\text{tr}}$, there is a following analytical solution, which looks similar to Eq. (8a–c), but with replacement of ${\nu }_{\mathrm{j}}$ by ${\nu }_{\mathrm{i}}$:

${\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}=\frac{4{\omega }_{\mathrm{\lambda }}^{\text{tr}}}{{\xi }_{\mathrm{\lambda }}^2-{\nu }_{\mathrm{i}}^2}\left(E_{\mathrm{\lambda }}^{\mathrm{i}}+\frac{2-{\nu }_{\mathrm{i}}}{2-\xi }\frac{A{E}_{\mathrm{\lambda }}^{\text{dif}}+B/E_{\mathrm{\lambda }}^{\text{dif}}}{{\left(E_{\mathrm{\lambda },0}^{\text{dif}}\right)}^2-{\zeta }_{\lambda }^2}\right),{\zeta }_{\mathrm{\lambda }}=\frac{2+{\xi }_{\lambda }}{2-{\xi }_{\lambda }},(\mathrm{21a})$

$A=\psi {\zeta }_{\mathrm{\lambda }}-E_{\mathrm{\lambda },0}^{\mathrm{i}}{E}_{\mathrm{\lambda },0}^{\text{dif}},B=E_{\mathrm{\lambda },0}^{\text{dif}}\left({\zeta }_{\mathrm{\lambda }}{E}_{\mathrm{\lambda },0}^{\mathrm{i}}-\psi E_{\mathrm{\lambda },0}^{\text{dif}}\right),\psi =\frac{2+{\nu }_{\mathrm{i}}}{2-{\nu }_{\mathrm{i}}},(\mathrm{21b})$

$E_{\mathrm{\lambda },0}^{\mathrm{i}}=\exp \left(-{\nu }_{\mathrm{i}}{\tau }_{\mathrm{\lambda },0}^{\text{tr}}\right),E_{\mathrm{\lambda }}^{\text{dif}}=\exp \left(-{\xi }_{\lambda }{\tau }_{\mathrm{\lambda }}^{\text{tr}}\right),E_{\mathrm{\lambda },0}^{\text{dif}}=\exp \left(-{\xi }_{\lambda }{\tau }_{\mathrm{\lambda },0}^{\text{tr}}\right).(\mathrm{21c})$

In the limit of ${\tau }_{\mathrm{\lambda },0}^{\text{tr}}={\beta }_{\mathrm{\lambda }}^{\text{tr}}{d}_{\text{snow}}\to \infty$, this solution coincides with the solution derived by Dombrovsky et al. (2019).

The optical properties of snow were calculated in the same way as in (Dombrovsky et al., 2019). The analytical solution for single spherical ice grains obtained by Kokhanovsky and Zege (1995) in the geometrical optics approximation was used. As usual, it was assumed that the ice grains have a mean radius $a=100$ µm and their volume fraction is equal to $f_{\mathrm{v}}=0.33$.

The real parameters of the problem may differ from the accepted values. However, the effect of this choice on the subsequent physical analysis is expected to be insignificant. The possible contamination of snow by particles suspended in the atmosphere is not considered. This effect was considered, for example, by He et al. (2018) and Dombrovsky and Kokhanovsky (2020a).

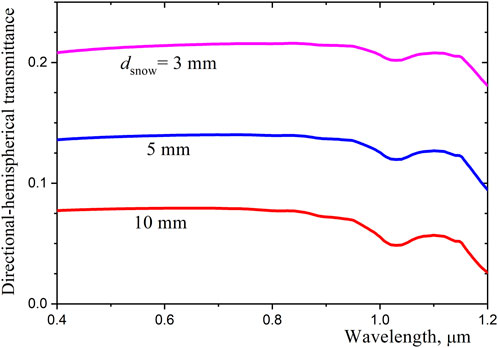
The effect of snow layer thickness on the directional-hemispherical transmittance of snow, $T_{\mathrm{\lambda }}^{\mathrm{d}-\mathrm{h}}$, is shown in Figure 4. The value of $T_{\mathrm{\lambda }}^{\mathrm{d}-\mathrm{h}}$ was calculated at a solar zenith angle ${\theta }_{\mathrm{i}}={60}^{\mathrm{o}}$. One can see that even a 5 mm thick snow layer transmits only about 10%–14% of the incident radiation whereas a thicker snow layer practically does not transmit solar radiation to the ice surface. Note that this result agrees well with the measurements by Perovich (2007). In addition, a small reflection of light from the ice surface and also small scattering of light by gas bubbles in the ice allows a significant simplification of the radiative transfer problem: one can assume that the sunlight transmitted through the snow layer does not return back.

Figure 4

Figure 4. Effect of snow layer thickness on the transmittance of snow.

Consider now the heat transfer problem for solar heating and possible snow melting on the ice surface, taking into account the conductive heating of the ice layer. The temperature of the lower surface of the ice (at the ice-water interface) is 0°C. This boundary condition allows one not to consider the heat transfer under the ice, which is necessary when the ice layer is located, for example, on bare ground. At the same time, when analyzing the thermal state of the snow layer illuminated by the Sun, it is necessary to take into account the heat conducted away from the snow into the ice layer. In other words, the energy equation should be solved in the computational domain including both the snow cover and the ice layer:

$\rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+P,t>0,0<z<d_{\text{th}}=d_{\text{snow}}+d_{\text{ice}},(\mathrm{22a})$

$T\left(0,z\right)=T_{\text{init}}\left(z\right),(\mathrm{22b})$

$z=0,-k\frac{\partial T}{\partial z}=h\left(T_{\text{air}}-T\right)+q_{\inf }^{\text{sol}}-\epsilon q_{\text{rc}},z=d_{\text{th}},T\left(t,z\right)=T_0,(\mathrm{22c})$

$q_{\inf }^{\text{sol}}={\int }_{{\lambda }_{*}}^{{\lambda }_{\text{op}}}{q}_{\mathrm{\lambda }}^{\text{sol}}\left(t\right)\mathrm{d}\lambda ,q_{\text{rc}}=\pi {\displaystyle \underset{{\lambda }_{\mathrm{w}1}}{\overset{{\lambda }_{\mathrm{w}2}}{\int }}}{I}_{\mathrm{\lambda },\mathrm{b}}\left(T,\lambda \right)\mathrm{d}\lambda .(\mathrm{22d})$

where $T\left(t,z\right)$ is the medium temperature which depends on current time $t$ and coordinate $z$ measured from the upper surface of the snow layer, $P\left(t,z\right)$ is the solar radiation power absorbed in the medium, $T_{\text{air}}\left(t\right)$ is the air temperature outside the thermal boundary layer, $T_0=0℃$, $q_{\inf }^{\text{sol}}\left(t\right)$ is the integral infrared solar radiative flux in the opacity range of ${\lambda }_{*}<\lambda <{\lambda }_{\text{op}}$ (the upper boundary of this range was taken equal to ${\lambda }_{\text{op}}=2.4$ µm). Specific volumetric heat capacity $\rho c$ and thermal conductivity $k$ of the medium are:

$\rho c=\left\{\begin{array}{c}{\left(\rho c\right)}_{\text{snow}}\text{\hspace{1em}when\hspace{1em}}0<z<d_{\text{snow}}\\ {\left(\rho c\right)}_{\text{ice}}\text{\hspace{1em}when\hspace{1em}}{d}_{\text{snow}}<z<d_{\text{th}},\end{array}\right.k=\left\{\begin{array}{c}{k}_{\text{snow}}\text{\hspace{1em}when\hspace{1em}}0<z<d_{\text{snow}}\\ k_{\text{ice}}\text{\hspace{1em}when\hspace{1em}}{d}_{\text{snow}}<z<d_{\text{th}}.\end{array}\right.(23)$

The initial temperature profile was assumed to be as follows:

$T_{\text{init}}\left(z\right)=\{\begin{array}{l}{T}_{\text{air}}\text{\hspace{1em}when\hspace{1em}}z\le d_{\text{snow}}\\ T_{\text{air}}+\left(T_0-T_{\text{air}}\right)\left(z-d_{\text{snow}}\right)/d_{\text{ice}}\text{\hspace{0.17em}when\hspace{0.17em}}z>d_{\text{snow}}.\end{array}(24)$

When modeling the effect of the snow layer on the opening of the lake from ice, it would be incorrect to consider the solar heating conditions typical of the high-mountain lakes of northeastern Tibet, when, due to low precipitation and constantly strong winds, the ice on these lakes is not covered by snow. In addition, at low altitudes, unlike in high mountains, not only direct solar radiation but also diffuse radiation from the light-scattering atmosphere should be taken into account. In this problem, we use the same data as in the papers by Dombrovsky et al. (2019) and Dombrovsky and Kokhanovsky (2022) for the summer solstice during the Arctic polar summer at latitude 70^o.

The motion of the Sun across the sky during the day was calculated in the same way as in (Dombrovsky et al., 2019). At the same time, taking into account the diffuse atmospheric radiation requires additional relations, which are obtained by solving the following boundary-value problem for spectral irradiation:

${\left({\overline{G}}_{\mathrm{\lambda }}\right)}^{″}-{\xi }^2{\overline{G}}_{\mathrm{\lambda }}=0,(\mathrm{25a})$

${\tau }_{\mathrm{\lambda }}^{\text{tr}}=0,{\left({\overline{G}}_{\mathrm{\lambda }}\right)}^{\prime }=2\left({\overline{G}}_{\mathrm{\lambda }}-2\right),{\tau }_{\mathrm{\lambda }}^{\text{tr}}={\tau }_{\mathrm{\lambda },0}^{\text{tr}},{\left({\overline{G}}_{\mathrm{\lambda }}\right)}^{\prime }=-2{\overline{G}}_{\mathrm{\lambda }}.(\mathrm{25b})$

The analytical solution to this problem is given by:

${\overline{G}}_{\mathrm{\lambda }}=\frac{4}{2-\xi }\frac{\zeta E_{\mathrm{\lambda }}^{\text{dif}}-{\left(E_{\mathrm{\lambda },0}^{\text{dif}}\right)}^2/E_{\mathrm{\lambda }}^{\text{dif}}}{{\zeta }^2-{\left(E_{\mathrm{\lambda },0}^{\text{dif}}\right)}^2},(26)$

In the limit of ${\tau }_{\mathrm{\lambda },0}^{\text{tr}}\to \infty$, Equation 26 reduces to the following one : ${\overline{G}}_{\mathrm{\lambda }}=4E_{\mathrm{\lambda }}^{\text{dif}}/\left(2+\xi \right)$.

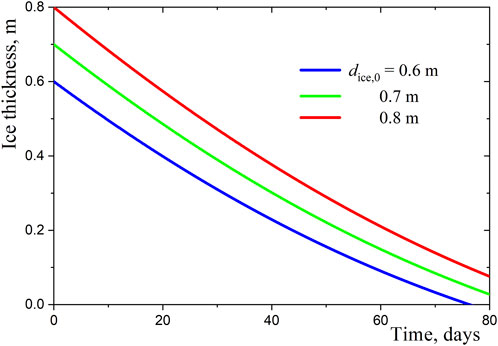
To exclude the influence of the initial temperature profile, we consider the calculated temperature profiles on day 14 from $t=0$. For certainty, the ice layer thickness is assumed to be equal to $d_{\text{ice}}=40$ cm, whereas the thickness of the snow layer varies widely. The computational results presented in Figure 5 for three values of $d_{\text{snow}}$ differ most markedly at midnight when the snow has time to cool by 0.3–0.4°C as a result of convective and radiative cooling. It is interesting that the maximum heating of snow occurs in the second half of the day and even at $d_{\text{snow}}=200$ mm only the surface layer of snow 2–3 mm thick melts. This result is qualitatively different from the case of thick snow cover considered in (Dombrovsky et al., 2019; Dombrovsky and Kokhanovsky, 2022) due to heat sinking into the ice layer. Of course, this heat sink is more noticeable in case of a thin snow layer, but remains significant even at $d_{\text{snow}}=200$ mm. Calculations have shown that snow less than $d_{\text{snow}}^{*}\approx 15$ mm thick does not melt at all due to cooling by the ice layer. The found threshold value $d_{\text{snow}}^{*}$ of the non-melting snow layer is another characteristic parameter of the considered problem. It is important that in all the variants, the ice layer is far from melting.

Figure 5

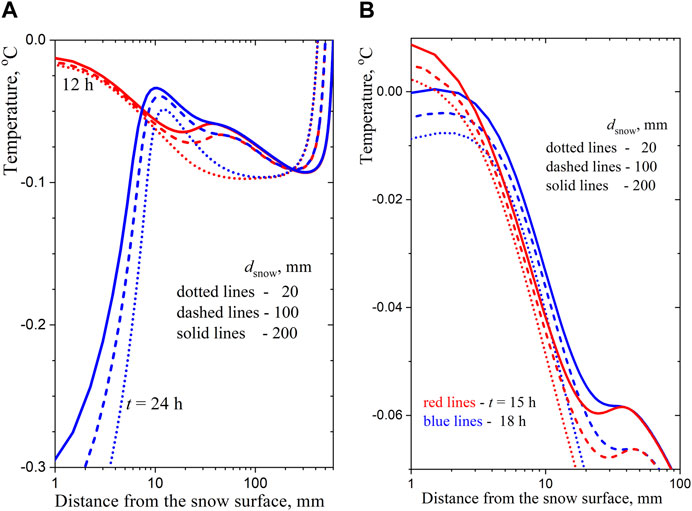
Figure 5. Temperature profiles in the snow and ice layers underneath at different times of the day: (A)–at noon and midnight, (B)–in the afternoon.

The above computational study gives the following general picture of solar heating of the ice layer covered by snow. When the upper surface of ice on a lake is illuminated by the spring Sun, the thick ice layer begins to melt even in very cold air and melting occurs from the lower surface of the ice layer. But if there is a thin layer of snow on the surface of the ice (even less than 1 cm thick) the snow does not allow much of the sunlight to penetrate into ice and makes melting of the ice surface underneath impossible. At the same time, the snow itself on the ice surface does not heat up because it scatters a significant part of the visible solar radiation, and the absorbed solar heat is almost immediately transferred to the relatively thick layer of ice. Snow melting can only begin when the snow layer is thicker than $d_{\text{snow}}^{*}\approx 15$ mm and only when the snow layer is $d_{\text{snow}}\approx 200$ mm thick does melting become significant. Of course, the produced water flows down through the pores in the snow and freezes again at some distance from the ice surface. If the initial thickness of the snow layer is more than 300 mm, melting of the snow near the sunlit surface continues and leads to the formation of a kind of mushy zone on the ice with ice particles suspended in water, which tend to float to the water surface. This stage of the process can be quite long, but as a result the ice surface turns out to be covered with a layer of water.

An estimate of the effect of melt pond on melting of ice

Meltwater, formed initially by snowmelt, does not cover the ice surface uniformly. This is evidenced by numerous observations both for ice-covered lakes and for the much better-studied Arctic Sea ice. Note that the abnormally strong melting of sea ice in the Arctic during the polar summer is an important process that has been intensively analyzed over the last decade. One should name a number of studies that are specifically devoted to the formation and evolution of melt ponds on the Arctic Sea ice. In chronological order, these are experimental and analytical works by Polashenski et al. (2012), Hudson et al. (2013), Schröder et al. (2014), Popović et al. (2018), Malinka et al. (2018), Ma et al. (2019), König and Oppelt (2020), Perovich et al. (2021), Sterlin et al. (2021), Lei et al. (2022), and Rosenburg et al. (2023). Photographs in the literature show numerous melt ponds and the change in the ice surface area occupied by these ponds in the polar summer. Note that similar melt ponds are also observed on glaciers (Rockström and Gaffney, 2021). In most of the above-mentioned works on sea ice, the authors are focused on positive feedback that leads to an enormous increase in the total area of the melt ponds. The point is that the albedo of snow in the visible range of the spectrum is very high, and when snow melts in polar summer, forming melt ponds, the reflection of solar radiation is radically reduced. As a result, sea ice receives much more solar heat, causing it to melt and increasing the area occupied by melt ponds. This positive feedback over a large surface area of the Arctic Sea is accompanied by an increase in the water vapor content of the atmosphere and is important for the continuation of global warming.

Even visual observations allow us to distinguish between two types of melt ponds: the so-called bright ponds and dark ponds. The ice on the bottom of the bright pond is mostly smooth and dense but with small cracks and highly light-scattering porous areas with fine pores. The bottom of the dark pond is more heterogeneous and has relatively large cracks and voids (König and Oppelt, 2020). This is related to the different structure of the first-year ice and multiyear ice (Li et al., 2020). The experimental work by König and Oppelt (2020) confirmed the qualitative results of the analytical study of melt pond reflectivity by Malinka et al. (2018). Note that the work by Malinka et al. (2018) was based on the same methodological framework as the present paper, including the transport approximation and the two-flux model for radiative transfer.

For simplicity, we will focus on a more simple melting problem for the first-year ice. The formation of a layer of water on the ice surface and the subsequent melting of ice are complex processes that deserve special modeling. Nevertheless, it is possible to suggest a simple physical model for ice melting under a meltwater layer. It is obvious that on both surfaces of the ice layer, the temperature is constant and equal to 0°C. Of course, the total radiation power absorbed in the ice volume leads not to increase the ice temperature, but to its melting. The heat flux from water under the ice, as was shown above, is insignificant. Indeed, there is a stable temperature stratification of water directly under the ice, and the thermal conductivity of water is rather small. On the contrary, the natural convection of water in a melt pond can give a noticeably larger contribution to ice melting, and this should be taken into consideration. This effect is more significant in the case of a small ice layer thickness.

The temperature profile along the depth of the melt pond is non-monotonic and has a maximum at some depth below the surface. Indeed, the heating of the water surface by infrared solar radiation is compensated by convective cooling and radiative cooling in the middle-infrared transparency window of the cloudless atmosphere. Even at temporary heating of the surface layer of water to the temperature $T_{*}=4℃$, this water, as denser, goes down to some depth $d_{*}<d_{\mathrm{p}}$, where $d_{\mathrm{p}}$ is the depth of the melt pond. At the bottom of the melt pond, at a depth of $d_{*}<d{<d}_{\mathrm{p}}$, the water temperature decreases from $T_{*}$ at ${d=d}_{*}$ to $T_0=0℃$ at ${d=d}_{\mathrm{p}}$ (at the ice surface). Intensive natural convection takes place in this lower layer. Obviously, most of the solar radiative flux absorbed in the water volume is transferred to the ice in this lower layer of the melt pond. This is so because in the upper layer of the pond water (at a depth of ${d<d}_{*}$) due to stable temperature stratification, the only heat transfer mode–heat conduction–operates, and the thermal conductivity of water is small: $k_{\mathrm{w}}=0.57$ W/(m K). As a result, for example, at ${d-d}_{*}=10$ cm and temperature difference $T_{*}-T_0=4℃$ the upward heat flux is very small: $q_{\text{cond}}\approx 23$ W/(m² K). Therefore, in the suggested approximate model, it is assumed that the main part of solar radiation in the spectral range of water semitransparency absorbed in the volume of the melt pond is transferred to the ice layer. We will consider only the day-averaged radiative flux at the melt pond surface. The change of heat transfer conditions on the surface of the melt pond during the day does not matter for the considered ice melting because of the large heat capacity of the ice layer.

Small reflection of sunlight from water can be neglected. In subsequent calculations, the cosine of the refraction angle is assumed constant and equal to ${\mu }_{\mathrm{j}}=0.75$, which approximately corresponds to the zenith angle of the Sun ${\theta }_{\mathrm{i}}=60°$. As before, the insignificant difference between the refractive indices of water and ice makes it possible to neglect the reflection and refraction of light both at the bottom of the melt pond and at the lower surface of the ice layer. To simplify the calculations, the propagation of only the direct solar radiation is considered. Of course, a 1D approach that does not take into account the size of the melt pond and its unequal depth in the central part and at the periphery is acceptable for the model problem. Perovich et al. (2021) found that the depth of melt ponds during ice melt varies little with time because it is regulated by the flow of horizontal and vertical water drainage to the ocean. As a result, some of the solar heat absorbed by the water in the pond is not transferred to the ice layer. This should be taken into account, especially for small ponds.

To calculate the transfer of solar radiation in the ice layer under the melt pond, the above suggested method with the spectral irradiation ${\overline{G}}_{\mathrm{\lambda }}={\overline{G}}_{\mathrm{\lambda }}^{\text{dif}}+E_{\mathrm{\lambda }}^{\mathrm{j}}$ and the diffuse component calculated by analytical solution (Eq. 10a–10c) is used. Since we are not interested in the distribution of absorbed radiation over the thickness of the ice layer, it is sufficient to consider the spectral irradiation integrated over the optical thickness of the ice. However, the profile of the ice scattering parameter is not known. In addition, the solution depends on physical parameters related to solar illumination and the depth of the melt pond. The natural uncertainty of these data does not allow one to expect accurate results of detailed calculations. Under these conditions, relying on the field measurement data available in the literature is reasonable. The experimental data on geometric parameters and heat fluxes for first-year Arctic Sea ice in advanced stages of melt are given in Hudson et al. (2013).

The following approximation of the radiation power absorbed in the ice layer is used:

$P=P_{\max }\exp \left(-z/d_{\text{ice}}^{*}\right).(27)$

According to Figure 1, at the scattering parameter $S=2$ m⁻¹ this dependence with the value $d_{\text{ice}}^{*}=0.8$ m is universal for ice layers of different thicknesses in the range $0.2\le d_{\text{ice}}\le 0.8$ m. The integration of Eq. 30 gives the following formula for the radiative flux absorbed in an ice layer:

$q_{\text{ice}}=q_{\text{ice}}^{\text{inc}}\left[1-\exp \left(-d_{\text{ice}}/d_{\text{ice}}^{*}\right)\right].(28)$

Of course, the dependences of $q_{\text{ice}}\left(d_{\text{ice}}\right)$ at the real scattering parameter, which, in general, varies with the ice thickness, may differ significantly from function (Equation 28), but retrieval of profiles $S\left(z\right)$ from the available limited experimental data is impossible. Therefore, Equation 28 should be considered an essential assumption adopted in the approximate model.

The integral radiative flux absorbed in a melt pond is given by the following equation:

$q_{\mathrm{w}}={\int }_{{\lambda }_{\text{uv}-\text{vis}}}^{{\lambda }_{*}}{q}_{\mathrm{\lambda }}^{\mathrm{w}}d\lambda ,q_{\mathrm{\lambda }}^{\mathrm{w}}=q_{\mathrm{\lambda },\mathrm{w}}^{\text{inc}}\left[1-\exp \left(-{\alpha }_{\mathrm{\lambda }}^{\mathrm{w}}{d}_{\mathrm{p}}/{\mu }_{\mathrm{j}}\right)\right].(29)$

It is assumed that $q_{\mathrm{\lambda },\mathrm{w}}^{\text{inc}}$ is constant during a large part of the polar summer and its spectral dependence roughly coincides with the Planck function at temperature $T_{\text{sol}}=5800$ K. A day-averaged integral incident flux of solar radiation in the range of water and ice semitransparency $q_{\text{inc}}=q_{\mathrm{w}}+q_{\text{ice}}^{\text{inc}}$ can be taken from Hudson et al. (2013).

Using the approximate value of $q_{\text{ice}}$, one can estimate the linear rate of ice melting using the heat balance equation:

${\rho }_{\text{ice}}L{\dot{d}}_{\text{ice}}=-\left({\left(1-K_{\text{loss}}\right)q}_{\mathrm{w}}+q_{\text{ice}}\right),d_{\text{ice}}\left(0\right)=d_{\text{ice},0}.(30)$

The value $K_{\text{loss}}<1$ is introduced to account the heat losses with horizontal drainage of water. The results of calculations at $K_{\text{loss}}=0.2$ presented in Figure 6 show two periods of the process: first, the ice melts faster due to the absorption of solar radiation passing through it, and then the heat is transferred to ice mainly from the melt pond. The characteristic time of melting of thick ice is comparable to the duration of the warmest period of the polar summer.

Figure 6

Figure 6. Time variation of ice layer thickness during the ice melting.

The suggested model can be considered only as a simple physical assessment. The real process needs a more sophisticated analysis which is beyond the scope of the present paper. However, it is clear that a relatively simple approach to solving the radiative transfer problem may be useful in the physical modeling of one of the stages of ice melting and the complex evolution of melt ponds.

As a result of the strong melting of sea ice during the polar summer, significant areas of the Arctic Sea may become ice-free. Most likely, this will not prevent the restoration of the ice cover during the polar winter, which would be an extremely undesirable effect of global warming. The fact is that the surface layer of water in the Arctic Sea cannot heat up above the melting point of ice due to the natural convection of water in its unstable temperature stratification. Thus, the unique physical properties of water allow us to count on serious negative feedback and retain some optimism about the rate of global climate change accompanied by intensive seasonal melting of polar ice.

Conclusion

Physical and computational models of solar radiative heating and melting of ice on water surface were developed. In the semitransparency range of ice and snow, the multiple scattering of radiation in the ice which contains gas bubbles and in the snow cover that may be present on the ice surface is described using the transport approximation for the scattering phase function and two-flux model for the diffuse component of the spectral radiation intensity. Analytical solution derived for the radiative transfer are coupled with a numerical solution for the transient energy equation. The heat transfer model takes into account convective heat transfer with the atmospheric air, infrared solar radiation absorbed at the illuminated surface, and radiative cooling in the mid-infrared transparency window of the cloudless atmosphere.

It was shown that a thick layer of ice not covered with snow begins to melt at the ice-water interface due to solar heating of ice. The computational data are in good agreement with the field observations for Ngoring Lake in the Qinghai–Tibet Plateau. The theoretical analysis showed a dramatic change in the process if there is a layer of snow on the ice. Even in the case of a thin snow layer less than 1 cm thick, the snow does not transmit most of the sunlight and makes ice melting impossible. At the same time, the snow itself on the ice surface does not heat up because it scatters a significant part of visible solar radiation, and the absorbed solar heat is transferred almost instantly to the relatively thick layer of ice.

Snow melting can only begin when the snow layer is about 15 mm thick, and only when the snow layer is about 200 mm thick does melting become significant. If the initial thickness of the snow layer exceeds 300 mm, snow melting near the sunlit surface leads to the formation of a melt pond on the ice surface. Such melt pools are regularly observed in polar summer on the ice of the Arctic Sea. Abnormally strong melting of sea ice in the Arctic during polar summer is an extremely important process that has been intensively studied in recent years. The last part of the paper provided an estimate of ice melting under a melt pond. The results obtained are in qualitative agreement with in-situ observations.

The general approach and particular solutions suggested for approximate calculations of solar heating and melting of lake and sea ice with possible snow cover on the ice surface can be used as the basis of more specific computational models for a variety of combined heat transfer problems in geophysics and other research areas.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LD: Conceptualization, Investigation, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The work was financially supported by the Ministry of Science and Higher Education of the Russian Federation (project no. FEWZ-2023-0002).

Acknowledgments

The author is grateful to Professor Alexander Kokhanovsky for useful discussions.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bohren, C. F., and Huffman, D. R. (1998). Absorption and scattering of light by small particles. New York: Wiley.

Google Scholar

Chen, Z., Zhu, L., Raman, A., and Fan, S. (2016). Radiative cooling to deep sub-freezing temperatures through a 24-h day-night cycle. Nat. Commun. 7, 13729. doi:10.1038/ncomms13729

PubMed Abstract | CrossRef Full Text | Google Scholar

Defraeye, T., Blocken, B., and Carmeliet, J. (2011). Convective heat transfer coefficients for exterior building surfaces: existing correlations and CFD modelling. Energy Convers. Manag. 52 (1), 512–522. doi:10.1016/j.enconman.2010.07.026

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (2004). The propagation of infrared radiation in a semitransparent liquid containing gas bubbles. High. Temper. 42 (1), 146–153. doi:10.1023/B:HITE.0000020103.82678.13

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (2012). The use of transport approximation and diffusion-based models in radiative transfer calculations. Comput. Therm. Sci. 4 (4), 297–315. doi:10.1615/ComputThermalScien.2012005050

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (2019). “Scattering of radiation and simple approaches to radiative transfer in thermal engineering and bio-medical applications,” in Springer series in light scattering. Editor A. Kokhanovsky (Cham (Switzerland): Springer Nature), 4, 71–127.

CrossRef Full Text | Google Scholar

Dombrovsky, L. A. (2022). Laser-induced thermal treatment of superficial human tumors: an advanced heating strategy and non-Arrhenius law for living tissues. Front. Therm. Eng. 1, 807083. doi:10.3389/fther.2021.807083

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Baillis, D. (2010). Thermal radiation in disperse systems: an engineering approach. New York: Begell House.

Google Scholar

Dombrovsky, L. A., and Kokhanovsky, A. A. (2020a). Light absorption by polluted snow cover: internal versus external mixture of soot. J. Quant. Spectrosc. Radiat. Transf. 242C, 106799. doi:10.1016/j.jqsrt.2019.106799

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Kokhanovsky, A. A. (2020b). Solar heating of ice sheets containing gas bubbles. J. Quant. Spectrosc. Radiat. Transf. 250, 106991. doi:10.1016/j.jqsrt.2020.106991

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Kokhanovsky, A. A. (2021). “Solar heating of the cryosphere: snow and ice sheets,”. Springer series in light scattering. Editor A. Kokhanovsky (Cham (Switzerland): Springer Nature), 6, 53–109.

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Kokhanovsky, A. A. (2022). Deep heating of a snowpack by solar radiation. Front. Therm. Eng. 2, 882941. doi:10.3389/fther.2022.882941

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., and Kokhanovsky, A. A. (2023). Solar heating of ice-covered lake and ice melting. J. Quant. Spectrosc. Radiat. Transf. 294, 108391, 108391. doi:10.1016/j.jqsrt.2022.108391

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Kokhanovsky, A. A., and Randrianalisoa, J. H. (2019).On snowpack heating by solar radiation: a computational model. J. Quant. Spectrosc. Radiat. Transf. 227, 72–85. doi:10.1016/j.jqsrt.2019.02.004

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Nenarokomova, N. B., Tsiganov, D. I., and Zeigarnik, Y. A. (2015). Modeling of repeating freezing of biological tissues and analysis of possible microwave monitoring of local regions of thawing. Int. J. Heat. Mass Transf. 89, 894–902. doi:10.1016/j.ijheatmasstransfer.2015.05.117

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Reviznikov, D. L., Kryukov, A. P., and Levashov, V. Y. (2017). Self-generated clouds of micron-sized particles as a promising way of a solar probe shielding from intense thermal radiation of the Sun. J. Quant. Spectrosc. Radiat. Transf. 200, 234–243. doi:10.1016/j.jqsrt.2017.06.025

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Solovjov, V. P., and Webb, B. W. (2022). Effect of ground-based environmental conditions on the level of dangerous ultraviolet solar radiation. J. Quant. Spectrosc. Radiat. Transf. 279, 108048. doi:10.1016/j.jqsrt.2021.108048

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Timchenko, V., and Jackson, M. (2012). Indirect heating strategy for laser induced hyperthermia: an advanced thermal model. Int. J. Heat. Mass Transf. 55 (17-18), 4688–4700. doi:10.1016/j.ijheatmasstransfer.2012.04.029

CrossRef Full Text | Google Scholar

Dombrovsky, L. A., Levashov, V. Y., Kryukov, A. P., Dembele, S., and Wen, J. X. (2020). A comparative analysis of shielding of thermal radiation of fires using mist curtains containing droplets of pure water or sea water. Int. J. Therm. Sci. 152, 106299. doi:10.1016/j.ijthermalsci.2020.106299

CrossRef Full Text | Google Scholar

Eisel, M., Ströbl, S., Pongrats, T., Stepp, H., Rühm, A., and Sroka, R. (2018). Investigation of optical properties of dissected and homogenized biological tissue. J. Biomed. Opt. 23 (9), 091418. doi:10.1117/1.jbo.23.9.091418

PubMed Abstract | CrossRef Full Text | Google Scholar

Hale, G. M., and Querry, M. P. (1973). Optical constants of water in the 200nm to 200μm wavelength region. Appl. Opt. 12 (3), 555–563. doi:10.1364/AO.12.000555

PubMed Abstract | CrossRef Full Text | Google Scholar

He, C., Liou, K.-N., Takano, Y., Yang, P., Qi, L., and Chen, F. (2018). Impact of grain shape and multiple black carbon internal mixing on snow albedo: parameterization and radiative effect analysis. J Geophys Res. Atmos. 123 (2), 1253–1268. doi:10.1002/2017JD027752

CrossRef Full Text | Google Scholar

Hossain, M. M., and Gu, M. (2016). Radiative cooling: principles, progress, and potentials. Adv. Sci. 3 (7), 1500360. doi:10.1002/advs.201500360

PubMed Abstract | CrossRef Full Text | Google Scholar

Howell, J. R., Mengüç, M. P., Daun, K., and Siegel, R. (2021). Thermal radiation heat transfer. 7th Edition. New York: CRC Press.

Google Scholar

Hudson, S. R., Granskog, M. A., Sundfjord, A., Randelhoff, A., Renner, A. H. H., and Divine, D. V. (2013). Energy budget of first-year Arctic sea ice in advanced stages of melt. Geophys Res. Lett. 40 (11), 2679–2683. doi:10.1002/grl.50517

CrossRef Full Text | Google Scholar

Jacques, S. L. (2013). Optical properties of biological tissues: a review. Phys. Med. Biol. 58 (11), R37–R61. doi:10.1088/0031-9155/58/11/R37

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirillin, G., Leppäranta, M., Terzhevik, A., Granin, N., Bernhard, J., Engelhardt, C., et al. (2012). Physics of seasonally ice-covered lakes: a review. Aquat. Sci. 74 (4), 659–682. doi:10.1007/s00027-012-0279-y

CrossRef Full Text | Google Scholar

Kirillin, G. V., Shatwell, T., and Wen, L. (2021). Ice-covered lakes of Tibetan Plateau as solar heat collectors. Geophys Res. Lett. 48 (14), e2021GL093429. doi:10.1029/2021GL093429

CrossRef Full Text | Google Scholar

Kokhanovsky, A. A., and Zege, E. P. (1995). Local optical parameters of spherical polydispersions: simple approximations. Appl. Opt. 34 (24), 5513–5519. doi:10.1364/AO.34.005513

PubMed Abstract | CrossRef Full Text | Google Scholar

König, M., and Oppelt, N. (2020). A linear model to derive melt pond depth on Arctic sea ice from hyperspectral data. Cryosphere 14 (8), 2567–2579. doi:10.5194/tc-14-2567-2020

CrossRef Full Text | Google Scholar

Lazhu, Y. K., Hou, J., Wang, J., Lei, Y., Zhu, L., Chen, Y., et al. (2021). A new finding on the prevalence of rapid water warming during lake ice melting on the Tibetan Plateau. Sci. Bull. 66, 2358–2361. doi:10.1016/j.scib.2021.07.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei, R., Cheng, B., Hoppmann, M., Zhang, F., Zuo, G., Hutchings, J. K., et al. (2022). Seasonality and timing of sea ice mass balance and heat fluxes in the Arctic transpolar drift during 2019–2020. Elem. Sci. Anth 10 (1), 1–22. doi:10.1525/elementa.2021.000089

CrossRef Full Text | Google Scholar

Leppäranta, M. (2015). Freezing of lakes and the evolution of their ice cover. Berlin: Springer.

Google Scholar

Li, Q., Zhou, C., Zheng, L., Liu, T., and Yang, X. (2020). Monitoring evolution of melt ponds on first-year and multiyear sea ice in the Canadian Arctic Archipelago with optical satellite data. Ann. Glaciol. 61 (82), 154–163. doi:10.1017/aog.2020.24

CrossRef Full Text | Google Scholar

Ma, Y.-P., Sudakov, I., Strong, C., and Golden, K. M. (2019). Ising model for melt ponds on Arctic sea ice. New J. Phys. 21, 063029. doi:10.1088/1367-2630/ab26db

CrossRef Full Text | Google Scholar

Malinka, A., Zege, E., Istomina, L., Heygster, G., Spreen, G., Perovich, D., et al. (2018). Reflective properties of melt ponds on sea ice. Cryosphere 12 (6), 1921–1937. doi:10.5194/tc-12-1921-2018

CrossRef Full Text | Google Scholar

Mirsadeghi, M., Cóstola, D., Blocken, B., and Hensen, J. L. M. (2013). Review of external convective heat transfer coefficient models in building energy simulation programs: implementation and uncertainty. Appl. Therm. Eng. 56 (1-2), 134–151. doi:10.1016/j.applthermaleng.2013.03.003

CrossRef Full Text | Google Scholar

Mishchenko, M. I. (2014). Electromagnetic scattering by particles and particle groups: an introduction. Cambridge (UK): Cambridge University Press.

Google Scholar

Mishchenko, M. I. (2018). “Independent” and “dependent” scattering by particles in a multi-particle group. OSA Contin. 1 (1), 243–260. doi:10.1364/OSAC.1.000243

CrossRef Full Text | Google Scholar

Modest, M. F., and Mazumder, S. (2021). Radiative heat transfer. 4th Edition. New York: Academic Press.

Google Scholar

Perovich, D., Smith, M., Light, B., and Webster, M. (2021). Meltwater sources and sinks for multiyear Arctic sea ice in summer. Cryosphere 15 (9), 4517–4525. doi:10.5194/tc-15-4517-2021

CrossRef Full Text | Google Scholar

Perovich, D. K. (2007). Light reflection and transmission by a temperate snow cover. J. Claciol 53 (181), 201–210. doi:10.3189/172756507782202919

CrossRef Full Text | Google Scholar

Picard, G., Libois, Q., and Arnaud, L. (2016). Refinement of the ice absorption spectrum in the visible using radiance profile measurements in Antarctic snow. Cryosphere 10 (6), 2655–2672. doi:10.5194/tc-10-2655-2016

CrossRef Full Text | Google Scholar

Polashenski, C., Perovich, D., and Courville, Z. (2012). The mechanisms of sea ice melt pond formation and evolution. J. Geophys Res. 117 (C1), C01001. doi:10.1029/2011JC007231

CrossRef Full Text | Google Scholar

Popović, P., Cael, B. B., Silber, M., and Abbot, D. S. (2018). Simple rules govern the patterns of Arctic sea ice melt ponds. Phys. Rev. Lett. 120, 148701. doi:10.1103/PhysRevLett.120.148701

PubMed Abstract | CrossRef Full Text | Google Scholar

Raman, A. P., Anoma, M. A., Zhu, L., Rephaeli, E., and Fan, S. (2014). Passive radiative cooling below ambient air temperature under direct sunlight. Nature 515, 540–544. doi:10.1038/nature13883

PubMed Abstract | CrossRef Full Text | Google Scholar

Rockström, J., and Gaffney, O. (2021). Breaking boundaries: the science of our planet. London: Penguin Random House.

Google Scholar

Rosenburg, S., Lange, C., Jäkel, E., Schäfer, M., Ehrlich, A., and Wendisch, M. (2023). Retrieval of snow layer and melt pond properties on Arctic sea ice from airborne imaging spectrometer observations. Atmos. Meas. Techn 16 (16), 3915–3930. doi:10.5194/amt-16-3915-2023

CrossRef Full Text | Google Scholar

Roy, P. K., Shoval, S., Shvalb, N., Dombrovsky, L. A., Gendelman, O., and Bormashenko, E. (2023). Apple-like shape of freezing paraffin wax droplets and its origin. Materials 16 (16), 5514. doi:10.3390/ma16165514

PubMed Abstract | CrossRef Full Text | Google Scholar

Sandell, J. L., and Zhu, T. C. (2011). A review of in-vivo optical properties of human tissues and its impact on PDT. J. Biophot. 4 (11-12), 773–787. doi:10.1002/jbio.201100062

PubMed Abstract | CrossRef Full Text | Google Scholar

Schröder, D., Feltham, D. L., Flocco, D., and Tsamados, M. (2014). September Arctic sea-ice minimum predicted by spring melt-pond fraction. Nat. Clim. Change Lett. 4, 353–357. doi:10.1038/nclimate2203

CrossRef Full Text | Google Scholar

Sterlin, J., Fishefet, T., Massonnet, F., Lecomte, O., and Vancoppenolle, M. (2021). Sensitivity of Arctic Sea ice to melt pond processes and atmospheric forcing: a model study. Ocean. Model 167, 101872. doi:10.1016/j.ocemod.2021.101872

CrossRef Full Text | Google Scholar

Su, D., Hu, X., Wen, L., Lyu, S., Gao, X., Zhao, L., et al. (2019). Numerical study on the response of the largest lake in China to climate change. Hydrol. Earth Syst. Sci. 23 (4), 2093–2109. doi:10.5194/hess-23-2093-2019

CrossRef Full Text | Google Scholar

Su, D., Wen, L., Gao, X., Leppäranta, M., Song, X., Shi, Q., et al. (2020). Effects of the largest lake of the Tibetan Plateau on the regional climate. J. Geophys Res. Atmos. 125 (22), e2020JD033. doi:10.1029/2020JD033396

CrossRef Full Text | Google Scholar

Tuchin, V. V. (2007). Tissue optics: light scattering methods and instruments for medical diagnosis. second ed. Bellingham (WA): SPIE Press. v. PM166.

Google Scholar

Wang, M., Wen, L., Li, Z., Leppäranta, M., Stepanenko, V., Zhao, Y., et al. (2022). Mechanisms and effects of under-ice warming water in Ngoring Lake of qinghai-tibet plateau. Cryosphere 16 (9), 3635–3648. doi:10.5194/tc-16-3635-2022

CrossRef Full Text | Google Scholar

Warren, S. G., and Brandt, R. E. (2008). Optical constants of ice from the ultraviolet to the microwave: a revised compilation. J. Geophys Res. Atmos. 113 (D14), D14220. doi:10.1029/2007JD009744

CrossRef Full Text | Google Scholar

Zhang, G., and Duan, S. (2021). Lakes as sentinels of climate change on the Tibetan Plateau. All Earth 33 (1), 161–165. doi:10.1080/27669645.2021.2015870

CrossRef Full Text | Google Scholar

Zhou, F., Yao, M., Fan, X., Yin, G., Meng, X., and Lin, Z. (2022). Evidence of warming from long-term records of climate and permafrost in the hinterland of the Qinghai-Tibet Plateau. Front. Environ. Sci. 10, 836085. doi:10.3389/fenvs.2022.836085

CrossRef Full Text | Google Scholar

Nomenclature