Computational reconstitution of spine calcium transients from individual proteins

We have built a stochastic model in the program MCell that simulates Ca²⁺ transients in spines from the principal molecular components believed to control Ca²⁺ entry and exit. Proteins, with their kinetic models, are located within two segments of dendrites containing 88 intact spines, centered in a fully reconstructed 6 × 6 × 5 μm³ cube of hippocampal neuropil. Protein components include AMPA- and NMDA-type glutamate receptors, L- and R-type voltage-dependent Ca²⁺ channels, Na⁺/Ca²⁺ exchangers, plasma membrane Ca²⁺ ATPases, smooth endoplasmic reticulum Ca²⁺ ATPases, immobile Ca²⁺ buffers, and calbindin. Kinetic models for each protein were taken from published studies of the isolated proteins in vitro. For simulation of electrical stimuli, the time course of voltage changes in the dendritic spine was generated with the desired stimulus in the program NEURON. Voltage-dependent parameters were then continuously re-adjusted during simulations in MCell to reproduce the effects of the stimulus. Nine parameters of the model were optimized within realistic experimental limits by a process that compared results of simulations to published data. We find that simulations in the optimized model reproduce the timing and amplitude of Ca²⁺ transients measured experimentally in intact neurons. Thus, we demonstrate that the characteristics of individual isolated proteins determined in vitro can accurately reproduce the dynamics of experimentally measured Ca²⁺ transients in spines. The model will provide a test bed for exploring the roles of additional proteins that regulate Ca²⁺ influx into spines and for studying the behavior of protein targets in the spine that are regulated by Ca²⁺ influx.

Introduction

One major goal of cellular neuroscience is to understand the molecular mechanisms that control the changes in synaptic strength governing learning and the formation of memory. It is well-established that the trigger for changes in synaptic strength in the CNS is influx of Ca²⁺ into dendritic spines (Franks and Sejnowski, 2002; Sjöström and Nelson, 2002). Thus, to understand the rules that govern changes in synaptic strength during normal brain function, and to clarify the interactions of pharmaceuticals with excitatory synapses, it is important to understand Ca²⁺ control mechanisms at a quantitative level. The basal level of Ca²⁺ in spines and dendrites and the size and timing of transient increases in Ca²⁺ during electrical activity are tightly controlled. Several decades of biochemical and biophysical work on individual enzymes and channels has resulted in detailed characterizations of the kinetic properties of proteins that are believed to regulate Ca²⁺ in spines and dendrites. At the same time, electrophysiologists have used fluorescent dyes that are sensitive to Ca²⁺ concentration to measure Ca²⁺ transients in spines produced by electrical signals in intact neurons. Here we use computer simulations to ask whether the aggregate behavior of the enzymes and channels believed to regulate Ca²⁺ in spines can account quantitatively for Ca²⁺ transients observed in spines in living neurons.

Synaptic strength is regulated by biochemical pathways driven by Ca²⁺ influx through N-methyl-D-aspartate-type glutamate receptors (NMDARs) and voltage-dependent Ca²⁺ channels (VDCCs) in dendritic spines (Kennedy, 2013). The direction of change in synaptic strength is critically dependent on the timing and amplitude of the Ca²⁺ influx (Magee and Johnston, 1997; Markram et al., 1997; Bi and Poo, 1998). Because NMDARs are sensitive to both voltage and glutamate, a few milliseconds difference in the timing of presynaptic release and postsynaptic depolarization can dramatically alter the amplitude and timing of Ca²⁺ transients and the direction of resulting changes in synaptic strength. It is particularly important to understand the complex mechanisms that regulate synaptic strength because mutations in several proteins that influence its regulation have been correlated with increased risk of mental diseases or with intellectual disability (Selkoe, 2002; Pinto et al., 2010; Hamdan et al., 2011; Sklar et al., 2011; Network and Pathway Analysis Subgroup of the Psychiatric Genomics, 2015).

As a first step, we have asked whether the properties of the crucial proteins that biochemists, pharmacologists, electrophysiologists and biophysicists have studied in vitro, together with our present understanding of their relative numbers and locations, are sufficient to explain the timing of Ca²⁺ transients observed experimentally in situ in stimulated spines. For a simpler system, biochemists would use a reconstitution experiment to try to reproduce the cellular behavior in question by combining purified proteins in a test tube (e.g., Kinoshita et al., 2001). However, full reconstitution experiments are not experimentally feasible for a complex function like control of Ca²⁺ concentration in spines because this function depends on the precise locations of the proteins on membranes and cytosolic structures.

As an alternative approach to experimental reconstitution, we generated a computer model in the program MCell (Kerr et al., 2008). The model incorporates realistic dendritic geometry, and includes the experimentally measured kinetics of the major Ca²⁺-handling proteins that are believed to control Ca²⁺ flux in spines of pyramidal neurons in area CA1 of the hippocampus (Table 1). It also incorporates their experimentally estimated numbers and spatial localizations. We show that application of a simulated electrophysiological stimulus to the model can produce Ca²⁺ transients that replicate the timing and amplitude of Ca²⁺ transients measured in spines in response to a back-propagating action potential (bAP; Sabatini et al., 2002). The successful reconstitution required adjustment of nine parameters within their range of experimental uncertainty.

TABLE 1

Table 1. Chemical kinetic rates and diffusion constants of molecules in model.

The calibration of parameters was done by adding appropriate fluorescent Ca²⁺ indicators to the model, simulating the response of the indicators to a bAP, and then comparing the simulated responses to experimental results obtained in the presence of the same indicators (Sabatini et al., 2002; Scheuss et al., 2006). After calibration, we removed the indicators so that the model better approximated the in vivo state, and again applied simulated electrophysiological stimuli. The cytosolic Ca²⁺ transients produced in this way had a faster rise time and higher amplitude than those previously calculated from experimental fluorescence data (Maravall et al., 2000; Sabatini et al., 2002; Yasuda et al., 2003). We believe that our estimates are likely to be more accurate because the previous calculations were made with equations that were derived assuming steady-state conditions for Ca²⁺ binding to proteins in the spine (Neher and Augustine, 1992); but, our simulations show that a steady state is not reached during the rapid Ca²⁺ transients produced by a single bAP.

Methods

The model was encoded in version 3.2 of the MCell Monte Carlo simulator (Kerr et al., 2008). MCell is a particle-based simulator of 3D reaction-diffusion systems. It permits the specification of a detailed cellular geometry and the assignment of discrete molecules, with their associated kinetics, to positions in the membrane, cytosol, or extracellular space. During the simulation, the diffusion of individual molecules is modeled as a pseudo-random walk constrained by the assigned diffusion constants. Fixed molecules have a diffusion constant of zero. Molecules can diffuse in two dimensions on the membrane, or in three dimensions in the cytosol and extracellular space. Interactions of molecules are detected by ray-tracing (Kerr et al., 2008), and binding events and/or first-order reactions are set to occur stochastically based on probabilities calculated from the kinetic rate constants assigned to each reaction. The global time step for all simulations was 1 μs. In MCell's reaction/diffusion algorithms, diffusion of individual molecules is simulated by a Monte Carlo random walk. The random walk is generated by scheduling each particle to move at a certain time in discrete spatial steps the length and direction of which are chosen by Monte Carlo sampling of the solution to the diffusion equation. During the simulation, time progresses by processing scheduled events in temporal order and the minimum elapsed time between events can be arbitrarily small. However, for internal accounting purposes the researcher specifies a global fixed timestep for keeping track of the states of most molecules. To balance computational efficiency and accuracy, molecules that move or react quickly can be scheduled to move/react with a finer temporal granularity than those that move/react more slowly. In our simulatins, we used this adaptive time stepping feature to simulate interaction of Ca²⁺ with a time step of 0.1 μs. Counting of reactions and molecules is described below. Data analysis was performed with custom Python scripts using Python-3.4, NumPy-1.9.2, SciPy-0.15.1, and matplotlib-1.4.3. Visualizations were created with the open source program Blender (blender.org) using the CellBlender addon. Both MCell and CellBlender are available at mcell.org.

Geometry

We started with a 6 × 6 × 5 μm cube of neuropil from stratum radiatum of the hippocampus reconstructed from electron micrographs of 100 serial sections (Figure 1, see Mishchenko et al., 2010; Kinney et al., 2013). The process of reconstruction, adjustment of extracellular space, and creation of water-tight triangulated surfaces for computer simulation is described in detail in Kinney (2009), Kinney et al. (2013), and Edwards et al. (2014). The reconstruction of the extent and tortuosity of the extracellular space permits accurate modeling of the time-course of diffusion of glutamate through and out of the synaptic cleft. The cube is centered on two segments of dendrite that are entirely included within the volume. We used these two for the reconstitution study (Figure 1C). The larger proximal apical dendritic segment has a mean diameter of 2.1 μm and contains 72 spines that are located completely within the volume (Figure 1D). The smaller dendritic segment has a diameter of 0.8 μm and contains 16 complete spines (Figure 1E). In these two dendrites, endoplasmic reticulum (ER) and mitochondria were traced and included in the reconstruction and simulations (Figures 1F,G). Protrusions of the smooth endoplasmic reticulum (SER) into the spine neck and head are present in 14 spines in the larger dendrite and three in the smaller dendrite (about 19% of the spines of both dendrites). This percentage is comparable to that reported by Spacek and Harris (1997) and Cooney et al. (2002). Although all of the membranous structures in the cube were included in the simulations to allow for appropriate glutamate diffusion and re-uptake, we collected data about Ca²⁺ flux only from these two dendritic segments and their spines.

FIGURE 1

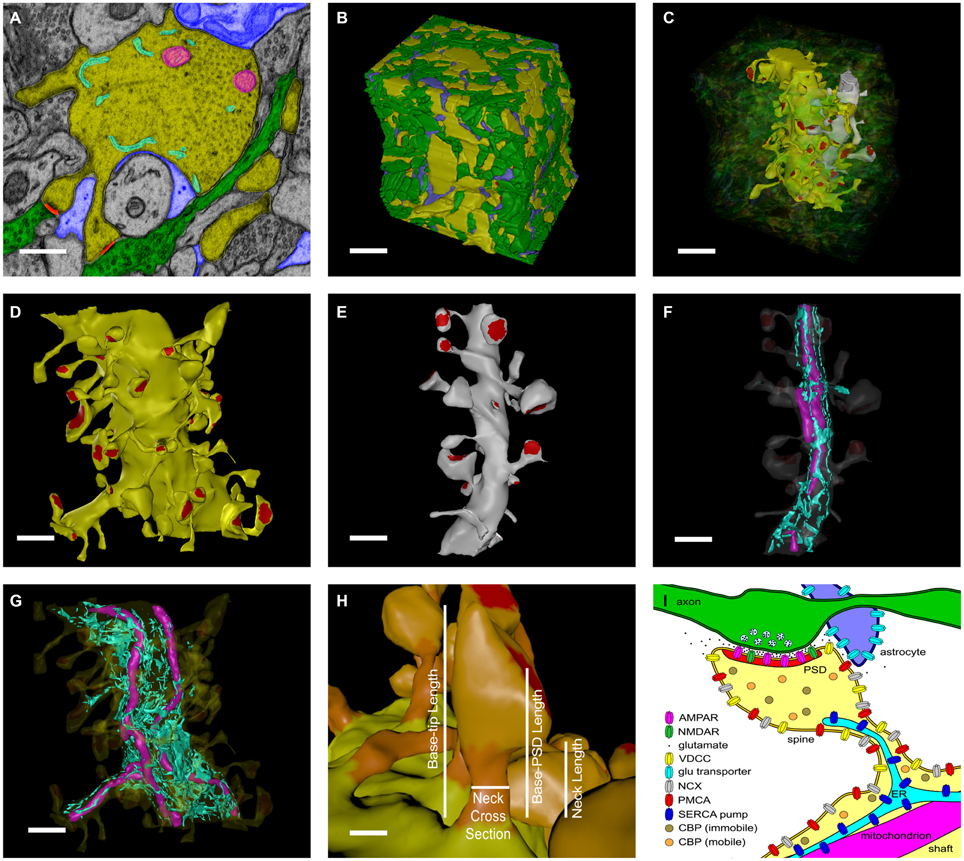
Figure 1. Reconstruction of hippocampal neuropil. (A) Hand segmentation of 2D-objects within a single EM thin section. The entire reconstruction consisted of 100 serial EM thin sections 50 nm thick. Each plasma membrane bound structure was traced in each thin section but only a few structures are highlighted here for illustrative purposes. A large apical dendrite is highlighted in yellow along with its enclosed endoplasmic reticulum (cyan) and mitochondria (magenta). Spines that are part of the principal dendrite, also shown in yellow, sometimes appear disjoint from the dendrite in a given thin section. Two axons that make synaptic contacts with two spines of the large apical dendrite in this plane of section are shown in green. PSDs and presynaptic active zones were annotated by enclosing them in a separate close-fitting contour (red). Processes of an astrocytic glial cell are shown in blue. Scale bar is 0.5 μm. (B) Reconstructed volume of neuropil. Dendrites are yellow. Axons are green. Astrocyte is blue. The extracellular space was adjusted so that the distance between components was 20 nm using an algorithm described in Kinney et al. (2013). Scale bar is 1 μm. (C) Two dendrites in the reconstructed volume were selected for simulations of glutamatergic synaptic transmission and postsynaptic calcium dynamics. A large apical dendrite is shown in yellow and a smaller branch dendrite is shown in light gray. The selected dendrites are shown in relation to one another embedded in the semitransparent neuropil. The synaptic contact areas (red) on the two selected dendrites were identified and labeled as shown in (D,E). Scale bar is 1 μm. (D,E) The PSD regions (red) of the large apical dendrite (D) and the smaller branch dendrite (E) were annotated. Scale bar is 1 μm. (F,G) Intracellular organelles of the small branch dendrite (F) and large apical dendrite (G), including the reconstructed endoplasmic reticulum (cyan) and mitochondria (magenta). Scale bar is 1 μm. (H) The spine head (light-orange), neck (dark-orange), and dendritic shaft (yellow) were also annotated. Geometric measurements used in the analysis are shown as annotations. The neck cross section area was measured at a point halfway along the length of the neck. Scale bar is 0.25 μm. (I) Summary of all neuropil elements included in the model. The PSD was used to lasso a region of the spine surface for NMDAR and AMPAR placement. Presynaptic vesicles are shown for illustration only and were not included in simulations; instead glutamate was released directly into the synaptic cleft (see Methods Section). Note that about 19% of spines in the reconstruction contained ER protruding from the dendritic shaft into the spine neck and head.

The locations of postsynaptic densities (PSDs) were defined by first tracing the contours of each PSD and active zone (AZ) on each original micrograph on which they appeared. The stack of such contours for a given PSD-AZ pair encloses the synaptic junction. The reconstructed contours include the intracellular extent of both the PSD and the AZ and intersect with the pre- and postsynaptic membrane associated with each. Therefore, we used the outer boundaries of the contours as a “3D-lasso” to tag surface mesh triangles representing the postsynaptic membrane and the location of the associated PSD (labeled in red for the large dendrite in Figure 1D).

MCell permits counting and tracking of molecules within a defined volume and also tracking of molecular fluxes across a defined surface. In the simulations reported here we tracked molecules of free Ca²⁺, Ca²⁺-bound to calcium binding proteins, and Ca²⁺ bound to indicator molecules in each spine head by creating “counting boxes” in which changing levels of each species were counted during the simulation. To count species in the spine head, a continuous form-fitting mesh was defined with its surface 5 nm from the outside surface of the spine head, and closed where the head connects with the neck. To count species in the entire spine, and to track the flux of Ca²⁺ through the base of the spine neck into the shaft, a second continuous form-fitting mesh was defined with its surface 10 nm from the outside surface of the spine (both head and neck), and closed at the place where the neck of the spine meets the dendritic shaft. Numbers of molecules within each counting box, and the flux between each spine and the shaft were measured at each time step of the simulations (1 μs), except for Ca²⁺, which was measured every 0.1 μs. All counts were recorded in an output file every 100 μs. Counts of molecules were sometimes converted to concentrations by converting to moles and dividing by the volume of the spine after subtracting the volume of any ER or mitochondria that intersected the sampling volume.

Stimuli

The simulations reported here were initiated by release of glutamate from a single site on the presynaptic membrane (see Keller et al., 2008). The release was accompanied by a simulated voltage change in the postsynaptic membrane represented by 1 μs step changes in voltage read from a file generated in the program NEURON. Stimuli were simulated by adapting a NEURON model of a layer 5 neocortical pyramidal cell (Mainen et al., 1995). The NEURON model was implemented in pyramidal neuron “j4,” and included I_Na, I_K, I_KM (K channel blocked by Ach acting through the muscarinic receptor), I_KCa [Ca²⁺-dependent K channels (e.g., I_BK, I_K, I_SK, and I_AHP currents), passive K (resting K channel), I_CaHVA (HVA-type Ca²⁺ channel), I_CaLVA (LVA, or T-type Ca²⁺ channel) in spines only], PMCA pump mediating Ca²⁺ decay. Its geometry consists of the soma, 11 primary dendrites, and 87 branches, divided into 164 compartments. Details are available in the NEURON ModelDB (https://senselab.med.yale.edu/ModelDB/ShowModel.cshtml?model=2488).

Backpropagating action potentials (bAP) were simulated by injecting current into the axon hillock and recording the voltages experienced at a spine located on a dendritic branch ~100 μm from the soma, as described in Keller et al. (2008). The NEURON model did not contain glutamate receptors. The excitatory postsynaptic potential (EPSP) was simulated by injecting current into the spine head as an alpha function such that a 5.8 mV peak EPSP was produced (see Keller et al., 2008). The peak of the EPSP occurred about 0.3 ms after release and decayed in ~2 ms. The EPSP plus bAP was simulated by injecting current into a spine to create an EPSP and 10 ms later injecting current into the axon hillock to initiate an action potential. The time-varying voltages recorded at the spine during these three stimuli were used to drive voltage-dependent transition rates in the models of VDCCs and NMDARs. The voltage changes alter the kinetic constants for relief of the Mg²⁺ block of the NMDARs, determine the flux of Ca²⁺ through open NMDAR and VDCC channels, and alter the kinetic constants that drive gating of VDCCs. An NMDAR channel opens and fluxes Ca²⁺ in the simulation only when glutamate is bound to the receptor at the time that the Mg²⁺ block is relieved.

Proteins

Proteins were placed onto the membrane surfaces of the reconstructed dendrites or in the volume of the cytosol as shown in the cartoon in Figure 1I, and described in detail below. For each simulation initiated by a distinct random seed, proteins were placed randomly at a specified density or concentration, within each specified membrane or spatial compartment. Thus, the exact spatial locations of molecules and the sequences of stochastic binding events and enzymatic reactions vary randomly and depend on the seed used to initiate the simulation.

Sources of Ca²⁺ Influx

Glutamate receptors

AMPARs and NMDARs were placed into the postsynaptic membranes overlying the PSDs. The number of AMPARs is not a critical parameter in this study because the simulations are primarily concerned with Ca²⁺ influx through NMDARs and VDCCs. AMPARs are included in the simulation because AMPARs compete with NMDARs for binding of glutamate. Thus, the competition for binding of glutamate is modeled directly, allowing an accurate estimate of the activation of NMDARs. The density of AMPARs was set to 1200 μm⁻² of PSD surface (120 receptors for a PSD of diameter 350 nm). In vivo, the number of AMPA receptors in spines is highly variable and is altered by synaptic plasticity (Nusser et al., 1998; Kharazia and Weinberg, 1999; Takumi et al., 1999; Racca et al., 2000). We have not included calcium-permeable AMPARs because they are relatively rare in excitatory synapses onto CA1 pyramidal neurons and are usually not a major source of Ca²⁺ flux. We used a kinetic model for activation of AMPARs by glutamate (Figure 2A; Table 1) based on an empirical model from Jonas et al. (1993) that describes recordings at 22–24°C from hippocampal slices of 15 to 24 day old rats. The model represents the behavior of AMPARs that contain a mixture of GluA1 and GluA2 subunits. We adjusted the parameters to 34°C using a Q₁₀ of 2.0, because protein functions most commonly display a Q10 that is close to 2; thus, the adjustment is an approximation.

FIGURE 2

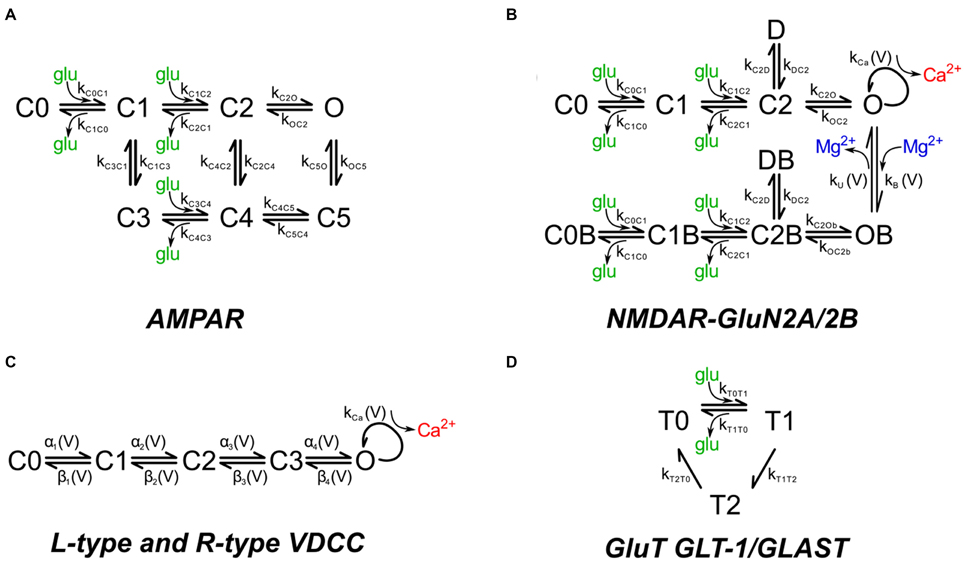
Figure 2. Chemical kinetic schemes of receptors, Ca²⁺ channels, and glutamate transporter. The kinetic rate constants for the reaction pathways are given in Table 1. (A) Glutamate-gated AMPAR with a mixture of GluA1 and GluA2 subunits and (B) glutamate-gated NMDA receptor with a mixture of GluN2A (NR2A) and GluN2B (NR2B) subunits were distributed on the dendritic spine head plasma membrane associated with the PSD. Mg²⁺ block was modeled by the asymmetric trapping block model of Vargas-Caballero and Robinson (2004). (C) Voltage-dependent Ca²⁺ channels on the spine head and neck are the sole source of calcium during backpropagating action potentials. (D) Glutamate transporter representing a combination of GLT-1 and GLAST transporter subtypes were distributed on the astrocytic glial processes.

NMDARs were placed in the membranes overlying PSDs at a density of 150 μm⁻² (15 receptors for a PSD of diameter 350 nm). This number is consistent with estimates of receptor numbers per PSD in the literature (e.g., 5–30 NMDARs per PSD, Spruston et al., 1995). We used the asymmetric trapping block kinetic model for activation of NMDARs, which includes distinct activation and deactivation rates for Mg²⁺ free and Mg²⁺ bound channels (Vargas-Caballero and Robinson, 2004; Figure 2B; Table 1). Their measurements were made at a temperature of 24–25°C; as we did for the AMPA receptors, we multiplied the rates for the NMDA receptors by a factor of 2 to adjust them to 34°C. The peak opening of NMDAR channels (whether blocked or unblocked) occurs at an average of 20 ms after glutamate release. The extra synaptic NMDARs on which this kinetic scheme is based contain GluN1 and a mixture of GluN2A and GluN2B subunits and are believed to have a higher proportion of GluN2B subunits than synaptic receptors (Stocca and Vicini, 1998).

We simulated the behavior of the NMDAR channel during a bAP, or during an EPSP followed by a bAP, by adapting a previously published model of the electrical behavior of a layer 5 neocortical pyramidal cell made in the program NEURON (Mainen et al., 1995), as described in detail in Keller et al. (2008), and above under Stimulus. Briefly, we used NEURON to generate a time series of dendritic membrane voltages for dendrites at the appropriate apical location, and a current–voltage (I–V) curve indicating the Ca²⁺ current through the open channel at each voltage. For the calculation, Ca²⁺ conductance was set at 4.5 pS (10% of 45 pS) and E_NMDA was set to 3 mV (Jahr and Stevens, 1993). The voltages were read by MCell and used to calculate probabilities of blocking and unblocking by Mg²⁺ from the equations for k_B and k_U in Table 1. When a receptor adopted an opened, unblocked state, the Ca²⁺ current through the pore was read from the I-V curve, and converted into the rate of Ca²⁺ flux per second according to the simple electrical equation,

$\begin{array}{cc}J=\frac{1}{2F}\times 6.02\times {10}^{23}\frac{\text{ions}}{\text{mole}}& (1)\end{array}$

with flux, J, in ions/s, current, I, in amperes, and F as Faraday's constant. For example, if a Ca²⁺ current of 1 pA flows through a receptor, MCell would use a flux rate of 3.12 × 10⁶ s⁻¹ to generate Ca²⁺ ions at the cytosolic mouth of the pore. To simulate the flux of individual ions through an ionotropic receptor, MCell randomly samples the Poisson distribution of time of the next flux event calculated from the flux rate constant. Thus, ions move one at a time through the open pore and the time between flux events has a Poisson distribution, generating the correct stochastic noise.

Voltage-Dependent Calcium Channels (VDCCs)

Rapid, transient increases in dendritic Ca²⁺ occur when VDCCs in the membranes of spines and shafts are activated by excitatory postsynaptic potentials (EPSPs) or by bAPs. For the stimuli used in the simulations reported here, they are the largest source of Ca²⁺ influx. The precise complement of VDCCs in spines and shafts of pyramidal neurons is uncertain for two reasons. First, subtypes of VDCCs are sometimes difficult to separate pharmacologically. For example, CaV_1.3 channels (one of two L-type channels) are difficult to distinguish from CaV_2.3 channels (R-type) because both are resistant to inhibition by dihydropyridines (Higley and Sabatini, 2008). Second, neurons in different parts of the brain, such as the hippocampus and cortex, have distinct complements of Ca²⁺ channels in their dendrites (e.g., Markram et al., 1995; Koester and Sakmann, 2000; Bloodgood and Sabatini, 2007; Higley and Sabatini, 2008). Nonetheless, it is generally agreed that spines on pyramidal neurons in area CA1 of the hippocampus contain primarily R-type VDCCs with a small contribution from T-type channels; while the shafts of these same dendrites contain L, R, and T-type channels (Bloodgood and Sabatini, 2007).

The voltage sensitivity and activation kinetics of L and R-type channels are similar. However, R-type channels undergo slow inactivation during a depolarization of several 100 ms; whereas L-type channels do not (Magee and Johnston, 1995a). In this study, the activating stimuli were a single EPSP, and/or a single bAP. Therefore, we assumed that inactivation of the R-type VDCCs was not significant in the simulations reported here. This assumption permitted us to use a single kinetic scheme to represent both L- and R-type channels (Figure 2C). We adopted a five state kinetic scheme from Bischofberger et al. (2002; Figure 2C; Table 1). The scheme generated correct voltage sensitivity and activation curves at 23°C for L or R-type channels activated by single stimuli. We adjusted the parameters to 34°C using a Q₁₀ of 2.0. A single channel conductance of 2.5 pS was reported by Church and Stanley (1996) based on measurements at 25°C of single channel conductances of VDCCs in chick ciliary ganglia at physiological Ca²⁺ concentration. As they suggested, we adjusted the conductance to 3.72 pS for 34°C using a Q₁₀ of 1.55.

The probabilities of changes in state of individual channels and the Ca²⁺ ion influx through the open state was simulated by MCell in a manner similar to that described above for NMDA receptors. The time series of dendritic membrane voltages generated in NEURON was read by MCell and used to calculate α_i and β_i according to the equations in Table 1. The rate of Ca²⁺ flux through open channels at each membrane voltage (k_Ca) was calculated from Equation (2) (Bischofberger et al., 2002).

$\begin{array}{cc}{k}_{Ca}(V_m)=\frac{3.72V_m{N}_A\left[0.3993-e^{\left(\frac{-V_m}{80.36}\right)}\right]}{2F\left(1-e^{\left[\frac{V_m}{80.36}\right]}\right)}& (2)\end{array}$

The rate constant k_Ca(V_m) has the units s⁻¹.

VDCCs have been estimated to have a density of ~2 μm⁻² in apical dendrites when measured in membrane patches (Magee and Johnston, 1995a). We arrived at a calibrated density for VDCC's on spines of 1.20 μm⁻² and on shafts of 2.67 μm⁻², as described under Results Section.

T-type channels are also present in spines; however, they are largely inactivated at the resting potential that we used in our model, and that was used in the experiments of Sabatini et al. (2002; −65 to −70 mV; Fraser and MacVicar, 1991). Thus, they would contribute only a small proportion of Ca²⁺ influx after a single bAP stimulus (Magee and Johnston, 1995b). Therefore, they are not included in this model.

Glutamate transporters

After its release, the excitatory transmitter glutamate is removed from the extracellular space by glutamate transporters in the astrocyte membrane. We placed transporters in the astrocytes at a density of 10,000 μm⁻² in agreement with the measurements of Lehre and Danbolt (1998). Crystal structures of related transporters suggest that its diameter is ~5 to 8 nm, indicating a range of maximum packing densities of 16,000–40,000 μm⁻² (Yernool et al., 2004; Penmatsa et al., 2013). Thus, the glutamate transporter occupies a large fraction of the surface of astrocytes.

We used a simplified kinetic scheme (Figure 2D), implemented by Geiger et al. (1999), that reproduces the major binding, unbinding, and translocation characteristics of glutamate transport in cerebellar Purkinje cells, which is primarily attributed to EAAT4 transporters (Otis and Jahr, 1998). In hippocampal astrocytes, glutamate transport is mediated predominantly by EAAT1 (GLT-1) with a lesser contribution by EAAT2 (GLAST; Danbolt, 2001); but see Hu et al. (2003) on EAAT4 expression. Full kinetic models, with rate constants, for EAAT1, including Na⁺, K⁺, H⁺, and voltage dependence (Bergles et al., 2002), and for EAAT2 (Wadiche and Kavanaugh, 1998) have been published. However, the reduced model accurately reflects the slow turnover rate and the binding affinity for glutamate in the μM range of EAAT1 and EAAT2 (Arriza et al., 1994; Wadiche et al., 1995; Bergles et al., 2002). Thus, we believe it is sufficient for the present study in which we release single quanta of glutamate at individual synapses.

This model is primarily concerned with understanding the major proteins contributing to Ca²⁺ flux in the postsynaptic spine, therefore, we didn't include glutamate transporters on presynaptic axonal processes, although they have been shown to be present there in neuronal cultures and in perfusion fixed brain tissue (Wang et al., 1998; Chen et al., 2004). We also didn't include them on the postsynaptic membrane, although some studies have suggested they can modulate NMDA receptor activation (Diamond, 2001). In our reconstructed neuropil, not all spines are immediately adjacent to an astroglial process, therefore, the time-course of persistence of glutamate in the synaptic cleft is likely to be highly variable from spine to spine in the simulations (Ventura and Harris, 1999; Witcher et al., 2007). Glutamate transporters in the synaptic membrane would reduce this variability, but are not likely to have a large effect on the overall activation of NMDA receptors.

Cytosolic Ca²⁺ Binding Proteins

Immobile cytosolic Ca²⁺-binding Proteins

Ca²⁺ ion is buffered in the cytosol by binding to mobile and immobile “buffers.” The immobile buffers are considered to be immobile proteins with a mixture of low and high affinities for calcium (Neher and Augustine, 1992). To simulate these proteins we have used a single immobile buffer at a concentration of 78.7 μM with a K_D of 2.0 μM (Figure 3A). These values were chosen by calibrating the model so that it reproduces measurements of calcium fluxes after bAPs as described under Results Section. The concentration of immobile Ca²⁺ buffers in neurons have been estimated in the range of tens to a few 100 μM (Neher and Augustine, 1992; Maravall et al., 2000)

FIGURE 3

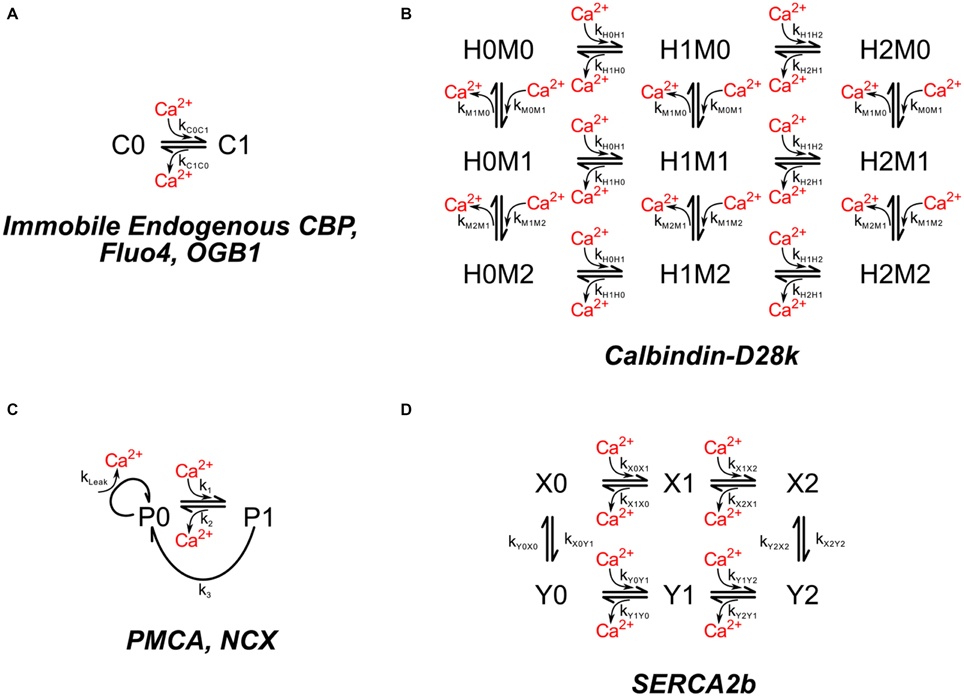
Figure 3. Chemical kinetic schemes of endogenous Ca²⁺ buffer, calbindin-D28k, Ca²⁺ pumps, and Na⁺–Ca²⁺ exchanger. (A) The interaction of Ca²⁺ with immobile endogenous CBPs was modeled as a simple first-order reversible reaction. Molecules of immobile endogenous CBPs were distributed throughout the volume of the dendritic and spine cytoplasm. (B) The mobile high affinity calcium buffer calbindin-D28k was included in the dendritic and spine cytoplasm. (C) Ca²⁺ pumps PMCA, and NCX were modeled with identical kinetic schemes but different rate constants. PMCA and NCX pumps were placed on the spines and dendritic shafts. (D) The SERCA pump was placed on ER membrane.

Calbindin

Calbindin is a major calcium buffering protein present in spines of hippocampal neurons. Its concentration in spines is debated. For simulations in which calbindin is included, we used 45 μM, the value reported for pyramidal neurons in area CA1 by Müller et al. (2005). We used the kinetic model for binding of Ca²⁺ to two high affinity sites and two medium affinity sites on calbindin published by Nagerl et al. (2000; Figure 3B; Table 1).

Fluorescent Ca²⁺ indicators

We calibrated parameters of the model by fitting the characteristic of simulated Ca²⁺ transients to measurements from Ca²⁺ transients in individual spines carried out with the use of the fluorescent Ca²⁺ indicators, Fluo-4 and Oregon Green 488-BAPTA (OGB-1; Sabatini et al., 2002). For the calibration process, a model of the appropriate fluorescent indicator was added to the dendritic cytosol as described under Results Section. The kinetic model for binding of Ca²⁺ by these indicators is shown in Figure 3A, and parameters are listed in Table 1. The diffusion constants were calculated from the Stokes/Einstein equation $D=\frac{kT}{6\pi \nu r}$. We set ν equal to $\frac{1}{3}$ the viscosity of water (0.001 $\frac{kg\times m}{s}$) to approximate the cytosol. To calculate r (the hydrodynamic radius of the diffusing particle), we first calculated the volume (V) from the molecular masses of Fluo4 and OGB1 (1100 and 1200 g/mol, respectively) and their densities (~1.4 g/cc). Both values were obtained from LifeTechnologies.com. We then assumed that $V=\frac{4\pi r^3}{3}$.

Removal of Ca²⁺ from the Cytosol

Experiments with fluorescent Ca²⁺ indicators and pharmacological agents indicate that Ca²⁺ is removed from the spine cytosol by the combined action of three transmembrane proteins, Na⁺/Ca²⁺ exchangers (NCX's), smooth endoplasmic reticulum Ca²⁺ ATPases (SERCA's), and plasma membrane Ca²⁺ ATPases (PMCA's).

NCX's

The NCX's have a relatively low affinity for Ca²⁺ (K_D ~ 3 μM), but a large exchange capacity with turnover numbers sometimes as high as several thousand per second (Hilgemann et al., 1991; Carafoli et al., 2001). During calibration, the density of NCX's was set to 142 μm⁻² on spines and 488 μm⁻² on the shaft plasma membrane. These numbers are consistent with the finding of Lörincz et al. (2007) that shafts have a considerably higher density of NCXs than do spines. The kinetics of NCX were modeled by a Michaelis–Menten-like scheme (Figure 3C; Table 1). The turnover rate (k₃) at which a pump with Ca²⁺ bound extrudes Ca²⁺ from the cell, was setat 600 s⁻¹. The concentration of Ca²⁺ at which the pump operates at half maximum velocity (K_M) was set at 3 μM (Blaustein and Lederer, 1999).

PMCA's

PMCA's, in contrast to NCX's, have a high affinity for Ca²⁺ (K_D < 0.5 μM) and use the energy of ATP hydrolysis to reduce the Ca²⁺ concentration to its resting level with a turnover rate of ~12 s⁻¹ measured in vitro (Penheiter et al., 2003; Caride et al., 2007). We used the same kinetic scheme to model PMCA kinetics as for NCXs, but with parameters of 12 s⁻¹ for turnover rate and 0.18 μM for K_M (Figure 3C; Table 1). The best fit to experimental measurements during the calibration (see Results and Discussion Sections), was obtained with a density of 998 μm⁻² for PMCAs on the spine membrane and 488 μm⁻² on the shaft plasma membrane.

SERCA's

About 19% of the spines in our sample contain SER. However, the ratio of spine SER membrane to spine plasma membrane is small, even in those spines. Nonetheless, we included SERCA pumps in the SER. The hippocampus expresses high levels of the SERCA2b isoform (Baba-Aissa et al., 1996), and only low levels of SERCA3 (Wuytack et al., 1995). We made the simplifying assumption that all of the SERCA pumps in CA1 pyramidal neurons are SERCA2B. SERCA pumps were placed on the SER membrane at a density of 1000 μm⁻² (about half the density measured in RBL-2H3 mast cells by Means et al. (2006). The behavior of SERCA pumps is not fit well by the simple scheme that describes PMCA pumps (Figure 3C). Therefore, we modeled SERCA2b pumps according to a modification of the kinetic scheme from Higgins et al. (2006; Figure 3D; Table 1) for the SERCA pump at 37°C. We added individual Ca²⁺ binding events to the four state model in Higgins et al. (2006) to make a six state model, choosing a k_on of 1 × 10⁸ M⁻¹ s⁻¹ for binding of each Ca²⁺ to states X0 and X1 to satisfy the requirement for fast transition rates between X0, X1, and X2. We calculated the k_off values to maintain the K_D's specified in Higgins et al. (2006). The k_on rates for binding of Ca²⁺ to Y0 and Y1 were set to 1 × 10⁵ M⁻¹ s⁻¹ and the k_off rates were calculated according to the specified K_D's. These values allowed us to satisfy the Gibbs free energy constraints for binding and ATP hydrolysis as discussed in Higgins et al. (2006). We assumed a constant Ca²⁺ concentration of 60 μM in the ER lumen.

Boundary Conditions

Accurate modeling of a biochemical reaction–diffusion system requires appropriate treatment of the boundary conditions. We used a Neumann boundary condition; that is, we made the truncated ends of the two simulated dendritic segments reflective to Ca²⁺. This configuration causes Ca²⁺ flux to behave as if each dendritic segment were connected to a much greater length of dendrite, all seeing the same stimulus. Thus, when a back propagating action potential (bAP) activates VDCCs in a 5 μm length of dendrite, we assume that the electrical length constant of the dendrite would cause the bAP to activate VDCCs in the neighboring length of dendrite equally, causing Ca²⁺ ions to flow into and out of the segments at an equal rate.

The basal steady-state Ca²⁺ concentration was maintained at 100 nM by adjusting the leak rates of the PMCA's and NCX's (Figure 3C; Table 1). In addition to translocating Ca²⁺ out of the cell, PMCA's and NCX's allow a small leak of Ca²⁺ back into the cell. A leaky pump model is consistent with thermodynamic principles of reversibility and has significant advantages for calibration. If the rate of leaking and pumping is properly balanced in the rate constants of the kinetic scheme, then the resting [Ca²⁺] will be independent of pump density, and the proper resting [Ca²⁺] will be maintained with any number of pump molecules. The leaky pump model prevents the accidental introduction of standing gradients of Ca²⁺ or steady-state fluxes of Ca²⁺ along the length of the resting dendrite or between the spines and dendritic shaft. In contrast, standing gradients and fluxes would be virtually impossible to eliminate if the pumps and leaks were implemented as separate proteins. We used Michaelis–Menten equations to calculate the leak rate as follows. We assumed that the pump has an average basal extrusion rate (r_ex) at 100 nM Ca²⁺ that is related to the fraction of pumps with bound Ca²⁺ (f_b) at that concentration: $r_{ex}=f_b{}^{\ast }{k}_3$. The fraction of pumps with bound Ca²⁺, both at rest and after a stimulus, depends on the Ca²⁺ concentration. The quasi-steady-state assumption (Briggs and Haldane, 1925) yields the relations:

$\begin{array}{cc}\left[P_{C{a}^{2+}}\right]=\frac{{\left[P\right]}_{tot}\left[C{a}^{2+}\right]}{K_M+\left[C{a}^{2+}\right]},& (3)\end{array}$

and

$\begin{array}{cc}{K}_m=\frac{k_2+k_3}{k_1},& (4)\end{array}$

where $\left[P_{C{a}^{2+}}\right]$ is the number of pumps with Ca²⁺ bound.

$\begin{array}{cc}{f}_b=\frac{\left[P_{C{a}^{2+}}\right]}{{\left[P\right]}_{tot}},& (5)\end{array}$

therefore, substituting for K_M and multiplying by k₁ gives the relation:

$\begin{array}{cc}{f}_b=\frac{k_1\left[C{a}^{2+}\right]}{k_2+k_3+k_1\left[C{a}^{2+}\right]},& (6)\end{array}$

which relates f_b to [Ca²⁺].

Thus, we calculated f_b and r_ex at resting [Ca²⁺] = 100 nM from the rate constants for PMCA's and NCX's in Table 1. We then set their leak rates equal to the calculated basal r_ex to produce a resting steady-state [Ca²⁺] of 100 nM. We set the Ca²⁺ leak rate for PMCA's at 4.3 s⁻¹ and for NCX's at 19.4 s⁻¹ (Table 1). These rates produced a steady-state basal [Ca²⁺] of 100 nM in simulations in which no stimulus was applied.

Modeling of Fluorescence Experiments

To simulate experimental results obtained with Ca²⁺ sensitive fluorescent dyes, we added 20 μM Fluo4, 50 μM Oregon Green Bapta 1 (OGB1), or 100 μM OGB1 to dendrites, as appropriate (Figure 3A; Table 1); and then simulated interaction of Ca²⁺ with the indicator with a time step of 0.1 μs during a simulated bAP stimulus, using MCell's adaptive time stepping. We directly recorded the amount of Ca²⁺ bound to indicator, the amount of unbound indicator, and the amount of free Ca²⁺ in the spines and shafts every 100 μs. Thus, we did not need to simulate the resulting fluorescence to obtain information about Ca²⁺ transients. To directly compare our simulation results to the experimental results of Sabatini et al. (2002), which they calculated using the method of Maravall et al. (2000), we estimated the Ca²⁺ transient by assuming that Ca²⁺ reaches rapid equilibrium with the fluorescent dye. At equilibrium,

$\begin{array}{cc}\left[C{a}^{2+}\right]=\frac{K_D\left[B\right]}{\left[U\right]},& (7)\end{array}$

where K_D is the dissociation constant of Ca²⁺ from the dye, [B] is the concentration of dye bound to Ca²⁺, and [U] is the concentration of unbound dye.

Therefore, the estimated Ca²⁺ transient at each time step, $\Delta {\left[C{a}^{2+}\right]}_{estim}$, will be:

$\begin{array}{cc}\Delta {\left[C{a}^{2+}\right]}_{estim}=\left(\frac{K_D\left[B\right]}{\left[U\right]}\right)-{\left[C{a}^{2+}\right]}_0,& (8)\end{array}$

where ${\left[C{a}^{2+}\right]}_0$ is the steady state resting concentration of Ca²⁺ with no stimulus (i.e., 100 nM). To accurately simulate the data of Sabatini et al. (2002), we lowpass filtered the simulated transients ($\Delta {\left[C{a}^{2+}\right]}_{estim}$) in the spine head and adjacent shaft (captured with a resolution of 1 μs) with a 250 Hz four-pole Bessel lowpass filter and sampled at 500 Hz to correspond with the experimental measurements.

Statistics

One hundred individual simulations, each with a new random seed, were carried out with each set of parameters. Ca²⁺ transients were recorded in the large spines (≥0.05 fl in volume) on the smaller diameter dendrite (seven spines) for calibration and in all spines on the larger diameter dendrite for later tests. The individual simulations were averaged for each spine, and then the means from each spine were averaged and the standard error of the mean was determined. This procedure closely recapitulates the statistical analysis of the experimental data (see Section Results). The random placement of membrane molecules for each simulation with a new random seed introduces more variability into simulations in each spine than would be observed in repeated scans of the same spine in an experiment, because it introduces stochastic variation of channel numbers within each individual simulated spine. Thus, the simulations mimic sampling of 100 spines with the same shape and size, but slightly different numbers and arrangements of proteins.

Results

Morphological Analysis

To compare the range of shapes and sizes of spines in the reconstructed neuropil to those reported previously in fixed hippocampal tissue, we measured several morphological parameters of the 72 spines (Figure 4A) on the larger reconstructed dendrite (Figures 4B–K). Spine head volumes ranged from 0.004 to 0.2 fl; base-to-tip lengths of spines from 0.48 to 1.45 μm; diameters of spine necks from 0.04 to 0.5 μm; and spine neck lengths from 0.08 to 1.1 μm. The average volume of spine heads was 0.03 μm³ (0.03 fl) and the average base-tip length of spines was 0.85 μm. These measurements are consistent with those of Harris and Stevens (1989) and as reviewed in Sorra and Harris (2000). The measurements were made after the extracellular volume fraction of the reconstruction was expanded from 8 to 20% to account for shrinkage artifacts during fixation (Kinney, 2009; Kinney et al., 2013). Thus, the good agreement with previous measurements shows that no significant distortions of the geometry were introduced by our correction methods.

FIGURE 4

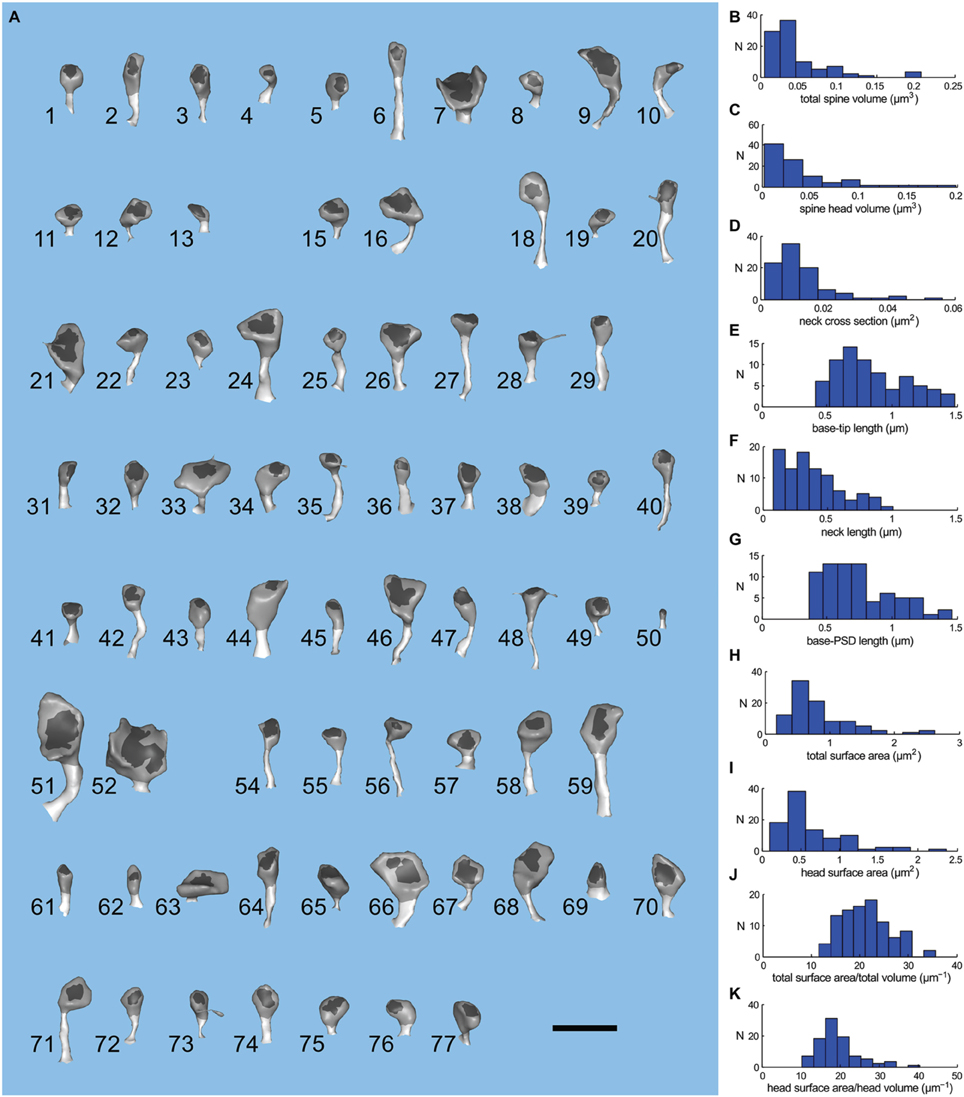
Figure 4. Geometry of spines of the large apical dendrite. (A) Visual index of the spines of the large apical dendrite. Spines have been oriented to view both head and neck. The PSD region is dark gray; spine head, medium gray; and spine neck, light gray. The spines are numbered 1–77 and have not been sorted. Five spines (numbers 14, 17, 30, 53, and 60) were omitted from the simulations because they were clipped by the boundary of the reconstructed volume. Thus, the apical dendritic segment contains 72 intact spines. The scale bar is 1 μm. (B–K) Distribution of geometric parameters of the spines. (B) Total spine volume. (C) Spine head volume. The average spine head volume in the sample was 0.03 μm³. (D) Spine neck cross sectional area. (E) Base-tip length. The average spine length from the base of the spine to the apex of the head was 0.85 μm. (F) Spine neck length. (G) Base to PSD length. (H) Total surface area. (I) Head surface area. (J) Ratio of total spine surface area to total spine volume. (K) Ratio of head surface area to head volume.

Calibration and Parameter Sensitivities

Although most of the kinetic parameters listed in Table 1 are reasonably well-constrained by values in the literature; the concentrations of some of the proteins within neurons are not known as precisely as others because they have been estimated based upon relatively low resolution data. Thus, to bring the Ca²⁺ transients predicted by the model into agreement with experiments of Sabatini et al. (2002), we adjusted nine parameters within reasonable previously measured physiological ranges, seven concentration parameters and the k_on and k_off of the endogenous buffer. The concentration parameters that we adjusted were: the densities of the PMCA, NCX, and VDCCs on spine and on shaft membranes; and the concentration of the immobile endogenous CBPs, which represent the sum of endogenous Ca²⁺-binding proteins (Table 2). In adjusting the concentrations of the PMCA and NCX pumps, we used an additional experimental constraint from Scheuss et al. (2006), who reported that PMCAs and NCXs each remove approximately the same amount of Ca²⁺ in response to a bAP. Thus, we adjusted the ratio of PMCA to NCX pumps such that they would extrude equal amounts of Ca²⁺ in spines of the size measured by Sabatini et al. (2002). This constraint reduced the number of free parameters to seven. The range over which each parameter was tested by manual trial and error to obtain initial preliminary best fit values is indicated in Table 2. The data upon which the ranges are based is discussed for each protein in the Methods Section under Proteins.

TABLE 2

Table 2. Parameter sensitivity in four dimensional measurement space.

In their experiments, Sabatini et al. (2002) placed whole-cell clamps on the somas of CA1 pyramidal neurons and perfused them with three different fluorescent Ca²⁺ indicators at different concentrations to generate data from spines with a gradient of Ca²⁺ buffering capacities when buffering by the dyes is included. During the perfusion, as indicator diffused throughout the neuron, we assume that calbindin was washed out of spines because its size and diffusion constant are similar to those of the fluorescent indicators. Sabatini et al. then used a two-photon laser-scanning microscope, scanning at 500 Hz, to record the fluorescent transients in spines and the adjacent dendritic shafts in response to a bAP stimulus triggered by injecting current through the patch pipette. They state that Ca²⁺ transients were measured on small apical dendrites less than 2 μm in diameter and on spines in which the fluorescent signal could be reliably detected. Their data was gathered from 7 to 14 spines at four concentrations of indicator with six scans of each spine during which a single bAP was delivered. The fluorescent transients were converted into an estimate of the size of the Ca²⁺ transient, Δ[Ca²⁺]_estim, using a previously published method (Maravall et al., 2000). Transients calculated from the six scans were then averaged for each spine, and then the means from each spine were averaged and the standard error of that mean was calculated. They determined the resting Ca²⁺ concentration in spines and shafts, the change in Ca²⁺ in response to a backpropagating action potential, and the decay time constant of the Ca²⁺ transient (τ), at each concentration of Ca²⁺ indicator. The endogenous buffering capacity, κ_e, of spines and shafts was then calculated by the method of Neher and Augustine (1992) in which the relationship of the size of the Ca²⁺ transient to the buffering capacity of the Ca²⁺ indicators is extrapolated to zero indicator concentration (see Figure 5).

FIGURE 5

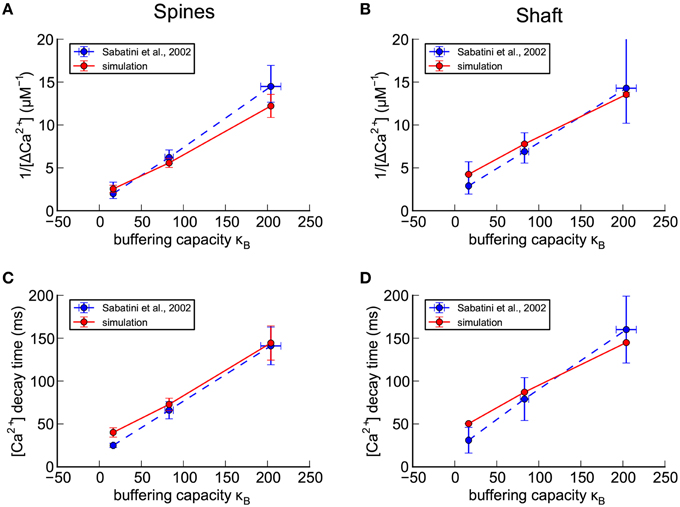
Figure 5. Calibration of nine parameters in spines and shafts of the small branch spine. (A–D) Confirmation of calibration of the shape of a Ca²⁺ transient in response to a bAP in the absence of calbindin (see Methods Section). For comparison with experimental results of Sabatini et al. (2002; shown as blue dashed lines), concentrations of exogenous fluorescent calcium indicators in the model were set to 20 μM Fluo4, 50 μM OGB1, or 100 μM OGB1. The simulated results for the best calibrated parameters, averaged for seven spines with volumes ≥ 0.05 fl, are shown as red lines. (A) For each concentration of indicator, the reciprocal of the averaged peaks of the calcium transients in the spines, 1/Δ[Ca²⁺], is plotted against the buffering capacity in the presence of indicator (κ_B) calculated as in Sabatini et al. (2002). The Δ[Ca²⁺], extrapolated to zero indicator, was in the range 0.5 to 1.0 μM (reciprocal of y-axis intercept) with κ_e in the range 16–50 (x-axis intercept). (B) The reciprocal of the averaged peaks of the calcium transients in the dendritic shaft is plotted against buffering capacity. The Δ[Ca²⁺], extrapolated to zero indicator, was 0.3 μM with κ_e = 62. (C) The averaged time constant of calcium decay in the spines is plotted against calcium buffering capacity. The calcium decay time constant, extrapolated to zero indicator in the spines was in the range 20–40 ms (y-axis intercept) with κ_e in the range 30–80 (x-axis intercept). (D) The averaged time constant of calcium decay in the dendritic shafts was plotted against buffering capacity. The calcium decay time constant, extrapolated to zero indicator in the dendritic shafts was 42 ms with κ_e = 75.

To simulate the Sabatini et al. (2002) experiments, we set the calbindin concentration in our model to zero, and added different Ca²⁺-sensing dyes to the model as described under Methods Section. We recorded the amount of Ca²⁺ bound to each indicator over time during a simulated bAP stimulus. For calibration, we used simulation data collected from spines on the smaller dendrite (shaft diameter 0.8 μm, Figure 1E) because its dimensions are closest to those in which Sabatini et al. (2002) made their measurements. In addition, we used only spines with volumes of 0.05 fl or larger (seven spines) because we reasoned that only the larger spines would have provided readily detectable and reliable fluorescence signals in an experimental setting.

We set four target values from the Sabatini et al. data, for each of the three different Ca²⁺ indicator concentrations: 1/peak Δ[Ca²⁺] and decay time (τ) for transients in the spine head, and the same two values for transients in the shaft (Figure 5). We then determined these four values from each of our simulations, as described in Methods Section, for each indicator concentration and parameter set.

To obtain preliminary values for the seven parameters that best fit the target values, we made manual systematic iterative adjustments of the densities of PMCAs, NCXs, and VDCCs, in the membranes, varying their values within the boundaries of estimates of their concentrations in the literature (see Methods Section and Table 2). We estimated the ratio of PMCA and NCX pumps that would remove equal amounts of Ca²⁺ from the spine head, as found in Sabatini et al. (2002), by calculating the mean concentration of Ca²⁺ during a typical transient and then using the K_M's and turnover numbers of the two pumps to calculate the ratio of the pumps that would be required for each to remove an equal amount of Ca²⁺ at that concentration. The pumps were then kept at that ratio in both spine and shaft membranes, and the numbers of the pumps in spines and shafts were adjusted to keep this ratio constant during the trials to find preliminary best fit parameters. In other words, the densities of the two pumps in the spine head and in the shaft were each treated as one parameter, reducing the number of free parameters from nine to seven (Table 2). Before proceeding to the refinement stage described below, the ratio of their densities was readjusted slightly so that each of the pumps removed equal amounts of Ca²⁺ from both the shafts and the large spine heads. The concentration and Ca²⁺-binding rates of the immobile endogenous CBP in the cytoplasm were also adjusted until a reasonably good fit was obtained to the experimental plots of total buffer capacity, κ_B, against the amplitudes and decay times of the Ca²⁺ transients, in the presence of three different concentrations of fluorescent sensors (Figure 5).

We next refined the local fit and determined approximate parameter sensitivities using a form of Principal Component Analysis as follows. First, we constructed three 4 × 4 covariance matrices (Σ, Equation 9) for the three sets of four output values determined from the simulation data we collected from the seven spines. The calculations are summarized in Equations (10–12), where n is the number of spines observed (n = 7), x_i and y_i are the ith observation of output values x or y, respectively. Likewise, μ_x and μ_y are the mean output value for x or y, across n = seven spines.

$\begin{array}{cc}{\displaystyle \sum _{xy}=}\left[\begin{array}{cccc}va{r}_1& co{v}_{12}& co{v}_{13}& co{v}_{14}\\ co{v}_{21}& va{r}_2& co{v}_{23}& co{v}_{24}\\ co{v}_{31}& co{v}_{32}& va{r}_3& co{v}_{34}\\ co{v}_{41}& co{v}_{42}& co{v}_{43}& va{r}_4\end{array}\right],& (9)\end{array}$

where

$\begin{array}{cc}va{r}_x=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(x_i-{\mu }_x\right)}^2},& (10)\end{array}$

$\begin{array}{cc}co{v}_{xy}=\frac{1}{n}{\displaystyle \sum _{i=1}^n(x_i-{\mu }_x)(y_i-{\mu }_y)},& (11)\end{array}$

and

$\begin{array}{cc}{\mu }_x=\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}_i}.& (12)\end{array}$

We then averaged the three matrices together, element by element, to create an average covariance matrix. For this calculation, it would be ideal to use the experimental covariances. However, because we don't have access to the raw experimental data, we instead computed the average of the three covariance matrices from the simulation results. To the extent that we have chosen the correct arrangement of proteins for the simulations, this matrix should be similar to an experimental covariance matrix. The averaging reduces the dimensionality of the aggregate “output value space” from 12D (3 × 4D), which would be underdetermined by our seven variable parameters, to 4D, which is, instead, overdetermined by the seven variable parameters. This method is adequate for estimating parameter sensitivies and checking the goodness of fit, given the boundaries on the variable parameters, and the inherent noisiness of the original experimental measurements of Ca²⁺ transients by fluorescence methods.

We know from computational statistics and Principle Component Analysis that the four eigenvalues of this covariance matrix are the interdependent variances of each of the four output measurements in the direction of the eigenvectors (axes of the principle components). Thus, the square root of the eigenvalues equals 1 standard deviation (i.e., 1 sigma) in the direction of its associated eigenvector. We used the eigenvalues and eigenvectors to refine the fit and determine the parameter sensitivities by the following method. We ran 14 simulations in which each of the seven parameters was varied independently either increasing it to 1.5 times its preliminary best fit value, or decreasing it to 0.9 times its preliminary best fit value (14 groups of parameters). These increments were chosen so that the resulting change in the output value was large enough not to be occluded by the Monte–Carlo trial-to-trial variability, but small enough to ensure rough linearity between the change in output value and the change in the parameter value. These simulations were run for each of the three indicator concentrations. For each set of parameters, the four output values were calculated for each of the seven spines, averaging 100 simulation runs. Then the mean output values were averaged over the seven spines to obtain three sets of four averaged output values for each set of parameters at the three indicator concentrations. The three sets of four values were then averaged to obtain a single set of four values for each of the 14 sets of parameters. The target (experimental) values were represented as a point in four-space and each group of output values for the 14 sets of parameters was also represented as a point in four-space. The radial distances from the point in four-space representing the target (experimental) values to the point in four-space for each set of parameters was then calculated, and normalized by the square root of the corresponding eigenvalue (i.e., the standard deviation of the corresponding principal component) (Note that, after normalizing the radial distance we obtain, z, the Z-score in four dimensions). To do this calculation, the origins of the four eigenvectors with lengths scaled to 1 sigma, as derived from the corresponding eigenvalues, were placed at the four-dimensional point representing the four target experimental values. Then the distances (z) between the four experimental target values and the corresponding output values for the 14 sets of parameters was calculated by projecting the 14 four-dimensional points onto the four scaled eigenvectors. The ratio of the length of each projection to the length of the eigenvectors is a measure that represents the number of standard deviations, or Z-score, of one of the simulated values from the target value (i.e., 1/Δ[Ca²⁺] in the spine head or shaft, or decay time (τ) in the spine head or shaft). This operation projects, or transforms, the four original values into a new four-dimensional measurement space where the four transformed values are the coordinates of a point, m, whose distance, z (normalized by the standard deviation in each dimension) from the point representing the target value is given by the equation:

$\begin{array}{cc}z=\sqrt{{\displaystyle \sum _{i=1}^4{\left(m_i^s-m_i^t\right)}^2}},& (13)\end{array}$

where the subscript, i, is the i^th dimension of point m, the superscript s indicates the transformed simulated value, and superscript t indicates the transformed target experimental value. The change in z, Δz, over the fractional change in parameter value p, $\frac{\Delta p}{p}$, is $\frac{\Delta z·p}{\Delta p}$ = $\frac{\Delta z}{0.6}$ for each parameter, where Δp = 1.5p − 0.9p or 0.6 × the preliminary best fit value. In the language of Principal Component Analysis, this calculation means that the difference vector between simulated and target measurements was projected onto the four principal components, and the resulting difference vector components were normalized by the standard deviations of these principal components.

We expressed the parameter sensitivity in Table 2 in two different ways. The first measure, $\frac{\Delta z}{0.6}$, is a dimensionless measure that reflects the change in goodness of fit to the experimental target that results from changing p from 0.9*p to 1.5*p. The second measure, $\frac{\Delta p}{\Delta z}$ is a measure that indicates the change in p necessary to produce a change of +1σ in the goodness of fit to the experimental target. The values of $\frac{\Delta z}{0.6}$ in Table 2 indicate that VDCC density and pump density in the spine (2.8 and 1.5, respectively) are the least sensitive parameters and that the CBP concentration and pump density in the shaft (14.5 and 21.1, respectively) are the most sensitive parameters affecting the goodness of fit. It is important to note that z measures the goodness of fit in all four dimensions simultaneously. Furthermore, the goodness of fit is weighted equally by the variance of the simulation data in each of the four dimensions. This means that the simulation measurements that have smaller variances will affect the fit more sensitively than those with larger variances. It is evident in Figures 5B,D, that the variances of simulation measurements in the shaft are smaller than those in the spine. For this reason, the fit is more sensitive to parameters in the shaft than the corresponding parameters in the spine.

The column headed “Range of exploration” in Table 2 shows the range of values explored for each parameter during the manual search for the preliminary best fit. These ranges are consistent with the range of experimental measurements, as discussed in Methods Section. Though we cannot guarantee with certainty that other combinations of parameters will not fit as well as the values shown in Table 3, we found no such combinations within the indicated ranges of values.

TABLE 3

Table 3. Calibrated parameters.

To further improve the fit, we re-adjusted each parameter in the initial best-fit parameter set by an appropriate amount to decrease the final distance z, based on its $\frac{\Delta z·p}{\Delta p}$. We assumed linearity of Δzover the change in parameter values (Δp = 0.6p) and extrapolated to minimum z. The output values calculated from the simulations showed a small improvement in fit and are plotted in Figures 5A–D. Additional adjustments of the parameters didn't significantly improve the overall fit. Table 3 shows the final parameters. For comparison, it also shows the corresponding experimental estimates of the parameters available in the literature.

The simulations predicted endogenous buffering capacities (κ_e) in the same range as reported by Sabatini et al. (2002) with values from 16 to 80 when the concentration of indicator was extrapolated to zero (see Methods Section and Figures 5A–D). The decay time constant for the Δ[Ca²⁺]_estim transient was 42 ms in the dendrites and 20–40 ms in the spines when extrapolated to zero indicator, again in the same range reported by Sabatini et al. (2002). The extrapolated peak Δ[Ca²⁺]_estim during the bAP was 0.3 μM in the dendrites and 0.5–1.0 μM in the spines, also in the range reported by Sabatini et al.

Relationship of Buffering Capacity to Amplitude and Decay Time of Δ[Ca²⁺]_estim in the Large Dendrite

After we calibrated the model to match experimental data using the small dendrite, we used the same parameters to simulate Ca²⁺ transients for large spines on the large dendrite (13 spines ≥ 0.05 fl, shaft diameter ~2.1 μm (Figures 6A–D). The most striking difference between Ca²⁺ transients in the two dendrites is seen in the shafts. For each concentration of indicator, the simulated transient in the large shaft has a smaller amplitude (e.g., 1/Δ[Ca²⁺] is larger) than in the small shaft, and the decay time is longer, reflecting the smaller surface to volume ratio of the shaft with the larger diameter.

FIGURE 6

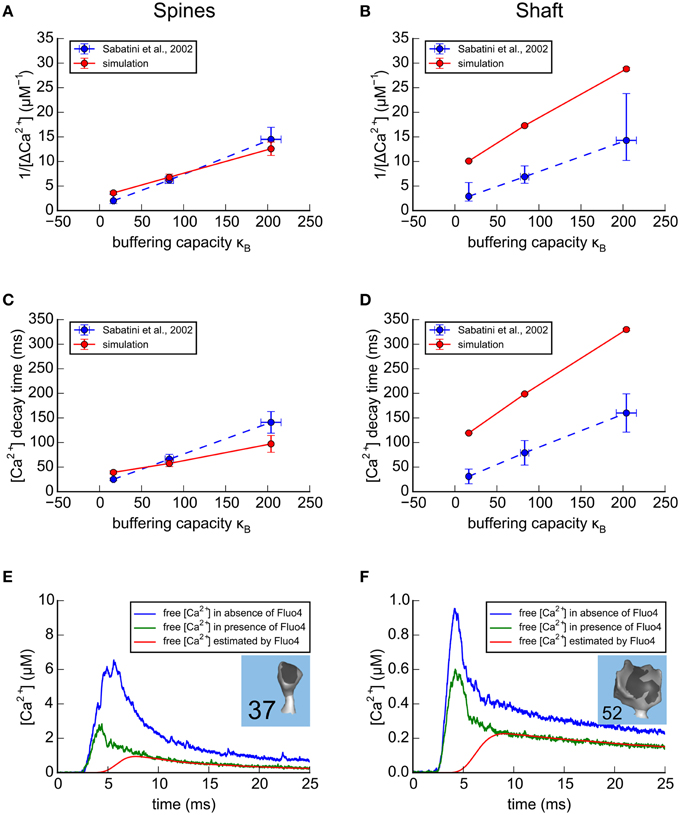
Figure 6. Results of simulations in the spines and shafts of the large apical dendrite using parameters optimized for the small branch dendrite. (A–D) Simulation of Ca²⁺ transients in response to a bAP in the absence of calbindin. As in Figure 5, for comparison with experimental results of Sabatini et al. (2002; shown as blue dashed lines), concentrations of exogenous fluorescent Ca²⁺ indicators in the model were set to 20 μM Fluo4, 50 μM OGB1, or 100 μM OGB1. The simulated results in the large apical dendrite, averaged for the 13 spines with volumes ≥0.05 fl are shown as red lines. (A) For each concentration of indicator, the reciprocal of the averaged peaks of the Ca²⁺ transients in the spines of the large apical dendrite, 1/Δ[Ca²⁺], is plotted against the buffering capacity in the presence of indicator (κ_B) calculated as in Sabatini et al. (2002). The Δ[Ca²⁺], extrapolated to zero indicator, was in the range 0.3–0.6 μM (reciprocal of y-axis intercept) with κ_e in the range 40–75 (x-axis intercept). (B) The reciprocal of the averaged peaks of the Ca²⁺ transients in the dendritic shaft is plotted against buffering capacity. The Δ[Ca²⁺], extrapolated to zero indicator, was 0.12 μM with κ_e = 75. (C) The averaged time constant of Ca²⁺ decay in the spines is plotted against Ca²⁺ buffering capacity. The Ca²⁺ decay time constant, extrapolated to zero indicator in the spines was 25 to 40 ms (y-axis intercept) with κ_ein the range 60–120 (x-axis intercept). (D) The averaged time constant of Ca²⁺ decay in the dendritic shafts was plotted against buffering capacity. The Ca²⁺ decay time constant, extrapolated to zero indicator in the dendritic shafts was 100 ms with κ_e = 80. (E,F) Ca²⁺ transients in two spines of the calibrated model, in response to a bAP. Simulations were run in the presence and absence of 20 μM Fluo4 in a median size spine (E, spine #37, average of 32 trials) and in a large-size spine (F, spine #52, average of 59 trials). The average Ca²⁺ transients that would be estimated from the fluorescence of 20 μM Fluo4 are shown in red. The average Ca²⁺ transients, measured in the simulation by counting actual free Ca²⁺, are shown in the presence of Fluo4 (green), and in its absence (blue).

Effect of the Presence of Fluorescent Indicators on the Free Ca²⁺ Transient

One advantage of this model is that after it is calibrated to agree with experiments that were performed with Ca²⁺ indicators, they can be removed from the simulations to explore Ca²⁺ dynamics in the absence of indicators. We know that exogenous indicators alter the free Ca²⁺ transient, but their effect can't be measured by direct experiments. We used the calibrated model to simulate and compare free Ca²⁺ transients in a small (Figure 6E) and a large (Figure 6F) spine in response to a bAP as estimated from fluorescence measurements by the method of Maravall (red), and as recorded in the simulation in the presence (green) and absence (blue) of Fluo4. The peak of the free Ca²⁺ estimated from fluorescence is much smaller than the free Ca²⁺ transients recorded during the simulations, either in the presence or absence of Fluo4. This is because the response of the indicator is too slow to follow the rapid initial phase of the transient. Note that the indicator does accurately follow the slow decay phase of the transient when the free [Ca²⁺] is changing slowly enough that the indicator is able to track it.

Responses to EPSP, bAP, and EPSP+bAP Stimuli in a Median-size Spine

We examined simulated Ca²⁺ transients in the absence of indicator in more detail in a single median-size spine (#37), in response to three different stimuli; an EPSP alone, a bAP alone, and an EPSP preceding a bAP by 10 ms (EPSP+bAP; Figure 7). During the stimuli that included an EPSP, 1500 molecules of glutamate was released from a single site and bound to and activated AMPARs and NMDARs. We previously found that release of 1500 molecules of glutamate produces activation that most closely matches experimental estimates (Keller et al., 2008). The EPSP voltage was simulated as described under “Stimuli” in Methods Section.

FIGURE 7

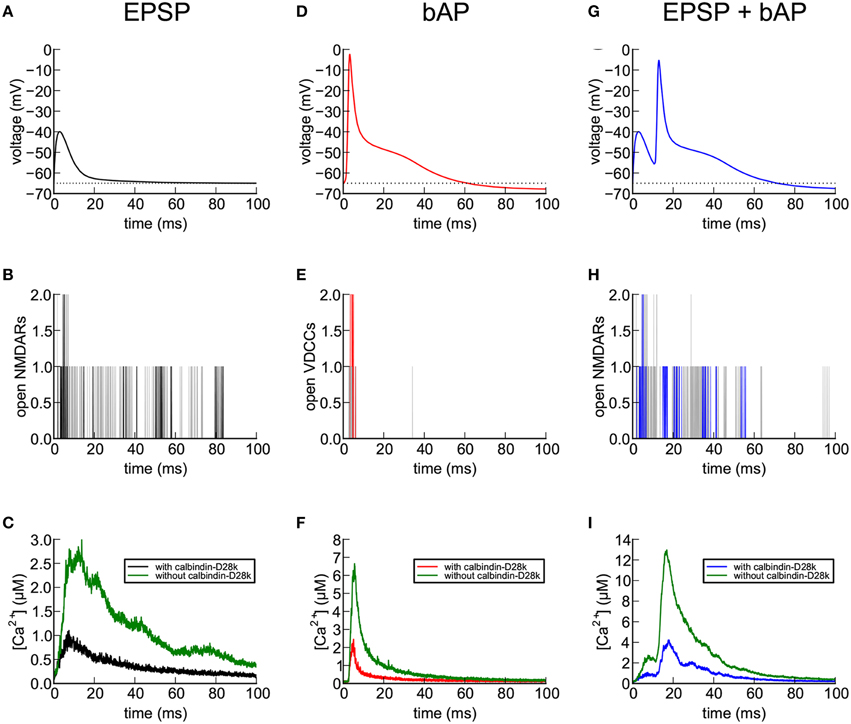
Figure 7. Calcium entry into spines in response to EPSP, bAP, and EPSP+bAP stimuli. Unless otherwise stated, the dendrite contained 45 μM calbindin-D28k and the signals are those recorded in spine #37. (A) Depolarization of the spine head following an EPSP stimulus. The voltage signal was generated from a NEURON simulation, as described in Methods Section. (B) NMDARs flickered between open and closed states during an EPSP. The black trace shows a single trial. Gray traces are superposition of five additional trials. (C) Ca²⁺ transients in the spine head in response to a single EPSP stimulus averaged over 56 trials in the presence (black) and absence (green) of calbindin-D28k. (D) Depolarization of the spine head following a bAP stimulus. The voltage signal was generated from a NEURON simulation as described in Methods Section). (E) VDCCs flickered between open and closed states during the bAP. The red trace shows a single trial. Gray traces are superposition of five additional trials. (F) Ca²⁺ transients in the spine head in response to a single bAP stimulus averaged over 32 trials in the presence (red) and absence (green) of calbindin-D28k. (G) Depolarization of the spine head following an EPSP+bAP stimulus. The voltage signal was generated from a NEURON simulation as described in Methods Section. (H) NMDARs flickered between open and closed states during an EPSP+bAP. The blue trace shows a single trial. Gray traces are superposition of five additional trials. (I) Ca²⁺ transients in the spine head in response to a single EPSP+bAP stimulus averaged over 86 trials in the presence (blue) and absence (green) of calbindin-D28k.

During a single EPSP (Figure 7A), activated NMDARs are mostly blocked by Mg²⁺. Thus, in the simulation, only a few flickered open stochastically (Figure 7B). The size of the EPSP (25 mV) is the average size for hippocampal CA1 pyramidal neurons, calculated by Harnett et al. (2012). Many of the EPSP trials in this simulation resulted in no Ca²⁺ influx at all because of the small number of activated and unblocked NMDARs. We computed the average of Ca²⁺ transients during the successful trials both in the presence (black) and absence (green) of calbindin (Figure 7C). In the presence of calbindin, successful trials produced a slow rising phase to a peak amplitude of about 1 μM, followed by a slow decay. In the absence of calbindin, the average peak amplitude was about 2.6 μM. Thus, the principal effect of calbindin on the Ca²⁺ transient is to reduce its overall magnitude. The noisiness in the averaged trace of the Ca²⁺ transient in Figure 7C is a result of stochastic opening and closing of the NMDARs and binding and unbinding of Ca²⁺ to the CBPs and pumps.

During a bAP (Figure 7D), the depolarization of the spine head caused the small number of VDCCs to flicker open and closed stochastically (Figure 7E) and Ca²⁺ flowed into the spine head through the open channels (Figure 7F). As with the EPSP stimulus, many trials with the bAP stimulus failed to open any VDCC channels and no Ca²⁺ influx occurred. We averaged the successful Ca²⁺ responses to a bAP and observed a rapid rising phase to a peak amplitude of about 2.2 μM in the presence of calbindin, followed by a rapid decay, and a peak of 6.5 μM in its absence. During the sustained influx of Ca²⁺, the rate of influx exceeded the rate at which internal Ca²⁺-binding proteins could bind the Ca²⁺, resulting in a rapid rise of free Ca²⁺ levels. When the Ca²⁺ influx stopped, the Ca²⁺-binding proteins and free Ca²⁺ rapidly reached a quasi-equilibrium. The Ca²⁺ was then removed from the spine by the Ca²⁺ pumps and by diffusion through the spine neck.

After a simulated EPSP+bAP stimulus (Figure 7G), only zero, one, or (rarely) two NMDARs became doubly bound by glutamate immediately after its release. Those that did cycled stochastically between closed and open states for much longer than VDCCs (Figure 7H). Because the Mg²⁺ block was relieved by the bAP, a large Ca²⁺ influx was observed in the spine head, followed by decay to baseline (Figure 7I). In the presence of calbindin (blue), the average amplitude of the Ca²⁺ transients during trials that resulted in Ca²⁺ influx was 4.0 μM and the time to decay to 10% of the peak was 65 ms. In the absence of calbindin (green), the peak amplitude was nearly 13 μM and the time to decay to 10% of the peak was 50 ms.

A visualization of simulated release and Ca²⁺ influx at spine #37 after an EPSP+bAP stimulus in the absence of calbindin is shown in Figure 8. Glutamate is released, diffuses, and activates receptors (Figures 8A–D). Ca²⁺ flows in through an opened NMDA receptor (Figure 8E) and is pumped out as the voltage decreases (Figure 8F). The visualization illustrates the level of detail that the simulations can reveal.

FIGURE 8

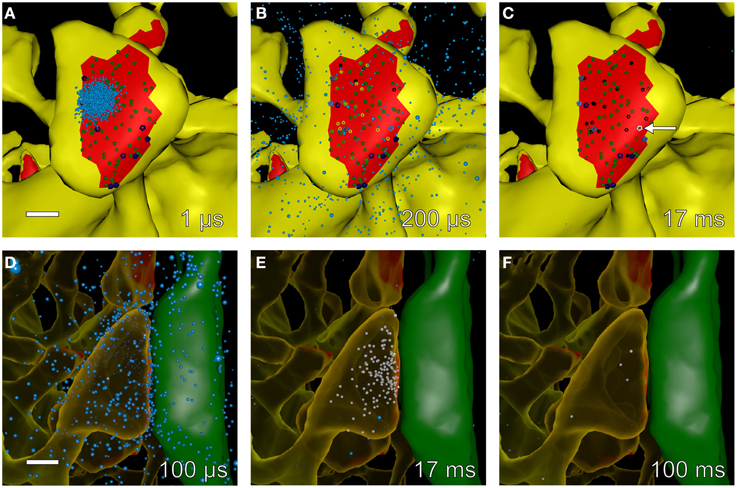
Figure 8. Snapshots of simulated glutamate release and postsynaptic calcium dynamics at different times during an EPSP+bAP stimulus. We used Cell Blender (see Methods Section) to visualize simulated glutamate release and calcium entry into spine #37 (see Figure 4A) during an EPSP+bAP stimulus. All other components of the neuropil were present in the simulation but are not displayed in the visualization. All scale bars are 0.25 μm. (A–C) Time-lapse sequence of glutamate (cyan dots) released onto a dendritic spine with unbound AMPARs (smaller, dark-green glyphs) and unbound NMDARs (larger, dark-blue glyphs). Snapshots (A–C) were made from data generated by MCell during a single trial and taken at 1, 200 μs, and 17 ms after glutamate release, respectively. Glutamate diffused rapidly throughout the synaptic cleft, binding to AMPARs and NMDARs. Singly bound AMPARs are shown as medium-green glyphs, doubly bound AMPARs as bright-green glyphs, open AMPARs as yellow glyphs, and desensitized AMPARs as black glyphs. Singly bound NMDARs are shown as medium-blue glyphs, doubly bound NMDARs as bright-blue glyphs, and open NMDARs as white glyphs. During this trial the peak of AMPAR activation occurred at ~200 μs and the peak of NMDAR activation occurred at ~17 ms when a single NMDAR flickered open (white glyph indicated by white arrow in C). (D–F) Time-lapse sequence of glutamate decay and calcium influx after stimulation. Snapshots for (D–F) were made from data generated by MCell during a single trial and taken at 100 μs, 17, and 100 ms after glutamate release, respectively. The presynaptic axon (green) on the right makes an en passant synapse with the postsynaptic spine (translucent yellow) on the left. Free glutamate molecules (cyan dots) diffuse from the synaptic cleft within a few microseconds and are taken up within a 100 ms by astroglial transporters (not visualized but present in the simulation). Some glutamate remains bound and activates NMDARs for many tens of microseconds allowing influx of calcium (white dots) as NMDARs flicker open and closed. In this example, calcium entered the spine through a single open NMDAR and was cleared from the spine head via calcium pumps in the spine membrane and by diffusion through the spine neck.

Fate of Calcium Entering Spines during a bAP and an EPSP+bAP Stimulus

During the first 100 ms of a bAP stimulus, we monitored the fate of all the Ca²⁺ that entered the spine in the absence or presence of calbindin (Figures 9A–D). For comparison, we also monitored the fate of Ca²⁺ after an EPSP+bAP stimulus in the presence of calbindin (Figures 9E,F). The Ca²⁺ fates following the three stimuli are shown for a median-sized spine (#37, Figures 9A,C,E) and a large spine (#52; Figures 9B,D,F). Ca²⁺ was tracked after its influx through both VDCCs and NMDARs. We recorded its binding to CBPs, NCXs and PMCAs, and its eventual efflux out of the spine via the pumps and via diffusion through the neck into the shaft. The pumps and CBPs bound Ca²⁺ as soon as it entered the spine (yellow). Only a tiny fraction of Ca²⁺ remained free in the spine (blue). Ca²⁺ that bound to pumps was eventually pumped out of the spine (red and white) unless it unbound before being pumped. Ca²⁺ bound to immobile CBPs was released gradually to be captured by pumps or to diffuse out of the spine neck either while free or while bound to calbindin (green).

FIGURE 9

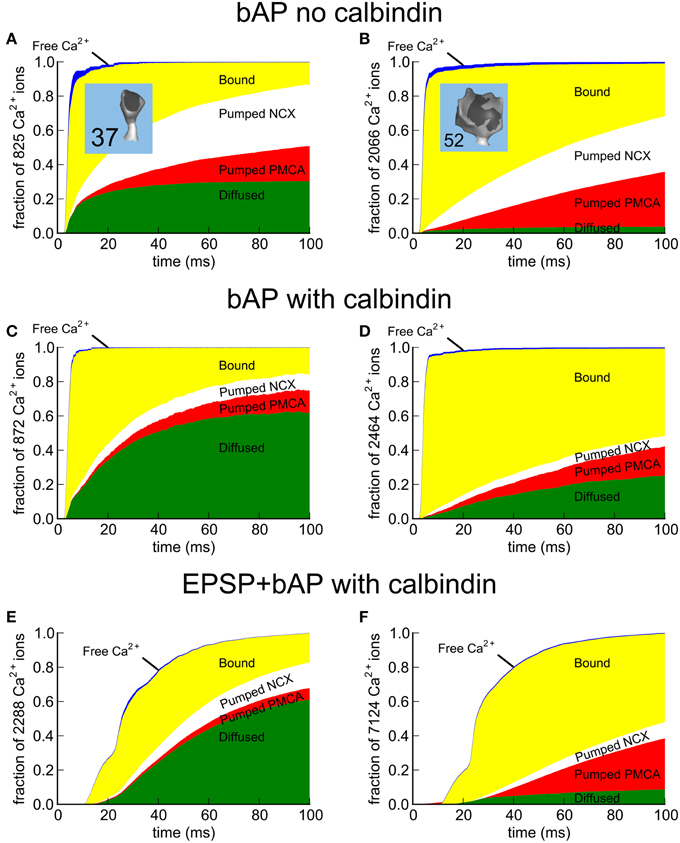
Figure 9. Fate maps of Ca²⁺ entering spines #37 and #52 in response to EPSP+bAP. The fate of all Ca²⁺ entering the spines was tracked for 100 ms after the stimulus. While inside the spine, Ca²⁺ can diffuse freely (blue) or bind to Ca²⁺-binding proteins and pumps (yellow). To restore the resting state, Ca²⁺ that enters is removed from the spine by PMCA pumps (red), NCX exchangers (white), or via diffusion through the spine neck (green) as free Ca²⁺ or while bound to mobile calbindin. (A,C,E) Fate of Ca²⁺ in median-size spine #37; (A) after a bAP in the absence of calbindin, (C) a bAP in the presence of calbindin, or (E) an EPSP+bAP in the presence of calbindin. (B,D,F) Fate of Ca²⁺ in large spine #52; (B) after a bAP in the absence of calbindin, (D) a bAP in the presence of calbindin, or (F) an EPSP+bAP in the presence of calbindin. Data is represented as a fraction of the total Ca²⁺ influx. The actual number of Ca²⁺ ions tracked is indicated in the y-axis label.

As expected, a larger fraction of total Ca²⁺ exits the median-size spine than the large spine by diffusion into the shaft. The principal effect of calbindin is to decrease the fraction of Ca²⁺ exiting via the pumps and to accelerate diffusion of Ca²⁺ into the shaft while it is bound to calbindin. Sabatini et al. (2002) reported that the length of time required for equilibration of Ca²⁺ between the spine and dendritic shaft during a bAP averaged 89 ± 31 ms, varying from 12 to 190 ms. They concluded that, in the absence of indicator (which diffuses faster than the endogenous CBPs), the time required for complete equilibration between the spine and shaft is likely to be longer than 1 s. Because the Ca²⁺ transient decays much faster than Ca²⁺ is cleared by diffusion, they concluded that diffusion through the spine neck is not likely to be a major determinant of the decay time of a Ca²⁺ transient produced by a bAP. Our simulations of Ca²⁺ movements are consistent with this conclusion.

Discussion

One goal of this study was to perform a “computational” reconstitution assay. We tested whether the locations, estimated numbers, and kinetic behavior, determined in vitro, of the major proteins believed to control the influx and efflux of Ca²⁺ in spines can account for the measured size and decay time of Ca²⁺ transients in a computer reconstruction of intact dendrites and spines. We have shown that the properties of these proteins can indeed account for the size and decay of the Ca²⁺ transients when incorporated into our model. This conclusion comes with several qualifications. Some of the required parameters, in particular, the densities of individual classes of proteins in subcellular membranes, are difficult to measure experimentally. Hence, we have sometimes used molecular numbers, and/or membrane protein densities measured in non-neuronal cells, to establish biologically reasonable densities. For example, the densities of Na⁺/Ca²⁺ exchangers (NCXs) and plasma membrane Ca²⁺ ATPases (PMCAs) on the membrane of the spine head have not been measured directly. In our calibrations, we found that the required density of PMCAs in the spine head is higher by a factor of 2–3 than their measured density in plasma membranes of other cell types (see below). The values of the densities of NCXs and PMCAs that fit our calibration depend, in part, on their assigned turnover numbers. However, it is not possible to be certain that the enzymatic turnover numbers measured in vitro for these two pumps accurately reflect the turnover numbers in vivo. For example, if the turnover rate for PMCAs is higher in vivo than the rate measured in vitro, a lower density of PMCAs would be sufficient to account for the transients observed in vivo. Nonetheless, all of the final parameters in this model are within reasonable physiological limits. Thus, we conclude that the set of proteins we have used in the model, to a first approximation, can serve as the principal regulators of Ca²⁺ transients in spines. In addition, we conclude that the properties of these proteins, measured in vitro in the studies we have chosen (see Methods Section), are not likely to be grossly different than their properties displayed in vivo. Another area of experimental uncertainty is the immobile endogenous buffer, which represents the aggregate concentration and binding rates of the set of cytosolic proteins that bind Ca²⁺. The concentration (79.7 μM) and K_D of the CBP that we established during the calibration are reasonable considering the high total protein concentration in the cytosol, and the weak binding properties of most immobile Ca²⁺ binding proteins. Because the concentration of the immobile buffer is not well-constrained by experiments, one might wonder whether a different concentration of CBP's would result in an equally good fit with a different set of values for the other parameters. However, there was not another good fit within the range of each of the parameters that we searched (Table 2). Because the range of parameters that we searched was determined by the range of their values measured previously in vitro, we conclude that there are not multiple sets of physiologically realistic parameters that are compatible with a global fit of the cellular experimental data we have used.

The distribution of PMCA and NCX pumps between spine and shaft is qualitatively consistent with studies showing that Ca²⁺ pumps are distributed unevenly in dendrites and spines. In some situations, PMCA pumps appear to cluster at the neck and base of the spine head or in the PSD (Burette and Weinberg, 2007; Burette et al., 2010; Weinberg, personal communication). There have been no direct experimental estimates of the density of PMCA's on spine or dendritic membranes. However, in non-neuronal cells, PMCAs have been estimated to be 0.1% of plasma membrane proteins and 0.3–1% in neuronal cells (Stauffer et al., 1995). Quinn et al. (1984) estimated the density of total proteins in the plasma membrane of a BHK cell at 30,000 μm⁻². Those numbers suggest that the neuronal membrane density of PMCA pumps would be estimated to be as high as 300 μm⁻². Our final calibrated density of 998 μm⁻² in the spine membrane is about three times that value. Biochemical estimates of densities of the pump on plasma membrane have some uncertainty because it is difficult to know what proportion of an isolated membrane fraction is plasma membrane, and because the measures by immunoblot of labeled phosphorylation intermediates are often semi-quantitative (Stauffer et al., 1995). Nonetheless, because of the importance of rapid Ca²⁺ transients in spines, one might expect them to have a higher PMCA density than BHK cells, particularly at the postsynaptic interface. A prediction of our model is that one of three things is true (or some combination): 1. PMCAs are present at a higher density in spines than in non-neuronal cells; 2. they have a higher turnover number in vivo than measured in vitro; or 3. there are additional factors important for removing Ca²⁺ from the spine that are not well-understood by molecular neurobiologists. We favor the idea that PMCAs are expressed at unusually high levels in the spine membrane because spines have evolved to exert tight control over Ca²⁺ fluxes.

The model presented here doesn't include several additional spine membrane components that can modulate the timing and/or amplitude of Ca²⁺ transients under particular conditions, or in particular synaptic types. These components include SK channels, calcium-permeable AMPARs, metabotropic receptors, and inositol trisphosphate (IP3) and ryanodine receptors in SER. SK channels hyperpolarize the spine membrane in response to an initial Ca²⁺ influx, and thus strongly modulate the influx of Ca²⁺ during repetitive stimulation (Ngo-Anh et al., 2005). They do not have a large effect during a single bAP or EPSP+bAP. Their influence on Ca²⁺ influx during the kinds of repetitive stimuli that lead to synaptic plasticity will be important to add to this model for future studies. Ca²⁺-permeable AMPARs are believed to play a role in excitatory synapses onto inhibitory GABAergic neurons (Mahanty and Sah, 1998; Laezza and Dingledine, 2004). Under some circumstances, they may also play a transient role in Ca²⁺ influx into spine synapses during consolidation of LTP (Plant et al., 2006). They don't appear to be an important source of Ca²⁺ influx in the majority of glutamatergic synapses onto excitatory neurons. Ca²⁺ stores in SER containing IP3 or ryanodine receptors are present in a small proportion of spine synapses in the hippocampus (~20%). We have not modeled those spines in the present study. It will be interesting to examine the effect of the presence of Ca²⁺-permeable AMPARs and Ca²⁺ stores on spine Ca²⁺ transients in future studies.

Our model of Ca²⁺-handling permits accurate simulation of diffusion of Ca²⁺ and mobile Ca²⁺-binding proteins through spine necks and into the nearby dendritic shafts, assuming a fairly uniform cytosol. However, we have not included agents that might mediate changes in the diffusional barrier in the spine neck, such as highly cross-linked actin cytoskeleton or mobile organelles that might move transiently into the neck (Bloodgood and Sabatini, 2005). Thus, our results do not reflect these influences.

We found that the single exponential decay of the fluorescence of Fluo-4 and OGB1 observed in the experiments of Sabatini et al. (2002) constrained the values of the on-rate and the K_D of the immobile CBP. When the on-rate of the immobile CBP was set significantly slower than the on-rates of Fluo4 or OGB1, the decay of the simulated fluorescence transient (i.e., Ca²⁺-bound to the indicator) was best fit by two exponential curves, one fast and one slow. As the on-rate of the immobile CBP was increased and approached the on-rate of the indicator, the shape of the decay phase of the fluorescence transient was better fit by a single exponential. Furthermore, the off-rate (and therefore the overall K_D) of the immobile CBP also had to be balanced against that of the indicator to avoid a biphasic exponential decay of the fluorescence transient. This phenomenon can be understood by noting that during the rising phase of a transient, the buffer or dye with the higher on-rate will initially bind most of the Ca²⁺, but during the decay phase the buffer or dye with the lower K_D (i.e., highest affinity and slowest off-rate) will eventually bind the most Ca²⁺ (Markram et al., 1998). The best-fit parameters we found for the immobile CBP allows the indicator to bind and retain most of the Ca²⁺ throughout the fluorescence transient while also fitting the experimental measurements of endogenous buffering capacity.

To understand and model the biochemical responses to Ca²⁺ in the postsynaptic spine, including the interaction of Ca²⁺ with calmodulin and its target proteins, it is important to know the precise height and time course of the Ca²⁺ transients. Since our simulations allow us to measure free [Ca²⁺], with or without added indicator and with or without lowpass filtering, we were able to measure both the perturbation of free Ca²⁺ due to the added indicator, and the error in the estimation of free Ca²⁺ based on the fluorescence signal (Figures 6E,F). The error in the estimation arises from two factors: (1) the estimation method requires the assumption that free and indicator-bound Ca²⁺ are in quasi-equilibrium; in other words, the indicator binds Ca²⁺ fast enough to track the Ca²⁺ transient accurately; and (2) the estimation method assumes that the data acquisition and subsequent lowpass filtering of the fluorescence signal are fast enough to track the fluorescence transient. The model shows that both of these assumptions are false. Ca²⁺ does not approach equilibrium with the indicator during the transient, and the Ca²⁺ peak is significantly attenuated by the lowpass filter.

The comparison of Ca²⁺ fluxes into a median size spine and a large spine (Figures 6E,F, 9) reveal that, although a larger amount of Ca²⁺ flows into the larger spine, the effective concentration of free Ca²⁺ reached in that spine is smaller because the Ca²⁺ is averaged over a much larger volume. Our future studies will examine in more detail, in different sizes and shapes of spines, the relationship between the surface to volume ratio of a spine and the concentrations and local interactions of Ca²⁺ in the spine cytosol after a stimulus.

The model presented here will be a useful adjunct to experimental studies of the regulatory systems that control synaptic strength. For example, the basic model of Ca²⁺ handling in spines provides a test bed in which the sensitivity of Ca²⁺ transients to changes in the numbers and parameters of other modulating proteins can be predicted both independently and in combination. The model will also enable future studies in which calmodulin and its target enzymes will be added to the spine cytosol to test and predict how Ca²⁺ influx, triggered by a wide variety of stimuli, can affect activation of Ca²⁺-regulated enzymes that control synaptic plasticity.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by NIH grants NS21184, MH095980, and NS074644 (KH), NIH grants NS44306 and DA030749 (MK, TS, TB), NIH grants MH079076 and P41-GM103712 (TJS, TB), NIH grant EB00487 (CB), NSF grant OCI-1216701 (CB), the Howard Hughes Medical Institute, the Texas Emerging Technologies Fund, and the Gordon and Betty Moore Foundation. We thank B. Dylan Bannon for comments on the manuscript.

References

Allbritton, N. L., Meyer, T., and Stryer, L. (1992). Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science 258, 1812–1815. doi: 10.1126/science.1465619

PubMed Abstract | CrossRef Full Text | Google Scholar

Arriza, J. L., Fairman, W. A., Wadiche, J. I., Murdoch, G. H., Kavanaugh, M. P., and Amara, S. G. (1994). Functional comparisons of three glutamate transporter subtypes cloned from human motor cortex. J. Neurosci. 14, 5559–5569.

PubMed Abstract | Google Scholar

Baba-Aissa, F., Raeymaekers, L., Wuytack, F., De Greef, C., Missiaen, L., and Casteels, R. (1996). Distribution of the organellar Ca^2C transport ATPase SERCA2 isoforms in the cat brain. Brain Res. 743, 141–153. doi: 10.1016/S0006-8993(96)01037-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Bartol, T. M. (1992). A Study of Miniature Endplate Current Generation at the Vertebrate Neuromuscular Junction using Electrophysiology and Monte Carlo Simulation. Ph.D. thesis, Cornell University, Ithaca, NY.

Bergles, D. E., Tzingounis, A. V., and Jahr, C. E. (2002). Comparison of coupled and uncoupled currents during glutamate uptake by GLT-1 transporters. J. Neurosci. 22, 10153–10162.

PubMed Abstract | Google Scholar

Bi, G., and Poo, M.-M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.

PubMed Abstract | Google Scholar

Bischofberger, J., Geiger, J. R., and Jonas, P. (2002). Timing and efficacy of Ca2C channel activation in hippocampal mossy fiber boutons. J. Neurosci. 22, 10593–10602.

PubMed Abstract | Google Scholar

Blaustein, M. P., and Lederer, W. J. (1999). Sodium/calcium exchange: its physiological implications. Physiol. Rev. 79, 763–854.

PubMed Abstract | Google Scholar

Bloodgood, B. L., and Sabatini, B. L. (2005). Neuronal activity regulates diffusion across the neck of dendritic spines. Science 310, 866–869. doi: 10.1126/science.1114816

PubMed Abstract | CrossRef Full Text | Google Scholar

Bloodgood, B. L., and Sabatini, B. L. (2007). Nonlinear regulation of unitary synaptic signals by CaV(2.3) voltage-sensitive calcium channels located in dendritic spines. Neuron 53, 249–260. doi: 10.1016/j.neuron.2006.12.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Briggs, G. E., and Haldane, J. B. (1925). A note on the kinetics of enzyme action. Biochem. J. 19, 338–339. doi: 10.1042/bj0190338

PubMed Abstract | CrossRef Full Text | Google Scholar

Brini, M., and Carafoli, E. (2009). Calcium pumps in health and disease. Physiol. Rev. 89, 1341–1378. doi: 10.1152/physrev.00032.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Burette, A. C., Strehler, E. E., and Weinberg, R. J. (2010). A plasma membrane Ca2C ATPase isoform at the postsynaptic density. Neuroscience 169, 987–993. doi: 10.1016/j.neuroscience.2010.05.062

PubMed Abstract | CrossRef Full Text | Google Scholar

Burette, A., and Weinberg, R. J. (2007). Perisynaptic organization of plasma membrane calcium pumps in cerebellar cortex. J. Comp. Neurol. 500, 1127–1135. doi: 10.1002/cne.21237

PubMed Abstract | CrossRef Full Text | Google Scholar

Carafoli, E., Santella, L., Branca, D., and Brini, M. (2001). Generation, control, and processing of cellular calcium signals. Crit. Rev. Biochem. Mol. Biol. 36, 107–260. doi: 10.1080/20014091074183

PubMed Abstract | CrossRef Full Text | Google Scholar

Caride, A. J., Filoteo, A. G., Penniston, J. T., and Strehler, E. E. (2007). The plasma membrane Ca^2C pump isoform 4a differs from isoform 4b in the mechanism of calmodulin binding and activation kinetics: implications for Ca^2C signaling. J. Biol. Chem. 282, 25640–25648. doi: 10.1074/jbc.M701129200

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, W., Mahadomrongkul, V., Berger, U. V., Bassan, M., Desilva, T., Tanaka, K., et al. (2004). The glutamate transporter GLT1a is expressed in excitatory axon terminals of mature hippocampal neurons. J. Neurosci. 24, 1136–1148. doi: 10.1523/JNEUROSCI.1586-03.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Church, P. J., and Stanley, E. F. (1996). Single L-type calcium channel conductance with physiological levels of calcium in chick ciliary ganglion neurons. J. Physiol. 496(Pt 1), 59–68. doi: 10.1113/jphysiol.1996.sp021665

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooney, J. R., Hurlburt, J. L., Selig, D. K., Harris, K. M., and Fiala, J. C. (2002). Endosomal compartments serve multiple hippocampal dendritic spines from a widespread rather than a local store of recycling membrane. J. Neurosci. 22, 2215–2224.

PubMed Abstract | Google Scholar

Danbolt, N. C. (2001). Glutamate uptake. Prog. Neurobiol. 65, 1–105. doi: 10.1016/S0301-0082(00)00067-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Diamond, J. S. (2001). Neuronal glutamate transporters limit activation of NMDA receptors by neurotransmitter spillover on CA1 pyramidal cells. J. Neurosci. 21, 8328–8338.

PubMed Abstract | Google Scholar

Edwards, J., Daniel, E., Kinney, J., Bartol, T., Sejnowski, T., Johnston, D., et al. (2014). VolRoverN: enhancing surface and volumetric reconstruction for realistic dynamical simulation of cellular and subcellular function. Neuroinformatics 12, 277–289. doi: 10.1007/s12021-013-9205-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ellis, R. J. (2001). Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr. Opin. Struct. Biol. 11, 114–119. doi: 10.1016/S0959-440X(00)00172-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Elowitz, M. B., Surette, M. G., Wolf, P. E., Stock, J. B., and Leibler, S. (1999). Protein mobility in the cytoplasm of Escherichia coli. J. Bacteriol. 181, 197–203.

PubMed Abstract | Google Scholar

Franks, K. M., and Sejnowski, T. J. (2002). Complexity of calcium signaling in synaptic spines. Bioessays 24, 1130–1144. doi: 10.1002/bies.10193

PubMed Abstract | CrossRef Full Text | Google Scholar

Fraser, D. D., and MacVicar, B. A. (1991). Low-threshold transient calcium current in rat hippocampal lacunosum-moleculare interneurons: kinetics and modulation by neurotransmitters. J. Neurosci. 11, 2812–2820.

PubMed Abstract | Google Scholar

Geiger, J. R. P., Roth, A., Taskin, P., and Jonas, P. (1999). “Glutamate-mediated synaptic excitation of cortical interneurons,” in Ionotropic Glutamate Receptors in the CNS, eds P. Jonas and H. Monyer (Heidelberg: Springer-Verlag), 363–398. doi: 10.1007/978-3-662-08022-1_11

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamdan, F. F., Daoud, H., Piton, A., Gauthier, J., Dobrzeniecka, S., Krebs, M. O., et al. (2011). De novo SYNGAP1 mutations in nonsyndromic intellectual disability and autism. Biol. Psychiatry 69, 898–901. doi: 10.1016/j.biopsych.2010.11.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Harnett, M. T., Makara, J. K., Spruston, N., Kath, W. L., and Magee, J. C. (2012). Synaptic amplification by dendritic spines enhances input cooperativity. Nature 491, 599–602. doi: 10.1038/nature11554

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, K. M., and Stevens, J. K. (1989). Dendritic spines of CA1 pyramidal cells in the rat hippocampus: serial electron microscopy with reference to their biophysical characteristics. J. Neurosci. 9, 2982–2997.

PubMed Abstract | Google Scholar

Higgins, E. R., Cannell, M. B., and Sneyd, J. (2006). A buffering SERCA pump in models of calcium dynamics. Biophys. J. 91, 151–163. doi: 10.1529/biophysj.105.075747

PubMed Abstract | CrossRef Full Text | Google Scholar

Higley, M. J., and Sabatini, B. L. (2008). Calcium signaling in dendrites and spines: practical and functional considerations. Neuron 59, 902–913. doi: 10.1016/j.neuron.2008.08.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Hilgemann, D. W., Nicoll, D. A., and Philipson, K. D. (1991). Charge movement during Na^C translocation by native and cloned cardiac Na^C/Ca^2C exchanger. Nature 352, 715–718. doi: 10.1038/352715a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, W. H., Walters, W. M., Xia, X. M., Karmally, S. A., and Bethea, J. R. (2003). Neuronal glutamate transporter EAAT4 is expressed in astrocytes. Glia 44, 13–25. doi: 10.1002/glia.10268

PubMed Abstract | CrossRef Full Text | Google Scholar

Jahr, C. E., and Stevens, C. F. (1993). Calcium permeability of the N-methyl-D-aspartate receptor channel in hippocampal neurons in culture. Proc. Natl. Acad. Sci. U.S.A. 90, 11573–11577. doi: 10.1073/pnas.90.24.11573

PubMed Abstract | CrossRef Full Text | Google Scholar

Jonas, P., Major, G., and Sakmann, B. (1993). Quantal components of unitary EPSCs at the mossy fibre synapse on CA3 pyramidal cells of rat hippocampus. J. Physiol. (Lond). 472, 615–663. doi: 10.1113/jphysiol.1993.sp019965

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller, D. X., Franks, K. M., Bartol, T. M. Jr., and Sejnowski, T. J. (2008). Calmodulin activation by calcium transients in the postsynaptic density of dendritic spines. PLoS ONE 3:e2045. doi: 10.1371/journal.pone.0002045

PubMed Abstract | CrossRef Full Text | Google Scholar

Kennedy, M. B. (2013). Synaptic signaling in learning and memory. Cold Spring Harb. Perspect. Biol. a016824. doi: 10.1101/cshperspect.a016824

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerr, R. A., Bartol, T. M., Kaminsky, B., Dittrich, M., Chang, J.-C. J., Baden, S. B., et al. (2008). Fast Monte Carlo simulation methods for biological reaction-diffusion systems in solution and on surfaces. SIAM J. Sci. Comput. 30, 3126–3149. doi: 10.1137/070692017

PubMed Abstract | CrossRef Full Text | Google Scholar

Kharazia, V. N., and Weinberg, R. J. (1999). Immunogold localization of AMPA and NMDA receptors in somatic sensory cortex of albino rat. J. Comp. Neurol. 412, 292–302.

PubMed Abstract | Google Scholar

Kinney, J. P. (2009). Investigation of Neurotransmitter Diffusion in Three-dimensional Reconstructions of Hippocampal Neuropil. Thesis, University of California, San Diego, CA.

Kinney, J. P., Spacek, J., Bartol, T. M., Bajaj, C. L., Harris, K. M., and Sejnowski, T. J. (2013). Extracellular sheets and tunnels modulate glutamate diffusion in hippocampal neuropil. J. Comp. Neurol. 521, 448–464. doi: 10.1002/cne.23181

PubMed Abstract | CrossRef Full Text | Google Scholar

Kinoshita, K., Arnal, I., Desai, A., Drechsel, D. N., and Hyman, A. A. (2001). Reconstitution of physiological microtubule dynamics using purified components. Science 294, 1340–1343. doi: 10.1126/science.1064629

PubMed Abstract | CrossRef Full Text | Google Scholar

Koester, H. J., and Sakmann, B. (2000). Calcium dynamics associated with action potentials in single nerve terminals of pyramidal cells in layer 2/3 of the young rat neocortex. J. Physiol. 529(Pt 3), 625–646. doi: 10.1111/j.1469-7793.2000.00625.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Laezza, F., and Dingledine, R. (2004). Voltage-controlled plasticity at GluR2-deficient synapses onto hippocampal interneurons. J. Neurophysiol. 92, 3575–3581. doi: 10.1152/jn.00425.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehre, K. P., and Danbolt, N. C. (1998). The number of glutamate transporter subtype molecules at glutamatergic synapses: chemical and stereological quantification in young adult rat brain. J. Neurosci. 18, 8751–8757.

PubMed Abstract | Google Scholar

Lörincz, A., Rózsa, B., Katona, G., Vizi, E. S., and Tamás, G. (2007). Differential distribution of NCX1 contributes to spine-dendrite compartmentalization in CA1 pyramidal cells. Proc. Natl. Acad. Sci. U.S.A. 104, 1033–1038. doi: 10.1073/pnas.0605412104

PubMed Abstract | CrossRef Full Text | Google Scholar

Magee, J. C., and Johnston, D. (1995a). Characterization of single voltage-gated NaC and Ca2C channels in apical dendrites of rat CA1 pyramidal neurons. J Physiol. 487(Pt 1), 67–90. doi: 10.1113/jphysiol.1995.sp020862

PubMed Abstract | CrossRef Full Text | Google Scholar

Magee, J. C., and Johnston, D. (1995b). Synaptic activation of voltage-gated channels in the dendrites of hippocampal pyramidal neurons. Science 268, 301–304. doi: 10.1126/science.7716525

PubMed Abstract | CrossRef Full Text | Google Scholar

Magee, J. C., and Johnston, D. (1997). A synaptically controlled, associative signal for Hebbian plasticity in hippocampal neurons. Science 275, 209–213. doi: 10.1126/science.275.5297.209

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahanty, N. K., and Sah, P. (1998). Calcium-permeable AMPA receptors mediate long-term potentiation in interneurons in the amygdala. Nature 394, 683–687. doi: 10.1038/29312

PubMed Abstract | CrossRef Full Text | Google Scholar

Mainen, Z. F., Joerges, J., Huguenard, J. R., and Sejnowski, T. J. (1995). A model of spike initiation in neocortical pyramidal neurons. Neuron 15, 1427–1439. doi: 10.1016/0896-6273(95)90020-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Maravall, M., Mainen, Z. F., Sabatini, B. L., and Svoboda, K. (2000). Estimating intracellular calcium concentrations and buffering without wavelength ratioing. Biophys. J. 78, 2655–2667. doi: 10.1016/S0006-3495(00)76809-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Markram, H., Helm, P. J., and Sakmann, B. (1995). Dendritic calcium transients evoked by single back-propagating action potentials in rat neocortical pyramidal neurons. J. Physiol. 485(Pt 1), 1–20. doi: 10.1113/jphysiol.1995.sp020708

CrossRef Full Text | Google Scholar

Markram, H., Lübke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215. doi: 10.1126/science.275.5297.213

PubMed Abstract | CrossRef Full Text | Google Scholar

Markram, H., Roth, A., and Helmchen, F. (1998). Competitive calcium binding: implications for dendritic calcium signaling. J. Comput. Neurosci. 5, 331–348. doi: 10.1023/A:1008891229546

PubMed Abstract | CrossRef Full Text | Google Scholar

Means, S., Smith, A. J., Shepherd, J., Shadid, J., Fowler, J., Wojcikiewicz, R. J., et al. (2006). Reaction diffusion modeling of calcium dynamics with realistic ER geometry. Biophys. J. 91, 537–557. doi: 10.1529/biophysj.105.075036

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishchenko, Y., Hu, T., Spacek, J., Mendenhall, J., Harris, K. M., and Chklovskii, D. B. (2010). Ultrastructural analysis of hippocampal neuropil from the connectomics perspective. Neuron 67, 1009–1020. doi: 10.1016/j.neuron.2010.08.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, A., Kukley, M., Stausberg, P., Beck, H., Muller, W., and Dietrich, D. (2005). Endogenous Ca2C buffer concentration and Ca2C microdomains in hippocampal neurons. J. Neurosci. 25, 558–565. doi: 10.1523/JNEUROSCI.3799-04.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagerl, U. V., Novo, D., Mody, I., and Vergara, J. L. (2000). Binding kinetics of calbindin-D28k determined by flash photolysis of caged Ca^2C. Biophys. J. 79, 3009–3018. doi: 10.1016/S0006-3495(00)76537-4

PubMed Abstract | CrossRef Full Text

Naraghi, M. (1997). T-jump study of calcium binding kinetics of calcium chelators. Cell Calcium 22, 255–268. doi: 10.1016/S0143-4160(97)90064-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Network Pathway Analysis Subgroup of the Psychiatric Genomics, C. (2015). Psychiatric genome-wide association study analyses implicate neuronal, immune and histone pathways. Nat. Neurosci. 18, 199–209. doi: 10.1038/nn.3922

PubMed Abstract | CrossRef Full Text | Google Scholar

Neher, E., and Augustine, G. J. (1992). Calcium gradients and buffers in bovine chromaffin cells. J. Physiol. 450, 273–301. doi: 10.1113/jphysiol.1992.sp019127

PubMed Abstract | CrossRef Full Text | Google Scholar

Ngo-Anh, T. J., Bloodgood, B. L., Lin, M., Sabatini, B. L., Maylie, J., and Adelman, J. P. (2005). SK channels and NMDA receptors form a Ca2C-mediated feedback loop in dendritic spines. Nat. Neurosci. 8, 642–649. doi: 10.1038/nn1449

PubMed Abstract | CrossRef Full Text | Google Scholar

Nusser, Z., Lujan, R., Laube, G., Roberts, J. D. B., Molnar, E., and Somogyi, P. (1998). Cell type and pathway dependence of synaptic AMPA receptor number and variability in the hippocampus. Neuron 21, 545–559. doi: 10.1016/S0896-6273(00)80565-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Otis, T. S., and Jahr, C. E. (1998). Anion currents and predicted glutamate flux through a neuronal glutamate transporter. J. Neurosci. 18, 7099–7110.

PubMed Abstract | Google Scholar

Penheiter, A. R., Bajzer, Z., Filoteo, A. G., Thorogate, R., Török, K., and Caride, A. J. (2003). A model for the activation of plasma membrane calcium pump isoform 4b by calmodulin. Biochemistry 42, 12115–12124. doi: 10.1021/bi027098C

PubMed Abstract | CrossRef Full Text | Google Scholar

Penmatsa, A., Wang, K. H., and Gouaux, E. (2013). X-ray structure of dopamine transporter elucidates antidepressant mechanism. Nature 503, 85–90. doi: 10.1038/nature12533

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinto, D., Pagnamenta, A. T., Klei, L., Anney, R., Merico, D., Regan, R., et al. (2010). Functional impact of global rare copy number variation in autism spectrum disorders. Nature 466, 368–372. doi: 10.1038/nature09146

PubMed Abstract | CrossRef Full Text | Google Scholar

Plant, K., Pelkey, K. A., Bortolotto, Z. A., Morita, D., Terashima, A., McBain, C. J., et al. (2006). Transient incorporation of native GluR2-lacking AMPA receptors during hippocampal long-term potentiation. Nat. Neurosci. 9, 602–604. doi: 10.1038/nn1678

PubMed Abstract | CrossRef Full Text | Google Scholar

Quinn, P., Griffiths, G., and Warren, G. (1984). Density of newly synthesized plasma membrane proteins in intracellular membranes II. Biochemical studies. J. Cell Biol. 98, 2142–2147. doi: 10.1083/jcb.98.6.2142

PubMed Abstract | CrossRef Full Text | Google Scholar

Racca, C., Stephenson, F. A., Streit, P., Roberts, J. D., and Somogyi, P. (2000). NMDA receptor content of synapses in stratum radiatum of the hippocampal CA1 area. J. Neurosci. 20, 2512–2522.

PubMed Abstract | Google Scholar

Sabatini, B. L., Oertner, T. G., and Svoboda, K. (2002). The life cycle of Ca^2C ions in dendritic spines. Neuron 33, 439–452. doi: 10.1016/S0896-6273(02)00573-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabatini, B. L., and Svoboda, K. (2000). Analysis of calcium channels in single spines using optical fluctuation analysis. Nature 408, 589–593. doi: 10.1038/35046076

PubMed Abstract | CrossRef Full Text | Google Scholar

Scheuss, V., Yasuda, R., Sobczyk, A., and Svoboda, K. (2006). Nonlinear [Ca2C] signaling in dendrites and spines caused by activity-dependent depression of Ca2C extrusion. J. Neurosci. 26, 8183–8194. doi: 10.1523/JNEUROSCI.1962-06.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Selkoe, D. J. (2002). Alzheimer's disease is a synaptic failure. Science 298, 789–791. doi: 10.1126/science.1074069

PubMed Abstract | CrossRef Full Text | Google Scholar

Sjöström, P. J., and Nelson, S. B. (2002). Spike timing, calcium signals and synaptic plasticity. Curr. Opin. Neurobiol. 12, 305–314. doi: 10.1016/S0959-4388(02)00325-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Sklar, P., Ripke, S., Scott, L. J., Andreassen, O. A., Cichon, S., Craddock, N., et al. (2011). Large-scale genome-wide association analysis of bipolar disorder identifies a new susceptibility locus near ODZ4. Nat. Genet. 43, 977–983. doi: 10.1038/ng.943

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorra, K. E., and Harris, K. M. (2000). Overview on the structure, composition, function, development, and plasticity of hippocampal dendritic spines. Hippocampus 10, 501–511. doi: 10.1002/1098-1063(2000)10:5<501::AID-HIPO1>3.0.CO;2-T

PubMed Abstract | CrossRef Full Text | Google Scholar

Spacek, J., and Harris, K. M. (1997). Three-dimensional organization of smooth endoplasmic reticulum in hippocampal CA1 dendrites and dendritic spines of the immature and mature rat. J. Neurosci. 17, 190–203.

PubMed Abstract | Google Scholar

Spruston, N., Jonas, P., and Sakmann, B. (1995). Dendritic glutamate receptor channels in rat hippocampal CA3 and CA1 pyramidal neurons. J. Physiol. (Lond). 482, 325–352. doi: 10.1113/jphysiol.1995.sp020521

PubMed Abstract | CrossRef Full Text | Google Scholar

Stauffer, T. P., Guerini, D., and Carafoli, E. (1995). Tissue distribution of the four gene products of the plasma membrane Ca2C pump. A study using specific antibodies. J. Biol. Chem. 270, 12184–12190. doi: 10.1074/jbc.270.20.12184

PubMed Abstract | CrossRef Full Text | Google Scholar

Stocca, G., and Vicini, S. (1998). Increased contribution of NR2A subunit to synaptic NMDA receptors in developing rat cortical neurons. J. Physiol. 507(Pt 1), 13–24. doi: 10.1111/j.1469-7793.1998.013bu.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Takumi, Y., Ramirez-León, V., Laake, P., Rinvik, E., and Ottersen, O. P. (1999). Different modes of expression of AMPA and NMDA receptors in hippocampal synapses. Nat. Neurosci. 2, 618–624. doi: 10.1038/10172

PubMed Abstract | CrossRef Full Text | Google Scholar

Vargas-Caballero, M., and Robinson, H. P. (2004). Fast and slow voltage-dependent dynamics of magnesium block in the NMDA receptor: the asymmetric trapping block model. J. Neurosci. 24, 6171–6180. doi: 10.1523/JNEUROSCI.1380-04.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Ventura, R., and Harris, K. M. (1999). Three-dimensional relationships between hippocampal synapses and astrocytes. J. Neurosci. 19, 6897–6906.

PubMed Abstract | Google Scholar

Wadiche, J. I., Arriza, J. L., Amara, S. G., and Kavanaugh, M. P. (1995). Kinetics of a human glutamate transporter. Neuron 14, 1019–1027. doi: 10.1016/0896-6273(95)90340-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wadiche, J. I., and Kavanaugh, M. P. (1998). Macroscopic and microscopic properties of a cloned glutamate transporter/chloride channel. J. Neurosci. 18, 7650–7661.

PubMed Abstract | Google Scholar

Wang, G. J., Chung, H. J., Schnuer, J., Pratt, K., Zable, A. C., Kavanaugh, M. P., et al. (1998). High affinity glutamate transport in rat cortical neurons in culture. Mol. Pharmacol. 53, 88–96.

PubMed Abstract | Google Scholar

Witcher, M. R., Kirov, S. A., and Harris, K. M. (2007). Plasticity of perisynaptic astroglia during synaptogenesis in the mature rat hippocampus. Glia 55, 13–23. doi: 10.1002/glia.20415

PubMed Abstract | CrossRef Full Text | Google Scholar

Wuytack, F., Dode, L., Baba-Aissa, F., and Raeymaekers, L. (1995). The SERCA3-type of organellar Ca2C pumps. Biosci. Rep. 15, 299–306. doi: 10.1007/BF01788362

PubMed Abstract | CrossRef Full Text | Google Scholar

Yasuda, R., Sabatini, B. L., and Svoboda, K. (2003). Plasticity of calcium channels in dendritic spines. Nat. Neurosci. 6, 948–955. doi: 10.1038/nn1112

CrossRef Full Text | Google Scholar

Yernool, D., Boudker, O., Jin, Y., and Gouaux, E. (2004). Structure of a glutamate transporter homologue from Pyrococcus horikoshii. Nature 431, 811–818. doi: 10.1038/nature03018

PubMed Abstract | CrossRef Full Text | Google Scholar