Tip and vibration control of space robots using estimated flexible coordinates

This paper provides an extension to previous work on end-effector control of flexible space manipulators. Those works considered the use of a special output called the $\mu$-tip rate for feedback control of desired end-effector trajectories with simultaneous vibration control. Implementation of this special output requires measurement of end-effector position or the use of flexible forward kinematics to determine it. For the latter, one requires measurements of the joint angles and flexible coordinates. The second of these is difficult to measure in space scenarios, so this paper looks at the use of an estimation scheme to approximate it and use it in a task-space control law. Multiple simulations are conducted to investigate the use of these approximated elastic coordinates in robustly controlling a one-link and two-link flexible manipulator with a payload mass. The error between desired and actual trajectory is calculated, and the results are juxtaposed with results from a joint-space feedback scheme. There is an emphasis on comparing the estimated elastic coordinates with the actual simulated coordinates. Using the estimated elastic coordinates to determine the end-effector location via forward kinematics, yielded similar results to when the actual elastic coordinates were used. Overall, the estimation equation used is shown to provide reasonable end-effector tracking results with the end-effector being able to track various types of trajectories.

1 Introduction

The control of structurally flexible robot manipulators represents a significant challenge when compared with that of their rigid counterparts. In the latter case, the desired motions of the end-effector position and orientation are easily translated into a prescription for the joint motions. The latter are typically collocated with torque actuation provided by motors. This leads to the desirable property of passivity for the input-output mapping relating joint torques to joint rates. The passivity theorem (Desoer and Vidyasagar, 1975) then guarantees the stability provided by the negative feedback of strictly passive controllers such as proportional-integral control applied to joint rates [i.e., proportional-derivative (PD) control applied to the joint angle motions].

For structurally flexible manipulators, the passivity property of the joint torque to joint rate mapping continues to hold given the collocation (Benhabib et al., 1981) but this is less useful because control of the joint motions does not necessarily produce the correct motion for the end-effector coordinates. However, it is fair to say that many researchers (Benosman and Le Vey, 2004) have opted to control flexible manipulators by tracking desired joint trajectories (obtained from rigid inverse kinematics) coupled with vibration suppression of the flexible coordinates. This is often misguided because the inverse kinematical solution for a prescribed end-effector motion does typically require some deformations of the links as shown by Bayo et al. (1989).

Robust control is necessitated when there is a need for stability despite model uncertainties and environmental disturbances. For flexible manipulators, a specific issue arises in terms of the model uncertainty created by uncertain vibration frequencies and mode shapes as well as different numbers of modes in the plant model used for design compared to those in the actual structure. The vast majority of models consider each link in the manipulator as a beam with a truncated set of modes. In most cases, this truncation is not an issue and is seen to agree well with experimental results, given an appropriate number of modes have been included in the model. In a few exceptional circumstances, however, cases of spillover instability have been seen to arise as seen in Sayahkarajy and Mohamed (2014). With the passivity theorem, simple controllers can be used to robustly control systems when model uncertainty does not destroy the passivity of the plant. Hence, if passivity is achievable, then the manipulator could be robustly stabilized by a simple PD controller despite having truncated numbers of modes in the dynamics modelling.

In task-space control, actuator and sensor collocation is not possible, and it has been shown in Pota and Vidyasagar (1991) that the input-output mapping relating joint torque to tip-rate is not passive for a single flexible link. This can be explained by the fact that the transfer matrix for this mapping is nonminimum phase (hence not positive real) as shown in Cannon Jr. and Schmitz (1984). With the actual tip-rate output not being viable for task-space control of flexible manipulators, past research has focused on finding alternative task-space outputs that could perhaps achieve passivity. Given the relative ease with which passive input-output pairs can be stabilized, there has been some work done on establishing passivity for systems whose output contains the end-effector motion.

Wang and Vidyasagar (1992) were able to effectively realize the passivity property for a single flexible link system by using a reflected tip-rate output and with the assumption that the moments of inertia produced by the link and payload are much greater than the moment of inertia of the hub. These results were extended in Damaren (1995) for a multi-degree-of-freedom space manipulator attached to a rigid spacecraft and with an end-effector payload. Damaren posed an modified tip-rate output, ${\dot{\mathit{\rho }}}_{\mu }$, with which passivity could be achieved. To characterize this output, first the actual tip-rate $\dot{\mathit{\rho }}$ must be defined. Let the Cartesian end-effector (translational and rotational) displacements be defined as $\mathit{\rho }=\mathcal{F}(\mathit{\theta },{\mathbf{q}}_e)$ where $\mathcal{F}$ is the forward kinematics map, $\mathit{\theta }$ are the joint angles, and ${\mathbf{q}}_e$ are the elastic coordinates. Then the velocity kinematics are given by the following:

$\dot{\mathit{\rho }}={\mathbf{J}}_{\theta }\left(\mathit{\theta },{\mathbf{q}}_e\right)\dot{\mathit{\theta }}+{\mathbf{J}}_e\left(\mathit{\theta },{\mathbf{q}}_e\right){\dot{\mathbf{q}}}_e(1)$

where ${\mathbf{J}}_{\theta }$ and ${\mathbf{J}}_e$ are Jacobian matrices. The modified tip-rate output can then be defined as the following:

${\dot{\mathit{\rho }}}_{\mu }={\mathbf{J}}_{\theta }\dot{\mathit{\theta }}+\mu {\mathbf{J}}_e{\dot{\mathbf{q}}}_e(2)$

where $\mu$ is a real parameter. The parameter $\mu$ can help characterize the stability region, with a critical ${\mu }^{*}$ representing the boundary for which system stabilization can be achieved using simple PD laws. Notably, ${\mu }^{*}$ for a given system can be determined analytically and is directly related to the payload-to-link mass ratio of the manipulator (Damaren, 2000). As long as $\mu$ obeying $0\le \mu <{\mu }^{*}$ is used to compute ${\dot{\mathit{\rho }}}_{\mu }$, the joint-torque to ${\dot{\mathit{\rho }}}_{\mu }$ pairing can be shown to be passive, and a PD law can be employed for control.

With large payloads, ${\mu }^{*}\to 1$ and the modified output, ${\dot{\mathit{\rho }}}_{\mu }$, asymptotically approaches the true tip-rate, while still maintaining passivity. This behaviour is due to the modal properties of flexible manipulators. In Damaren (1995) it was shown how the unconstrained mode shapes of the links increasingly followed pinned-clamped behaviour as the mass of the payload increased. This created a favourable node at the end-effector, and vibrations were seen mainly along the length of the links and not at the tip. The nonminimum phase property of the task-space mapping was shown to be mitigated in this asymptotic case of large payloads. With the use of ${\dot{\mathit{\rho }}}_{\mu }$ as an output, a task-space control scheme utilizing the passivity property proven in Damaren (1995) can be used to control flexible manipulators in space. In order to obtain this modified output however, measurement or estimation of the elastic coordinates is needed which motivates the present study.

Obtaining the elastic coordinates through sensors has proven difficult, historically. In some experimental papers the elastic deflection of a flexible link is measured using optical sensors such as cameras as seen in Wang and Vidyasagar (1992) or laser diodes as seen in Tso et al. (2003). Notably, this was done for the single-link manipulator in both Wang and Vidyasagar (1992) and Tso et al. (2003). With multi-degree-of-freedom manipulators, these optical systems would be more expensive and complicated to implement and are less feasible. Another major problem with these optical sensing systems is that they become unusable if an object comes in between the camera and the manipulator. Another strategy is to use resistive strain gauges, which was done in Stanway et al. (1998) to obtain values for elastic coordinates experimentally. Christoforou and Damaren (2000) used strain gauges to estimate three flexible coordinates for each of two flexible links on a three-link planar manipulator. This required calibration of the strain gauges before each use of the manipulator system and was more labour-intensive overall. Additionally, strain gauges have reliability issues in the space environment due to thermal effects.

With the difficulty in measuring elastic coordinates directly, the next best solution would be to find a way to reliably estimate these coordinates. Then, $\mathit{\rho }$ can be computed using $\widehat{\mathit{\rho }}=\mathcal{F}(\mathit{\theta },{\widehat{\mathbf{q}}}_e)$ where ${\widehat{\mathbf{q}}}_e$ is the estimated ${\mathbf{q}}_e$. Classical state estimation schemes, such as the Kalman filter or reduced-order observers, being linear, are unsuitable to handle estimation for the highly nonlinear manipulator systems. In Moallem (1996) a nonlinear observer was developed for a two-link manipulator. This observer used three measurements, however: joint rates and angles, along with elastic coordinate measurements from strain gauges. Only the elastic coordinate rates were unmeasured and to be estimated. While suitable for a nonlinear problem, this solution still had the issue of strain gauges, which cannot be used in space, and was overall very complex to design and implement. More sophisticated techniques for designing observers for nonlinear systems were put forward in Bernard (2017). Its route of action was to normalize the given nonlinear system into a standard form with normalized coordinates, observe these normalized coordinates, and then inversely map them back to the original system to determine the original coordinates. This process can be computationally expensive for controllers, however, and real-time implementation has to be tested. The normalizing process for a multi-degree-of-freedom flexible manipulator has also not been done in literature and a suitable transformation and change of coordinates is not guaranteed to exist. Another non-linear estimation scheme was seen in Fenili (2013) which used a state-dependent Riccati equation-based estimator to estimate the elastic coordinates of a flexible-link manipulator. This estimation scheme is complex and requires that one find an observer gain L through trial and error. Additionally, even with an acceptable gain chosen, the estimator had large overshoots in the results presented in Fenili (2013).

More recently, virtual sensor theory has been used to estimate the generalized elastic coordinates and find the end-effector position of flexible manipulators. This was done in Bengoa et al. (2017) very successfully though with a note on the computational load required for real-time implementation. In Adel et al. (2022) virtual sensor theory was combined with function approximation schemes found in machine learning literature. Results were also promising with this method although the computational load was still high, albeit lower than in Bengoa et al. (2017).

Overall, sensor solutions to measure elastic coordinates are lacking with current technology. Furthermore, most observer schemes to estimate these coordinates are either highly complex, so requiring a large computation load, or are not feasible for nonlinear systems in a space setting. In contrast, Damaren (1995) offers a closed-form estimation formula, valid for flexible manipulators with large payloads. It is given by

${\mathbf{K}}_{ee}{\widehat{\mathbf{q}}}_e\left(t\right)=-{\mathbf{J}}_e^T{\mathbf{J}}_{\theta }^{-T}\mathit{\tau }\left(t\right)(3)$

where ${\mathbf{K}}_{ee}$ is the elastic portion of the stiffness matrix and $\mathit{\tau }$ are the joint torques.

The present paper looks at the simulated behaviour of flexible robots in response to a task-space controller that uses the above estimate of the flexible coordinates to determine ${\mathit{\rho }}_{\mu }$. Planar one-link and two-link manipulators with flexible links are studied. In the second section of this paper, the methods employed to model a flexible manipulator are laid out. Additionally, the task-space control scheme utilized in subsequent simulations is defined. The third section presents the results obtained from simulating multiple end-effector trajectories with the given control scheme. A discussion on these results is also included. The final section includes concluding thoughts from the results and summarizes key findings.

2 Methods

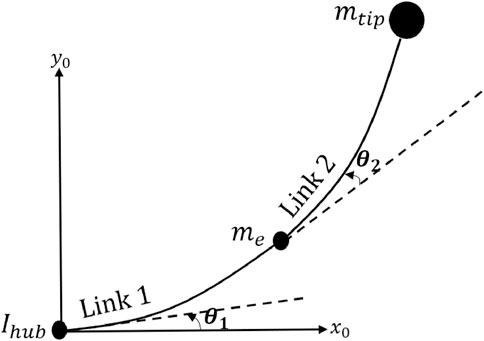
In this paper, a space robot comprised of a topological chain of $N$ linearly elastic flexible bodies was considered. The bodies were connected by revolute joints with joint angles $\mathit{\theta }\in {\mathfrak{R}}^N$. The flexibility was limited to the links and assumed to be only in the direction traverse to the link length, with no longitudinal motions or out-of-plane deflections. The totality of the flexible coordinates can be given by ${\mathbf{q}}_e\in {\mathfrak{R}}^{N_e}$, generated using clamped-free modelling for the deflections of each link. Let $\mathbf{q}=\mathrm{c}\mathrm{o}\mathrm{l}\{\mathit{\theta },{\mathbf{q}}_e\}$ be the column matrix of generalized coordinates. Additionally, there was an inertia $I_{\mathit{hub}}$ assigned to the hub and a point tip mass $m_{\mathit{tip}}$ at the end-effector. Particularly for this investigation, planar one-link and two-link manipulators were the subject of study. Figures 1, 2 show a visual representation of the one-link and two-link manipulators, respectively. In the one-link case, the tip position $\mathit{\rho }$ translates to the arc length traversed from the initial position of $\theta =0$. In the two-link case, the tip position is expressed in the traditional Cartesian inertial frame, in $x$ and $y$.

Figure 1

Figure 1. One-link flexible manipulator.

Figure 2

Figure 2. Two-link flexible manipulator.

2.1 Equations of motion

The modelling techniques from Damaren (1995), Wong (2006), and Fraser and Daniel (1991) were used to develop the equations of motion. For a general flexible manipulator, these equations are as follows:

$\mathbf{M}\left(\mathbf{q}\right)\ddot{\mathbf{q}}+\mathbf{c}\left(\mathbf{q},\dot{\mathbf{q}}\right)+\mathbf{K}\mathbf{q}=\mathbf{B}\mathit{\tau }(4)$

where $\mathbf{M}$ is the mass matrix, $\mathbf{K}$ is the stiffness matrix, $\mathbf{B}$ is the input matrix, and $\mathit{\tau }\in {\mathfrak{R}}^N$ are the joint torques:

$\mathbf{M}=\left[\begin{array}{cc}\hfill {\mathbf{M}}_{\theta \theta }\hfill & \hfill {\mathbf{M}}_{\theta e}\hfill \\ \hfill {\mathbf{M}}_{\theta e}^T\hfill & \hfill {\mathbf{M}}_{ee}\hfill \end{array}\right],\mathbf{K}=\left[\begin{array}{cc}\hfill \mathbf{O}\hfill & \hfill \mathbf{O}\hfill \\ \hfill \mathbf{O}\hfill & \hfill {\mathbf{K}}_{ee}\hfill \end{array}\right],\mathbf{B}=\left[\begin{array}{c}\hfill \mathbf{1}\hfill \\ \hfill \mathbf{O}\hfill \end{array}\right](5)$

for the above matrices, the matrix structure is consistent with $\mathbf{q}=\mathrm{c}\mathrm{o}\mathrm{l}\{\mathit{\theta },{\mathbf{q}}_e\}$. The elastic portion of the stiffness matrix can be defined as ${\mathbf{K}}_{ee}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\{K_{ee,1},\dots ,K_{ee,N_e}\}$, where $K_{ee,n}=EI{\int }_0^L{{\psi }_{n^{″}}}^{2}dx$ as per Chen et al. (2023). The nonlinear inertial terms are $\mathbf{c}(\mathbf{q},\dot{\mathbf{q}})$, which are quadratic in $\dot{\mathbf{q}}$, and are given by the following:

$\mathbf{c}{\left(\mathbf{q},\dot{\mathbf{q}}\right)}_i={\mathbf{e}}_i^T{\displaystyle \sum _{j=1}^{N+N_e}}{\dot{q}}_j\frac{\partial \mathbf{M}}{\partial q_j}\dot{\mathbf{q}}-\frac{1}{2}{\dot{\mathbf{q}}}^T\frac{\partial \mathbf{M}}{\partial q_i}\dot{\mathbf{q}}$

where ${\mathbf{e}}_i$ is a unit vector, non-zero in the $i^{th}$ degree of freedom. Notably for the one-link case, the nonlinear term collapses to zero.

2.2 Control scheme

With the equations of motion defined, a task-space control scheme can be implemented. This control scheme utilized the approximated elastic coordinates to determine the modified task-space output, ${\dot{\mathit{\rho }}}_{\mu }$ and is defined as follows:

$\mathit{\tau }={\mathbf{M}}_{\theta \theta }\left({\mathit{\theta }}_d,\mathit{0}\right){\ddot{\mathit{\theta }}}_d+\mathbf{c}\left(\left({\mathit{\theta }}_d,\mathit{0}\right),\left({\dot{\mathit{\theta }}}_d,\mathit{0}\right)\right)-{\mathbf{J}}_{\theta }^T\left[K_P\left[{\widehat{\mathit{\rho }}}_{\mu }-{\mathit{\rho }}_d\right]+K_D\left[{\widehat{\dot{\mathit{\rho }}}}_{\mu }-{\dot{\mathit{\rho }}}_d\right]\right](6)$

where ${\mathbf{M}}_{\theta \theta }({\mathit{\theta }}_d,\mathit{0})$ is an approximation of the mass matrix, $\mathbf{c}\left(({\mathit{\theta }}_d,\mathit{0}),({\dot{\mathit{\theta }}}_d,\mathit{0})\right)$ is the matrix of nonlinear terms, ${\mathbf{J}}_{\theta }$ is the rigid Jacobian, $K_P$, $K_D$ are the proportional and derivative control gains, respectively, and ${\mathit{\rho }}_d$, ${\dot{\mathit{\rho }}}_d$ are the desired end-effector positions and rates, respectively. The desired joint variables, ${\mathit{\theta }}_d,{\dot{\mathit{\theta }}}_d$, and ${\ddot{\mathit{\theta }}}_d$ are all obtained from the rigid inverse kinematic solution of ${\mathit{\rho }}_d$. The motivation for the feedforward in Equation 6 is described by Stanway et al. (1998).

The modified tip-rate output is as follows:

${\dot{\mathit{\rho }}}_{\mu }={\mathbf{J}}_{\theta }\dot{\mathit{\theta }}+\mu {\mathbf{J}}_e{\dot{\mathbf{q}}}_e+\mu {\mathbf{J}}_{\theta }\dot{\mathit{\theta }}-\mu {\mathbf{J}}_{\theta }\dot{\mathit{\theta }}=\mu \left({\mathbf{J}}_{\theta }\dot{\mathit{\theta }}+{\mathbf{J}}_e{\dot{\mathbf{q}}}_e\right)+\left(1-\mu \right){\mathbf{J}}_{\theta }\dot{\mathit{\theta }}=\mu \dot{\mathit{\rho }}+\left(1-\mu \right){\mathbf{J}}_{\theta }\dot{\mathit{\theta }}(7)$

the above equation assumes the true end-effector rate $\dot{\mathit{\rho }}$ is known, as to bypass the need to approximate ${\dot{\mathbf{q}}}_e$.

If the Jacobian is approximated by ${\mathbf{J}}_{\mathit{\theta }}\approx {\mathbf{J}}_{\theta }(\mathit{\theta },\mathbf{0})$, then the integral of Equation 7 gives the following:

${\mathit{\rho }}_{\mu }=\int {\dot{\mathit{\rho }}}_{\mu }dt=\int \left(\mu \dot{\mathit{\rho }}+\left(1-\mu \right){\mathbf{J}}_{\theta }\dot{\mathit{\theta }}\right)dt=\mu \mathit{\rho }+\left(1-\mu \right)\mathcal{F}\left(\mathit{\theta },\mathbf{0}\right)(8)$

hence, for $\mu =1$, ${\mathit{\rho }}_{\mu }=\mathit{\rho }$ is the true tip position and for $\mu =0$, ${\mathit{\rho }}_{\mu }={\mathcal{F}}_r(\mathit{\theta })\stackrel{\mathrm{\Delta }}{=}\mathcal{F}(\mathit{\theta },\mathbf{0})$ is the rigid forward kinematics solution. To obtain $\mathit{\rho }$, the forward kinematics map with the approximated flexible coordinates can be used. Then Equation 8 becomes the following:

${\widehat{\mathit{\rho }}}_{\mu }=\left(1-\mu \right)\mathcal{F}\left(\mathit{\theta },\mathbf{0}\right)+\mu \widehat{\mathit{\rho }}=\left(1-\mu \right)\mathcal{F}\left(\mathit{\theta },\mathbf{0}\right)+\mu \mathcal{F}\left(\mathit{\theta },{\widehat{\mathbf{q}}}_e\right)(9)$

additionally, it is to be noted that to use Equation 7, the rigid Jacobian is needed. In multi-degree-of-freedom manipulators, this Jacobian is a function of elastic coordinates and so the approximation must be used for computation of the term. Then Equation 7 can be rewritten as the following:

${\dot{\mathit{\rho }}}_{\mu }=\mu \dot{\mathit{\rho }}+\left(1-\mu \right){\widehat{\mathbf{J}}}_{\theta }\dot{\mathit{\theta }}(10)$

where ${\widehat{\mathbf{J}}}_{\theta }$ is the rigid Jacobian, calculated using the estimated elastic coordinates. Note that in Equation 10 $\dot{\mathit{\rho }}$ is needed. This rate can be taken as a measurement with an accelerometer attached to the end-effector. The approximation of the elastic coordinates, used to compute ${\widehat{\mathit{\rho }}}_{\mu }$ and ${\widehat{\dot{\mathit{\rho }}}}_{\mu }$, is slightly changed from Equation 3 as follows:

${\widehat{\mathbf{q}}}_e\left(t\right)=-{\mathbf{K}}_{ee}^{-1}{\mathbf{J}}_e^T{\mathbf{J}}_{\theta }^{-1}\mathit{\tau }\left(t-k\right)(11)$

where $k$ is the time between consecutive time steps. It should be noted that as the joint torques $\mathit{\tau }(t)$ are not immediately available, the values from the previous time-step of the simulation are used to estimate the elastic coordinate values for the current time-step. This approximation came forth in Damaren (1995) as a result of assuming a state of static equilibrium for the manipulator. This is noticeably the reason for the mass matrix not appearing in the approximation, as system acceleration is assumed to be zero. Therefore, the use of the approximation during highly dynamic modes of the manipulator is one of the objects of interest for the simulations done in this paper.

3 Results and discussion

3.1 One-link

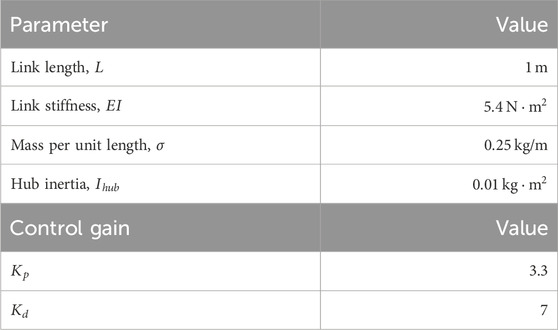
Multiple simulations were done in MATLAB implementing the control scheme given by Equation 6. Table 1 below lists the sizing parameters and control gains used in all one-link simulations.

Table 1

Table 1. Sizing parameters and control gains used in one-link manipulator simulations.

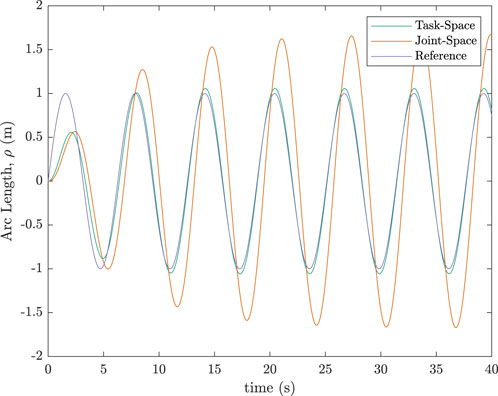
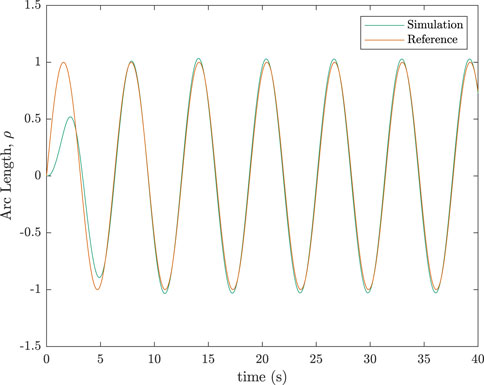
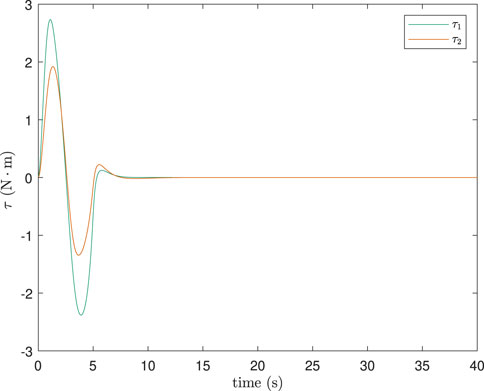
A sinusoidal trajectory was simulated for the one-link manipulator. Results are shown in Figure 3. The worst tracking occurred in the initial few seconds of the simulation. This follows from the fact that the approximation given by Equation 11 is derived assuming a quasi-static state, whilst the period when the manipulator is first moved from rest is highly dynamic. Figure 3 includes results from an appropriate joint-space control scheme as well, for easier comparison. The following joint-space control scheme was used:

$\mathit{\tau }={\mathbf{M}}_{\theta \theta }\left({\mathit{\theta }}_d,\mathit{0}\right){\ddot{\mathit{\theta }}}_d-\left(K_P\left[\mathit{\theta }-{\mathit{\theta }}_d\right]+K_D\left[\dot{\mathit{\theta }}-{\dot{\mathit{\theta }}}_d\right]\right)(12)$

Note that the desired joint angle, rate, and acceleration used in the joint-space scheme were obtained from the rigid inverse kinematic solution of the desired end-effector trajectory. The task-space scheme using the elastic coordinate approximation fared much better than the joint-space scheme as seen in the simulation results in Figure 3. The proportional and derivative gains, $K_p$ and $K_d$, were kept identical in both the task-space and joint-space control laws.

Figure 3

Figure 3. Trajectory tracking of one-link manipulator, $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

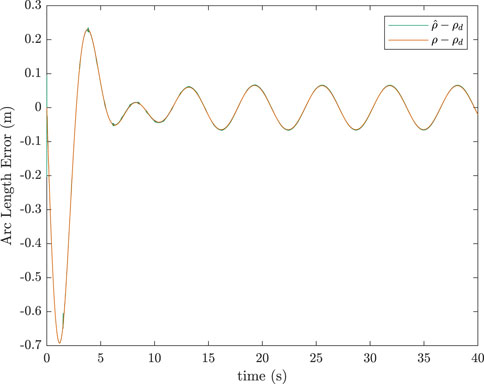
Figure 4 shows the tracking error for this same simulation. The two graphs of $\rho -{\rho }_d$ and $\widehat{\rho }-{\rho }_d$ almost coincide, signaling that subpar performance in Figure 3 is most likely not due to the elastic coordinate approximation being inaccurate. This also suggests that performance can be improved with finer tuning of the control gains and/or $\mu$. Additionally, the approximate generalized elastic coordinates were plotted against the actual coordinates, determined from simulation. This is seen in Figure 5 and results show the approximate coordinates closely followed the actual coordinates.

Figure 4

Figure 4. Error between true tip-position and desired position of one-link manipulator, $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

Figure 5

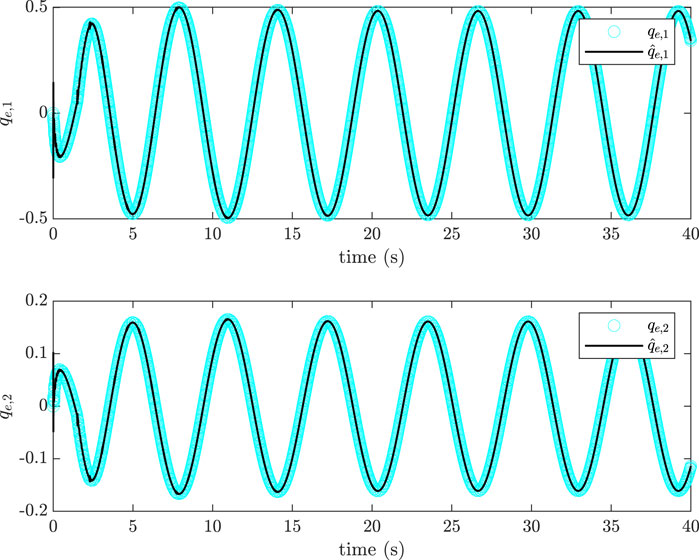
Figure 5. Comparison of approximated generalized elastic coordinates with actual, simulated values, $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and ${\mu }_{\mathit{final}}=0.9$.

The following equation was used to calculate the error between the actual elastic coordinates and the estimated ones:

$E_{qe}=\sqrt{\frac{{\int }_0^T{\left({\widehat{\mathbf{q}}}_e-{\mathbf{q}}_e\right)}^T\left({\widehat{\mathbf{q}}}_e-{\mathbf{q}}_e\right)dt}{{\int }_0^T{\mathbf{q}}_e^T{\mathbf{q}}_{e}dt}}(13)$

This error was calculated for multiple simulations, across which, the trajectory followed and the $\mu$ used was kept identical ($\mu =0.6$) and only the size of payload mass at the end-effector was changed. This allowed the creation of Figure 6 which plots the error between ${\mathbf{q}}_e$ and ${\widehat{\mathbf{q}}}_e$ for varying payload masses. There was a downward trend noted in error as the payload mass increased, and from the logarithmic plot it is clear that this downward trend was algebraic. These results suggest that Equation 11 is more accurate as $m_{\mathit{tip}}/m_{\mathit{link}}$ increases. This can be extended by saying that the approximation becomes better as the value of ${\mu }^{*}$ increases. In the asymptotic case of ${\mu }^{*}\to 1$, not only is the task-space output almost exactly the real tip-rate, the elastic coordinate approximation is also the most accurate.

Figure 6

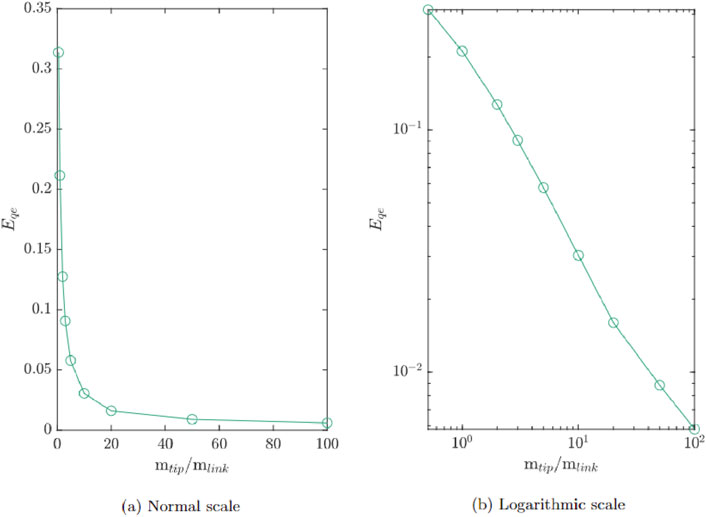
Figure 6. Generalized elastic coordinate estimation error on (A) normal scale and (B) logarithmic scale for varying ratios of $m_{\mathit{tip}}/m_{\mathit{link}}$, done using $\mu =0.6$.

Notably, the elastic component of the link’s displacement was modelled using only two basic functions in all results thus far, hence the two elastic coordinates generated in Figure 5. As one issue with controlling flexible structures is their infinite elastic degrees of freedom, it is important to investigate if truncating these degrees of freedom to elastic modes caused a loss of stability.

To check this, a simulation was done where the number of degrees of freedom in the controller was set to be different from the number in the plant. All terms in Equation 6 were calculated using a truncated model of two flexible degrees of freedom, $N_{e,controller}=2$, while the plant was programmed to have five degrees, $N_{e,plant}=5$. With higher numbers of elastic modes, a numerical degeneracy was seen in Wong (2006) for the Rayleigh-Ritz Method. To prevent this from occurring in the investigation, the highest number of modes were capped to $N_{e,plant}=5$ for the plant. From Figure 7 it can be seen that stability was still preserved in such a case. Moreover, there was no significant loss in performance, and accurate tracking was still maintained.

Figure 7

Figure 7. One-link tracking for different modes in plant and controller for $m_{\mathit{tip}}/m_{\mathit{link}}=20$, ${\mu }_{\mathit{final}}=0.9$, $N_{e,plant}=5$, $N_{e,controller}=2$.

3.2 Two-link

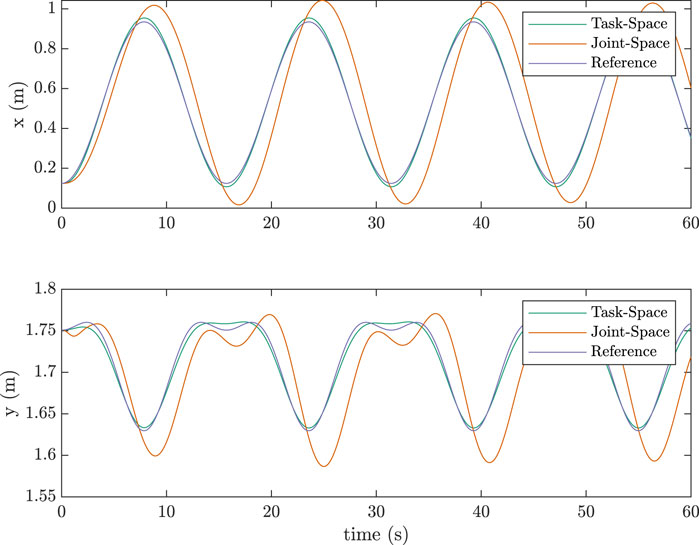
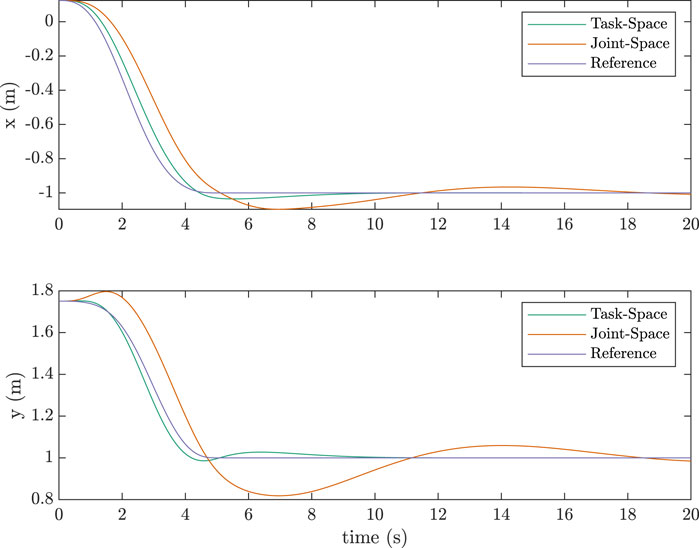
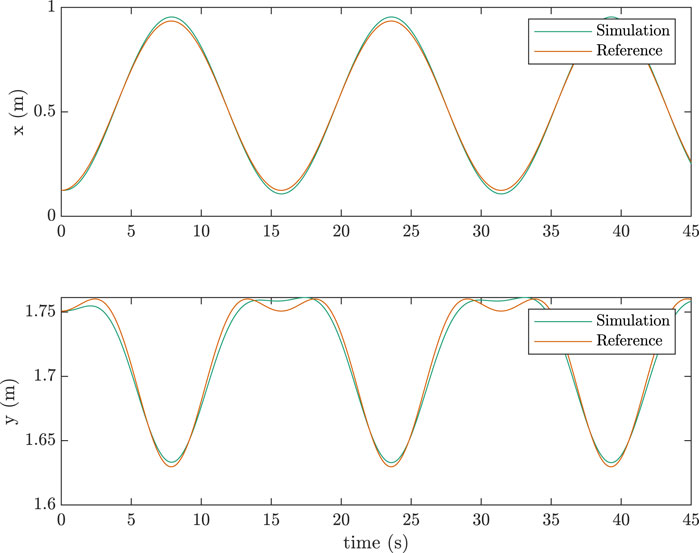
Simulations for the two-link case were also done similarily. Table 2 lists the parameters used in the simulations along with the control gains.Figure 8 shows the task-space tracking as compared to a joint-space scheme for a sinusoidal trajectory. Figure 9 shows the equivalent for a pick-and-place trajectory generated using a quintic polynomial. The performance with the task-space scheme proved to be considerably better than its joint-space counterpart for both trajectory types. The joint-space scheme used in Figures 8, 9 is as follows:

$\mathit{\tau }={\mathbf{M}}_{\theta \theta }\left({\mathit{\theta }}_d,\mathit{0}\right){\ddot{\mathit{\theta }}}_d+\mathbf{c}\left(\left({\mathit{\theta }}_d,\mathit{0}\right),\left({\dot{\mathit{\theta }}}_d,\mathit{0}\right)\right)-\left(K_P\left[\mathit{\theta }-{\mathit{\theta }}_d\right]+K_D\left[\dot{\mathit{\theta }}-{\dot{\mathit{\theta }}}_d\right]\right)(14)$

As tracking performance for the two-link case was slightly worse than the one-link case, especially for the sinusoidal trajectory, an investigation was done to see how much of this performance loss was due to the elastic coordinates being estimated rather than measured. Figures 10, 11 show the tracking error for both the sinusoidal and pick-and-place trajectories, respectively. As one can see, the graphs of $\mathit{\rho }-{\mathit{\rho }}_d$ and $\widehat{\mathit{\rho }}-{\mathit{\rho }}_d$ almost coincide, and so subpar performance is most likely not due to the elastic coordinate approximation being inaccurate. It is also possible that the frequency of the desired sinusoidal trajectory is simply faster than the time it takes for the actuation wave to reach the end of the links. With such long, flexible links, there is naturally time needed for the actuation at the joints to traverse the length of the link to reach the end-effector. Only trajectories that are slower than the period of this wave can be realistically achieved by the manipulator with any degree of accuracy.

Table 2

Table 2. Sizing parameters and control gains used in two-link manipulator simulations.

Figure 8

Figure 8. Sinusoidal trajectory tracking of two-link manipulator for $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

Figure 9

Figure 9. Pick-and-place trajectory tracking of two-link manipulator for $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

Figure 10

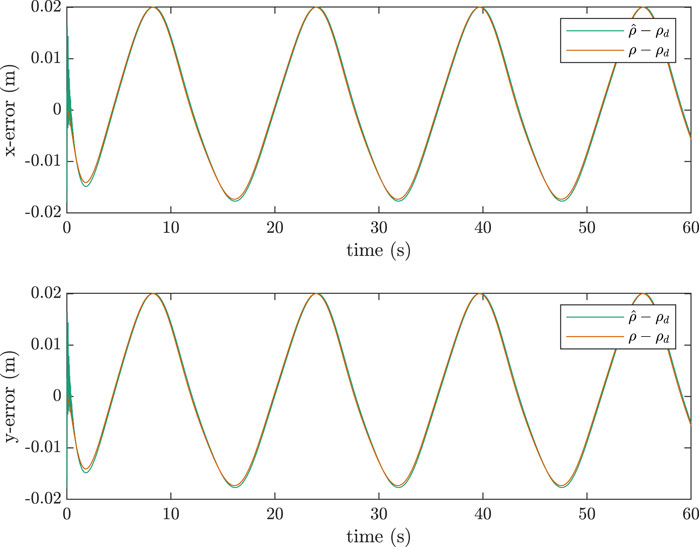
Figure 10. Error between true tip-position and desired position for a two-link manipulator, sinusoidal trajectory, $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

Figure 11

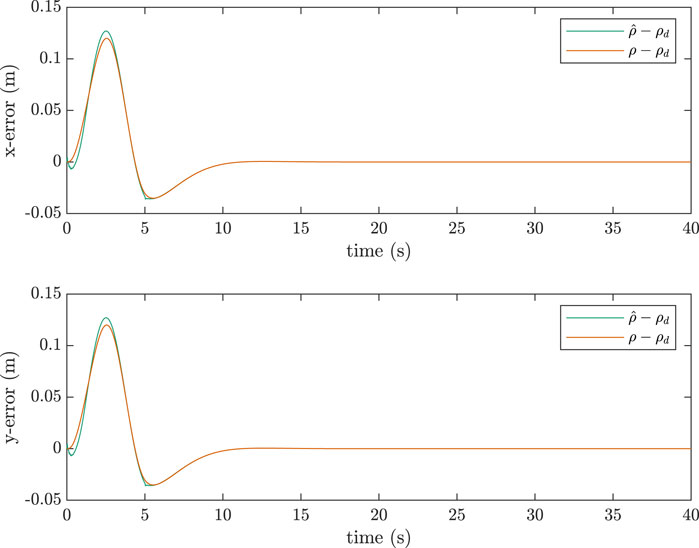
Figure 11. Error between true tip-position and desired position for a two-link manipulator, quintic trajectory, $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

The slight oscillations visible in Figure 10 at the beginning of the simulation can be explained by the assumptions behind the approximation equation, namely that it was derived in Damaren (1995) assuming a quasi-static state of the manipulator. When the manipulator is first moved from rest, it is highly dynamic and the approximation equation is not able to estimate the elastic coordinates as accurately in this initial highly dynamic period. This explains the deviations present at the beginning of Figure 10.

As the Jaocbians in the two-link case are a function of ${\mathbf{q}}_e$, the simulations in this case required that the Jacobians be calculated using ${\widehat{\mathbf{q}}}_e$ from the previous time step. These Jacobians could then be used to calculate the current ${\widehat{\mathbf{q}}}_e$ as follows:

${\widehat{\mathbf{q}}}_e\left(t\right)=-{\mathbf{K}}_{ee}^{-1}{\left[{\widehat{\mathbf{J}}}_e\left(\mathit{\theta }\left(t\right),{\widehat{\mathbf{q}}}_e\left(t-k\right)\right)\right]}^T{\left[{\widehat{\mathbf{J}}}_{\theta }\left(\mathit{\theta }\left(t\right),{\widehat{\mathbf{q}}}_e\left(t-k\right)\right)\right]}^{-T}\mathit{\tau }\left(t-k\right)(15)$

To bypass the need to use the approximated elastic coordinates of the previous time-step in the calculation of the current ${\widehat{\mathbf{q}}}_e$, the use of a modified approximation of coordinates was investigated. In this modified approximation, the Jacobians were calculated using only the measured rigid degrees of freedom, and ${\mathbf{q}}_e$ was set to $\mathit{0}$ as follows:

${\widehat{\widehat{\mathbf{q}}}}_e\left(t\right)=-{\mathbf{K}}_{ee}^{-1}{\left[{\mathbf{J}}_e\left(\mathit{\theta },\mathit{0}\right)\right]}^T{\left[{\mathbf{J}}_{\theta }\left(\mathit{\theta },\mathit{0}\right)\right]}^{-T}\mathit{\tau }\left(t-k\right)(16)$

Equations 1, 2, 4, 5, 9, 12-15 summarize the kinematics, dynamics, and control. In Figures 12, 13, corresponding to the sinusoidal and pick-and-place trajectories, respectively, the approximate elastic coordinates, ${\widehat{\mathbf{q}}}_e$ were compared with the real coordinates, ${\mathbf{q}}_e$, which were obtained from simulation. Additionally, the modified approximation, ${\widehat{\widehat{\mathbf{q}}}}_e$ from Equation 16 was also plotted in both figures. It is apparent, especially in the pick-and-place trajectory, that the approximation ${\widehat{\mathbf{q}}}_e$ followed the real values more closely than the approximation ${\widehat{\widehat{\mathbf{q}}}}_e$. Figures 14, 15 show the joint actuator torques for the sinusoidal and pick-and-place trajectories, respectively. For both cases, torques were relatively low and stayed within a reasonable range.

Figure 12

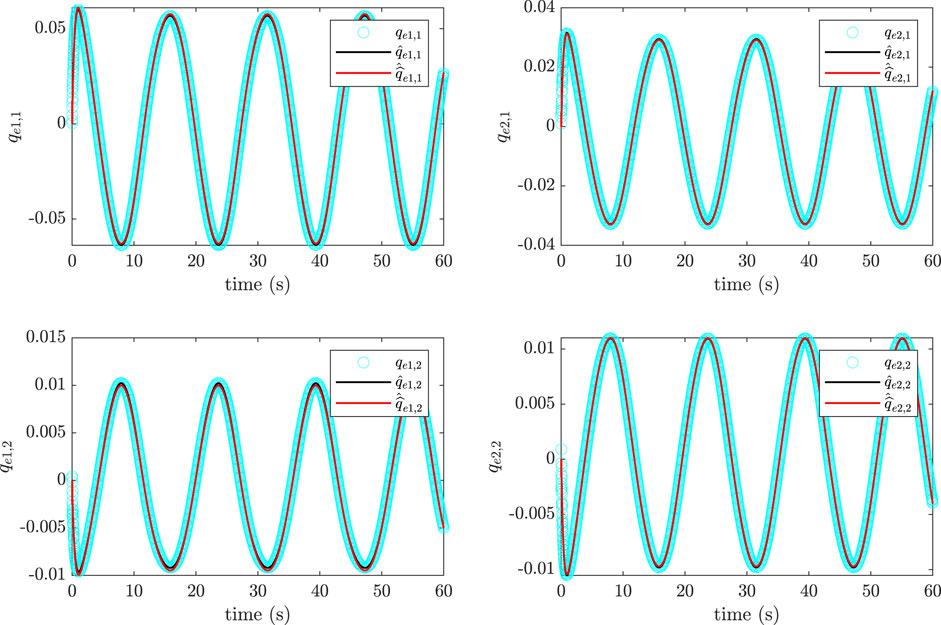
Figure 12. Comparison of approximated generalized elastic coordinates with actual, simulated values for two-link manipulator, sinusoidal trajectory, $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

Figure 13

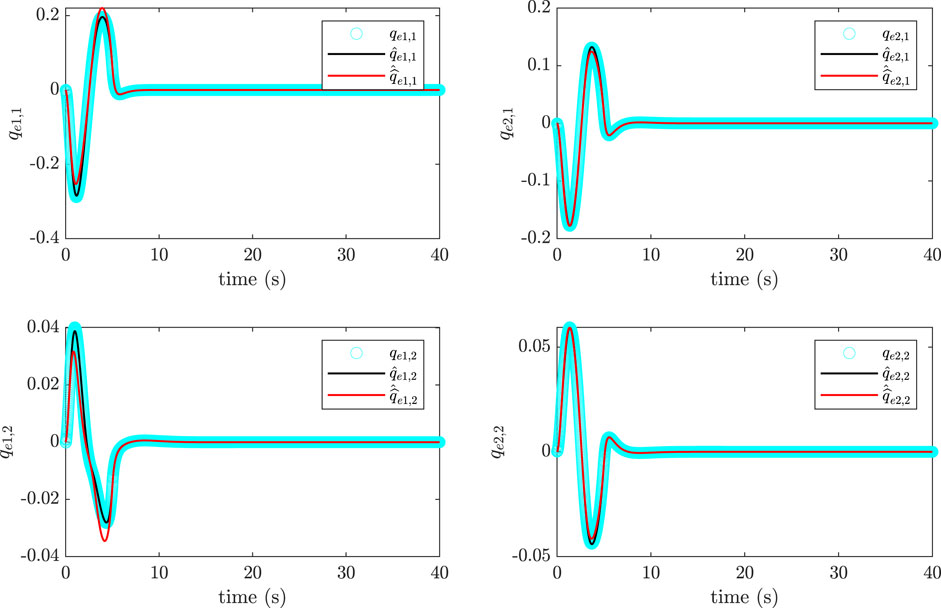
Figure 13. Comparison of approximated generalized elastic coordinates with actual, simulated values for two-link manipulator, quintic trajectory, $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

Figure 14

Figure 14. Joint Torques for two-link manipulator, sinusoidal trajectory, $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

Figure 15

Figure 15. Joint Torques for two-link manipulator, quintic trajectory, $m_{\mathit{tip}}/m_{\mathit{link}}=20$ and $\mu =0.9$.

Lastly, simulations were done with a different number of modes for the plant and controller to check if truncating the dynamics to a finite dimension caused instability. Results showed no spillover effects as shown in Figure 16 below. The total number of elastic modes used were $N_{e,controller}=4$ and $N_{e,plant}=8$, with the modes divided equally between the two links.

Figure 16

Figure 16. Two-link tracking for different modes in plant and controller for $m_{\mathit{tip}}/m_{\mathit{link}}=20$, $\mu =0.9$, $N_{e.plant}=8$, $N_{e,controller}=4$.

4 Conclusion

In this work, one-link and two-link flexible manipulators were modelled and a task-space control scheme that utilized the passivity theorem was implemented for end-effector trajectory tracking. This tracking was accomplished using the elastic coordinate approximation given by Equation 11. In all cases, the ${\mathbf{q}}_e$ approximation was used successfully to track various end-effector trajectories. The largest discrepancies between the approximated and actual elastic coordinate values were found to be during the initial few seconds of simulation when the manipulator was at its most dynamic. This follows from the fact that Equation 11 is derived assuming a quasi-static state.

In the one-link results, it was seen that the elastic coordinate approximation given by Equation 11 was more accurate as the ratio of $m_{\mathit{tip}}/m_{\mathit{link}}$ increased. The one-link and two-link results showed that even when the plant was modelled with more elastic degrees of freedom than the controller assumed, the results were still stable. Overall, it can be seen that the approximation given by Equation 11 is a powerful tool and advantageous in the fact that it provides a closed-form analytical method to estimate the generalized elastic coordinates.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

DP: Visualization, Writing–original draft, Writing–review and editing. CD: Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by a Discovery Grant provided by the Natural Sciences and Engineering Research Council (Canada).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adel, M., Ahmed, S. M., and Fanni, M. (2022). End-effector position estimation and control of a flexible interconnected industrial manipulator using machine learning. IEEE Access 10, 30465–30483. doi:10.1109/ACCESS.2022.3157817

CrossRef Full Text | Google Scholar

Bayo, E., Papadopoulos, P., Stubbe, J., and Serna, M. A. (1989). Inverse dynamics and kinematics of multilink elastic robots: an iterative frequency domain approach. Int. J. Robotics Res. 8, 49–62. doi:10.1177/027836498900800604

CrossRef Full Text | Google Scholar

Bengoa, P., Zubizarreta, A., Cabanes, I., Mancisidor, A., Pinto, C., and Mata, S. (2017). Virtual sensor for kinematic estimation of flexible links in parallel robots. Sensors 17 (9), 1934. doi:10.3390/s17091934

PubMed Abstract | CrossRef Full Text | Google Scholar

Benhabib, R. J., Iwens, R. P., and Jackson, R. L. (1981). Stability of large space structure control systems using positivity concepts. J. Guid. Control, Dyn. 4, 487–494. doi:10.2514/3.56100

CrossRef Full Text | Google Scholar

Benosman, M., and Le Vey, G. (2004). Control of flexible manipulators: a survey. Robotica 22, 533–545. doi:10.1017/s0263574703005642

CrossRef Full Text | Google Scholar

Bernard, P. (2017). Observer design for nonlinear systems, automatic control engineering. Paris, France: Université Paris sciences et lettres. Ph.D. thesis.

Google Scholar

Cannon, Jr. R. H., and Schmitz, E. (1984). Initial experiments on the end-point control of a flexible one-link robot. Int. J. Robotics Res. 3, 62–75. doi:10.1177/027836498400300303

CrossRef Full Text | Google Scholar

Chen, T., Wang, Y., Wen, H., and Kang, J. (2023). Autonomous assembly of multiple flexible spacecraft using RRT* algorithm and input shaping technique. Nonlinear Dyn. 111, 11223–11241. doi:10.1007/s11071-023-08445-3

CrossRef Full Text | Google Scholar

Christoforou, E. G., and Damaren, C. J. (2000). The control of flexible-link robots manipulating large payloads: theory and experiments. J. Robotic Syst. 17, 255–271. doi:10.1002/(sici)1097-4563(200005)17:5<255::aid-rob3>3.0.co;2-k

CrossRef Full Text | Google Scholar

Damaren, C. J. (1995). Passivity analysis for flexible multilink space manipulators. J. Guid. Control, Dyn. 18, 272–279. doi:10.2514/3.21380

CrossRef Full Text | Google Scholar

Damaren, C. J. (2000). Passivity and noncollocation in the control of flexible multibody systems. J. Dyn. Syst. Meas. Control 122, 11–17. doi:10.1115/1.482423

CrossRef Full Text | Google Scholar

Desoer, C. A., and Vidyasagar, M. (1975). Feedback systems: input-output properties. New York: Academic Press.

Google Scholar

Fenili, A. (2013). The rigid-flexible robotic manipulator: nonlinear control and state estimation considering a different mathematical model for estimation. Shock Vib. 20, 1049–1063. doi:10.1155/2013/681846

CrossRef Full Text | Google Scholar

Fraser, A. R., and Daniel, R. W. (1991). Perturbation techniques for flexible manipulators. Massachusetts: Kluwer Academic Publishers.

Google Scholar

Moallem, M. (1996). Control and design of flexible-link manipulators. Montreal, Canada: Concordia University. Ph.D. thesis.

Google Scholar

Pota, H., and Vidyasagar, M. (1991). Passivity of flexible beam transfer functions with modified outputs. Proc. 1991 IEEE Int. Conf. Robotics Automation 3, 2826–2831. doi:10.1109/robot.1991.132061

CrossRef Full Text | Google Scholar

Sayahkarajy, M., and Mohamed, Z. (2014). Mixed sensitivity H2/Hinfinity control of a flexible-link robotic arm. Int. J. Mechani. Mechatron. Enginee. 14, 21–27. doi:10.1007/bf00932903

CrossRef Full Text | Google Scholar

Stanway, J., Sharf, I., and Damaren, C. (1998). Comparison and validation of dynamics simulation models for a structurally flexible manipulator. ASME J. Dyn. Syst. Meas. Control 120, 404–409. doi:10.1115/1.2805417

CrossRef Full Text | Google Scholar

Tso, S., Yan, T., Xu, W., and Sun, Z. (2003). Vibration control for a flexible-link robot arm with deflection feedback. Int. J. Non-Linear Mech. 38, 51–62. doi:10.1016/s0020-7462(01)00040-3

CrossRef Full Text | Google Scholar

Wang, D., and Vidyasagar, M. (1992). Passive control of a stiff flexible link. Int. J. Robotics Res. 11, 572–578. doi:10.1177/027836499201100606

CrossRef Full Text | Google Scholar

Wong, V. Y. K. (2006). Passivity analysis of a single link flexible manipulator. University of Toronto. B.A.Sc. Thesis.

Google Scholar