ICEEMDAN–VMD denoising method for enhanced magnetic memory detection signal of micro-defects

Ferromagnetic materials are extensively utilized in industrial settings where the early detection and repair of defects is paramount for ensuring industrial safety. During the enhanced magnetic memory detection of micro-defects, many interference signals appear in the detection signal, which makes it difficult to accurately extract the characteristics of the micro-defect signals, significantly affecting detection effectiveness. When improved complete ensemble empirical mode decomposition with adaptive noise (ICEEMDAN) is employed independently for signal denoising, the noise and feature signals of the transition components are retained or removed. When variational mode decomposition (VMD) is employed independently for signal denoising, the denoising effect is restricted because of the difficulty in determining the penalty factor $\alpha$ and the number of decomposition layers m. To solve these problems, a denoising method for enhanced magnetic memory detection signals based on ICEEMDAN and VMD, called ICEEMDAN–VMD, is proposed in this paper. First, a comprehensive index (CI) combining information entropy (IE) and the correlation coefficient R is proposed, then the signal components obtained by performing decomposition with the ICEEMDAN method are divided into noise-dominant components, transition components, and useful signal components based on the CI. Subsequently, VMD is employed to perform secondary decomposition on the transition components obtained from the ICEEMDAN method and calculate the correlation coefficients. Ultimately, the optimal VMD components and useful signal components obtained by the ICEEMDAN method are selected for signal reconstruction to obtain a denoised signal. To validate the effectiveness of the proposed method, the denoising effects of the ICEEMDAN–VMD, ICEEMDAN, and VMD methods were compared based on the signal-to-noise ratio (SNR) and fuzzy entropy (FE). The comparison indicated that the ICEEMDAN–VMD denoising method significantly enhanced the denoising effect, and the SNRs of the components of the magnetic field signal could be increased by up to 69.426%. The SNR of each gradient component of the magnetic field signal could be improved by up to ten times, and the FEs of the signal components and their corresponding gradient components could be reduced by 24.198%–81.011%, respectively.

1 Introduction

Ferromagnetic materials are essential raw materials for modern industry and are widely used in various load-bearing structures, such as pipelines, pressure vessels, and bridges. Due to environmental and load factors, ferromagnetic components inevitably develop a variety of defects that can adversely affect their performance and safety, potentially leading to serious failures (Shi et al., 2020). Metal magnetic memory, as a nascent non-destructive testing method, fulfills the objective of identifying defects or stress concentrations in ferromagnetic materials by detecting changes in the magnetic field of the object under test due to defects or stress concentrations. Nevertheless, it possesses the disadvantage of weak changes in the magnetic field, which is readily drowned out by ambient noise. Enhancing magnetic memory detection by applying a magnetic field of a certain magnitude to the object to be tested so that the sample reaches unsaturation magnetization achieves the effect of enhancing the magnetic signal in the anomalous area and suppressing noise. Enhanced magnetic memory testing can not only detect micro-defects such as plastic deformation and stress concentration but also improve the detection rate of macro-defects such as cracks and corrosion, and thus has broad application prospects (Liu et al., 2022; Zhang and Liu, 2024; Liu et al., 2018). However, when there is strong interference in the detection environment, the enhanced magnetic memory signal and its gradient signal will still be severely affected, especially for the signals of micro-defects, which can easily lead to missed detection. Therefore, establishing an effective denoising method for the enhanced magnetic memory signals of micro-defects is of great significance.

The face of micro-defects when the magnetic field anomaly region is weak is easily covered in strong interference environments, and defects cannot be detected. Currently, the empirical mode decomposition (EMD) and related improved methods have been widely used in signal denoising for magnetic detection. Leng et al. (2010) and Chen et al. (2016) proposed an improved EMD method with different adaptive decomposition methods, and they achieved good application results in metal magnetic memory gradient signal denoising. However, they did not solve the problems of mode aliasing and endpoint effects that occur during EMD, and the loss of useful signals occurred due to the direct removal of high-order components. Luo et al. (2023) proposed an EMD-wavelet threshold denoising (WTD) method for metal magnetic memory signals and experimentally verified its feasibility. Song et al. (2019) and Bai (2019) applied an improved denoising method of ensemble empirical mode decomposition (EEMD) to metal magnetic memory detection. However, EEMD faces the problem that auxiliary white noise cannot be completely removed. Shi et al. (2019) and Liang (2020) proposed complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) to solve the auxiliary white noise residual problem of the EEMD method. However, this can result in the emergence of spurious modes. Zhang et al. (2019) and Zhang et al. (2023) found that the improved complete ensemble empirical mode decomposition with adaptive noise (ICEEMDAN) method can achieve a better signal-to-noise ratio (SNR) and root mean square error than CEEMDAN, but there are still noise residuals and characteristic losses. Zhang et al. (2022) applied VMD to magnetic flux leakage detection and demonstrated that its noise reduction effect is better than that of EMD.

To effectively process the enhanced magnetic memory signals of micro-defects, we propose a denoising method for enhanced magnetic memory signals based on ICEEMDAN–VMD by comparing ICEEMDAN with VMD. SNR and fuzzy entropy (FE) were selected as evaluation indicators to compare the denoising effects of ICEEMDAN–VMD, ICEEMDAN, and VMD, and the result indicated that ICEEMDAN–VMD yielded a better denoising effect for the enhanced magnetic recording detection signal of micro-defects.

2 Test program and micro-defect signals using enhanced magnetic memory detection

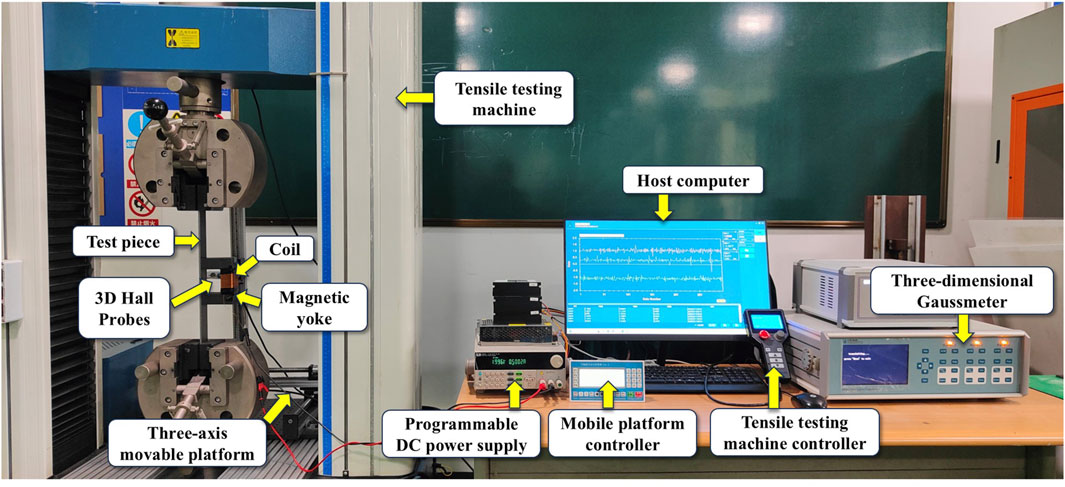
As shown in Figure 1, the enhanced magnetic memory detection system used in this study was composed of a loading device, magnetization device, and magnetic signal acquisition device. The loading device was a DF13.305T electronic universal testing machine, which was used to apply tensile loads to the specimens. The magnetization device was composed of an IT6862A programmable DC power supply and a U-shaped magnetic yoke. The tested area of the specimen was magnetized to a non-saturated state by applying excitation currents to a U-shaped magnetic yoke. The magnetic signal acquisition device consisted of a CH3600 three-dimensional Gaussian meter and a three-axis displacement control platform, enabling automatic scanning of magnetic signals of the tested area.

Figure 1

Figure 1. Enhanced magnetic memory detection system.

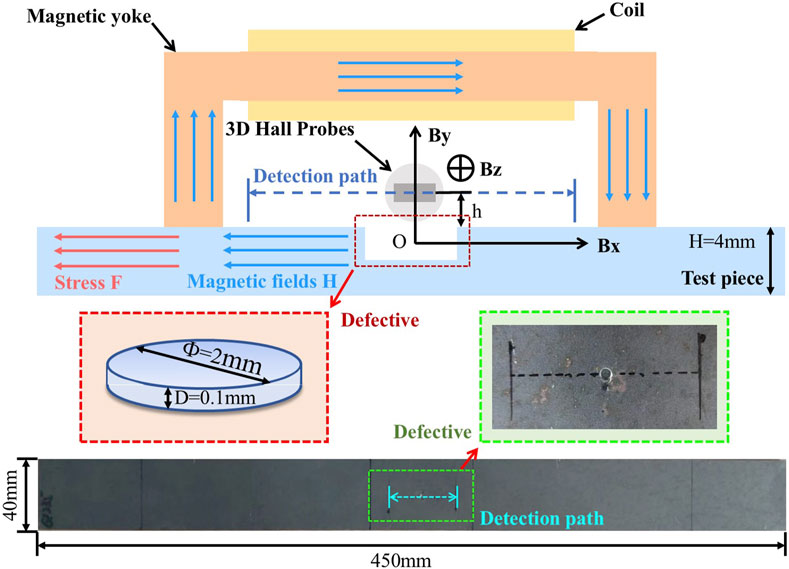
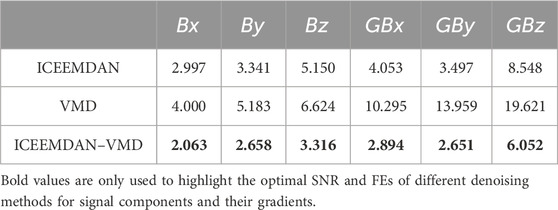
As shown in Figure 2, the specimens were made of Q235 steel with dimensions of 450 mm × 40 mm × 4 mm (length × width × thickness). A micro-defect 0.1 mm deep was simulated by a plastic indentation formed by pressing a Ø2 mm indenter at the center of the specimen. The excitation current was 0.5 A. The specimen was loaded to 400 MPa and was then kept loaded. The probe was lifted to a height of 1 mm. The horizontal component $B_x$, normal component $B_y$, and tangential component $B_z$ of the magnetic field within a range of ±20 mm from the center of the indentation were measured by the magnetic signal acquisition device, then the gradient values of the three components—represented respectively by $G{B}_x$, $G{B}_y$, and $G{B}_z—$were calculated along the x direction.

Figure 2

Figure 2. Schematic diagram of enhanced magnetic memory test detection.

The original detection signals of $B_x$, $B_y$, and $B_z$ are shown in Figures 3A–C, and the $B_x$, $B_y$, and $B_z$ with the trend components of the excitation magnetic field removed are shown in Figures 3D–F. It can be observed in Figures 3A–F that there were only minor abnormal fluctuations of $B_x$, $B_y$, and $B_z$, and that $B_x$ had an indistinct peak at the indentation at the indentation site due to the interference factors. Furthermore, as shown in Figures 3G–I, $G{B}_x$, $G{B}_y$, and $G{B}_z$ at the indentation were completely overwhelmed by noise signals, making it impossible to accurately identify the location of the micro-defect.

Figure 3

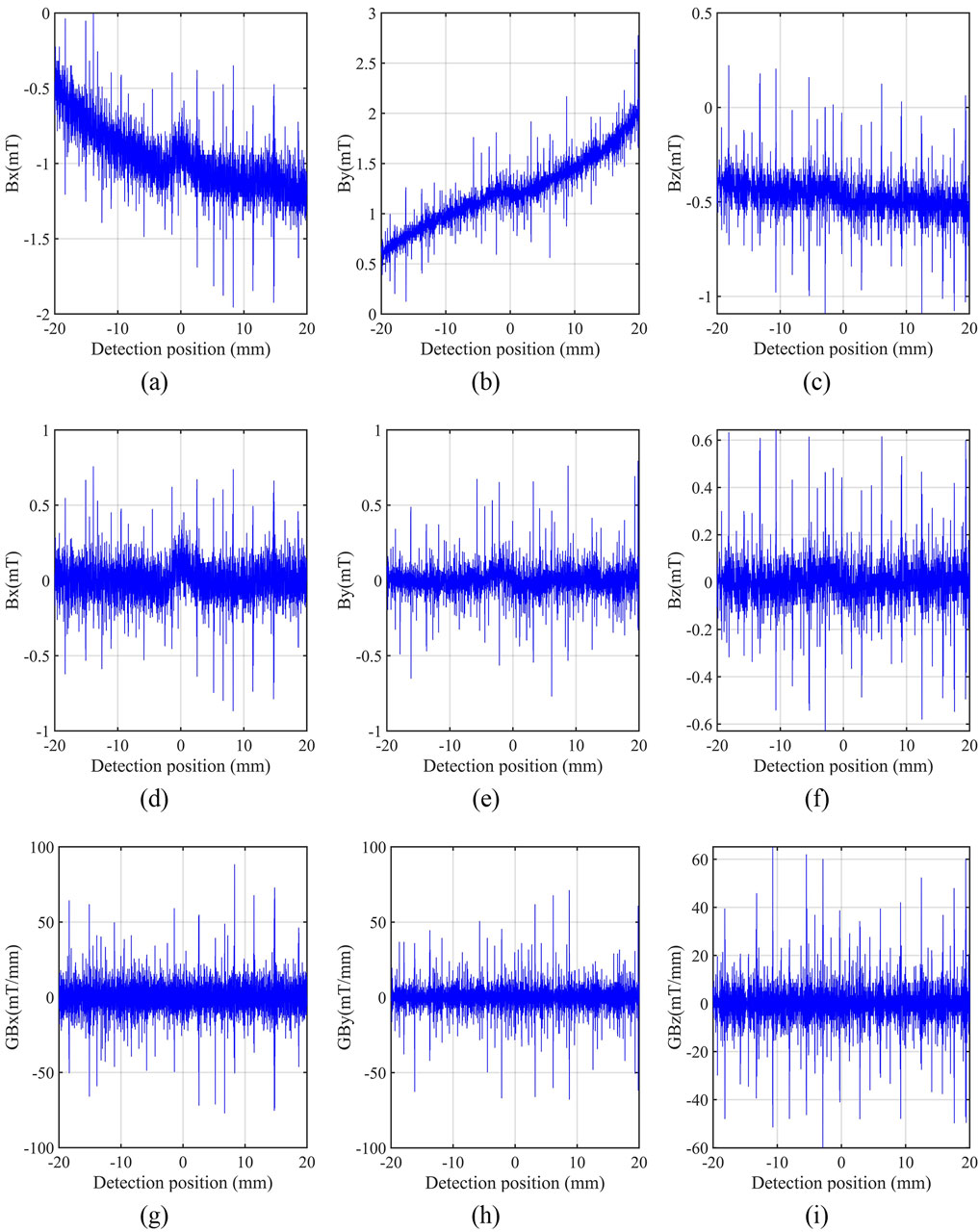
Figure 3. Detection signals and their gradient signals with trending components removed. (A) Original horizontal component $B_x$, (D) $B_x$ without the trend components of the excitation magnetic field, and (G) its gradient $G{B}_x$. (B) Original normal component $B_y$, (E) $B_y$ without the trend components of the excitation magnetic field, and (H) its gradient $G{B}_y$. (C) Original tangential component $B_z$, (F) $B_z$ without the trend components of the excitation magnetic field, and (I) its gradient $G{B}_z$.

3 Analysis of ICEEMDAN and VMD denoising effects

3.1 Denoising processing steps and effect of ICEEMDAN

ICEEMDAN is an improved algorithm of CEEMDAN, which replaces the Gaussian white noise by the kth-order intrinsic mode function (IMF) component noise resulting from the original EMD during the CEEMDAN process. The process of ICEEMDAN is as follows (Marcelo et al., 2014).

Step 1: Adaptive Gaussian white noise is added to the original signal:

${B_1}^{\left(i\right)}\left[t\right]=B_1\left[t\right]+{\epsilon }_0{E}_1\left(p^{\left(i\right)}\left[t\right]\right)\left(i=1,2...n\right),(1)$

where $B_1\left[t\right]$ denotes the original signal, $E_1$ denotes that the EMD is performed once, $p^{\left(i\right)}\left[t\right]$ denotes the i^th-order component of the noise added to the original signal, and ${\epsilon }_0$ denotes the ratio of the SNR to the standard deviation of the added noise.

Step 2: EMD is conducted on the noise-added signal to obtain the first-order residual $R_1\left[t\right]$ and first-order intrinsic mode function $IM{F}_1$:

$\left\{\begin{array}{l}{R}_1\left[t\right]={\displaystyle \sum _{i=1}^{\mathrm{n}}}\mathrm{M}\left({B_1}^{\left(i\right)}\left[t\right]+{\epsilon }_1{E}_1\left(p^{\left(\mathrm{i}\right)}\left[t\right]\right)\right)\\ IM{F}_1=\mathrm{M}\left({B_1}^{\left(i\right)}\left[t\right]\right)-R_1\left[t\right],\end{array}\right.(2)$

where $\mathrm{M}\left(•\right)$ denotes the calculation of the local mean, and $R_1\left[t\right]$ denotes residual signal.

Step 3: The residual signal $R_1\left[t\right]$ is treated as a new signal, and further repetitive processing is carried out in accordance with steps (1) and (2) to obtain the i^th-order residual $R_i\left[t\right]$ and the i^th-order intrinsic mode function $IM{F}_i$:

$\left\{\begin{array}{l}{R}_i\left[t\right]={\displaystyle \sum _{i=1}^n}\mathrm{M}(R_{i-1}\left[t\right]+{\epsilon }_{i-1}{E}_n\left(p^{\left(\mathrm{i}\right)}\left[t\right]\right)\\ IM{F}_i=R_{i-1}\left[t\right]-R_i\left[t\right].\end{array}\right.(3)$

Step 4: The above steps are repeated until the residual cannot be decomposed, and the original signal is decomposed into a series of intrinsic mode functions and the residuals:

$B_1\left[t\right]={\displaystyle \sum _{i=1}^n}IM{F}_i+R_i\left[t\right].(4)$

Step 5: In order to achieve more accurate judgment of the transition component, the comprehensive index $CI$ combined the information entropy $IE$ with the correlation coefficient $R$ is proposed, which is calculated:

$CI=N\left(IE\right)*N\left(R\right),(5)$

where $N\left(x\right)$ represents normalization processing, the information entropy $IE$ represents the uncertainty of possible events occurring in the information source, calculated by $IE=-{\displaystyle \sum _{i=1}^n}p\left(if{m}_i\right)\log p\left(if{m}_i\right)$, and the correlation coefficient $R$ is calculated by.

$R\left(s,IM{F}_j\right)=\frac{{\displaystyle \sum _{i=1}^N}\left(s-\overline{s}\right)\left(IM{F}_j-{\overline{IMF}}_j\right)}{\sqrt{{\displaystyle \sum _{i=1}^N}{\left(s-\overline{s}\right)}^2}\sqrt{{\displaystyle \sum _{i=1}^N}{\left(IM{F}_j-{\overline{IMF}}_j\right)}^2}}.(6)$

Step 6: The comprehensive index $CI$ between each order component and the original signal are calculated. The k^th-order component $IM{F}_k$ is selected as the transition component, the $CI$ of which is the local extremum. Then, the denoised signal is reconstructed with the k^th-order transition component $IM{F}_k$ and its subsequent order components, and the 1^st-through k^th-order components before the boundary component are discarded.

According to the ICEEMDAN process, the $CI$ of IFM components of $B_x$, $B_y$, and $B_z$, shown in Figure 4A, exhibits an initial trend of rapid decline followed by a minor increase, and then a further decline. The local maximum value of $B_x$ was located at $IM{F}_7$, and the local maximum values of $B_y$ and $B_z$ were located at $IM{F}_8$, which is consistent with the characteristics of the IFM components of $B_x$, $B_y$, and $B_z$. Figures 4B–D reveals that the eighth-order components of $B_y$ and $B_z$ are mainly low-frequency signals with obvious defect signal characteristics, while the first- to seventh-order components are mainly high-frequency noise signals. The seventh-order component of $B_x$ has a more obvious characteristic of the micro defect, while the first- to sixth-order components of $B_x$ are mainly high-frequency noise signals.

Figure 4

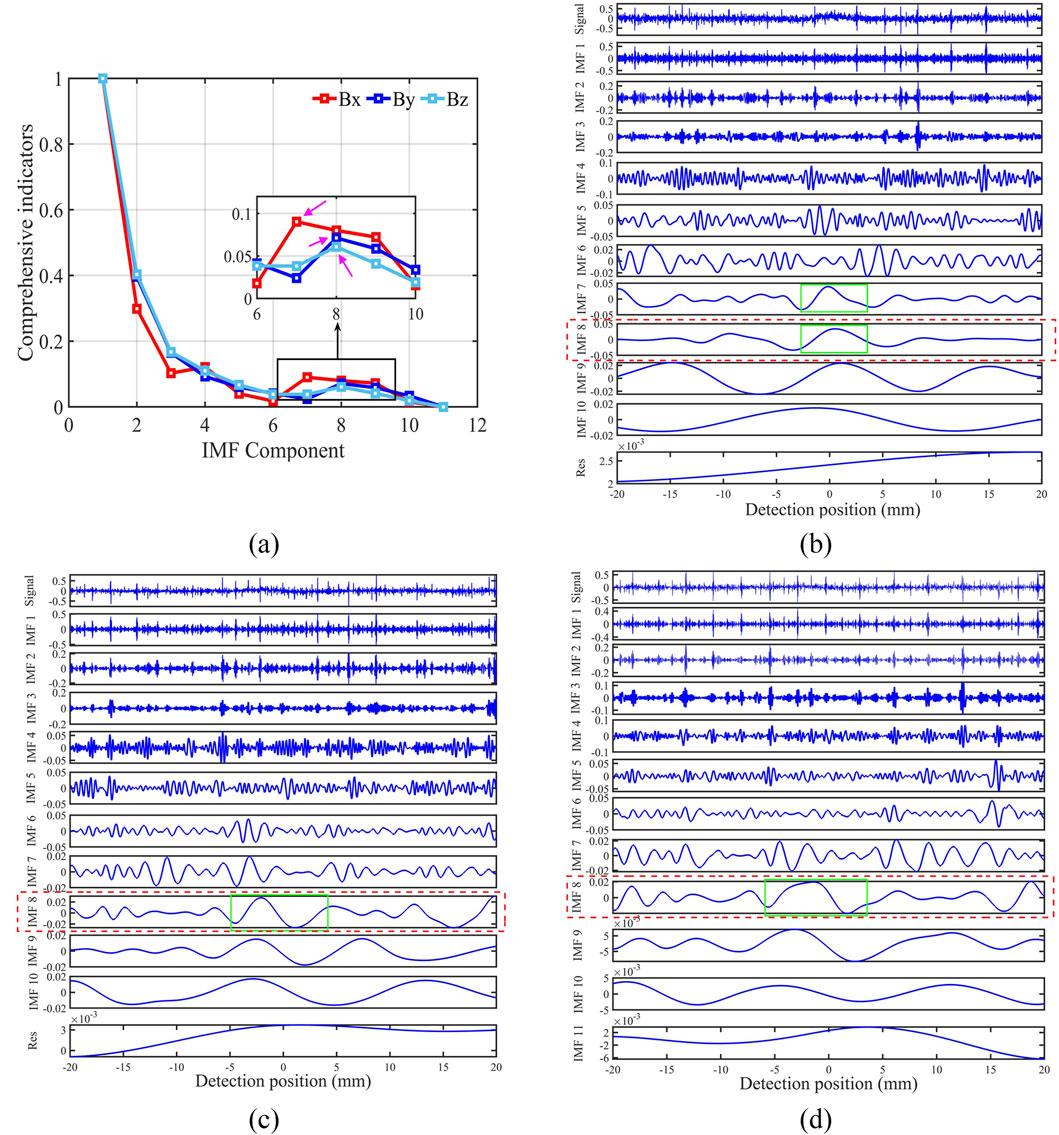
Figure 4. ICEEMDAN correlation coefficient selection and typical decomposition result charts. (A) Correlation coefficients of $B_x$, $B_y$, and $B_z$, (B) IFM components of $B_x$, (C) IFM components of $B_y$, and (D) IFM components of $B_z$.

Using $IM{F}_7$ as the transition component of $B_x$ and $IM{F}_8$ as the transition component of $B_y$ and $B_z$, the ICEEMDAN denoising results of the enhanced magnetic memory signal of the micro-defect are shown in Figure 5. The results indicate that the signal anomalies of $B_x$, $B_y$, $B_z$, and their gradient values were significantly enhanced at the micro-defect location. $B_x$ presents a peak and $G{B}_x$ a peak and valley at the location the micro-defect. Furthermore, $B_y$ and $B_z$ present peaks and valleys, and $G{B}_y$ and $G{B}_z$ present valleys at the location of the micro-defect. Nevertheless, due to the presence of noise signals in the transition component obtained via ICEEMDAN, a certain amount of noise was still present in the non-defect area, resulting in fluctuations in the signal of this area. When calculating the gradient values for each component of the magnetic field, the noise signals were further amplified, causing a significant increase in the fluctuation amplitudes of $G{B}_x$, $G{B}_y$ , and $G{B}_z$ in the non-defect area, leading to difficulties in defect identification using $G{B}_x$, $G{B}_y$, and $G{B}_z$. Moreover, the components before the transition component often contained defective feature signals, especially the first component $IM{F}_{k-1}$ before the transition component $IM{F}_k$. Directly discarding $IM{F}_{k-1}$ often resulted in the loss of useful signals.

Figure 5

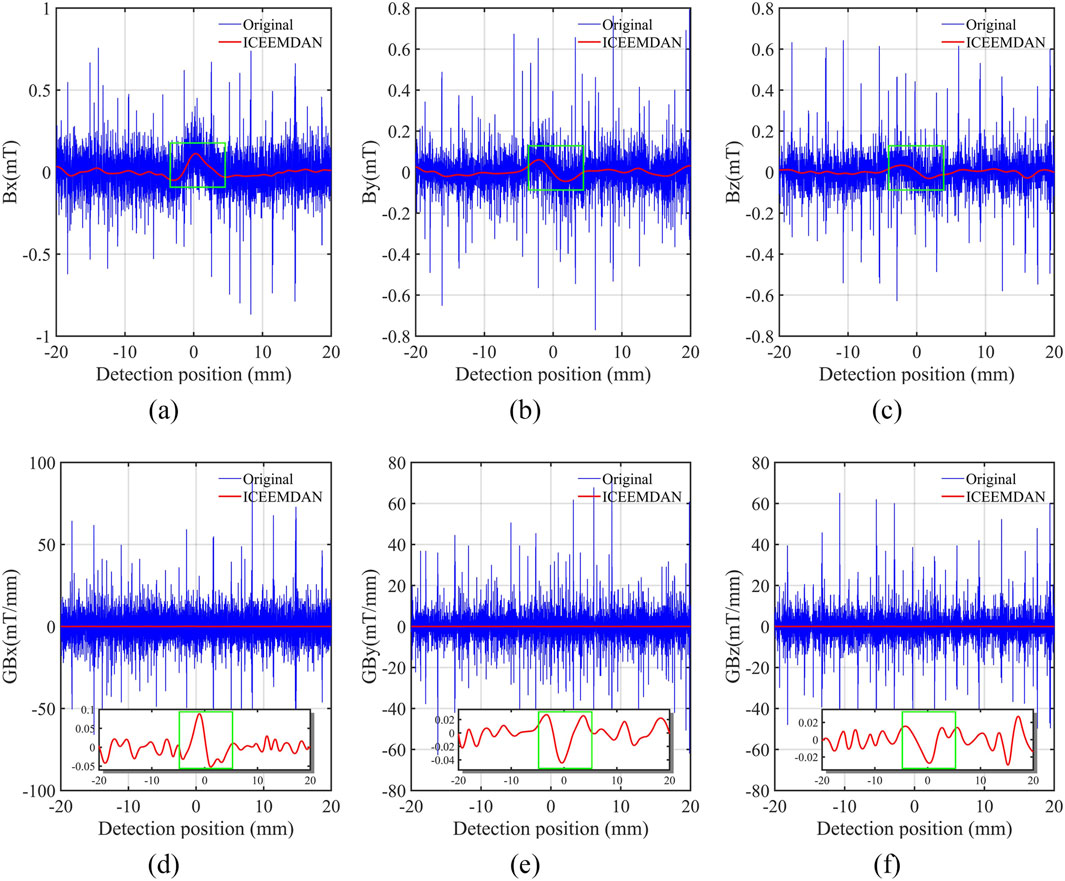
Figure 5. Denoising result of ICEEMDAN. (A) Horizontal component $B_x$ and (D) its gradient $G{B}_x$. (B) Normal component $B_y$ and (E) its gradient $G{B}_y$. (C) Tangential component $B_z$ and (F) its gradient $G{B}_z$.

3.2 Denoising processing steps and the effect of VMD

VMD is an adaptive denoising method based on EMD. The decomposition process is based on the following formula (Zhang et al., 2022):

$\begin{array}{l}\left\{\begin{array}{l}\underset{\left\{u_m,{\omega }_m\right\}}{\min }\left\{{\displaystyle \sum _m}{‖{\partial }_t\left[\delta \left(t\right)+j/\pi t)*u_m\left(t\right)\right]e^{-j{\omega }_{m}t}‖}_2^2\right\}\\ s.t.{\displaystyle \sum _{m=1}^M}{u}_m=B\left(t\right),\end{array}\right.\end{array}(7)$

where $m$ is the number of modal decompositions, $u_m$ is the m^th-order mode corresponding to the decomposition, ${\omega }_m$ is the center frequency corresponding to the m^th-order mode, $\delta \left(t\right)$ is the Fermi–Dirac distribution, * denotes the convolution, and $B\left(t\right)$ is the detection signal. To solve the constrained variational problem, an augmented Lagrangian function $L\left(\left\{u_m\right\},\left\{{\omega }_m\right\},\lambda \right)$ is introduced:

$\begin{array}{l}L\left(\left\{u_m\right\},\left\{{\omega }_m\right\},\lambda \right)=\alpha {\displaystyle \sum _m}{\displaystyle \underset{2}{\overset{2}{‖{\partial }_r\left[\left(\delta \left(t\right)+j/\pi t\right)*u_m\left(t\right)\right]e^{-j{\omega }_{m}t}‖}}}\\ +{‖B\left(t\right)-{\displaystyle \sum _m}{\nu }_m\left(t\right)‖}_2^2+〈\lambda \left(t\right),B\left(t\right)-{\displaystyle \sum _m}\nu m\left(t\right)〉\end{array}(8)$

where $\lambda$ denotes the Lagrange multiplier, and $\alpha$ denotes the penalty factor. After being updated, the $\left\{{\mu }_m,{\omega }_m,\left(\lambda \right)\right\}$ is calculated as shown in Equation 9:

$\left\{\begin{array}{l}{\widehat{\mu }}_m^{n+1}\left(\omega \right)=\frac{\widehat{f}\left(\omega \right)-{\displaystyle \sum _{i\ne m}}{\widehat{\mu }}_i\left(\omega \right)+\frac{\widehat{\lambda }\left(\omega \right)}{2}}{1+2\alpha \left(\omega -{\omega }_m\right)}\\ {\widehat{\omega }}_m^{n+1}\left(\omega \right)=\frac{{\int }_0^{\infty }\omega {\left|{\widehat{\mu }}_m^{n+1}\left(\omega \right)\right|}^2\mathrm{d}\omega }{{\int }_0^{\infty }{\left|{\widehat{\mu }}_m^{n+1}\left(\omega \right)\right|}^2\mathrm{d}\omega }\\ {\widehat{\lambda }}^{n+1}\left(\omega \right)={\widehat{\lambda }}^n\left(\omega \right)+\gamma \left[\widehat{f}\left(\omega \right)-{\displaystyle \sum _m}{\widehat{\mu }}_m^{n+1}\left(\omega \right)\right].\end{array}\right.(9)$

During the VMD, it is necessary to determine different optimal penalty factors $\alpha$ and the number of decompositions $m$ based on the complexity of the signal. According to experience and the comparison of the decomposition effects for different $\alpha$ and $m$, the optimal $\alpha$ and $m$ combinations for $B_x$, $B_y$, and $B_z$ were respectively determined to be ($\alpha$, $m$) = (5 × 10⁵, 7), (7 × 10⁵, 7), and (1.2 × 10⁶, 15). The denoising results of the VMD are shown in Figure 6.

Figure 6

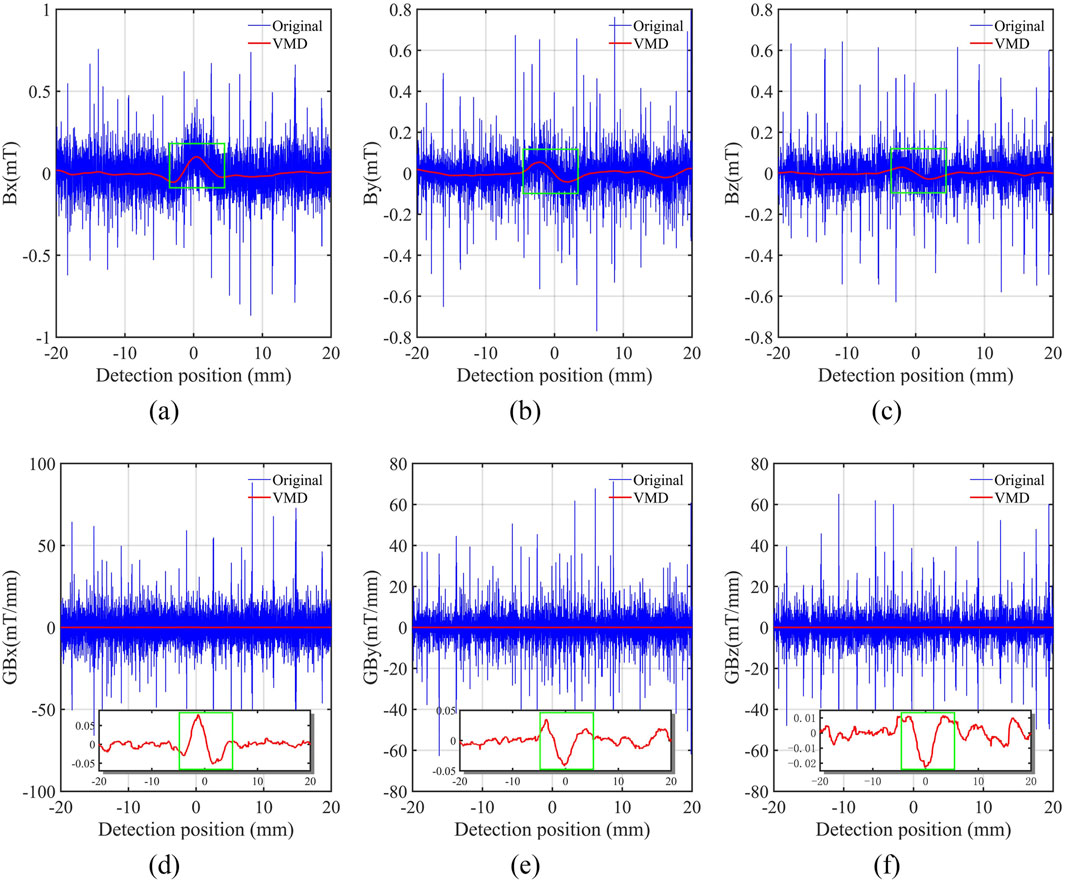
Figure 6. Denoising result of VMD. (A) Horizontal component $B_x$ and (D) its gradient $G{B}_x$. (B) Normal component $B_y$ and (E) its gradient $G{B}_y$. (C) Tangential component $B_z$ and (F) its gradient $G{B}_z$.

The results indicated that the signal anomalies of $B_x$, $B_y$, $B_z$, and their gradient values were more conspicuous at the site of the micro-defect after VMD denoising. $B_x$ presents a peak and $G{B}_x$ presented a peak and valley at the location micro-defect. $B_y$ and $B_z$ present peaks and valleys, respectively, $G{B}_y$ and $G{B}_z$ present valleys at the site of the micro-defect. Compared with the signals after ICEEMDAN denoising, the signal obtained by VMD denoising had smaller signal fluctuations in the non-defect region, suggesting that VMD could eliminate more noise signals. Nevertheless, there were minor continuous fluctuations in the gradient values. The main reason for these fluctuations some extremely small noise signals in $B_x$, $B_y$, and $B_z$ after VMD denoising, which would affect the subsequent extraction of micro-defect feature signals.

4 Denoising processing steps and effect of ICEEMDAN–VMD

4.1 Denoising processing steps of ICEEMDAN–VMD

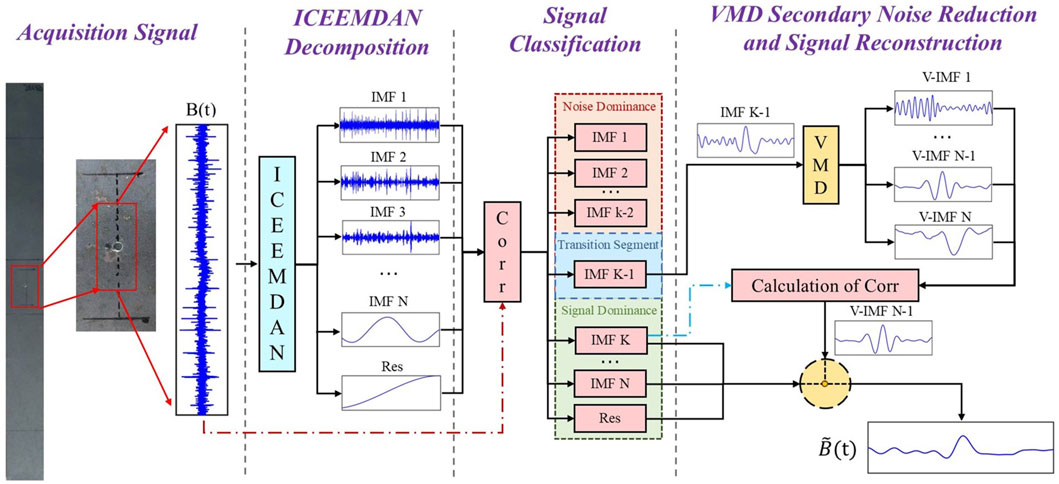
In response to the deficiencies of the ICEEMDAN and VMD methods, the ICEEMDAN–VMD joint signal denoising method is proposed, the process of which includes main four steps. The steps are shown in Figure 7 and described as follows:

Step 1: ICEEMDAN is performed on the original enhanced magnetic memory signals of the micro-defect to obtain m IMF components.

Step 2: IMF component classification. The correlation coefficients between the IMF components obtained in step 1 and the original signal are calculated, and the decomposition components are classified into three types—the noise-dominated components from $IM{F}_1$ to $IM{F}_{k-2}$, the transition components $IM{F}_{k-1}$ and $IM{F}_k$, and the useful-signal-dominated components from $IM{F}_{k+1}$ to $IM{F}_m$.

Step 3: Secondary denoising by VMD. The penalty factors and the number of decompositions are selected based on experience, and a secondary decomposition on the transition component $IM{F}_k$ is performed via VMD to obtain a series of $V-IM{F}_n$ components. Then, the correlation coefficients between the obtained $V-IM{F}_n$ components and $IM{F}_k$ are calculated to obtain the most relevant $V-IM{F}_j$ component to $IM{F}_k$.

Step 4: Signal reconstruction. The component $V-IM{F}_{n-1}$, $IM{F}_k$, and the components $IM{F}_{k+1}$ to $IM{F}_m$ obtained in Step 2 are reconstructed to obtain the denoising signal of $B_{\left(t\right)}$.

Figure 7

Figure 7. Denoising processing steps of ICEEMDAN–VMD.

Compared with ICEEMDAN, ICEEMDAN–VMD can effectively remove noise signals in the transition components, reduce signal noise in non-defect areas, and make the gradient values more stable, as well as minimize the loss of useful signals to the greatest extent. Compared with VMD, ICEEMDAN–VMD can effectively solve the problem of the difficult selection of penalty factors and the number of decomposition layers and avoids the problem of small fluctuations in the signal gradient values caused by the extremely small noise signals after VMD denoising.

4.2 Analysis of the noise reduction effect of the ICEEMDAN–VMD signal processing method

The ICEEMDAN–VMD denoising method was used to process the detected signals of a micro-defect. The selection of penalty factor α and the number of decomposition layers m for the VMD method was made according to the predictions outlined in Xiaoya et al. (2022), with the stipulated values set to α = 3,600 and m = 4, with the results shown in Figure 8. The results indicate that the ICEEMDAN–VMD denoising method could effectively reduce the influence of noise signals on the defect characteristic signals $B_x$, $B_y$, and $B_z$ as well as their gradient values, and it could significantly reduce abnormal signal fluctuations in non-defect areas, making the signal anomalies at defect locations clearer.

Figure 8

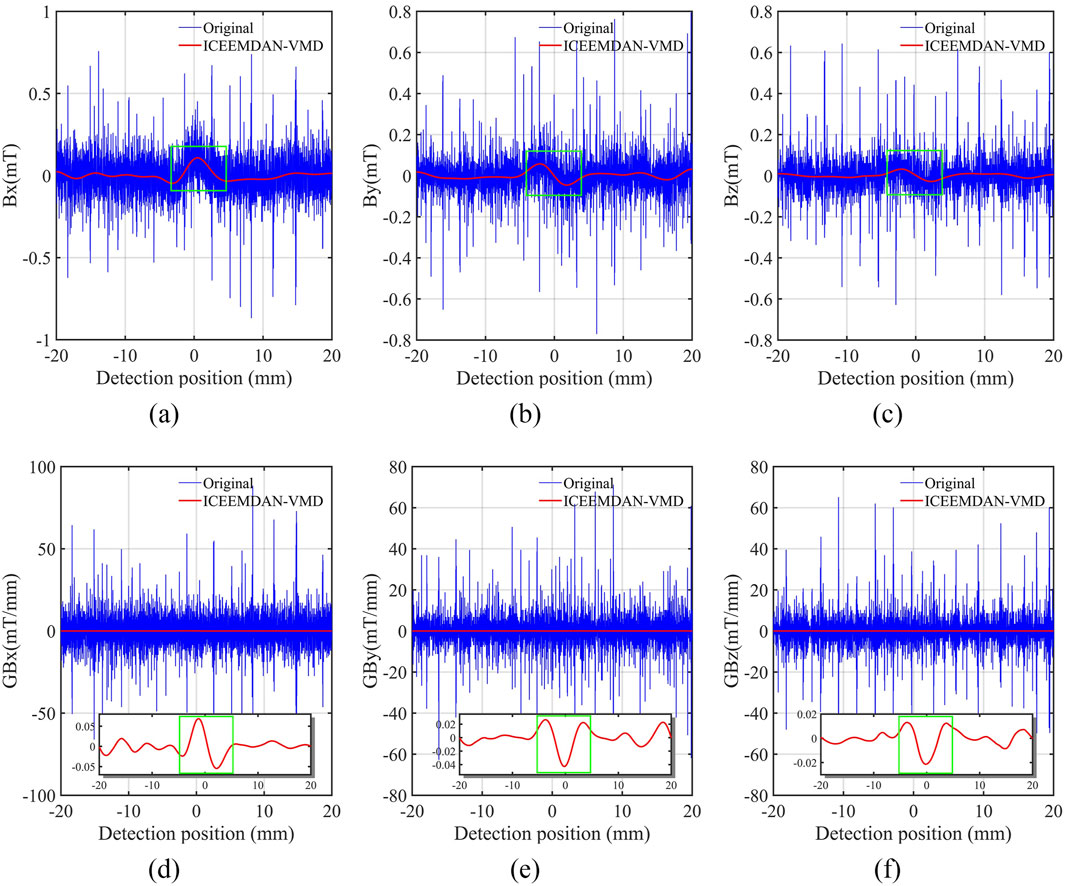
Figure 8. Denoising results of ICEEMDAN–VMD. (A) Horizontal component $B_x$ and (D) its gradient $G{B}_x$. (B) Normal component $B_y$ and (E) its gradient $G{B}_y$. (C) Tangential component $B_z$ and (F) its gradient.

Comparing the signals processed by ICEEMDAN, VMD, and ICEEMDAN-VMD, the signal components and their gradient curves processed by ICEEMDAN-VMD are smoothest, especially in non-defect areas where the signal fluctuation amplitude is smallest (Figure 9).

Figure 9

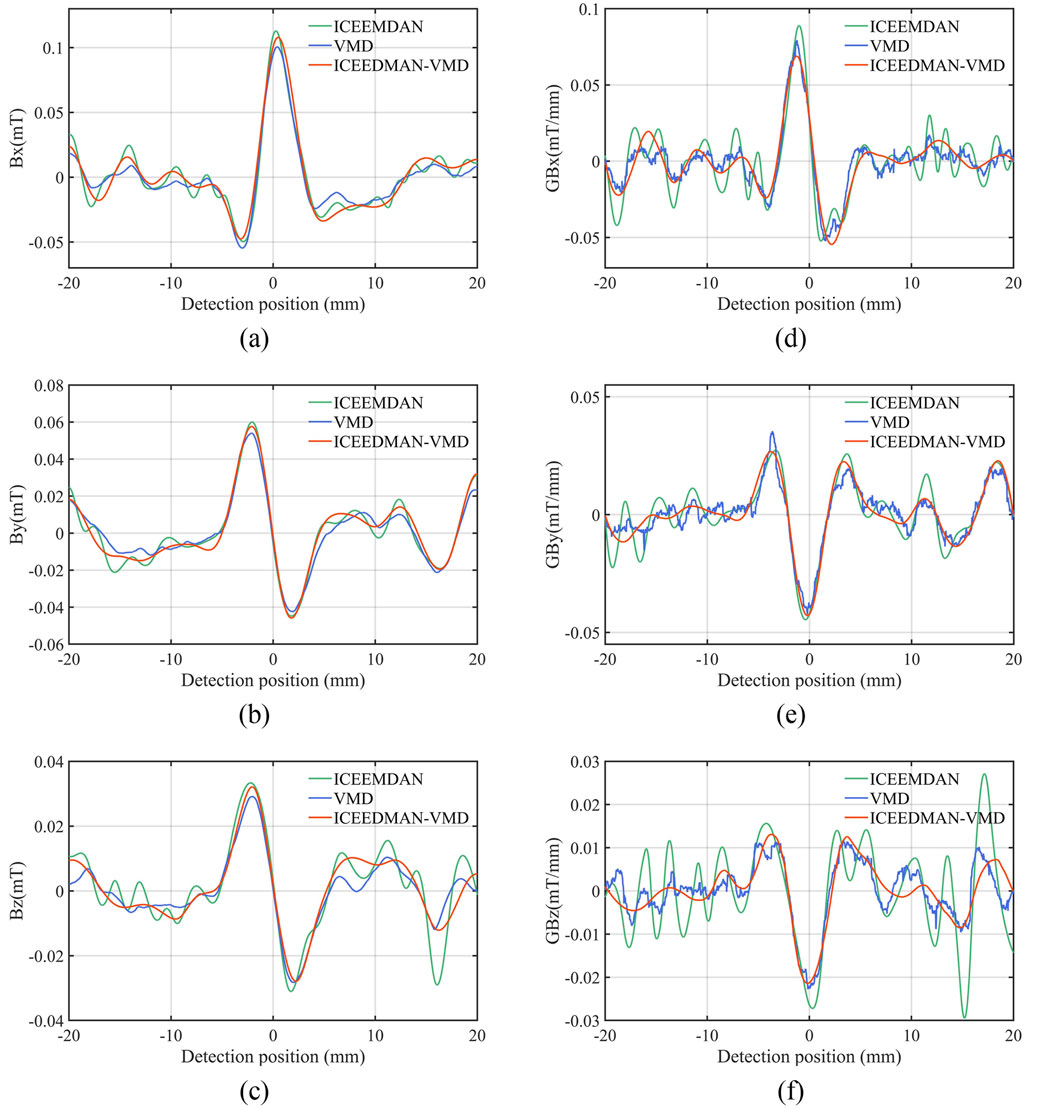
Figure 9. Comparison of ICEEMDAN, VMD, and ICEEMDAN–VMD results. (A) Horizontal component $B_x$ and (D) its gradient $G{B}_x$. (B) Normal component $B_y$ and (E) its gradient $G{B}_y$. (C) Tangential component $B_z$ and (F) its gradient $G{B}_z$.

Furthermore, to quantitatively compare the improved effect of the ICEEMDAN–VMD method, the SNR and FE were selected to evaluate its effect. The SNR is the ratio of useful signal energy to noise energy; the larger the SNR, the better the denoising effect. Since the original pure signal could not be obtained, the maximum amplitude of the useful signal was selected for comparison with the maximum amplitude of the noise signal for calculation. The SNR formula is shown as follows (Ren et al., 2021):

$SNR=20\lg \frac{B\left[t\right]}{N\left[t\right]},(10)$

where $B\left[t\right]$ represents the maximum magnitude of the useful signal, and $N\left[t\right]$ represents the maximum magnitude of the noise signal.

FE serves as a measurement of the probability that a time series will generate new patterns when the dimensionality varies. The higher the probability that the time series generates new patterns and the higher the complexity of the time series, the higher the FE of the time series. Therefore, the smaller the FE of the denoised signal, the better the denoising effect (Zhu et al., 2024) The FE calculation formula is:

$\left\{\begin{array}{l}FE\left(m,n,r\right)=\underset{N\to \infty }{\lim }\left[\ln {\phi }^m\left(n,r\right)-\ln {\phi }^{m+1}\left(n,r\right)\right]\\ {\phi }^m\left(n,r\right)=\frac{1}{N-m}{\displaystyle \sum _{i=1}^{N-m}}\left[\frac{1}{N-m-1}{\displaystyle \sum _{j=1,j\ne i}^{N-m}}{D}_{ij}^{m,n,r}\right]\\ D_{ij}^{m,n,r}=e^{-\frac{d{\left(X_i^m,X_j^m\right)}^n}{r}},\end{array}\right.(11)$

Where $N$ denotes the test sample data, and $X_i^m$ is the vector of the signal in m dimensions. $X_i^m=\left[x\left(i\right),x\left(i+1\right),\dots ,x\left(i+m-1\right)\right]i=1,2,\dots ,N-m+1$, $\frac{d{\left(X_i^m,X_j^m\right)}^n}{r}$ is the maximum absolute value of the difference between the element values, r denotes the similarity tolerance, and n denotes the similarity tolerance boundary gradient.

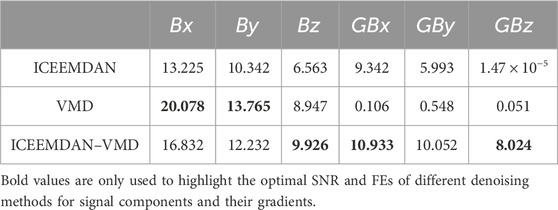
According to the results in Table 1, for $B_x$ and $B_y$, the SNRs after VMD denoising were the highest, followed by those after ICEEMDAN–VMD denoising, and the SNRs after ICEEMDAN denoising were the lowest. In terms of $B_z$, the SNR after ICEEMDAN–VMD denoising was the highest, followed by that after VMD denoising, and the SNR after ICEEMDAN denoising was the lowest. The SNR of $B_z$ after ICEEMDAN–VMD denoising was improved by 51.25% and 10.94%, respectively, compared with those after ICEEMDAN and VMD denoising. For the gradient values $G{B}_x$, $G{B}_y$ , and $G{B}_z$, the SNRs after ICEEMDAN–VMD denoising were higher than those after ICEEMDAN denoising, increasing by 17.03%, 67.73%, and 445.85%, respectively, and the ICEEMDAN–VMD yielded an order-of-magnitude improvement in the SNR compared with VMD.

Table 1

Table 1. Signal-to-noise ratios (SNRs) of different denoising methods.

According to the results in Table 2, the FEs of $B_x$, $B_y$, $B_z$, and their gradient values after ICEEMDAN–VMD denoising were the smallest. After ICEEMDAN–VMD denoising processing, the FE of $B_x$ decreased by 31.142% and 48.412%, and the FE of $G{B}_x$ decreased by 28.59% and 71.89% compared with those after ICEEMDAN and VMD denoising, respectively. Similarly, the FE of $B_y$ respectively decreased by 20.47% and 48.73%, and the FE of $G{B}_y$ respectively decreased by 24.20% and 81.01% compared with those after ICEEMDAN and VMD denoising. Finally, the FE of $B_z$ respectively decreased by 35.61% and 49.94%, and the FE of $G{B}_z$ respectively decreased by 29.20% and 69.16% compared with those after ICEEMDAN and VMD denoising. Therefore, the above results indicated that ICEEMDAN–VMD yielded the fewest new modes after processing and the denoising effect was improved significantly. Based on the comparison of the SNR and FE, the denoising effect of ICEEMDAN–VMD was best for the enhanced magnetic signals of micro-defects.

Table 2

Table 2. Fuzzy entropies (FEs) of different denoizing methods.

The VMD demonstrates the highest SNR at $B_x$ and $B_y$, which can be attributed to the fact that the Gaussian white noise added by the ICEEMDAN method is not fully removed, resulting in some of the noise being retained. However, an examination of $G{B}_x$ and $G{B}_y$ reveals that the ICEEMDAN-VMD method yields a substantial enhancement in SNR. This can be attributed to the fact that the signal obtained by the VMD is characterized by a lack of smoothness and is amplified following the solution of the gradient values. This phenomenon is further substantiated by the observed change in FE. The efficacy of the method for ICEEMDAN with VMD enhancement has been demonstrated.

To verify the applicability of ICEEMDAN-VMD to various paths, it was used to process detection signals from different paths within a 20 mm × 20 mm area near the defect, and the processed signals were used to create a pseudo-color map (Figure 10). Figures 10A–F display the unprocessed detection signals $B_x$, $B_y$, $B_z$ and their gradient signals $G{B}_x$, $G{B}_y$, and $G{B}_z$, and Figures 10G–L show the processed detection signals and their gradient signals obtained after applying ICEEMDAN-VMD. It becomes evident that slight signal anomalies are observed in the defect area in the absence of denoising methods, rendering it a challenge to identify and locate defects through these anomalous signal regions. However, after denoising with ICEEMDAN-VMD, the noise signals are significantly eliminated, revealing distinct abnormal signal areas near the defect. This enables effective identification and localization of defects through these abnormal signal regions. In summary, the proposed ICEEMDAN-VMD method demonstrates effectiveness in processing magnetic field signals from various paths.

Figure 10

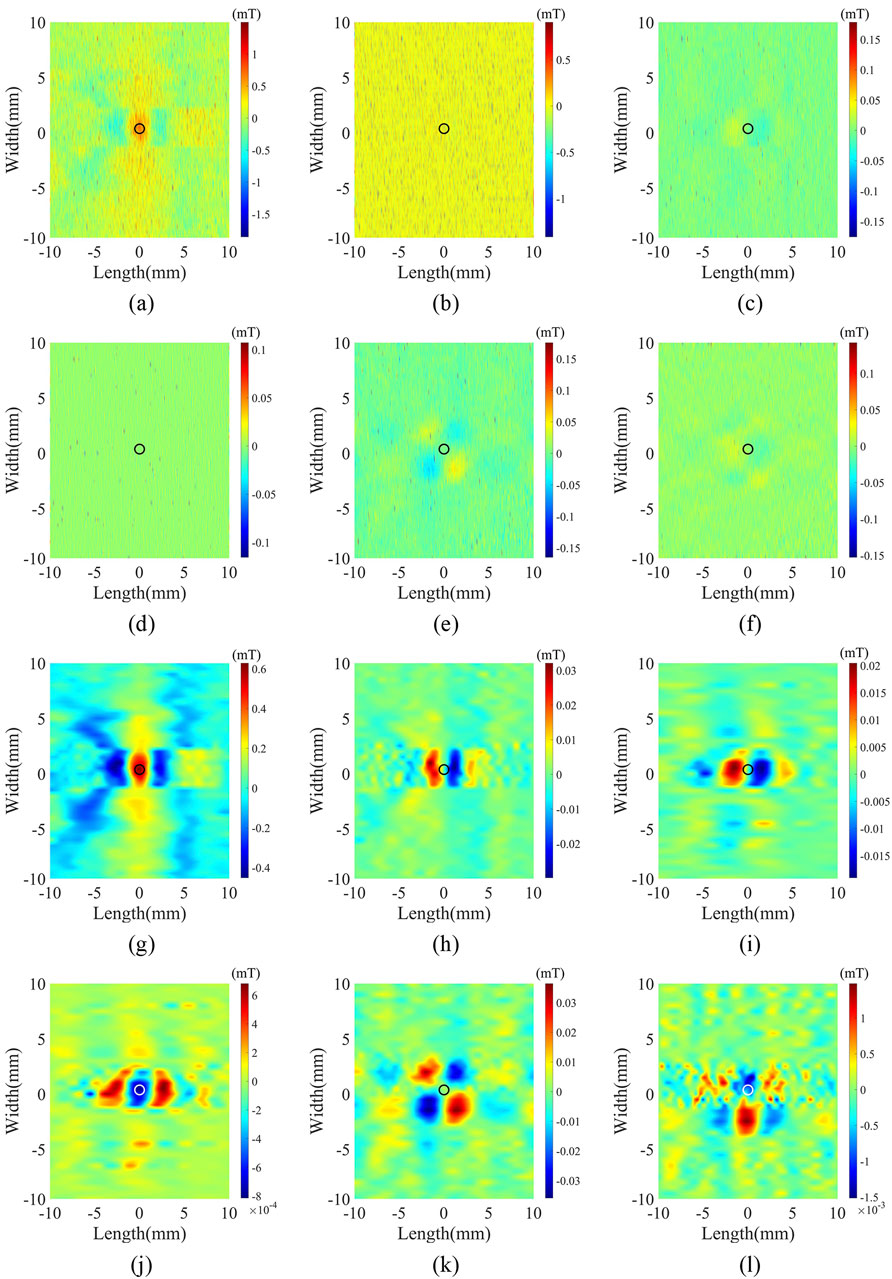
Figure 10. (A–F) specifically denote the unprocessed detection signals $B_x$, $B_y$, and $B_z$ and their gradient signals $G{B}_x$, $G{B}_y$, and $G{B}_z$; (G–L) specifically denote the processed signals $B_x$, $B_y$, and $B_z$ and their gradient signals $G{B}_x$, $G{B}_y$, and $G{B}_z$ obtained after applying ICEEMDAN-VMD.

5 Conclusion

To overcome the difficulty of identifying micro-defect feature signals caused by signal interference during enhanced magnetic memory detection, the ICEEMDAN–VMD denoising method is here proposed. The denoising effects of ICEEMDAN, VMD, and ICEEMDAN–VMD were analyzed in detail through experiments, and the improvement effect of ICEEMDAN–VMD was verified. The findings were as follows:

1. When ICEEMDAN is employed for the enhanced magnetic memory signal denoising, the transition component $IM{F}_k$ contains both useful and noise signals. Directly discarding $IM{F}_k$ would result in the loss of useful feature signals, while retaining $IM{F}_k$ would result in the retention of noise signals in the reconstructed signal, affecting the denoising effect of the signal. When VMD is employed for the enhanced magnetic memory signal denoising, it is difficult to select the optimal penalty factor $\alpha$ and the number of decomposition layers m. After processing the experimental results, there were still some extremely small noise signals in $B_x$, $B_y$, and $B_z$ after VMD denoising, resulting in minor continuous fluctuations in the gradient values.

2. The denoising method of ICEEMDAN–VMD could effectively overcome the shortcomings of ICEEMDAN and VMD, and it had a better denoising effect on enhanced magnetic memory signals. Compared with ICEEMDAN, ICEEMDAN–VMD could effectively reduce the noise signals of the transition components and non-defect areas, making $B_x$, $B_y$, $B_z$, and their gradient values more stable. Compared with VMD, ICEEMDAN–VMD could effectively solve the problem of the difficult selection of the optimal penalty factor $\alpha$ and the number of decomposition layers m, and it could avoid the problem of small fluctuations in the signal gradient values caused by extremely small noise signals in $B_x$, $B_y$, and $B_z$.

3. After the ICEEMDAN–VMD denoising process, the SNRs of $B_x$ and $B_z$ were larger than those of ICEEMDAN, and the SNRs of $B_z$ and its gradient values were significantly improved. In particular, the SNRs of each magnetic gradient value component signal yielded an order-of-magnitude improvement compared with those obtained via VMD processing. Compared with the FEs of the signals processed by ICEEMDAN and VMD, the FEs of $B_x$, $B_y$, $B_z$, and their gradient values decreased by 20.469%–81.011% after ICEEMDAN–VMD processing. Therefore, ICEEMDAN–VMD is better suited to the enhanced magnetic memory signals of micro-defects than ICEEMDAN or VMD.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SJ: conceptualization, software, supervision, validation, writing–original draft, and writing–review and editing. JY: formal analysis, investigation, supervision, visualization, and writing–original draft. YL: data curation, formal analysis, funding acquisition, and writing–original draft. GH: conceptualization, formal analysis, funding acquisition, investigation, methodology, resources, and writing–review and editing.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

Authors SJ, JY, YL, and GH were employed by National Pipeline Network Group Zhejiang Natural Gas Pipeline Network Co. Ltd.

Generative AI statement

The authors declare that no generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, B. (2019). Research on signal noise mechanism and noise reduction method of pipe pulse magnetic eddy current detection based on EEMD. M.s. thesis. Beijing, China: China University Petroleum.

Google Scholar

Chen, H., Wang, C., and Zuo, X. (2016). Metal magnetic memory gradient tensor signal processing method. Syst. Eng. Electron., 488–493. doi:10.3969/j.issn.1001-506X.2017.03.05

CrossRef Full Text | Google Scholar

Leng, J., Xu, M., and Zhang, J. (2010). Application of empirical mode decomposition in early diagnosis of magnetic memory signal. J. Central South Univ. Technol. 17 (03), 549–553. doi:10.1007/s11771-010-0521-5

CrossRef Full Text | Google Scholar

Liang, X. (2020). Research on intelligent diagnosis and risk assessment methods of natural gas pipeline defects. Ph.D. dissertation. Beijing, China: China University Petroleum. doi:10.27643/d.cnki.gsybu.2020.000111

CrossRef Full Text | Google Scholar

Liu, B., Zhang, J., and Zhang, Z. (2022). Modeling, simulation and experimental exploration of metal magnetic memory under weak magnetic excitation. Sn Appl. Sci. 4 (6), 167. doi:10.1007/s42452-022-05059-z

CrossRef Full Text | Google Scholar

Liu, Z., Fei, Z., Huang, H., and Qian, Z. (2018). Study on strengthening mechanism of excitation magnetic field to stress-magnetization coupling effects. China Mech. Eng. 29 (09), 1108–1114. doi:10.3969/j.issn.1004-132X.2018.09.015

CrossRef Full Text | Google Scholar

Luo, X., Wang, L., Cao, S., Xiao, Q., Yang, H., and Zhao, J. (2023). Signal processing methods of enhanced magnetic memory testing. Processes 11 (2), 302. doi:10.3390/pr11020302

CrossRef Full Text | Google Scholar

Marcelo, A. C., Gastón, S., and María, E. T. (2014). Improved complete ensemble EMD: a suitable tool for biomedical signal processing. Biomed. Signal Process. Control 14, 19–29. doi:10.1016/j.bspc.2014.06.009

CrossRef Full Text | Google Scholar

Ren, L., Liu, Z., and Zhou, J. (2021). Shaking noise elimination for detecting local flaw in steel wire ropes based on magnetic flux leakage detection. Ieee Trans. Instrum. Meas., 70: 1–9. doi:10.1109/tim.2021.3112792

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, M., Zhao, H., Huang, Z., and Liu, Q. (2019). Signal extraction using complementary ensemble empirical mode in pipeline magnetic flux leakage nondestructive evaluation. Rev. Sci. Instrum. 90 (7), 075101. doi:10.1063/1.5089475

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, P., Su, S., and Chen, Z. (2020). Overview of researches on the nondestructive testing method of metal magnetic memory: status and challenges. J. Nondestruct. Eval. 39 (2), 43. doi:10.1007/s10921-020-00688-z

CrossRef Full Text | Google Scholar

Song, H., Dong, H., Yuan, Z., Zhu, J., Zhang, H., and Huang, Y. (2019). An EEMD-based electromagnetic induction method for nondestructive testing of buried metal conductors. Ieee Access 7, 142261–142271. doi:10.1109/ACCESS.2019.2944549

CrossRef Full Text | Google Scholar

Xiaoya, W., Feng, G., Qi, T., Guo, J., Li, Z., Zhao, D., et al. (2022). Reduce the noise of transient electromagnetic signal based on the method of SMA-VMD-WTD. IEEE Sensors J., 22(15): 14959–14969. doi:10.1109/jsen.2022.3184697

CrossRef Full Text | Google Scholar

Zhang, J., Chen, Q., and Ye, Q. (2023). Nondestructive testing of steel wire rope based on gagnetic signal and infrared information. Russ. J. Nondestruct. Test. 59 (9), 991–1004. doi:10.1134/S1061830923600399

CrossRef Full Text | Google Scholar

Zhang, J., and Liu, P. (2024). Quantitative study on cross section damage of steel wire rope based on magnetic signal characteristics under weak magnetic excitation. IEEE Trans. Instrum. Meas. 73, 1–7. doi:10.1109/tim.2024.3353842

CrossRef Full Text | Google Scholar

Zhang, M., Wang, D., Guo, Y., Zhang, M., and Zhang, Z. (2022). Characteristics extraction and identification of pipeline magnetic flux leakage internal testing signals based on VMD-SVM. Oil Field Equip. 51 (06), 9–17. doi:10.3969/j.issn.1001-3482.2022.06.002

CrossRef Full Text | Google Scholar

Zhang, T., Wang, X., Chen, Y., Zia, U., Ju, H., and Zhao, Y. (2019). Non-contact geomagnetic detection using improved complete ensemble empirical mode decomposition with adaptive noise and teager energy operator. Electronics 8 (3), 309. doi:10.3390/electronics8030309

CrossRef Full Text | Google Scholar

Zhu, L., Xia, Y., Zhu, C., and Deng, F. (2024). Power load prediction method based on CEEMDAN and spectral time graph convolutional networks. Comput. Eng. doi:10.19678/j.issn.1000-3428.0068925

CrossRef Full Text | Google Scholar