- 1Department of Mechanical, Industrial and Systems Engineering, University of Rhode Island, Kingston, RI, United States
- 2Graduate School of Oceanography, University of Rhode Island, Kingston, RI, United States
- 3Department of Electrical, Computer, and Biomedical Engineering, University of Rhode Island, Kingston, RI, United States
Introduction: This paper addresses the critical need for adaptive formation control in Autonomous Underwater Vehicles (AUVs) without requiring knowledge of system dynamics or environmental data. Current methods, often assuming partial knowledge like known mass matrices, limit adaptability in varied settings.
Methods: We proposed two-layer framework treats all system dynamics, including the mass matrix, as entirely unknown, achieving configuration-agnostic control applicable to multiple underwater scenarios. The first layer features a cooperative estimator for inter-agent communication independent of global data, while the second employs a decentralized deterministic learning (DDL) controller using local feedback for precise trajectory control. The framework's radial basis function neural networks (RBFNN) store dynamic information, eliminating the need for relearning after system restarts.
Results: This robust approach addresses uncertainties from unknown parametric values and unmodeled interactions internally, as well as external disturbances such as varying water currents and pressures, enhancing adaptability across diverse environments.
Discussion: Comprehensive and rigorous mathematical proofs are provided to confirm the stability of the proposed controller, while simulation results validate each agent’s control accuracy and signal boundedness, confirming the framework’s stability and resilience in complex scenarios.
1 Introduction
Robotics and autonomous systems have a wide range of applications, spanning from manufacturing and surgical procedures to exploration in challenging environments (Ghafoori et al., 2024; Jandaghi et al., 2023). However, controlling robots in such settings, especially in space and underwater, presents significant difficulties due to unpredictable dynamics. In the context of underwater exploration, AUVs have become essential tools, offering cost-effective, reliable, and versatile solutions for adapting to dynamic conditions. Effective use of AUVs is critical for unlocking the mysteries of marine environments, making advancements in their control and operation essential. As the demand for efficient underwater exploration increases and the complexity of tasks assigned to AUVs grows, there is a pressing need to enhance their operational capabilities. This includes developing sophisticated formation control strategies that allow multiple AUVs to operate in coordination, drawing inspiration from natural behaviors observed in fish schools and bird flocks (Zhou et al., 2023; Yang et al., 2021). By leveraging multi-agent systems, AUVs can work in coordinated groups, enhancing efficiency, stability, and coverage while navigating dynamic and complex underwater environments. These strategies are essential for ensuring precise operations in varied underwater tasks, ranging from pipeline inspections and seafloor mapping to environmental monitoring (Yan et al., 2023).
Despite challenges from intricate nonlinear dynamics, complex interactions among AUVs, and the uncertain dynamic nature of underwater environments, effective multi-AUV formation control is increasingly critical in modern ocean industries (Yan et al., 2018; Hou and Cheah, 2009). Historically, formation control research has predominantly utilized the behavioral approach (Balch and Arkin, 1998; Lawton, 2000), which divides the overall control design into subproblems, with each vehicle’s action determined by a weighted average of solutions, though selecting appropriate weighting parameters can be challenging. The leader-following approach (Cui et al., 2010; Rout and Subudhi, 2016) designates one vehicle as the leader while others follow, maintaining predefined geometric relationships, and controlling formation behavior by designing specific motions for the leader. Alternatively, the virtual structure approach (Millán et al., 2013).
Despite advancements in formation control and path planning for multi-AUV systems, challenges such as environmental disturbances, complex underwater dynamics, and communication limitations continue to pose difficulties (Hadi et al., 2021). To address these challenges, there is a critical need for controllers that are independent of both robot dynamics and environmental disturbances. Developing such controllers would enhance formation control by allowing for decentralized application, which increases flexibility in formation structures and improves robustness against communication constraints. Addressing these gaps is essential for advancing the capabilities and reliability of multi-AUV systems. On the other hand, communication constraints in underwater environments make decentralized control with a virtual leader-following topology ideal for AUVs, enabling coordination using local information despite communication delays or interruptions (Yan et al., 2023).
Reinforcement learning (RL) has also been extensively applied in robotic control (Christen et al., 2021; Cao et al., 2022). RL approaches, such as deep reinforcement learning (DRL), offer advantages in learning complex, non-linear control policies directly from data. However, RL methods generally lack the ability to provide mathematical stability proofs and guarantees for the controller’s behavior, making it challenging to ensure safety and reliability, especially in critical applications. Besides, while Zhang et al. (2018) developed various direct neural adaptive laws that lead to increased oscillations with higher adaptation gains, indirect neural adaptive laws using prediction error methods were proposed to mitigate this issue, though they could not guarantee parameter convergence. However, NN-based learning control methods, such as those utilizing adaptive neural networks or deterministic learning frameworks Jandaghi et al. (2024), can incorporate stability analysis and provide rigorous mathematical proofs for parameter convergence. These methods enable researchers to establish theoretical guarantees for the stability and robustness of the controller, which is essential for deploying controllers in real-world applications where safety and reliability are critical. Most recently, Tutsoy et al. (2024) proposed an optimization-based approach for path planning in Unmanned Air Vehicles (UAVs) with actuator failures using particle swarm optimization and genetic algorithms. Their method focuses on minimizing both time and distance by optimizing predefined cost functions through heuristic methods, while incorporating system constraints such as actuator limits, kinematic, and dynamic constraints, as well as parametric uncertainties.
Despite extensive literature in the field, to the best of our knowledge, existing researches assume homogeneous dynamics and certain system parameters for all AUV agents, which is unrealistic in unpredictable underwater environments. Factors such as buoyancy, drag, and varying water viscosity significantly alter system dynamics and behavior. Additionally, AUVs may change shape during tasks like underwater sampling or when equipped with robotic arms, further complicating control. Typically, designing multi-AUV formation control involves planning desired formation paths and developing tracking controllers for each AUV. However, accurately tracking these paths is challenging due to the complex nonlinear dynamics of AUVs, especially when precise models are unavailable. Implementing a fully distributed and decentralized formation control system is also difficult, as centralized control designs become exceedingly complex with larger AUV groups. To address these challenges previous work, such as Yuan et al. (2017) and Dong et al. (2019), developed adaptive learning controllers that relied on the assumption of a known mass matrix, which is not practical in real-world applications. These controllers relied on known system parameters that can fail due to varying internal forces caused by varying external environmental conditions. The solution is to develop environment-independent controllers that do not rely on any specific system dynamical parameters.
The framework’s control architecture is ingeniously divided into a first-layer Cooperative Estimator Observer and a lower-layer Decentralized Deterministic Learning (DDL) Controller. The first-layer observer is pivotal in enhancing inter-agent communication by sharing crucial system estimates, operating independently of any global information. Concurrently, the second-layer DDL controller utilizes local feedback to finely adjust each AUV’s trajectory, ensuring resilient operation under dynamic conditions heavily influenced by hydrodynamic forces and torques by considering system uncertainty completely unknown. This dual-layer setup not only facilitates acute adaptation to uncertain AUV dynamics but also leverages RBFNN for precise local learning and effective knowledge storage. Such capabilities enable AUVs to efficiently reapply previously learned dynamics after the system restarts. This tow-layer framework achieves a significant advancement by considering all system dynamics parameters as unknown, enabling a universal application across all AUVs, regardless of their operating environments. This universality is crucial for adapting to environmental variations such as water flow, which increases the AUV’s effective mass via the added mass phenomenon and affects the vehicle’s inertia. Additionally, buoyancy forces that vary with depth, along with hydrodynamic forces and torques, stemming from water flow variations, the AUV’s unique shape, its appendages, and drag forces due to water viscosity, significantly impact the damping matrix in the AUV’s dynamics. This framework not only improves operational efficiency but also significantly advances the field of autonomous underwater vehicle control by laying a robust foundation for future enhancements in distributed adaptive control systems and fostering enhanced collaborative intelligence among multi-agent networks in marine environments. Extensive simulations have underscored the effectiveness of the framework, demonstrating its potential to elevate the adaptability and resilience of AUV systems under the most demanding conditions. In summary, the contribution of this paper is as follows:
• The universal controller works in any environment and condition, such as currents or depth.
• Each AUV controller operates independently.
• The controller functions without needing information about the robot’s dynamic parameters, like mass, damping, or inertia. Each AUV can also have different dynamic parameters.
• The system learns the dynamics once and reuses the pre-trained weights, avoiding the need for retraining.
• The use of localized RBFNN reduces real-time computational demands.
• Providing rigorous stability analysis of the controller while providing mathematical proofs to ensure and guarantee the reliability of the controller.
The rest of the paper is organized as follows: Section 2 provides an initial overview of graph theory, RBFNN, and the problem statement. The design of the distributed cooperative estimator and the decentralized deterministic learning controller are discussed in Section 3. The formation adaptive control and formation control using pre-learned dynamics are explored in Section 4 and Section 5, respectively. Simulation studies are presented in Section 6, and Section 7 concludes the paper.
2 Preliminaries and problem statement
2.1 Notation and graph theory
Denoting the set of real numbers as
A directed graph
2.2 Radial basis function neural networks (RBFNN)
The RBFNN Networks can be described as
Lemma 1. Consider any continuous recurrent trajectory1
2.3 Problem statement
A multi-agent system comprising
In this study, the subscript
The vector
Unlike previous work Yuan et al. (2017), which assumed known values for the AUV’s inertia and rotation matrices, this study considers all matrix coefficients, including
Internally, it handles unknown parameters such as mass and damping coefficients, as well as unmodeled nonlinear interactions and couplings. Externally, it accounts for unpredictable disturbances, including fluctuating water currents, depth-dependent pressures, and changes in hydrodynamic forces.
By avoiding reliance on predefined models, the proposed approach is robust and adaptable to diverse mission scenarios and unexpected environmental changes, ensuring reliable performance even in highly uncertain conditions.
In the context of leader-following formation tracking control, the following virtual leader dynamics generates the tracking reference signals:
with “0” marking the leader node, the leader state
Considering the system dynamics of multiple AUVs (Equation 1) along with the leader dynamics (Equation 2), we establish a non-negative matrix
Assumption 1. All the eigenvalues of
Assumption 2. The directed graph
Assumption 1 is crucial for ensuring that the leader dynamics produce stable, meaningful reference trajectories for formation control. It ensures that all states of the leader, represented by
Additionally, Assumption 2 reveals key insights into the structure of the Laplacian matrix
where
Problem 1. In the context of a multi-AUV system (Equation 1) integrated with virtual leader dynamics (Equation 2) and operating within a directed network topology
1) Formation Control: Each of the
2) Decentralized Learning: The nonlinear uncertain dynamics of each AUV will be identified and learned autonomously during the formation control process. The insights gained from this learning process will be utilized to enhance the stability and performance of the formation control system.
Remark 1. The leader dynamics described in Equation 2 are designed as a neutrally stable LTI system. This design choice facilitates the generation of sinusoidal reference trajectories at various frequencies which is essential for effective formation tracking control. This approach to leader dynamics is prevalent in the literature on multiagent leader-following distributed control systems like Yuan (2017) and Jandaghi et al. (2024).
Remark 2. It is important to emphasize that the formulation assumes formation control is required only within the horizontal plane, suitable for AUVs operating at a constant depth, and that the vertical dynamics of the 6 degrees of freedom (DOF) AUV system, as detailed in Prestero (2001), are entirely decoupled from the horizontal dynamics.
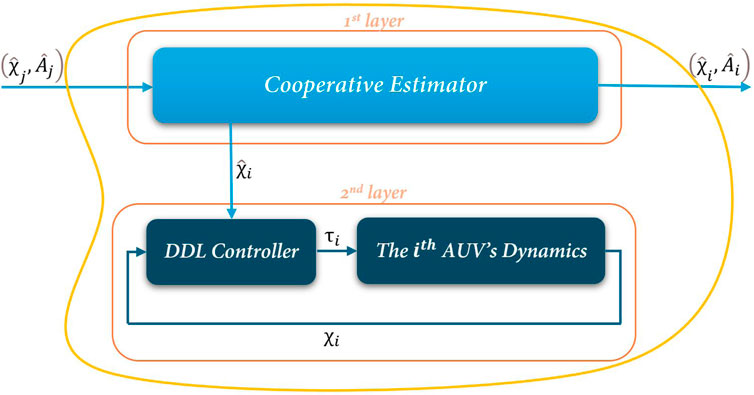
As shown in Figure 1, a two-layer hierarchical design approach is proposed to address the aforementioned challenges. The first layer, the Cooperative Estimator, enables information exchange among neighboring agents. The second layer, known as the Decentralized Deterministic Learning (DDL) controller, processes only local data from each individual AUV. The development and formulation of the first layer are discussed in detail in Section 3.1, while the DDL control strategy, along with its corresponding controller design and analysis, is provided in Section 3.2.
3 Two-layer distributed controller architecture
3.1 First layer: cooperative estimator
In the context of leader-following formation control, not all AUV agents may have direct access to the leader’s information, including tracking reference signals
The observer states for each
which borrowed from Ren and Beard (2008) as well. The constants
Remark 3. Each AUV agent in the group is equipped with an observer configured as specified in Equations 3, 4, comprising two state variables,
To verify the convergence properties, we need to compute the error dynamics. Now we define the estimation error for the state and the system matrix for agent
Define the collective error states and adaptation matrices:
Theorem 1. Consider the error system Equation 5. Under Assumptions 1, 2, and given that
This convergence is facilitated by the independent adaptation of each agent’s parameters within their respective error dynamics, represented by the block diagonal structure of
Proof: We begin by examining the estimation error dynamics for
Under Assumption 2, all eigenvalues of
is exponentially stable, then
Now, each individual agent can accurately estimate both the state and the system matrix of the leader through cooperative observer estimation Equations 3, 4. This information will be utilized in the DDL controller design for each agent’s second layer, which will be discussed in the following subsection.
3.2 Second layer: decentralized deterministic learning controller
To fulfill the overall formation learning control objectives, in this section, we develop the DDL control law for the multi-AUV system defined in Equation 1. We use
To design the DDL control law that addresses the formation tracking control and the precise learning of the AUVs’ complete nonlinear uncertain dynamics at the same time, we will integrate renowned backstepping adaptive control design method outlined in Krstic et al. (1995) along with techniques from Wang and Hill (2018) and Yuan et al. (2017) for deterministic learning using RBFNN. Specifically, for the
To frame the problem in a more tractable way, we assume
A positive definite gain matrix
Now we derive the first derivatives of the virtual control input and the desired control input as follows:
As previously discussed, unlike earlier research that only identified the matrix coefficients
where
where
Then, from Equations 1, 13 we have:
By subtracting
For updating
where
where, for all
Remark 4. Unlike the first-layer DA observer design, the second-layer control law is fully decentralized for each local agent. It utilizes only the local agent’s information for feedback control, including
Theorem 2. Consider the local closed-loop system (Equation 15). For each
Proof: 1) Consider the following Lyapunov function candidate for the closed-loop system (Equation 15):
Evaluating the derivative of
Choose
where
It follows that
For all
2) For the second part, it will be shown that
The derivative of
Similar to the proof of part one, we let
Also
where
which together with Equation 16 implies that:
also
Consequently, it is straightforward that given
By integrating the outcomes of Theorems 1, 2, the following theorem is established, which can be presented without additional proof:
Theorem 3. By Considering the multi-AUV system (Equation 1) and the virtual leader dynamics (Equation 2) with the network communication topology
Remark 5. With the proposed two-layer formation learning control architecture, inter-agent information exchange occurs solely in the first-layer DA observation. Only the observer’s estimated information, and not the physical plant state information, needs to be shared among neighboring agents. Additionally, since no global information is required for the design of each local AUV control system, the proposed formation learning control protocol can be designed and implemented in a fully distributed manner.
Remark 6. It is important to note that the eigenvalue constraints on
4 Accurate learning from formation control
It is necessary to demonstrate the convergence of the RBFNN weights in Equations 13, 14 to their optimal values for accurate learning and identification. The main result of this section is summarized in the following theorem.
Theorem 4. Consider the local closed-loop system (Equation 15) with Assumptions 1, 2. For each
where
Proof: From Theorem 3, we have shown that for all
Thus, to prove accurate convergence of local neural weights
where
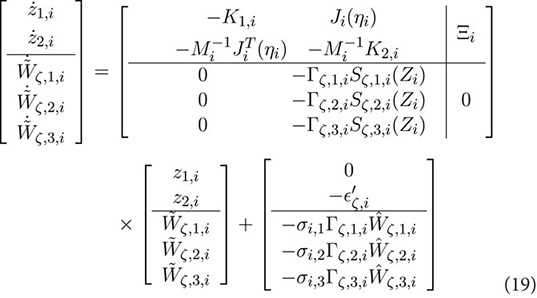
and
where
for all
where for all
with the approximation accuracy level of
Remark 7. The key idea in the proof of Theorem 4 is inspired by Wang and Hill (2018). For more detailed analysis on the learning performance, including quantitative analysis on the learning accuracy levels
Remark 8. Based on Equation 18, to obtain the constant RBFNN weights
Remark 9. It is shown in Theorem 4 that locally accurate learning of each individual AUV’s nonlinear uncertain dynamics can be achieved using localized RBFNNs along the periodic trajectory
5 Formation control with pre-learned dynamics
In this section, we will further address objective 2 of Problem 1, which involves achieving formation control without readapting to the AUV’s nonlinear uncertain dynamics. To this end, consider the multiple AUV systems (Equation 1) and the virtual leader dynamics (Equation 2). We employ the estimator observer Equations 3, 4 to cooperatively estimate the leader’s state information. Instead of using the DDL feedback control law (Equation 13), and self-adaptation law (Equation 4), we introduce the following constant RBFNN controller, which does not require online adaptation of the NN weights:
where
Theorem 5. Consider the multi-AUV system (Equation 1) and the virtual leader dynamics (Equation 3) with the network communication topology
Proof: The closed-loop system for each local AUV agent can be established by integrating the controller (Equation 20) with the AUV dynamics (Equation 1).
where
Selecting
which implies that:
where
Remark 10. Building on the locally accurate learning outcomes discussed in Section 4, the newly developed distributed control protocol comprising Equations 3, 4, 20 facilitates stable formation control across a repeated formation pattern. Unlike the formation learning control approach outlined in Section 3.2, which involves Equations 3, 4 coupled with Equations 13, 14, the current method eliminates the need for online RBFNN adaptation for all AUV agents. This significantly reduces the computational demands, thereby enhancing the practicality of implementing the proposed distributed RBFNN formation control protocol. This innovation marks a significant advancement over many existing techniques in the field.
6 Simulation
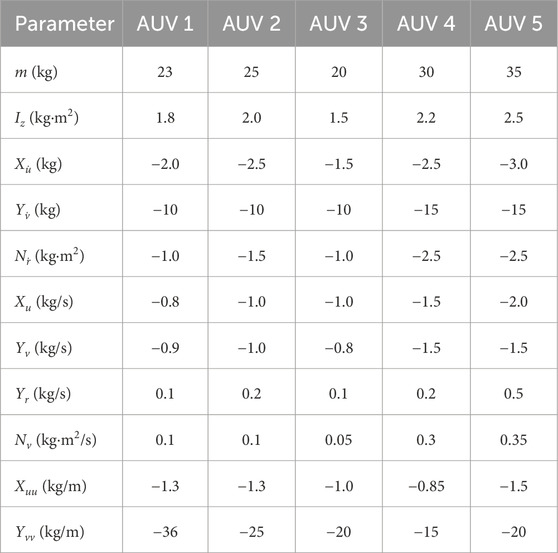
We consider a multi-AUV heterogeneous system composed of 5 AUVs for the simulation. The dynamics of these AUVs are described in THE system (Equation 1). The system parameters for each AUV are specified as follows:
where the mass and damping matrix components for each AUV
According to the notations in Prestero (2001) and Skjetne et al. (2005) the coefficients
Figure 2 illustrates the communication topology and the spanning tree where agent 0 is the virtual leader and is considered as the root, in accordance with Assumption 2. The desired formation pattern requires each AUV,
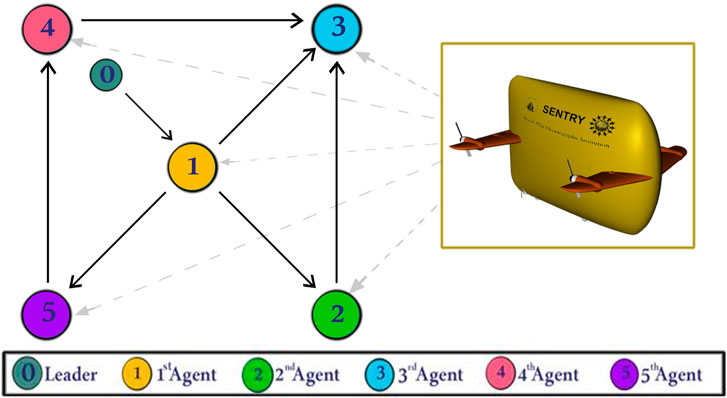
Figure 2. The communication network topology and spanning tree of multi-AUV system of the simulation with 0 as virtual leader.
The initial conditions and system matrix are structured to ensure all eigenvalues of
Each AUV tracks its respective position in the formation by adjusting its location to
6.1 DDL formation learning control simulation
The estimated virtual leader’s state, derived from the cooperative estimator in the first layer (see Equations 3, 4), is utilized to estimate each agent’s complete uncertain dynamics within the DDL controller (second layer) using Equations 13, 14. The uncertain nonlinear functions
The observer and controller parameters are chosen as
Figure 3 displays the simulation results of the cooperative estimator (first layer) for all five agents. It illustrates how each agent’s estimated states,
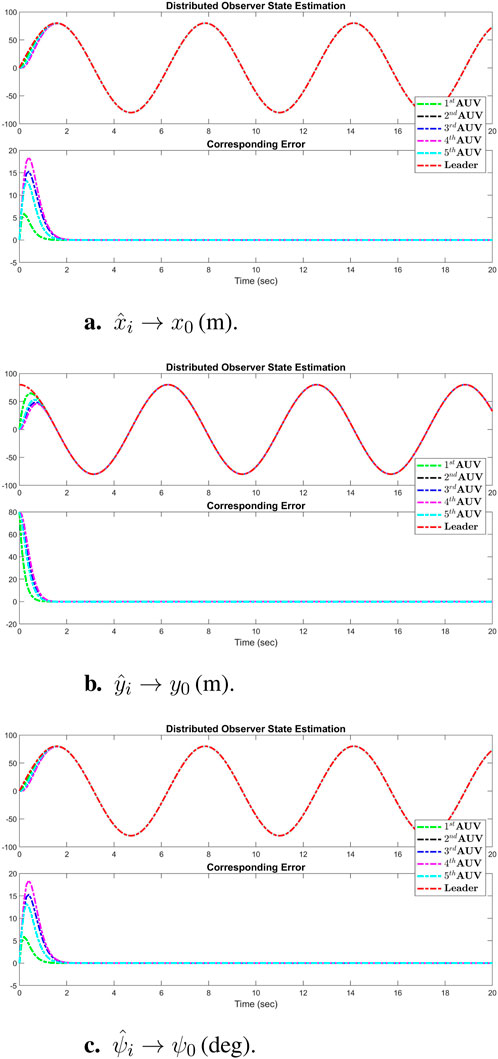
Figure 3. Simulation results of the cooperative observer (first layer) for all three states (x-axis, y-axis, and vehicle heading) of each AUV: (A)
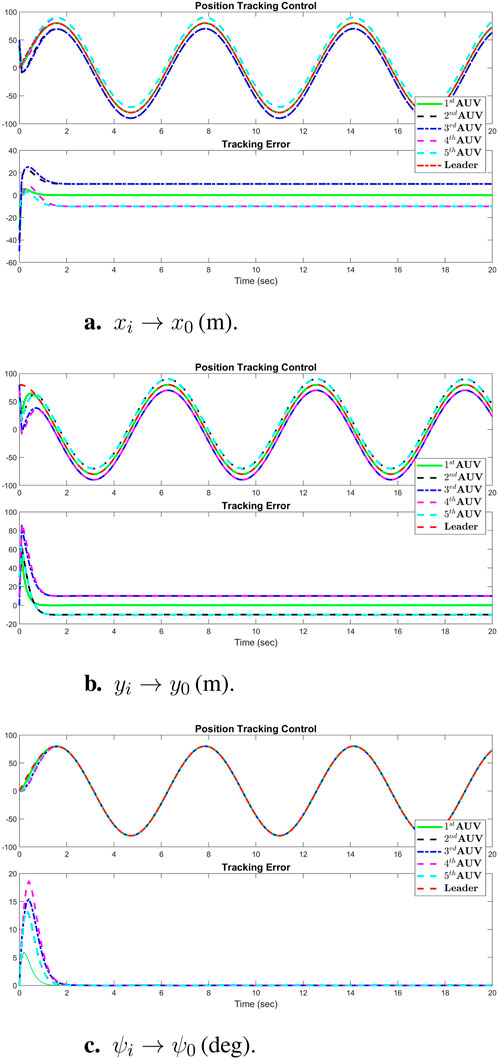
Figure 4. Simulation results of position tracking control performance of all agents: (A)
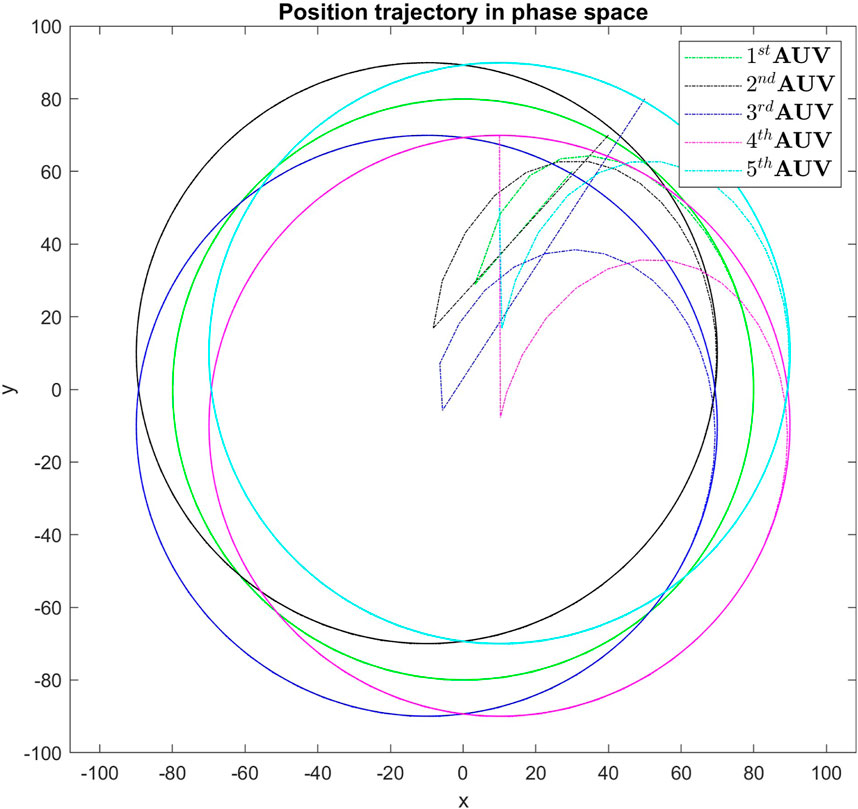
Figure 5. Real-time control performance in simulation for all agents, demonstrating the tracking strategy’s effectiveness in maintaining the formation pattern.
The sum of the absolute values of the neural network weights in Figure 6. This convergence reflects the network’s ability to maintain consistent performance, as further adjustments to the weights become minimal. Also, updating neural network weights and their convergence throughout the learning process into their optimal valies depicted in Figure 7. This convergence of all neural network weights to their optimal values during the training process, aligns with Theorem 4 as well. This leads to achieving accurate function approximation in the second layer. Figure 8 represents the successful function approximation results for the unknown system dynamics
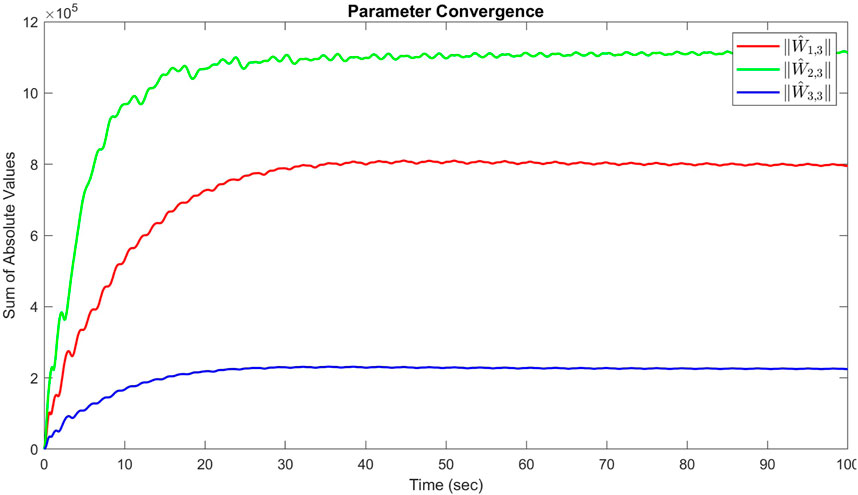
Figure 6. Sum of the absolute values of neural network weights in simulation for the third agent, showing the network stabilized and learns a consistent tracking pattern.
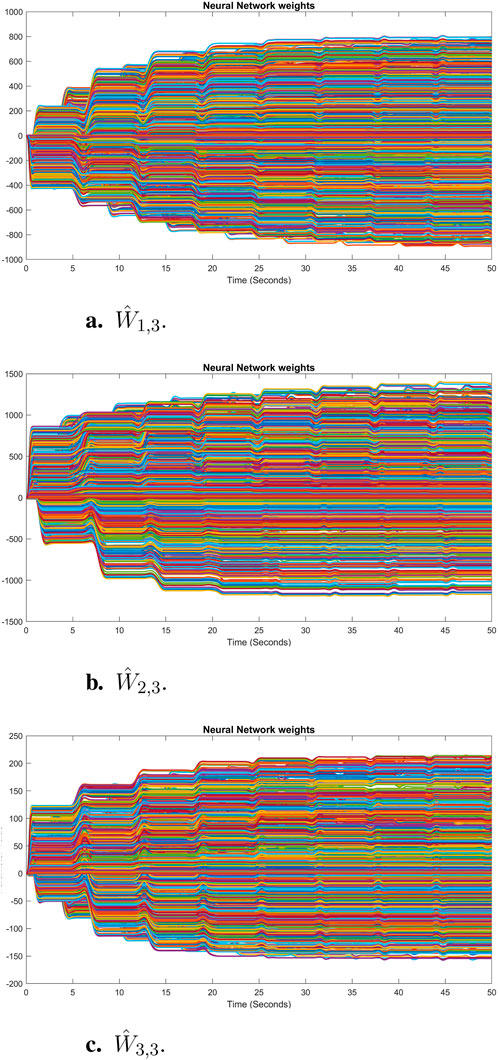
Figure 7. Convergence of neural network weights of each state to their optimal values in simulation for the third agent: (A)
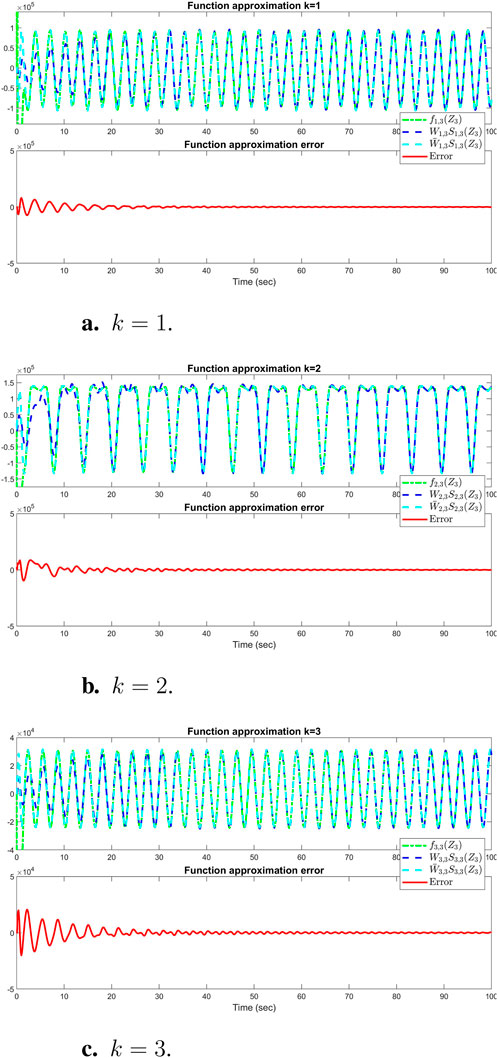
Figure 8. Simulation results of successful function approximation for all three states (k = 1, 2, 3) of the
6.2 Simulation for formation control with pre-learned dynamics
To evaluate the distributed control performance of the multi-AUV system, we implemented the pre-learned distributed formation control law. This strategy integrates the estimator observer Equations 3, 4, this time coupled with the constant RBFNN controller (Equation 21). We employed the virtual leader dynamics described in Equation 21 to generate consistent position tracking reference signals, as previously discussed in Section 6.1. To ensure a fair comparison, identical initial conditions and control gains and inputs were used across all simulations. Figure 9 illustrates the comparison of the tracking control results from Equations 13, 14 with the results using pre-trained weights
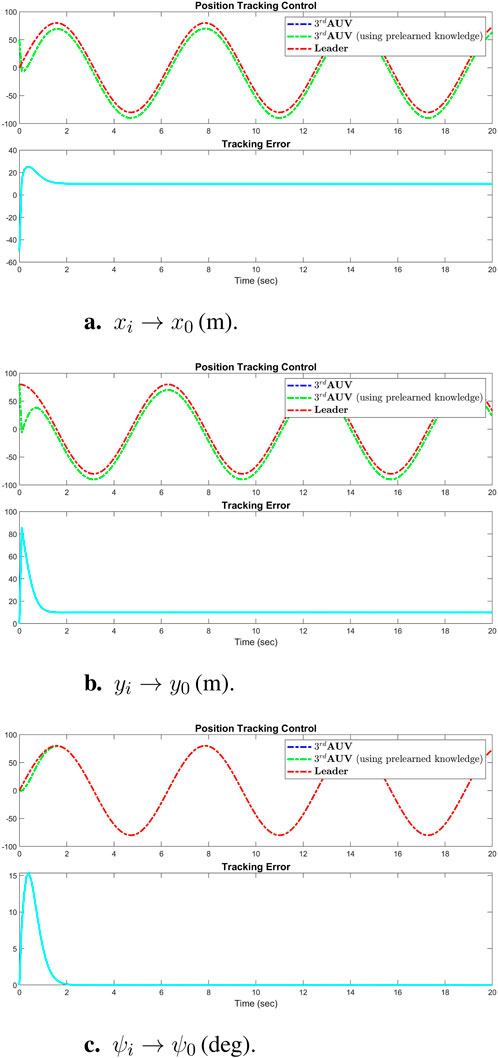
Figure 9. Simulation results of successful performance of position tracking control using pretrained weights
The control experiments and simulation results presented demonstrate that the constant RBFNN control law (Equation 4) can achieve satisfactory tracking control performance comparable to that of the adaptive control laws (Equations 13, 14), but with no computational demand. The elimination of online recalculations or readaptations of the NN weights under this control strategy significantly reduces the computational load whenever system restarts without needing to retrain again. This reduction is particularly advantageous in scenarios involving extensive neural networks with a large number of neurons, thereby conserving system energy and enhancing operational efficiency in real-time applications.
Before concluding the paper, a brief contribution of the paper is provided:
• Distributed Observer Results: Simulations showed that the distributed observer effectively estimated the leader’s state, allowing for accurate formation control without needing global information.
• Tracking Control Results: The controller demonstrated reliable tracking of reference signals, maintaining performance even under varying conditions and unknown system dynamics.
• Formation Control: The proposed controller maintained accurate formation control relative to a virtual leader in simulations, even when the system dynamics were unknown with different AUVs.
• Neural Network Weight Convergence: The simulation results demonstrated that the neural network weights converged effectively, ensuring accurate function approximation and reliable performance in controlling AUVs under uncertainties.
• Adaptability and Stability: The framework ensured stable tracking performance across various environmental conditions by relying on the RBFNN’s learning capabilities, allowing the AUVs to use prelearned information and maintain formation control without needing to relearn dynamics whenever system restarts.
• Reduction in Computational Load: The use of pre-trained neural network weights significantly reduced the computational burden during real-time operation, particularly when large neural networks were employed.
7 Conclusion
In conclusion, this paper has introduced a novel two-layer control framework designed for Autonomous Underwater Vehicles (AUVs), aimed at universal applicability across various AUV configurations and environmental conditions. This framework assumes all system dynamics to be unknown, thereby enabling the controller to operate independently of specific dynamic parameters and effectively handle any environmental challenges, including hydrodynamic forces and torques. The framework consists of a first-layer distributed observer estimator that captures the leader’s dynamics using information from adjacent agents, and a second-layer decentralized deterministic learning controller. Each AUV utilizes the estimated signals from the first layer to determine the desired trajectory, simultaneously training its own dynamics using Radial Basis Function Neural Networks (RBFNN). This innovative approach not only sustains stability and performance in dynamic and unpredictable environments but also allows AUVs to efficiently utilize previously learned dynamics after system restarts, facilitating rapid resumption of optimal operations. The robustness and versatility of this framework have been rigorously confirmed through comprehensive simulations, demonstrating its potential to significantly enhance the adaptability and resilience of AUV systems. By embracing total uncertainty in system dynamics, this framework establishes a new benchmark in autonomous underwater vehicle control and lays a solid groundwork for future developments aimed at minimizing energy use and maximizing system flexibility. We plan to expand this framework by accommodating more general leader dynamics and conducting experimental applications to validate its performance in real-world settings. Moreover, a more accurate model of some source of uncertainty could improve performance which we will address in our future research. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
EJ: Conceptualization, Writing–original draft, Writing–review and editing. MZ: Conceptualization, Funding acquisition, Supervision, Writing–review and editing. PS: Conceptualization, Supervision, Writing–review and editing. CY: Conceptualization, Formal Analysis, Funding acquisition, Supervision, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported in part by the National Science Foundation under Grant CMMI-1952862 and CMMI-2154901.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1A recurrent trajectory represents a large set of periodic and periodic-like trajectories generated from linear/nonlinear dynamical systems. A detailed characterization of recurrent trajectories can be found in Wang and Hill (2018).
References
Balch, T., and Arkin, R. (1998). Behavior-based formation control for multirobot teams. IEEE Trans. Robotics Automation 14, 926–939. doi:10.1109/70.736776
Cai, H., Lewis, F. L., Hu, G., and Huang, J. (2015). “Cooperative output regulation of linear multi-agent systems by the adaptive distributed observer,” in 2015 54th IEEE Conference on Decision and Control (CDC) (IEEE), 5432–5437.
Cao, X., Ren, L., and Sun, C. (2022). Dynamic target tracking control of autonomous underwater vehicle based on trajectory prediction. IEEE Trans. Cybern. 53, 1968–1981. doi:10.1109/tcyb.2022.3189688
Christen, S., Jendele, L., Aksan, E., and Hilliges, O. (2021). Learning functionally decomposed hierarchies for continuous control tasks with path planning. IEEE Robotics Automation Lett. 6, 3623–3630. doi:10.1109/lra.2021.3060403
Cui, R., Ge, S. S., How, B. V. E., and Choo, Y. S. (2010). Leader–follower formation control of underactuated autonomous underwater vehicles. Ocean. Eng. 37, 1491–1502. doi:10.1016/j.oceaneng.2010.07.006
Dong, X., Yuan, C., Stegagno, P., Zeng, W., and Wang, C. (2019). Composite cooperative synchronization and decentralized learning of multi-robot manipulators with heterogeneous nonlinear uncertain dynamics. J. Frankl. Inst. 356, 5049–5072. doi:10.1016/j.jfranklin.2019.04.028
Fossen, T. I. (1999). “Guidance and control of ocean vehicles,”. Norway: University of Trondheim. Doctors Thesis.
Ghafoori, S., Rabiee, A., Cetera, A., and Abiri, R. (2024). Bispectrum analysis of noninvasive eeg signals discriminates complex and natural grasp types. arXiv Prepr. arXiv:2402.01026, 1–5. doi:10.1109/embc53108.2024.10782163
Hadi, B., Khosravi, A., and Sarhadi, P. (2021). A review of the path planning and formation control for multiple autonomous underwater vehicles. J. Intelligent and Robotic Syst. 101, 67–26. doi:10.1007/s10846-021-01330-4
Hou, S. P., and Cheah, C. C. (2009). “Coordinated control of multiple autonomous underwater vehicles for pipeline inspection,” in Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference (IEEE), 3167–3172.
Ioannou, P. A., and Sun, J. (1996). Robust adaptive control, 1. Upper Saddle River, NJ: PTR Prentice-Hall.
Jandaghi, E., Chen, X., and Yuan, C. (2023). “Motion dynamics modeling and fault detection of a soft trunk robot,” in 2023 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM) (IEEE), 1324–1329.
Jandaghi, E., Stein, D. L., Hoburg, A., Stegagno, P., Zhou, M., and Yuan, C. (2024). “Composite distributed learning and synchronization of nonlinear multi-agent systems with complete uncertain dynamics,” in 2024 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), 1367–1372. doi:10.1109/aim55361.2024.10637197
Krstic, M., Kokotovic, P. V., and Kanellakopoulos, I. (1995). Nonlinear and adaptive control design. John Wiley and Sons, Inc.
Lawton, J. R. T. (2000). A Behavior-Based Approach to Multiple Spacecraft Formation Flying (Ph.D. thesis). Brigham Young University, Provo, UT, United States.
Millán, P., Orihuela, L., Jurado, I., and Rubio, F. R. (2013). Formation control of autonomous underwater vehicles subject to communication delays. IEEE Trans. Control Syst. Technol. 22, 770–777. doi:10.1109/tcst.2013.2262768
Park, J., and Sandberg, I. W. (1991). Universal approximation using radial-basis-function networks. Neural Comput. 3, 246–257. doi:10.1162/neco.1991.3.2.246
Peng, Z., Wang, D., Shi, Y., Wang, H., and Wang, W. (2015). Containment control of networked autonomous underwater vehicles with model uncertainty and ocean disturbances guided by multiple leaders. Inf. Sci. 316, 163–179. doi:10.1016/j.ins.2015.04.025
Peng, Z., Wang, J., and Wang, D. (2017). Distributed maneuvering of autonomous surface vehicles based on neurodynamic optimization and fuzzy approximation. IEEE Trans. Control Syst. Technol. 26, 1083–1090. doi:10.1109/tcst.2017.2699167
Prestero, T. (2001). “Development of a six-degree of freedom simulation model for the remus autonomous underwater vehicle,” in MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No.01CH37295), Honolulu, HI, USA, 2001, pp.450–455 vol.1, doi:10.1109/OCEANS.2001.968766
Ren, W., and Beard, R. W. (2005). Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. automatic control 50, 655–661. doi:10.1109/tac.2005.846556
Ren, W., and Beard, R. W. (2008). Distributed consensus in multi-vehicle cooperative control, 27. Springer.
Rout, R., and Subudhi, B. (2016). A backstepping approach for the formation control of multiple autonomous underwater vehicles using a leader–follower strategy. J. Mar. Eng. and Technol. 15, 38–46. doi:10.1080/20464177.2016.1173268
Skjetne, R., Fossen, T. I., and Kokotović, P. V. (2005). Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica 41, 289–298. doi:10.1016/j.automatica.2004.10.006
Su, Y., and Huang, J. (2011). Cooperative output regulation of linear multi-agent systems. IEEE Trans. Automatic Control 57, 1062–1066. doi:10.1109/TAC.2011.2169618
Tutsoy, O., Asadi, D., Ahmadi, K., Nabavi-Chashmi, S. Y., and Iqbal, J. (2024). Minimum distance and minimum time optimal path planning with bioinspired machine learning algorithms for faulty unmanned air vehicles. IEEE Trans. Intelligent Transp. Syst. 25, 9069–9077. doi:10.1109/tits.2024.3367769
Wang, C., and Hill, D. J. (2018). Deterministic learning theory for identification, recognition, and control. CRC Press. doi:10.1201/9781315221755
Yan, T., Xu, Z., Yang, S. X., and Gadsden, S. A. (2023). Formation control of multiple autonomous underwater vehicles: a review. Intell. and Robotics 3, 1–22. doi:10.20517/ir.2023.01
Yan, Z., Liu, X., Zhou, J., and Wu, D. (2018). Coordinated target tracking strategy for multiple unmanned underwater vehicles with time delays. IEEE Access 6, 10348–10357. doi:10.1109/access.2018.2793338
Yang, Y., Xiao, Y., and Li, T. (2021). A survey of autonomous underwater vehicle formation: performance, formation control, and communication capability. IEEE Commun. Surv. and Tutorials 23, 815–841. doi:10.1109/comst.2021.3059998
Yuan, C. (2017). Leader-following consensus of parameter-dependent networks via distributed gain-scheduling control. Int. J. Syst. Sci. 48, 2013–2022. doi:10.1080/00207721.2017.1309597
Yuan, C., Licht, S., and He, H. (2017). Formation learning control of multiple autonomous underwater vehicles with heterogeneous nonlinear uncertain dynamics. IEEE Trans. Cybern. 48, 2920–2934. doi:10.1109/tcyb.2017.2752458
Yuan, C., and Wang, C. (2011). Persistency of excitation and performance of deterministic learning. Syst. and control Lett. 60, 952–959. doi:10.1016/j.sysconle.2011.08.002
Yuan, C., and Wang, C. (2012). Performance of deterministic learning in noisy environments. Neurocomputing 78, 72–82. doi:10.1016/j.neucom.2011.05.037
Zhang, Y., Li, S., and Liu, X. (2018). Neural network-based model-free adaptive near-optimal tracking control for a class of nonlinear systems. IEEE Trans. neural Netw. Learn. Syst. 29, 6227–6241. doi:10.1109/tnnls.2018.2828114
Keywords: environment-independent controller, autonomous underwater vehicles (AUV), dynamic learning, formation learning control, multi-agent systems, neural network control, adaptive control, robotics
Citation: Jandaghi E, Zhou M, Stegagno P and Yuan C (2025) Adaptive formation learning control for cooperative AUVs under complete uncertainty. Front. Robot. AI 11:1491907. doi: 10.3389/frobt.2024.1491907
Received: 05 September 2024; Accepted: 12 December 2024;
Published: 14 February 2025.
Edited by:
Giovanni Iacca, University of Trento, ItalyReviewed by:
Önder Tutsoy, Adana Science and Technology University, TürkiyeDi Wu, Harbin University of Science and Technology, China
Copyright © 2025 Jandaghi, Zhou, Stegagno and Yuan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chengzhi Yuan, Y3l1YW5AdXJpLmVkdQ==
 Emadodin Jandaghi
Emadodin Jandaghi Mingxi Zhou
Mingxi Zhou Paolo Stegagno
Paolo Stegagno Chengzhi Yuan
Chengzhi Yuan