Improving remote sensing dehazing quality through local hybrid correction and optimization of atmospheric attenuation model based on wavelength

Near-ground remote sensing image dehazing is crucial for accurately monitoring land resources. An effective dehazing technique and a precise atmospheric attenuation model are fundamental to acquiring real-time ground data with high fidelity. The dark channel prior (DCP) is a widely used method for improving visibility in hazy conditions, but it often results in reduced image clarity and artifacts, that limit its practical utility. To address these limitations, we propose a novel hybrid correction method, local hybrid correction (LHC), which integrates gamma correction for high-contrast regions and logarithmic correction for low-contrast regions within a dehazed image. We calculated the cumulative distribution function (CDF) of Weber contrast for the dehazed image and analyzed the impact of different contrast thresholds on the effectiveness of improving image clarity and reducing artifacts. Our results showed that a contrast threshold corresponding to the 90% CDF significantly improved image sharpness and reduced artifacts compared to other thresholds. Furthermore, LHC outperformed both gamma and logarithmic corrections in terms of image clarity and artifact reduction, even after applying additional post-processing methods such as multi-exposure fusion and guided filtering. The quantitative analysis of the dehazed images, using gray-level co-occurrence matrix (GLCM) metrics, indicated that the LHC method offered a balanced advantage in enhancing image details, texture consistency, and structural complexity. Specifically, images processed by LHC exhibit moderate contrast and correlation, low homogeneity and high entropy, all these made the LHC method a very suitable solution for near-ground remote sensing tasks that required enhanced image detail and reduced artifacts. We also examined the atmospheric attenuation coefficient, observing that it increased with distance, deviating progressively from empirical values, this phenomenon underscored the complex effects of atmospheric scattering on dehazing accuracy, especially at extended ranges. Additionally, we refined the transmittance attenuation model using light reflection at the 550 nm wavelength from verdant landscapes, which improved the model’s alignment with real-world conditions. This approach was not only effective for this wavelength but could adapt to other wavelengths in future studies. Overall, our research advanced the precision of remote sensing dehazing techniques, promising improved decision-making for land resource management and a variety of environmental applications.

1 Introduction

Near-ground remote sensing image dehazing occupies a vital role in land resource monitoring, delivering precise, high-resolution data essential for assessing land utilization, soil health, and vegetative cover (Liang et al., 2025; Akay and Sami, 2024; Wang D. et al., 2024; Zheng et al., 2024). This technology enables the timely identification of land degradation (Ebrahimi et al., 2024), unlawful land use (Liu et al., 2024), and environmental transformations (Qiao et al., 2023; Cavalli and Maria, 2024), thereby supporting robust land management and conservation strategies. It is imperative to pursue approaches in near-ground remote sensing image dehazing that are not only precise and real-time but also extensive in range and cost-effective.

In near-ground remote sensing image dehazing, haze thickness and distribution as well as atmospheric scattering frequently diminish dehazed image quality, posing challenges to the effective dehazing of remote sensing images (Singh et al., 2024; Georgeot et al., 2024; Wei et al., 2024). Particularly in near-ground contexts, the complexity of haze and ground scenes severely impacts the dehazing effect and the fidelity of information extraction (Shen et al., 2020). Thus, dehazing has emerged as a critical research area to enhance image visibility and bolster the accuracy of object recognition. Investigating dehazing techniques for near-ground remote sensing imagery is of great importance not only for land monitoring but also as an interdisciplinary focus linking computer vision and remote sensing science. In hazy natural settings, remote sensing images often suffer from diminished contrast and brightness due to the scattering effects caused by airborne particles and water vapor. This degradation not only complicates visual assessment but also hinders the accurate extraction of ground data (Zheng et al., 2024). To counteract these issues, researchers have developed various dehazing algorithms, generally classified into physical model-based approaches and image enhancement-based approaches (Jiang et al., 2021). Physical model-based methods employ atmospheric scattering models to restore authentic colors and detail, typically achieving higher accuracy, albeit with considerable computational demands (Yan and Cui, 2024). In contrast, image enhancement-based methods improve image visibility by modulating contrast and brightness, allowing for faster processing but with trade-offs in maintaining natural coloration (Zhang et al., 2023).

Physical model-based techniques rely heavily on the atmospheric scattering model, which attributes image degradation primarily to the combined effects of direct radiation, scattered light, and ambient illumination (Yan and Cui, 2024). One of the most prominent physical model-based approaches is the dark channel prior (DCP) algorithm. The DCP method capitalizes on the observation that, in haze-free images, some pixels have very low intensities in at least one color channel (usually the dark channel), which can be used as a prior to estimate the transmission map of the image and subsequently recover the scene’s details (Fu et al., 2024a). While DCP enhances image clarity to an extent, it encounters limitations, such as easy-to-produce color distortion, artifacts and unclear details, and challenges in haze images with extensive bright regions. More refined methods have been introduced to overcome these challenges. For instance, the color attenuation prior (CAP) method incorporates brightness and saturation data to accurately estimate haze density (Zhu et al., 2015). Another method based on transparency and brightness information, leverages local statistical data within scenes to estimate atmospheric light, thus improving dehazing outcomes (Lei et al., 2024). Guided filtering is another key technique in this category, which helps improve the accuracy of atmospheric light estimation (Sun et al., 2021). It preserves the edges while removing noise, thus enhancing the dehazing process and overall image clarity. Despite their strong performance, physical model-based methods face some challenges, including the reliance on accurate parameter estimation. The effectiveness of dehazing heavily depends on the accuracy of these parameters, and inaccuracies can lead to suboptimal results. Furthermore, the significant computational demands of these methods can restrict their use in real-time applications.

In contrast to physical model-based approaches, image enhancement techniques bypass intricate physical models and instead refine visual quality through adjustments in histogram or contrast. Histogram equalization (HE), one of the earliest enhancement techniques, was celebrated for its simplicity and computational efficiency. However, it struggled with effectively addressing dehazing challenges, especially in images with non-uniform haze or insufficient contrast (Huang et al., 2019). More recent developments have drawn from the Retinex theory, which is based on the human visual system’s ability to perceive illumination and reflectance separately (Lu S. et al., 2024). These Retinex-inspired methods are particularly effective in enhancing dehazing image details, but they also face some challenges, especially in terms of handling computational complexity, color accuracy, and noise management. Other practical techniques are gamma and logarithm correction, forms of contrast adjustment that modify the image’s brightness curves, which can be useful for enhancing visibility and improving the perceived clarity of hazy images (Soleimany et al., 2021). But they also have limitations, especially in high-contrast or complex scenes, where they may lead to loss of details or image distortion. Multi-exposure fusion (MEF) is another popular image enhancement technique where multiple images with varying exposure levels are fused together to improve image details and contrast (Lu S. et al., 2024). Although these techniques can appreciably improve the visual appeal of an image, they overlook atmospheric scattering effects, limiting their efficacy in dehazing compared to physical model-based approaches. The rapid advancements in deep learning have introduced a new paradigm in image dehazing. Convolutional neural networks (CNNs) and generative adversarial networks (GANs) are increasingly being utilized for dehazing tasks, offering substantial improvements over traditional methods (Shen et al., 2024; Lu Q. et al., 2024). These approaches transcend the need for explicit physical models, learning instead to map features for dehazing through robust data-driven training. The resulting techniques offer marked improvements in both image quality and computational efficiency.

Despite significant progress in dehazing, there remain several unresolved challenges. First, although physical model-based methods offer high accuracy, their computational complexity is substantial, restricting their applications in real-time processing. Second, while image enhancement methods offer fast computation, their dehazing performance is limited under complex haze conditions. Additionally, deep learning methods require large amounts of labeled data, but existing haze-related data about near-ground remote sensing are relatively insufficient, which impacts model generalization. To achieve efficient and practical dehazing methods for near-ground remote sensing images, the following aspects are worth exploring: first, combining physical model and image enhancement techniques to achieve efficient dehazing; second, improving the dehazing effect with as few steps as possible; Finally, further optimizing atmospheric attenuation model to improve the accuracy and efficiency of image dehazing. So, in this study, we aim to develop a simple and efficient dehazing method for near-ground remote sensing images by focusing on several objectives: (1) investigating the impact of transmission parameters and atmospheric light on image clarity and artifact depth after using dark channel prior to dehazing. (2) investigating simple and efficient methods to improve the detail clarity and reduce artifacts in dehazed images by jointly using the gamma and logarithmic correction; (3) employing image processing techniques to estimate atmospheric transmittance and attenuation coefficients under various haze conditions, supported by visibility and distance measurements using visibility meters and laser rangefinders; and (4) comparing empirical and experimental values of atmospheric attenuation coefficient, and building an optimization model aligning with real-world conditions for the atmospheric attenuation. This work aspires to advance the accuracy and efficiency of dehazing for near-ground remote sensing images, paving the way for improved practical applications in land resources monitoring, agriculture and urban analysis.

2 Materials and methods

2.1 Data collection and processing methods

To obtain haze images under varying ground and atmospheric conditions, we conducted a series of near-ground remote sensing image collection experiments across multiple regions of China from January 2022 to October 2024. These experiments employed a drone (DJI Matrice 300 RTK, DJI Innovations Technology Co., Ltd., China) equipped with an onboard remote sensing camera (Zenmuse P1, DJI Innovations Technology Co., Ltd., China). During haze conditions, the drone was positioned at a fixed altitude and angle to capture multiple sets of images with varying exposure times for subsequent selection. Concurrently, a visibility meter (PWD20, Vaisala Ltd., Finland) was used to measure atmospheric visibility (V), and it took multiple measurements to calculate the average value.

On clear days when the haze had dissipated, two distant green plant sites on the ground were selected as reference points for the study. At location A on the ground, directly beneath the drone’s fixed filming position B, a laser rangefinder (TP320, Apresys Shanghai Precision Optoelectronics Co., Ltd., China) was employed to measure the distance (L_AB) from point A to the drone’s filming point B, as well as the distance (L_AC) from point A to plant site C. Using the known distances L_AB and L_AC, and the angle between the straight lines AB and AC, we calculated the distance (x) from plant site C to the drone’s filming point B. The visibility (V) and the calculated distance (x) were then used to compute the atmospheric attenuation coefficient (β) for subsequent analysis.

For the dehazing of the collected near-ground remote sensing images, we utilized Python and OpenCV for image processing. These tools were employed for the development and execution of several dehazing algorithms, including dark channel prior, correlation correction, multi-exposure fusion, guided filtering, and other post-processing techniques. Additionally, we leveraged Python and OpenCV to compute the initial transmission maps of the haze images. Based on these initial transmission maps, the transmission values at 22 plant sites were calculated and used to determine the atmospheric attenuation coefficient and optimize the atmospheric attenuation model.

2.2 Physical model of atmospheric attenuation of light

The image dehazing method used in this study was based on physics-based approaches, which made it essential to understand how light propagates through the atmosphere. In the atmosphere, light intensity decreases exponentially with distance due to the combined effects of absorption and scattering by atmospheric molecules, aerosols, haze, and other pollutants. This process of light attenuation can be described by the Beer-Lambert Law (Motiee et al., 2024), a classical physical model that quantifies how light intensity diminishes as it travels through a medium. The Beer-Lambert Law is mathematically expressed as follows:

$I\left(x\right)=I_0\exp \left(-\beta x\right),(1)$

where I(x) is the light intensity after traveling a distance x, I₀ is the initial light intensity, and β is the attenuation coefficient, accounting for both absorption and scattering. In atmospheric conditions, especially under haze, the attenuation coefficient β reflects the impact of aerosols and haze particles, which strongly scatter and absorb light in the visible and near-infrared spectrum, reducing visibility. To further quantify light attenuation in hazy conditions, an empirical formula for β has been developed, incorporating atmospheric visibility and wavelength of light:

$\beta \left(V,\lambda \right)=\frac{3.91}{V}\times {\left(\frac{\lambda }{0.55}\right)}^{-q},(2)$

where β(V, λ) is the attenuation coefficient, V is the visibility of the atmosphere, and q = 1.6 (V ≥ 10 km), 1.3(1 km ≤ V < 10 km) and 0.585V^1/3 (V < 1 km) (Fayaz et al., 2024). Equations 1, 2 reflect the increased scattering and absorption at shorter visibility distances, which intensifies light attenuation in hazy conditions. Light attenuation also varies with the wavelength of light, as different wavelengths are absorbed and scattered to varying degrees. In remote sensing applications, silicon-based sensors are typically used to detect light in the visible and near-infrared range, particularly from 400 to 1,200 nm. Consequently, when capturing images in hazy conditions, these sensors are significantly affected by wavelength-dependent attenuation, which must be accounted for to achieve accurate image readings. Based on these insights, the physical model describing light transport through a hazy atmosphere can be formulated as follows:

$I\left(x\right)=I_0\exp \left\{-\frac{3.91}{V}\times {\left(\frac{\lambda }{0.55}\right)}^{-q}]x\right\}.(3)$

This expression in Equation 3 demonstrates that light attenuation in haze is influenced by factors such as atmospheric visibility, light wavelength, and transmission distance. To optimize the estimation of the atmospheric attenuation coefficient under near-ground haze conditions, the later sections of the article will focus on calculating attenuation coefficients using both the empirical formula (Equation 2) and those derived from dehazing image processing techniques. This aims to refine the attenuation coefficient model, enhancing its applicability for accurate remote sensing in hazy environments.

The imaging process of haze images can be described using an atmospheric transport model (Yan and Cui, 2024), which provides the foundation for dehazing techniques aimed at recovering a clear image:

$I\left(x\right)=J\left(x\right)t\left(x\right)+A\left[1-t\left(x\right)\right],(4)$

where $I\left(x\right)$ is the observed hazy image, $J\left(x\right)$ is the dehazed image, $t\left(x\right)$ is the transmission map, and $A$ is the atmospheric light. While this model represented by Equation 4 explains haze formation, dehazing requires additional techniques to recover a clear image. In the following sections, our approach began with dark channel prior (DCP) dehazing, which estimated atmospheric light and transmission by assuming that certain pixels in clear images exhibited low intensity in at least one color channel. Although effective in many cases, DCP may encounter limitations in scenes with extensive bright areas or complex lighting, necessitating additional steps. Correlation correction was then applied to minimize sensor noise and color bias, improving alignment between the spectral data and the real scene. Guided filtering was used next to preserve edge details, enhancing the clarity of the dehazed image. To further improve detail and contrast, multi-exposure fusion (MEF) combined images with different exposure levels, providing a more comprehensive depiction of the scene. Finally, additional post-processing was conducted to restore natural colors and reduce noise while preserving edge details. These steps formed the core of our dehazing methodology, though some steps may be omitted in certain cases to streamline the procedure, resulting in variations of the dehazing method. Subsequent sections will provide a detailed description of each step and demonstrate its effectiveness in enhancing clarity and reducing artifacts in dehazed images.

2.3 Dark channel prior dehazing

The dark channel prior (DCP) is a classical image dehazing algorithm based on the observation that, in most natural haze-free images, at least one color channel has a very low intensity in a local patch (Fu et al., 2024b). This assumption holds especially well in scenes with shadows, foliage, and textured surfaces but may encounter limitations in images containing extensive bright regions, such as skies or overexposed areas. By leveraging this prior, DCP enables effective estimation of atmospheric light and the transmission map, which are essential components in removing haze. To calculate the dark channel image, the algorithm selects the minimum value among the RGB channels for each pixel. For an input image, the dark channel value at the pixel position x can be defined as follows:

$I^{dark}\left(x\right)=\underset{y\in \mathrm{\Omega }\left(x\right)}{\min }\left(\underset{C\in \left\{r,g,b\right\}}{\min }{I}^C\left(y\right)\right),(5)$

where $I^C\left(y\right)$ represents the pixel value of the image I at position y in the C color channel, $\mathrm{\Omega }\left(x\right)$ is a local window centered at the pixel $x$, $\underset{C\in \left\{r,g,b\right\}}{\min }$ refers to the minimum value among the three color channels (red, green, and blue), and $\underset{y\in \mathrm{\Omega }\left(x\right)}{\min }$ refers to the minimum value within the local window (Okamoto et al., 2024).

In the first experiment of this paper, the DCP method represented by Equation 5 was applied to dehaze two remote sensing images: one from a field scene and the other from an urban scene. The field scene, shown in Figure 1A, is relatively simple, with mainly green plants and minimal variation in brightness. The urban scene, shown in Figure 1F, is more complex, with green plants, white high-rise buildings, and other structures, as well as significant variation in brightness. To estimate the transmission map, an empirical formula that adjusts transmittance based on haze density is given as follows:

$t\left(x\right)=1-\omega \cdot \underset{y\in \mathrm{\Omega }\left(x\right)}{\min }\left(\underset{C\in \left\{r,g,b\right\}}{\min }\left(I^C\left(y\right)/A^C\right)\right),(6)$

where ω is an empirical parameter, introduced to control transmittance levels and prevent excessive dehazing. The results of applying the DCP method to two remote sensing images are shown in Figure 1. These images were processed using different values for the transmittance correction parameter ω and varying percentages (P) of the brightest pixels, selected to estimate the atmospheric light A. The results showed that a lower ω value (0.85) resulted in better visual quality, showing fewer artifacts, richer colors, and increased clarity compared to a higher ω value (0.95), and this effect became more noticeable in haze images with complex scene, for example, the urban scene, as illustrated in Figure 1. Changes in the percentage of brightest pixels P used to estimate atmospheric light (ranging from 0.1% to 0.5%) had no significant effect on image quality. Based on our visual assessment and the balance between clarity, color fidelity and artifact depth, we selected ω = 0.85 and P = 0.1% as optimal values for generating the rough transmission map (see Figure 11), for these values provided the most satisfactory dehazing results. Further quantitative evaluation will be discussed in the subsequent sections.

Figure 1

Figure 1. Dark channel prior to dehazing. (A) Original image for a field scene. (F) Original image for an urban scene. Transmittance correction parameter ω and the percent P of the brightest pixels selected to estimate the atmospheric light in the figure were as follows: (B, G) $\omega$ = 0.85, P = 0.1%; (C, H) $\omega$ = 0.85, P = 0.5%; (D, I) $\omega$ = 0.95, P = 0.1%; (E, J) $\omega$ = 0.95, P = 0.5%.

To enhance the detail clarity and reduce artifacts in dehazed images at a microscopic level, the micro-characteristics of the dehazed images generated by the DCP method were further evaluated. The cumulative distribution function (CDF) of local contrast was calculated in the dehazed images, as shown in Figure 2 (Wu et al., 2024). The local contrast was computed using the Weber contrast, defined as follows:

$C_W\left(x,y\right)=\frac{I\left(x,y\right)-\underset{m\in \mathrm{\Omega }}{I}\left(x,y\right)}{\underset{m\in \mathrm{\Omega }}{I}\left(x,y\right)},(7)$

where C_W (x, y) is Weber contrast at the pixel position (x, y), $\mathrm{\Omega }$ is the local window containing pixel (x, y), I(x, y) is the intensity at pixel (x, y), and $\underset{m\in \mathrm{\Omega }}{I}\left(x,y\right)$ represents the average pixel value in the local window centered at (x, y). The CDF illustrates the cumulative frequency of Weber contrast (Equation 7) values in the dehazed images, indicating the proportion of pixels with contrast values less than or equal to a given level. The results show that, for the dehazed images, higher ω and lower P values appear to make a larger number of pixels to preserve or enhance contrast. Among these two factors, the impact of ω appears to be more significant than that of P, as evidenced by the CDF curves being less steep and shifted toward higher Weber contrast values. This suggests that increasing ω has a stronger effect on enhancing contrast compared to lowering P. However, it is important to note that a larger number of pixels with high local contrast does not necessarily correlate with improved image quality. In fact, higher contrast can sometimes be indicative of artifacts resulting from over-processing or noise amplification. These artifacts may arise from algorithmic issues such as insufficient noise handling or aggressive contrast enhancement, leading to unnatural features in the image. While many image processing techniques aim to address these artifacts and improve the detail clarity of dehazed images after DCP processing, they are often complex and time-consuming. Therefore, exploring simple and effective methods to handle these artifacts and enhance the detail clarity of dehazed images is crucial.

Figure 2

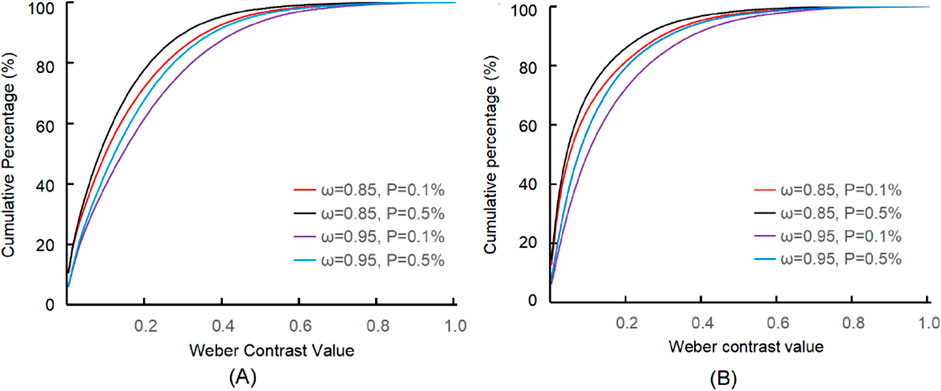
Figure 2. The curves show the cumulative distribution function (CDF) of Weber contrast values across the images after operating DCP. (A) The CDF curves for the field scene image; (B) The CDF curves for the urban scene image. The horizontal axis represents the Weber contrast values, indicating the relative difference between local pixel intensity and the local mean intensity normalized by the local mean. Higher values on the horizontal axis correspond to regions with greater local contrast. The vertical axis represents the cumulative probability of pixels with Weber contrast values less than or equal to the corresponding value on the horizontal axis.

2.4 Correlation correction

Remote sensing images often suffer from uneven brightness due to sensor and environmental factors, which can introduce biases and distort the spectral information. At the same time, DCP dehazing methods tend to increase unevenness and image distortion due to the formation of excessive artifacts. To address this, correlation correction techniques are used to eliminate these biases, ensuring that the spectral data in the image better aligns with the real-world scene. Gamma correction is a commonly used method for applying a non-linear transformation to pixel brightness values (Soleimany et al., 2021). It enhances the image contrast by adjusting the intensity of the pixels, particularly in the dark and bright areas, while also balancing the overall brightness of the image. This transformation is particularly useful for improving the visibility of details that may be obscured by haze or low contrast. In this experiment, gamma correction was applied for the images Figures 1B, G, and the results were shown in Figure 3, which exhibited varying degrees of brightness and contrast. The formula used for gamma correction is:

$I_{out}={\left(I_{in}\right)}^{\gamma },(8)$

where $I_{in}$ is the input normalized pixel intensity, $I_{out}$ is the corrected output intensity, and the exponent γ is adjusted based on the characteristics of the scene. The remote sensing images were processed with gamma values ranging from 0.8 to 3.0 according to the Equation 8. The processed results reveal that when γ < 1, the dark areas of the image are brightened, resulting in an overall lighter image (Figures 3A, C). In contrast, when γ > 1, the contrast in the highlighted areas is reduced, and the image becomes darker than the images before gamma correction (Figures 3B, D; Supplementary Figure S1). These results suggest that gamma correction can enhance the visibility of details in images with low contrast, particularly by boosting dark regions when γ < 1. However, the choice of γ value depends on the specific characteristics of the scene, as applying extreme values of gamma can lead to loss of detail in dark areas, as shown in Supplementary Figures S1B, E.

Figure 3

Figure 3. Gamma or logarithmic correction after DCP. (A–D) and (E–H) were processed by gamma and logarithmic corrections, respectively. The γ and a were the exponent of the gamma function and base of the logarithm function, respectively. (A, C) γ = 0.8; (B, D) γ = 1.2; (E, G) a = 2.0; (F, H) a = 3.0.

To explore a more effective method of dehazing, logarithmic correction was applied for the images in Figures 1B, G. It has a tendency to stretch the low-brightness pixels, which can enhance the details in dark areas and help retain more image information (Wu et al., 2024). The logarithmic correction is defined as:

$I_{out}={\log }_a\left(I_{in}+1\right),(9)$

where a was the base of the logarithm, which was varied in our experiment within the range of 1.2 ≤ a ≤ 5.0. When compared to the gamma correction, the two functions produce distinct patterns for low input values (I_in < 0.22). Specifically, the logarithmic correction (Equation 9) results in a stronger increase in brightness for low pixel values compared to gamma correction, which is reflected in the fact that the detailed areas of the image processed with logarithmic correction are brighter, as shown in Figure 3 and Supplementary Figure S1 (except for γ = 0.8 and a = 2, where the two methods behave similarly because their function values are close). This suggests that logarithmic correction can more effectively enhance the dark regions of a dehazed image compared to gamma correction, particularly for values of γ other than 0.8. Additionally, the maximum output of the logarithmic correction is typically smaller than that of the gamma correction, which implies that the dynamic range of the logarithmic output is narrower. This can lead to lower contrast but may allow for better detail retention in certain image areas. However, it is important to note that when a = 1.2, the images showed significant distortion, as the output values exceeded the maximum intensity limit of 1, leading to potential image artifacts (Supplementary Figure S1).

Although gamma and logarithmic corrections could make the image clearer and reduce image distortion, the artifacts still appeared, especially in gamma-corrected images, where the artifacts were more pronounced (Figure 3). To address the artifacts that affected the quality of dehazed images, a hybrid correction approach, referred to as local hybrid correction (LHC), was proposed. LHC applies gamma correction to high-contrast regions and logarithmic correction to low-contrast regions of the dehazed image. The key to LHC lies in determining the boundary between high and low contrast, known as the contrast threshold. In the previous analysis, the cumulative distribution function (CDF) of Weber contrast for the dehazed image was calculated, revealing the contrast values for the majority of pixels. Since artifacts typically occurred in high-contrast regions, and most pixels in dehazed images were in low-contrast regions in near-ground remote sensing images, the contrast value corresponding to 90% of the CDF was selected as the threshold. In subsequent experiments, LHC was applied using this threshold and compared with results from different contrast thresholds (such as CDF = 82%, CDF = 90%, CDF = 95%) to demonstrate the operational process and effects. For all images processed with LHC, the local window size was set to 10 × 10, the gamma function exponent was set to 1.2, and the base of the logarithmic function was set to 3. The results of LHC with thresholds 0.27 (CDF = 82%), 0.36 (CDF = 90%) and 0.45 (CDF = 95%) were showed in Figures 4A–C, and the results of thresholds 0.20 (CDF = 82%), 0.30 (CDF = 90%) and 0.40 (CDF = 95%) were shown in Figures 4D–F, respectively. The results indicated that as the threshold decreased, the images became darker, suggesting that more pixels were affected by gamma correction. By comparing Figure 4 with Figure 3, it was found that artifacts in the dehazed image are notably reduced with LHC. This suggests that LHC may help mitigate artifacts. We would demonstrate this with subsequent operations.

Figure 4

Figure 4. Local hybrid correction (LHC) after DCP. The gamma correction to high-contrast regions set γ = 1.2 and the logarithmic correction to low-contrast regions set a = 3. When we processed the LHC on all these images, the contrast threshold T is as follows: (A) T = 0.36; (B) T = 0.27; (C) T = 0.45; (D) T = 0.3; (E) T = 0.2; (F) T = 0.4.

2.5 Additional post-processing

In addition to the previously mentioned corrections, color restoration techniques could adjust the image’s color distribution to improve its appearance, making it more visually consistent with expected color balances. Similarly, filtering techniques, such as bilateral filtering, were used to reduce noise and artifacts, while striving to preserve important edge details. In our experiment, white balance correction was applied to adjust color distortions, and bilateral filtering was used to reduce noise while maintaining edge clarity (Mirzaee et al., 2024; Krishnaraj and Palanisamy, 2024). Subsequently, the overall brightness and contrast of the image were fine-tuned to enhance the clarity of the dehazed image, producing the clearest possible visual representation. The results indicated that images processed with logarithmic correction exhibited clearer detail compared to those processed with gamma correction, particularly in Figure 5B. While the depth of the artifacts was similar. However, while the white balance correction and bilateral filtering were applied to the dehazed images after the LHC operation, they showed negligible improvement in the image quality, but fine-tuning of the contrast and brightness led to a noticeable enhancement of clarity (Figure 6). It was also observed that images processed with LHC, using the contrast threshold corresponding to 90% of the CDF (Figures 6A, D), were clearer in details and exhibited lighter artifacts compared to other contrast thresholds and those processed with gamma or logarithmic correction. These results suggest that LHC can effectively reduce the artifacts and improve image quality when the appropriate threshold is applied. Subsequently, further investigation would be carried out to understand the specific impact of LHC on artifact reduction and clarity improvement.

Figure 5

Figure 5. The results of image dehazing by combining DCP, correlation correction, white balance correction and bilateral filtering. Images (A, C) were processed by gamma correction with γ = 1.2; (B, D) were processed by logarithmic correction with a = 3.0. The red boxes in the images mark the regions selected for magnified observation. The magnified white flowers and tops of the buildings in the top-left corners are used to compare the detail clarity of different dehazed images, while the magnified boxed images in the top-right corners are used to compare the depth of artifacts in different dehazed images.

Figure 6

Figure 6. The results of image dehazing combined with DCP, LHC and fine-tuning of the contrast and brightness. The images (A–F) were the results of processing fine-tuning of the contrast and brightness in Figures 4A–F.

2.6 Multi-exposure fusion

To examine whether the advantages of LHC in attenuating artifacts and clarifying images persisted after subsequent image quality optimization operations, we applied a multi-exposure fusion (MEF) method to the dehazed images and evaluated the results. The MEF technique utilizes two parameters: α, which adjusts the spatial frequency or contrast of the exposure images, and β, which is the weight factor for adjusting exposure levels (Han H. et al., 2024). In our experiment, we used α = 1.2 and β = 40. The images processed with DCP (ω = 0.85 and P = 0.1%), gamma or logarithmic correction, and LHC were subjected to MEF, as shown in Figure 7. The results showed that MEF improved image clarity. However, images processed with logarithmic correction (Figures 7G, I) exhibited slightly clearer details compared to gamma correction (Figures 7A, C). This effect was observed consistently after white balance correction and bilateral filtering, as shown in Figures 7B, D, H, J. When comparing the LHC with gamma and logarithmic corrections, it was found that images processed with LHC (Figures 7E, K) exhibited more uniform brightness after MEF, and these resulted in lighter artifacts and slightly improved detail clarity (Figures 7F, L). These findings suggested that LHC can help reduce the severity of artifacts while improving image quality.

Figure 7

Figure 7. Dehazing processes of combining DCP, correlation correction and multi-exposure fusion (MEF). (A, C) show the results of MEF with α = 1.2 and β = 40 after gamma correction with γ = 1.2; (G, I) show the results of MEF with α = 1.2 and β = 40 after logarithmic correction with a = 3; (E, K) show the results of MEF with α = 1.2 and β = 40 after LHC with contrast threshold corresponding to 90% of the CDF; (B, D, H, J) show the final results after white balance correction and bilateral filtering; (F, L) show the final results after fine-tuning the contrast and brightness.

2.7 Transmittance refinement

To demonstrate the advantages of the LHC method in attenuating artifacts and enhancing image detail clarity, it will be compared with the guided filtering method in the following sections. In the dehazing process, the initial transmittance estimate can be relatively coarse. To refine this, guided filtering is applied using a grayscale image (converted from the color image) as a guide, improving the accuracy of the transmittance estimate and thus enhancing the quality of the dehazed image. This process helps create a more realistic and natural image by reducing artifacts and preserving important image details. In the experiment, guided filtering was applied to the images after DCP ($\omega$ = 0.85 and $r$ = 0.1%) and gamma or logarithmic correction. The formula for the refined transmittance after guided filtering is given by:

$t_{\text{refined}}\left(x\right)=\frac{1}{\left|{\mathrm{\Omega }}_k\right|}{\displaystyle \sum _{k\in {\mathrm{\Omega }}_k}}\left(a_k{I}_{gray}\left(x\right)+b_k\right),(10)$

where ${\mathrm{\Omega }}_k$ is the local window centered at pixel k, $\left|{\mathrm{\Omega }}_k\right|$ is the total number of pixels within the window, and $I_{gray}\left(x\right)$ is the guide image, typically the grayscale map derived from the original haze map. The parameters $a_k$ and $b_k$ control the linear transmittance, and a regularization parameter ε is introduced to avoid excessive smoothing of high-frequency details (Wang J. et al., 2024). For the purpose of the experiment, the local window radius was set to 60, and the regularization parameter ε = 0.001, based on prior studies that balanced edge preservation with noise reduction. After applying the guided filtering (Equation 10), the refined transmission maps showed smoother edges in the grayscale images Figure 8 compared to the rough initial transmission maps (Figure 11), while still maintaining local structural details. The images processed with guided filtering (as shown in Figure 9) demonstrated improved clarity, particularly in the images processed with logarithmic correction, which were clearer and showed more detailed information than those processed with gamma correction. However, they showed similar artifact depth with gamma correction. This effect remained even after the subsequent application of MEF, white balance correction and bilateral filtering (Figures 9C, F, I, L). There is no significant difference in the artifact depth and image detail clarity between the results of the guided filtering after logarithmic correction and LHC operation (comparison among Figures 9I, L, 7F). This suggested that the LHC method attenuates artifacts similarly to guided filtering but with simpler and more efficient operation.

Figure 8

Figure 8. Refined transmission maps performed by guided filtering. (A) Refined transmission map for the field scene image; (B) Refined transmission map for the urban scene image.

Figure 9

Figure 9. The dehazing processes of combining DCP, gamma or logarithmic correction, guided filtering, MEF, white balance correction and bilateral filtering. (A, D) guided filtering applied after gamma correction with γ = 1.2; (G, J) guided filtering applied after logarithmic correction with $a$ = 3; (B, E, H, K) MEF with α = 1.2 and β = 40; (C, F, I, L) white balance correction and bilateral filtering.

3 Experiment results

3.1 Quantitative analysis of dehazed images

To quantitatively evaluate the advantages of the LHC method in image dehazing, we conducted an analysis based on four key texture metrics derived from the gray-level co-occurrence matrix (GLCM) of the dehazed images: contrast, correlation, homogeneity, and entropy, which were particularly suitable for the evaluation of local features of dehazed images (Saini and Nagpal, 2024). Contrast measures the intensity of local variations in the image, with higher values typically indicating sharper details and more pronounced texture (Du et al., 2024; Zhang et al., 2017). Correlation evaluates the linear dependence between pixel values, where higher values reflect a more structured and consistent texture. Homogeneity quantifies the similarity of pixel pairs, with higher values signifying smoother and more uniform regions, often associated with less noise. Finally, Entropy measures the complexity and uncertainty of the image content, where higher entropy values indicate more intricate and detailed textures.

The results of the quantitative evaluation for the dehazed images are presented in Table 1. Based on these results, Figures 6, 7F, L, which were processed with the LHC method, exhibit a balanced advantage in terms of the GLCM metrics. These images show moderate contrast, which helps preserve fine image details while avoiding the distortion that can result from over-sharpening. Specifically, Figure 6D (contrast = 615.20) and Figure 9L (contrast = 492.46) achieve a balance between detail retention and preventing excessive sharpness, which prevents unwanted artifacts. Additionally, the lower homogeneity and higher entropy values observed in these images suggest more texture details and greater image complexity. For example, Figure 6A has an entropy value of 14.73, indicating that it contains more intricate texture patterns, making it suitable for remote sensing tasks that require high detail and complexity. But moderate correlation made the texture keep a good consistency, and this made the artifacts less pronounced in Figure 6A. In contrast, Figure 7C, which was processed using gamma correction, exhibits extremely high contrast (1,435.22) and entropy (15.72), and the lowest homogeneity, leading to significant distortion. While higher contrast can sometimes enhance image sharpness, in this case, it causes visual artifacts that compromise the quality of the image. In comparison, Figure 9, which was processed using guided filtering after gamma or logarithmic correction, has lower contrast values, higher correlation, and lower entropy, resulting in a smoother image appearance but at the cost of a lack of sufficient detail and complexity, which limits its applicability for analysis tasks that require a more nuanced understanding of the image content.

Table 1

Table 1. Quantitative analysis of contrast, correlation, homogeneity, and entropy for the dehazed images of Figures 1A, F. The highest and lowest scores for each metric are highlighted in bold black.

Therefore, the LHC method, when used as post-processing for dehazed images after DCP, demonstrates clear advantages in terms of detail representation, texture consistency, and complexity. The LHC-processed images not only preserve finer details but also exhibit more complex and visual lighter textures, which are crucial for tasks that demand high levels of detail and sophistication, such as near-ground remote sensing analysis.

3.2 The attenuation coefficient of the atmosphere

To accurately calculate the atmospheric attenuation coefficient in haze conditions near the ground and restore the actual scene map, it is essential to compare both the experimental and empirical values of the attenuation coefficient of light in hazy air and to analyze the causes of any deviations between them. In this study, we processed a series of near-ground remote sensing haze images using the promising method (DCP, LHC, and fine-tuning of the contrast and brightness), based on the results of quantitative analysis. The resulting dehazed images are shown in Figure 10. These images were chosen to represent real-world scenes, including agricultural land, forests, and urban environments. The results demonstrated that the LHC method significantly improves image clarity and suppresses noise across diverse environmental contexts, validating its practical utility for remote sensing tasks. The rough transmission maps for each haze image were initially calculated using appropriate transmittance and atmospheric light parameters as defined in Equation 6. To refine these estimates, 22 representative plant sites were selected from the rough transmission maps for transmittance calculation, based on visual inspection and comparison with grayscale reference scales by image processing software in Python (see Figure 11). The atmospheric attenuation coefficients (β_expt) for the 22 plant sites were then calculated using the theoretical transmittance formula $t\left(x\right)=e^{-\beta x}$, where the transmittance t(x) was substituted with the values derived from the rough transmission maps. The distance (x) from the scene to the camera was calculated as mentioned in Section 2.1. For the empirical values, the attenuation coefficient (β_emp) was determined by substituting the measured visibility and the distance x (as mentioned in Section 2.1) into the empirical atmospheric attenuation equation (Equation 2).

Figure 10

Figure 10. Dehazing of near-ground remote sensing images. (A) Original haze images; (B) Dehazing using dark channel prior (DCP); (C) Image after DCP and LHC; (D) Image after DCP, LHC, and fine-tuning of the contrast and brightness.

Figure 11

Figure 11. Rough transmission maps for scenes 1 to 22. (A) Rough transmission map for the field scene image; (B) Rough transmission map for the urban scene image; (C–A) Rough transmission maps for the other nine scene images.

To simplify the calculations, the wavelength of 550 nm (green light) was chosen, as this wavelength is commonly used in atmospheric studies and corresponds well with the reflection properties of vegetation, which was the primary feature of interest in our plant sites. The green plants in the images were selected as representative of areas that primarily reflect green light. Finally, we compared the experimental and empirical values and calculated the deviations using error assessment methods. The results are presented in Table 2. It was found that the experimental attenuation coefficients (β_expt) generally increased with distance (x), and the deviations between the experimental and empirical values also increased as distance increased. These findings suggest that while the experimental method provides reasonable estimates, there is a growing discrepancy with increasing distance, which could be attributed to factors such as atmospheric scattering and measurement limitations that need further investigation.

Table 2

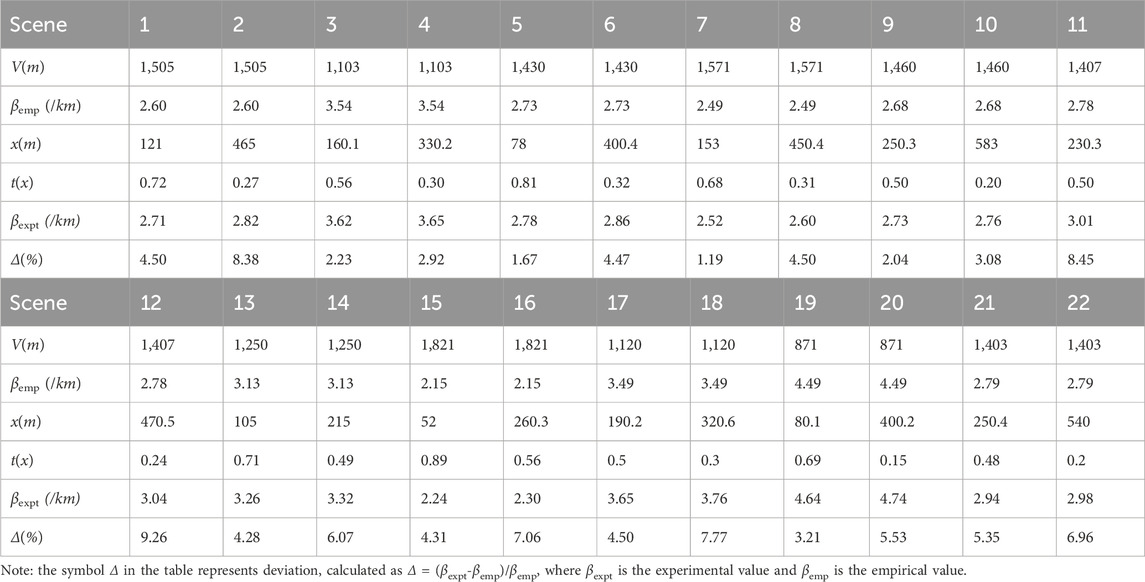
Table 2. Comparison of the atmospheric attenuation coefficients between empirical and experimental values.

3.3 Optimization of the atmospheric attenuation model

The mathematical relationships between the atmospheric attenuation coefficients (both empirical and experimental) and visibility are depicted in the scatter plots in Figure 12. By fitting these experimental values, the optimized transmittance attenuation curve was derived, expressed as follows:

${\beta }_{expt}\left(V\right)=\frac{4.0879}{V^{0.989}}(11)$

Figure 12

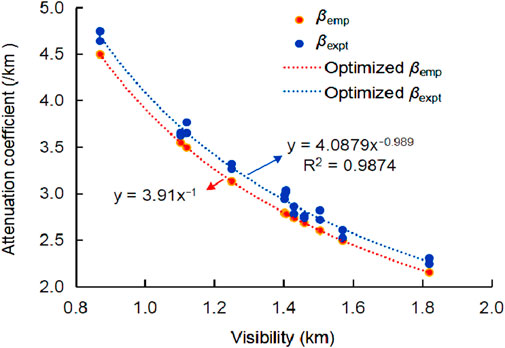
Figure 12. Scatter plots showing the relationship between the atmospheric attenuation coefficients (empirical and experimental values) and visibility. The curves represent the optimized transmittance attenuation model fitted to the experimental data.

The coefficient of determination (R² = 0.9874) indicates a strong correlation between the experimental data and the optimized model. This suggests that the optimized Equation 11 fits the experimental data well. However, while the model demonstrates a good fit under specific experimental conditions, its applicability as a general atmospheric attenuation coefficient model should be further validated. Additional testing in diverse environmental conditions and across different wavelengths would be necessary to assess its robustness and generalizability.

4 Discussion

This study explored and developed a simple yet efficient dehazing method for near-ground remote sensing images, with a focus on improving image clarity, reducing artifacts, and preserving fine details. The dark channel prior (DCP) method, which leverages the principle that pixels in haze-free images typically exhibit relatively low intensity in the dark channel, proved particularly useful for initial haze removal. While DCP has been shown to be effective in many studies (Han Y. et al., 2024; Suo et al., 2023), it is important to note that its performance may degrade due to the decrease in clarity and the formation of artifacts. Thus, while DCP is a useful starting point for haze removal, additional methods are often required to enhance image quality further.

To further improve the clarity of image details, gamma and logarithmic corrections were applied. Our analysis found that logarithmic correction was more effective than gamma correction in enhancing dark regions of the image, which was particularly crucial for remote sensing image analysis, where fine details in low-light areas were often obscured by haze. However, this result differed from those found in the studies by Suo et al. (2023) and Wang and Yang (2022), and the discrepancy may be due to differences in haze conditions or other environmental factors. This highlighted the need for further investigation into how different haze conditions affect the effectiveness of these corrections.

Despite the improvements in image clarity and distortion reduction, both gamma and logarithmic corrections introduced noticeable artifacts. In particular, gamma-corrected images exhibited more pronounced artifacts, likely due to excessive contrast enhancement, which may led to distortion in the final images. Although other post-processing techniques, such as multi-exposure fusion (MEF) and guided filtering, played an important role in retaining image details, reducing artifacts and enhancing overall image quality, they often resulted in images with lower contrast and higher correlation (Li, 2023; Li et al., 2022; Mu et al., 2024; Deng et al., 2021). This smoothing effect diminished the image’s complexity and fine detail. These results indicated that applying a uniform correction to the entire image using the gamma and logarithmic corrections is imperfect for detail enhancement and artifact reduction. Localized correction methods targeting these issues are needed. Therefore, it is crucial to strike a balance between smoothness and detail preservation in remote sensing image processing, a challenge that traditional dehazing methods often struggle with.

The local hybrid correction (LHC) method, applied as a post-processing step to the dehazed images, proved to be a promising solution for mitigating these artifacts. Unlike gamma or logarithmic corrections, which adjust overall sharpness and amplify some noise, LHC applies gamma correction to high-contrast regions and logarithmic correction to low-contrast regions of the dehazed image. This approach effectively preserved image details while suppressing noise. The choice of contrast threshold is a critical factor in LHC, and our results indicated that the contrast value corresponding to the 90% cumulative distribution function (CDF) significantly improved image sharpness and reduced artifacts. However, the optimal threshold may vary for different dehazed images, and closely related to the original hazy images. While the LHC method is primarily a post-processing correction technique applied after DCP, its optimal threshold is indirectly influenced by imaging conditions, such as haze intensity, camera resolution, and spectral characteristics of the sensor. Meanwhile, its effectiveness is also influenced by the quality of the input hazy image, which depends on factors such as light scattering, atmospheric pressure, humidity and aerosol concentration during image acquisition. These factors impact the initial haze formation and optical properties of the atmosphere, and while they are more relevant to the dehazing process itself, their effects on the dehazed images may affect the subsequent corrections made by LHC. We have highlighted these in our study while also emphasizing the need for testing the LHC method on dehazed images obtained from diverse environmental conditions, such as urban, arid, and mountainous landscapes. So, this study also demonstrated the effectiveness of the LHC method in improving the clarity of dehazed images across a variety of real-world scenarios, including agricultural land, forests, and urban environments. These findings validate the practical utility of the LHC method for land management, environmental monitoring, and urban planning. Further research should focus on quickly determining the optimal threshold for different remote sensing images and assessing the method’s robustness under different atmospheric conditions to maximize the performance of the LHC method in diverse real-world applications.

Additionally, the white balance correction and bilateral filtering applied to the dehazed images after the LHC operation showed negligible improvement in image quality, suggesting that LHC may have already optimized both the color and denoising aspects of the image. This further underscored the superiority of LHC in noise suppression and efficient correction for dehazed images. Moreover, this study also highlighted the similarities and differences between guided filtering and the LHC method. Both were capable of reducing noise, but guided filtering sacrificed detail and contrast in the process, limiting its application in tasks that require complex image analysis. In contrast, the LHC method reduced noise while better preserving image details, making it more suitable for applications where detail retention was crucial. Therefore, these methods are suited for different dehazing tasks: guided filtering is more appropriate for noise reduction in relatively simple environments, while LHC is ideal for high-quality image enhancement in detailed analysis or remote sensing tasks. Nevertheless, additional post-processing may still provide marginal improvements, and further research could explore the interactions between LHC and other post-processing techniques.

Although the LHC method significantly improves the quality of dehazed images, evaluating its computational efficiency is essential, particularly for real-time remote sensing applications. To assess its efficiency, we compared the processing time of the LHC method with that of traditional gamma and logarithmic corrections under controlled conditions, including consistent hardware and dataset sizes (Supplementary Tables S1, S2). Our results indicate that the total processing time of the LHC method is generally shorter than gamma and logarithmic corrections for images of similar size, which suggests its relative computational advantage. However, for large-scale remote sensing datasets, such as aerial and satellite imagery, the processing time of the LHC method is expected to grow linearly with data size, assuming no major bottlenecks. While this linear growth is manageable for moderately sized datasets, optimizing computational load becomes critical for real-time applications. This could include scenarios where high-resolution images or time-sensitive decision-making is required, such as monitoring environmental changes or urban planning. Further research is needed to validate the scalability of the LHC method under diverse conditions, including varying resolutions, environmental factors, and sensor types. Additionally, future studies should explore strategies to enhance algorithm performance through parallel computing, GPU-based acceleration, or other optimization techniques. Such advancements would improve the practicality of the LHC method for large-scale, real-world remote sensing applications.

In our study, we also examined the behavior of the atmospheric attenuation coefficient. We observed that the experimental attenuation coefficient (β_expt) increased with distance, leading to greater deviations from empirical values. This underscored the complexity of atmospheric scattering and its significant effect on dehazing accuracy, particularly at larger distances where haze-induced distortions become more pronounced. These findings were in agreement with Tian’s study (Li et al., 2024), which also highlighted the challenges posed by atmospheric scattering in remote sensing.

We also explored the optimization of the transmittance attenuation model based on initial transmission maps, which was critical for accurately modeling haze in remote sensing images. Recent studies have focused on optimizing the transmittance attenuation curve using various techniques such as weighted multi-exposure fusion (Gao et al., 2019), deep learning-based deblurring methods (Deng et al., 2021), and considering environmental factors like visibility, relative humidity, and aerosol particle size distribution (Peng et al., 2020; Zhang et al., 2024). In contrast, our approach leveraged green landscapes and the reflected 550 nm light from these landscapes to optimize the attenuation coefficient model, offering a more realistic representation of real-world conditions. However, we acknowledge that its applicability to other wavelengths or non-verdant environments remains a limitation and requires further investigation. While this model provides promising results, future work should evaluate its performance across various environmental conditions, such as urban, arid, and mountainous regions. These diverse landscapes present unique challenges, including differences in atmospheric scattering, aerosol concentration, and terrain complexity. Additionally, we recognize the potential complementarity of our method with other techniques, such as deep learning, which could further enhance its robustness. Future studies should also explore refining the model to optimize for other wavelengths, which could potentially improve its performance across a broader range of atmospheric conditions.

5 Conclusion

In this study, we proposed an efficient method to enhance the dehazing quality of near-ground remote sensing images, improving clarity, reducing artifacts, and preserving fine details. The local hybrid correction (LHC) technique outperformed traditional methods like gamma and logarithmic corrections by enhancing sharpness and reducing artifacts, making it especially useful for applications in land resource monitoring, agricultural analysis, and urban planning. However, further testing under varied environmental conditions and with diverse datasets is needed to fully assess its robustness.

We also investigated the behavior of the atmospheric attenuation coefficient, observing that it increased with distance and deviated from empirical values at longer ranges. This underscores the need to refine the transmittance attenuation model for better dehazing. Our optimization using 550 nm wavelength reflections from green landscapes showed promising results, aligning well with real-world conditions. However, its applicability to other wavelengths and non-verdant environments requires further study.

Future research should expand the attenuation model to include a wider range of atmospheric conditions and wavelengths, and explore the combination of LHC with the optimized attenuation model for improved remote sensing accuracy. Additionally, enhancing the LHC method’s computational efficiency, especially for large-scale datasets like aerial and satellite imagery, is crucial for real-time applications. Optimizing processing speed through parallel computing or GPU-based acceleration could further improve its practicality for time-sensitive tasks. This study lays the groundwork for future advancements in remote sensing dehazing, with potential impacts on environmental monitoring, land management, and urban planning.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

DZ: Conceptualization, Investigation, Methodology, Resources, Supervision, Writing–original draft. KS: Conceptualization, Investigation, Methodology, Resources, Supervision, Writing–original draft, Writing–review and editing. ZL: Data curation, Investigation, Software, Visualization, Writing–original draft. MC: Data curation, Validation, Visualization, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research was financially supported by the “Integrated Air-Space-Ground Intelligent Ecological Situation Sensing and Comprehensive Monitoring Platform Social Service Project (No. FJGY-[GK]-202404039)” based in Fuzhou, China. This funding enabled the development of the study and contributed to the resources necessary for data collection and analysis.

Acknowledgments

The authors would like to acknowledge the financial support received from the project “Integrated Air-Space-Ground Intelligent Ecological Situation Sensing and Comprehensive Monitoring Platform Social Service Project (No. FJGY-[GK]-202404039)”, Fuzhou, China.

Conflict of interest

Author KS was employed by Beijing Outlook Shenzhou Technology Co., Ltd. Author ZL was employed by Zhejiang Outlook Shenzhou Technology Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2024.1543342/full#supplementary-material

References

Akay, S., and Sami, O. (2024). Exploring land use/land cover dynamics and statistical assessment of various indicators. Appl. Sci. 14, 2434. doi:10.3390/app14062434

CrossRef Full Text | Google Scholar

Cavalli, R., and Maria, L. (2024). Remote data for mapping and monitoring coastal phenomena and parameters: a systematic review. Remote Sens. 16, 446. doi:10.3390/rs16030446

CrossRef Full Text | Google Scholar

Deng, X., Zhang, Y., Xu, M., Gu, S., and Duan, Y. (2021). Deep coupled feedback network for joint exposure fusion and image super-resolution. IEEE Trans. Image Process. 30, 3098–3112. doi:10.1109/tip.2021.3058764

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, S., Xing, J., Wang, S., Wei, L., and Zhang, Y. (2024). STMNet: scene classification-assisted and texture feature-enhanced multiscale network for large-scale urban informal settlement extraction from remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 17, 13169–13187. doi:10.1109/jstars.2024.3432200

CrossRef Full Text | Google Scholar

Ebrahimi, A., Zolfaghari, F., Ghodsi, M., and Narmashiri, F. (2024). Assessing the accuracy of spectral indices obtained from Sentinel images using field research to estimate land degradation. PLoS One 19, e0305758. doi:10.1371/journal.pone.0305758

PubMed Abstract | CrossRef Full Text | Google Scholar

Fayaz, M., Nam, J., Dang, L. M., Song, H. K., Moon, H., and Hyeonjoon, L. (2024). Land-cover classification using deep learning with high-resolution remote-sensing imagery. Appl. Sci. 14, 1844. doi:10.3390/app14051844

CrossRef Full Text | Google Scholar

Fu, F., Zhang, Z., Geng, X., Xu, J., and Fang, M. (2024a). Optimized dehazing algorithm based on dark channel prior with Gabor filter and multiscale minimum filter. IET Image Process 18, 2918–2929. doi:10.1049/ipr2.13143

CrossRef Full Text | Google Scholar

Fu, H., Gong, Q., Wang, P., and Lu, Y. R. (2024b). Synthetic aperture radar remote sensing scene classification based on fuzzy co-occurrence networks. J. Appl. Remote Sens. 18 (1). doi:10.1117/1.jrs.18.016510

CrossRef Full Text | Google Scholar

Gao, Y., Lan, X. D., Cai, R. S., and Li, J. (2019). Single fog image dehazing via fast multi-scale image fusion. IFAC-PapersOnLine 52 (24), 225–230. doi:10.1016/j.ifacol.2019.12.412

CrossRef Full Text | Google Scholar

Georgeot, A., Ceamanos, X., and Attie, J. L. (2024). Quantitative assessment of the potential of optimal estimation for aerosol retrieval from geostationary weather satellites in the frame of the iAERUS-GEO algorithm. Atmos. Sci. Lett. 25, e1199. doi:10.1002/asl.1199

CrossRef Full Text | Google Scholar

Han, H., Feng, Z., Du, W., Guo, S., Wang, P., Xu, T., et al. (2024). Remote sensing image classification based on multi-spectral cross-sensor super-resolution combined with texture features: a case study in the Liaohe planting area. IEEE Access 12, 16830–16843. doi:10.1109/access.2024.3358812

CrossRef Full Text | Google Scholar

Han, Y., Kim, J., Lee, J., Nah, J. H., Ho, Y. S., and Park, W. C. (2024). Efficient haze removal from a single image using a DCP-based lightweight U-Net neural network model. Sensors 24, 3746. doi:10.3390/s24123746

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, S. Q., Li, D., Zhao, W. W., and Liu, Y. (2019). Haze removal algorithm for optical remote sensing image based on multi-scale model and histogram characteristic. IEEE Access 7, 104179–104196. doi:10.1109/ACCESS.2019.2929591.8

CrossRef Full Text | Google Scholar

Jiang, B., Chen, G., Wang, J., Ma, H., Wang, L., Chen, X., et al. (2021). Deep dehazing network for remote sensing image with non-uniform haze. Remote Sens. 13, 4443. doi:10.3390/rs13214443

CrossRef Full Text | Google Scholar

Krishnaraj, V., and Palanisamy, J. (2024). Analyzing the impact of climate data using geospatial techniques on land use and land cover changes in the Kaveri River Basin, Manmangalam Taluk, Karur District, Tamil Nadu. Water Air Soil Pollut. 235 (3), 168. doi:10.1007/s11270-024-06963-3

CrossRef Full Text | Google Scholar

Lei, L., Cai, Z., and Fan, Y. L. (2024). Single image dehazing enhancement based on retinal mechanism. Multimed. Tools Appl. 83, 61083–61101. doi:10.1007/s11042-023-17935-w

CrossRef Full Text | Google Scholar

Li, J. (2023). Enhanced edge-perceptual guided image filtering. IEEE Trans. Image Process. 32, 1234–1245. doi:10.48550/arXiv.2310.10387

CrossRef Full Text | Google Scholar

Li, Y., Li, Z., Zheng, C., and Wu, S. (2022). Adaptive weighted guided image filtering for depth enhancement in shape-from-focus. IEEE Trans. Image Process. 31, 567–578. doi:10.1016/j.patcog.2022.108900

CrossRef Full Text | Google Scholar

Li, Z., Xiao, X., and Zhang, N. (2024). IDACC: image dehazing avoiding color cast using a novel atmospheric scattering model. IEEE Access 12, 70160–70169. doi:10.1109/access.2024.3402084

CrossRef Full Text | Google Scholar

Liang, Y., Ding, F., Liu, L., Hao, F., Kang, T., Zhao, C., et al. (2025). Monitoring water quality parameters in urban rivers using multi-source data and machine learning approach. J. Hydrol. 648, 132394–132415. doi:10.1016/j.jhydrol.2024.132394

CrossRef Full Text | Google Scholar

Liu, B., Li, B., Sreeram, V., and Li, S. (2024). MBT-UNet: multi-branch transform combined with UNet for semantic segmentation of remote sensing images. Remote Sens. 16, 2776. doi:10.3390/rs16152776

CrossRef Full Text | Google Scholar

Lu Q, Q., Li, C., and Yin, L. (2024). Multi-path parallel enhancement of low-light images based on multiscale spatially aware Retinex decomposition. Expert Syst. Appl. 252 (Part B), 124301. doi:10.1016/j.eswa.2024.124301

CrossRef Full Text | Google Scholar

Lu S, S., Liu, F., Ye, Y., Tang, J., Li, P., Lin, W., et al. (2024). Analysis of the spatio-temporal characteristics of winter surface urban heat island: a case study in Beijing, China. J. Earth Sci. 35, 1640–1653. doi:10.1007/s12583-023-1880-9

CrossRef Full Text | Google Scholar

Mirzaee, S., Nafchi, A., Mirzakhani Ostovari, Y., Seifi, M., Ghorbani-Dashtaki, S., Khodaverdiloo, H., et al. (2024). Monitoring and assessment of spatiotemporal soil salinization in the Lake Urmia region. Environ. Monit. Assess. 196 (10), 958–1019. doi:10.1007/s10661-024-13055-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Motiee, S., Motiee, H., Ahmadi, A., and Azadeh, A. (2024). Analysis of rapid snow and ice cover loss in mountain glaciers of arid and semi-arid regions using remote sensing data. J. Arid. Environ. 222, 105153–105210. doi:10.1016/j.jaridenv.2024.105153

CrossRef Full Text | Google Scholar

Mu, P., Du, Z., Liu, J., and Bai, C. (2024). Little strokes fell great oaks: boosting the hierarchical features for multi-exposure image fusion. Proc. IEEE/CVF Int. Conf. Comput. Vis., 5678–5687. doi:10.48550/arXiv.2404.06033

CrossRef Full Text | Google Scholar

Okamoto, R., Ide, R., Oguma, H., and Hiroyuki, S. (2024). Automatically drawing vegetation classification maps using digital time-lapse cameras in alpine ecosystems. Remote Sens. Ecol. Conserv. 10, 188–202. doi:10.1002/rse2.364

CrossRef Full Text | Google Scholar

Peng, Y., Wang, H., Hou, M., Jiang, T., Zhang, M., Zhao, T., et al. (2020). Improved method of visibility parameterization focusing on high humidity and aerosol concentrations during fog-haze events: application in the GRAPES_CAUCE model in Jing-Jin-Ji, China. Atmos. Environ. 222, 117139–118000. doi:10.1016/j.atmosenv.2019.117139

CrossRef Full Text | Google Scholar

Qiao, B., Leng, Z., Mao, S., Wang, Q., and Liu, H. (2023). Remote sensing-based assessment of soil and water pollution in deep excavation scenario. J. Biobased Mat. Bioenergy. 17, 460–468. doi:10.1166/jbmb.2023.2289

CrossRef Full Text | Google Scholar

Saini, P., and Nagpal, B. (2024). PSO-CNN-Bi-LSTM: a hybrid optimization-enabled deep learning model for smart farming. Environ. Model. Assess. 29 (3), 517–534. doi:10.1007/s10666-023-09920-2

CrossRef Full Text | Google Scholar

Shen, Q., Gao, G., Duan, Y., and Chen, L. (2024). Long-term continuous changes of vegetation cover in desert oasis of a hyper-arid endorheic basin with LandTrendr algorithm. Ecol. Indic. 166, 112418–112512. doi:10.1016/j.ecolind.2024.112418

CrossRef Full Text | Google Scholar

Singh, J., Mandal, L., Pathak, B., Narayanamurthy, C. S., and Ganesan, A. R. (2024). Anisoplanatic effects on wave propagation through dynamic pseudo-random phase plate mimicking atmospheric turbulence. Opt. Commun. 557, 130360–130368. doi:10.1016/j.optcom.2024.130360

CrossRef Full Text | Google Scholar

Shen, H. F., Zhang, C., Li, H. F., Yuan, Q., and Zhang, L. P. (2020). A spatial-spectral adaptive haze removal method for visible remote sensing images. IEEE Trans. Geosci. Remote Sens. 58 (9), 6168–6180. doi:10.1109/TGRS.2020.2974807

CrossRef Full Text | Google Scholar

Soleimany, A., Grubliauskas, R., and Sereviciene, V. (2021). Application of satellite data and GIS services for studying air pollutants in Lithuania (case study: kaunas city). Health 14, 411–429. doi:10.1007/s11869-020-00946-z

CrossRef Full Text | Google Scholar

Sun, F. X., Wang, S. F., Zhao, G., and Chen, M. X. (2021). Single-image dehazing based on dark channel prior and fast weighted guided filtering. J. Electron. Imaging 30 (2), 021005–021005. doi:10.1117/1.JEI.30.2.021005

CrossRef Full Text | Google Scholar

Suo, H., Guan, J., Ma, M., Huo, Y., Cheng, Y., Wei, N., et al. (2023). Dynamic dark channel prior dehazing with polarization. Appl. Sci. 13, 10475. doi:10.3390/app131810475

CrossRef Full Text | Google Scholar

Wang, R., and Yang, Y. (2022). A dehazing algorithm based on transform domain and adaptive gamma correction. Comput. Eng. Sci. 44 (9), 1630–1637. doi:10.3969/j.issn.1007-130X.2022.09.013

CrossRef Full Text | Google Scholar

Wang D, D., Tang, B. H., and Li, Z. L. (2024). Evaluation of five atmospheric correction algorithms for multispectral remote sensing data over plateau lake. Ecol. Inf. 82, 102666. doi:10.1016/j.ecoinf.2024.102666

CrossRef Full Text | Google Scholar

Wang J, J., Wu, Y., Zhang, Y., Wang, H., Yan, H., Jin, J., et al. (2024). A genetic algorithm-optimized backpropagation neural network model for predicting soil moisture content using spectral data. J. Soils Sediments 24, 2816–2828. doi:10.1007/s11368-024-03792-z

CrossRef Full Text | Google Scholar

Wei, H., Gao, K., Wang, J., Tang, Q., Tang, X., and Xu, F. (2024). Optical imaging degradation simulation and transformer-based image restoration for remote sensing. IEEE Geosci. Remote Sens. Lett. 21, 1–5. doi:10.1109/lgrs.2024.3381581

CrossRef Full Text | Google Scholar

Wu, T., Eising, C., Glavin, M., and Jones, E. (2024). An efficient and effective image decolorization algorithm based on cumulative distribution function. J. Imaging. 10 (3), 51. doi:10.3390/jimaging10030051

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, W., and Cui, L. (2024). Image dehaze algorithm based on improved atmospheric scattering models. IEEE Access 12, 98971–98976. doi:10.1109/access.2024.3428568

CrossRef Full Text | Google Scholar

Zhang, X., Cui, J., Wang, W., and Lin, C. (2017). A study for texture feature extraction of high-resolution satellite images based on a direction measure and gray level co-occurrence matrix fusion algorithm. Sensors 17 (7), 1474. doi:10.3390/s17071474

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Wang, Y., Yuan, C., and Zhuang, Z. (2024). Study on visibility forecast optimization based on aerosol-meteorological feedbacks in wet conditions. Urban Clim. 55, 101951. doi:10.1016/j.uclim.2024.101951

CrossRef Full Text | Google Scholar

Zhang, Y. J., Zhong, J. P., Liu, Z. G., and Han, Z. W. (2023). ECF-STPM: a robust crack detection method for railway catenary components. IEEE Trans. Instrum. Meas. 72, 1–14. doi:10.1109/tim.2023.3307181

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, Z., Yu, J., Zhang, X., and Du, S. (2024). Development of a 30 m resolution global sand dune/sheet classification map (GSDS30) using multi-source remote sensing data. Remote Sens. Environ. 302, 113973–114016. doi:10.1016/j.rse.2023.113973

CrossRef Full Text | Google Scholar

Zhu, Q., Mai, J., and Shao, L. (2015). A fast single image haze removal algorithm using color attenuation prior. IEEE Trans. Image Process. 24, 3522–3533. doi:10.1109/TIP.2015.2446191

PubMed Abstract | CrossRef Full Text | Google Scholar