Advancing terrestrial snow depth monitoring with machine learning and L-band InSAR data: a case study using NASA’s SnowEx 2017 data

Current terrestrial snow depth mapping from space faces challenges in spatial coverage, revisit frequency, and cost. Airborne lidar, although precise, incurs high costs and has limited geographical coverage, thereby necessitating the exploration of alternative, cost-effective methodologies for snow depth estimation. The forthcoming NASA-ISRO Synthetic Aperture Radar (NISAR) mission, with its 12-day global revisit cycle and 1.25 GHz L-band frequency, introduces a promising avenue for cost-effective, large-scale snow depth and snow water equivalent (SWE) estimation using L-band Interferometric SAR (InSAR) capabilities. This study demonstrates InSAR’s potential for snow depth estimation via machine learning. Using 3 m resolution L-band InSAR products over Grand Mesa, Colorado, we compared the performance of three machine learning approaches (XGBoost, ExtraTrees, and Neural Networks) across open, vegetated, and the combined (open + vegetated) datasets using Root Mean Square Error (RMSE), Mean Bias Error (MBE), and R² metrics. XGBoost emerged as the superior model, with RMSE values of 9.85 cm, 10.46 cm, and 9.88 cm for open, vegetated, and combined regions, respectively. Validation against in situ snow depth measurements resulted in an RMSE of approximately 16 cm, similar to in situ validation of the airborne lidar. Our findings indicate that L-band InSAR, with its ability to penetrate clouds and cover extensive areas, coupled with machine learning, holds promise for enhancing snow depth estimation. This approach, especially with the upcoming NISAR launch, may enable high-resolution (∼10 m) snow depth mapping over extensive areas, provided suitable training data are available, offering a cost-effective approach for snow monitoring. The code and data used in this work are available at https://github.com/cryogars/uavsar-lidar-ml-project.

1 Introduction

Accurately measuring snow depth is critical for applications in hydrologic science, water resource management, and climate modeling (Lievens et al., 2022). Seasonal snowpacks act as natural reservoirs, storing winter precipitation and gradually releasing meltwater in spring and summer as the temperature rises (Simpkins, 2018; Livneh and Badger, 2020; Vano, 2020; Lievens et al., 2022). Tracking snow accumulation and melt is instrumental in understanding how snowpack storage affects water resources. For instance, in California, the Sierra Nevada seasonal snowpack contributes approximately 70% of additional water storage to supplement the existing artificial reservoir system (Dettinger and Anderson, 2015; Hedrick et al., 2018; Henn et al., 2020). However, monitoring snow depth, especially on a large scale, is fraught with challenges. The diverse and rugged terrain of mountainous regions makes it particularly difficult (Deems et al., 2006).

Traditionally, snow depth monitoring has relied on in situ measurements and airborne observations (Deems et al., 2013; Marshall et al., 2015; Dong, 2018; Webb et al., 2021). However, these methods are often limited by geographical reach, temporal frequency, and financial resources. In situ measurements are known for their accuracy and reliability, as they are often conducted manually using instruments such as snow probes, snow coring, or through automated snow telemetry stations (SNOTEL) (Serreze et al., 1999). However, access to mountainous regions can be difficult during winter when snow monitoring is essential. Additionally, the resources required for frequent and widespread in situ measurements, including financial and human capital, can be prohibitively high (Deems et al., 2013). Moreover, in situ measurements have limited support (i.e.,; representativeness) and cannot fully resolve the spatial heterogeneity of snowpack properties (e.g.,; snow depth, snow water equivalent (SWE), and snow density) across a landscape (Trujillo and Lehning, 2015; Bühler et al., 2016), as snow has a spatial autocorrelation length on the order of 100 m [e.g.,; Trujillo et al. (2009)].

Remote sensing technologies such as Light Detection and Ranging (lidar) provide high-precision snow depth estimates, but the high cost limits comprehensive monitoring (Deems et al., 2013). Airborne lidar and structure-from-motion (i.e.,; photogrammetry using aerial photography) deliver detailed snow depth maps but are geographically limited (Harder et al., 2020; Meyer et al., 2022). Satellite passive microwave sensors estimate basin average SWE yet suffer from coarse resolution (∼25 km) and saturate at 150 mm SWE, preventing application in mountainous areas (Chen and Wang, 2018; Taheri and Mohammadian, 2022). Optical remote sensing is weather-dependent and unable to penetrate dense forest cover (Sinha et al., 2015; Aquino et al., 2021). Additionally, while initiatives like the Airborne Snow Observatory (ASO) are making strides towards the broader use of lidar for snow mapping, snow depth data is primarily collected in the western United States (US) (Ferraz et al., 2018), leaving a significant geographical gap in global snow monitoring. Consequently, the development of new spaceborne capabilities to map snow depth continues to be an active area of research.

Amid the limitations of traditional snow monitoring methods and the challenges of lidar acquisition on a global scale, the pursuit of alternative remote sensing technologies is imperative. The forthcoming NASA-ISRO (NASA-Indian Space Research Organization) Synthetic Aperture Radar (NISAR) mission, scheduled for launch in March 2025, appears promising in this regard. NISAR, equipped with an L-band radar, is set to observe nearly all of Earth’s terrestrial and ice surfaces at an approximate resolution of 10 m, with a revisit frequency of twice every 12 days (Kellogg et al., 2020; LAL et al., 2022). Operating within the 1–2 GHz frequency range (L-band) with wavelengths between 15 and 30 cm, it can penetrate cloud cover and 10+ meters of snow, facilitating all-weather, day-night snow monitoring in a wide range of conditions.

Guneriussen et al. (2001) first developed a theoretical framework describing the relationship between the InSAR phase and changes in SWE under dry snow conditions. They demonstrated the sensitivity of InSAR phase to SWE changes but highlighted challenges such as phase wrapping errors and temporal decorrelation when using C-band frequencies due to their short wavelengths. To mitigate these issues, the authors suggested exploring L-band frequencies, which have longer wavelengths, to improve SWE estimation. Leinss et al. (2015) extended the work of Guneriussen et al. (2001) by deriving a linear relationship between phase delay and changes in SWE that is less sensitive to temporal decorrelation and phase wrapping errors. Their approach is optimized to determine changes in SWE from a time series of differential interferograms and depends minimally on snow density and stratigraphy. Deeb et al. (2011) investigated the use of InSAR to generate time-series SWE maps in the Kuparuk watershed of Alaska using C-band ERS-1 data. They demonstrated that InSAR-derived SWE maps captured spatial patterns of snow redistribution and emphasized the potential of L-band data (e.g., PALSAR on the Advanced Land Observing Satellite) for operational SWE retrieval due to its longer wavelength advantage.

Further advancements have leveraged dual-polarimetric data for snow depth estimation. Varade et al. (2020) improved snow depth estimates in mountainous regions of Dhundi using dual-polarimetric Sentinel-1 data with bias correction techniques. They enhanced snow depth estimation accuracy by combining VV and VH polarization data and applying bias corrections based on snow-free areas. Mahmoodzada et al. (2020) extended the work of Varade et al. (2020) by addressing snow volume scattering effects within the DInSAR displacement framework rather than through snow phase corrections. Feng et al. (2024) introduced a dual-polarimetric radar snow depth estimation framework using Sentinel-1 data in the Scandinavian Mountains. Their method, based on the dual-polarimetric radar vegetation index, outperformed existing techniques, achieving a 26.9% improvement in the coefficient of determination compared to the cross-polarization ratio method and a 20% reduction in the mean absolute error. Palomaki and Sproles (2023) assessed L-band InSAR snow estimation techniques over shallow and heterogeneous prairie snowpacks in Montana, United States. While they found that L-band InSAR is sensitive to differences in snow cover, they noted challenges in accurately estimating SWE due to sub-pixel snow depth variability and recommended further refinement of InSAR-based techniques for such environments.

During 2017–2021, the NASA SnowEx Mission performed repeat InSAR surveys with UAVSAR, with initial physics-based retrievals showing promise (Marshall et al., 2021). A recent study by Hoppinen et al. (2023) employing repeat pass InSAR for monitoring SWE over Idaho found strong correlations between retrieved SWE changes from SAR images and both in situ and modeled results. Tarricone et al. (2023) used repeat-pass L-band InSAR to estimate SWE changes in an environment with both snow accumulation and ablation, showcasing the capability of L-band InSAR for tracking SWE changes. Studies have also shown promise in retrieving snow depth information from InSAR coherence, phase, and incidence angle data. Li et al. (2017) used repeat-pass InSAR measurements for estimating snow depth and SWE in the Northern Piedmont Region of the Tianshan Mountains and found the snow depth estimation to be consistent with field measurements. With the promising capabilities of InSAR, the NISAR mission may be able to provide high-resolution (∼10–50 m) snow depth estimates over large areas if appropriate snow depth observations are available for training machine learning models. While physics-based retrievals have shown promise, machine learning techniques can be advantageous as they often require fewer assumptions about snow conditions, such as whether the snow is dry or wet, and can be effective in scenarios where traditional inversion methods may be limited by data availability.

Our goal in this work is to use a pair of repeat-pass L-band InSAR products from the 2017 NASA SnowEx campaign on Grand Mesa to estimate total snow depth (e.g.,; bulk snowpack depth to the ground) using Machine Learning algorithms. While previous work has focused on physics-based retrievals, in 2017, we only had one lidar flight measuring total snow depth, and therefore, physics-based inversion is not possible. While InSAR is inherently more related to changes in snow depth rather than total snow depth, snow accumulation patterns tend to exhibit consistency. As such, snow depth before the onset of melt displays similar patterns to snow depth changes (Mason, 2020). Snow distribution patterns have been shown to exhibit intra- and inter-seasonal consistency despite differences in weather patterns and seasonal snowfall amounts (Deems et al., 2008; Sturm and Wagner, 2010; Schirmer and Lehning, 2011; Pflug and Lundquist, 2020). While the actual snow depths may change, the locations of deeper and shallower snow areas generally tend to be consistent.

Since the 1990s, machine learning algorithms have gained prominence in environmental remote sensing (Reichstein et al., 2019; Zhang et al., 2019; Yuan et al., 2020) and, over time, have proliferated across various application areas such as snow depth retrieval (Tedesco et al., 2004; Wang et al., 2019; King et al., 2022a; Ofekeze et al., 2022; Ofekeze et al., 2023; Alabi et al., 2023), snow density (Alabi et al., 2022; Feng et al., 2022), and SWE (Bair et al., 2018; Broxton et al., 2019) predictions. Hu et al. (2021) conducted a study using machine learning algorithms to fuse gridded snow depth datasets with inputs including geolocation, topography, and in situ observations. The Random Forest algorithm proved to be the most proficient of the three learning machines tested. Liang et al. (2015) applied the Support Vector Machine (SVM) to estimate snow depth in northern Xinjiang using data from visible and infrared surface reflectance, brightness temperature, and auxiliary information. The SVM method outperformed the Artificial Neural Networks (ANN) utilized in Finland (Tedesco et al., 2004). King et al. (2022a) utilized a random forest model trained on vertical radar reflectivity profiles from the VertiX X-band radar instrument in Egbert, Ontario, and atmospheric temperature estimates from the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis version 5 (ERA-5) for snow accumulation predictions resulting in a mean square error (MSE) of ∼1.8 × 10⁻³ mm² when compared to collocated in situ measurements.

These works and others have highlighted the potential of machine learning in producing improved snow depth predictions. However, a common limitation across many of these studies is the constrained spatial coverage of validation datasets, which can be attributed to the scarcity of global snow depth data and the prohibitive costs associated with acquiring lidar data globally. This study aims to develop a snow depth prediction system using L-band InSAR (which can be deployed over large areas) products and ML algorithms. Specifically, we will compare the performance of three machine learning algorithms: eXtreme Gradient Boosting (XGBoost) (Chen and Guestrin, 2016), Extremely Randomized Tress (ExtraTrees) (Geurts et al., 2006), and Artificial Neural Networks (ANN). We will also investigate the impact of vegetation on snow depth prediction accuracy.

The objective of this work is divided into three broad aspects:

1. To test the effectiveness of L-band InSAR products in estimating total snow depth using ML algorithms,

2. To analyze the effect of vegetation on the performance of the ML models, and

3. To understand the relative importance of each input feature in snow depth estimation.

The study area is stratified into open areas and vegetated areas, using a 0.5 m threshold on lidar vegetation height observations, to evaluate the impact of vegetation on model performance. Machine learning algorithms can be used to extract snow depth information from L-band InSAR data in a robust and efficient manner.

We believe that our research has the potential to complement existing snow monitoring practices by facilitating cost-effective, high-resolution, and extensive snow depth estimation. Our findings could lead to the development of a global snow depth prediction system that provides valuable information for water resource management, flood forecasting, and avalanche hazard assessment, provided that accurate and representative training data is available.

2 Materials and methods

2.1 Study area

This study was conducted on Grand Mesa, a flat-topped mesa in Western Colorado, United States (39.1°N, 107.9°W). Grand Mesa is one of the largest flat-topped mesas in the world (Chesnutt et al., 2017; Gatebe et al., 2018), with elevations from 2,000 to 3,400 m above sea level (Kulakowski et al., 2004). The climate is continental (Kulakowski et al., 2004), with the coldest, warmest, and windiest months being January, July, and June, respectively (Time and Date website, 2024: https://www.timeanddate.com/weather/@5423575/climate).

2.2 Data

The data for our study was sourced from NASA’s 2017 SnowEx campaign (Kim et al., 2017). The 2017 campaign aimed to evaluate the sensitivity of snow remote sensing techniques through a gradient of forest densities (NSIDC: https://nsidc.org/data/snowex). This campaign was primarily conducted in two locations in Colorado, United States: Grand Mesa and Senator Beck Basin. Our focus is on Grand Mesa (Figure 1). SnowEx datasets are publicly available through the National Snow and Ice Data Center (NSIDC: https://nsidc.org/data/snowex).

Figure 1

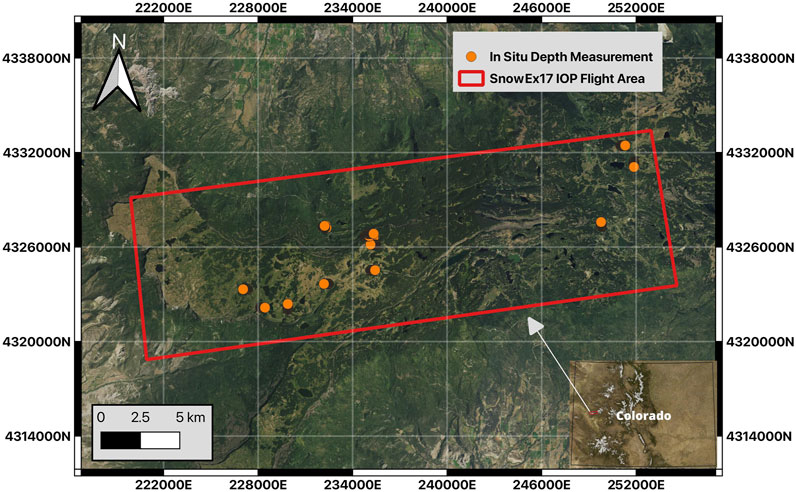
Figure 1. Study Site: Grans Mesa, Colorado. The large red rectangle outlines a 9.25 × 32 km target area that was imaged by all airborne sensors during the 2012 SnowEx Intense Observation Period (IOP). Orange circles indicate in situ depth measurement locations collected on February 8. While the orange circles may appear to overlap due to the map scale (in kilometers), the actual measurement points are spaced 3 m apart. The inset map shows the location of Grand Mesa within Colorado, United States. The natural gradient of Snow Water Equivalent (SWE) increases from west to east, and the forest cover also naturally varies across the region (Kim et al., 2017).

The 2017 SnowEx campaign spanned from September 2016 to July 2017, with the Intense Observation Period (IOP) taking place between February 6 and 25 February 2017 (Brucker et al., 2017). During this period, a multitude of measurements were collected, including data from cloud-absorption radar, ground-penetrating radar, synthetic aperture radar, lidar, airborne video, Global Navigation Satellite Systems (GNSS) measurements, and snow pit measurements (Brucker et al., 2017; Kim et al., 2017). In this study, we focus on the L-band InSAR products (phase change, coherence, amplitude, incidence angle) and high-resolution airborne lidar data collected during the campaign (snow depth, bare ground elevation, vegetation height). Our study site within Grand Mesa spans approximately 70 km², and all data used in this study has a resolution of 3 m, which was the resolution of the airborne lidar. The InSAR products were resampled to have the same resolution and align with the lidar raster. The details of each data type’s collection and use are outlined in the following sections.

2.2.1 Lidar snow depth measurements

Lidar, an acronym for Light Detection and Ranging (Brucker et al., 2017; King et al., 2022b), is a remote sensing method that uses the travel time of a laser pulse to measure distances (Killinger, 2014; Revuelto et al., 2014). The lidar data used in this study was collected by the NASA Airborne Snow Observatory (ASO) as part of the 2017 SnowEx campaign on two dates: 20 September 2016, and 8 February 2017. The September 20 flight was a “snow-free” flight, which means that the lidar data was collected before any snow had fallen on the ground. The February 8 flight was a “snow-on” flight, which means that the lidar data was collected when a snowpack had developed on the ground. The initial gridded ASO lidar product has a spatial resolution of 3 m and a vertical accuracy characterized by a root mean square difference of 8 cm when compared to near-coincident median values from 52 snow-probe transects (Currier et al., 2019). Snow depths were then calculated by differencing the two DEMs (snow-on minus snow-off). In addition to snow depth, bare ground elevation and vegetation height to the top of the canopy at matching 3-m resolution were produced from the lidar data (Figure 2).

Figure 2

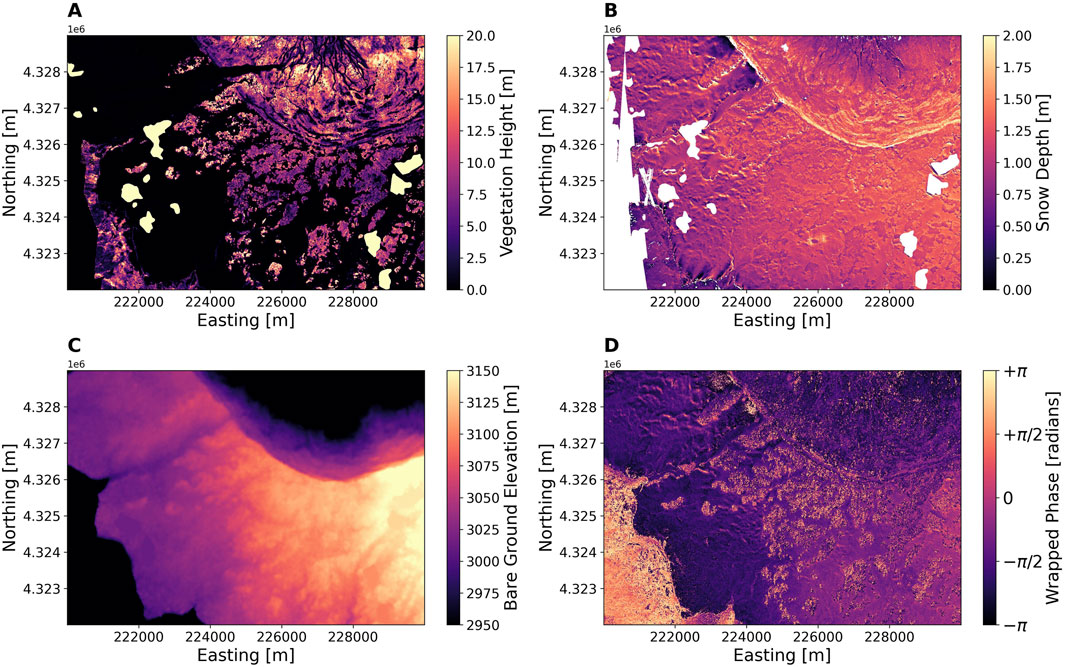
Figure 2. Lidar-derived products (UTM Zone 13) (A–C) from the study site. (A) Vegetation height with a color range from 0 to 20 m, (B) Snow depth with a color range from 0 to 2 m. (C) Bare ground elevations with a color range spanning approximately 2,950–3,150 m. (D) L-Band InSAR Wrapped Phase (UTM Zone 13) with a color scale ranging from -π to +π radians.

For this work, we divided the data into three categories based on vegetation:

• Open areas: areas with no vegetation or vegetation heights <0.5 m.

• Vegetated areas: areas with vegetation height≥0.5 m

• Combined dataset: a combination of both open and vegetated areas.

The resulting training dataset contains 3.174 × 10⁶ (48% of the total samples), 2.166 × 10⁶ (32% of the total samples), and 5.341 × 10⁶ (80% of the total samples) 3-m resolution snow depths for open areas, vegetated areas, and a combination of both, respectively (Table 1). In this work, we used 80% of the data for training the model, 10% for tuning hyperparameters, and 10% for testing. In machine learning, the splitting percentage depends on the size of the dataset. Studies have shown that an 80/10/10 split is appropriate for datasets containing more than 1 million samples (Muraina, 2022). Table 1 shows the snow depth statistics for each category in the training data. The mean snow depth is approximately 1.06 m in open areas, which is slightly lower than that of the vegetated areas at 1.10 m. The range of snow depth across all areas is from 0 m to a maximum of 3 m.

Table 1

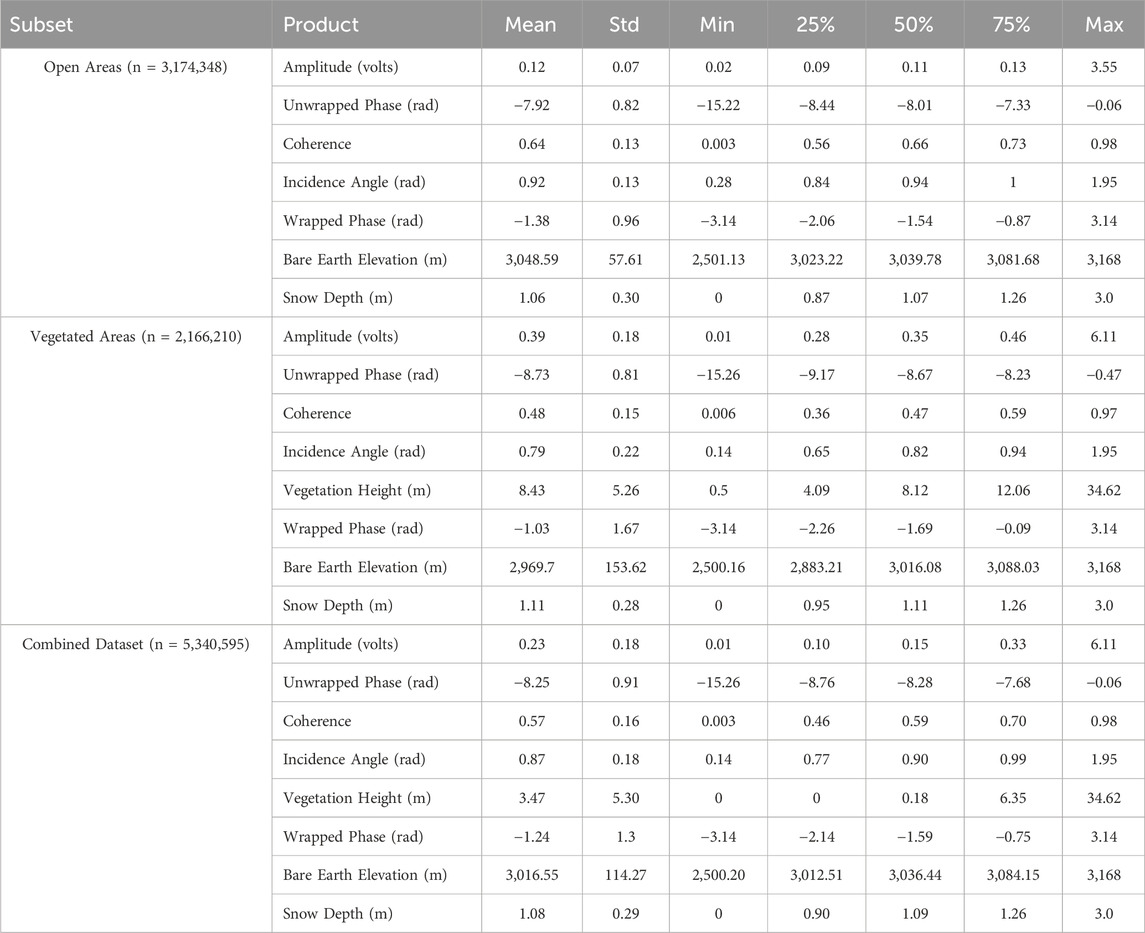
Table 1. Summary Statistics of L-band InSAR products, lidar snow depths, bare ground elevation, and vegetation height (all at 3 m resolution) in the training set. The table provides the count, mean, standard deviation (Std), minimum (Min), 25th percentile (25%), median (50%), 75th percentile (75%), and maximum (Max) values for each product within open, vegetated, and the combined dataset (open + vegetated). Units are included for variables where applicable; coherence is unitless.

2.2.2 L-band InSAR products

Interferometric Synthetic Aperture Radar (InSAR) is a radar technique that calculates changes in the distance between the radar antenna and the ground surface by comparing the phase difference of two or more radar images (Lu et al., 2007). Repeat-pass InSAR uses two or more InSAR images of the same scene taken at different times to generate an interferogram, which measures the phase shift between the image acquisitions. InSAR can be used to measure a variety of surface changes, including deformation, subsidence, and ice sheet movement. More recently, repeat-pass InSAR has been used to measure SWE changes (Tarricone et al., 2023).

The L-band InSAR frequency range is 1–2 GHz, corresponding to a wavelength range of 15–30 cm (Ulaby et al., 1981). These longer wavelengths allow L-band signals to penetrate clouds and penetrate deeper into dry snow and vegetation canopies compared to higher-frequency bands like C- or X-band. Generally, radar waves with longer wavelengths experience less backscatter and attenuation than shorter wavelengths (Awasthi and Varade, 2021). For dry snow, radar backscatter primarily originates from the snow–soil interface, as dry snow has low attenuation of radar signals at frequencies below 10 GHz (Marshall et al., 2005; Tarricone et al., 2023). As the radar wave propagates through the snow layer, it undergoes refraction (change in the radar propagation direction) and slows down due to the dielectric properties of snow, which differ from those of the atmosphere. This refraction and reduction in wave speed are governed by the refractive index of snow, which is a function of snow density for dry snow. The refraction results in a phase shift relative to radar signals when less snow is present. The phase difference between two InSAR acquisitions can be used to estimate changes in snow depth and SWE. L-band SAR signals are also less affected by snowfall and atmospheric conditions (e.g., water vapor) due to their longer wavelength, which reduces scattering and attenuation effects compared to shorter wavelengths like C- or X-band (Ulaby et al., 1981). This makes L-band InSAR data more reliable under varying weather conditions.

As part of the 2017 SnowEx campaign, the NASA Jet Propulsion Laboratory (JPL) flew the L-Band UAVSAR sensor over Grand Mesa in February and March. A total of five flights were conducted on February 6, 22, 25, and March 8 and 31. For this work, we used the pair of flights closest to the lidar acquisition. Since the lidar was acquired on February 8, we used the HH polarization for February 6 and 22 as the InSAR features for our ML models. We analyzed both HH and VV polarizations to determine which provided higher coherence over our study area. Our analysis showed that HH polarization provided higher median coherence. In InSAR, higher coherence indicates greater confidence in the phase information, which implies a more accurate retrieval. UAVSAR products come at a native resolution of 2 m. However, we resampled the UAVSAR features to 3 m to match the lidar resolution.

The following L-band InSAR products, all of which are resampled to 3-m resolution, were used in this study: coherence (CO), local incidence angle (IA), amplitude (AM), wrapped phase (WP), and unwrapped phase (UW). For a detailed description of these products and InSAR methodologies in general, refer to Ulaby et al. (1981), Awasthi and Varade (2021), Marshall et al. (2021), Hoppinen et al. (2023), and Tarricone et al. (2023).

To use InSAR for estimating total snow depth, we assume that the total snow depth patterns before melt starts within a season are relatively consistent (Sturm and Wagner, 2010), with the patterns of snow depth change detected by the InSAR instrument being representative of the distribution of total snow depth. This assumption is generally valid, but there are instances and locations where this may not be the case, depending on weather patterns, landscape and vegetation changes, and other processes affecting snow distribution. L-band InSAR data will be available from the NISAR mission at a 12-day temporal resolution, which has the potential to complement existing snow depth measurement practices. In addition, with a continuously operating InSAR, 12-day snow depth/SWE changes can be summed to estimate total depth (Oveisgharan et al., 2024). The InSAR products used in this work are shown in Figure 3, and their summary statistics are included in Table 1.

Figure 3

Figure 3. L-band InSAR products from the study site (UTM Zone 13): (A) Incidence angles with values from 0.5 to 1.5 radians, (B) Coherence metrics with values from 0.50 to 0.80, (C) Amplitudes with signal intensities between 0.0 and 0.5 V, and (D) Unwrapped Phase with phase shift values from ∼ −11 to −6 radians.

2.3 Methods

Our methodology for estimating snow depth from InSAR products using machine learning models comprised several key steps, which are outlined below.

2.3.1 Data preprocessing

Data preprocessing was the foundational step in our methodology, preparing the dataset for compatibility with our Machine Learning algorithms. The raw remote sensing data spanned numerous raster layers at a 3-m resolution. Each raster layer represents approximately a 7 km × 10 km area on the ground, with each pixel representing an average value over a 3 m × 3 m area. We first restructured the raster into pixel-wise tabular data frames to enable vector-based preprocessing. After concatenating all variables, we inspected for noise and outliers that could potentially affect the models’ learning.

Noise in the data was identified through pixel values coded as −9,999, which are standard no-data flags, and these values were dropped from the analyses. Outliers were defined based on the physical plausibility of measurements, with snow depth values greater than 3 m classified as outliers. This threshold was chosen after inspecting the in situ snow depth distribution for the day (February 8), which showed a maximum snow depth of 3 m. Extreme values (e.g., snow depths of 13 m) were unrealistic and likely due to errors such as the lidar laser hitting the top of vegetation during the snow-on flight.

No missing value imputation was done as we have an abundance of data points (∼6.7 million observations after data cleaning). Imputation is a process where missing data points are filled in using various statistical methods, which can sometimes introduce uncertainties. By avoiding imputation, we maintained dataset integrity. These data cleaning steps resulted in a dataset of 6,675,745 usable observations.

After data cleaning, we randomly split our data into three disjoint subsets:

• Training Set: 80% of the data was used for training the models.

• Tuning Set: 10% of the data was used for hyperparameter tuning to optimize model performance and to prevent overfitting during model training. Hyperparameter tuning involves adjusting the parameters of the learning algorithm itself to find the best configuration. This process can help improve predictive accuracy and robustness. Overfitting occurs when a model learns the training data too well, capturing noise and details that do not generalize to new data. By using a tuning set, we can ensure the model generalizes well and performs effectively on unseen data. Note that using a tuning set for hyperparameter optimization is an alternative to cross-validation for large datasets.

• Testing Set: The remaining 10% of the data was used to test the models’ performance.

We have chosen random sampling to minimize sampling bias and ensure that the testing data is representative of the training data. Following the partitioning, all input features were converted into a common dimensionless scale with a mean of zero and a standard deviation of one using the z-score standardization approach following Equation 1. This will prevent potential domineering effects from variables with larger raw value ranges during model training. We have chosen the z-score standardization approach because it ensures outliers are handled more properly (Ozdemir, 2022). The normalized version of every observation $X_{i,j}$ in feature $X_j$ is obtained by:

$X_{i,j}^z=\frac{X_{i,j}-{\mu }_j}{{\sigma }_j}(1)$

where $X_{i,j}^z$ is the standardized value, ${\mu }_j$ and ${\sigma }_j$ are the mean and standard deviation of variable $X_j$ from the training set.

For each data stratum (open, vegetated, and their combination), we trained three models:

• Model 1: The first model uses only bare ground elevation as input, and this model serves as the baseline model in this work. Mathematically, we write:

$SD=f\left(BGE\right)(2)$

• Model 2: This model uses InSAR products and bare ground elevation as input features. The model is represented mathematically as follows:

$SD=f\left(CO,IA,BGE,WP,AM,UP\right)(3)$

• Model 3: This model combines the InSAR products, bare ground elevation, and vegetation height as features. This configuration is used to evaluate the effect of vegetation height on the model performance.

$SD=f\left(CO,IA,BGE,WP,AM,UP,VH\right)(4)$

where $f$ is the various learning algorithms compared, $VH$ is the vegetation height, BGE is the bare ground elevation, and $SD$ is the snow depth. Note that the open areas only have models 1 and 2 because, in the open areas, vegetation height is 0 or buried under the snow cover (<0.5 m).

2.3.2 Model selection and training

Once the data were appropriately prepared, we proceeded to the next phase: model selection and training. We trained and compared three machine learning algorithms: Extremely Randomized Trees (Extra Trees), eXtreme Gradient Boosting (XGBoost), and artificial neural networks (ANN). These models were chosen because they have been shown to perform well on a variety of remote sensing data (Maxwell et al., 2018; Meloche et al., 2022). For hyperparameter tuning, we used the Optuna framework (Akiba et al., 2019). Optuna is an open-source hyperparameter optimization framework in Python that is designed to optimize the hyperparameters for machine learning models. Unlike traditional grid search, Optuna utilizes a Tree-structured Parzen Estimator (TPE) algorithm (Bergstra et al., 2011; Bergstra et al., 2013), a Bayesian optimization algorithm, which tends to find optimal hyperparameters faster and with fewer function evaluations compared to grid search. This efficient search approach proved to be especially advantageous given the large dataset involved in our study. The details of the hyperparameters tuned for each model can be found in Supplementary Tables S1–S3 of the supplementary material, and the flowchart illustrating the step-by-step methodology of our model training can be found in Figure 4.

Figure 4

Figure 4. A flowchart illustrating the step-by-step methodology of our model training.

2.3.2.1 Extremely Randomized Trees

Extra Trees is an ensemble algorithm that averages predictions across a pre-defined number of randomized decision trees to improve accuracy and control overfitting. The “extra” in Extra Trees stands for extremely randomized, indicating that at each split in the learning process, the features and cut points are chosen in a random manner, hence reducing the variance of the model. Due to this extreme randomization, Extra Trees are faster than Random Forest and hence suitable for large datasets. Mathematically, the prediction ${\widehat{f}}_{EXT}\left(\mathit{x}\right)$ from an extra tree regressor can be expressed as Equation 5:

${\widehat{f}}_{EXT}\left(\mathit{x}\right)=\frac{1}{T}{\displaystyle \sum _{t=1}^T}{\widehat{f}}^t\left(\mathit{x}\right)(5)$

Where $T$ is the total number of trees in the ensemble and ${\widehat{f}}^t\left(\mathit{x}\right)$ is the prediction of the tth tree for the input vector $\mathit{x}$.

In our analysis, the optimal hyperparameters for the Extra Trees model were identified using Optuna. The optimal number of trees in the forest was found to be 150. The maximum depth of the trees was set to None, indicating that the nodes are expanded until they contain fewer than the minimum samples required to split, allowing the trees to grow to their full depth. Finally, the mean squared error (MSE) was used as the measure of split quality at each node. These hyperparameter settings were found to provide the best performance on the tuning set. The details of these hyperparameters can be found in Supplementary Table S1 of the supplementary material.

2.3.2.2 eXtreme Gradient Boosting

XGBoost is another ensemble algorithm, but unlike Extra Trees, it builds a sequence of decision trees instead of a forest of decision trees. XGBoost operates by sequentially constructing weak learners (decision trees), with each tree aiming to correct the errors made by the previous one. This process of sequential error correction is known as Boosting. At each iteration, a weak learner is trained to approximate the gradient of the loss function (the residual errors). Boosting is then achieved by iteratively updating the residual errors when a new learner is added to the ensemble. This methodology of leveraging the gradient of the loss function to guide the boosting process is known as Gradient Boosting. XGBoost uses a variant of the Gradient Boosting algorithm called Newton boosting, which attaches weights to the residuals through the Hessian (second-order derivative of the loss function). With this, observations with larger errors have more weight. XGBoost takes Newton boosting to the extreme by regularizing the loss functions and introducing efficient tree learning with parallelizable implementation. This “extreme” attribute of XGBoost makes it suitable for large datasets. Moreover, XGBoost can also benefit from GPU (CUDA support only) acceleration, making it suitable for large datasets.

In our analysis, the optimal hyperparameters for the XGBoost model were identified using Optuna, as detailed in Supplementary Table S2 of the supplementary material. The objective was set to minimize the MSE between the predicted and true snow depth values. We used a learning rate of 0.05 to control the step size at each iteration while moving toward a minimum of the loss function. The depth of the trees was set to grow unrestricted to allow the model to learn complex relationships in the data. A total of 1,000 trees were grown using a histogram-based training method to accelerate the training process.

2.3.2.3 Artificial neural network

Artificial Neural Network (ANN) is an ensemble of linked artificial neurons organized into input, hidden, and output layers. Each neuron receives inputs, performs mathematical operations on these inputs, and passes the output to the next layer. Every connection between nodes has an associated weight; the optimal weights are learned during training. The input layer holds the features, with one node per input feature, and the output layer holds the network’s prediction. The number of neurons in the hidden layers is determined through hyperparameter tuning. In this study, we employed a Feed-forward Neural Network (FNN), a type of ANN where connections between nodes do not form a cycle. Specifically, we chose the FNN because we converted our raster data into a data frame, and FNN is well-suited for tabular datasets.

We designed a five-layer FNN using the PyTorch framework for our analysis. The architecture comprises one input layer, three densely connected hidden layers with 2048, 1,500, and 1,000 nodes, respectively, and one output layer. Rectified Linear Unit (ReLU) activation functions were used in the hidden layers to introduce non-linearity, while a linear activation function was employed in the output layer for snow depth estimation. The model was trained using the Adam (Kingma and Ba, 2015) optimization algorithm with a learning rate of 0.0001 to minimize the Mean Squared Error Loss (MSELoss) between the predicted and lidar-derived snow depths. The training was conducted over 15 epochs with a batch size of 128. We terminated the training at 15 epochs because no substantial improvement was noticed after this point. The hyperparameters for the FNN model were optimized using Optuna, with the details of the tuned hyperparameters presented in Supplementary Table S3 of the supplementary material.

Model performance was evaluated using root mean squared error (RMSE), mean bias error (MBE), and coefficient of determination (R²). RMSE measures the average magnitude of the errors between the predicted and observed values, providing insight into the model’s overall accuracy. MBE assesses the average bias in the predictions, indicating whether the model systematically overestimates or underestimates the true values. R² measures how well the predicted values match the true values using a 1:1 line, with higher values indicating a better fit. RMSE has a lower bound of zero, with smaller values indicating better performance. MBE is unbounded and can be positive or negative, with values closer to zero in absolute value being preferable. Note that R², in this case, is not the square of the correlation coefficient; hence, it can be negative for a bad model.

2.4 Feature importance

To quantify the contribution of individual features to snow depth prediction, we employed two complementary methods: the gain metric from the XGBoost model and SHapley Additive exPlanations (SHAP) (Lundberg and Lee, 2017). The gain, derived from the XGBoost framework, measures the average contribution of each feature to reducing the mean squared error loss across all trees within the model. This method offers an initial insight into the relative importance of features based on their utility in constructing the predictive model. However, gain-based importance can be misleading for high cardinality (many unique values) features and may not fully capture the nuanced interactions between features. To address this, we also utilized SHAP values, which provide a more comprehensive and stable measure of feature importance by considering the contribution of each feature to every possible combination of features in the dataset (Man and Chan, 2021). SHAP originates from concepts in cooperative game theory, and it computes the importance of a feature by distributing the predictive contribution among features in a model, akin to dividing payoffs among collaborating players. Although SHAP analysis is computationally expensive, particularly for large datasets, its ability to offer clear and consistent interpretations of the features’ impact on the model’s output makes it a valuable tool for in-depth feature importance analysis.

3 Results

3.1 Snow depth estimation

Comparing the performance of Models 1 (Equation 2), 2 (Equation 3), and 3 (Equation 4) allowed us to evaluate the incremental value of remote sensing predictors for improving snow depth estimation beyond using bare ground elevation alone. Across most configurations and areas, XGBoost consistently outperformed other models (Table 2, Figure 5). Therefore, our discussion will focus on the XGBoost results.

Table 2

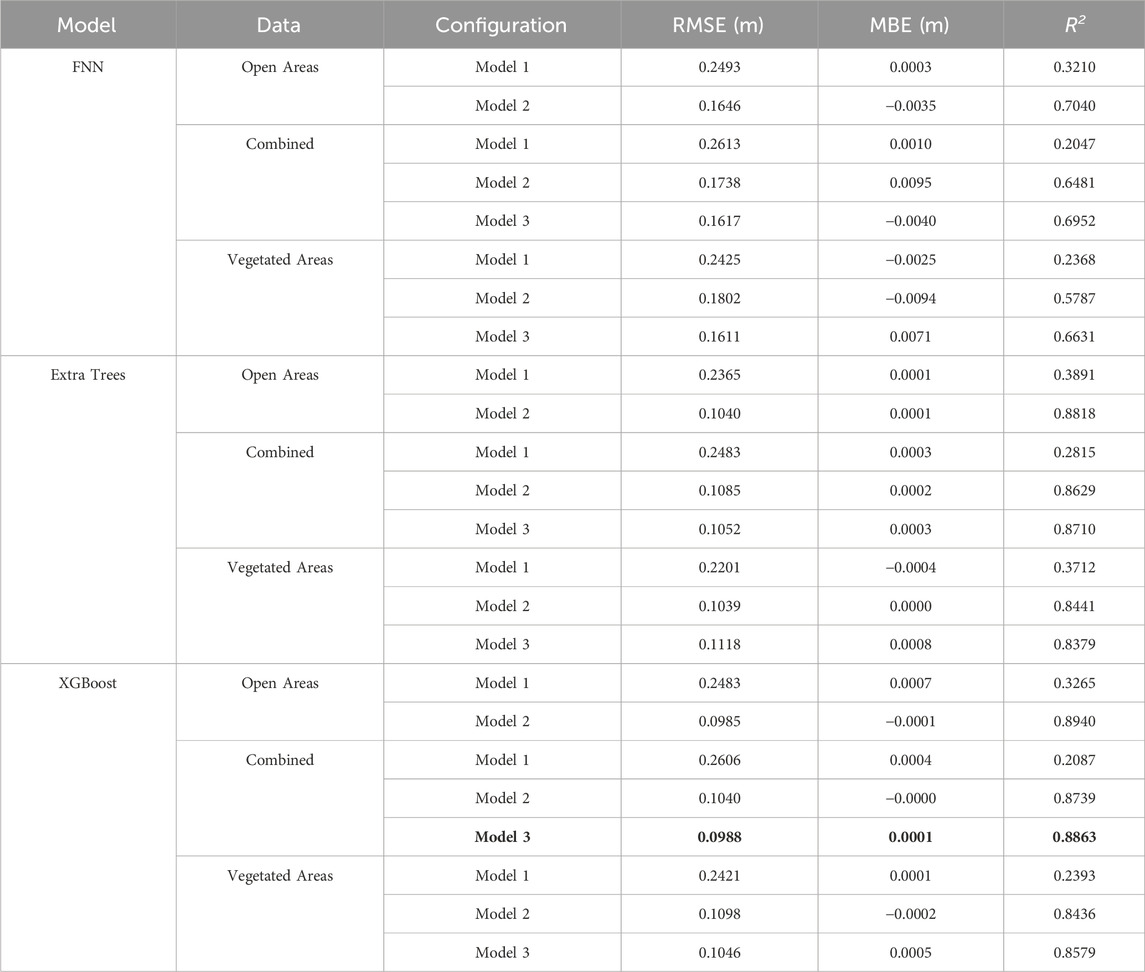
Table 2. Comparative Performance of FNN, Extra Trees, and XGBoost across Vegetated, Open, and their combination on the Held-out Test Set. The most preferred model is highlighted in bold fonts.

Figure 5

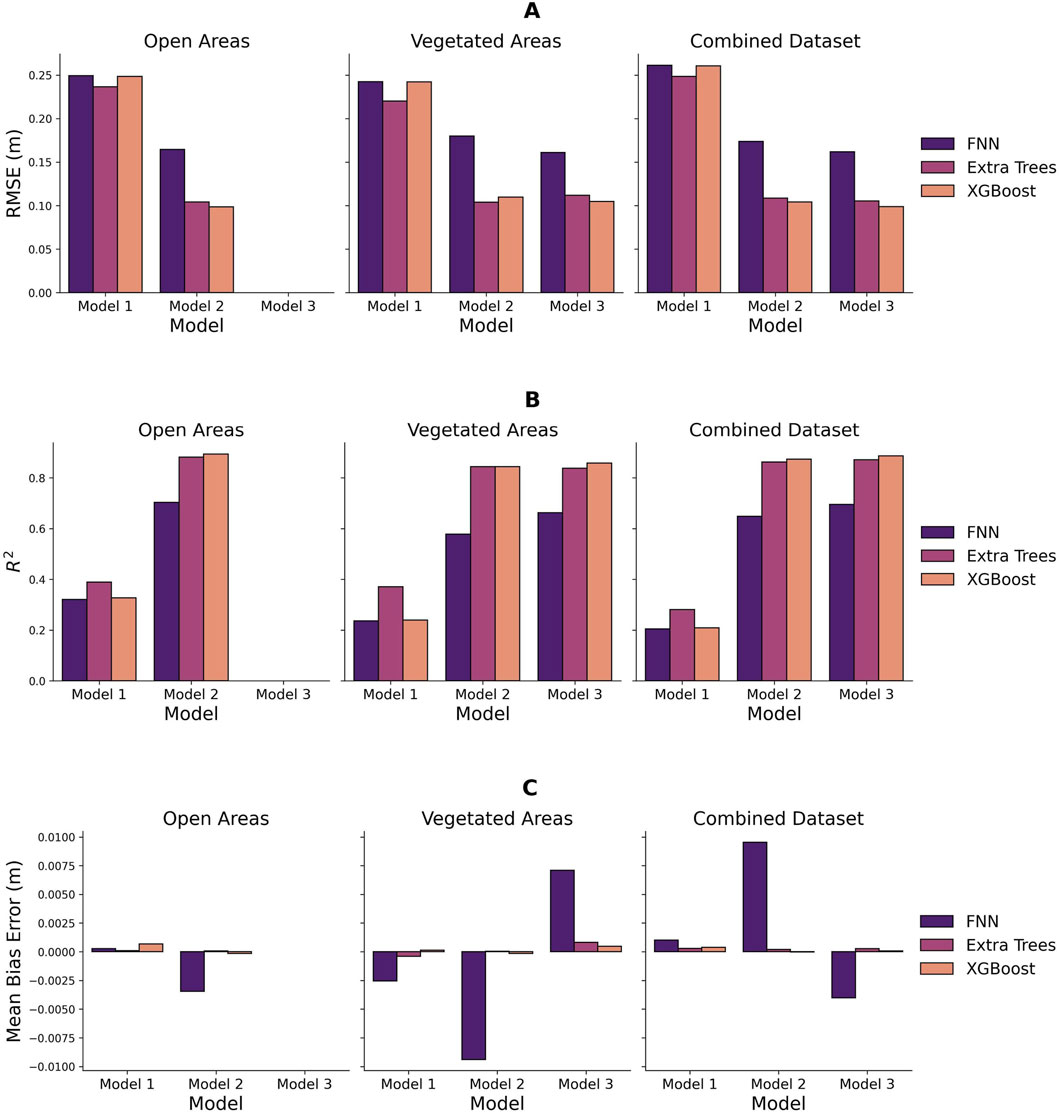
Figure 5. Comparative performance metrics of snow depth estimation Models on the testing set. Panel (A) displays the RMSE across all models and data strata, illustrating the accuracy of snow depth predictions. Panel (B) presents the R² values, and Panel (C) presents the MBE.

The model comparison revealed distinct performance across different model configurations. The baseline model (Model 1) provided a foundational understanding but demonstrated limited predictive power with R² values ranging from 0.21 to 0.33 across the open, vegetated, and mixed areas. However, incorporating InSAR-derived features (Model 2) markedly increased the precision of snow depth estimates.

Model 2 increased the R² value from 0.33 to 0.89 in the open areas, from 0.24 to 0.84 in the vegetated areas, and from 0.21 to 0.87 for the combined data, with the addition of the InSAR data. This improvement underscores the potential of InSAR data in capturing key variables influencing snow depth. The highest R² was observed in open areas. The performance in vegetated areas also improved, which indicates that InSAR products contribute valuable information even in vegetated landscapes. For the combined (open + vegetated) dataset, Model 2 attained an R² of 0.87, which is also a substantial increase from the baseline performance (0.21).

Introducing vegetation height as an additional predictor alongside InSAR products in Model 3 yielded minimal performance gains in model accuracy across vegetated and combined areas (since open areas have no vegetation or they are buried under the snow over). In vegetated areas, Model 3 increased the R² from 0.84 to 0.86, while for the combined dataset, the R² improved from 0.87 to 0.89. Despite these incremental improvements, the overall best performance was observed in open areas (Model 2: RMSE = 9.85 cm, R² = 0.894), followed closely by the combined dataset (Model 3: RMSE = 9.88 cm, R² = 0.886). Vegetated areas exhibited the least performance (Model 3: RMSE = 10.46 cm, R² = 0.858), although still maintaining a high level of accuracy.

Based on the performance comparison, Model 3 for the combined dataset appears to be the optimal choice. This model demonstrated comparable results (Table 2) to those obtained in open areas (Model 2), effectively eliminating the need for separate models for open and vegetated regions. Adopting a single model approach offers several advantages, including saving time and resources while allowing more focus on refining and optimizing this unified model. Figures 6–8, Figure 9B and Table 3 are based on Model 3 for the combined dataset, as Model 3 provides a comprehensive and efficient solution for our application.

Figure 6

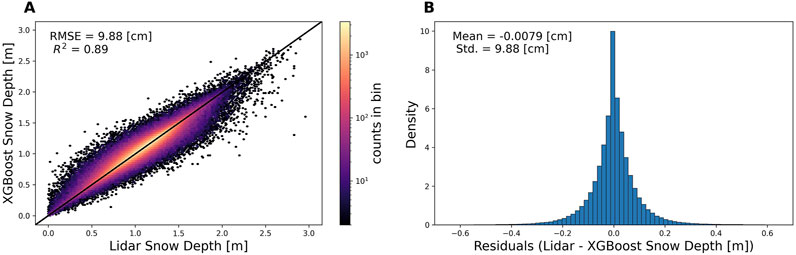
Figure 6. XGBoost Residual Analysis (Model 3 on the combined dataset). (A) Hexbin density plot comparing lidar measured snow depths with predictions from the XGBoost model, with each bin containing at least 2 data points. (B) Histogram of the residuals (lidar minus XGBoost predicted snow depths).

Table 3

Table 3. In situ validation results.

The XGBoost modeled snow depths showed strong correspondence with lidar snow depths at the 3-m scale (RMSE = 9.88 cm, R² = 0.89; Figure 6A), illustrating the model’s ability to reproduce the observed snow depth variability. Similarly, the residuals (i.e., lidar minus XGBoost predicted snow depth; Figure 6B) are concentrated around zero with a mean of −7.9 × 10⁻³ cm and a standard deviation of 9.9 cm, indicating minimal errors and biases, and an error similar to that reported for airborne lidar.

Figure 7B (predicted depths) visually appears to capture the spatial variability observed in the lidar data (Figure 7A), suggesting good model performance. Figure 7C quantifies the prediction error, visually encoded to emphasize areas of underestimation or overestimation by the model. Figure 7C indicates minimal bias based on the color map.

Figure 7

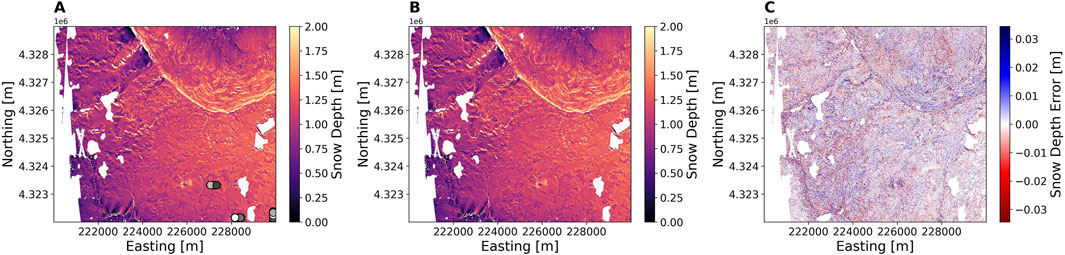
Figure 7. Spatial Residual Analysis. (A) Lidar-derived snow depth. (B) The XGBoost predicted snow depth. (C) The prediction error (lidar minus predicted snow depths), with a diverging color bar (blue for positive values, white for zero, and red for negative values) to visualize over- and under-predictions. Gray circles in the bottom right of panel A indicate in situ depth measurement locations collected on February 8.

3.2 Feature importance

Using SHAP values (Figure 8A), the most influential variables were unwrapped phase, bare ground elevation, and amplitude. Gain-based importance (Figure 8B) also showed unwrapped phase, bare ground elevation, and amplitude as the top 3 predictors, aligning with SHAP. This indicates their high explanatory power for estimating snow depth from InSAR.

Figure 8

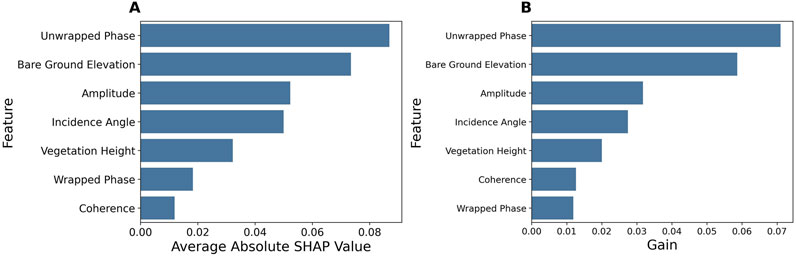
Figure 8. Feature Importance for Model 3 on the combined dataset: (A) SHAP importance (B) XGBoost impurity-based importance.

When stratified into open and vegetated areas, the feature importance ranks were the same as Figure 8 in open areas. However, for vegetated areas, bare ground elevation was the leading feature, highlighting the complex relationship between the topography and snow accumulation beneath the canopy. Vegetation height also became more important in forests, ranking 3rd compared to 5th overall. Feature importance plots for forested and open areas can be found in Supplementary Figures S1, S2 of the supplementary material.

3.3 In situ validation

To provide an independent assessment of model accuracy, predicted snow depths were validated against in situ observations collected as part of the 2017 NASA SnowEx campaign (Brucker et al., 2018). Manual measurements were taken using either a standard, handheld 3-m snow probe or a shorter GPS-equipped 1.2-m MagnaProbe. The GPS technology in the MagnaProbe provides a position accuracy of ±2.5 m (Sturm and Holmgren, 2018). During the intense observation period (February 6–25), a total of 27,081 snow depth measurements were taken at intervals of approximately 3 m (Brucker et al., 2018).

Validation was done using a 3-m buffer approach, where the average snow depth (both from lidar and our predictions) within a 3-m radius of each in situ observation was calculated. We used lidar snow depth data from 8 February 2017, for developing our models, so our validation focused on in situ measurements taken on the same date to ensure temporal consistency. Initially, we had 1777 in situ snow depth measurements from February 8. However, the lidar data used in this study did not cover the entire area where in situ measurements were taken. Hence, we considered only points where the 3-meter buffer contained lidar/modeled depths.

This spatial filtering reduced the number of usable in situ measurements to 234, as only these points were within the lidar swath coverage area. These 234 measurements were used for comparison against the average of the lidar dataset and the model predictions (training or testing) within their respective 3-m buffers.

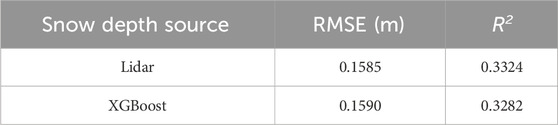
When compared to in situ measurements (Table 3), the lidar-derived snow depths achieved an RMSE of 15.85 cm and R² of 0.332, while snow depths predicted by XGBoost achieved a slightly worse performance (RMSE = 15.90 cm and R² = 0.328). Overall, the in situ validation provides confidence in the modeling framework, with XGBoost predictions showing accuracy approaching the lidar training data.

4 Discussion

4.1 Model performance

This study explored the potential of machine learning for snow depth prediction using data from NASA JPL’s UAVSAR sensor, which employs L-band radar for InSAR measurements. We developed and compared three machine learning algorithms–Extra Trees, XGBoost, and FNN, each selected for their robustness in handling complex datasets and their fast training and prediction time, with XGBoost and FNN capable of benefiting from GPU acceleration. XGBoost consistently outperforms other algorithms. Hence, the results are based on the XGBoost model. To investigate the potential differences in model performance across open and vegetated areas and assess the feasibility of using a single model for snow depth prediction across the entire study area, we partitioned the study area into three distinct categories: vegetated regions, open regions, and a combination of both.

Within each category, we developed three distinct models: a baseline model using only elevation data (model 1), a second model incorporating InSAR parameters and elevation (model 2), and a third model combining InSAR parameters, elevation, and vegetation height (model 3). The addition of vegetation height improved model performance for both vegetated and mixed areas (assuming open areas have no vegetation or are buried beneath the snow cover). In vegetated areas, including vegetation height as a feature reduced the RMSE from 10.98 cm to 10.46 cm, while for the combined dataset, the RMSE reduced from 10.40 cm to 9.88 cm.

These findings suggest that while vegetation height contributes to the model’s predictive power, its impact is less pronounced compared to the inclusion of InSAR-derived features. In open areas, adding InSAR-derived features reduced the RMSE from 24.83 cm to 9.85 cm compared to the baseline; in vegetated areas, the RMSE reduced from 24.21 cm to 10.98 cm; and for the combined dataset, the RMSE reduced from 26.06 cm to 10.40 cm. The marginal improvements in model accuracy from model 2 to model 3 indicate that the InSAR parameters capture a larger portion of the variability in snow depth, even in the presence of vegetation.

The model performed better in open areas than in vegetated areas. This is likely because forests have a more complex structure than open areas, which can scatter and attenuate the InSAR signal. Additionally, trees can intercept snowfall, making it more difficult to measure snow depth beneath the canopy accurately. Although our models performed better in open areas, the results from the vegetated areas also maintained high accuracy. For model 2, the difference in RMSE between open and vegetated areas is 1.13 cm. The high accuracy in vegetated areas can be attributed to the fact that L-band data is less sensitive to the forest structure. This finding is consistent with the work of Hosseini (Hosseini and Garestier, 2021), where he found the L-band to be less sensitive to forest structure than the P-band.

Considering the performance metrics across different areas, Model 3 for the combined dataset emerges as the best choice, offering a balance between accuracy and practicality. By incorporating both InSAR-derived attributes and vegetation height, Model 3 effectively captures the variability in snow depth across open and vegetated areas, achieving an impressive R² of 0.89 and an RMSE of 9.88 cm. This single model approach for mixed areas eliminates the need to develop separate models for open and vegetated regions, saving time and resources while maintaining high predictive power. The inclusion of vegetation height in Model 3 successfully differentiates between open and vegetated areas, as evidenced by the comparable performance metrics obtained when the combined dataset’s predictions are divided into their respective subsets when separate models are not trained (vegetated areas: RMSE = 10.46 m, R² = 0.86; open areas: RMSE = 9.5 cm, R² = 0.90; data not shown). These results further validate the robustness and versatility of Model 3 in estimating snow depth across vegetated and non-vegetated areas. This enhanced performance implies the potential of a single and robust model to reliably estimate snow depth in both vegetated and open areas, which can enhance the efficiency of large-scale snow monitoring efforts.

4.2 Feature importance

We conducted feature importance using SHAP and gain metrics from XGBoost. This is because the SHAP feature importance provides a more reliable and stable ranking, and the gain metrics can be misleading for features with high cardinality. We found an agreement between the importance of the feature from both SHAP’s and XGBoost’s gain (Figure 8). Unwrapped phase, bare earth elevation, and amplitude are the top three influential features. Unwrapped phase emerged as the most influential predictor, as it is a direct indicator of snow depth changes, hence its strong influence on the model’s predictive power. The bare ground elevation’s importance is similarly intuitive; it represents the underlying topography, which is fundamental in understanding snow accumulation patterns. Topography relates to snow depth through factors like elevation, slope, and aspect (Trujillo et al., 2007; Hojatimalekshah et al., 2021).

Higher elevations experience more snowfall, north-facing slopes retain snowpack longer in the northern hemisphere, and leeward areas develop drifts. The bare ground elevation provides the terrain context to model these topological influences on snow accumulation. Amplitude, ranking third in importance, suggests that the backscatter intensity, which is affected by surface characteristics, including roughness and snow density, is also an important predictor. This aligns with findings in literature where backscatter properties have been directly correlated with snow depth. King et al. (2015) found a strong correlation between Ku-band backscatter and snow depth in the tundra. The remaining features, like incidence angle and coherence, showed lower importance. Further analysis is warranted to fully explain the relative feature contributions. Additionally, from a remote sensing perspective, SAR imagery captures details about the Earth’s surface by recording both the strength (amplitude) and timing (phase) of the backscattered radar signal. Given the rich information contained in the amplitude and phase components of SAR images, it is reasonable to expect that these features would rank high on the feature importance scale when used in various remote sensing applications, such as snow depth estimation.

When the data was stratified by open versus vegetated areas, some notable differences emerged in the feature importance (Supplementary Figures S1, S2 of the supplementary material). In open areas, unwrapped phase and bare earth elevation remained the top two predictors, followed by incidence angle and then amplitude. This aligns with the overall importance rankings and reinforces the primacy of phase and topography for snow depth estimation in open regions. However, in vegetated regions, bare earth elevation was the top performer, followed by incidence angle and vegetation height. Unwrapped phase dropped to fourth. The decreased ranking of the unwrapped phase in forests is likely because dense vegetation attenuates and scatters the radar signal, reducing the phase’s sensitivity to snow depth variations below the canopy. Meanwhile, vegetation height became the third most important variable, likely because it plays a role in correcting for signal attenuation effects in vegetated areas. These land cover-specific feature importance findings provide useful insights. The unwrapped phase appears most valuable in open areas where radar penetration is uncompromised, while bare earth elevation and vegetation structure take precedence in forests. These results point to potential pathways for improving InSAR snow depth retrieval through optimal parameterization tailored to different land cover regimes. Additionally, these results can guide future research and data collection efforts, making them more focused, and may lead to more sophisticated physics-based models and physics-informed machine learning.

4.3 In situ validation

Validation against in situ snow depth measurements provides an independent assessment of model accuracy. The lidar training data achieved 15.9 cm RMSE versus in situ points. For the optimized XGBoost model, we achieved 16 cm RMSE compared to in situ data. We observe from Figures 9A, B that the lidar data and XGBoost’s predictions generally underestimated the in situ snow depth measurements. Currier et al. (2019) also reported this negative bias between the lidar and in situ probe measurements. The close alignment between lidar and ML model errors suggests that our model effectively learned the patterns present in the lidar data. However, this also means that the ML model inherited the biases present in the lidar measurements (Figure 9). We observed a general underestimation of snow depth by lidar, which was consequently reflected in our ML predictions. This underscores a fundamental principle in machine learning: the model’s performance is inherently limited by the quality of its training data.

Figure 9

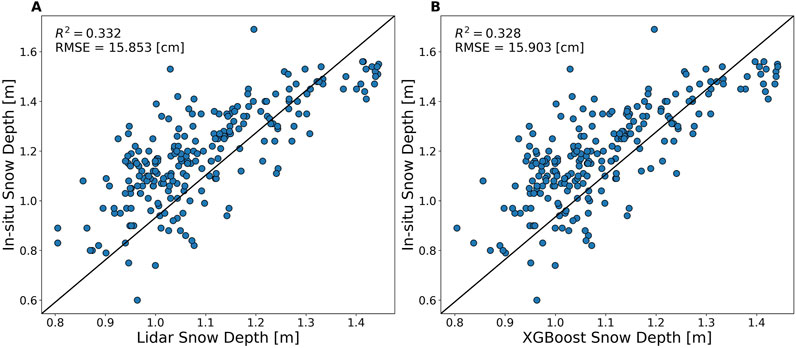
Figure 9. Snow depth validation using in situ measurements. (A): Lidar-derived depths versus in situ depths. (B) XGBoost predicted depths versus in situ depths. The evaluation metrics (RMSE and R²) show a comparable accuracy between the lidar-derived and the XGBoost-predicted snow depths. Both methods exhibit a negative bias, as the in situ measurements are generally larger than the corresponding modeled snow depths.

The estimated ±5 cm uncertainty in in situ snow depth probe measurements, arising from factors such as probe penetration into the soil and low vegetation impacts (Sturm and Holmgren, 2018; Currier et al., 2019), sets a practical limit on the achievable accuracy of our model validations. Additionally, potential geolocation errors from the probe introduce spatial discrepancies when comparing point-based in situ measurements with grid-based lidar or model predictions. These factors introduce a margin of error that must be considered when interpreting the validation results.

Our findings show a larger discrepancy between lidar and in situ snow depths compared to the work of Currier et al. (2019) on the same dataset. While we found an RMSE of 15.9 cm, they reported a root-mean-square difference of 8 cm between the lidar-derived snow depths and in situ measurements. This difference in error magnitudes can be attributed to methodological distinctions. The difference might be due to Currier et al. (2019) comparing median values from 52 snow-probe transects collected over 4 days (February 8, 9, 16, and 17) to near-coincident lidar data from February, while we compared 234 individual point measurements with lidar from February 8 alone. Their use of transect medians likely smoothed out local variations and reduced the influence of outliers, potentially reducing the overall error.

In summary, while the ML model successfully replicated the patterns in the lidar data, it also replicated its biases. This serves as a cautionary note for the application of ML in snow monitoring: while ML can be a powerful tool for pattern recognition and prediction, it is not a panacea for underlying data quality issues. Enhancing the accuracy of lidar measurements would likely improve the model’s predictive capabilities. Addressing geolocation errors and understanding the inherent measurement uncertainties can further refine the validation process and the interpretation of model performance.

4.4 Limitations, scope, and future work

This study provides initial insights into using InSAR products to estimate snow depth. However, several limitations and assumptions must be acknowledged to contextualize the findings.

The key assumption of our approach is that the spatial patterns of total snow depth remain consistent between the time of snow accumulation and the subsequent InSAR acquisition. This implies that the snow depth change detected by the InSAR instrument is representative of the total snow depth distribution. However, external factors, such as strong winds from unusual directions or melting events, could alter snow accumulation patterns during this interval, potentially compromising the accuracy of the estimates. Therefore, the effectiveness of this approach is influenced by the stability of snow depth patterns between acquisitions.

This study focuses on relatively flat terrain, where the effects of phase decorrelation and geometric distortions are minimal. While this may be suitable for establishing a proof of concept, the method’s transferability to rugged terrain remains untested. In mountainous areas, terrain-induced effects on InSAR signals—such as layover, shadowing, and foreshortening—introduce additional complexities (Zebker and Villasenor, 1992). These effects can lead to signal distortions and loss of coherence, affecting the accuracy of snow depth estimations. Although previous studies (e.g., Hoppinen et al., 2023) have shown promise in using physics-based InSAR methods in rugged terrain, the applicability of machine learning (ML)-driven approaches in these environments is yet to be evaluated. This work is the first in a series of ML-based snow depth retrieval studies from L-band data in preparation for the upcoming NISAR mission.

Our study was conducted in February, a period when snow cover is typically stable, and other InSAR-based methods, such as physics-based approaches, have demonstrated promising results even in rugged terrain (Hoppinen et al., 2023; Palomaki and Sproles, 2023; Tarricone et al., 2023; Bonnell et al., 2024). This raises the question of how users benefit from the additional complexity of machine learning methods, given the large amount of data required to train them. While this is a valid consideration, physics-based InSAR approaches (e.g., Guneriussen et al., 2001) require snow properties, such as snowpack bulk density and permittivity, to model the phase delay introduced by the snowpack. However, these properties may not always be readily available in an operational context. Additionally, physics-based methods often require atmospheric corrections using models like the ECMWF Reanalysis v5 (ERA5) to account for temporal and spatial variations in radar wave propagation caused by changes in pressure, temperature, and moisture (Hoppinen et al., 2023). While the ML approach may potentially benefit from these corrections, our results indicate that the ML model learned the patterns in the lidar data without them, suggesting that it is promising without explicit atmospheric corrections.

Physics-based approaches for InSAR-based SWE and snow depth monitoring typically require a complete time series of SAR images capturing snow accumulation and ablation across the winter season (Tarricone et al., 2023). This is due to the rapid decorrelation in snow-covered regions, which makes single or sparse acquisitions insufficient for robust modeling. In contrast, the machine learning approach does not depend on a complete time series as long as there is a coincident depth map. Instead, it directly learns patterns from available data. Moreover, the ML approach can efficiently handle large datasets, which is advantageous given the expected data volumes from NISAR. ML methods offer the opportunity to incorporate diverse input datasets and derive nuanced patterns in snow depth distributions that physics-based approaches may not capture. However, a key limitation of ML is its reliance on representative and high-quality training data, which must be carefully curated to ensure accurate predictions. This reliance may present challenges in operational contexts, particularly in regions with no lidar or in situ data to train the model. Future research could focus on developing optimal strategies for generating or acquiring quality training datasets to enhance the applicability and scalability of ML methods. As InSAR data becomes more widely available through missions like NISAR, the advantages of ML methods are expected to outweigh their additional complexity and data requirements.

Future research will focus on extending the applicability of the proposed ML approach to more complex terrains and varying snow conditions. Specifically, future work will:

• Evaluate Transferability to Rugged Terrain: Testing the ML models in mountainous regions, where phase decorrelation, shadowing, and layover effects introduce additional challenges, will assess their robustness in the presence of terrain-induced effects on InSAR signals.

• Validate Across Different Snow Conditions and Seasons: The current work was conducted in a dry snow environment and during the accumulation period of the snow season. Expanding the temporal scope of the study to include melting periods (e.g., post-peak SWE) and wet snow conditions will help assess the model’s generalizability and operational scalability.

• Incorporate Snow-Free Baseline Acquisitions for Backscatter Ratios: Future work should include snow-free baseline acquisitions to calculate multi-temporal backscattering ratios. This would help reduce noise and enhance the accuracy of snow depth retrievals by better isolating snow-related backscatter.

• Examine the Accuracy-Resolution Trade-off: This study used 3 m spatial resolution data, which may be impractical for operational hydrology requiring coarser scales (e.g., 10–50 m). Future work will investigate accuracy changes as resolution scales are adjusted to coarser levels.

• Incorporate Advanced Computer Vision Techniques: Future iterations of this work will explore advanced computer vision approaches, such as convolutional neural networks and transformer-based architectures, to further enhance snow depth estimation accuracy and efficiency.

• Incorporate Auxiliary Datasets: Future research should include auxiliary datasets, such as snow stratigraphy, temperature profiles, and meteorological conditions, where available to enhance model performance.

• Explore Physics-Informed ML Models: Future research should incorporate physical process-based knowledge into ML models and investigate the sensitivity of the models to the various input features to provide deeper insights into the mechanism driving snow depth variation.

Addressing these questions will allow us to further advance the field of machine learning-based snow depth prediction and contribute to more accurate and reliable snow monitoring and forecasting systems.

5 Conclusion

This study serves as a proof of concept for the potential of machine learning to estimate snow depth using L-band InSAR data. The XGBoost model demonstrated promising performance, and the feature importance analysis provided insights into the relationships between L-band InSAR features and snow depth. The upcoming NISAR mission, with its global L-band InSAR coverage, presents a unique opportunity to further advance this approach. With the availability of NISAR data, we can expand the training dataset, incorporate additional polarizations, and explore alternative machine learning approaches, potentially leading to even more accurate snow depth estimation. The success of the ML approach depends on the availability of quality training data, as the accuracy of the ML model approaches that of lidar when validated against the in situ measurements. With sufficient, representative, and diverse training data, machine learning models can effectively capture the complex relationships between snow depth and its influencing factors, enabling accurate snow depth prediction. With the advent of NISAR and continued research efforts, we can harness the power of machine learning to potentially improve water resource management.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

IA: Formal Analysis, Methodology, Validation, Visualization, Writing–original draft, Writing–review and editing, Software. H-PM: Conceptualization, Data curation, Funding acquisition, Supervision, Writing–review and editing. JM: Writing–review and editing. ET: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was partially funded by the U.S. Army Cold Regions Research and Engineering Laboratory (CRREL) under contract W913E523C0002.

Acknowledgments

The authors would like to thank the NASA Terrestrial Hydrology Program and all participants of the SnowEx campaign for providing the lidar and in situ data. We also thank Yunling Lou, the UAVSAR Project Manager at NASA JPL, for the UAVSAR data. We thank the reviewers (Mukesh Gupta, Divyesh Varade, and Surendar Manickam) for improving our manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsen.2024.1481848/full#supplementary-material

References

Akiba, T., Sano, S., Yanase, T., Ohta, T., and Koyama, M. (2019). “Optuna: a next-generation hyperparameter optimization framework,” in Proceedings of the ACM SIGKDD international conference on knowledge discovery and data mining, 2623–2631. doi:10.1145/3292500.3330701

CrossRef Full Text | Google Scholar

Alabi, I. O., Marshall, H.-P., Mead, J., and Ofekeze, E. (2022). “How transferable are our models? A case study of Idaho SNOTEL sites,” in AGU fall meeting abstracts, C52C-0365.

Google Scholar

Alabi, I. O., Marshall, H.-P., Mead, J., Trujillo, E., and Ofekeze, E. (2023). Harnessing L-band InSAR and lidar data through machine learning for accurate snow depth estimation in Grand mesa, Colorado. AGU23.

Google Scholar

Aquino, C., Mitchard, E., McNicol, I., Carstairs, H., Burt, A., Vilca, B. L. P., et al. (2021). “Using experimental sites in tropical forests to test the ability of optical remote sensing to detect forest degradation at 0.3-30 M resolutions,” in 2021 IEEE international geoscience and remote sensing symposium IGARSS (IEEE), 677–680.

CrossRef Full Text | Google Scholar

Awasthi, S., and Varade, D. (2021). Recent advances in the remote sensing of alpine snow: a review. GIsci Remote Sens. 58, 852–888. doi:10.1080/15481603.2021.1946938

CrossRef Full Text | Google Scholar

Bair, E. H., Abreu Calfa, A., Rittger, K., and Dozier, J. (2018). Using machine learning for real-time estimates of snow water equivalent in the watersheds of Afghanistan. Cryosphere 12, 1579–1594. doi:10.5194/tc-12-1579-2018

CrossRef Full Text | Google Scholar

Bergstra, J., Bardenet, R., Bengio, Y., and Kégl, B. (2011). Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process Syst. 24.

Google Scholar

Bergstra, J., Yamins, D., and Cox, D. (2013). “Making a science of model search: hyperparameter optimization in hundreds of dimensions for vision architectures,” in International conference on machine learning (PMLR), 115–123.

Google Scholar

Bonnell, R., McGrath, D., Tarricone, J., Marshall, H.-P., Bump, E., Duncan, C., et al. (2024). Evaluating L-band InSAR snow water equivalent retrievals with repeat ground-penetrating radar and terrestrial lidar surveys in northern Colorado. Cryosphere 18, 3765–3785. doi:10.5194/tc-18-3765-2024

CrossRef Full Text | Google Scholar

Broxton, P. D., Van Leeuwen, W. J. D., and Biederman, J. A. (2019). Improving snow water equivalent maps with machine learning of snow survey and lidar measurements. Water Resour. Res. 55, 3739–3757. doi:10.1029/2018wr024146

CrossRef Full Text | Google Scholar

Brucker, L., Hiemstra, C., Marshall, H., and Elder, K. (2018). SnowEx17 community snow depth probe measurements. Version 1. doi:10.5067/WKC6VFMT7JTF

CrossRef Full Text | Google Scholar

Brucker, L., Hiemstra, C., Marshall, H.-P., Elder, K., De Roo, R., Mousavi, M., et al. (2017). “A first overview of SnowEx ground-based remote sensing activities during the winter 2016--2017,” in 2017 IEEE international geoscience and remote sensing symposium (IGARSS), 1391–1394.

Google Scholar

Bühler, Y., Adams, M. S., Bösch, R., and Stoffel, A. (2016). Mapping snow depth in alpine terrain with unmanned aerial systems (UASs): potential and limitations. Cryosphere 10, 1075–1088. doi:10.5194/tc-10-1075-2016

CrossRef Full Text | Google Scholar

Chen, L., and Wang, L. (2018). Recent advance in earth observation big data for hydrology. Big Earth Data 2, 86–107. doi:10.1080/20964471.2018.1435072

CrossRef Full Text | Google Scholar

Chen, T., and Guestrin, C. (2016). “Xgboost: a scalable tree boosting system,” in Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 785–794.

Google Scholar

Chesnutt, J. M., Wegmann, K. W., Cole, R. D., and Byrne, P. K. (2017). “Landscape evolution comparison between sacra mensa, mars and the Grand mesa, Colorado, USA,” in AGU fall meeting abstracts, EP53B-1690.

Google Scholar

Currier, W. R., Pflug, J., Mazzotti, G., Jonas, T., Deems, J. S., Bormann, K. J., et al. (2019). Comparing aerial lidar observations with terrestrial lidar and snow-probe transects from NASA’s 2017 SnowEx campaign. Water Resour. Res. 55, 6285–6294. doi:10.1029/2018wr024533

CrossRef Full Text | Google Scholar

Deeb, E. J., Forster, R. R., and Kane, D. L. (2011). Monitoring snowpack evolution using interferometric synthetic aperture radar on the North Slope of Alaska, USA. Int. J. Remote Sens. 32, 3985–4003. doi:10.1080/01431161003801351

CrossRef Full Text | Google Scholar

Deems, J. S., Fassnacht, S. R., and Elder, K. J. (2006). Fractal distribution of snow depth from LiDAR data. J. Hydrometeorol. 7, 285–297. doi:10.1175/jhm487.1

CrossRef Full Text | Google Scholar

Deems, J. S., Fassnacht, S. R., and Elder, K. J. (2008). Interannual consistency in fractal snow depth patterns at two Colorado mountain sites. J. Hydrometeorol. 9, 977–988. doi:10.1175/2008jhm901.1

CrossRef Full Text | Google Scholar

Deems, J. S., Painter, T. H., and Finnegan, D. C. (2013). Lidar measurement of snow depth: a review. J. Glaciol. 59, 467–479. doi:10.3189/2013jog12j154

CrossRef Full Text | Google Scholar

Dettinger, M. D., and Anderson, M. L. (2015). Storage in California's reservois and snowpack in this time of drought. San Franc. Estuary Watershed Sci. 13. doi:10.15447/sfews.2015v13iss2art1

CrossRef Full Text | Google Scholar

Dong, C. (2018). Remote sensing, hydrological modeling and in situ observations in snow cover research: a review. J. Hydrol. (Amst) 561, 573–583. doi:10.1016/j.jhydrol.2018.04.027

CrossRef Full Text | Google Scholar

Feng, T., Huang, C., Huang, G., Shao, D., and Hao, X. (2024). Estimating snow depth based on dual polarimetric radar index from Sentinel-1 GRD data: a case study in the Scandinavian Mountains. Int. J. Appl. Earth Observation Geoinformation 130, 103873. doi:10.1016/j.jag.2024.103873

CrossRef Full Text | Google Scholar

Feng, T., Zhu, S., Huang, F., Hao, J., Mind’je, R., Zhang, J., et al. (2022). Spatial variability of snow density and its estimation in different periods of snow season in the middle Tianshan Mountains, China. Hydrol. Process 36, e14644. doi:10.1002/hyp.14644

CrossRef Full Text | Google Scholar

Ferraz, A., Saatchi, S., Bormann, K. J., and Painter, T. H. (2018). Fusion of NASA Airborne Snow Observatory (ASO) lidar time series over mountain forest landscapes. Remote Sens. (Basel) 10, 164. doi:10.3390/rs10020164

CrossRef Full Text | Google Scholar

Gatebe, C., Li, W., Chen, N., Fan, Y., Poudyal, R., Brucker, L., et al. (2018). “Snow-covered area using machine learning techniques,” in IGARSS 2018-2018 IEEE international geoscience and remote sensing symposium (IEEE), 6291–6293.

Google Scholar

Geurts, P., Ernst, D., and Wehenkel, L. (2006). Extremely randomized trees. Mach. Learn 63, 3–42. doi:10.1007/s10994-006-6226-1

CrossRef Full Text | Google Scholar

Guneriussen, T., Hogda, K. A., Johnsen, H., and Lauknes, I. (2001). InSAR for estimation of changes in snow water equivalent of dry snow. IEEE Trans. Geoscience Remote Sens. 39, 2101–2108. doi:10.1109/36.957273

CrossRef Full Text | Google Scholar

Harder, P., Pomeroy, J. W., and Helgason, W. D. (2020). Improving sub-canopy snow depth mapping with unmanned aerial vehicles: lidar versus structure-from-motion techniques. Cryosphere 14, 1919–1935. doi:10.5194/tc-14-1919-2020

CrossRef Full Text | Google Scholar

Hedrick, A. R., Marks, D., Havens, S., Robertson, M., Johnson, M., Sandusky, M., et al. (2018). Direct insertion of NASA Airborne Snow Observatory-derived snow depth time series into the iSnobal energy balance snow model. Water Resour. Res. 54, 8045–8063. doi:10.1029/2018wr023190

CrossRef Full Text | Google Scholar

Henn, B., Musselman, K. N., Lestak, L., Ralph, F. M., and Molotch, N. P. (2020). Extreme runoff generation from atmospheric river driven snowmelt during the 2017 Oroville Dam spillways incident. Geophys Res. Lett. 47, e2020GL088189. doi:10.1029/2020gl088189

CrossRef Full Text | Google Scholar

Hojatimalekshah, A., Uhlmann, Z., Glenn, N. F., Hiemstra, C. A., Tennant, C. J., Graham, J. D., et al. (2021). Tree canopy and snow depth relationships at fine scales with terrestrial laser scanning. Cryosphere 15, 2187–2209. doi:10.5194/tc-15-2187-2021

CrossRef Full Text | Google Scholar

Hoppinen, Z., Oveisgharan, S., Marshall, H., Mower, R., Elder, K., and Vuyovich, C. (2023). Snow water equivalent retrieval over Idaho, Part B: using L-band UAVSAR repeat-pass interferometry, 1–24.

Google Scholar

Hosseini, S., and Garestier, F. (2021). Pol-InSAR sensitivity to hemi-boreal forest structure at L-and P-bands. Int. J. Appl. Earth Observation Geoinformation 94, 102213. doi:10.1016/j.jag.2020.102213

CrossRef Full Text | Google Scholar

Hu, Y., Che, T., Dai, L., and Xiao, L. (2021). Snow depth fusion based on machine learning methods for the Northern Hemisphere. Remote Sens. (Basel) 13, 1250. doi:10.3390/rs13071250

CrossRef Full Text | Google Scholar

Kellogg, K., Hoffman, P., Standley, S., Shaffer, S., Rosen, P., Edelstein, W., et al. (2020). “NASA-ISRO synthetic aperture radar (NISAR) mission,” in 2020 IEEE aerospace conference (IEEE), 1–21.

CrossRef Full Text | Google Scholar

Killinger, D. K. (2014). “Lidar (light detection and ranging),” in Laser spectroscopy for sensing (Elsevier), 292–312.

Google Scholar

Kim, E., Gatebe, C., Hall, D., Newlin, J., Misakonis, A., Elder, K., et al. (2017). OVERVIEW of snowex year 1 activities NASA goddard space flight center, 2 usra, 3 aerospace corp., 4 ata aerospace, 5 US forest service, igarss, 1388–1390.

Google Scholar

King, F., Duffy, G., and Fletcher, C. G. (2022a). A centimeter-wavelength snowfall retrieval algorithm using machine learning. J. Appl. Meteorol. Climatol. 61, 1029–1039. doi:10.1175/jamc-d-22-0036.1

CrossRef Full Text | Google Scholar

King, F., Kelly, R., and Fletcher, C. G. (2022b). Evaluation of lidar-derived snow depth estimates from the iPhone 12 pro. IEEE Geoscience Remote Sens. Lett. 19, 1–5. doi:10.1109/lgrs.2022.3166665

CrossRef Full Text | Google Scholar

King, J., Kelly, R., Kasurak, A., Duguay, C., Gunn, G., Rutter, N., et al. (2015). Spatio-temporal influence of tundra snow properties on Ku-band (17.2 GHz) backscatter. J. Glaciol. 61, 267–279. doi:10.3189/2015jog14j020

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. L. (2015). “Adam: a method for stochastic optimization,” in 3rd international conference on learning representations, ICLR 2015 - conference track proceedings, 1–15.

Google Scholar

Kulakowski, D., Veblen, T. T., and Drinkwater, S. (2004). The persistence of quaking aspen (Populus tremuloides) in the Grand Mesa area, Colorado. Ecol. Appl. 14, 1603–1614. doi:10.1890/03-5160

CrossRef Full Text | Google Scholar

Lal, P., Singh, G., Das, N. N., and Entekhabi, D. (2022). “A data-driven snapshot algorithm for high-resolution soil moisture retrievals for the upcoming NISAR mission,” in AGU fall meeting abstracts, H42G-–1379.

Google Scholar

Leinss, S., Wiesmann, A., Lemmetyinen, J., and Hajnsek, I. (2015). Snow water equivalent of dry snow measured by differential interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 8, 3773–3790. doi:10.1109/jstars.2015.2432031

CrossRef Full Text | Google Scholar

Li, H., Wang, Z., He, G., and Man, W. (2017). Estimating snow depth and snow water equivalence using repeat-pass interferometric SAR in the northern piedmont region of the Tianshan Mountains. J. Sens. 2017, 1–17. doi:10.1155/2017/8739598

CrossRef Full Text | Google Scholar

Liang, J., Liu, X., Huang, K., Li, X., Shi, X., Chen, Y., et al. (2015). Improved snow depth retrieval by integrating microwave brightness temperature and visible/infrared reflectance. Remote Sens. Environ. 156, 500–509. doi:10.1016/j.rse.2014.10.016

CrossRef Full Text | Google Scholar

Lievens, H., Brangers, I., Marshall, H.-P., Jonas, T., Olefs, M., and De Lannoy, G. (2022). Sentinel-1 snow depth retrieval at sub-kilometer resolution over the European Alps. Cryosphere 16, 159–177. doi:10.5194/tc-16-159-2022

CrossRef Full Text | Google Scholar

Livneh, B., and Badger, A. M. (2020). Drought less predictable under declining future snowpack. Nat. Clim. Chang. 10, 452–458. doi:10.1038/s41558-020-0754-8

CrossRef Full Text | Google Scholar

Lu, Z., Kwoun, O., and Rykhus, R. (2007). Interferometric synthetic aperture radar (InSAR): its past, present and future. Photogramm. Eng. Remote Sens. 73, 217.

Google Scholar

Lundberg, S. M., and Lee, S.-I. (2017). A unified approach to interpreting model predictions. Adv. Neural Inf. Process Syst. 30. doi:10.48550/arXiv.1705.07874

CrossRef Full Text | Google Scholar

Mahmoodzada, A. B., Varade, D., and Shimada, S. (2020). Estimation of snow depth in the Hindu Kush Himalayas of Afghanistan during peak winter and early melt season. Remote Sens. (Basel) 12, 2788. doi:10.3390/rs12172788

CrossRef Full Text | Google Scholar

Man, X., and Chan, E. (2021). The best way to select features? comparing mda, lime, and shap. J. Financial Data Sci. Winter 3, 127–139. doi:10.3905/jfds.2020.1.047

CrossRef Full Text | Google Scholar

Marshall, H., Hawley, R. L., and Tedesco, M. (2015). Field measurements for remote sensing of the cryosphere. Remote Sens. Cryosphere, 345–381. doi:10.1002/9781118368909.ch14

CrossRef Full Text | Google Scholar

Marshall, H.-P., Deeb, E., Forster, R., Vuyovich, C., Elder, K., Hiemstra, C., et al. (2021). “L-band InSAR depth retrieval during the NASA SnowEx 2020 campaign: Grand mesa, Colorado,” in 2021 IEEE international geoscience and remote sensing symposium IGARSS (IEEE), 625–627.

Google Scholar

Marshall, H.-P., Koh, G., and Forster, R. R. (2005). Estimating alpine snowpack properties using FMCW radar. Ann. Glaciol. 40, 157–162. doi:10.3189/172756405781813500

CrossRef Full Text | Google Scholar

Mason, M. A. (2020). Snow depth distribution patterns and consistency from airborne lidar time series.

Google Scholar

Maxwell, A. E., Warner, T. A., and Fang, F. (2018). Implementation of machine-learning classification in remote sensing: an applied review. Int. J. Remote Sens. 39, 2784–2817. doi:10.1080/01431161.2018.1433343

CrossRef Full Text | Google Scholar

Meloche, J., Langlois, A., Rutter, N., McLennan, D., Royer, A., Billecocq, P., et al. (2022). High-resolution snow depth prediction using Random Forest algorithm with topographic parameters: a case study in the Greiner watershed, Nunavut. Hydrol. Process 36. doi:10.1002/hyp.14546

CrossRef Full Text | Google Scholar

Meyer, J., Deems, J. S., Bormann, K. J., Shean, D. E., and Skiles, S. M. (2022). Mapping snow depth and volume at the alpine watershed scale from aerial imagery using Structure from Motion. Front. Earth Sci. (Lausanne) 10, 989792. doi:10.3389/feart.2022.989792

CrossRef Full Text | Google Scholar

Muraina, I. (2022). “Ideal dataset splitting ratios in machine learning algorithms: general concerns for data scientists and data analysts,” in 7th international Mardin Artuklu scientific research conference, 496–504.

Google Scholar

Ofekeze, E., Marshall, H.-P., Mead, J., and Alabi, I. O. (2022). “A machine learning framework for active and passive microwave observation from snow water equivalent synthetic aperture radar and radiometer (SWESARR) for snow depth estimation,” in AGU fall meeting abstracts, C52C--0364.

Google Scholar

Ofekeze, E., Marshall, H.-P., Mead, J., Trujillo, E., and Alabi, I. O. (2023). Advancing snow water equivalent estimation with SWESARR. AGU23.

Google Scholar

Oveisgharan, S., Zinke, R., Hoppinen, Z., and Marshall, H. P. (2024). Snow water equivalent retrieval over Idaho–Part 1: using Sentinel-1 repeat-pass interferometry. Cryosphere 18, 559–574. doi:10.5194/tc-18-559-2024

CrossRef Full Text | Google Scholar

Ozdemir, S. (2022). Feature engineering bookcamp. Simon & Schuster.

Google Scholar

Palomaki, R. T., and Sproles, E. A. (2023). Assessment of L-band InSAR snow estimation techniques over a shallow, heterogeneous prairie snowpack. Remote Sens. Environ. 296, 113744. doi:10.1016/j.rse.2023.113744

CrossRef Full Text | Google Scholar

Pflug, J. M., and Lundquist, J. D. (2020). Inferring distributed snow depth by leveraging snow pattern repeatability: investigation using 47 lidar observations in the Tuolumne watershed, Sierra Nevada, California. Water Resour. Res. 56, e2020WR027243. doi:10.1029/2020wr027243

CrossRef Full Text | Google Scholar

Reichstein, M., Camps-Valls, G., Stevens, B., Jung, M., Denzler, J., Carvalhais, N., et al. (2019). Deep learning and process understanding for data-driven Earth system science. Nature 566, 195–204. doi:10.1038/s41586-019-0912-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Revuelto, J., López-Moreno, J. I., Azor\’\in-Molina, C., Zabalza, J., Arguedas, G., and Vicente-Serrano, S. M. (2014). Mapping the annual evolution of snow depth in a small catchment in the Pyrenees using the long-range terrestrial laser scanning. J. Maps 10, 379–393. doi:10.1080/17445647.2013.869268

CrossRef Full Text | Google Scholar

Schirmer, M., and Lehning, M. (2011). Persistence in intra-annual snow depth distribution: 2. Fractal analysis of snow depth development. Water Resour. Res. 47. doi:10.1029/2010wr009429

PubMed Abstract | CrossRef Full Text | Google Scholar

Serreze, M. C., Clark, M. P., Armstrong, R. L., McGinnis, D. A., and Pulwarty, R. S. (1999). Characteristics of the western United States snowpack from snowpack telemetry (SNOTEL) data. Water Resour. Res. 35, 2145–2160. doi:10.1029/1999wr900090

CrossRef Full Text | Google Scholar

Simpkins, G. (2018). Snow-related water woes. Nat. Clim. Chang. 8, 945. doi:10.1038/s41558-018-0330-7

CrossRef Full Text | Google Scholar

Sinha, S., Jeganathan, C., Sharma, L. K., and Nathawat, M. S. (2015). A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 12, 1779–1792. doi:10.1007/s13762-015-0750-0

CrossRef Full Text | Google Scholar

Sturm, M., and Holmgren, J. (2018). An automatic snow depth probe for field validation campaigns. Water Resour. Res. 54, 9695–9701. doi:10.1029/2018WR023559

CrossRef Full Text | Google Scholar

Sturm, M., and Wagner, A. M. (2010). Using repeated patterns in snow distribution modeling: an Arctic example. Water Resour. Res. 46. doi:10.1029/2010wr009434

CrossRef Full Text | Google Scholar

Taheri, M., and Mohammadian, A. (2022). An overview of snow water equivalent: methods, challenges, and future outlook. Sustainability 14, 11395. doi:10.3390/su141811395

CrossRef Full Text | Google Scholar

Tarricone, J., Webb, R. W., Marshall, H. P., Nolin, A. W., and Meyer, F. J. (2023). Estimating snow accumulation and ablation with L-band interferometric synthetic aperture radar (InSAR). Cryosphere 17, 1997–2019. doi:10.5194/tc-17-1997-2023

CrossRef Full Text | Google Scholar

Tedesco, M., Pulliainen, J., Takala, M., Hallikainen, M., and Pampaloni, P. (2004). Artificial neural network-based techniques for the retrieval of SWE and snow depth from SSM/I data. Remote Sens. Environ. 90, 76–85. doi:10.1016/j.rse.2003.12.002

CrossRef Full Text | Google Scholar

Trujillo, E., and Lehning, M. (2015). Theoretical analysis of errors when estimating snow distribution through point measurements. Cryosphere 9, 1249–1264. doi:10.5194/tc-9-1249-2015

CrossRef Full Text | Google Scholar

Trujillo, E., Ram\’\irez, J. A., and Elder, K. J. (2007). Topographic, meteorologic, and canopy controls on the scaling characteristics of the spatial distribution of snow depth fields. Water Resour. Res. 43. doi:10.1029/2006wr005317

PubMed Abstract | CrossRef Full Text | Google Scholar

Trujillo, E., Ramirez, J. A., and Elder, K. J. (2009). Scaling properties and spatial organization of snow depth fields in sub-alpine forest and alpine tundra. Hydrological Process. Int. J. 23, 1575–1590. doi:10.1002/hyp.7270

CrossRef Full Text | Google Scholar

Ulaby, F. T., Moore, R. K., and Fung, A. K. (1981). Microwave remote sensing: active and passive. volume 1-microwave remote sensing fundamentals and radiometry.

Google Scholar

Vano, J. A. (2020). Implications of losing snowpack. Nat. Clim. Chang. 10, 388–390. doi:10.1038/s41558-020-0769-1

CrossRef Full Text | Google Scholar

Varade, D., Maurya, A. K., Dikshit, O., Singh, G., and Manickam, S. (2020). Snow depth in Dhundi: an estimate based on weighted bias corrected differential phase observations of dual polarimetric bi-temporal Sentinel-1 data. Int. J. Remote Sens. 41, 3031–3053. doi:10.1080/01431161.2019.1698076

CrossRef Full Text | Google Scholar

Wang, J., Yuan, Q., Li, T., Shen, H., and Zhang, L. (2019). “Estimating snow-depth by fusing satellite and station observations: a deep learning approach,” in IGARSS 2019-2019 IEEE international geoscience and remote sensing symposium (IEEE), 4109–4112.

CrossRef Full Text | Google Scholar

Webb, R. W., Marziliano, A., McGrath, D., Bonnell, R., Meehan, T. G., Vuyovich, C., et al. (2021). In situ determination of dry and wet snow permittivity: improving equations for low frequency radar applications. Remote Sens. (Basel) 13, 4617. doi:10.3390/rs13224617

CrossRef Full Text | Google Scholar

Yuan, Q., Shen, H., Li, T., Li, Z., Li, S., Jiang, Y., et al. (2020). Deep learning in environmental remote sensing: achievements and challenges. Remote Sens. Environ. 241, 111716. doi:10.1016/j.rse.2020.111716

CrossRef Full Text | Google Scholar

Zebker, H. A., and Villasenor, J. (1992). Decorrelation in interferometric radar echoes. IEEE Trans. geoscience remote Sens. 30, 950–959. doi:10.1109/36.175330

CrossRef Full Text | Google Scholar

Zhang, B., Chen, Z., Peng, D., Benediktsson, J. A., Liu, B., Zou, L., et al. (2019). Remotely sensed big data: evolution in model development for information extraction [point of view]. Proc. IEEE 107, 2294–2301. doi:10.1109/jproc.2019.2948454

CrossRef Full Text | Google Scholar