- 1College of Educational Science, Xinjiang Normal University, Urumqi, China
- 2Department of Preschool Education, Hebei Normal University, Shijiazhuang, China
- 3Shanghai Institute of Early Childhood Education, Shanghai Normal University, Shanghai, China
Background: Executive Function and the Approximate Number System are well-established as critical components in developing the Cardinality Principle in young children. However, most existing studies explore the relationship between these variables in isolation without examining whether Approximate Number System mediates the relationship between Executive Function and the Cardinality Principle and the role of age in this. This study aimed to address this gap by investigating the mediating role of the Approximate Number System in the relationship between Executive Function and the Cardinality Principle and the moderating role of age in young children.
Methods: This cross-sectional study was conducted in China from February to June 2024. A total of 203 young children (97 boys and 106 girls, Mean age = 68.93 ± 7.076 months) participated. Participants were assessed using a range of tests: the Day-Night Stroop Task, Digit Recall Task, Dimensional Change Card Sort Task, Panamath Test Software, How Many Task, and Give-N Task to measure Executive Function, Approximate Number System, and Cardinality Principle. Data were analyzed using SPSS 26.0 and PROCESS v4.1 (Model 4) to explore the relationships among Executive Function, the Approximate Number System, and the Cardinality Principle through Pearson correlations, multivariate regression, and mediation analysis with 5000 bootstrap samples.
Results: Correlation analysis revealed that the Cardinality Principle was significantly and positively correlated with Inhibitory Control, Working Memory, Cognitive Flexibility, Executive Function, and the Approximate Number System. Regression analyses indicated that Executive Function positively predicted young children's Cardinality Principle. Specifically, Working Memory and Cognitive Flexibility were positive predictors of the Cardinality Principle, while Inhibitory Control was not. Mediation analysis results demonstrated that the Approximate Number System mediated the relationships between Inhibitory Control and the Cardinality Principle, Working Memory and the Cardinality Principle, and Cognitive Flexibility and the Cardinality Principle, respectively. In addition, the study found that young children's age negatively moderated the relationship between the Approximate Number System and the Cardinality Principle.
Conclusions: The study emphasizes that in developing young children's Cardinality Principle, emphasis should be placed on improving their Executive Function and Approximate Number System while considering the age differences of young children and developing appropriate educational methods for different age groups.
1 Introduction
The Cardinality Principle (CP) refers to the understanding that the final number in a counting sequence represents the total number of items in the set (Paliwal and Baroody, 2020; Simon et al., 2023). This principle is fundamental for young children's acquisition of ordinal knowledge (Colomé and Noël, 2012), quantitative comparison (Abreu-Mendoza et al., 2013), spatial concepts (Berteletti et al., 2010), mathematical language (Hornburg et al., 2018), and early arithmetic skills (Paliwal and Baroody, 2020). It serves as a cornerstone for grasping formal mathematics and significantly influences young children's mathematical achievement in school (Paliwal and Baroody, 2020). Given its importance, the CP is pivotal to early mathematical cognition and forms the bedrock of effective math education.
However, the development of the CP is not an isolated process but rather one that intertwines with various cognitive factors. Despite extensive research, there is no consensus on the extent to which different cognitive abilities contribute to mathematics learning. Nonetheless, it is widely accepted that both domain-general and domain-specific abilities play crucial roles (Passolunghi et al., 2014). Research trends in recent years have shown that scholars are increasingly focusing on the key critical roles of Executive Function (EF, a domain-generalized ability) and Approximate Number System (ANS, a domain-specific ability) in CP formation and development (Odic et al., 2015; vanMarle et al., 2018; Sella et al., 2021; Bachman et al., 2022; Skagerlund et al., 2024).
EF is generally considered an umbrella term for higher-order cognitive processes necessary for the behavior of goal-directed individuals and is a domain-general ability. Its core elements includes inhibitory control, working memory, and cognitive flexibility (Diamond, 2013; Ganesan and Steinbeis, 2021). Inhibitory control involves the ability to suppress irrelevant information or inappropriate behavior to focus on a goal (Carlson and Wang, 2007). Working memory refers to the capacity to retain and manipulate task-related information during complex cognitive activities (Dunning and Holmes, 2014). Cognitive flexibility is the ability to adapt one's thinking and strategies in response to changing tasks or conditions (Highgate and Schenk, 2020). EF is critical for behavioral regulation, attention, and task-switching, and plays a foundational role in learning, particularly in mathematics (Bull and Lee, 2014; Zhang, 2016). While extensive research has demonstrated the importance of EF in early mathematical learning (Noël, 2009; Bull et al., 2011; Verdine et al., 2014; Mcclelland et al., 2014), most studies have focused on older children (Zhang, 2016). Few have explored how EF and its components affect the development of the CP in young children, leaving gaps in understanding the specific mechanisms involved.
The ANS is a domain-specific cognitive ability that enables individuals to make rapid, approximate quantitative judgments without relying on exact counting or symbolic numbers (Xu and Spelke, 2000). Cognitive neuroscience research indicates that the intraparietal sulcus, a key brain region, underpins the ANS (Dehaene et al., 1996). The ANS is considered crucial for developing CP, with empirical studies supporting this link (Halberda and Feigenson, 2008; Inglis and Gilmore, 2014). For instance, Fuhs et al. (2016) found a strong association between young children's ANS acuity and their development of the CP. vanMarle et al. (2018) also identified significant predictive relationships between the ANS and CP development. However, most research on this topic has been conducted outside China, and it remains unclear whether these findings apply to Chinese children.
Some scholars have pointed out that skills in general domains indirectly influence the development of mathematical competence through domain-specific skills (Östergren, 2013). This implies that from the theoretical level, there is a specific link between EF, ANS and CP and that ANS may be able to explain the relationship between EF and CP. Some scholars at home and abroad have conducted empirical studies on the relationship between EF, ANS and the development of the CP in young children. For example, a meta-analysis by Santana et al. (2022) covering 23 studies (mean = 69.6 months) found that higher cognitive flexibility contributes to improved comprehension of numbers. Ouyang et al. (2021) followed 138 young children (mean= 59.76 months) and showed a positive correlation between working memory and the accuracy of the ANS. Shusterman et al. (2016) studied 46 young children (mean= 50 months) between the ages of 36 and 60 months and showed that mastery of the CP time is synchronized with the development of their ANS. Not to be overlooked. The age of the young child is also one of the key factors. The association between young children's ANS and math ability has been found to decrease as they get older (Fazio et al., 2014; Peng et al., 2017; Schneider et al., 2017). This suggests that age may largely influence young children's link between the ANS and CP understanding, not only in terms of the existence of such a link but also in the strength of its effect. However, there are still gaps in our understanding of how EF affects CP, how ANS mediates this relationship, and the moderating role of age. In addition, the age of the subjects in previous studies has not been uniform, while some studies have shown that 4–7 years of age is an important period for the development of EF, ASN, and CP in young children (Jordan et al., 2006; Liu, 2013; Zhou, 2004). Therefore, the study used 4–7 young children as research subjects to explore whether ANS mediates the relationship between EF and CP and the moderating role of age, which can more effectively explore the relationship between young children's EF, ANS, and CP development, as well as provide educators with theoretical and practical insights in developing young children's mathematical skills.
1.1 Executive Function and young children's Cardinality Principle
The relationship between EF and mathematical abilities is well-documented, yet the specific link between EF and CP in young children remains less explored. Existing literature suggests that EF and the CP may share underlying physiological and cognitive processes. Research has identified brain regions such as the prefrontal cortex, orbitofrontal cortex, and anterior cingulate gyrus as critical for EF (Gao, 2009), while areas like the occipital-parietal-frontal regions are active during numerical processing (Thioux et al., 2001; Vandecruys et al., 2024).
In theoretical discussions, scholars have suggested that excellent inhibitory control is crucial for children when performing basic maths tasks such as counting and cardinal numbers. This ability helps children accurately recognize and count objects by following counting rules and effectively ignoring irrelevant distracting information (Fuhs and McNeil, 2013). In addition, the role of working memory cannot be underestimated, as it enables individuals to quickly and efficiently extract number facts and problem representations from long-term memory and to save the required counting information during problem-solving temporarily (Hubber et al., 2014). Further, cognitive flexibility is a key competency in children's mathematics learning, enabling them to switch flexibly between different mathematical strategies and concepts (Santana et al., 2022). As children progress from mere understanding of counting sequences to mastery of quantitative concepts, they must shift their thinking from a procedural to a conceptual level. This cognitive flexibility helps them better understand the quantitative information provided by counting (Purpura et al., 2017).
Empirical studies on EF and CP show mixed results. For instance, Scalise et al. (2021) found that inhibitory control predicted the CP, while Fuhs et al. (2016) did not find a significant correlation. Similarly, research on working memory has yielded conflicting findings, with some studies showing a positive correlation with the CP and others finding no significant relationship (Skagerlund et al., 2024; Goffin and Ansari, 2016). In some studies, cognitive flexibility has been linked to CP development, but the results are not universally consistent (Van der Ven et al., 2012; Fuhs et al., 2016; Santana et al., 2022). This lack of consensus highlights the need for further investigation into how different components of EF relate to the CP (Bull and Lee, 2014). Thus, this study hypothesizes:
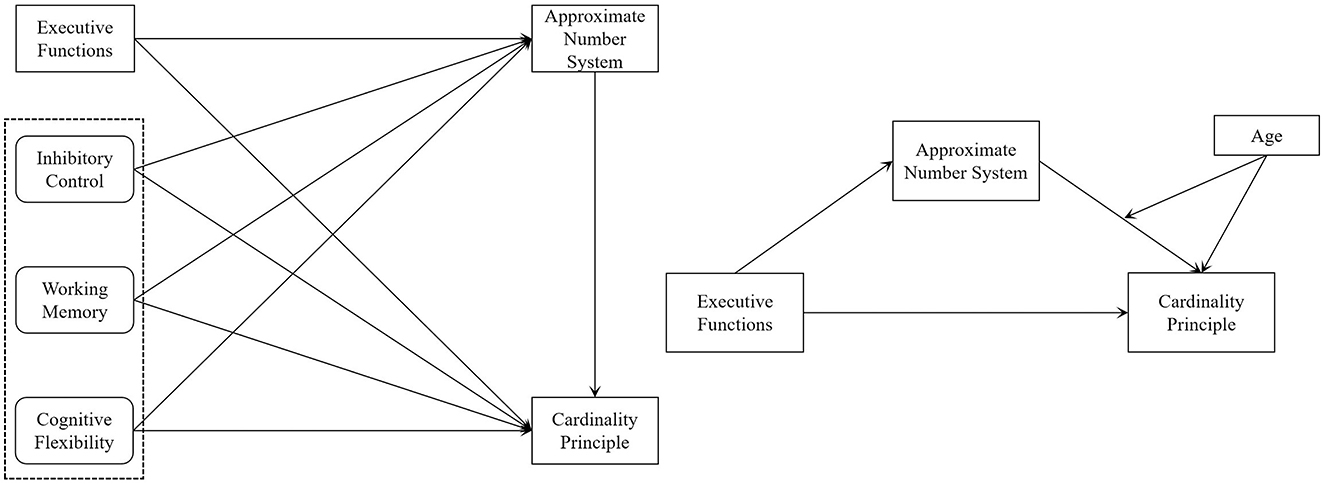
Hypothesis 1a (H1a): EF positively affects the CP.
Hypothesis 1b (H1b): Inhibitory Control positively affects the CP.
Hypothesis 1c (H1c): Working Memory positively affects the CP.
Hypothesis 1d (H1d): Cognitive Flexibility positively affects the CP.
1.2 Executive Function and the Approximate Number System
The role of EF in ANS tasks has been explored from various perspectives. According to dual processing theory, cognitive processing involves both intuitive and analytical levels. Intuitive processing is rapid and unconscious, while analytical processing is deliberate and conscious (Evans and Stanovich, 2013; Keren, 2013). The ANS, which supports intuitive processing, allows for quick quantitative estimates without detailed counting. EF, linked to analytical processing, regulates and optimizes these intuitive estimates, ensuring their accuracy and flexibility (Evans, 2008).
Empirical studies have examined the relationship between EF and the ANS. Mueller and Brand (2018) found a negative correlation between errors in EF tasks and ANS performance, indicating that better EF is associated with higher ANS accuracy. Research focusing on sub-components of EF, such as inhibitory control, working memory and cognitive flexibility, has also explored their roles in ANS tasks. For instance, Fuhs and McNeil (2013) found that better inhibitory control was associated with higher ANS acuity. Similarly, Ouyang et al. (2021) showed a positive correlation between working memory and ANS accuracy. Cognitive flexibility has been linked to improved ANS performance, as demonstrated by Purpura and Simms (2018), who found significant correlations between cognitive flexibility and ANS accuracy.
1.3 Approximate Number System and the Cardinality Principle
Researchers have divided the human non-symbolic number system into the Exact Number System and the ANS. The ANS, present in both humans and animals, improves with age and is critical for understanding number concepts and developing mathematical skills (Halberda and Feigenson, 2008; Gilmore et al., 2011; Halberda et al., 2012). The intraparietal sulcus is crucial for number cognition and underpins the ANS (Dehaene et al., 1996). Studies have shown that the ANS is essential for developing the CP (Dehaene et al., 1998; Feigenson et al., 2004, 2013; Mussolin et al., 2016; Piazza, 2010). For example, Shusterman et al. (2016) found that the development of the CP coincided with ANS maturation, and vanMarle et al. (2018) identified significant predictive relationships between the ANS and the CP.
Contrary views exist, such as Schröder et al. (2022), who found no significant effect of ANS acuity at 1.5 years on later CP acquisition. Some researchers argue that the ANS and mathematical ability are independent (Carey, 2001, 2004; Rips et al., 2008; Butterworth, 2010; Libertus et al., 2014; Carey et al., 2017). Despite these conflicting views, most evidence supports a correlation between the ANS and mathematical ability. Empirical research on this topic is limited in China, and no studies have investigated the role of the ANS in mediating the relationship between EF and the CP. Thus, this study aims to examine this mediation effect in Chinese children.
Hypothesis 2a (H2a): EF affects the CP through the ANS.
Hypothesis 2b (H2b): Inhibitory Control affects the CP through the ANS.
Hypothesis 2c (H2c): Working Memory affects the CP through the ANS.
Hypothesis 2d (H2d): Cognitive Flexibility affects the CP through the ANS.
1.4 The moderating role of age
Recent findings suggest that age influences children's ANS acuity and CP. Specifically, as age increases, young children show a positive correlation in the acuity of ANS (Sekuler and Mierkiewicz, 1977; Holloway and Ansari, 2009). Zhou (2004) study noted that young children's understanding of CP was strongly correlated with their age. Hornburg et al. (2018) found that young children's age was significantly and positively correlated with their performance on the Give-n task but not with their performance on the how many tasks. Notably, recent studies have shown that the relationship between ANS and math ability diminishes with age (Fazio et al., 2014; Peng et al., 2017; Schneider et al., 2017; Inglis et al., 2011; Mussolin et al., 2012). For example, Inglis et al. (2011) found that young children's correctness and Weber coefficients on a quantity comparison task were significantly and positively correlated with scores on the Mathematics Achievement Test (Woodcock-Johnson III-Calculation). In contrast, this relationship was not significant in adults. A study by Mussolin et al. (2012) among preschoolers found that the correlation between ANS acuity and symbolic math ability was significant among 3- to 4-year-olds but not among 5- to 6-year-olds. However, this hypothesis was not supported by the results of Chen and Li (2014) meta-analysis, which found that the correlation between young children's ANS acuity and math proficiency did not change with age. This suggests that no academic consensus exists on the relationship between age, ANS acuity, and math ability. In addition, few studies have further explored whether age moderates the relationship between ANS acuity and young children's CP. Based on this, one of the goals of this study was to investigate whether age plays a moderating role in the relationship between ANS acuity and young children's CP.
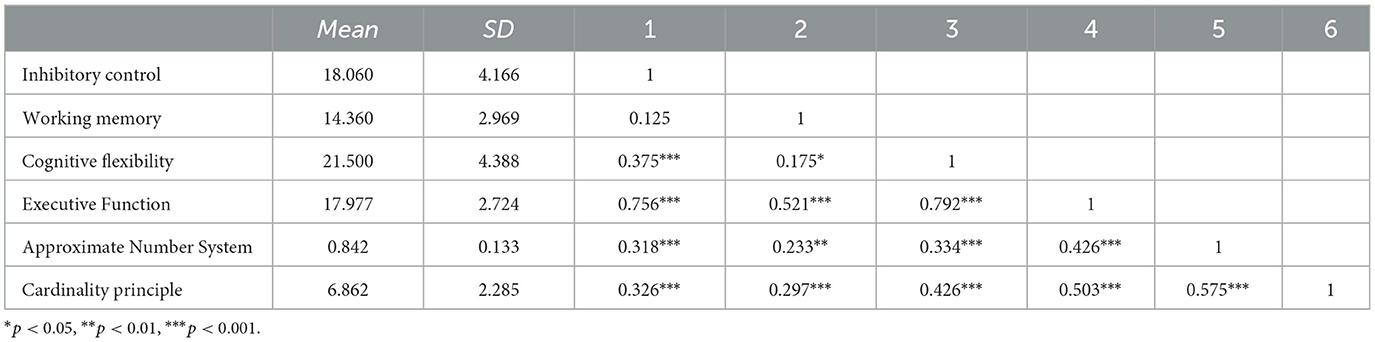
Hypothesis 3 (H3): Age negatively moderates the relationship between ANS acuity and young children's CP.
1.5 The present study
Research has explored the relationships between young children's EF, ANS, and the development of the CP. Studies have examined the connections between EF and ANS, EF and the CP, and ANS and the CP. These investigations have provided valuable insights into mathematical development in young children. However, several issues remain unresolved. First, the relationship between EF and CP is still debated, and there is a lack of research on the specific mechanisms through which EF influences the development of CP in young children. Second, while some studies have investigated how various sub-dimensions of EF—such as inhibitory control, working memory, and cognitive flexibility—affect the ANS, there is no consensus on these mechanisms. Lastly, there has been limited research on the interrelationships among young children's EF, ANS, and the development of the CP. In addition, few scholars have explored the moderating role of age in the relationship between ans and cp. To fill these gaps, the present study examined the mechanisms by which EF influences CP development, whether ANS mediates this relationship, and the moderating role of age. The following hypotheses were proposed in this study (see Figure 1).
Hypothesis 1a (H1a): EF positively affects the CP.
Hypothesis 1b (H1b): Inhibitory Control positively affects the CP.
Hypothesis 1c (H1c): Working Memory positively affects the CP.
Hypothesis 1d (H1d): Cognitive Flexibility positively affects the CP.
Hypothesis 2a (H2a): EF affects the CP through the ANS.
Hypothesis 2b (H2b): Inhibitory Control affects the CP through the ANS.
Hypothesis 2c (H2c): Working Memory affects the CP through the ANS.
Hypothesis 2d (H2d): Cognitive Flexibility affects the CP through the ANS.
Hypothesis 3 (H3): Age negatively moderates the relationship between ANS acuity and young children's CP.
2 Method
2.1 Participants
Participants were recruited from preschools and kindergartens in Urumqi. Parental consent was obtained for 210 young children, but due to absences during testing, complete data were available for 203 young children. The sample consisted of 97 boys and 106 girls, aged 53–88 months (Mean age = 68.93 ± 7.076 months). Testing occurred in the young children's classrooms, and they received stickers or small prizes for their participation.
2.2 Measures
2.2.1 Executive Function
EF was assessed through three sub-dimensions: inhibitory control, working memory, and cognitive flexibility. Based on this, the mean scores of the three sub-dimensions were summarized to become the young children's EF scores.
2.2.1.1 Inhibitory control—Day-Night Stroop Task
Based on Marcovitch et al. (2015) Day-Night Stroop Task, young children were shown images of the sun and moon and instructed to say “night” when they saw the sun and “day” when they saw the moon. The task included 10 pictures of each image, with 20 formal tests following five practice trials. Scores ranged from 0 to 20 points. In this study, the Cronbach's α of this task is 0.948.
2.2.1.2 Working memory—Digit Recall Task
Adapted from Gathercole et al. (2004), this task involved recalling sequences of digits read at a rate of one per second. The test started with sequences of 1 digit and increased in length until the child failed to recall three consecutive sets. The task consisted of seven lists ranging from 1 to 7 digits, with scores ranging from 0 to 21 points. In this study, the Cronbach's α of this task is 0.793.
2.2.1.3 Dimensional Change Card Sort Task
Based on Zelazo (2006) Dimensionally Variable Card Categorization Task, young children sorted cards by color and shape. The test included six practice trials and 24 formal tests, with scores ranging from 0 to 24 points. The Cronbach's α for this task was 0.931.
2.2.2 Approximate Number System
The ANS was evaluated using the Panamath test software developed by Halberda and Feigenson (2008), primarily using a dot-matrix comparison task. The task began with a “+” focus point on the computer screen, and when the “space” key was pressed, the left and right sides of the screen were provided with yellow dots and blue dots, respectively. The task requires the child to select the higher number of dots from the two dots and respond by pressing the appropriate key (labeled with the proper color on the keyboard beforehand). If the child failed to respond within the presentation time (2,128 milliseconds), the stimulus disappeared, a masking stimulus was presented, and a response box was presented with a key-press response to proceed to the next trial. The number of dots in each dot matrix ranged from 5 to 21, and the ratio of the number of yellow dots to blue dots ranged from 1.2 to 2.8 for random presentation. A total of eight practice trials and 80 formal trials were included, of which 40 trials had more yellow dots and another 40 had more blue dots. The 40 tests consisted of dots with the same number of dots and the same size of the total area of the dots, and the other 40 tests consisted of dots with the same number of dots and the same size of the total area of the dots. Test results were generated at the end of the test, i.e., the three metrics of accuracy, namely reaction time, accuracy and Weber's coefficient, were used as measures of ANS acuity (Peng et al., 2017; Inglis and Gilmore, 2014), and the test has been validated for use with Chinese children (Ouyang et al., 2021; Guo et al., 2021).
2.2.3 Cardinality Principle
CP was assessed using the “Base Number Concept Measurement Task” and “Counting by Objects and Saying the Total Task” from Zhao (2006) and Zhang (2017). The mean scores of the two sub-tasks were summarized to become the young children's CP scores. The tasks involved:
2.2.3.1 How Many Task
Young children were asked to count and report the number of blocks in sets of varying sizes, with scores ranging from 0 to 9 points. In this study, the Cronbach's α of this task is 0.846.
2.2.3.2 Give-N Task
Young children were asked to provide a specific number of blocks from larger sets, with scores ranging from 0 to 9 points. In this study, the Cronbach's α of this task is 0.872.
2.3 Procedure
Ethical approval was obtained from the Shanghai Normal University Ethics Committee. Testing was conducted in schools with parental and school principal consent. Parents and teachers were informed that data would be used solely for research purposes and kept confidential. Trained researchers conducted the tests from May to June 2024. Each child participated in individual, one-on-one testing sessions lasting ~25–40 min.
2.4 Analysis
Data were analyzed using SPSS 29.0. Descriptive statistics were used to assess the current state of development in EF, ANS, and Cardinality. Correlation analyses examined relationships between these variables. Given that numerous studies have pointed out that gender and age affect EF, ANS, and CP (Sekuler and Mierkiewicz, 1977; Sabbagh et al., 2006; Holloway and Ansari, 2009; Acar, 2018; Hornburg et al., 2018), we tested the predictive power of EF and its subdimensions on CP by using gender and age as covariates. Mediation analyses using SPSS Process 4.1 tested whether the ANS mediated the relationships between EF sub-dimensions and the CP.
3 Results
3.1 Descriptive statistics and correlation
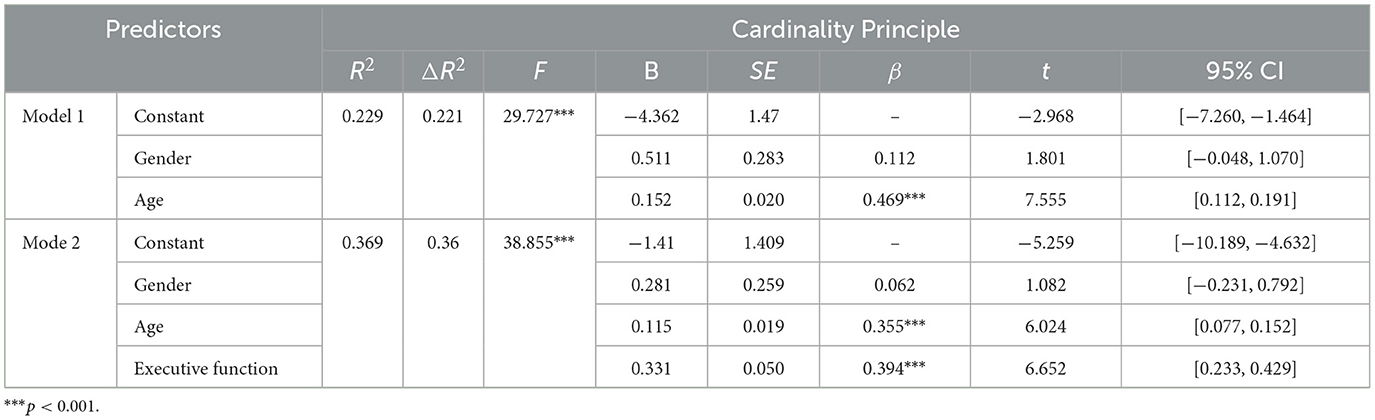
Descriptive statistics and Pearson's correlation coefficients are detailed in Table 1. The CP was significantly correlated with Inhibitory Control (r = 0.326, p < 0.001), Working Memory (r = 0.297, p < 0.001), Cognitive Flexibility (r = 0.426, p < 0.001), EF (r = 0.503, p < 0.001), and ANS (r = 0.575, p < 0.001). ANS was significantly correlated with Inhibitory Control (r = 0.318, p < 0.001), Working Memory (r = 0.233, p < 0.01), Cognitive Flexibility (r = 0.334, p < 0.001), and EF (r = 0.426, p < 0.001).
3.2 Direct associations between Executive Function and young children's Cardinality Principle
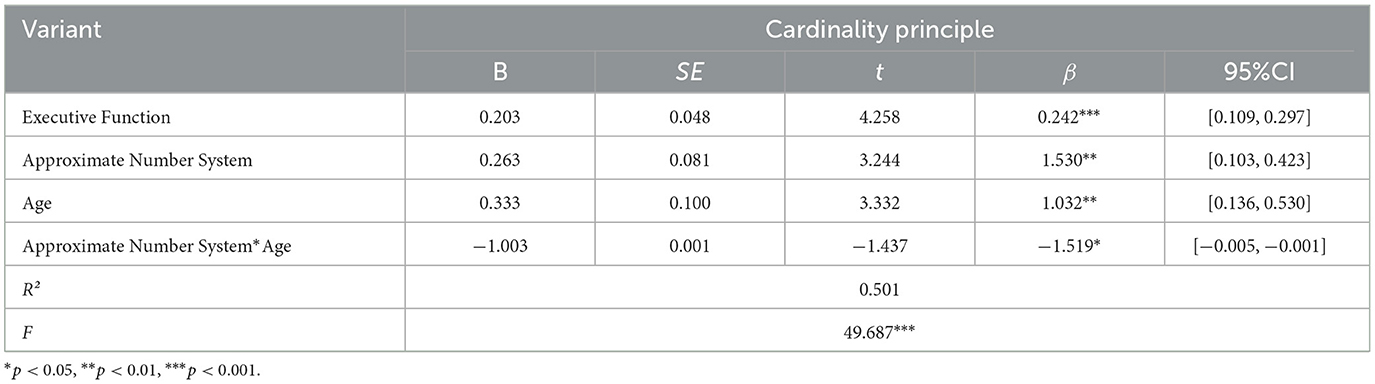
After controlling for gender and age, linear regression analysis (Table 2) showed that EF (β = 0.394, p < 0.001) positively influences the CP, supporting Hypothesis 1a. Regarding sub-dimensions (see Table 3), Inhibitory Control (β = 0.112, p > 0.05) did not significantly impact the CP, refuting Hypothesis 1b. Working Memory (β = 0.179, p < 0.01) and Cognitive Flexibility (β = 0.272, p < 0.001) positively influenced the CP, supporting Hypotheses 1c and 1d.
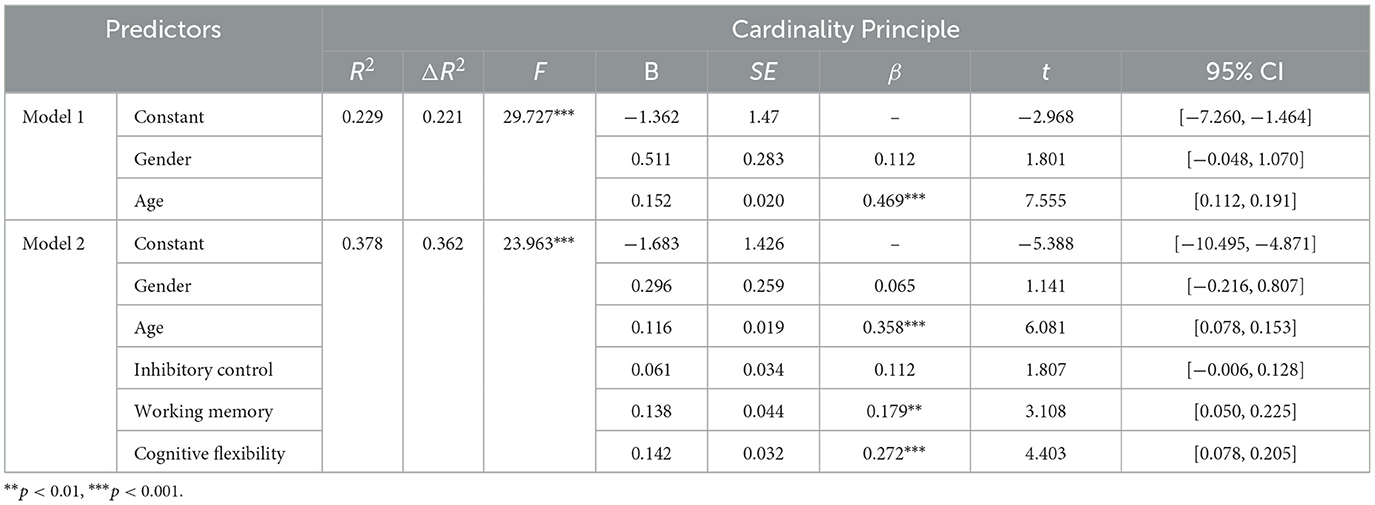
Table 3. Regression analysis of the effect of Executive Function's sub-dimensions on Cardinality Principle.
3.3 The mediating role of the Approximate Number System
Since only one covariate, age, was significant in the linear regression, it was continued as a covariate in the mediation analysis. To more effectively explore the mediating role of ANS between the EF's sub-dimensions and CP, when mediation was analyzed for a sub-dimension, we added the other two sub-dimensions to the model as covariates. Mediation analysis (Tables 4, 5) revealed that EF was positively associated with the ANS (β = 0.381, p < 0.001), which in turn positively affected the CP (β = 0.389, p < 0.001). The residual direct effect was also significant (β = 0.255, p < 0.001), indicating that the ANS partially mediated the relationship between EF and the CP [indirect effect =0.148, bootstrap 95% CI (0.070–0.231)]. The mediating impact accounted for 36.725% of the total effect of EF on the CP. Inhibitory Control's effect on the CP was fully mediated by the ANS [indirect effect = 0.072, bootstrap 95% CI (0.006–0.145)], with the mediating impact accounting for 60.504% of the total effect. For Working Memory, the ANS partially mediated the relationship with the CP [indirect effect = 0.058, bootstrap 95% CI (0.006–0.113)], with the mediating impact accounting for 32.584% of the total effect. Cognitive Flexibility's effect was also partially mediated by the ANS [indirect effect = 0.080, bootstrap 95% CI (0.017–0.154)], with the mediating impact accounting for 28.777% of the total effect. The final path coefficients are illustrated in Figure 2.
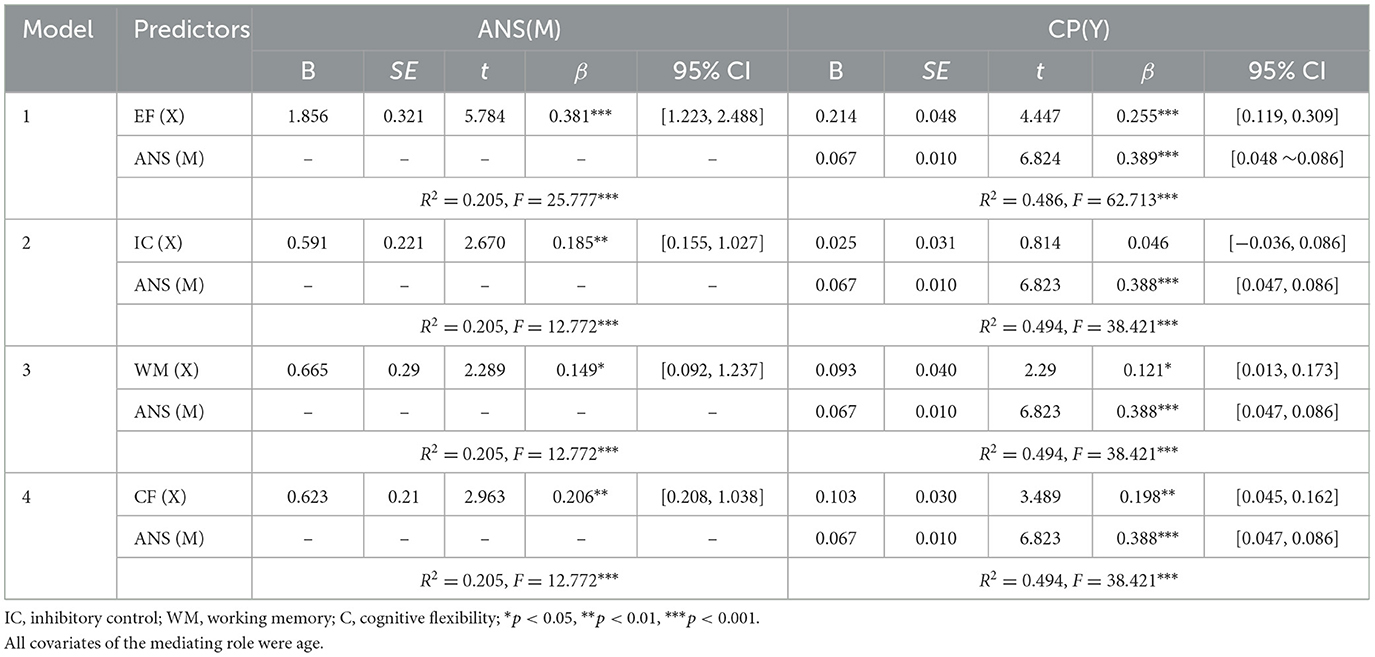
Table 4. Analysis of the mediating role of the Approximate Number System between Executive Function and its sub-dimensions and the Cardinality Principle.
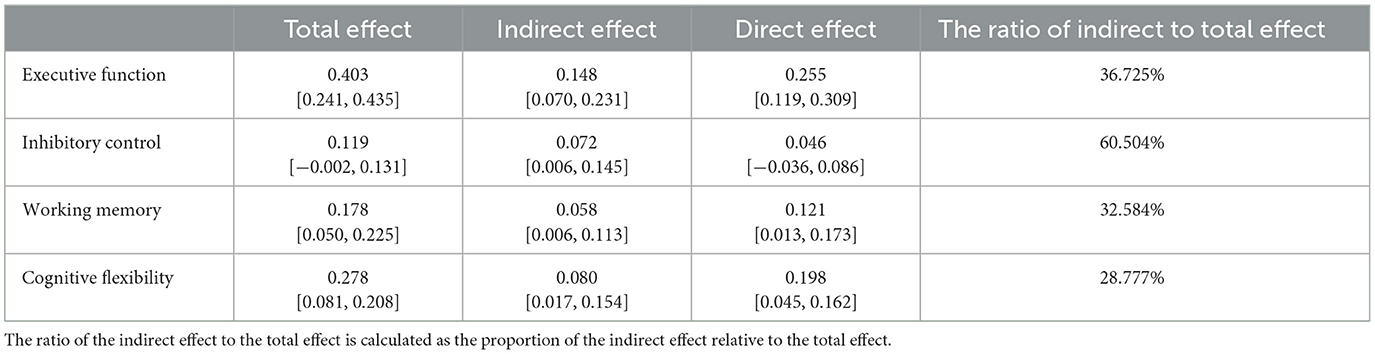
Table 5. Analysis of the mediating effect of the Approximate Number System between Executive Function and its sub-dimensions and the Cardinality Principle.
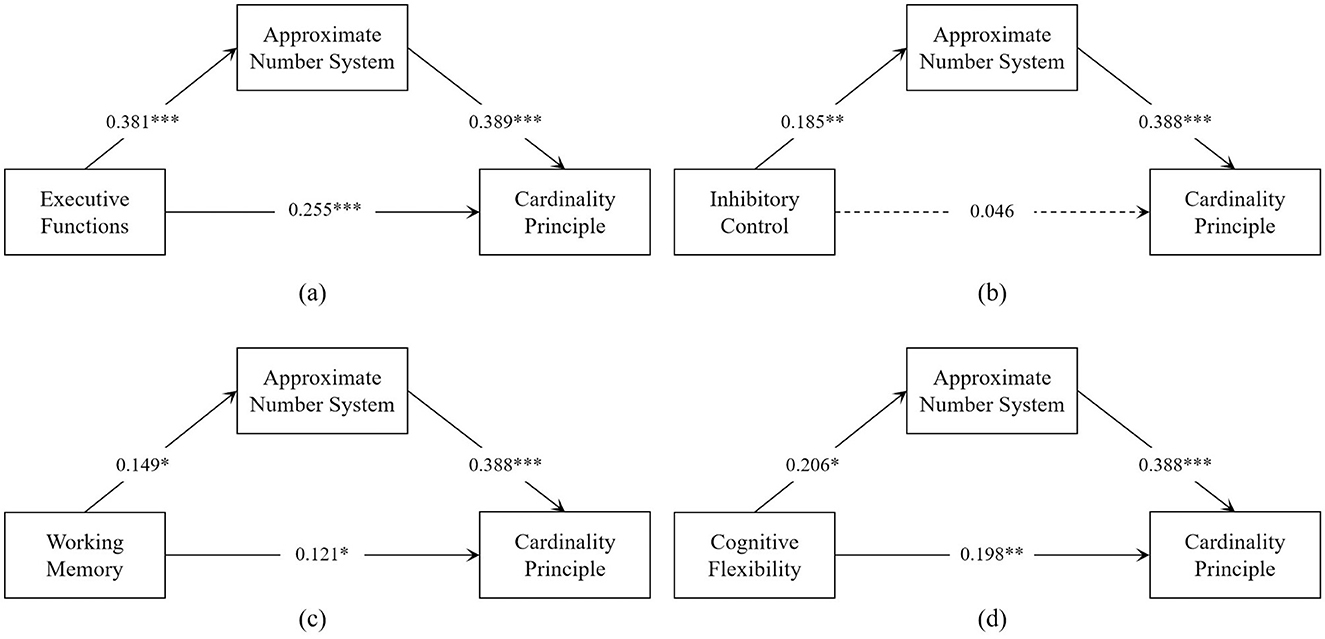
Figure 2. Approximate Number System mediated Executive Function and its sub-dimensions with Cardinality Principle. *p < 0.05, **p < 0.01, ***p < 0.001.
3.4 Mediation and moderated mediation models
To further investigate the relationship between the ANS and CP for young children in different age groups, the study analyzed the moderating role of young children's age in the mediator model by using the PROCESS macro program (model 14), and the results are shown in Table 6 and Figure 3. Both ANS (β = 1.530, p < 0.01) and young children's age (β = 1.032, p < 0.01) significantly and positively predicted cp, whereas the interaction term between ANS and young children's age (β = −1.519, p < 0.05) significantly and negatively predicted CP, suggesting that the young children's age plays a negatively moderating role in the relationship between ANS and CP. We then conducted a simple slope analysis to explore the nature of the moderating effect further (see Table 7; Figure 4). The results showed that in the low age level (mean – 1 SD), the effect was β = 0.086 [p < 0.001) (p < 0.001, 95% CI (0.062, 0.111)], and in the middle age level (mean), the effect was β = 0.066 [p < 0.001, 95% CI (0.047, 0.085)]. At high age level (mean + 1 SD), the effect was β =0.046 (p < 0.01, 95% CI (0.020–0.071)]. This suggests that the predictive effect of ANS on CP diminishes with age.
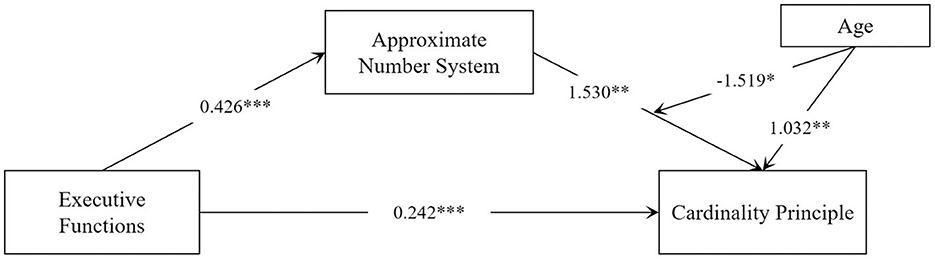
Figure 3. The moderating role of age as an Approximate Number System with Cardinality Principles. *p < 0.05, **p < 0.01, ***p < 0.001.

Table 7. Indirect effects of Approximate Number System on Cardinality Principle under different age conditions.
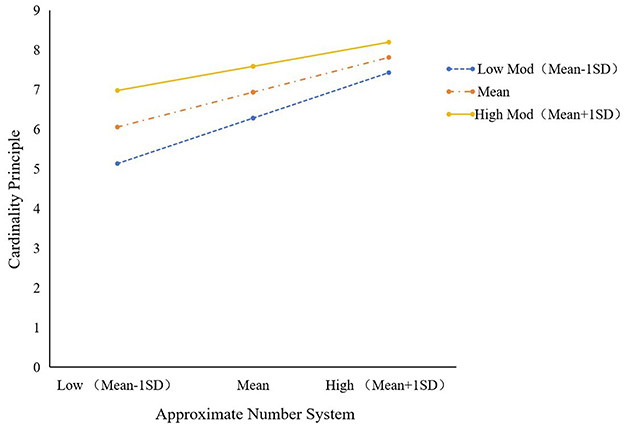
Figure 4. Indirect effects of Approximate Number System on Cardinality Principle under different age conditions.
4 Discussion
Previous research has explored the relationships among young children's EF, ANS, and CP. However, there is a lack of consensus in the findings, and few studies have simultaneously examined the interactions among these three variables. This study aims to clarify the pathways through which EF influences the CP and to evaluate the mediating role of the ANS. Our findings yield two primary conclusions: (1) EF positively impacts the development of the CP in young children, (2) the ANS mediates the relationship between EF and the CP, and (3) Age Negatively Moderates the Relationship Between ANS and CP.
4.1 Executive Function and young children's Cardinality Principle
Consistent with previous studies (Purpura et al., 2017; Simanowski and Krajewski, 2019), our research confirms that EF positively predicts the CP. Young children with stronger EF exhibit a higher understanding of cardinality. Within EF, working memory and cognitive flexibility are found to be more significant predictors of CP compared to inhibitory control.
The lack of a significant direct correlation between inhibitory control and the CP may be attributed to the nature of the Day-Night Stroop Task used in this study. Gerstadt et al. (1994) noted that this task is challenging for younger children (3.5–4.5 years) but relatively easier for older children (6–7 years), which may reduce variability in inhibitory control among the participants. Additionally, young children's development of the CP may rely more on direct interactions with quantities and mathematical guidance rather than on inhibitory control alone (Levine et al., 2010). While inhibitory control plays a role in some mathematical tasks, it does not directly impact the CP as significantly as working memory and cognitive flexibility.
Empirical evidence supports that working memory and cognitive flexibility are more directly related to the CP (Fuhs et al., 2016; Skagerlund et al., 2024). Working memory is crucial for math learning as it involves retaining and manipulating numerical information. Early counting often relies on finger movements, which help young children track counted objects and reduce cognitive load (Kirsh and Maglio, 1994). Young children with robust working memory are better equipped to master the CP because they can manage and process numerical information more effectively.
Cognitive flexibility also plays a critical role by allowing young children to switch between different mathematical strategies and concepts (Santana et al., 2022). As young children progress from understanding counting sequences to grasping the concept of quantity, they must adapt their thinking from a procedural to a conceptual level. This flexibility enables them to better understand that counting provides quantitative information (Purpura et al., 2017), thus improving their mastery of the CP.
4.2 The mediating role of the Approximate Number System
Our study demonstrates that the ANS mediates the relationship between EF and CP. Specifically, the ANS mediates the effects of inhibitory control, working memory, and cognitive flexibility on the CP. As young children's EF components—such as inhibitory control, working memory, and cognitive flexibility—improve, their ANS acuity also increases, which in turn enhances their understanding of cardinality.
This finding aligns with Kang et al. (2020) theory. Inhibitory control positively influences the CP through its effect on the ANS. Young children with higher inhibitory control can better manage interferences during quantity estimation, allowing the ANS to focus more effectively on the quantity being estimated (Fuhs and McNeil, 2013). This enhanced focus improves the accuracy of estimation and provides a more reliable foundation for developing CP.
Similarly, working memory positively affects the CP by enhancing ANS acuity. Since working memory is essential for processing and controlling numerical information, improvements in working memory contribute to better ANS performance (Baddeley, 2018; Ouyang et al., 2021), which supports the development of CP.
Cognitive flexibility also impacts the CP through the ANS. In tasks requiring non-symbolic number comparison, young children with higher cognitive flexibility can effectively shift their focus and maintain the ANS's functionality (Kang et al., 2020). This flexibility aids in the formation and development of CP.
4.3 The moderating role of the age
The study showed that young children's age negatively moderated the relationship between ANS and CP. Specifically, the effect of ANS on CP gradually weakened as toddlers aged. This finding validated research hypothesis 3 and the theory previously proposed by Liang et al. (2021) that age may influence the strength of the relationship between ANS and math proficiency.
According to Piaget (1977) theory of stages of cognitive development, young children's cognitive abilities develop with age, and young children understand quantities primarily through visual and concrete information. At this time, their understanding of quantities may be based on ANS. As they grow older, children begin to use logic and more abstract thinking to understand quantities, reducing their reliance on ANS.
On the one hand, young children's symbolic quantity systems mature with age. Due to the symbolic quantity system's precision characteristics, young children's reliance on ANS in quantity processing gradually decreases, while their reliance on the symbolic quantity system gradually increases (Geary et al., 2013; Wong, 2020; Liang et al., 2021). On the other hand, early formal math education helps young children focus on quantitative attributes, increasing the quality and efficiency of their performance on ANS tasks, with a resulting greater effect on ANS (Shusterman et al., 2016).
5 Contributions, limitations, and future directions
This study reveals the relationship between EF, ANS and CP and explores the moderating role of age in this process. These findings have important implications for the practice of early childhood mathematics education. First, strengthening young children's EF training can help improve their understanding of CP. Educators should design rich and varied cognitive flexibility and working memory activities to promote the development of young children's abilities in these areas. Second, the mediating role of ANS between EF and CP suggests that improving young children's cognitive skills in non-symbolic quantities helps them better grasp mathematical concepts. Therefore, educational practices should focus on developing young children's intuitive perception of quantities and estimation skills. In addition, the negative moderating effect of age on the relationship between ANS and CP reminds us that educational strategies should be adjusted for young children of different ages. For younger children, educators should pay more attention to the cultivation of ANS ability and help them establish a basic understanding of quantity through concrete and intuitive mathematical activities. Older children should be gradually guided to transition from intuitive to abstract thinking, reduce their reliance on ANS, and strengthen the training of the symbolic quantity system. In conclusion, the results of this study show that in the process of mathematics education for young children, EF, ANS and age factors should be considered to develop a targeted educational program. At the same time, it provides useful references for parents and teachers to guide them on better assisting young children in learning mathematics daily to promote their all-round development.
Despite these contributions, the study has limitations. First, the cross-sectional design limits our ability to explore the temporal dynamics of these relationships. Future research should employ longitudinal designs to further investigate how these variables interact over time. Second, the study's focus on a specific age range of preschoolers may limit the generalizability of the findings to other age groups. Expanding the age range in future studies could provide a more comprehensive understanding of these developmental processes. Third, it has been shown that EF can mediate the relationship between ANS and young children's mathematical ability (Price and Wilkey, 2017; Lonnemann et al., 2019), but this was not taken into account in this study, and the relationship between the three can be further explored in the future by starting with the interactions between ANS and EF. Lastly, variables such as family socioeconomic status (SES) (Starkey et al., 2004; Mcneil et al., 2011; Ouyang et al., 2021) and vocabulary skills (Negen and Sarnecka, 2012), which might influence the ANS and the CP, were not included in this study. Future research should incorporate these additional variables to deepen the exploration of developmental mechanisms in mathematical cognition.
6 Conclusion
This study revealed the relationship between EF, ANS and CP in young children. The conclusions are as follows: first, EF has a positive effect on the development of CP in young children, with working memory and cognitive flexibility being more important predictors of CP. Second, ANS mediated the relationship between EF and CP, suggesting that EF promotes CP development by increasing the acuity of ANS. Finally, age negatively moderated the relationship between ANS and CP, with the effect of ANS on CP diminishing with age. This finding suggests that, in the process of young children's mathematics education, we should pay attention to the development of EF while focusing on the role of ANS and considering the influence of age factors on the development of mathematical cognition. Therefore, educators should design targeted teaching strategies according to young children's age characteristics and cognitive development level to promote the comprehensive development of young children's mathematical abilities.
Data availability statement
The data is not publicly available due to ethical requirements. Requests to access the datasets should be directed to the corresponding author or Huanhuan Li, aHVhbmh1YW5saUB4am51LmVkdS5jbg==.
Ethics statement
The studies involving humans were approved by University Committee on Human Research Protection of Shanghai Normal University with approval number “2023035”. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin.
Author contributions
HL: Conceptualization, Funding acquisition, Methodology, Writing – original draft, Writing – review & editing. HD: Conceptualization, Funding acquisition, Methodology, Writing – original draft, Writing – review & editing. BD: Data curation, Formal analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing. ML: Data curation, Investigation, Writing – review & editing, Project administration. YW: Supervision, Writing – review & editing. ZW: Funding acquisition, Supervision, Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was supported by the Youth Fund Project of Humanities and Social Sciences, Ministry of Education (22YJC880032), Major Bidding Project under the “14th Five-Year Plan” for Educational Sciences in Hebei Province (2201053), 2024 Annual Think Tank Bidding Topic of the “Tianchi Talent Introduction Plan” in Xinjiang Uygur Autonomous Region (XJEDU2024J148), and Social Science Fund Project of Xinjiang Uygur Autonomous Region (2024BJYX150).
Acknowledgments
We are very grateful for the voluntary participation of the children and the support and help provided by the kindergarten director, teachers and parents of young children.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abreu-Mendoza, R. A., Soto-Alba, E. E., and Arias-Trejo, N. (2013). Area vs. density: influence of visual variables and cardinality knowledge in early number comparison. Front. Psychol. 4:805. doi: 10.3389/fpsyg.2013.00805
Acar, I. H. (2018). Examining the regulatory and reactive temperamental characteristics as predictors of low income preschool children's executive function. Curr. Psychol. 37, 748–759. doi: 10.1007/s12144-017-9562-3
Bachman, H., Miller, P., Elliott, L., Duong, S., Libertus, M., and Votruba-Drzal, E. (2022). Associations among socioeconomic status and preschool-aged children's, number skills, and spatial skills: the role of executive function. J. Exp. Child Psychol. 221:105453. doi: 10.1016/j.jecp.2022.105453
Baddeley, A. (2018). Exploring Working Memory: Selected Works of Alan Baddeley. London: Routledge/Taylor & Francis Group.
Berteletti, I., Lucangeli, D., Piazza, M., Dehaene, S., and Zorzi, M. (2010). Numerical estimation in preschoolers. Dev. Psychol. 46, 545–551. doi: 10.1037/a0017887
Bull, R., Espy, K. A., Wiebe, S. A., Sheffield, T. D., and Nelson, J. M. (2011). Using confirmatory factor analysis to understand executive control in preschool children: sources of variation in emergent mathematic achievement. Dev. Sci. 44, 575–587. doi: 10.1111/j.1467-7687.2010.01012.x
Bull, R., and Lee, K. (2014). Executive functioning and mathematics achievement. Child Dev. Perspect. 8, 36–41. doi: 10.1111/cdep.12059
Butterworth, B. (2010). Foundational numerical capacities and the origins of dyscalculia. Trends Cogn. Sci. 14, 534–541. doi: 10.1016/j.tics.2010.09.007
Carey, S. (2001). Cognitive foundations of arithmetic: evolution and ontogenisis. Mind Lang. 16, 37–55. doi: 10.1111/1468-0017.00155
Carey, S. (2004). Bootstrapping & the origin of concepts. Daedalus 133, 59–68. doi: 10.1162/001152604772746701
Carey, S., Shusterman, A., Haward, P., and Distefano, R. (2017). Do analog number representations underlie the meanings of young children's verbal numerals? Cognition 168, 243–255. doi: 10.1016/j.cognition.2017.06.022
Carlson, S. M., and Wang, T. S. (2007). Inhibitory control and emotion regulation in preschool children. Cogn. Dev. 22, 489–510. doi: 10.1016/j.cogdev.2007.08.002
Chen, Q., and Li, J. (2014). Association between individual differences in non-symbolic number acuity and math performance: a meta-analysis. Acta Psychol. 148, 163–172. doi: 10.1016/j.actpsy.2014.01.016
Colomé, À., and Noël, M. P. (2012). One first? Acquisition of the cardinal and ordinal uses of numbers in preschoolers. J. Exp. Child Psychol. 113, 233–247. doi: 10.1016/j.jecp.2012.03.005
Dehaene, S., Dehaene-Lambertz, G., and Cohen, L. (1998). Abstract representations of numbers in the animal and human brain. Trends Neurosci. 21, 355–361. doi: 10.1016/S0166-2236(98)01263-6
Dehaene, S., Tzourio, N., Frak, V., Raynaud, L., Cohen, L., Mehler, J., et al. (1996). Cerebral activations during number multiplication and comparison: a PET study. Neuropsychologia 34, 1097–1106. doi: 10.1016/0028-3932(96)00027-9
Diamond, A. (2013). Executive functions. Annu. Rev. Psychol. 64, 135–168. doi: 10.1146/annurev-psych-113011-143750
Dunning, D. L., and Holmes, J. (2014). Does working memory training promote the use of strategies on untrained working memory tasks? Mem. Cognit. 42, 854–862. doi: 10.3758/s13421-014-0410-5
Evans, J. S. (2008). Dual-processing accounts of reasoning, judgment, and social cognition. Annu. Rev. Psychol. 59, 255–278. doi: 10.1146/annurev.psych.59.103006.093629
Evans, J. S. B. T., and Stanovich, K. E. (2013). Dual-process theories of higher cognition: advancing the debate. Perspect. Psychol. Sci. 8, 223–241. doi: 10.1177/1745691612460685
Fazio, L. K., Bailey, D. H., Thompson, C. A., and Siegler, R. S. (2014). Relations of different types of numerical magnitude representations to each other and to mathematics achievement. J. Exp. Child. Psychol. 123, 53–72. doi: 10.1016/j.jecp.2014.01.013
Feigenson, L., Dehaene, S., and Spelke, E. (2004). Core systems of number. Trends Cogn. Sci. 8, 307–314. doi: 10.1016/j.tics.2004.05.002
Feigenson, L., Libertus, M. E., and Halberda, J. (2013). Links between the intuitive sense of number and formal mathematics ability. Child Dev. Perspect. 7, 74–79. doi: 10.1111/cdep.12019
Fuhs, M. W., Hornburg, C. B., and McNeil, N. M. (2016). Specific early number skills mediate the association between executive functioning skills and mathematics achievement. Dev. Psychol. 52, 1217–1235. doi: 10.1037/dev0000145
Fuhs, M. W., and McNeil, N. M. (2013). ANS acuity and mathematics ability in preschoolers from low-income homes: contributions of inhibitory control. Dev. Psychol. 16, 136–148. doi: 10.1111/desc.12013
Ganesan, K., and Steinbeis, N. (2021). Development and plasticity of executive functions: a value-based account. Curr. Opin. Psychol. 44, 215–219. doi: 10.1016/j.copsyc.2021.09.012
Gao, Y. X. (2009). The Cognitive-Neural Mechanism of Children's Inhibition Processes——the ERP Evidence From Audio-Visual Cross-Modal (Master's thesis). Shandong Normal University, Jinan, China.
Gathercole, S. E., Pickering, S. J., Ambridge, B., and Wearing, H. (2004). The structure of working memory from 4 to 15 years of age. Dev. Psychol. 40, 177–190. doi: 10.1037/0012-1649.40.2.177
Geary, D. C., Hoard, M. K., Nugent, L., and Bailey, D. H. (2013). Adolescents' functional numeracy is predicted by their school entry number system knowledge. PLOS ONE. 8:e54651. doi: 10.1371/journal.pone.0054651
Gerstadt, C. L., Hong, Y. J., and Diamond, A. (1994). The relationship between cognition and action: performance of children 3 1/2-7 years old on a Stroop-like day-night test. Cognition 53, 129–153. doi: 10.1016/0010-0277(94)90068-X
Gilmore, C., Attridge, N., and Inglis, M. (2011). Measuring the approximate number system. Q. J. Exp. Psychol. 64, 2099–2109. doi: 10.1080/17470218.2011.574710
Goffin, C., and Ansari, D. (2016). Beyond magnitude: judging ordinality of symbolic number is unrelated to magnitude comparison and independently relates to individual differences in arithmetic. Cognition 150, 68–76. doi: 10.1016/j.cognition.2016.01.018
Guo, L. Y., Xu, X. P., Dai, D., and Deng, C. P. (2021). Foundations for early mathematics skills: the interplay of approximate number system, mapping ability, and home numeracy activities. Cogn. Dev. 59:101083. doi: 10.1016/j.cogdev.2021.101083
Halberda, J., and Feigenson, L. (2008). Developmental change in the acuity of the “number sense”: The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Dev. Psychol. 44, 1457–1465. doi: 10.1037/a0012682
Halberda, J., Ly, R., Wilmer, J. B., Naiman, D. Q., and Germine, L. (2012). Number sense across the lifespan as revealed by a massive Internet-based sample. Proc. Natl. Acad. Sci. U. S. A. 109, 11116–11120. doi: 10.1073/pnas.1200196109
Highgate, Q., and Schenk, S. (2020). Cognitive flexibility in humans and other laboratory animals. J. Roy. Soc. New Zeal. 51, 1–31. doi: 10.1080/03036758.2020.1784240
Holloway, I. D., and Ansari, D. (2009). Mapping numerical magnitudes onto symbols: the numerical distance effect and individual differences in children's mathematics achievement. J. Exp. Child Psychol. 103, 17–29. doi: 10.1016/j.jecp.2008.04.001
Hornburg, C. B., Schmitt, S. A., and Purpura, D. J. (2018). Relations between preschoolers' mathematical language understanding and specific numeracy skills. J. Exp. Child Psychol. 176, 84–100. doi: 10.1016/j.jecp.2018.07.005
Hubber, P. J., Gilmore, C., and Cragg, L. (2014). The roles of the central executive and visuospatial storage in mental arithmetic: a comparison across strategies. Q. J. Exp. Psychol. 67, 936–954. doi: 10.1080/17470218.2013.838590
Inglis, M., Attridge, N., Batchelor, S., and Gilmore, C. (2011). Non-verbal number acuity correlates with symbolic mathematics achievement: but only in children. Psychon. Bull. Rev. 18, 1222–1229. doi: 10.3758/s13423-011-0154-1
Inglis, M., and Gilmore, C. (2014). Indexing the approximate number system. Acta Psychol. 145, 147–155. doi: 10.1016/j.actpsy.2013.11.009
Jordan, N. C., Kaplan, D., Oláh, L. N., and Locuniak, M. N. (2006). Number sense growth in kindergarten: a longitudinal investigation of children at risk for mathematics difficulties. Child. Dev. 77, 153–175. doi: 10.1111/j.1467-8624.2006.00862.x
Kang, D., Zhang, L., Cai, S., Liu, J. P., Lu, M. Y., and Liu, Q. X. (2020). The relationship between the accuracy of children's approximate number system and their mathematical ability. J. Math. Teach. Educ. 29, 19–24+31.
Keren, G. (2013). A tale of two systems: a scientific advance or a theoretical stone soup? Commentary on Evans & Stanovich (2013). Perspect. Psychol. Sci. 8, 257–262. doi: 10.1177/1745691613483474
Kirsh, D., and Maglio, P. (1994). On distinguishing epistemic from pragmatic action. Cogn. Sci. 18, 513–549. doi: 10.1207/s15516709cog1804_1
Levine, S. C., Suriyakham, L. W., Rowe, M. L., Huttenlocher, J., and Gunderson, E. A. (2010). What counts in the development of young children's number knowledge? Dev. Psychol. 46, 1309–1319. doi: 10.1037/a0019671
Liang, X., Kang, J. M., and Wang, L. J. (2021). The relationship between the approximate number system and mathematical abilities: evidence from developmental research. Adv. Psychol. Sci. 29, 827–837. doi: 10.3724/SP.J.1042.2021.00827
Libertus, M. E., Feigenson, L., Halberda, J., and Landau, B. (2014). Understanding the mapping between numerical approximation and number words: evidence from Williams syndrome and typical development. Dev. Sci. 17, 905–919. doi: 10.1111/desc.12154
Liu, H. Q. (2013). The Research on the Relationships Between Executive Function and Practical Consciousness of 4~7 yea rs o ld Children (Master's thesis). Liaoning Normal University, Dalian, China.
Lonnemann, J., Müller, C., Büttner, G., and Hasselhorn, M. (2019). The influence of visual-spatial skills on the association between processing of nonsymbolic numerical magnitude and number word sequence skills. J. Exp. Child Psychol. 178, 184–197. doi: 10.1016/j.jecp.2018.09.018
Marcovitch, S., O'Brien, M., Calkins, S. D., Leerkes, E. M., Weaver, J. M., and Levine, D. W. (2015). A longitudinal assessment of the relation between executive function and theory of mind at 3, 4, and 5 years. Cogn. Dev. 33, 40–55. doi: 10.1016/j.cogdev.2014.07.001
Mcclelland, M. M., Cameron, C. E., Duncan, R., Bowles, R. P., Acock, A. C., Miao, A., et al. (2014). Predictors of early growth in academic achievement: the head-toes-knees-shoulders task. Front. Psychol. 5:599. doi: 10.3389/fpsyg.2014.00599
Mcneil, N. M., Fuhs, M. W., Keultjes, M. C., and Gibson, M. H. (2011). Influences of problem format and ses on preschoolers' understanding of approximate addition. Cogn. Dev. 26, 57–71. doi: 10.1016/j.cogdev.2010.08.010
Mueller, S. M., and Brand, M. (2018). Approximate number processing skills contribute to decision making under objective risk: interactions with executive functions and objective numeracy. Front. Psychol. 9:1202. doi: 10.3389/fpsyg.2018.01202
Mussolin, C., Nys, J., and Leybaert, J. (2016). How approximate and exact number skills are related to each other across development: a review. Dev. Rev. 39, 1–15. doi: 10.1016/j.dr.2014.11.001
Mussolin, C., Nys, J., Leybaert, J., and Content, A. (2012). Relationships between approximate number system acuity and early symbolic number abilities. Trends. Neurosci. Educ. 1, 21–31. doi: 10.1016/j.tine.2012.09.003
Negen, J., and Sarnecka, B. W. (2012). Number-concept acquisition and general vocabulary development. Child Dev. 83, 2019–2027. doi: 10.1111/j.1467-8624.2012.01815.x
Noël, M. P. (2009). Counting on working memory when learning to count and to add: a preschool study. Dev. Psychol. 45, 1630–1643. doi: 10.1037/a0016224
Odic, D., Corre, M. L., and Halberda, J. (2015). Children's mappings between number words and the approximate number system. Cognition 138, 102–121. doi: 10.1016/j.cognition.2015.01.008
Östergren, R. (2013). Mathematical Learning Disability: Cognitive Conditions, Development and Predictions. Sweden: Linköping University Electronic Press.
Ouyang, X., Yang, Y., Zhang, X., and Zhang, Q. (2021). Longitudinal relations between the approximate number system and symbolic number skills in preschool children. J. Exp. Child Psychol. 212:105254. doi: 10.1016/j.jecp.2021.105254
Paliwal, V., and Baroody, A. J. (2020). How best to teach the cardinality principle? Early Child. Res. Q. 44, 152–160. doi: 10.1016/j.ecresq.2018.03.012
Paliwal, V., and Baroody, A. J. (2020). Cardinality principle understanding: the role of focusing on the subitizing ability. Zdm Math. Educ. 52, 649–661. doi: 10.1007/s11858-020-01150-0
Passolunghi, M. C., Cargnelutti, E., and Pastore, M. (2014). The contribution of general cognitive abilities and approximate number system to early mathematics. Br. J. Educ. Psychol. 84 Pt 4, 631–649. doi: 10.1111/bjep.12054
Peng, P., Yang, X., and Meng, X. (2017). The relation between approximate number system and early arithmetic: the mediation role of numerical knowledge. J. Exp. Child Psychol. 157, 111–124. doi: 10.1016/j.jecp.2016.12.011
Piaget, J. (1977). Psychology and Epistemology: Towards a Theory of Knowledge. London: Penguin Books.
Piazza, M. (2010). Neurocognitive start-up tools for symbolic number representations. Trends Cogn. Sci. 14, 542–551. doi: 10.1016/j.tics.2010.09.008
Price, R. G., and Wilkey, D. E. (2017). Cognitive mechanisms underlying the relation between nonsymbolic and symbolic magnitude processing and their relation to math. Cogn. Dev. 44, 139–149. doi: 10.1016/j.cogdev.2017.09.003
Purpura, D. J., Schmitt, S. A., and Ganley, C. M. (2017). Foundations of mathematics and literacy: the role of executive functioning components. J. Exp. Child Psychol. 153, 15–34. doi: 10.1016/j.jecp.2016.08.010
Purpura, D. J., and Simms, V. (2018). Approximate number system development in preschool: what factors predict change? Cogn. Dev. 45, 31–39. doi: 10.1016/j.cogdev.2017.11.001
Rips, L. J., Bloomfield, A., and Asmuth, J. (2008). From numerical concepts to concepts of number. Behav. Brain Sci. 31, 623–687. doi: 10.1017/S0140525X08005566
Sabbagh, M. A., Xu, F., Carlson, S. M., Moses, L. J., and Lee, K. (2006). The development of executive functioning and theory of mind. A comparison of Chinese and U.S. preschoolers. Psychol. Sci. 17, 74–81. doi: 10.1111/j.1467-9280.2005.01667.x
Santana, A. N., Roazzi, A., and Nobre, A. P. M. C. (2022). The relationship between cognitive flexibility and mathematical performance in children: a meta-analysis. Trends Neurosci. Educ. 28:100179. doi: 10.1016/j.tine.2022.100179
Scalise, N. R., Daubert, E. N., and Ramani, G. B. (2021). When one size does not fit all: a latent profile analysis of low-income preschoolers' math skills. J. Exp. Child Psychol. 209:105156. doi: 10.1016/j.jecp.2021.105156
Schneider, M., Beeres, K., Coban, L., Merz, S., Susan, S. S., Stricker, J., et al. (2017). Associations of non-symbolic and symbolic numerical magnitude processing with mathematical competence: a meta-analysis. Dev. Sci. 20:e12372. doi: 10.1111/desc.12372
Schröder, E., Gredebäck, G., Forssman, L., and Lindskog, M. (2022). Predicting children's emerging understanding of numbers. Dev. Psychol. 25:e13207. doi: 10.1111/desc.13207
Sekuler, R., and Mierkiewicz, D. (1977). Children's judgments of numerical inequality. Child Dev. 48, 630–633. doi: 10.2307/1128664
Sella, F., Slusser, E., Odic, D., and Krajcsi, A. (2021). The emergence of children's natural number concepts: current theoretical challenges. Child Dev. Perspect. 15, 265–273. doi: 10.1111/cdep.12428
Shusterman, A., Slusser, E., Halberda, J., and Odic, D. (2016). Acquisition of the cardinal principle coincides with improvement in approximate number system acuity in preschoolers. PLoS ONE 11:e0153072. doi: 10.1371/journal.pone.0153072
Simanowski, S., and Krajewski, K. (2019). Specific preschool executive functions predict unique aspects of mathematics development: a 3-year longitudinal study. Child Dev. 90, 544–561. doi: 10.1111/cdev.12909
Simon, M. A., Della Volpe, D., and Velamur, A. (2023). Construction of the cardinality principle through counting: critique and conjecture. Math Think. Learn. 25, 1–16. doi: 10.1080/10986065.2021.2012737
Skagerlund, K., Skagenholt, M., and Träff, U. (2024). Mathematics anxiety and number processing: the link between executive functions, cardinality, and ordinality. Q. J. Exp. Psychol. doi: 10.1177/17470218241234041. [Epub ahead of print].
Starkey, P., Klein, A., and Wakeley, A. (2004). Enhancing young children's mathematical knowledge through a pre-kindergarten mathematics intervention. Early Child. Res. Q. 19, 99–120. doi: 10.1016/j.ecresq.2004.01.002
Thioux, M., Pesenti, M., De Volder, A., and Seron, X. (2001). Category-specific representation and processing of numbers and animal names across semantic tasks: a PET study. Neuroimage 13, 617–617. doi: 10.1016/S1053-8119(01)91960-3
Van der Ven, S. H., Kroesbergen, E. H., Boom, J., and Leseman, P. P. (2012). The development of executive functions and early mathematics: a dynamic relationship. Br. J. Educ. Psychol. 82 (Pt 1), 100–119. doi: 10.1111/j.2044-8279.2011.02035.x
Vandecruys, F., Vandermosten, M., and De Smedt, B. (2024). The inferior fronto-occipital fasciculus correlates with early precursors of mathematics and reading before the start of formal schooling. Cortex 174, 149–163. doi: 10.1016/j.cortex.2024.02.014
vanMarle, K., Chu, F. W., Mou, Y., Seok, J. H., Rouder, J., and Geary, D. C. (2018). Attaching meaning to the number words: contributions of the object tracking and approximate number systems. Dev. Sci. 21:12495. doi: 10.1111/desc.12495
Verdine, B. N., Irwin, C. M., Golinkoff, R. M., and Hirsh-Pasek, K. (2014). Contributions of executive function and spatial skills to preschool mathematics achievement. J. Exp. Child Psychol. 126, 37–51. doi: 10.1016/j.jecp.2014.02.012
Wong, T. T. (2020). Are the acuities of magnitude representations of different types and ranges of numbers related? Testing the core assumption of the integrated theory of numerical development. Cogn. Dev. 54:100888. doi: 10.1016/j.cogdev.2020.100888
Xu, F., and Spelke, E. S. (2000). Large number discrimination in 6-month-old infants. Cognition 74, B1–B11. doi: 10.1016/S0010-0277(99)00066-9
Zelazo, P. D. (2006). The Dimensional Change Card Sort (DCCS): a method of assessing executive function in children. Nat. Protoc. 1, 297–301. doi: 10.1038/nprot.2006.46
Zhang, J. Y. (2017). Relationships Between Approximate Number System Accuracy and Mathematical Competence in Young Children Aged 5-6 (Master's thesis). East China Normal University, Shanghai, China.
Zhang, X. (2016). Linking language, visual-spatial, and executive function skills to number competence in very young Chinese children. Early Child. Res. Q. 36, 178–189. doi: 10.1016/j.ecresq.2015.12.010
Zhao, Z. G. (2006). The Study on the Development of Number Sense and Estimation in Young Childrenaged 3-6 (Master's thesis). East China Normal University, Shanghai, China.
Keywords: Executive Function, Cardinality Principle, Approximate Number System, mediating role, moderating role
Citation: Li H, Di H, Duan B, Luo M, Wang Y and Wang Z (2024) Executive Function and young children's Cardinality Principle: the mediating role of the Approximate Number System and the moderating role of age. Front. Psychol. 15:1495489. doi: 10.3389/fpsyg.2024.1495489
Received: 16 September 2024; Accepted: 28 October 2024;
Published: 13 November 2024.
Edited by:
Yoshifumi Ikeda, Tokyo Gakugei University, JapanReviewed by:
Maria Silvia Saccani, San Camillo Hospital (IRCCS), ItalyChen Cheng, Hong Kong University of Science and Technology, Hong Kong SAR, China
Copyright © 2024 Li, Di, Duan, Luo, Wang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhenglu Wang, emhlbmdsdUB4am51LmVkdS5jbg==
†These authors have contributed equally to this work and share first authorship
 Huanhuan Li
Huanhuan Li Huijuan Di
Huijuan Di Bingyu Duan
Bingyu Duan Mengzhen Luo
Mengzhen Luo Yifang Wang
Yifang Wang Zhenglu Wang
Zhenglu Wang