- 1Department of Psychology, Northwest Normal University, Lanzhou, Gansu, China
- 2Graduate School of Education, Incheon National University, Incheon, Republic of Korea
This study presents a comprehensive meta-analysis of fMRI data to explore the neural correlates of mathematical creativity, a vital competence in mathematics education. Utilizing Activation Likelihood Estimation (ALE) and Meta-Analytic Connectivity Modeling (MACM) techniques, we analyzed studies published up to 2022 to identify brain regions activated during mathematical and creative tasks. The findings reveal significant activation in the left inferior frontal gyrus (IFG) and the left superior frontal gyrus (SFG) during both mathematical and creative tasks, emphasizing their roles in idea generation, working memory, and executive control. The MACM analysis further highlights the importance of the frontoparietal network, a key player in cognitive control, for mathematical creativity. This network’s involvement in attention, working memory, and goal orientation aligns with the demands of mathematical problem-solving. Our results offer valuable insights into the neural mechanisms underlying mathematical creativity, providing a foundation for developing targeted educational strategies to enhance this crucial competence in learners.
1 Introduction
Mathematics is a core subject in most countries’ educational systems, and one of the goals of any educational system should be fostering creative people. Creativity plays an important role in the development of individuals and societies and is recognized as one of the key skills necessary for learners in the 21st century, as well as being a core attribute in contemporary economic, social, and educational environments (Swanzy-Impraim et al., 2022). Creativity is also recognized as an essential skill that students must master in higher education due to its direct relationship to the development of content knowledge and skills (Egan et al., 2017; Livingston, 2010). Creativity is defined as an ability to interact with cognitive abilities, personal qualities, and environmental factors to produce novel and effective ways of solving problems.
Doing meaningful science has been considered a creative act, and the nature of mathematics provides a suitable platform for developing creativity. Hence, the importance of mathematical creativity is apparent and needs no further emphasis, even though the definitions of mathematical creativity are various depending on researchers. Although research on creativity has been a hot topic, unfortunately, there has been not only a dearth of research on mathematical creativity, but even the definition of its concept still lacks a common definition (Mann, 2006; Tubb et al., 2020). Mathematical creativity is often considered a key component of mathematical ability, which includes flexible thinking, providing valuable and novel solutions to mathematical problems, analyzing mathematical problems in a variety of ways, the ability to perceive mathematical relationships using complex thinking, and generating original and novel mathematical products through identification and selection (Kattou et al., 2013; Sadak et al., 2022).
Yet the focus on mathematical creativity in mathematics education still never stops, such as the assessment of students’ mathematical creativity, how to better develop students’ mathematical creativity, and the eye-tracking characteristics of mathematical creativity (Schindler and Lilienthal, 2020; Suherman and Vidákovich, 2022). With the development of educational neuroscience, more and more studies have begun to explore the neural regions and networks of the brain that are related to creativity in an attempt to come up with more scientific educational strategies to improve students’ creativity because traditional educational research methods are difficult to investigate the relationship of mathematics and creativity despite providing some useful information (Agnoli et al., 2018; Sun et al., 2016; Zhou, 2018). Moreover, their relationship has never been explored explicitly in cognitive neuroscience.
Cognitive neuroscience can not only examine behavioral changes but also study the correlation of these behavioral changes with brain structure and function. This research approach can provide ample evidence for the effectiveness of educational interventions (Zhou, 2018). It has been suggested that mathematical creativity is a combination of general domain creativity and domain-specific mathematical ability (Schoevers et al., 2020). Based on this, this study intends to further investigate which educational strategies can scientifically and effectively promote students’ mathematical creativity based on exploring the cognitive neural basis of creativity and mathematical competence through a cognitive neural meta-analytic approach. Specifically, the research questions are as follows:
1. Which brain regions are activated during doing mathematical tasks and which brain regions are activated during doing creativity tasks?
2. Which brain regions overlap and which brain regions are unique?
3. How is the composition of brain networks related to overall mathematical creativity?
2 Materials and methods
2.1 Literature and methods
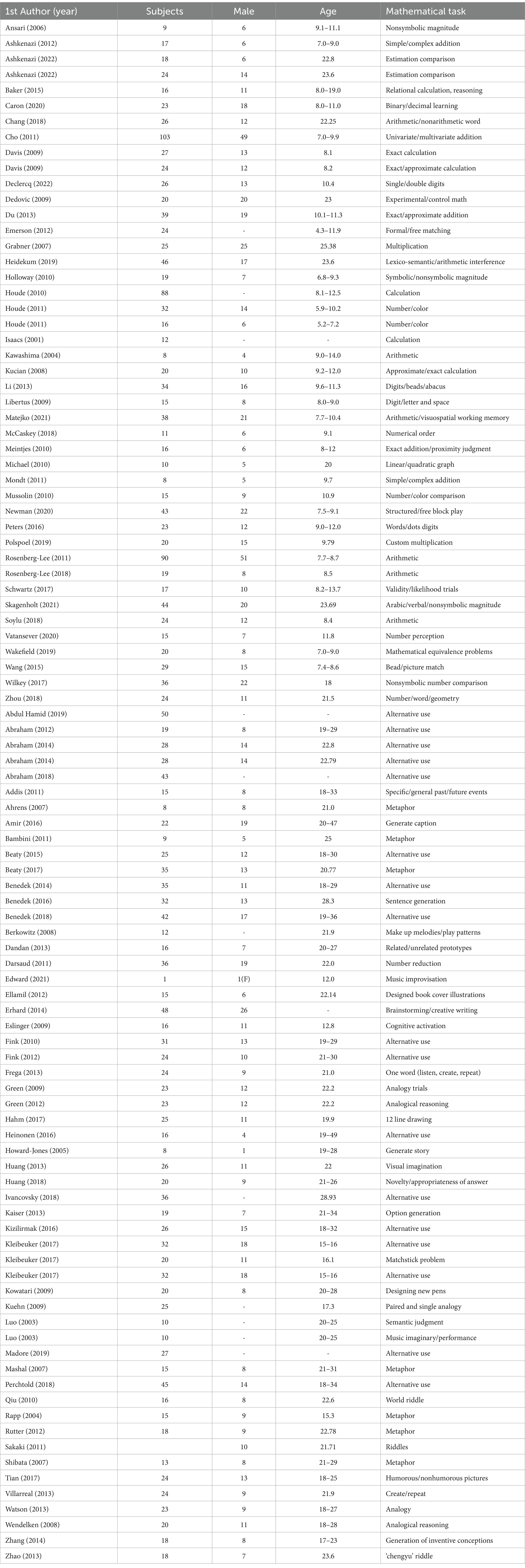
Potential articles were identified by searching empirical papers published by Web of Science, PLOS, APA through 2022. The research for articles related to mathematics keywords such as “mathematics,” “arithmetic,” “problem solving,” “addition,” “subtraction,” “division,” “multiplication,” “mental math,” and “numeral” were combined with technical terms such as “neuroimaging,” “brain imaging,” “cerebral correlates,” “neural correlates,” “functional magnetic resonance imaging” and its abbreviation. The research for articles related to creativity keywords such as “creativity,” “divergent thinking,” “creative idea generation,” “insight,” “metaphor,” “improvisation,” “aha,” “original idea,” “remote associates,” “heuristic prototype,” “creative thinking” AND “neuroimaging,” “brain imaging,” “cerebral correlates” “functional magnetic resonance imaging” and its abbreviation. We complemented these results with PubMed and NeuroQuery.
Studies were eligible for the present meta-analysis included: (1) whole brain analysis had to be used and ROI studies were excluded, (2) MNI or Talairach coordinates had to be provided, (3) tasks were limited to mathematics and creativity, and (4) subjects had to be healthy and right-handed. A PRISMA flow chart of the selection process is illustrated below. A total of 44 papers on mathematics and 56 papers on creativity were included in the final meta-analysis (see Table 1; Figure 1).
2.2 ALE meta-analysis
As a coordinate-based meta-analysis ALE focuses on finding consistency in spatial location by counting the coordinate values reported in the article. The basic principle of ALE meta-analysis of coordinate information is to fit the activation points in each experiment to a probability distribution, that is, the magnitude of the probability that the activation points fall on each voxel of the brain (Eickhoff et al., 2009).
Significant activation of brain regions associated with mathematical creativity was detected using the ALE (Activation Likelihood Estimation) approach. A meta-analysis of mathematical tasks of a total of 958 foci reported in 44 experiments and creative tasks of a total of 1,177 foci reported in 56 was conducted using the ALE approach with GingerALE 3.0.2 software.1 Activation foci reported in Talairach space were converted to MNI space before being put into GingerALE. ALE-maps of single analyses were constructed using 1,000 permutations and a cluster level of FWE of p < 0.05 with a cluster forming a voxel level threshold of p < 0.001. ALE maps of contrast analyses were constructed using 5,000 permutations at p < 0.001 and a minimum volume of 50 mm3 (Müller et al., 2018). Each ALE map was visualized using the Mango 4.0.1 software.2
2.3 MACM analysis
Based on the brain regions derived from the findings of the ALE meta-analysis, and to explore the cognitive neural mechanisms of mathematical creativity, we performed a MACM analysis to detect synergistic activation patterns in these regions of interest. It allows for ALE analysis of BrainMap database (see Footnote 1) co-activation foci, which further reveals other important brain regions co-activated with the ROI through the functional connectivity of the task. MACM collects data from a variety of neural databases (e.g., Brain map) and utilizes meta-analysis algorithms, such as ALE, to assess or examine which brain regions are co-activated with a given seed region. The basic principle of MACM is that if two brain regions are functionally related, they are more likely to be activated by the same task (Kotkowski et al., 2018; Langner and Camilleri, 2021).
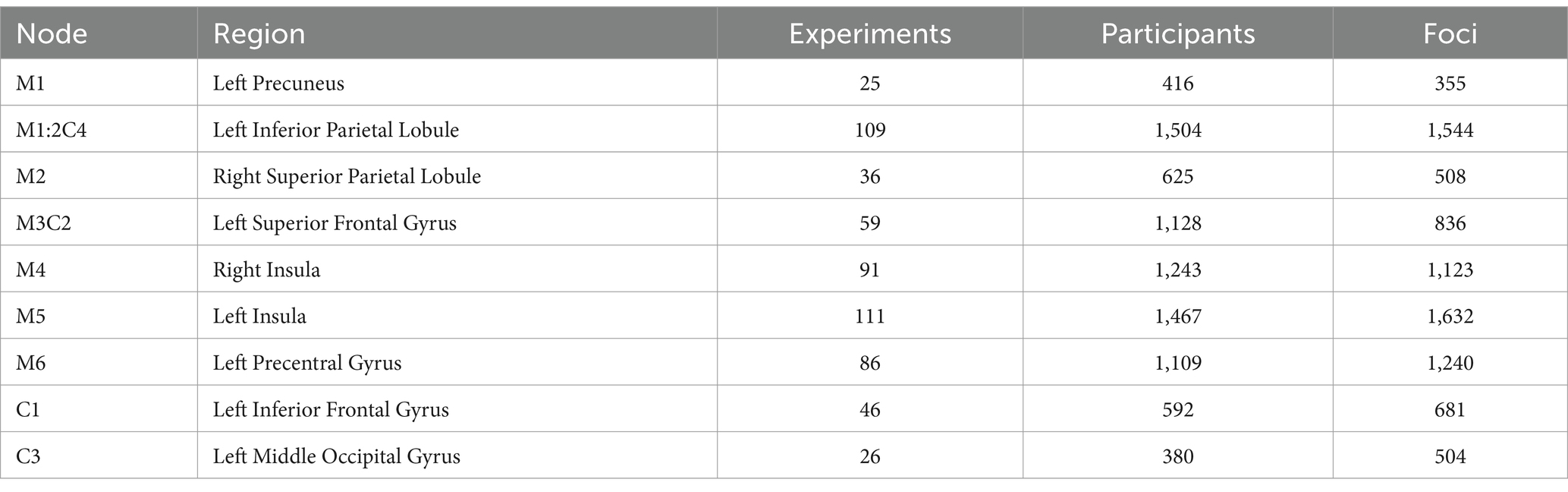
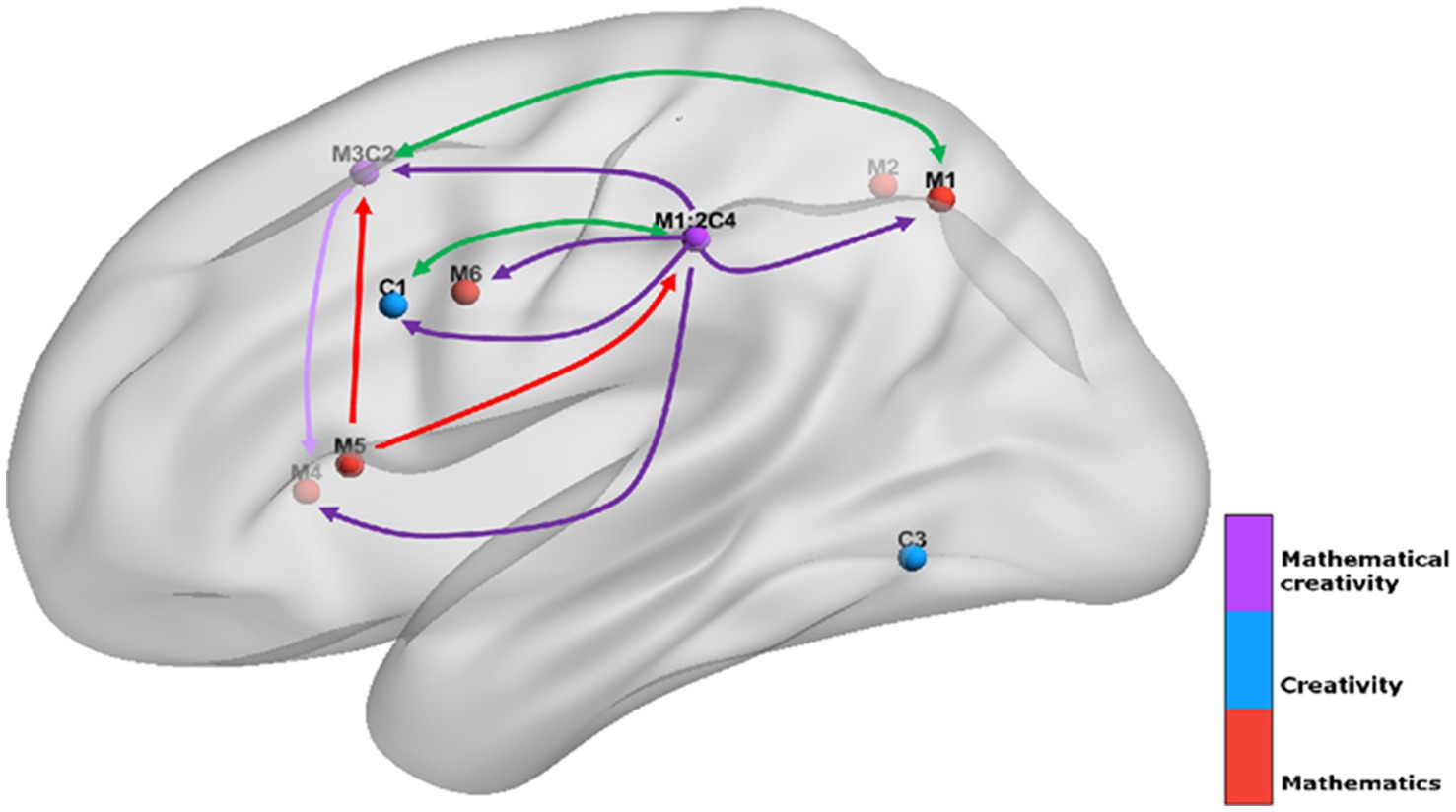
For the MACM analysis, we first selected the 9 regions derived from the ALE analysis described above as ROIs, including left precuneus, left inferior parietal lobule (IPL), right superior parietal lobule (SPL), left superior frontal gyrus (SFG), right insula, left insula, left precentral gyrus, left inferior frontal gyrus (IFG), left middle occipital gyrus (MOG), where the left inferior parietal lobule (IPL) and left superior frontal gyrus (SFG) is the region where creativity and mathematical ability are co-activated. Each ROI contains experiments, participants, and foci information as shown in Table 2. MACM map was visualized using the BrainNet Viewer software3 (Xia et al., 2013).
3 Results
3.1 Subsection
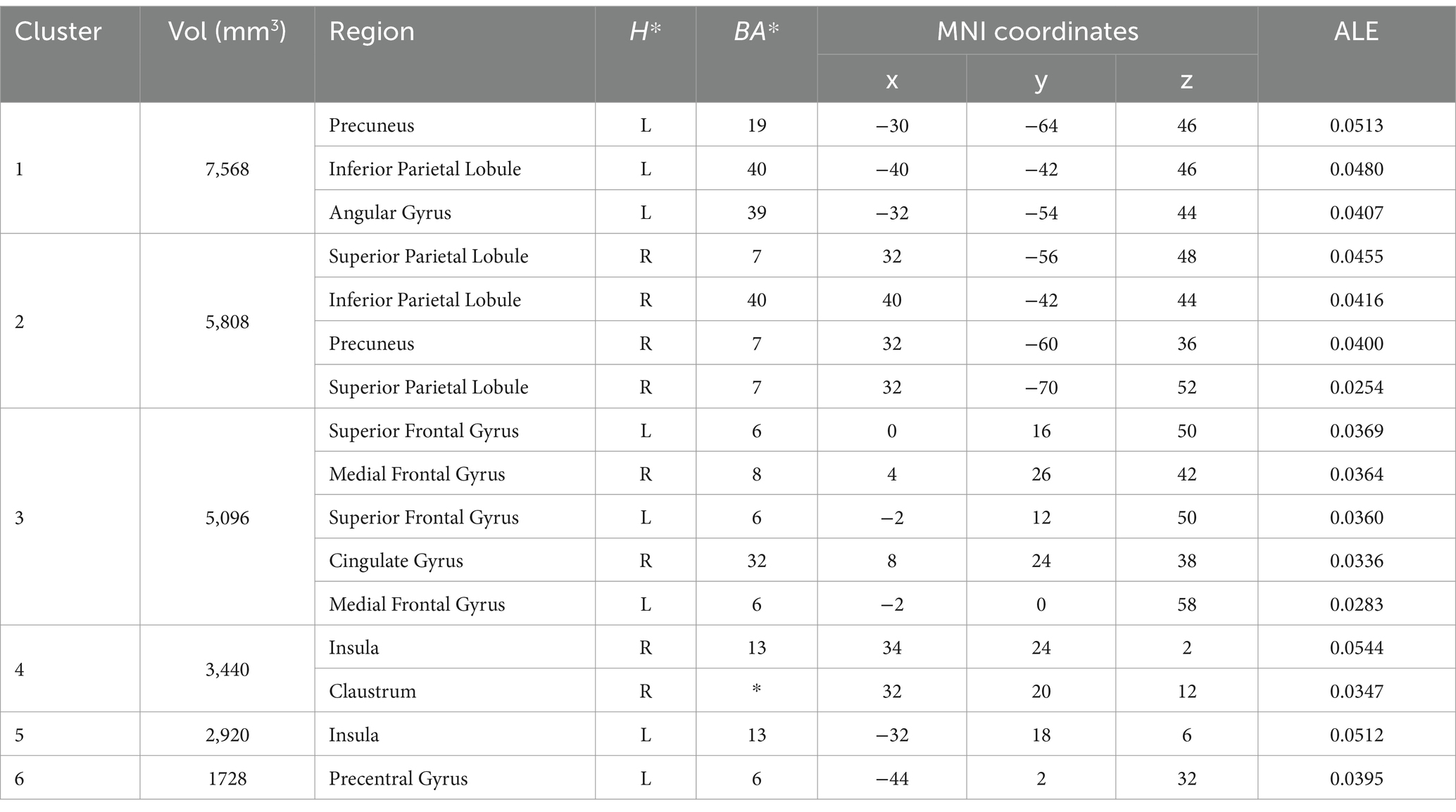
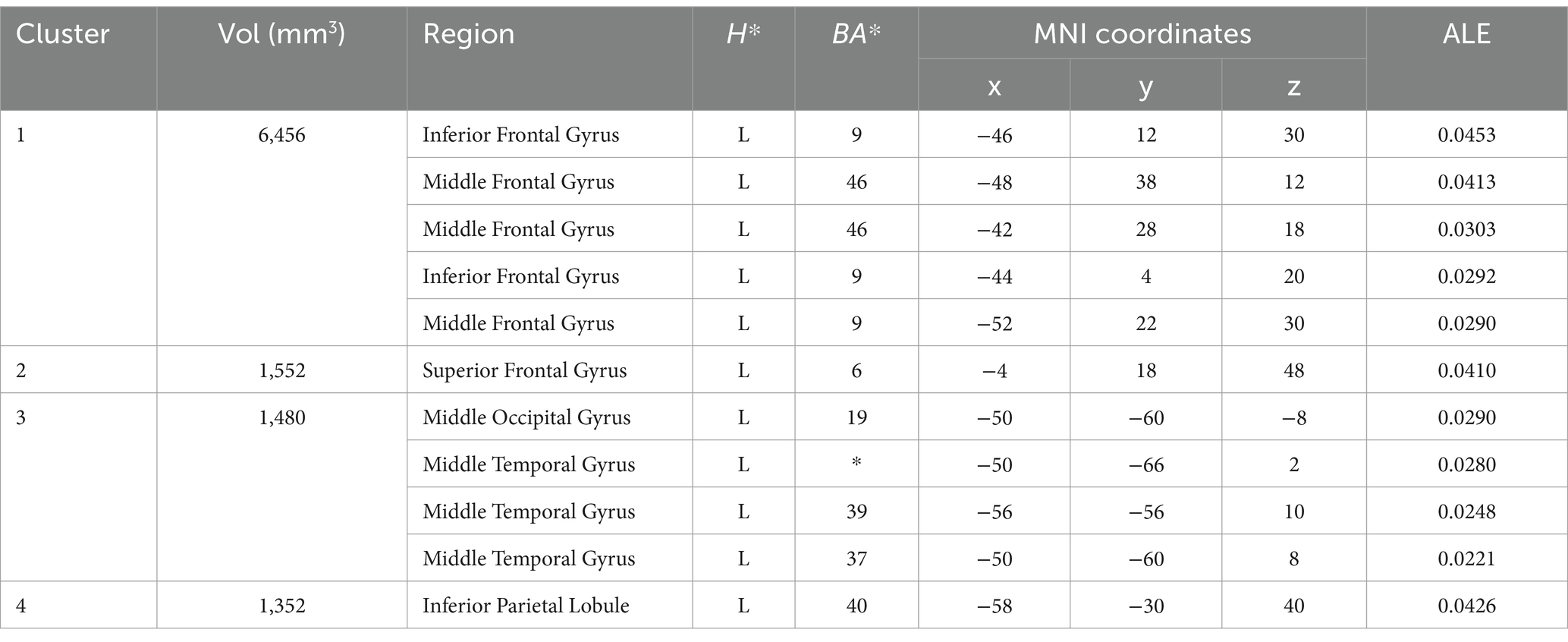
The ALE meta-analysis on 44 studies for mathematics revealed 6 clusters of significant activation, including the bilateral inferior parietal lobule, the left superior parietal lobule, the left superior frontal gyrus, the right medial frontal gyrus, the left me-dial frontal gyrus, the bilateral insula, the left precentral gyrus (see Table 3; Figure 2).
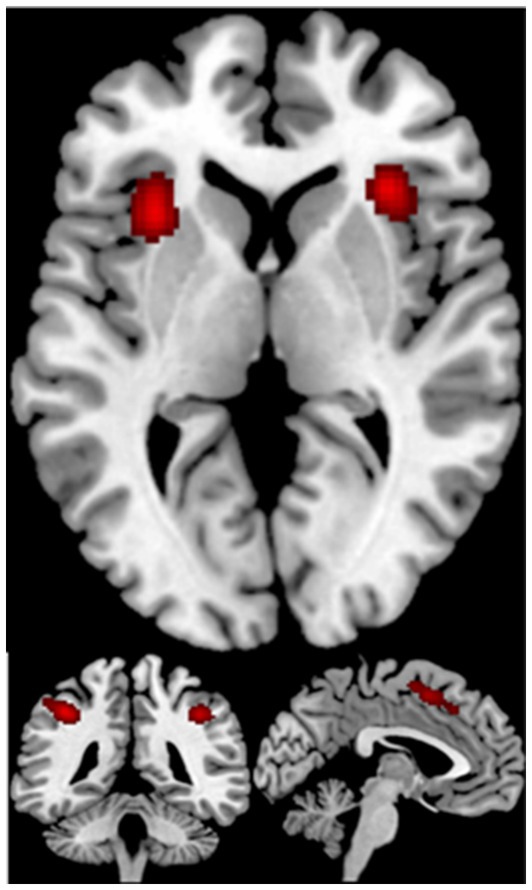
The ALE meta-analysis on 56 studies in creativity resulted in 4 significant clusters of activation, including the left inferior frontal gyrus, the left middle frontal gyrus, the left superior frontal gyrus, the left middle occipital gyrus, the left middle temporal gyrus, the left inferior parietal lobule (see Table 4; Figure 3).
3.2 ALE meta-analysis
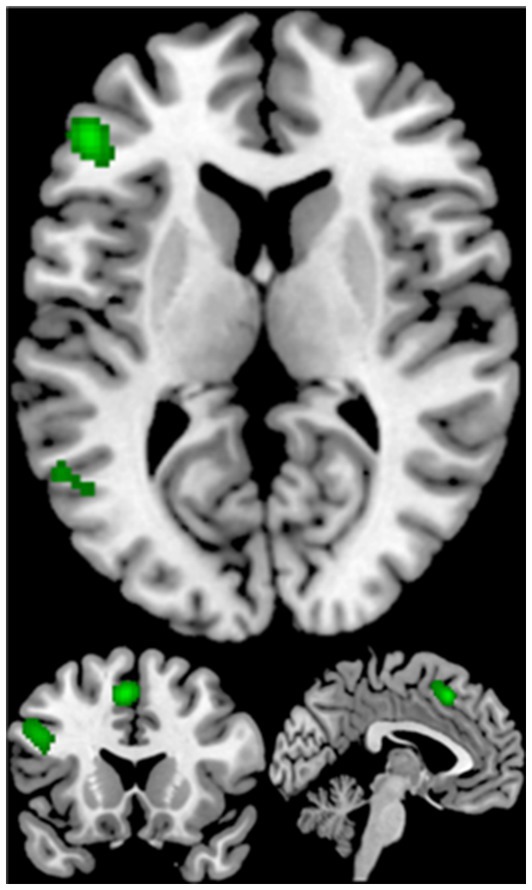
The contrast analysis for increased activation during mathematics compared to creativity with a total of 5 clusters, including the bilateral precuneus, the bilateral claustrum, the right superior parietal lobule, the right angular gyrus, the right insula, and the right inferior parietal lobule. Creativity revealed 3 clusters of significant activation compared to mathematics. The left inferior frontal gyrus, the left inferior parietal lobule, and the left middle frontal gyrus are included. The common brain regions activated by both mathematical and creative tasks were the left inferior frontal gyrus and the left superior frontal gyrus (see Table 5; Figure 4).
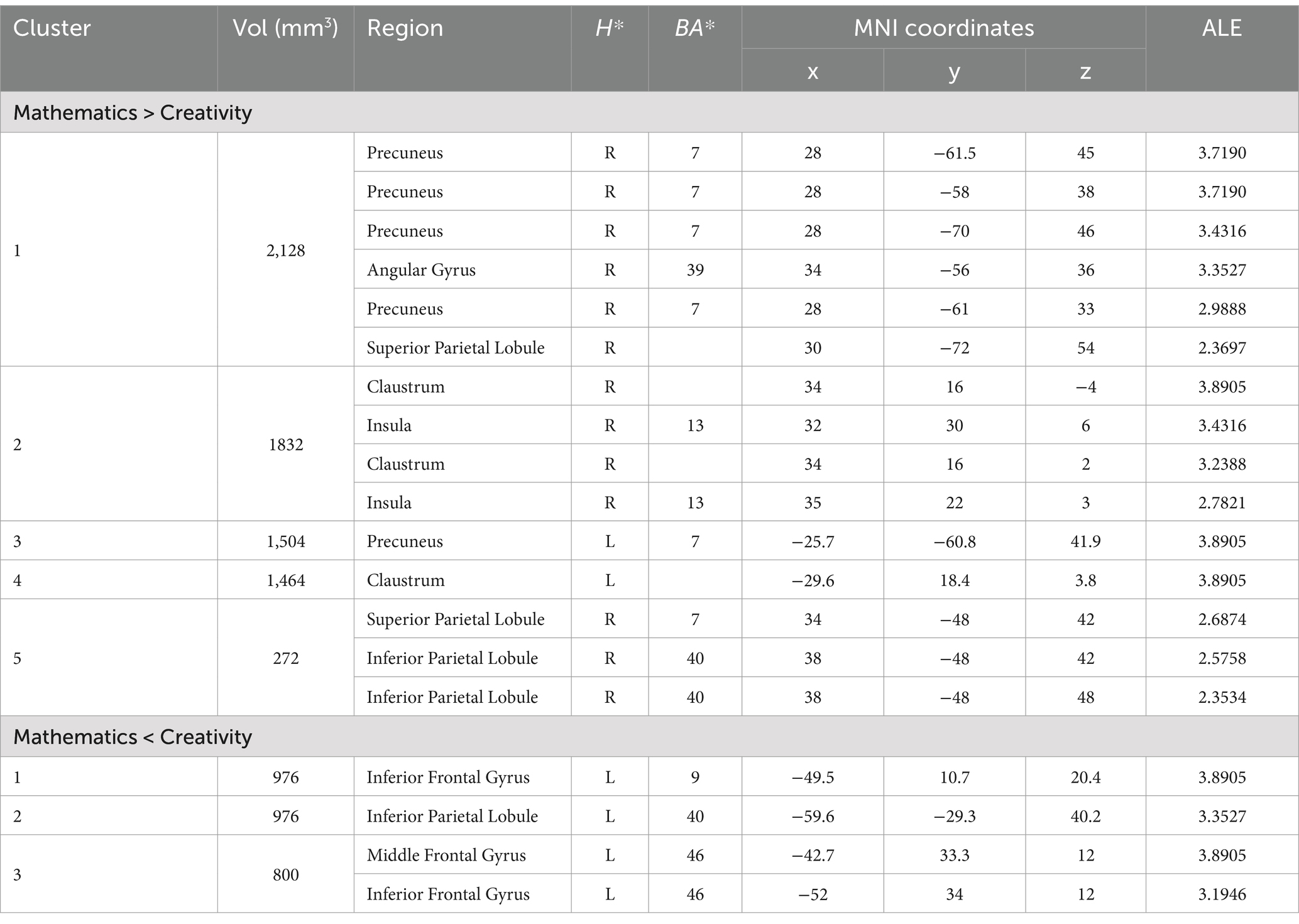
Table 5. Regions of activations resulting from the contrast analysis of the conditions “mathematics” and “creativity.”
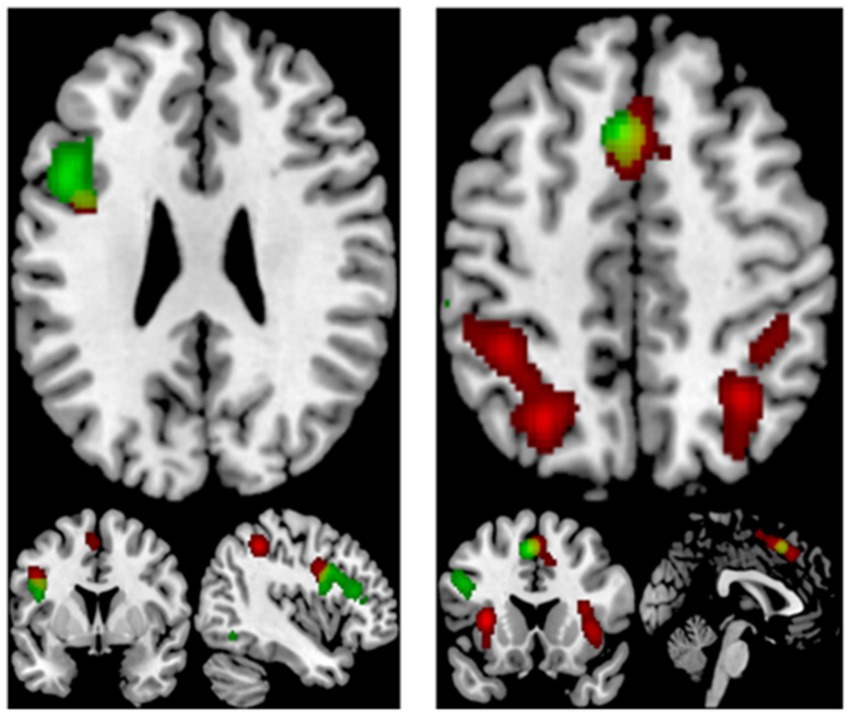
Figure 4. Displayed are significant results from the meta-analysis common of mathematics and creativity.
3.3 MACM analysis
The focus of this study is on the cognitive neural mechanisms of mathematical creativity, so the results of the MACM analyses of the left inferior parietal lobule (IPL) and the left superior frontal gyrus (SFG), the regions where mathematical ability and creativity are co-activated, will be analyzed specifically. Results related to other regions can be viewed in the Appendix. Co-activation maps for the left inferior parietal lobule were significant for the right inferior parietal lobule (BA 40), the bilateral medial frontal gyrus (BA 6), the right sub-gyral (BA 6), the left middle frontal gyrus (BA 6), the left insula (BA 13, 47), the right claustrum, the left inferior frontal (BA 9), the right superior temporal gyrus (BA 41, 22) (see Table 5; Figure 5). For the left superior frontal gyrus significant co-activation was observed in the right angular gyrus (BA 39), the left middle frontal gyrus (BA 9), the left precuneus (BA 19), the left inferior parietal lobule (BA 40), the left sub-gyrus (BA 6), the bilateral middle frontal gyrus (BA 6), and the left insula (BA 13) (see Tables 6, 7; Figure 5).
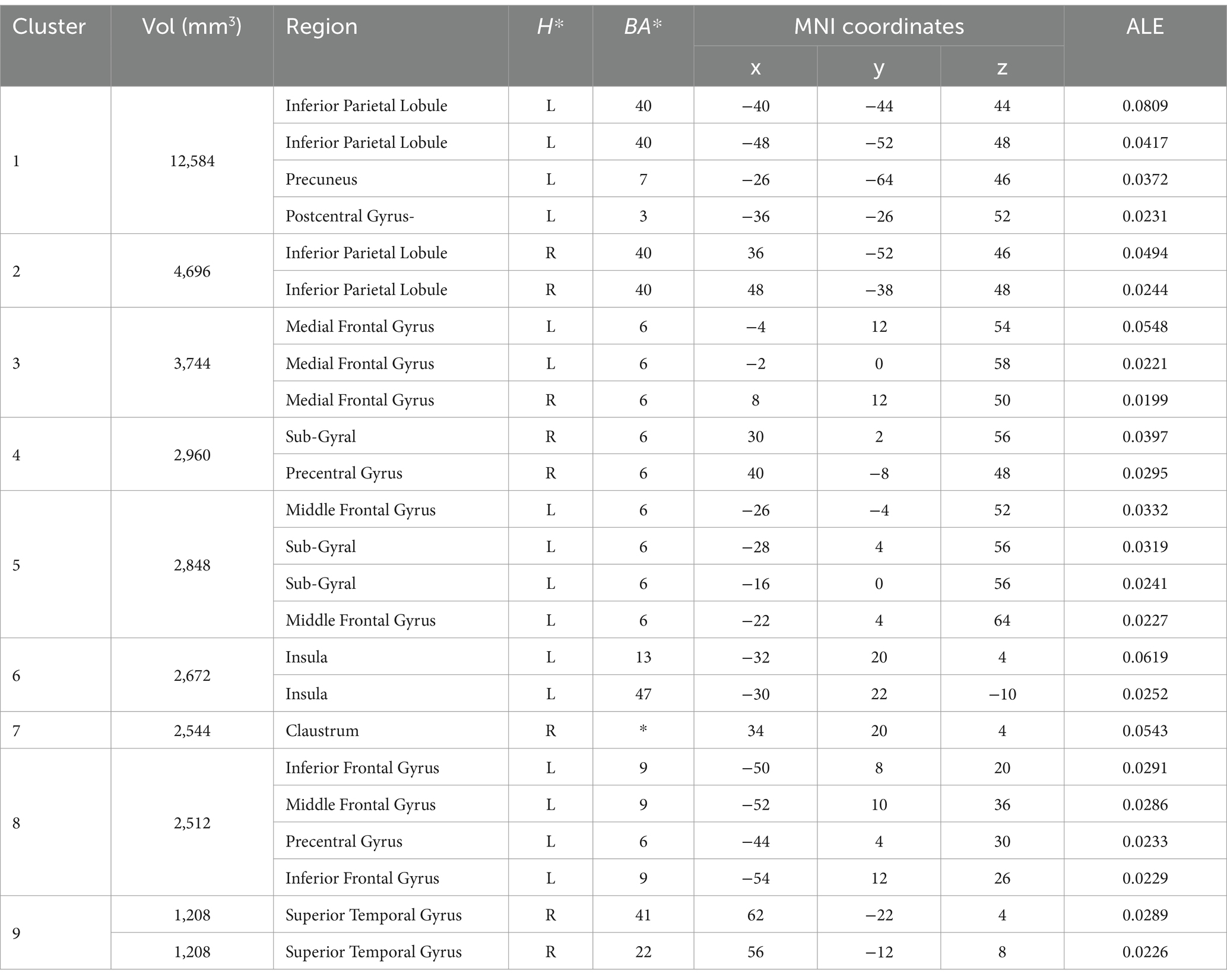
Table 6. MACA results: regions of functional coactivation associated with left Inferior Parietal Lobule.
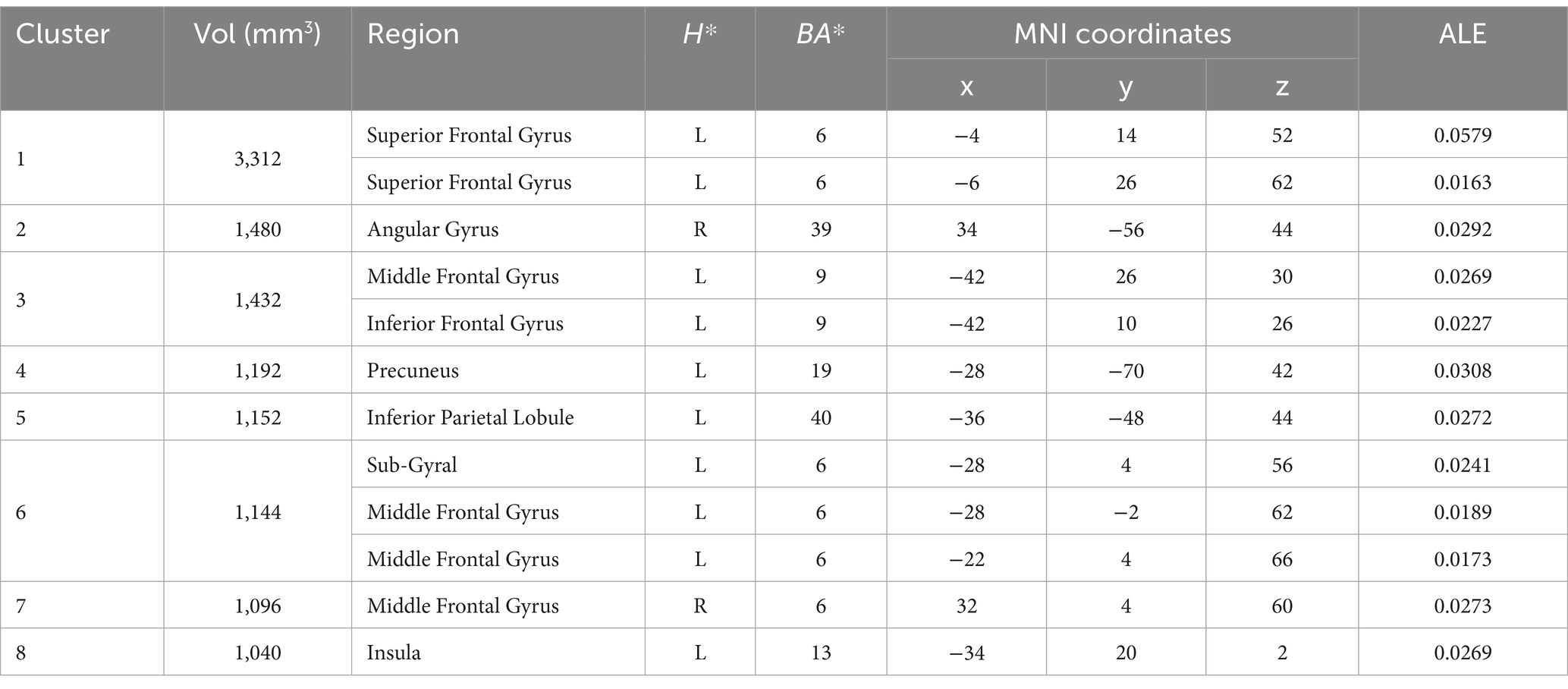
Table 7. MACA results: regions of functional coactivation associated with left Superior Frontal Gyrus.
4 Discussion
4.1 ALE meta-analysis
The results of the ALE for creative thinking showed that the activated brain regions were mainly concentrated in the left hemisphere, which included the inferior frontal gyrus (BA 9, 46), the superior frontal gyrus (BA 6), the middle occipital gyrus (BA 19), and the inferior parietal lobule (BA 40) regions. It has been shown that the IFG generates creative ideas through the retrieval of loosely related semantic concepts, the screening of creative ideas, and the evaluation of originality (Cogdell-Brooke et al., 2020). Numerous previous meta-analyses of creative thinking have also found this region to be activated because it involves integrating semantic concepts and ideas in new ways (Boccia et al., 2015; Wu et al., 2015). The SFG has also been shown to be activated in numerous meta-analyses, and existing meta-analyses suggest that this region may be activated in different creative tasks because of its need to flexibly manipulate semantic information, so that the generation of many original ideas is associated with this region (Cogdell-Brooke et al., 2020). The SFG plays an important role in cognitive functions such as working memory, mental manipulation, and spatial orientation processing, and there is a stable correlation between this region and creative thinking skills, especially with insight (Lin et al., 2018). The MOG is primarily associated with mental imagery, which plays an important role in creative thinking (Beaty et al., 2018). The IPL is an important region for semantic processing and has been shown to play a key role in situational memory retrieval, and cognitive operations that facilitate situational retrieval can be effective in promoting creative thinking (Madore et al., 2016). Also, this region has been shown to promote divergent thinking (Kuang et al., 2022). These activation regions suggest that prefrontal regions are critical in creativity. And the importance of this region has been repeatedly demonstrated in individuals with prefrontal damage, where creativity is also impaired to some extent (Khalil and Moustafa, 2022; Ovando-Tellez et al., 2019).
The results of the ALE for mathematics cognition revealed that the activated brain regions were predominantly located in the bilateral inferior parietal lobule (IPL) (BA 40), the left superior parietal lobule (SPL) (BA 32), the left superior frontal gyrus (SFG) (BA 6), the right medial frontal gyrus (MFG) (BA 8), the left medial frontal gyrus (MFG) (BA 6), the bilateral insula, and the left precentral gyrus. The meta-analysis of mathematical brain region associations in the present study indicated that the frontal–parietal region plays a key role in mathematical ability, which is generally consistent with the results of the prior meta-analysis (Istomina and Arsalidou, 2024). The IPL, particularly in its bilateral manifestation, is crucial for numerical processing and arithmetic reasoning. This region is known to be involved in the manipulation and representation of numerical quantities, as well as in spatial attention and number sense (Hubbard et al., 2005). The SPL, especially on the left side, plays a significant role in visuospatial processing and the integration of sensory information, which are essential in understanding and solving mathematical problems (Friedman and Miyake, 2017). The SFG, located in the left hemisphere, is associated with higher cognitive functions such as working memory and executive control, both of which are integral to complex mathematical problem-solving and abstract reasoning (Christoff et al., 2009). The MFG, particularly in the right hemisphere, contributes to decision-making and cognitive control, which are vital in tasks requiring logical reasoning and the application of mathematical principles (Arsalidou and Taylor, 2011). On the contrary, the left MFG is implicated in processes related to calculation and mathematical operations, reflecting its role in more structured and rule-based aspects of mathematics. The bilateral insula is involved in risk and uncertainty assessment, which can be crucial in mathematical decision-making and problem-solving scenarios (Preuschoff et al., 2008). The left precentral gyrus plays a role in motor planning and execution, and its involvement in mathematical cognition might be related to the mental manipulation of numbers and symbols, a process often metaphorically described as ‘mental gymnastics’ (Andres et al., 2008). These activation regions emphasize the multifaceted nature of mathematical cognition, involving a network of brain areas responsible for numerical processing, spatial reasoning, working memory, decision-making, and symbolic manipulation. This complex interplay of cognitive functions highlights the integral role of these regions in the understanding and application of mathematics.
The results of the ALE for both mathematics and creativity indicated that the activated brain regions were crucially located in the left inferior frontal gyrus (IFG) and the superior frontal gyrus (SFG). The IFG plays a key role in generating creative mathematical ideas by retrieving and integrating diverse mathematical concepts, thereby fostering innovative problem-solving approaches (Beaty et al., 2016). Its ability to manipulate and recombine existing mathematical knowledge is essential for producing original and effective solutions. Meanwhile, the SFG is vital for higher cognitive functions like working memory and executive control, which are integral to mathematics and creativity. It helps maintain and manipulate complex mathematical information, enabling the exploration of various problem-solving strategies and their evaluation (Dietrich and Kanso, 2010). The SFG is particularly important in abstract mathematical reasoning and in shifting between different problem-solving methods. In addition, the SFG’s role in attentional control is important in maintaining focus on complex mathematical tasks, thus facilitating deeper engagement and persistence in finding creative solutions (Zabelina and Robinson, 2010). The combined functions of the IFG and SFG highlight the intricate cognitive processes involved in both the generation of novel ideas and the sustained manipulation and evaluation of these ideas. These activated brain regions associated with creativity and math are largely similar to previous meta-analysis results, but this study not only explored the brain regions, but also further explored the brain networks associated with math creativity through the MACM method.
4.2 MACM analysis
The results of the MACM analysis indicate that the frontoparietal network has a key role in mathematical creativity. This region is a core network for cognitive control and plays an important role in the processes of goal orientation, working memory, inhibitory switching, attention, cognitive control, and other cognitive abilities (Uddin et al., 2019). It has been shown that the frontoparietal network is the core network for creative performance and that stimulation of the frontoparietal network can effectively promote the enhancement of an individual’s creative ability (Lifshitz-Ben-Basat and Mashal, 2021; Tabatabaeian and Jennings, 2023). In addition, greater activation of this region also occurred when individuals solved math problems. Intervention training for children with math deficits has also shown that increased activation in the frontal–parietal region was found in these children after two weeks of numeracy training (Liang, 2022; Soltanlou et al., 2022). Recent research suggests that functional connectivity within the frontoparietal network plays a key role in mathematical ability and that individuals with high levels of mathematical ability may rely on this network for effective neural communication and information processing (Ren and Libertus, 2023). It can be seen that the frontoparietal network not only plays an important role in mathematics and creativity skills but also has a role in mathematical creativity that cannot be ignored.
5 Conclusion
Findings from the current meta-analysis on mathematical creativity provide valuable insights into the neural mechanisms underlying this complex cognitive process. Specifically, we focused on exploring brain regions associated with mathematical creativity using the ALE and MACM analytic approaches. Based on the ALE meta-analysis, we identified key brain regions activated during mathematical and creative tasks, with a particular focus on the left IFG and SFG. These findings were further substantiated by an MACM analysis, which highlighted the frontoparietal network’s critical role in mathematical creativity. These results demonstrate that the left IFG and SFG are essential in both mathematical reasoning and creative thinking. The IFG facilitates the generation of innovative mathematical ideas through the integration of diverse concepts, while the SFG supports higher cognitive functions such as working memory and executive control, essential for complex problem-solving in mathematics. The overlap in these regions during tasks requiring mathematical and creative cognition underscores their importance in the cognitive processes that underlie mathematical creativity. Compared to creativity tasks, mathematical tasks show increased concordance in the precuneus, claustrum, and superior parietal lobule. On the other hand, creativity tasks show increased concordance in the inferior frontal gyrus, inferior parietal lobule, and middle frontal gyrus. Moreover, the frontoparietal network, identified as a core network for cognitive control, was found to be significantly activated in tasks involving mathematical creativity. This network’s involvement in goal orientation, working memory, and cognitive control suggests its integral role in both domain-specific mathematical abilities and general creative performance.
To foster mathematical creativity, teachers can be suggested to use students’ episodic knowledge about the problem-solving process, an abacus, diagrams, gestures, graphs, symbols, etc., as visualization while explaining mathematical contents, and speech with gesture strategy when students solve the problems. In addition, not only focused on cognitive aspects, teachers help students build intrinsic motivation and affective goals to cause their effort in attention and complex processing. Our study contributes to the ongoing efforts to understand and enhance creativity in educational settings, particularly within the domain of mathematics. Our findings may shed light on potential avenues for the development of effective educational strategies to promote students’ mathematical creativity.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
QL: Conceptualization, Data curation, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. SK: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2022R1A2C1010310).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
References
Agnoli, S., Zanon, M., Mastria, S., Avenanti, A., and Corazza, G. E. (2018). Enhancing creative cognition with a rapid right-parietal neurofeedback procedure. Neuropsychologia 118, 99–106. doi: 10.1016/j.neuropsychologia.2018.02.015
Andres, M., Olivier, E., and Badets, A. (2008). Actions, words, and numbers: a motor contribution to semantic processing? Curr. Dir. Psychol. Sci. 17, 313–317. doi: 10.1111/j.1467-8721.2008.00597.x
Arsalidou, M., and Taylor, M. J. (2011). Is 2 + 2 = 4? Meta-analyses of brain areas needed for numbers and calculations. NeuroImage 54, 2382–2393. doi: 10.1016/j.neuroimage.2010.10.009
Beaty, R. E., Benedek, M., Silvia, P. J., and Schacter, D. L. (2016). Creative cognition and brain network dynamics. Trends Cogn. Sci. 20, 87–95. doi: 10.1016/j.tics.2015.10.004
Beaty, R. E., Thakral, P. P., Madore, K. P., Benedek, M., and Schacter, D. L. (2018). Core network contributions to remembering the past, imagining the future, and thinking creatively. J. Cogn. Neurosci. 30, 1939–1951. doi: 10.1162/jocn_a_01327
Boccia, M., Piccardi, L., Palermo, L., Nori, R., and Palmiero, M. (2015). Where do bright ideas occur in our brain? Meta-analytic evidence from neuroimaging studies of domain-specific creativity. Front. Psychol. 6:1195. doi: 10.3389/fpsyg.2015.01195
Christoff, K., Keramatian, K., Gordon, A. M., Smith, R., and Mädler, B. (2009). Prefrontal organization of cognitive control according to levels of abstraction. Brain Res. 1286, 94–105. doi: 10.1016/j.brainres.2009.05.096
Cogdell-Brooke, L. S., Sowden, P. T., Violante, I. R., and Thompson, H. E. (2020). A meta-analysis of functional magnetic resonance imaging studies of divergent thinking using activation likelihood estimation. Hum. Brain Mapp. 41, 5057–5077. doi: 10.1002/hbm.25170
Dietrich, A., and Kanso, R. (2010). A review of EEG, ERP, and neuroimaging studies of creativity and insight. Psychol. Bull. 136, 822–848. doi: 10.1037/a0019749
Egan, A., Maguire, R., Christophers, L., and Rooney, B. (2017). Developing creativity in higher education for 21st century learners: a protocol for a scoping review. Int. J. Educ. Res. 82, 21–27. doi: 10.1016/j.ijer.2016.12.004
Eickhoff, S. B., Laird, A. R., Grefkes, C., Wang, L. E., Zilles, K., and Fox, P. T. (2009). Coordinate-based activation likelihood estimation meta-analysis of neuroimaging data: a random-effects approach based on empirical estimates of spatial uncertainty. Hum. Brain Mapp. 30, 2907–2926. doi: 10.1002/hbm.20718
Friedman, N. P., and Miyake, A. (2017). The relations among inhibition and interference control functions: a latent-variable analysis. J. Exp. Psychol. Gen. 133, 101–135. doi: 10.1037/0096-3445.133.1.101
Hubbard, E. M., Piazza, M., Pinel, P., and Dehaene, S. (2005). Interactions between number and space in parietal cortex. Nat. Rev. Neurosci. 6, 435–448. doi: 10.1038/nrn1684
Istomina, A., and Arsalidou, M. (2024). Add, subtract and multiply: Meta-analyses of brain correlates of arithmetic operations in children and adults. Dev. Cogn. Neurosci. 69:101419. doi: 10.1016/j.dcn.2024.101419
Kattou, M., Kontoyianni, K., Pitta-Pantazi, D., and Christou, C. (2013). Connecting mathematical creativity to mathematical ability. ZDM 45, 167–181. doi: 10.1007/s11858-012-0467-1
Khalil, R., and Moustafa, A. A. (2022). A neurocomputational model of creative processes. Neurosci. Biobehav. Rev. 137:104656. doi: 10.1016/j.neubiorev.2022.104656
Kotkowski, E., Price, L. R., Fox, P. M., Vanasse, T. J., and Fox, P. T. (2018). The hippocampal network model: a transdiagnostic metaconnectomic approach. NeuroImage: Clinical 18, 115–129. doi: 10.1016/j.nicl.2018.01.002
Kuang, C., Chen, J., Chen, J., Shi, Y., Huang, H., Jiao, B., et al. (2022). Uncovering neural distinctions and commodities between two creativity subsets: a meta-analysis of fMRI studies in divergent thinking and insight using activation likelihood estimation. Hum. Brain Mapp. 43, 4864–4885. doi: 10.1002/hbm.26029
Langner, R., and Camilleri, J. (2021). “A meta-analytic connectivity modelling (MACM): a tool for assessing region-specific functional connectivity patterns in task-constrained states” in Brain Network Dysfunction in Neu-ropsychiatric Illness: Methods, Applications, and Implications (Berlin: Springer Nature), 93–104.
Liang, C. (2022). Problem solving by agricultural extension students with various levels of creativity through a neurocognitive Lens. Sustain. For. 14:16371. doi: 10.3390/su142416371
Lifshitz-Ben-Basat, A., and Mashal, N. (2021). Enhancing creativity by altering the frontoparietal control network functioning using transcranial direct current stimulation. Exp. Brain Res. 239, 613–626. doi: 10.1007/s00221-020-06023-2
Lin, J., Cui, X., Dai, X., Chen, Y., and Mo, L. (2018). Neural correlates of creative insight: amplitude of low-frequency fluctuation of resting-state brain activity predicts creative insight. PLoS One 13:e0203071. doi: 10.1371/journal.pone.0203071
Livingston, L. (2010). Teaching creativity in higher education. Arts Education Policy Review, 111, 59–62. doi: 10.1080/10632910903455884
Madore, K. P., Jing, H. G., and Schacter, D. L. (2016). Divergent creative thinking in young and older adults: extending the effects of an episodic specificity induction. Mem. Cogn. 44, 974–988. doi: 10.3758/s13421-016-0605-z
Mann, E. (2006). Creativity: the essence of mathematics. J. Educ. Gift. 30, 236–260. doi: 10.4219/jeg-2006-264
Müller, V. I., Cieslik, E. C., Laird, A. R., Fox, P. T., Radua, J., Mataix-Cols, D., et al. (2018). Ten simple rules for neuroimaging meta-analysis. Neurosci. Biobehav. Rev. 84, 151–161. doi: 10.1016/j.neubiorev.2017.11.012
Ovando-Tellez, M. P., Bieth, T., Bernard, M., and Volle, E. (2019). The contribution of the lesion approach to the neuroscience of creative cognition. Curr. Opin. Behav. Sci. 27, 100–108. doi: 10.1016/j.cobeha.2018.10.011
Preuschoff, K., Quartz, S. R., and Bossaerts, P. (2008). Human insula activation reflects risk prediction errors as well as risk. J. Neurosci. 28, 2745–2752. doi: 10.1523/jneurosci.4286-07.2008
Ren, X., and Libertus, M. E. (2023). Identifying the neural bases of math competence based on structural and functional properties of the human brain. J. Cogn. Neurosci. 35, 1212–1228. doi: 10.1162/jocn_a_02008
Sadak, M., Incikabi, L., Ulusoy, F., and Pektas, M. (2022). Investigating mathematical creativity through the connection between creative abilities in problem posing and problem solving. Think. Skills Creat. 45:101108. doi: 10.1016/j.tsc.2022.101108
Schindler, M., and Lilienthal, A. J. (2020). Students’ creative process in mathematics: insights from eye-tracking-stimulated recall interview on students’ work on multiple solution tasks. Int. J. Sci. Math. Educ. 18, 1565–1586. doi: 10.1007/s10763-019-10033-0
Schoevers, E. M., Kroesbergen, E. H., and Kattou, M. (2020). Mathematical creativity: a combination of domain-general creative and domain-specific mathematical skills. J. Creat. Behav. 54, 242–252. doi: 10.1002/jocb.361
Soltanlou, M., Dresler, T., Artemenko, C., Rosenbaum, D., Ehlis, A. C., and Nuerk, H. C. (2022). Training causes activation increase in temporo-parietal and parietal regions in children with mathematical disabilities. Brain Struct. Funct. 227, 1757–1771. doi: 10.1007/s00429-022-02470-5
Suherman, S., and Vidákovich, T. (2022). Assessment of mathematical creative thinking: a systematic review. Think. Skills Creat. 44:101019. doi: 10.1016/j.tsc.2022.101019
Sun, J., Chen, Q., Zhang, Q., Li, Y., Li, H., Wei, D., et al. (2016). Training your brain to be more creative: brain functional and structural changes induced by divergent thinking training. Hum. Brain Mapp. 37, 3375–3387. doi: 10.1002/hbm.23246
Swanzy-Impraim, E., Morris, J. E., Lummis, G. W., and Jones, A. (2022). Promoting creativity: secondary visual art teachers’ perceptions and understanding of creativity in Ghana. Think. Skills Creat. 45:101057. doi: 10.1016/j.tsc.2022.101057
Tabatabaeian, S., and Jennings, C. (2023). Dynamic attentional mechanisms of creative cognition. Philosophy Mind Sci. 4, 2699–2723. doi: 10.33735/phimisci.2023.10020
Tubb, A. L., Cropley, D. H., Marrone, R. L., Patston, T., and Kaufman, J. C. (2020). The development of mathematical creativity across high school: increasing, decreasing, or both? Think. Skills Creat. 35:100634. doi: 10.1016/j.tsc.2020.100634
Uddin, L. Q., Yeo, B. T., and Spreng, R. N. (2019). Towards a universal taxonomy of macro-scale functional human brain networks. Brain Topogr. 32, 926–942. doi: 10.1007/s10548-019-00744-6
Wu, X., Yang, W., Tong, D., Sun, J., Chen, Q., Wei, D., et al. (2015). A meta-analysis of neuroimaging studies on divergent thinking using activation likelihood estimation. Hum. Brain Mapp. 36, 2703–2718. doi: 10.1002/hbm.22801
Xia, M., Wang, J., and He, Y. (2013). BrainNet viewer: a network visualization tool for human brain connectomics. PLoS One 8:e68910. doi: 10.1371/journal.pone.0068910
Zabelina, D. L., and Robinson, M. D. (2010). Creativity as flexible cognitive control. Psychol. Aesthet. Creat. Arts 4, 136–143. doi: 10.1037/a0017379
Keywords: creativity, fMRI, mathematics, mathematical creativity, meta-analysis
Citation: Li Q and Kim S (2025) Meta-analysis of fMRI studies related to mathematical creativity. Front. Psychol. 15:1400328. doi: 10.3389/fpsyg.2024.1400328
Edited by:
Ann Dowker, University of Oxford, United KingdomReviewed by:
Andy Wai Kan Yeung, University of Hong Kong, ChinaPei Xie, Sichuan Normal University, China
Copyright © 2025 Li and Kim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sungyeun Kim, c3lrQGludS5hYy5rcg==
 Qingqing Li
Qingqing Li Sungyeun Kim
Sungyeun Kim