- 1School of Psychology, Aristotle University of Thessaloniki, Thessaloniki, Greece
- 2Department of Education, University of Nicosia, Nicosia, Cyprus
- 3Department of Primary Education, Democritus University of Thrace, Alexandroupolis, Greece
- 4School of Philosophy and Education, Aristotle University of Thessaloniki, Thessaloniki, Greece
The present study investigated conceptual understanding in learning science in relation to four cognitive variables: logical thinking, field-dependence/field-independence, and divergent and convergent thinking. The participants were fifth- and sixth-grade elementary school pupils involved in different mental tasks, where they had to describe and interpret phenomena related to changes of matter. This brief report presents data from the students’ understanding of evaporation, and the method of analysis, a person-centered approach, is explicated. Latent class analysis (LCA) was applied to reveal distinct clusters of cases sharing similar patterns of responses. The use of LCA aligns with theoretical conjectures related to a stepwise conceptual change process, and the hypothetical steps correspond to the identified discrete latent classes (LCs). Subsequently, the LCs were associated with the four cognitive variables as covariates, thus providing empirical evidence for the role of the above-mentioned individual differences in children’s learning in sciences. Methodological issues and theoretical implications are discussed.
1. Introduction
The literature on children’s conceptual understanding of science is rich in reports focusing on erroneous or alternative ideas. Over decades, a crucial amount of knowledge has accrued, which has helped practitioners design teaching interventions, and academic scholars and theorists postulate assumptions about the nature of children’s representations. One of the most challenging themes in science teaching is the transformations of matter and related concepts (Liu and Lesniak, 2005, 2006; Papageorgiou and Johnson, 2005; García-Franco and Taber, 2009; Tsitsipis et al., 2010, 2012). Researchers’ strategies in probing children’s ideas include attempts to classify them and often identifying fundamental conceptions that facilitate or prevent the attainment of the scientific view. For example, the lack of understanding of the particulate nature of matter affects apprehending changes in the states of matter.
Interestingly, cross-cultural studies have revealed similar misconceptions, such as the content of the bubbles in boiling water being air, heat, carbon dioxide, or a mixture of hydrogen and oxygen, showing that children confuse such phenomena with chemical changes (Papageorgiou and Johnson, 2005; Talanquer, 2009; Papageorgiou et al., 2010). Inquiries regarding physical transformations of matter, such as evaporation, have shown that children’s cognitive obstacles originate from a lack of understanding of fundamental particle concepts and also from individual differences, e.g., logical thinking and cognitive styles (Johnson, 1998a,b; Tsitsipis et al., 2010, 2012). Researchers have also acknowledged that some kind of hierarchical levels of understanding exist in the progression from naïve ideas to the scientific view, often explicated via a specific level scheme (e.g., Hadenfeldt et al., 2014). Such putative levels imply a stepwise rather than a linear conceptual change process. Scholars from earlier times have postulated two theoretical perspectives about this. The first approach considers children’s knowledge before entirely acquiring the scientific view consistent or theory-like with explanatory power (Vosniadou and Brewer, 1992). The second approach supports the notion that these ideas are fragments of knowledge (p-prims) that come loosely together in situ, i.e., when a child needs to complete any task (DiSessa, 1993). The debate on these antithetical hypotheses is enduring since both have demonstrated empirical support. For the coherent knowledge hypothesis, explicit mental models have been proposed, while subsequent discussions have raised several methodological issues (Vosniadou and Brewer, 1992; Ioannides and Vosniadou, 2002; DiSessa et al., 2004; Nobes and Panagiotaki, 2007, 2009; Straatemeier et al., 2008). However, regardless of any argumentation, stepwise progression in learning processes remains an intriguing hypothesis, which, nevertheless, needs exploration via robust methodologies. One of the limitations of the past endeavors is that they relied on a simple analysis of empirical indicators, ignoring latent variable theory and contemporary models of psychological measurement (Bartholomew, 1987; Borsboom, 2008). Among them, latent class analysis (LCA) assumes that both observable and latent variables are categorical, and it is the proper measurement model for the coherent knowledge theory since the latter considers the children’s mental models as a categorical type of entities. Its applications have been demonstrated in exploratory and confirmatory approaches (Straatemeier et al., 2008; Vaiopoulou et al., 2017).
Moreover, most investigations on science learning have aimed merely to describe students’ hitches by labeling the difficulties of the specific topic without implementing independent variables within a more comprehensive explanatory framework. However, some researchers have found associations of conceptual change in science with several individual differences and notably cognitive variables, such as logical thinking, field dependence/independence, divergence, and convergence (BouJaoude et al., 2004; Tsitsipis et al., 2010, 2012; Tsikalas et al., 2014; Papageorgiou et al., 2016). In this endeavor, the selection of the above variables was made from among potential individual differences that were theory and evidence-based, while some others were excluded, e.g., working memory, which is associated with problem-solving and mathematical calculations.
The nature of children’s knowledge and the encountered cognitive obstacles, along with the role of individual differences in attaining conceptual change, are taken into account in designing pedagogical interventions, contributing to a theoretical framework aiming to identify, understand, and propose strategies to help children to overcome learning difficulties (Danili and Reid, 2004; Stamovlasis, 2006).
The present paper presents the implementation of the above cognitive variables within a person-centered approach and supports a stepwise conceptual change process, adding to the theoretical growth of the field. Next, a brief description of the above-mentioned psychometric variables follows.
1.1. Cognitive variables
1.1.1. Logical thinking or formal reasoning
Logical thinking (LTH), or formal reasoning, is a Piagetian construct referring to one’s ability to successfully implement concrete and formal operational reasoning (Lawson, 1978, 1985, 1993). Measuring LTH includes proportional, combinational, and probabilistic thinking and reasoning related to the isolation and control of variables, conservation of mass, and displaced volume. Formal reasoning is associated with students’ achievement in numerous studies (Lawson, 1982; Niaz, 1996; Tsaparlis and Angelopoulos, 2000; Stamovlasis and Tsaparlis, 2001; BouJaoude et al., 2004; Tsitsipis et al., 2010, 2012) and, in general, it has been proven to be one of the most important predictors of academic performance.
1.1.2. Field dependence/independence (FDI)
FDI is a cognitive style that concerns a person’s ability to separate relevant information from a complex and confusing context (Witkin et al., 1977). When individuals are dominated by a strong frame of reference and have difficulties separating an item from its context, they are characterized as field-dependent. On the contrary, individuals who can identify the item from the misleading context are called field-independent (Witkin and Goodenough, 1981). This cognitive style is considered continuous, and persons that fall in the middle of the FDI scale are defined as field-intermediate. FDI is a crucial cognitive variable involved in mental tasks, and learning science research has found that it is one of the main predictors of academic achievement (Tinajero and Páramo, 1998). In addition, FDI is a moderator variable within the information processing model due to the mental capacity and higher information processing ability required to process irrelevant information (Johnstone and Al-Naeme, 1991; Tsaparlis and Angelopoulos, 2000). Specifically, science education research has highlighted the critical role of field independence in conceptual understanding, learning, and problem-solving (Danili and Reid, 2004; Kang et al., 2005; Stamovlasis and Tsaparlis, 2005; Tsaparlis, 2005).
1.1.3. Convergent and divergent thinking
Convergence (CONV) refers to the ability to focus on the one correct answer in order to solve a problem, whereas divergence (DIV) regards the ability to respond flexibly and successfully to problems requiring the production of multiple solutions (Child and Smithers, 1973). It is important to emphasize that even though the terms used indicate that they are opposites, they are two distinct cognitive styles (Heller, 2007) which represent two unique aspects of intelligence and can be complementary characteristics. Given that a scientific problem can be quite complex, both attributes are essential, i.e., divergent thinking in the first stages and convergence in the latter steps for decision-making and conclusions (Facaoaru, 1985; Heller, 2007). Indeed, in science education research, these psychometric variables are highly correlated to students’ achievement (Danili and Reid, 2006; Tsitsipis et al., 2010, 2012; Tsikalas et al., 2014).
2. Method
2.1. Theoretical and methodological issues
The present study fosters the theoretical perspective that advocates the existence of hierarchical progression steps toward conceptual change, i.e., the conceptual understanding process’s evolution is not linear but passes through discrete stages. This is a theoretical assumption that requires empirical support while it embraces the intriguing research question of whether a latent construct, such as conceptual understanding, is continuous or categorical (or taxon), regardless of the level of measurement of the observable indicators, which are the choice of the researcher. This question is the aim of taxometrics, a branch of psychometric modeling that seeks to identify if a latent construct is a taxon/categorical or dimensional/continuous variable (Haslam et al., 2012). Alternatively, the usual psychometric practice is the implementation of a suitable psychometric model, e.g., a factor model or a latent class model, and scrutinizing the model fit with empirical data. Therefore, the measurement model that ensures access to the latent variable in question should align with the theoretical conjectures. The appropriate method for investigating conceptual change under the theory of coherent mental models is LCA, a psychometric measurement model that considers both latent and observable variables at the nominal level of measurement. The above supports a cogent rationale for implementing LCA, especially when the empirical indices implemented are at the nominal level of measurement, identified as correct responses or misconceptions/incorrect responses. (Van der Maas and Straatemeier, 2008; Hofman et al., 2015). Furthermore, LCA is an adept procedure to identify distinct groups in the participants that provide distinct patterns of responses, which according to latent variable theory, are due to different latent representations. That is, the latent construct possessed by participants exhibits discrete levels rather than being a continuous variable. These represent stages of conceptual understanding that emerge from the analysis of the empirical data. LCA is an effective method to detect discrete mental representations, thinking patterns, and cognitive change (Van der Maas and Straatemeier, 2008; Hofman et al., 2015).
Moreover, exploring conceptual understanding requires an explanatory framework and independent predictors that could be statistically associated with the hypothetical stages. To this end, the present endeavor explores the theoretical conjecture of a stage-wise progression in conjunction with the explanatory role of four cognitive variables. The choice of the psychometric variables to be associated with the levels of understanding is theory-driven and evidence-based. These constructs operationalize mental resources theoretically involved in the cognitive processes of learning the subject matter. For instance, divergent thinking that is associated with imagination is required to comprehend phenomena of state change of matter at the sub-micro level of molecules. Analogous elaborations and association of all cognitive variables with the mental processes involved in learning sciences have been presented and can be found elsewhere, along with the empirical evidence (Tsitsipis et al., 2010, 2012).
There are two interrelated fundamental research hypotheses:
H1. The first relates to identifying the existence of steps or stages along the conceptual change progression in science learning.
H2. The second concerns the association of the four psychometric variables: logical thinking, field dependence/independence, divergent thinking, and convergent thinking, with children’s understanding of the changes of matter under study.
2.2. Participants and measures
Three hundred and seventy-five pupils taking a mandatory science course in the fifth and sixth grades of elementary school (aged 11–12, 50.9% boys and 49.1% girls) participated in the study. They were from different schools in the broad area of Macedonia, Greece. Data were collected during one school year through paper-pencil tests. Children were involved in various tasks related to matter and its transformational properties, and they had to describe and explain phenomena. The open-ended questionnaire included selected items utilized in related studies (Johnson, 1998a,b,c; Papageorgiou et al., 2010), preserving enhanced validity. The assessment instrument included illustrations that facilitated the representation of the phenomena in question. There were items emphasizing knowledge recall and the interpretation of phenomena, which comprised the dimensions of the underlying construct and were context specific depending on what had been taught. Three graders applied a marking scheme of incorrect (misconception), partially correct, and correct. This marking scheme provided three-level ordinal variables, treated as categorical and used as the input for the subsequent LCA. After discussing the ensuing discrepancies among the graders, the agreement was 100%.
In addition, the participants had to complete psychometric tests extensively used in science learning research over the last decades to measure the psychometric variables in question. Specifically:
Logical thinking (LTH) or formal reasoning was assessed using the Lawson test, measuring logical thinking levels (Lawson, 1978). A Cronbach’s alpha reliability coefficient of 0.78 was obtained.
Field dependence/independence (FDI) or disembedding ability is usually evaluated utilizing the Group Embedded Figures Test (GEFT); however, a similar test, the Hidden-Figures Test (HFT), was used, which has been devised and calibrated (Johnstone and El-Banna, 1986) from Witkin’s original test materials. Cronbach’s alpha reliability coefficient was 0.84.
Divergent thinking (DIV) was measured using a six-item test designed by Bahar (Bahar, 1999). Each item is substantially a mini-test in itself lasting for 2–5 min that asks students to: generate words with similar meanings to those given (Test 1); construct up to four sentences using the words in the form as given (Test 2); draw up to five different sketches relevant to a given idea (Test 3); write down as many things as possible that have a common trait (Test 4); write down as many words as possible that begin with one specific letter and end with another specific letter (Test 5); and list all the ideas about a given topic (test 6). This instrument was used first with Greek students by Danili and Reid (2006) and by Tsitsipis et al. (2010). Cronbach’s alpha reliability coefficient was 0.74.
Convergent thinking (CONV) was assessed using a five-item timed test (Hindal et al., 2009) translated into Greek and modified to fit Greek idioms. Students answered each question separately for a total time of 20 min. Test 1 asked students to find two patterns that link to a group of words given (question 1), to form two words from the letters given (question 2), and to write down and explain a number missing from three sequences given (question 3). For Test 2, students had to read about a topic and classify three main ideas in a diagram. The task of Test 3 was to pick out a different object from a group of four and explain why they selected it. Test 4 comprised writing down two true things for all four given graphs. For Test 5, students marked a route on a map and described it in a few words. For the present sample, Cronbach’s alpha reliability coefficient was 0.77.
2.3. Latent class analysis
LCA is a psychometric method that uses Bayesian statistics to classify a set of responses or observable categories into clusters or latent classes (LCs) based on a set of conditional probabilities, which are the probabilities of having a response pattern y given the specific latent class c (Clogg, 1995; Dayton, 1998). Based on several criteria, such as the classification error, entropy R2, the number of parameters, likelihood ratio statistic (L2), Bayesian information criterion (BIC), Akaike’s information criterion (AIC), degrees of freedom, and bootstrapped p-value, the researcher decides on LC model fitting to empirical data (Magidson and Vermunt, 2004).
An advantage of LCA is the option to include external variables in the model, functioning as covariates or distal outcomes. Incorporating such variables defines an LC model comprising two parts: the measurement part, consisting of information on how the clusters are derived, and the structural part, dealing with the relationships between the ensued clusters and the external variables (Bakk et al., 2013). The process to carry out LCA can be either one-step or stepwise. The latter method includes three steps: (i) The identification of the underlying latent variable based on a set of indicators, (ii) The assignment of cases (individuals) to latent classes, and (iii) The analysis of the results into class membership and the covariates, accordingly. The stepwise method is preferable when the predictive validity of the covariate is of interest, while different classification methods can be applied along with bias-correction procedures (Bolck et al., 2004; Vermunt, 2010).
LCA has numerous applications in a wide range of disciplines and fields. For example, in educational research, LCA has been proven effective in deriving participants’ profiles and answering challenging research questions. Some indicative investigations include exploring students’ predictions and explanations of physical phenomena (Schneider and Hardy, 2013; van Schaik et al., 2020) and testing contradictory theoretical perspectives, such as the coherence vs. fragmented knowledge hypotheses (Straatemeier et al., 2008; Vaiopoulou and Papageorgiou, 2018; Stamovlasis et al., 2020).
3. Results
3.1. The ensuing latent classes
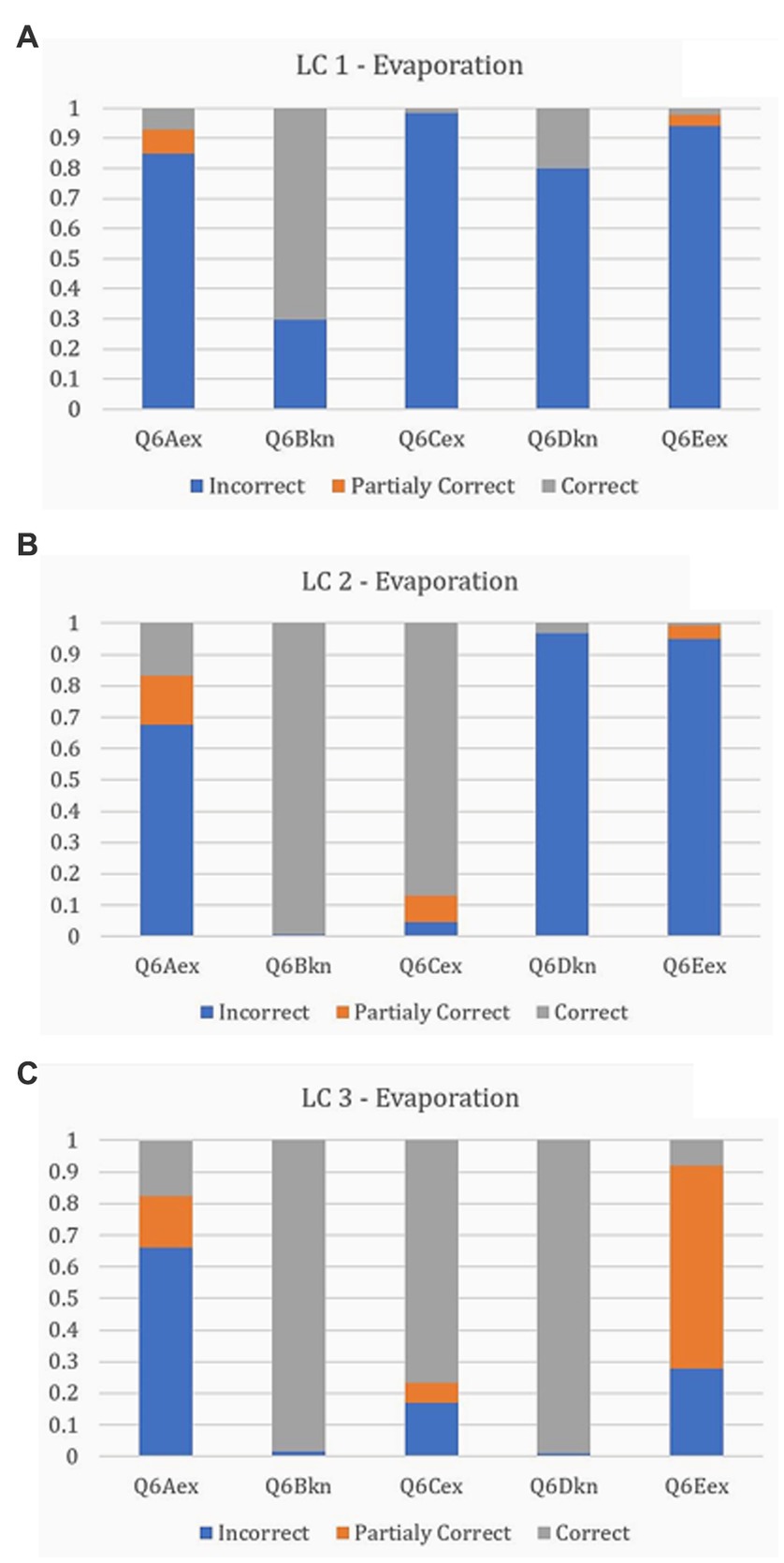
This short report analyzes and presents part of the data, specifically children’s responses to tasks related to the evaporation phenomenon, via LCA. The analysis, including the five corresponding items, led to the results in Table 1, where the three latent classes (LC) were identified as the best parsimonious model (entropy-R2 = 0.87, df = 324, classification error = 0.0445, BIC = 2343.12, Npar = 40).
A set of conditional probabilities concerning the responses in each item characterizes each of the ensuing latent classes (LC). In a graph showing the cumulative probabilities of a latent class, it is possible to visualize a pattern depicting the consistency of responses regarding the levels of judgment: correct, partially correct, and incorrect. These patterns designate the progression level; that is, a pattern where the incorrect responses (misconceptions) prevail denotes a lower level than a pattern dominated by correct responses.
Figure 1 depicts the three latent classes. LC1 (20.54%) includes children who provided primarily incorrect responses, i.e., misconceptions (Figure 1A). LC2 (43.04%) consists of children who, compared to LC1, provided some correct or partially correct answers and demonstrated a nuanced understanding. LC2 possesses an evident degree of heterogeneity regarding the responses in the five items, given that the analysis provided a pattern with a mixture of incorrect, correct, and partially correct answers (Figure 1B). LC3 (36.42%) includes children mainly providing correct responses. This pattern, compared to LC2, appears less fragmented and relatively homogeneous, with the correct answers prevailing (Figure 1C).
The three LCs are evidently hierarchical, representing three stages that children could have reached through a learning process, and these groups are the categories of the latent variable under investigation. The crucial question is how they are associated with the cognitive variables, which are anticipated to function as predictors of learning outcomes.
3.2. Effect of the four cognitive variables on latent classes
In the next step, latent classes were associated with the four covariates, considered independent variables, and predicted the LC membership.
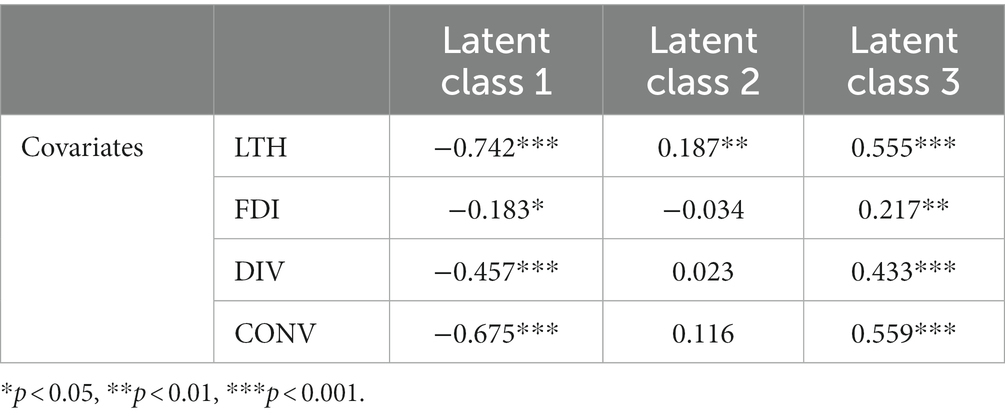
Table 2 shows the effects of cognitive variables on the three latent classes. LC1 is negatively associated with LTH (b = −0.742, p < 0.0001), FDI (b = −0.183, p < 0.05), DIV (b = −0.457, p < 0.001), and CONV (b = −0.675, p < 0.001). On the other hand, LC3 is positively associated with all covariates: LTH (b = 0.555, p < 0.0001), FDI (b = 0.217, p < 0.01), DIV (b = 0.433, p < 0.001), and CONV (b = 0.559, p < 0.001). In between LC1 and LC3, LC2 is non-significantly associated with the psychometric variables with the exception of LTH (b = 0.187, p < 0.01).
In conclusion, LCA applied to children’s responses revealed distinct clusters corresponding to discrete conceptual understanding levels. The roles of the four cognitive variables examined as covariates of LC memberships follow a consistent pattern, associated negatively and positively with the lower and higher levels of conceptual understanding, respectively. The interpretation of the coefficient in Table 2 is analogous to the logistic regression coefficients, i.e., the higher the LTH value, the higher the odds of belonging to LC3. The above relationships indicate the crucial role of mental resources in the underlying learning process and imply their involvement in forming various performance levels.
4. Discussion
4.1. Interpretation of the findings and theoretical perspectives
LCA suggests that the latent variable under study can be considered categorical. In this study, it revealed certain clusters/LC where, in each LC, children shared similar response patterns, which according to psychometric measurement theory are due to a latent construct that is the common cause of the observed responses. Thus, children within the same LC possess the same latent mental representations. LCA was used in an exploratory mode since the clusters were not defined a priori, but they emerged from the analysis. Note that elsewhere (Straatemeier et al., 2008; Vaiopoulou et al., 2017; Vaiopoulou and Papageorgiou, 2018; Stamovlasis et al., 2020), the method was used in a confirmatory mode to validate specific mental models explicitly stated in the literature (Vosniadou and Brewer, 1992; Ioannides and Vosniadou, 2002). These proposed mental models/latent classes were identified and characterized by specific concurrent misconceptions, which, in fact, have been used in the classification process to obtain those mental models. To construct the hypothesized mental models via exploratory processes while proposing them as the stages being sought. This approach adheres to the epistemological view of substance philosophy, contrary to the process philosophy (Seibt, 2022) which is the view fostered in the present interpretation.
Given the existence of discrete levels of understanding and their association with cognitive variables, it is essential to pursue an interpretation of the findings and explicate the nature of these stages in conjunction with their predictors. The insight here is to reconsider the involvement of cognitive variables and explain the findings by fostering a process-based approach that identifies cognitive phenomena situated and time-dependent in nature (Van Geert and de Ruiter, 2022). The meta-theoretical framework of complex adaptive systems (CDS) and non-linear dynamics may provide a suitable vocabulary description of the process under investigation. The well-known concept of attractor fits the notion of the stages sought in the present endeavor. An attractor is a stable state or a set of stages toward which a system’s evolution tends to move (Freeman and Barrie, 1994; Kelso, 1995), while the changes in the system are understood as transitions between attractors. Ergo, the CDS framework can reasonably provide a theoretical justification for the existence of discrete stages.
If the detected LCs are viewed or related to a kind of attractor state, their association with psychometric variables implies that the corresponding mental resources are part of or are involved in forming the attractor. From the CDS perspective, the mental operators corresponding to LTH, FDI, DIV, and CONV act successively in a dynamical and iterative process, where potential failed synergies among them trap the mind into a lower performance attractor stage. Dynamical causes stemming from insufficient cooperation among mental resources might lead to a sub-optimal conceptual understanding, a state that could be characterized as a conceptual attractor. Such a description explicitly assumes that the temporal outcome is not an additive function of the contributing components, i.e., the underlying process is not linear.
The above explanation from the CDS perspective adds to conceptual change research by proposing the operation of mental resources and their dynamical co-actions as contributing to the formation of dynamical attractors, in which the LCs are detected as distinct stages.
4.2. Limitations and future research
The present research has limitations that originate from the cross-sectional type of design and the opportunity sampling procedure. Given that it is the first endeavor investigating participants of the young age of 11–12, the findings need replication with different samples. Moreover, the theoretical interpretation attempted via CDS needs further refinement and a complete elaboration to establish a definite amalgamation of conceptual change theories within the complexity theory and non-linear dynamical system framework. Additionally, this perspective’s development needs empirical evidence by means of non-linear methodological analyses. Research has shown that the psychometric constructs under investigation that operationalize active mental resources are predictive variables in children’s cognitive performance, while applications of catastrophe theory models have associated them with non-linear changes that explicate transitions between stages (Stamovlasis, 2006, 2011; Stamovlasis and Tsaparlis, 2012; Vaiopoulou et al., 2021; Stamovlasis et al., 2023). Thus, a following inquiry may seek potential non-linear changes between the discovered stages (or attractors)—that is, transitions, for instance, between LC1 and LC2—revealed in the various cognitive tasks as a function of the cognitive variables under study.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved by the Greek Ministry of Education (protocol code “υπ. Αριθ. Φ. 15/545/83146/Γ1/19-7-12” on 19 July 2012). Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author contributions
JV, TT, DS, and GP contributed to the conception and design of the study and wrote sections of the manuscript. JV organized the database, performed the statistical analysis, and wrote the first draft of the manuscript. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bahar, M. (1999). Investigation of biology students’ cognitive structure through word association tests, mind maps and structural communication grids. PhD thesis, University of Glasgow.
Bakk, Z., Tekle, F. B., and Vermunt, J. K. (2013). Estimating the association between latent class membership and external variables using Bias-adjusted three-step approaches. Sociol. Methodol. 43, 272–311. doi: 10.1177/0081175012470644
Bartholomew, D. J. (1987). Latent variable models and factor analysis. Oxford: Oxford University Press.
Bolck, A., Croon, M., and Hagenaars, J. (2004). Estimating latent structure models with categorical variables: one-step versus three-step estimators. Polit. Anal. 12, 3–27. doi: 10.1093/pan/mph001
Borsboom, D. (2008). Latent variable theory. Measurement Interdiscip. Res. Perspect. 6, 25–53. doi: 10.1080/15366360802035497
BouJaoude, S., Salloum, S., and Abd-El-Khalick, F. (2004). Relationships between selective cognitive variables and students’ ability to solve chemistry problems. Int. J. Sci. Educ. 26, 63–84. doi: 10.1080/0950069032000070315
Child, D., and Smithers, A. (1973). An attempted validation of the Joyce-Hudson scale of covergence and divergence. Br. J. Educ. Psychol. 43, 57–62. doi: 10.1111/j.2044-8279.1973.tb00738.x
Clogg, C. C. (1995). “Latent class models” in Handbook of statistical modeling for the social and behavioral sciences. (New York, NY: Springer US), 311–359.
Danili, E., and Reid, N. (2004). Some strategies to improve performance in school chemistry, based on two cognitive factors. Res. Sci. Technol. Educ. 22, 203–226. doi: 10.1080/0263514042000290903
Danili, E., and Reid, N. (2006). Cognitive factors that can potentially affect pupils’ test performance. Chem. Educ. Res. Pract. 7, 64–83. doi: 10.1039/B5RP90016F
DiSessa, A. A. (1993). Toward an epistemology of physics. Cogn. Instr. 10, 105–225. doi: 10.1080/07370008.1985.9649008
DiSessa, A. A., Gillespie, N. M., and Esterly, J. B. (2004). Coherence versus fragmentation in the development of the concept of force. Cogn. Sci. 28, 843–900. doi: 10.1016/j.cogsci.2004.05.003
Facaoaru, C. (1985). Kreativität in Wissenschaft und Technik [Creativity in science and technology]. Bern: Huber.
Freeman, W. J., and Barrie, J. M. (1994). “Chaotic oscillations and the genesis of meaning in cerebral cortex” in Temporal coding in the brain. eds. G. Buzsáki, R. Llinás, W. Singe, A. Berthoz, and Y. Christen (Berlin, Heidelberg: Springer), 13–37.
García-Franco, A., and Taber, K. S. (2009). Secondary students’ thinking about familiar phenomena: learners’ explanations from a curriculum context where “particles” is a key idea for organising teaching and learning. Int. J. Sci. Educ. 31, 1917–1952. doi: 10.1080/09500690802307730
Hadenfeldt, J. C., Liu, X., and Neumann, K. (2014). Framing students’ progression in understanding matter: a review of previous research. Stud. Sci. Educ. 50, 181–208. doi: 10.1080/03057267.2014.945829/SUPPL_FILE/RSSE_A_945829_SM5354.DOCX
Haslam, N., Holland, E., and Kuppens, P. (2012). Categories versus Dimensions in Personality and Psychopathology: A Quantitative Review of Taxometric Research. Psychol. Med. 42, 903–920. doi: 10.1017/S0033291711001966
Heller, K. A. (2007). Scientific ability and creativity. High Abil. Stud. 18, 209–234. doi: 10.1080/13598130701709541
Hindal, H., Reid, N., and Badgaish, M. (2009). Working memory, performance and learner characteristics. Res. Sci. Technol. Educ. 27, 187–204. doi: 10.1080/02635140902853640
Hofman, A. D., Visser, I., Jansen, B. R. J., and van der Maas, H. L. J. (2015). The balance-scale task revisited: a comparison of statistical models for rule-based and information-integration theories of proportional reasoning. PLoS One 10:e0136449. doi: 10.1371/journal.pone.0136449
Johnson, P. M. (1998a). Children’s understanding of changes of state involving the gas state, part 1: boiling water and the particle theory. Int. J. Sci. Educ. 20, 567–583. doi: 10.1080/0950069980200505
Johnson, P. M. (1998b). Children’s understanding of changes of state involving the gas state, part 2: evaporation and condensation below boiling point. Int. J. Sci. Educ. 20, 695–709. doi: 10.1080/0950069980200607
Johnson, P. M. (1998c). Progression in children’s understanding of a ‘basic’ particle theory: a longitudinal study. Int. J. Sci. Educ. 20, 393–412. doi: 10.1080/0950069980200402
Johnstone, A. H., and Al-Naeme, F. F. (1991). Room for scientific thought? Int. J. Sci. Educ. 13, 187–192. doi: 10.1080/0950069910130205
Johnstone, A. H., and El-Banna, H. (1986). Capacities, demands and processes: a predictive model for science education. Educ. Chem. 23, 80–84.
Kang, S., Scharmann, L. C., Noh, T., and Koh, H. (2005). The influence of students’ cognitive and motivational variables in respect of cognitive conflict and conceptual change. Int. J. Sci. Educ. 27, 1037–1058. doi: 10.1080/09500690500038553
Kelso, J. A. S. (1995). Dynamic patterns: the self-organization of brain and behavior. Cambridge, MA: The MIT Press.
Lawson, A. E. (1978). The development and validation of a classroom test of formal reasoning. J. Res. Sci. Teach. 15, 11–24. doi: 10.1002/tea.3660150103
Lawson, A. E. (1982). Formal reasoning, achievement, and intelligence: an issue of importance. Sci. Educ. 66, 77–83. doi: 10.1002/sce.3730660110
Lawson, A. E. (1985). A review of research on formal reasoning and science teaching. J. Res. Sci. Teach. 22, 569–617. doi: 10.1002/tea.3660220702
Lawson, A. E. (1993). Classroom test of scientific reasoning: revised paper–pencil edition. Tempe, AZ: Arizona State University.
Liu, X., and Lesniak, K. M. (2005). Students’ progression of understanding the matter concept from elementary to high school. Sci. Educ. 89, 433–450. doi: 10.1002/sce.20056
Liu, X., and Lesniak, K. M. (2006). Progression in children’s understanding of the matter concept from elementary to high school. J. Res. Sci. Teach. 43, 320–347. doi: 10.1002/tea.20114
Magidson, J., and Vermunt, J. K. (2004). “Latent class models” in The Sage handbook of quantitative methodology for the social sciences. ed. D. Kaplan (Thousand Oaks, CA: Sage), 175–198.
Niaz, M. (1996). Reasoning strategies of students in solving chemistry problems as a function of developmental level, functional M-capacity and disembedding ability. Int. J. Sci. Educ. 18, 525–541. doi: 10.1080/0950069960180503
Nobes, G., and Panagiotaki, G. (2007). Adults’ representations of the earth: implications for children’s acquisition of scientific concepts. Br. J. Psychol. 98, 645–665. doi: 10.1348/000712607X178119
Nobes, G., and Panagiotaki, G. (2009). Mental models or methodological artefacts? Adults’ ‘naïve’ responses to a test of children’s conceptions of the earth. Br. J. Psychol. 100, 347–363. doi: 10.1348/000712608X332909
Papageorgiou, G., Grammaticopoulou, M., and Johnson, P. M. (2010). Should we teach primary pupils about chemical change? Int. J. Sci. Educ. 32, 1647–1664. doi: 10.1080/09500690903173650
Papageorgiou, G., and Johnson, P. M. (2005). Do particle ideas help or hinder pupils’ understanding of phenomena? Int. J. Sci. Educ. 27, 1299–1317. doi: 10.1080/09500690500102698
Papageorgiou, G., Markos, A., and Zarkadis, N. (2016). Students’ representations of the atomic structure-the effect of some individual differences in particular task contexts. Chem. Educ. Res. Pract. 17, 209–219. doi: 10.1039/c5rp00201j
Papageorgiou, G., Stamovlasis, D., and Johnson, P. M. (2010). Primary teachers’ particle ideas and explanations of physical phenomena: effect of an in-service training course. Int. J. Sci. Educ. 32, 629–652. doi: 10.1080/09500690902738016
Schneider, M., and Hardy, I. (2013). Profiles of inconsistent knowledge in children’s pathways of conceptual change. Dev. Psychol. 49, 1639–1649. doi: 10.1037/a0030976
Seibt, J. (2022). “Process philosophy” in The Stanford encyclopedia of philosophy (winter 202). eds. E. N. Zalta and U. Nodelman (Stanford, CA: Metaphysics Research Lab, Stanford University)
Stamovlasis, D. (2006). The nonlinear dynamical hypothesis in science education problem solving: a catastrophe theory approach. Nonlinear Dynamics Psychol. Life Sci. 10, 37–70.
Stamovlasis, D. (2011). Nonlinear dynamics and neo-Piagetian theories in problem solving: perspectives on a new epistemology and theory development. Nonlinear Dynamics Psychol. Life Sci. 15, 145–173.
Stamovlasis, D., and Tsaparlis, G. (2001). Application of complexity theory to an information processing model in science education. Nonlinear Dynamics Psychol. Life Sci. 5, 267–286. doi: 10.1023/A:1009514607622
Stamovlasis, D., and Tsaparlis, G. (2005). Cognitive variables in problem solving: a nonlinear approach. Int. J. Sci. Math. Educ. 3, 7–32. doi: 10.1007/s10763-004-3918-5
Stamovlasis, D., and Tsaparlis, G. (2012). Applying catastrophe theory to an information-processing model of problem solving in science education. Sci. Educ. 96, 392–410. doi: 10.1002/sce.21002
Stamovlasis, D., Vaiopoulou, J., and Papageorgiou, G. (2020). A comparative evaluation of dissimilarity-based and model-based clustering in science education research: the case of children’s mental models of the earth. Int. J. Data Anal. Tech. Strat. 12:247. doi: 10.1504/IJDATS.2020.10028869
Stamovlasis, D., Vaiopoulou, J., Tsikalas, T., and Papageorgiou, G. (2023). A punctuation equilibrium model for conceptual change and the role of neo-Piagetian constructs: Methodology, empirical evidence, and theoretical perspectives. Nonlinear Dynamics, Psychology, and Life Sciences (in press).
Straatemeier, M., van der Maas, H. L. J., and Jansen, B. R. J. (2008). Children’s knowledge of the earth: a new methodological and statistical approach. J. Exp. Child Psychol. 100, 276–296. doi: 10.1016/j.jecp.2008.03.004
Talanquer, V. (2009). On cognitive constraints and learning progressions: the case of “structure of matter.”. Int. J. Sci. Educ. 31, 2123–2136. doi: 10.1080/09500690802578025
Tinajero, C., and Páramo, M. F. (1998). Field dependence-independence cognitive style and academic achievement: a review of research and theory. Eur. J. Psychol. Educ. 13, 227–251. doi: 10.1007/BF03173091
Tsaparlis, G. (2005). Non-algorithmic quantitative problem solving in university physical chemistry: a correlation study of the role of selective cognitive factors. Res. Sci. Technol. Educ. 23, 125–148. doi: 10.1080/02635140500266369
Tsaparlis, G., and Angelopoulos, V. (2000). A model of problem solving: its operation, validity, and usefulness in the case of organic-synthesis problems. Sci. Educ. 84, 131–153. doi: 10.1002/(SICI)1098-237X(200003)84:2<131::AID-SCE1>3.0.CO;2-4
Tsikalas, T., Stamovlasis, D., and Papageorgiou, G. (2014). Mental representations of 12 year-old children about boiling and evaporation: a probabilistic association with convergent and divergent thinking. Preschool Primary Educ. 2:17. doi: 10.12681/ppej.87
Tsitsipis, G., Stamovlasis, D., and Papageorgiou, G. (2010). The effect of three cognitive variables on students’ understanding of the particulate nature of matter and its changes of state. Int. J. Sci. Educ. 32, 987–1016. doi: 10.1080/09500690902893605
Tsitsipis, G., Stamovlasis, D., and Papageorgiou, G. (2012). A probabilistic model for students’ errors and misconceptions on the structure of matter in relation to three cognitive variables. Int. J. Sci. Math. Educ. 10, 777–802. doi: 10.1007/s10763-011-9288-x
Vaiopoulou, J., and Papageorgiou, G. (2018). Primary students’ conceptions of the earth: re-examining a fundamental research hypothesis on mental models. Preschool Primary Educ. 6, 23–34. doi: 10.12681/ppej.14210
Vaiopoulou, J., Stamovlasis, D., and Papageorgiou, G. (2017). “New perspectives for theory development in science education: rethinking mental models of force in primary school” in Progress in education. ed. R. V. Nata, vol. 47 (Hauppauge, NY: Nova Science Publishers, Inc), 1–16.
Vaiopoulou, J., Tsikalas, T., Stamovlasis, D., and Papageorgiou, G. (2021). Nonlinear dynamic effects of convergent and divergent thinking in conceptual change process: empirical evidence from primary education. Nonlinear Dynamics Psychol. Life Sci. 25, 335–355.
Van der Maas, H. L. J., and Straatemeier, M. (2008). How to detect cognitive strategies: commentary on ‘differentiation and integration: guiding principles for analyzing cognitive change.’. Dev. Sci. 11, 449–453. doi: 10.1111/j.1467-7687.2008.00690.x
Van Geert, P. L. C., and de Ruiter, N. (2022). Toward a process approach in psychology: stepping into Heraclitus’ river Cambridge, Cambridge University Press.
Van Schaik, J. E., Slim, T., Franse, R. K., and Raijmakers, M. E. J. J. (2020). Hands-on exploration of cubes’ floating and sinking benefits Children’s subsequent buoyancy predictions. Front. Psychol. 11:1665. doi: 10.3389/fpsyg.2020.01665
Vermunt, J. K. (2010). Latent class modeling with covariates: two improved three-step approaches. Polit. Anal. 18, 450–469. doi: 10.1093/pan/mpq025
Vosniadou, S., and Brewer, W. F. (1992). Mental models of the earth: a study of conceptual change in childhood. Cogn. Psychol. 24, 535–585. doi: 10.1016/0010-0285(92)90018-W
Witkin, H. A., and Goodenough, D. R. (1981). Cognitive styles: essence and origins. Field dependence and field independence. Psychol Issues, 1–141.
Keywords: conceptual change, divergent and convergent thinking, field-dependence/field-independence, logical thinking, latent class analysis, science learning, conceptual understanding, congitive variables
Citation: Vaiopoulou J, Tsikalas T, Stamovlasis D and Papageorgiou G (2023) Conceptual understanding in science learning and the role of four psychometric variables: a person-centered approach. Front. Psychol. 14:1204868. doi: 10.3389/fpsyg.2023.1204868
Edited by:
Igor Douven, Université Paris-Sorbonne, FranceReviewed by:
Lina Bendifallah, KU Leuven, BelgiumTzung-Jin Lin, National Taiwan Normal University, Taiwan
Copyright © 2023 Vaiopoulou, Tsikalas, Stamovlasis and Papageorgiou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Julie Vaiopoulou, Y3ZhaW9wb3Vsb3VAcHN5LmF1dGguZ3I=
 Julie Vaiopoulou
Julie Vaiopoulou Themistocles Tsikalas3
Themistocles Tsikalas3 Dimitrios Stamovlasis
Dimitrios Stamovlasis George Papageorgiou
George Papageorgiou