- 1Department of Psychology, National and Kapodistrian University of Athens, Athens, Greece
- 2Department of Self Skills Development, King Saud University, Riyadh, Saudi Arabia
- 3Education and Training Evaluation Commission (ETEC), Riyadh, Saudi Arabia
The aim of this study was threefold: First, to examine the dimensionality of the construct of General Academic Ability (GAA) at the subscale level providing additional insights over and above on the conceptualization of the construct. Second, to explore different degrees of measurement invariance of the GAA across gender using more recent advancements in the examination of Measurement Invariance (i.e., Bias-Corrected bootstrap Confidence Intervals). Third, to examine gender differences across the different facets of the GAA at the latent mean level. The sample consisted of 1,800 high school graduates who applied for higher education in Saudi Arabia. The results from the analysis indicated that the hierarchical model with one higher-order factor (i.e., general academic ability) and four lower-order cognitive factors (i.e., verbal ability, quantitative ability, scholastic aptitude, and GPA) exhibited an excellent fit to the data. In terms of the measurement invariance hypothesis, it was found that the hierarchical model exhibits full configural and metric invariance and partial scalar invariance. Finally, using the Latent Mean Difference procedure, the results showed gender differences in the Verbal and GPA domains. Although significant differences were also found in the Scholastic aptitude domain, this finding is not stable due to several non-invariant items within the domain. In both cases, females scored higher than males. Finally, regarding the higher-order factor (GAA), the results showed that females scored higher than males. There were no significant differences in the Quantitative domain.
Introduction
Academic performance is a crucial research topic, particularly for college admission purposes. Though there is no agreed-upon of its measures, literature determined three group factors that affect the quality of academic performance: Aptitude, instruction, and environment (Walberg, 1981). For admission purposes, the most common way of measuring academic performance is through standardized tests. Literature suggests that these tests are affected by several individual and contextual factors. For example, researchers found that ethnicity is one of the factors that affect academic performance. White students are more likely to have a higher cumulative general point average (CGPA; Weissberg et al., 2003; Laskey and Hetzel, 2011; Bronkema and Bowman, 2019) than students of color or other ethnicities. Parental status is another factor that affects academic success. Several studies have demonstrated that parental education significantly predicts cumulative general point average (CGPA; Kelly, 2004; Dayioğlu and Türüt-Aşik, 2007; Dika, 2012). Another factor that is affecting academic performance is age. Several researchers found that age significantly predicts both first semester and first-year GPA (Gibbison et al., 2011; Ferrão and Almeida, 2019). Finally, pre-college academic preparation was found to be influential for academic success. Several studies affirmed that students with higher high school grade point average (HSGPA) were more likely to achieve a higher college grade point average (CGPA; Dayioğlu and Türüt-Aşik, 2007; Dika, 2012; Komarraju et al., 2013; Wurf and Croft-Piggin, 2015; Saunders-Scott et al., 2018; Sulphey et al., 2018; Bronkema and Bowman, 2019; Caviglia-Harris and Maier, 2020).
Gender is another factor assumed to affect students’ academic scores considerably. Many studies have shown that boys and girls perform differently (e.g., O’Reilly and McNamara, 2007; Abubakar and Bada, 2012). However, contrary to the compelling evidence regarding the effect of other individual and contextual variables on academic performance, the gender role in academic performance is still an issue that attracts increased scientific interest, mainly due to the inconclusive reported findings. For example, studies pointed out no significant gender difference in students’ academic achievement. In a meta-analytic study, Else-Quest et al. (2010) showed negligible gender differences in the results of standardized mathematics tests. Similarly, Ajai and Imoko (2015) found that male and female students did not significantly differ in achievement and retention scores in mathematics.
On the other hand, other studies have reported significant differences, with the boys or the girls performing better. For example, several studies suggest that females outperform males in language-based subjects and verbal tests (e.g., Deary et al., 2007; Spinath et al., 2010), and males outperform their female counterparts in STEM-related subjects (e.g., math, engineering, etc.) and visuospatial tests (e.g., Strand et al., 2006; Lakin, 2013). Evidence from TIMSS 2015 indicated that 4th-grade boys outperformed girls in mathematics in about one-third of the countries that took place, while for 8th grade, this figure is reduced to one-sixth (Mullis et al., 2016). In a meta-analytic study, Voyer and Voyer (2014) found that females appear to have higher school grades in language-based subjects and STEM subjects than males.
Gibb et al. (2008) introduced a biological perspective and the way the human brain is organized across gender as a possible explanation for obtained gender differences in achievement, while Carvalho (2016) highlighted the role of personality dimensions (e.g., aggressiveness) as potential mediators in the relationship between gender and academic performance.
The gender gap in academic performance has been examined not only in terms of school grades and performance but also in terms of other aspects of academic life. For example, Bugler et al. (2015) suggested that females have higher motivation levels and better adaptation. Similarly, Ghazvini and Khajehpour (2011) found that female students showed more internal locus of control in academic performance than male students. However, no differences were found in academic self-concept as a function of gender. They also found that boys use learning strategies to a lesser degree than do girls and that girls take greater responsibility for their academic failures.
A possible explanation for the inconsistencies in the obtained results might lie in the method of analysis applied by the researchers to examine the phenomenon. For example, almost all reported studies have used conventional mean difference statistics (e.g., t-test, ANOVA, etc.) to examine possible gender differences in academic achievement. However, this approach is based on the assumption that the measurement properties of the scale used to measure academic performance are equivalent across the compared groups (Vandenberg and Lance, 2000). Despite its appeal, this assumption is highly problematic since it is not always true. Thus, findings that are based on this assumption could be questioned since one can never be sure that the reported differences are due to actual group differences or are due to the different conceptualization (i.e., factor structure) of the construct being measured across groups (Reise et al., 1993).
An alternative and more robust statistical technique for comparing groups would be examining the latent means derived from the multi-group comparisons performed via structural equation modeling and measurement invariance techniques (Cheung and Rensvold, 2002; Millsap, 2011). Measurement invariance is determined if the trait scores between different groups are comparable and have the same meaning. On the other hand, although determining measurement invariance across groups is a logical prerequisite to conducting meaningful cross-group comparisons (e.g., males vs. females), measurement invariance is rarely tested in psychological research (Horn and McArdle, 1992).
Based on the above and given the lack of agreement among researchers on the role of gender in academic performance, the aims of this study were threefold: first, to provide additional insights over and above on the conceptualization of the construct of General Academic Ability (GAA) as introduced and discussed by Dimitrov et al. (2015). Second, to explore different degrees of measurement invariance of the GAA construct across gender. Using more recent advancements in Measurement Invariance (i.e., Bias-Corrected bootstrap Confidence Intervals), we will attempt to understand the factorial structure of the GAA in more depth. Third, to examine gender differences across the different facets of the GAA at the latent mean level.
Materials and methods
Participants and procedure
The sample consisted of 1,800 high school graduates who applied for higher education in Saudi Arabia. Along with other admission requirements that Saudi higher education institutions have toward their applicants, a key factor in the decision on acceptance is a composite score of the applicants based on their high school grade (GPA) and test scores on two standardized tests, namely General Aptitude Test (GAT) and Standardized Achievement Admission Test (SAAT). Nine hundred (50.0%) of the participants were males, and 900 (50.0%) were females, with a mean age of 17.50 years (SD = 1.12), ranging between 17 and 32 years. Regarding the type of school, 1,259 individuals (69.1%) graduated from a public school and 541 (30.1%) from a private school. In terms of their socio-economic status, 548 (30.4%) participants were coming from families with <5,000$ annual income, 554 (30.8%) from families with 5,000–1,000$ annual income, 321 (17.8%) from families with 10,000–15,000$ annual income, 211 (11.7%) from families with 15,000–20,000$ annual income and 166 (9.2%) from families with annual income >20,000$. In terms of origin, all participants were coming from the 13 regions of Saudi Arabia. Although not representative, the characteristics of a sample approximate the characteristics of the Saudi population. Ethical approval for the present study was granted by the Education and Training Evaluation Commission’s Ethics Committee (Ref No.TR332-2021). All participants were informed that their responses would be utilized as a part of a larger study to evaluate the psychometric properties of the measure. Completion of the test comprised their informed consent for their participation. No participants reported any psychological or emotional issues that would inhibit their full performance.
Measures
The general aptitude test for science major
This is a general cognitive ability test developed developed by the Qiyas (Education & Training Evaluation Commission), which measures two different cognitive areas: (a) verbal and (b) numerical. This GAT version contains 95 dichotomous items (right-wrong) and measures seven different cognitive skills: (i) word meaning (12 items), (ii) sentence completion (15 items), (iii) analogy (15 items), (iv) reading comprehension (23 items), (v) arithmetic (17 items), (vi) analysis (seven items), and (vii) geometry (six items). The first four subscales measure verbal ability and the remaining numerical ability. A global cognitive ability factor composed of the scores from the two domain scales (i.e., verbal and numerical) is also available. There are five different versions of the GAT (Form A to E). Previous studies have shown that GAT is a very reliable test, with alpha reliabilities ranging from 0.73 to 0.82 for both sections (Verbal and Numerical; e.g., Dimitrov, 2013; Dimitrov et al., 2015; Dimitrov and Shamrani, 2015). Additionally, several studies have shown that GAT is an instrument with solid psychometric properties (e.g., Alanazi, 2014; Alamoudi et al., 2021; Aldurayheem, 2022).
The standard achievement admission test
Standard achievement admission test is an admission test developed by the Qiyas (Education & Training Evaluation Commission), covering four basic subject areas: Biology, Chemistry, Physics, and Mathematics, and focuses on the material of the official 3-year (scientific) curriculum of the Saudi High Schools. Standard achievement admission test is comprised of 88 multiple-choice items (four alternative options), which are distributed as follows: 20% of each subject for the first year of the high school syllabus, 30% of each subject for the second year of the high school syllabus, and 50% of each subject for the third year of the high school syllabus. The test time for each section is 25 min. Previous studies reported reliability indices ranging from 0.62 to 0.74 (e.g., Tsaousis et al., 2018). Additionally, several studies have demonstrated that SAAT is a valid predictor for various outcome criteria (e.g., Alamoudi et al., 2021; Alsagoafi, 2021; Vista and Alkhadim, 2022).
High school grade point average
The Ministry of Education provided the high school grades for the 1st and 2nd semesters and the Grade Point Average for each student at the end of the academic year.
Data analysis strategy
To test the latent structure of the GAA, a hierarchical (second-order) factor model with 16 observed variables that are a function of four lower-order cognitive factors (i.e., verbal ability, quantitative ability, school scholastic aptitude, and GPA) and one higher-order factor (GAA) that accounts for the commonality shared by the lower order factors, was examined. We used the following indices to assess model fit to the data: the chi-square (χ2) statistic and the related degrees of freedom (df), the Comparative Fit Index (CFI), the Tucker–Lewis Index (TLI), the Root Mean Square Error of Approximation (RMSEA), and the Standardized Root Mean Square Residual (SRMR). A CFI and TLI value above 0.90 indicates an acceptable fit (with values >0.95 being ideal; Brown, 2015). Further, RMSEA and SRMR values up to 0.08 indicate a reasonable fit to the data, while values up to 0.05 indicate an excellent fit (Hu and Bentler, 1999). Maximum likelihood with robustness to non-normality and non-independence of observations (MLR; Muthén and Muthén, 1998-2016) was the model’s estimation method.
To test whether GAA sub-scales exhibited measurement invariance across gender, a multi-group confirmatory factor analysis (MGCFA) was conducted (Vandenberg and Lance, 2000; Milfont and Fischer, 2015). Τhree different (nested) models were examined: configural, metric, and scalar invariance. In configural invariance, the extent to which the scale’s factor structure is conceptualized similarly across groups was tested. To do that, the item factor loadings and item thresholds were allowed to vary across both groups (unconstrained model). This model also serves as the baseline model with which the other two models are compared for invariance. Next, apart from fixing construct dimensionality to be invariant, additional equality constraints were imposed on the item factor loadings across the two groups. In that way, the metric (or weak) invariance was tested. If a scale exhibits metric invariance, the respondents across groups attribute the same meaning to the latent construct under study. Then, additional constraints to factor loadings and item intercepts were imposed to test for scalar invariance. Establishing scalar invariance indicates that participants with the same score on the latent construct would obtain the same score on the observed variable irrespective of their group membership (Putnick and Bornstein, 2016). When scalar invariance is established, comparisons among group means are meaningful (Vandenberg and Lance, 2000; Millsap, 2011).
Finally, latent mean differences were evaluated to examine for possible gender differences. In an SEM framework, to estimate the difference between two group means at a latent level, one of the groups should be served as a reference group, and its mean should be fixed to zero. In this case, the latent mean of the other group represents the difference between the latent means of the two groups (Hong et al., 2003). Thus, a significant mean of a compared group would indicate that this group has a different level of the latent construct relative to the reference group. In this analysis, females were chosen as reference groups (coded as 0).
It should be noted that Cheung and Rensvold (2002) suggest a protocol of eight steps when the measurement invariance of a scale is examined: apart from the configural, metric, and scalar invariance, and before the examination of latent means, additional constraints could be imposed to examine invariance of uniqueness variances, factor variances, factor covariances or path coefficients across groups. However, these additional forms of invariance are useful only when specific hypotheses regarding the relationship among the dimensions of the measured construct may be of interest (Cheung and Rensvold, 2000; Byrne, 2011). In this study, these additional steps were omitted since the main objective of this study was the examination of gender differences at the latent mean level. According to Cheung and Lau (2012), only scalar invariance is a prerequisite for comparing latent means.
The most frequently used method for evaluating invariance among different consecutive models is examining the changes in various fit indices such as ΔCFI, ΔRMSEA, and ΔSRMR (e.g., Vandenberg and Lance, 2000; Chen, 2007; Cheung, 2008). However, this method raises several issues which put in question its effectiveness in testing invariant parameters. For example, almost all fit indices are based on the χ2 statistic; it is widely known, however, that this statistic is sensitive to sample size (Kelloway, 1995). Thus, in large sample sizes, even small differences in any parameter across groups may lead to the rejection of the null hypothesis of invariance. Another major limitation is that criteria such as ΔCFI have no known sampling distribution, and therefore, it is not possible to establish any significance testing for evaluating invariant parameters. As a result, several scholars argue that the suggested cut-off criteria seem arbitrarily defined. Some other scholars argue that it is not statistically correct to apply the same cut-off criteria for evaluating models with different levels of complexity (e.g., Cheung and Rensvold, 2002) since more complex models may need different cut-off values compared to less complex models.
Another concern is related to the sample size of the compared groups. It has been argued that several fit indices (e.g., CFI, RMSEA, SRMR) and their corresponding changes in fit across the different invariance models (e.g., ΔCFI, ΔRMSEA, ΔSRMR) are less powerful when the sample sizes are equal rather than equal across groups (Chen, 2007). This may be because the sample with the larger sample size affects more the parameter estimation process of the constrained model.
An issue of equal importance is when full measurement invariance cannot be established, and as a result, latent means cannot be examined. One solution to this problem is to relax one by one the invariance constraints based on the modification indices (MIs), starting with the parameter with the largest MI until the minimum cut-off criterion is met. In this case, a partial metric or scalar invariance is established, and this model can then be used to test latent means (Marsh and Hocevar, 1985; Byrne et al., 1989). However, Cheung and Rensvold (1998) argue that all constrained parameters in a fully constrained model must be invariant apart from the relaxed one to get robust MI values. If more than one of the constrained parameters is non-invariant, there is an increased risk for inaccurate identification of non-invariant items.
An alternative approach to examining measurement invariance that addresses most of the abovementioned issues is using the Bias Corrected (BC) bootstrap confidence intervals (Cheung and Lau, 2012). This approach automatically generates 1,000 bootstrap samples (or more), and parameter differences (e.g., in factor loadings or intercepts) between groups are calculated across samples. Then, confidence intervals for each bootstrap sample are calculated, adjusting the bootstrap distribution of the parameters. This idea is based on past work where BC bootstrap confidence intervals have been used to test the significance of factor loading differences (Meade and Bauer, 2007) and differences in indirect effects across groups (Lau and Cheung, 2012).
This method exhibits several advantages over the standard approach of testing measurement invariance. The most important one is that it provides more accurate parameter estimates since it does not calculate the estimates from the original data but rather is based on bootstrap resamples. Moreover, the so-called bias-corrected approach corrects for bias and skewness in the distribution of bootstrap estimates. Another important advantage is that it provides a significance test for evaluating the magnitude of the difference in parameters across groups, avoiding arbitrary conclusions from unjustified cut-off criteria. Moreover, it allows examining multiple parameters across groups simultaneously as it provides a separate table with all estimated parameters. Finally, the BC bootstrap confidence intervals method is less restricted in the normality assumption than standard methods used in measurement invariance. In addition, it overcomes issues related to sample size across groups since it is based on a resampling technique (Cheung and Lau, 2012). All analyses were conducted with Mplus version 8.2 (Muthén and Muthén, 1998-2016).
Results
Descriptive statistics, normality indices, and inter-correlations among the study variables are presented in Table 1. As can be seen, all variables had skewness and kurtosis values within the acceptable range (i.e., <2.0), indicating that the data are normally distributed. Additionally, all variables are intercorrelated to a considerable degree, especially the variables within each domain (i.e., GAT Verbal, GAT Quantitative, SAAT, and GPA).
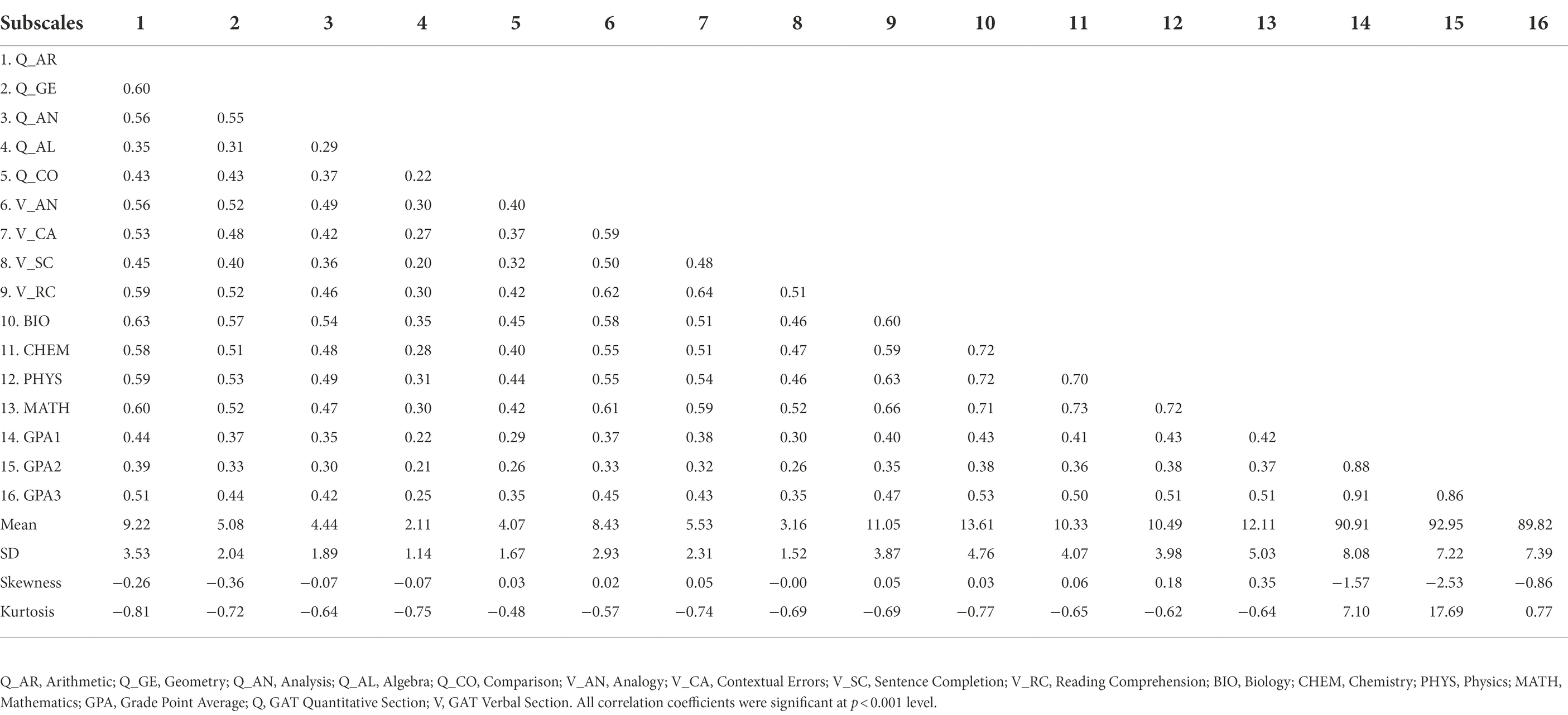
Table 1. Descriptive statistics and inter-correlations among the variables of the study (N = 1,800).
GAA dimensionality results
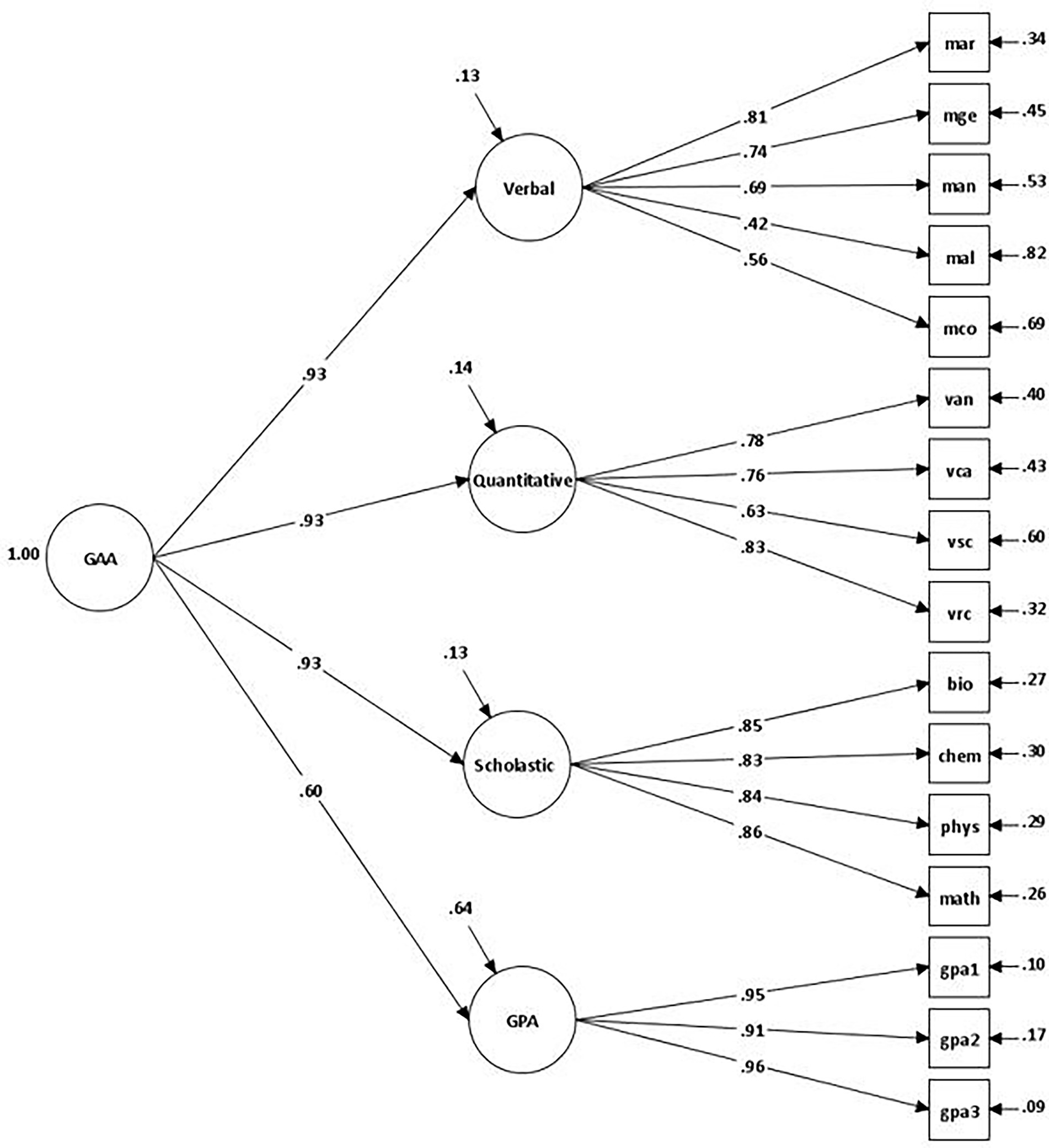
Previous empirical evidence suggested a dominant GAA dimension underlies the students’ domain scores on GPA, GAT-Verbal domain, GAT-Quantitative domain, and SAAT total score (Dimitrov et al., 2015). In this study, we are expanding the investigation of the dimensionality of the GAA by using different subsets of indicators from the four cognitive domains: five indicators for the Quantitative domain (i.e., arithmetic, geometry, analysis, algebra, and comparison), four indicators for Verbal domain (i.e., analogy, contextual errors, sentence completion, and reading comprehension), four scholastic aptitude indicators (i.e., biology, chemistry, physics, and mathematics), and three indicators of school performance across the academic year (1st semester, 2nd semester, final grade). The results from the analysis indicated that the hierarchical model with one higher-order factor (i.e., general academic ability) and four lower-order cognitive factors (i.e., verbal ability, quantitative ability, scholastic aptitude, and GPA) exhibited an excellent fit to the data: χ2 = 546.68, df = 100; CFI = 0.971; TLI = 0.965; RMSEA (90% CIs) = 0.050 (0.046–0.054), and SRMR = 0.027. A graphical representation of this model is presented in Figure 1.
Measurement invariance
First, configural invariance across groups was examined to test whether the overall factor structure (i.e., hierarchical model) holds for both groups. Results indicated that the hierarchical model fit the two groups well (Males: χ2 = 271.25, df = 100; CFI = 0.983; TLI = 0.979; RMSEA (90% CIs) = 0.044 (0.037–0.050), and SRMR = 0.027, and Females: χ2 = 359.57, df = 100; CFI = 0.960; TLI = 0.952; RMSEA (90% CIs) = 0.054 (0.048–0.060), and SRMR = 0.031). Next, the Bias-Corrected (BC) bootstrap confidence intervals technique was applied to test metric invariance across groups. For identification purposes, one item from each latent variable was selected (i.e., the first indicator) as a referent indicator, and the factor loading of this indicator was fixed to 1. The results from the analysis indicated an excellent model fit to the data: χ2 = 612.49, df = 200; CFI = 0.980; TLI = 0.976; RMSEA (90% CIs) = 0.048 (0.044–0.052), and SRMR = 0.029. To examine whether all factor loadings across gender groups were equal, new parameters were defined as the difference in the factor loadings across groups, and a BC bootstrap confidence interval for this difference was generated (Table 2). It should be noted that 99% BC bootstrap confidence intervals were chosen to test the significance of the new parameters. When zero is located within the confidence interval, the null hypothesis of invariance is accepted. As can be seen, all new parameters related to the four latent variables are not significantly different across male and female groups. Thus, metric invariance exists for this construct.
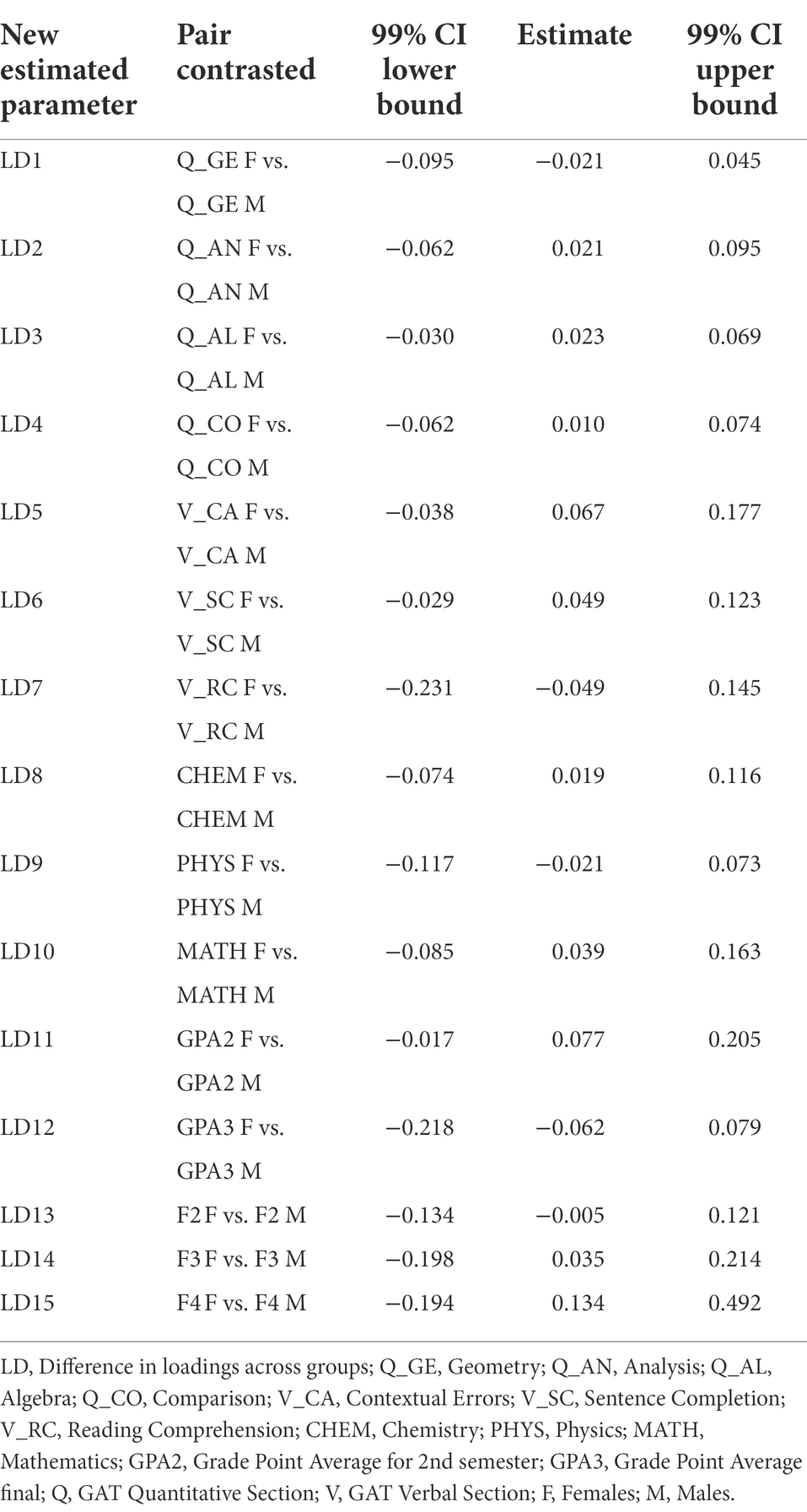
Table 2. Bias-Corrected bootstrap confidence intervals for testing metric measurement invariance (N = 1,800).
Next, scalar invariance across groups was examined by constraining the item intercepts to be invariant across the contrasted groups. The results from the analysis indicated an excellent model fit to the data: χ2 = 659.43, df = 215; CFI = 0.978; TLI = 0.976; RMSEA (90% CIs) = 0.048 (0.044–0.052), and SRMR = 0.061. Again, new parameters were defined as the difference in the item intercepts across groups, and then a BC bootstrap confidence interval for this difference was estimated. The results from this analysis are presented in Table 3. As can be seen, although the scalar model had an excellent fit, a closer examination of the individual scalar parameters did not support full scalar invariance. Items Q_GE (Geometry) from the Quantitative domain, V_CA (Contextual Errors) from the Verbal domain, CHEM (Chemistry), and MATH (Mathematics) from the scholastic aptitude domain, and GPA3 (final GPA) were not invariant across groups.
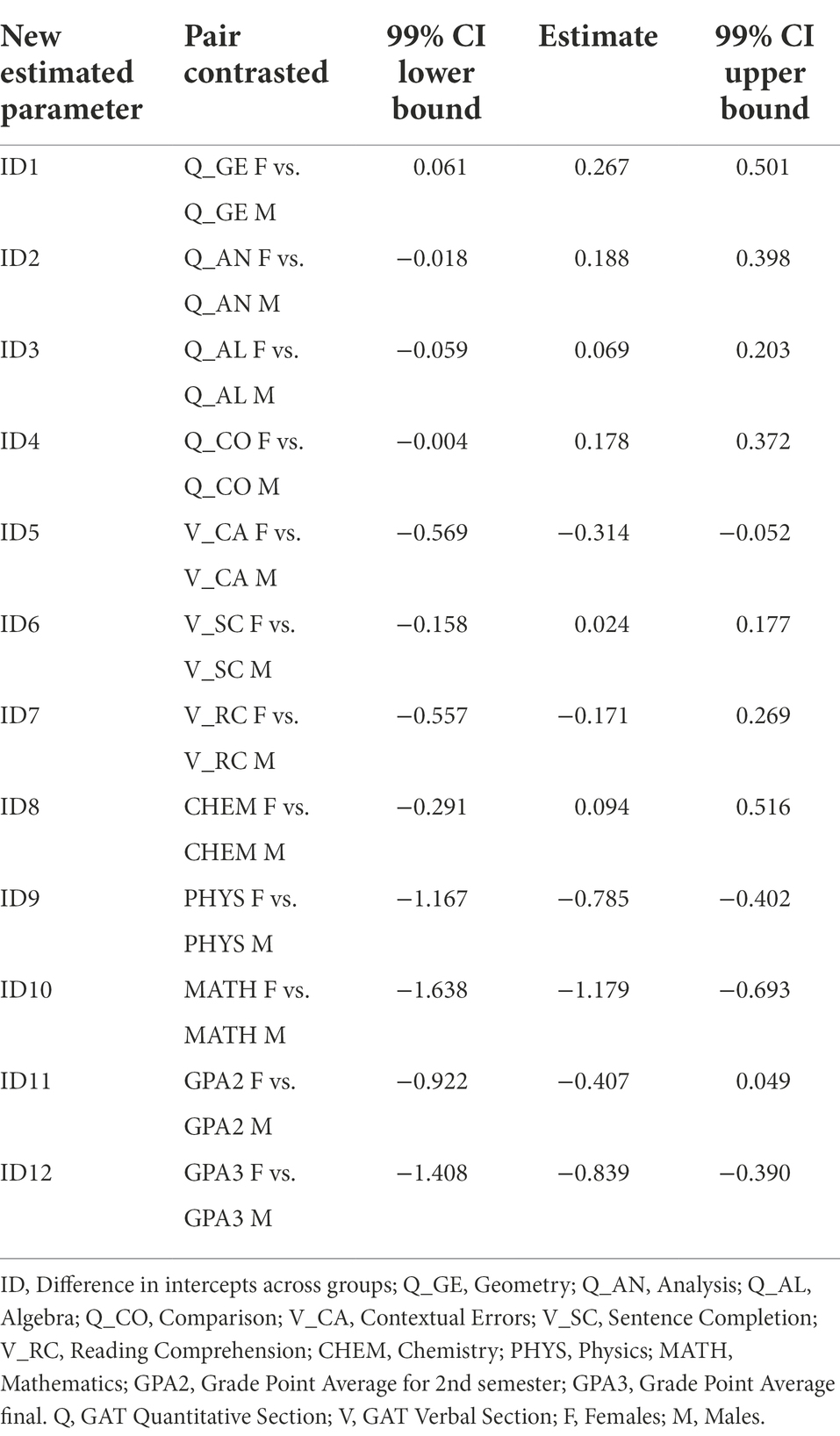
Table 3. Bias-Corrected bootstrap confidence intervals for testing scalar measurement invariance (N = 1,800).
As discussed earlier, if the invariance of item intercepts is not supported, partial scalar invariance could be established as an alternative. An important consideration is how many items are allowed to be invariant to establish partial measurement invariance (metric or scalar). Several scholars suggest that robust partial invariance is accomplished if the majority of the items in a latent variable are invariant across groups (Reise et al., 1993; Vandenberg and Lance, 2000; Cheung and Lau, 2012). This assumption is met for all latent variables in our study, apart from the scholastic aptitude variables (two out of four variables were non-invariant). Thus, for this latent variable, the comparison of latent means across gender was not conducted. For all the other latent variables, latent means using the BC bootstrap confidence interval approach were performed.
Given that the configural, metric, and partial scalar invariance assumptions were satisfied, the next step was to test for possible gender differences at the latent mean level. Since partial scalar invariance was established in the previous step, the non-invariant items (i.e., Q_GE, V_CA, CHEM, MATH, and GPA3) were left to be freely estimated. This model demonstrated an acceptable model fit, indicating that partial scalar invariance was achieved (χ2 = 685.27, df = 215; CFI = 0.977; TLI = 0.974; RMSEA (90% CIs) = 0.049 (0.045–0.053), and SRMR = 0.055). The results from the analysis showed that there were gender differences in the Verbal domain and the GPA domain (Table 4). Although significant differences were also found in the Scholastic aptitude domain, as mentioned earlier, this finding is not stable due to a large number of non-invariant items within the domain. In both cases, females scored higher than males. There were no significant differences in the Quantitative domain. In terms of the higher-order factor (GAA), the results showed a significant gender effect and that females scored higher than males.
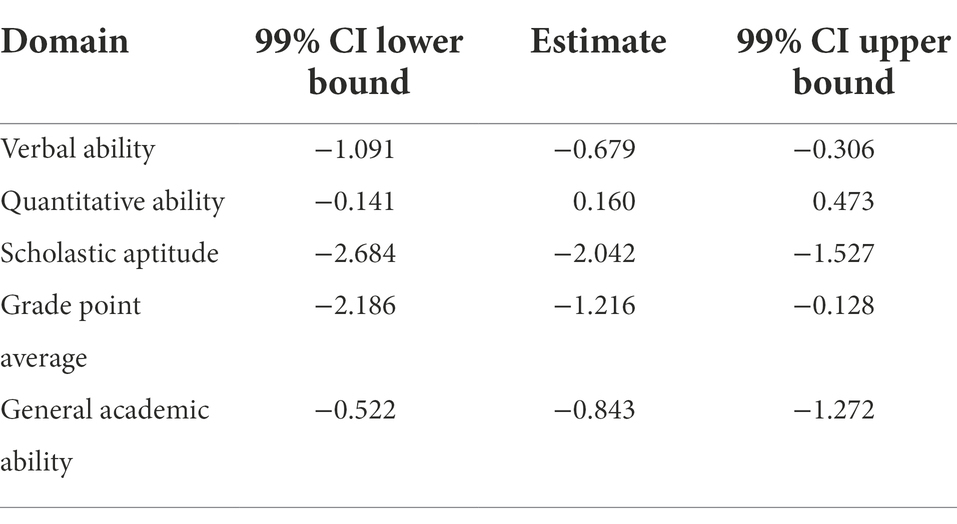
Table 4. Bias-corrected bootstrap confidence intervals for comparing GAA latent means across gender.
Discussion
The main aim of this study was threefold: first, to examine the factorial structure of the General Academic Ability (GAA), a construct developed to measure the academic performance of high school graduates in Saudi Arabia and used as the key criterion in the decision on acceptance to higher education in Saudi Arabia. The second aim of this project was to explore different degrees of measurement invariance of the GAA construct across gender. Using more recent advancements in Measurement Invariance (i.e., Bias-Corrected bootstrap Confidence Intervals), we will attempt to understand the factorial structure of the GAA in more depth. Finally, the third aim of this study was to examine whether there are gender differences across the different facets of the GAA at the latent mean level.
Dimitrov et al. (2015) introduced the GAA higher-order factor as a function of four different composites: (a) verbal ability, (b) quantitative ability, (c) scholastic aptitude, and (d) Grade Point Average (GPA). Previous findings provided sufficient evidence to support the psychometric quality of the construct and its usefulness as a key criterion for university entrance. However, this information originated from the analysis at the domain-only level (four main variables). Therefore, in this study, we attempted to provide additional insights on the conceptualization of the construct by examining its factor structure using as indicators the subscales from which these four domains were composed, that is 4 for verbal ability, 5 for quantitative ability, 4 for scholastic aptitude, and 3 for GPA (total of 16 variables).
To examine the factor structure of the GAA, a hierarchical model with one higher-order factor (i.e., general academic ability) and four lower-order cognitive factors (i.e., verbal ability, quantitative ability, scholastic aptitude, and GPA) was examined. The results from the analysis showed an excellent fit to the data, providing further support to the findings reported by Dimitrov et al. (2015). The GAA is a higher-order construct that underlies the students’ scores on several cognitive criteria coming from standardized tests and school performance. In this context, this study demonstrated that these criteria are valid indicators of this higher-order dimension and could be used as a valid criterion for entrance to higher education.
The second aim of this study was to examine whether GAA exhibits measurement invariance across gender. In other words, whether males and females conceptualize the latent constructs in identical ways (configural), respond to the items in the same way (metric), and have the same score on each latent construct obtain the same score on the observed variable regardless of their group membership (scalar). Previous research has demonstrated that standard methods typically used to test measurement invariance and identify non-invariant items (e.g., the likelihood ratio test – LRT across compared models or the change in goodness-of-fit indices among constrained models such as ΔCFI) share certain limitations and pitfalls (e.g., the sensitivity of the Δχ2 to large sample sizes, arbitrarily determined cut-off values in the reduction of a fit index across compared models, lack of any significance test; see Cheung and Lau, 2012).
In this study, we used an alternative approach via the Bias-Corrected (BC) bootstrap confidence intervals. BC bootstrap confidence intervals have been previously used in other statistical procedures, including estimating factor loading differences (Meade and Bauer, 2007) or evaluating differences in indirect effects across groups (Lau and Cheung, 2012). In this study, we use this approach as an extension of the above applications. Some of the most important advantages of this approach in testing measurement invariance are that it allows us to estimate more accurate parameter estimates and the presence of a robust significance test to identify non-invariant items.
The results showed that the hierarchical model exhibits full configural and metric invariance and partial scalar invariance. However, items Q_GE (Geometry) from the Quantitative domain, V_CA (Contextual Errors) from the Verbal domain, CHEM (Chemistry) and MATH (Mathematics) from the scholastic aptitude domain, and GPA3 (final GPA) were not invariant across gender. This finding suggests that males and females with the same score on each latent construct do not obtain the same score on these observed variables (i.e., one group might find these subscales easier than the other group). This finding is particularly important since it contributes to the better justification of the validity of the factorial structure of the GAA. It should also be noted that when standard approaches for testing measurement invariance were applied (i.e., LRT and ΔCFI, ΔRMSEA), all observed variables were invariant across gender.
Next, differences in academic performance between female and male students were examined by estimating Latent Mean differences. Although only partial scalar invariance was achieved at the previous level of analysis, it is possible to conduct valid cross-group comparisons across gender between different latent domains since the majority of the items in a latent variable were invariant across groups (Reise et al., 1993; Vandenberg and Lance, 2000).
Gender differences or “gender gap” in academic achievement have continuously attracted scientific interest not only in educational research but also from a political and economic context (e.g., Hausmann et al., 2009; UNESCO, 2015) and have raised important questions with educational, political, and economic consequences (e.g., Klasen, 2002; EGREES, 2005). In previous years, international organizations and scientific collaborations have attempted to highlight the issue and provide convincing evidence regarding the role of gender in academic achievement (e.g., Nguyen and Ryan, 2008; UNESCO, 2015; OECD, 2016). Unfortunately, these attempts have not returned consistent results resulting in ambiguity and vagueness in terms of the factors that might cause this inconsistency. This paper adds to existing research into the gender gap in academic attainment by proposing the application of a novel statistical approach to re-examine a research question that has been attracting researchers’ interest continually and has not been clarified yet, mainly due to the inconclusive findings: The Bias-Corrected (BC) bootstrap confidence intervals. Some of the most important advantages of this approach in testing measurement invariance across groups are that it allows us to estimate more accurate parameter estimates and uses a robust significance test to identify non-invariant items. Therefore, we believe this statistical approach could offer more compelling evidence for the unresolved issue of whether there is a gender gap in academic attainment.
Using the Latent Mean Difference procedure, the results from this study showed gender differences in the Verbal domain and the GPA domain. In both cases, females scored higher than males. Although significant differences were also found in the Scholastic aptitude domain, this finding is not stable due to many non-invariant items within the domain. Regarding the higher-order factor (GAA), the results also showed that females scored higher than males. There were no significant differences in the Quantitative domain. The findings from this study support the general hypothesis that female students outperform their male counterparts in almost every aspect of academic life and provide further support to the gender gap in educational attainment. (e.g., Holmlund and Sund, 2008; Hausmann et al., 2009; Bugler et al., 2015). Most of the findings from this study are in line with previous results showing that females outperform males in language-based skills (e.g., Deary et al., 2007; Steinmayr and Spinath, 2008; Spinath et al., 2010) as well as that overall, they achieve higher average grades (Voyer and Voyer, 2014; Marcenaro-Gutierrez et al., 2017).
Although there are studies in the past arguing that males outperform females in STEM-related subjects such as mathematics and engineering (e.g., Strand et al., 2006; Lakin, 2013), more recent research using more advanced methodological and statistical techniques (e.g., meta-analysis) has demonstrated that are negligible or no gender differences in the results of standardized mathematics tests there is no gender effect in mathematical ability (Else-Quest et al., 2010; Ajai and Imoko, 2015). The findings from this study support the above argument.
The present study’s findings should be viewed in light of the below-mentioned limitations. One limitation is related to the characteristics of the participants, who were predominantly high school students and were Saudi in origin, which might constrain the generalizability of the findings. Further research is thus required to test the current findings in more diverse samples (e.g., university students, other cultures, etc.). Additionally, an issue not addressed in this study was the factorial invariance of the GAA across other groups. For example, it might be interesting to examine whether other demographic variables such as age could have long-run effects on academic performance. For example, Pellizzari and Billari (2012) found that older participants in a given class or a cohort perform better than younger participants. The same pattern of results has been reported by other researchers (e.g., Dhuey and Bedrad, 2006; Crawford et al., 2007). Thus, it would be interesting to compare possible GAA differences across high school students, university students, and more mature individuals (e.g., employees). It would also be interesting to examine the mechanisms leading to the gender gap in academic performance. Thus, future research might not only focus on detecting mean differences in predictor variables but also concentrate on the relations between potential predictors and specific individual (e.g., self-esteem, personality, etc.) as well as contextual (e.g., public vs. private schools, parenting, etc.) factors vary as a function of gender. For example, it would be interesting to examine parental factors such as parenting style (Masud et al., 2019) or parental involvement and support (Topor et al., 2010; Jeynes, 2016) as possible determinants of the observed gender inequality in academic performance.
Overall, measurement invariance is an important research topic when researchers hope to investigate whether the measurement model of the latent constructs (including pattern and magnitude) holds across groups and whether the mean levels of the latent constructs hold across groups. The results from this study showed that there are gender differences in academic ability and that females generally outperform males in verbal abilities and GPA. However, no gender differences were found in terms of quantitative skills.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved by Education and Training Evaluation Commission’s Ethics Committee. The patients/participants provided their written informed consent to participate in this study.
Author contributions
IT designed the research project, performed the statistical analysis, and completed the original version of the manuscript. MA contributed to the development of the article, polished, revised, and approved the final version of the manuscript. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abubakar, R. B., and Bada, I. A. (2012). Age and gender as determinants of academic achievements in college mathematics. Asian J. Nat. Appl. Sci. 1, 121–127.
Ajai, J. T., and Imoko, B. I. (2015). Gender differences in mathematics achievement and retention scores: a case of problem-based learning method. Int. J. Res. Educ. Sci. 1, 45–50.
Alamoudi, A. A., Fallatah, H. I., Eldakhakhny, B. M., Kamel, F. O., AlShawwa, L. A., and Elsamanoudy, A. Z. (2021). Relationship between admission criteria and academic performance in basic science courses in health science colleges in KAU. BMC Med. Educ. 21:94. doi: 10.1186/s12909-021-02502-4
Alanazi, N. K. (2014). The Validity of the general Aptitude test (GAT) to Predict male Saudi students’ academic Performance in the first Semester. Unpublished Ph.D. Dissertation, University of Northern Colorado.
Aldurayheem, A. (2022). The effectiveness of the general aptitude test in Saudi Arabia in predicting performance of English as a foreign language. PSU Research Review. Advance online publication. doi: 10.1108/PRR-01-2021-0002
Alsagoafi, A. (2021). Exploring Saudi Students’ perceptions of national exams: a washback study. Revista Romaneasca pentru Educatie Multidimensionala 13, 213–234. doi: 10.18662/rrem/13.1Sup1/393
Bronkema, R. H., and Bowman, N. A. (2019). Close campus friendships and college student success. J. Coll. Stud. Retention Res. Theory Pract. 21, 270–285. doi: 10.1177/1521025117704200
Brown, A. T. (2015). Confirmatory Factor Analysis for Applied Research. 2nd Edn. New York: The Guilford Press.
Bugler, M., McGeown, S. P., and St Clair-Thompson, H. (2015). Gender differences in adolescents’ academic motivation and classroom behaviour. Educ. Psychol. 35, 541–556. doi: 10.1080/01443410.2013.849325
Byrne, B. M. (2011). Structural Equation Modeling with Mplus: Basic Concepts, Applications, and Programming. New York: Routledge.
Byrne, B. M., Shavelson, R. J., and Muthén, B. (1989). Testing for the equivalence of factor covariance and mean structures: the issue of partial measurement invariance. Psychol. Bull. 105, 456–466. doi: 10.1037/0033-2909.105.3.456
Carvalho, R. G. G. (2016). Gender differences in academic achievement: the mediating role of personality. Personal. Individ. Differ. 94, 54–58. doi: 10.1016/j.paid.2016.01.011
Caviglia-Harris, J., and Maier, K. (2020). It’s not all in their heads: the differing role of cognitive factors and non-cognitive traits in undergraduate success. Educ. Econ. 28, 245–262. doi: 10.1080/09645292.2020.1729702
Chen, F. F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Struct. Equ. Model. 14, 464–504. doi: 10.1080/10705510701301834
Cheung, G. W. (2008). Testing equivalence in the structure, means, and variances of higher-order constructs with structural equation modeling. Organ. Res. Methods 11, 593–613. doi: 10.1177/1094428106298973
Cheung, G. W., and Lau, R. S. (2012). A direct comparison approach for testing measurement invariance. Organ. Res. Methods 15, 167–198. doi: 10.1177/1094428111421987
Cheung, G. W., and Rensvold, R. B. (1998). Cross-cultural comparisons using non-invariant measurement items. Appl. Behav. Sci. Rev. 6, 93–110. doi: 10.1016/S1068-8595(99)80006-3
Cheung, G. W., and Rensvold, R. B. (2000). Assessing extreme and acquiescence response sets in cross-cultural research using structural equations modeling. J. Cross-Cult. Psychol. 31, 187–212. doi: 10.1177/0022022100031002003
Cheung, G. W., and Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Struct. Equ. Model. 9, 233–255. doi: 10.1207/S15328007SEM0902_5
Crawford, C., Dearden, L., and Meghir, С. (2007). When you are born Matters: the impact of the date of Birth on child Cognitive Outcomes in England. London: Institute for Fiscal Studies.
Dayioğlu, M., and Türüt-Aşik, S. (2007). Gender differences in academic performance in a large public university in Turkey. High. Educ. 53, 255–277. doi: 10.1007/s10734-005-2464-6
Deary, I. J., Strand, S., Smith, P., and Fernandes, C. (2007). Intelligence and educational achievement. Intelligence 35, 13–21. doi: 10.1016/j.intell.2006.02.001
Dika, S. L. (2012). Relations with faculty as social capital for college students: evidence from Puerto Rico. J. Coll. Stud. Dev. 53, 596–610. doi: 10.1353/csd.2012.0051
Dimitrov, D. M. (2013). General Aptitude Test-Quantitative: IRT and Trues-Core Analysis. Unpublished Technical Report Riyadh, Saudi Arabia. National Center for Assessment in Higher Education.
Dimitrov, D. M., Raykov, T., and Al-Qataee, A. (2015). Developing a measure of general academic ability: an application of maximal reliability and optimal linear combination to high school students’ scores. Educ. Psychol. Meas. 75, 475–490. doi: 10.1177/0013164414543179
Dimitrov, D. M., and Shamrani, A. R. (2015). Psychometric features of the general aptitude test–verbal part (GAT-V): a large-scale assessment of High School Graduates in Saudi Arabia. Meas. Eval. Couns. Dev. 48, 79–94. doi: 10.1177/0748175614563317
Dhuey, E., and Bedard, K. (2006). The persistence of early childhood maturity: international evidence of long-run age effects. Q. J. Econ. 121, 1437–1472. doi: 10.1162/qjec.121.4.1437
EGREES (2005). Equity in European educational systems: a set of indicators. Eur. Educ. Res. J. 4, 1–151.
Else-Quest, N. M., Hyde, J. S., and Linn, M. C. (2010). Cross-national patterns of gender differences in mathematics: a meta-analysis. Psychol. Bull. 136, 103–127. doi: 10.1037/a0018053
Ferrão, M., and Almeida, L. (2019). Differential effect of university entrance score on first-year students’ academic performance in Portugal. Assess. Eval. High. Educ. 44, 610–622. doi: 10.1080/02602938.2018.1525602
Ghazvini, S. D., and Khajehpour, M. (2011). Gender differences in factors affecting academic performance in high school students. Procedia Social Behav. Sci. 15, 1040–1045. doi: 10.1016/j.sbspro.2011.03.236
Gibb, S. J., Fergusson, D. M., and Horwood, L. J. (2008). Gender differences in educational achievement to age 25. Aust. J. Educ. 52, 63–80. doi: 10.1177/000494410805200105
Gibbison, G. A., Henry, T. L., and Perkins-Brown, J. (2011). The chicken soup effect: the role of recreation and intramural participation in boosting freshman grade point average. Econ. Educ. Rev. 30, 247–257. doi: 10.1016/j.econedurev.2010.09.003
Hausmann, R., Tyson, L. T., and Zahidi, S. (2009). The Global Gender gap Report. Geneva: World Economic Forum.
Holmlund, H., and Sund, K. (2008). Is the gender gap in school performance affected by the sex of the teacher? Labour Econ. 15, 37–53. doi: 10.1016/j.labeco.2006.12.002
Hong, S., Malik, M. L., and Lee, M. K. (2003). Testing configural, metric, scalar, and latent mean invariance across genders in sociotropy and autonomy using a non-western sample. Educ. Psychol. Meas. 63, 636–654. doi: 10.1177/0013164403251332
Horn, J. L., and McArdle, J. J. (1992). A practical guide to measurement invariance in aging research. Exp. Aging Res. 18, 117–144. doi: 10.1080/03610739208253916
Hu, L. T., and Bentler, P. M. (1999). Cut-off criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives. Struct. Equ. Model. 6, 1–55. doi: 10.1080/10705519909540118
Jeynes, W. H. (2016). A meta-analysis: the relationship between parental involvement and Latino student outcomes. Educ. Urban Soc. 49, 4–28. doi: 10.1177/0013124516630596
Kelloway, E. K. (1995). Sturctural equation modelling in perspective. J. Organ. Behav. 16, 215–224. doi: 10.1002/job.4030160304
Kelly, S. (2004). Do increased levels of parental involvement account for social class differences in track placement? Soc. Sci. Res. 33, 626–659. doi: 10.1016/j.ssresearch.2003.11.002
Klasen, S. (2002). Low schooling for girls, slower growth for all? Cross-country evidence on the effect of gender inequality in education on economic development. World Bank Econ. Rev. 16, 345–373. doi: 10.1093/wber/lhf004
Komarraju, M., Ramsey, A., and Rinella, V. (2013). Cognitive and non-cognitive predictors of college readiness and performance: role of academic discipline. Learn. Individ. Differ. 24, 103–109. doi: 10.1016/j.lindif.2012.12.007
Lakin, J. M. (2013). Sex differences in reasoning abilities: surprising evidence that male-female ratios in the tails of the quantitative reasoning distribution have increased. Intelligence 41, 263–274. doi: 10.1016/j.intell.2013.04.004
Laskey, M. L., and Hetzel, C. J. (2011). Investigating factors related to retention of at-risk college students. Learn. Assistance Rev. 16, 31–43.
Lau, R. S., and Cheung, G. W. (2012). Estimating and comparing specific mediation effects in complex latent variable models. Organ. Res. Methods 15, 3–16. doi: 10.1177/1094428110391673
Marcenaro-Gutierrez, O., Lopez-Agudo, L. A., and Ropero-Garcia, M. A. (2017). Gender differences in adolescents’ academic achievement. Young 26, 1–21.
Marsh, H. W., and Hocevar, D. (1985). Application of confirmatory factor analysis to the study of self-concept: first- and higher-order factor models and their invariance across groups. Psychol. Bull. 97, 562–582. doi: 10.1037/0033-2909.97.3.562
Masud, S., Mufarrih, S. H., Nada, Q. Q., Qaisar, Q., Khan, F., Khan, S., et al. (2019). Academic performance in adolescent students: The role of parenting styles and socio-demographic factors: a cross-sectional study from Peshawar, Pakistan. Front. Psychol. 10:2497. doi: 10.3389/fpsyg.2019.02497
Meade, A. W., and Bauer, D. J. (2007). Power and precision in confirmatory factor analytic tests of measurement invariance. Struct. Equ. Model. 14, 611–635. doi: 10.1080/10705510701575461
Milfont, T. L., and Fischer, R. (2015). Testing measurement invariance across groups: applications in cross-cultural research. Int. J. Psychol. Res. 3, 111–130.
Millsap, R. E. (2011). Statistical Approaches to Measurement Invariance. New York: Routledge/Taylor & Francis Group.
Mullis, I. V. S., Martin, M. O., and Loveless, T. (2016). Years of TIMSS: International Trends in Mathematics and Science Achievement, Curriculum, and Instruction. Vol. 20. Chestnut Hill, MA: IEA.
Muthén, L. K., and Muthén, B. O. (1998-2016). Mplus User’s Guide. 8th Edn. Los Angeles, CA: Muthén & Muthén.
Nguyen, H.-H. D., and Ryan, A. M. (2008). Does stereotype threat affect test performance of minorities and women? A meta-analysis of experimental evidence. J. Appl. Psychol. 93, 1314–1334. doi: 10.1037/a0012702
OECD (2016). PISA 2015 Results (Volume 1): Excellence and Equity in Education. PISA: Paris: OECD Publishing.
O’Reilly, T., and McNamara, D. S. (2007). The impact of science knowledge, reading skill and reading strategy knowledge on more traditional ‘High-Stakes’ measures of high school students’ science achievement. Am. Educ. Res. J. 44, 161–196. doi: 10.3102/0002831206298171
Pellizzari, M., and Billari, F. C. (2012). The younger, the better? Age-related differences in academic performance at university. J. Popul. Econ. 25, 697–739. doi: 10.1007/s00148-011-0379-3
Putnick, D. L., and Bornstein, M. H. (2016). Measurement invariance conventions and reporting: the state of the art and future directions for psychological research. Dev. Rev. 41, 71–90. doi: 10.1016/j.dr.2016.06.004
Reise, S. P., Widaman, K. F., and Pugh, R. H. (1993). Confirmatory factor analysis and item response theory: two approaches for exploring measurement invariance. Psychol. Bull. 114, 552–566. doi: 10.1037/0033-2909.114.3.552
Saunders-Scott, D., Braley, M. B., and Stennes-Spidahl, N. (2018). Traditional and psychological factors associated with academic success: investigating best predictors of college retention. Motiv. Emot. 42, 459–465. doi: 10.1007/s11031-017-9660-4
Spinath, B., Harald Freudenthaler, H., and Neubauer, A. C. (2010). Domain-specific school achievement in boys and girls as predicted by intelligence, personality, and motivation. Personal. Individ. Differ. 48, 481–486. doi: 10.1016/j.paid.2009.11.028
Steinmayr, R., and Spinath, B. (2008). Sex differences in school achievement: what are the roles of personality and achievement motivation? Eur. J. Personal. 22, 185–209. doi: 10.1002/per.676
Strand, S., Deary, I. J., and Smith, P. (2006). Sex differences in cognitive abilities test scores: a UK national picture. Br. J. Educ. Psychol. 76, 463–480. doi: 10.1348/000709905X50906
Sulphey, M. M., Al-Kahtani, N. S., and Syed, A. M. (2018). Relationship between admission grades and academic achievement. Entrepreneurship Sustainability Issues 5, 648–658. doi: 10.9770/jesi.2018.5.3(17)
Topor, D. R., Keane, S. P., Shelton, T. L., and Calkins, S. D. (2010). Parent involvement and student academic performance: a multiple mediational analysis. J. Prev. Interv. Community 38, 183–197. doi: 10.1080/10852352.2010.486297
Tsaousis, I., Sideridis, G., and Al-Saawi, F. (2018). Differential distractor functioning as a method for explaining DIF: the case of a National Admissions Test in Saudi Arabia. Int. J. Test. 18, 1–26. doi: 10.1080/15305058.2017.1345914
UNESCO (2015). Education for All Global Monitoring Report 2015: Gender Summary. Available at: https://unesdoc.unesco.org/ark:/48223/pf0000234809
Vandenberg, R. J., and Lance, C. E. (2000). A review and synthesis of the measurement invariance literature: suggestions, practices, and recommendations for organizational research. Organ. Res. Methods 3, 4–70. doi: 10.1177/109442810031002
Vista, A., and Alkhadim, G. S. (2022). Pre-university measures and university performance: a multilevel structural equation modeling approach. Front. Educ. 7:723054. doi: 10.3389/feduc.2022.723054
Voyer, D., and Voyer, S. D. (2014). Gender differences in scholastic achievement: a meta-analysis. Psychol. Bull. 140, 1174–1204. doi: 10.1037/a0036620
Walberg, H. J. (1981). “A psychological theory of educational productivity,” in Psychology and Education. eds. F. H. Farley and N. U. Gordon (Berkeley, CA: McCutchan).
Weissberg, N. C., Owen, D. R., Jenkins, A. H., and Harburg, E. (2003). The incremental variance problem: enhancing the predictability of academic success in an urban, commuter institution. Genet. Soc. Gen. Psychol. Monogr. 129, 153–180.
Keywords: general academic ability, academic performance, gender differences, measurement invariance, BC bootstrap confidence intervals
Citation: Tsaousis I and Alghamdi MH (2022) Examining academic performance across gender differently: Measurement invariance and latent mean differences using bias-corrected bootstrap confidence intervals. Front. Psychol. 13:896638. doi: 10.3389/fpsyg.2022.896638
Edited by:
Holmes Finch, Ball State University, United StatesReviewed by:
Joevarian Hudiyana, University of Indonesia, IndonesiaAntonia Cascales-Martinez, University of Murcia, Spain
Copyright © 2022 Tsaousis and Alghamdi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ioannis Tsaousis, aW9hbnRzYW91c2lzQHBzeWNoLnVvYS5ncg==
 Ioannis Tsaousis
Ioannis Tsaousis Mohammed H. Alghamdi
Mohammed H. Alghamdi