- 1Department of Counseling, National Chiayi University, Chiayi, Taiwan
- 2Department of Educational Psychology and Counseling, National Pingtung University, Pingtung, Taiwan
- 3Graduate Institute of Educational Information and Measurement, National Taichung University of Education, Taichung, Taiwan
- 4Department of Psychology, Assessment Research Centre, The Education University of Hong Kong, Tai Po, Hong Kong SAR, China
The existing differential item functioning (DIF) detection approaches relying on item difficulty or item discrimination are limited for understanding the associates of DIF items, and consequently, DIF items were conventionally either deleted or ignored. Given the importance of minimizing DIF items in test construction, teachers or testing practitioners need more information regarding possible associates of DIF items. Using an example of a teacher-made mathematics achievement test, this study aimed to examine how the Poly-BW indices (power, defenselessness, disturbance, and hint) contributed to the properties of gender-related DIF items. Data from a 34-item mathematics achievement test that involved 1,439 seventh-grade students from Taiwan (51.01% boys and 48.99% girls) showed that the differences of the defenselessness (mp) and power (cp) indices between men and women served as salient predictors of the DIF measures estimated by the Poly Simultaneous Item Bias Test (Poly-SIBTEST) procedure and with satisfactory accuracy of hit rates. Items with relatively large defenselessness for men were likely to present male-favoring DIFs, whereas items with relatively large power for men were likely to present female-favoring DIFs. The Poly-BW indices yielded directions for modifying items for teachers in practice.
Introduction
Differential item functioning (DIF) indicates the situation where participants from different memberships (e.g., age and gender) on the same level of the latent trait (e.g., math performance) have a different probability of a certain response to a particular item (Holland and Thayer, 1988). DIF may hamper the interpretation of mean comparisons or even lead to misleading conclusions as an item with DIF yields either constant benefits for a particular membership (uniform DIF) or benefits differing in direction and magnitude across various memberships (non-uniform DIF).
Given the distorting consequences of DIF, various DIF techniques have been advanced to assess invariance in both person and item parameters. However, most DIF detection approaches and the estimation of DIF effect sizes are limited in providing the possible associates of DIF items (Kim et al., 2007; Li, 2014a,b, 2015). The possible associates of DIF-flagged items entail the possible reasons why the DIF occurs and through which we could determine whether these items should be deleted or revised. On the other hand, if the information on possible associates of DIF items is limited, the DIF items cannot be treated appropriately. Consequently, some researchers chose to remove a DIF-flagged item from the item bank, while others might conduct further analyses (e.g., Wang et al., 2012; Chen and Hwu, 2018). Furthermore, by reviewing 27 studies on DIF item treatment, Cho et al. (2016) found that 30% of the studies removed the DIF items while 26% of the studies ignored them.
The associates of DIF are complex and could be examined from several perspectives. Some studies developed multi-dimensional DIF detection methods to explain DIF resulting from the secondary dimension (e.g., Roussos and Stout, 1996; Mazor et al., 1998; Lee et al., 2016). Some studies explore differential distractor functioning (DDF) to express that DIF could be derived from distractors being attracted differently by individuals from different groups (e.g., Suh and Bolt, 2011; Suh and Talley, 2015) and others argued that the presence of DIF is not directly related to the defined groups but associated with a latent or unknown group (De Ayala et al., 2002; Cohen and Bolt, 2005). Item characteristics, person effects, and the interaction between item and person effects could be accounted for DIF. To provide implications for teacher-made tests in classrooms (e.g., modifications for DIF items based on properties of items), however, this study would investigate the associates of DIF with an emphasis on item effects (e.g., properties of items).
The properties of items delineate item characteristics (e.g., item difficulty), which could provide teachers or testing practitioners directions to modify or revise items exhibiting DIF. Two common properties are item difficulty and item discrimination. However, both of them are limited in addressing possible associates of DIF. Beyond that, aberrant response indices derived from a response pattern in an item could be alternative options to identify possible associates in DIFs. Due to the function of detecting the aberrant response patterns by assessing the agreement of difficulty within an item response pattern, the caution index (SCI, Sato, 1975) or modified caution index (MCI, Harnisch and Linn, 1981) developed by early researchers could be used to identify possible associates in DIF items. However, they are still limited by their ineffectiveness in distinguishing extreme levels of item difficulty (Huang and Wu, 2013). For example, a response pattern, such as 000| 00000111, consisting of “0” (representing a wrong response) and “1” (representing a correct response) is ranged by difficulty levels from left-easy items to right-hard items. Two different response patterns of the within-difficulty response pattern (000 before the symbol “|”) and the beyond-difficulty response pattern (111 after the symbol “|”) are handled by the MCI or SCI identically, even though these two response patterns might be due to different item characteristics. That is, possible intrinsic properties of item response patterns might not be distinguished by the SCI or by the MCI measures alone.
As an extension of the SCI measure, the beyond-surprise/within-concern dichotomous BW indicators (Huang, 2012; Huang and Wu, 2013) have yielded more useful information for the intrinsic properties of items. The dichotomous BW indicators provide the information of item characteristics about power (c), defenselessness (m), disturbance (b), and hint (w) for each item. The four indicators are useful for exploring the intrinsic properties of an item (Huang and Wu, 2013). Recently, the original dichotomous BW indicators have been extended to the Poly-BW indices for polytomously scored items (Huang and Lu, 2017), in which they are recorded as cp, mp, bp, and wp, respectively. However, no studies have yet examined the association between these four polytomous indices and DIFs. Furthermore, since the Poly-BW indices are non-parametric-based to yield diagnostic information for items (e.g., whether the items respond normally or aberrantly), they can provide information on item classifications by means of the approximate permutation test (APT, Edgington, 1995). Through the APT process, many data matrixes can be approximately simulated according to an original data matrix so that the 95th percentile values of individual indices in an item can be set and classified. This analysis enables us to disclose possible associates in suspective DIF items and by which DIF items could be more appropriately dealt with. Details of the item classification procedures are provided in the “Materials and Methods” section.
On the other hand, although recently, there are several existing DIF detection methods depending on different assumptions of their models, the Poly Simultaneous Item Bias Test (Poly-SIBTEST) approach is a wildly used non-parametric-based DIF-detecting procedure in polytomously scoring situations (Chang et al., 1996). Capitalizing on its non-parametric-based and polytomously scoring characteristics, the Poly-SIBTEST procedure was chosen in the current study as a reference method to estimate DIFs for examining the associations between the estimated DIF measures and the non-parametric-based Poly-BW indices measures.
Given the importance of the possible associates of DIF items, this study exemplifies the advantages of the four Poly-BW indices by assessing their predictive effects on the gender-related DIFs measured from the Poly-SIBTEST approach in a teacher-made math test. A gender-related DIF in a math text is a particularly important issue because gender difference in math performance has been debated for some decades. Some researchers argued that there were no gender differences in math performance (Hyde and Mertz, 2009; Lindberg et al., 2010), but others proposed that boys outperformed girls since third grade (Fryer and Levitt, 2010; Robinson and Theule Lubienski, 2011), and still other researchers showed that girls performed similarly or better than boys in terms of classroom grades (Pomerantz et al., 2002; Ding et al., 2006). However, these comparisons are valid only when a math test is established freely with the gender invariance. Accordingly, two main research questions guide this study: (1) Do the four Poly-BW indices predict effectively a DIF measure obtained from the Poly-SIBTEST approach? (2) How accurately do the four Poly-BW indices predict a DIF item?
Dichotomous BW Indicators
Aberrant responses, known as inconsistent or unexpected responses compared to the overall responses in a test, can provide diagnostic information for persons and items (Kogut, 1986; Seol, 1998). Indices developed for detecting a person’s aberrant response patterns were usually labeled as person-fit indices, while for detecting an item’s aberrant responses was called item-fit indices. Some indices are based on the characteristics of a group, and others are based on item response theory (IRT) models (Harnisch and Linn, 1981; Kogut, 1986; Meijer and Sijtsma, 1999). Based on the group-based Guttman (1944) principles (1944) (i.e., able persons should answer those items correctly, which exhibited difficulty levels lower than those persons’ ability levels), the dichotomous BW indicators (Huang, 2002) were designed to detect persons’ aberrant responses patterns, i.e., person-fit oriented, and were subsequently extended to detect aberrant responses of items, i.e., item-fit oriented. The person-fit BW indicators originally (Huang, 2002) measured a person’s tendency of “guess” (B indicator) and “carelessness” (W indicator) and later (Huang and Wu, 2013) extended to measure a person’s tendency of “mastery” (C indicator) and “misconception” (M indicator), respectively. Huang (2011) investigated the robustness of BW aberrance indices against test length and found that the person-fit BW indicators were almost unrelated to test length. Later, Huang (2012) compared the aberrance detection powers among the person-fit BW indicators, other four group-based indicators (SCI, MCI, NCI, and Wc & Bs), and five IRT-based indicators (OUTFITz, INFITz, ECI2z, ECI4z, and lz) under the conditions of content category, type of aberrance, the severity of aberrance, and the ratios of aberrance persons. He found the person-fit BW indicators and the four group-based indices exhibited higher detection rates (over 90%) than the five IRT-based indicators, and furthermore, the BW indicators exhibited the best stability across different situations.
According to symmetrical characteristics, the properties of the item-fit BW indicators are the same as those of the person-fit BW indicators. Specifically, the dichotomous BW item-fit indicators (Huang, 2002) were developed to detect the tendency of “disturbance” (b indicator) and “hint” (w indicator) in an item beyond and within the item’s difficulty level, respectively. In addition to the two aberrant indicators, Huang and Wu (2013) incorporated another two indicators with normal responses for an item, called “power” (c indicator) and “defenselessness” (m indicator) within and beyond the item’s difficulty level, respectively. Here, normal responses mean those responses that obey the Guttman’s principles. In their study, a cognitive diagnostic model based on the WBstar program was used to examine the quality of a teacher-made test (22 items) on the contents of fractions and decimals and found that the BW-based cognitive diagnostic model performed effectively for detecting the misfit of items in small-sample scenario of 32 fourth-grade students.
For applying to a DIF scenario, Huang and Lin (2017) conducted a Monte Carlo study to investigate the predictive effects of the dichotomous BW indicators on DIFs. They simulated data under five conditions (sample size, item number, DIF type, DIF ratio, and DIF severity) and found that the power indicator and the defenselessness indicator could significantly explain the variances of DIFs. Moreover, the four dichotomous BW indicators also exhibited over 90% of the accuracy rate of prediction on the flagged-DIF items. However, Huang and Lin’s study was limited in the dichotomously scoring system and not suitably interpreted in polytomously scoring scenarios. In recognition of limited usage of the dichotomous BW indicators, Huang and Lu (2017) extended these indicators to fit in polytomously scored scenarios, called the Poly-BW indices. In their study, they developed the PWBstar1.0 program1 for estimating the Poly-BW indices, but they did not investigate the associations between the Poly-BW indices and DIF measures. Therefore, the predictive effectiveness of the Poly-BW indices to DIF measures is unknown.
Poly-BW Indices
Similar to the dichotomous situations, the main idea of the Poly-BW indices was based on the concept of a discrepancy, which would reflect the level of aberrant or normal responses. The discrepancy distances between persons’ abilities and an item’s difficulty would be calculated according to normal or aberrant responses beyond and within an item’s difficulty level, respectively. Specifically, suppose in a K-item test participated by N examinees, we can first rank ability levels by individual person scores from the bottom (low) to top (high) and then rank difficulty levels by individual item scores from left (low) to right (high). Let the jth item has a maximum score of sj and the ith person has an earned score xij on the jth item, then xij ≤ sj. Since the N examinees are ranked by individual’s total earned scores on the K-item test from bottom to top, we can define as the ith person’s potential ability. Then we correspondingly calculate the accumulated maximum score by defining a specified Ij (1 ≤ Ij ≤ N) such that for all N examinees from bottom to top, indicating a certain item score (Qj) defined as the difference between the maximum score and the earned score is falling between two sequential accumulated maximum scores and thus exhibits the item’s robustness so as for all N examinees not to answer it correctly. Ideally, the ith person who possesses the complete potential ability ti should gain the accumulated maximum score on the jth item.
Therefore, the true item difficulty () for the jth item can be expressed by two sequential persons’ potential ability levels (ti and ti+1) through interpolation technique with a 0.5 error unit as Equation 1 shows:
Adding a 0.5 error unit in Equation 1 is because the score unit is 1 and using half of the score unit for correction will be helpful to distinguish difficulty levels when the examinee sample is too small.
With the true item difficulty () and based on the dichotomous logic, the Poly-BW indices (cp, mp, bp, and wp) designed to measure the degree of power, defenselessness, disturbance, and, hint for an item, respectively, are given from Equations 2 to 5 as follows:
The properties of the four Poly-BW indices are delineated as follows. First, the power index (cp) refers to the power of an item, that is, the examinees would answer it incorrectly just truly due to their ability is lower than the item difficulty (i.e., within the difficulty level). Second, the defenselessness index (mp) refers to the possible inefficiencies of an item, that is, examinees whose ability levels were higher than the difficulty level of the item (i.e., beyond the difficulty level) would easily answer this item correctly. The cp and mp indices differ from the difficulty index in the classical test theory (CTT). In CTT, the computation of the difficulty index does not distinguish “within” or “beyond” an item difficulty level. In this study, the cp index measures the part of “not correct” responses within the item difficulty, and the mp index measures the part of “correct” responses beyond the item difficulty. An item with a greater value of power index is more likely to be answered “incorrectly” than another item with a lower value of power index. Therefore, when comparing power index between two groups (gender groups), a greater value of power index for a particular item in the focal group (e.g., men) indicates that this item is more likely to be answered incorrectly by male examinees than by female examinees, given those examinees’ ability within this item difficulty. In contrast, an item with a greater value of defenselessness index is more likely to be answered “correctly” than another item with a lower value of defenselessness index. Therefore, when comparing the defenselessness index between two groups (gender groups), a greater value of defenselessness index for a particular item in the focal group (e.g., men) means that this item is more likely to be answered correctly by male examinees than by female examinees, given those examinees’ ability beyond this item difficulty.
On the other hand, the bp and wp indices indicate that an item displays possible aberrances of disturbances or hints that examinees might encounter, respectively. The disturbance index (bp) measures the property of an item with possible pitfalls, that is, examinees answer the item incorrectly even though their ability levels are beyond the difficulty level of the item. An item with a greater value of disturbance index is more likely to be answered “incorrectly” than another item with a lower value of disturbance index. Therefore, when comparing the disturbance index between two groups (gender groups), a greater value of disturbance index for a particular item in the focal group (e.g., men) suggests that this item has more likelihood to be answered wrongly for male examinees than female examinees, even given those examinees’ abilities beyond the item difficulty. In contrast, the hint index (wp) measures the possible prompts in an item, that is, examinees answer the item correctly even though their ability levels are within the difficulty level of this item. An item with a greater value of hint index is more likely to be answered “correctly” than another item with a lower value of hint index. Thus, a greater value of hint index for a particular item in the focal group (e.g., men) delineates that this item has more likelihood to be answered “correctly” for male examinees than female examinees, even given those examinees’ abilities are within the item difficulty.
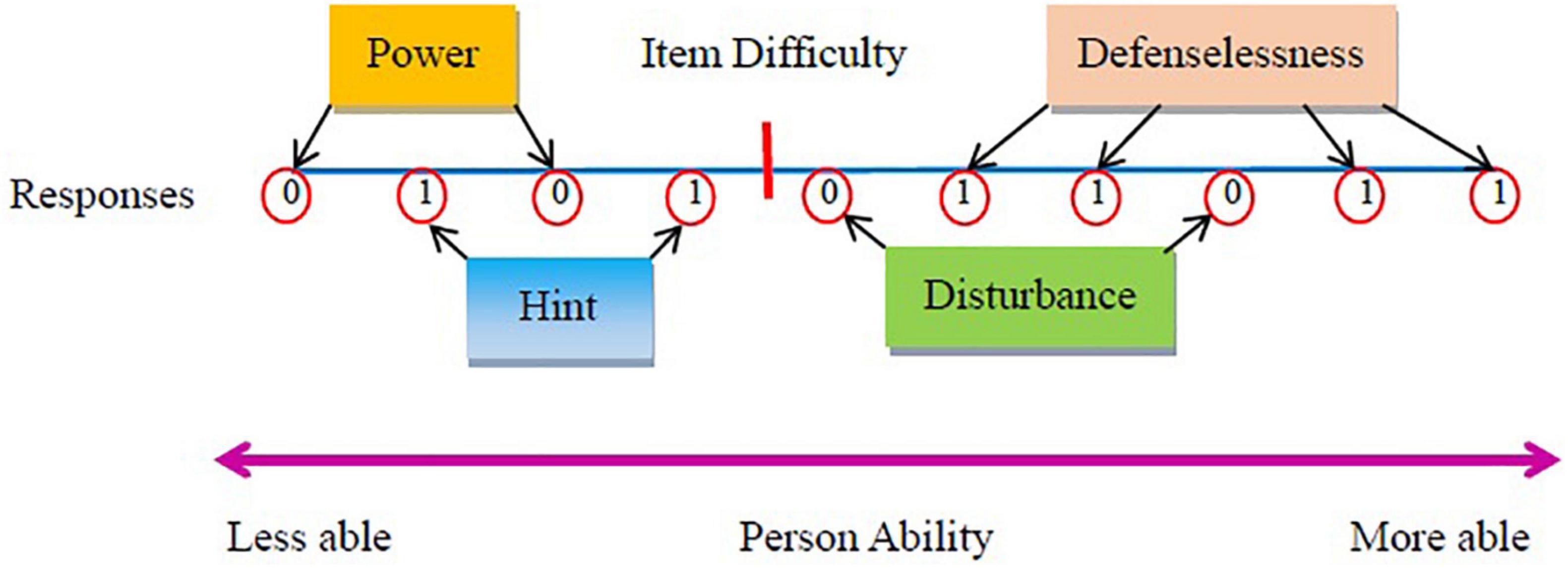
Figure 1 provides a visualization for the idea of the four Poly-BW indices in different situations of normal and aberrant responses. Ideally, an item is supposed to be answered incorrectly when examinees’ abilities are lower than the item difficulty (i.e., power) and to be answered correctly when examinees’ abilities are higher than the item difficulty (i.e., defenselessness). On the other hand, when the ideal principles of responses are violated, the levels of discrepancy will reflect the levels of aberrance. The disturbance situation occurs when an item is still answered incorrectly even though examinees’ abilities are higher than the item difficulty. The hint situation occurs when an item is still answered correctly even though examinees’ abilities are lower than the item difficulty.
Materials and Methods
Participants
A total of 1,439 seventh-grade students from central Taiwan (51.01% men and 48.99% women) participated in the study. They were selected from 40 classes in eight junior high schools. The students completed a math test in a math class within around 40 min. In Taiwan, all math textbooks are developed based on directions governing the Basic Education Curricula and the contents of math textbooks should be approved by the Ministry of Education. Therefore, all junior-high-school students with the same grade are taught similar contents or units of math. Before administering this math test, all participants were supposed to have learned the contents of arithmetic, algebra, and geometry during their math class. We confirmed that all teachers had taught these contents before giving this math test.
Instrument
The math test was developed by our research team, i.e., three junior-high-school teachers and two experts in math and psychological measurement. It was a criterion-referenced and formative assessment. The objective of this test was to evaluate what the students had learned and assessed whether students obtained the required knowledge. Therefore, all items were developed according to the directions governing the Basic Education Curricula in Taiwan. The test comprised 34 items involving the three major components of math: 14 items for arithmetic (such as addition/subtraction of integers, multiplication/division of integers, operations on fractions, and the concept of factors/multiples), 16 items for algebra (such as the operation/application of integers and fractions), and 4 items for geometry (such as the concepts of the number line and absolute numbers). Each item required more than two problem-solving steps to solve and was scored on the basis of the number of steps taken by the students (according to the rubric of the math test). Supplementary Appendix A presents the specifications of items by contents and formats. Supplementary Appendix B presents the original teacher-made math test.
Rubric of Test
The rubric was established on the basis of the rationale of the partial credit model (PCM) (Masters, 1982). According to the PCM, to proceed with the next problem-solving step, the previous step is required to be correct. For instance, in the case of a three-step item, if a student answers the first step correctly but fails in the second step, it is reasonable to assume that he/she cannot answer correctly in the third step. Thus, based on the requirement of the PCM, each correct step, given that the previous steps were correct, was given one point, but a step was not given a point if any previous step was incorrect. Thus, the possible scores for each item in this study, ranging from 0 to 2, 0 to 3, 0 to 4, and 0 to 5, depended on the total number of solution steps and the corresponding previous correct steps for each item. To validate the step scores, two raters were asked to judge the step scores and to add the total scores for all the examinees on each item. The Pearson product-moment correlations were calculated between the two columns of total scores from the two raters for all the examinees on each item and ranged from 0.88 to 0.99, indicating good levels of inter-rater consistency for all items. All intracorrelations between items were significant at 0.01 alpha level and shown in Supplementary Appendix C by the male and female groups, respectively.
Poly-SIBTEST Procedure
The Poly-SIBTEST, a confirmatory and theory-driven approach to detect associates of DIF, was designed to address the problem of DIF identification in polytomously scoring situations (Chang et al., 1996). Poly-SIBTEST is a non-parametric method (i.e., it did not assume the parametric shape of the item response function) and it was a Shealy-Stout multidimensional model (MDM; Shealy and Stout, 1993) used for DIF detection. The MDM model delineates that a DIF is a result of the second construct that is not intended to measure in a test (Shealy and Stout, 1993). Put differently, a DIF item measures more than one construct and the focal group (studied group) have different scores in the second construct. Therefore, according to MDM, a DIF occurs when the reference and focal groups that are matched on the same level of the intended (main) construct have different scores (distributions) on the second construct.
Based on Poly-SIBTEST theory and prior research, when items are hypothesized to have a common secondary construct, they could be bundled together and assessed for differential bundle functioning (DBF). Specifically, the inequality TjF(θ) < TjR(θ), where θ represents the measured target ability, T represents the marginal item response functions on item j for the focal group (F) and the reference group (R), respectively. The difference between the subtest response functions gives a preliminary index of DBF, given the examinees’ ability level. If all ability levels are considered, an index of DBF, i.e., Bu, can be estimated. The estimate of Bu can be tested by the standardized statistic, which has an approximately normal distribution with a mean 0 and SD of 1 for a large sample. Items with values greater than 1.96 or less than − 1.96 are deemed as DIF items. In Poly-SIBTEST analysis, we set the female group as the reference group so that the values of Bu greater than 0 indicate male-favoring potential and values of Bu less than 0 indicate female-favoring potential. However, for a DIF-flagged item, only the values of the standardized Bu greater than 1.96 or less than − 1.96 were considered.
Valid Matching Subtest
Before DIF estimation, a valid matching subset was required previously in the Poly-SIBTEST procedure. There were 18 of 34 items of interest, such as mathematics content (arithmetic, algebra, and geometry), number type (fraction and integer), and item format (operation and word problem), which were classified into five bundles of the studied subtest. The remaining 16 items, after precluding the items in the studied subtest, were used in the matching subtest for the purpose of purification in the first automatic DIF analysis (Stout and Roussos, 1995). After conducting automatic DIF analysis three times and canceling five items that displayed significant DIFs, a valid matching subtest consisting of 11 non-DIF items was found (item 1, 6, 8, 10, 12, 13, 15, 20, 22, 27, and 32). These uncontaminated items were used to identify the ability levels of male and female students in Poly-SIBTEST analysis.
Analysis
In this study, we set women as the referenced group in both Poly-SIBTEST analysis and Poly-BW differences estimation. A positive DIF measure in Poly-SIBTEST analysis indicated a male-favoring item and a negative DIF measure indicated a female-favoring item. A positive index difference in Poly-BW analysis implied a certain Poly-BW index estimated from the male group greater than that estimated from the female group, and vice versa. Thus, for research question 1, the Poly-BW indices were calculated for the male and female groups separately through the PWBstar1.0 program, and the differences in individual indices between the two groups were used as predictors for the DIF measure (Bu) obtained from Poly-SIBTEST through stepwise multiple regression analysis. For research question 2, the accuracy of classification for a DIF-flagged item by the four Poly-BW indices from the APT procedure was assessed by multiple discriminant analysis.
Specifically, the study used a 100-repetition APT procedure through the following steps: (1) setting three types of cp values (high, middle, and low, using 33% ranks as cutoffs); (2) setting two types of levels (high and low) by using upper or lower the 95% percentile value for each mp, bp, and wp index in the male and female groups, respectively. After these APT steps, all information on the item classifications can be provided by the PWBstar 1.0 program by labeling the types of item classifications as (letter + number)’, in which the letters represent high (H), middle (M), and low (L) power levels of the cp index; while the numbers 1, 2, 3, and 4 refer to normal, disturbance, hint, and hybrid (disturbance plus hint) types of responses, respectively. Further, the prime symbol (′) indicates a significantly high defenselessness value of the mp index. The item classifications provide insights into the associates of DIF. For example, if a DIF item is labeled as L1′ and L2′ for men and women, respectively, it implies that this DIF item displays a low level of power (L) and a high level of defenselessness (′) for both genders, but with normal performances (“1”) for the male groups and aberrant disturbances (“2”) for women. Suspiciously, disturbance might be an associate of DIF.
Results
Descriptive Statistics and Preliminary Analysis of Dimensionality
Descriptive statistics of item level performance and parameters estimated by the Poly-WB item indices formula for men (N = 734) and women (N = 705) were displayed in Supplementary Appendix D. Due to different problem-solving steps required in individual items, the scores of items were ranged from 0 to 2, 0 to 3, 0 to 4, and 0 to 5. As can be seen in Supplementary Appendix D, the mean scores on an item earned by male students ranged from 0.54 (max score 3 in item 29) to 3.48 (max score 5 in item 26) and ranged from 0.78 (max score 2 in item 30) to 3.85 (max score 5 in item 26) by female students. The smallest SDs for both groups occurred on item 19 (0.81 and 0.74 for men and women, respectively) and the largest SDs occurred on item 23 (2.34 and 2.42 for men and women, respectively). Before examining DIFs, the dimensionality of these 34 items was preliminarily checked. Principal components analysis of standardized residuals showed that unexplained variance explained by the main dimension was only 0.8%, indicating this math test exhibited a unidimensionality.
Prediction
Table 1 summarizes the stepwise multiple regression analysis. Two Poly-BW indices explain almost 78% of the variance (63.8% from the predictor of mpM–F and 14.2% from the predictor of cpM–F) of the DIF measures (Bu) obtained from Poly-SIBTEST analysis (F4,29 = 28.53, p < 0.001). Specifically, the defenselessness (mp) index has the largest contribution (63.8%), followed by the power (cp) index (14.2%). This finding indicates that the defenselessness (mp) and power (cp) indices could be used to predict the gender DIF measures in the math test (β = 0.734, p < 0.001 for mpM–F; β = − 0.286, p < 0.05 for cpM–F)2. Because the women were regarded as the referenced group in both Poly-SIBTEST analysis and Poly-BW difference estimations, a positive regression coefficient implied that the larger the defenselessness differences (mpM–F), the larger are the DIF measures (i.e., the items were more likely to favor men when they had a relatively large defenselessness for men). Likewise, a negative regression coefficient indicated that the larger the power differences, the smaller are the DIF measures (i.e., the items were more likely to favor women when they had a relatively large power for men). In summary, the defenselessness (mp) and power (cp) indices were significant predictors of DIF properties in this case. From the definitions of these two indices, these findings indicated that if an item was perceived as more defenseless (easy to be answered correctly beyond the item’s difficulty) or powerful (hard to be answered correctly within the item’s difficulty) by one gender group, then the item was more likely to exhibit a DIF. Interestingly, the abnormal indices (hint wp and disturbance bp) did not contribute significantly to the DIF properties. This finding indicated that these two abnormal indices were less likely to be the possible associates of DIFs in this case.
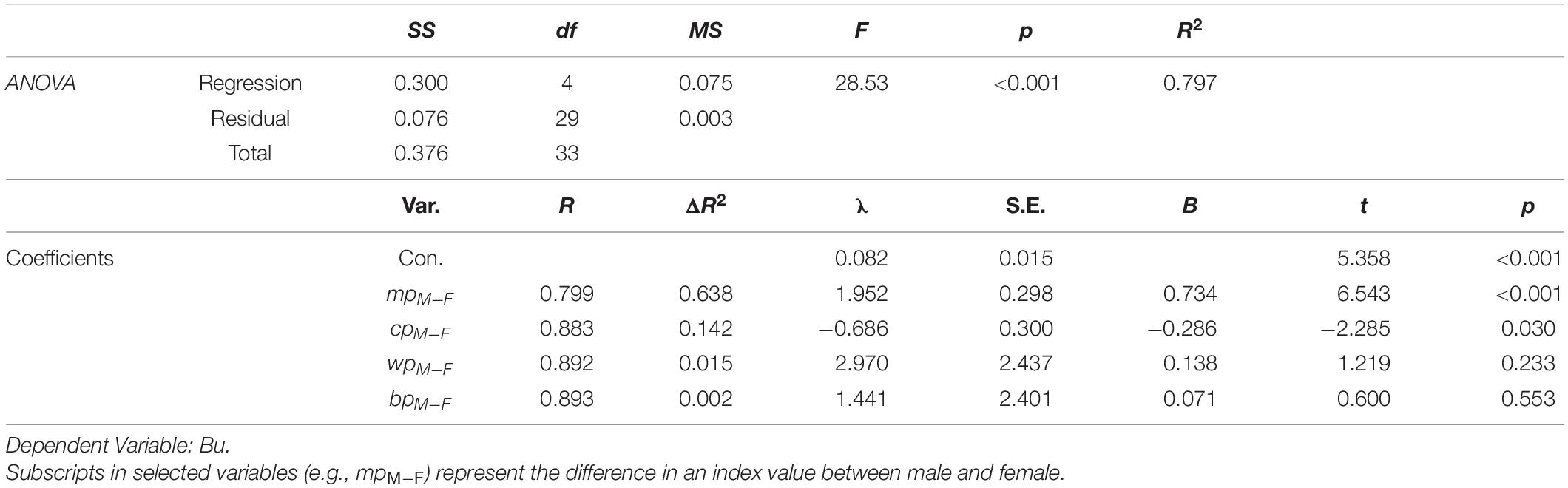
Table 1. Regression model summary for Poly-BW indices on differential item functioning (DIF) measures.
Furthermore, to demonstrate the Poly-BW indices outperformed the difficulty index of CTT, i.e., P = (PH + PL)/2 in terms of DIF variance explained, we compared DIF variance explained from the P index and the Poly-BW indices. Results showed that the CTT difficulty index explained 53.4% variance of DIF measures (F1,32 = 36.68, p < 0.001), but it was lower than the variance explained by the defenselessness (mp) index (63.8%). Since the difficulty index based on CTT is calculated based on total scores, it confounded the within-difficulty and the beyond-difficulty effect in a person’s responses. Instead, the within-difficulty and beyond-difficulty effects can be distinguished by the power (cp) index and the defenselessness (mp) index, respectively, so that the intrinsic properties in DIFs can be more disclosed.
Accuracy
For research question 2, we examined how accurately the four Poly-BW indices predicted the DIF-flagged items using multiple discriminant analysis. Based on the standardized values of Bu obtained from the Poly-SIBTEST procedure (i.e.,|Bu| > 1.96), 12 items were detected with DIFs: 6 items favoring men (items 2, 5, 7, 11, 14, and 17) and 6 items favoring women (items 4, 18, 19, 21, 29, and 31). The remaining 22 items were neutral to both genders. The average hit rate of the DIFs (see Figure 2) was 82.4%. Without considering the group favored by the DIF items, the DIFs were perfectly (100%) predicted by the four Poly-BW indices. But the neutral category was predicted with an accuracy of 72.7% with six undetermined items. There were five neutral items (items 22, 23, 26, 27, and 28) classified as female-favoring items and one neutral item (item 25) classified as a male-favoring item.
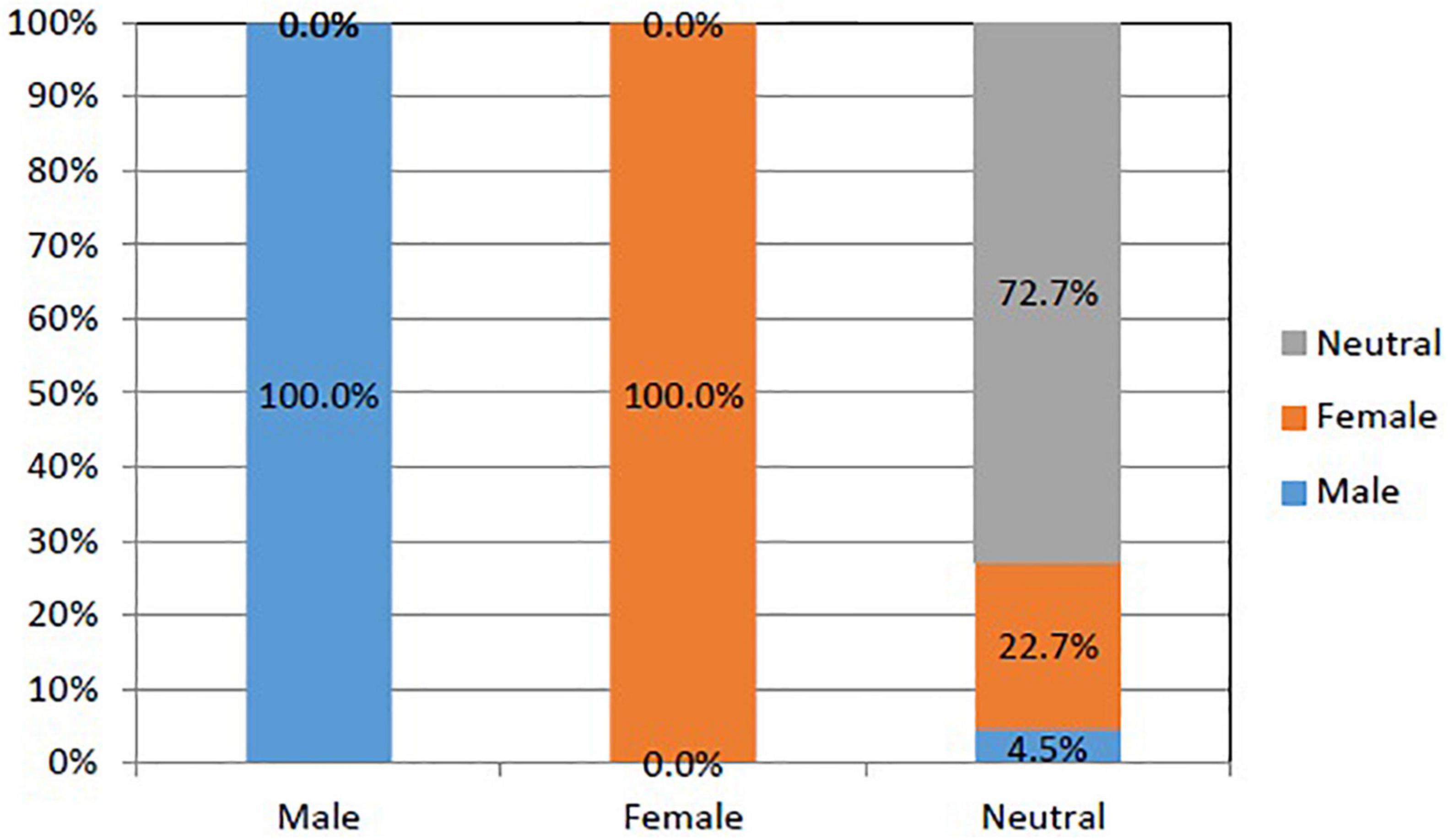
Figure 2. Hit rates of differential item functioning (DIF)-flagged items according to multiple discriminant analysis.
When examining the values of Poly-BW indices (see Table 2), we found that five of six male-favoring items (except item 7) have higher mp values in the male group than in the female group, and all six female-favoring items have higher mp values in the female group than in the male group. For the undetermined items, the six neutral items displayed higher cp values in the male group than in the female group, but different magnitudes of mp values in both groups. All the five female-favoring items displayed higher mp values in the female group than in the male group, but in contrast, the male-favoring item (item 25) displayed a higher mp value in the male group than in the female group (0.094 vs. 0.076). This implies that the mp index (defenselessness) dominates the key reasons of item transformation from no DIF to favoring one group. Other Poly-BW indices values of remaining items can be seen in Supplementary Appendix D.
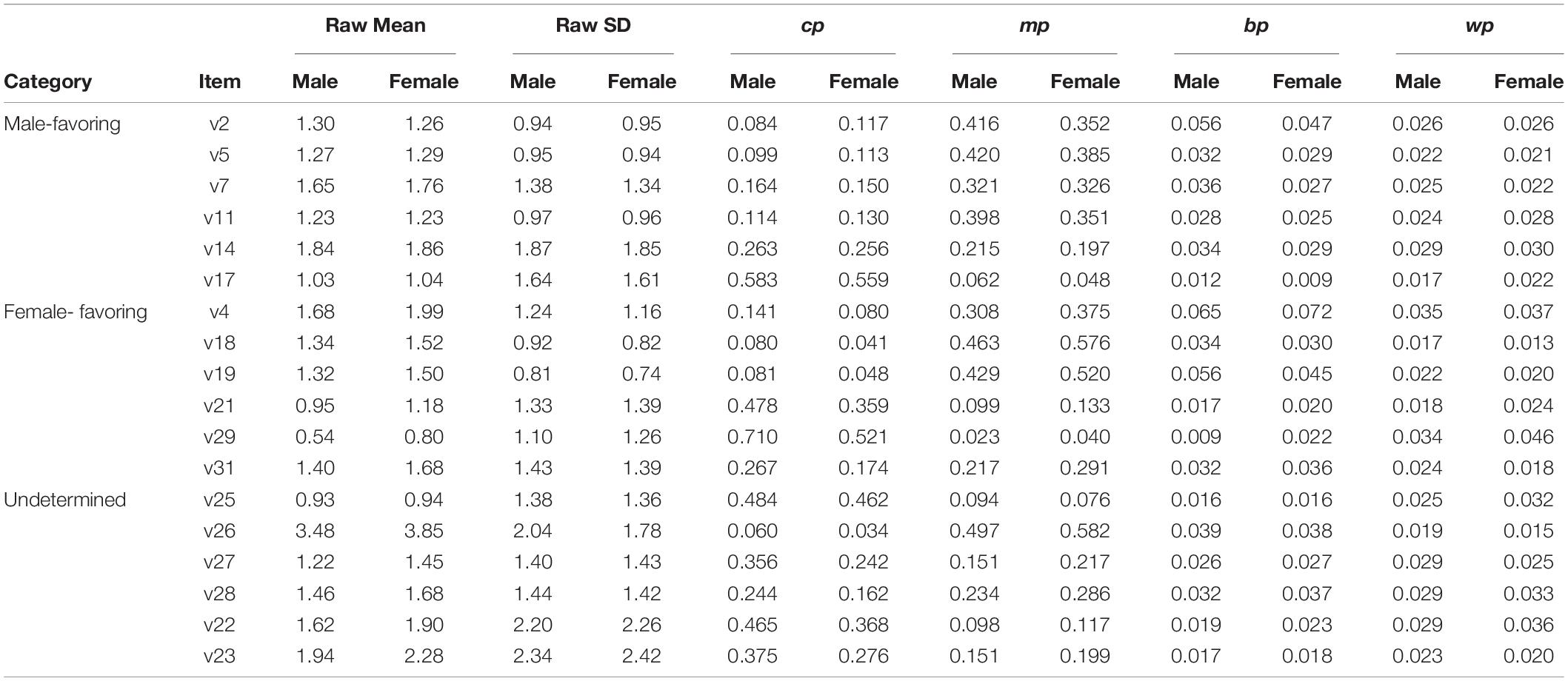
Table 2. Values of Poly-BW indices for differential item functioning (DIF) items and undetermined items.
Furthermore, after excluding the six undetermined items, the remaining 28 items predicted by the defenselessness (mp) and power (cp) indices as male-favoring, female-favoring, and neutral are shown in Figure 3. As can be seen, in terms of the Q values from CTT, men mostly perceived an item as more difficult than women across all items, suggesting that CTT item difficulty cannot explain the possible associates of gender DIFs. Nevertheless, the mp and cp indices provide useful information on the associates of a DIF. First, in the female-favoring part (the left part of Figure 3), most of the female-favoring items exhibited low values of defenselessness (mp) but high values of power (cp) between men and women. Here, the values of defenselessness (mp) and power (cp) were the difference values between the gender groups (where women were the referenced group). Accordingly, when the items had lower defenselessness and higher power for men, they were likely to be female-favoring items. Second, in the male-favoring part (the right part of Figure 3), most of the male-favoring items exhibited high values of defenselessness (mp) but low values of power (cp) between men and women. Thus, when the items had higher defenselessness and lower power for men, they were likely to be male-favoring items.
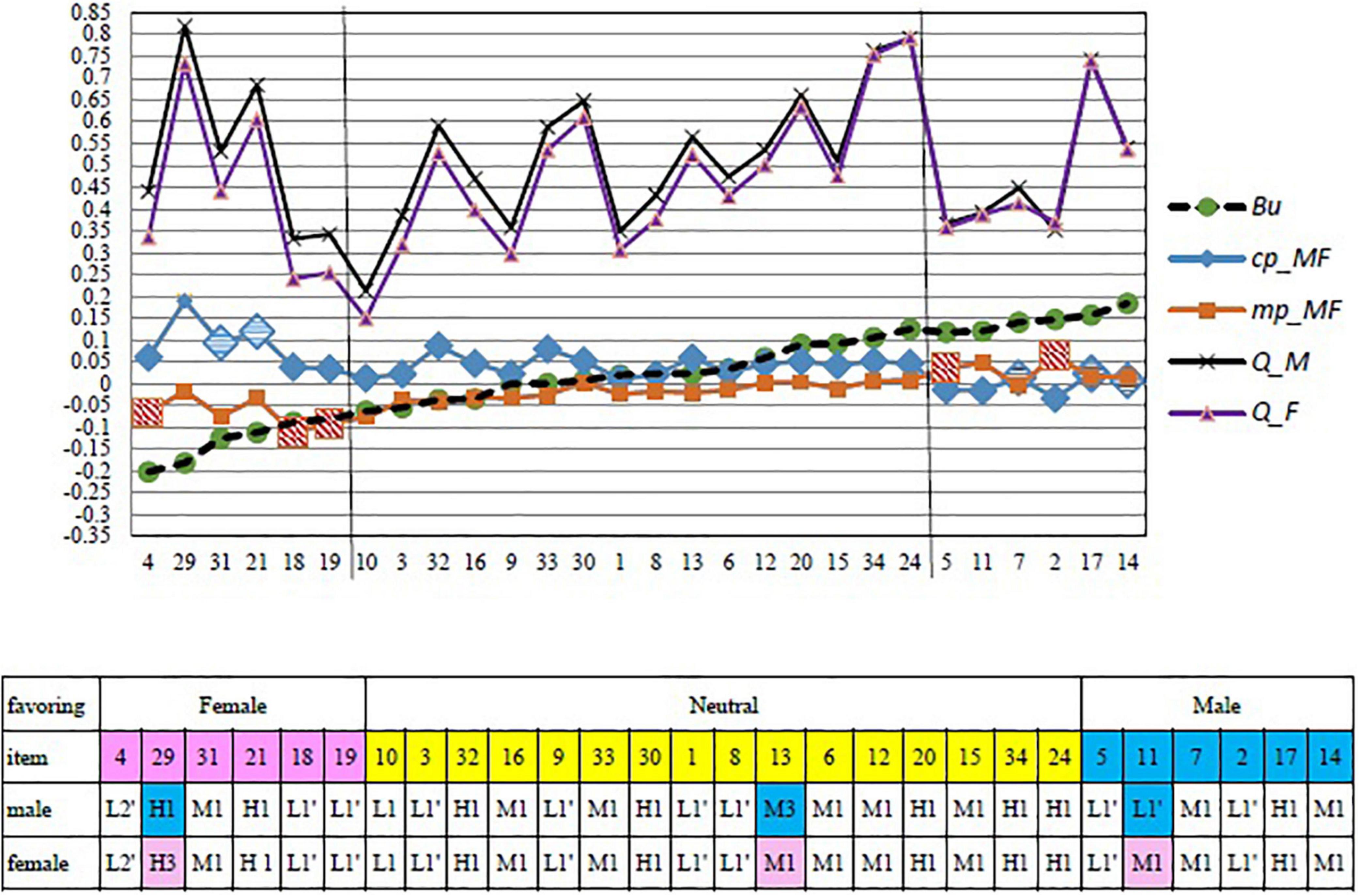
Figure 3. Differential item functioning (DIF) predicted by mp and cp indices and classifications for favoring items.
Furthermore, the item classifications from the APT yielded more insightful information for DIF item treatment. In the female-favoring part, three items (i.e., items 4, 18, and 19) with high values of defenselessness (mp) exhibited consistent item types (L2′, L1′, and L1′, respectively) for both men and women. This implied that men and women consistently perceived the three items as defenseless. Moreover, they consistently perceived item 4 as defenseless and with disturbance (L2′), and items 18 and 19 as normal (L1′). Two other DIF items (items 31 and 21) with relatively high values of power (cp) exhibited consistent item types (M1 and H1, respectively) for both men and women, indicating that the two groups perceived the two items as having middle to high levels of power, respectively. On the other hand, only the item classification of item 29 was different for the gender groups: H3 for women and H1 for men. Thus, item 29 was perceived as having a high level of power for both groups but with a hint only for the female group. The Hint was likely an associate of this DIF item (item 29).
In the male-favoring part, six items exhibited male-favoring properties. Two of them (items 5 and 2) exhibited the same defenselessness item types (L1′) and three of them (items 7, 17, and 14) exhibited the same power item types (M1, H1, and, M1, respectively) for both groups. Thus, these findings implied that men and women consistently perceived the former two items as defenseless but the latter three items as having middle to have high levels of power. Interestingly, only item 11 was labeled as L1′ and M1 for men and women, respectively, suggesting that men perceived this item as more defenseless than women did, which likely resulted in its male-favoring property. In the neutral part, all 15 of 16 items performed consistently across the male and female groups. Only item 13 was labeled as M3 and M1 for men and women, respectively, indicating the item performed middle power for both groups, but men perceived more hints than women. Interestingly, item 13 did not perform DIF. This might be due to middle power performed by the item and, according to Table 1, the variances of DIFs explained by the power (cp) index are low (only 14.2%).
In summary, a 100-repetition APT found only two items (items 29 and 11) to be perceived with different item classifications for men and women among the 12 DIF items.
Discussion
Given that the possible associates of DIF items have not attracted much attention, this study employed the Poly-SIBTEST approach as a reference method to demonstrate how the Poly-BW indices contribute to DIF measures with an example of the math test. To our best knowledge, this study may be the first study to investigate how the Poly-BW indices explain the possible associates of DIFs. There are several significant findings which were reported. First, two of the Poly-BW indices (defenselessness and power) significantly contributed to the Poly-SIBTEST-based DIF measures. This finding was largely consistent with the Monte Carlo study of Huang and Lin (2017), in which they simulated dichotomous data under five conditions (sample size, item number, DIF type, DIF ratio, and DIF severity) for Rasch-based DIF measures. In their study, they found that the power index and defenselessness index could on average predict Rasch-based DIFs with significant absolute beta values as 0.41 and 0.26, respectively, and explain 22.4% of total variances of DIFs.
In our polytomously-scoring study, the defenselessness index (mp) explained most of the variance of the DIF measures in this case, indicating that the extent to which an item is more likely to be answered correctly by the examinees whose ability levels were higher than the difficulty level of the item in one group than those in the other group is a significant predictor of the occurrence of DIF. More specifically, if an item is perceived as weak and exhibits high defenselessness so that persons with ability levels higher than the difficulty level are very easy to answer it correctly, then the item is likely to be identified as a DIF item. In addition and importantly, when compared with the difficulty index based on CTT, defenselessness index (mp) explained more variance of DIF measures because the Poly-BW index could clearly distinguish “within” or “beyond” the item difficulty level. If we ignore the within-beyond effect on DIF associates and just wholly deal with traditional difficulty index as an indicator of DIFs, then we may lose some useful information of possible associates in a DIF item. This is because the effects of power and defenselessness may be washed out in a single item.
Second, the Poly-BW indices provide clearer clues for understanding the different associates of DIFs for men and women in the math test. In this case, if an item has relatively high defenselessness and relatively low power for men, it is likely to be a male-favoring DIF item. By contrast, if an item has relatively low defenselessness and relatively high power for women, it is likely to be a female-favoring DIF item. The gaps of defenselessness or power between genders may be the possible reasons for gender-related DIF in the math test. Given the gap of defenselessness explaining the large DIF variance (63.8%), this study revealed that DIF mainly occurs in a certain situation where a person ability is beyond item difficulty. More specifically, the more difference on defenselessness exists between both genders, the more likely DIF occurs. In line with this finding, we suggest that the treatment of DIF items should depend on the type of assessment. If the assessment is a norm-referenced test, the DIF items with high defenselessness for both genders may be modified. Such an item should be modified as a more difficult item. By contrast, if the assessment is a criterion-referenced test, the DIF items with high defenselessness for both genders may be retained. Because the objective of criterion-referenced tests is simply to inspect whether the students have learned the materials, the items (relatively defenseless items) measuring the basic concept of the materials are commonly or necessarily included in the test.
Third, although we found the Poly-BW indices can precisely classify most of the DIF items identified by Poly-SIBTEST procedures, there were six neutral items misclassified as the female-favoring or male-favoring items. With more specific inspections, the mp index (defenselessness) dominates the key associates of DIF items and major transformation reasons from no DIF to favoring one group. The possible main reason for this discrepancy might be due to the Poly-SIBTEST procedures assessing a DIF based on the concept of a “whole” item score; however, the Poly-BW indices distinguish two response patterns (within-difficulty response pattern and the beyond-difficulty response pattern).
The findings in this study have some important implications. Teachers or testing practitioners could modify or revise DIF items based on the Poly-BW indices. When an item is flagged as DIF in practice, the possible reasons of DIF items, such as defenselessness or power, should be examined through the Poly-BW indices. From the Poly-BW indices, researchers and practitioners can understand possible associates of DIF items on math performance. Further treatment of the DIF items depends on the item classifications and the types of assessment. In addition, although the disturbance (bp) and hint (wp) are not significant predictors of DIF measures in this study, it does not mean that disturbance or hint is not the associates of DIFs in this case. It is likely that the effects of disturbance and hint on the DIF measures of all items are offset and negligible, but they may be significant for some items. Finally, item classifications involving complicated procedures in APTs could be easily conducted using the PWBstar1.0 program; thus, practitioners or teachers could employ this program to examine the intrinsic properties of tests.
This study has the following limitations. First, this study is the first study to explore how the Poly-BW indices contribute to DIF measures in a teacher-made mathematics achievement test; thus, the findings are more exploratory in the context of teacher-made math tests, and additional evidence is required for similar or different fields. For example, additional evidence as to whether the defenselessness property is the primary associate for DIF items in criterion-referenced tests should be obtained. Second, the significant predictors (Poly-BW indices) for DIF measures in norm-referenced tests still need to be explored. Third, this study used the Poly-SIBTEST index as a reference method, limiting to examine uniform DIF. The Crossing SIBTEST (e.g., Li, 2020) in assessing non-uniform DIF could be included in further studies. Finally, the Poly-BW indices include four indices for both persons and items. This study emphasizes the use of the Poly-BW indices for items; thus, future studies could investigate examinees’ performance using the Poly-BW person-fit indices.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. All participants voluntarily joined this study. The procedures of this study follow ethics principles for human research.
Author Contributions
T-WH contributed for creating ideas, data collection, data analysis, and writing. P-CW contributed to data analysis, discussion of ideas, and revision of the manuscript. MM yielded feedback and critically revised the article for important intellectual content. All authors contributed to the interpretation of the results and read and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyg.2022.821459/full#supplementary-material
Footnotes
- ^ https://www.ncyu.edu.tw/gcweb/content.aspx?site_content_sn=44700
- ^ We also chose a 1-parameter Rasch model to estimate the DIF contrasts (men minus women). The results showed that three Poly-BW indices explain almost 88% of the variance (70% from the predictor of mpM–F, 15% from the predictor of cpM–F, and 3% from the predictor of wM–F) of the DIF contrast obtained from Rasch DIF analysis. The findings were similar to those from the Poly-SIBTEST analysis. Because Rasch DIF analysis is not a non-parametric-based method, the results for further analyses were not conducted.
References
Chang, H. H., Mazzeo, J., and Roussos, L. A. (1996). Detecting DIF for polytomously scored items: an adaptation of the SIBTEST procedure. J. Educ. Measure. 33, 333–353. doi: 10.1111/j.1745-3984.1996.tb00496.x
Chen, C. T., and Hwu, B.-S. (2018). Improving the assessment of differential item functioning in large-scale programs with dual-scale purification of Rasch models: the PISA example. Appl. Psychol. Measure. 42, 206–220. doi: 10.1177/0146621617726786
Cho, S. J., Suh, Y., and Lee, W.-Y. (2016). After differential item functioning is detected: IRT item calibration and scoring in the presence of DIF. Appl. Psychol. Measure. 40, 573–591. doi: 10.1177/0146621616664304
Cohen, A. S., and Bolt, D. M. (2005). A mixture model analysis of differential item functioning. J. Educ. Measure. 42, 133–148. doi: 10.1111/j.1745-3984.2005.00007
De Ayala, R. J., Kim, S. H., Stapleton, L. M., and Dayton, C. M. (2002). Differential item functioning: a mixture distribution conceptualization. Int. J. Test. 2, 243–276. doi: 10.1080/15305058.2002.9669495
Ding, C. S., Song, K., and Richardson, L. J. (2006). Do mathematical gender differences continue? A longitudinal study of gender difference and excellence in mathematics performance in the U.S. Educ. Studies 40, 279–295. doi: 10.1080/00131940701301952
Fryer, R. G., and Levitt, S. D. (2010). An Empirical Analysis of the Gender Gap in Mathematics. Am. Econ. J. Appl. Econ. 2, 210–240. doi: 10.1257/app.2.2.210
Guttman, L. (1944). A basis for scaling qualitative data. Am. Sociol. Rev. 9, 139–150. doi: 10.2307/2086306
Harnisch, D. L., and Linn, R. L. (1981). Analysis of item response patterns: questionable test data and dissimilar curriculum practices. J. Educ. Measure. 18, 133–146. doi: 10.1111/j.1745-3984.1981.tb00848.x
Holland, P. W., and Thayer, D. T. (1988). “Differential item performance and the Mantel Haenszel procedure,” in Test validity, eds H. Wainer and H. I. Braun (New Jersey: Lawrence Erlbaum Associates, Inc), 129–145.
Huang, T. W. (2002). The power of the Beyond-Ability-Surprise Index and the Within-Ability Concern Index for detecting person/item aberrances: A Monte Carlo study. Unpublished doctorate dissertation. Ohio: The Ohio State University.
Huang, T. W. (2011). Robustness of BW aberrance indices against test length. Know. Manage. E Learn. 3, 310–318. doi: 10.34105/j.kmel.2011.03.023
Huang, T. W. (2012). Aberrance detection powers of the BW and Person-Fit Indices. J. Educ. Technol. Soc. 15, 28–37.
Huang, T. W., and Lin, S. Y. (2017). “Predictions of DIFs by the BW item-fit indices: a monte carlo study,” in Paper presented at The Seventh Asian Conference on Psychology & the Behavioral Sciences 2017(ACP2017) (Kobe).
Huang, T. W., and Lu, C. M. (2017). Develop BW Cognitive Diagnostic Models and Program to Assess Students’ Learning Statuses,”2017 6th IIAI International Congress on Advanced Applied Informatics (IIAI-AAI), Hamamatsu, Japan: IEEE
Huang, T. W., and Wu, P. C. (2013). A classroom-based cognitive diagnostic model for teacher-made tests: an example with fractions and decimals. J. Educ. Technol. Soc. 16, 347–361.
Hyde, J. S., and Mertz, J. E. (2009). Gender, culture, and mathematics performance. Proc. Natl. Acad. Sci. 106, 8801–8807. doi: 10.1073/pnas.0901265106
Kim, S. H., Cohen, A. S., Alagoz, C., and Kim, S. (2007). DIF detection and effect size measures for polytomously scored items. J. Educ. Measure. 44, 93–116.
Kogut, J. (1986). Review of IRT-based indices for detecting and diagnosing aberrant response patterns (Research Report No. 86-4). Enschede, Netherlands: University of Twente.
Lee, S., Bulut, O., and Suh, Y. (2016). Multidimensional extension of multiple indicators multiple causes models to detect DIF. Educ. Psychol. Measure. 77, 545–569. doi: 10.1177/0013164416651116
Li, Z. (2014a). A power formula for the SIBTEST procedure for differential item functioning. Appl. Psychol. Measure. 38, 311–328. doi: 10.1177/0146621613518095
Li, Z. (2014b). Power and sample size calculations for logistic regression tests for differential item functioning. J. Educ. Measure. 51, 441–462. doi: 10.1111/jedm.12058
Li, Z. (2015). A power formula for the Mantel–Haenszel test for differential item functioning. Appl. Psychol. Measure. 39, 373–388. doi: 10.1177/0146621614568805
Li, Z. (2020). The Power of Crossing SIBTEST. Appl. Psychol. Measure. 44, 393–408. doi: 10.1177/0146621620909907
Lindberg, S. M., Hyde, J. S., Petersen, J. L., and Linn, M. C. (2010). New trends in gender and mathematics performance: a meta-analysis. Psychol. Bull. 136, 1123–1135. doi: 10.1037/a0021276
Masters, G. N. (1982). A Rasch model for partial credit scoring. Psychometrika 47, 149–174. doi: 10.1590/S0120-41572011000300013
Mazor, K. M., Hambleton, R. K., and Clauser, B. E. (1998). Multidimensional DIF analyses: the effects of matching on unidimensional subtest scores. Appl. Psychol. Measure. 22, 357–367. doi: 10.1177/014662169802200404
Meijer, R. R., and Sijtsma, K. (1999). A review of methods for evaluating the fit of item score patterns on a test (Research Report No. 99-01). Enschede, Netherlands: University of Twente.
Pomerantz, E. M., Altermatt, E. R., and Saxon, J. L. (2002). Making the grade but feeling distressed: gender differences in academic performance and internal distress. J. Educ. Psychol. 94, 396–404. doi: 10.1037/0022-0663.94.2.396
Robinson, J. P., and Theule Lubienski, S. (2011). The development of gender achievement gaps in mathematics and reading during elementary and middle school: examining direct cognitive assessments and teacher ratings. Am. Educ. Res. J. 48, 268–302. doi: 10.3102/0002831210372249
Roussos, L. A., and Stout, W. F. (1996). A multidimensionality-based DIF analysis paradigm. Appl. Psychol. Measure. 20, 353–371. doi: 10.1177/014662169602000404
Seol, H. (1998). Sensitivity of five Rasch-model-based fit indices to selected person and item aberrances: A simulation study. Unpublished dissertation. Ohio: The Ohio State University.
Shealy, R. T., and Stout, W. F. (1993). A model-biased standardization approach that separates true bias/DIF from group ability differences and detects test bias/DIF as well as item bias/DIF. Psychometrika 54, 159–194. doi: 10.1007/bf02294572
Suh, Y., and Bolt, D. M. (2011). A nested logit approach for investigating distractors as causes of differential item functioning. J. Educ. Measure. 48, 188–205. doi: 10.1111/j.1745-3984.2011.00139.x
Suh, Y., and Talley, A. E. (2015). An empirical comparison of DDF detection methods for understanding the causes of DIF in multiple-choice items. Appl. Measure. Educ. 28, 48–67. doi: 10.1080/08957347.2014.973560
Keywords: differential item functioning (DIF), Poly-SIBTEST, Poly-BW indices, teacher-made mathematics test, item-fit statistics
Citation: Huang T-W, Wu P-C and Mok MMC (2022) Examination of Gender-Related Differential Item Functioning Through Poly-BW Indices. Front. Psychol. 13:821459. doi: 10.3389/fpsyg.2022.821459
Received: 24 November 2021; Accepted: 28 January 2022;
Published: 25 February 2022.
Edited by:
Laura Girelli, University of Salerno, ItalyReviewed by:
Zhushan Li, Boston College, United StatesKubra Atalay Kabasakal, Hacettepe University, Turkey
Copyright © 2022 Huang, Wu and Mok. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tsai-Wei Huang, dHdodWFuZ0BtYWlsLm5jeXUuZWR1LnR3
 Tsai-Wei Huang
Tsai-Wei Huang Pei-Chen Wu
Pei-Chen Wu Magdalena Mo Ching Mok
Magdalena Mo Ching Mok