
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Psychol., 19 January 2023
Sec. Educational Psychology
Volume 13 - 2022 | https://doi.org/10.3389/fpsyg.2022.1111600
Motivation, the teacher–student relationship, the use of resources, and the time spent studying, in addition to the family economic and social context, are some of the factors that affect academic performance and directly influence student failure. This paper evaluates the motivation in mathematics students’ performances by analyzing indicators of the mathematics learning dimensions. A total of 2,018 secondary students were evaluated in this cross-sectional study. Motivation, teaching, resources, and study time were analyzed with a validated 20-item questionnaire. Statistical analysis revealed that student motivation appears to be significantly related to perceptions of teaching practices and the use of resources for study. Students with high motivation have positive perceptions of teaching practices. Gender differences were not observed. In addition, the motivation indicator allowed for grouping students into various motivational profiles.
In general, secondary school students do not develop mathematical competence correctly due to their difficulties with understanding the basic theoretical concepts and the proper interpretations of data (Cipkova et al., 2019). Moreover, a negative perception of the subject, which is dependent on the interests of teenagers (Husein et al., 2018; Abin et al., 2020), has a negative impact on both a student’s academic performance (Ozhan and Kocadere, 2020) and their choice of STEAM studies (Hine, 2018).
Academic achievement is primarily associated with educational attainment (Williams et al., 2022). Therefore, grades are one of the reliable reference indicators of a student’s academic performance (Neuendorf et al., 2022). Moreover, a student regularly finishing their math homework was a significant predictor of academic performance (Xu, 2022). However, the amount of homework completed in secondary school did not have an association with a student’s academic performance (Tsang et al., 2022).
On the other hand, variables responsible for low academic performance can be classified into internal and external variables. Internal variables are associated with cognitive factors such as aptitude, intelligence, cognitive style, and personality factors such as motivation (Lim, 2021; Mercader Rubio et al., 2022), self-esteem (Smith et al., 2022), and self-confidence (Estrada-Madariaga, 2017; Vinni-Laakso et al., 2019). Several findings have suggested positive relationships between academic performance and emotional intelligence (Buenrostro and Radinsky, 2019).
External variables include socioeconomic status (Bardach et al., 2022; Musaddiq et al., 2022; Williams et al., 2022), family (Stavrulaki et al., 2021), and economic and school context (Siebecke and Jarl, 2022; Tan, 2022). With respect to social context, marginality, poverty, delinquency, drug use, etc., stand out (Perdereau-Noel et al., 2017; Martin et al., 2022). As for school context, a high ratio in a student’s classroom (INEE, 2021) and the role of teachers (Kim, 2020) stand out. In 2021, Spanish State School Board stated that low academic performance generally led to student failure.
One of the consequences of low academic performance and student failure is early school dropout (Cuenca Carrión et al., 2021). In 2019 and 2021, Spanish State School Board reports defined early school dropout as “the percentage of young people between 18 and 24 years of age whose highest academic qualification is Compulsory Secondary Education and who do not continue their education.” These data were provided by Eurostat from a labor force survey. For 2020, Europe set an early dropout rate of below 10% (15% for Spain) as a target (Cuenca Carrión et al., 2021).
Numerous studies have analyzed the effects of educational environment on a student’s academic performance. Warwick et al. (2019) highlighted the teacher–student relationship as the most relevant element of performance (Warwick et al., 2019), and the scientific literature shows that the influences of personal motivation and classroom climate are key elements (Ozhan and Kocadere, 2020; Prieto, 2020; Rojo-Robas et al., 2020).
Results from other studies appear to confirm that the use of technology for educational purposes for learning mathematics is not significant in the academic performance of secondary mathematics students (Hossein-Mohand et al., 2021a). However, other studies have suggested that the excessive use of technologies has an influence on student failure in high school (Gómez-García et al., 2020a).
The role of a teacher is vital in the teaching–learning process. A motivated teacher introduces technological (Gómez-García et al., 2020b), pedagogical, and methodological innovations in the teaching of mathematics (Trujillo-Torres et al., 2020a). Their role is fundamental to adequately assessing the classroom climate and to developing interventions that favor safe learning environments (Quijada et al., 2020). However, some authors have suggested a significant association between truancy and a negative classroom climate (Rathmann et al., 2018). In this sense, inadequate intervention is associated with an increase in disruptive behaviors (Lerang et al., 2019).
Regarding groupings of students within a classroom, several authors have argued that natural distributions are produced by antagonistic acceptance–rejection and popularity–unpopularity criteria (Reihenova, 2018; Laninga-Wijnen et al., 2019; Tereshchenko et al., 2019). Scientific evidence supports that the popularity–unpopularity criteria clustered similar pairs of both high and low performers and the effects of like-peer groupings that significantly impact students in ethnically mixed classrooms (Keller and Takacs, 2019). Additionally, boys with both high and low academic performance levels have significantly higher risks of being bullied than girls with the same academic profiles (Bergold et al., 2020).
However, the literature has established significant associations between the teacher–student relationship and student academic achievement (Holzberger et al., 2019; Klapproth and Fischer, 2019). Moreover, good teacher–student communication allows teachers to adequately assess their students’ mathematical competencies (Sánchez-Matamoros et al., 2019; Uner and Akkus, 2019) and develop effective pedagogical strategies within the classroom (Van-Kleij, 2019; Hossein-Mohand et al., 2021b).
The teacher–student relationship is significantly positively associated with the methodology used by the teacher. However, Roorda et al. (2019) pointed out that if a student has a bad relationship with their teacher, they also have a negative perception of the corresponding subject. This may explain the results showing low performance levels in mathematics in secondary schools (Lazarides et al., 2019; Ozdemir and Ozdemir, 2019). Moreover, the teacher–student relationship has a major influence on socioeconomically disadvantaged groups of students (Munter and Haines, 2019).
However, discrepant positions regarding the impact of the teacher–student relationship have been observed. Timmermans and Rubie-Davies (2018) suggested that the overall effects for the majority are insignificant, but for a minority, they could be very significant. In contrast, Goellner et al. (2018) claimed that long-lasting relationships between a student and teacher over time (in primary and secondary education) broaden the spectrum of dyadic effects on the student body. An example of the effect of this relationship is its impact on both academic and non-academic motivation in students (Trujillo-Torres et al., 2020b).
In addition to the inherent capacity of a student, academic performance in mathematics has significant associations with self-discipline and perseverance (Hagger and Hamilton, 2019). The resilience needed to cope with learning this subject is supported by motivation (Sagone et al., 2020). Therefore, in this multifactorial analysis, it is worth highlighting the role of motivation as a fundamental variable for learning mathematics (Rojo-Robas et al., 2020; Trujillo-Torres et al., 2020b).
Intrinsic motivation arises from an individual’s own motivation by providing enjoyment in the face of challenges (Diseth et al., 2020). This motivation increases with personal development and perseverance and strengthens an individual’s resilience (Cheng, 2019). External motivation, on the other hand, stimulates an individual through different types of external rewards and recognition (Liu et al., 2020a). These stimuli detract from the intrinsic value of the activity performed and negatively affect a student’s performance (Gillison et al., 2019).
Different findings have suggested that extrinsic motivation has a significant negative impact on intrinsic motivation (Cheng, 2019). However, other authors have claimed that both types of motivation affect each other (Hidi et al., 2019; Liu et al., 2020a,b) and that this effect is not summative but multiplicative. Furthermore, they have pointed out that the effect of extrinsic motivation depends on an individual’s level of intrinsic motivation (Sheldon and Prentice, 2019). Past scientific findings have shown that the effect of a reward is negative only if the level of intrinsic motivation of a learner is high (Liu et al., 2020b). Otherwise (i.e., for unmotivated individuals or for individuals with very low levels of intrinsic motivation), rewards or instrumental motivation are important stimuli that arouse interest in a task’s “situational interest,” reinforce intrinsic motivation, and support an individual’s academic performance (Liu et al., 2020a).
Similarly, several authors have suggested significant correlations between autonomous motivation and positive perceptions toward studies in STEAM (Hagger and Hamilton, 2018; Hodis, 2018). They have pointed out significant positive correlations between students’ autonomous and controlled motivations and between students’ socio-cognitive beliefs toward scientific activities and their academic performance in these areas. On the other hand, there is evidence that shows that external stimuli (rewards, prizes, etc.) can impact superficial, non-durable cognitive effects. On the other hand, internal stimuli (commitment, self-improvement, etc.) can provoke deep, permanent cognitive effects and motivate students in a decisive way (Rican et al., 2022).
In terms of gender, the difference in motivational perceptions regarding mathematics has impacted the low number of young women studying STEAM (Hsieh, 2019; Vinni-Laakso et al., 2019). Possible causes of this include gender roles (Ehrtmann and Wolter, 2018; Steegh et al., 2019), which are influenced by sociocultural factors (Melak and Singh, 2021). The 2020 report by the Spanish Youth Institute (INJUVE) concluded that gender and sexual orientation are associated with the choice of STEAM in university studies (INJUVE, 2020). This report argued that, in general, the female gender and the homosexual collective show preferences toward artistic and humanistic studies, while the male gender prefers STEAM studies.
However, interest in STEAM among female students is positively correlated with the resources employed, time devoted to studying, and career prospects (Loh et al., 2019). In this sense, mathematics teachers can motivate students with appropriate pedagogical and methodological interventions (Vergara et al., 2019). Effective interventions significantly impact the mathematical competence acquired by a student (Garrido-Yserte et al., 2019; Levrini et al., 2019) and can favor their interest in STEAM (Barth et al., 2018). Preventing and acting against demotivation and avoiding consequent early school dropout is an arduous task that requires specific training for mathematics teachers (Gil et al., 2019; Hossein-Mohand et al., 2021b).
The early school dropout rate for Spain (20.2%) is well above the European average (11.8%). The Autonomous City of Melilla (a Spanish city in north of Africa with a special administrative structure) has reached an extreme value in this respect, with an early school dropout rate of 22.8% (Cuenca Carrión et al., 2021). Since 2010, the A.C. of Melilla is among the two European cities with the highest rates. Although there was evidence of a decrease in these rates for the period 2008–2018, they were still far from attaining the European Council’s target of 10% by 2020 (Martínez-Abad et al., 2020). On the other hand, the gross secondary school graduation rate in Spain is 78.8%, but in the A.C. of Melilla, with the second lowest rate in the country, it is 52.7% (67.5% for females and 48.1% for males). Furthermore, the PISA 2018 report indicated that 75% of Spanish students had the minimum level of competence in mathematics, compared to the European average of 78% (Gamazo and Martínez-Abad, 2020). In terms of ranking in autonomous regions, the two lowest values were found in the autonomous cities of Ceuta (44%) and Melilla (53%) (INEE, 2021).
In this context, a cross-sectional analysis of academic variables that could influence the motivational profile of secondary and high school mathematics students is proposed. Due to the general profile of a student body, only the possible effect of extrinsic or instrumental motivation is evaluated. This quantitative study also evaluates the teacher’s role and the resources and study time of students.
The main objective of the present study was to determine the effect of motivation on the mathematics students in the A.C. of Melilla through the analysis of indicators of the dimension “Learning Mathematics.” The associated specific objectives are: first, to examine the relationship between the variables related to gender, educational level, teaching, study time, resources employed, and extrinsic motivation, and second, to establish the optimal number of clusters necessary to subdivide the sample according to the motivational profiles of the mathematics students in the A.C. of Melilla.
The hypotheses associated with personal and academic factors are as follows:
H1. The variables associated with the indicators—instrumental or extrinsic motivation, teaching, study time, employment of resources for study—and the variables—educational level and gender—do not have the same influence on the same secondary students, nor do they influence these students in the same way.
H2. There will not be a statistically significant correlation between each pair of the variables (gender and educational level) and the indicators (teaching, study time, resources used, and extrinsic motivation).
H3. The regressors (teaching, study time, employment of resources for study, educational level, and gender) do not significantly influence instrumental or extrinsic motivation through either main or interaction effects.
H4. There are no statistically significant differences between the genders of the students and their educational level, teaching, study time, resources used, and motivation.
The present cross-sectional study is a non-experimental, ex post facto method which uses a closed questionnaire as the data collection instrument. Mathematics grades are used as a reference predictor for students’ mathematics academic performance (Barca et al., 2011; Córdoba et al., 2012).
The study sample corresponds to mathematics students in the A.C. of Melilla. The study population was obtained by applying the following inclusion criteria: (1) being under 18 years old, (2) residing in the City, and (3) studying in secondary and high school during the 2018/2019 academic year. With these criteria, the population amounts to 5,875 individuals (50.84% of which are female). The sample selection criterion was comprised of a non-probabilistic convenience sampling.
The initial sample had 2,039 students, but an initial analysis identified 21 incomplete questionnaires, and these were removed from the present study. Finally, a total of 2,018 students (53.40% females) from all schools and educational levels in the C. A. of Melilla participated in this study. The sample was differentiated by educational levels, compulsory secondary schools, and post-16 education, as follows: 1 secondary school (417), 2 secondary school (473), 3 secondary school (394), 4 secondary school (417), 1 Baccalaureate (233), and 2 Baccalaureate (84).
The present study is part of a broad investigation focused on secondary and high school students in the A.C. of Melilla. An instrument with 135 closed-ended items of six dimensions and 31 indicators was used in this study, and it followed the Rosenbluth et al. (2016) procedure for the development of the questionnaire.
This work shows partial results related to 20 items of the dimension “B. Learning Mathematics” of the general questionnaire. It was taken to determine the possible relationship between the figures for the mathematics teacher, academic motivation, study time, and the use of different resources to study. The variables analyzed, their relationship with the corresponding indicators, and the dimensions are shown in Table 1.
The questionnaire was previously subjected to content validation by the judgment of ten experts with more than 15 years of academic experience (four researchers in mathematics education, three secondary school principals, and four heads of mathematics departments) in terms of the level of writing, as well as the degree of appropriateness of the items used. In addition, a pilot test was administered to 20 students to detect the last aspects that were susceptible to improvement.
Finally, the internal data matrix was validated by verifying that, in its composition, the conjunction of the heterogeneous items was coherent, using the Kaiser–Guttman criterion and the Tucker–Lewis index. First, the optimal number of dimensions of the instrument was assessed through the Kaiser–Guttman criterion and used to identify the optimal number of axes. The initial number was structured around 6 dimensions. However, the algorithm established that the optimal number of axes is three.
The generalized low-rank models (GLRM) and principal component analysis (PCA) were used for validation, taking the following parameters as references:
• loss = “Quadratic.”
• regularization_x = “L1.”
• gamma_x = 0.5.
• gamma_y = 0.
• max_iterations = 1,000.
The results obtained were as follows:
• The instrument can be reduced to four dimensions.
• The first dimension explains 24% of the variance, the second 18%, the third 16%, and the fourth 15%.
Based on the previous results, it was confirmed that, in order to optimize the instrument, it could be reduced from 6 to 4 dimensions.
To complete the validation, a double exploratory factor analysis was carried out, with the first one testing the previous statement about the dimensions and the second, using varimax rotation, identifying the variables that could be eliminated.
The results of the first exploratory factor analysis are as follows:
• Mean item complexity = 1.2.
• Test of the hypothesis that five factors are sufficient.
• The degrees of freedom for the null model are 15 and the objective function is 0.15, with chi-square value of 302.63.
• The degrees of freedom for the model are −5 and the objective function is 0.
• The root mean square of the residuals (RMSR) is 0.
• The Tucker–Lewis index of factoring reliability = 1.052.
• Fit based upon the off-diagonal values = 1.
Considering the original dimensions of the instrument, and given that the Tucker–Lewis index of factoring reliability is higher than 0.9, the instrument can be optimized with the choice of five axes.
These axes were then compared with the six axes initially established in the original instrument. The Bayesian information criterion (BIC) was lower by taking five dimensions, which confirmed this as the optimal solution.
For the second exploratory factor analysis using varimax rotation, uniqueness was calculated, and the residual matrix was analyzed. The proportion of variability is denoted as communality. One way to calculate it is to subtract uniqueness from one. An appropriate factor model results in low values for uniqueness and high values for communality. These results were met for the validation of the instrument. As a result, seven variables were removed from the set.
For the calculation of the residual matrix, the following scripts were used:
• Lambda < data$loadings.
• Psx < diag(data.fa$uniquenesses).
• S < data.fa$correlation.
• Sigma < Lambda%*% t(Lambda) + Psx.
The results showed for all cases where values were close to 0, those variables were well-represented.
Finally, the power of the statistical test was calculated. For this purpose, the following procedure was used: Two datasets were defined, with x1 selecting only the variable gender and x2, teaching (with level = 0), and an analogous one, y, which selected the same type of variables, but took a PMT level of one. Then, Cohen’s d was used for both datasets (d estimate = 0.11). For calculation of the power calculations for the t-tests of the means, the d value was replaced by the d estimate above and a power of 95% was defined. The results showed that 1,955 subjects (N = 1,955,106) are necessary to detect significant differences in the study, a result that is otherwise within the sample size.
The analyses of the present work are conducted using the R language in R studio (R Studio_Team, 2020; R Core_Team, 2021) to evaluate in a gender-differentiated analysis the possible association between the extrinsic motivation (MO) indicator and the academic variables that are detailed below.
The initial dataset consisted of 2018 observations and 137 variables. However, for this study, only the following variables and indicators are taken into consideration (Table 1):
The MO indicator groups together six questions from the global instrument belonging to the dimension “B. Learning Mathematics” (items B.82–B.87). The responses are adjusted based on a Likert scale of four (1, none; 2, a little; 3, enough; and 4, a lot).
The teaching indicator (PMT) focuses on a student’s perception of their mathematics teacher’s practices and includes six questions from the global instrument (items B.41–B.46). The study time indicator (ST) is associated with the average time spent by a student studying mathematics on working days (LJM) and on public holidays (VSM) (items B.52 and B.53). A different Likert scale of four is used for these items (1, none; 2, less than 1 h; 3, from 1 to 2 h; and 4, more than 2 h). As for the resources (RE) indicator, it focuses on the different resources (technological and non-technological) used by a student for learning mathematics and includes four questions from the global instrument (items B61–B.64) as references. The responses are adjusted based on a Likert scale of four (1, none; 2, a little; 3, enough; and 4, a lot).
This study also aims to assess whether there are gender differences (ECC) and the influence of educational level (NEC). The Likert-scale for the study variables is: ECC (1, female and 2, male); NEC (1, 1 secondary; 2, 2 secondary; 3, 3 secondary; 4, 4 secondary; 5, 1 high school; and 6, 2 high school).
Table 1 provides an overview of the interconnectedness of the above elements.
The data collection procedure was complex as it was conducted during school hours, but it was the only one that guaranteed the reliability of the data. This required the active collaboration of the management, the ICT coordinator, and the mathematics and technology departments of each center to implement the questionnaires with the least possible impact on school operations. It was also necessary to organize classroom and technological resources. The reliability of data collection was guaranteed using Google Forms, and a procedure was chosen to eliminate coder transcription errors (Cohen and Manion, 1990). The questionnaires were circulated in a computer classroom during school time to avoid bias, and they were given to all the secondary and high schools in the A.C. of Melilla.
Throughout the data collection process, a mathematics teacher was always assigned to each school to answer questions about the questionnaire, and another teacher from the technology department was assigned to deal with technical issues. At the end of the online questionnaire, each student returned to their classroom to continue with their studies.
The variables analyzed in this study, their relationship with the corresponding indicators, and the dimensions are shown in Table 1.
Because our participants are under 18 years-old, the questionnaire was reviewed by the local educational authorities and received authorization from the Provincial Director of the Ministry of Education to distribute the questionnaires in the educational centers of the city during school hours. In addition, all subjects who participated voluntarily were fully informed of the nature of the research.
The study complies with the ethical criteria of the Declaration of Helsinki. In addition, it follows the AERA (American Educational Research Association) code of ethics for research in education.
In our previous studies, we evaluated the incidence of some variables on performance and the relationships between them. However, this study aims to globally analyze the effect of motivation on some factors. Therefore, it was considered appropriate to group the variables of the dimension “B. Learning Mathematics” around the corresponding indicator (see Table 1):
• Gender (ECC)
• Educational level (NEC)
• Teaching (PMT): PMC + PME + PMR + PMM + PCT + PRE
• Study time (ST): LJM + VSM
• Resources used (ER): ULT + UAE + UVI + UAI
• Motivation (MO): MRP + MGA + MEF + MFM + MAM + MPM.
We note that the grouping of the variables of the motivation indicator quantifies their overall effect. The present study does not attempt to distinguish between the intrinsic and extrinsic motivation of the subjects. Furthermore, we note that the above groupings are not to be interpreted as a linear combination of variables.
Complementarily, each of the independent variables were factored and converted into numerical variables. They were then binned as follows:
• If the mean of PMT > 10.4∼1
• If the mean of ER > 5.8∼1
• If the mean of MO > 10∼1
• Otherwise, 0. It is important to note that the values 0 and 1 were factored. This latter procedure was performed to test the Mann–Whitney U-test values.
To achieve objective ¨OE1.1 To examine MO, PMT, ST, ER, NEC, and ECC variables and their relationships¨; and ¨OE1.2 To determine the optimal number of clusters necessary to subdivide the sample around the motivational profiles of the mathematics students of the A.C. of Melilla¨, the relationships between indicators B4 and B8 were analyzed. Figures 1, 2 presented in-depth correlation analyses of the motivational profile.
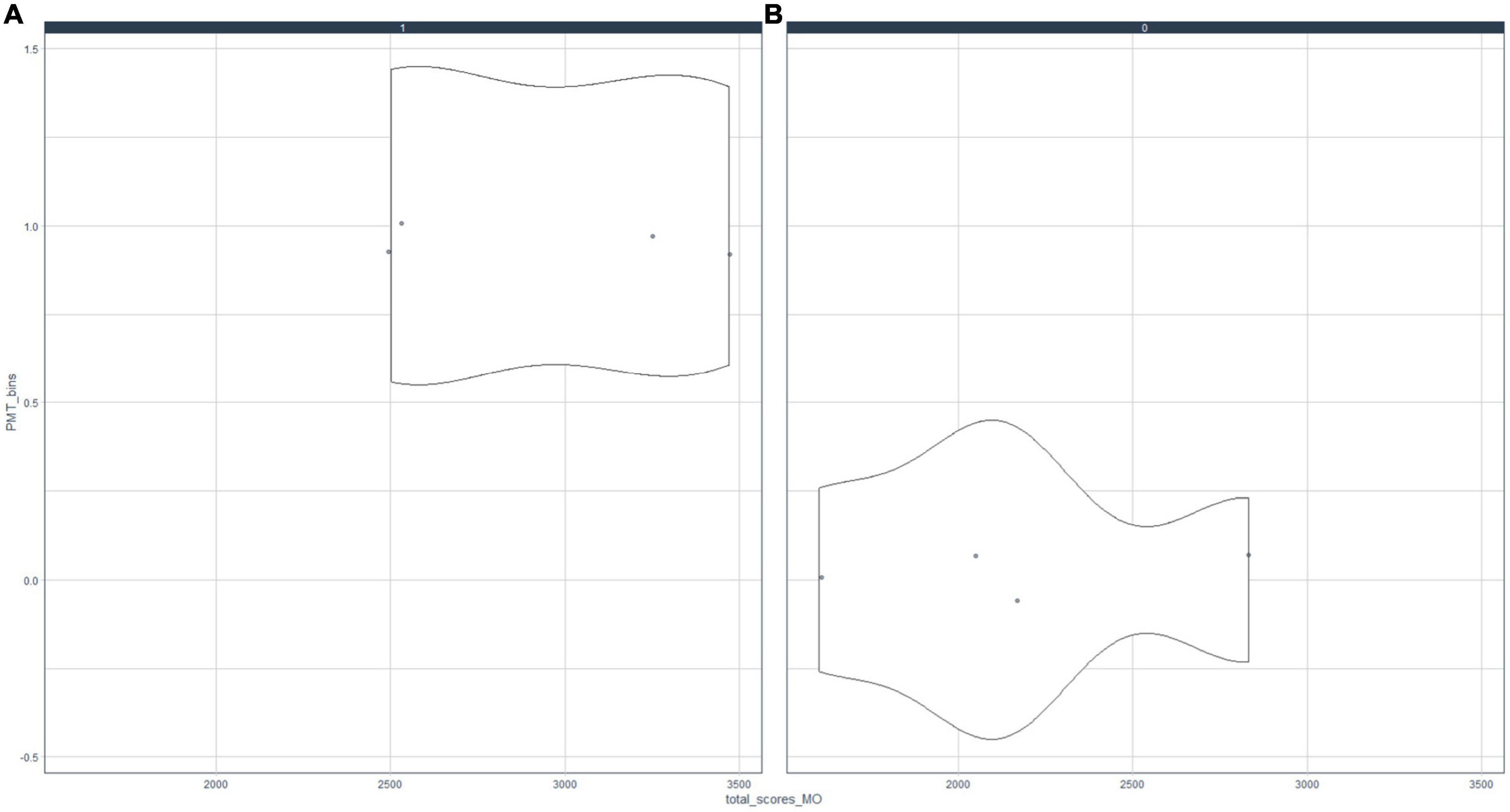
Figure 1. Relationship between motivation (MO) and teaching (PMT). Association of motivation and teaching indicators; (A) MO = 0, (B) MO = 1.
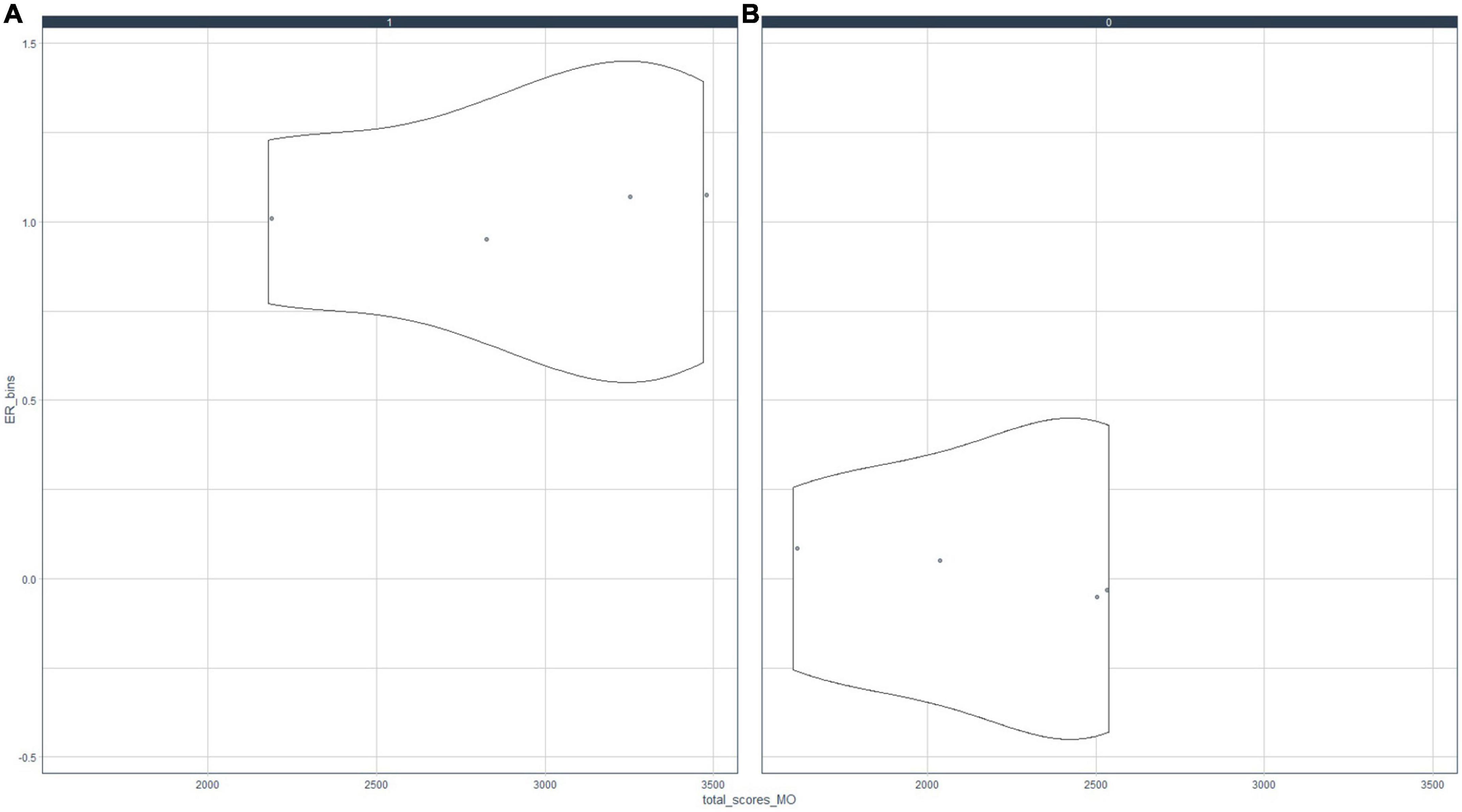
Figure 2. Relationship between motivation (MO) and resources used (ER). Association of motivation and resources for study; (A) MO = 0, (B) MO = 1.
Figure 1 shows that the behavior of motivated subjects with respect to PMT is significantly different from when they are not motivated, i.e., if a student is highly motivated (academically, by rewards, by their family, etc.), they will have a high perception of the teaching practices of their mathematics teacher. Otherwise, a student’s perceptions about teaching methodologies will be negative. Similarly, Figure 2 illustrates that the MO and RE scores are strongly positively correlated. In general, if students are motivated, they tend to use different resources to study. The impact is different for unmotivated students, who tend to obtain low values in using different resources for studying mathematics.
Another instrument used to evaluate the motivational profile of mathematics students in the A.C. of Melilla is the funnel correlation analysis shown in Figure 3.
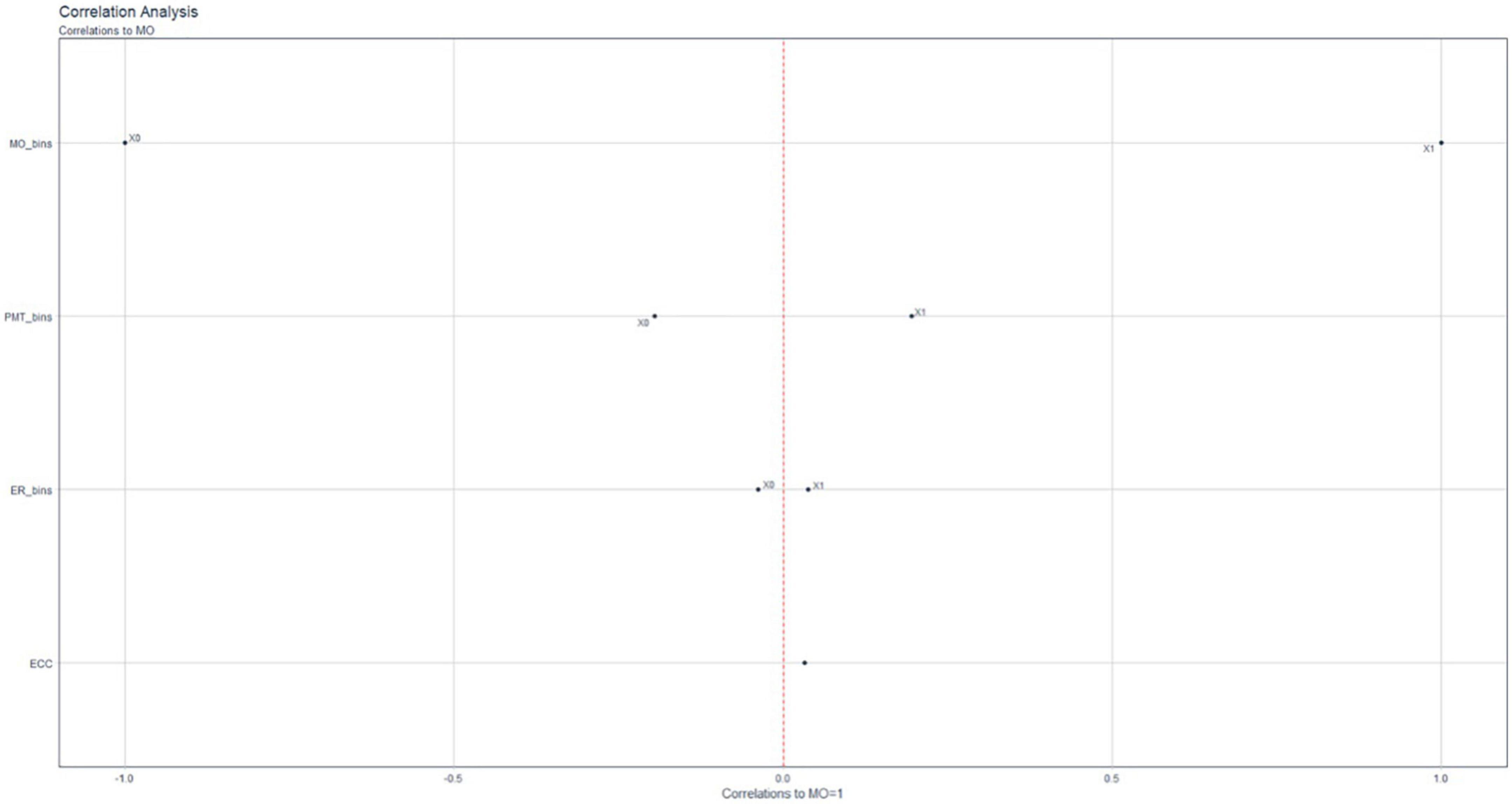
Figure 3. Correlation Funnel. Scores of studying and teaching resources to the motivation indicator.
Figure 3 shows that the variables MO, PMT, and ER are binary (yes/no), i.e., the subject’s motivation could be either No = 0 or Yes = 1. In the case of MO = 1, there is a strong correlation between a PMT of one and an ER of one. On the other hand, when MO takes a value of zero, there is a correlation with an ER of zero and a PMT of zero. These results imply that if the students are motivated, their perceptions of the teaching function improve and they use the appropriate didactic resources to study.
In the analysis differentiated by gender, our results suggest that there are no gender differences in the motivation associated with learning mathematics. Therefore, hypothesis H1 is rejected. “The relation between the variable MO with PMT, ST, ER, NEC, and ECC does not follow a similar pattern.”
To investigate further, the correlations between the variables of gender, educational level, teaching, study time, different resources used, and motivation are evaluated. The results are shown in Figure 4.
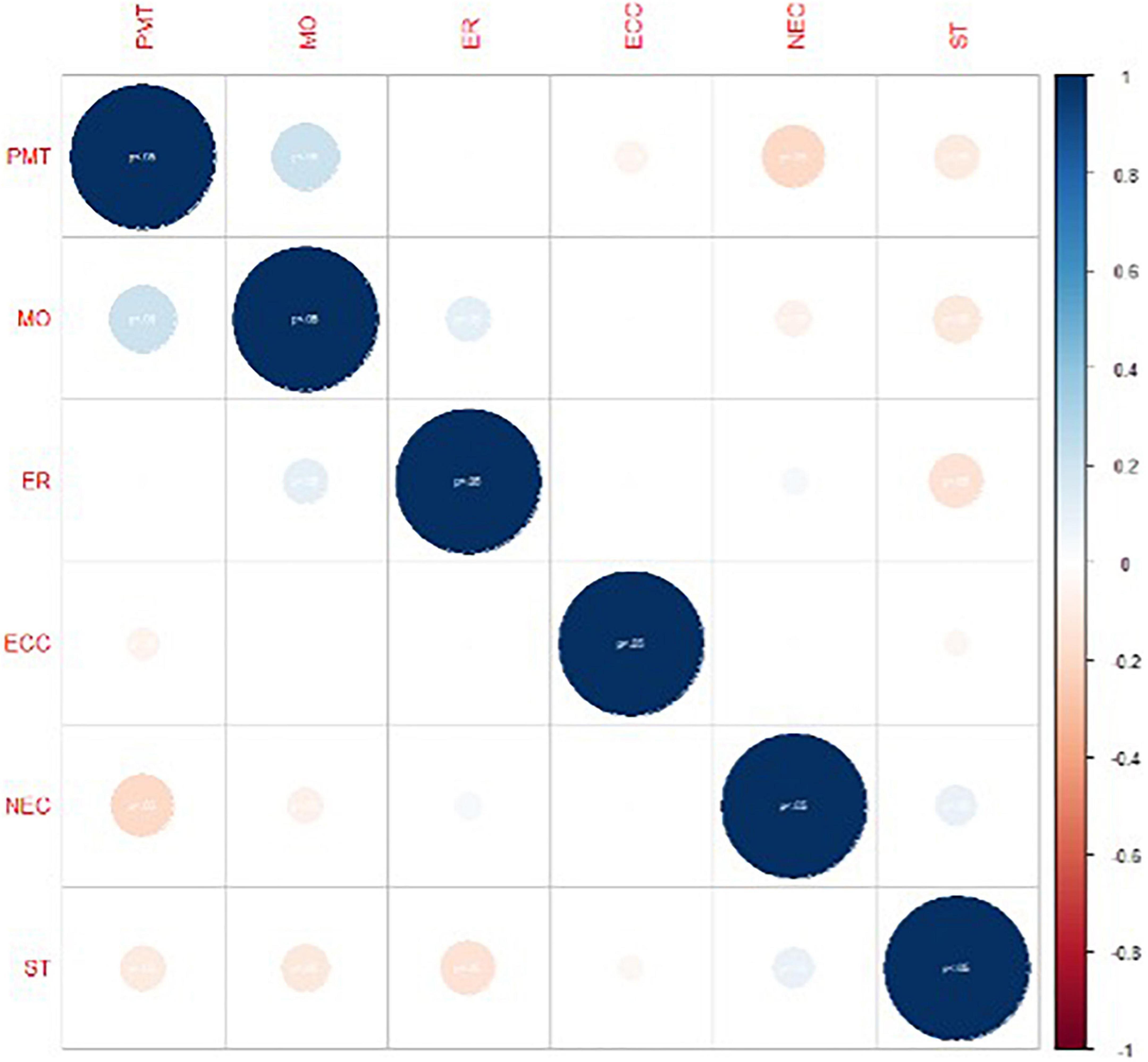
Figure 4. Correlation between the variables gender, educational level, teaching, study time, resources used, and motivation.
Figure 4 shows that in most cases, the correlations are weak and inverse. In addition, the strongest correlation is between PMT and MO. Based on these results, the null hypothesis H2 is accepted.
In order to answer hypothesis H4 on the existence of significant differences between the genders of students in relation to educational level, teaching, study time, different resources used, and motivation, the Mann–Whitney U-test is used. The results show that there are only significant differences between males and females with respect to the teaching variable (W = 547,220, p-value = 0.02431). Consequently, the null hypothesis H4 is partially rejected.
A study is then carried out to answer the research question: can mathematics students be grouped into clusters according to their motivational profile, and if so, what would be the optimal number of clusters? A principal component analysis (PCA) is performed to evaluate possible groupings, as shown in Figure 5.
Figure 5 illustrates that the optimal number of optimal clusters to subdivide the sample is nine. In other words, the mathematics students in the A.C. of Melilla can be grouped around nine differentiated profiles. Furthermore, the algorithm employs 14 classifier models for its analysis: EII, VII, EEI, VEI, EVI, VVI, EEE, EVE, VEE, VVE, EEV, VEV, EVV, and WWW, of which the optimal model is EII. Therefore, hypothesis H5 is rejected. “It is not possible to classify students according to their motivational profile.” This interesting finding has sparked the authors’ interest in conducting a new comprehensive and independent study to determine the nature and classification of students according to their motivational profiles, and it will be published soon.
To address objective 2, to determine if the variables PMT, ST, ER, and ECC have a significant impact on MO, a linear regression analysis is performed for the motivation variable. To quantify the weight of the most influential regressors, the analysis also identifies the level of each variable and their combined role. In other words, the effect of each variable as the main element and the interaction of two or more variables are analyzed. Table 2 shows the results.
Table 2 shows that the model is significant (p-value of <2.2 e–16), but it presents a low R2 (8.6% of the variation in student motivation depends on the variables ECC, NEC, PMT, ST, and ER). Less than 10% of the variability in motivation is explained by gender, educational level, teaching, study time, and use of different resources for study. We expect that there must be other factors associated with motivation that are not contemplated in the present paper and whose weight accounts for more than 90% of the variability.
The variables ER, NEC2: PMT, NEC3:ER, NEC4:ER, and NEC2: PMT:ST, NEC2:PMT:ST:ER had a significant contribution with respect to student motivation. In other words, the profiles that correlated highly significantly with motivation were as follows: (1) the student body, in general, employs different resources for study, and the highest correlations were found among students in 2 secondary school and 3 secondary school; (2) students in the 2 years of high school, in general; and (3) the highest scores were found among those who value teaching, dedicate time to study, and use different resources to learn mathematics.
Based on the above results, the null hypothesis H3 is partially rejected. “The regressors PMT, ST, ER, NEC, and ECC do not significantly influence MO, either through main or interaction effects.”
The low impact of the regressors in our study on motivation (<10%) suggests the existence of others of greater relevance that are affecting mathematics students in the A.C. of Melilla.
This study aims to determine the possible relationship between the figures of the mathematics teacher, academic motivation, study time, and use of different resources to study.
The present paper shows a significant association between a student’s extrinsic motivation and their positive perception of their mathematics teacher (Figure 1). Similarly, this study suggests a strongly positively correlation between student motivation with the use of different resources to study (Figure 2). In this sense Liu et al. (2020b) evidenced that instrumental motivation reinforces intrinsic motivation and arouses “situational interest,” and it has an especially important impact on students with poor academic performance (Liu et al., 2020a). Other authors have suggested that an individual’s intrinsic and extrinsic motivation influence each other (Hidi et al., 2019; Liu et al., 2020b), producing a multiplicative effect on a student’s academic performance (Sheldon and Prentice, 2019). Roorda et al. (2019) pointed out that a good student–teacher relationship has a significant positive effect on a student’s perception of the subject. Additionally, this influence is highly significant in socioeconomically disadvantaged groups of students (Munter and Haines, 2019; Martin et al., 2022). Additionally, Warwick et al. (2019) suggested a relevant association between teacher–student relationship and academic failure. In this sense, if a student’s perception of their mathematics teacher is negative, their interest in the subject declines (Rojo-Robas et al., 2020). Consequently, their low academic results lead to school failure (Al-Shannaq and Leppavirta, 2020) and early school dropout (Cuenca Carrión et al., 2021). Other findings have pointed to associations between early school dropout with a negative classroom climate (Rathmann et al., 2018) and an increase in disruptive behaviors among high school students (Lerang et al., 2019).
In the analysis differentiated by gender to find possible correlations between gender, educational level, teaching, study time, different resources used, and motivation (Figure 3), our results suggest that there are no gender differences in motivation associated with learning mathematics. Other analysis shows that in most cases, the correlations are weak and inverse (Figure 4). Furthermore, the Mann–Whitney U-test shows that there are only significant differences between males and females with respect to their perceptions of their mathematics teachers.
In comparison to our results, the scientific literature shows contradictory findings. They point out the differences in motivational perceptions regarding mathematics in young women’s choices of undergraduate studies in STEAM (Hsieh, 2019; Vinni-Laakso et al., 2019). The low participation is due to the gender roles assumed by women during adolescence (Ehrtmann and Wolter, 2018; Steegh et al., 2019), which are influenced by sociocultural factors (Melak and Singh, 2021). However, the literature demonstrates that interest in STEAM among female students is positively correlated with different resources employed, time spent studying, and career prospects (Loh et al., 2019).
To further assess the possible relationship between the variables of study, in a linear regression analysis, the profiles that correlated highly significantly with motivation are the following: (1) the student body, in general, employs different resources for study, and the highest correlations were found among students in 2° secondary school and 3° secondary school; (2) students in the 2 years of high school, in general; and (3) the highest scores were found among those who value teaching, dedicate time to study, and use different resources to learn mathematics. The low impact of the regressors in our study on motivation (<10%) suggests the existence of others of greater relevance that are affecting mathematics students in the A.C. of Melilla. Along the same lines, other findings have shown a significant effect of technologies on academic performance (Gómez-García et al., 2020a). In addition, socioeconomic status (Bardach et al., 2022; Musaddiq et al., 2022; Williams et al., 2022) and family (Stavrulaki et al., 2021) are factors that should be contemplated.
The present manuscript quantifies the optimal clusters of mathematics students, which are grouped according to their motivational profile (Figure 5). This result is very interesting as it suggests that the mathematics teacher should attend to nine training realities in the classroom from the motivational point of view. In line with the above, Mora et al. (2020) recommended using appropriate teaching strategies that awaken the interest and participation of students in STEAM. In addition, the differences in preferences associated with gender should be contemplated (INJUVE, 2020). These actions could reduce the high early school dropout rate in the A.C. of Melilla (Roca Cobo et al., 2019).
The association between the study variables and motivation has followed a similar pattern. Therefore, the results have confirmed the possibility of classifying students into nine groups according to their motivational profile. On the one hand, the regressors of teaching, study time, employment of resources for study, and educational level have shown an influence on motivation, confirming our study hypothesis H3.
Our results have also shown a significant correlation between PMT and MO, accepting the null hypothesis (H2) there is no statistically significant correlation between each pair of variables (gender and educational level and teaching indicators, study time, resources used and motivation).
Finally, our results present certain limitations associated primarily with the cross-sectional nature of this study. Furthermore, the present study focuses only on mathematics in a specific geographical area.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
The studies involving human participants were reviewed and approved by Dirección Provincial de Educación de Melilla. Written informed consent for participation was not required from the participants or their legal guardians/next of kin. Because the students were under 18 years-old, the questionnaire was previously reviewed and authorized by the local authorities of the Ministry of Education.
HoH-M performed the formal analysis and conducted the validation. HaH-M wrote the first draft of the manuscript. Both authors contributed to conception of the study, manuscript revision, read, and approved the submitted version.
We thank the Provincial Director of Education, the Principals, the Heads of Mathematics and Technology Departments of the secondary schools in A.C. of Melilla for their help in the data collection process.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abin, A., Nunez, J. C., Rodriguez, C., Cueli, M., Garcia, T., and Rosario, P. (2020). Predicting mathematics achievement in secondary education: The role of cognitive, motivational, and emotional variables. Front. Psychol. 11:876.
Al-Shannaq, M. M. M., and Leppavirta, J. (2020). Comparing math anxiety of scientific facilities students as related to achievement, and some variables. Int. J. Instr. 13, 341–352. doi: 10.29333/iji.2020.13123a
Barca, A., Peralbo, M., Porto, A., Marcos, J., and Brenlla, J. (2011). Metas académicas del alumnado de educación secundaria obligatoria (eso) y bachillerato con alto y bajo rendimiento escolar. Revista De Educ. 354, 341–368.
Bardach, L., Klassen, R. M., and Perry, N. E. (2022). Teachers’ psychological characteristics: Do they matter for teacher effectiveness, teachers’ well-being, retention, and interpersonal relations? An integrative review. Educ. Psychol. Rev. 34, 259–300. doi: 10.1007/s10648-021-09614-9
Barth, J. M., Kim, H., Eno, C. A., and Guadagno, R. E. (2018). Matching abilities to careers for others and self: Do gender stereotypes matter to students in advanced math and science classes? Sex Roles 79, 83–97. doi: 10.1007/s11199-017-0857-5
Bergold, S., Kasper, D., Wendt, H., and Steinmayr, R. (2020). Being bullied at school: The case of high-achieving boys. Soc. Psychol. Educ. 23, 315–338. doi: 10.1007/s11218-019-09539-w
Buenrostro, P., and Radinsky, J. (2019). Looking at my (real) world through mathematics: Memories and imaginaries of math and science learning. Cogn. Instr. 37, 390–407. doi: 10.1080/07370008.2019.1624546
Cheng, W. (2019). How intrinsic and extrinsic motivations function among college student samples in both Taiwan and the US. Educ. Psychol. 39, 430–447. doi: 10.1080/01443410.2018.1510116
Cipkova, E., Karolcik, S., and Scholzova, L. (2019). Are secondary school graduates prepared for the studies of natural sciences? - evaluation and analysis of the result of scientific literacy levels achieved by secondary school graduates. Res. Sci. Technol. Educ. 38, 146–167. doi: 10.1080/02635143.2019.1599846
Córdoba, L., García, V., Luengo, L., Vizuete, M., and Feu, S. (2012). How academic career and habits related to the school environment influence on academic performance in the physical education subject. Retos. Nuevas Tendencias sEduc. Física Deportey Recreat. 21, 9–13.
Cuenca Carrión, E., Jiménez Sánchez, J., Zárate Muñiz, Y., Frías del Val, A. S., Barrio de Miguel, M. A., Collado Martin, M. A., et al. (2021). Informe 2021 sobre el estado del sistema educativo. Curso 2019-2020. Madrid: Secretaría General Técnica. Centro de Publicaciones. Ministerio de Educación y Formación Profesional.
Diseth, A., Mathisen, F. K. S., and Samdal, O. (2020). A comparison of intrinsic and extrinsic motivation among lower and upper secondary school students. Educ. Psychol. 40, 961–980. doi: 10.1080/01443410.2020.1778640
Ehrtmann, L., and Wolter, I. (2018). The impact of students’ gender-role orientation on competence development in mathematics and reading in secondary school. Learn. Individ. Differ. 61, 256–264. doi: 10.1016/j.lindif.2018.01.004
Estrada-Madariaga, M. d. M. (2017). Estudio descriptivo sobre el abandono escolar temprano e influjo de variables personales y socio-culturales en la Ciudad Autónoma de Melilla.Tesis (Doctoral). Granada: Universidad de Granada.
Gamazo, A., and Martínez-Abad, F. (2020). An exploration of factors linked to academic performance in PISA 2018 through data mining techniques. Front. Psychol. 11:575167. doi: 10.3389/fpsyg.2020.575167
Garrido-Yserte, R., Crecente-Romero, F., and Gallo-Rivera, M.-T. (2019). The relationship between capacities and entrepreneurial intention in secondary school students. Econ. Res. 33, 2322–2341. doi: 10.1080/1331677x.2019.1697328
Gil, A. J., Antelm-Lanzat, A. M., Cacheiro-González, M. L., and Pérez-Navio, E. (2019). School dropout factors: A teacher and school manager perspective. Educ. Stud. 45, 756–770. doi: 10.1080/03055698.2018.1516632
Gillison, F. B., Rouse, P., Standage, M., Sebire, S. J., and Ryan, R. M. (2019). A meta-analysis of techniques to promote motivation for health behaviour change from a self-determination theory perspective. Health Psychol. Rev. 13, 110–130. doi: 10.1080/17437199.2018.1534071
Goellner, R., Wagner, W., Eccles, J. S., and Trautwein, U. (2018). Students’ idiosyncratic perceptions of teaching quality in mathematics: A result of rater tendency alone or an expression of dyadic effects between students and teachers? J. Educ. Psychol. 110, 709–725. doi: 10.1037/edu0000236
Gómez-García, M., Hossein-Mohand, H., Trujillo-Torres, J. M., and Hossein-Mohand, H. (2020a). The Training and Use of ICT in teaching perceptions of melilla’s (Spain) mathematics teachers. Mathematics 8:1641. doi: 10.3390/math8101641
Gómez-García, M., Hossein-Mohand, H., Trujillo-Torres, J. M., Hossein-Mohand, H., and Aznar-Díaz, I. (2020b). Technological factors that influence the mathematics performance of secondary school students. Mathematics 8:1935. doi: 10.3390/math8111935
Hagger, M. S., and Hamilton, K. (2018). Motivational predictors of students’ participation in out-of-school learning activities and academic attainment in science: An application of the trans-contextual model using Bayesian path analysis. Learn. Individ. Differ. 67, 232–244. doi: 10.1016/j.lindif.2018.09.002
Hagger, M. S., and Hamilton, K. (2019). Grit and self-discipline as predictors of effort and academic attainment. Br. J. Educ. Psychol. 89, 324–342. doi: 10.1111/bjep.12241
Hidi, S. E., Renninger, K. A., Renninger, K. A., and Hidi, S. E. (2019). Motivation and its relation to learning introduction. Cambridge: Cambridge University Press.
Hine, G. (2018). Teachers’ perceptions on declining student enrolments in Australian senior secondary mathematics courses. Issues Educ. Res. 28, 635–654.
Hodis, F. A. (2018). Underpinnings of expectancies of success in mathematics: An analysis of general, school-related, and domain-specific motivation antecedents. J. Educ. Psychol. 110, 407–430. doi: 10.1037/edu0000218
Holzberger, D., Praetorius, A.-K., Seidel, T., and Kunter, M. (2019). Identifying effective teachers: The relation between teaching profiles and students’ development in achievement and enjoyment. Eur. J. Psychol. Educ. 34, 801–823. doi: 10.1007/s10212-018-00410-8
Hossein-Mohand, H., Gómez-García, M., Trujillo-Torres, J.-M., Hossein-Mohand, H., and Boumadan-Hamed, M. (2021a). Uses and Resources of Technologies by Mathematics Students Prior to COVID-19. Sustainability 13:1630. doi: 10.3390/su13041630
Hossein-Mohand, H., Trujillo-Torres, J.-M., Gómez-García, M., Hossein-Mohand, H., and Campos-Soto, A. (2021b). Analysis of the Use and integration of the flipped learning model, project-based learning, and gamification methodologies by secondary school mathematics teachers. Sustainability 13:2606. doi: 10.3390/su13052606
Hsieh, T.-L. (2019). Gender differences in high-school learning experiences, motivation, self-efficacy, and career aspirations among Taiwanese STEM college students. Int. J. Sci. Educ. 41, 1870–1884. doi: 10.1080/09500693.2019.1645963
Husein, N. A., Rahman, N. F. A., Phang, F. A., Abu Bakar, A. H., Ahmad, R. R., Kasim, N., et al. (2018). The Relationship Between Mentoring in Students’. Perception Towards STEM Education. Adv. Sci. Lett. 24, 72–73. doi: 10.1166/asl.2018.11923
Keller, T., and Takacs, K. (2019). Peers that count: The influence of deskmates on test scores. Res. Soc. Stratif. Mobil. 62:100408. doi: 10.1016/j.rssm.2019.05.003
Kim, H.-K. (2020). Meta analysis on the improvement of academic performance by the teaching method for underachievers of learning mathematics. Math. Educ. 59, 31–45.
Klapproth, F., and Fischer, B. D. (2019). Preservice teachers’ evaluations of students’ achievement development in the context of school-track recommendations. Eur. J. Psychol. Educ. 34, 825–846. doi: 10.1007/s10212-018-0405-x
Laninga-Wijnen, L., Gremmen, M. C., Dijkstra, J. K., Veenstra, R., Vollebergh, W. A. M., and Harakeh, Z. (2019). The role of academic status norms in friendship selection and influence processes related to academic achievement. Dev. Psychol. 55, 337–350. doi: 10.1037/dev0000611
Lazarides, R., Gaspard, H., and Dicke, A.-L. (2019). Dynamics of classroom motivation: Teacher enthusiasm and the development of math interest and teacher support. Learn. Instr. 60, 126–137. doi: 10.1016/j.learninstruc.2018.01.012
Lerang, M. S., Ertesvag, S. K., and Havik, T. (2019). Perceived classroom interaction, goal orientation and their association with social and academic learning outcomes. Scandinavian. J. Educ. Res. 63, 913–934. doi: 10.1080/00313831.2018.1466358
Levrini, O., Tasquier, G., Branchetti, L., and Barelli, E. (2019). Developing future-scaffolding skills through science education. Int. J. Sci. Educ. 41, 2647–2674. doi: 10.1080/09500693.2019.1693080
Lim, S. A. (2021). The longitudinal relationship between academic motivation and engagement: A self-determination theory perspective [자기결정성이론에 근거한 학습동기와 수업참여의 종단적 관계]. Korean J. Educ. Res. 59, 163–184.
Liu, Y., Hau, K.-T., and Zheng, X. (2020a). Does instrumental motivation help students with low intrinsic motivation? Comparison between Western and confucian students. Int. J. Psychol. 55, 182–191. doi: 10.1002/ijop.12563
Liu, Y., Hau, K.-T., Liu, H., Wu, J., Wang, X., and Zheng, X. (2020b). Multiplicative effect of intrinsic and extrinsic motivation on academic performance: A longitudinal study of Chinese students. J. Pers. 88, 584–595. doi: 10.1111/jopy.12512
Loh, C. E., Sun, B., and Majid, S. (2019). Do girls read differently from boys? Adolescents and their gendered reading habits and preferences. Eng. Educ. 54, 174–190. doi: 10.1080/04250494.2019.1610328
Martin, A. J., Burns, E. C., Collie, R. J., Cutmore, M., MacLeod, S., and Donlevy, V. (2022). The role of engagement in immigrant students’ academic resilience. Learn. Instr. 82:101650. doi: 10.1016/j.learninstruc.2022.101650
Martínez-Abad, F., Gamazo, A., and Rodríguez-Conde, M.-J. (2020). Educational data mining: Identification of factors associated with school effectiveness in PISA assessment. Stud. Educ. Eval. 66:100875. doi: 10.3389/fpsyg.2019.02583
Melak, A., and Singh, S. (2021). Women’s participation and factors affecting their academic performance in engineering and technology education: A study of Ethiopia. Sustainability 13:2246. doi: 10.3390/su13042246
Mercader Rubio, I., Oropesa Ruiz, N. F., Gutierrez Angel, N., and Fernandez Martinez, M. M. (2022). Motivational profile, future expectations, and attitudes toward study of secondary school students in Spain: Results of the PISA report 2018. Int. J. Environ. Res. Public Health 19:3864. doi: 10.3390/ijerph19073864
Mora, H., Signes-Pont, M. T., Fuster-Guillo, A., and Pertegal-Felices, M. L. (2020). A collaborative working model for enhancing the learning process of science & engineering students. Comput. Hum. Behav. 103, 140–150. doi: 10.1016/j.chb.2019.09.008
Munter, C., and Haines, C. (2019). Mathematics teachers’ enactment of cognitively demanding tasks and students’ perception of racial differences in opportunity. Math. Think. Learn. 21, 155–177. doi: 10.1080/10986065.2019.1576002
Musaddiq, M. H., Sarfraz, M. S., Shafi, N., Maqsood, R., Azam, A., and Ahmad, M. (2022). Predicting the impact of academic key factors and spatial behaviors on students’ performance. Appl. Sci. Basel 12:10112. doi: 10.3390/app121910112
Neuendorf, C., Jansen, M., Kuhl, P., and Vock, M. (2022). Who is a high achiever? Operationalisation of high achievement in empirical educational research since the year 2000. Z. Padagogische Psychol. 19, 1–19. doi: 10.1024/1010-0652/a000343
Ozdemir, S. B., and Ozdemir, M. (2019). How do adolescents’ perceptions of relationships with teachers change during upper-secondary school years? J. Youth Adolesc. 49, 921–935. doi: 10.1007/s10964-019-01155-3
Ozhan, S. C., and Kocadere, S. A. (2020). The effects of flow, emotional engagement, and motivation on success in a gamified online learning environment. J. Educ. Comput. Res. 57, 2006–2031. doi: 10.1177/0735633118823159
Perdereau-Noel, M., Saliou, P., and Vic, P. (2017). Prevalence of teenage sleeping disorders. Arch. Pediatrie 24, 336–345. doi: 10.1016/j.arcped.2017.01.009
Prieto, J. M. A. (2020). A systematic review about gum cation, motivation and learning in high school. Teoria De La Educ. 32, 73–99. doi: 10.14201/teri.20625
Quijada, A., Ruiz, M. A., Huertas, J. A., and Alonso-Tapia, J. (2020). Development and validation of the School Climate Questionnaire for Secondary and High School Teachers (SCQ- SHST). Anales De Psicol. 36, 155–165. doi: 10.6018/analesps.341001
Rathmann, K., Herke, M., Hurrelmann, K., and Richter, M. (2018). Class climate, academic well-being and self-rated health among school children in germany: Findings of the national educational panel study (NEPS). Gesundheitswesen 80, 334–343. doi: 10.1055/s-0043-121886
Reihenova, A. (2018). “Secondary school students’ types of thinking in learning mathematics,” in Society, integration, education, eds V. Lubkina, S. Usca, and A. Zvaigzne (Latvia: School Pedagogy Preschool Pedagogy), 405–417. doi: 10.17770/sie2018vol1.3427
Rican, J., Chytry, V., and Medova, J. (2022). Aspects of self-regulated learning and their influence on the mathematics achievement of fifth graders in the context of four different proclaimed curricula. Front. Psychol. 13:963151. doi: 10.3389/fpsyg.2022.963151
Roca Cobo, E., Zárate Muñiz, Y. S., Frías del VaI, A., Barrio de Miguel, M. Á, Collado Martín, M. A., and González Albo Arévalo, R. (2019). Informe 2019 sobre el estado del sistema educativo. Curso 2017_2018. Available online at: https://www.educacionyfp.gob.es/eu/mc/cee/publicaciones/informes-del-sistema-educativo/informe-2019.html
Rojo-Robas, V., Madariaga, J. M., and Domingo-Villarroel, J. (2020). Secondary education students’ beliefs about mathematics and their repercussions on motivation. Mathematics 8:368. doi: 10.3390/math8030368
Roorda, D. L., Jorgensen, T. D., and Koomen, H. M. Y. (2019). Different teachers, different relationships? Student-teacher relationships and engagement in secondary education. Learn. Individ. Dif. 75:101761. doi: 10.1016/j.lindif.2019.101761
Rosenbluth, A., Cruzat-Mandich, C., and Ugarte, M. L. (2016). Methodology to Validate a Competencies Assessment Tool for Psychology Students. Univ. Psychol. 15, 303–314.
Sagone, E., De Caroli, M. E., Falanga, R., and Indiana, M. L. (2020). Resilience and perceived self-efficacy in life skills from early to late adolescence. Int. J. Adolesc. Youth 25, 882–890. doi: 10.1080/02673843.2020.1771599
Sánchez-Matamoros, G., Fernández, C., and Llinares, S. (2019). Relationships among prospective secondary mathematics teachers’ skills of attending, interpreting and responding to students’ understanding. Educ. Stud. Math. 100, 83–99. doi: 10.1007/s10649-018-9855-y
Sheldon, K. M., and Prentice, M. (2019). Self-determination theory as a foundation for personality researchers. J. Pers. 87, 5–14. doi: 10.1111/jopy.12360
Siebecke, D. E., and Jarl, M. (2022). Does the material well-being at schools successfully compensate for socioeconomic disadvantages? Analysis of resilient schools in Sweden. Large Scale Assess. Educ. 10:11. doi: 10.1186/s40536-022-00130-y
Smith, J., Nadeau, M. F., Archambault, I., Guimond, F. A., St-Amand, J., Fitzpatrick, C., et al. (2022). Linking high school students’ achievement goal orientations with their competence beliefs and their perception of teachers’ emotional support during the COVID-19 pandemic. Front. Educ. 7:762766. doi: 10.3389/feduc.2022.762766
Stavrulaki, E., Li, M., and Gupta, J. (2021). Perceived parenting styles, academic achievement, and life satisfaction of college students: The mediating role of motivation orientation. Eur. J. Psychol. Educ. 36, 693–717. doi: 10.1007/s10212-020-00493-2
Steegh, A. M., Hoeffler, T. N., Keller, M. M., and Parchmann, I. (2019). Gender differences in mathematics and science competitions: A systematic review. J. Res. Sci. Teach. 56, 1431–1460. doi: 10.1002/tea.21580
Tan, M. D. (2022). School socioeconomic desegregation and student academic performance: Evidence from a longitudinal study on middle school students in China. Soc. Psychol. Educ. 25, 1135–1155. doi: 10.1007/s11218-022-09710-w
Tereshchenko, A., Francis, B., Archer, L., Hodgen, J., Mazenod, A., Taylor, B., et al. (2019). Learners’ attitudes to mixed-attainment grouping: Examining the views of students of high, middle and low attainment. Res. Pap. Educ. 34, 425–444. doi: 10.1080/02671522.2018.1452962
Timmermans, A. C., and Rubie-Davies, C. M. (2018). Do teachers differ in the level of expectations or in the extent to which they differentiate in expectations? Relations between teacher -level expectations, teacher background and beliefs, and subsequent student performance. Educ. Res. Eval. 24, 241–263. doi: 10.1080/13803611.2018.1550837
Trujillo-Torres, J.-M., Hossein-Mohand, H., Gómez-García, M., Hossein-Mohand, H., and Cáceres-Reche, M.-P. (2020a). Mathematics teachers’ perceptions of the introduction of ICT: The relationship between motivation and use in the teaching function. Mathematics 8:2158.
Trujillo-Torres, J.-M., Hossein-Mohand, H., Gómez-García, M., Hossein-Mohand, H., and Hinojo-Lucena, F.-J. (2020b). Estimating the academic performance of secondary education mathematics students: A gain lift predictive model. Mathematics 8:2101. doi: 10.3390/math8122101
Tsang, A., Dang, B. Y. Y., and Moorhouse, B. L. (2022). An examination of learners’ homework engagement, academic achievement, and perceptions. Educ. Stud. 1–15.
Uner, S., and Akkus, H. (2019). Secondary students’ perceptions of their teachers’ pedagogical content knowledge: A scale development study. Teach. Dev. 23, 566–587. doi: 10.1080/13664530.2019.1674685
Van-Kleij, F. M. (2019). Comparison of teacher and student perceptions of formative assessment feedback practices and association with individual student characteristics. Teach. Teach. Educ. 85, 175–189. doi: 10.1186/s12913-016-1423-5
Vergara, D., Fernández, M. L., and Lorenzo, M. (2019). Enhancing student motivation in secondary school mathematics courses: A methodological approach. Educ. Sci. 9:83. doi: 10.3390/educsci9020083
Vinni-Laakso, J., Guo, J., Juuti, K., Loukomies, A., Lavonen, J., and Salmela-Aro, K. (2019). The relations of science task values, self-concept of ability, and STEM aspirations among finnish students from first to second grade. Front. Psychol. 10:1449. doi: 10.3389/fpsyg.2019.01449
Warwick, P., Vrikki, M., Karlsen, A. M. F., Dudley, P., and Vermunt, J. D. (2019). The role of pupil voice as a trigger for teacher learning in Lesson Study professional groups. Cambridge J. Educ. 49, 435–455. doi: 10.1080/0305764x.2018.1556606
Williams, M. E., Clarkson, S., Hastings, R. P., Watkins, R. C., McTague, P., and Hughes, J. C. (2022). Factors from middle childhood that predict academic attainment at 15-17 Years in the UK: A systematic review. Front. Educ. 7:849765. doi: 10.3389/feduc.2022.849765
Keywords: secondary education, academic performance, learning, motivation, mathematics
Citation: Hossein-Mohand H and Hossein-Mohand H (2023) Influence of motivation on the perception of mathematics by secondary school students. Front. Psychol. 13:1111600. doi: 10.3389/fpsyg.2022.1111600
Received: 29 November 2022; Accepted: 20 December 2022;
Published: 19 January 2023.
Edited by:
Belen Garcia-Manrubia, University of Murcia, SpainReviewed by:
Milagros Elena Rodriguez, Universidad de Oriente, VenezuelaCopyright © 2023 Hossein-Mohand and Hossein-Mohand. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hossein Hossein-Mohand,  aG9zc2Vpbi5oLm1AdWdyLmVz
aG9zc2Vpbi5oLm1AdWdyLmVz
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.