- 1Boston College, Chestnut Hill, MA, United States
- 2Department of Psychology, Utah State University, Logan, UT, United States
Prominent theories suggest that time and number are processed by a single neural locus or a common magnitude system (e.g., Meck and Church, 1983; Walsh, 2003). However, a growing body of literature has identified numerous inconsistencies between temporal and numerical processing, casting doubt on the presence of such a singular system. Findings of distinct temporal and numerical biases in the presence of emotional content (Baker et al., 2013; Young and Cordes, 2013) are particularly relevant to this debate. Specifically, emotional stimuli lead to temporal overestimation, yet identical stimuli result in numerical underestimation. In the current study, we tested adults’ temporal and numerical processing under cognitive load, a task that compromises attention. Under the premise of a common magnitude system, one would predict cognitive load to have an identical impact on temporal and numerical judgments. Inconsistent with the common magnitude account, results revealed baseline performance on the temporal and numerical task was not correlated and importantly, cognitive load resulted in distinct and opposing quantity biases: numerical underestimation and marginal temporal overestimation. Together, our data call into question the common magnitude account, while also providing support for the role of attentional processes involved in numerical underestimation.
Introduction
Throughout our daily lives, we constantly track temporal and numerical information. However, this process is never void of context; in fact, it is often coupled with distractions. We often calculate a tip at a restaurant while simultaneously talking to our friends or estimate how long it will take us to drive home while listening to a child crying in the backseat. Although research has most frequently tested quantity processing in controlled laboratory settings, recent work has revealed quantity processing biases in the presence of external stimuli. For example, these studies have revealed durations to be overestimated and numerosities to be underestimated in the presence of emotional content, namely angry faces (see Gil et al., 2007; Baker et al., 2013; Young and Cordes, 2013). These findings have led many researchers to re-think prominent theories of quantity processing, while also unveiling questions regarding the cognitive mechanism(s) involved in quantity processes. In the current study, we investigated adults’ temporal and numerical processing under cognitive load – an attention-distracting working memory task. This manipulation not only mimics real-world quantity processing, but allows us to directly test theories of quantity processing.
Evidence from behavioral, neural, and clinical data reveal many striking parallels in numerical and temporal processing (Dormal et al., 2006; Feigenson, 2007; Provasi et al., 2011; Dormal and Pesenti, 2012, 2013; Vicario et al., 2013). For example, behavioral data indicate that the ease of numerical and temporal judgments relies on Weber’s Law (Stevens, 1957). That is, it is easier to discriminate between two numerosities or durations when they differ by a larger ratio. Other behavioral work shows that rats and infants are able to generalize a rule learned in a numerical domain to a temporal domain and vice versa (Meck and Church, 1983; de Hevia et al., 2012). Neuroimaging and clinical work also reveals similarities between numerical and temporal processing. For instance, adults’ intraparietal sulcus (IPS) is activated while processing both numerical and temporal stimuli (Dormal et al., 2012; Skagerlund et al., 2016). Relatedly, Hayashi et al. (2013); Experiment (1) show comparable activations in the intraparietal cortex and inferior frontal gyrus during temporal and numerical discrimination tasks. Moreover, many individuals’ suffering from clinical disorders, such as Turner Syndrome, also experience comorbid quantity processing deficits (e.g., Vicario et al., 2013), further emphasizing commonalities in quantity processing. These findings have led researchers to propose that a single neural locus, or a common magnitude system, is responsible for processing both time and number (Meck and Church, 1983; Walsh, 2003; Cantlon et al., 2009).
Despite reports of numerous similarities in numerical and temporal processing, researchers have also identified many striking inconsistencies in processing these two types of quantity (e.g., Baker et al., 2013; Young and Cordes, 2013; Odic, 2017). Although number and time follow comparable developmental trajectories in infancy, different developmental trajectories occur in childhood (Odic, 2017). While some work has suggested that the IPS is activated during both temporal (e.g., Schubotz et al., 2000; Rao et al., 2001) and numerical (e.g., Cantlon et al., 2006; Piazza et al., 2007; Ashkenazi et al., 2008) tasks, the overall consensus is that the IPS is implicated in numerical, but not temporal, processing (Rammsayer and Classen, 1997; Nenadic et al., 2003; Mattel and Meck, 2004; Koch et al., 2009). Research revealing unique numerical and temporal biases when making quantity judgments in the presence of emotional content has been particularly damaging to the common magnitude account. In these studies, participants passively view a happy, angry, or neutrally valenced face immediately before making a numerical or temporal judgment. Results show that both children and adults consistently underestimate numerosity in the presence of both negatively and positively valenced stimuli (both happy and angry faces). In contrast, durations are overestimated in the presence of negatively valenced stimuli1 (angry faces; Gil et al., 2007; Baker et al., 2013; Young and Cordes, 2013). That is, the exact same emotional stimuli differentially bias numerical and temporal processing, challenging claims of a common magnitude system. In the current study, we investigate the effect of cognitive load on temporal and numerical judgments. While comparable temporal and numerical biases would provide evidence in favor of a common magnitude system, unique temporal and numerical biases under cognitive load would call this account into question.
Distinct biases in the presence of emotional content have not only challenged claims of a common magnitude system, but also led researchers to speculate about the cognitive mechanism(s) underlying numerical and temporal processing. Because distinct patterns of estimation occur in the presence of emotional faces – only angry faces lead to temporal overestimation, but both angry and happy faces lead to numerical underestimation – some have explained these results by the differential effects of arousal and attention on quantitative processing (Young and Cordes, 2013). While previous work has tested the effects of altered attention or heightened arousal on temporal and numerical judgments separately (e.g., Thomas and Brown, 1974; Rammsayer and Lima, 1991; Brown and Stubbs, 1992; Macar et al., 1994; Brown, 1997, 2008; Casini and Macar, 1997; Fortin and Rousseau, 1998; Zakay, 1998; Khan et al., 2006; Wearden et al., 2007; Block and Zakay, 2008; Ortega and Lopez, 2008; see Block et al., 2010; Hamamouche et al., 2017), these studies have rarely investigated these manipulations on temporal and numerical processing in the same individuals using the same task. Moreover, attention and arousal are closely related constructs, and are inevitably involved in both temporal and numerical estimation. Thus, in the current study, we aimed to solely manipulate attention – defined as “the appropriate allocation of processing resources to relevant stimuli” (Coull, 1998, p. 344) – by introducing cognitive load during temporal and numerical processing in the same individuals. Using this manipulation, we will be able to (1) assess the impact of attention manipulations on temporal and numerical processing, and (2) determine whether comparable biases occur in the presence of an attention distracting task.
The Current Study
In the current study, adults made temporal and numerical judgments under cognitive load – a distracting, working memory task – in order to assess the likelihood of the common magnitude system. Under the premise of a common magnitude system, one would predict altered attention from the cognitive load manipulation to identically impact numerical and temporal judgments. However, if numerical and temporal processing are dictated by distinct cognitive systems, temporal and numerical biases under cognitive load may not track together.
Materials and Methods
Participants
Eighty Boston College undergraduates participated in this study for course credit or cash compensation (58 females, Mage = 19.15 years). After exclusions (see criteria below), there were 71 participants with complete data.
Experimental Design and Procedure
Participants completed both a numerical and a temporal bisection task. Within each task, there were two blocks: a baseline block and a cognitive load block. The order of the tasks (numerical vs. temporal) and the order of the blocks within each task (baseline vs. cognitive load) were counterbalanced. However, the order remained consistent within each participant – if the participant completed the cognitive load trials first in the temporal bisection task, s/he would also complete the cognitive load trials first in the numerical bisection task.
In the numerical bisection task, participants were first familiarized to a small (15 dots) and a large (60 dots) standard value (modeled after Lewis et al., 2017). Each display was shown twice and labeled both on the screen and by the experimenter with the appropriate size (i.e., small or large). To confirm that participants knew the standard values before beginning the test trials, participants first completed four standard practice trials in which they had to classify the dot arrays containing the standard values as either small or large (by pressing a button on the keyboard). Participants received feedback on each of the four standard practice trials. No other feedback was provided during the experiment.
In the baseline block of the numerical task, participants then completed additional practice trials in which they were presented with arrays containing intermediate numerosities (19, 24, 30, 38, 48) in addition to the standard values and were asked to indicate whether the numerosity of the display was more similar to the small or large standard. Each numerosity (standard values and intermediate values) was shown once in a randomized order, resulting in seven baseline practice trials. Participants completed these baseline practice trials to familiarize them to the demands of the task. After completing the practice trials, participants then completed the baseline test trials, during which each of the seven numerosities were presented 12 times each in a random order, resulting in a total of 84 test trials. Dot arrays were presented for 750 ms. For each numerosity, there were twelve different configurations of dots. Within each array, the size of all dots was held constant; however, dot sizes varied across arrays. Half of the arrays controlled for cumulative surface area, such that regardless of the numerosity, the cumulative area of the array was held constant (approximately 133.6 cm2). Thus, individual dots were smaller as the number of dots in the array increased. The other half of the dot arrays controlled for dot size such that each dot, regardless of the numerosity of the array, had an area of 4.01 cm2. Thus, dot arrays with fewer dots also had a smaller cumulative surface area (cumulative areas ranged from 59.9 to 239.99 cm2).
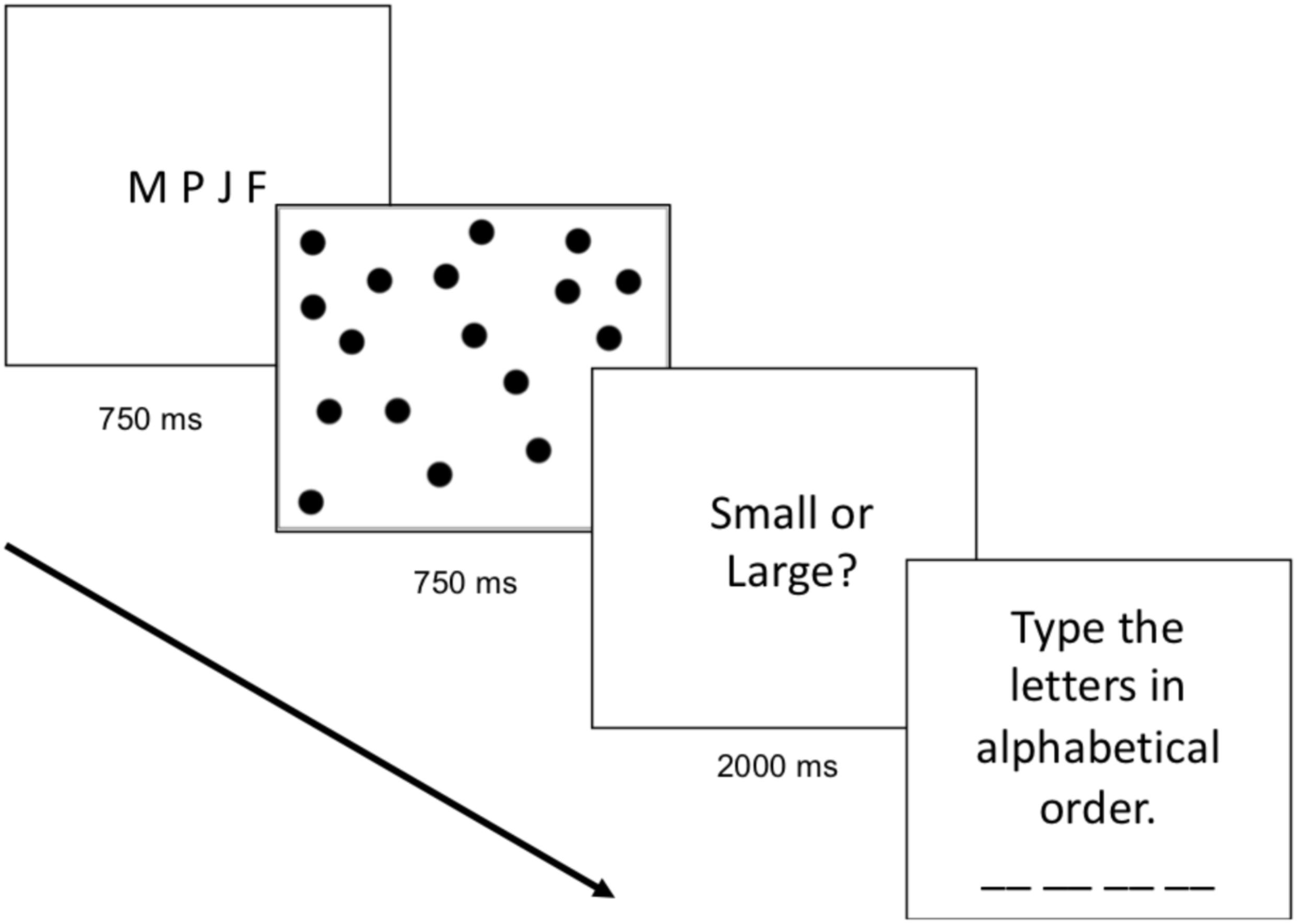
The cognitive load block was identical to the baseline block except that participants were required to remember and alphabetize four letters while simultaneously completing the numerical task. On every trial, participants saw four letters on the screen (e.g., M K F J) for 750 ms and were told to remember and alphabetize the letters. Participants were then presented with the dot array. After making their numerical judgment (whether the array was more similar to small or large standard), participants were shown a text box in which they were instructed to type the four letters in alphabetical order (e.g., F J K M). The participants first completed seven practice trials (one with each numerosity), and then completed 84 test trials (12 displays of each numerosity). During test, participants were only asked to type the letters alphabetically on a random two-thirds of the trials; however, participants did not know when they would be required to type the letters in alphabetical order, thus they were required to perform the working memory task on every trial in anticipation of receiving the prompt. The progression of the cognitive load trials can be found in Figure 1.
The temporal bisection task was identical to the numerical bisection, except participants saw a blue oval in the center of the screen for a specified duration instead of a dot array. Participants were familiarized to two standard durations, a short standard (400 ms) and a long duration (1600 ms; modeled after Young and Cordes, 2013). Again, participants began with four standard practice trials during which they classified the two standard durations and received trial-by-trial feedback. Participants then completed seven additional practice trials with each standard value and the intermediate durations (504, 635, 800, 1008, and 1270 ms) intermixed, during which they were instructed to decide whether the oval’s duration was more similar to the short standard or the long standard. Then during the baseline block, participants completed 84 test trials (7 durations × 12 presentations = 84 test trials). The cognitive load block was identical – participants were again shown four letters prior to every temporal stimulus and were asked to remember and alphabetize them during the temporal task as described above.
Data Coding
Exclusion Criteria
Five participants only completed one of the two bisection tasks (numerical or temporal) and an additional three participants only completed one trial type (baseline or cognitive load). Thus, performance on the task or block that was not completed was coded as missing data.
Data from participants who performed poorly on test trials involving the standard values (<75% accuracy on the standard values combined) were excluded (Number: NBaseline = 1, NCognitiveLoad = 2; Time: NBaseline = 1; NCognitiveLoad = 2).
Cognitive load
To assess participants’ accuracy on the cognitive load task, we calculated the percentage of trials during which each participant correctly alphabetized the letters for the numerical and temporal bisection separately. Participants who typed in the letters without alphabetizing them were removed from the cognitive load analyses (NNumber = 2, NTime = 5).
Bisection task dependent measures
Two dependent measures were taken from the bisection task:
(1) Relative Point of Subjective Equality (PSE). The PSE corresponds to the value at which 50% of the responses were classified as “large” (or “long”). First, the proportion of responses during which the participant judged the numerosities (or durations) as being closer to the large (long) standard was plotted as a function of the stimulus numerosity (or duration) and these data were fit with a Cumulative Gaussian function (as per Çoşkun et al., 2015). These curves were then used to determine each participant’s PSE, or the value at which 50% of responses were “large” (or “long”). PSEs were calculated separately for each bisection task (numerical and temporal) and block type (baseline and cognitive load). It should be noted that a higher PSE is indicative of a leftward shift in the curve, indicative of a lower likelihood of the participant judging the value as similar to the long/large standard; i.e., it is indicative of underestimation. PSE values that were three standard deviations above or below the mean were replaced with the next highest/lowest value within that range (Time: NBaseline = 1, NCognitiveLoad = 1). Because PSE varies based on the range of values for each task (15–60 for number and 400–1600 for time), we calculated a Relative PSE for each task and trial block separately. The Relative PSE was calculated by dividing each participant’s PSE by the geometric mean of the standard values (30 for the numerical task and 800 for the temporal task), thus allowing for direct comparisons between temporal and numerical performance.
(2) Relative Difference Limen (DL). The DL is a measure of the participant’s consistency in responding and corresponds to the value halfway between the set sizes corresponding to a 75% probability of a large/long response and a 25% probability of a large/long response. Outliers were replaced with the next largest/smallest value within the range (Time: NBaseline = 1, NCognitiveLoad = 1; Number: NBaseline = 1). Again, we calculated the Relative DL by dividing each participants’ DL by the geometric mean of the standard values.
Results
First, we confirmed that the order in which participants completed the bisection task (numerical versus temporal first) and/or the block order (baseline trials versus cognitive load trials first) did not interact with our variables of interest (Relative PSE, Relative DL). Neither the order in which participants completed the bisection tasks (numerical versus temporal first) nor the order of the blocks (baseline vs. cognitive load) interacted with our variables of interest (p’s > 0.05); thus, we collapsed data across these variables in the subsequent analyses.
The Relation Between Time and Number
The common magnitude account would predict a correlation between baseline performance on the numerical and temporal bisection. However, performance on the baseline numerical and temporal tasks was not correlated (Relative PSE: r = 0.090, p = 0.445, Relative DL: r = 0.132, p = 0.263).
Cognitive Load Performance
Next, we tested whether cognitive load accuracy (i.e., correctly alphabetizing the four letters) differed as a function of the task (numerical versus temporal bisection). This was done to ensure that cognitive load affected participants in each task approximately equally. A paired samples t-test revealed no significant difference in cognitive load accuracy across the two tasks, t(72) = 0.723, p = 0.472 (Temporal Task: M = 0.70, SE = 0.02; Numerical Task: M = 0.69, SE = 0.02).
Effect of Cognitive Load on Temporal and Numerical Judgments
Relative PSE
In order to directly compare biases on the numerical and temporal task, we conducted a 2 (Task: numerical vs. temporal bisection) × 2 (Block: baseline versus cognitive load) repeated measures ANOVA on the Relative PSE. There was a significant Task × Block interaction, F(1, 71) = 22.063, p < 0.001, = 0.237 (See Figure 2). No other main effects reached significance, p’s > 0.2. To follow up on the Task × Block interaction, we next conducted paired samples t-tests comparing the baseline and cognitive load trials within the numerical and temporal task separately. Cognitive load trials (M = 1.13, SE = 0.02) were significantly underestimated compared to baseline trials (M = 1.04, SE = 0.02) in the numerical bisection, t(75) = -4.634, p < 0.001, See Figures 3A, 4A whereas cognitive load trials (M = 1.05, SE = 0.02) were marginally overestimated compared to baseline trials (M = 1.10, SE = 0.02) in the temporal bisection, t(75) = 1.890, p = 0.063, See Figures 3B, 4B providing support for the role of attention in numerical processing by indicating numerical underestimation under cognitive load. Lastly, we conducted additional paired samples t-tests to compare numerical and temporal processing in each block separately. Performance at baseline was comparable on the numerical and temporal task during the baseline trials t(73) = -1.990, p = 0.05. However, under cognitive load performance, the relative PSE on the numerical task was significantly greater than the temporal, t(71) = 2.743, p = 0.008, emphasizing the unique effect of cognitive load on the two bisection tasks.
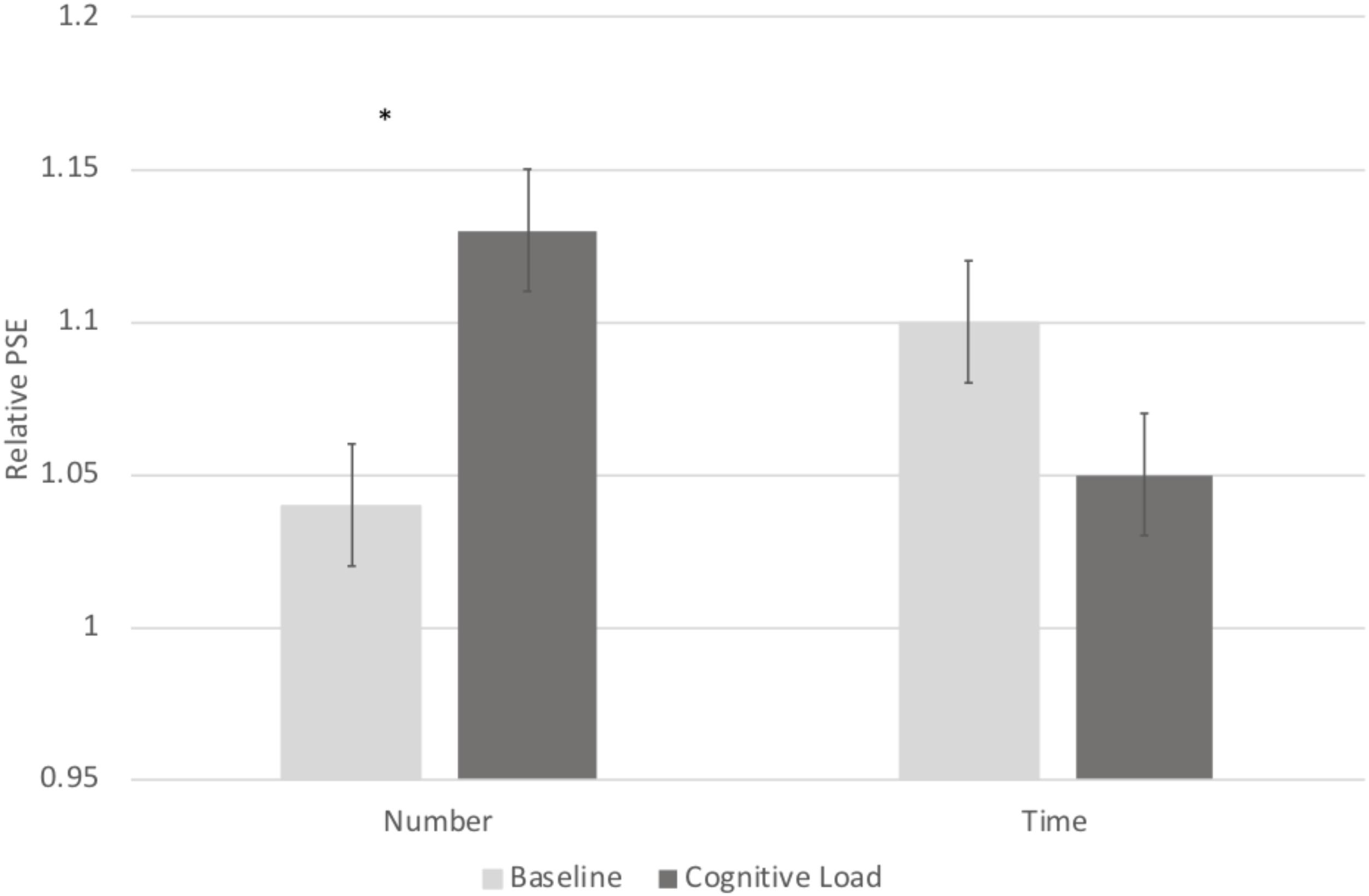
FIGURE 2. A significant Block × Trial Type interaction revealed differential effects of cognitive load on temporal and numerical judgments.
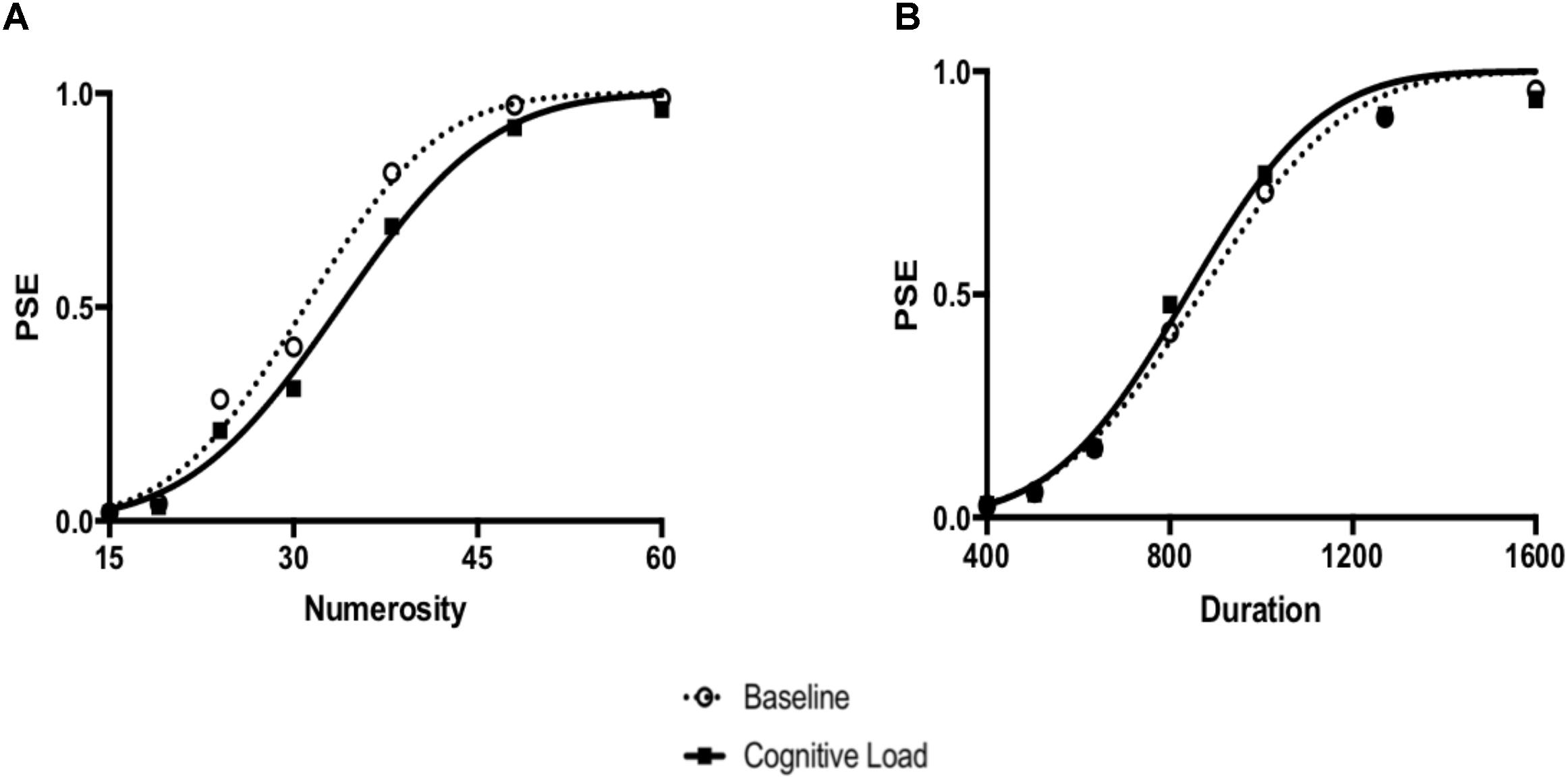
FIGURE 3. (A) Numerical bisection data and the best fitting Cumulative Gaussian functions using the group average. (B) Temporal bisection data and best fitting Cumulative Gaussian functions using the group average.
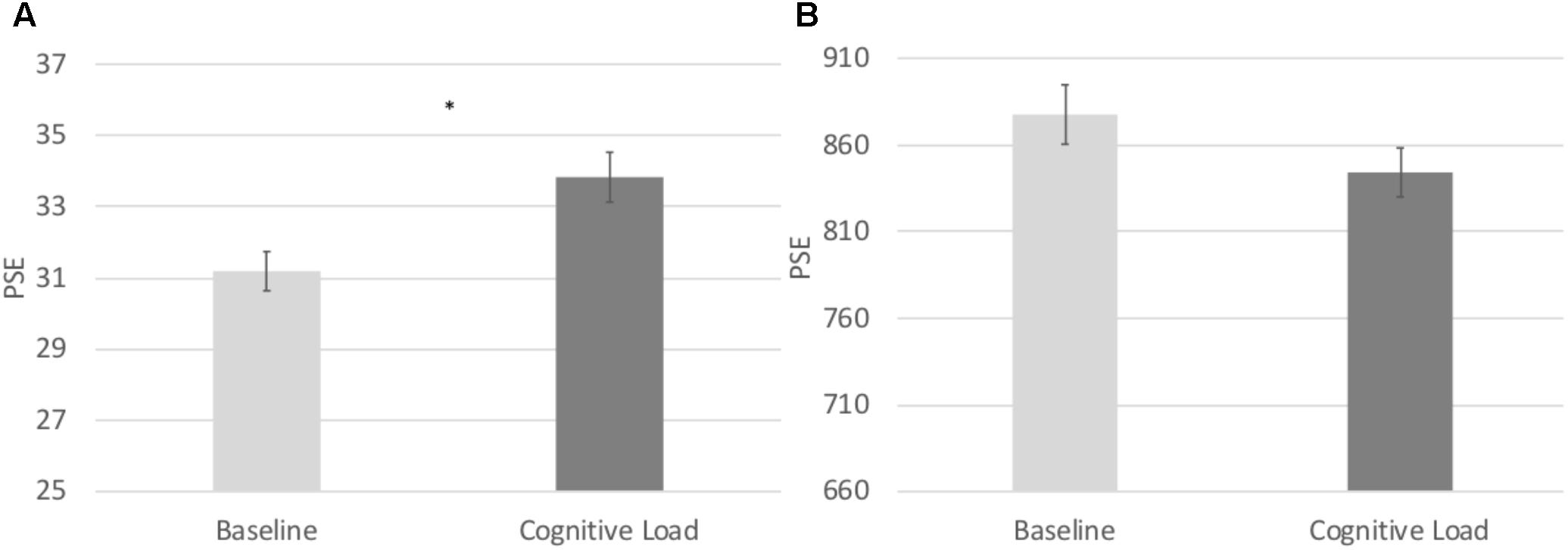
FIGURE 4. (A) Point of subjective equality estimates from the Numerical Bisection Task. (B) Point of subjective equality estimates from the Temporal Bisection Task.
Relative DL
In order to test the effects of cognitive load on the consistency of participants’ responding, we conducted identical repeated measures ANOVA on the Relative DL in both the numerical and temporal tasks. There was a main effect of task, F(1, 71) = 4.841, p = 0.031, = 0.064, such that the Relative DL on the numerical task (M = 0.147, SE = 0.006) was significantly lower to that of the temporal task (M = 0.165, SE = 0.007), indicative of more consistent responding in the numerical task across both Blocks. No other main effects or interactions reached significance, p’s > 0.8 (see Figure 5).
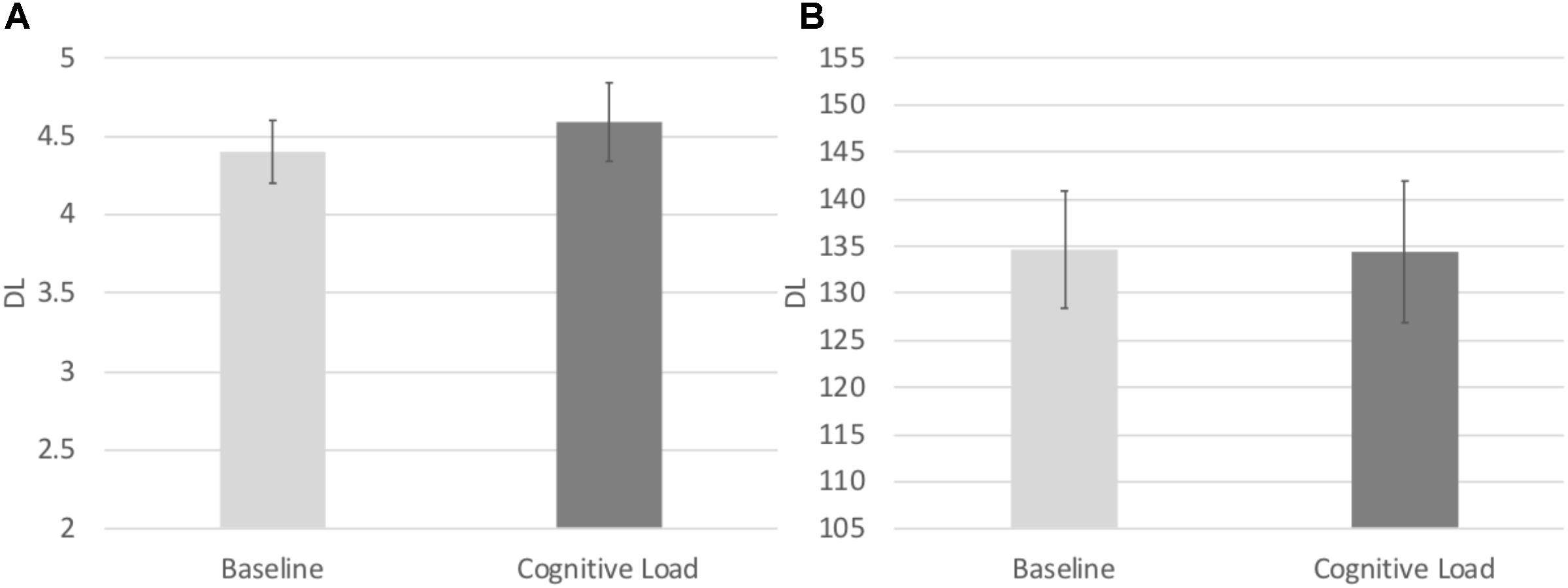
FIGURE 5. (A) Difference limen estimates from the Numerical Bisection Task. (B) Difference limen estimates for the Temporal Bisection Task.
Discussion
Understanding how quantity processing occurs in the real world is critical for assessing prominent theories of quantity processing and can also shed light on the cognitive mechanism(s) underlying these processes. Previous research identified numerous similarities in processing quantities such as time and number, leading to the prominent common magnitude system theory (see Walsh, 2003). However, newer work revealing many discrepancies in quantity processing (e.g., Baker et al., 2013; Odic, 2017) has undercut the common magnitude account. Of particular interest to this line of work are findings that angry face stimuli lead to numerical underestimation, yet temporal overestimation. These results have led researchers to rethink the prominent theory of a common magnitude system and consider the alternative that distinct cognitive mechanism(s) may underlie numerical and temporal processing. In the current study, we used a cognitive load manipulation to directly test the effect of altered attention during temporal and numerical processing in adults.
Temporal and Numerical Processing in Baseline Conditions
First, the common magnitude system would predict performance on comparable temporal and numerical tasks to be correlated. Replicating previous work, our baseline data revealed no correlation between performance on our temporal and numerical tasks (see Agrillo et al., 2013; Young and Cordes, 2013; Odic et al., 2016). This finding matches several null results from other research groups, further undercutting the common magnitude account by suggesting that one’s ability to track time and number are dictated by distinct patterns of representational acuity even within the same individuals.
Quantity Biases Under Cognitive Load
The common magnitude system would not only predict a correlation between temporal and numerical processing, but also temporal and numerical biases to track in the same direction under identical conditions. Despite this, several studies have demonstrated unique temporal and numerical biases in the presence of emotional content (Gil et al., 2007; Baker et al., 2013; Young and Cordes, 2013; Lewis et al., 2017). While these biases have previously been observed in the presence of emotional content, our data provide additional evidence for differential biases in temporal and numerical processing in a new context – during cognitive load. Mirroring earlier work with emotional content, our data reveal that cognitive load led to numerical underestimation. Temporal judgments, however, were marginally overestimated during cognitive load trials. Our findings join others challenging claims of the common magnitude system by identifying distinct and opposing biases in temporal and numerical processing (Gil et al., 2007; Baker et al., 2013; Young and Cordes, 2013; Lewis et al., 2017).
Our study also aimed to further explore the effect of attention on temporal and numerical processing. While previous work has suggested heightened arousal leads to temporal overestimation, but altered attention leads to numerical underestimation (Young and Cordes, 2013), attention and arousal are related constructs. Thus, our study attempted to solely test the effect of altered attention – through the induction of cognitive load – on both temporal and numerical processing within the same individuals. As predicted, numerical judgments were underestimated during the critical cognitive load trials, suggesting that numerical processing was disrupted while concurrently performing a distracting working memory task.
It is also important to note that temporal judgments were also marginally impacted by cognitive load, but in a different direction and less robustly. Unlike the findings with the numerical data, cognitive load resulted in the marginal overestimation of durations. These findings somewhat replicate previous work demonstrating that individuals tend to overestimate time in the presence of angry stimuli (e.g., Gil et al., 2007; Young and Cordes, 2013). However, they are counter to findings suggesting that altered attention leads to shorter duration estimates (e.g., Brown and Stubbs, 1992; Brown, 1997, 2008; Block and Zakay, 2008; Block et al., 2010). The opposing findings of our study compared to previous work may be accounted for by methodological differences, such as the type of temporal task employed and the durations used. Although prior work has primarily explored attentional manipulations on timing in the context of production or reproduction tasks (which typically assess estimation), the current study employed a bisection task that assesses subjective temporal judgments. In line with this possibility is work revealing differential impacts of arousing stimuli on temporal judgments across different timing tasks. Although angry faces lead to temporal overestimation in bisection, estimation, and production tasks, emotion does not impact temporal performance on reproduction or generalization tasks (Gil and Droit-Volet, 2011). While differences in the task demands could have led to discrepancies between our study and others, research employing bisection tasks, like the one used in the current study, has also revealed temporal underestimation (see Casini and Macar, 1997; Droit-Volet et al., 2010; Tipples, 2010). Moreover, our task focused on short durations (<1600 ms), yet previous work has typically, although not exclusively, tested the effect of cognitive load on longer durations (>2 s). This is particularly important given substantial evidence for two separate timing systems for timing sub-seconds (<1 s) and supra-seconds (>1 s, e.g., Lewis and Miall, 2003; Buhusi and Cordes, 2011; Gooch et al., 2011). Thus, it is possible that either the task employed, or the specific durations tested, may have led our findings to conflict with previous work on timing and attention. Regardless, our data further emphasize the need to investigate the effect of cognitive load on both sub- and supra-second judgments across tasks to determine whether how attentional manipulations impact timing judgments.
Lastly, because cognitive load was expected to impact attention, it was predicted that the inclusion of a dual task paradigm would have led to less consistent responding on the cognitive load trials. Surprisingly, this was not the case. Our data analyses revealed that introducing cognitive load did not impact participants’ consistency in making temporal or numerical judgments. In fact, our only finding in regards to response consistency was an overall main effect of task, such that numerical judgments were more precise than temporal judgments. This finding is consistent with evidence indicating that numerical judgments are more accurate than temporal judgments across the lifespan (Droit-Volet et al., 2008, Expt 1; Odic et al., 2016; Odic, 2017).
While our goal was to directly manipulate attention, it is important to note that our cognitive load manipulation not only altered attention, but also necessarily engaged other domain-general abilities such as working memory. Although we intentionally chose a cognitive load manipulation that has been used in the literature for manipulating attention (e.g., Postle et al., 1999), it is clear that this secondary task confounded attention and working memory. Thus, it is possible that the biases obtained in our data may be the result of manipulations to another domain general cognitive process, rather than attention specifically. Future work will be important for teasing apart this alternative. In particular, studies employing eyetracking methods, in which implicit measures of attention could be directly measured, would be particularly beneficial for investigating this possibility.
Conclusion
These data provide evidence against a common magnitude system by (a) demonstrating inconsistencies in representing different types of quantity within individuals, and (b) showing numerical underestimation, but slight temporal overestimation during an attention distracting task. Although our findings suggest that attention is critical for numerical processing, more work is needed to shed light on how attentional manipulations impact quantity processing. Future research will be critical for understanding the unique representational formats of quantities, and additional work exploring the role of attention and arousal as cognitive mechanisms underlying quantity processing may be particularly fruitful for shedding light on the representational patterns of quantitative information.
Ethics Statement
This study was carried out in accordance with the recommendations of Institutional Review Board, Boston College. The protocol was approved by the Institutional Review Board, Boston College. All subjects gave written informed consent in accordance with the Declaration of Helsinki.
Author Contributions
KH and MK completed all data collection. KH wrote the manuscript. MK, KJ, and SC provided thoughtful feedback on the manuscript. All authors contributed to the design of the study and approved of this version of the manuscript.
Funding
Funding was provided by a Boston College Research Expense Grants to SC.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank Kylie Gallo and Taylor Reader for their assistance with data collection and coding.
Footnotes
- ^While temporal overestimation typically occurs in the presence of angry faces, this effect seems to depend on the temporal measure used (see Gil and Droit-Volet, 2011; Lui et al., 2011).
References
Agrillo, C., Piffer, L., and Adriano, A. (2013). Individual differences in non-symbolic numerical abilities predict mathematical achievements but contradict ATOM. Behav. Brain Funct. 9:26. doi: 10.1186/1744-9081-9-26
Ashkenazi, S., Henik, A., Ifergane, G., and Shelef, I. (2008). Basic numerical processing in left intraparietal sulcus (IPS) acalulia. Cortex 44, 439–448. doi: 10.1016/j.cortex.2007.08.008
Baker, J. M., Rodzon, K. S., and Jordan, K. (2013). The impact of emotion on numerosity estimation. Front. Psychol. 4:521. doi: 10.3389/fpsyg.2013.00521
Block, R. A., Hancock, P. A., and Zakay, D. (2010). How cognitive load affects duration judgments: a meta-analytic review. Acta Psychol. 134, 330–343. doi: 10.1016/j.actpsy.2010.03.006
Block, R. A., and Zakay, D. (2008). “Timing and remembering the past, the present, and the future,” in Psychology of Time, ed. S. Grondin (Bingley: Emerald), 367–394.
Brown, S. W. (1997). Attentional resources in timing: interference effects in concurrent temporal and nontemporal working memory tasks. Percept. Psychophys. 59, 1118–1140. doi: 10.3758/BF03205526
Brown, S. W. (2008). “Time and attention: review of the literature,” in Psychology of Time, ed. S. Grondin (Bingley: Emerald), 111–138.
Brown, S. W., and Stubbs, D. A. (1992). Attention and interference in prospective and retrospective timing. Perception 21, 545–557. doi: 10.1068/p210545
Buhusi, C. V., and Cordes, S. (2011). Time and number: the privileged status of small values in the brain. Front. Integr. Neurosci. 5:67. doi: 10.3389/fnint.2011.00067
Cantlon, J. F., Brannon, E. M., Carter, E. J., and Pelphrey, K. A. (2006). Functional imaging of numerical processing in adults and 4-y-old children. PLoS Biol. 4:e125. doi: 10.1371/journal.pbio.0040125
Cantlon, J. F., Platt, M. L., and Brannon, E. M. (2009). Beyond the number domain. Trends Cogn. Sci. 13, 83–91. doi: 10.1016/j.tics.2008.11.007
Casini, L., and Macar, F. (1997). Effects of attention manipulation on judgments of duration and of intensity in the visual modality. Mem. Cogn. 25, 812–818. doi: 10.3758/BF03211325
Çoşkun, F., Sayalı, Z. C., Gürbüz, E., and Balcí, F. (2015). Optimal time discrimination. Q. J. Exp. Psychol. 68, 381–401. doi: 10.1080/17470218.2014.944921
Coull, J. T. (1998). Neural correlates of attention and arousal: insights from electrophysiology, functional neuroimaging and psychopharmacology. Prog. Neurobiol. 55, 343–361. doi: 10.1016/S0301-0082(98)00011-2
de Hevia, M. D., Girelli, L., and Cassia, V. M. (2012). Minds without language represent number through space: origins of the mental number line. Front. Psychol. 3:466. doi: 10.3389/fpsyg.2012.00466
Dormal, V., Dormal, G., Joassin, F., and Pesenti, M. (2012). A common right fronto-parietal network for numerosity and duration processing: an fMRI study. Hum. Brain Mapp. 33, 1490–1501. doi: 10.1002/hbm.21300
Dormal, V., and Pesenti, M. (2012). Processing magnitudes within the parietal cortex. Hor. Neurosci. Res. 8, 107–140.
Dormal, V., and Pesenti, M. (2013). Processing numerosity, length and duration in a three-dimensional Stroop-like task: towards a gradient of processing automaticity? Psychol. Res. 77, 116–127.
Dormal, V., Seron, X., and Pesenti, M. (2006). Numerosity-duration interference: a Stroop experiment. Acta Psychol. 121, 109–124. doi: 10.1016/j.actpsy.2005.06.003
Droit-Volet, S., Bigand, E., Ramos, D., and Bueno, J. L. O. (2010). Time flies with music whatever its emotional valence. Acta Psychol. 135, 226–232. doi: 10.1016/j.actpsy.2010.07.003
Droit-Volet, S., Clément, A., and Fayol, M. (2008). Time, number and length: similarities and differences in discrimination in adults and children. Q. J. Exp. Psychol. 61, 1827–1846. doi: 10.1080/17470210701743643
Feigenson, L. (2007). The equality of quantity. Trends Cogn. Sci. 11, 185–187. doi: 10.1016/j.tics.2007.01.006
Fortin, C., and Rousseau, R. (1998). Interference from short-term memory processing on encoding and reproducing brief durations. Psychol. Res. 61, 269–276. doi: 10.1007/s004260050031
Gil, S., and Droit-Volet, S. (2011). “Time flies in the presence of angry faces” depending on the temporal task used! Acta Psychol. 136, 354–362. doi: 10.1016/j.actpsy.2010.12.010
Gil, S., Niedenthal, P. M., and Droit-Volet, S. (2007). Anger and time perception in children. Emotion 7, 219–225. doi: 10.1037/1528-3542.7.1.219
Gooch, C. M., Wiener, M., Hamilton, C. A., and Coslett, B. H. (2011). Temporal discrimination of sub-and suprasecond time intervals: a voxel-based lesion mapping analysis. Front. Integr. Neurosci. 5:59. doi: 10.3389/fnint.2011.00059
Hamamouche, K. A., Niemi, L., and Cordes, S. (2017). Quantifying a threat: evidence of a numeric processing bias. Acta Psychol. 177, 1–9. doi: 10.1016/j.actpsy.2017.04.001
Hayashi, M. J., Kanai, R., Tanabe, H. C., Yoshida, Y., Carlson, S., and Walsh, V. (2013). Interaction of numerosity and time in prefrontal and parietal cortex. J. Neurosci. 33, 883–893. doi: 10.1523/JNEUROSCI.6257-11.2013
Khan, A., Sharma, N. K., and Dixit, S. (2006). Effect of cognitive load and paradigm on time perception. J. Indian Acad. Appl. Psychol. 32, 37–42.
Koch, G., Oliveri, M., and Caltagirone, C. (2009). Neural networks engaged in milliseconds and seconds time processing: evidence from transcranial magnetic stimulation and patients with cortical or subcortical dysfunction. Philos. Trans. R. Soc. Lond. B 364, 1907–1918. doi: 10.1098/rstb.2009.0018
Lewis, E. A., Zax, A., and Cordes, S. (2017). The impact of emotion on numerical estimation: a developmental perspective. Q. J. Exp. Psychol. 71, 1300–1311. doi: 10.1080/17470218.2017.1318154
Lewis, P. A., and Miall, R. C. (2003). Brain activation patterns during measurement of sub-and supra-second intervals. Neuropsychologia 41, 1583–1592. doi: 10.1016/S0028-3932(03)00118-0
Lui, M. A., Penney, T. B., and Schirmer, A. (2011). Emotion effects on timing: attention versus pacemaker accounts. PLoS One 6:e21829. doi: 10.1371/journal.pone.0021829
Macar, F., Grondin, S., and Casini, L. (1994). Controlled attention sharing influences time estimation. Mem. Cogn. 22, 673–686. doi: 10.3758/BF03209252
Mattel, M. S., and Meck, W. H. (2004). Cortico-striatal circuits and interval timing: coincidence detection of oscillatory processes. Cogn. Brain Res. 21, 139–170. doi: 10.1016/j.cogbrainres.2004.06.012
Meck, W. H., and Church, R. M. (1983). A mode control model of counting and timing processes. J. Exp. Psychol. 9, 320–334.
Nenadic, I., Gaser, C., Volz, H. P., Rammsayer, T., Häger, F., and Sauer, H. (2003). Processing of temporal information and the basal ganglia: new evidence from fMRI. Exp. Brain Res. 148, 238–246. doi: 10.1007/s00221-002-1188-4
Odic, D. (2017). Children’s intuitive sense of number develops independently of their perception of area, density, length, and time. Dev. Sci. 21:e12533. doi: 10.1111/desc.12533
Odic, D., Lisboa, J. V., Eisinger, R., Olivera, M. G., Maiche, A., and Halberda, J. (2016). Approximate number and approximate time discrimination each correlate with school math abilities in young children. Acta Psychol. 163, 17–26. doi: 10.1016/j.actpsy.2015.10.010
Ortega, L., and Lopez, F. (2008). Effects of visual flicker on subjective time in a temporal bisection task. Behav. Process. 78, 380–386. doi: 10.1016/j.beproc.2008.02.004
Piazza, M., Pinel, P., Le Bihan, D., and Dehaene, S. (2007). A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53, 293–305. doi: 10.1016/j.neuron.2006.11.022
Postle, B. R., Berger, J. S., and D”Esposito, M. (1999)). Functional neuroanatomical double dissociation of mnemonic and executive control processes contributing to working memory performance. Proc. Natl. Acad. Sci. U.S.A. 96, 12959–12964.
Provasi, J., Rattat, A. C., and Droit-Volet, S. (2011). Temporal bisection in 4-month-old infants. J. Exp. Psychol. 37, 108–113. doi: 10.1037/a0019976
Rammsayer, T., and Classen, W. (1997). Impaired temporal discrimination in Parkinson’s disease: temporal processing of brief durations as an indicator of degeneration of dopaminergic neurons in the basal ganglia. Int. J. Neurosci. 91, 45–55. doi: 10.3109/00207459708986364
Rammsayer, T. H., and Lima, S. D. (1991). Duration discrimination of filled and empty auditory intervals: cognitive and perceptual factors. Percept. Psychophys. 50, 565–574. doi: 10.3758/BF03207541
Rao, S. M., Mayer, A. R., and Harrington, D. L. (2001). The evolution of brain activation during temporal processing. Nat. Neurosci. 4, 317–323. doi: 10.1038/85191
Schubotz, R. I., Friederici, A. D., and Von Cramon, D. Y. (2000). Time perception and motor timing: a common cortical and subcortical basis revealed by fMRI. Neuroimage 11, 1–12. doi: 10.1006/nimg.1999.0514
Skagerlund, K., Karlsson, T., and Träff, U. (2016). Magnitude processing in the brain: an fMRI study of time, space, and numerosity as a shared cortical system. Front. Hum. Neurosci. 10:500.
Thomas, E., and Brown, I. (1974). Time perception and the filled-duration illusion. Percept. Psychophys. 16, 449–458. doi: 10.3758/BF03198571
Tipples, J. (2010). Time flies when we read taboo words. Psychon. Bull. Rev. 17, 563–568. doi: 10.3758/PBR.17.4.563
Vicario, C. M., Yates, M. J., and Nicholls, M. E. (2013). Shared deficits in space, time, and quantity processing in childhood genetic disorders. Front. Psychol. 4:43. doi: 10.3389/fpsyg.2013.00043
Walsh, V. (2003). A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn. Sci. 7, 483–488. doi: 10.1016/j.tics.2003.09.002
Wearden, J. H., Norton, R., Martin, S., and Montford-Bebb, O. (2007). Internal clock processes and the filled-duration illusion. J. Exp. Psychol. 33, 716–729.
Young, L. N., and Cordes, S. (2013). Fewer things, lasting longer: the effect of emotion on quantity judgments. Psychol. Sci. 24, 1057–1059. doi: 10.1177/0956797612465294
Keywords: quantity processing, time perception, number processing, cognitive load, quantity estimation
Citation: Hamamouche K, Keefe M, Jordan KE and Cordes S (2018) Cognitive Load Affects Numerical and Temporal Judgments in Distinct Ways. Front. Psychol. 9:1783. doi: 10.3389/fpsyg.2018.01783
Received: 02 June 2018; Accepted: 04 September 2018;
Published: 02 October 2018.
Edited by:
Fuat Balcı, Koç University, TurkeyReviewed by:
Giovanna Mioni, Università degli Studi di Padova, ItalyJennifer T. Coull, Aix-Marseille Université, France
Copyright © 2018 Hamamouche, Keefe, Jordan and Cordes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Karina Hamamouche, aGFtYW1vdWNAYmMuZWR1
 Karina Hamamouche
Karina Hamamouche Maura Keefe
Maura Keefe Kerry E. Jordan
Kerry E. Jordan Sara Cordes
Sara Cordes