The role of inertia in modeling decisions from experience with instance-based learning

One form of inertia is the tendency to repeat the last decision irrespective of the obtained outcomes while making decisions from experience (DFE). A number of computational models based upon the Instance-Based Learning Theory, a theory of DFE, have included different inertia implementations and have shown to simultaneously account for both risk-taking and alternations between alternatives. The role that inertia plays in these models, however, is unclear as the same model without inertia is also able to account for observed risk-taking quite well. This paper demonstrates the predictive benefits of incorporating one particular implementation of inertia in an existing IBL model. We use two large datasets, estimation and competition, from the Technion Prediction Tournament involving a repeated binary-choice task to show that incorporating an inertia mechanism in an IBL model enables it to account for the observed average risk-taking and alternations. Including inertia, however, does not help the model to account for the trends in risk-taking and alternations over trials compared to the IBL model without the inertia mechanism. We generalize the two IBL models, with and without inertia, to the competition set by using the parameters determined in the estimation set. The generalization process demonstrates both the advantages and disadvantages of including inertia in an IBL model.

Introduction

People’s reliance on inertia, the tendency to repeat the last decision irrespective of the obtained outcomes (successes or failures), has been documented in literature concerning managerial and organizational sciences as well as behavioral sciences (Samuelson, 1994; Reger and Palmer, 1996; Hodgkinson, 1997; Tripsas and Gavetti, 2000; Gladwell, 2007; Biele et al., 2009; Gonzalez and Dutt, 2011; Nevo and Erev, 2012). For example, inertia acts like a status quo bias and helps to account for the commonly observed phenomenon whereby managers fail to update and revise their understanding of a situation when it changes, a phenomenon that acts as a psychological barrier to organizational change (Reger and Palmer, 1996; Tripsas and Gavetti, 2000; Gladwell, 2007). In these situations, inertia is generally believed to have a negative effect on decision making (Sandri et al., 2010).

Inertia has also been incorporated to account for human behavior in existing computational models of decisions from experience (DFE). DFE are choices that are based on previous encounters with one’s alternatives; as opposed to decisions from description, which are based on summary descriptions detailing all possible outcomes and their respective likelihoods of each option (Hertwig and Erev, 2009). In DFE, researchers have studied both the risk-taking behavior and alternations between alternatives in repeated binary-choice tasks, where decision makers consequentially choose between risky and safe alternatives repeatedly (Samuelson, 1994; Börgers and Sarin, 2000; Barron and Erev, 2003; Erev and Barron, 2005; Biele et al., 2009; Hertwig and Erev, 2009; Erev et al., 2010a; Gonzalez and Dutt, 2011; Nevo and Erev, 2012). The alternations explain how individuals search information and how this search pattern changes over repeated trials. Thus, alternations tell us about the information-search patterns and learning in DFE (Erev et al., 2010a). Accounting for both risk-taking and alternations helps to develop a complete understanding about how decision makers reach certain long-term outcomes, which cannot be determined by solely studying one of these measures in the isolation of the other (Gonzalez and Dutt, 2011).

Most recently, models based upon the Instance-Based Learning Theory (IBLT; and “IBL models” hereafter), a theory of dynamic DFE, have shown to account for both the observed risk-taking and alternations in a binary-choice task better than most of the best known computational models. A number of these IBL models have incorporated some form of the inertia mechanism (Gonzalez and Dutt, 2011; Gonzalez et al., 2011), while others have not incorporated inertia and still accounted for the risk-taking behavior (Lejarraga et al., 2012). For example, Lejarraga et al. (2012) have shown that a single IBL model, without inertia, is able to explain observed risk-taking and generalize across several variants of the repeated binary-choice task. Therefore, it appears that inertia may not be needed in computational models to account for the observed risk-taking. However, Lejarraga et al. (2012) model does not demonstrate how alternations are accounted for or how alternations and risk-taking are accounted for simultaneously. As discussed above, people’s experiential decisions may likely rely on inertia, and computational models might need some form of inertia to account for both observed risk-taking and alternations. Yet, the role that inertia mechanisms play in existing computational models is unclear and needs to be systematically investigated.

In this paper, we evaluate the role of an inertia mechanism in an IBL model. We evaluate a model with inertia and another without inertia for their ability to account for observed risk-taking and alternation behaviors. In order to evaluate the inertia mechanism, we use two large human datasets that were collected in the Technion Prediction Tournament (TPT) involving the repeated binary-choice task (Erev et al., 2010b). In what follows, we first discuss the current understanding of the role of inertia in accounting for DFE. Next, we present the results of calibrating two existing IBL models, with and without inertia, in the TPT’s estimation dataset and evaluate the added value and contribution of including inertia. Finally, we present the results that generalize these models into the TPT’s competition dataset. We close this paper by discussing our results and highlighting some future directions in this ongoing research program.

The Role of Inertia in Decisions from Experience

Inertia may be a psychological barrier to changes in an organization if decision makers fail to update their understanding of a situation when it changes (Reger and Palmer, 1996; Hodgkinson, 1997; Tripsas and Gavetti, 2000; Gladwell, 2007). For example, Tripsas and Gavetti (2000) provided a popular example of inertia in a managerial setting concerning the Polaroid Corporation. Polaroid believed that it could only make money by producing consumables and not the hardware. Thus, it decided to stick to producing only consumables. This decision led the company to neglect the growth in digital imaging technologies. Because of the prevailing inertial “mental model” of their business, the corporation failed to adapt effectively to market changes. Furthermore, Gladwell (2007) has suggested that inertia is one powerful explanation as to why established firms are not as innovative as young, less established firms. For example, as an established firm, Kodak’s management is reported to have suffered from a status quo bias due to inertia: They believed that what has worked in the past will also work in the future (Gladwell, 2007).

In judgment and decision making, inertia has been shown to play a role in determining the proportion of risk-taking due to the timing of a descriptive warning message (Barron et al., 2008). Barron et al. (2008) compared the effect of a descriptive warning received before or after making risky decisions in a repeated binary-choice task. In this task, participants made a choice between a safe option with a sure gain and a risky option with the possibility of incurring a loss or a gain such that the probability of incurring the loss was very small (p = 0.001). Thus, most of the time, the task offered gains for both safe and risky choices. These authors show that when an early warning coincides with the beginning of a decision making process, the warning is both weighted more heavily in future decisions and induces safer behavior (i.e., a decrease in the proportion of risky choices), which becomes the status quo for future choices. Thus, although the proportion of risk-taking is lower for an early warning message compared to a late warning message, the risky and safe choices in both cases show excessive reliance on inertia to repeat the last choice made. Here, inertia acts like a double-edged sword: It is likely to encourage or discourage ongoing risky behavior depending upon the timing of a warning.

Some researchers have depicted inertia as an irrational behavior in which individuals hold onto choices that clearly do not provide the maximizing outcome for too long (Sandri et al., 2010). However, these authors have only shown that behavior may be inconsistent with one specific rational model of maximization, which may be an arbitrary standard that is difficult to generalize to other rational models of maximization. There are certain other situations where inertia is likely to produce positive effects as well. In psychology, inertia is also believed to be a key component of love, trust, and friendship (Cook et al., 2005). If evidence shows that a friend is dishonest, then the decision to mistrust the friend in future interactions would demand much more instances of dishonesty from the friend than that required to form an opinion about a stranger. Thus, the inertia of continuing to trust the friend makes it difficult to break the friendship.

Inertia has been incorporated in a number of existing cognitive models of DFE. It is believed that inertia helps these models account for both observed risk-taking and alternations in the repeated binary-choice (Samuelson, 1994; Börgers and Sarin, 2000; Biele et al., 2009; Erev et al., 2010a; Gonzalez and Dutt, 2011; Nevo and Erev, 2012). For example, Erev et al. (2010a) observed that in the repeated binary-choice task, participants selected the alternative that led to an observed high outcome in the last trial in 67.4% of the trials, while they repeated their last choice for an alternative, irrespective of it being high or low, in 75% of the trials. These observations suggest that participants tend to repeat their last choice even when it does not agree with the high outcome in their last experience, exhibiting robust reliance on inertia that seems to be independent of observed outcomes. Some researchers have suggested that in situations where estimating the choice that yields high outcomes from observation is costly, difficult, or time consuming, relying on inertia might be the most feasible course of action (Samuelson, 1994). But other researchers have found this inertia effect even when the forgone outcome (i.e., what respondents would have gotten had they chosen the other alternative) is greater than the obtained outcome (Biele et al., 2009).

In order to account for these observations, recent computational models of DFE have explicitly incorporated three different forms of inertia as part of their specification (Erev et al., 2010a; Gonzalez and Dutt, 2011; Gonzalez et al., 2011). In the first form, inertia increases over time as a result of a decrease in surprise, where surprise is defined as the difference in expected values of the two alternatives (Erev et al., 2010a). This definition of inertia has been included in the Inertia Sampling and Weighting (I-SAW) model. The I-SAW model was designed for a repeated binary-choice market-entry task, and it distinguishes between three explicit response modes: exploration, exploitation, and inertia (Erev et al., 2010a; Chen et al., 2011). The I-SAW model also provides reasonable predictions in the repeated binary-choice task (Nevo and Erev, 2012). Inertia is represented in this model with the assumption that individuals tend to repeat their last choice, and the probability of inertia in a trial is a function of surprise. Surprise is calculated as the difference in the expected value of the two alternatives due to the observed outcomes in each alternative in previous trials. The probability of inertia is assumed to increase over trials, as surprise decreases over trials. This definition based upon surprise incorporates the idea of learning over repeated trials of game play where, due to repeated presentations of the same set of outcomes, participants tend to get increasingly less surprised and begin to stick to an option that they prefer (i.e., show inertia in their decisions).

In the second form (that is similar to the first form), inertia increases over time as a result of a decrease in surprise, which is based upon the difference in blended values (a measure of utility of alternatives based on past experience in Gonzalez et al., 2011 model). This definition of inertia has been included in the IBL model that was runner-up in the market-entry competition (Gonzalez et al., 2011). This model includes an inertia mechanism that is driven by surprise like in the I-SAW model; however, surprise here is calculated as the difference between the blended values of two alternatives.

In the third and simpler form, inertia is a probabilistic process that is triggered randomly over trials, where the random occurrences of inertia are based upon a calibrated probability parameter, pInertia (Gonzalez and Dutt, 2011). This definition of inertia is the one we evaluate in this paper, as it was recently included in an IBL model that produced robust predictions superior to many existing models (Gonzalez and Dutt, 2011). According to Gonzalez and Dutt (2011), the IBL model with the pInertia parameter accounts for both observed risk-taking and alternations simultaneously in different paradigms of DFE and performs consistently better than most existing computational models of DFE that competed in the TPT.

Although computational models have included inertia in several forms, Lejarraga et al. (2012) have recently shown that a single IBL model without any inertia assumption is also able to account for the observed risk-taking behavior in different tasks that included probability-learning, binary-choice with fixed probability, and binary-choice with changing probability. Although the use of some form of inertia seems necessary in many computational models of DFE (Erev et al., 2010a; Chen et al., 2011; Gonzalez and Dutt, 2011; Gonzalez et al., 2011; Nevo and Erev, 2012), its role in accounting for risk-taking and alternations in DFE is still unclear and a systematic investigation of its role in computational models is needed.

Given the wide use of inertia in computational models, it is likely that incorporating inertia assumptions might make them more ecologically valid. That seems likely because if a model accounts for risk-taking behavior already, then incorporating a form of inertia in its specification might directly influence its ability to account for alternations as well. However, we currently do not know how inertia in a model might impact its ability to account for both the risk-taking behavior and the alternations simultaneously. The incorporation of inertia in a model is likely to be beneficial only if it improves the model’s ability to account for both risk-taking and alternations, and not solely one of these measures.

Materials and Methods

Risk-taking and Alternations in the Technion Prediction Tournament

The TPT (Erev et al., 2010b) was a modeling competition organized in 2008 in which different models were submitted to predict choices made by human participants. Competing models were evaluated following the generalization criterion method (Busemeyer and Wang, 2000), by which models were fitted to choices made by participants in 60 problems (the estimation set) and later tested in a new set of 60 problems (the competition set) with the parameters obtained in the estimation set. Although the TPT involved three different experimental paradigms, here we use data from the E-repeated paradigm that involved consequential choices in a repeated binary-choice task with immediate feedback on the chosen alternative. We use this dataset to evaluate the inertia mechanism in an IBL model.

The TPT dataset’s 120 problems involved a choice between a safe alternative that offered a medium (M) outcome with certainty; and a risky alternative that offered a high (H) outcome with some probability (pH) and a low (L) outcome with the complementary probability. The M, H, pH, and L were generated randomly, and a selection algorithm assured that the 60 problems in each set were different in domain (positive, negative, and mixed outcomes) and probability (high, medium, and low pH). The positive domain was such that each of the M, H, and L outcomes in a problem were positive numbers (>0). The mixed domain was such that one or two of the outcomes among M, H, and L (but not all three) in a problem were negative (<0). The negative domain was such that each of the M, H, and L outcomes in a problem were negative numbers (<0). The low, medium, and high probability in a problem corresponded to the value of pH between 0.01–0.09, 0.1–0.9, and 0.91–0.99, respectively. The selection algorithm ensured that there were 20 problems each for the three domains and about 20 problems each for the three probability values in the estimation and the competition sets. The resulting set of problems in the three domains and the three probability values was large and representative. For each of the 60 problems in the estimation and competition set, a sample of 100 participants was randomly assigned into 5 groups, and each group completed 12 of the 60 problems. Each participant was instructed to repeatedly and consequentially select between two unlabeled buttons on a computer screen in order to maximize long-term rewards for a block of 100 trials per problem (the end point on trials was not provided or known to participants). One button was associated with a risky alternative and the other button with a safe alternative. Clicking a button corresponding to either the safe or risky alternative generated an outcome associated with the selected button (i.e., there was only partial feedback and participants were not shown the foregone outcome on the unselected button). The alternative with the higher expected value, which could be either the safe or risky, could maximize a participant’s long-term rewards. Other details about the E-repeated paradigm are reported in Erev et al. (2010b).

The models submitted to the TPT were not provided with the alternation data (i.e., the A-rate), and they were evaluated only according to their ability to account for risk-taking behavior (i.e., the R-rate; Erev et al., 2010b). Gonzalez and Dutt (2011) had calculated the A-rate for analyses of alternations from the TPT datasets and we followed the exact same procedures in this paper. First, alternations were either coded as 1 s (a respondent switched from making a risky or safe choice in the last trial to making a safe or risky choice in the current trial) or as 0 s (the respondent repeated the same choice in the current trial as that in the last trial). Then, the A-rate is computed as the proportion of alternations in each trial starting in trial 2 (the A-rate in trial 1 is undefined as there is no preceding trial to calculate alternations). The proportion of alternations in each trial is computed by averaging the alternations over 20 participants per problem and 60 problems in each dataset. The R-rate is the proportion of risky choices (i.e., choices of the risky alternative) in each trial averaged over 20 participants per problem and 60 problems in each dataset.

Figure 1 shows the overall R-rate and A-rate over 99 trials from trial 2 to 100 in the estimation and competition sets. As seen in both datasets, the R-rate decreases slightly across trials, although there is a sharp decrease in the A-rate. The sharp decrease in the A-rate shows a change in the exploration (information-search) pattern across repeated trials. Overall, the R-rate and A-rate curves suggest that participants’ risk-taking behavior remains relatively steady across trials, while they learn to alternate less and choose one of the two alternatives more often. Later in this paper, we evaluate the role of inertia mechanism to account for these R- and A-rate curves in Figure 1 in a computational IBL model.

FIGURE 1

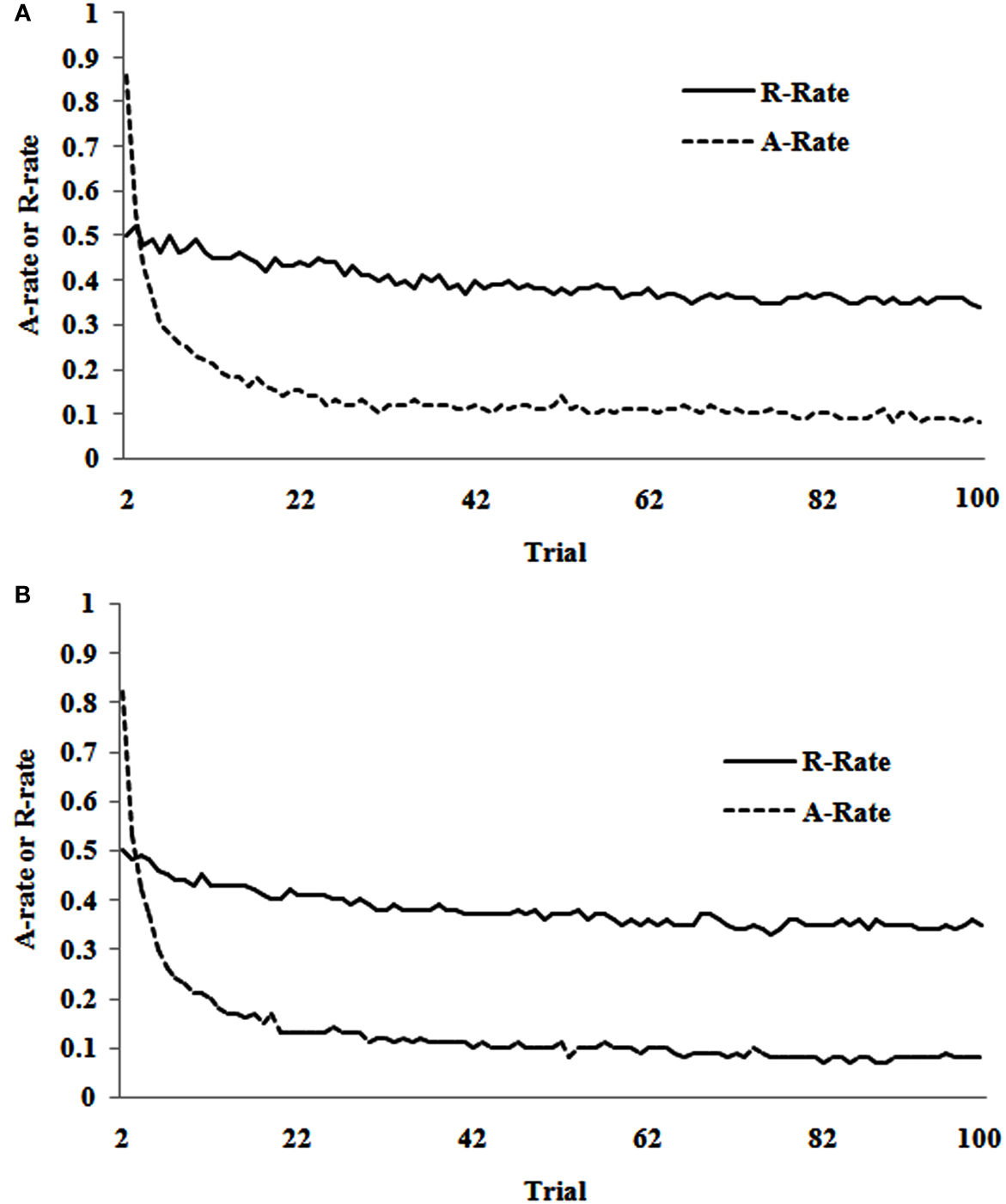
Figure 1. (A) The R-rate and A-rate across trials observed in human data in the estimation set of the TPT between trial 2 and trial 100. (B) The R-rate and A-rate across trials observed in human data in the competition set of the TPT between trial 2 and trial 100.

An Instance-Based Learning Model of Repeated Binary-Choice

Instance-Based Learning Theory has been used for developing computational models that explain human behavior in a wide variety of dynamic decision making tasks. These tasks include dynamically complex tasks (Gonzalez and Lebiere, 2005; Gonzalez et al., 2003; Martin et al., 2004), training paradigms of simple and complex tasks (Gonzalez et al., 2010), simple stimulus-response practice and skill acquisition tasks (Dutt et al., 2009), and repeated binary-choice tasks (Lebiere et al., 2007; Gonzalez and Dutt, 2011; Gonzalez et al., 2011; Lejarraga et al., 2012) among others. Its applications to these diverse tasks illustrate its generality and its ability to explain DFE in multiple contexts.

Here, we briefly discuss an IBL model that has shown to successfully account for both risk-taking and alternation behaviors in DFE (Gonzalez and Dutt, 2011). This model assumes reliance on recency, frequency, and random inertia to make choice selections. Here, we evaluate how the same IBL model, with and without the random inertia mechanism, can simultaneously account for risk-taking and alternation in repeated binary-choice. This evaluation will enable us to better understand the role of this particular simpler formulation of inertia in computational IBL models.

IBL model

All IBL models propose an “instance” as a key representation of cognitive information. An instance is a representation of each decision alternative and consists of three parts: a situation (a set of attributes that define the alternative), a decision for one of the many alternatives, and an outcome resulting from making that decision. An IBL model of repeated binary-choice has assumed a simple instantiation of inertia mechanism (Gonzalez and Dutt, 2011): A free parameter, called pInertia, determines the repetition of the previous choice in the current decision according to this probabilistic mechanism (see the Appendix for the formal definitions of all the mechanisms of the IBL model for repeated binary-choice and the pInertia parameter). If a uniformly distributed random number is less than the probability pInertia, then the model repeats its last choice; otherwise, the model compares blended values for the risky and safe alternatives, and makes a choice for the alternative with the higher blended value.

In this paper, we call this IBL model implementation with the random inertia mechanism, the “IBL-Inertia model.” In addition, we consider another version of the same model, but without this inertia mechanism (Lejarraga et al., 2012) as a baseline to compare against the IBL-Inertia model. We call this implementation without inertia, the “IBL model.” In the absence of inertia, this model relies solely on the comparison between the blended values for the risky and safe alternatives to make choice selections in each trial (the IBL-Inertia model also compares blended values to make choice selections; however, blended values are used only in the IBL-Inertia model when a random number is greater than or equal to the pInertia parameter in a trial). With the exception of the presence of pInertia in the IBL-Inertia model and its absence in the IBL model, both models are identical in all other respects.

Blending, as proposed in both model implementations, is a function of the probability of retrieving instances from memory multiplied by their respective outcomes stored in instances (Lebiere, 1999; Gonzalez and Dutt, 2011; Lejarraga et al., 2012). Each instance consists of a label that identifies a decision alternative in the task and the outcome obtained. For example (A, $32) is an instance where the decision was to choose the risky alternative (A) and the outcome obtained was $32. The probability of retrieving an instance from memory is a function of its activation (Anderson and Lebiere, 1998). A simplified version of the activation mechanism, which relies on recency and frequency of using instances and noise in retrieval, has been shown to be sufficient to capture human choices in several repeated binary-choice and probability-learning tasks (Gonzalez and Dutt, 2011; Lejarraga et al., 2012). The activation is influenced by the decay parameter d that captures the rate of forgetting or reliance on recency. The higher the value of the d parameter, the greater is the model’s reliance on recent experiences. The activation is also influenced by a noise parameter s that is important for capturing the variability in human behavior from one participant to another.

For the first trial, both model implementations, IBL-Inertia and IBL, have no instances in memory from which to calculate blended values. Therefore, these implementations make a selection between instances that are pre-populated in their memory. We used a value of +30 in the outcome slot of the two alternatives’ instances (Gonzalez and Dutt, 2011). The +30 value is arbitrary, but most importantly, it should be greater than any possible outcomes in the TPT problems to trigger an initial exploration of the two alternatives. For the first trial, the choice between the two alternatives in both implementations is solely based on the blended values. From the second trial onward, the inertia mechanism is used along with blending in IBL-Inertia model and only blending is used in the IBL model.

Results

Model Calibration and Evaluation of Inertia

The IBL model is compared with the IBL-Inertia model for their ability to account for both the proportion of risk-taking (R-rate) and alternations (A-rate) across trials. We will first calibrate the models’ shared parameters, noise s and decay d, to the data in the TPT’s estimation set. Then, we explore the role of adding the pInertia parameter to the IBL model (i.e., the IBL-Inertia model) by recalibrating all its parameters. Then, we generalize both the calibrated models, IBL and IBL-Inertia, to the TPT’s competition set.

Calibrating a model to human data means finding the parameter values that minimize the mean-squared deviation (MSD) between the model’s predictions and the observed human performance on a dependent measure. We used a genetic algorithm program to calibrate the model’s parameters. The genetic algorithm tried different combinations of parameters to minimize the sum of MSDs between the model’s average R-rate per problem and the average A-rate per problem measures and the corresponding values in human data (we call this sum as the combined R-rate and A-rate measure). Calibrating on the combined R-rate and A-rate measure is expected to produce the best account for both measures in human data compared to using only one of these measures (Dutt and Gonzalez, under review). Also, calibrating on the combined R-rate and A-rate measure allows us to test the IBL model’s maximum potential to account for both these measures.

In order to compare results on the R-rate and A-rate during calibration, we use the AIC (Akaike Information Criterion) measure in addition to the MSD (mean-squared deviation) measure. The AIC definition takes into account both a model’s complexity (estimated by the number of free parameters in the model), as well as its accuracy (estimated by G², defined the “lack of fit” between model and human data; Pitt and Myung, 2002; Busemeyer and Diederich, 2009). The AIC definition and the computation procedures used here are the same as those used by Gonzalez and Dutt, 2011; for more details on the AIC definition refer to the Appendix). The use of AIC during calibration is relevant because the IBL and IBL-Inertia models are hierarchical (or nested) models (Maruyama, 1997; Loehlin, 2003; Kline, 2004) and they differ only in terms of the inertia mechanism. Thus, the IBL model can be simply derived from the IBL-Inertia model by restricting the pInertia parameter’s value to 0 during model calibration. Furthermore, in order to capture the trend of R-rate and A-rate from a model over trials, we used the Pearson’s correlation coefficient (r) between model and human data across trials (for the A-rate we used trials 2–100 and for the R-rate we used trials 1–100; the A-rate is undefined for trial 1). Also, we computed the MSE (mean-squared error) between model and human data across trials. For the MSE, we averaged the R-rate and A-rate in model and human data across all participants and problems in a dataset for each trial. Then, we calculated the mean of the squared differences between model and human data for each trial. Because the MSE is computed across trials, it measures the distance between the model and human data curves trial-by-trial (for more details on the MSE definition refer to the Appendix).

For the purpose of calibration, the average R-rate per problem and the average A-rate per problem were computed by averaging the risky choices and alternations in each problem over 20 participants per problem and 100 trials per problem (for the A-rate per problem, only 99 trials per problem were used for computing the average). Later, the MSDs were calculated across the 60 problems by using the average R-rate per problem and the average A-rate per problem measures from the model and human data in the estimation set. Some researchers suggest calibrating models to the data of each participant per problem rather than to aggregate measures (Pitt and Myung, 2002; Busemeyer and Diederich, 2009); however, the calibration to aggregate behavior is quite common in the cognitive and behavioral sciences (e.g., Anderson et al., 2004; Erev et al., 2010a; Gonzalez and Dutt, 2011; Lejarraga et al., 2012). In fact, calibrating to aggregate measures is especially meaningful when the participant-to-participant variability in the dependent measure is small compared to the value of the dependent measure itself (Busemeyer and Diederich, 2009). In the estimation and competition sets, the standard deviations for the A-rate and R-rate were similar and very small (∼0.1) compared to the values of the R-rate (∼0.5) and the A-rate (∼0.3) measures themselves. Thus, we use the average dependent measures for the purposes of model calibration in this paper.

For calibrating the models, both the s parameter and the d parameters were varied between 0.0 and 10.0, and the pInertia parameter was varied between 0.0 and 1.0. Although the genetic algorithm can continue to indefinitely optimize parameters, it was stopped when there was no change in the parameter values obtained for a consecutive period of 200 generations. The assumed range of variation for the pInertia, s, and d parameters, and the decision process to stop the genetic algorithm are expected to provide good optimal parameter estimates (Gonzalez and Dutt, 2011). Also, the large range of parameters’ variation ensures that the optimization process does not miss the minimum sum of MSDs (for more details about genetic algorithm optimization, please see Gonzalez and Dutt (2011).

We calibrated both the IBL and IBL-Inertia models to the combined R-rate and A-rate in TPT’s estimation set. The purpose of the calibration was to obtain optimized values of d and s parameters in the IBL model and pInertia, d, and s parameters in the IBL-Inertia model. Later, keeping d and s parameters at their optimized values in the IBL-Inertia model, we varied the pInertia parameter from 0.0 to 1.0 in increments of 0.05. By only varying the pInertia parameter and keeping the other parameter values fixed at their optimized values, we were able to determine the inertia mechanism’s full contribution in the model.

Table 1 shows the values of calibrated parameters, MSD, r, AIC, and MSE compared to baseline for IBL and IBL-Inertia models in TPT’s estimation set. First, both models’ d and s parameters have values in the same range as those reported by Lejarraga et al. (2012). Lejarraga et al. (2012) reported d = 5 and s = 1.5 for a MSD = 0.0056 calibrated on R-rate using the IBL model. As documented by Lejarraga et al. (2012), the values of both d and s reported in Table 1 are high compared to the ACT-R default values of d = 0.5 and s = 0.25 (the default values were reported by Anderson and Lebiere(1998, 2003). A high d value points to a quick decay in memory and a strong dependence on recently experienced outcomes (i.e., reliance on recency). The high s value allows the model to exhibit participant-to-participant variability in capturing the R-rate and A-rate. The pInertia value in IBL-Inertia model (=0.62) is high and it shows that on a trial, this model is likely to repeat its previous choice with a 62% chance. In general, the results from both models are generally good (MSDs <0.05 and MSEs <0.05), where both models perform slightly better at capturing the human A-rate than the human R-rate.

TABLE 1

Table 1. The values of calibrated parameters for IBL and IBL-Inertia models and the MSD, r, AIC, and MSE in TPT’s estimation set.

Secondly, the individual MSDs, MSEs, and AICs on the R-rate and A-rate in the IBL model are larger than those in the IBL-Inertia model. For example, in the IBL-Inertia model, the MSDs for the R-rate, A-rate, and the sum of R-rate and A-rate are consistently smaller than those in the IBL model (0.008 < 0.016, an improvement of +0.008; 0.003 < 0.005, an improvement of +0.002; and, 0.011 < 0.021, an improvement of +0.010). Also, the relative AIC in the IBL-Inertia model is negative (i.e., better) for both the R-rate and the A-rate. Thus, even with an extraparametric complexity (the pInertia parameter), the IBL-Inertia model performs more accurately compared to the IBL model. Although the MSE in the IBL model is larger than that in the IBL-Inertia model for both R-rate and A-rate; however, as is also shown in Table 1, the IBL-Inertia model does not account for the trends in the R-rate and the A-rate across trials compared with the IBL model (the r in the IBL model is greater than that in the IBL-Inertia model for both the R-rate and the A-rate).

Figure 2 presents the R-rate and A-rate across trials predicted by the calibrated IBL and IBL-Inertia models and that observed in human data in the TPT’s estimation set. In general, these results reveal that both models generate good accounts for both observed risk-taking and alternation behaviors. The IBL model is able to capture the gradual decreasing trend in the A-rate as well as the slightly decreasing trend in risk-taking across trials. However, the model’s account for the R-rate exhibit as lightly greater decrease compared with that observed in human data across increasing number of trials. Also, the model’s account for the A-rate shows more alternations during about the first half of the trials than that observed in human data. This latter observation is likely due to the +30 pre-populated instances initially put in model’s memory, which make it explore both options for a longer time and causes a higher A-rate in the first few trials. However, with increasing trials, the activation of these pre-populated instances becomes weak (as these values are not observed in the problems) and their influence on the A-rate diminishes, causing the A-rate to decrease sharply and meet the human data.

FIGURE 2

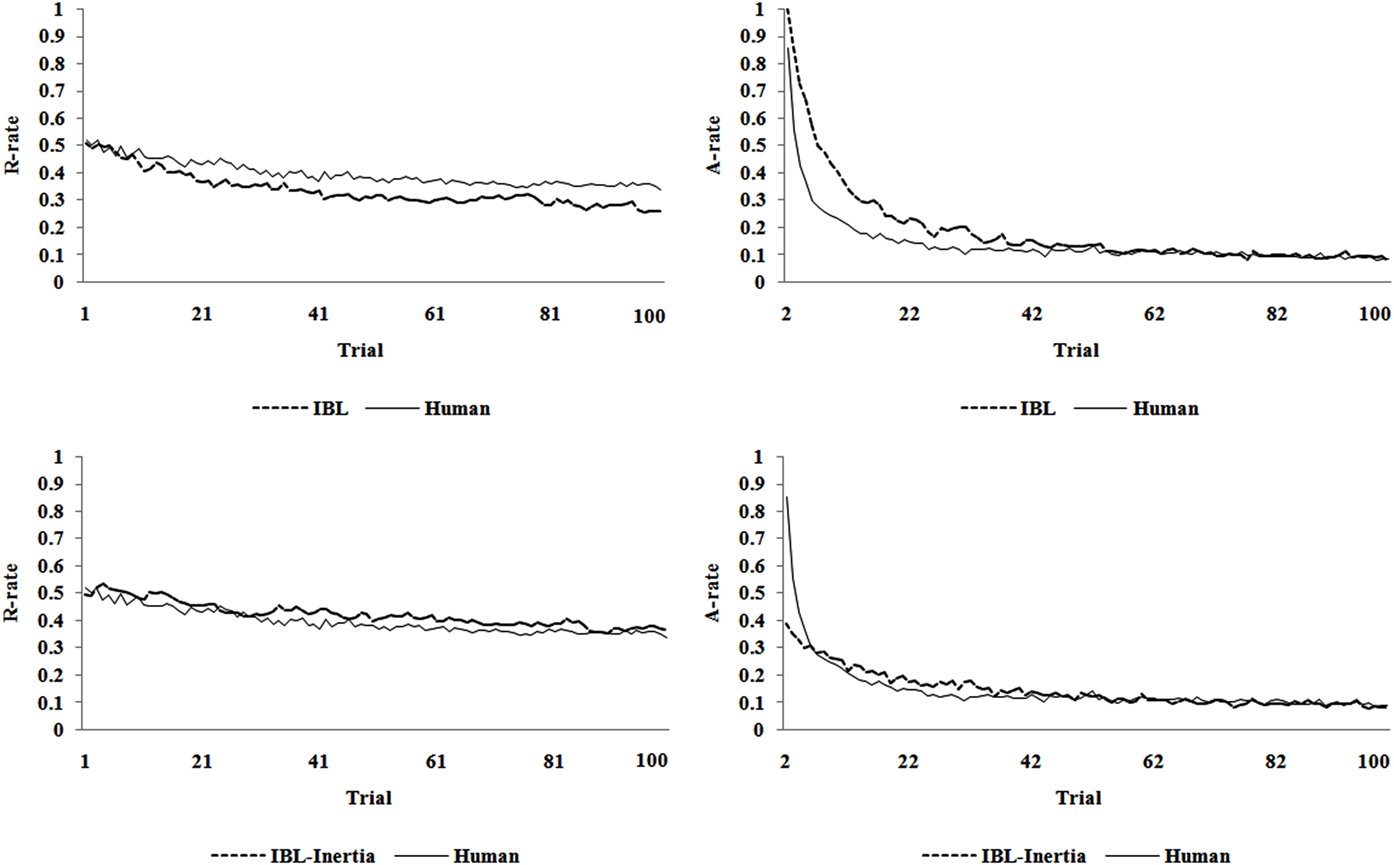
Figure 2. The R-rate and A-rate across trials predicted by the IBL and IBL-Inertia models and that observed in human data in the TPT’s estimation set.

As shown in the bottom graphs of Figure 2, the IBL-Inertia model corrects for the under-estimation and over-estimation in the R-rate and A-rate. However, because of the pInertia parameter, the model is unable to account for the initial decrease in the A-rate in the first few trials as well as the IBL model, which does so naturally. A likely reason is the high calibrated value of pInertia parameter (=0.62) that overshadows the effect of pre-populated instances in the first few trials. Also, it seems that the random effect of pInertia across trials causes disruptions in IBL-Inertia model’s R-rate trends over trials. Overall, these observations explain why the IBL-Inertia accounts for overall behavior better than the IBL model, but it does not account for the trends in the R-rate and the A-rate.

Evaluating the Inertia Mechanism

Although the analyses above provide some benefits of including pInertia in the IBL model, one would like to understand these benefits more thoroughly for different values of the pInertia parameter over its entire range. If including pInertia in the IBL model is beneficial, then we should observe smaller MSDs on the R-rate and A-rate across a large part of the parameter’s range of variation compared with the IBL model without pInertia. Also, this analysis is important because the calibrated value of pInertia in the IBL model was found to be high (=0.62), minimizing the role of the blending mechanism.

For this investigation, we used the IBL-Inertia model with its optimized parameters calibrated on the combined R-rate and A-rate measure (i.e., d = 6.71; s = 1.40) and varied the pInertia parameter from 0.0 to 1.0 in increments of 0.05 in TPT’s estimation set. Varying pInertia like so allows us to determine the range of values for which the sum of the MSDs computed on the average R-rate per problem and the average A-rate per problem are minimized.

Figure 3 shows the MSDs for the IBL-Inertia model calibrated on the combined R-rate and A-rate as a function of pInertia values in the estimation set. It also shows the three corresponding MSDs from the original IBL model (shown as dotted lines in Figure 3) for comparison purposes (these MSDs are also reported in Table 1). The MSDs for the R-rate, the A-rate, and the sum of the MSDs for the R-rate and A-rate in the IBL-Inertia model are below the corresponding MSDs in the IBL model for all values of pInertia greater than 0.05 and less than 0.90. Thus, including inertia in the IBL model and calibrating all model parameters improves the model’s ability to account for the average R-rate and A-rate compared with the IBL model without inertia. Also, the advantages of including pInertia parameter seem to be present over a large range of this parameter’s variation.

FIGURE 3

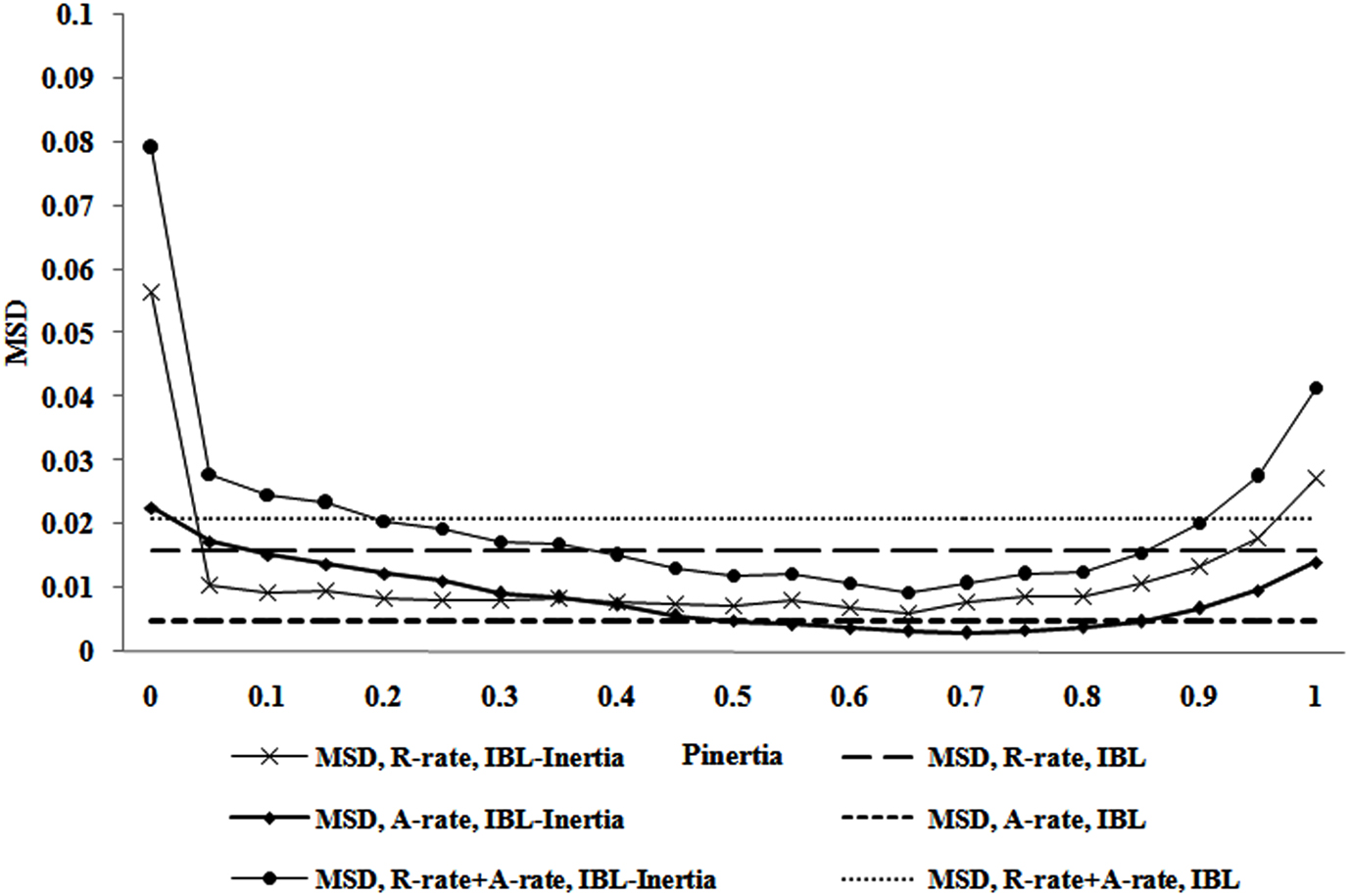
Figure 3. The MSD for the R-rate, the MSD for the A-rate, and the MSD for the combined R-rate and A-rate for different values of pInertia parameter in IBL-Inertia model (the corresponding MSDs for the IBL model are also plotted as dotted lines for comparison). The IBL-Inertia model used the calibrated parameters for d and s parameters (i.e., d = 6.41 and s = 1.40).

Generalizing the IBL Models to the Competition Set

A popular method of comparing models of different complexity is through models’ generalization in novel conditions (Stone, 1977; Busemeyer and Wang, 2000; Ahn et al., 2008). In generalization, the calibrated models with different complexities (number of free parameters) are run in novel conditions to compare their performance. The novel conditions would minimize any advantage the model with more parameters has over the model with fewer parameters. In fact, TPT also accounted for model complexity among submitted models by generalization, i.e., by running models in the new competition set with the parameters obtained in the estimation set (Erev et al., 2010b). We used the same procedures as used in the TPT and generalized the calibrated IBL and IBL-Inertia models to TPT’s competition set.

In related research, we have claimed that the TPT’s estimation and competition data sets are too similar, raising questions regarding the value of using the competition set for generalization (Gonzalez and Dutt, 2011; Gonzalez et al., 2011). These similarities arise because the problems used in the estimation and competition sets were generated by using the same algorithm. However, given that the TPT competition set was collected in a new experiment, involving new problems, and involving a different set of participants from that of the estimation set, testing the models in the competition set is still a relevant exercise to determine the robustness of the models. This generalization further helps us to take into account both models’ complexity (number of parameters) and their accuracy of predictions (MSDs; Busemeyer and Diederich, 2009).

The IBL model and IBL-Inertia model were run in the TPT’s competition set problems using the parameters determined in the estimation set: d = 6.71, s = 1.40, and pInertia = 0.62 (the pInertia parameter is only for the IBL-Inertia model). As previously mentioned, these parameter values had resulted in the lowest MSDs on the combined R-rate and A-rate measure for the two models in the estimation set. Table 2 shows the values of MSD, r, and MSE for the IBL and IBL-Inertia models upon their generalization in TPT’s competition set. The IBL-Inertia model’s predictions resulted in overall MSDs and MSEs for the R-rate and the A-rate that were smaller than those for the IBL model. Like in the estimation set, however, the IBL-Inertia model did not account for the over trial trend in the R-rate and the A-rate compared with the IBL model (demonstrated by the r calculations). These results demonstrate that the IBL-Inertia model can generalize to new problems more accurately (in terms of average overall performance in both the A-rate and R-rate measures across problems and across trials compared with the IBL model; but the IBL-Inertia model also cannot account for trends across trials in these measures compared with the IBL model without inertia).

TABLE 2

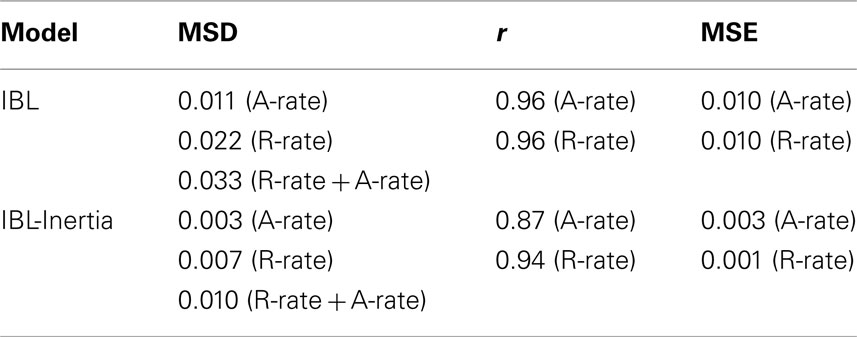
Table 2. The values of MSD, r, and MSE for IBL and IBL-Inertia models upon their generalization in TPT’s competition set.

Figure 4 shows the R-rate and the A-rate over trials for human data, and how the IBL and IBL-Inertia models generalized in the competition set. The IBL model, upon generalization, underestimates the observed R-rate and overestimates the observed A-rate in the competition set. These patterns of under- and over-estimations are similar to those observed in the model’s predictions in the estimation set in Figure 2. The IBL-Inertia model’s predictions about the human R-rate and A-rate in the competition set, however, were very good with very little under- and over-estimations of the observed R-rate and A-rate curves. Furthermore, because the pInertia parameter (=0.62) is fixed across trials at a high value in the IBL-Inertia model, the model does not alternate as much as humans in the first few trials. As seen in the lower right graph, the IBL-Inertia model’s A-rate starts around 40%, rather than the 85% as observed in human data. Thus, the IBL-Inertia model is not able to account for the initially high A-rate and the rapid decrease in the A-rate in the first few trials compared with the IBL model in its predictions.

FIGURE 4

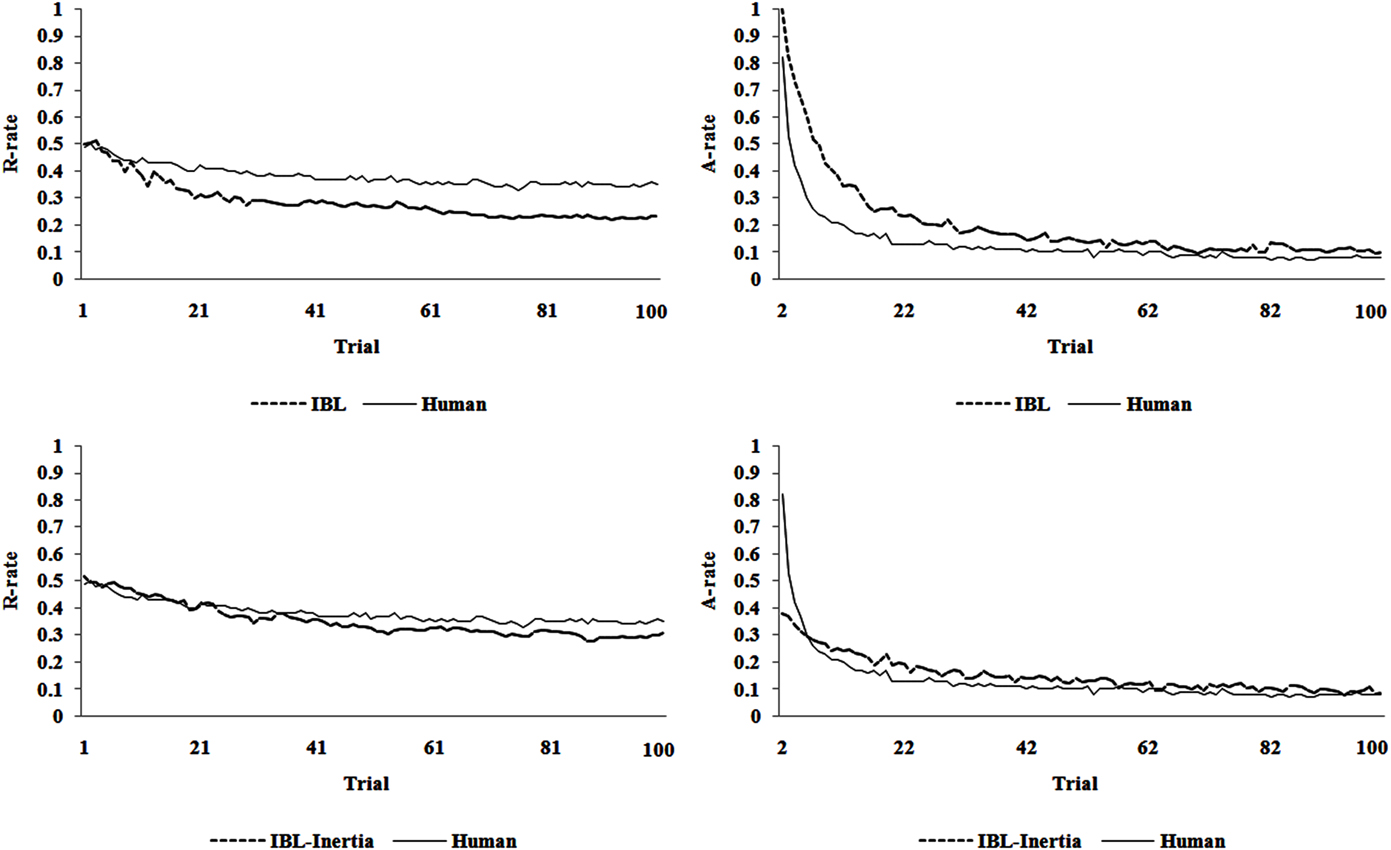
Figure 4. The R-rate and A-rate over trials predicted by the IBL and IBL-Inertia models upon their generalization in the competition set. The R-rate and A-rate observed in human data in the competition set are also shown.

Discussion

Some computational models of DFE do not include any inertia assumptions and are still able to account for the observed risk-taking behavior (Lejarraga et al., 2012). However, a number of recent computational models have included some form of inertia to account for observed DFE (Erev et al., 2010a; Gonzalez and Dutt, 2011; Gonzalez et al., 2011). Three different inertial forms have been proposed: random inertia (Gonzalez and Dutt, 2011); inertia as a function of surprise determined by the differences in expected values (Erev et al., 2010a); and inertia as a function of surprise determined by the differences in blended values (Gonzalez et al., 2011). This research uses the particular case of random inertia in an IBL model and determines the benefits of this mechanism by considering two IBL models with and without this mechanism. We selected the random inertia form for our evaluation because of its simplistic formulation, but also because an existing IBL model with this definition accounts for DFE better than other best known models of DFE (Gonzalez and Dutt, 2011).

Our results reveal that a simple instantiation of the inertia mechanism can be used to improve the ability of the IBL model to account for the average risk-taking (R-rate) and alternations (A-rate; based upon MSDs, MSEs, and AICs) observed in human data. However, we also find that the inclusion of random inertia does not help the model to account for the trends across trials in the R-rate and A-rate compared with the same model without inertia (based upon correlation coefficients, r). We draw our conclusions based upon model calibration and model generalization that is known to account for increased model complexity (number of parameters) in novel test environments (Busemeyer and Diederich, 2009).

Most current models of DFE have been successful at capturing the risk-taking behavior, but not the underlying alternations observed in repeated binary-choice; such as the tendency to repeat choices irrespective of the obtained outcome in the last trial (Biele et al., 2009). This observation is perhaps not a coincidence, because predicting risk-taking behavior and alternation effects simultaneously is a very challenging task (Rapoport et al., 1997; Erev and Barron, 2005; Estes and Maddox, 2005). In order to overcome some of the challenges, a number of computational models have considered the inclusion of some form of inertia with some initial success (Erev et al., 2010a; Gonzalez and Dutt, 2011; Gonzalez et al., 2011). As can be seen in our results, the random inertia’s inclusion into the IBL model helps the model to account for both the average A-rate and R-rate in terms of MSDs, MSEs, and AICs, but not in terms of trends in these rates over trials. Because random inertia accounts for the average A-rate and R-rate in human data, it helps to reduce the observed under-estimation and over-estimation of the observed R-rate and A-rate, respectively, which is seen in the model without the inertia mechanism. This finding might suggest that the inclusion of some form of inertia into computational models might be ecologically plausible for capturing the average risk-taking and alternation behaviors more accurately, but not for the trend in these behaviors over time.

Although the introduction of inertia into the IBL model generally improves the fits to the average human data (based upon MSDs, MSEs, and AICs), it is likely that few modelers may be impressed by this particular result. It is well-known that a model with more parameters (i.e., greater model complexity) can fit a dataset better than a model with fewer parameters (Pitt and Myung, 2002). We dealt with this issue through model generalization (Stone, 1977). The generalization helped to test models with different parametric assumptions in a novel environment (Busemeyer and Diederich, 2009). We used these procedures and generalized the IBL and the IBL-Inertia models to the TPT’s competition dataset to compare their performance.

Although the error across trials between IBL-Inertia model and human data was smaller compared to that between IBL model and human data; however, unlike the IBL model, the IBL-Inertia model did not capture the trends in the R-rate and A-rate across trials. The most likely reason is that the inertia parameter in its current formulation is a noisy selection of choices across trials, which disregards the choices derived based upon blended values. Gonzalez et al. (2011) had assumed an inertia formulation that was based upon surprise, where surprise was a function of the difference in blended values of the two alternatives. Perhaps, if the inertia mechanism in the model is formulated as described by Gonzalez et al. (2011), then the trends across trials might be better accounted for compared to that based upon inertia’s current formulation. Overall, these observations indicate that there are many aspects still left in the literature to explore. For example, it is unclear whether people exhibit inertia after receiving both rewards and punishments. Although inertia has been defined as the tendency to repeat the last choice irrespective of the obtained outcomes (Biele et al., 2009), it is clear that inertia needs to be defined more precisely. Some researchers have argued inertia as an irrational behavior in which individuals hold onto choices that clearly do not provide the maximizing outcome for too long (Sandri et al., 2010). Inertia has also been portrayed as desirable, however, as it believed to be a key component of love, trust, and friendship in the real world (Cook et al., 2005). Even when we consider inertia as we defined it in this paper, it may be the result of strong preferences for the high outcomes or the result of an apparently irrational behavior of holding on too long to non-maximizing (low) outcomes. As part of our future research, we propose to define the reasons for inertia more precisely by investigating its relationship with the exploration of alternatives due to the nature of outcomes, high or low. One way we may do this analysis is by controlling for the nature of rewards or punishments received after a decision choice and by evaluating its effects on repeating the last choice as the current decision. Also, we would like to consider the alternation behaviors of individuals depending upon the nature of rewards or punishments received by them in the last trial.

Finally, as part of future research, we would also like to compare the different formulations of inertia in computational models of DFE. As detailed above, there have been at least three different inertia formulations proposed: A random variation across trials (Gonzalez and Dutt, 2011), a function of surprise determined by the difference in expected values (Erev et al., 2010a), and a function of surprise determined by the differences in blended values (Gonzalez et al., 2011). Which one of these formulations performs best in different DFE tasks? How well do these different formulations account for the over trial trends in the R-rates and A-rates? Still, how are these formulations impacted by task complexity: by the nature and number of outcomes on each alternative, and the nature of the probability distribution of outcomes on each alternative? These are also some important questions that we would like to attend to as part of future research.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research is supported by the Defense Threat Reduction Agency (DTRA) grant number: HDTRA1-09-1-0053 to Dr. Cleotilde Gonzalez. We thank Ms. Hau-Yu Wong and Dr. Noam Ben-Asher of the Dynamic Decision Making Laboratory for their help in proofreading this manuscript and providing insightful comments. We would also like to thank Dr. Ido Erev of the Technion-Israel Institute of Technology for making the data from the Technion Prediction Tournament available.

References

Ahn, W. Y., Busemeyer, J. R., Wagenmakers, E. J., and Stout, J. C. (2008). Comparison of decision learning models using the generalization criterion method. Cogn. Sci. 32, 1376–1402.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Anderson, J. R., Bothell, D., Byrne, M. D., Douglass, S., Lebiere, C., and Qin, Y. (2004). An integrated theory of the mind. Psychol. Rev. 111, 1036–1060.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Anderson, J. R., and Lebiere, C. (1998). The Atomic Components of Thought. Mahwah, NJ: Erlbaum.

Anderson, J. R., and Lebiere, C. (2003). The Newell test for a theory of mind. Behav. Brain Sci. 26, 587–639.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barron, G., and Erev, I. (2003). Small feedback-based decisions and their limited correspondence to description-based decisions. J. Behav. Decis. Mak. 16, 215–233.

CrossRef Full Text

Barron, G., Leider, S., and Stack, J. (2008). The effect of safe experience on a warnings’ impact: sex, drugs, and rock-n-roll. Organ. Behav. Hum. Decis. Process. 106, 125–142.

CrossRef Full Text

Biele, G., Erev, I., and Ert, E. (2009). Learning, risk attitude and hot stoves in restless bandit problems. J. Math. Psychol. 53, 155–167.

CrossRef Full Text

Börgers, T., and Sarin, R. (2000). Naive reinforcement learning with endogenous aspirations. Int. Econ. Rev. 41, 921–950.

CrossRef Full Text

Busemeyer, J. R., and Diederich, A. (2009). Cognitive Modeling. Thousand Oaks: Sage Publications, Inc.

Busemeyer, J. R., and Wang, Y. (2000). Model comparisons and model selections based on the generalization criterion methodology. J. Math. Psychol. 44, 171–189.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chen, W., Liu, S.-Y., Chen, C.-H., and Lee, Y.-S. (2011). Bounded memory, inertia, sampling and weighting model for market entry games. Games 2, 187–199.

CrossRef Full Text

Cook, K. S., Hardin, R., and Levi, M. (2005). Cooperation without Trust? New York: Russell Sage Foundation Publications.

Dutt, V., Yamaguchi, M., Gonzalez, C., and Proctor, R. W. (2009). “An instance-based learning model of stimulus-response compatibility effects in mixed location-relevant and location-irrelevant tasks,” in Proceedings of the 9th International Conference on Cognitive Modeling – ICCM2009, eds A. Howes, D. Peebles, and R. Cooper (Manchester: University of Huddersfield).

Erev, I., and Barron, G. (2005). On adaptation, maximization and reinforcement learning among cognitive strategies. Psychol. Rev. 112, 912–931.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Erev, I., Ert, E., and Roth, A. E. (2010a). A choice prediction competition for market entry games: an introduction. Games 1, 117–136.

CrossRef Full Text

Erev, I., Ert, E., Roth, A. E., Haruvy, E., Herzog, S. M., Hau, R., Hertwig, R., Stewart, T., West, R., and Lebiere, C. (2010b). A choice prediction competition: choices from experience and from description. J. Behav. Decis. Mak. 23, 15–47.

CrossRef Full Text

Estes, W. K., and Maddox, W. T. (2005). Risks of drawing inferences about cognitive processes from model fits to individual versus average performance. Psychon. Bull. Rev. 12, 403–408.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gladwell, M. (2007). Blink. New York: Back Bay Books.

Gonzalez, C., Best, B. J., Healy, A. F., Bourne, L. E. Jr., and Kole, J. A. (2010). A cognitive modeling account of simultaneous learning and fatigue effects. Cogn. Syst. Res. 12, 19–32.

CrossRef Full Text

Gonzalez, C., and Dutt, V. (2011). Instance-based learning: integrating sampling and repeated decisions from experience. Psychol. Rev. 118, 523–551.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gonzalez, C., Dutt, V., and Lejarraga, T. (2011). A loser can be a winner: comparison of two instance-based learning models in a market entry competition. Games 2, 136–162.

CrossRef Full Text

Gonzalez, C., and Lebiere, C. (2005). “Instance-based cognitive models of decision making,” in Transfer of Knowledge in Economic Decision-Making, eds D. Zizzo, and A. Courakis (New York: Palgrave Macmillan), 148–165.

Gonzalez, C., Lerch, F. J., and Lebiere, C. (2003). Instance-based learning in real-time dynamic decision making. Cogn. Sci. 27, 591–635.

CrossRef Full Text

Hertwig, R., and Erev, I. (2009). The description-experience gap in risky choice. Trends Cogn. Sci. (Regul. Ed.) 13, 517–523.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hodgkinson, G. P. (1997). Cognitive inertia in a turbulent market: the case of UK residential estate agents. J. Manage. Stud. 34, 921–945.

CrossRef Full Text

Kline, R. B. (2004). Principles and Practice of Structural Equation Modeling (Methodology in the Social Sciences), 2nd Edn. New York: The Guilford Press.

Lebiere, C. (1999). “Blending,” in Proceedings of the Sixth ACT-R Workshop (Fairfax, VA: George Mason University).

Lebiere, C., Gonzalez, C., and Martin, M. (2007). “Instance-based decision making model of repeated binary choice,” in Proceedings of the 8th International Conference on Cognitive Modeling, Ann Arbor, MI.

Lejarraga, T., Dutt, V., and Gonzalez, C. (2012). Instance-based learning: a general model of repeated binary choice. J. Behav. Decis. Mak. 25, 143–153.

CrossRef Full Text

Loehlin, J. C. (2003). Latent Variable Models: An Introduction to Factor, Path, and Structural Equation Analysis. Mahwah, NJ: Lawrence Erlbaum.

Martin, M. K., Gonzalez, C., and Lebiere, C. (2004). “Learning to make decisions in dynamic environments: ACT-R plays the beer game,” in Proceedings of the Sixth International Conference on Cognitive Modeling (Pittsburgh, PA: Carnegie Mellon University), 178–183.

Maruyama, G. M. (1997). Basics of Structural Equation Modeling. Thousand Oaks, CA: Sage Publications, Inc.

Nevo, I., and Erev, I. (2012). On surprise, change, and the effect of recent outcomes. Front. Psychol. 3:24.

CrossRef Full Text

Pitt, M. A., and Myung, I. J. (2002). When a good fit can be bad. Trends Cogn. Sci. (Regul. Ed.) 6, 421–425.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rapoport, A., Erev, I., Abraham, E. V., and Olson, D. E. (1997). Randomization and adaptive learning in a simplified poker game. Organ. Behav. Hum. Decis. Process. 69, 31–49.

CrossRef Full Text

Reger, R. K., and Palmer, T. B. (1996). Managerial categorization of competitors: using old maps to navigate new environments. Organ. Sci. 7, 22–39.

CrossRef Full Text

Samuelson, L. (1994). Stochastic stability in games with alternative best replies. J. Econ. Theory 64, 35–65.

CrossRef Full Text

Sandri, S., Schade, C., Mußhoff, O., and Odening, M. (2010). Holding on for too long? An experimental study on inertia in entrepreneurs’ and non-entrepreneurs’ disinvestment choices. J. Econ. Behav. Organ. 76, 30–44.

CrossRef Full Text

Stone, M. (1977). Asymptotics for and against cross-validation. Biometrika 64, 29–35.

CrossRef Full Text

Tripsas, M., and Gavetti, G. (2000). Capabilities, cognition, and inertia: evidence from digital imaging. Strateg. Manage. J. 21, 1147–1161.

CrossRef Full Text

Appendix

IBL Model Equations

Inertia mechanism

A choice is made in the model in trial t + 1 as:

If

The draw of a random value in the uniform distribution U (0, 1) < pInertia,

Then

Repeat the choice as made in the previous trial

Else

$\begin{array}{r}\text{Select}\text{an}\text{alternative}\text{with}\text{the}\text{highest}\text{blended}\text{value}\text{as}\text{per}\\ \text{Eq.}\text{ A2}\text{(below)}\hfill & \hfill \text{(A1)}\end{array}$

The pInertia parameter could vary between 0 and 1, and it does not change across trials or participants.

Blending and activation mechanisms

The blended value of alternative j is defined as

${\text{V}}_j=\sum _{i=1}^n{p}_i{x}_i$(A2)

Where x_i is the value of the observed outcome in the outcome slot of an instance i corresponding to the alternative j, and p_i is the probability of that instance’s retrieval from memory (for the case of our binary-choice task in the experience condition, the value of j Eq. A2 could be either risky or safe). The blended value of an alternative is the sum of all observed outcomes x_i in the outcome slot of corresponding instances, weighted by the instances’ probability of retrieval.

Probability of retrieving instances

In any trial t, the probability of retrieving instance i from memory is a function of that instance’s activation relative to the activation of all other instances corresponding to that alternative, given by

$p_{i,t}=\frac{{\text{e}}^{A_{i,t}∕\tau }}{\sum _j{\text{e}}^{A_{j,t}∕\tau }}$(A3)

Where τ is random noise defined as $s\times \sqrt{2},$ and s is a free noise parameter. The noise parameter s captures the imprecision of retrieving instances from memory.

Activation of instances

The activation of each instance in memory depends upon the activation mechanism originally proposed in ACT-R (Anderson and Lebiere, 2003). According to this mechanism, for each trial t, activation A_i,t of instance is:

$A_{i,t}=ln\left(\sum _{t_i\in \left\{1,\dots ,t-1\right\}}{\left(t-t_i\right)}^{-d}\right)+s\times \text{1n}\left(\frac{1-{\gamma }_{i,t}}{{\gamma }_{i,t}}\right)$(A4)

Where d is a free decay parameter, and t_i is a previous trial when the instance i was created or its activation was reinforced due to an outcome observed in the task (the instance i is the one that has the observed outcome as the value in its outcome slot). The summation will include a number of terms that coincides with the number of times an outcome has been observed in previous trials and the corresponding instance i’s activation that has been reinforced in memory (by encoding a timestamp of the trial t_i). Therefore, the activation of an instance corresponding to an observed outcome increases with the frequency of observation and with the recency of those observations. The decay parameter d affects the activation of an instance directly, as it captures the rate of forgetting or reliance on recency.

Noise in activation

The γ_i,t term is a random draw from a uniform distribution U (0, 1), and the $s\times ln\text{(}\frac{1-{\gamma }_{i.t}}{{\gamma }_{i,t}}\text{)}$ term represents Gaussian noise important for capturing the variability of human behavior.

Definition of akaike information criterion

$\begin{array}{rcl}\text{AIC =}& G^2+2\ast k\hfill & \text{(A5)}\hfill \\ G^2=& t\ast ln\frac{\text{SSE}}{t}\hfill & \text{(A6)}\\ \text{SSE}=& \sum _{i=1}^t{\left(x_{\text{model},i}-x_{\text{human},i}\right)}^2& \text{(A7)}\end{array}$

Where, G² is defined as the lack of fit between model and human data (Gonzalez and Dutt, 2011). Furthermore, the x_{model, i} and x_human,i refer to the average dependent measure (e.g., average R-rate or A-rate) in the model and human data over t trials of a task (t = 100 for the R-rate and t = 99 for the A-rate). The average in the dependent measure (R-rate or A-rate) has been taken over all problems and participants. The SSE is the sum of squared errors between human and model datasets that is calculated for the average dependent measure (A-rate or R-rate). The mean-squared error (MSE) is defined as SSE/100 for the R-rate measure and SSE/99 for the A-rate measure. The t is the number of trials in the task, and k is the number of parameters in the model. The AIC in its formulation incorporates both the effect of an MSD (the G² term) as well as the number of free parameters in a model (the 2 ∗ k term). The smaller the value of AIC, the better the respective model is.