- 1 GION –Institute for Educational Research, University of Groningen, Groningen, The Netherlands
- 2 Department of Psychology, University of Groningen, Groningen, The Netherlands
A valid interpretation of most statistical techniques requires that one or more assumptions be met. In published articles, however, little information tends to be reported on whether the data satisfy the assumptions underlying the statistical techniques used. This could be due to self-selection: Only manuscripts with data fulfilling the assumptions are submitted. Another explanation could be that violations of assumptions are rarely checked for in the first place. We studied whether and how 30 researchers checked fictitious data for violations of assumptions in their own working environment. Participants were asked to analyze the data as they would their own data, for which often used and well-known techniques such as the t-procedure, ANOVA and regression (or non-parametric alternatives) were required. It was found that the assumptions of the techniques were rarely checked, and that if they were, it was regularly by means of a statistical test. Interviews afterward revealed a general lack of knowledge about assumptions, the robustness of the techniques with regards to the assumptions, and how (or whether) assumptions should be checked. These data suggest that checking for violations of assumptions is not a well-considered choice, and that the use of statistics can be described as opportunistic.
Introduction
Most statistical techniques require that one or more assumptions be met, or, in the case that it has been proven that a technique is robust against a violation of an assumption, that the assumption is not violated too extremely. Applying the statistical techniques when assumptions are not met is a serious problem when analyzing data (Olsen, 2003; Choi, 2005). Violations of assumptions can seriously influence Type I and Type II errors, and can result in overestimation or underestimation of the inferential measures and effect sizes (Osborne and Waters, 2002). Keselman et al. (1998) argue that “The applied researcher who routinely adopts a traditional procedure without giving thought to its associated assumptions may unwittingly be filling the literature with non-replicable results” (p. 351). Vardeman and Morris (2003) state “…absolutely never use any statistical method without realizing that you are implicitly making assumptions, and that the validity of your results can never be greater than that of the most questionable of these” (p. 26). According to the sixth edition of the APA Publication Manual, the methods researchers use “…must support their analytic burdens, including robustness to violations of the assumptions that underlie them...” [American Psychological Association (APA, 2009); p. 33]. The Manual does not explicitly state that researchers should check for possible violations of assumptions and report whether the assumptions were met, but it seems reasonable to assume that in the case that researchers do not check for violations of assumptions, they should be aware of the robustness of the technique.
Many articles have been written on the robustness of certain techniques with respect to violations of assumptions (e.g., Kohr and Games, 1974; Bradley, 1980; Sawilowsky and Blair, 1992; Wilcox and Keselman, 2003; Bathke, 2004), and many ways of checking to see if assumptions have been met (as well as solutions to overcoming problems associated with any violations) have been proposed (e.g., Keselman et al., 2008). Using a statistical test is one of the frequently mentioned methods of checking for violations of assumptions (for an overview of statistical methodology textbooks that directly or indirectly advocate this method, see e.g., Hayes and Cai, 2007). However, it has also been argued that it is not appropriate to check assumptions by means of tests (such as Levene’s test) carried out before deciding on which statistical analysis technique to use because such tests compound the probability of making a Type I error (e.g., Schucany and Ng, 2006). Even if one desires to check whether or not an assumption is met, two problems stand in the way. First, assumptions are usually about the population, and in a sample the population is by definition not known. For example, it is usually not possible to determine the exact variance of the population in a sample-based study, and therefore it is also impossible to determine that two population variances are equal, as is required for the assumption of equal variances (also referred to as the assumption of homogeneity of variances) to be satisfied. Second, because assumptions are usually defined in a very strict way (e.g., all groups have equal variances in the population, or the variable is normally distributed in the population), the assumptions cannot reasonably be expected to be satisfied. Given these complications, researchers can usually only examine whether assumptions are not violated “too much” in their sample; for deciding on what is too much, information about the robustness of the technique with regard to violations of the assumptions is necessary.
The assumptions of normality and of homogeneity of variances are required to be met for the t-test for independent group means, one of the most widely used statistical tests (Hayes and Cai, 2007), as well as for the frequently used techniques ANOVA and regression (Kashy et al., 2009). The assumption of normality is that the scores in the population in case of a t-test or ANOVA, and the population residuals in case of regression, be normally distributed. The assumption of homogeneity of variance requires equal population variances per group in case of a t-test or ANOVA, and equal population variances for every value of the independent variable for regression. Although researchers might be tempted to think that most statistical procedures are relatively robust against most violations, several studies have shown that this is often not the case, and that in the case of one-way ANOVA, unequal group sizes can have a negative impact on the technique’s robustness (e.g., Havlicek and Peterson, 1977; Wilcox, 1987; Lix et al., 1996).
Many textbooks advise that the assumptions of normality and homogeneity of variance be checked graphically (Hazelton, 2003; Schucany and Ng, 2006), such as by making normal quantile plots for checking for normality. Another method, which is advised in many other textbooks (Hayes and Cai, 2007), is to use a so-called preliminary test to determine whether to continue with the intended technique or to use an alternative technique instead. Preliminary tests could, for example, be used to choose between a pooled t-test and a Welch t-test or between ANOVA and a non-parametric alternative. Following the argument that preliminary tests should not be used because, amongst others, they can inflate the probability of making a Type I error (e.g., Gans, 1981; Wilcox et al., 1986; Best and Rayner, 1987; Zimmerman, 2004, 2011; Schoder et al., 2006; Schucany and Ng, 2006; Rochon and Kieser, 2011), it has also been argued that in many cases unconditional techniques should be the techniques of choice (Hayes and Cai, 2007). For example, the Welch t-test, which does not require homogeneity of variance, would be seen a priori as preferable to the pooled variance t-test (Zimmerman, 1996; Hayes and Cai, 2007).
Although the conclusions one can draw when analyzing a data set with statistical techniques depend on whether the assumptions for that technique are met, and, if that is not the case, whether the technique is robust against violations of the assumption, no work, to our knowledge, describing whether researchers check for violations of assumptions in practice has been published. When possible violations of assumptions are checked, and why they sometimes are not, is a relevant question given the continuing prevalence of preliminary tests. For example, an inspection of the most recent 50 articles published in 2011 in Psychological Science that contained at least one t-test, ANOVA or regression analysis, revealed that in only three of these articles was the normality of the data or the homogeneity of variances discussed, leaving open the question of whether these assumptions were or were not checked in practice, and how. Keselman et al. (1998) showed in a review of 61 articles that used a between-subject univariate design that in only a small minority of articles anything about the assumptions of normality (11%) or homogeneity (8%) was mentioned, and that in only 5% of the articles something about both assumptions was mentioned. In the same article, Keselman et al. present results of another study in which 79 articles with a between-subject multivariate design were checked for references to assumptions, and again the assumptions were rarely mentioned. Osborne (2008) found similar results: In 96 articles published in high quality journals, checking of assumptions was reported in only 8% of the cases.
In the present paper a study is presented in which the behavior of researchers while analyzing data was observed, particularly with regard to the checking for violations of assumptions when analyzing data. It was hypothesized that the checking of assumptions might not routinely occur when analyzing data. There can, of course, be rational reasons for not checking assumptions. Researchers might, for example, have knowledge about the robustness of the technique they are using with respect to violations of assumptions, and therefore consider the checking of possible violations unnecessary. In addition to observing whether or not the data were checked for violations of assumptions, we therefore also administered a questionnaire to assess why data were not always checked for possible violations of assumptions. Specifically, we focused on four possible explanations for failing to check for violations of assumptions: (1) lack of knowledge of the assumption, (2) not knowing how to check whether the assumption has been violated, (3) not considering a possible violation of an assumption problematic (for example, because of the robustness of the technique), and (4) lack of knowledge of an alternative in the case that an assumption seems to be violated.
Materials and Methods
Participants
Thirty Ph.D. students, 13 men and 17 women (mean age = 27, SD = 1.5), working at Psychology Departments (but not in the area of methodology or statistics) throughout The Netherlands, participated in the study. All had at least 2 years experience conducting research at the university level. Ph.D. students were selected because of their active involvement in the collection and analysis of data. Moreover, they were likely to have had their statistical education relatively recently, assuring a relatively up-to-date knowledge of statistics. They were required to have at least once applied a t-procedure, a linear regression analysis and an ANOVA, although not necessarily in their own research project. Ten participants were randomly selected from each of the Universities of Tilburg, Groningen, and Amsterdam, three cities in different regions of The Netherlands. In order to get 30 participants, 41 Ph.D. students were approached for the study, of whom 11 chose not to participate. Informed consent was obtained from all participants, and anonymity was ensured.
Task
The task consisted of two parts: data analysis and questionnaire. For the data analysis task participants were asked to analyze six data sets, and write down their inferential conclusions for each data set. The t-test, ANOVA and regression (or unconditional alternatives to those techniques) were intended to be used, because they are relatively simple, frequently used, and because it was expected that most participants would be familiar with those techniques. Participants could take as much time as they wanted, and no limit was given to the length of the inferential conclusions. The second part of the task consisted of filling in a questionnaire with questions about the participants’ choices during the data analysis task, and about the participants’ usual behavior with respect to assumption checking when analyzing data. All participants needed between 30 and 75 min to complete the data analysis task and between 35 and 65 min to complete the questionnaire. The questionnaire also included questions about participants’ customs regarding visualization of data and inference, but these data are not presented here. All but three participants performed the two tasks at their own workplace. The remaining three used an otherwise unoccupied room in their department. During task performance, the first author was constantly present.
Data analysis task
The data for the six data sets that the participants were asked to analyze were offered in SPSS format, since every participant indicated using SPSS as their standard statistical package. Before starting to analyze the data, the participants were given a short description of a research question without an explicit hypothesis, but with a brief description of the variables in the SPSS file. The participants were asked to analyze the data sets and interpret the results as they do when they analyze and interpret their own data sets. Per data set, they were asked to write down an answer to the following question: “What do these results tell you about the situation in the population? Explain how you came to your conclusion”. An example of such an instruction for which participants were expected to use linear regression analysis, translated from the Dutch, is shown in Figure 1. Participants were explicitly told that consultation of any statistical books or the internet was allowed, but only two participants availed themselves of this opportunity.
Figure 1. An example of one of the research question descriptions. In this example, participants were supposed to answer this question by means of a regression analysis.
The short description of the six research questions was written in such a way as to suggest that two t-tests, two linear regression analyses and two ANOVAs should be carried out, without explicitly naming the analysis techniques. Of course, non-parametric or unconditional alternatives were considered appropriate, as well. The results of a pilot experiment indicated that the descriptions were indeed sufficient to guide people in using the desired technique: The five people tested in the pilot used the intended technique for each of the six data sets. All six research question descriptions, also in translated form, can be found in the Appendix to this study.
The six data sets differed with respect to the effect size, the significance of the outcomes, and to whether there was a “strong” violation of an assumption. Four of the six data sets contained significant effects, one of the two data sets for which a t-test was supposed to be used contained a clear violation of the assumption of normality, one of the two data sets for which ANOVA was supposed to be used contained a clear violation of the assumption of homogeneity of variance, and effect size was relatively large in three data sets and relatively small in the other data sets (see Table 1 for an overview).
Table 1. An overview of the properties of the six scenarios.
To get more information on which choices were made by the participants during task performance, and why these choices were made, participants were asked to “think aloud” during task performance. This was recorded on cassette. During task performance, the selections made within the SPSS program were noted by the first author, in order to be able to check whether there was any check for the assumptions relevant for the technique that was used. Furthermore, participants were asked to save the SPSS syntax files. For the analysis of task performance, the information from the notes made by the first author, the tape recordings and the syntax files were combined to examine behavior with respect to checking for violations of the assumptions of normality and homogeneity of variance. Of course, had participants chosen unconditional techniques for which one or both of these assumptions were not required to be met, their data for the scenario in question would not have been used, provided that a preliminary test was not carried out to decide whether to use the unconditional technique. However, in no cases were unconditional techniques used or even considered. The frequency of selecting preliminary tests was recorded separately.
Each data set was scored according to whether violations of the assumptions of normality and homogeneity of variance were checked for. A graphical assessment was counted as correctly checking for the assumption, provided that the assessment was appropriate for the technique at hand. A correct check for the assumption of normality was recorded if, for the t-test and ANOVA, a graphical representation of the different groups was requested, except when the graph was used only to detect outliers. Merely looking at the numbers, without making a visual representation was considered insufficient. For regression analysis, making a plot of the residuals was considered to be a correct check of the assumption of normality. Deciding whether this was done explicitly was based on whether the participant made any reference to normality when thinking aloud. A second option was to make a QQ- or PP-plot of the residuals. Selecting the Kolmogorov–Smirnov test or the Shapiro–Wilk test within SPSS was considered checking for the assumption of normality using a preliminary test.
Three ways of checking for the assumption of homogeneity of variance for the t-test and ANOVA were considered adequate. The first was to make a graphical representation of the data in such a way that difference in variance between the groups was visible (e.g., boxplots or scatter plots, provided that they are given per group). A second way was to make an explicit reference to the variance of the groups. A final possibility was to compare standard deviations of the groups in the output, with or without making use of a rule of thumb to discriminate between violations and non-violations. For regression analysis, a scatter plot or a residual plot was considered necessary to check the assumption of homogeneity of variance. Although the assumption of homogeneity of variance assumes equality of the population variations, an explicit reference to the population was not required. The preliminary tests that were recorded included Levene’s test, the F-ratio test, Bartlett’s test, and the Brown–Forsythe test.
The frequency of using preliminary tests was reported separately from other ways of checking for assumptions. Although the use of preliminary tests is often considered an inappropriate method for checking assumptions, their use does show awareness of the existence of the assumption. Occurrences of checking for irrelevant assumptions, such as equal group sizes for the t-test, or normality of all scores for one variable (instead of checking for normality per group) for all three techniques were also counted, but scored as incorrectly checking for an assumption.
Questionnaire
The questionnaire addressed four explanations for why an assumption was not checked: (1) Unfamiliarity with the assumption, (2) Unfamiliarity with how to check the assumptions, (3) Violation of the assumption not being regarded problematic, and (4) Unfamiliarity with a remedy against a violation of the assumption. Each of these explanations was operationalized before the questionnaires were analyzed. The experimenter was present during questionnaire administration to stimulate the participants to answer more extensively, if necessary, or ask them to reformulate their answer when they seemed to have misread the question.
Unfamiliarity with the assumptions. Participants were asked to write down the assumptions they thought it was necessary to check for each of the three statistical techniques used in the study. Simply mentioning the assumption of normality or homogeneity of variance was scored as being familiar with the assumption, even if the participants did not specify what, exactly, was required to follow a normal distribution or which variances were supposed to be equal. Explaining the assumptions without explicitly mentioning them was also scored as being familiar with this assumption.
Unfamiliarity with how to check the assumptions. Participants were asked if they could think of a way to investigate whether there was a violation of each of the two assumptions (normality and homogeneity of variance) for t-tests, ANOVA and regression, respectively. Thus, the assumptions per technique were explicitly given, whether or not they had been correctly reported in answer to the previous question. For normality, specifying how to visualize the data in such a way that a possible violation was visible was categorized as a correct way of checking for assumption violations (for example: making a QQ-plot, or making a histogram), even when no further information was given about how to make such a visualization. Mentioning a measure of or a test for normality was also considered correct. For studying homogeneity of variance, rules of thumb or tests, such as Levene’s test for testing equality of variances, were categorized as a correct way of checking this assumption, and the same holds for eyeballing visual representations from which variances could be deduced. Note that the criteria for a correct check are lenient, since they include preliminary tests that are usually considered inappropriate.
Violation of the assumption not being regarded problematic. For techniques for which it has been shown that they are robust against certain assumption violations, it can be argued that it makes sense not to check for these assumptions, because the outcome of this checking process would not influence the interpretation of the data anyway. To study this explanation, participants were asked per assumption and for the three techniques whether they considered a possible violation to be influential. Afterward, the answers that indicated that this influence was small or absent were scored as satisfying the criteria for this explanation.
Unfamiliarity with a remedy against a violation of an assumption. One could imagine that a possible violation of assumptions is not checked because no remedy for such violations is known. Participants were thus asked to note remedies for possible violations of normality and homogeneity of variance for each of the three statistical analysis techniques. Correct remedies were defined as transforming the data (it was not required that participants specify which transformation), using a different technique (e.g., a non-parametric technique when the assumption of normality has been violated) and increasing the sample size.
Data Analysis
All results are presented as percentages of the total number of participants or of the total number of analyzed data sets, depending on the specific research question. Confidence intervals (CIs) are given, but should be interpreted cautiously because the sample cannot be regarded as being completely random. The CIs for percentages were calculated by the so-called Score CIs (Wilson, 1927). All CIs are 95% CIs.
Results
Of the six datasets that the 30 participants were required to analyze, in all but three instances the expected technique was chosen. In the remaining three instances, ANOVA was used to analyze data sets that were meant to be analyzed by means of a t-test. Since ANOVA is in this case completely equivalent to an independent-samples t-test, it can be concluded that an appropriate technique was chosen for all data sets. In none of these cases, an unconditional technique was chosen.
Violations of, or conformance with, the assumptions of normality and homogeneity of variance were correctly checked in 12% (95%CI = [8%, 18%]) and 23% (95%CI = [18%, 30%]), respectively, of the analyzed data sets. Figure 2 shows for each of the three techniques how frequently possible violations of the assumptions of normality and homogeneity of variance occurred, and whether the checking was done correctly, or whether a preliminary test was used. Note that the assumption of normality was rarely checked for regression, and never correctly. In the few occasions that normality was checked the normality of the scores instead of the residuals was examined. Although this approach might be useful for studying the distribution of the scores, it is insufficient for determining whether the assumption of normality has been violated.
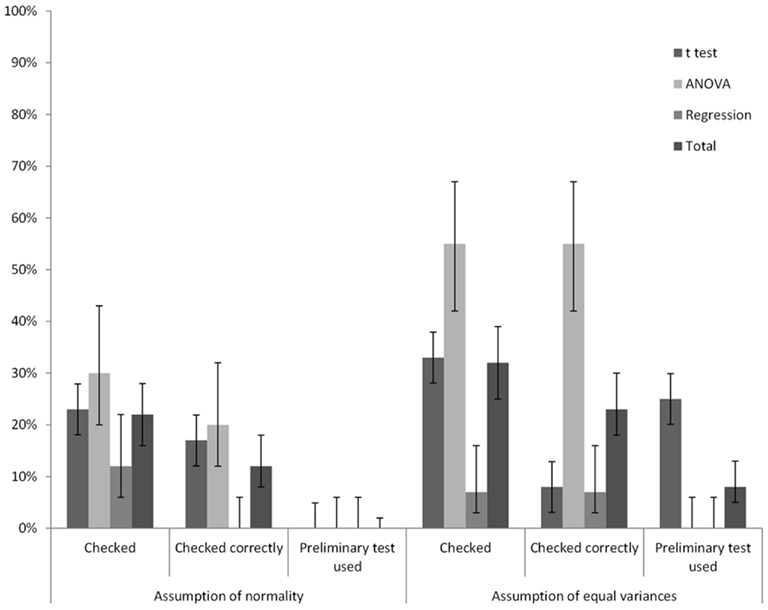
Figure 2. The frequency of whether two assumptions were checked at all, whether they were checked correctly, and whether a preliminary test was used for three often used techniques in percentages of the total number of cases. Between brackets are 95% CIs for the percentages.
The percentages of participants giving each of the four reasons for not checking assumptions as measured by the questionnaire are given in Figure 3. A majority of the participants were unfamiliar with the assumptions. For each assumption, only a minority of participants mentioned at least one of the correct ways to check for a violation of the assumption. The majority of the participants failed to indicate that the alleged robustness of a technique against violations of the relevant assumption was a reason not to check these assumptions in the first place. Many participants did not know whether a violation of an assumption was important or not. Only in a minority of instances was an acceptable remedy for a violation of an assumption mentioned. No unacceptable remedies were mentioned. In general, participants indicated little knowledge of how to overcome a violation of one of the assumptions, and most participants reported never having looked for a remedy against a violation of statistical assumptions.
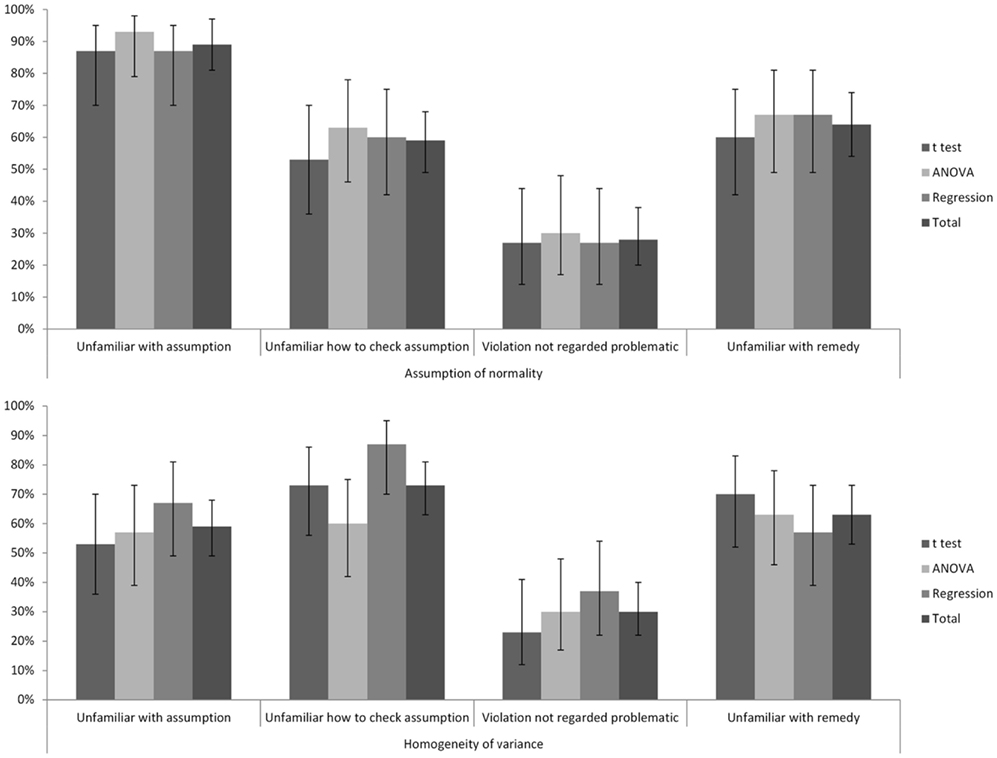
Figure 3. Percentages of participants giving each of the explanations for not checking assumptions as a function of assumption and technique. Error bars indicate 95% CIs.
Participants had been told what the relevant assumptions were before they had to answer these questions. Therefore, the results for the last three explanations per assumption in Figure 3 are reported for all participants, despite the fact that many participants reported being unfamiliar with the assumption. This implies that, especially for the assumption of normality and to a lesser extent for the assumption of equal variances, the results regarding the last three explanations should be interpreted with caution.
Discussion
In order to examine people’s understanding of the assumptions of statistical tests and their behavior with regard to checking these assumptions, 30 researchers were asked to analyze six data sets using the t-test, ANOVA, regression or a non-parametric alternative, as appropriate. All participants carried out nominally appropriate analyses, but only in a minority of cases were the data examined for possible violations of assumptions of the chosen techniques. Preliminary test outcomes were rarely consulted, and only if given by default in the course of carrying out an analysis. The results of a questionnaire administered after the analyses were performed revealed that the failure to check for violations of assumptions could be attributed to the researchers’ lack of knowledge about the assumptions, rather than to a deliberate decision not to check the data for violations of the assumptions.
Homogeneity of variance was checked for in roughly a third of all cases and the assumption of normality in less than a quarter of the data sets that were analyzed. Moreover, for the assumption of normality checks were often carried out incorrectly. An explanation for the finding that the assumption of homogeneity of variance was checked more often than the assumption of normality is the fact that a clear violation of this assumption can often be directly deduced from the standard deviations, whereas measures indicating normality are less common. Furthermore, many participants seemed familiar with a rule of thumb to check whether the assumption of homogeneity of variance for ANOVA is violated (e.g., largest standard deviation is larger than twice the smallest standard deviation), whereas such rules of thumb for checking possible violations of the assumption of normality were unknown to our participants. It was also found that Levene’s test was often used as a preliminary test to choose between the pooled t-test and the Welch t-test, despite the fact that the use of preliminary tests is often discouraged (e.g., Wilcox et al., 1986; Zimmerman, 2004, 2011; Schucany and Ng, 2006). An obvious explanation for this could be that the outcomes of Levene’s test are given as a default option for the t procedure in SPSS (this was the case in all versions that were used by the participants). The presence of Levene’s test together with the corresponding t-tests may have led researchers to think that they should use this information. Support for this hypothesis is that preliminary tests were not carried out in any other cases.
It is possible that researchers have well-considered reasons for not checking for possible violations of assumption. For example, they may be aware of the robustness of a technique with respect to violations of a particular assumption, and quite reasonably chose not to check to see if the assumption is violated. Our questionnaire, however, revealed that many researchers simply do not know which assumptions should be met for the t-test, ANOVA, and regression analysis. Only a minority of the researchers correctly named both assumptions, despite the fact that the statistical techniques themselves were well-known to the participants. Even when the assumptions were provided to the participants during the course of filling out the questionnaire, only a minority of the participants reported knowing a means of checking for violations, let alone which measures could be taken to remedy any possible violations or which tests could be used instead when violations could not be remedied.
A limitation of the present study is that, although researchers were asked to perform the tasks in their own working environment, the setting was nevertheless artificial, and for that reason the outcomes might have been biased. Researchers were obviously aware that they were being watched during this observation study, which may have changed their behavior. However, we expect that if they did indeed conduct the analyses differently than they would normally do, they likely attempted to perform better rather than worse than usual. A second limitation of the study is the relatively small number of participants. Despite this limited number and the resulting lower power, however, the effects are large, and the CIs show that the outcomes are unlikely to be due to chance alone. A third limitation is the possible presence of selection bias. The sample was not completely random because the selection of the universities involved could be considered a convenience sample. However, we have no reason to think that the sample is not representative of Ph.D. students at research universities. A fourth and last limitation is the fact that it is not clear what training each of the participants had on the topic of assumptions. However, all had their education in Psychology Departments in The Netherlands, where statistics is an important part of the basic curriculum. It is thus unlikely that they were not subjected to extensive discussion on the importance of meeting assumptions.
Our findings show that researchers are relatively unknowledgeable when it comes to when and how data should be checked for violations of assumptions of statistical tests. It is notable that the scientific community tolerates this lack of knowledge. One possible explanation for this state of affairs is that the scientific community as a whole does not consider it important to verify that the assumptions of statistical tests are met. Alternatively, other scientists may assume too readily that if nothing is said about assumptions in a manuscript, any crucial assumptions were met. Our results suggest that in many cases this might be a premature conclusion. It seems important to consider how statistical education can be improved to draw attention to the place of checking for assumptions in statistics and how to deal with possible violations (including deciding to use unconditional techniques). Requiring that authors describe how they checked for the violation of assumptions when the techniques applied are not robust to violations would, as Bakker and Wicherts (2011) have proposed, force researchers on both ends of the publishing process to show more awareness of this important issue.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
American Psychological Association. (2009). Publication Manual of the American Psychological Association, 6th Edn. Washington, DC: American Psychological Association
Bakker, M., and Wicherts, J. M. (2011). The (mis)reporting of statistical results in psychology journals. Behav. Res. Methods 43, 666–678.
Bathke, A. (2004). The ANOVA F test can still be used in some unbalanced designs with unequal variances and nonnormal data. J. Stat. Plan. Inference 126, 413–422.
Best, D. J., and Rayner, J. C. W. (1987). Welch’s approximate solution for the Behrens–Fisher problem. Technometrics 29, 205–210.
Bradley, J. V. (1980). Nonrobustness in Z, t, and F tests at large sample sizes. Bull. Psychon. Soc. 16, 333–336.
Choi, P. T. (2005). Statistics for the reader: what to ask before believing the results. Can. J. Anaesth. 52, R1–R5.
Gans, D. J. (1981). Use of a preliminary test in comparing two sample means. Commun. Stat. Simul. Comput. 10, 163–174.
Havlicek, L. L., and Peterson, N. L. (1977). Effects of the violation of assumptions upon significance levels of the Pearson r. Psychol. Bull. 84, 373–377.
Hayes, A. F., and Cai, L. (2007). Further evaluating the conditional decision rule for comparing two independent means. Br. J. Math. Stat. Psychol. 60, 217–244.
Kashy, D. A., Donnellan, M. B., Ackerman, R. A., and Russell, D. W. (2009). Reporting and interpreting research in PSPB: Practices, principles, and pragmatics. Pers. Soc. Psychol. Bull. 35, 1131–1142.
Keselman, H. J., Algina, J., Lix, L. M., Wilcox, R. R., and Deering, K. N. (2008). A generally robust approach for testing hypotheses and setting confidence intervals for effect sizes. Psychol. Methods 13, 110–129.
Keselman, H. J., Huberty, C. J., Lix, L. M., Olejnik, S., Cribbie, R., Donahue, B., Kowalchuk, R. K., Lowman, L. L., Petoskey, M. D., Keselman, J. C., and Levin, J. R. (1998). Statistical practices of educational researchers: an analysis of their ANOVA, MANOVA and ANCOVA. Rev. Educ. Res. 68, 350.
Kohr, R. L., and Games, P. A. (1974). Robustness of the analysis of variance, the Welch procedure and a Box procedure to heterogeneous variances. J. Exp. Educ. 43, 61–69.
Lix, L. M., Keselman, J. C., and Keselman, H. J. (1996). Consequences of assumption violations revisited: a quantitative review of alternatives to the one-way analysis of variance F test. Rev. Educ. Res. 66, 579–620.
Olsen, C. H. (2003). Review of the use of statistics in infection and immunity. Infect. Immun. 71, 6689–6692.
Osborne, J. (2008). Sweating the small stuff in educational psychology: how effect size and power reporting failed to change from 1969 to 1999, and what that means for the future of changing practices. Educ. Psychol. 28, 151–160.
Osborne, J. W., and Waters, E. (2002). Four assumptions of multiple regression that researchers should always test. Pract. Assess. Res. Evalu. 8. Available at: http://www-psychology.concordia.ca/fac/kline/495/osborne.pdf
Rochon, J., and Kieser, M. (2011). A closer look at the effect of preliminary goodness-of-fit testing for normality for the one-sample t-test. Br. J. Math. Stat. Psychol. 64, 410–426.
Sawilowsky, S. S., and Blair, R. C. (1992). A more realistic look at the robustness and type II error properties of the t test to departures from population normality. Psychol. Bull. 111, 352–360.
Schoder, V., Himmelmann, A., and Wilhelm, K. P. (2006). Preliminary testing for normality: some statistical aspects of a common concept. Clin. Exp. Dermatol. 31, 757–761.
Schucany, W. R., and Ng, H. K. T. (2006). Preliminary goodness-of-fit tests for normality do not validate the one-sample Student t. Commun. Stat. Theory Methods 35, 2275–2286.
Vardeman, S. B., and Morris, M. D. (2003). Statistics and ethics: some advice for young statisticians. Am. Stat. 57, 21.
Wilcox, R. R., Charlin, V. L., and Thompson, K. L. (1986). New Monte Carlo results on the robustness of the ANOVA F, W, and F* statistics. Commun. Stat. Simul. Comput. 15, 933–943.
Wilcox, R. R., and Keselman, H. J. (2003). Modern robust data analysis methods: measures of central tendency. Psychol. Methods 8, 254–274.
Wilson, E. B. (1927). Probable inference, the law of succession, and statistical inference. J. Am. Stat. Assoc. 22, 209–212.
Zimmerman, D. W. (1996). Some properties of preliminary tests of equality of variances in the two-sample location problem. J. Gen. Psychol. 123, 217–231.
Zimmerman, D. W. (2004). A note on preliminary tests of equality of variances. Br. J. Math. Stat. Psychol. 57, 173–181.
Zimmerman, D. W. (2011). A simple and effective decision rule for choosing a significance test to protect against non-normality. Br. J. Math. Stat. Psychol. 64, 388–409.
Appendix
Research question descriptions
In this Appendix, the six research question descriptions are presented in translated form. Descriptions 1 and 2 were supposed to be answered by means of a t-test, Descriptions 3 and 4 by means of regression analysis, and Descriptions 5 and 6 by means of ANOVA.
1. A researcher is interested in the extent to which group A and group B differ in cognitive transcentivity. He has scores of 25 randomly selected participants from each of the two groups on a cognitive transcentivity test (with the range of possible scores from 0 to 25). In Column 1 of the SPSS file, the scores of the participants on the test are given, and in column 2 the group membership (group A or B) is given.
2. A researcher is interested in the extent to which group C and group D differ in cognitive transcentivity. He has scores of 25 randomly selected participants from each of the two groups on a cognitive transcentivity test (with the range of possible scores from 0 to 25). In Column 1 of the SPSS file, the scores of the participants on the test are given, and in column 2 the group membership (group C or D) is given.
3. A researcher is interested to what extent the weight of men can predict their self-esteem. She expects a linear relationship between weight and self-esteem. To study the relationship, she takes a random sample of 100 men, and administers a questionnaire to them to measure their self-esteem (on a scale from 0 to 50), and measures the participants’ weight. In Column 1 of the SPSS file, the scores on the self-esteem questionnaire are given. The second column shows the weights of the men, measured in kilograms.
4. A researcher is interested to what extent the weight of women can predict their self-esteem. She expects a linear relationship between weight and self-esteem. To study the relationship, she takes a random sample of 100 women, and administers a questionnaire to them to measure their self-esteem (on a scale from 0 to 50), and measures the participants’ weight. In Column 1 of the SPSS file, the scores on the self-esteem questionnaire are given. The second column shows the weights of the women, measured in kilograms.
5. A researcher is interested to what extent young people of three nationalities differ with respect to the time in which they can run the 100 meters. To study this, 20 persons between 20 and 30 years of age per nationality are randomly selected, and the times in which they run the 100 meters is measured. In Column 1 of the SPSS file, their times are given in seconds. The numbers “1, “2,” and “3” in Column 2 represent the three different nationalities.
6. A researcher is interested to what extent young people of three
Keywords: assumptions, robustness, analyzing data, normality, homogeneity
Citation: Hoekstra R, Kiers HAL and Johnson A (2012) Are assumptions of well-known statistical techniques checked, and why (not)?. Front. Psychology 3:137. doi: 10.3389/fpsyg.2012.00137
Received: 07 November 2011; Accepted: 20 April 2012;
Published online: 14 May 2012.
Edited by:
Jason W. Osborne, Old Dominion University, USAReviewed by:
Jason W. Osborne, Old Dominion University, USAJelte M. Wicherts, University of Amsterdam, The Netherlands
Copyright: © 2012 Hoekstra, Kiers and Johnson. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Rink Hoekstra, GION, University of Groningen, Grote Rozenstraat 3, 9712 TG Groningen, The Netherlands e-mail: r.hoekstra@rug.nl