Intrinsic noise within viscous solids and impact on material exploration

This paper introduces the concept of the intrinsic-noise-atom (i.e., intrinsic-noise-element) and its applications. We propose a method to extract intrinsic noise generated within viscous solids and discuss its impact on material exploration and analysis. The analysis is designed to improve our ability to explore viscous material, enhancing the inversion of physical formation characteristics in acoustic logging while drilling. We show that under a harmonic single-frequency force, the medium viscosity and the particles’ inertia inside the viscous solids lead to a transient process from the static state to the stable state of a harmonic single-frequency vibration. The spectrum corresponding to this transient process reveals information on the intrinsic noise within viscous solids. A damped oscillatory spring model of particle vibration corresponding to longitudinal wave propagation is established, and the acoustic impulse response and system function are obtained, where we can extract the intrinsic noise signal from the vibration state generated by the particle under the action of harmonic single-frequency force. Based on a representative frequency spectrum, the characteristics of the physical formation around the drilled oil well can be retrieved to determine whether it is a hydrocarbon reservoir and if there are deformations, such as fractures, or if it is in good condition. With its reliability, this method can effectively extract the intrinsic noise and successfully retrieve the characteristics of the physical formation of solid media.

1 Introduction

Owing to the particle’s inertia and medium viscosity within viscous solids, a stationary particle undergoes a critical transition from a static state to a stable harmonic single-frequency vibration under a harmonic single-frequency force. The spectrum associated with this transient transition process corresponds to the intrinsic noise generated by the vibrating particle. We define the intrinsic noise produced by a harmonic single-frequency force acting on a particle as an “intrinsic-noise-atom.” Based on the principles of linear superposition and Fourier transform, the intrinsic noise induced by multifrequency forces can be considered as the superposition of intrinsic-noise-atoms caused by each harmonic frequency component of the multifrequency force. The combination or superposition of different intrinsic-noise-atoms can constitute the intrinsic noise generated by any complex multifrequency force applied to a particle. Studying the intrinsic-noise-atom is crucial in understanding the complex vibrational particle behavior and the propagation property of waves in viscous solids. Intrinsic noise is a natural physical phenomenon of particle vibration in viscous solids under external disturbances. At the same time, the intrinsic-noise-atom is a key concept and a critical factor in acoustic measurement for practical applications.

The physical properties and microstructures of different solid media exhibit distinct characteristics. For instance, when the harmonic single-frequency force is applied to particles inside different mediums or objects, the transient transition processes generated during their vibrations, along with the corresponding spectra and central frequencies, vary accordingly. Consequently, the information conveyed by intrinsic-noise-atoms (or intrinsic noise) is helpful to infer the physical properties of the media and their internal structures.

Extensive research has been conducted on intrinsic-noise-atom or intrinsic noise at the micro/macro scale, leading to applications across various fields. Based on frequency domain analysis, Michael et al. described a frequency-domain technique for analyzing intrinsic noise generated in negatively self-regulating genetic circuits [1]. Ramaswamy et al. studied how intrinsic spectral noise affects mesoscopic oscillating chemical reactions [2]. Alex et al. introduced an extended mathematical framework for analyzing classical intrinsic/extrinsic noise [3]. Jangir et al. demonstrated that intrinsic randomness in biochemical reactions (intrinsic noise) and variability in cellular states (extrinsic noise) reduce information transfer through signaling networks [4]. Villegas et al. investigated intrinsic noise and critical deviation in Boolean gene regulatory networks [5]. Hong et al. highlighted that acoustic stress and wave resonance play crucial roles in plasma bubbles, providing novel approaches for sustainable chemical processes [6]. Fa and Zhao also reported intrinsic noise generated during the vibration of particles in viscous media and piezoelectric transducers, along with its potential applications [7].

The transient transition process and the intrinsic noise generated by the whole motion of some objects have also been studied. Piquette theoretically and experimentally studied the transient response of piezoelectric transducers, revealing that harmonic single-frequency voltage excitation of piezoelectric transducers produces a transient process from a stationary state to a steady harmonic single-frequency vibration [8, 9]. Similarly, Fa and Zhao et al. confirmed the transient process of piezoelectric transducers transitioning from stationary to steady harmonic single-frequency vibration under harmonic single-frequency electrical excitation [10–13]. The frequency spectrum corresponding to this transient process represents the intrinsic noise generated during the vibration of the transducer. They verified the existence of the intrinsic-noise-atom generated by the piezoelectric transducer. Fa and Zhao at al. Have also experimentally confirmed the presence of intrinsic noise generated during piezoelectric transducers’ vibration when excited by a multifrequency electric-voltage signal [14]. Zha et al. studied novel piezoelectric surface and bulk acoustic wave resonators for communication technologies, which also involved intrinsic noise applications [15].

The transient responses of piezoelectric transducers with mechanical loads have also been investigated. Moon et al. found that the center frequency of a piezoelectric transducer varies with the mechanical load and environmental conditions. They proposed a method to track the resonant frequency by using the transient characteristics of the transducer [16]. Wang et al. studied the relationship between the central frequency of intrinsic noise and the early strength development of cement mortar by using piezoelectric transducers. Their findings showed that the central frequency of intrinsic noise is related to the properties of the cement mortar surrounding the transducer, which represents the combined response of the mechanical load of cement mortar and the electric-acoustic (or acoustic-electric) conversion of the piezoelectric transducer [17].

From the foregoing analysis and discussion, it is evident that whether considering a particle within a viscous solid medium, a composite structure formed by two media, or an entire object, any alteration in their motion state due to external perturbations will generate associated intrinsic noise. The transient process of harmonic states and the corresponding spectra are influenced by the medium’s viscosity, density, stiffness, and other properties, as well as the geometry of the particle or object.

The concept of the intrinsic-noise-atom holds significant implications for the forward modeling of intrinsic noise and for inverting physical properties of the measured medium and its geometric structure using the intrinsic noise information contained within acoustic signals. Leveraging the matching pursuit algorithm [19, 20], Zhang and Castagna developed a wavelet dictionary for seismic exploration signals derived from the well logging data. They used logging data from several oil wells (including density and acoustic velocity) and specialized algorithms to construct a wavelet dictionary for seismic exploration signals. By matching and tracking the recorded seismic exploration data against the basic wavelet element in this wavelet dictionary, they successfully reconstructed information on the characteristics and structures of underground rock formations (such as reflection coefficient sequences), aiding in the search for hydrocarbon reservoirs [21, 22]. We propose replacing the logging data with intrinsic noise data from limited acoustic signals that measure homogeneous or heterogeneous media with varying internal structures. Employing algorithms of interpolation, extrapolation, scaling and squeeze/stretch of frequency, we also can construct a dictionary of intrinsic-noise-atoms by using some intrinsic noises generated from vibration particles in media with diverse physical properties and structures [19]. This intrinsic noise dictionary and the intrinsic noise extracted from the measured acoustic signal are then used for matching-pursuing and iterative calculations to reconstruct the physical characteristics (such as reflection coefficients and acoustic velocities) and internal structure of the measured medium. Meanwhile, the intrinsic noise extracted from acoustic signals and density data measured by Logging while drilling (LWD) are valuable elements for reconstructing the acoustic wave propagation velocity in the formation.

This allows for the accurate acquisition of formation wave first arrivals and enables the inversion of formation properties around the drilled well using spectral information. It helps determine whether reservoirs and fractures are present, as well as oil/gas content and evaluates the cement bond quality of the cased well. Although substantial research has been conducted on intrinsic noise, the physical mechanisms of its generation still require study, and its potential applications merit further exploration, such as the study of intrinsic noise provides one of the essential conditions for the parallel/series acoustic lumped particle vibrational transmission network model which can describe the whole acoustic measurement process more accurately from the physical mechanism.

2 Physical model

2.1 The model of viscous solid with particle vibrations

The vibrating “particles” in acoustics are fundamental tangible substances with mass and energy. When the harmonic single-frequency force compelling the particle to vibrate near its equilibrium position in a viscous solid suddenly disappears, the amplitude of the particle’s vibration diminishes over time due to energy dissipation from frictional resistance force. When a harmonic single-frequency force is applied to the stationary particle in a viscous solid, a particle transitions from stationary to stable harmonic single-frequency vibration due to the particle’s inertia and the medium’s viscosity.

Therefore, in addition to the frequency component of the steady-state harmonic single-frequency vibration, the particle vibration also contains the frequency component corresponding to the transient process of the particle vibration, i.e., the frequency component of the intrinsic noise.

Damping can be used to measure the attenuation of a particle’s vibration amplitude inside a medium near its equilibrium position as time increases. Then, we may analyze the intrinsic noise corresponding to the transient process experienced by the vibration of a particle inside a viscous solid.

Particle vibration in a viscous medium will be affected by frictional resistance force. The magnitude of this frictional resistance is not only related to the viscosity of the medium but also to the geometric shape and size of the object, the mode of movement, and the speed. For instance, when a small ball moves within a viscous liquid at a constant speed, it encounters a frictional resistance force,

$f_f=6\mathrm{\pi }r\eta v=R_{0}v(1)$

In Equation 1, the frictional resistance force is proportional to friction resistance ($R_0=6\mathrm{\pi }r\eta$), and it is proportional to the radius of the ball (r), its speed (v), and the viscosity coefficient of the viscous liquid (η).

Considering particle vibration in viscous solid media, let’s assume the particles behave like tiny balls with a constant radius. During their vibrational motion, the influence of the geometric parameter of particles on the friction resistance remains unchanged. The key impact factors are the vibration speed and viscosity of the solid media. In analogy to Equation 1, we assume that the frictional resistance force of the vibrating particles in the viscous solid medium is proportional to the vibration speed and the viscosity coefficient of the medium surrounding the particles, and the direction of the frictional resistance force is opposite to that of movement of the particles.

The P-wave corresponds to the compression and extension strain of the solid medium. Elastic damping is a complex phenomenon associated with the strain mode within a solid medium caused by the vibration of the particles. When the particle vibrates, the size and density of the volume element in a solid medium will change. As shown in Figure 1A, the compression deformation of the uniform compression rod, we will use such a model to analyze the particle vibration process corresponding to the P-wave. As shown in Figure 1B, the compression strain of the compression rod is equivalent to a spring oscillator model. Assume that the length of the spring when the particle is in the equilibrium position is $l_0$, the instantaneous length during the vibration process is l, and the displacement of the particle is u. It yields an analytical solution of its particle vibration by solving the corresponding second-order differential motion equation with constant coefficients.

Figure 1

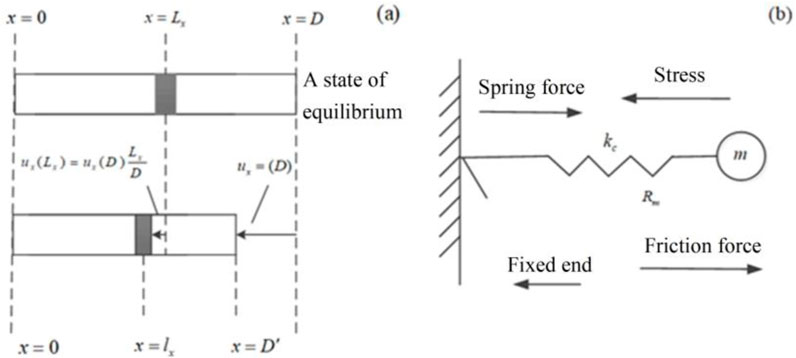
Figure 1. Mechanical analogy model of particle damped vibration corresponding to P-wave: (a) Compression deformation of a uniformly compressed rod; (b) Equivalent spring oscillator.

Assuming that the P-wave propagates along the x-axial direction, the displacement direction of the particle corresponding to the P-wave is parallel to the x-axial direction, which is the horizontal direction in Figure 1B. In such a spring oscillator model of compression/extension strain, the particle is initially at the equilibrium position with the length of the spring $l_0$, and the corresponding particle displacement is equal to zero. During the particle vibration, it yields a measured length of the spring ($l$) and the corresponding particle displacement ($u=l-l_0$). In the P-wave spring oscillator model, the lengthening and shortening of the spring changes periodically, i.e., the spring length ($l$) can be longer or shorter than the length at equilibrium ($l_0$).

As shown in Figure 1, in addition to the ideal microscopic elastic force, the vibrating particles in the viscous solid medium are also subject to frictional resistance force ($f_f$). Assuming that the frictional resistance ($R_m$) to the spherical particles in viscous solid media is an analogy with the frictional resistance ($R_0$) of the small ball moving at a constant speed in the viscous liquid described in Equation 1, then the size of the frictional resistance ($R_m$) is also proportional to the viscosity of the solid media. So, the frictional resistance-force ($f_f$) generated by the viscosity of the solid medium on the vibrating particles is always parallel to the horizontal direction and opposite to the direction of motion of the particles, which can be written by

$f_f=-R_m\frac{\mathrm{d}u}{\mathrm{d}t}(2)$

The particle displacement corresponding to the P-wave is

$u=x=l-l_0=\Delta l(3)$

For a given stiffness coefficient ($k$), the elastic force on the corresponding vibrating particle is

$f_k=-k\Delta l=-kx=-ku(4)$

2.2 Impulse response and system function

When a harmonic single-frequency external force ($f_{ext}$) acts upon a particle in a viscous solid medium, based on Equations 2–4, the resultant force can be written by

$f_{total}=f_{ext}+f_f+f_k=f_{ext}-R_m\frac{\mathrm{d}u}{\mathrm{d}t}-ku(5)$

In accordance with Newton’s Second Law and Equation 5, we can derive a second-order linear differential equation with constant coefficients that describes the motion of a particle as follows,

$m\frac{{\mathrm{d}}^{2}u}{\mathrm{d}{t}^2}+R_m\frac{\mathrm{d}u}{\mathrm{d}t}+ku=f_{ext}(6)$

The displacement velocity of the particle ($v=\mathrm{d}u/\mathrm{d}t$) is analogous to the current in the electrical network ($I=\mathrm{d}Q/\mathrm{d}t$); the mass (m) is analogous to the inductance ($L$); the force compliance ($C_m=1/k_c$) is analogous to the capacitance (C); the friction-resistance ($R_m$) is analogous to the resistance ($R$); the action force ($f_{ext}$) is analogous to the voltage source ($V$). The equation of motion, i.e., Equation 6, provides the corresponding time domain network, as shown in Figure 2A. Converting an equivalent mechanical network to the s-domain can help solve the acoustic impulse response and system function, as shown in Figure 2B.

Figure 2

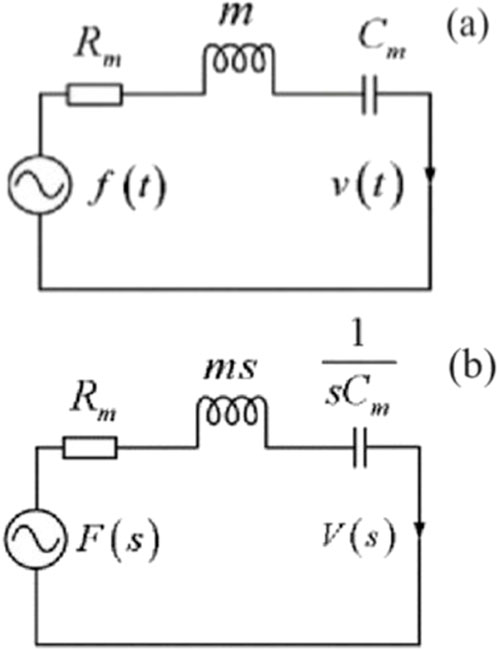
Figure 2. Equivalent mechanical network of particle motion in viscous solids: (a) Time domain; (b) s-domain.

The displacement velocity ($v\left(t\right)$) and the external force ($f_{ext}\left(t\right)$) acting on the particle are functions of time in the time domain. The corresponding quantities are $V\left(s\right)$ and $F_{ext}\left(s\right)$ in s-domain. So, we can get the expressions of the displacement velocity and the system function of the mechanical network (i.e., the ratio of displacement velocity and the external force) in the s-domain as follows,

$V\left(s\right)=\frac{F_{ext}\left(s\right)}{R_m+ms+\frac{1}{C_{m}s}}(7)$

$H\left(s\right)=\frac{V\left(s\right)}{F_{ext}\left(s\right)}=\frac{C_{m}s}{m{C}_m{s}^2+R_m{C}_{m}s+1}(8)$

Using the residue theorem, we can get the analytical expression of the mechanical network impulse response corresponding to the particle motion in the time domain as follows,

$h\left(t\right)={\displaystyle \sum _{j=1}^N}\text{Res}\left[H\left(s_j\right){\mathrm{e}}^{s_{j}t}\right](9)$

where, N is the number of singular points of system function ($H\left(s\right)$) and $s_j$ is the roots of the denominator in Formula 8, which is a quadratic polynomial [$m{C}_m{s}^2+R_m{C}_{m}s+1=\left(s+s_1\right)\left(s+s_2\right)$]. So we have

$s_{1,2}=\frac{-R_m{C}_m\pm \sqrt{{\left(R_m{C}_m\right)}^2-4m{C}_m}}{2m{C}_m}=-\beta \pm \alpha (10)$

here $\alpha =\sqrt{{\left(R_m{C}_m\right)}^2-4m{C}_m}/\left(2m{C}_m\right)$; $\beta =R_m/\left(2m\right)$.

Equation 10 would provide a few different potential solutions.

1) There are two different real roots [${\left(R_m{C}_m\right)}^2>4m{C}_m$]. The mechanical network impulse response in Equation 9 yields

$h\left(t\right)=\left(A_1{\mathrm{e}}^{-\alpha t}+A_2{\mathrm{e}}^{-\beta t}\right)\epsilon \left(t\right)(11)$

where $A_1=C_m\beta /\left(\beta -\alpha \right)$; $A_2=-C_m\alpha /\left(\beta -\alpha \right)$; $\epsilon \left(t\right)$ is the unit step function.

This solution indicates that the particle in a viscous solid medium is in an overdamped physical state, which is not a solution for the particle being in a vibrational state.

2) The system is in the case of two identical real roots where [${\left(R_m{C}_m\right)}^2=4m{C}_m$; $s_{1,2}=-\frac{R_m}{2m}$]. The mechanical network impulse response in Equation 9 yields,

$h\left(t\right)=\left(A_{1}t+A_2\right){\mathrm{e}}^{-\beta t}\epsilon \left(t\right)(12)$

where $\alpha =0$; $\beta =-s_{1,2}=\frac{R_m}{2m}$; $A_1=C_m\beta$; $A_2=C_m$.

The mechanical network impulse response is in exponential decay with time, indicating that the particle system in the viscous solid medium is in a critical damping state, which is also not a solution that conforms to the actual particle vibration.

3) There is a pair of conjugate complex roots [${\left(R_m{C}_m\right)}^2<4m{C}_m$; $s_{1,2}=-\beta \pm i\alpha$]. The mechanical network impulse response is then,

$h\left(t\right)=A{\mathrm{e}}^{-\beta t}\cos \left({\omega }_{d}t+\theta \right)\epsilon \left(t\right)(13)$

where $A=C_m\sqrt{1+{\left(\frac{\beta }{\alpha }\right)}^2}$; $\theta ={\tan }^{-1}\left(\frac{\beta }{\alpha }\right)={\tan }^{-1}\left(\frac{1}{\sqrt{1-4m/\left(R_m^2{C}_m\right)}}\right)$; ${\omega }_d=\frac{\sqrt{4m{C}_m-{\left(R_m{C}_m\right)}^2}}{2m{C}_m}$.

Equations 11, 12 are not solutions in practical physical sense. Equation 13 indicates that the particle system is underdamped and that the mechanical network impulse response is described well for particle vibrational state motion. The amplitude ($A$), angular frequency (${\omega }_d$), and phase shift angle ($\theta$) are determined only by the physical properties of the viscous solid medium. The impulse response amplitude in the viscous solid medium ($A{\mathrm{e}}^{-\beta t}$) is no longer a constant but decays exponentially with time.

The system function of the particle vibration system in the viscous solid medium, i.e., the frequency domain expression corresponding to the impulse response of the particle system, can be obtained from Equation 8,

$H\left(i\omega \right)=H\left(s\right){|}_{s=i\omega }=\frac{i\omega C_m}{-m{C}_m{\omega }^2+i{R}_m{C}_m\omega +1}(14)$

Equations 13, 14 show that this case is a linear time-invariant system whose impulse response and system function are functions of the physical properties and parameters of the viscous solid. Consequently, by inverting the impulse response or system function with the measured acoustic wave signal, we can gain information on the physical properties of the viscous solid media and discover its internal structural anomalies.

Finally, when an external force ($f_{ext}$) is acting on a particle inside a viscous medium, its vibration velocity, i.e., the derivative of the particle displacement with time, can be expressed based on the mechanical network impulse response,

$v\left(t\right)=f_{ext}\left(t\right)*h\left(t\right)(15)$

where Equation 15 is a time-domain expression of Equation 7.

3 Calculation and analysis

We selected a few solid medium samples for calculation and analysis, neglecting the anisotropy of the rocks, where their physical parameters [18] are shown in Table 1.

Table 1

Table 1. Parameters of three isotropic rocks.

3.1 A system of particle vibration in viscous solid media

From the physical properties of the selected rock samples (Table 1), we can obtain the friction resistance of the vibrating particle ($R_m=a_1{\eta }_{11}$), its mass ($m=a_2\rho$), and the stiffness coefficient of the spring oscillator ($k=1/C_m=a_3{c}_{11}$). Here, a₁, a_2, and a₃ are the proportional coefficients between the frictional resistance of the particle and the viscosity coefficient of the solid medium, the mass of the particle and the density of the solid, and the stiffness and the stiffness coefficient of the spring vibrator, respectively, which are determined by the physical properties and internal structure of the viscous solid medium and the geometrical-size of the particle. Based on the physical parameters of the three types of viscoelastic solid media samples presented in Table 1, and setting the proportional coefficient as follows: $a_1=1\times {10}^{-11}$, $a_2=1\times {10}^{-7}$, and $a_3=1\times {10}^{-1}$, we can calculate the acoustic impulse response and system function of the three aforementioned rock samples. We selected two scenarios for this analysis and comparison: one where the viscosity coefficient is set to ${\eta }_{11}=3\times {10}^4\mathrm{N}\cdot \mathrm{s}/{\mathrm{m}}^2$, as illustrated in Figure 3, and another one where the viscosity coefficient is set to ${\eta }_{11}=9\times {10}^4\mathrm{N}\cdot \mathrm{s}/{\mathrm{m}}^2$, as illustrated in Figure 4. Among these, the waveform and amplitude spectrum of the acoustic impulse response of the shale particle vibration system exhibit the biggest values respectively. The maximum value obtained from the shale calculations was used to normalize the results for all three rock types.

Figure 3

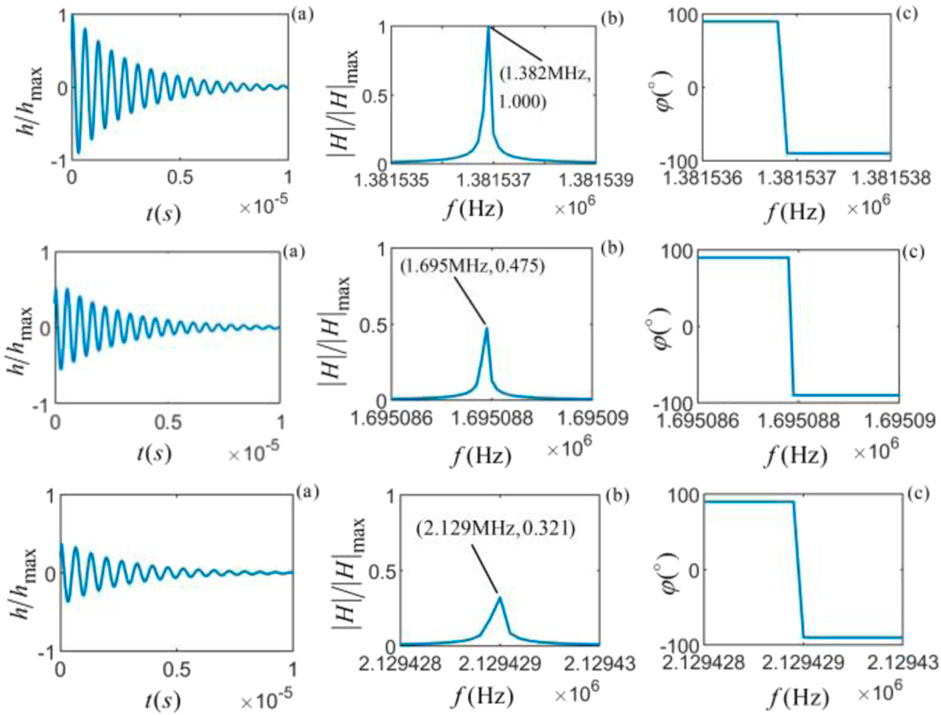
Figure 3. From top to bottom, the vibrational system (${\eta }_{11}=3\times {10}^4\mathrm{N}\cdot \mathrm{s}/{\mathrm{m}}^2$) of Shale, M-sandstone, and C-sandstone: (a) time domain waveform; (b) amplitude spectrum; (c) phase spectrum.

Figure 4

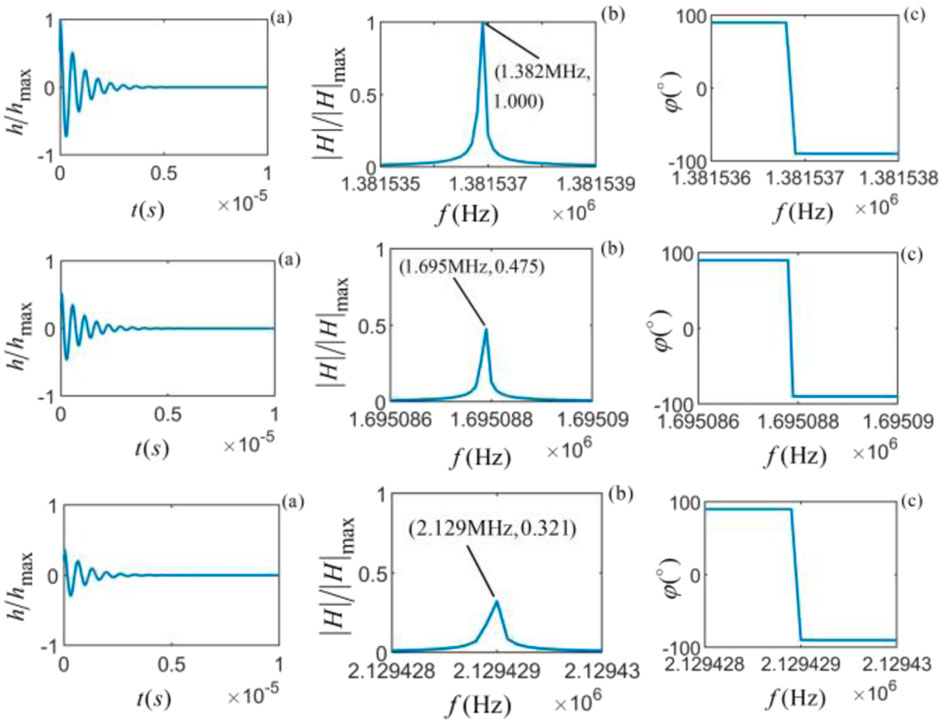
Figure 4. From top to bottom, the vibrational system (${\eta }_{11}=9\times {10}^4\mathrm{N}\cdot \mathrm{s}/{\mathrm{m}}^2$) of Shale, M-sandstone, and C-sandstone: (a) time domain waveform; (b) amplitude spectrum; (c) phase spectrum.

The calculation results show that for different rocks with the same viscosity coefficient, the waveform amplitude in the time domain decays exponentially with time until it decays to zero; under the same viscosity coefficient, the amplitude of the time domain waveform and amplitude spectrum of the internal particle vibration of shale is the largest, and that of C-sandstone is the smallest; the amplitude spectrum of the particle vibration increases with frequency until it reaches the maximum amplitude at a specific frequency, and then the amplitude starts to decrease with frequency. The frequency corresponding to the maximum amplitude of the amplitude spectrum is defined as the center frequency ($f_0$) of the particle system.

For the same rock with different viscosities, the center frequency of the particle vibration is independent of the viscosity of the medium, but the amplitude of the spectrum will decrease with the increase of viscosity; the center frequency of the particle vibration inside C-sandstone is the highest (2.129 MHz) and followed by M-sandstone (1.695 MHz), where the shale stone has the lowest center frequency (1.382 MHz). This further supports our understanding of the influence of the stiffness coefficient on the center frequency. The larger the stiffness coefficient, the larger the center frequency corresponding to the particle vibration system; at the center frequency, the phase of the system function has a 180° mutation.

In summary, the viscosity of solid media will affect the amplitude of the particle vibration system function but will not affect its center frequency. The stiffness coefficient will affect the center frequency of the particle vibration system. Therefore, the mechanical properties of viscous solid media’s particle vibration are related to the shape and geometric parameters of the particles and the viscosity and stiffness coefficient of the medium solid.

3.2 Harmonic single-frequency force acting on a particle inside a medium

Let’s consider and compare the particle vibrations within solid media under the action of harmonic single-frequency forces with different frequencies (f = 0.8 $f_0$, 1.0 $f_0$, and 1.2 $f_0$) in the units of central frequency, as shown in Figures 5–7, for the time domain waveforms, amplitude, and phase spectra.

Figure 5

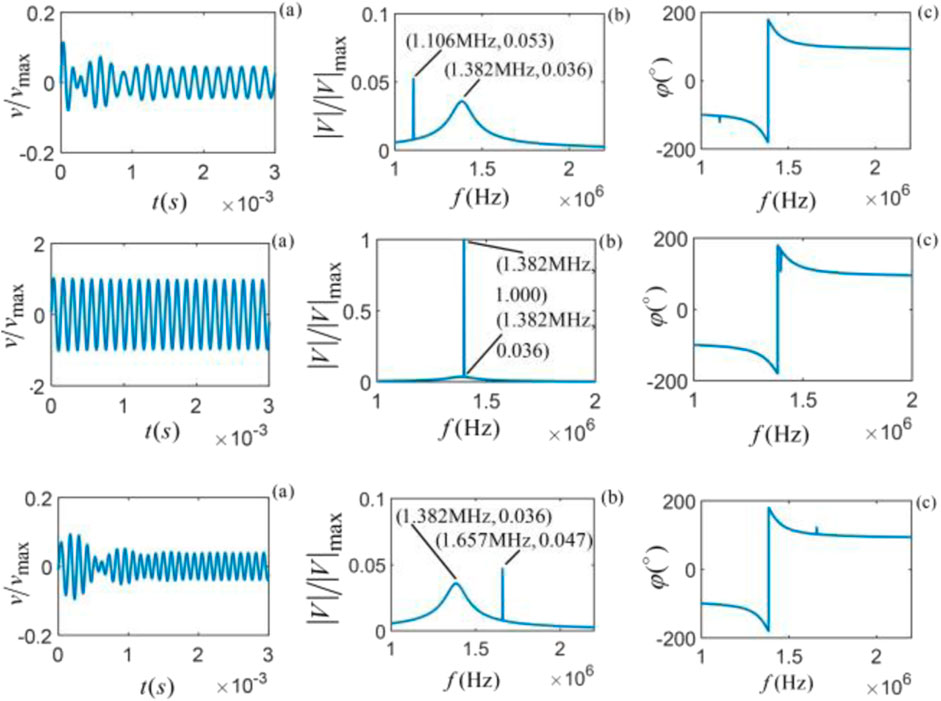
Figure 5. Vibrational state of Shale stone at different frequencies, from top to bottom ($f=0.8f_0$, $f=1.0f_0$, and $f=1.2f_0$): (a) time domain waveform; (b) amplitude spectrum; (c) phase spectrum.

Figure 6

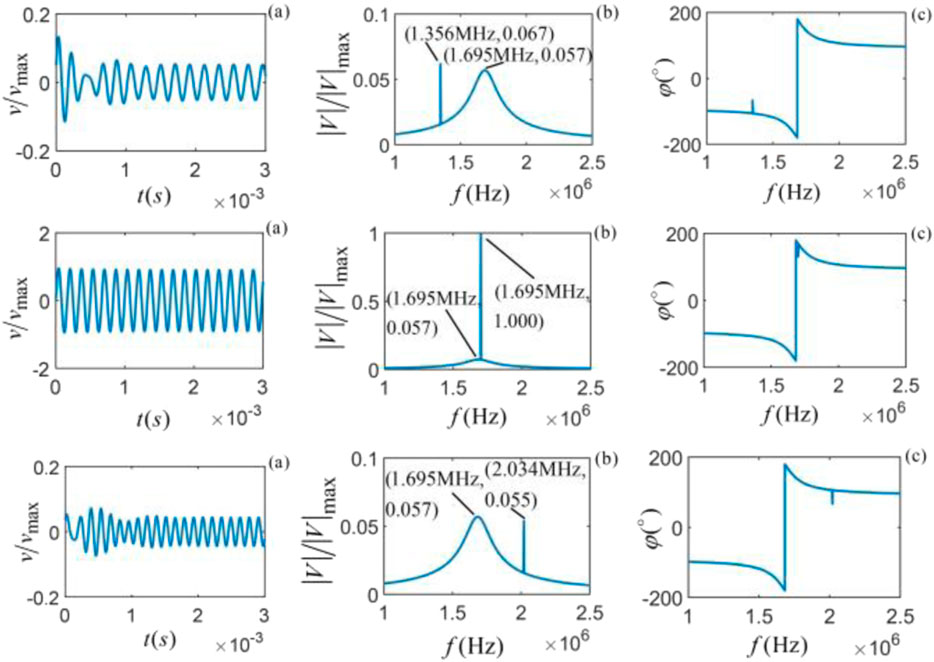
Figure 6. Vibrational state of M-sandstone at different frequencies, from top to bottom ($f=0.8f_0$, $f=1.0f_0$, and $f=1.2f_0$): (a) time domain waveform; (b) amplitude spectrum; (c) phase spectrum.

Figure 7

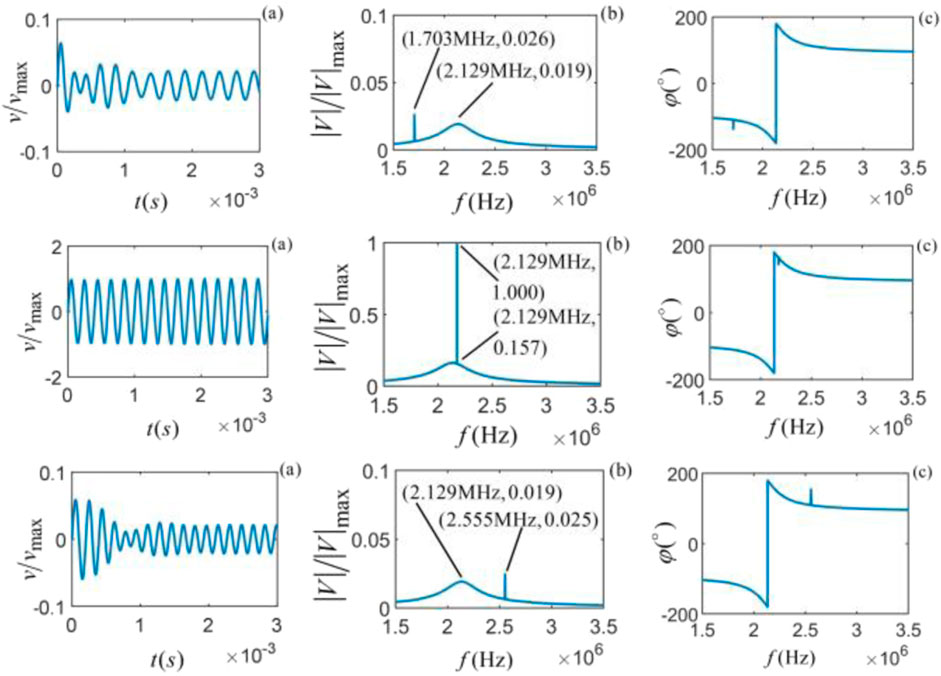
Figure 7. Vibrational state of C-sandstone at different frequencies, from top to bottom ($f=0.8f_0$, $f=1.0f_0$, and $f=1.2f_0$): (a) time domain waveform; (b) amplitude spectrum; (c) phase spectrum.

When the single-frequency harmonic force frequency is equal to the center frequency of the particle vibration, resonance occurs, and the amplitude of the time domain waveform and the corresponding amplitude spectrum is the largest, as shown in the middle penal (the second from top to bottom). The time domain waveform and amplitude spectrum are normalized by the maximum values of the time domain waveform and amplitude spectrum at resonance.

As shown in the first column of the figures for each sample, its time domain waveform consists of two parts, i.e., a transient transition process and a steady-state harmonic single-frequency vibration with the frequency of the harmonic force. The time domain waveform of the particle vibration has different transient processes at the beginning but gradually stabilizes to a sinusoidal vibration over time. The closer the harmonic single-frequency force (excitation signal) frequency is to the center frequency of the particle system, the greater the amplitude of the particle vibration and the shorter the duration of the transient transition process. When harmonic single-frequency excitation signals of different frequencies act on the particles, the time domain waveform generated by the particle vibration shows different transient processes and gradually stabilizes a harmonic single-frequency vibration with the frequency of over time.

The corresponding amplitude spectrum contains two types of spectrum information: one is the spectrum corresponding to the harmonic single-frequency signal of steady-state harmonic single-frequency oscillation, i.e., the impulse pulse in the frequency domain, which is the frequency of the harmonic single-frequency force, and the other is the spectrum corresponding to the transient process, which is the frequency component of the intrinsic noise generated by the particles inside the viscous solid medium under the action of the harmonic single-frequency force.

The phase spectrum’s behavior at the intrinsic noise center frequency is a key indicator for understanding the vibration spectrum. At this frequency, the phase spectrum exhibits a positive jump, and at the regular frequency of the harmonic single-frequency force, the phase spectrum shows an impulse. The phase jump and impulse coincide when the harmonic single-frequency force frequency aligns with the intrinsic noise center frequency. This alignment provides a crucial insight: when the frequency of the harmonic single-frequency force is significantly different from the center frequency of the intrinsic noise, it becomes easier to isolate the intrinsic noise from the particle vibration spectrum.

3.3 External force with multiple frequencies

The excitation force signal acting on the particle in viscous solids is usually a wavelet containing many frequency components. A complex multifrequency signal can be decomposed into separate single-frequency components with different amplitudes, frequencies, and phases based on discrete Fourier transform. The more frequency components are used, the more accurate the waveform shape is to represent the original wavelet.

It is common to use the gate-selected sinusoidal force applied to the particle with a time domain expression,

$f_{ext}\left(t\right)=A_0\sin \left({\omega }_{s}t\right)\left[H\left(t\right)-H\left(t-t_0\right)\right](16)$

By Fourier transform, we can get its spectrum expression and the corresponding phase spectrum:

$S_{ext}\left(\omega \right)=U_0\left\{{\omega }_s-\left({\omega }_s\cos {\omega }_s{t}_0+i\omega \sin {\omega }_s{t}_0\right)\exp \left(-i\omega t_0\right)/\left({\omega }_s^2-{\omega }^2\right)\right\}(17)$

$\varphi \left(\omega \right)=\arctan \frac{\text{Im}\left[S_1\left(\omega \right)\right]}{\text{Re}\left[S_1\left(\omega \right)\right]}(18)$

where $A_0$ and ${\omega }_s$ are the amplitude and angular frequency (${\omega }_s=2\pi f_s$).

Taking the center frequency of the particle system inside shale ($f_0={\omega }_0/2\pi =1.382\text{MHz}$) as an example, let’s choose a gate-selected sinusoidal force and apply it to the shale sample, where we have a harmonic frequency gate width ($t_0=3{\mathrm{T}}_0=6\pi /{\omega }_{\mathrm{s}}$), and amplitude ($A_0=1$) of the gate-selected sinusoidal force with a gate-selected sinusoidal force period (T₀), as shown in Figure 8. Based on Equations 17, 18, the amplitude and phase spectra of the gate-selected sinusoidal force are illustrated in Figures 8A, B respectively. Utilizing Equations 16–18, the calculated and fitted time-domain waveforms of the gate-selected sinusoidal force are represented by the solid and circled lines in Figure 8C. It shows that the waveform fitted by the amplitude and phase spectra is virtually consistent with the excitation signal, ensuring the accuracy of subsequent analysis. For the equivalent mechanical network of the particle vibration (see Figure 2), based on the linear superposition principle, each frequency component in the gate-selected sinusoidal force can act on the particle as a separate action force to excite the particle. The superposition of the contribution of all frequency components of the gate-selected sinusoidal force to the particle vibration provides the final vibration state of the particle.

Figure 8

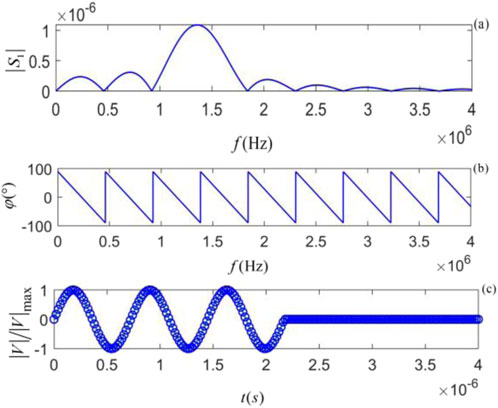
Figure 8. The gate-selected sinusoidal signal: (a) amplitude spectrum, (b) phase spectrum, and (c) time domain waveform.

By exploring a few selected frequency components of a gate-selected sinusoidal force at frequencies ($f$ = 0.2 $f_0$, 0.6 $f_0$, 1.2 $f_0$, and 1.4 $f_0$) for the selected three rocks, we can observe amplitude variations with respect to these frequencies (|S₁ (1.2 $f_0$)|>|S₁ (0.2 $f_0$)|>|S₁ (0.6 $f_0$)|>|S₁ (1.4 $f_0$)). Figures 9–11 are the calculated time-domain waveforms for the selected harmonic force frequency components ($f$ = 0.2 $f_0$, 0.6 $f_0$, 1.2 $f_0$, and 1.4 $f_0$) acting on the particles inside the selected three rock samples, and there is the relation of |v_s (1.2 $f_0$)|>|v_s (0.2 $f_0$)|>|v_s (0.6 $f_0$)|>|v_s (1.4 $f_0$)|, where $v_s\left(\cdot \right)$ denotes the amplitude of the steady-state harmonic single-frequency oscillation of the particle in response to the different frequency components of the gate-selected sinusoidal force. For example, take shale stone, whose internal particle system has the center frequency of $f_0$ = 1.382 MHz, at the frequencies of $f$ = 0.2 $f_0$ (0.2764 MHz), 0.6$f_0$ (0.8292 MHz), 1.2 $f_0$ (1.6584 MHz)and 1.4$f_0$ (1.9348 MHz), the magnitudes of the frequency components of the gate-selected sinusoidal force are 2.2824$\times {10}^{-7}$, 2.1042 $\times {10}^{-7}$, 4.9681 $\times {10}^{-7}$, and 1.4109 $\times {10}^{-7}$, respectively, and the amplitudes of the steady-state harmonic single-frequency oscillation of the particle in the shale stone are 0.0231, 0.0215, 0.0421, 0.0147, which is $v_s\left(1.2f_0\right)$ >$v_s\left(0.2f_0\right)$ >$v_s\left(0.6f_0\right)>v_s\left(1.4f_0\right)$. The same rules also apply to M-sandstone and C-sandstone, as shown in Figures 10, 11.

Figure 9

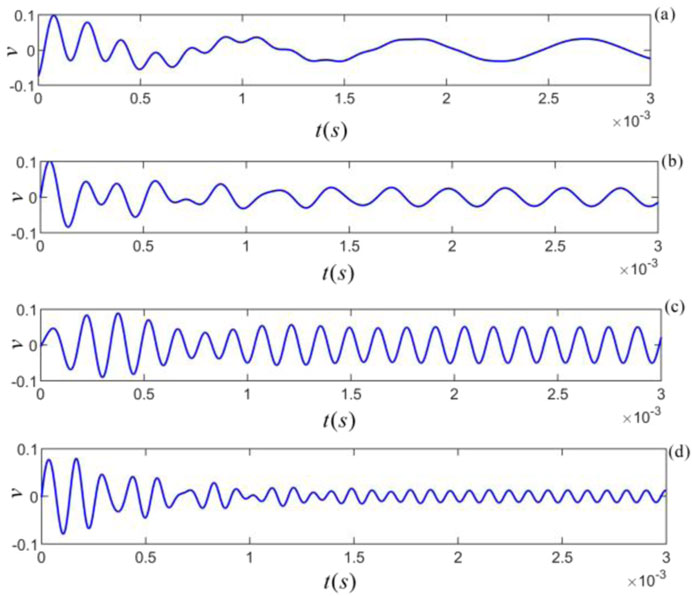
Figure 9. Different frequency components of the gate-selected sinusoidal force acting on the particles inside the shale: (a) $f$ = 0.2 $f_0$; (b) $f$ = 0.6 $f_0$; (c) $f$ = 1.2 $f_0$; (d) $f$ = 1.4 $f_0$.

Figure 10

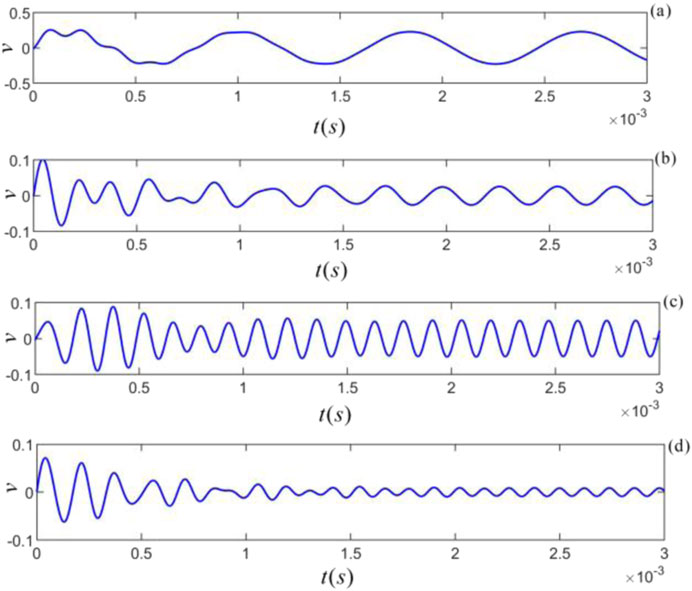
Figure 10. Different frequency components of the gate-selected sinusoidal force acting on M-sandstone: (a) $f$ = 0.2 $f_0$; (b) $f$ = 0.6 $f_0$; (c) $f$ = 1.2 $f_0$; (d) $f$ = 1.4 $f_0$.

Figure 11

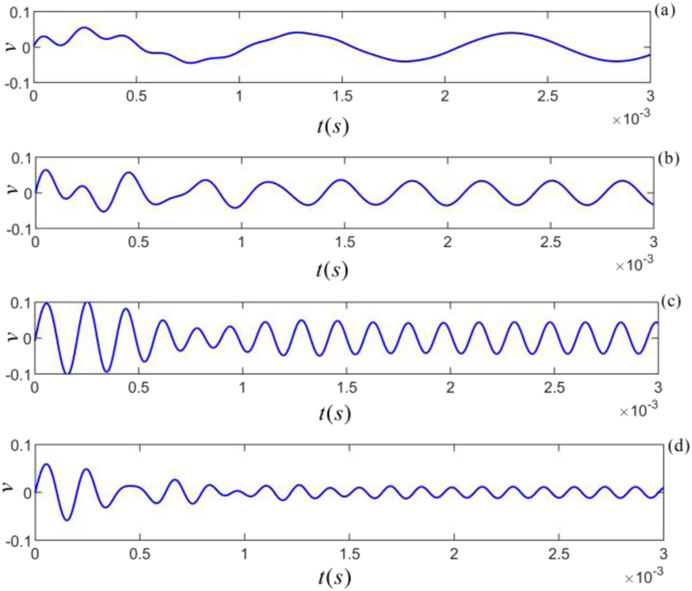
Figure 11. Different frequency components of the gate-selected sinusoidal force acting on C- sandstone: (a) $f$ = 0.2 $f_0$; (b) $f$ = 0.6 $f_0$; (c) $f$ = 1.2 $f_0$; (d) $f$ = 1.4 $f_0$.

Figures 9–11 shows that each frequency component provided by the gate-selected sinusoidal force acting on the particle yields a distinctive transient process and steady-state harmonic single-frequency vibrations with different frequencies and amplitudes. For frequency components of the gate-selected sinusoidal force applied to the particle far away from the intrinsic noise center frequency, the transient transition of the particle vibration is long. When the gate-selected sinusoidal force frequency applied to the particle is equal to the center frequency of the intrinsic noise, the duration of the transient process of the particle vibration is the shortest, and the gate-selected sinusoidal force frequency is superimposed on the center frequency of the intrinsic noise. The frequency and magnitude of the intrinsic noise and the corresponding force frequency component determine the amplitude of the transient process. In contrast, the magnitude of this frequency component determines the steady-state harmonic vibration’s amplitude.

The vibration state of a particle inside the viscous solid medium is a summary contribution of all frequency components. Figures 12–14 shows the vibration states of the particles inside the three types of rocks (shale, M-sandstone, and C-sandstone) under the gate-selected sinusoidal forces of frequencies ($f_s<f_0$, $f_s=f_0$, $f_s>f_0$). The time domain waveform and frequency domain amplitude spectrum were normalized by the maximum values of the time domain waveform and amplitude spectrum for each rock at $f_s=f_0$.

Figure 12

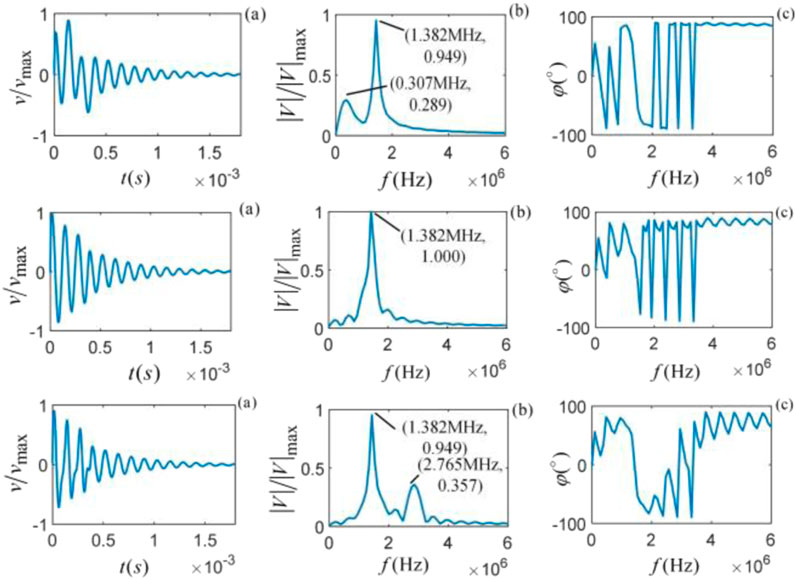
Figure 12. Shale vibration state from top to bottom ($f_s<f_0$, $f_s=f_0$, $f_s>f_0$): (a) time domain waveform; (b) amplitude spectrum; (c) phase spectrum.

Figure 13

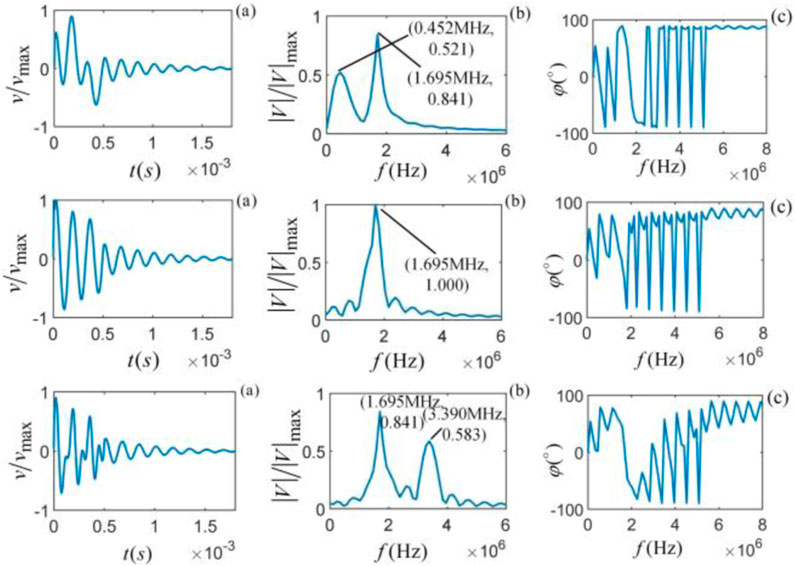
Figure 13. M-sandstone vibration state from top to bottom ($f_s<f_0$, $f_s=f_0$, $f_s>f_0$): (a) time domain waveform; (b) amplitude spectrum; (c) phase spectrum.

Figure 14

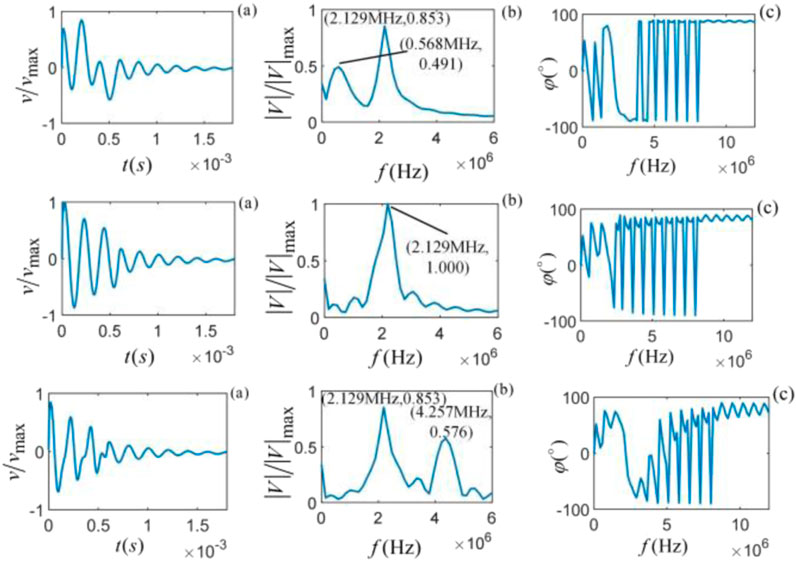
Figure 14. C-sandstone vibration state from top to bottom ($f_s<f_0$, $f_s=f_0$, $f_s>f_0$): (a) time domain waveform; (b) amplitude spectrum; (c) phase spectrum.

Figures 12–14 shows that different frequencies of gate-selected sinusoidal wavelet acting on its internal particles for a given rock medium yield different vibration states. The particle vibration has different time domain waveforms, amplitude, and phase spectra. When the gate-selected sinusoidal force frequency equals the central frequency of the intrinsic noise corresponding to the rock, the time domain waveform and amplitude spectrum will be at their maximum.

When the gate-selected sinusoidal force frequency overlaps with the intrinsic noise central frequency ($f_s=f_0$), the amplitude spectrum has only one peak, which is the imposition of the peak upon another. If the excitation frequency is lower than the noise central frequency ($f_s<f_0$), there are two peaks in the amplitude spectrum. The left peak is the contribution from the gate-selected sinusoidal force, and the right peak is the contribution from the intrinsic noise generated by the particle vibration. If the excitation frequency is higher than the noise central frequency ($f_s>f_0$), there are also two peaks in the amplitude spectrum. The left peak is the contribution from the intrinsic noise, and the right peak is from the gate-selected sinusoidal force. Regardless of the type of excitation force, either a harmonic single-frequency signal or a multifrequency wavelet, the vibrational state of the particle always contains the excitation frequency components and the intrinsic noise generated by the vibrating particles. The medium’s physical properties and geometric structure are the sole factors in determining the spectral characteristics of the intrinsic noise.

Figures 12–14 shows that, in the near frequency region around the spectrum of intrinsic noise and force, the fluctuation of the phase spectrum is more pronounced due to the influence of the spectrum distribution and characteristics of intrinsic noise, especially with multifrequency force. In the frequency range far away from the spectrum of intrinsic noise and excitation force, the fluctuation of the phase spectrum tends to become smaller. We found that the phase spectrum of the intrinsic noise generated by the internal particles of the different sample rock media under the action of the same type of force has similar changes and trends. Comparing Figures 9–11 with Figures 12–14 shows that when a single-frequency force acts on a particle, extracting the intrinsic noise generated by the vibrating particle is easier than that of multiple-frequency excitation.

4 Concluding remarks

We have introduced the concept of “intrinsic-noise-atom”. Through algorithms of interpolation, extrapolation, squeeze/stretch, and scaling, we can construct a dictionary that contains intrinsic-noise-atoms produced by vibrating particles within the viscous media with various physical properties and structures.

The combination or superposition of different intrinsic-noise-atoms can constitute the intrinsic noise generated when any complex multifrequency force is applied to a particle, and vice versa.

The generation and disappearance of particle vibrations have their own transient transition processes. The spectrum corresponding to the transient process is the intrinsic noise generated by the particle vibration system.

Intrinsic noise is closely related to the physical properties of the solid media and their internal structure. Applying the matching-pursuit algorithm on and the intrinsic noise extracted from measured acoustic wave signal with the atoms in dictionary can invert the physical properties of the solid media and their internal structure more accurately. Such as,in LWD acoustic logging, The intrinsic noise information can be used to reduce or eliminate the influence of the drill-collar direct wave on the measured acoustic wave efficiently, so that obtain propagation velocity of acoustic wave in the formation around the wellbore accurately.

This research lays a theoretical foundation for extracting the progressive intrinsic noise generated by the sequential vibration of all particles on the acoustic wave propagation path from the measured acoustic wave signal and the parallel-series lumped particle vibration model to describe the acoustic measurement process. The next step will be to establish a quantitative relationship between intrinsic noise and acoustic attenuation. A new lumped particle vibration transmission network that takes into account the influence of factors such as particle vibration-damping attenuation, wave propagation attenuation, progressive intrinsic noise generated by particles inside the medium, and the electric-acoustic (or acoustic-electric) conversion of the acoustic transducer on the measured acoustic wave signal (the electrical signal at the electrical end of the receiving transducer) is established to describe the acoustic measurement process.

This research has theoretically derived and simulated the intrinsic noise signal generated by the particle in viscous solid media and has not yet been verified by relevant experiments. In the subsequent process, some rock samples can be constructed for experimental measurement, combining theory with engineering, and we can develop corresponding software to interpret and process the physical properties of the inversion medium and the internal structural anomalies using the progressive intrinsic noise signal. It also lays the foundation for developing a new intrinsic noise logging tool.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

LF: Conceptualization, Validation, Writing–original draft, Writing–review and editing. SM: Data curation, Software, Writing–original draft. HY: Validation, Writing–review and editing. JL: Investigation, Writing–review and editing. YH: Project administration, Writing–review and editing. KZ: Supervision, Writing–review and editing. YX: Formal Analysis, Writing–review and editing. MZ: Conceptualization, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the National Natural Science Foundation of China (grant no. 41974130), Xi’an Fanyi University, Xi’an University of Posts and Telecommunications, and the Physical Sciences Division at The University of Chicago.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Simpson ML, Cox CD, Sayler GS. Frequency domain analysis of noise in autoregulated gene circuits. Proc Natl Acad Sci (2003) 100(8):4551–6. doi:10.1073/pnas.0736140100

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Ramaswamy R, Sbalzarini IF. Intrinsic noise alters the frequency spectrum of mesoscopic oscillatory chemical reaction systems. Scientific Rep (2011) 1(1):154. doi:10.1038/srep00154

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Rhee A, Cheong R, Levchenko A. Noise decomposition of intracellular biochemical signaling networks using nonequivalent reporters. Proc Natl Acad Sci (2014) 111(48):17330–5. doi:10.1073/pnas.1411932111

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Selimkhanov J, Taylor B, Yao J, Pilko A, Albeck J, Hoffmann A, et al. Accurate information transmission through dynamic biochemical signaling networks. Science (2014) 346(6215):1370–3. doi:10.1126/science.1254933

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Villegas P, Ruiz-Franco J, Hidalgo J, Muñoz MA. Intrinsic noise and deviations from criticality in Boolean gene-regulatory networks. Scientific Rep (2016) 6(1):34743. doi:10.1038/srep34743

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Hong J, Zhang T, Zhou R, Zhou R, Ostikov K, Rezaeimotlagh A, et al. Plasma bubbles: a route to sustainable chemistry. AAPPS Bull (2021) 31:26–14. doi:10.1007/s43673-021-00027-y

CrossRef Full Text | Google Scholar

7. Fa L, Yang H, Fa Y, Meng S, Bai J, Zhang Y, et al. Progress in acoustic measurements and geoacoustic applications. AAPPS Bull (2024) 34(1):23. doi:10.1007/s43673-024-00127-5

CrossRef Full Text | Google Scholar

8. Piquette JC. Method for transducer transient suppression. I: theory. The J Acoust Soc America (1992) 92(3):1203–13. doi:10.1121/1.403970

CrossRef Full Text | Google Scholar

9. Piquette JC. Method for transducer transient suppression. II: experiment. J Acoust Soc America (1992) 92(3):1214–21. doi:10.1121/1.403971

CrossRef Full Text | Google Scholar

10. Fa L, Castagna JP, Hovem JM. Derivation and simulation of source function for acoustic logging. In: 1999 IEEE Ultrasonics Symposium. Proceedings. International Symposium (Cat. No. 99CH37027); 17-20 Oct. 1999; USA. IEEE (1999).

Google Scholar

11. Fa L, Mou J, Fa Y, Zhou X, Zhang Y, Liang M, et al. On transient response of piezoelectric transducers. Front Phys (2018) 6:123. doi:10.3389/fphy.2018.00123

CrossRef Full Text | Google Scholar

12. Fa L, Tu N, Qu H, Wu Y, Sun K, Zhang Y, et al. Physical characteristics of and transient response from thin cylindrical piezoelectric transducers used in a petroleum logging tool. Micromachines (2019) 10(12):804. doi:10.3390/mi10120804

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Fa L, Kong L, Gong H, Li C, Li L, Guo T, et al. Numerical simulation and experimental verification of electric–acoustic conversion property of tangentially polarized thin cylindrical transducer. Micromachines (2021) 12(11):1333. doi:10.3390/mi12111333

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Fa L, Liu D, Gong H, Chen W, Zhang Y, Wang Y, et al. A frequency-dependent dynamic electric–mechanical network for thin-wafer piezoelectric transducers polarized in the thickness direction: physical model and experimental confirmation. Micromachines (2023) 14(8):1641. doi:10.3390/mi14081641

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zha X, Luo JT, Tao R, Fu C. Surface and bulk acoustic wave resonators based on aluminum nitride for bandpass filters. AAPPS Bull (2024) 34(1):14. doi:10.1007/s43673-023-00104-4

CrossRef Full Text | Google Scholar

16. Moon J, Park S, Lim S. A novel high-speed resonant frequency tracking method using transient characteristics in a piezoelectric transducer. Sensors (2022) 22(17):6378. doi:10.3390/s22176378

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wang G, Qiu W, Wang D, Chen H, Wang X, Zhang M. Monitoring the early strength development of cement mortar with piezoelectric transducers based on eigenfrequency analysis method. Sensors (2022) 22(11):4248. doi:10.3390/s22114248

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Thomsen L. Weak elastic anisotropy. Geophysics (1986) 51(10):1954–66. doi:10.1190/1.1442051

CrossRef Full Text | Google Scholar

19. Mallat S, Zhang Z. Matching pursuit with time-frequency dictionaries. IEEE Trans Signal Process (1993) 41(12):3397–419. doi:10.1109/78.258082

CrossRef Full Text | Google Scholar

20. Davis G, Mallat S, Avellaneda M. Adaptive greedy approximations. Constructive approximation (1997) 13:57–98. doi:10.1007/s003659900033

CrossRef Full Text | Google Scholar

21. Zhang R, Castagna J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition (2011) 76(6). R147–58. doi:10.1190/geo2011-0103.1

CrossRef Full Text | Google Scholar

22. Wang YH. Seismic time-frequency spectral decomposition by matching pursuit. Geophysics (2007) 72(1):V13–20. doi:10.1190/1.2387109

CrossRef Full Text | Google Scholar