A novel approach to pseudorandom number generation using Hamiltonian conservative chaotic systems

High-quality random number generators are required for various applications such as cryptography, secure communications, Monte Carlo simulations, and randomized algorithms. Existing pseudorandom number generators (PRNGs) face limitations such as periodic behavior, dependence on high-quality entropy sources, or computational inefficiency. On the other hand, chaotic systems are widely used for pseudorandom sequence generation due to their sensitivity to initial conditions and rich dynamical properties. The dissipative chaotic systems settle into low-dimensional attractors; however, the conservative chaotic systems (CCSs) conserve phase space volume and exhibit superior ergodicity, making them particularly suitable for chaos-based cryptographic applications. However, challenges remain with existing approaches, such as limited phase space and periodic behavior, necessitating more robust CCS-based solutions for secure and efficient implementations. To address these challenges, in this paper, we propose a pseudorandom number generator based on a Hamiltonian conservative chaotic system (HCCS) constructed using the 4D Euler equations of rigid body rotations. Although the proposed method is described using a specific chaotic system, the approach can be easily extended to other Hamiltonian conservative chaotic systems (HCCSs) following a careful analysis of their behaviour in phase space. We provide a detailed description of the pre-analysis, followed by two methods that utilize the Poincaré sections of HCCS to extract pseudorandom sequences, along with their corresponding pseudo codes. Additionally, we present the results of the performance analysis of the two pseudorandom number generation methods using the NIST randomness test suite, which confirm their robustness and compliance with randomness standards. Our innovative approach demonstrates significant potential to enhance the quality, unpredictability, and efficiency of pseudorandom number generation, making it highly suitable for cryptographic applications.

1 Introduction

Random number generators are highly required in a variety of applications ranging from Monte Carlo simulations, cryptography and secure communications, gambling and gaming, statistical sampling, modelling and simulations, randomized algorithms, machine learning and data science, genetic algorithms and evolutionary computing, hardware testing etc. In most of applications, the requirement of high-quality randomness is critical as the predictability and structure of random sequences may lead to inaccurate analysis/simulations and compromised security [1]. Generating truly random sequences is impractical, expensive or very slow as these are generated from unpredictable natural physical processes like radioactive decay, electronic or thermal noise, quantum fluctuations, photon emission/detection, disk drive latency, Brownian motion etc. It therefore leads to a widespread requirement and use of pseudorandom number generators (PRNGs) which are deterministic algorithms designed to generate number sequences that approximate the properties of random sequences. In general, the PRNG takes an initial seed as input and generates the sequence of numbers using a deterministic recursive/iterative relation. The output sequence is the same as long as the same seed is provided as input to these deterministic relations [2]. PRNGs have become essential for many applications requiring a high-speed and repeatable random sequence. Well-designed PRNGs should produce sequences possessing longer periods, unpredictability, uniform distributions and involving an efficient computational process. Before the 20th century, randomness was typically achieved using natural physical processes, as mentioned above. However, with the advent of computers, the concept of pseudorandom number generation emerged. The first such PRNG was proposed by John von Neumann in 1949 [3], based on the middle square method, which was later found to have several statistical weaknesses. Later in the second half of the 20th century, PRNGs like Linear Congruential Generator (LCG) [1,4] and Mersenne Twister [5] became very popular and were widely used in various software systems. A surge in cryptographic applications in 21st century led to the development of cryptographically secure PRNGs that aim to prevent attackers from predicting future sequences. Mersenne Twister [5], developed in 1997, gained popularity in the early 21st century, along with other cryptographically secure PRNGs like Yarrow [6], Fortuna [7, 8], Blum-Blum-Shub [9], and more recently, the Permuted Congruential Generators (PCGs) [10], the Xoshiro/XORSHIFT family of PRNGs [11] and QRNGs [12]. Each of the above-mentioned PRNGs has its limitations: the Mersenne Twister is not cryptographically secure; Yarrow and Fortuna rely heavily on high-quality entropy sources and are complex to implement; and Blum-Blum-Shub is slow and computationally intensive. QRNGs may require specialized hardware, while Permuted Congruential Generators (PCGs) and the Xoshiro/XORSHIFT family, although fast, may lack cryptographic security and exhibit statistical weaknesses if not implemented with due care. PRNGs can be broadly classified into the following categories:Deterministic Algorithm-Based PRNGs- These include Linear Congruential Generators (LCG), Lagged Fibonacci Generators (LFG), Linear Feedback Shift Registers (LFSR), the Mersenne Twister, and others;Cryptographically Secure PRNGs- Examples include Blum Shub (BBS), Yarrow, and Fortuna; Cryptographic Hash Function-Based PRNGs- These use cryptographic hash functions such as SHA-256; Cellular Automata-Based Algorithms- Examples include PRNGs based on specific rules like Rule 30 and Rule 110; Quantum Random Number Generators (QRNGs)- These rely on quantum phenomena, such as superposition and entanglement; Hardware-Based PRNGs- These are non-deterministic and closely approximate true randomness by utilizing sources like thermal noise and radioactive decay; Chaos-Based Deterministic PRNGs- These rely on chaotic systems to generate pseudorandom sequences. For a recent detailed survey and classification of various state-of-the-art PRNGs, refer to Bhattacharjee and Das [13]. Additionally, James and Moneta [14] provides further insights and advocates for high-quality pseudorandom number generators (PRNGs) rooted in chaotic dynamical systems exhibiting Kolmogorov-Anosov mixing (K-mixing) and ergodicity, which ensure exponential divergence of trajectories (via positive Lyapunov exponents) and uniform phase space exploration. It also includes a comprehensive review of high-quality pseudorandom number generators.

Chaotic dynamical systems exhibit exponential divergence of nearby trajectories, a hallmark of sensitivity to initial conditions characterized by positive Lyapunov exponents. This divergence arises from geometric mechanisms such as stretching and folding, which also induce mixing in the system. Despite this extreme sensitivity, the system’s trajectories remain bounded in phase space and exhibit aperiodic behaviour. Furthermore, chaotic systems are typically ergodic, meaning their long-term temporal averages converge to spatial averages over the entire state space. Many chaotic systems also demonstrate topological transitivity, ensuring that trajectories eventually approach arbitrarily close to any region within the bounded state space [15–17]. In general chaotic dynamical system can be classified into two major classes: dissipative chaotic dynamical systems and conservative chaotic systems. Dissipative chaotic systems lose energy over time due to the existence of some form of dissipative force resulting it their phase space contracts over time and the long-term behaviour of such systems settle onto an attractor (equilibrium points, nodes/no spirals, chaotic strange attractor) in low dimension. Some of the examples are: the Lorenz system, Rossler System, forced damped Duffing oscillator, etc. Such low-dimensional attractors may be reconstructed using a delayed reconstruction from one or two variable time trajectories [16, 17]. In recent years, several chaos-based pseudorandom number generators have been proposed in the literature based on the chaotic logistic map, Henon map, standard map, Lorenz systems, and various hybrid-chaotic maps [18–25]. Most of them have been successfully used for developing secure image encryption systems, however they face critical limitations due to use of low-dimensional chaos or existence of dissipative attractors in their dynamics resulting in the shrinkage of available phase space, periodic windows under finite precision, and statistical weaknesses due to low entropy or dissipative dynamics [26].

On the other hand, Conservative chaotic systems are mainly characterized by their property of conserving phase space volume and energy. The long-term asymptotic dynamics of such a system do not approach an attractor. The elliptic (centre), hyperbolic (saddle) points and chaotic stochastic orbits may co-exist for various ranges of control/system parameters and initial conditions. As a general scenario of the dynamical behaviour of such systems: for some range of control parameter the entire phase space is filled with regular orbit i.e., invariant tori, above a certain critical value of parameter the volume occupied by the invariant tori decreases abruptly and variety of orbits including the chaotic (stochastic) orbits appear for different sets of initial conditions with further increase in the parameters. The chaotic (stochastic) orbits in such systems fill the entire accessible phase space and the basin of attraction is identical to the region occupied by them. Under such conditions, the dimension of the chaotic orbit is always same as the dimension of the phase space and is an integer, and possesses an invariant measure and a high order of ergodicity. Some of the various popular examples of such systems are Henon Heiles systems, undamped forced Duffing oscillator, standard map etc., [16, 17]. Due to the nonexistence of attractor (contrary to dissipative systems) in phase space, identical size of phase space and chaotic orbit’s basin, stronger or richer ergodic property along with the interesting property of sensitivity on initial conditions and system parameters make conservative chaotic systems (CCSs) [17] more suitable for their applications in pseudorandom sequence generation [22, 27] and their further use in chaos-based permutation and substitution for image encryption [28]. Conservative chaotic systems (CCSs) are further divided into two categories: (i) Hamiltonian Conservative Chaotic Systems (HCCSs) and (ii) Non-Hamiltonian Conservative Chaotic Systems (Non-HCCSs). The HCCSs are categorized by the zero sum of Lyapunov exponents along with both energy and volume of phase space conservation (Henon-Hiles, undamped forced, standard map, Cang’s system-A [29] etc.) however non-HCCSs possess only zero sum of Lyapunov exponents (Sprott’s system A [30–32]). Some systems have constant Hamiltonian but the traces of Jacobian are not zero are also termed as non HCCSs (e.g., Cang’s system-B [29]).

Recent advancements in the construction of Hamiltonian conservative chaotic systems have significantly expanded the scope of chaos-based applications, particularly in pseudorandom number generation (PRNG). Ji’e et al. [33] introduced a simplified framework for designing Hamiltonian systems, emphasizing structural symmetry and energy conservation, which enables systematic generation of chaotic dynamics. Dong et al. [34] demonstrated how multistable Hamiltonian systems with adjustable parameters can enhance unpredictability, directly linking their chaotic outputs to robust PRNGs validated through statistical tests like NIST. Extensions to higher-dimensional systems, such as 5D hyperchaotic models by Dong et al. [35] and Zhang and Huang [36], leverage symmetry and coexisting attractors to amplify entropy, critical for high-security encryption. Kong et al. [37] further generalized these principles to odd-dimensional (2n+1) Hamiltonian systems, balancing simplicity with high-dimensional complexity and showcasing their efficacy in fast image encryption. Notably, hardware implementation challenges are addressed in works like Yu et al. [38] and Yan and Li [39], which validate the feasibility of FPGA-based realizations of multistable Hamiltonian systems, ensuring practical applicability in resource-constrained environments. Adding to this, Yuan et al. [40] introduce a novel class of nD Hamiltonian systems incorporating a three-terminal memristor, merging memristive nonlinearity with conservative chaos. Their work demonstrates enhanced dynamical richness, including tunable hyperchaotic regimes and improved entropy, while providing a hardware-efficient FPGA implementation framework tailored for PRNGs. Collectively, these studies highlight a paradigm shift toward Hamiltonian conservative chaos as a cornerstone for reliable PRNGs, combining mathematical elegance (energy conservation, symmetry, memristive adaptability) with engineering pragmatism (scalability, multistability, hardware feasibility). However, open challenges remain in optimizing the trade-off between system complexity, memristor integration, and computational efficiency for real-time cryptographic applications.

In this paper, we propose a pseudorandom number generator (PRNG) based on a Hamiltonian conservative chaotic system (HCCS) constructed using the 4D Euler equations of rigid body rotations. The novelty of our proposed work lies in the systematic pre-analysis of HCCSs to ensure a uniform and ergodic distribution of phase space variables used in the PRNG development, along with their invariant measure to achieve the desired pseudorandomness. This analysis also helps in selecting the appropriate parameters/initial conditions ranges to be used as seed values for the proposed PRNG. Such recommendations are often overlooked in existing chaos-based PRNGs, including those based on HCCSs. We detail this preliminary analysis for a specific HCCS constructed using the 4D Euler equations of rigid body rotations and use it to describe the proposed PRNG approach. This approach can be readily extended to other HCCSs, provided their phase space behavior is carefully analyzed as outlined in this paper. In the next section, we describe the details of the Hamiltonian conservative chaotic system, its dynamical behavior, and the pre-analysis required for effective pseudorandom number generation.

2 Hamiltonian conservative chaotic system based on 4D Euler equations

The 3D Euler equations for rigid body dynamics describe the rotational motion of a rigid body about the centre of mass without external torque. These equations date back to the 18th century, derived by Leonhard Euler and express how the angular velocity changes over time based on the body’s moment of inertia [41, 42]. These are nonlinear coupled differential equations that preserve the conservation of angular momentum and energy and predict the rotational motion of the rigid body that can range from smooth rotation to a very complex even chaotic depending on the body’s geometry and initial conditions. These are widely used in the field like mechanical engineering and aerospace engineering.

$\begin{array}{cc}\hfill I_1\frac{d{\omega }_1}{dt}& =\left(I_2-I_3\right){\omega }_2{\omega }_3,\hfill \\ \hfill I_2\frac{d{\omega }_2}{dt}& =\left(I_3-I_1\right){\omega }_3{\omega }_1,\hfill \\ \hfill I_3\frac{d{\omega }_3}{dt}& =\left(I_1-I_2\right){\omega }_1{\omega }_2.\hfill \end{array}(1)$

Here ${\omega }_1,{\omega }_2,{\omega }_3$ are the components of the angular velocity in the body-fixed frame, and $I_1,I_2,I_3$ are the principal moments of inertia about the three principal axes.

A 4D extension of these equations describes the rotational dynamics in four-dimensional space involving the six independent angular velocities $({\omega }_{12},{\omega }_{13},{\omega }_{14},{\omega }_{23},{\omega }_{24},{\omega }_{34})$ corresponding to the six independent planes of rotation in 4D space (i.e., combinations of the four coordinate axes) [43]. In 4D, a $4\times 4$ matrix represents the inertia tensor $(I_{ij};i,j\in \{\mathrm{1,2,3,4}\})$ that describes how the mass is distributed with respect to six independent planes. The more complex structure of the moment of inertia leads to richer dynamics including potential chaotic behaviour.

The 4D Euler equations for rigid body rotation can be written in terms of the Hamiltonian vector field where the six angular velocities can be organized into an angular momentum vector $\mathbf{L}$ in the 6D space of rotations.

The 4D Euler equations in Hamiltonian form have the following general form:

$\frac{d{L}_{ij}}{dt}={\displaystyle \sum _{k\ne i,j}}\left(I_{ik}^{-1}-I_{jk}^{-1}\right)L_{ik}{L}_{jk}(2)$

where $L_{ij}$ is the angular momentum in the $ij$-plane, and $I_{ij}$ are the components of the moment of inertia tensor in the 4D space. The corresponding Hamiltonian function related to the total kinetic energy of the system, in terms of angular momentum and moment of inertia in 4D space, is given as

$H=T=\frac{1}{2}{\displaystyle \sum _{ij}}{I}_{ij}^{-1}{L}_{ij}^2(3)$

A Hamiltonian form of 3D Euler equation may be written by assuming $x_i=I_i{\omega }_i$ and ${\alpha }_i=I_i^{-1}$

$\begin{array}{c}\hfill {\dot{x}}_1=\left({\alpha }_3-{\alpha }_2\right)x_2{x}_3,\\ \hfill {\dot{x}}_2=\left({\alpha }_1-{\alpha }_3\right)x_1{x}_3,\\ \hfill {\dot{x}}_3=\left({\alpha }_2-{\alpha }_1\right)x_1{x}_2.\end{array}(4)$

with the Hamiltonian $H(x)=\frac{1}{2}\left({\alpha }_1{x}_1^2+{\alpha }_2{x}_2^2+{\alpha }_3{x}_3^2\right)$

The Euler equations may also be written in the form

$\dot{x}=J\left(x\right)\nabla H\left(x\right),(5)$

where $J(x)$ is symplectic

$\begin{array}{c}\hfill J\left(x\right)=-J^T\left(x\right)=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill -x_3\hfill & \hfill x_2\hfill \\ \hfill x_3\hfill & \hfill 0\hfill & \hfill -x_1\hfill \\ \hfill -x_2\hfill & \hfill x_1\hfill & \hfill 0\hfill \end{array}\right]\end{array}(6)$

equivalently, the Euler equations may be written in Lie–Poisson bracket or cross-product form

$\dot{x}=\left\{x,H\left(x\right)\right\}=x\times \nabla H\left(x\right),(7)$

with $\{x,H\}$ determining the Lie–Poisson structure.

Qi [44] extends these equations to 4D for four sub-rigid bodies, introducing six complete 4D Euler equations that preserve symplectic structure, Hamiltonians, and Casimir energies. Based on these equations, six types of Hamiltonian conservative chaotic systems are constructed, revealing the mechanism that generates and enhances chaos. The approach has been summarized briefly in the following paragraph. For a system with dimension more than 3, the Lie-Poisson structure can not be written in the cross-product form as in Equation 7. For this purpose four 3D rigid sub-bodies $S{B}_{123},S{B}_{124},S{B}_{134},\text{\hspace{0.17em}and\hspace{0.17em}}S{B}_{234}$ are considered, and the generalized 4D sub-Euler equation for the sub-body $S{B}_{\mathit{ijk}}$ are expressed as follows:

$\begin{array}{c}\hfill {\dot{\mathbf{x}}}_{\mathit{ijk}}={\mathbf{x}}_{\mathit{ijk}}\times \nabla H\left({\mathbf{x}}_{\mathit{ijk}}\right)=\det \left[\begin{array}{ccc}\hfill {\mathbf{e}}_i\hfill & \hfill {\mathbf{e}}_j\hfill & \hfill {\mathbf{e}}_k\hfill \\ \hfill x_i\hfill & \hfill x_j\hfill & \hfill x_k\hfill \\ \hfill {\alpha }_i{x}_i\hfill & \hfill {\alpha }_j{x}_j\hfill & \hfill {\alpha }_k{x}_k\hfill \end{array}\right]\end{array}(8)$

In the above equation $ijk$ is one of the ordered triplets from the set $(\mathrm{123,124,134,234})$. The cross-product calculation is same as 3D crossproduct and the result is generalized in 4D vector form with zero as the remaining component. By integrating these sub-bodies, six complete 4D bodies Euler’s equations are constructed e.g., ${\sum }_{24}$ is constructed by combining $S{B}_{124}$ & $S{B}_{234}$ in the following way:

$\dot{\mathbf{x}}={\mathbf{x}}_{124}\times \nabla H\left({\mathbf{x}}_{124}\right)+{\mathbf{x}}_{234}\times \nabla H\left({\mathbf{x}}_{234}\right)(9)$

$\dot{\mathbf{x}}=J_{24}\left(\mathbf{x}\right)\nabla H\left(\mathbf{x}\right),(10)$

where

$J_{24}\left(x\right)=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill -x_4\hfill & \hfill 0\hfill & \hfill x_2\hfill \\ \hfill x_4\hfill & \hfill 0\hfill & \hfill -x_4\hfill & \hfill x_3-x_1\hfill \\ \hfill 0\hfill & \hfill x_4\hfill & \hfill 0\hfill & \hfill -x_2\hfill \\ \hfill -x_2\hfill & \hfill x_1-x_3\hfill & \hfill x_2\hfill & \hfill 0\hfill \end{array}\right](11)$

with the Hamiltonian $H(x)=\frac{1}{2}\left({\alpha }_1{x}_1^2+{\alpha }_2{x}_2^2+{\alpha }_3{x}_3^2+{\alpha }_4{x}_4^2\right)$

Similarly, we may construct ${\sum }_{12}{\sum }_{13}$, ${\sum }_{14}$, ${\sum }_{23}$, and ${\sum }_{34}$ by combining $S{B}_{123}$ & $S{B}_{124}$, $S{B}_{123}$ & $S{B}_{134}$, $S{B}_{124}$ & $S{B}_{134}$, $S{B}_{123}$ & $S{B}_{234}$, and $S{B}_{134}$ & $S{B}_{234}$ respectively. All six 4D Euler’s equations are conservative in Hamiltonian form, and the Casimir energy function (also known as energy-momentum) is also conserved. The rate of change of the Casimir function, referred to as the Casimir power, may serve as a criterion for determining whether the system exhibits chaos. Hamiltonian conservative chaotic systems (HCCS) may be generated by breaking the conservation of Casimir energy and preserving the Hamiltonian in the above six 4D Euler’s equations. The generated six HCCS are denoted by ${\sum }_{ij}^H$ where $ij$ is one of the elements of the set (12, 13, 14, 23, 24, 34). One of the Hamiltonian conservative chaotic systems (HCCS) ${\sum }_{24}^H$ generated in the above mentioned way is as follows:

$\dot{\mathbf{x}}=J_{24}^H\left(\mathbf{x}\right)\nabla H\left(\mathbf{x}\right),(12)$

where

$J_{24}^H\left(x\right)=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill -x_4\hfill & \hfill b\hfill & \hfill x_2\hfill \\ \hfill x_4\hfill & \hfill 0\hfill & \hfill -x_4\hfill & \hfill x_3-x_1\hfill \\ \hfill -b\hfill & \hfill x_4\hfill & \hfill 0\hfill & \hfill -x_2\hfill \\ \hfill -x_2\hfill & \hfill x_1-x_3\hfill & \hfill x_2\hfill & \hfill 0\hfill \end{array}\right].(13)$

in the expanded form, the HCCS ${\sum }_{24}^H$ may be written as:

$\left[\begin{array}{c}\hfill \dot{x_1}\hfill \\ \hfill \dot{x_2}\hfill \\ \hfill \dot{x_3}\hfill \\ \hfill \dot{x_4}\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill -x_4\hfill & \hfill b\hfill & \hfill x_2\hfill \\ \hfill x_4\hfill & \hfill 0\hfill & \hfill -x_4\hfill & \hfill x_3-x_1\hfill \\ \hfill -b\hfill & \hfill x_4\hfill & \hfill 0\hfill & \hfill -x_2\hfill \\ \hfill -x_2\hfill & \hfill x_1-x_3\hfill & \hfill x_2\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\alpha }_1{x}_1\hfill \\ \hfill {\alpha }_2{x}_2\hfill \\ \hfill {\alpha }_3{x}_3\hfill \\ \hfill {\alpha }_4{x}_4\hfill \end{array}\right],(14)$

with the substitutions [45] ${\alpha }_4-{\alpha }_2=a$, ${\alpha }_4-{\alpha }_3=c$, ${\alpha }_1-{\alpha }_4=d$, and ${\alpha }_3-{\alpha }_2=0$, and $(x_1,x_2,x_3,x_4)\equiv (x,y,z,w)$, the HCCS takes the following form:

$\begin{array}{cc}\hfill \dot{x}& =ayw+bz,\hfill \\ \hfill \dot{y}& =czw+dxw,\hfill \\ \hfill \dot{z}& =-cyw-bx,\hfill \\ \hfill \dot{w}& =-\left(a+d\right)xy.\hfill \end{array}(15)$

We use the above mentioned HCCS as an example to demonstrate the generation of pseudorandom numbers.

The above system has been integrated for the parameters $(a,b,c,d)=(0.5,\mathrm{10,6,5.5})$ and initial conditions $(x_0,y_0,z_0,w_0)=(\mathrm{1,1,1,1})$ [45] for $16\times 10^6$ steps with a time step of 0.01 for generating a bit sequence of $10^6$ bits. The system trajectory has been observed continuously and the Poincare points $(y_n,z_n,w_n)$, $(x_n,z_n,w_n)$, $(x_n,y_n,w_n)$ and $(x_n,y_n,z_n)$ are recorded when the trajectory crosses the planes $x=0$, $y=0$, $z=0$ and $w=0$ respectively. We have depicted the 2D projections of these Poincare points and histograms of the variables in Figures 1–4. Particularly in the left column of these figures the 2D projections of 3D Poincare points have been depicted and in the right column the histograms of all three variables of Poincare points. These Poincare sections and histograms are obtained for the time asymptotic behaviour of the system under the parameter values and initial conditions mentioned above. The distribution of points in the 2D projections as well as the shape of the histograms remain invariant under time asymptotic behaviour. As we observe that the phase space of the above system is a hypersphere defined by $-2\le x\le 2$; $-2\le y\le 2$; $-2\le z\le 2$; $-2\le w\le 2$ and the Poincare sections of the phase trajectories through the planes give 3D spheres whose projections on various 2D planes are circles of radius 2 with origin (0,0).

Figure 1

Figure 1. 2D projections of the Poincare section $x=0$ and histograms of the corresponding variables.

Figure 2

Figure 2. 2D projections of the Poincare section $y=0$ and histograms of the corresponding variables.

Figure 3

Figure 3. 2D projections of the Poincare section $z=0$ and histograms of the corresponding variables.

Figure 4

Figure 4. 2D projections of the Poincare section $w=0$ and histograms of the corresponding variables.

For the purpose of a pseudorandom number generation, we require a uniform and ergodic distribution of points in phase space, with invariant probability distributions for all phase variables. It is well known that for a uniform distribution of points in a 2D square space, both variables must individually follow a uniform distribution over the same range. Similarly, for a uniform distribution of points in a 2D circular space, both variables should follow a normal-like distribution (more precisely, a uniform distribution in 2D polar space) over the same range.

In our analysis, when we closely examine the distribution of points in the 2D projections of Poincaré sections and their corresponding histograms of variables, we clearly observe from Figure 1 that the projection of points in the 2D phase space $(y,w)$, as well as the individual distributions of variables $y$ and $w$ for a Poincaré section defined by $x=0$, satisfies the above criteria. This behavior is fully ergodic in the time-asymptotic sense. However, any other cases in Figures 1–4 do not meet this criterion.

3 The proposed method for pseudorandom number generation

After selecting a suitable pair of variables namely, $a$ and $b$, there are two ways to generate pseudorandom bit sequences by comparing these variables.

In the first method, we divide the entire circular phase space into four equal parts (quadrants) and assign a pair of bits to each part. We then integrate the Hamiltonian conservative system and obtain the Poincaré points for the selected pair of variables. When the Poincaré points fall into a particular quadrant of the phase space, we add the corresponding pair of bits to our bit sequence. This process continues until the sequence reaches the desired length. We have illustrated the division of the phase space and the corresponding pairs of bits in Figure 5 and presented the corresponding algorithm in Algorithm 1.

Figure 5

Figure 5. The division of the phase space $(a,b)$ into four parts and the corresponding pairs of bits.

Algorithm 1

Algorithm 1. Generate the pair of bits using Method 1.

In the second method, we divide the circular phase space into eight equal parts and assign a triplet of bits to each part. We then integrate the Hamiltonian conservative chaotic system and sequentially obtain the Poincaré points for the selected pair of variables. When the Poincaré points fall into a specific part of the phase space, we add the corresponding triplet to our bit sequence. This process continues until the sequence reaches the desired length. We have illustrated the division of the phase space and the corresponding pairs of bits in Figure 6 and presented the corresponding algorithm in Algorithm 2.

Figure 6

Figure 6. The division of the phase space $(a,b)$ into eight parts and the corresponding triplets of bits.

Algorithm 2

Algorithm 2. Generate the triplet of bits using Method 2.

The second method generates bit sequences faster than the first method, as each iteration (each time the trajectory crosses the selected Poincaré plane) produces three bits. In contrast, the first method only produces two bits. Therefore, the second method is 1.5 times faster than the first.

Based on the dynamic analysis of the Hamiltonian conservative chaotic system presented in the previous section, we select the variables $y$ and $w$ corresponding to the Poincaré section defined by $x=0$ for pseudorandom number generation. We now explore three different schemes for each of the two methods mentioned above.

3.1 Method 1: Through the divison of Poincare phase space into four parts

We integrate two identical Hamiltonian conservative chaotic systems, starting with random and different initial conditions but the same system parameter values corresponding to chaotic ergodic behavior.

3.1.1 Scheme 1.1

Consider the Poincare phase space of variables $y_1$ (each time the trajectory crosses the Poincaré section at $x_1=0$) and $y_2$ (each time the trajectory crosses the Poincaré section at $x_2=0$). This space is divided into four parts and pairs of bits are generated as described in Method 1 above. This process is carried out using Algorithm 1 with $a=y_1$ and $b=y_2$.

3.1.2 Scheme 1.2

Consider the Poincare space of variables $w_1$ (each time the trajectory crosses the Poincaré section at $x_1=0$) and $w_2$ (each time the trajectory crosses the Poincaré section at $x_2=0$). This space is divided into four parts, and pairs of bits are generated as described in Method 1 above. This process is carried out using Algorithm 1 with $a=w_1$ and $b=w_2$.

3.1.3 Scheme 1.3

Consider the Poincare phase space of variables $y_1$ (each time the trajectory crosses the Poincaré section at $x_1=0$) and $w_2$ (each time the trajectory crosses the Poincaré section at $x_2=0$), or alternatively, the Poincare space of variables $y_2$ (each time the trajectory crosses the Poincaré section at $x_1=0$) and $w_1$ (each time the trajectory crosses the Poincaré section at $x_2=0$). This space is divided into four parts and pairs of bits are generated as described in Method 1 above. This process is carried out using Algorithm 1 with $a=y_1$ and $b=w_2$ or, alternatively, $a=y_2$ and $b=w_1$.

3.2 Method 2: Through the divison of Poincare phase space into eight parts

We integrate two identical Hamiltonian conservative chaotic systems, starting with random and different initial conditions but the same system parameter values corresponding to chaotic ergodic behavior.

3.2.1 Scheme 2.1

Consider the Poincare phase space of variables $y_1$ (each time the trajectory crosses the Poincaré section at $x_1=0$) and $y_2$ (each time the trajectory crosses the Poincaré section at $x_2=0$). This space is divided into eight parts, and triplets of bits are generated as described in Method 2 above. This process is carried out using Algorithm 2 with $a=y_1$ and $b=y_2$.

3.2.2 Scheme 2.2

Consider the Poincare phase space of variables $w_1$ (each time the trajectory crosses the Poincaré section at $x_1=0$) and $w_2$ (each time the trajectory crosses the Poincaré section at $x_2=0$). This space is divided into eight parts, and triplets of bits are generated as described in Method 2 above. This process is carried out using Algorithm 2 with $a=w_1$ and $b=w_2$.

3.2.3 Scheme 2.3

Consider the Poincare phase space of variables $y_1$ (each time the trajectory crosses the Poincaré section at $x_1=0$) and $w_2$ (each time the trajectory crosses the Poincaré section at $x_2=0$), or alternatively, the Poincare space of variables $y_2$ (each time the trajectory crosses the Poincaré section at $x_1=0$) and $w_1$ (each time the trajectory crosses the Poincaré section at $x_2=0$). This space is divided into eight parts, and triplets of bits are generated as described in Method 2 above. This process is carried out using Algorithm 2 with $a=y_1$ and $b=w_2$ or, alternatively, $a=y_2$ and $b=w_1$.

In the proposed approach for pseudorandom number generation, we describe two primary methods, dividing the phase space into four parts and into eight parts, each with multiple schemes. These methods can be applied to any HCCS, provided that the selected phase variables for partitioning satisfy the pre-analysis criteria of uniformity, ergodicity, and invariant measure. The number of schemes within each method depends on the available phase variables meeting these criteria. At least two such phase variables are required, along with their corresponding 2D projections. If more qualifying phase variables exist, additional schemes can be designed by considering all possible permutations of phase-variable pairs and their respective 2D projections. In this paper, we present three schemes for each method and demonstrate that pseudorandom number generation is feasible for all possible pairwise permutations of the chosen phase variables.

It is also important to mention that we have explained our method using an example of an HCCS, specifically a continuous-time dynamical system, through the Poincaré surface of section approach. However, the method can also be applied to discrete-time HCCS (e.g., 2D Hamiltonian conservative chaotic standard map) as long as the stated criteria are met. In such cases, the Poincaré surface of section is not needed; instead, phase variables and their corresponding 2D projections can be directly obtained at discrete time steps from the following map (difference) equations:

$\begin{array}{c}\hfill X_{n+1}=\left(X_n+K\sin Y_n\right)\mathrm{mod}2\pi ,\\ \hfill Y_{n+1}=\left(X_{n+1}+Y_n\right)\mathrm{mod}2\pi .\end{array}(16)$

In Figure 7, we depict the phase space $(X,Y)$ behavior of the 2D Hamiltonian conservative chaotic Standard Map and the histograms of both phase variables for $10^6$ iterations and the parameter value $K=259.14$. We observe that both phase variables exhibit a uniform and invariant distribution in the asymptotic time limit, and the phase space distribution is ergodic. Hence, it satisfies the criteria stated above for pseudorandom number generation. Therefore, these phase variables may be used for pseudorandom number generation as described in the two methods (and their respective schemes) mentioned above.

Figure 7

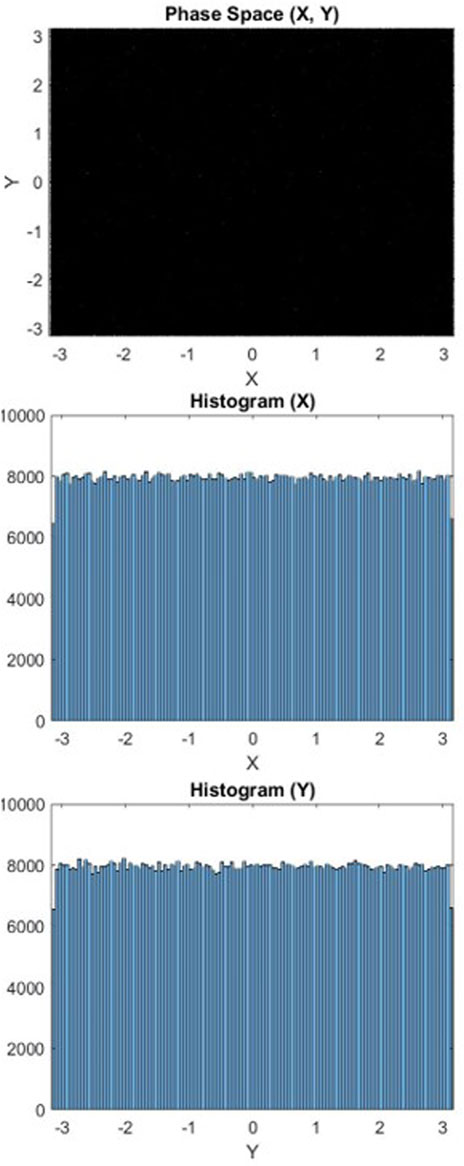
Figure 7. Phase space $(X,Y)$ and histograms of the phase variables $X$ and $Y$ of the 2D Hamiltonian conservative chaotic standard map.

4 The performance analysis and statistical testing

We use the NIST randomness test suite [46] to analyze the output of our proposed pseudorandom number generator. For this purpose, for each scheme (explained in Section 3), we generate 1,000 sequences, each of length $10^6$ bits. To generate each bit sequence, we randomly choose a set of initial conditions from the hyperspherical phase space of radius 2, and the system parameters are selected to ensure complete ergodic behavior throughout the entire phase space (as explained in the previous section).

All the generated sequences are tested using the NIST randomness test suite, which comprises 15 tests, including both parametric and non-parametric tests. The NIST test suite primarily conducts tests based on specific test statistics and generates a p-value that indicates the success or failure of each test, depending on the p-value’s magnitude (with the significance level $(\alpha )=0.01$ chosen for our analysis). A p-value is generated for each sequence and test statistic, and the sequence passes the test if $p-value\ge \alpha =0.01$.

Thus, for our 1,000 sequences generated by the proposed pseudorandom number generator, the NIST test suite computes 1,000 p-values for each test statistic. There are 15 main tests, several of which include multiple sub-tests based on different templates, parameter sets, or criteria. In total, 188 tests are performed by the NIST test suite on each sequence, determining whether that particular sequence passes or fails each test. For a detailed description of all the tests in NIST randomness test suite, we refer the readers to Bassham et al. [46].

We then calculate the proportion of sequences that pass each test by dividing the number of sequences that passed by the total number tested, providing a comprehensive evaluation of the randomness of the sequences generated by our pseudorandom number generator. We also check the uniformity of the p-values generated for each sequence by applying the ${\chi }^2$ test and computing a $p-valu{e}_T$ for each test statistic. If the $p-valu{e}_T\ge 0.001$ the distribution of the p-values is considered uniform.

The results of $p-valu{e}_T$ and proportions of sequences passing the tests for all the six schemes have been summarized in Table 1, 2, and are also depicted in Figures 8, 9. We clearly observe that the pseudorandom sequences generated by our novel approach pass all the tests in the NIST randomness test suite. Therefore, the proposed PRNG is robust and complies with the randomness standards required for cryptographic applications.

Table 1

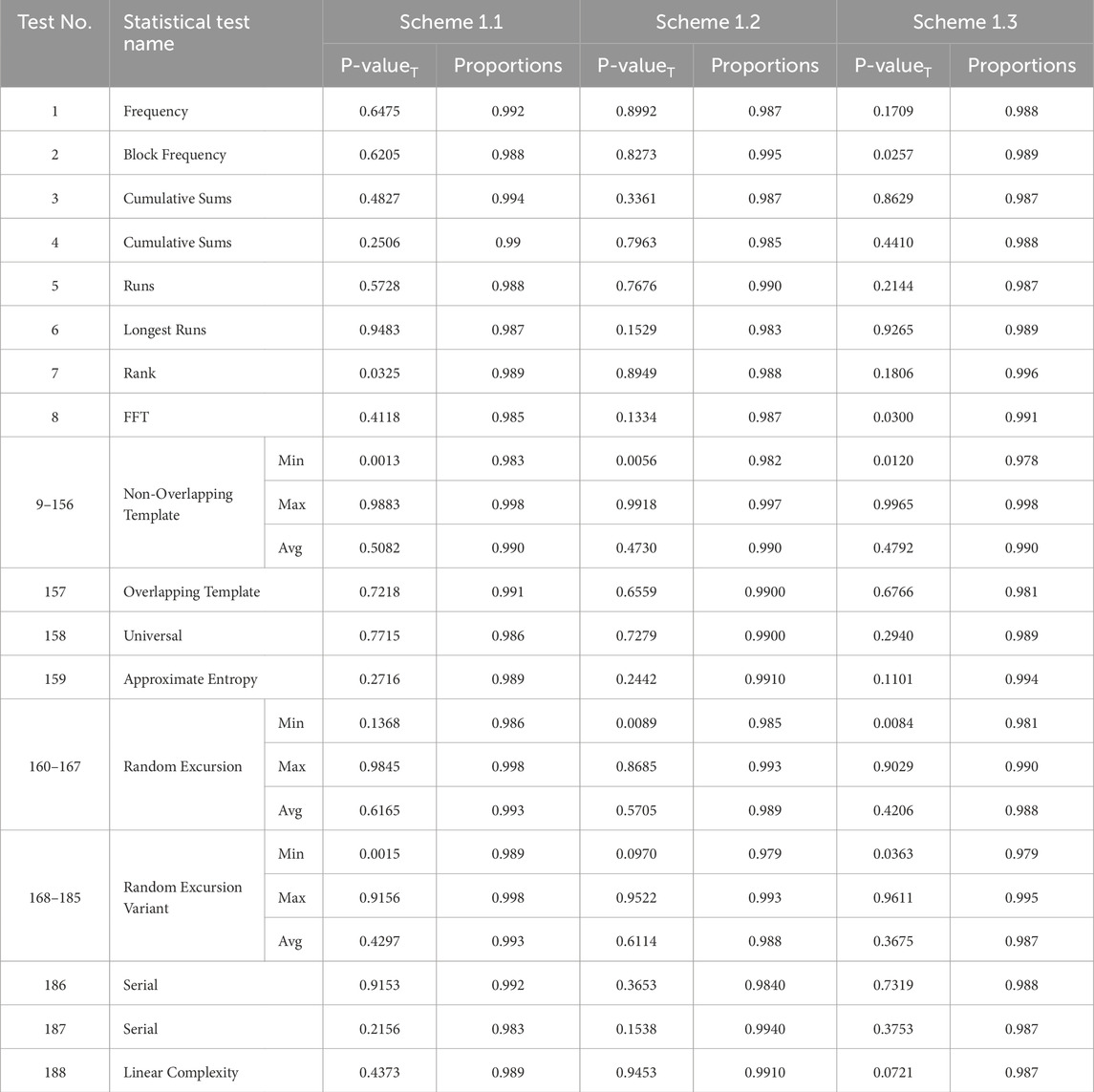
Table 1. Performance analysis of the three schemes in Method 1 using the NIST randomness test suite.

Table 2

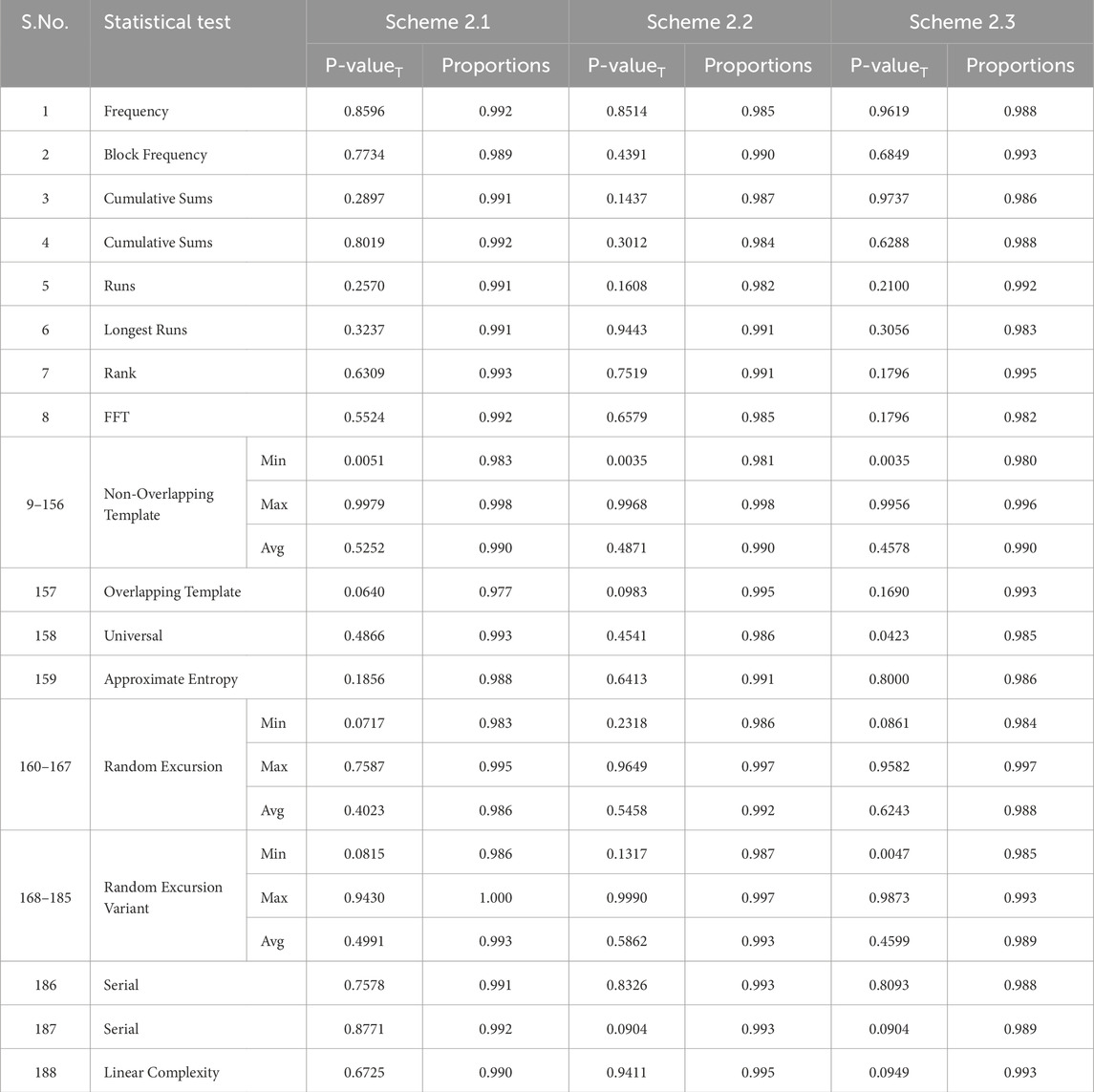
Table 2. Performance analysis of the three schemes in Method 2 using the NIST randomness test suite.

Figure 8

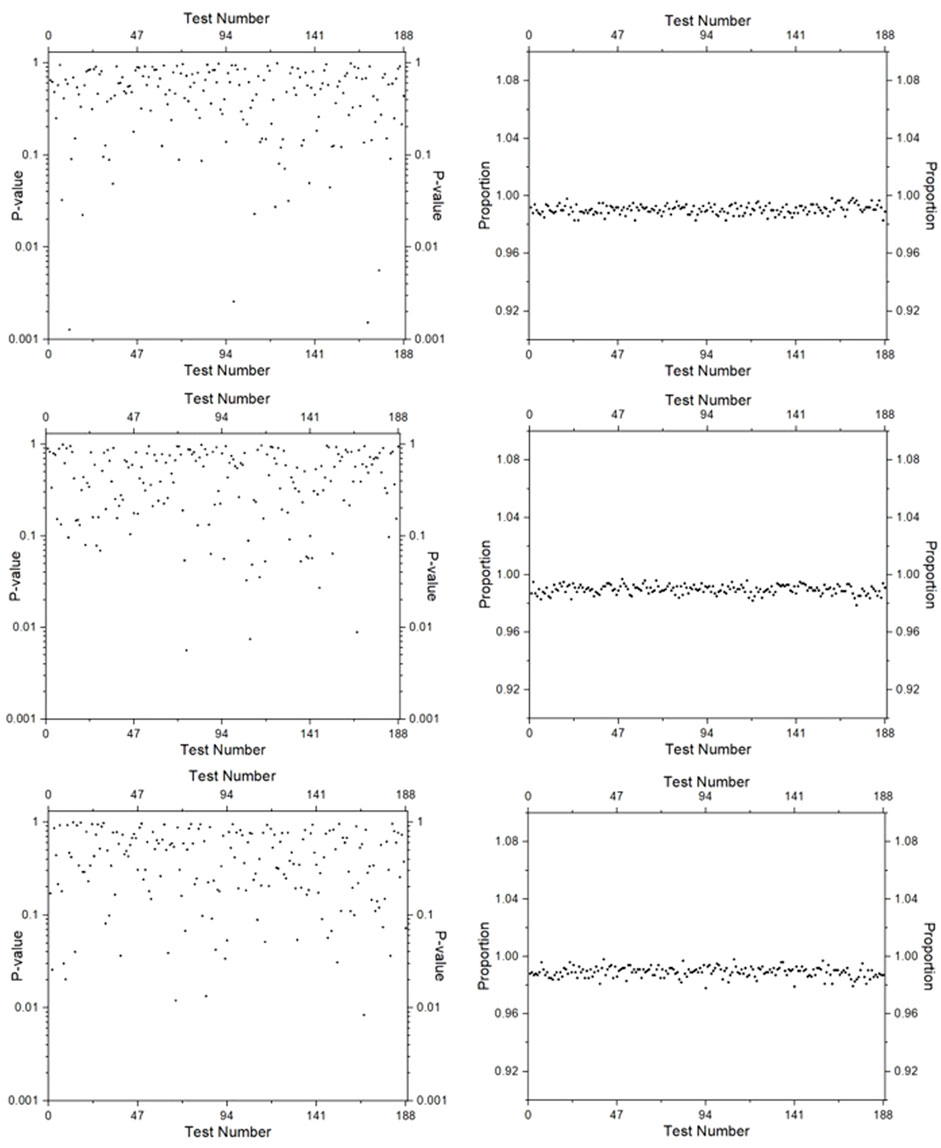
Figure 8. NIST Test Suite Results for Method 1: The first, second, and third rows correspond to Scheme 1.1, Scheme 1.2, and Scheme 1.3, respectively.

Figure 9

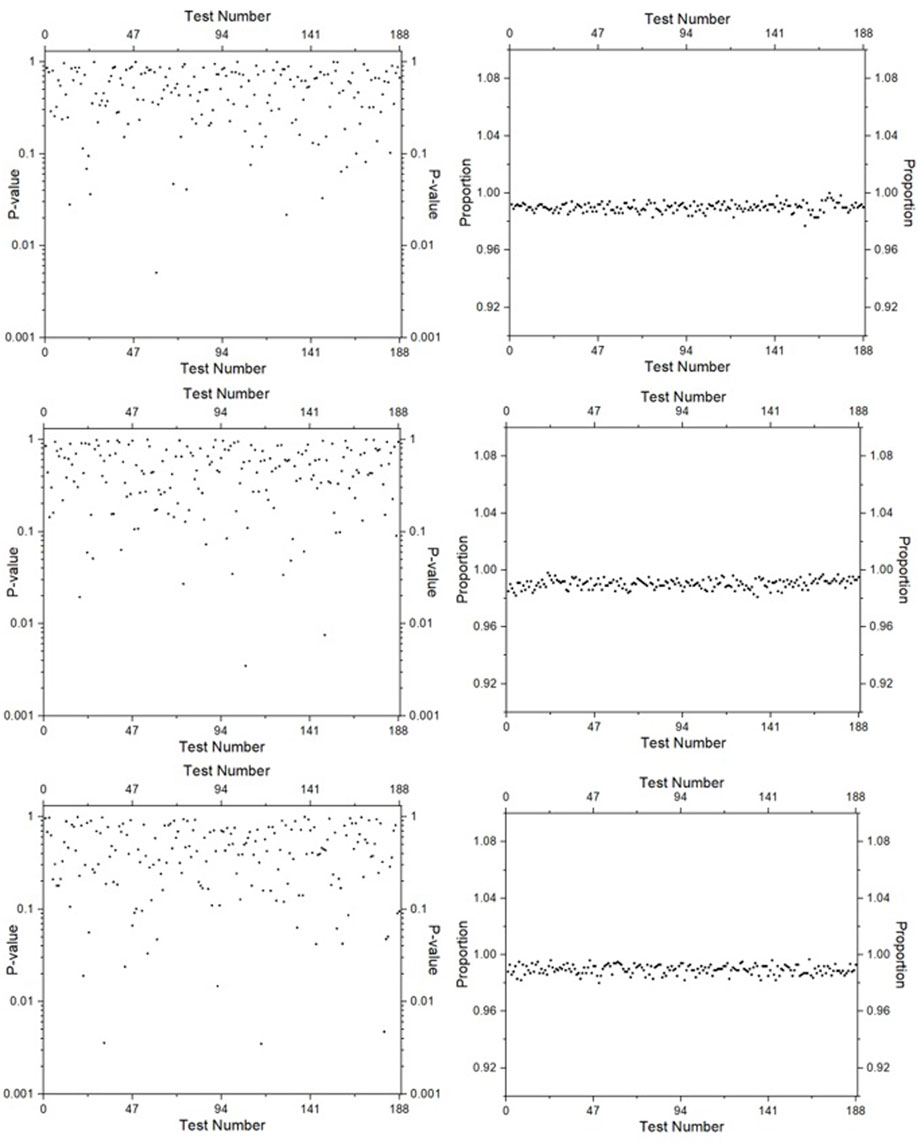
Figure 9. NIST Test Suite Results for Method 2: The first, second, and third rows correspond to Scheme 2.1, Scheme 2.2, and Scheme 2.3, respectively.

As pointed out earlier, the Method 2 is 1.5 times faster than Method 1, giving it a computational speed advantage. Both methods have different variants (as referred to by schemes) based on the number of phase variables and their corresponding 2D projections that satisfy the predefined criterion. A higher-dimensional HCCS inherently employs more phase variables, leading to a greater number of valid 2D projections and, consequently, more scheme variants. Ideally, the superiority amongst the schemes corresponding to the same method is trivial. However, the suitability of a method for pseudorandom number generation is ultimately determined by its performance in the NIST statistical test suite. This evaluation hinges on two key metrics: (i) Uniformity of p-values across the test (assessed by $p-valu{e}_T)$ and (ii) Proportions of sequences that pass the tests. A method is considered cryptographically secure if its results fall within the allowable ranges specified by the NIST guidelines (based on the chosen significance level). Importantly, direct numerical comparisons of p-values or passing proportions are not inherently meaningful. Instead, the focus should remain on adherence to the NIST criteria. Furthermore, valid comparisons between methods require identical testing environments (e.g., significance level, number of sequences, and bit-length per sequence). For this reason, we avoid explicit comparisons based on raw p-value magnitudes or passing rates and instead emphasize compliance with the NIST recommendations.

The Dependence on high-entropy sources and periodic behavior are common challenges in most pseudorandom number generators (PRNGs). Every PRNG has a characteristic period after which its sequence repeats. A PRNG is considered secure for a specific application only if its period significantly exceeds the required sequence length. Additionally, all PRNGs require a seed value to initialize pseudorandom sequence generation. A larger seed space (i.e., more possible seed values) corresponds to higher entropy, which directly enhances security. In our approach, we ensure the Hamiltonian Conservative Chaotic System (HCCS) exhibits ergodic behavior before employing it for PRNG applications. By leveraging the entire phase space of the HCCS as the seed domain, a feature unattainable in dissipative chaotic systems or conservative systems with coexisting regular and chaotic dynamics (which are non-ergodic), the number of possible seed values becomes theoretically infinite. However, in practice, finite computational precision imposes a finite (albeit extremely large) upper bound on the seed space, a limitation shared by most chaos-based PRNGs. For an HCCS-based PRNG with ergodic behaviour, the periodicity is theoretically infinite, as the system can traverse its entire phase space without repetition. Nevertheless, finite computational precision restricts the practical implementation to a finite period length. Although this period remains astronomically large compared to conventional PRNGs, it underscores the inherent constraints of digital computation in chaotic systems.

5 Conclusion

This paper presents a novel approach to pseudorandom number generation (PRNG) using a Hamiltonian conservative chaotic system (HCCS) derived from the 4D Euler equations. The key contribution of our work lies in the systematic pre-analysis of HCCSs to ensure a uniform and ergodic distribution of phase space variables along with their invariant measure, which is crucial for achieving robust pseudorandomness. This pre-analysis framework, which involves identifying suitable Poincaré sections and phase space variables, not only ensures the statistical rigor of the generated sequences but also guides the selection of parameter ranges for initial seeds-an aspect often overlooked in existing chaos-based PRNGs, including those based on HCCSs. The proposed approach is readily extendable to any Hamiltonian conservative chaotic system exhibiting the desired ergodic behavior, provided the pre-analysis steps outlined in this paper are rigorously followed. We demonstrate the proposed approach by generating high-quality pseudorandom sequences using two alternative methods and multiple schemes associated with each method, tailored to the number of variables satisfying the uniformity and ergodicity criteria. Comprehensive testing with the NIST randomness test suite confirms the excellent statistical properties of the sequences, meeting the stringent standards required for cryptographic applications.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

VP: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–original draft, Writing–review and editing. TS: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Knuth DE. The art of computer programming: Seminumerical algorithms. Reading, MA: Addison-Wesley (1969).

Google Scholar

2. L’Ecuyer P. Random numbers for simulation. Commun ACM (1990) 33:85–97. doi:10.1145/84537.84555

CrossRef Full Text | Google Scholar

3. Von Neumann J. 13. various techniques used in connection with random digits. Appl Math Ser (1951) 12(5):36–38.

Google Scholar

4. Lehmer DH. Mathematical models in large-scale computing units, 26. Ann. Comput. Lab. Harvard University (1951). p. 141–6.

Google Scholar

5. Matsumoto M, Nishimura T. Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans Model Comp Simulation (Tomacs) (1998) 8:3–30. doi:10.1145/272991.272995

CrossRef Full Text | Google Scholar

6. Kelsey J, Schneier B, Ferguson N. Yarrow-160: notes on the design and analysis of the yarrow cryptographic pseudorandom number generator. In: International workshop on selected areas in cryptography. Springer (1999). p. 13–33.

Google Scholar

7. Ferguson N, Schneier B. Practical cryptography, 141. New York: Wiley (2003).

Google Scholar

8. McEvoy R, Curran J, Cotter P, Murphy C. Fortuna: cryptographically secure pseudo-random number generation in software and hardware. In: 2006 IET Irish signals and systems conference (IET) (2006). p. 457–62.

Google Scholar

9. Blum L, Blum M, Shub M. A simple unpredictable pseudo-random number generator. SIAM J Comput (1986) 15:364–83. doi:10.1137/0215025

CrossRef Full Text | Google Scholar

10. O’neill ME. Pcg: a family of simple fast space-efficient statistically good algorithms for random number generation. ACM Trans Math Softw (2014).

Google Scholar

11. Marsaglia G. Xorshift rngs. J Stat Softw (2003) 8:1–6. doi:10.18637/jss.v008.i14

CrossRef Full Text | Google Scholar

12. Haider Z, Saeed MH, Zaheer ME-u.-H, Alvi ZA, Ilyas M, Nasreen T, et al. Quantum random number generator (qrng): theoretical and experimental investigations. The Eur Phys J Plus (2023) 138:797. doi:10.1140/epjp/s13360-023-04421-3

CrossRef Full Text | Google Scholar

13. Bhattacharjee K, Das S. A search for good pseudo-random number generators: survey and empirical studies. Comp Sci Rev (2022) 45:100471. doi:10.1016/j.cosrev.2022.100471

CrossRef Full Text | Google Scholar

14. James F, Moneta L. Review of high-quality random number generators. Comput Softw Big Sci (2020) 4:2–12. doi:10.1007/s41781-019-0034-3

CrossRef Full Text | Google Scholar

15. Strogatz SH. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. Boca Raton, FL: CRC Press (2018).

CrossRef Full Text | Google Scholar

16. Hilborn RC. Chaos and nonlinear dynamics: an introduction for scientists and engineers. Oxford, Great Britain: Oxford University Press (2000).

Google Scholar

17. Lakshmanan M, Rajaseekar S. Nonlinear dynamics: integrability, chaos and patterns. Springer Science and Business Media (2012).

Google Scholar

18. Alawida M. Enhancing logistic chaotic map for improved cryptographic security in random number generation. J Inf Security Appl (2024) 80:103685. doi:10.1016/j.jisa.2023.103685

CrossRef Full Text | Google Scholar

19. Sun F, Lv Z, Wang C. Pseudo-random number generation based on spatial chaotic map of logistic type and its cryptographic application. Int J Mod Phys C (2024) 36:2450172. doi:10.1142/s0129183124501729

CrossRef Full Text | Google Scholar

20. Calderon MJA, Lucas LJL, Rosli SAB, Ying SSH, Yu JLE, Xiang M, et al. Logistic map pseudo random number generator in fpga (2024). arXiv preprint arXiv:2404.19246.

Google Scholar

21. Murillo-Escobar D, Murillo-Escobar MÁ, Cruz-Hernández C, Arellano-Delgado A, López-Gutiérrez RM. Pseudorandom number generator based on novel 2d hénon-sine hyperchaotic map with microcontroller implementation. Nonlinear Dyn (2023) 111:6773–89. doi:10.1007/s11071-022-08101-2

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Patidar V, Sud K. A novel pseudo random bit generator based on chaotic standard map and its testing. Electron J Theor Phys (2009) 6:327–44.

Google Scholar

23. Patidar V, Kaur G. A novel conservative chaos driven dynamic dna coding for image encryption. Front Appl Maths Stat (2023) 8:1100839. doi:10.3389/fams.2022.1100839

CrossRef Full Text | Google Scholar

24. Krishnamoorthi S, Dhanaraj RK, Hafizul Islam S. Ccm-prng: pseudo-random bit generator based on cross-over chaotic map and its application in image encryption. Multimedia Tools Appl (2024) 83:80823–46. doi:10.1007/s11042-024-18668-0

CrossRef Full Text | Google Scholar

25. Madouri Z, Hadj Said N, Ali Pacha A. A new pseudorandom number generator based on chaos in digital filters for image encryption. J Opt (2024) 53:3548–63. doi:10.1007/s12596-023-01606-y

CrossRef Full Text | Google Scholar

26. AbdElHaleem SH, Abd-El-Hafiz SK, Radwan AG. Analysis and guidelines for different designs of pseudo random number generators. IEEE Access (2024) 12:115697–715. doi:10.1109/access.2024.3445277

CrossRef Full Text | Google Scholar

27. Cang S, Kang Z, Wang Z. Pseudo-random number generator based on a generalized conservative sprott-a system. Nonlinear Dyn (2021) 104:827–44. doi:10.1007/s11071-021-06310-9

CrossRef Full Text | Google Scholar

28. Patidar V, Pareek N, Purohit G, Sud K. A robust and secure chaotic standard map based pseudorandom permutation-substitution scheme for image encryption. Opt Commun (2011) 284:4331–9. doi:10.1016/j.optcom.2011.05.028

CrossRef Full Text | Google Scholar

29. Cang S, Wu A, Wang Z, Chen Z. Four-dimensional autonomous dynamical systems with conservative flows: two-case study. Nonlinear Dyn (2017) 89:2495–508. doi:10.1007/s11071-017-3599-6

CrossRef Full Text | Google Scholar

30. Jia H, Shi W, Wang L, Qi G. Energy analysis of sprott-a system and generation of a new Hamiltonian conservative chaotic system with coexisting hidden attractors. Chaos, Solitons and Fractals (2020) 133:109635. doi:10.1016/j.chaos.2020.109635

CrossRef Full Text | Google Scholar

31. Cang S, Li Y, Kang Z, Wang Z. Generating multicluster conservative chaotic flows from a generalized sprott-a system. Chaos, Solitons and Fractals (2020) 133:109651. doi:10.1016/j.chaos.2020.109651

CrossRef Full Text | Google Scholar

32. Cang S, Li Y, Kang Z, Wang Z. A generic method for constructing n-fold covers of 3d conservative chaotic systems. Chaos: Interdiscip J Nonlinear Sci (2020) 30:033103. doi:10.1063/1.5123246

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Ji’e M, Yan D, Sun S, Zhang F, Duan S, Wang L. A simple method for constructing a family of Hamiltonian conservative chaotic systems. IEEE Trans Circuits Syst Regular Pap (2022) 69:3328–38. doi:10.1109/tcsi.2022.3172313

CrossRef Full Text | Google Scholar

34. Dong E, Yuan M, Du S, Chen Z. A new class of Hamiltonian conservative chaotic systems with multistability and design of pseudo-random number generator. Appl Math Model (2019) 73:40–71. doi:10.1016/j.apm.2019.03.037

CrossRef Full Text | Google Scholar

35. Dong Q, Zhou S, Zhang Q, Kasabov NK. A class of 5d Hamiltonian conservative hyperchaotic systems with symmetry and multistability. Nonlinear Dyn (2022) 110:2889–912. doi:10.1007/s11071-022-07735-6

CrossRef Full Text | Google Scholar

36. Zhang Z, Huang L. A new 5d Hamiltonian conservative hyperchaotic system with four center type equilibrium points, wide range and coexisting hyperchaotic orbits. Nonlinear Dyn (2022) 108:637–52. doi:10.1007/s11071-021-07197-2

CrossRef Full Text | Google Scholar

37. Kong X, Yu F, Yao W, Xu C, Zhang J, Cai S, et al. A class of 2n+ 1 dimensional simplest Hamiltonian conservative chaotic systems and fast image encryption schemes. Appl Math Model (2024) 125:351–74. doi:10.1016/j.apm.2023.10.004

CrossRef Full Text | Google Scholar

38. Yu F, Yuan Y, Wu C, Yao W, Xu C, Cai S, et al. Modeling and hardware implementation of a class of Hamiltonian conservative chaotic systems with transient quasi-period and multistability. Nonlinear Dyn (2024) 112:2331–47. doi:10.1007/s11071-023-09148-5

CrossRef Full Text | Google Scholar

39. Yan M, Li S. Research on shape-controllable generalized multi-cluster Hamiltonian conservative chaotic flow systems and their fpga implementation. Eur Phys J Plus (2024) 139:466–15. doi:10.1140/epjp/s13360-024-05289-7

CrossRef Full Text | Google Scholar

40. Yuan Y, Yu F, Tan B, Huang Y, Yao W, Cai S, et al. A class of nd Hamiltonian conservative chaotic systems with three-terminal memristor: modeling, dynamical analysis, and fpga implementation. Chaos: Interdiscip J Nonlinear Sci (2025) 35:013121. doi:10.1063/5.0238893

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Marsden JE, Ratiu TS. Introduction to mechanics and symmetry: a basic exposition of classical mechanical systems, 17. Springer Science and Business Media (2013).

Google Scholar

42. Shamolin M. Classification of complete integrability cases in four-dimensional symmetric rigid-body dynamics in a nonconservative field. J Math Sci (2010) 165:743–54. doi:10.1007/s10958-010-9838-8

CrossRef Full Text | Google Scholar

43. Perelomov A. Motion of four-dimensional rigid body around a fixed point: an elementary approach i. J Phys A: Math Gen (2005) 38:L801–7. doi:10.1088/0305-4470/38/47/l03

CrossRef Full Text | Google Scholar

44. Qi G. Modelings and mechanism analysis underlying both the 4d euler equations and Hamiltonian conservative chaotic systems. Nonlinear Dyn (2019) 95:2063–77. doi:10.1007/s11071-018-4676-1

CrossRef Full Text | Google Scholar

45. Dong E, Liu G, Wang Z, Chen Z. Energy conservation, singular orbits, and fpga implementation of two new Hamiltonian chaotic systems. Complexity (2020) 2020:1–15. doi:10.1155/2020/8693157

CrossRef Full Text | Google Scholar

46. Bassham LE, Rukhin AL, Soto J, Nechvatal JR, Smid ME, Leigh SD, et al. Astatistical test suite for random and pseudorandom number generators forcryptographic applications (2010).

Google Scholar