He’s frequency formulation for fractal-fractional nonlinear oscillators: a comprehensive analysis

This mini-review focuses on He’s frequency formulation for fractal-fractional nonlinear oscillators. It examines the significance and applications of this formulation in understanding and analyzing the frequency-amplitude relationship within a fractal space. The review analyses the key features and advantages of He’s frequency formulation, highlighting its role in providing a straightforward approach to fractal vibration systems compared to traditional methods. Furthermore, it discusses an open problem for future research.

1 Introduction

The study of nanobeam vibrations is of great importance for the advancement of microelectromechanical systems (MEMS) [1]. The vibration of a nanobeam is not merely a mechanical phenomenon; rather, it is a critical element that drives the development of these highly sophisticated systems. In 6G communication technology, the stability of nano-antenna arrays directly depends on the precise control of nano-beam vibrations. Any instability in the vibrations can lead to signal interference and a decrease in transmission efficiency. For example, by optimizing the vibration modes of nano-beams, the radiation pattern can be adjusted and signal gain can be enhanced, thereby improving the overall performance of the communication system. Sensors based on the vibration of nanobeams can detect subtle changes in biomolecule concentrations, enabling early disease diagnosis. By modulating the vibrational characteristics (such as resonant frequency), the sensitivity of these sensors can be significantly enhanced, to the point where the presence of individual biomarkers can be detected. For instance, in early cancer screening, nanobeam sensors identify specific proteins at very low concentrations in the blood, offering new avenues for precision medicine. MEMS, with the potential to precipitate a revolutionary transformation in domains such as sixth-generation (6G) communications [2], quantum computing [3], and healthcare [4], rely heavily on an accurate understanding and control of nanobeam vibrations.

Minor disturbances, such as those caused by air pollution and changes in humidity, can impact the precision and dependability of the system by influencing the vibration characteristics of the nanobeam. Tian et al. were the first mathematicians to model these factors in a fractal space, and they concluded that in the fractal space, the pull-in instability can be eliminated [5]. As a consequence, a new branch of knowledge, known as fractal vibration theory [6, 7], has emerged. This innovative theory is specifically crafted to handle the complex and unconventional vibrating behaviors that traditional theories fall short in explaining. In the editorial article [8], the fundamental characteristics of fractional vibration theory and the fractal vibration theory are elucidated in meticulous and transparent detail.

Traditional vibration analysis methods are typically based on integer-order derivatives and assume that the system has regular geometric shapes and linear behavior. However, these assumptions no longer hold in fractal-fractional systems. For instance, when dealing with the vibration of nanostructures that have self-similar or irregular geometric structures, traditional methods cannot accurately describe the inherent non-locality and memory effects in the system. They often oversimplify complex physical processes, leading to significant errors in predicting the frequency-amplitude relationship and dynamic behavior of oscillators. In contrast, He’s frequency formula, by considering fractal and fractional-order characteristics, provides a more precise and powerful tool for analyzing such complex systems.

He’s frequency formulation [9, 10] represents an exceptionally potent analytical instrument within the domain of fractal vibration theory. This formulation not only presents a profound method of analysis but also offers significant promise for advancing our comprehension and practical applications in this intricate field. The formulation provides an efficient and highly efficacious means of determining the complex frequency-amplitude relationship of nonlinear oscillators. This relationship is of crucial importance for understanding the behavior and characteristics of a broad spectrum of systems, ranging from mechanical vibrations to electrical circuits and beyond.

The importance of He’s frequency formulation is further reinforced by a series of subsequent studies. He and Liu extended it to fractal oscillators [11], and numerous authors have demonstrated the applicability and versatility of He’s formulation in diverse contexts, including the case of the Toda oscillator [12] and various fractal vibration systems [13]. Moreover, numerous researchers have further expanded and refined the understanding of He’s frequency formulation for their applications, and a considerable amount of literature has contributed to the expanding body of knowledge surrounding He’s frequency formulation [14–18]. The extensive applications and continuous development of He’s frequency formulation are documented in Refs. [19, 20]. Moreover, the integration of this approach with other methods, such as the homotopy perturbation method [21, 22], has the potential to expand the research landscape of nonlinear oscillations. In conclusion, He’s frequency formulation represents a fundamental contribution to the field of nonlinear oscillations, offering a valuable and powerful tool for both researchers and practitioners. The continued exploration and application of this concept in a variety of studies serves to demonstrate its significance and potential for further advancements in our understanding and control of nonlinear systems. This paper presents a concise overview of the applications of this formulation to fractal-fractional oscillators.

2 Fractal-fractional nonlinear oscillator

Different from fractional models [23–26], the fractal-fractional nonlinear oscillator [27, 28] constitutes a captivating area of study within the domain of nonlinear dynamics. It amalgamates the concepts of fractals and fractional calculus to model complex systems. Fractals provide a means to depict irregular structures, whereas fractional calculus offers a more accurate representation of systems with memory and non-local effects. In a fractal-fractional nonlinear oscillator, these elements converge to create a model that can capture the intricate behavior of diverse physical and engineering systems. This might include phenomena such as damping, resonance, and chaos. By understanding and analyzing these oscillators, researchers can obtain valuable insights into the behavior of complex systems and potentially develop new techniques for control and optimization [29–37].

Here, we consider a fractal-fractional (Equation 2) describes the nonlinear vibration system of a restrained cantilever beam with an intermediate lumped mass. [38].

$\left(1+a{u}^2+b{u}^4\right)\frac{d^{2\alpha }u}{d{x}^{2\alpha }}+\left(au+2b{u}^3\right){\left(\frac{d^{\alpha }u}{d{x}^{\alpha }}\right)}^2+{\mathrm{\Omega }}^{2}u+m{u}^3+n{u}^5=0(1)$

with the boundary conditions

$u\left(0\right)=B,\frac{d^{\alpha }u}{d{x}^{\alpha }}\left(0\right)=0(2)$

where $\frac{d^{\alpha }u}{d{x}^{\alpha }}$ is the two-scale fractal derivative [39–42], a and b respectively represent the contributions of the high - order terms of the nonlinear stiffness coefficient, m and n are the coefficients of the fifth - order terms of the nonlinear restoring force, $\mathrm{\Omega }$ is the linear natural frequency, and $\alpha$ is the order of the fractal derivative, which reflects the fractal characteristics of the system [42–45].

The two-scale fractal derivative is defined as:

$\frac{d^{2\alpha }u}{d{x}^{2\alpha }}u\left(x\right)=\frac{1}{\mathrm{\Gamma }\left(1-2\alpha \right)}{\int }_{-\infty }^{\infty }\frac{u\left(x^{\prime }\right)-u\left(x\right)}{{\left(x^{\prime }-x\right)}^{1+2\alpha }}g\left(x,x^{\prime },l_1,l_2\right)d{x}^{\prime }$

Among them, $g\left(x,x^{\prime },l_1,l_2\right)$ is a weighting function related to the fractal structure and the scales $l_1,l_2$. Consider the fluid velocity field $v\left(x\right)$ in the fractal porous medium, and its governing equation is:

$\rho \frac{\mathrm{\partial }v}{\mathrm{\partial }t}=-\nabla p+\mu \left(\frac{d^{2\alpha }v}{d{x}^{2\alpha }}+\beta \frac{d^{\alpha }v}{d{x}^{\alpha }}\right)$

where $\rho$ is the fluid density, p is the pressure, $\mu$ is the viscosity, and $\beta$ is a coefficient related to the fractal characteristics. By solving this equation with the two-scale fractal derivative, we can accurately predict the flow patterns and velocities of the fluid in the fractal porous medium, which is not possible using traditional derivatives.

The two-scale fractal derivative [39, 40] is an innovative concept in the realm of mathematics and physics. It extends the traditional derivative to take into account fractal behavior. Through two-scale fractal derivatives, the flow patterns of fluids in fractal pores can be accurately predicted, whereas traditional derivatives cannot capture such complex behaviors.

This derivative considers two distinct scales, providing a more accurate description of processes that display non-integer scaling. It can be applied to various fields like fluid dynamics, material science, and signal processing. The two-scale fractal derivative aids in understanding complex phenomena involving irregular or self-similar structures. It offers new insights and tools for analyzing and modeling systems with fractal characteristics.

The nonlinear vibrations of a restrained cantilever beam with an intermediate lumped mass are an important area of study. This system exhibits complex behavior due to the combination of nonlinearities and the added mass. Understanding these vibrations is helpful in designing more robust structures and analyzing their dynamic responses.

Sun and his colleagues dedicated themselves to arduous research on Equation 1 and finally obtained the following frequency - amplitude relationship [38].

${\omega }^2=\frac{8{\Omega }^2+6m{B}^2+5n{B}^4}{8+4a{B}^2+3b{B}^4}=\frac{{\Omega }^2+0.75m{B}^2+0.625n{B}^4}{1+0.5a{B}^2+0.375b{B}^4}(3)$

Their endeavors in this regard were truly outstanding. They engaged in complex analysis that demanded a high degree of expertise and intellectual rigor. Given the intricacy of their approach, there is currently a significant need for a one-step simple method, such as He’s frequency formulation [9, 10], which can offer a more streamlined and accessible means to achieve similar results.

3 A brief review He’s frequency formulation

Equation 4 presents the basic form of a fractional-order nonlinear vibration system.

$\frac{d^{2\alpha }u}{d{x}^{2\alpha }}+f\left(u\right)=0,u\left(0\right)=B,\frac{d^{\alpha }u}{d{x}^{\alpha }}\left(0\right)=0(4)$

The most used frequency formulations are respectively expressed as [9, 10]

${\omega }^2={\left\{\frac{f}{u}\right\}}_{\begin{array}{c}u=\sqrt{3}B/2\end{array}}(5)$

and

${\omega }^2={\left\{\frac{df}{du}\right\}}_{u=B/2}(6)$

More generally, we can choose more than one location points [34]:

${\omega }_i^2={\left\{\frac{f}{u}\right\}}_{u=N_{i}B}(7)$

and

${{\omega }_j}^2={\left\{\frac{df}{du}\right\}}_{\begin{array}{c}{u}_j=N_{i}B\end{array}}(8)$

Where 0<N_i<1 and 0<N_j<1, and (Equation 9) provides the average value of the frequency squared at multiple location points.

${\omega }^2=\frac{1}{n}\left({{\omega }_1}^2+{{\omega }_2}^2+\cdots +{{\omega }_n}^2\right)(9)$

Equation 10 demonstrates the method for calculating the average frequency at multiple location points.

$\omega =\frac{1}{n}\left({\omega }_1+{\omega }_2+\cdots +{\omega }_n\right)(10)$

The selection of $u=\sqrt{3}B/2$ in Equation 5 is derived from the sensitivity of the nonlinear system to frequency changes near the critical amplitude. While the selection of $u=B/2$ in Equation 6 captures the trend of frequency changes through the local behavior of the derivative at the mid - amplitude point. Sampling at multiple position points (Equations 7, 8) takes the average values over different amplitude ranges, which effectively reduces the error of single - point estimation and is applicable to highly nonlinear systems.

Equations 11–17 illustrate the frequency calculation methods at different location points and the derivation process of their average values.

$\frac{d^{2\alpha }u}{d{x}^{2\alpha }}+f\left(u,\frac{d^{\alpha }u}{d{x}^{\alpha }},\frac{d^{2\alpha }u}{d{x}^{2\alpha }}\right)=0,u\left(0\right)=B,\frac{d^{\alpha }u}{d{x}^{\alpha }}\left(0\right)=0(11)$

The frequency formulation is

${\omega }^2={\left\{\frac{f}{u}\right\}}_{u=\sqrt{3}B/2,\frac{d^{\alpha }u}{d{x}^{\alpha }}=-\omega B/2,\frac{d^{2\alpha }u}{d{x}^{2\alpha }}=-\sqrt{3}B{\omega }^2/2}(12)$

or

${\omega }^2={\left\{\frac{f}{u}\right\}}_{u=NB,\frac{d^{\alpha }u}{d{x}^{\alpha }}=-\sqrt{1-N^2}B\omega ,\frac{d^{2\alpha }u}{d{x}^{2\alpha }}=-NB{\omega }^2}(13)$

He-Liu frequency formulation [11] recommends the form

${\omega }^2=\frac{{\int }_0^A\left(wf\right)du}{{\int }_0^A\left(wu\right)du}(14)$

where w is a weighting function.

4 An example

For Equation 1, f can be expressed as

$f=\left(a{u}^2+b{u}^4\right)\frac{d^{2\alpha }u}{d{x}^{2\alpha }}+\left(au+2b{u}^3\right){\left(\frac{d^{\alpha }u}{d{x}^{\alpha }}\right)}^2+{\mathrm{\Omega }}^{2}u+m{u}^3+n{u}^5=0(15)$

By the frequency formulation, we have

${\omega }^2={\left\{\left(au+b{u}^3\right)\frac{d^{2\alpha }u}{d{x}^{2\alpha }}+\left(a+2b{u}^2\right){\left(\frac{d^{\alpha }u}{d{x}^{\alpha }}\right)}^2+{\mathrm{\Omega }}^2+m{u}^2+n{u}^4\right\}}_{\begin{array}{l}u=\sqrt{3}B/2\\ \frac{d^{\alpha }u}{d{x}^{\alpha }}=-\omega B/2\\ \frac{d^{2\alpha }u}{d{x}^{2\alpha }}=-\sqrt{3}B{\omega }^2/2\end{array}}=\left(a\frac{\sqrt{3}}{2}B+b\frac{3\sqrt{3}}{8}{B}^3\right)\left(-\frac{\sqrt{3}}{2}B{\omega }^2\right)+\left(a+2b\frac{3}{4}{B}^2\right)\left(\frac{1}{4}{\omega }^2{B}^2\right)+{\mathrm{\Omega }}^2+m\frac{3}{4}{B}^2+n\frac{9}{16}{B}^4(16)$

After a simple calculation, we obtain

${\omega }^2=\frac{{\Omega }^2+\frac{3}{4}m{B}^2+\frac{9}{16}n{B}^4}{1+\frac{1}{2}a{B}^2+\frac{3}{16}b{B}^4}(17)$

The result obtained through this approach is much closer to Equation 3. When we consider adopting the simple approach, it truly stands out. As Ji-Huan He said, “The simpler is better.” The simplicity of this approach not only brings convenience in implementation but also leads to a remarkable result. It offers a more straightforward way to reach a conclusion that is highly comparable to what would be expected from more complex methods. The obtained result is indeed remarkable in that it showcases the effectiveness and efficiency of a less convoluted approach. It proves that sometimes simplicity can lead to outcomes that are just as valuable, if not more so, than those achieved through intricate and time-consuming methods.

Using a different location point, we have

${\omega }^2={\left\{\left(au+b{u}^3\right)\frac{d^{2\alpha }u}{d{x}^{2\alpha }}+\left(a+2b{u}^2\right){\left(\frac{d^{\alpha }u}{d{x}^{\alpha }}\right)}^2+{\mathrm{\Omega }}^2+m{u}^2+n{u}^4\right\}}_{\begin{array}{l}u=NB\\ \frac{d^{\alpha }u}{d{x}^{\alpha }}=-\sqrt{1-N^2}\omega B\\ \frac{d^{2\alpha }u}{d{x}^{2\alpha }}=-NB{\omega }^2\end{array}}=\left(aNB+b{N}^3{B}^3\right)\left(-NB{\omega }^2\right)+\left(a+2b{N}^2{B}^2\right)\left(\left(1-N^2\right){\omega }^2{B}^2\right)+{\mathrm{\Omega }}^2+m{N}^2{B}^2+n{N}^4{B}^4(18)$

From Equations 18, 19 further analyzes the frequency squared values under different parameter combinations.

${\omega }^2=\frac{{\mathrm{\Omega }}^2+0.69m{B}^2+n{N}^4{B}^4}{1+a\left(2N^2-1\right)B^2+b\left(3N^4-N^2\right)B^4}(19)$

To further analyze the comparison between the results of He’s frequency formulation and Equation 3, we calculate the relative error for various parameter values. The results are given in Table 1 and illustrated in Figure 1.

Table 1

Table 1. Relative errors for different cases: Case 1 a = 0.1; b = 0.05; m = 2.0; n = 0.5; case 2 a = 0.3; b = 0.1; m = 1.5; n = 0.8.

Figure 1

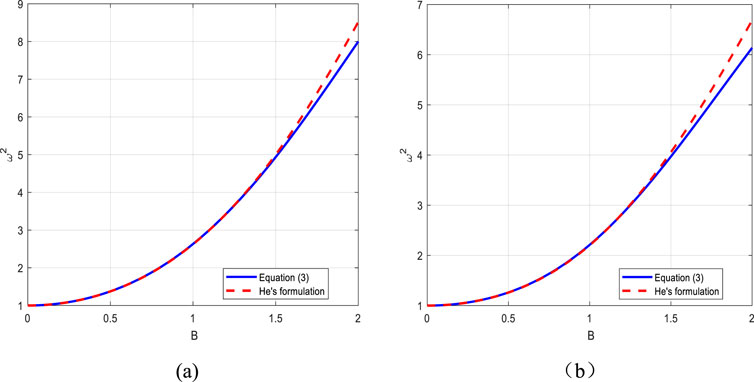
Figure 1. Comparison of the He formula and Equation 3 under different conditions:(a) a = 0.1; b = 0.05; m = 2.0; n = 0.5; (b) a = 0.3; b = 0.1; m = 1.5; n = 0.8.

From the table, it can be seen that the relative error varies with different parameter values. The error mainly stems from the approximation and neglect of higher-order terms in the He formula, while the numerical solution of Equation 3 may produce deviations due to the accumulation of algorithmic truncation errors. Additionally, the selection of position points may not fully cover the system response in strongly nonlinear regions.

Figure 1 illustrates the comparison of the frequency squared values obtained from He’s frequency formulation and Equation 3 as a function of the amplitude. The blue curve represents the results from He’s frequency formulation, while the red curve represents those from Equation 3.

The potential sources of discrepancy between the two methods are multi-faceted. He’s frequency formulation makes certain approximations to simplify the calculation. For example, in the process of deriving the formula, some higher-order terms might be neglected. In contrast, Equation 3 is obtained through a more comprehensive and complex analysis process. Numerical errors also play a role. The calculation of Equation 3 may involve more complex numerical algorithms, and small errors in these algorithms can accumulate and lead to differences in the final results. Moreover, the choice of location points in He’s formulation is based on general principles, but it may not cover all the characteristics of the system in some special cases.

In practical applications, the implications of these differences are significant. For applications with relatively low accuracy requirements, the simplicity of He’s formulation makes it a convenient choice. However, for applications that demand high precision, such as in the design of high-performance MEMS devices, understanding these differences is essential. It allows engineers and researchers to make more informed decisions when choosing the appropriate method and provides a basis for further improving the formulations to achieve better accuracy.

The question of how to choose an optimal value of N remains an open problem that has yet to be fully resolved. There are possible approaches to optimization of its choice by various modern technologies, e.g., the genetic algorithm, the gradient descent method, and AI-powered problem solving method [46].

5 Conclusion

In conclusion, He’s frequency formulation for fractional nonlinear oscillators represents a valuable contribution to the field of nonlinear dynamics. This formulation offers a novel approach to analyzing and understanding the complex behavior of fractional nonlinear oscillatory systems. By providing a more accurate description of frequency and other characteristics, it has the potential to enhance our understanding of various physical phenomena and engineering applications. Future research could further explore the generalization and extension of this formulation, as well as its application in different types of nonlinear systems. Additionally, combining He’s frequency formulation with other advanced techniques may lead to even more powerful tools for the study of fractional nonlinear oscillators. Overall, He’s frequency formulation holds great promise for advancing our knowledge and capabilities in dealing with nonlinear oscillatory systems.

Looking ahead, several promising research directions emerge in the context of He’s frequency formulation. One avenue is to explore its integration with advanced numerical techniques. For instance, combining it with the finite element method would enable a more detailed analysis of complex systems with irregular geometries and varying material properties. In such an approach, the domain of the problem could be discretized using finite elements, and He’s frequency formulation could be applied within each element to account for the fractal-fractional behavior. This would enhance the accuracy of predicting the vibration characteristics of structures like those found in MEMS devices with intricate designs.

Another exciting direction lies in its application to emerging fields. In nanorobotics, where the precise control of nanoscale motions is essential, He’s frequency formulation can potentially be used to optimize the design of actuators and sensors. By understanding the frequency-amplitude relationships of the nanocomponents, we can improve the performance and reliability of nanorobotic systems. In biomolecular dynamics, it could offer new perspectives on the study of molecular vibrations and their role in biological processes. For example, it may help in elucidating the energy transfer mechanisms within biomolecules, which could have implications for drug design and understanding diseases at the molecular level.

Moreover, the development of more efficient parameter determination algorithms is of utmost importance. With the increasing complexity of systems, traditional methods for finding optimal parameters in He’s frequency formulation may become computationally expensive. Incorporating machine learning algorithms, such as genetic algorithms or neural networks, could potentially accelerate the search process and improve the accuracy of the determined parameters. This would make the application of He’s frequency formulation more practical and efficient in dealing with large-scale and complex systems.

In summary, the future of He’s frequency formulation research is rich with opportunities, and continued efforts in these directions are expected to yield significant advancements in our understanding and control of nonlinear oscillatory systems.

Author contributions

LZ: Writing–original draft, Writing–review and editing. KG: Writing–original draft, Funding acquisition. JY: Funding acquisition, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TUDSPP-2024-45). Research supported by the Fundamental Research Funds for Hohhot Minzu College (ZSQNTS202427).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor CH declared a shared affiliation with the author LZ at the time of review.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mohammadi M, Farajpour A, Moradi A, Hosseini M. Vibration analysis of the rotating multilayer piezoelectric Timoshenko nanobeam. Eng Anal Boundary Elem (2022) 145:117–31. doi:10.1016/j.enganabound.2022.09.008

CrossRef Full Text | Google Scholar

2. Tian D, Huang ZX, Xiang JJ. A modeling and experimental analysis of fractal geometric potential mems in the context of the development of 6g and beyond. Fractals (2024) 32. doi:10.1142/S0218348X2450124X

CrossRef Full Text | Google Scholar

3. Bhosale KS, Li SS. Multi-harmonic phononic frequency comb generation in capacitive CMOS-MEMS resonators. Applied Physics Letters (2024) 124(16):163505. doi:10.1063/5.0197773

CrossRef Full Text | Google Scholar

4. Padha B, Yadav I, Dutta S, Arya S. Recent developments in wearable NEMS/MEMS-Based smart infrared sensors for healthcare applications. ACS APPLIED ELECTRONIC MATERIALS (2023) 5(10):5386–411. doi:10.1021/acsaelm.3c00860

CrossRef Full Text | Google Scholar

5. Tian D, Ain QT, Anjum N, He CH, Cheng B. Fractal N/MEMS: from pull-in instability to pull-in stability. Fractals (2021) 29:2150030. doi:10.1142/S0218348X21500304

CrossRef Full Text | Google Scholar

6. Tian D, He CH. A fractal micro-electromechanical system and its pull-in stability. J Low Frequency Noise Vibration Active Control (2021) 40(3):1380–6. doi:10.1177/1461348420984041

CrossRef Full Text | Google Scholar

7. Niu JY, Feng GQ, Gepreel KA. A simple frequency formulation for fractal-fractional non-linear oscillators: a promising tool and its future challenge. FRONTIERS PHYSICS (2023) 11:1158121. doi:10.3389/fphy.2023.1158121

CrossRef Full Text | Google Scholar

8. He CH, He JH, Sedighi HM, El-Dib YO, Marinkovic D, Alsolami AA. Editorial: analytical methods for nonlinear oscillators and solitary waves. FRONTIERS PHYSICS (2023) 11:1309182. doi:10.3389/fphy.2023.1309182

CrossRef Full Text | Google Scholar

9. He JH. The simplest approach to nonlinear oscillators. Results Phys (2019) 15:102546. doi:10.1016/j.rinp.2019.102546

CrossRef Full Text | Google Scholar

10. He J-H. The simpler, the better: analytical methods for nonlinear oscillators and fractional oscillators. Journal of Low Frequency Noise. Vibration and Active Control (2019) 38(3-4):1252–60. doi:10.1177/1461348419844145

CrossRef Full Text | Google Scholar

11. He CH, Liu C. A modified frequency-amplitude formulation for fractal vibration systems. Fractals (2022) 30(3):2250046. doi:10.1142/S0218348X22500463

CrossRef Full Text | Google Scholar

12. Feng GQ. Dynamic pull-down theory for the Toda oscillator. Int J Mod Phys B (2024) 38(22):2450292. doi:10.1142/S0217979224502928

CrossRef Full Text | Google Scholar

13. Tian Y. Frequency formula for a class of fractal vibration system. Rep Mech Eng (2022) 3(1):55–61. doi:10.31181/rme200103055y

CrossRef Full Text | Google Scholar

14. Feng GQ. He's frequency formula to fractal undamped duffing equation. J Low Frequency Noise Vibration Active Control (2021) 40(4):1671–6. doi:10.1177/1461348421992608

CrossRef Full Text | Google Scholar

15. Feng GQ, Niu JY. He’s frequency formulation for nonlinear vibration of a porous foundation with fractal derivative. GEM-International on Geomathematics (2021) 12(1):14. doi:10.1007/s13137-021-00181-3

CrossRef Full Text | Google Scholar

16. Tsaltas K. An improved one-step amplitude-frequency relation for nonlinear oscillators. Results Phys (2023) 54(2023):107090. doi:10.1016/j.rinp.2023.107090

CrossRef Full Text | Google Scholar

17. Ismail GM, Moatimid GM, Yamani MI. Periodic solutions of strongly nonlinear oscillators using He's frequency formulation. Eur J Pure Appl Maths (2024) 17(3):2155–72. doi:10.29020/nybg.ejpam.v17i3.5339

CrossRef Full Text | Google Scholar

18. He CH, Liu C, He JH, Gepreel K. Low frequency property of a fractal vibration model for a concrete beam. Fractals (2021) 29(5):2150117. doi:10.1142/S0218348X21501176

CrossRef Full Text | Google Scholar

19. El-Dib YO. The frequency estimation for non-conservative nonlinear oscillation. ZAMM (2021) 101(12):e202100187. doi:10.1002/zamm.202100187

CrossRef Full Text | Google Scholar

20. Zhang JG, Song QR, Wang F. Application of he’s frequency formula to nonlinear oscillators with generalized initial conditions. Facta Universitatis, Ser Mech Eng(2023) 21(4):701–12. doi:10.22190/fume230909047z

CrossRef Full Text | Google Scholar

21. He CH, El-Dib YO. A heuristic review on the homotopy perturbation method for non-conservative oscillators. J Low Freq N A(2022) 41(2):572–603. doi:10.1177/14613484211059264

CrossRef Full Text | Google Scholar

22. He JH, He CH, Alsolami AA. A good initial guess for approximating nonlinear oscillators by the homotopy perturbation method. Facta Universitatis, Ser Mech Eng(2023) 21(1):021–9. doi:10.22190/FUME230108006H

CrossRef Full Text | Google Scholar

23. Gao XL, Li ZY, Wang YL. Chaotic dynamic behavior of a fractional-order financial system with constant inelastic demand. Int J Bifurcation Chaos(2024) 34(9):2450111. doi:10.1142/S0218127424501116

CrossRef Full Text | Google Scholar

24. Li ZY, Chen QT, Wang Y, Li X. Solving two-sided fractional super-diffusive partial differential equations with variable coefficients in a class of new reproducing kernel spaces. Fractal and Fractional(2022) 6(9):492. doi:10.3390/fractalfract6090492

CrossRef Full Text | Google Scholar

25. Han C, Wang YL, Li ZY. A high-precision numerical approach to solving space fractional Gray-Scott model. Appl Maths Lett(2022) 125:107759. doi:10.1016/j.aml.2021.107759

CrossRef Full Text | Google Scholar

26. Che H, Yu-Lan W, Zhi-Yuan L. Novel patterns in a class of fractional reaction-diffusion models with the Riesz fractional derivative. Mathematics Comput Simulation(2022) 202:149–63. doi:10.1016/j.matcom.2022.05.037

CrossRef Full Text | Google Scholar

27. He J-H, Jiao M-L, He C-H. Homotopy perturbation method for fractal Duffing oscillator with arbitrary conditions. Fractals(2022) 30(9). doi:10.1142/S0218348X22501651

CrossRef Full Text | Google Scholar

28. He J-H, Moatimid GM, Zekry MH. Forced nonlinear oscillator in a fractal space. Facta Universitatis Ser Mech Eng(2022) 20(No 1):001–20. doi:10.22190/FUME220118004H

CrossRef Full Text | Google Scholar

29. El-Dib YO, Elgazery NS, Gad NS. A novel technique to obtain a time-delayed vibration control analytical solution with simulation of He's formula. J Low Frequency Noise Vibration Active Control (2023) 42(3):1379–89. doi:10.1177/14613484221149518

CrossRef Full Text | Google Scholar

30. Kawser MA, Alim MA, Sharif N. Analyzing nonlinear oscillations with He's frequency-amplitude method and numerical comparison in jet engine vibration system. Heliyon (2024) 10(2):e24261. doi:10.1016/j.heliyon.2024.e24261

PubMed Abstract | CrossRef Full Text | Google Scholar

31. He JH, Yang Q, He CH, Alsolami AA. Pull-down instability of the quadratic nonlinear oscillators. Facta Universitatis Ser Mech Eng (2023) 21(2):191–200. doi:10.22190/FUME230114007H

CrossRef Full Text | Google Scholar

32. He JH. Periodic solution of a micro-electromechanical system, Facta Universitatis. Ser Mech Eng (2024) 22(2):187–98. doi:10.22190/FUME240603034H

CrossRef Full Text | Google Scholar

33. He JH, He CH, Qian MY, Alsolami AA. Piezoelectric Biosensor based on ultrasensitive MEMS system. Sensors and Actuators A (2024) 376:115664. doi:10.1016/j.sna.2024.115664

CrossRef Full Text | Google Scholar

34. Lyu GJ, He JH, He CH, Hamid M. Straightforward method for nonlinear oscillators. J Donghua Univ (English Edition) (2023) 40(1):105–9. doi:10.3969/j.issn.1673-0066.2023.01.013

CrossRef Full Text | Google Scholar

35. He JH, Kou SJ, He CH, Zhang ZW, Gepreel KA. Fractal oscillation and its frequency-amplitude property. Fractals (2021) 29(4):2150105. doi:10.1142/S0218348X2150105X

CrossRef Full Text | Google Scholar

36. Shen Y. The Lagrange interpolation for He's frequency formulation. J Low Frequency Noise Vibration Active Control (2021) 40(3):1387–91. doi:10.1177/1461348420972824

CrossRef Full Text | Google Scholar

37. Mohammadian M. Application of He's new frequency-amplitude formulation for the nonlinear oscillators by introducing a new trend for determining the location points. Chin J Phys (2024) 89:1024–40. doi:10.1016/j.cjph.2024.03.047

CrossRef Full Text | Google Scholar

38. Sun Y, Lu J, Zhu M, Alsolami AA. Numerical analysis of fractional nonlinear vibrations of a restrained cantilever beam with an intermediate lumped mass. J Low Frequency Noise, Vibration Active Control (2024) 0(0). doi:10.1177/14613484241285502

CrossRef Full Text | Google Scholar

39. He JH. Seeing with a single scale is always unbelieving: from magic to two-scale fractal. Therm Sci (2021) 25(2B):1217–9. doi:10.2298/TSCI2102217H

CrossRef Full Text | Google Scholar

40. Anjum N, He CH, He JH. Two-scale fractal theory for the population dynamics. Fractals (2021) 29(7):150182. doi:10.1142/S0218348X21501826

CrossRef Full Text | Google Scholar

41. Li X-X, Luo Y-C, Ali Alsolami A, He J-H. Elucidating the fractal nature of the porosity of nanofiber members in the electrospinning process. Fractals (2024) 32. doi:10.1142/S0218348X24501093

CrossRef Full Text | Google Scholar

42. He CH, Liu C. Fractal dimensions of a porous concrete and its effect on the concrete’s strength. Facta Universitatis Ser Mech Eng (2023) 21(1):137–50. doi:10.22190/FUME221215005H

CrossRef Full Text | Google Scholar

43. He CH, Liu SH, Liu C, Mohammad-Sedighi H. A novel bond stress-slip model for 3-D printed concretes. Discrete and Continuous dynamical Systems-Series S (2022) 15(7):1669–83. doi:10.3934/dcdss.2021161

CrossRef Full Text | Google Scholar

44. He CH, Liu HW, Liu C. A fractal-based approach to the mechanical properties of recycled aggregate concretes. Facta Universitatis, Ser Mech Eng (2024) 22(2):329–42. doi:10.22190/FUME240605035H

CrossRef Full Text | Google Scholar

45. He CH. A variational principle for a fractal nano/microelectromechanical (N/MEMS) system. Int J Numer Methods Heat Fluid Flow (2022) 33(1):351–9. doi:10.1108/hff-03-2022-0191

CrossRef Full Text | Google Scholar

46. He JH. Transforming frontiers: the next decade of differential equations and control processes. Adv Differential Equations Control Process (2025) 32(1):2589. doi:10.59400/adecp2589

CrossRef Full Text | Google Scholar