Performance evaluation of photovoltaic scenario generation

Photovoltaic scenario generation plays a critical role in power systems characterized by high diversity and fluctuation. Despite recent theoretical advancements, effectively evaluating the performance of photovoltaic scenario generation remains a significant challenge. Existing studies predominantly rely on metrics such as mean, variance, and probability density functions for assessment. However, these approaches struggle to disentangle the underlying mechanisms of morphological features and environmental stochastic factors (e.g., cloud cover, seasonal variations) from individual or batch-generated samples. To address these limitations, this paper proposes an evaluation framework based on the wide-sense stationary process. By analyzing historical photovoltaic scenario data, a solar irradiance distribution model is first constructed to characterize its dynamic behavior. Subsequently, an autoregressive model is employed to quantify the influence of environmental randomness on photovoltaic scenarios. The proposed evaluation model not only comprehensively validates the reliability of various photovoltaic scenario generation techniques but also identifies the corresponding month or season of generated samples through scenario feature analysis. Experimental results demonstrate that, compared to conventional probability-based metrics, the proposed model more effectively reveals the performance characteristics of photovoltaic scenario generation technologies. This advancement provides a novel technical foundation for optimizing photovoltaic scenario generation in practical power systems.

1 Introduction

Electricity produced from solar photovoltaic (PV) panels is a vital source of clean energy, where much research has been done in recent years owing to its low pollution. As integration of PV powers into traditional power grid increases, a challenge surfaces due to regulation requirements of balancing existing supply-demand in energy markets [1, 2]. One solution to this problem is PV energy prediction in solar reception process using PV scenario generation to simulate real PV energy [3–5]. Key to informative analysis of PV scenario is accurate representation that describes the variability and uncertainty of solar generation from both spatial and temporal aspects [6, 7]. Two attributes of PV systems make it difficult to generate reliable PV scenario. One is that solar generation is mostly dominated by the accessibility of solar irradiation that changes across a day and during a year following the movement round the Sun and the Earth’s rotation [8–10]. Compared with traditional energy generation techniques, PV systems involves strong uncertain and environmental variables (e.g., cloud and season). The other is PV systems contain highly scalable ranging from a few kilowatts (kW) to hundreds of megawatts (MW) [11], which indicates the diversity of PV scenarios. Thereby, exploring the most accurate information on the PV generation characteristics determines the reliability of generated PV scenarios.

A lot of studies have devoted to improve the effectiveness and precision of PV scenario generation [12], categorized as model-based and model-free approaches. The former represents solar reception process with a specific model of presupositions, and the accuracy of model determines the reliability of PV scenario generation. Most of these techniques utilize probability models to simulate solar reception process. A modular statistical modeling approach is presented to predict power generation of both PV and wind power systems [13]. A pseudo-random number generation technique is proposed to reduce prediction error of PV scenario generation with considering uncertainty and variability indices [14]. Aggregated power curves are also analyzed and contributes to PV generation [15]. Gaussian copulas are established to produce multivariate PV scenarios [16]. The advantages of these techniques are simple models and easy implementation, yet the disadvantage is its limited ability of representing the uncertainty. Overcoming the weakness of model-based methods, model-free techniques learn the inherent distribution of solar reception process through analyzing existing PV scenario data. Support vector regression is used to forecast regional PV power generation with past PV data [17]. Artificial neural network is built to predict the solar irradiance in PV systems [18]. A recurrent neural network (RNN) is utilized to produce PV scenarios with month and weather information, which requires no mathematical modelling [19]. Conditional generative adversarial networks (CGAN) and Wasserstein GAN (WGAN) are constructed to generate PV scenarios with sufficient diversity and good representation of environmental uncertainty [20]. These techniques are capable of capturing the details of PV scenarios caused by particular operation of solar receptions. The drawbacks of model-free techniques are severe computation complexity and unexplained characteristics in operation processes. While either approach claims its accuracy and effectiveness, there are no standards evaluating them.

Although existing methods for PV scenario generation have demonstrated certain advantages, they also face notable limitations. Model-based approaches, such as AR and autoregressive moving average (ARMA) models, rely on fixed assumptions about the underlying process, making it challenging to capture non-linear and abrupt changes in PV power caused by sudden weather shifts. Model-free approaches, such as generative adversarial networks (GANs) and other deep learning models, have greater flexibility but require large datasets and significant computational resources. Their generalization performance may also be affected when applied to unseen weather or seasonal conditions.

Hence, it is important to evaluate the effectiveness of PV scenario generation methods. Typically, probabilistic properties of produced PV scenarios (e.g., mean value, variance, and probability density function (pdf)) are common indicators of evaluating the performance of PV scenario generation, because these indicators are easily calculated. In particular, hourly PV generation is used to estimate variable changes between times in the system and optimize future expansion plans. PV energy curves have high fluctuations due to the diversity and variety of solar reception process, i.e., the differences between any 2 sampling values in a PV scenario could be large. In this regard, mean value is weak to represent the uncertainty (e.g., cloud) in PV scenarios. Furthermore, variance is useful to evaluate the pattern of sunrise and sunset. Only averaging the variances of existing PV data is hard to determine which month or season that a generated sample belongs to. Additionally, pdf stands for purely solar energies from the Sun without environmental randomness, which is hard to assess the influence by cloud.

Therefore, unlike simple probability indicators such as mean and variance, we propose a novel evaluation model that explicitly assesses the reliability and effectiveness of photovoltaic (PV) scenario generation. While recent research, such as those relying on mean and variance, have been widely used, they are limited in their ability to capture the temporal dependencies and environmental randomness that significantly affect PV generation. These methods primarily focus on statistical summaries, which fail to account for abrupt changes caused by environmental factors like cloud movement, leading to less accurate predictions. In contrast, our autoregressive (AR)-based model provides a more comprehensive evaluation framework by explicitly modeling the temporal structure and stochastic fluctuations in PV scenarios. This AR model simulates the movement of clouds and its impact on solar reception, offering a more precise characterization of the underlying randomness in PV generation. Additionally, by incorporating month- and season-specific AR parameters, our approach is capable of categorizing PV scenarios into temporal categories, such as specific months and seasons, something that traditional mean and variance-based methods cannot achieve. This enhanced ability to classify and evaluate PV scenarios allows for more robust and context-aware PV energy predictions, making our approach not only more accurate but also more scalable and practical for real-world applications.

1. Proposed evaluation model has stronger ability of assessing the reliability of generated PV scenarios than simple probability indicators, which is conducive to improving the studies of PV scenario generation and promoting the application of PV systems.

2. Proposed evaluation model can estimate the corresponding month and season that a credible PV sample is geared to. To our knowledge, this is the first work evaluating the specific month and season of a generated PV scenario.

3. We discover the representative properties (e.g., the effect of cloud) of solar reception process and use the discovery to assess the inherent movement of cloud, which fills a gap of estimating the environmental randomness of PV scenario generation.

The rest of this paper is organized as follows. Section 2 motivates the introduction of the details of AR model in both time and frequency domains. Section 3 is devoted to the details of proposed approach. In Section 4, experimental results are discussed and analyzed. Finally, Section 5 concludes this paper.

2 Autoregressive model

In regard to time series events, correlations exist among the behaviors at certain intervals. Considering the correlations, an autoregressive (AR) model is able to predict future variables of interest according to their past values. AR model is basically a linear regression of current values against past values in the same time series [21]. An AR(p) model is mathematically defined as:

$\phi \left[n\right]=-c-a_1\phi \left[n-1\right]-a_2\phi \left[n-2\right]-\cdots -a_p\phi \left[n-p\right]+ϵ\left[n\right](1)$

where $\phi [n]$ is $n$th value of variable observation; $ϵ[n]$ is driving noise; $p$ is the order of AR model; $\{a_1,a_2,\dots ,a_p\}$ are AR parameters. $c$ denotes the energy of the observation, which is defined as:

$c=\left(1-{\displaystyle \sum _{t=1}^p}{a}_t\right)\mu (2)$

where $\mu$ is the process mean.

AR parameters $\{a_t|t=\mathrm{1,2},\dots ,p\}$ dominate the performance of AR model, which could be estimated by several techniques, e.g., Yule-Walker, burg method, Kalman filter, least-square, expectation-maximization, forward-backward. Changing the value of $p$ and the parameter $a_t$ leads to different time series patterns [22].

Taking Z-transforms of Equation 1, AR model as a LTI filter is depicted as:

$H\left(z\right)=\frac{{\sigma }_{ϵ}^2}{A_p\left(z\right)}=\frac{{\sigma }_{ϵ}^2}{c+{\sum }_{t=1}^p{a}_t{z}^{-t}}(3)$

AR(p) model is used to model the observation $\phi [n]$ as the response of a LTI filter with $p$ order to an input $ϵ[n]$ (illustrated as in Figure 1). The purpose is to discover the filter coefficients (AR parameters $\{a_t|t=\mathrm{1,2},\dots ,p\}$) and the input $ϵ[n]$ that make the estimated $\widehat{\phi }[n]$ as close to $\phi [n]$ as possible. From Equation 3, AR model is an all-poles model. AR system could be unstable if the poles are outside the unit circle.

Figure 1

Figure 1. AR model as a LTI filter.

The AR parameters could be solved by Yule-Walker equations. Equation 1 can be reformed in a vector form.

$\left(\phi \left[n\right],\phi \left[n-1\right],\dots ,\phi \left[n-p\right]\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill a_1\hfill \\ \hfill ⋮\hfill \\ \hfill a_p\hfill \end{array}\right)=ϵ\left[n\right]-c(4)$

Multiple both sides by $\phi [n]$ and take the expectation, we have:

$E\phi \left[n\right]x\left[n\right]=E\left\{\phi \left[n\right]\left(\phi \left[n\right],\phi \left[n-1\right],\dots ,\phi \left[n-p\right]\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill a_1\hfill \\ \hfill ⋮\hfill \\ \hfill a_p\hfill \end{array}\right)\right\}$

$=E\left\{ϵ\left[n\right]-c\right\}$

Then,

$\left(r_0,r_1,\dots ,r_p\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill a_1\hfill \\ \hfill ⋮\hfill \\ \hfill a_p\hfill \end{array}\right)={\sigma }_{ϵ}^2(5)$

where $\{r_0,r_1,\dots ,r_p\}$ are autocorrelation function. Then,

$\left[\begin{array}{cccc}\hfill r_0\hfill & \hfill r_1\hfill & \hfill \dots \hfill & \hfill r_p\hfill \\ \hfill r_1\hfill & \hfill r_0\hfill & \hfill \dots \hfill & \hfill r_{p-1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill r_p\hfill & \hfill r_{p-1}\hfill & \hfill \dots \hfill & \hfill r_0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 1\hfill \\ \hfill a_1\hfill \\ \hfill ⋮\hfill \\ \hfill a_p\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\sigma }_{ϵ}^2\hfill \\ \hfill 0\hfill \\ \hfill ⋮\hfill \\ \hfill 0\hfill \end{array}\right](6)$

While deleting the first equation in Equation 6, the formula, termed Yule-Walker equations, is obtained as follows.

$\left[\begin{array}{cccc}\hfill r_0\hfill & \hfill r_1\hfill & \hfill \dots \hfill & \hfill r_p\hfill \\ \hfill r_1\hfill & \hfill r_0\hfill & \hfill \dots \hfill & \hfill r_{p-1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill r_{p-1}\hfill & \hfill r_{p-2}\hfill & \hfill \dots \hfill & \hfill r_0\hfill \end{array}\right]\left[\begin{array}{c}\hfill a_1\hfill \\ \hfill a_2\hfill \\ \hfill ⋮\hfill \\ \hfill a_p\hfill \end{array}\right]=-\left[\begin{array}{c}\hfill r_1\hfill \\ \hfill r_2\hfill \\ \hfill ⋮\hfill \\ \hfill r_p\hfill \end{array}\right](7)$

3 The proposed model

Figure 2 illustrates the overall methodology of our proposed autoregressive-based PV scenario assessment framework. By analyzing the time dependency and random fluctuations in PV data, the AR model can capture short-term variations caused by environmental factors, thereby providing a more robust evaluation of PV scenario reliability. This framework introduces an autoregressive process to model environmental disturbances in PV generation, taking into account the temporal dependence of PV output as well as abrupt fluctuations due to environmental changes. Meanwhile, the framework integrates AR model parameters with monthly and seasonal PV generation characteristics. By estimating AR parameters for different months and seasons, it assigns generated PV samples to the appropriate time period, enabling more accurate handling of both seasonal variations and longer-term fluctuations in the PV data.

Figure 2

Figure 2. Diagram of the AR model–based evaluation framework for monthly and Quarterly analysis.

3.1 PV dataset analysis

Take 4 data sets from existing PV data for observation, shown in Figure 3. To address the month-to-month and seasonal variations in solar radiation, we conducted an in-depth analysis of the distribution characteristics of photovoltaic data for specific months and seasons. Solar radiation exhibits significant differences not only in its mean values but also in its variability and distribution patterns across months and seasons. For instance, summer months like July and August demonstrate higher average solar radiation and smoother temporal patterns due to stable weather conditions, while winter months like December and January are characterized by lower average radiation levels and more frequent fluctuations caused by cloud cover and shorter daylight hours. Seasonally, summer shows the highest consistency in solar radiation, while winter has the highest variability. In addition, the distribution characteristics of solar radiation, such as its skewness and kurtosis, were analyzed for each month and season to capture subtle temporal differences. Winter months generally exhibit a higher skewness due to irregular peaks in solar radiation, whereas summer months tend to have lower kurtosis, reflecting more consistent radiation patterns, as shown in Figures 3A, B.

Figure 3

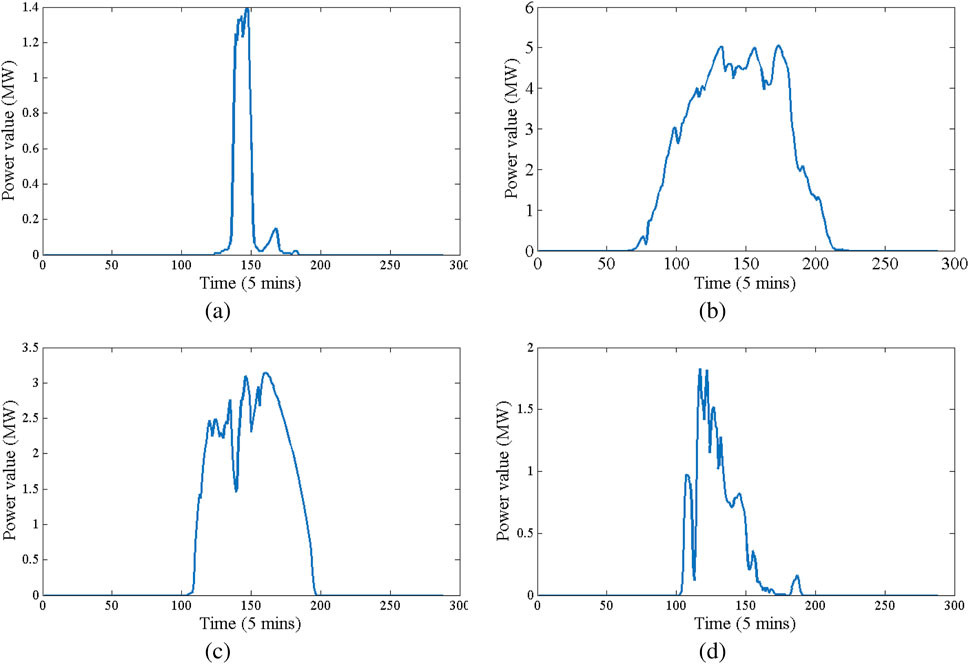
Figure 3. PV scenario samples, where data are sampled every 5 min (a) A daily PV output profile under relatively clear weather conditions. (b) A PV output profile exhibiting moderate fluctuations due to intermittent cloud cover. (c) A high-fluctuation scenario sharing the same average output as (d), but showing distinctly different variability patterns. (d) A contrasting scenario with the same mean power as (c), yet reflecting different environmental randomness in its generation curve.

While the clouds shade PV panels from the light, a downward peak occurs. The duration of these peaks depends on the moving speed of clouds. Additionally, as shown in Figures 3C, d, even though mean values of these 2 PV samples are the same, their representation are extremely different. Consequently, it is hard to utilize mean value and variance to evaluate the performance and diversity of PV scenario generation. The normalization is applied to the energy ratio $\lambda [n]$ and the normalized solar power $g[n]$. The energy ratio $\lambda [n]$ is normalized to follow a Gaussian distribution $G({\mu }_{\lambda },{\sigma }_{\lambda }^2)$, where ${\mu }_{\lambda }$ and ${\sigma }_{\lambda }^2$ are the mean and variance estimated from historical data. Similarly, $g[n]$ is transformed to follow $G({\mu }_g,{\sigma }_g^2)$, with ${\mu }_g$ and ${\sigma }_g^2$ reflecting the peak solar power time and its variability within a day. These normalization steps standardize the feature distributions, ensuring consistent input for the evaluation models and improving the robustness of the analysis.

We first normalized the raw photovoltaic output power data in the data preprocessing phase. Specifically, each historical sample $x_o[n]$ is transformed into $x[n]$ using the following equation:

$x\left[n\right]=\lambda \left[n\right]\cdot \left(g\left[n\right]+\epsilon \left[n\right]\right)(8)$

Where $\lambda [n]$ represents the energy ratio, $g[n]$ is the normalized solar power, and $\epsilon [n]$ accounts for the environmental interference, such as cloud cover and weather variations. All photovoltaic data are normalized to ensure consistency across the dataset following a Gaussian distribution. The energy ratio $\lambda [n]$ is normalized as follows:

$\lambda \left[n\right]\sim G\left({\mu }_{\lambda },{\sigma }_{\lambda }^2\right)(9)$

Where ${\mu }_{\lambda }$ and ${\sigma }_{\lambda }^2$ are the mean and variance of the energy ratio, respectively. Similarly, the normalized solar power $g[n]$ follows a Gaussian distribution, given by:

$g\left[n\right]\sim G\left({\mu }_g,{\sigma }_g^2\right)(10)$

Where ${\mu }_g$ indicates the time of maximum solar power during the day, and ${\sigma }_g^2$ represents the time interval between sunrise and sunset. To model the environmental disturbances impacting the photovoltaic power, the interference term $\epsilon [n]$ is modeled as an autoregressive process:

$\epsilon \left[n\right]=-{\displaystyle \sum _{t=1}^p}{a}_t\cdot \epsilon \left[n-t\right]+u\left[n\right](11)$

Where $a_t$ are the AR model paremeters, $p$ is the order of the model, and $u[n]$ is the noise term, which follows a Gaussian distribution. These preprocessing steps ensure the data are appropriately normalized and standardized, providing consistent and reliable input for subsequent model training.

We establish the evaluation model according to month and season. In other words, we could assess a generated PV sample whether belongs to a specific month or season. For each $x$ in historical data, a set of parameter values ${\mathrm{\Theta }}_x:({\lambda }^x,{\mu }_g,{\sigma }_g^2,a_1,a_2,\dots ,a_p,{\sigma }_u^2)$ could be gained by Equation 1. Denote each generated sample as $y$, with a group of parameter values ${\mathrm{\Theta }}_y:({\lambda }^y,{\mu }_g^y,{({\sigma }_g^y)}^2,a_1^y,a_2^y,\dots ,a_p^y,{({\sigma }_u^y)}^2)$ are also evaluated. While the proposed evaluation framework assumes WSS for month-specific and season-specific PV data, this assumption may not hold under significant non-stationary conditions, such as those caused by extreme weather events or rapid environmental changes. To mitigate this limitation, the evaluation process could incorporate adaptive mechanisms, such as recalibrating AR parameters for shorter time intervals to better capture transient dynamics. Furthermore, reflection coefficients and residual errors from the AR process could provide additional indicators of non-stationarity, allowing for more flexible evaluation criteria under such conditions.

The proposed model relies on several key assumptions for effective modeling and evaluation. The solar reception process is assumed to exhibit WSS within each month and season, allowing the AR model to capture temporal dependencies. Additionally, the energy ratio $\lambda [n]$ and normalized solar power $g[n]$ are assumed to follow Gaussian distributions, facilitating parameter estimation. Environmental fluctuations cause by weather changes, such as cloud movement, are modeled using a linear AR process, which enables the model to capture short-term dependencies. While these assumptions are reasonable for most PV scenarios, deviations, such as seasonal transitions or extreme weather conditions, may impact the model’s generalization ability. The model is tested on PV data from multiple months and seasons to ensure robustness, reflecting a wide range of environmental conditions. This approach improves the model’s generalization capacity and practical applicability.

3.2 Month-evaluation

For $j$th month in a year, evaluation model is determined by ${\mathrm{\Theta }}_x^j:\{{\widehat{\lambda }}^j,{\widehat{\mu }}_g^j,{\widehat{\sigma }}_g^j,{\widehat{a}}_t^j,{({\widehat{\sigma }}_u^j)}^2\}$, $j=\{\mathrm{1,2},\dots ,12\}$. We arrange ${\mathrm{\Theta }}_x^j$ into three parts in accordance with three indicators $\{{\widehat{r}}_{\lambda }^y[j],{\widehat{r}}_g^y[j],{\widehat{r}}_u^y[j]\}$ to evaluate a given generated PV sample $y$ being “reliable”. If the sample is reliable, the indicators would obtain the month that this sample belongs to.

1) In the first part, ${\widehat{r}}_{\lambda }^y[j]$ manifests the probability that energy ratio of generated sample $y$ follows the distribution of energy ratio of the $j$th month.

In term of the $j$th month, from Equation 2, the distribution of energy ratio is dominated by ${\widehat{\mu }}_{\lambda }^j$ and ${({\widehat{\sigma }}_{\lambda }^j)}^2$ which are gained by the following formulas:

${\widehat{\mu }}_{\lambda }^j=\frac{1}{d}{\displaystyle \sum _{i=1}^d}{\lambda }^x\left[i\right](12)$

${\left({\widehat{\sigma }}_{\lambda }^j\right)}^2=\frac{1}{d}{\displaystyle \sum _{i=1}^d}{\left({\lambda }^x\left[i\right]-{\widehat{\mu }}_{\lambda }^j\right)}^2(13)$

where $d$ is the total days in the $j$th month. ${\lambda }^x[i]$ is the value of energy ratio in the $i$th day of $j$th month.

For each generated PV sample $y$, $\{r_{\lambda }^y[j]|j=\mathrm{1,2},\dots ,12\}$ are calculated separately as follows.

${\widehat{r}}_{\lambda }^y\left[j\right]=\frac{1}{\sqrt{2\pi {\left({\widehat{\sigma }}_{\lambda }^j\right)}^2}}{e}^{-\frac{1}{2}{\left(\frac{{\lambda }^y-{\widehat{\mu }}_{\lambda }^j}{{\widehat{\sigma }}_{\lambda }^j}\right)}^2}(14)$

2) In the second part, ${\widehat{r}}_g^y[j]$ describes the difference of sunshine duration between generated samples and the $j$th month, which is evaluated by ${\widehat{\mu }}_g^j$ and ${({\widehat{\sigma }}_g^j)}^2$.

${\widehat{r}}_g^y\left[j\right]=\sqrt{{\left({\mu }_g-{\widehat{\mu }}_g^j\right)}^2+\left({\sigma }_g^2-{\left({\widehat{\sigma }}_g^j\right)}^2\right)},(15)$

${\widehat{\mu }}_g^j=\frac{1}{d}{\displaystyle \sum _{i=1}^d}{\mu }_g\left[i\right](16)$

${\left({\widehat{\sigma }}_g^j\right)}^2=\frac{1}{d}{\displaystyle \sum _{i=1}^d}{\sigma }_g^2\left[i\right](17)$

3) In the third part, ${\widehat{r}}_u^y[j]$ represents the learning ability of generated samples for environmental randomness of $j$th month. An AR(p) model is designed to imitate the uncertainties. An importance of AR model is that all poles must be within unit circle to ensure system stability [23]. If $p>2$, all $\{a_t|t=\mathrm{1,2},\dots ,p\}$ are not necessary to be less than 1. Thereby, averaging $a_t$’s may result in poles falling outside the unit circle. Instead of averaging the values of $a_t$, we implement reflection coefficients $\{k_t|t=\mathrm{1,2},\dots ,p\}$ to obtain the “averaged” AR parameters. $k_t$ has a good property that it is bounded by 1. To find $k_t$ by step-down (SD) procedure, we need to obtain $\{a_t[m]|m=\mathrm{1,2},\dots ,t-1;t=p,p-1,\dots ,2\}$, where $a_t[m]$ is the $m$th AR parameter for model order $p=t$.

In SD procedure,

$a_{t-1}\left[i\right]=\frac{a_t\left[i\right]-a_t\left[t\right]a_t^{*}\left[t-i\right]}{1-|a_t\left[t\right]{|}^2}(18)$

where * means transposition. Prediction error powers of each model order in the procedure is defined as:

${\upsilon }_{t-1}=\frac{{\upsilon }_t}{1-|a_t\left[t\right]{|}^2}(19)$

SD procedure is completed while ${\upsilon }_t<{({\widehat{\sigma }}_g^j)}^2$. Furthermore, the procedure is initialized with $a_t[m]=a_t$ in ${\mathrm{\Theta }}_x$ for $t=\mathrm{1,2},\dots ,p$ and ${\upsilon }_p={\sigma }_u^2$. After displaying SD procedure, reflection coefficients are obtained as $k_t=a_t[t]$, $t=\mathrm{1,2},\dots ,p$. Averaged $k_t$ is calculated as:

${\widehat{k}}_t=\frac{1}{d}{\displaystyle \sum _{i=1}^d}{k}_t\left[i\right](20)$

With ${\widehat{k}}_t$, $\{{\widehat{a}}_t|t=\mathrm{1,2},\dots p\}$ is calculated using Levinson recursion.

${\widehat{a}}_t\left[m\right]=\left\{\begin{array}{c}{\widehat{a}}_{t-1}\left[m\right]+{\widehat{k}}_t{\widehat{a}}_{t-1}\left[t-m\right]\widehat{k}=\mathrm{1,2},\dots ,t-1\hfill \\ {\widehat{k}}_{t}m=t\hfill \end{array}\right.(21)$

${\left({\widehat{\sigma }}_u^j\right)}^2=\widehat{r}\left[0\right]{\displaystyle \prod _{t=1}^p}\left(1-{\widehat{k}}_t^2\right)(22)$

$\widehat{r}\left[0\right]=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\epsilon }^2\left[n\right]$

${\widehat{r}}_u^y[j]$ is measured by Euclidean distance between AR parameters $\{a_t^y|t=\mathrm{1,2},\dots ,p\}$ in a generated sample $y$ and coefficients $\{{\widehat{a}}_t^j|t=\mathrm{1,2},\dots ,p\}$ in the $j$th month.

${\widehat{r}}_u^y\left[j\right]=\sqrt{{\displaystyle \sum _{t=1}^p}{\left({\widehat{a}}_t^j-a_t^y\right)}^2+\left({\left({\widehat{\sigma }}_u^j\right)}^2-{\left({\sigma }_u^y\right)}^2\right)}(23)$

For each generated sample $y$, a set of $\{{\widehat{r}}_{\lambda }^y[j],{\widehat{r}}_g^y[j],{\widehat{r}}_u^y[j]\}$ is obtained. Based on maximum likelihood theory, we search the largest values of these 3 coefficients with highest probability for finding the month that $y$ belongs to.

$\left\{\begin{array}{c}{j}_1=\underset{j}{argmax}{\widehat{r}}_{\lambda }^y\left[j\right],j=\mathrm{1,2},\dots ,12\hfill \\ j_2=\underset{j}{argmin}{\widehat{r}}_g^y\left[j\right],j=\mathrm{1,2},\dots ,12\hfill \\ j_3=\underset{j}{argmin}{\widehat{r}}_u^y\left[j\right],j=\mathrm{1,2},\dots ,12\hfill \end{array}\right.(24)$

To place the assessment, state null hypothesis and alternate hypothesis, respectively:

  $H_0$: $y$ is a reliable sample for PV scenario.

  $H_1$: $y$ is not a reliable sample for PV scenario.

Because two neighboring months have some similar solar receptions, we set a bias $\delta$ to adjust the evaluation. Considering the comparability between any two neighboring months, while $|j_1-j_2|\le \delta$, $|j_1-j_3|\le \delta$, and $|j_2-j_3|\le \delta$ are all satisfied, accept $H_0$. Otherwise, accept $H_1$. To further quantify the confidence in the evaluation results, we calculated the 95% confidence intervals (CIs) for the likelihood ratios ${\widehat{r}}_{\lambda }^y[j]$, ${\widehat{r}}_g^y[j]$, ${\widehat{r}}_u^y[j]$ using the following formula:

$\text{CI}=\widehat{r}\pm z\cdot \frac{\sigma }{\sqrt{n}}(25)$

where $\widehat{r}$ is the maximum likelihood estimate, $\sigma$ is the standard deviation of the likelihood ratios across the samples, $n$ is the number of observations, and $z$ is the critical value for a 95% confidence level. We use corresponding to a 95% confidence interval. This 5% significance level is a widely accepted convention in statistical inference, as it offers a practical balance between Type I and Type II errors in hypothesis testing [24–26]. Many studies in related fields (e.g., power systems, reliability analysis) similarly adopt the 95% CI when evaluating model performance or uncertainty quantification [27–29], ensuring that our approach remains consistent with standard practice. Additionally, statistical significance tests were conducted to validate the reliability of the classification results. We employed a one-sample t-test to assess whether the mean likelihood ratio for each month or season significantly differed from a pre-defined threshold ${\mu }_0$, representing unreliable PV scenarios. The test statistic is given by:

$t=\frac{\bar{r}-{\mu }_0}{\frac{\sigma }{\sqrt{n}}}(26)$

where $\bar{r}$ is the mean likelihood ratio, and $\sigma$ is its standard deviation. The p-value corresponding to the test statistic determines whether to reject $H_0$. A significance level of 0.05 was used as the cutoff for statistical significance, which is a widely adopted threshold in statistical hypothesis testing across various fields, including the social sciences, engineering, and environmental studies. The choice of a 0.05 significance level, corresponding to a 95% confidence interval. This threshold means that there is a 5% chance of incorrectly rejecting the null hypothesis when it is actually true, which provides a practical balance between precision and practical decision-making. In our study, using this significance level allowed us to confidently assess whether the observed differences in likelihood ratios were statistically significant, thus providing reliable classification of PV scenarios. This choice of significance level aligns with commonly accepted practices in similar research studies [30–32]. By adopting this 0.05 significance level, we ensured that our results met established statistical standards, offering a reliable and robust evaluation of the PV scenario classification process.

Normally, $\delta =1$. The parameter $\delta$ is used as a threshold to account for the natural similarity between neighboring months, ensuring that minor deviations do not lead to misclassification of PV scenarios. Based on empirical analysis, $\delta$ is set to 1, which balances classification accuracy and robustness. A larger $\delta$ increases the tolerance for classification, potentially leading to misclassifications, while a smaller $\delta$ may cause overly strict categorization, especially in transitional months with similar solar patterns (e.g., March and April or September and October). Algorithm 1 describes the details of Month-Evaluation model.

Algorithm 1

Algorithm 1.Month-Evaluation Procedure.

3.3 Season-Evaluation

This model is similar to Month-Evaluation model, in which $s$ replaces d and represents the total days in each season. Season-Evaluation model is assessed by $\{{\tilde{r}}_{\lambda }^y[j],{\tilde{r}}_g^y[j],{\tilde{r}}_u^y[j]\}$. $h=\{\mathrm{1,2,3,4}\}$ represents spring, summer, autumn, and winter, respectively. Season-Evaluation model is used to identify whether a generated sample $y$ as a reliable PV scenario belongs to a specific season, in which the three-step procedure is also designed with a season of ${\mathrm{\Theta }}_x^h:\{{\tilde{\lambda }}^h,{\tilde{\mu }}_g^h,{\tilde{\sigma }}_g^h,{\tilde{a}}_t^h,{({\tilde{\sigma }}_u^h)}^2\}$.

1) Firstly, ${\tilde{r}}_{\lambda }^y[j]$ is obtained through evaluation of distribution of energy ration according to Gaussian distribution which is determined by its mean value and variance.

${\tilde{\mu }}_{\lambda }^h=\frac{1}{s}{\displaystyle \sum _{q=1}^s}{\lambda }^x\left[q\right](27)$

${\left({\tilde{\sigma }}_{\lambda }^h\right)}^2=\frac{1}{s}{\displaystyle \sum _{q=1}^s}{\left({\lambda }^x\left[q\right]-{\tilde{\mu }}_{\lambda }^h\right)}^2(28)$

where ${\lambda }^x[q]$ is $q$th day in $h$th season that contains $s$ days.

Given a generated PV sample $y$, $\{{\tilde{r}}_{\lambda }^y[h]|h=\mathrm{1,2,3,4}\}$ are evaluated separately using the following formula.

${\tilde{r}}_{\lambda }^y\left[h\right]=\frac{1}{\sqrt{2\pi {\left({\tilde{\sigma }}_{\lambda }^h\right)}^2}}{e}^{-\frac{1}{2}{\left(\frac{{\lambda }^y-{\tilde{\mu }}_{\lambda }^h}{{\tilde{\sigma }}_{\lambda }^h}\right)}^2}(29)$

2) Secondly, owing to the particularity of sunshine duration in each season, the pattern of sunrise and sunset of seasons is depicted with ${\tilde{\mu }}_g^h$ and ${({\tilde{\sigma }}_g^h)}^2$.

${\tilde{\mu }}_g^h=\frac{1}{s}{\displaystyle \sum _{q=1}^s}{\mu }_g\left[q\right](30)$

${\left({\tilde{\sigma }}_g^h\right)}^2=\frac{1}{s}{\displaystyle \sum _{q=1}^s}{\sigma }_g^2\left[q\right](31)$

${\tilde{r}}_g^y[h]$ is to evaluate the given sample $y$ based on the discovery of the Gaussian distribution of solar reception process.

${\tilde{r}}_g^y\left[h\right]=\sqrt{{\left({\mu }_g-{\tilde{\mu }}_g^h\right)}^2+\left({\sigma }_g^2-{\left({\tilde{\sigma }}_g^h\right)}^2\right)},(32)$

3) Thirdly, reflection coefficients $\widetilde{k_t}$ are also used to gain averaged AR parameters ${\tilde{a}}_t^h$ and ${({\tilde{\sigma }}_u^h)}^2$ to guarantee system stability.

${\tilde{k}}_t=\frac{1}{s}{\displaystyle \sum _{q=1}^s}{k}_t\left[q\right](33)$

$k_t[q]$ is obtained with $a_t$ using SD procedure in Equation 10. Then, $\{{\tilde{a}}_t^h|t=\mathrm{1,2},\dots ,p;h=\mathrm{1,2,3,4}\}$ and ${({\tilde{\sigma }}_u^h)}^2$ are evaluated with $\{{\tilde{k}}_t|t=\mathrm{1,2},\dots ,p\}$ using Levinson recursion. ${\tilde{r}}_a^m[h]$ is designed as:

${\tilde{r}}_a^m\left[h\right]=\sqrt{{\displaystyle \sum _{t=1}^p}{\left({\tilde{a}}_t^h-a_t^y\right)}^2+\left({\left({\tilde{\sigma }}_u^h\right)}^2-{\left({\sigma }_u^y\right)}^2\right)}(34)$

With a series of $\{{\tilde{r}}_{\lambda }^y[h],{\tilde{r}}_g^y[h],{\tilde{r}}_u^y[h]\}$, the appropriate season that $y$ belongs to is discovered with the highest probabilities using maximum likelihood theory.

$\left\{\begin{array}{c}{h}_1=\underset{h}{argmax}{\tilde{r}}_{\lambda }^y\left[h\right],h=\mathrm{1,2,3,4}\hfill \\ h_2=\underset{h}{argmin}{\tilde{r}}_g^y\left[h\right],h=\mathrm{1,2,3,4}\hfill \\ h_3=\underset{h}{argmin}{\tilde{r}}_u^y\left[h\right],h=\mathrm{1,2,3,4}\hfill \end{array}\right.(35)$

To place the assessment, state null hypothesis and alternate hypothesis, respectively:

  $H_0$: $y$ is a reliable PV sample in $h^{*}$ season

  $H_1$: $y$ is not a reliable sample for PV scenario.

Only while $h_1=h_2=h_3$, accept $H_0$, where $h*=h_1$. Otherwise, accept $H_1$. Algorithm 2 describes the details of Season-Evaluation.

3.4 Correlation between month and seasonal evaluation

The monthly and seasonal evaluation methods differ in their temporal granularity and parameter estimation processes. The monthly evaluation classifies PV scenarios into 12 specific months, using month-specific parameters to capture fine-grained temporal differences in PV power generation. In contrast, the seasonal evaluation classifies scenarios into four broader seasonal categories, where seasonal parameters are aggregated from monthly data. This approach increases robustness to short-term fluctuations but reduces temporal resolution. Together, these methods provide a complementary framework, with the monthly evaluation offering higher precision and the seasonal evaluation providing more excellent stability in the presence of temporal variability.

4 Experimental results

4.1 Software settings

The experiments presented in this study were implemented using Matlab 2015, a powerful tool for numerical computations, statistical analysis, and time series modeling. Matlab’s robust environment allowed us to efficiently handle the large datasets required for evaluating photovoltaic (PV) scenarios and implementing the autoregressive (AR) model. For the AR and ARMA modeling, we utilized Matlab’s built-in toolboxes, which provide comprehensive functions for time series analysis and statistical testing. Additionally, other techniques such as Generative Adversarial Networks (GAN) and Conditional GAN (CGAN) were implemented using TensorFlow to handle the deep learning-based generation of PV scenarios.

Algorithm 2

Algorithm 2. Season-Evaluation Procedure.

4.2 Experiment settings

With Solar Integration datasets [33], we choose solar data from both 32 solar power plants in the State of Washington to train all PV scenario generation techniques in the simulation. The Solar Integration dataset is selected for its wide acceptance and representativeness in PV scenario generation research. This dataset provides real-world operational data from 32 PV power plants, capturing the natural variability of solar power influenced by weather conditions, geographical differences, and seasonal changes. Unlike synthetic datasets, the Solar Integration dataset reflects the stochastic nature of PV power generation, allowing for a more comprehensive evaluation of the model’s generalization ability. Its diverse feature distribution and realistic noise levels ensure that the model is tested under practical conditions, enhancing the credibility of the experimental results. Potential biases in the dataset are primarily introduced by weather-related randomness and seasonal shifts in solar irradiance. These factors may result in an imbalanced sample distribution, especially during months with more frequent weather disturbances. To mitigate this, the proposed model incorporates month-specific and season-specific parameter estimation, allowing it to account for these natural variations. The model aims to achieve more robust evaluation performance by explicitly modeling temporal and seasonal effects. Including these statistical characteristics ensures that the evaluation method’s assumptions are transparent and justified.

All experiments of evaluation are operated in Matlab R2014b software with 8 GB memory. In order to generate PV scenario data with different techniques, we implement AR and autoregressive and moving average (ARMA) toolbox in Matlab and display Gaussian copula Matlab codes. Additionally, GAN, CGAN, and CGAN-filtering models are established in tensorflow with a single Nvidia TITAN Xp GPU to obtain new PV scenario samples. Furthermore, three popular date generation techniques are also used to produce PV scenarios: random oversample (ROS), synthetic minority over-sampling technique (SMOTE), and adaptive synthetic sampling (ADASYN). The parameter settings of these 9 techniques are as follows:

1. AR: p = 6, which is the order of AR model.

2. ARMA: p = 6, and q = 5. q is the order of MA model.

3. Gaussian copula: solar energy has a wide range between different seasons. Thus, we normalize the existing PV scenarios as pretreatment.

4. GAN: the generator is initialized as a 4-layer neural network in which the sizes of hidden layers are $\{\mathrm{128,1024,256,288}\}$. As the discriminator, 4 hidden layers whose sizes are $\{\mathrm{288,256,1024,128}\}$ and a softmax layer are involved.

5. CGAN: in addition to GAN parameters, mean values of powers are calculated for each sample, and the results are classified into 5 categories: $\mu (X_i)<$0.2 (class 1), 0.2$<\mu (X_i)<$0.5 (class 2), 0.5$<\mu (X_i)<$1 (class 3), 1$<\mu (X_i)<$2 (class 4), and $\mu (X_i)>$2 (class 5).

6. CGAN-filtering: in addition to CGAN settings, there are 2 parameters in the filtering. The orders of zeros and poles are initialized as 10 and 5, respectively.

7. ROS: random state = 42, which represents the random number generator.

8. SMOTE and ADASYN: k = 3, and m = 5. k is the number of nearest neighbours that construct synthetic samples, and m is the number of nearest neighbours that determine if a minority sample is in danger.

Normally, solar energy has a wide range between different seasons. Thus, we normalize the existing PV scenarios as pretreatment. 6 generated PV scenarios from these 8 generation techniques chosen by random are shown in Figure 4. Obviously, AR and ARMA methods generate PV scenarios with diversity, while Gaussian copula and GAN family specialize in learning the environment randomness (i.e., the shape of PV scenario), and SMOTE and ADASYN focus on the energy of PV scenarios.

Figure 4

Figure 4. Generated PV scenarios by different approaches.

4.3 Comparisons with evaluation metrics

4.3.1 Comparisons on generated PV samples

We compare the proposed model (termed as $\mathbb{A}$) with 2 popular evaluation metrics, i.e., mean value (denoted as $\mathbb{M}$) and variance (denoted as $\mathbb{V}$). 6 samples produced by 8 techniques (illustrated in Figure 3) are used to obtain evaluation results both for month and season estimation. We compare the proposed model (termed as $\mathbb{A}$) with 2 popular evaluation metrics, i.e., mean value (denoted as $\mathbb{M}$) and variance (denoted as $\mathbb{V}$). 6 samples produced by 8 techniques (illustrated in Figure 3) are used to obtain evaluation results both for month and season estimation. Moreover, the inability of mean value and variance-based metrics to capture these temporal and statistical characteristics often leads to higher evaluation errors, particularly in months or seasons with extreme variations in solar radiation. For instance, the AR-generated PV scenarios for January showed unrealistic consistency in solar energy levels during midday, which is against natural solar radiation patterns. While the mean value and variance metrics failed to identify such anomalies, the proposed AR-based evaluation model effectively detected these inconsistencies by analyzing the temporal correlations and stochastic fluctuations in the data.

In contrast, GAN-generated samples displayed distinct characteristics that influenced their evaluation. First, GANs excel in capturing the overall shape and variability of PV scenarios, as they learn the underlying data distribution from historical datasets. This allows GAN-generated samples to exhibit temporal dependencies that closely mimic real-world PV scenarios, particularly in months with stable solar radiation, such as July and August. However, the stochastic nature of GANs introduces noise into the generated samples, which can manifest as small, high-frequency fluctuations that deviate from natural solar radiation patterns. These noise-induced deviations are subtle and often escape detection by mean value and variance-based metrics but are effectively captured by the proposed AR-based evaluation model due to its sensitivity to temporal correlations. Additionally, the evaluation results revealed that the performance of GAN-generated samples varied with the complexity of the temporal patterns in the target data. For example, in winter months like January, where solar radiation patterns are highly irregular due to frequent cloud cover, GAN-generated samples tended to exhibit over-smoothed temporal trends, failing to replicate the abrupt changes observed in real data. The proposed model successfully identified these limitations by analyzing the AR parameters and residuals, which highlighted the discrepancies in the stochastic dynamics between the generated samples and the actual data.

To observe the performance of evaluation methods, we specially choose some non-PV samples. Experimental results are shown in Tables 1, 2. $‘i/j^{\prime }$ means that this PV scenario actually belongs to $j$th month or season which is evaluated as a sample in $i$th month or season. $‘{\times }^{\prime }$ indicates that this sample cannot be deemed as a reliable PV scenario in line with existing solar reception pattern. According to the similarity between the generated samples and existing PV scenarios, we denote the month or season that generated samples belong to (i.e., the value of $j$).

Table 1

Table 1. Evaluation performance of generated PV scenario in specific months.

Table 2

Table 2. Evaluation performance of generated PV scenario in specific seasons.

In regard to month attribution of a PV sample set, the proposed model outperforms mean value and variance estimations. Table 1. shows mean value and variance have higher evaluation errors of the months that produced PV samples belongs to. In particular, while a generated PV sample does not follow solar reception principles, mean and variance have difficulties in observing it. Take the 5th sample from AR model for instance, it is impossible that solar energies remain the highest value between around 12 p.m. and 16 p.m., which is against nature law leading to an unreliable PV sample. This is because AR parameters in an AR model are sensitive and could result in unstable state. The proposed model is capable of estimating the unreliability of PV samples. On the opposite, mean and variance evaluation cannot identify the unreliability. Typically, PV scenarios among neighbouring months have analogous attributes, e.g., daylight hours that affects the width of PV scenarios. For example, the generated PV samples from SMOTE belong to August, yet they are deemed as scenarios in July by mean evaluation. Furthermore, the months in spring and autumn have similar solar conditions, e.g., solar reception amount in a day. Therefore, mean and variance are unable to tell the difference, e.g., October and March. At last, when learned representations of environmental changes are not precise, the fluctuations in PV samples are abnormal (e.g., PV samples generated by CGAN). In that case, these samples are unreliable, but mean value and variance cannot detect them.

For season attribution of a PV sample, the proposed model outperforms traditional mean value and variance estimations, as shown in Table 2). The improved performance for season classification is attributed to the autoregressive (AR) model used in the proposed approach, which captures temporal dependencies and seasonal variations more effectively than simple statistical summaries. The AR model was implemented using Matlab 2015 due to its robust capabilities for time-series modeling and statistical analysis. In particular, we utilized Matlab’s Econometrics Toolbox, which includes functions for autoregressive and moving average modeling, to analyze the PV data and assess the seasonal attributes of the generated scenarios. These basic statistical techniques were applied to evaluate the solar data and assess the seasonality of PV output based on average values and variances, which do not account for the underlying temporal correlations. In contrast to month evaluation, evaluation techniques display well on season attribute. This is because that the differences in solar movement and environment changes among seasons are more significant than months. To assess the seasonal performance, the confidence intervals for likelihood ratios were calculated for each season, using the one-sample t-test approach implemented in Matlab. The p-values corresponding to these tests were computed to determine the statistical significance of the seasonal differences in the PV samples.

4.3.2 Comparisons of evaluation performance

In order to verify the effectiveness of the proposed model, we implement mean value, variance, and the proposed model displaying on 100 samples generated by these 8 techniques, separately. Evaluation errors of these 3 measurements are shown in Figure 5, 6, in which the proposed model outperforms other 2 measurements. This validates that mean value and variance are unable to identify unreliable generated samples, leading to high evaluation errors with AR and ARMA approaches. By contrast, the proposed model exhibits strong ability of estimating the reliability of generated samples, resulting in low evaluation errors. Moreover, with increased diversity of generation by Gaussian copula, GAN, and CGAN-filter, mean value and variance measurements are easily trapped into misidentification between neighboring months or seasons. Furthermore, because the generated samples by SMOTE and ADASYN distributes in a narrow region, these 3 evaluation approaches also gain good performances. Compared with month evaluation, evaluation results for seasons achieve better performance.

Figure 5

Figure 5. Comparisons of evaluation errors by 3 approaches for month.

Figure 6

Figure 6. Comparisons of evaluation errors by 3 approaches for season.

4.3.3 Analysis of computational efficiency

To evaluate the computational efficiency of the proposed model, we analyze its time complexity, resource requirements, and runtime performance for datasets of varying sizes. The computational complexity of the key components is assessed to ensure the model’s feasibility for large-scale and high-frequency PV data. Our experiments showed that the confidence intervals for likelihood ratios across months and seasons were within a range of $\pm$2% of the maximum likelihood estimates, indicating high reliability of the evaluation results. Furthermore, p-values from the t-tests confirmed the statistical significance of the classification results, with all p-values below the 0.05 threshold for reliable PV scenarios. These quantitative measures not only validate the evaluation results but also demonstrate the robustness of the proposed model under varying conditions. The AR model fitting process, with an order of p, has a computational complexity of $O(N\cdot p^2)$, where N denotes the number of samples. The month-based and season-based evaluation models, which involve parameter estimation and hypothesis testing, have a complexity of $O(N\cdot p)$. To provide practical insight into runtime performance, we conduct experiments on datasets with sizes ranging from 10,000 to 100,000 samples. The results show that the total runtime increases approximately linearly with the dataset size. This demonstrates that the proposed model maintains computational efficiency even when applied to large datasets, making it suitable for high-frequency PV data applications.

The superior performance of the proposed method, mainly when applied to GAN-generated PV scenarios, can be attributed to its ability to capture the temporal dependencies and stochastic nature of PV power fluctuations. GAN-generated samples often exhibit diversity in overall shape and randomness. However, they may need to accurately reflect the fine-grained temporal structure and dynamic changes caused by weather and cloud movements. Unlike traditional mean and variance-based evaluation methods, which only consider statistical summaries, the proposed AR–based model analyzes the temporal correlations within PV scenarios. By incorporating AR parameters and assessing the consistency of month- and season-specific temporal patterns, the proposed method can identify subtle deviations in the dynamic characteristics of GAN-generated scenarios. This capability allows for more precise detection of abnormal or unreliable samples that traditional metrics might overlook. The enhanced capacity to track and evaluate temporal patterns is a key reason for the superior performance of the proposed method when evaluating scenarios generated by GANs.

5 Conclusion

Solar photovoltaic had caught plenty of attentions due to its little pollution, and PV scenario generation was going to be an effective way to facilitate integrating solar energy into traditional energy systems. In order to effectively evaluate the performance of PV scenario generation, we proposed an evaluation model based on AR theory. After analyzing existing PV samples, we found out the shape of PV scenarios was an important representation of environmental randomness. In the simulation, we produced PV samples with 8 popular generation approaches. Compared with mean value and variance measurements, experiments showed the proposed model achieved better performance, especially in a unreliable PV scenario. Moreover, mean value and variance estimation confused with months that have similar solar movement and environmental changes. With 100 generated PV scenarios, we simulated the evaluation among the proposed model and compared measurements. Simulations showed that the proposed model obtained better evaluation results than mean value and variance estimations.

In addition to its theoretical evaluation performance, the proposed model offered practical value for real-world applications, particularly power dispatching. Accurate classification of PV scenarios into month- and season-specific categories enabled system operators to predict solar power availability more effectively. By capturing the temporal patterns of solar power generation, the model supported power dispatching decisions, allowing grid operators to adjust dispatch schedules in response to seasonal and weather-induced fluctuations. The month-specific evaluation provided higher temporal resolution, enabling short-term dispatch adjustments, while the seasonal evaluation offered long-term insights for seasonal dispatch planning. This dual-level evaluation approach enhanced the robustness and flexibility of power-dispatching strategies.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SR: Conceptualization, Writing–original draft. TY: Investigation, Software, Writing–review and editing. JL: Methodology, Supervision, Writing–review and editing. GW: Formal Analysis, Project administration, Validation, Writing–review and editing. KM: Resources, Visualization, Writing–review and editing. BL: Data curation, Funding acquisition, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The funding for this research was provided by the Special Key Project for Technological Innovation and Application Development in Chongqing, under grant number NO.CSTB2024TIAD-KPX0093.

Conflict of interest

Author GW was employed by Chongqing Carbon Energy Technology Co., Ltd. and Sichuan Aizhong Comprehensive Energy Technology Service Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Esram T, Kimball JW, Krein PT, Chapman PL, Midya P. Dynamic maximum power point tracking of photovoltaic arrays using ripple correlation control. IEEE Trans Power Electronics (2008) 21:1282–91. doi:10.1109/tpel.2006.880242

CrossRef Full Text | Google Scholar

2. Wai RJ, Wang WH, Lin CY. High-performance stand-alone photovoltaic generation system. IEEE Trans Ind Electronics (2008) 55:240–50. doi:10.1109/tie.2007.896049

CrossRef Full Text | Google Scholar

3. Basore PA, Cole WJ. Comparing supply and demand models for future photovoltaic power generation in the usa. Prog Photovoltaics Res Appl (2018) 26:414–8. doi:10.1002/pip.2997

CrossRef Full Text | Google Scholar

4. De Brito MAG, Galotto L, Sampaio LP, e Melo Gd. A, Canesin CA. Evaluation of the main mppt techniques for photovoltaic applications. IEEE Trans Ind Electron (2013) 60:1156–67. doi:10.1109/tie.2012.2198036

CrossRef Full Text | Google Scholar

5. Renaudineau H, Donatantonio F, Fontchastagner J, Petrone G, Spagnuolo G, Martin J-P, et al. A pso-based global mppt technique for distributed pv power generation. IEEE Trans Ind Electronics (2015) 62:1047–58. doi:10.1109/tie.2014.2336600

CrossRef Full Text | Google Scholar

6. Golestaneh F, Pinson P, Gooi HB. Very short-term nonparametric probabilistic forecasting of renewable energy generation— with application to solar energy. IEEE Trans Power Syst (2016) 31:3850–63. doi:10.1109/tpwrs.2015.2502423

CrossRef Full Text | Google Scholar

7. De la Fuente DV, Rodríguez CLT, Garcerá G, Figueres E, González RO. Photovoltaic power system with battery backup with grid-connection and islanded operation capabilities. IEEE Trans Ind Electron (2013) 60:1571–81. doi:10.1109/TIE.2012.2196011

CrossRef Full Text | Google Scholar

8. Estébanez EJ, Moreno VM, Pigazo A, Liserre M, Dell’Aquila A. Performance evaluation of active islanding-detection algorithms in distributed-generation photovoltaic systems: two inverters case. IEEE Trans Ind Electronics (2011) 58:1185–93. doi:10.1109/TIE.2010.2044132

CrossRef Full Text | Google Scholar

9. Yang T, Huang Q, Cai F, Li J, Jiang L, Xia Y. Vital characteristics cellular neural network (vcenn) for melanoma lesion segmentation: a biologically inspired deep learning approach. J Imaging Inform Med (2024) 1–18. doi:10.1007/s10278-024-01257-w

PubMed Abstract | CrossRef Full Text | Google Scholar

10. An Y, Zhang K, Chai Y, Zhu Z, Liu Q. Gaussian mixture variational-based transformer domain adaptation fault diagnosis method and its application in bearing fault diagnosis. IEEE Trans Ind Inform (2024) 20:615–25. doi:10.1109/TII.2023.3268750

CrossRef Full Text | Google Scholar

11. Parsons H, Cochran SBatra. Variability of power from large-scale solar photovoltaic scenarios in the state of Gujarat: preprint. In: To be presented at the renewable energy world conference and expo–India, 5-7 may 2014. New Delhi, India (2014).

Google Scholar

12. Osório GJ, Lujano-Rojas JM, Matias JCO, Catalão JPS. A new scenario generation-based method to solve the unit commitment problem with high penetration of renewable energies. Int J Electr Power Energ Syst (2015) 64:1063–72. doi:10.1016/j.ijepes.2014.09.010

CrossRef Full Text | Google Scholar

13. Ekstrom J, Koivisto M, Mellin I, Millar J, Lehtonen M. A statistical model for hourly large-scale wind and photovoltaic generation in new locations. IEEE Trans Sustainable Energ (2017) PP:1383–93. doi:10.1109/tste.2017.2682338

CrossRef Full Text | Google Scholar

14. Luis LM (2018). Phdthesis: framework for scenario generation and reduction in photovoltaic-integreated generation commitment.

Google Scholar

15. Nuno E, Cutululis N. Generation of large-scale pv scenarios using aggregated power curves. In: IEEE General Meeting Power & Energy Society, 2017 IEEE Power & Energy Society General Meeting (2017). p. 1–5.

Google Scholar

16. Golestaneh F, Gooi HB. Multivariate prediction intervals for photovoltaic power generation (2018)

Google Scholar

17. Junior JGDSF, Oozeki T, Ohtake H, Shimose KI, Takashima T, Ogimoto K. Forecasting regional photovoltaic power generation - a comparison of strategies to obtain one-day-ahead data. Energ Proced (2014) 57:1337–45. doi:10.1016/j.egypro.2014.10.124

CrossRef Full Text | Google Scholar

18. Mellit A, Pavan AM. A 24-h forecast of solar irradiance using artificial neural network: application for performance prediction of a grid-connected pv plant at trieste, Italy. Solar Energy (2010) 84:807–21. doi:10.1016/j.solener.2010.02.006

CrossRef Full Text | Google Scholar

19. Yona A, Senjyu T, Funabashi T. Application of recurrent neural network to short-term-ahead generating power forecasting for photovoltaic system. In: Power engineering society general meeting (2007). p. 1–6.

Google Scholar

20. Chen Y, Wang Y, Kirschen DS, Zhang B. Model-free renewable scenario generation using generative adversarial networks. IEEE Trans Power Syst (2017) PP:1. doi:10.1109/TPWRS.2018.2794541

CrossRef Full Text | Google Scholar

21. Kay SM Fundamentals of statistical signal processing: practical algorithm development, 3. Pearson Education IEEE Transactions on Signal Processing (2013).

Google Scholar

22. Kirshner H, Unser M, Ward JP. On the unique identification of continuous-time autoregressive models from sampled data. IEEE Trans Signal Process (2014) 62:1361–76. doi:10.1109/tsp.2013.2296879

CrossRef Full Text | Google Scholar

23. Kay S. Fundamentals of statistical signal processing: estimation theory. Technometrics (1993) 37:465–6. doi:10.2307/1269750

CrossRef Full Text | Google Scholar

24. Lee S, Moon S, Kim K, Sung S, Hong Y, Lim W, et al. A comparison of green, delta, and Monte Carlo methods to select an optimal approach for calculating the 95 population-attributable fraction: guidance for epidemiological research. J Prev Med Public Health = Yebang Uihakhoe chi (2024) 45:78–89. doi:10.3961/jpmph.2012.45.2.78

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Özkale MR, Hüsniye A. Bootstrap confidence interval of ridge regression in linear regression model: a comparative study via a simulation study. Commun Stat - Theor Methods (2023) 52:7405–41. doi:10.1080/03610926.2022.2045024

CrossRef Full Text | Google Scholar

26. Yuichiro S, Takashi S, Hiroto H. Testing parallelism and confidence intervals of level difference in an intraclass correlation model with monotone missing data. Commun Stat - Theor Methods (2023) 52:6147–60. doi:10.1080/03610926.2022.2026961

CrossRef Full Text | Google Scholar

27. Chitralok H, Mani K, Harsha B, Rashmi R. Application of isotonic regression in estimating ED_g and its 95% confidence interval by bootstrap method for a biased coin up-and-down sequential dose-finding design. Indian J Anaesth (2023) 67:828–31. doi:10.4103/ija.ija_431_23

CrossRef Full Text | Google Scholar

28. Chittaranjan A. How to understand the 95 risk, odds ratio, and hazard ratio: as simple as it gets. J Clin Psychiatry (2023) 84. doi:10.4088/JCP.23f14933

CrossRef Full Text | Google Scholar

29. Talsma PA. Estimation of median survival time and its 95 using sas proc lifetest. J Biopharm Stat (2023) 34:11–3.

Google Scholar

30. Kolawole OJ, Oje MM, Betiku OA, Ijarotimi O, Adekanle O, Ndububa DA. Correlation of alanine aminotransferase levels and a histological diagnosis of steatohepatitis with ultrasound-diagnosed metabolic-associated fatty liver disease in patients from a centre in Nigeria. BMC Gastroenterol (2024) 24:147.

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Rubanovich AV. Redefining the critical value of significance level (0.005 instead of 0.05): the bayes trace. Biol Bull (2019) 46:1449–57. doi:10.1134/s1062359019110086

CrossRef Full Text | Google Scholar

32. Kenanidis P, Llompart M, Santos SF, Dabrowska E. Redundancy can hinder adult l2 grammar learning: evidence from case markers of varying salience levels. Front Psychol (2024) 15:1368080. doi:10.3389/fpsyg.2024.1368080

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Draxl C, Clifton A, Hodge BM, Mccaa J. The wind integration national dataset (wind) toolkit. Appl Energ (2015) 151:355–66. doi:10.1016/j.apenergy.2015.03.121

CrossRef Full Text | Google Scholar

Nomenclature

Indices

$j$ Index of month

$t$ Index of time (hours)

$h$ Index of season

$P_{PV}$ Photovoltaic power output (W)

Variables

$E_{\mathit{solar}}$ Solar energy received (J)

$\lambda$ Energy ratio

$g[n]$ Normalized solar power

$ϵ[n]$ Environmental interference (e.g., cloud cover)

Models

AR Autoregressive model

ARMA Autoregressive moving average model

GAN Generative adversarial network

CGAN Conditional generative adversarial network

WGAN Wasserstein generative adversarial network

Parameters

$\mu$ Mean value of a variable

${\sigma }^2$ Variance of a variable

$a_t$ Autoregressive model parameters

$\rho$ Friction index

$k_t$ Reflection coefficients in AR model

$p$ Order of AR model

${\sigma }_u^2$ Noise variance in AR model

$\mathcal{N}$ Set of participants in scenario generation

Statistical distributions

Gaussian distribution Normal distribution, often used to model randomness