An advanced deep learning framework for simulating information propagation dynamics

The warehouse model, based on differential equations, has been widely employed in the field of network information propagation for an extended period. Numerous studies have revolved around the construction, fitting and simulation of these models. However, there has not been a universal and efficient fitting method applicable to all warehouse models in the realm of information propagation, mainly due to the often challenging nature of solving differential equations in practical scenarios. In this article, we introduce a deep learning-based framework for simulating information propagation dynamics. This framework is grounded in a model that embeds a physical neural network and can be employed for fitting data from sentiment analysis platforms. We apply our framework to classic information propagation dynamic models, achieving favorable fitting results and consistent experimental outcomes, underscoring the advancement of our approach.

1 Introduction

Over the past decade, the swift evolution of mobile Internet technology has exerted a profound influence on both production and daily life for all individuals. Simultaneously, the internet has progressively assumed a central role in how people engage with current events and news. While the Internet offers convenience for disseminating public opinion [1], it also poses substantial challenges to the management of public sentiment. The systematic investigation of network communication patterns and a comprehensive understanding of propagation mechanisms represent pivotal topics in contemporary research. Furthermore, these aspects constitute the focal points of government and regulatory agencies tasked with safeguarding network security and governing public sentiment [2]. Hence, a plethora of information propagation models have been proposed for simulating and forecasting public sentiment, conducting interventions and control, or studying policy patterns [3–5]. These models can be broadly categorized into differential equation-based compartment models and topology-based complex network models. In comparison, compartment models have garnered richer research attention due to their clarity in addressing macroscopic factors. This paper primarily focuses on the simulations of compartment models, encompassing the evolution of various groups during the information propagation process and the inverse problem-solving for pertinent propagation parameters.

Deep learning, owing to its formidable feature extraction capabilities, has found extensive applications across diverse domains [6]. It autonomously acquires high-dimensional information from extensive datasets, thereby reducing the need for conventional feature engineering. Nevertheless, the adoption of pure data-driven deep learning methods within the realm of information dissemination remains limited due to the reliance on large-scale and high-quality data [7]. In the domain of information dissemination, the acquisition of high-quality labeled data is challenging, and privacy concerns often hinder access to a significant portion of information. These factors present substantial obstacles to the integration of deep learning techniques. Furthermore, deep learning, functioning as a black-box model, lacks interpretability in its underlying mechanisms, thus impeding its broad applicability to various scientific problems. Physics-informed neural networks (PINNs) [8, 9] have, to a certain extent, alleviated these issues. They merge data-driven deep learning with differential equations, enhancing the interpretability of deep learning and streamlining the solving of differential equations. With the advancement of technology, PINNs have made significant research contributions in various fields, including fluid dynamics [10], materials science [11], aerospace engineering [12], and biochemistry [13]. Furthermore, numerous derivative models rooted in PINNs have emerged to cater to diverse tasks, such as those involving restricted initial or boundary conditions [8].

Since the onset of the COVID-19 pandemic, a variety of compartmental models have been introduced, serving as enhanced versions of the Susceptible-Infected-Recovered (SIR) compartmental model to investigate various aspects of disease spread [14]. Yin et al. applied the traditional SIR model to the field of information propagation and proposed the Susceptible-Forwarding-Immune (SFI) model based on the cumulative retweet volume of the Sina-microblog platform to predict the dissemination trend of a single piece of information [15]. Xiao et al. fully considered the anti-rumor information and user’s psychology, and constructed the SKIR rumor propagation model [16], which can effectively grasp the dynamic change laws of anti-rumor information on the information propagation process. Yin et al. constructed the Multiple-Information Susceptible-Discussion-Immune (M-SDI) dynamic model to understand the propagation pattern of public opinion on social networks by creatively considering public repeated participation in new topics [17]. Moreover, many scholars have extended the traditional SIR model to information dissemination from various perspectives, such as forgetting mechanisms, individual characteristics, and behaviors [18–20]. Recently, the application of deep learning in infectious disease models has become a research hotspot. For instance, Malinzi et al. applied a Physics-Informed Neural Network (PINN) to a Susceptible-Infected-Recovered-Deceased (SIRD) model, indicating that their PINN model outperformed all other data analysis models, even when trained with minimal data [21]. Heldmann et al. explored different models involving integer-order, fractional-order, and time-delay systems expressed as systems of Ordinary Differential Equations (ODEs). Research on complex systems based on systems of ODEs is very common and widely used in the field of mathematical physics, such as in laser physics, among others [22, 23]. PINNs were chosen for their capability to simultaneously perform parameter inference and simulate both observed and unobserved dynamics [24]. Cai et al. employed the novel fractional Physics-Informed Neural Networks (fPINNs) deep learning framework to calibrate the unknown parameters of a Susceptible-Exposed-Infected-Removed (SEIR) model [25]. Hao et al. also used the PINN method to model the compartment model and used first-order local sensitivity analysis to investigate the most influential parameters in the basic SIR model, and the results showed that reproduction/mortality had the greatest impact on all compartments of the SIR model [26].

Therefore, our objective is to develop a PINN framework for simulating the dynamics of network information propagation. Although there are certain similarities between infectious disease dynamics and network information dissemination, and the effectiveness of the PINNs method has been demonstrated in various domains, it is important to note that limited availability of real-world data and the complexity of mechanisms and influencing factors in information dissemination pose challenges in this field. Hence, constructing such a simulation system and validating its efficacy are crucial for advancing research on information propagation dynamics, providing valuable methodological guidance for subsequent related studies.

The organization of this article is as follows: Section 2 provides a foundation in single-information propagation dynamics and the fundamentals of PINNs. Section 3 outlines our proposed simulation framework for information propagation dynamics. Section 4 presents numerical experiments conducted using our proposed framework on classic information propagation dynamic models. Finally, Section 5 offers a summary and analysis of our work.

2 Preliminaries

Describing the information propagation process often necessitates the introduction of partial differential equations (PDEs) or ordinary differential equations (ODEs) to depict the dynamic state of information dissemination [27]. Analogous to dynamic equations used in infectious disease modeling, a multitude of ordinary differential equations, grounded in various propagation models or laws, have been employed to simulate the information propagation process, which makes it possible for real-world data fitting and validations of the propagation dynamic model. However, traditional methods for solving differential equations tend to be intricate and susceptible to the influence of initial conditions or boundary conditions [28]. Furthermore, the data employed for fitting often contains noise, significantly impacting the solutions derived from these differential equations. It is worth noting that problem-solving within the domain of information propagation can be categorized into two distinct types: forward problem-solving and inverse problem-solving. Forward problem-solving involves scenarios where the equation’s parameters are known, and the focus is on changes in each dependent variable within the differential equation. In contrast, inverse problem-solving pertains to situations in which the unknown parameters of the differential equation are reverse-engineered, leveraging partial data on dependent variables obtained from real-world observations, where the parameters serve to characterize the system’s propagation characteristics. In addressing inverse problems, the least squares method is frequently introduced for parameter fitting, which is often contingent on well-designed initial values or boundaries [8].

2.1 Dynamics for single-information network propagation

Single information dissemination is the basic structure of network public opinion information dissemination, and the process of an individual participating in single information dissemination is also the basis of single information dissemination analysis [15]. The dynamic model of single information spreading based on forwarding is called Susceptible-Forwarding-Immune (SFI) model. Here, the sum of the total number of people in susceptible state ($S$), forwarding state ($F$), and immune state ($I$) remains the same. Therefore, the SFI dynamic model of single information propagation in the form of a differential equation is established as Equations 1-3:

$\frac{d}{dt}S\left(t\right)=-\beta S\left(t\right)F\left(t\right)(1)$

$\frac{d}{dt}F\left(t\right)=p\beta S\left(t\right)F\left(t\right)-\alpha F\left(t\right)(2)$

$\frac{d}{dt}I\left(t\right)=\left(1-p\right)\beta S\left(t\right)F\left(t\right)+\alpha F\left(t\right)(3)$

where the average contact rate $\beta$ represents the average rate at which an individual in the susceptible state can access the information, the average forwarding rate $p$ represents the average rate that an individual in the susceptible state forwards the information after being exposed to the information, and the average immune rate $\alpha$ represents the average rate at which an individual changes from the forwarding state to the immune state. In the SFI dynamic model of single information transmission, another variable defined by the researchers is the cumulative number of forwarding users, which is a quantity that can be directly obtained from the network transmission platform and is also a crucial quantity for the analysis of the model. It is defined as Equation 4:

$C\left(t\right)={\int }_0^{t}p\beta S\left(t\right)F\left(t\right)dt(4)$

For the SFI dynamic model with single information dissemination, when fitting the actual case data, the above three key variables in the model will be formed as an unknown parameter vector and estimated to make the cumulative number consistent with the real data. Therefore, to find the best fit for the data is to find the best combination of parameters to minimize the error between the estimated and real values. In general, the least squares method is the most widely used in the fitting of information propagation dynamics research, where other machine learning methods such as the Monte Carlo method are also used. Since the model does not have an analytical formula and its form is very complex, minimizing the sum of squared deviations becomes a nonlinear least squares problem.

2.2 Physics informed neural networks

According to the universal approximation theorem, the neural network can be regarded as a general nonlinear function approximator, and the modeling process of a differential equation is to find nonlinear functions that meet relevant constraints [8]. Using neural networks to approximate model differential equations has become a research hotspot. The automatic differentiation technology in deep neural networks can be naturally applied to the calculation in differential equations and the constraint conditions of differential form are integrated into the loss function design of neural networks, so as to obtain neural networks with physical model constraints, which is the most basic idea to design embedded physical neural networks [29]. The PINNs model aims to establish a correlation between deep neural networks and various physical phenomena represented as systems of differential equations, thereby enhancing the interpretability of neural networks and expediting the resolution of differential equations. In the common application model of PINNs, the incorporation of physical information is primarily manifested in the loss function. The implementation of PINNs involves the integration of physics principles and neural networks through a well-designed approach, which does not pose significant challenges. First, the neural network is constructed, where the parameters are randomly initialized. The initialized neural network takes in the independent variables of the system of differential equations and produces the solutions that are needed to be optimized for the dependent variable of the system. Secondly, the output value of the dependent variable generated by the neural network fails to provide evidence for the validity of the equation, and this discrepancy constitutes the loss of equations. At the same time, the loss of the data level and the loss of the boundary condition are introduced to combine with the given weights, which become the loss of the whole model. Finally, the gradient descent method and other optimization methods are used to train the model and fit the differential equation.

Before data-driven machine learning made great progress, many physics and engineering fields were physically model-driven. Over the years, these fields had accumulated a wealth of physical models, most of which were described in the form of partial differential equations, such as Navier-Stokes equations in fluid dynamics [30], Maxwell equations in electromagnetic field theory [31] and Schrodinger equation in quantum mechanics [32]. Directly solving the physical model can make accurate predictions, but it faces the problems of too large errors caused by simple physical models, too high solution complexity caused by complex physical models and too large solution errors caused by missing or inaccurate measurement of physical model parameters and initial boundary values. The traditional numerical methods of partial differential equations face great challenges in solving inverse problems, complex geometric regions and high-dimensional space. In contrast, the classical machine learning algorithms are purely data-driven. The task of training a supervised machine learning model is to establish a functional mapping from the input data to the output data, that is, to learn a specific model from the pre-obtained training data and the pre-defined algorithm structure. However, in many physical and engineering fields, these training data often imply part of the prior knowledge, such as the law of conservation of momentum, the law of conservation of mass and so on [29]. PINNs combine the advantages of data-driven machine learning models and physical models. Under the condition of a small amount of training data, physics-based neural networks can train models satisfying physical constraints automatically, have better generalization performance while ensuring accuracy, and predict important physical parameters of the model [33].

3 Methods

3.1 Dynamic equations of information propagation

The information propagation process in the compartment model can be abstracted into a dynamic pattern, as illustrated in Figure 1. Here, $u^T$ represents the system state at time $t$, which is influenced by both the initial value condition $a$ and the boundary condition $\partial X$ over time, and undergoes transformation according to the propagation law $f^{*}$. Typically described by differential equations, this propagation law $f^{*}$ is approximated using embedded physical information neural networks to facilitate the solving of the entire dynamics process or other tasks.

Figure 1

Figure 1. The abstract process of the dynamics mechanism of information propagation.

Throughout this paper, we make the assumption that the underlying model of single-information network propagation follows the structure depicted in the SFI model, which can be mathematically represented by a system of ordinary differential equations. All propagation dynamics based on compartment models can be described using either systems of partial differential equations or ordinary differential equations. Therefore, our focus lies on the SFI model as it serves as a fundamental framework for studying information dissemination. This foundation allows us to derive various single information dissemination models under different scenarios or influence factors, which share similar and universal sets of differential equations. Taking the SFI model as an illustrative example, it is important to note that the total number of users in different states within the compartment model remains constant throughout its dynamic process, where changes are reflected through mutual transformations between different groups.

In order to fit the real data combined with the platform data, relevant scholars introduce the cumulative forwarding number $C\left(t\right)\left[5\right]$, which is the same as other similar models. In the system of ordinary differential equations with single information propagation such as SFI, the initial values are designed as follows: $F_0={\left.F\left(t\right)\right|}_{t=0}=C_0={\left.C\left(t\right)\right|}_{t=0}=1,I_0={\left.I\left(t\right)\right|}_{t=0}=0.$ In different information propagation models, whether ordinary differential equations or partial differential equations, the initial value or boundary value is related to the numbers of each state, which can be obtained from the real data. Based on the ordinary differential equations of single information propagation, some scholars introduce the latency period and other factors affecting the propagation, such as opinion, emotion, etc [34–36]. This kind of propagation dynamic equations is similar to the equations of single information propagation, and their solution methods are also universal.

3.2 PINN framework for dynamics of information propagation

Based on the method of physics-informed neural networks, we introduce a deep learning framework informed by the information propagation dynamic equations that describe the single information propagation processes and their derivatives. Most studies express the information propagation dynamics as ordinary differential equations, and some introduce other factors besides time as independent variables of the equations to construct partial differential equations. Our PINN modeling framework takes into account the two types of equations simultaneously, the only difference between the two ways is that the input of the neural network is one or more.

In our framework shown in Figure 2, the Application Program Interface (API) is used to obtain real propagation data from the social media platform, including the changes of the cumulative forwarding number of a certain news over time. Therefore, the time $t$ and other independent variables are the input of the neural network, and the cumulative forwarding number $C\left(t\right)$ is supervised and studied as real data, which is applied to design the loss functions of our model. In different information propagation dynamic problems, the supervision information we use may also be different. For example, considering the information propagation dynamics driven by the emotion factors, the real data we focus on for fitting can be the cumulative forwarding numbers under different categories of emotion. Moreover, when using the ordinary differential equations to represent the information propagation, the independent variable of the input model is only time $t$, namely, the input layer of our proposed neural network model has only one variable; When applying the partial differential equations to describe the information propagation, the independent variables of the input model can be time $t$ and social distance $x$, namely, the input layer of our proposed neural network model has two inputs: time $t$ and social distance $x$.

Figure 2

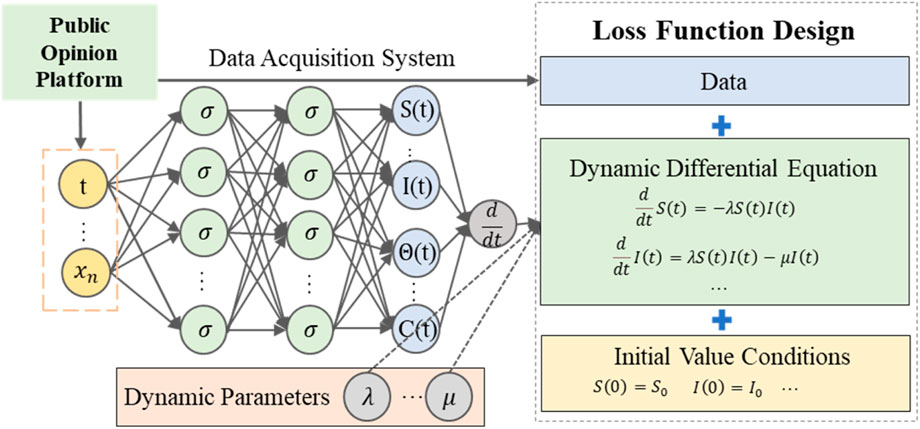
Figure 2. The embedded physical neural network framework for information propagation dynamics, which consists of three parts: a data acquisition system, a fully connected neural network, and a loss function.

A neural network with parameters $\theta$ takes time $t$ and other independent variables affecting information propagation as the input and outputs a vector of the state variables as a surrogate of the PDE solution, such as $S\left(t\right)$, $C\left(t\right)$ and $\mathrm{\Theta }\left(\mathrm{t}\right)$ which represent the other possible variables. We use multiple fully connected layers as the hidden layers of a deep neural network because fully connected neural networks can in some sense be used to approximate arbitrary functions. It should be noted that in the dynamic equations of information propagation, there are often dynamic parameters that need to be fitted, such as $\beta$, $p$ and so on, which are directly involved in the calculation of the equations. Therefore, we use independent neurons to represent these dynamic parameters that need to be optimized and use the automatic differentiation mechanism of neural networks to design and optimize the loss function. Finally, this kind of inverse problem is solved.

The next key step is to constrain the neural network to satisfy the scattered observations of $C\left(t\right)$ and its variants as well as the PDE system (including ODEs), which is realized by constructing the loss function considering terms corresponding to the observations and the PDE system. Specifically, we assume that we have the measurements of $y_1,y_2,···,y_M$ at the time $t_1,t_2,···,t_N$ respectively and we enforce the neural network to satisfy the PDE system at the time point ${\tau }_1,{\tau }_2,···,{\tau }_N$. The times $t_1,t_2,···,t_N$ and ${\tau }_1,{\tau }_2,···,{\tau }_N$ could be chosen at random. Then, the total loss is defined as a function of both $\theta$ and $\epsilon$, $\theta$ refers to all the parameters that need to be trained in the neural network, including the weights and biases of the neurons, and $\epsilon$ represents all the parameters that need to be predicted in PDEs:

$\mathcal{L}\left(\theta ,\epsilon \right)={\mathcal{L}}^{data}\left(\theta \right)+{\mathcal{L}}^{eq}\left(\theta ,p\right)+{\mathcal{L}}^{ic}\left(\theta \right)(5)$

${\mathcal{L}}^{\text{data}}\left(\theta \right)={\sum }_{m=1}^M{w}_m^{\text{data}}{\mathcal{L}}_m^{\text{data}}={\sum }_{m=1}^M{w}_m^{\text{data}}\left[\frac{1}{N^{\text{data}}}{\sum }_{n=1}^{N^{\text{data}}}{\left(y_m\left(t_n\right)-{\widehat{x}}_{s_m}\left(t_n;\theta \right)\right)}^2\right](6)$

${\mathcal{L}}^{\text{eq}}\left(\theta ,\epsilon \right)={\sum }_{s=1}^S{w}_s^{\text{eq}}{\mathcal{L}}_s^{\text{eq}}={\sum }_{s=1}^S{w}_s^{\text{eq}}\left[\frac{1}{N^{\text{eq}}}{\sum }_{n=1}^{N^{\text{eq}}}{\left({\left.\frac{d{\widehat{x}}_s}{dt}\right|}_{{\tau }_n}-f_s\left({\widehat{x}}_s\left({\tau }_n;\theta \right),{\tau }_n;\epsilon \right)\right)}^2\right](7)$

${\mathcal{L}}^{\text{ic}}\left(\theta \right)={\sum }_{s=1}^S{w}_s^{\text{ic}}{\mathcal{L}}_s^{\text{ic}}={\sum }_{s=1}^S{w}_s^{\text{ic}}\frac{{\left(x_s\left(T_0\right)-{\widehat{x}}_s\left(T_0;\theta \right)\right)}^2+{\left(x_s\left(T_1\right)-{\widehat{x}}_s\left(T_1;\theta \right)\right)}^2}{2}(8)$

The loss function is designed as shown in Equation 5, where the variable ${\mathcal{L}}^{\text{data}}$ represents the association between the data acquisition system’s M sets of observations y and the variable “data” as Equation 6, while ${\mathcal{L}}^{\text{eq}}$ enforces the dynamic equations for information propagation as Equation 7. In particular, $w_m^{\text{data}}$, $w_s^{\text{eq}}$ and $w_s^{\text{ic}}$ represent the weights of the data, the equations and the boundary conditions respectively, $m$ is the number of real data that can be obtained, and $s$ represents the number of PDE equations, in addition, $f_S$ represents a single equation in a PDE system, a total of $s$. We utilize automatic differentiation to analytically compute the derivative of the dependent variable in a PDE system. The third auxiliary loss term, ${\mathcal{L}}^{\text{ic}}$, is introduced as an additional source of information for system identification, which essentially contributes to the data loss component. $T_0$ represents the boundary conditions of the system at the initial moment, whereas $T_1$ denotes the boundary conditions at a subsequent arbitrary time point. It should be noted that both ${\mathcal{L}}^{\text{data}}$ and ${\mathcal{L}}^{\text{ic}}$ represent discrepancies between neural network outputs and measurements, making them supervised losses as Equation 8, whereas ${\mathcal{L}}^{\text{eq}}$, based on PDE systems for information propagation, is unsupervised. The weights are hyperparameters that can be manually adjusted, by default, the weights ​​are set to 1. In our final step, we simultaneously infer both neural network parameters $\theta$ and unknown parameters $\epsilon$ of the PDEs by minimizing the loss function using gradient-based optimizers such as Adam optimizer. It is important to note that our proposed method optimizes $\theta$ and $\epsilon$ concurrently, distinguishing it from meta-modeling.

The third auxiliary loss term ${\mathcal{L}}^{\text{ic}}$ is introduced as an additional source of information for system identification, serving as a crucial component in the data loss. It should be noted that both ${\mathcal{L}}^{\text{data}}$ and ${\mathcal{L}}^{\text{ic}}$ represent the disparities between neural network outputs and measurements, thus functioning as supervised losses. On the other hand, ${\mathcal{L}}^{\text{eq}}$, which relies on the PDE system for information propagation, operates as an unsupervised loss. In the final step, we simultaneously optimize both the neural network parameters $\theta$ and unknown parameters $\epsilon$ of the PDEs by minimizing the loss function using gradient-based optimizers like Adam optimizer. Importantly, our proposed method distinguishes itself from meta-modeling by optimizing $\theta$ and $\epsilon$ concurrently as Equation 9 shows.

${\theta }^{*},{\epsilon }^{*}=\mathit{arg}{\mathit{min}}_{\theta ,p}\mathcal{L}\left(\theta ,\epsilon \right)(9)$

Remark 1. In the actual training process, due to the extensive data requirements for neural network training and the limited data collected from social media platforms, our framework necessitates the sampling of points within the defined domain to acquire a more substantial dataset, which is essential to facilitate the training of our PINN model.

Remark 2. The algorithm is implemented in Python using paddlepaddle. The width and depth of the neural networks depend on the size of the equations and the complexity of the information propagation dynamics. We use the sigmoid activation function except for the last neural network layer which uses sigmoid function to scale the data at different dimensions. For the training, we use a combination of two optimizers, Adam and L-BFGS, to optimize the $\theta$ and $\epsilon$ in order to reduce the training time while ensuring accuracy and the learning rate of 0.001, where the training is performed using the full batch of data. Since the total loss consists of two supervised losses and one unsupervised loss, we perform the training using the following two-stage strategy, which is found in our experiments to speed up the network convergence:

Stage 1. The network is initially trained using the two supervised losses ${\mathcal{L}}^{\text{data}}$ and ${\mathcal{L}}^{\text{ic}}$ for a few iterations, taking into account the fact that supervised training is typically more straightforward than unsupervised training. This enables the network to rapidly align with the observed data points.

Stage 2. We further train the network using the three losses.

4 Numerical experiments

In this section, we demonstrate the application of the proposed framework in the context of dynamics in public opinion propagation. To showcase the advanced and generalized nature of the framework, based on data accessibility, we primarily utilize some classic works previously published by our team in numerical experiments. These studies mainly encompass the classical SFI model, the SFI model considering the emotional factors, the SFI model considering the different stages, and a propagation dynamic model based on differential equation systems. Due to slight variations among different variables of the SFI models, there need to be some differences in the fully connected neural network used in our framework - primarily regarding input neurons, output neurons, and neurons employed for training parameters in inverse problems. However, aspects such as activation functions and learning rates in our models remain consistent. To accommodate the efficiency requirements of our training model, adjustments can be made to vary the number of layers in our neural network according to practical considerations. More importantly, according to the given varying events of different propagation dynamics models during the actual data fitting process, scaling may be required at differing degrees, which will be described in subsequent parts. The data and codes in this section are publicly available at: https://github.com/zhangzhiqiangccm/PINN_attempt.

4.1 Simulation of the single information propagation model (SFI)

As mentioned in the second section of this paper, the SFI model [15], a classic compartmental model in the field of network information dissemination, serves as the foundational framework for numerous works. Consequently, we employed the proposed framework for simulating the dynamic process of single information propagation to compare with the traditional solution method in the SFI model, encompassing the fitting of population quantities for various states and the prediction of the propagation dynamic parameters. Similarly, we employed the same forwarding data collected from a hot topic on the Chinese Sina-microblog as the foundational dataset for our framework. To expedite the convergence of the neural network, we also applied data scaling and subsequently calculated the Mean Squared Error for the fitted results. The ultimate fitting performance is illustrated in Figure 3:

Figure 3

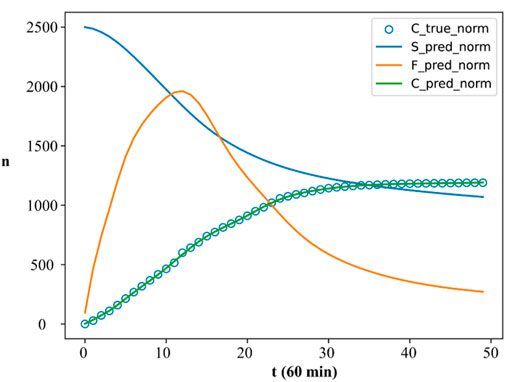
Figure 3. The fitting results of the SFI model based on our proposed framework. Note: The horizontal axis in the picture is time, and the vertical axis is the value of C(t). In the legend, “C_true_norm” represents the true value of the cumulative forwarding volume, “S_pred_norm”, “F_pred_norm” and “C_pred_norm” represent the predicted S(t), F(t) and C(t) respectively.

The total number $N$ of individuals in the SFI model remains constant, because the system operates on a compartmental framework. During simulation, we utilize the variables $S\left(t\right)$ and $F\left(t\right)$ to minimize computational complexity, with $I\left(t\right)$ being calculated based on these variables. Therefore, our proposed framework outputs results for $S\left(t\right)$, $F\left(t\right)$, and $C\left(t\right)$. To facilitate comparison, we have employed data from the SFI model. In our framework, the input layer of neural network consists of a single neuron representing time $t$, while the output layer comprises three neurons corresponding to $S\left(t\right)$, $F\left(t\right)$ and $C\left(t\right)$, The neural network employs six hidden layers with 32 neurons in each layer. However, due to insufficient data points (only 50), it is not feasible to train a deep-learning model. Therefore, we obtain additional training data by sampling at intervals along independent variables until we have collected 2000 points. The resulting fitting outcomes are depicted in Figure 3, demonstrating that our proposed framework exhibits superior capability in accurately capturing cumulative forwarding data with a final MSE value of 15.41. Additionally, for enhanced visualization purposes, we have scaled down the neural network’s output by a factor of ${2\times 10}^5$ for $S\left(t\right)$, $3\times {10}^2$ for $F\left(t\right)$, and ${10}^4$ for $C\left(t\right)$.

4.2 Simulation of the emotion-based information propagation model (E-SFI)

The emotion-based susceptible-forwarding-immune (E-SFI) [37] propagation dynamic model incorporates the categorization of emotions into positive, neutral, and negative, aiming to describe the process of emotional choices made by users in various states and investigate the information propagation that influences public sentiment. To accommodate this model in our framework, we have to increase the dimensions of the output layer in the neural network and expand the data for supervising model training. Consequently, we conducted simulations and training using original data from event one in the E-SFI model. The training process still utilized an 8-layer fully connected neural network with initial values determined by real data. The sampling and scaling approaches adopted in this part are similar to those in section 4.1, but with a greater number of neurons in the output layer to generate cumulative forwarding numbers under the three emotional states and produce propagation dynamics parameters. The fitting results in Figure 4 demonstrate that our framework outperforms the E-SFI model in accurately fitting real data including all the emotion types.

Figure 4

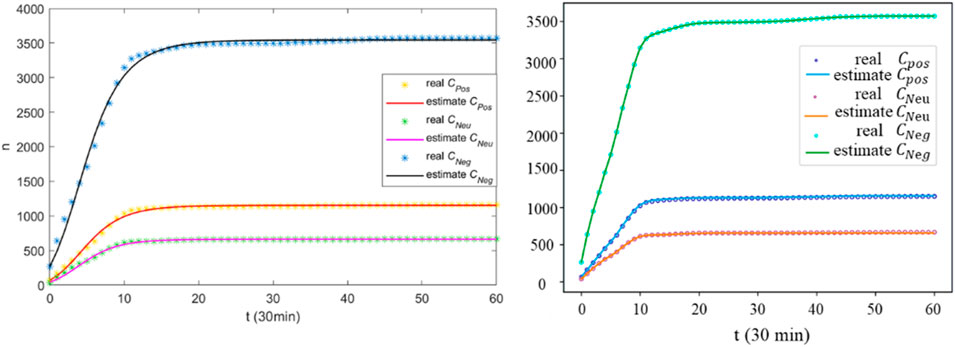
Figure 4. The comparison results between the original fitting outcomes of the E-SFI model (left) and those obtained from our proposed framework (right). Note: $C_{pos}$, $C_{neu}$ and $C_{neg}$ represent the cumulative forwarding number corresponding to the positive emotion group, neutral emotion group and negative emotion group respectively. The points in the figure represent the real data values, and the curves are the predicted variable values.

4.3 Simulation of the two-stage information propagation model (TS-SFI)

The two-stage rumor propagation dynamic model aims to design effective strategies for controlling rumors, where the first stage of rumor propagation is characterized by the susceptible/educated-infected-recovered (SO-S/EIR) dynamics and the second stage is characterized by the susceptible/educated-infected-denied-recovered (C-S/EIDR) dynamics [38]. The conventional least-squares fitting method is inadequate for modeling the two-stage rumor propagation dynamics discussed in this study, making it become necessary to separately fit each stage individually. The advantage of our framework lies in the robust fitting capability of neural networks, which enables us to accurately fit the data without the need for data splitting. Based on data and theory from the original paper, we applied the PINN framework for data fitting, of which notable results for both stages are depicted in Figure 5. Compared with the results in the original model, the fitting effect of our model is not satisfactory for the mutation in the two stages, but it performs well at other locations. Furthermore, our proposed framework demonstrates its capability to fit the curves from two distinct stages, thereby enhancing the efficiency of data fitting.

Figure 5

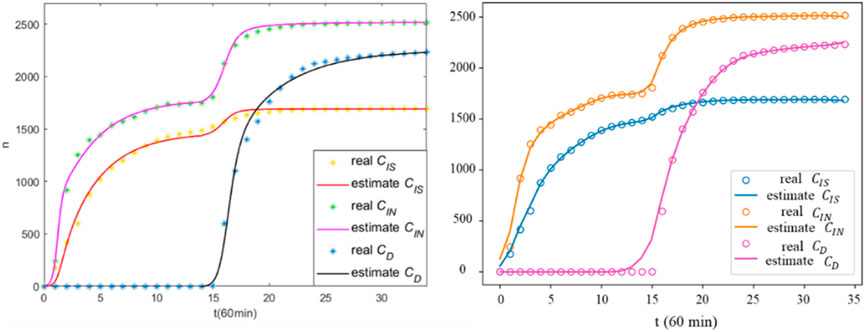
Figure 5. The comparison results between the original fitting outcomes of the TS-SFI model (left) and those obtained from our proposed framework (right). Note: $C_{IS}$, $C_{IN}$ and $C_D$ represent the cumulative number corresponding to the super infected users, normal infected users and denied users respectively. The points in the figure represent the real data values, and the curves are the predicted variable values.

4.4 Simulation of the PDE-based information propagation model (PSFI)

In addition to the time variable $t$, other independent variables such as distance can also be incorporated into the equation system governing network information propagation dynamics. Traditional methods often encounter challenges in solving partial differential equations compared to ordinary differential equations, and they may struggle to accurately fit real data. However, our framework offers a solution by avoiding complex partial differential equation solving altogether. Instead, we simply adjust the number of input layers in our neural network model to include both time $t$ and other independent variables for finding the equations’ solution. Notably, there is no need to modify the equations in loss function. Consequently, our framework significantly simplifies the resolution of high-dimensional systems involving partial differential equations. To validate its effectiveness in tasks involving multiple independent inputs, we collect data on the trending event “The arrest of the driver involved in the freight lesbian” from Sina-microblog platform, with a sampling time interval of 1 h. The social distance variable is defined based on the group that retweeted the initial message. For example, if user A posts a message and user B forwards it, the social distance between user A and user B is 1. If user C forwards the message forwarded by user B, the social distance between user C and user A is 2, and so on. As social distance increases, there is a decrease in the cumulative number of retweeters for the corresponding message over time. Figure 6 presents the fitting results based on the PSFI model: The fitting results demonstrate that our model effectively captures the variations in curves across various social distances.

Figure 6

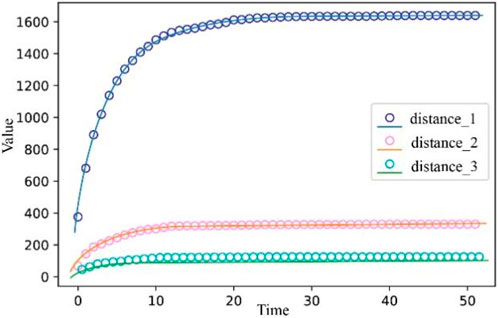
Figure 6. The fitting results of the SFI model for PDE based on our proposed framework. Note: Distance_1, distance_2, and distance_3 represent the three different social distances used in the experiment. The points in the figure represent the real data values, and the curves are the predicted variable values.

4.5 Model robustness testing

The aforementioned experiments have demonstrated the effectiveness of the proposed framework in the context of information dissemination dynamics. Additionally, we seek to validate the robustness of model by adjusting the weights in three key aspects in the SFI model: data, equations and initial conditions and corresponding results are depicted in Figure 7. The values after “Data”, “Eq”, and “Ic” represent the respective proportions of data loss, equation loss, and initial condition loss shown in Figure 7. There is significant fluctuation in results when altering the weights of equations, indicating their crucial role throughout the entire fitting process. Conversely, alterations of the curves are not prominently evident under the changes of initial value conditions. In traditional methods, simulation results are often heavily influenced by initial values, leading that only an appropriate initial value can obtain a reasonable fit. Our proposed framework reduces the susceptibility to variations in initial values while ensuring both fitting effectiveness and model robustness. Furthermore, the overall propagation trends of propagation populations remain unchanged, highlighting the intrinsic mechanisms inherent within the SFI model.

Figure 7

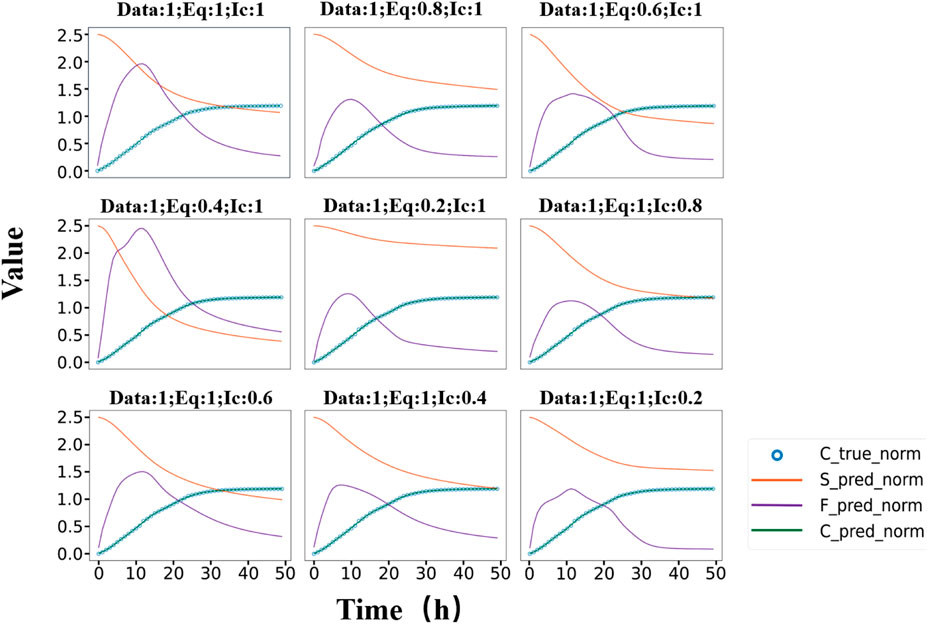
Figure 7. Fitting results of the SFI model under different loss weight configurations within the proposed framework. Note: The annotation “Data:1; Eq:1; Ic:1”indicates the weighting ratio assigned to data constraint, equations, and initial condition terms in the composite loss function. To better display the image, the values on the vertical axis have been reduced by a factor of 1,000; the actual quantities should be 1,000 times greater than those indicated in the figure.

4.6 Comparison of simulation results based on four types of models

The loss results of each model are computed after 100,000 iterations in Table 1. From the results, it is evident that the PSFI model outperforms both the SFI and E-SFI models in terms of training outcomes. Despite its more intricate structure and resulting complex system of differential equations, the PSFI model benefits from a larger amount of supervised signal data, enabling superior training. In contrast, the two-stage rumor propagation dynamic model based on the SFI model exhibits more complexity due to its lack of sufficient supervised signal data, leading to poorer fitting performance. Ultimately, simulation results based on partial differential equations slightly surpass those based on ordinary differential equations, with only minor differences observed in terms of independent variables in the input model. Thus, to some extent, incorporating social distance variable into the input model significantly impacts propagation dynamics fitting. Moreover, in our proposed framework, data loss often constitutes a substantial portion of the overall loss function, since losses at data level tend to be numerically greater than those incurred by the other two components.

Table 1

Table 1. Different loss results of each model from our framework.

Our framework integrates the forward and inverse problems in the context of information dissemination dynamics. In contrast to conventional approaches, which solve the model parameters and then conduct forward numerical simulations based on these parameters, our approach offers greater efficiency. However, it should be noted that the values of parameters obtained from our framework cannot be directly compared to those obtained through inverse problem-solving methods. This is because the parameters within the neural network in our framework are also an integral part of the overall system, despite its inherent complexity. Our framework primarily focuses on data fitting and predicting the numbers of user in each propagation state. While various modules within the framework interact and depend on each other, minor adjustments are still necessary to align with real-world scenarios. Among these adjustments, scaling pertaining to data handling is crucial way in our framework. Firstly, in propagation dynamic models, there can be substantial numerical disparities in representing different states or groups, ranging from a few to thousands or more, resulting in normalizing these numerical values becoming essential. In our framework, except for the final layer which lacks an activation function, the activation functions in the hidden layers of the neural network are chosen as $\mathit{Tan}h\left(\right)$ functions to aid in numerical normalization. Additionally, certain parameters involved in equations expressing information propagation may also exhibit significant differences. For instance, parameters like the average contact rate $\beta$ and the average forwarding probability $p$ both fall in the range of $\left(0,1\right)$, but only $\beta$ should be operated on an order of ${10}^{-4}$, which is scaled down $\beta$ by a factor of ${10}^4$ to facilitate neural network training. Furthermore, for the sake of visualization, we also apply scaling during the plotting process.

5 Conclusion

In this study, we introduce the method of embedded physical neural networks to construct a framework suitable for modeling the dynamics of public opinion propagation based on partial differential equations. This innovative approach combines the automatic differentiation mechanism of neural networks with partial differential equations through the design of a loss function, enabling more efficient fitting for real data. Unlike other methods, our approach does not require grid drawing and is insensitive to initial or boundary values [31]. Furthermore, it unifies ordinary and partial differential equations solving by converting time $t$ in dynamic problems into an input variable. The only difference between solving partial and ordinary differential equations problems lies in the input dimension of the neural network, reducing complexity when dealing with high-dimensional problems and significantly improving problem-solving efficiency [39]. Importantly, our framework can simultaneously solve both forward and inverse problems. In studying public opinion propagation dynamics, different events correspond to different parameters. Thus, solving the inverse problem becomes crucial but challenging. Our framework effectively fits parameter values while considering real-world data and accurately simulates the propagation dynamics of public opinion.

We apply this proposed framework to solve various classic scenarios such as the SFI and E-SFI models in public opinion propagation dynamics research. Comparative results demonstrate that our method outperforms existing models in terms of fitting accuracy without compromising computational efficiency. Although our proposed framework can obtain good results, there are also some shortcomings. Firstly, in the design of the loss function of the neural network, the weights of the data-related loss and the equation-related loss need to be determined by ourselves, because the two have large differences in absolute values, which need to be adjusted according to the specific problem and real data to avoid vanishing or exploding gradients. In addition, some noise can not be avoided to exist in the data we collected from public opinion platforms, which may lead to the phenomenon of overfitting.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YW: Methodology, Software, Data curation, Writing–review and editing. ZZ: Methodology, Software, Data curation, Writing–review and editing. JWu: Conceptualization, Methodology, Writing–review and editing. JWa: Formal Analysis, Validation, Visualization, Writing–review and editing. YZ: Methodology, Validation, Writing–review and editing. FY: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The work was supported by the Beijing Natural Science Foundation (No. 4232015); the National Natural Science Foundation of China (No. 62372418); the State Key Laboratory of Media Convergence and Communication, Communication University of China; the Fundamental Research Funds for the Central Universities; the High-quality and Cutting-edge Disciplines Construction Project for Universities in Beijing (Internet Information, Communication University of China). JW was funded by the Natural Science and Engineering Research Council of Canada; and by the Canada Research Chair Program.

Conflict of interest

Author YZ was employed by Baidu.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chen Y, Li Y, Wang Z, Quintero AJ, Yang C, Ji W. Rapid perception of public opinion in emergency events through social media. Nat hazards Rev (2022) 23(2):23. doi:10.1061/(asce)nh.1527-6996.0000547

CrossRef Full Text | Google Scholar

2. Barbara N, Clyde W. Trends in abortion attitudes: from roe to dobbs. Public Opin Q (2023)(2) 2. doi:10.1093/poq/nfad014

CrossRef Full Text | Google Scholar

3. Yin F, Pan Y, Tang X, Wu C, Jin Z, Wu J. An information propagation network dynamic considering multi-platform influences. Appl Math Lett (2022) 133:108231. doi:10.1016/j.aml.2022.108231

CrossRef Full Text | Google Scholar

4. Yin F, Wu Z, Shao X, Tang X, Liang T, Wu J. Topic-a cluster of relevant messages-propagation dynamics: a modeling study of the impact of user repeated forwarding behaviors. Appl Mathematics Lett (2022) 127:107819-. doi:10.1016/j.aml.2021.107819

CrossRef Full Text | Google Scholar

5. Yin F, Zhu X, Shao X, Xia X, Pan Y, Wu J. Modeling and quantifying the influence of opinion involving opinion leaders on delayed information propagation dynamics. Appl Mathematics Lett (2021) 121(4):107356. doi:10.1016/j.aml.2021.107356

CrossRef Full Text | Google Scholar

6. Vargas R, Mosavi A, Ruiz R. DEEP LEARNING: A REVIEW. Adv Intell Syst Comput (2017) 5(2). doi:10.20944/preprints201810.0218.v1

CrossRef Full Text | Google Scholar

7. Dong S, Wang P, Abbas K. A survey on deep learning and its applications. Computer Sci Rev (2021) 40:100379. doi:10.1016/j.cosrev.2021.100379

CrossRef Full Text | Google Scholar

8. Cuomo S, Di Cola VS, Giampaolo F, Rozza G, Raissi M, Piccialli F. Scientific machine learning through physics–informed neural networks: where we are and what's next. J Scientific Comput (2022) 92(3):88–62. doi:10.1007/s10915-022-01939-z

CrossRef Full Text | Google Scholar

9. Raissi M, Perdikaris P, Karniadakis GE. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys (2018) 378:686–707. doi:10.1016/j.jcp.2018.10.045

CrossRef Full Text | Google Scholar

10. Cai S, Mao Z, Wang Z, Yin M, Karniadakis GE. Physics-informed neural networks (PINNs) for fluid mechanics: a review. Chin J Theor Appl Mech (2021) 37(12):1727–38. doi:10.1007/s10409-021-01148-1

CrossRef Full Text | Google Scholar

11. Chen Y, Lu L, Karniadakis GE, Dal Negro L. Physics-informed neural networks for inverse problems in nano-optics and metamaterials. Opt Express (2020) 28(8):11618. doi:10.1364/oe.384875

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Almajid MM, Abu-Alsaud MO. Prediction of porous media fluid flow using physics informed neural networks. J Pet Sci Eng (2021) 208:109205. doi:10.1016/j.petrol.2021.109205

CrossRef Full Text | Google Scholar

13. Niaki SA, Haghighat E, Campbell T, Poursartib A, Vazir R. Physics-informed neural network for modelling the thermochemical curing process of composite-tool systems during manufacture. Compu. Meth. Appl. Mec. Eng (2020) 384 113959. doi:10.1016/j.cma.2021.113959

CrossRef Full Text | Google Scholar

14. Brugnano FZP, Iavernaro F, Zanzottera P. A multiregional extension of the SIR model, with application to the COVID-19 spread in Italy. Math Methods Appl Sci (2021) 44(6):4414–27. doi:10.1002/mma.7039

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Yin F, Shao X, Wu J. Nearcasting forwarding behaviors and information propagation in Chinese Sina-Microblog. Math Biosciences Eng (2019) 16(5):5380–94. doi:10.3934/mbe.2019268

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Xiao Y, Chen D, Wei S, Li Q, Wang H, Xu M. Rumor propagation dynamic model based on evolutionary game and anti-rumor. Nonlinear Dyn (2019) 95:523–39. doi:10.1007/s11071-018-4579-1

CrossRef Full Text | Google Scholar

17. Yin F, Lv J, Zhang X, Xia X, Wu J. COVID-19 information propagation dynamics in the Chinese Sina-microblog. Math Biosciences Eng (2020) 17(3):2676–92. doi:10.3934/mbe.2020146

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wang L, Song N, Ma C, He B, Huo L. Rumor spreading model considering the activity of spreaders in the homogeneous network. Physica A: Stat Mech its Appl (2017) 468:855–65. doi:10.1016/j.physa.2016.11.039

CrossRef Full Text | Google Scholar

19. Liu Y, Wang B, Wu B, Shang S, Zhang Y, Shi C. Characterizing super-spreading in microblog: an epidemic-based information propagation model. Physica A: Stat Mech its Appl (2016) 463:202–18. doi:10.1016/j.physa.2016.07.022

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Su Q, Huang J, Zhao X. An information propagation model considering incomplete reading behavior in microblog. Physica A: Stat Mech its Appl (2015) 419:55–63. doi:10.1016/j.physa.2014.10.042

CrossRef Full Text | Google Scholar

21. Malinzi J, Gwebu S, Motsa S. Determining COVID-19 dynamics using physics informed neural networks. Axioms (2022) 11(3):121. doi:10.3390/axioms11030121

CrossRef Full Text | Google Scholar

22. Meucci R, Euzzor S, Tito Arecchi F, Ginoux JM. Minimal universal model for chaos in laser with feedback. Int J Bifurcation Chaos (2021) 31(04):2130013. doi:10.1142/s0218127421300135

CrossRef Full Text | Google Scholar

23. Concas R, Montori A, Pugliese E, Perinelli A, Ricci L, Meucci R. Analysis of an improved circuit for laser chaos and its synchronization. IEEE Access (2024) 12:100602–10. doi:10.1109/access.2024.3409875

CrossRef Full Text | Google Scholar

24. Heldmann F, Berkhahn S, Ehrhardt M, Klamroth K. PINN training using biobjective optimization: the trade-off between data loss and residual loss. J Comput Phys (2023) 488:112211. doi:10.1016/j.jcp.2023.112211

CrossRef Full Text | Google Scholar

25. Cai M, Em Karniadakis G, Li C. Fractional SEIR model and data-driven predictions of COVID-19 dynamics of Omicron variant. Chaos: An Interdiscip J Nonlinear Sci (2022) 32(7):071101. doi:10.1063/5.0099450

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Hao Y. Modeling the COVID-19 pandemic: a model-driven and a data-driven analyses. (2023).

Google Scholar

27. Lazebnik T. Computational applications of extended SIR models: a review focused on airborne pandemics. Ecol Model (2023) 483:110422. doi:10.1016/j.ecolmodel.2023.110422

CrossRef Full Text | Google Scholar

28. Vadyala SR, Betgeri SN, Matthews JC, Matthews E. A review of physics-based machine learning in civil engineering. Results Eng (2022) 13:100316. doi:10.1016/j.rineng.2021.100316

CrossRef Full Text | Google Scholar

29. Karniadakis GE, Kevrekidis IG, Lu L, Perdikaris P, Wang S, Yang L. Physics-informed machine learning. Nat Rev Phys (2021) 3(6):422–40. doi:10.1038/s42254-021-00314-5

CrossRef Full Text | Google Scholar

30. Eivazi H, Tahani M, Schlatter P, Vinuesa R. Physics-informed neural networks for solving Reynolds-averaged Navier–Stokes equations. Phys Fluids (2022) 34(7). doi:10.1063/5.0095270

CrossRef Full Text | Google Scholar

31. Bennini A, Lanteri S, Valentin F, Gomes TA., Miguez da Silva L. PINNs for the time-domain Maxwell equations-Preliminary results. In: Performance Computing Conference; September, 2022; Porto Alegre (2023).

Google Scholar

32. Wang L, Yan Z. Data-driven rogue waves and parameter discovery in the defocusing nonlinear Schrödinger equation with a potential using the PINN deep learning. Phys Lett A (2021) 404:127408. doi:10.1016/j.physleta.2021.127408

CrossRef Full Text | Google Scholar

33. Lawal ZK, Yassin H, Lai DTC, Che Idris A. Physics-informed neural network (PINN) evolution and beyond: a systematic literature review and bibliometric analysis. Big Data Cogn Comput (2022) 6(4):140. doi:10.3390/bdcc6040140

CrossRef Full Text | Google Scholar

34. Geng L, Yang S, Wang K, Zhou Q. Modeling public opinion dissemination in a multilayer network with SEIR model based on real social networks. Eng Appl Artif Intelligence (2023) 125:106719. doi:10.1016/j.engappai.2023.106719

CrossRef Full Text | Google Scholar

35. Yan Z, Zhou X, Du R. An enhanced SIR dynamic model: the timing and changes in public opinion in the process of information diffusion. Electron Commerce Res (2024) 24(3):2021–44. doi:10.1007/s10660-022-09608-x

CrossRef Full Text | Google Scholar

36. Yuan J, Shi J, Wang J, Liu W. Modelling network public opinion polarization based on SIR model considering dynamic network structure. Alexandria Eng J (2022) 61(6):4557–71. doi:10.1016/j.aej.2021.10.014

CrossRef Full Text | Google Scholar

37. Yin F, Xia X, Zhang X, Zhang M, Lv J, Wu J. Modelling the dynamic emotional information propagation and guiding the public sentiment in the Chinese Sina-microblog. Appl Mathematics Comput (2021) 396:125884. doi:10.1016/j.amc.2020.125884

CrossRef Full Text | Google Scholar

38. Yin F, Jiang X, Qian X, Xia X, Pan Y, Wu J. Modeling and quantifying the influence of rumor and counter-rumor on information propagation dynamics. Chaos, Solitons and Fractals (2022) 162:112392. doi:10.1016/j.chaos.2022.112392

CrossRef Full Text | Google Scholar

39. Huang B, Wang J. Applications of physics-informed neural networks in power systems-a review. IEEE Trans Power Syst (2022) 38(1):572–88. doi:10.1109/tpwrs.2022.3162473

CrossRef Full Text | Google Scholar