Entangled quantum Stirling heat engine based on two particles Heisenberg model with Dzyaloshinskii-Moriya interaction

Quantum heat engines have attracted significant attention in recent years due to their potential to surpass classical thermodynamic limits by leveraging quantum effects such as entanglement and coherence. In this study, we analyze a quantum Stirling heat engine characterized by a working substance composed of a two-particle Heisenberg model with Dzyaloshinskii–Moriya (DM) interaction under an external magnetic field. We investigate the impact of the antisymmetric interaction on the engine’s efficiency across varying coupling parameters. Our findings demonstrate that the utilization of a two-qubit Heisenberg model in an entangled quantum Stirling heat engine can significantly enhance efficiency and performance. By optimizing the antisymmetric exchange parameters, we achieve substantial enhancements in engine efficiency, with results demonstrating that the efficiency attains remarkably high values compared to other cycles utilizing the same working substance. These enhancements are primarily influenced by the DM interaction and the entangled states of the working substance, leading to superior performance.

1 Introduction

Research in quantum thermodynamics has shown that incorporating innovative design elements and optimizing thermodynamic cycles can significantly enhance the performance of Quantum Heat Engines (QHEs) [1–5]. Over the past decade, researchers have made significant advancements in optimizing QHE performance by exploring and refining a wide range of thermodynamic cycles such as the Otto, Carnot, and Stirling cycles [6–11]. Various working substances have been suggested, including single spins, quantum oscillators, and the XYZ spin chain model with Dzyaloshinskii-Moriya (DM) interaction [12–23].

The examination of interacting qubits as operational entities within QHEs presents a compelling issue in quantum physics. In recent years, there has been significant investigation into the interplay of two qubits using the Heisenberg spin chain model, encompassing interactions between spins as well as spin-orbit coupling such as DM interaction [24]. Huang et al. [25] conducted an extensive examination of a quantum Otto heat engine using a three-qubit XXZ model, considering the influences of DM interaction and magnetic field. Their study explored the effects of interaction and anisotropic parameters on both the work output and efficiency of QHEs. Similarly, Purkait et al. [26] scrutinized the efficiency of quantum Stirling engines employing a working system of two Heisenberg-coupled spins near a Quantum Critical Point, attributing enhancements to the non-analytic nature of spin-spin correlation and entanglement. Additionally, Zhao et al. [27] investigated an entangled quantum Otto heat engine utilizing two-spin systems with DM interaction, revealing the significant role of DM interaction in the engine’s thermodynamics.

Moreover, scientists have explored how quantum coherence and entanglement affect QHE efficiency, providing new insights into improving their performance [28–33]. Various quantum thermodynamic cycles, including the Otto and Stirling cycles within two-spin working systems, have been studied to elucidate the impact of entanglement on QHE performance [5, 34–38].

In this context, our work focuses on elucidating the properties of an operational material and the theoretical framework for quantum heat engines (QHEs). We have studied a two-particle Heisenberg model with DM interaction under an external magnetic field as the working substance of a quantum Stirling heat engine. Unlike previous studies focusing on the Otto cycle [21, 27, 39], this work investigates the role of the Dzyaloshinskii–Moriya interaction within a Stirling cycle framework, which provides unique insights into the interplay between entanglement and antisymmetric exchange parameters. The study examines the impact of antisymmetric interaction on engine efficiency by altering coupling parameters and entanglement levels in the initial and third stages of the cycle. Our findings indicate that the DM interaction significantly enhances efficiency, revealing critical thresholds that optimize performance under different operational parameters. Optimizing these parameters can significantly improve efficiency, surpassing the Curzon-Ahlborn efficiency and reaching the Carnot limit. Additionally, fine-tuning entanglement levels has the potential to enhance efficiency. These results suggests that quantum heat engines have the potential to achieve higher performance levels through the exploration of antisymmetric aspects of spin systems.

2 Working substance: two-qubit isotropic Heisenberg XYZ model

Let us start by examining a two-qubit $XYZ$ spin chain employed as an operational material in a QHE system operating under the Stirling cycle. The Hamiltonian for the system is given by:

$\begin{array}{ll}\hfill \mathcal{H}& =\frac{B}{2}\left({\sigma }_1^z+{\sigma }_2^z\right)+J\left({\sigma }_1^x{\sigma }_2^x+{\sigma }_1^y{\sigma }_2^y+{\sigma }_1^z{\sigma }_2^z\right)\hfill \\ \hfill & +D\left({\sigma }_1^x{\sigma }_2^y-{\sigma }_1^y{\sigma }_2^x\right).\hfill \end{array}(1)$

where $J$ is the exchange constant, $D$ is the antisymmetric exchange parameter, and $B$ is the energy contribution associated with the external magnetic field. In this context, ${\sigma }^i$ denotes the standard Pauli operators. The first term signifies the interaction among adjacent spins, while the subsequent term represents the interaction with the external magnetic field. The exchange constant $(J)$ is crucial in describing different types of magnetic interactions; it can be positive or negative, indicating either antiparallel (entangled ground state) or parallel (separable ground state) scenarios [40, 41], respectively. This study focuses exclusively on the antiparallel scenario, considering the influence of the external magnetic field denoted by $B$.

The four eigenvalues of this Hamiltonian can be obtained as follows:

$\begin{array}{ll}\hfill E_1& =\frac{J}{2}+B,\hfill \\ \hfill E_2& =-\frac{J}{2}-\sqrt{J^2+D^2},\hfill \\ \hfill E_3& =-\frac{J}{2}+\sqrt{J^2+D^2},\hfill \\ \hfill E_4& =\frac{J}{2}-B.\hfill \end{array}$

We determine the occupation probabilities, denoted as $P_n$, of the system through a series of calculations. The probability for each state, with the normalization condition, is given by:

$P_n=\frac{e^{-\beta E_n}}{Z},$

where $Z={\sum }_{i=1}^4{e}^{-\beta E_i}$ is the partition function and $\beta =\frac{1}{k_{B}T}$. The entropy for the system at thermal equilibrium is:

$S=-{\displaystyle \sum _{i=1}^4}{P}_i\ln P_i.(2)$

3 Quantum stirling heat engine and the Heisenberg model

The universal behavior of quantum heat engines was extensively discussed in the academic literature, operating within the confines of all four thermodynamic regimes sanctioned by the Clausius formulation of the second law [40, 42–47]. This accomplishment is realized through the precise manipulation of reservoir temperatures and working parameters. In particular, quantum Stirling cycles applied in magnetic systems present themselves as promising alternatives for developing universal quantum heat engines. A quantum Stirling cycle is composed of two quantum isothermal processes and two quantum isochoric processes [48, 49]. It can be elucidated by analyzing the energy exchange in each step of the cycle:

Stage 1: An isothermal expansion occurs when the system is connected to a hot reservoir at a constant temperature $T_h$: [$A(J_A,T_h)\to B(J_B,T_h)$]. To ensure thermal equilibrium, the magnetic coupling transitions gradually from $J_A$ to $J_B$. In this step, the heat absorbed from the bath at temperature $T_h$, represented by $\mathrm{\Delta }{Q}_{AB}$, can be expressed through the entropy change:

$\mathrm{\Delta }{Q}_{AB}={\int }_A^B{T}_{h}dS=T_h\left[S\left(J_B,T_h\right)-S\left(J_A,T_h\right)\right].(3)$

Stage 2: A quantum isochoric process occurs in: [$B(J_B,T_h)\to C(J_B,T_c)$]. Throughout this stage, there is a transition in temperature within the system, moving from a hot bath at temperature $(T_h)$ to a cold one with temperature $(T_c)$. It is crucial to emphasize that the magnetic coupling constant, $J_B$, remains constant during this particular process. The system does not perform any work; instead, it releases heat, denoted as $\mathrm{\Delta }{Q}_{BC}$, which can be expressed in terms of the variation of the internal energy:

$\mathrm{\Delta }{Q}_{BC}=U\left(J_B,T_c\right)-U\left(J_B,T_h\right).(4)$

Stage 3: A quantum isothermal compression process is described: [$C(J_B,T_c)\to D(J_A,T_c)$], where the working substance is in contact with a cold reservoir at a fixed temperature $T=T_c$. The magnetic coupling transitions from $J_B$ to $J_A$. The amount of heat released in this process, denoted as $\mathrm{\Delta }{Q}_{CD}$, is given by the change in the entropy, Equation 2.

$\mathrm{\Delta }{Q}_{CD}={\int }_C^D{T}_{c}dS=T_c\left[S\left(J_A,T_c\right)-S\left(J_B,T_c\right)\right].(5)$

Stage 4: The final step is a quantum isochoric process: [$D(J_A,T_c)\to A(J_A,T_h)$]. During this fourth stage, the system transitions from the cold reservoir at $T_c$ to the hot reservoir at $T_h$. The mediation of this transition is carried out by the fixed magnetic coupling constant $J_A$. The attainment of thermal equilibrium marks the end of the isochoric thermalization process, resulting in a final temperature of $T_h$. This particular process involves no work, and the heat absorbed by the working substance (referred to as $\mathrm{\Delta }{Q}_{DA}$) can be expressed as follows:

$\mathrm{\Delta }{Q}_{DA}=U\left(J_A,T_h\right)-U\left(J_A,T_c\right).(6)$

To assess the impact of quantum entanglement on the energy exchange of the quantum Stirling cycle, we measure the entanglement present in the thermal equilibrium state using the widely recognized Wootters concurrence [50–52]. This allows us to evaluate the entanglement of the bipartite system, which is characterized as $c(\rho )=\max \left\{0,\sqrt{{\lambda }_1}-\sqrt{{\lambda }_2}-\sqrt{{\lambda }_3}-\sqrt{{\lambda }_4}\right\}$, where ${\lambda }_i$ are the eigenvalues of the matrix $\rho ({\sigma }_1^y\otimes {\sigma }_2^y)\rho *({\sigma }_1^y\otimes {\sigma }_2^y)$ arranged in descending sequence. Here $\rho *$ denotes the complex conjugate of $\rho$ [41, 50–53]. In the case of separable states, the parameter $c$ equals 0, whereas for Bell states, the parameter $c$ equals 1 [52]. From the Hamiltonian model given by Equation 1, the concurrence associated with the thermal equilibrium state is determined by the following equation:

$\begin{array}{ll}\hfill c& =\max \left\{\frac{\left[\sinh \beta \left(J+D\right)\right]-1}{2\left[\cosh \beta \left(J+D+B\right)\right]\left[\cosh \beta \left(J+D-B\right)\right]},0\right\},\hfill \\ \hfill & \hfill & \hfill \end{array}(7)$

Therefore, the entanglement at the end of the first stage and the third stage of the quantum Stirling cycle can be represented as $c_1$ and $c_2$ respectively, and they can be written as:

$\begin{array}{ll}\hfill c_1& =\frac{\sinh \left(\frac{J+D}{T_c}\right)-1}{2\cosh \left(\frac{J+D+B_1}{T_c}\right)\cosh \left(\frac{J+D-B_1}{T_c}\right)},\hfill \\ \hfill & \hfill & \hfill \end{array}$

$\begin{array}{ll}\hfill c_2& =\frac{\sinh \left(\frac{J+D}{T_h}\right)-1}{2\cosh \left(\frac{J+D+B_2}{T_h}\right)\cosh \left(\frac{J+D-B_2}{T_h}\right)}.\hfill \\ \hfill & \hfill & \hfill \end{array}(8)$

To understand how these interconnections affect important thermodynamic properties, we can analyze Equations 7, 8. By using these equations, we can express the magnetic field based on entanglement with an analytical solution given by:

$\begin{array}{ll}\hfill B_1& =T_c{\cosh }^{-1}\frac{\left[\sinh \left(\frac{J+D}{T_c}\right)-1-c_1\cosh \left(\frac{J+D}{T_c}\right)\right]}{c_1},\hfill \\ \hfill & \hfill & \hfill \end{array}(9)$

$\begin{array}{ll}\hfill B_2& =T_h{\cosh }^{-1}\frac{\left[\sinh \left(\frac{J+D}{T_h}\right)-1-c_2\cosh \left(\frac{J+D}{T_h}\right)\right]}{c_2}.\hfill \\ \hfill & \hfill & \hfill \end{array}(10)$

By substituting Equations 9, 10 to the heat exchanged in each step of the Stirling cycle, Equations 3–6, we can evaluate the heat absorbed $Q_{in}=\mathrm{\Delta }{Q}_{AB}+\mathrm{\Delta }{Q}_{DA}$, the heat released $Q_{\mathit{out}}=\mathrm{\Delta }{Q}_{BC}+\mathrm{\Delta }{Q}_{CD}$, the total work $W=Q_{in}+Q_{\mathit{out}}$ in terms of the entanglement $c_1$ and $c_2$, temperatures $T_c$, $T_h$, and the antisymmetric exchange parameters $D_1$ and $D_2$.

4 Results and discussion

In this section, we will study in detail the impact of the quantum entanglement, temperatures, and antisymmetric exchange parameters on the thermal efficiency of the two-qubit isotropic Heisenberg XYZ model used as a working substance in the quantum Stirling heat engine. The thermodynamic efficiency $(\eta )$ in the heat engine operation is characterized by the ratio between the extracted work $(W)$ and the absorbed heat $(Q_{in})$ of the working substance:

$\eta =\frac{W}{Q_{in}}$

Thus, one can examine the influences of DM interaction parameters on the efficiency and plot it as a function of the above-mentioned parameters.

The variation of the efficiency as a function of antisymmetric exchange parameters $D_1$ and $D_2$ has been presented in Figure 1.

Figure 1

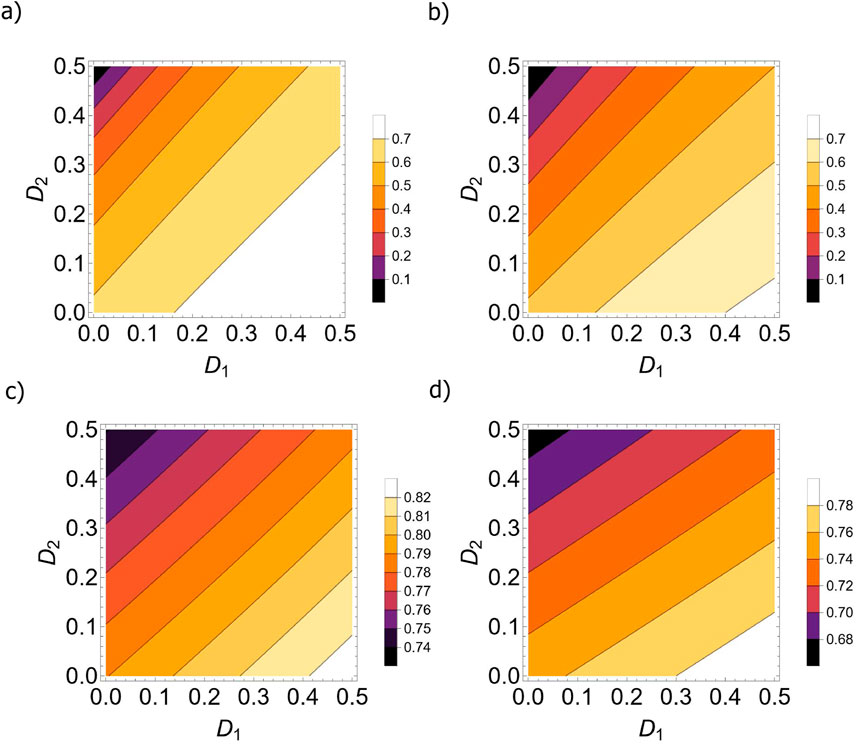
Figure 1. (Color online) Variation of the efficiency $\eta$ of the quantum Stirling Cycle, in terms of $D_1$ and $D_2$ in isoline map with $J_2=1.5J_1$, (A) $T_h=2T_c$, $c_1=2c_2$, (B) $T_h=4T_c$, $c_1=2c_2$, (C) $T_h=2T_c$, $c_1=4c_2$, (D) $T_h=4T_c$, $c_1=4c_2$. As can be seen, the efficiency of the quantum Stirling Cycle shows significant variations due to changes in antisymmetric exchange parameters ($D1$ and $D2$). Raising the hot reservoir temperature while keeping these parameters constant significantly impacts efficiency. The efficiency increases notably when the entanglement parameter $c1$ is doubled. However, decreasing the hot reservoir temperature from $Th=4Tc$ to $Th=2T_c$ also enhances efficiency.

The graphical representation demonstrates that variations in the antisymmetric exchange result in discernible fluctuations in the efficiency value. A comparative analysis between Figures 1A, B reveal that elevating the temperature of the hot reservoir while maintaining the antisymmetric parameter constant produces a significant impact on the efficiency. The upper limit of $\eta$ is contingent upon the specific values of $D_1$, $D_2$, $T_h$, and $T_c$. From the comparison of Figures 1B, C, it is noticeable that the increase of $c_1=2c_2$ to $c_1=4c_2$ has caused the efficiency to increase significantly. This shows that in the presence of the $D$ parameter, the increase in the entanglement leads to an enhancement in efficiency.

In Figure 1D, we plot a similar figure to Figure 1C except for $T_h=4T_c$. It is evident that the efficiency experiences a noticeable decrease. Upon comparing Figures 1C, D, it is observed that the efficiency rises as $T_h=4T_c$ transitions to $T_h=2T_c$, and the alteration in the ratio of the hot bath to the cold bath can result in an efficiency enhancement.

In Figure 2, we plot the efficiency of the Quantum Stirling heat engine in terms of the ratio between the antisymmetric exchange parameters $D_1/D_2$, fixing the parameters $\{c_1=4c_2,J_2=2J_1\}$ for different values of temperature (2 a) and $\{T_h=4T_c,J_2=2J_1\}$ (2 b), for different values of entanglement. As seen in the plot, the efficiency varies based on the relationship between the parameters $c_1$ and $c_2$. The figure clearly indicates that efficiency increases as the ratio between the concurrence $c_1/c_2$ increases. Thus, increasing the degree of entanglement in the first stage of the circle leads to an enhancement of the performance of the heat engine.

Figure 2

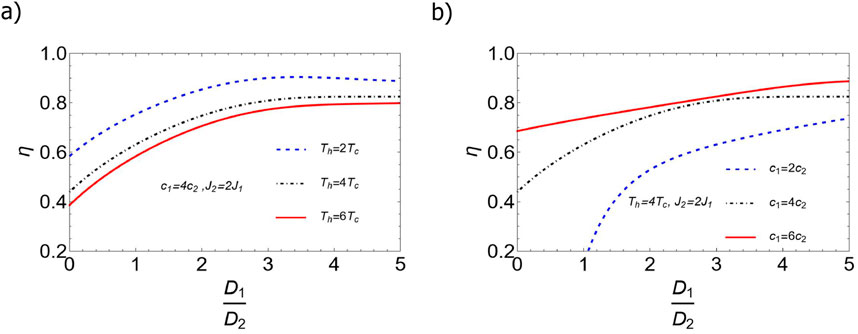
Figure 2. (Color online) Efficiency of the quantum Stirling heat engine as a function of $D_1/D_2$ with the parameters $J_2=2J_1$, (A) $c_1=4c_2$ and different relation between hot bath and cold bath, (B) $T_h=4T_c$ and different relation between $c_1$ and $c_2$. The efficiency varies based on the relationship between the parameters $c_1$ and $c_2$. It is evident that efficiency increases as the ratio between the concurrence $c_1/c_2$ increases.

To validate this improvement and highlight the potential of entangled heat engines to surpass traditional thermodynamic cycles under certain conditions, Figure 3 shows the efficiency $\eta$ of a quantum Stirling heat engine as a function of the ratio $D_1/D_2$ under different conditions, compared to the Carnot and Curzon–Ahlborn efficiencies [54]. Comparing these efficiencies benchmarks the quantum Stirling heat engine’s performance against established theoretical limits and provides insight into the practical and theoretical benefits of utilizing quantum effects in heat engines. We plot the efficiency $\eta$ of this quantum Stirling heat engine as a function of $D_1/D_2$ for $c_1=4c_2$ and $J_2=1.8J_1$, with (a) $T_h=4T_c$ and (b) $T_h=2T_c$. As can be seen, by increasing the ratio of $D_1/D_2$, the efficiency can surpass the Curzon–Ahlborn efficiency and achieve the Carnot limit asymptotically.

Figure 3

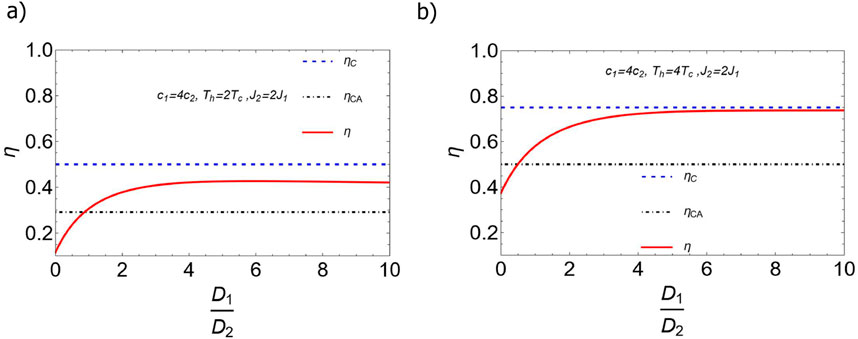
Figure 3. (Color online) Efficiency of the quantum Stirling heat engine as a function of $D_1/D_2$ is compared with the efficiencies of the Carnot $({\eta }_C)$ and Curzon-Ahlborn $({\eta }_{CA})$ [54] systems with (A) $T_h=4T_c$, $c_1=4c_2$ and $J_2=1.8J_1$, (B) $T_h=2T_c$, $c_1=4c_2$ and $J_2=2.5J_1$.

Furthermore, in order to compare our results with previous implementations of other quantum cycles [27], we provide a detailed comparison based on the efficiency as a function of the Dzyaloshinskii-Moriya (DM) interaction parameter $D$. In Figure 4, the solid red line represents the efficiency of our quantum Stirling engine model ${\eta }_D$, using the parameters reported in reference [27], while the data points correspond to the efficiency results $\eta$ and their respective upper bounds $et{a}_{ub}$ from the quantum Otto cycle analyzed by Zhao et al. [27].

Figure 4

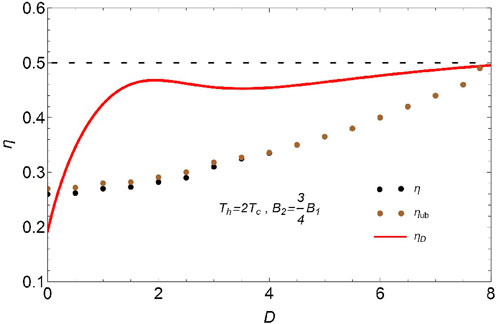
Figure 4. (Color online) Comparison of the efficiency of the quantum Stirling heat engine ${\eta }_D$ (solid red line) and the quantum Otto heat engine $\eta$ (black points), and their respective upper bounds $et{a}_{ub}$ (brown points), as a function of the Dzyaloshinskii-Moriya interaction parameter. As it can be seen, the implementation of the Stirling engine shows an increase in efficiency and reaches significantly higher values compared to the Otto engine, approaching the Carnot efficiency (0.5 - dashed black line) for high values of $D$, asymptotically.

Our results demonstrate that, given the parameter settings of the reference [27], the efficiency of the Stirling cycle surpasses the maximum efficiency of the Otto cycle for the observed range of the antisymmetric interaction. As can be seen, while the Otto cycle efficiency gradually increases at larger antisymmetric interaction, as observed from the brown and black data points, the Stirling efficiency exhibits a steeper increase, approaching asymptotically the Carnot efficiency $(\eta =0.5)$ for high values of antisymmetric interaction parameter. Therefore, the comparison highlights the distinct advantage of the Stirling cycle in leveraging the antisymmetric exchange interaction to enhance thermodynamic performance. Unlike the Otto cycle, where the efficiency improvement is constrained by the specific interaction dynamics and the heat exchange mechanisms, the Stirling cycle allows more effective utilization of the quantum resources introduced by the DM interaction.

5 Conclusion

In this letter, we study a four-level entangled quantum Stirling heat engine using a working substance composed of a two-particle Heisenberg model with Dzyaloshinskii-Moriya interaction under an external magnetic field. The effect of the antisymmetric interaction on the engine’s efficiency is studied by changing the coupling parameters and the degree of entanglement in the first and third steps of the cycle. Our findings indicate that optimizing the parameters associated with this interaction can lead to substantial improvements in efficiency, surpassing the value of Curzon–Ahlborn efficiency and reaching asymptotically the Carnot limit. These results highlight the potential for achieving higher performance levels in quantum heat engines exploring antisymmetric aspects of spin systems. Furthermore, our research suggests that fine-tuning the entanglement level in conjunction with the coupling parameters can result in even greater enhancements in efficiency. This demonstrates the intricate relationship between quantum effects and thermodynamic performance in spin-based systems.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

HR-S: Writing–original draft, Writing–review and editing. CC: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. C. Cruz thanks the Fundação de Amparo à Pesquisa do Estado da Bahia - FAPESB for its financial support (grant numbers APP0041/2023 and PPP006/2024).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Myers NM, Abah O, Deffner S, Quantum thermodynamic devices: from theoretical proposals to experimental reality. AVS Quantum Sci (2022) 4:027101. doi:10.1116/5.0083192

CrossRef Full Text | Google Scholar

2. Ptaszynski K. Non-Markovian thermal operations boosting the performance of quantum heat engines. Phys Rev E (2022) 106:014114. doi:10.1103/PhysRevE.106.014114

PubMed Abstract | CrossRef Full Text | Google Scholar

3. xiang Deng G, Ai H, Wang B, Shao W, Liu Y, Cui Z. Exploring the optimal cycle for a quantum heat engine using reinforcement learning. Phys Rev A (2024) 109:022246. doi:10.1103/physreva.109.022246

CrossRef Full Text | Google Scholar

4. Acharyya M, Chakrabarti BK. Quantum Ising heat engines: a mean field study. The Eur Phys J B (2024) 97:45. doi:10.1140/epjb/s10051-024-00681-9

CrossRef Full Text | Google Scholar

5. Rastegar-Sedehi H, Cruz C. Exploring entanglement effects in a quantum stirling heat engine. Physica Scripta (2024) 99:125936. doi:10.1088/1402-4896/ad8d8e

CrossRef Full Text | Google Scholar

6. Altintas F. Comparison of the coupled quantum Carnot and Otto cycles. Physica A: Stat Mech its Appl (2019) 523:40–7. doi:10.1016/j.physa.2019.01.144

CrossRef Full Text | Google Scholar

7. Peterson J, Batalhão TB, Herrera M, Souza AM, Sarthour RS, Oliveira IS, et al. Experimental characterization of a spin quantum heat engine. Phys Rev Lett (2019) 123:240601. doi:10.1103/physrevlett.123.240601

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Çakmak S. Benchmarking quantum Stirling and Otto cycles for an interacting spinsystem. J Opt Soc America B (2022) 39:1209. doi:10.1364/josab.447206

CrossRef Full Text | Google Scholar

9. Pili AHB, Khordad R, Sedehi HRR. Quantum Stirling heat engine in two-coupled-qubit Heisenberg XYZ model. Eur Phys J Plus (2023) 138:871. doi:10.1140/epjp/s13360-023-04516-x

CrossRef Full Text | Google Scholar

10. Pili AHB, Khordad R, Sedehi HRR, Sharifzadeh M. Influences of homogeneous and inhomogeneous magnetic fields on the performance of a quantum Stirling heat engine. Physica B: Condensed Matter (2024) 678:415748. doi:10.1016/j.physb.2024.415748

CrossRef Full Text | Google Scholar

11. Rojas O, Rojas M. Quantum machines using Cu₃-like compounds modeled by Heisenberg antiferromagnetic in a triangular ring. arXiv preprint arXiv:2406.01340 (2024). doi:10.48550/arXiv.2406.01340

CrossRef Full Text | Google Scholar

12. Feldmann T, Kosloff R. Characteristics of the limit cycle of a reciprocating quantum heat engine. Phys Rev E (2004) 70:046110. doi:10.1103/physreve.70.046110

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Rezek Y, Kosloff R. Irreversible performance of a quantum harmonic heat engine. New J Phys (2006) 8:83. doi:10.1088/1367-2630/8/5/083

CrossRef Full Text | Google Scholar

14. Altintas F, Hardal AÜC, Müstecaplıoglu ÖE. Phys Rev E (2014) 90:032102. doi:10.1103/PhysRevE.90.032102

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Insinga A, Andresen B, Salamon P. Thermodynamical analysis of a quantum heat engine based on harmonic oscillators. Phys Rev E (2016) 94:012119. doi:10.1103/physreve.94.012119

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Lin B, Chen J. Performance analysis of an irreversible quantum heat engine working with harmonic oscillators. Phys Rev E (2003) 67:046105. doi:10.1103/physreve.67.046105

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Kosloff R, Rezek Y. The quantum harmonic Otto cycle. Entropy (2017) 19:136. doi:10.3390/e19040136

CrossRef Full Text | Google Scholar

18. Huang X, Xu H, Niu X, Fu Y. A special entangled quantum heat engine based on the two-qubit Heisenberg XX model. Physica Scripta (2013) 88:065008. doi:10.1088/0031-8949/88/06/065008

CrossRef Full Text | Google Scholar

19. Stefanatos D. Optimal efficiency of a noisy quantum heat engine. Phys Rev E (2014) 90:012119. doi:10.1103/physreve.90.012119

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Huang XL, Wang T, Yi XX. Quantum Brayton cycle with coupled systems as working substance. Phys Rev E (2013) 87:012144. doi:10.1103/physreve.87.012144

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Khlifi Y, Allati AE, Salah A, Hassouni Y. Quantum heat engine based on spin isotropic Heisenberg models with Dzyaloshinskii–Moriya interaction. Int J Mod Phys B (2020) 34:2050212. doi:10.1142/S0217979220502124

CrossRef Full Text | Google Scholar

22. Chen L, Liu X, Wu F, Xia S, Feng H. Exergy-based ecological optimization of an irreversible quantum Carnot heat pump with harmonic oscillators. Physica A: Stat Mech its Appl (2020) 537:122597. doi:10.1016/j.physa.2019.122597

CrossRef Full Text | Google Scholar

23. Çakmak S. A feasible quantum heat engine driven by dipole-dipole interaction. Phys Lett A (2022) 422:127796. doi:10.1016/j.physleta.2021.127796

CrossRef Full Text | Google Scholar

24. Khedif Y, Errehymy A, Daoud M. On the thermal nonclassical correlations in a two-spin XYZ Heisenberg model with Dzyaloshinskii–Moriya interaction. Eur Phys J Plus (2021) 136:336. doi:10.1140/epjp/s13360-021-01254-w

CrossRef Full Text | Google Scholar

25. Huang X, Sun Q, Guo D, Yu Q. Quantum Otto heat engine with three-qubit XXZ model as working substance. Physica A: Stat Mech Appl (2018) 491:604–12. doi:10.1016/j.physa.2017.09.104

CrossRef Full Text | Google Scholar

26. Purkait C, Biswas A. Performance of Heisenberg-coupled spins as quantum Stirling heat machine near quantum critical point. Physica A: Stat Mech Appl (2022) 442:128180. doi:10.1016/j.physleta.2022.128180

CrossRef Full Text | Google Scholar

27. Zhao L-M, Zhang G-F. Entangled quantum Otto heat engines based on two-spin systems with the Dzyaloshinski–Moriya interaction. Quan Inf Process (2017) 16:216. doi:10.1007/s11128-017-1665-0

CrossRef Full Text | Google Scholar

28. Camati PA, Santos JFG, Serra R. Coherence effects in the performance of the quantum Otto heat engine. Phys Rev A (2018) 99:062103. doi:10.1103/PhysRevA.99.062103

CrossRef Full Text | Google Scholar

29. Brandner K, Bauer M, Seifert U. Universal coherence-induced power losses of quantum heat engines in linear response. Phys Rev Lett (2017) 119(17):170602. doi:10.1103/physrevlett.119.170602

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Dorfman K, Xu D, Cao J. Efficiency at maximum power of a laser quantum heat engine enhanced by noise-induced coherence. Phys Rev E (2018) 97(4-1):042120. doi:10.1103/physreve.97.042120

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Rahav S, Harbola U, Mukamel S. Heat fluctuations and coherences in a quantum heat engine. Phys Rev A (2012) 86:043843. doi:10.1103/physreva.86.043843

CrossRef Full Text | Google Scholar

32. Shi Y-H, Shi H-L, Wang X-H, Hu M, Liu S, Yang W-L, et al. Quantum coherence in a quantum heat engine. J Phys A: Math Theor (2019) 53:085301. doi:10.1088/1751-8121/ab6a6b

CrossRef Full Text | Google Scholar

33. Aimet S, Kwon H. Engineering a heat engine purely driven by quantum coherence. Phys Rev A (2022) 107:012221. doi:10.1103/PhysRevA.107.012221

CrossRef Full Text | Google Scholar

34. Thomas G, Johal RS. Coupled quantum Otto cycle. Phys Rev E (2011) 83:031135. doi:10.1103/physreve.83.031135

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Ma Y-H, Su S-H, Sun C-P. Quantum thermodynamic cycle with quantum phase transition. Phys Rev E (2017) 96:022143. doi:10.1103/physreve.96.022143

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Serafini G, Zippilli S, Marzoli I. Optomechanical Stirling heat engine driven by feedback-controlled light. Phys Rev A (2020) 102:053502. doi:10.1103/physreva.102.053502

CrossRef Full Text | Google Scholar

37. Yin Y, Chen L, Wu F. Performance of quantum Stirling heat engine with numerous copies of extreme relativistic particles confined in 1D potential well. Physica A: Stat Mech its Appl (2018) 503:58–70. doi:10.1016/j.physa.2018.02.202

CrossRef Full Text | Google Scholar

38. Gupt N, Bhattacharyya S, Ghosh A. Statistical generalization of regenerative bosonic and fermionic Stirling cycles. Phys Rev E (2021) 104:054130. doi:10.1103/physreve.104.054130

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Asadian M, Ahadpour S, Mirmasoudi F. Quantum correlated heat engine in XY chain with Dzyaloshinskii–Moriya interactions. Scientific Rep (2022) 12:7081. doi:10.1038/s41598-022-11146-3

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Cruz C, Rastegar-Sedehi H-R, Anka MF, de Oliveira TR, Reis M. Quantum science and technology, 8 (2023).035010.

Google Scholar

41. Cruz C, Alves Á, dos Santos R, Soares-Pinto D, de Jesus J, de Almeida J, et al. Influence of the external pressure on the quantum correlations of molecular magnets. Europhysics Lett (2017) 117:20004. doi:10.1209/0295-5075/117/20004

CrossRef Full Text | Google Scholar

42. Myers NM, McCready J, Deffner S. Quantum heat engines with singular interactions. Symmetry (2021) 13:978. doi:10.3390/sym13060978

CrossRef Full Text | Google Scholar

43. Sur S, Ghosh A. Quantum advantage of thermal machines with bose and fermi gases. Entropy (2023) 25:372. doi:10.3390/e25020372

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Singh V. Optimal operation of a three-level quantum heat engine and universal nature of efficiency. Phys Rev Res (2020) 2:043187. doi:10.1103/PHYSREVRESEARCH.2.043187

CrossRef Full Text | Google Scholar

45. Xu H-G, Jin J, Neto GDM, de Almeida NG. Universal quantum Otto heat machine based on the Dicke model. Phys Rev E (2024) 109:014122. doi:10.1103/physreve.109.014122

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Ono K, Shevchenko SN, Mori T, Moriyama S, Nori F. Analog of a quantum heat engine using a single-spin qubit. Phys Rev Lett (2020) 125 16:166802. doi:10.1103/PhysRevLett.125.166802

PubMed Abstract | CrossRef Full Text | Google Scholar

47. de Assis RJ, Sales JS, da Cunha JAR, de Almeida NG. Universal two-level quantum Otto machine under a squeezed reservoir. Phys Rev E (2020) 102:052131. doi:10.1103/physreve.102.052131

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Chatterjee S, Koner A, Chatterjee S, Kumar C. Temperature-dependent maximization of work and efficiency in a degeneracy-assisted quantum Stirling heat engine. Phys Rev E (2021) 103:062109. doi:10.1103/physreve.103.062109

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Solfanelli A, Falsetti M, Campisi M. Nonadiabatic single-qubit quantum Otto engine. Phys Rev B (2020) 101:054513. doi:10.1103/physrevb.101.054513

CrossRef Full Text | Google Scholar

50. Wootters WK. Entanglement of formation of an arbitrary state of two qubits. Phys Rev Lett (1998) 80:2245–8. doi:10.1103/physrevlett.80.2245

CrossRef Full Text | Google Scholar

51. Hill S, Wootters WK. Entanglement of a pair of quantum bits. Phys Rev Lett (1997) 78:5022–5. doi:10.1103/physrevlett.78.5022

CrossRef Full Text | Google Scholar

52. Horodecki R, Horodecki P, Horodecki M, Horodecki K. Quantum entanglement. Rev Mod Phys (2009) 81:865–942. doi:10.1103/revmodphys.81.865

CrossRef Full Text | Google Scholar

53. Cruz C, Soares-Pinto D, Brandao P, dos Santos A, Reis M. Carboxylate-based molecular magnet: one path toward achieving stable quantum correlations at room temperature. Europhysics Lett (2016) 113:40004. doi:10.1209/0295-5075/113/40004

CrossRef Full Text | Google Scholar

54. Curzon FL, Ahlborn B. Efficiency of a Carnot engine at maximum power output. Am J Phys (1975) 43:22–4. doi:10.1119/1.10023

CrossRef Full Text | Google Scholar