Weak measurements enhancing the quantum information facets of a driven Unruh–DeWitt detector

We developed a Hermitian operator representation of the Unruh channel for a driven accelerated detector in the presence of external noise. This representation is then used to provide a generalized analytical approach to a non-inertial evolution subjected to quantum weak measurements. The quantum information facets were then improved by performing weak measurements before and after the quantum channel. The external noise was modeled using a phase damping channel. The prominent oscillations of the quantum information are caused by vacuum fluctuations of the quantum fields coupled to the detector. Steady values are obtained for the quantum coherence and quantum Fisher information using the Unruh effect. Thus, quantum weak measurements can effectively suppress the decoherence induced by the relativistic acceleration. By comparing with cases without weak measurements, we demonstrate that there exist some regions with optimal measurement strengths that enhance the quantum coherence and quantum Fisher information. The effects of conditional improvement on the quantum information facets are still obvious in the presence of external noise.

1 Introduction

The Unruh–DeWitt (UdW) model [1, 2] has been widely used in the study of quantum field theory in curved spacetime. One of the great achievements of this model is based on witnessing the Unruh effect [3, 4]. In recent years, predicting the Unruh effect has become an active topic through observation of the relativistic acceleration motion in Minkowski vacuum. Researchers have realized the roles of quantum simulations [5, 6] as practical methods for studying quantum physics in accelerated systems. Meanwhile, such approaches are also expected to be utilized in the domain of black hole physics [7, 8], cosmology [9], and particle physics [10, 11]. With regard to the Unruh effect, it has been reported that for observing the thermal effect of 1 K, the system acceleration must satisfy the condition of ${10}^{21}m/s^2$ [12]. These effects are often difficult to observe owing to the complexity of the experimental conditions. By treating the atom as an open quantum system, the modification of vacuum fluctuations can be detected by measuring the geometric phase [13, 14]. The acceleration of the atom can decline to ${10}^{7}m/s^2$; this condition reduces the difficulty of realization and provides a new scheme for observing the quantum effects. In this work, we reveal some non-inertial effects indirectly by measuring the quantum information through quantum characteristics like quantum coherence and quantum Fisher information.

It is well known that quantum coherence plays a crucial role in quantum mechanics [15–19], making it possible to complete operations or tasks that are impossible to achieve with classical mechanical systems. Meanwhile, quantum coherence is regarded to have non-classical features and has been widely investigated by researchers as it has attracted much attention as an available physical resource. On the basis of feasibility experiments, we consider the $l_1$-norm coherence method to describe the mechanisms of quantum coherence. In addition to quantum coherence, we introduce a method for parameter estimation accuracy through the quantum Fisher information [22, 23]. We demonstrate the quantum effects indirectly from the perspective of quantum measurements. The Unruh effect produces a decoherence-like effect that can cause destruction of quantum information [24–26]. In an open quantum system, decoherence [27–29] is an inevitable phenomenon owing to interactions with the external environment. This leads to the decay of quantum correlation, which is the basic resource for quantum information processing. This result has motivated us to seek applicable methods to improve the quantum coherence and quantum Fisher information in relativistic acceleration motions as well as the means to achieve it. In this work, we introduce a method for suppressing the effects of decoherence using weak measurements and measurement reversal [30–33]. Weak measurement is an emerging quantum measurement technique that has shown great potential and application value for quantum information and precision measurements owing to its ability to obtain useful information while reducing the interference in quantum systems. Specifically, the advantages of weak measurements can be utilized when detecting a small number of photons. This powerful approach can effectively compensate for the shortcomings of the present detectors and has been experimentally implemented using optical methods and solid-state quantum control techniques over the last few years [34, 35]. Moreover, probabilistic measurement reversal has already been demonstrated on a superconducting phase qubit or photonic qubit. However, using measurement protocols to enhance quantum coherence remains a challenge. Our plan here is to set up a two-level atom coupled to a fluctuating vacuum scalar field in the Minkowski spacetime. The modification of vacuum fluctuations can be induced by accelerating the UdW model. We compare the variations of quantum coherence and quantum Fisher information by adding weak measurements and measurement reversal before and after the atom coupled to the environment, respectively. We expect that the system will inevitably be affected by other external factors in the process of evolution, so we examine what happens when the system is affected by multiple environments. The idea of multiple environments [36–38], such as phase damping (PD) noise, is introduced in the present work in the context of relativistic accelerated motion [39]. We examine whether the effects of weak measurements in multiple environments correspond with those of relativistic accelerated motion. We further analyze the effects of weak measurements on quantum coherence and quantum Fisher information in the context of multiple environments to obtain high-performance quantum resources.

The remainder of this paper is organized as follows. In Section 2, we mainly explain the dynamic evolution of the accelerated UdW model in an open quantum system and introduce the quantum coherence and quantum Fisher information facets. In Section 3, we introduce the approaches of weak measurement and measurement reversal to enhance the quantum information under relativistic accelerated motion. In Section 4, we explore the improvement of quantum information facets via weak measurements under multiple environments. Finally, we discuss our findings and conclusions in the last section.

2 Hermitian operator representation of the Unruh channel and quantum information facets

We formulate an Unruh channel for a two-level accelerated atom moving along a spatial trajectory using Hermitian operators. The Unruh channel characterizes relativistic evolution and is linearly coupled to a quantum scalar field through simple monopole interactions. This model can be driven using classical coherent fields. Herein, we consider the model inside a cylindrical electromagnetic cavity of radius R with a large length. The uniformly accelerating trajectory of motion can be expressed by the following path [40]:

$x\left(\tau \right)=\left(\frac{1}{a}\sinh \left(a\tau \right),\frac{1}{a}\cosh \left(a\tau \right),\mathrm{0,0}\right)(1)$

In addition, we assume that the interaction between the uniformly accelerated two-level atom and scalar field is weak. The total Hamiltonian of the system can thus be expressed as

$H=H^{\left(S\right)}+H^{\left(f\right)}+H^{\left(I\right)}(2)$

$H_S=\frac{1}{2}\mathrm{\Omega }{\sigma }_1$ According to Equation 2, is the Hamiltonian of the two-level atom, where $\mathrm{\Omega }$ is the transition between the excited and ground states and ${\sigma }_1$ is the Pauli operator. Here, ${\sigma }_1={\sigma }^{+}+{\sigma }^{-}$, where ${\sigma }^{+}$ and ${\sigma }^{-}$ are the atomic rising and lowering operators, respectively. $H^{\left(f\right)}={\displaystyle {\sum }_k}{\omega }_k{\varphi }_k^{+}\left(x\right){\varphi }_k^{-}\left(x\right)$ is the Hamiltonian of the scalar field, where ${\omega }_k$ is the vibration mode. $H^{\left(I\right)}=\lambda \left({\sigma }^{+}+{\sigma }^{-}\right)\mathrm{\Phi }\left(x\left(\tau \right)\right)$ denotes the interaction between the atom and quantum scalar field. The operator $\mathrm{\Phi }\left(x\left(\tau \right)\right)$ represents the external field, which is determined using the massless Klein–Gordon equation. This can be expanded as ${\mathrm{\Phi }}_{\mu }\left(x\right)={\displaystyle {\sum }_{k=1}^N}[{\chi }_{\mu }^k{\varphi }_k^{-}\left(x\right)+{\chi }_{\mu }^k{\varphi }_k^{+}\left(x\right)]$, where the field operators for positive-energy ${\varphi }_k^{+}\left(x\right)$ and negative-energy ${\varphi }_k^{-}\left(x\right)$ are related to a set of $N$ independent and massless scalar fields, and ${\chi }_{\mu }^k$ are the complex coefficients. In the framework of the moving model, the reduced density matrix $\rho \left(\tau \right)$ can be described using a quantum master equation in the Kossakowski–Lindblad form as

$\frac{\partial }{\partial \tau }\rho \left(\tau \right)=-i\left[H_{\mathit{eff}}^{\left(S\right)},\rho \left(\tau \right)\right]+\frac{1}{2}{\displaystyle \sum _{i,j=1}^3}{a}_{ij}{D}_{ij}\left[\rho \left(\tau \right)\right],(3)$

where the dissipator is $D_{ij}\left(\rho \right)=2{\sigma }_j\rho {\sigma }_i-{\sigma }_i{\sigma }_j\rho -\rho {\sigma }_i{\sigma }_j$, and ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$ are the three components of the Pauli operators from Equation 3. The Kossakowski matrix $a_{ij}$ takes the general form

$\begin{array}{ll}\hfill a_{ij}& =A{\delta }_{ij}-iB{\epsilon }_{\mathit{ijn}}{\delta }_{n1}+C{\delta }_{i1}{\delta }_{j1}\hfill \\ \hfill A& =\frac{{\lambda }^2}{2}\left(\mathcal{G}\left(\mathrm{\Omega }\right)+\mathcal{G}\left(-\mathrm{\Omega }\right)\right)\hfill \\ \hfill B& =\frac{{\lambda }^2}{2}\left(\mathcal{G}\left(\mathrm{\Omega }\right)-\mathcal{G}\left(-\mathrm{\Omega }\right)\right)\hfill \\ \hfill C& ={\lambda }^2\mathcal{G}\left(0\right)-A,\hfill \end{array}(4)$

The decay matrix elements $a_{ij}$ and effective Hamiltonian $H_{\mathit{eff}}$ are determined through Fourier and Hilbert transformations, respectively. The detailed process is provided in the Supplementary Appendix. By neglecting the Lamb shift term, the effective Hamiltonian $H_{\mathit{eff}}$ can be written as $H_{\mathit{eff}}^{\left(S\right)}=\frac{1}{2}[\mathrm{\Omega }+i{\lambda }^2\left(\mathcal{K}\left(-\mathrm{\Omega }\right)-\mathcal{K}\left(\mathrm{\Omega }\right)\right)]\left({\sigma }^{+}+{\sigma }^{-}\right)$.

Here, we study the relativistic accelerated motion, and the model is moving along a straight path in the x direction with uniform acceleration according to Equation 1. Therefore, we can derive the following decay parameters by Equation 4:

$\begin{array}{ll}\hfill A& =\frac{{\lambda }^2\mathrm{\Omega }}{4\pi }\coth \left(\frac{\pi \mathrm{\Omega }}{a}\right)\hfill \\ \hfill B& =\frac{{\lambda }^2\mathrm{\Omega }}{4\pi }\hfill \\ \hfill C& =\frac{{\lambda }^{2}a}{4{\pi }^2}-A,\hfill \end{array}(5)$

To illustrate the evolved state of the model perfectly, we use the Bloch vector instead of the reduced density matrix $\rho \left(\tau \right)$. The density matrix $\rho$can be expressed as $\rho =\frac{1}{2}\left(I+{\displaystyle {\sum }_{j=1}^3}{r}_j{\sigma }_j\right)$. According to the master equation, we can conveniently rewrite a Schrodinger-like equation for the Bloch vector as follows:

$\frac{d}{d\tau }\overrightarrow{r}\left(\tau \right)=-2H\cdot \overrightarrow{r}\left(\tau \right)+\overrightarrow{\chi }(6)$

where $H=\left(\begin{array}{ccc}\hfill 2A\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 2A+C\hfill & \hfill \mathrm{\Omega }/2\hfill \\ \hfill 0\hfill & \hfill -\mathrm{\Omega }/2\hfill & \hfill 2A+C\hfill \end{array}\right)$ is a decay matrix that depends on the effective Hamiltonian $H_{\mathit{eff}}$ and the real part of $a_{ij}$. $\vec{\chi }=\left(\begin{array}{c}\hfill -4B\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)$ is the inhomogeneous vector derived from the imaginary part of the Kossakowski matrix. Thus, we propose a quantum channel to describe the dynamic evolution of the UdW model using the Bloch vector. Now, the mapping matrix of the quantum channel is given by $\mathrm{\Gamma }\left(\tau \right)=\exp \left(-2\mathcal{H}\tau \right)=\left(\begin{array}{ccc}\hfill e^{-4A\tau }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{-2\left(2A+C\right)\tau }\cos \mathrm{\Omega }\tau \hfill & \hfill -e^{-2\left(2A+C\right)\tau }\sin \mathrm{\Omega }\tau \hfill \\ \hfill 0\hfill & \hfill e^{-2\left(2A+C\right)\tau }\sin \mathrm{\Omega }\tau \hfill & \hfill e^{-2\left(2A+C\right)\tau }\cos \mathrm{\Omega }\tau \hfill \end{array}\right)$, and the mapping vector is $\vec{\mathrm{\Lambda }}\left(\tau \right)=\frac{1}{2}\left[I-\mathrm{\Gamma }\left(\tau \right)\right]H^{-1}\cdot \vec{\chi }=\left(\begin{array}{c}\hfill \frac{B}{A}\left(e^{-4A\tau }-1\right)\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)$.Some parameters depend on Equation 5. We assume that the initial state of the atom is $\left|{\phi }_0\right.⟩=\cos \frac{\theta }{2}\left|1\right.⟩+e^{i\varphi }\sin \frac{\theta }{2}\left|0\right.⟩$ so that the Bloch vector of the initial state can be expressed as $\vec{r}\left(0\right)=\left(\sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta \right)$. Then, we calculate the time-dependent evolved Bloch vector by Equation 6 and the results are as follows:

$\begin{array}{c}\vec{r}\left(\tau \right)=\mathrm{\Gamma }\left(\tau \right)\cdot \vec{r}\left(0\right)+\vec{\mathrm{\Lambda }}\left(\tau \right)\hfill \\ =\left(\begin{array}{c}\hfill e^{-4A\tau }\sin \theta \cos \varphi +\frac{B}{A}\left(e^{-4A\tau }-1\right)\hfill \\ \hfill e^{-2\left(2A+C\right)\tau }\left(\cos \mathrm{\Omega }\tau \sin \theta \sin \varphi -\sin \mathrm{\Omega }\tau \cos \theta \right)\hfill \\ \hfill e^{-2\left(2A+C\right)\tau }\left(\sin \mathrm{\Omega }\tau \sin \theta \sin \varphi +\cos \mathrm{\Omega }\tau \cos \theta \right)\hfill \end{array}\right)\hfill \end{array}(7)$

It is very important that we use a proper evaluation method to measure the quantum coherence of the model. We consider the $l_1$-norm for measuring the coherence, that is, the absolute values of all the off-diagonal elements of the density matrix. Generally, the $l_1$-norm is expressed as $C_{l_1}\left(\rho \right)={\displaystyle {\sum }_{j\ne i}}\left|{\rho }_{ij}\right|$, where ${\rho }_{ij}$ denotes the element of the state density matrix. We can also represent the $l_1$-norm using the components of the Bloch vector, such that the quantum coherence of the model is given by

$C_{l_1}\left(\rho \right)=\sqrt{r_1^2+r_2^2}(8)$

where $r_k$ is the k-th component of the Bloch vector. Then, the quantum coherence with uniformly accelerated motion by Equation 8 can be calculated as

$C_a=\sqrt{{\left[e^{-4A\tau }\sin \theta \cos \varphi +L_1\right]}^2+{\left[J_1\left(\cos \mathrm{\Omega }\tau \sin \theta \sin \varphi -\sin \mathrm{\Omega }\tau \cos \theta \right)\right]}^2}(9)$

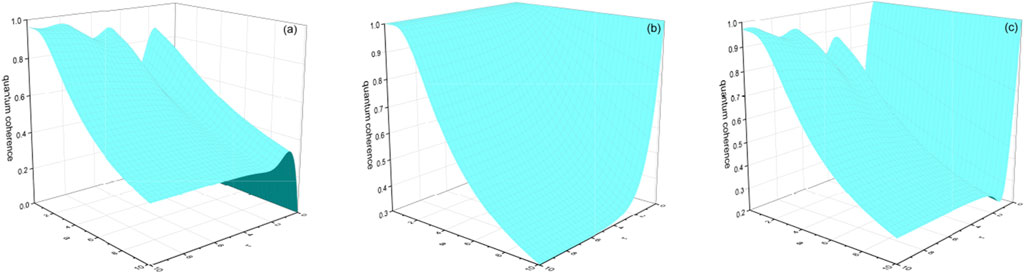
where $L_1=\frac{B}{A}\left(e^{-4A\tau }-1\right)$and $J_1=e^{-2\left(2A+C\right)\tau }$. It can be easily found that quantum coherence is dependent on the evolution of the parameterized states, which are closely related to the initial quantum properties of the atoms. In short, the changes to $\theta$ and $\varphi$ of the initial state will have a slight effect on the oscillation trend of the quantum coherence. Figure 1 shows the evolution of quantum coherence in the context of relativistic accelerated motion. The Unruh effect induced by the accelerated motion leads to attenuation of quantum coherence mainly owing to the vacuum fluctuations of the quantum fields coupled to the UdW detector. To illustrate the evolution of quantum coherence, we further analyze different situations from various perspectives. The changes to $\theta$ are considered first. When the initial state is pure, that is, $\theta =0,\varphi =\pi$, the resulting quantum coherence can be simplified as $C_a=\sqrt{{\left[\frac{B}{A}\left(e^{-4A\tau }-1\right)\right]}^2+{\left[e^{-2(2A+C)}\sin \mathrm{\Omega }\tau \right]}^2}$. From Figure 1A, it is seen that quantum coherence oscillates constantly with time and decays to a stable thermal equilibrium state based on the energy dissipation and quantum vacuum fluctuations. When the initial state is the maximum entangled state, that is, $\theta =\frac{\pi }{2},\varphi =\pi$, the quantum coherence can be written as $C_a=\left|-e^{-4A\tau }+\frac{B}{A}\left(e^{-4A\tau }-1\right)\right|$. It is observed that the quantum coherence tends to be relatively stable at the beginning of the dynamic evolution (Figure 1B). However, the quantum coherence gradually decays to a stable value under accelerated motion. Then, the effects of changes to $\varphi$ are considered. When $\theta =\frac{\pi }{2},\varphi =\frac{\pi }{2}$, the quantum coherence can be simplified as $C_a=\sqrt{{\left[\frac{B}{A}\left(e^{-4A\tau }-1\right)\right]}^2+{\left[e^{-2\left(2A+C\right)}\cos \mathrm{\Omega }\tau \right]}^2}$. It is observed that the oscillation of quantum coherence with time is more obvious when a tends to zero owing to the appearance of the oscillation term. At this point, we calculate $\frac{d{C}_a}{d\tau }=0$ by a numerical method. It is seen from Figure 1C that there is a minimum breakpoint. In the physical context, the energy provided is more than the energy dissipated at a small moment when the system interacts with the environment. Therefore, the quantum coherence value will still be improved during the very short period. The dissipation capacity becomes stronger with continuous evolution, such that the quantum coherence tends to decay. As the evolution progresses, the quantum coherence gradually decays to 0.

Figure 1

Figure 1. Evolution of quantum coherence is plotted as a function of time $\tau$ and acceleration a. (A) The parameters are chosen as $\theta =0$, $\varphi =\pi$, $\mathrm{\Omega }=1$, $\lambda =1$. (B) The parameters are chosen as $\theta =\frac{\pi }{2}$, $\varphi =\pi$, $\mathrm{\Omega }=1$, $\lambda =1$. (C) The parameters are chosen as $\theta =\frac{\pi }{2}$, $\varphi =\frac{\pi }{2}$, $\mathrm{\Omega }=1$, $\lambda =1$.

On the other hand, the Hamiltonian of the model can be expressed as $H_0=\frac{\mathrm{\Omega }}{2}\left({\sigma }^{+}+{\sigma }^{-}\right)$ when a tends toward 0. The unitary evolution operator can be written as $U\left(\tau \right)={\displaystyle {\sum }_{i=\mathrm{1,2}}}\exp \left(-i{\lambda }_i\tau \right)\left|{\phi }_i\right.⟩\left.⟨{\phi }_i\right|$. Under the assumption that the initial state is $\left|\mathrm{\Phi }\left(0\right)\right.⟩=\frac{1}{\sqrt{2}}\left(\left|e\right.⟩+e^{i\varphi }\left|g\right.⟩\right)$, the evolved state for an arbitrary interval $\tau$ can be written as $\left|\mathrm{\Phi }\left(\tau \right)\right.⟩=U\left(\tau \right)\left|\mathrm{\Phi }\left(0\right)\right.⟩=\exp \left(-\frac{i}{\hslash }{H}_0\tau \right)\left|\mathrm{\Phi }\left(0\right)\right.⟩=\frac{1}{\sqrt{2}}\left(\cos \frac{\mathrm{\Omega }}{2}\tau -i\sin \frac{\mathrm{\Omega }}{2}\tau \right)\left(\left|e\right.⟩+e^{i\varphi }\left|g\right.⟩\right)$. It is noted that the oscillatory behavior is dependent on different parameterized states. In quantum mechanics, the energy changes transiently at any position owing to quantum fluctuations; such small fluctuations cause the particles to remain in a fuzzy state. This uncertainty is one of the fundamental tenets of quantum mechanics. Similarly, the argument is valid for the situation where a approaches infinity. It is thus concluded that the quantum coherence gradually decays to 0 with evolution.

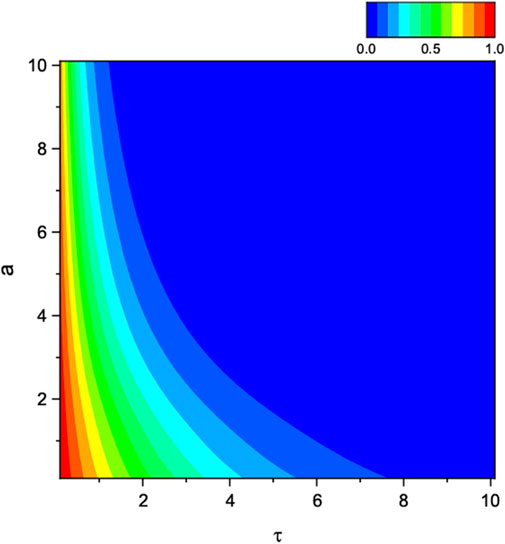
In addition to quantum coherence, which helps with observation of the Unruh effect, quantum Fisher information can be used to observe some non-inertial effects from the perspective of quantum measurements. In quantum statistical inference, the quantum Fisher information has great significance as a measure of the intrinsic information of the parameterized probability density. Furthermore, we introduce the quantum Fisher information for measuring the quantum information. The quantum Fisher information is used to determine the lower limit of the parameter estimation accuracy. For a general density matrix ${\rho }_{\theta }$, the quantum Fisher information about the parameter $\theta$ can be expressed as $\mathcal{F}\left(\theta \right)=Tr\left(L\rho L\right)=Tr\left(\rho L^2\right)=Tr\left({\partial }_{\theta }\rho L\right)$. Here, $L$ represents the symmetric logarithmic derivative operator. Then, the quantum Fisher information in terms of the Bloch vector is given by $F_q\left(\varphi \right)=\frac{{\left[\zeta \left(\varphi \right)\cdot {\partial }_{\varphi }\zeta \left(\varphi \right)\right]}^2}{1-{\left|\zeta \left(\varphi \right)\right|}^2}+{\left[{\partial }_{\varphi }\zeta \left(\varphi \right)\right]}^2$, where $q$ denotes quantum and $\varphi$ is the parameter to be estimated. Then, $r\left(\tau \right)$ is as given in Equation 7 and its terms are expressed by $F_1$, $F_2$, and $F_3$. We take the derivative of $r\left(\tau \right)$ to obtain ${\partial }_{\varphi }r\left(\tau \right)$, whose terms are expressed by $G_1$, $G_2$, and $G_3$ correspondingly. Then, the expression for the quantum Fisher information can be rewritten as Equation 10:

$\begin{array}{ll}\hfill F_{\varphi }& =\frac{{\left(F_1\cdot G_1+F_2\cdot G_2+F_3\cdot G_3\right)}^2}{1-\left(F_1^2+F_2^2+F_3^2\right)}+\left(G_1^2+G_2^2+G_3^2\right)\hfill \\ \hfill F_1& =e^{-4A\tau }\sin \theta \cos \varphi +\frac{B}{A}\left(e^{-4A\tau }-1\right)\hfill \\ \hfill F_2& =e^{-2\left(2A+C\right)\tau }\left(\cos \mathrm{\Omega }\tau \sin \theta \sin \varphi -\sin \mathrm{\Omega }\tau \cos \theta \right)\hfill \\ \hfill F_3& =e^{-2\left(2A+C\right)\tau }\left(\sin \mathrm{\Omega }\tau \sin \theta \sin \varphi +\cos \mathrm{\Omega }\tau \cos \theta \right)\hfill \\ \hfill G_1& =-e^{-4A\tau }\sin \theta \sin \varphi \hfill \\ \hfill G_2& =e^{-2\left(2A+C\right)\tau }\cos \mathrm{\Omega }\tau \sin \theta \cos \varphi \hfill \\ \hfill G_3& =e^{-2\left(2A+C\right)\tau }\sin \mathrm{\Omega }\tau \sin \theta \cos \varphi \hfill \end{array}(10)$

We set $\theta =\frac{\pi }{2}$ and consider $\varphi$ as the parameter to be estimated. Figure 2 shows the gradual decay of the quantum Fisher information caused by acceleration.

Figure 2

Figure 2. Quantum Fisher information is plotted as a function of time $\tau$ and acceleration a in the context of uniformly accelerated motion. The parameters are chosen as $\theta =\frac{\pi }{2}$, $\varphi =\pi$, $\mathrm{\Omega }=1$, $\lambda =1$.

3 Weak measurements enhance the quantum information of the UdW model

Quantum coherence is one of the types of available physical resources, but it is inevitably destroyed by external noise that can induce quantum decoherence. The assistive method via weak measurements and measurement reversal is introduced herein to protect the quantum states. In general, the weak measurement is of the form $M=diag\left.\left\{1,\sqrt{1-p_r}\right.\right\}$. This operation would not cause complete collapse of the quantum system, which can be recovered through some reversal operations [41]. Thus, the measurement reversal operator can be written as $N=diag\left\{\left.\sqrt{1-p},1\right\}\right.$. For simplicity, the weak measurement and measurement reversal operations can be directly expressed as $M=diag\left.\left\{1,m\right.\right\}$ and $N=diag\left.\left\{n,1\right.\right\}$, respectively, with $m,n\in \left[0+\infty \right)$. In quantum mechanics, the parameter describes the intensity of the measurement. Specifically, the parameter $m$ is related to the measurement operator $M$, which determines the degree to which the measurement affects the state of the quantum system. When $m=0$, $M$ is the projective measurement; in this case, the measurement operator $M$ causes the quantum system to collapse completely at certain eigenstates. This means that the state of the system can be completely determined after measurement and that the probability distribution of the measurement result is determined by the eigenvalues of the initial state of the system. When $m\in \left(\mathrm{0,1}\right)$ or $m\in \left(1,\infty \right)$, $M$ can be considered the measurement that partially collapses at the ground or excited state, respectively. This is a partial collapse measurement, which is a weak measurement. Here, the measurement operator $M$ is not a fully projective operator, and the measurement has little effect on the system such that the state of the quantum system only collapses partially to a certain eigenstate. This means that the state of the system still maintains a certain degree of superposition after measurement. A similar analogy is also valid for the measurement reversal $N$.

The main processes of weak measurement and measurement reversal can be described as follows. In general, we should perform two measurements of $M$ and $N$ before and after the atom enters the channel, respectively. Using the weak measurement and measurement reversal, the initial state can then be restored. Therefore, the final state [41] after two weak measurements can be expressed as ${\rho }_{\mathit{new}}=N{\mathrm{\Lambda }}_q\left(M\rho M^{+}\right)N^{+}$, where ${\mathrm{\Lambda }}_q$ denotes the mapping of the quantum channel.

Now, we analyze quantum coherence and quantum Fisher information with the weak measurement protocol under relative accelerated motion. The initial state can still be written as $\left|{\phi }_0\right.⟩=\cos \frac{\theta }{2}\left|1\right.⟩+e^{i\varphi }\sin \frac{\theta }{2}\left|0\right.⟩$. Upon adding the weak measurement before entering the uniformly accelerated environment, the normalized density matrix can be expressed as ${\rho }_M=\frac{1}{{\cos }^2\frac{\theta }{2}+m^2{\sin }^2\frac{\theta }{2}}\left(\begin{array}{cc}\hfill {\cos }^2\frac{\theta }{2}\hfill & \hfill \frac{1}{2}m{e}^{-i\varphi }\sin \theta \hfill \\ \hfill \frac{1}{2}m{e}^{i\varphi }\sin \theta \hfill & \hfill m^2{\sin }^2\frac{\theta }{2}\hfill \end{array}\right)$. Then, the density matrix can be reduced to the Bloch vector and written as ${\vec{\zeta }}^M=\left(\begin{array}{c}\hfill \frac{m\sin \theta \cos \varphi }{T_s}\hfill \\ \hfill \frac{m\sin \theta \sin \varphi }{T_s}\hfill \\ \hfill \frac{T_v}{T_s}\hfill \end{array}\right)$, where the normalized values are given by $T_s={\cos }^2\frac{\theta }{2}+m^2{\sin }^2\frac{\theta }{2}$ and $T_v={\cos }^2\frac{\theta }{2}-m^2{\sin }^2\frac{\theta }{2}$. Similarly, we add measurement reversal after the atom is coupled to the environment. The normalization of the final state can be expressed as Equation 11:

${\vec{\zeta }}^{MN}=\frac{1}{T}\left(\begin{array}{c}\hfill n\left(\frac{m\sin \theta \cos \varphi e^{-4A\tau }}{T_s}+L_1\right)\hfill \\ \hfill n\left(\frac{J_1}{T_s}\left(m\sin \theta \sin \varphi \cos \mathrm{\Omega }\tau -T_v\sin \mathrm{\Omega }\tau \right)\right)\hfill \\ \hfill \frac{1}{2}\left(\left(n^2-1\right)-\left(n^2+1\right)\frac{J_1}{T_s}\left(m\sin \theta \sin \varphi \sin \mathrm{\Omega }\tau +T_v\cos \mathrm{\Omega }\tau \right)\right)\hfill \end{array}\right)(11)$

where $L_1=\frac{B}{A}\left(e^{-4A\tau }-1\right)$ and $J_1=e^{-2\left(2A+C\right)\tau }$. Here, the normalized value can be expressed as $T=\frac{1}{2}$$\left\{\left(n^2+1\right)+\left(n^2-1\right)\frac{J_1}{T_s}\left(m\sin \theta \sin \varphi \sin \mathrm{\Omega }\tau +T_v\cos \mathrm{\Omega }\tau \right)\right\}$. Now, we can express the quantum coherence based on the $l_1$-norm as the estimate of the quantum signature of the UdW model after adding the weak measurement. This calculation can be written as Equation 12:

$C_{\mathit{aweak}}=\left|\frac{n}{T}\right|\sqrt{{\left[\frac{m\sin \theta \cos \varphi e^{-4A\tau }}{T_s}+L_1\right]}^2+{\left[\frac{J_1}{T_s}\left(m\sin \theta \sin \varphi \cos \mathrm{\Omega }\tau -T_v\sin \mathrm{\Omega }\tau \right)\right]}^2}(12)$

In this work, we compare quantum coherence with and without weak measurement. We describe the effect of weak measurement on quantum coherence through the following definition:

$\mathrm{\Delta }C=C_{\mathit{aweak}}-C_a(13)$

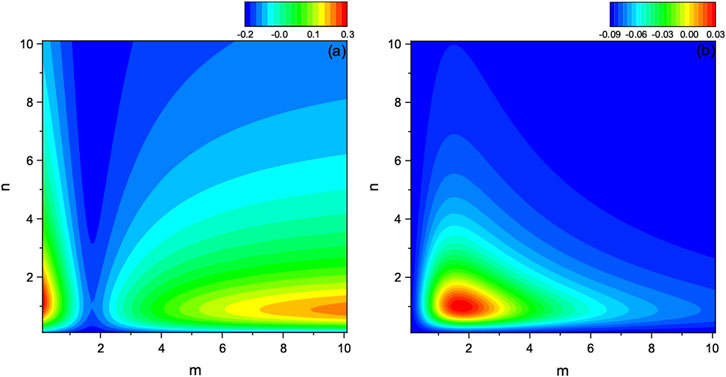
By Equation 13, if $\mathrm{\Delta }C>0$, it is considered that the weak measurement has a certain inhibitory effect on decoherence, indicating that the weak measurement indeed enhances the quantum coherence to a certain extent. If $\mathrm{\Delta }C<0$, then the opposite is considered. Figure 3 shows the plots of variation of the differences in quantum coherence and quantum Fisher information with the weak measurement parameters $m$ and $n$. The figure shows that $\mathrm{\Delta }C=0$ is a clear dividing line, and the area where $\mathrm{\Delta }C>0$ in Figure 3A indicates the presence of weak measurement. In the area where the color changes from green to a more vivid red, that is, when the parameters $m$ and $n$ are both small or when the parameter $m$ is large and $n$ is small, the difference in quantum coherence is more obvious. As evolution progresses, the influence of the environment continues to strengthen, and the role of the weak measurement gradually weakens until the evolution stabilizes.

Figure 3

Figure 3. (A) Variation of quantum coherence is plotted with weak measurement and measurement reversal. The parameters are chosen as $\theta =\frac{\pi }{3}$, $\varphi =0$, $\mathrm{\Omega }=1$, $\lambda =1$, $\tau =2$, $a=5$. (B) Variation of quantum Fisher information is plotted with weak measurement and measurement reversal. The parameters are chosen as $\theta =\frac{\pi }{3}$, $\varphi =0$, $\mathrm{\Omega }=1$, $\lambda =1$, $\tau =2$, $a=5$.

A similar method is used to analyze the quantum Fisher information under weak measurement, that is, we define it as $\mathrm{\Delta }F=F_{\mathit{aweak}}-F_a$. When $\mathrm{\Delta }F>0$, it is considered that the weak measurement improves the quantum Fisher information to a certain extent. In Figure 3B, the color ranges from yellow to a bright red, where the parameters $m$ and $n$ are small, and the effect of weak measurement is better. This indicates that weak measurements can enhance quantum coherence to a certain extent while also providing some protection for the quantum Fisher information. In theory, to obtain quantum resources with as high fidelity as possible, we can choose the conditions where the measurement values $m$ and $n$ are both small. This is because a weak measurement is essentially a probabilistic projective measurement with quantum statistical characteristics. The choice of the measurement parameters $m$ and $n$ results in some quantum statistical characteristics, which are helpful for enhancing quantum coherence. Our aim is to select a set of relatively appropriate parameters that can enhance the quantum statistical characteristics induced by weak measurements and measurement reversal. Through numerical calculations, we found that some parameters have no obvious effects on the changes to quantum statistical properties, that is, they have no effect on suppressing quantum decoherence.

4 Weak measurements enhance the quantum information in multiple environments

In the context of an open quantum system, there is increasing interest in the dynamic evolution of the system that takes into account the effects of external environments. In this work, we analyze the quantum coherence and quantum Fisher information under the influence of multiple environments. Accordingly, the effects of the proposed measurement protocol on quantum coherence and quantum Fisher information under multiple environments are explored. Herein, we consider PD noise as the external noise channel. In fact, the evolution of the quantum state can be expressed by the Kraus operator, that is, $\rho \to \rho \left(\tau \right)=\epsilon \left(\tau \right)={\sum }_i{K}_i\rho K_i^{+}$, where $K_i$ meets the condition ${\sum }_i{K}_i^{+}{K}_i=I\left(i=\mathrm{1,2}\dots ,n\right)$ and $I$ is the identity operator. We show that different environments can be expressed by different Kraus operators. Quantum states evolve from pure to mixed states under the influence of the environment, which can be represented using density operators. Accordingly, we obtain the Kraus operators of the PD channel as Equation 14:

$K_1=\sqrt{p}\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right),K_2=\sqrt{1-p}\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill \end{array}\right)(14)$

Here, $p\left(0\le p\le 1\right)$ is the range of the attenuation parameter in the PD noise channel.

In this work, we promote a more universal approach. For an arbitrary qubit state, the corresponding density matrix $\rho$ can be expressed using the vector form as $\rho =\frac{I+\vec{\zeta }\cdot \vec{\sigma }}{2}$. Here, $\vec{\zeta }$ is the Bloch vector of the state, and ${\sigma }_0$ and ${\sigma }_i\left(i=\mathrm{1,2,3}\right)$ denote the identity operator $I$ and three Pauli operators, respectively. Using the quantum channel, we describe the mapping from the initial state vector $\vec{X}=\left(1,\zeta \left(0\right)\right)$ to the evolved state vector $\vec{Y}=\left(1,\zeta \right)$ as [42]

$\vec{Y}=\mathrm{\Phi }\cdot \vec{X}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill {\vec{0}}^T\hfill \\ \hfill \vec{\lambda }\hfill & \hfill \vec{\mathrm{\Gamma }}\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1\hfill \\ \hfill {\vec{\zeta }}^{\left(0\right)}\hfill \end{array}\right)(15)$

where the vector ${\vec{0}}^T=\left(\mathrm{0,0,0}\right)$. In Equation 15, the quantum channel $\epsilon \left(\blacksquare \right)$ can determine the mapping vector $\vec{\lambda }$ and mapping matrix ${\mathrm{\Gamma }}_{ij}$, where ${\lambda }_i\left(i=\mathrm{1,2,3}\right)=Tr\left[{\sigma }_i\cdot \epsilon \left(\frac{I}{2}\right)\right]$ and ${\mathrm{\Gamma }}_{ij}\left(i,j=\mathrm{1,2,3}\right)=Tr\left[{\sigma }_i\cdot \epsilon \left(\frac{{\sigma }_j}{2}\right)\right]$. The Bloch vector of the evolved state can be obtained as $\vec{\zeta }=\mathrm{\Gamma }\cdot {\vec{\zeta }}^{\left(0\right)}+\vec{\lambda }$. From the above method, the mapping matrix and mapping vector can be respectively expressed as Equation 16:

${\mathrm{\Gamma }}_{PD}=\left(\begin{array}{ccc}\hfill 2p-1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 2p-1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),{\mathrm{\Lambda }}_{PD}=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)(16)$

in the case of the PD channel. Using this method, we can directly obtain the mapping matrix and mapping vector of the external noise without considering the initial state of the qubit.

We superimpose the effect of the external noise channel on the basis of the relative accelerated motion. We then obtain the new Bloch vector ${\vec{\zeta }}_{\mathit{new}}$, which is related to the original state as

$\begin{array}{ll}\hfill {\vec{\zeta }}_{\mathit{new}}& ={\mathrm{\Gamma }}_{PD}\cdot \vec{r}\left(\tau \right)+{\mathrm{\Lambda }}_{PD}\hfill \\ \hfill & ={\mathrm{\Gamma }}_{PD}\cdot \left(\mathrm{\Gamma }\left(\tau \right)\cdot \vec{r}\left(0\right)+\vec{\mathrm{\Lambda }}\left(\tau \right)\right)+{\mathrm{\Lambda }}_{PD}\hfill \\ \hfill & ={\mathrm{\Gamma }}_{PD}\mathrm{\Gamma }\left(\tau \right)\cdot \vec{r}\left(0\right)+{\mathrm{\Gamma }}_{PD}\vec{\mathrm{\Lambda }}\left(\tau \right)+{\mathrm{\Lambda }}_{PD}\hfill \\ \hfill & ={\mathrm{\Gamma }}_{\mathit{new}}\cdot \vec{r}\left(0\right)+{\mathrm{\Lambda }}_{\mathit{new}}\hfill \end{array}(17)$

Here, $\vec{r}\left(0\right)$and $\vec{r}\left(\tau \right)$ are as in Equation 7. From Equation 17, it can be seen that the effect of the external noise channel in the context of relative accelerated motion is encoded in ${\mathrm{\Gamma }}_{\mathit{new}}={\mathrm{\Gamma }}_{PD}\mathrm{\Gamma }\left(\tau \right)$ and ${\mathrm{\Lambda }}_{\mathit{new}}={\mathrm{\Gamma }}_{PD}\vec{\mathrm{\Lambda }}\left(\tau \right)+{\mathrm{\Lambda }}_{PD}$. By superimposing the effect of the PD channel, the Bloch vector can be expressed as Equation 18:

${\vec{\zeta }}_{PD}={\mathrm{\Gamma }}_{PD}\vec{r}\left(\tau \right)+{\mathrm{\Lambda }}_{PD}=\left(\begin{array}{c}\hfill \left(2p-1\right)\left(e^{-4A\tau }\sin \theta \cos \varphi +{Ł}_1\right)\hfill \\ \hfill \left(2p-1\right)J_1\left(\sin \theta \sin \varphi \cos \mathrm{\Omega }\tau -\cos \theta \sin \mathrm{\Omega }\tau \right)\hfill \\ \hfill J_1\left(\sin \theta \sin \varphi \sin \mathrm{\Omega }\tau +\cos \theta \cos \mathrm{\Omega }\tau \right)\hfill \end{array}\right)(18)$

and quantum coherence can be calculated as

$C_{PD}=\left|2p-1\right|\sqrt{{\left[e^{-4A\tau }\sin \theta \cos \varphi +{Ł}_1\right]}^2+{\left[J_1\left(\sin \theta \sin \varphi \cos \mathrm{\Omega }\tau -\cos \theta \sin \mathrm{\Omega }\tau \right)\right]}^2}(19)$

where ${Ł}_1=\frac{B}{A}\left(e^{-4A\tau }-1\right)$ and $J_1=e^{-2\left(2A+C\right)\tau }$. Comparing Equation 19 with Equation 9, we show that the quantum coherence is further attenuated owing to the action of the PD noise channel. From Figure 4A, we also observe that the quantum Fisher information in multiple environments is lower than that when considering only the relative accelerated motion. In other words, the effect of multiple environments further reduces the acquisition of quantum information. To obtain high-performance quantum resources as much as possible under multiple environments, the weak measurement method is also considered. The Bloch vector of the evolved state affer adding the weak measurement is expressed as Equation 20:

${\vec{\zeta }}^{\mathit{MNP}}=\frac{1}{T_{PD}}\left(\begin{array}{c}\hfill n\left(2p-1\right)\left(\frac{m{e}^{-4A\tau }\sin \theta \cos \varphi }{T_s}+{Ł}_1\right)\hfill \\ \hfill n\left(2p-1\right)\left(\frac{J_1}{T_s}\left(m\sin \theta \sin \varphi \cos \mathrm{\Omega }\tau -T_v\sin \mathrm{\Omega }\tau \right)\right)\hfill \\ \hfill \frac{1}{2}\left(\left(n^2-1\right)+\left(n^2+1\right)\frac{J_1}{T_s}\left(m\sin \theta \sin \varphi \sin \mathrm{\Omega }\tau +T_v\cos \mathrm{\Omega }\tau \right)\right)\hfill \end{array}\right)(20)$

The normalized value in the above formula can be expressed as $T_{PD}=\frac{1}{2}\left\{\left(n^2+1\right)+\left(n^2-1\right)\frac{J_1}{T_s}\left(m\sin \theta \sin \varphi \sin \mathrm{\Omega }\tau +T_v\cos \mathrm{\Omega }\tau \right)\right\}$. The quantum coherence can be expressed as

$C_{\mathit{PDweak}}=\left|\frac{nP}{T_{PD}}\right|\sqrt{{\left[\frac{m{J}_2\sin \theta \cos \varphi }{T_s}+{Ł}_1\right]}^2+{\left[\frac{J_1}{T_s}\left(m\sin \theta \sin \varphi \cos \mathrm{\Omega }\tau -T_v\sin \mathrm{\Omega }\tau \right)\right]}^2}(21)$

where $J_2=e^{-4A\tau }$ and $P=2p-1$. To show the effect of the weak measurement, we describe the result for quantum coherence as

${\mathrm{\Delta }C}_{PD}=C_{\mathit{PDweak}}-C_{PD}(22)$

where $C_{\mathit{PDweak}}$ and $C_{PD}$ are as described in Equations 19, 21, respectively. By Equation 22, if ${\mathrm{\Delta }C}_{PD}>0$, it implies that the weak measurement enhances quantum coherence to a certain extent under multiple environments with PD noise. If ${\mathrm{\Delta }C}_{PD}<0$, then the opposite is considered. We choose appropriate weak measurement parameters and plot the evolutionary trends of quantum coherence and quantum Fisher information under multiple environments. It is seen in Figure 4B that the quantum Fisher information is enhanced under weak measurement. Similarly, we define the difference analysis to study quantum coherence; we note that the part above the red line in Figure 4C indicates enhancement of quantum coherence via weak measurement. For both quantum coherence and quantum Fisher information, this enhancement is noted to become weaker with evolution of the system. In fact, we can clarify that weak measurements enhance the quantum coherence as well as quantum Fisher information under multiple environments.

Figure 4

Figure 4. (A) Quantum Fisher information is plotted under multiple environments. The parameters are chosen as $\theta =\frac{\pi }{3}$, $\varphi =0$, $\mathrm{\Omega }=1$, $\lambda =1$, $a=5$, $p=0.1$. (B) Evolution tendency of quantum Fisher information with weak measurement and measurement reversal is plotted under multiple environments. The parameters are chosen as $\theta =\frac{\pi }{3}$, $\varphi =0$, $\mathrm{\Omega }=1$, $\lambda =1$, $a=5$, $p=0.1$, $m=9$, $n=1$. (C) Evolution tendency of quantum coherence with weak measurement and measurement reversal is plotted under multiple environments. The parameters are chosen as $\theta =\frac{\pi }{3}$, $\varphi =0$, $\mathrm{\Omega }=1$, $\lambda =1$, $a=5$, $p=0.1$, $m=2$, $n=1$.

5 Discussion

We studied the quantum information of an atom coupled to the quantum scalar field in the context of relative accelerated motion using the UdW model. Accordingly, we simulated a linearly accelerated atom inside an electromagnetic cavity under certain conditions. The dynamic behavior of the detector was studied using the Hermitian operator representation. The $l_1$-norm provides an efficient means to observe the quantum coherence and quantum Fisher information as well as to evaluate the parameter estimation accuracy. We illustrate that the quantum information gradually stabilizes and decays to 0 due to the Unruh effect and presence of external noise, which are closely related to the initial quantum properties of atoms. This kind of oscillation is attributed to the vacuum fluctuations of the quantum scalar field coupled to the detector. An important feature of our work is that we provide unified treatment of the quantum channels to study the changes in quantum information using the Bloch vector. The results show that the decoherence behavior is more obvious under the superposition of quantum field noise. It is shown that quantum coherence and quantum Fisher information can be enhanced under optimal measurement strengths to a certain extent. We expect that these findings will contribute toward understanding and implementing relativistic quantum information.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and any further inquiries may be directed to the corresponding authors.

Author contributions

J-LX: conceptualization, investigation, and writing–original draft. C-JZ: writing–review and editing. JT: methodology and writing–review and editing. XH: writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by the Natural Science Foundation of China (no. 61875145) and Jiangsu Key Disciplines of the Fourteenth Five-Year Plan (no. 2021135). The authors were also supported by the Postgraduate Research and Practice Innovation Program of Jiangsu Province (no. KYCX23_3312).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. DeWitt BS. Quantum theory of gravity. I. The canonical theory. Phys Rev (1967) 160:1113–48. doi:10.1103/physrev.160.1113

CrossRef Full Text | Google Scholar

2. Brown EG, Martn-Martnez E, Menicucci NC, Mann RB. Phys Rev D (2013) 87:084062. doi:10.1103/PhysRevD.87.084062

CrossRef Full Text | Google Scholar

3. Unruh WG. Notes on black-hole evaporation. Phys Rev D (1976) 14:870–92. doi:10.1103/physrevd.14.870

CrossRef Full Text | Google Scholar

4. Crispino LCB, Higuchi A, Matsas GEA. The Unruh effect and its applications. Rev Mod Phys (2008) 80:787–838. doi:10.1103/revmodphys.80.787

CrossRef Full Text | Google Scholar

5. Feynman R. Simulating physics with computers. Int J Theor Phys (1982) 21:467–88. doi:10.1007/bf02650179

CrossRef Full Text | Google Scholar

6. Lloyd S. Universal quantum simulators. Sci. (1996) 273:1073–8. doi:10.1126/science.273.5278.1073

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Frolov VP. Two-dimensional black hole physics. Phys Rev D (1992) 46:5383–94. doi:10.1103/physrevd.46.5383

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Manikandan SK, Jordan AN. Andreev reflections and the quantum physics of black holes. Phys Rev D (2017) 96:124011. doi:10.1103/physrevd.96.124011

CrossRef Full Text | Google Scholar

9. Boersma JP. Averaging in cosmology. Phys Rev D (1998) 57:798–810. doi:10.1103/physrevd.57.798

CrossRef Full Text | Google Scholar

10. Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F, et al. Phys Rev D (2018) 98:030001. doi:10.1103/PhysRevD.98.030001

CrossRef Full Text | Google Scholar

11. Quigg C. Exploring futures for particle physics. Physics (2020) 13:156. doi:10.1103/physics.13.156

CrossRef Full Text | Google Scholar

12. Zhao Z, Yang B. Phys Rev D (2022) 106:036013. doi:10.1103/PhysRevD.106.036013

CrossRef Full Text | Google Scholar

13. Jaffino Stargen D, Lochan K. Cavity optimization for Unruh effect at small accelerations. Phys Rev Lett (2022) 129:111303. doi:10.1103/physrevlett.129.111303

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Lochan K, Ulbricht H, Vinante A, Goyal SK. Detecting acceleration-enhanced vacuum fluctuations with atoms inside a cavity. Phys Rev Lett (2020) 125:241301. doi:10.1103/physrevlett.125.241301

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Gour G. Physics magazine, PRX Quan, 3 (2022) 040323. doi:10.1103/PRXQuantum.3.040323

CrossRef Full Text | Google Scholar

16. Kollas NK, Blekos K. Faithful extraction of quantum coherence. Phys Rev A (2020) 101:042325. doi:10.1103/physreva.101.042325

CrossRef Full Text | Google Scholar

17. Sperling J, Walmsley IA. Quasiprobability representation of quantum coherence. Phys Rev A (2018) 97:062327. doi:10.1103/physreva.97.062327

CrossRef Full Text | Google Scholar

18. Yao Y, Dong L, Sun CP. Phys Rev A (2019) 100:032324. doi:10.1103/PhysRevA.102.032406

CrossRef Full Text | Google Scholar

19. Francica G, Binder FC, Guarnieri G, Mitchison MT, Goold J, Plastina F. Quantum coherence and ergotropy. Phys Rev Lett (2020) 125:180603. doi:10.1103/physrevlett.125.180603

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Zhu H, Hayashi M, Chen L. Axiomatic and operational connections between the l1-norm of coherence and negativity. Phys Rev A (2018) 97:022342. doi:10.1103/physreva.97.022342

CrossRef Full Text | Google Scholar

21. Zhao M-J, Ma T, Quan Q, Fan H, Pereira R. l1-norm coherence of assistance. Phys Rev A (2019) 100:012315. doi:10.1103/physreva.100.012315

CrossRef Full Text | Google Scholar

22. Yao Y, Xiao X, Ge L, Wang X-guang, Sun C-pu. Quantum Fisher information in noninertial frames. Phys Rev A (2014) 89:042336. doi:10.1103/physreva.89.042336

CrossRef Full Text | Google Scholar

23. Zhong W, Sun Z, Ma J, Wang X, Nori F. Fisher information under decoherence in Bloch representation. Phys Rev A (2013) 87:022337. doi:10.1103/physreva.87.022337

CrossRef Full Text | Google Scholar

24. Hu BL, Lin SY, Louko J. Relativistic quantum information in detectors–field interactions. Quan Grav. (2012) 29:224005. doi:10.1088/0264-9381/29/22/224005

CrossRef Full Text | Google Scholar

25. Sokolov B, Louko J, Maniscalco S, Vilja I. Unruh effect and information flow. Phys Rev D (2020) 101:024047. doi:10.1103/physrevd.101.024047

CrossRef Full Text | Google Scholar

26. Moustos D, Anastopoulos C. Non-Markovian time evolution of an accelerated qubit. Phys Rev D (2017) 95:025020. doi:10.1103/physrevd.95.025020

CrossRef Full Text | Google Scholar

27. Finkelstein J. Definition of decoherence. Phys Rev D (1993) 47:5430–3. doi:10.1103/physrevd.47.5430

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Robles-Prez S, Alonso-Serrano A, Gonzlez-Daz PF. Decoherence in an accelerated universe. Phys Rev D (2012) 85:063511. doi:10.1103/physrevd.85.063511

CrossRef Full Text | Google Scholar

29. Suzuki S, Nag T, Dutta A. Dynamics of decoherence: universal scaling of the decoherence factor. Phys Rev A (2016) 93:012112. doi:10.1103/physreva.93.012112

CrossRef Full Text | Google Scholar

30. Bromley TR, Cianciaruso M, Adesso G. Frozen quantum coherence. Phys Rev Lett (2015) 114:210401. doi:10.1103/physrevlett.114.210401

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Ma W-L, Wang P, Leong W-H, Liu R-B. Phase transitions in sequential weak measurements. Phys Rev A (2018) 98:012117. doi:10.1103/physreva.98.012117

CrossRef Full Text | Google Scholar

32. Basit A, Badsha F, Ali H, Guo-Qin G. EPL (2017) 118:30002. doi:10.1209/0295-5075/118/30002

CrossRef Full Text | Google Scholar

33. Wang S-C, Yu Z-W, Zou W-J, Wang X-B. Phys Rev A (2014) 89:022318. doi:10.1103/PhysRevA.89.022318

CrossRef Full Text | Google Scholar

34. Katz N, Neeley M, Ansmann M, Bialczak RC, Hofheinz M, Lucero E, et al. Reversal of the weak measurement of a quantum state in a superconducting phase qubit. Phys Rev Lett (2008) 101:200401. doi:10.1103/physrevlett.101.200401

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Banerjee S, Alok AK, Srikanth R, Hiesmayr BC. A quantum-information theoretic analysis of three-flavor neutrino oscillations: quantum entanglement, nonlocal and nonclassical features of neutrinos. Eur Phys J C (2015) 75:487. doi:10.1140/epjc/s10052-015-3717-x

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Omkar S, Banerjee S, Srikanth R, Alok AK. Quantum inf. Comput (2016) 16:0757. doi:10.1007/JHEP02(2017)082

CrossRef Full Text | Google Scholar

37. Alok AK, Banerjee S, Sankar SU. Nucl Phys B (2016) 909:65. doi:10.1016/j.nuclphysb.2016.05.001

CrossRef Full Text | Google Scholar

38. Srikanth R, Banerjee S. Squeezed generalized amplitude damping channel. Phys Rev A (2008) 77:012318. doi:10.1103/physreva.77.012318

CrossRef Full Text | Google Scholar

39. Benatti F, Floreanini R. Entanglement generation in uniformly accelerating atoms: reexamination of the Unruh effect. Phys Rev A (2004) 70:012112. doi:10.1103/physreva.70.012112

CrossRef Full Text | Google Scholar

40. Xiang H, Yan K, Tan J, Wu Q-Y. Quantum work extraction of an accelerated Unruh-DeWitt battery in relativistic motion. Phys Rev A (2023) 107:012207. doi:10.1103/physreva.107.012207

CrossRef Full Text | Google Scholar

41. Yang L, Xia Y, COL. 15(5), 052701(2017).

Google Scholar

42. Huang YM, Yan K, Wu YZ, Hao X. Eur Phys J (2019) 79:974. doi:10.1140/epjc/s10052-019-7491-z

CrossRef Full Text | Google Scholar

Appendix A

The coefficient $a_{ij}$ depends on the Fourier transform of the field vacuum correlations, which related with the trajectory, where

${\alpha }_{\mu \upsilon }\left(\lambda \right)={\int }_{-\infty }^{\infty }dt{e}^{i\lambda \tau }⟨0|{\mathrm{\Phi }}_{\mu }\left(x\left(\tau \right)\right){\mathrm{\Phi }}_{\upsilon }\left(x^{\prime }\left({\tau }^{\prime }\right)\right)|0⟩,(\mathrm{A1})$

$⟨0|{\mathrm{\Phi }}_{\mu }\left(x\right){\mathrm{\Phi }}_{\upsilon }\left(x^{\prime }\right)|0⟩={\displaystyle \sum _{k=1}^N}{\chi }_{\mu }^k{\left({\chi }_{\upsilon }^k\right)}^{*}{G}^{+}\left(x-x^{\prime }\right).(\mathrm{A2})$

The two-point correlation function is introduced for the scalar field

$G^{+}\left(x-x^{\prime }\right)=\langle 0|\mathrm{\Phi }\left(x\left(\tau \right)\right)\mathrm{\Phi }\left(x\left({\tau }^{\prime }\right)\right)|0⟩=\frac{1}{4{\pi }^2\left[{\left|\vec{x}-{\vec{x}}^{\prime }\right|}^2-\left(t-t^{\prime }-i\epsilon \right)\right]}.(\mathrm{A3})$

The Fourier and Hilbert transforms of the field correlation function can be respectively expressed as

$\mathcal{G}\left(\mathrm{\Omega }\right)={\int }_{-\infty }^{\infty }d\mathrm{\Delta }\tau e^{i\mathrm{\Omega }\mathrm{\Delta }\tau }{G}^{+}\left(\mathrm{\Delta }\tau \right),(\mathrm{A4})$

$\mathcal{K}\left(\mathrm{\Omega }\right)=\frac{\mathcal{P}}{\pi i}{\int }_{-\infty }^{\infty }d\omega \frac{\mathcal{G}\left(\omega \right)}{\omega -\mathrm{\Omega }},(\mathrm{A5})$

where $\mathrm{\Delta }\tau =\tau -{\tau }^{\prime }$and $\mathcal{P}$ denotes the principle value. With the help of the $3\times 3$ Hermitian matrices

${\psi }_{ij}^{\left(0\right)}=n_i{n}_j,{\psi }_{ij}^{\left(\pm \right)}=\frac{1}{2}\left({\delta }_{ij}-n_i{n}_j\pm i{ϵ}_{\mathit{ijm}}{n}_m\right).(\mathrm{A6})$

It proves convenient to define the transformed coupling coefficients ${\chi }_i^{{\left(\zeta \right)}_k}={\sum }_j{\chi }_j^k{\psi }_{ji}^{\left(\xi \right)}$, where $\zeta =0,+,-$. By means of them, the Kossakowski matrix reads,

$a_{ij}={\displaystyle \sum _{k=1}^N}\left[\mathcal{G}\left(0\right){\chi }_i^{\left(0\right)k}{\chi }_j^{\left(0\right)k}+\mathcal{G}\left(\mathrm{\Omega }\right){\chi }_i^{\left(+\right)k}{\chi }_j^{\left(+\right)k}+\mathcal{G}\left(\mathrm{\Omega }\right){\chi }_i^{\left(-\right)k}{\chi }_j^{\left(-\right)k}\right],(\mathrm{A7})$

In order to simplify the process, we assume that the coupling coefficients ${\chi }_{\mu }^k$ satisfy the condition

${\displaystyle \sum _{k=1}^N}{\chi }_{\mu }^k{\left({\chi }_{\upsilon }^k\right)}^{*}\propto {\delta }_{\mu \nu }.(\mathrm{A8})$

Then, the Kossakowski matrix $a_{ij}$ takes the general form

$\begin{array}{cc}{a}_{ij}\hfill & =A{\delta }_{ij}-iB{\epsilon }_{\mathit{ijn}}{\delta }_{n1}+C{\delta }_{i1}{\delta }_{j1}\hfill \\ A\hfill & =\frac{{\lambda }^2}{2}\left(\mathcal{G}\left(\mathrm{\Omega }\right)+\mathcal{G}\left(-\mathrm{\Omega }\right)\right)\hfill \\ B\hfill & =\frac{{\lambda }^2}{2}\left(\mathcal{G}\left(\mathrm{\Omega }\right)-\mathcal{G}\left(-\mathrm{\Omega }\right)\right)\hfill \\ C\hfill & ={\lambda }^2\mathcal{G}\left(0\right)-A.\hfill \end{array}(\mathrm{A9})$