Estimation of the freezeout parameters using strange hadrons with changing multiplicity in pp collisions at 7 TeV

We explore the spectra of transverse momenta of hadrons with strange quark content ($K_S^0$, $\varphi$, $\mathrm{\Lambda }+\bar{\mathrm{\Lambda }}$, $\bar{\mathrm{\Xi }}+{\bar{\mathrm{\Xi }}}^{+}$, and ${\mathrm{\Omega }}^{-}+{\bar{\mathrm{\Omega }}}^{+}$) produced in proton–proton collisions at $\sqrt{s_{NN}}$ = 7 TeV. We applied Tsallis statistics in a blast wave model $(TBW)$ to the ALICE Collaboration’s experimental data and extracted the freezeout parameters (Tsallis temperature, transverse flow velocity, and the parameter $q$, which is the non-extensive parameter). The changing trend of these parameters is studied with changing multiplicity. The parameter $q$ decreases while the parameter $T$ and ${\beta }_T$ increases toward higher multiplicities. ${\beta }_T$ is noted to drop to zero in the system with the lowest multiplicities. In addition, the interrelationships between the parameters $T$ with ${\beta }_T$ and $T$ with $q$ are presented where the former correlation is positive and the latter one is negative.

1 Introduction

Investigating the quantum chromodynamic (QCD) phase diagram is the primary aim of heavy-ion collisions at ultra-relativistic energies. The quark–gluon plasma (QGP) [1–6], which is believed to have existed shortly after the Big Bang, perhaps within microseconds, is a state of deconfined partons in thermal equilibrium formed by such collisions at the Large Hadron Collider (LHC) and the Relativistic Heavy Ion Collider (RHIC). Small collision systems, such as proton–proton (pp) as well as proton–nucleus (p-A) collisions, have traditionally been considered as baselines to probe heavy-ion collisions and describe the quark–gluon plasma’s (QGP) characteristics. However, recent experimental data have shown strong flow-like behavior in high multiplicity collisions of pp and p-A at LHC energies, displaying qualitative similarities to phenomena seen in collisions with heavy ions [7–14]. These observations include long-range two-particle angular correlations [10, 14, 15], non-zero second-order Fourier coefficients $({\nu }_2)$ in multi-particle cumulant analyses [13, 16], enhanced baryon-to-meson ratios at intermediate transverse momentum $(p_T)$ [17], and strangeness enhancement [18]. As a result, understanding the origins of collective behavior in small systems has become a significant area of both experimental and theoretical inquiry. The quarks and gluons are in a deconfined state in QGP matter, and it is very challenging to observe such deconfined matter directly. Rather, we use the invariant yield ($p_T$ spectra) of the particles.

Three types of temperatures are often studied in the literature of high energy collisions, which occur at different stages in the system evolution. Temperature is, of course, very crucial in the study of QGP. The three temperatures include 1) The initial temperature, which occurs at the initial stages of a collision; 2) the chemical freezeout temperature, which happens at the point of chemical freezeout; and 3) the kinetic freezeout temperature, which occurs at the kinetic freezeout stage. Particles stop colliding in an elastic manner, no new particles are created, and the yields of each type of particle become fixed during the chemical freezeout stage. Currently, the baryon chemical potential and chemical freezeout temperature are extracted using many available thermodynamics models [3, 19–21]. The kinetic freezeout occurs later than the chemical freezeout during system evolution. As the system evolves, it undergoes continuous expansion. When the system expands further and reaches the kinetic freezeout stage, the spacing between the particles widens, and the elastic collisions between them stop. Following this phase, particles begin to propagate in the direction of the detector as their momenta also become fixed. The collision system’s transverse excitation degree (in the form of temperature) and dynamic expansion (in the form of transverse flow velocity ${\beta }_T$) are revealed by the particles’ $p_T$ spectra [3, 19, 22, 23]. The details about the initial stages of collisions can be obtained by the string percolation theory [24, 25], while at the chemical freezeout stage, these details can be obtained by using the thermal model [26]. The information at the kinetic freezeout stage can be obtained by hydrodynamic models, such as the blast wave model with Boltzmann–Gibbs statistics [22] and with Tsallis statistics [45], the Erlang distribution [27], and others [28]. In this work, we will study the final state temperature and flow velocity using the blast wave model with Tsallis statistics. The final state temperature and the transverse flow velocity are very important because these two quantities together reflect the transition from the hot and dense phase of matter to hadronic matter as the system cools and expands. The above two quantities are very important in restraint of the equation of state (EOS) because they provide indirect measurements of the pressure, energy density, and temperature evolution of the system that is formed during the collision. In addition, strange hadrons are analyzed because they are suggested as useful probes to locate the phase boundary and the beginning of deconfinement. It has been suggested that an imprint of a quark–gluon plasma (QGP) in nucleus-nucleus collisions, relative to collisions between protons at the same center of mass energy, is the increased creation of hadrons with strange quark content in these collisions [29]. Strange hadron yields have so far been thoroughly measured in numerous experiments conducted at various accelerator facilities [30–35], where significant strangeness enhancement, particularly for multi-strange hyperons, has been noted. In nuclear collisions, the strange hadron yields are generally in close agreement with those predicted by statistical hadron gas models [36–38].

The structure of the paper is as follows: Section 2 outlines the methodology and formalism, while Section 3 presents the results and discussion. Finally, Section 4 provides a summary of the key findings and conclusions.

2 The method and formalism

The extraction of the thermodynamic parameters through different statistical distributions and thermodynamical models has been used in recent decades. These models have been distributed in two categories. Some of them are used in case of soft excitation process, where they can cover the low $p_T$ region, while some of them are used when the hard process involves, and they can cover the $p_T$ spectra up to maximum range. Models such as the blast wave model with Boltzmann–Gibbs statistics [22, 23, 39], standard distribution [40], and the Hagedorn thermal model [41] are employed to match the data of $p_T$ spectra up to 2 GeV/c or 2.5 GeV/c, while the Tsallis distribution [42, 43], the Tsallis-Pareto [44], the blast wave model with Tsallis distribution [45], and the modified Hagedorn model with embedded flow [46, 47, 49, 50] are used to fit the data of $p_T$ spectra up to a high $p_T$ range.

The blast wave model with Tsallis distribution will be employed, where it fits the current work’s $p_T$ spectra up to 12 GeV/c. The expression of the TBW model is given by

$\begin{array}{ll}\hfill f_1\left(p_T\right)& =\frac{1}{N}\frac{\mathrm{d}N}{\mathrm{d}{p}_{\text{T}}}=C{p}_T{m}_T{\int }_{-\pi }^{\pi }d\varphi {\int }_0^{R}rdr\hfill \\ \hfill & \times \left\{1+\frac{q-1}{T}\left[m_T\cosh \left(\rho \right)-p_T\sinh \left(\rho \right)\right.\right.\hfill \\ \hfill & {\left.\left.\times \cos \left(\varphi \right)\right]\right\}}^{\frac{-q}{\left(q-1\right)}}.\hfill \end{array}(1)$

The terms $C$, $N$, and $m_T$ denote the normalized constant, count of particles, and the transverse mass, respectively, where $m_T=\sqrt{p_T^2+m_0^2}$. The term $r$ represents the radial coordinate, whose highest limit is $R$ and $\varphi$ azimuthal angle. The freezeout parameters, namely, the Tsallis temperature, transverse flow velocity, and the non-extensive parameter, are represented by $T$, ${\beta }_T$, and $q$, respectively. $\rho ={\tanh }^{-1}[\beta (r)]$ is the boost angle, where $\beta (r)$ is the self-similar flow profile and is connected with ${\beta }_S$ by $\beta (r)={\beta }_S{(r/R)}^{n_0}$. ${\beta }_S$ is the flow velocity on the surface. The index $n_0$ is the flow profile and is a free parameter [23, 48]. The term ${\beta }_T$ is transverse flow velocity and is expressed by ${\beta }_T=(2/R^2){\int }_0^{R}r\beta (r)dr=2{\beta }_S/(n_0+2)$.

3 Results and discussion

This section examines the results of the $p_T$ spectra of strange hadrons at 7 TeV in pp collisions and discusses the results of the extracted parameters from high to lower multiplicity classes (MCs).

Figure 1 presents the $p_T$ spectra of strange hadrons, namely $K_S^0$, $\varphi$, $\mathrm{\Lambda }+\bar{\mathrm{\Lambda }}$, $\bar{\mathrm{\Xi }}+{\bar{\mathrm{\Xi }}}^{+}$, and ${\mathrm{\Omega }}^{-}+{\bar{\mathrm{\Omega }}}^{+}$, in panels (a)-(e), respectively. The $p_T$ spectra of these particles are analyzed in different MCs. We took the experimental data from [17, 18], which are represented by the symbols. The arrays of different symbols show different MCs from MC-I to MC-X, and the curve over them is the result of the TBW model from Equation 1. The lower panel consists of the data/fit ratio of the corresponding fit and shows the deviation of the fit from the data. The data/fit ratio between 0.5 and 2 is normal. One can see that the fit to data by the TBW model in Figure 1 is good, except at the tail for the MC-X for $K_S^0$ and $\varphi$. The departure of the fit curve from the data in $p_T<$0.5 is large compared to $p_T>$0.5 because the former is the very soft region where resonance decay is involved, which is not taken into account by the TBW model. Lower MCs are linked to higher multiplicity, and higher MCs are linked to lower multiplicity. Table 1 shows ${\chi }^2/dof$ and the values of the parameters that the TBW model extracts. It should be noted that $dof$ is calculated by subtracting the number of free parameters from the number of data points in the $p_T$ spectra of the corresponding hadron.

Figure 1

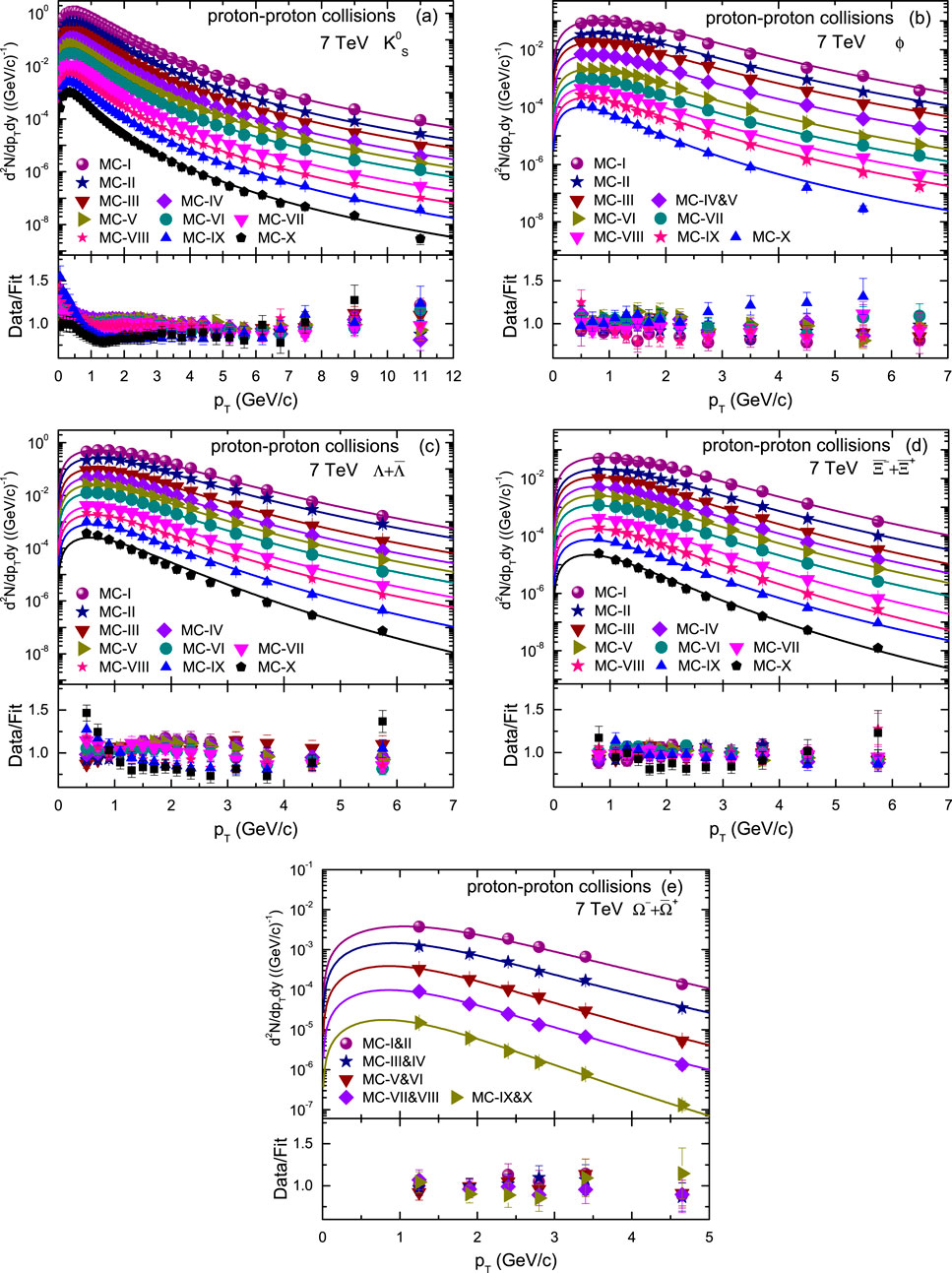
Figure 1. Transverse momentum spectra of strange hadrons ($K_S^0$, $\varphi$, $\mathrm{\Lambda }+\bar{\mathrm{\Lambda }}$, $\bar{\mathrm{\Xi }}+{\bar{\mathrm{\Xi }}}^{+}$, and ${\mathrm{\Omega }}^{-}+{\bar{\mathrm{\Omega }}}^{+}$) at 7 TeV produced in pp collisions in multiplicity class (MC) MC-I to MC-X. The lower panels of the figures display the corresponding fit data/fit ratios. Panel (A-E) shows the $p_T$ spectra for $K_S^0$, $\varphi$, $\mathrm{\Lambda }+\bar{\mathrm{\Lambda }}$, $\bar{\mathrm{\Xi }}+{\bar{\mathrm{\Xi }}}^{+}$, and ${\mathrm{\Omega }}^{-}+{\bar{\mathrm{\Omega }}}^{+}$, respectively.

Table 1

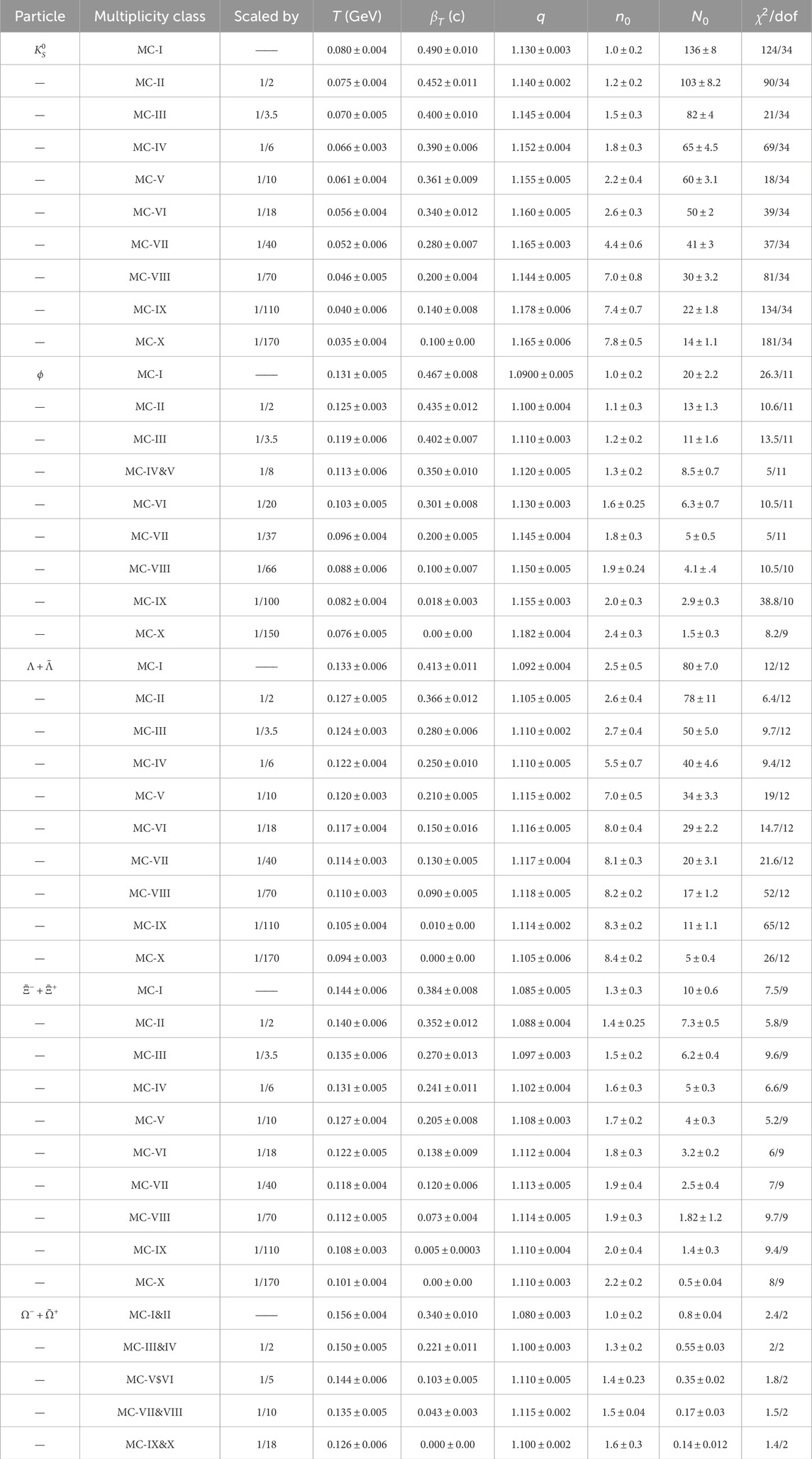
Table 1. Values of $T$, $q$, $N_0$, ${\chi }^2$, and degrees of freedom (dof) corresponding to the curves in Figure 1.

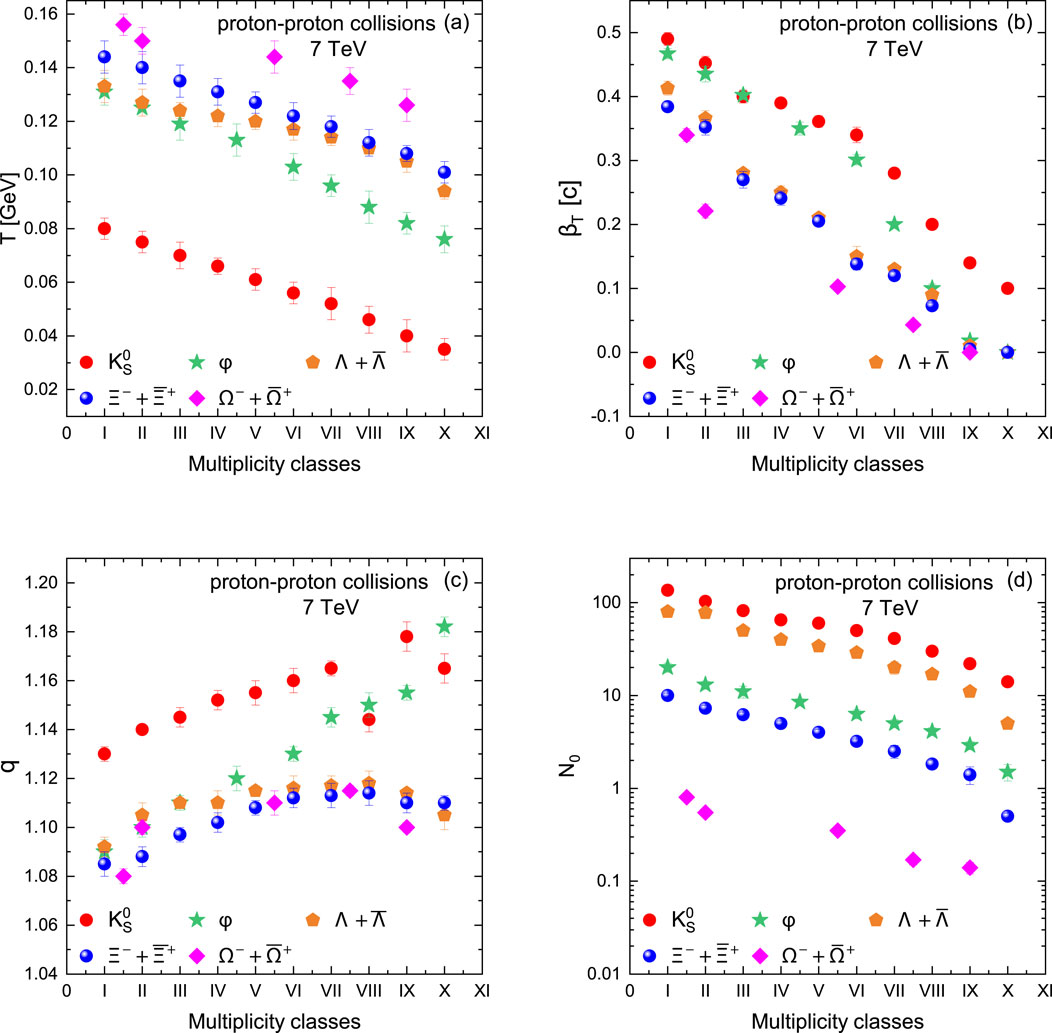
We have extracted $T$, ${\beta }_T$, the entropy parameter $(q)$, and the normalization parameter $(N_0)$. These parameters are displayed in Figure 2. Different panels in Figure 2 show the results of different parameters. For instance, panel (a) shows $T$ in relation to multiplicity, while panels (b), (c), and (d) show the dependence of ${\beta }_T$, $q$, and $N_0$ on multiplicity, respectively. The left-to-right trend of these parameters demonstrates how their multiplicity-related behavior changes. Higher multiplicity is associated with MC-I, whereas lower multiplicity is associated with MC-X, and the color variations represent various particles in the figure. Panel (a) in Figure 2 demonstrates the changing behavior of $T$ with respect to multiplicity. A decreasing trend of $T$ is observed with increasing MC (higher MC is associated with lower multiplicity). In the higher MC, that is, MC-X, a small portion of the colliding systems overlap where there is the transfer of a small amount of energy among nucleons within the colliding systems, which results in a lower excitation degree of the system and hence lower $T$. As the system progresses to lower MCs, the overlapping region of the colliding system becomes larger and larger, where the amount of energy transfer among the colliding systems becomes larger, which alternatively corresponds to a larger degree of excitation degree of the system and hence larger $T$. These results are similar to our previous results and other literature [50–52] of A-A collisions in different centrality intervals, where $T$is decreasing from central to peripheral collisions. In the present result, the lower MC has a resemblance with the central collisions, while the higher MC has a resemblance with peripheral collisions. In addition, the parameters from up to downward in panel (a) of Figure 2show a mass differential scenario where each particle freezes out at different times. This phenomenon has been observed in [50–52], although single freezeout [45], and double kinetic freezeout [53, 54] scenarios also exist. The dependence of $T$on $m_0$is more pronounced from $K_S^0$to $\mathrm{\Lambda }+\bar{\mathrm{\Lambda }}$and is less pronounced above it in ${\mathrm{\Xi }}^{-}+{\bar{\mathrm{\Xi }}}^{+}$and then is again more pronounced in ${\mathrm{\Omega }}^{-}+{\bar{\mathrm{\Omega }}}^{+}$. Furthermore, from high multiplicity to low multiplicity, $T$as a function of $m_0$for $K_S^0$and $\mathrm{\Lambda }+\bar{\mathrm{\Lambda }}$is seen to be very less pronounced and seen to be very close in lower MCs. Similarly, $\varphi$in higher multiplicity is very close to $\mathrm{\Lambda }+\bar{\mathrm{\Lambda }}$, and they show a divergence as one proceeds to lower multiplicity. Panel (b) in Figure 2is similar to panel (a); however, the result for ${\beta }_T$is displayed in it. From higher to lower MC, ${\beta }_T$is seen to decrease monotonically. The overlapping region of the colliding systems is comparatively larger than at higher MCs, which results in the transfer of a large amount of energy among nucleons within the colliding system. The pressure gradient is large, and consequently, ${\beta }_T$is larger. This pressure gradient decreases toward higher MCs and hence ${\beta }_T$. The behavior of ${\beta }_T$from lower to higher MCs resembles the behavior of ${\beta }_T$from central to peripheral collisions. Higher MCs resemble peripheral collisions, while lower MCs resemble the central collisions [50] where ${\beta }_T$decreases toward the periphery. Interestingly, we observed that in the last MC where the multiplicity is too small, ${\beta }_T$tends to zero, which may declare a remarkable variation in the system’s behavior. The abrupt drop in ${\beta }_T$ could indicate a transition from a regime where collective effects, like hydrodynamic flow, are dominant to one where other factors start to matter. This transition may be explained by a variety of adjustments to the energy density of the system, the predominance of distinct mechanisms for particle production, or modifications to the collision behaviors. Similar to $T$, ${\beta }_T$ also shows mass dependence: the more massive the particle, the lesser the flow velocity. However, this behavior from $K_S^0$ to $\varphi$ and from $\mathrm{\Lambda }+\bar{\mathrm{\Lambda }}$ to ${\mathrm{\Xi }}^{-}+{\bar{\mathrm{\Xi }}}^{+}$ is less pronounced.

Figure 2

Figure 2. Result of $T$, ${\beta }_T$, $q$and $N_0$as a function of multiplicity in panels (A–D), respectively.

Figure 2C displays the dynamics of $q$ in relation to the MC. One can see that there is an increasing trend of $q$ with respect to MCs. $q$ is smaller at lower MC and is larger at higher MC. We know that $q$ = 1 indicates a system closer to equilibrium. As the system departs from $q$ = 1, it tends to be far from equilibrium. The present work shows that $q$ is decreasing from higher MCs to lower MCs, which indicates that the system in higher MCs (lower multiplicity) is far from equilibrium, while the system in lower MCs (greater multiplicity) is close to equilibrium. We noticed that for all particles, the parameter $q$ is increasing continuously from lower to higher MCs; however, it decreases in the highest MCs, except $\varphi$, which does not have such change. This behavior can be explained as significant particle creation occurring in large-multiplicity events, resulting in more collisions and interactions between particles. The system becomes more thermalized and exhibits short-range correlations as a result, approaching equilibrium in behavior. As a result, there is a decrease in $q$, and the deviation from equilibrium is not large. The system becomes less thermalized as the multiplicity drops, showing more long-range correlations and weaker particle interactions. Because this pulls the system away from equilibrium, $q$ rises, and more non-extensive, non-equilibrium behavior is reflected. The system is strongly deviated from the Boltzmann–Gibbs distribution, which represents classical equilibrium. When the multiplicity is at its lowest, a simpler system with fewer particles produced can be the cause of the decline in $q$. In these situations, strong non-equilibrium behavior cannot be maintained due to a lack of interaction or complexity. All in all, the system is like a thin, almost perfect gas with very few correlations and interactions. When the system returns to equilibrium as a result of this behavior, $q$ falls. The system moves toward a more classical, weakly interacting regime where deviations from equilibrium are less noticeable, as indicated by this decrease in $q$ at the lowest multiplicity. In addition, panel (d) displays the result of the normalization parameter $(N_0)$. With lighter particles, $N_0$ is larger and comparatively smaller for the massive particles. In addition, it is larger in lower MCs and smaller in higher MCs. $N_0$ actually indicates the multiplicity.

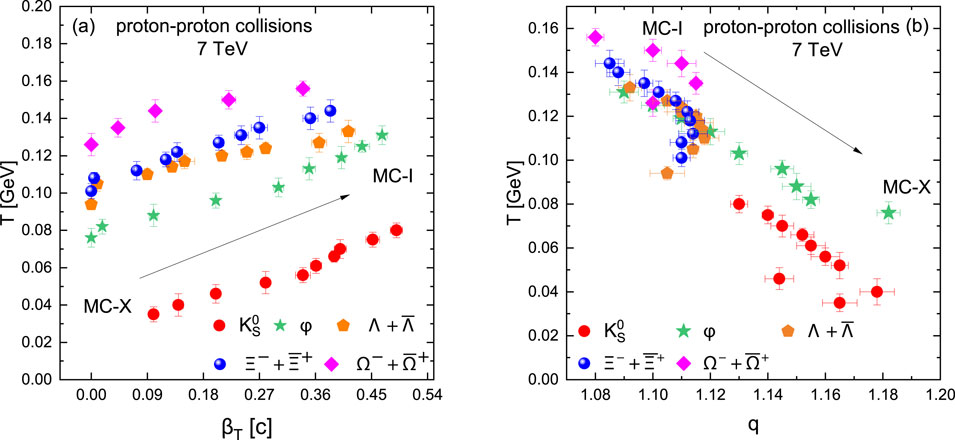
Figure 3 displays the correlation among the parameters. Panel (a) in Figure 3 presents the correlation between $T$ and ${\beta }_T$, while panel (b) shows the correlation between $T$ and $q$. Panel (a) reveals a positive correlation between $T$ and ${\beta }_T$. We can see that $T$ rises as ${\beta }_T$ increases from higher MCs to lower MCs. This renders the scenario of the early universe, where the system was very hot and was expanding quickly. This result is similar to our previous result [50], where such a scenario was observed from central to peripheral collisions. Panel (b) shows the negative correlation between $T$ and $q$. $T$ decreases with increasing $q$ from lower to higher MCs. There is a bending structure seen in the highest MC in the correlation of $T$ and $q$. This bending structure renders that the collective effects, such as flow or significant thermalization, are weaker at the lower multiplicities than they are at higher multiplicities. The system might behave more “ideally” in the absence of these collective behaviors, which would lessen the requirement for a high $q$ to account for non-equilibrium effects. Consequently, as the system becomes closer to a state that more closely resembles equilibrium, $q$ drops.

Figure 3

Figure 3. Correlation among $T$ and ${\beta }_T$ and $T$ and $q$ in panels (A, B), respectively.

4 Conclusion

We studied the freezeout properties of strange particles produced in proton–proton collisions at $\sqrt{s_{NN}}$ = 7 TeV. The particles under study include $K_S^0$, $\varphi$, $\mathrm{\Lambda }+\bar{\mathrm{\Lambda }}$, $\bar{\mathrm{\Xi }}+{\bar{\mathrm{\Xi }}}^{+}$, and ${\mathrm{\Omega }}^{-}+{\bar{\mathrm{\Omega }}}^{+}$. We investigated the $p_T$ spectra of the above particles in different MCs, where the higher MC is associated with less multiplicity and the lower MC is associated with larger multiplicity. The blast wave model with Tsallis statistics is used over the experimental data, and the freezeout parameters are extracted, including the $T$, ${\beta }_T$, and $q$. The behavior of these parameters with changing multiplicity is studied.

We observed that the parameter $T$ and ${\beta }_T$ decreases with the rise of the MC where the multiplicity is not large. There is a large overlap of colliding systems where much energy is exchanged between them and, consequently, larger $T$ and ${\beta }_T$. ${\beta }_T$ drops to zero in the highest MCs, which shows the transition from collective to non-collective effects in the highest MC. Both of these parameters are mass dependent, where the former is larger for massive particles, and the latter is larger for lighter particles. On the other hand, the parameter $q$ shows reverse behavior to that of $T$ and ${\beta }_T$, which shows that the system with higher multiplicity is close to an equilibrium, while it moves away from equilibrium as the multiplicity decreases. We also plotted the correlation between $T$ and ${\beta }_T$, which is positive and points toward the early birth of the universe where the system was very hot and the pressure gradient was incredibly large. However, the correlation between $T$ and $q$ is also plotted, which is negative, rendering the system with higher multiplicity close to equilibrium.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: hep data.

Author contributions

HA: software and writing–original draft. HZ: funding acquisition, supervision, validation, and writing–review and editing. F-HL: conceptualization, methodology, resources, supervision, and writing–review and editing. MW: conceptualization, investigation, methodology, supervision, validation, and writing–review and editing. MB: data curation, formal analysis, methodology, resources, validation, and writing–review and editing. RG: conceptualization, data curation, investigation, project administration, resources, visualization, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (Grant No. 11875039), the Research Project Supported by Shanxi Scholarship Council of China (Grant No. 2023-033 and 2022-033 and 2022-014), and the Fundamental Research Program of Shanxi Province (Grant No. 202303021221071). The authors also extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FFR-2024-2461-10”.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Adcoxbe K, Adlere SS, Afanasievt S, Aidalae C, Ajitanandaw NN, Akibaw Y PHENIX. Nucl Phys A (2005) 757:184–283. doi:10.1016/j.nuclphysa.2005.03.086[arXiv:nucl-ex/0410003

CrossRef Full Text | Google Scholar

2. Backa BB, Bakerb MD, Ballintijnd M PHOBOS. Nucl Phys A (2005) 757:28–101. doi:10.1016/j.nuclphysa.2005.03.084[arXiv:nucl-ex/0410022

CrossRef Full Text | Google Scholar

3. Adam J, Aggarwal MM, Ahammed Z, Amonett J, Anderson BD, Arkhipkin D STAR. Nucl Phys A (2005) 757:102–83. doi:10.1016/j.nuclphysa.2005.03.085[arXiv:nucl-ex/0501009

CrossRef Full Text | Google Scholar

4. Schukraft Alice J. Phil Trans Roy Soc Lond A (2012) 370:917–32. doi:10.1098/rsta.2011.0469

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cleymans J, Gavai RV, Suhonen E. Phys Rept (1986) 130:217. doi:10.1016/0370-1573(86)90169-9

CrossRef Full Text | Google Scholar

6. Shuryak EV. Theory and phenomenology of the QCD vacuum. Phys Rept (1984) 115:151–314. doi:10.1016/0370-1573(84)90037-1

CrossRef Full Text | Google Scholar

7. Abelev B, Adam J, Adamová D, Adare AM, Aggarwal MM, Aglieri Rinella G, et al. Transverse sphericity of primary charged particles in minimum bias proton–proton collisions at s√ = 0.9, 2.76 and 7 TeV. Eur Phys J C (2012) 72:2124. doi:10.1140/epjc/s10052-012-2124-9

CrossRef Full Text | Google Scholar

8. Chatrchyan S, Khachatryan V, Sirunyan A, Tumasyan A, Adam W, Aguilo E, et al. Observation of long-range, near-side angular correlations in pPb collisions at the LHC. Phys Lett B (2013) 718:795–814. doi:10.1016/j.physletb.2012.11.025

CrossRef Full Text | Google Scholar

9. Chatrchyan S, Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, et al. &gt;Study of the production of charged pions, kaons, and protons in pPb collisions at sqrt(sNN) = 5.02 TeV. Eur Phys J C (2014) 74(6):2847. doi:10.1140/epjc/s10052-014-2847-x

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Abelev B, Adam J, Adamova D, Adare AM, Aggarwal M, Aglieri Rinella G, et al. ALICE. Phys Lett B (2013) 719:29–41. doi:10.1016/j.physletb.2013.01.012

CrossRef Full Text | Google Scholar

11. Adare A, Afanasiev S, Aidala C, Ajitanand NN, Akiba Y, Al-Bataineh H, et al. PHENIX. Phys Rev C (2013) 88(2):024906. doi:10.1103/PhysRevC.88.024906

CrossRef Full Text | Google Scholar

12. Adam J, Adamová D, Aggarwal M, Aglieri Rinella G, Agnello M, Agrawal N, et al. ALICE. Phys Lett B (2016) 758:389–401. doi:10.1016/j.physletb.2016.05.027

CrossRef Full Text | Google Scholar

13. Acharya S, Adamová D, Adhya S, Adler A, Adolfsson J, Aggarwal M, et al. ALICE. Phys Rev Lett (2019) 123(14):142301. doi:10.1103/PhysRevLett.123.142301

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Hirono Y, Kharzeev DE, Yin Y ATLAS. Phys Rev Lett (2016) 116(17):172301. doi:10.1103/PhysRevLett.116.172301[arXiv:1509.04776

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Abelev BB, et al. ALICE. Phys Lett B (2013) 726:164–77. doi:10.1016/j.physletb.2013.08.024

CrossRef Full Text | Google Scholar

16. Khachatryan V, Sirunyan A, Tumasyan A, Adam W, Bergauer T, Dragicevic M, et al. CMS. Phys Rev Lett (2015) 115(1):012301. doi:10.1103/PhysRevLett.115.012301

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Acharya S, Acosta FT, Adamová D, Adler A, Adolfsson J, Aggarwal MM, et al. ALICE. Phys Rev C (2019) 99(2):024906. doi:10.1103/PhysRevC.99.024906

CrossRef Full Text | Google Scholar

18. Adam J, et al. ALICE. Nat Phys (2017) 13:535–9. doi:10.1038/nphys4111[arXiv:1606.07424

CrossRef Full Text | Google Scholar

19. Adamczyk L, Adkins JK, Agakishiev G, Aggarwal MM, Ahammed Z, Ajitanand NN, et al. Bulk properties of the medium produced in relativistic heavy-ion collisions from the beam energy scan program. Phys Rev C (2017) 96(4):044904. doi:10.1103/PhysRevC.96.044904

CrossRef Full Text | Google Scholar

20. Andronic A, Beutler F, Braun-Munzinger P, Redlich K, Stachel J. Phys Lett B (2009) 675:312–8. doi:10.1016/j.physletb.2009.04.024

CrossRef Full Text | Google Scholar

21. Wheaton S, Cleymans J, Hauer M. THERMUS—a thermal model package for ROOT. Comput Phys Commun (2009) 180:84–106. doi:10.1016/j.cpc.2008.08.001

CrossRef Full Text | Google Scholar

22. Schnedermann E, Sollfrank J, Heinz UW. Phys Rev C (1993) 48:2462–75. doi:10.1103/PhysRevC.48.2462[arXiv:nucl-th/9307020

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Abelev BI, Aggarwal MM, Ahammed Z, Anderson BD, Arkhipkin D, Averichev GS STAR. Phys Rev C (2009) 79:034909. doi:10.1103/PhysRevC.79.034909[arXiv:0808

CrossRef Full Text | Google Scholar

24. Mishra AN, Paić G, Pajares C, Scharenberg RP, Srivastava BK. Exploring the QGP phase above the deconfinement temperature in pp and A − A collisions at LHC energies. Nucl Phys A (2024) 1046:122865. doi:10.1016/j.nuclphysa.2024.122865

CrossRef Full Text | Google Scholar

25. Sahu D, Mishra AN, Sahoo R. PoS LHCP2021 (2021) 232. doi:10.22323/1.397.0232[arXiv:2110.03961

CrossRef Full Text | Google Scholar

26. Tawfik AN, Maher M, El-Kateb AH, Abdelaziz S. Adv High Energy Phys. (2020):2453476. doi:10.1155/2020/2453476

CrossRef Full Text | Google Scholar

27. He XW, Wei HR, Hong BH, Wu HY, Zhu WT, Wu FM. Centrality-dependent chemical potentials of light hadrons and quarks based on pT spectrum and particle yield ratio in Au-Au collisions at RHIC energies. Universe (2022) 8(8):420. doi:10.3390/universe8080420

CrossRef Full Text | Google Scholar

28. Wang Q, Liu FH, Olimov KK. Excitation functions of related temperatures of η and η0 emission sources from squared momentum transfer spectra in high-energy collisions. Universe (2023) 9(7):342. doi:10.3390/universe9070342

CrossRef Full Text | Google Scholar

29. Rafelski J, Muller B. Strangeness production in the quark-gluon Plasma. Phys Rev Lett (1982) 48:1066–9. doi:10.1103/PhysRevLett.48.1066

CrossRef Full Text | Google Scholar

30. Chung P, Ajitanand NN, Alexander JM, Anderson M, Best D, Brady FP, et al. E895. Phys Rev Lett (2003) 91:202301. doi:10.1103/PhysRevLett.91.202301

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Abelev BB, Adam J, Adamová D, Adare AM, Aggarwal MM, Aglieri Rinella G, et al. K(S)0 and Λ production in Pb-Pb collisions at √(s(NN))=2.76 TeV. Phys Rev Lett (2013) 111:222301. doi:10.1103/PhysRevLett.111.222301

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Albergo S, Bellwied R, Bennett M, Boemi D, Bonner B, Caines H, et al. Lambda spectra in 11.6A GeV/c Au-Au collisions. Phys Rev Lett (2002) 88:062301. doi:10.1103/PhysRevLett.88.062301

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Adcox K, Adler SS, Ajitanand NN, Akiba Y, Alexander J, Aphecetche L, et al. Measurement of Lambda and Lambda(macro) particles in Au+Au collisions at the square root of S(NN) = 130 GeV. Phys Rev Lett (2002) 89:092302. doi:10.1103/PhysRevLett.89.092302

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Back BB, Betts RR, Chang J, Chang WC, Chi CY, Chu YY, et al. Antilambda production in Au+Au collisions at 11.7A GeV/c. Phys Rev Lett (2001) 87:242301. doi:10.1103/PhysRevLett.87.242301

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Antinori F, Bacon PA, Badalà A, Barbera R, Belogianni A, Bloodworth IJ, et al. Strangeness enhancements at central rapidity in 40 A GeV/cPb–Pb collisions. J Phys G (2010) 37:045105. doi:10.1088/0954-3899/37/4/045105

CrossRef Full Text | Google Scholar

36. Redlich K, Tounsi A, Eur. Phys. J. C 24, 589–94. (2002) doi:10.1007/s10052-002-0983-1

CrossRef Full Text | Google Scholar

37. Becattini F, Cleymans J, Keranen A, Suhonen E, Redlich K. Features of particle multiplicities and strangeness production in central heavy ion collisions between1.7Aand158A GeV/c. Phys Rev C (2001) 64:024901. doi:10.1103/PhysRevC.64.024901

CrossRef Full Text | Google Scholar

38. Braun-Munzinger P, Cleymans J, Oeschler H, Redlich K. Nucl Phys A (2002) 697:902–12. doi:10.1016/S0375-9474(01)01257-X

CrossRef Full Text | Google Scholar

39. Abelev BI, Aggarwal MM, Ahammed Z, Alakhverdyants AV, Anderson BD, Arkhipkin D, et al. STAR. Phys Rev C (2010) 81:024911. doi:10.1103/PhysRevC.81.024911

CrossRef Full Text | Google Scholar

40. Cleymans J, Worku D. Relativistic thermodynamics: transverse momentum distributions in high-energy physics. Eur Phys J A (2012) 48:160. doi:10.1140/epja/i2012-12160-0

CrossRef Full Text | Google Scholar

41. Hagedorn R. Riv Nuovo Cim (1983) 6N10:1–50. doi:10.1007/BF02740917

CrossRef Full Text | Google Scholar

42. Olimov KK, Lebedev IA, Fedosimova AI, Liu FH, Dmitriyeva E, Musaev KA, et al. Correlations among parameters of the Tsallis distribution and Hagedorn function with embedded transverse flow in proton–proton collisions at (s)1/2 = 7 and 13 TeV. Eur Phys J Plus (2023) 138(5):414. doi:10.1140/epjp/s13360-023-04037-7

CrossRef Full Text | Google Scholar

43. Parvan AS. Hadron transverse momentum distributions in the Tsallis statistics with escort probabilities. J Phys G (2023) 50(12):125002. doi:10.1088/1361-6471/acfe23

CrossRef Full Text | Google Scholar

44. Alrebdi HI, Ajaz M, Waqas M, Ahmad MA, Maryam , Quraishi AM, et al. Chin J Phys (2024) 89:1669–77. doi:10.1016/j.cjph.2024.02.034

CrossRef Full Text | Google Scholar

45. Tang Z, Xu Y, Ruan L, van Buren G, Wang F, Xu Z. Spectra and radial flow in relativistic heavy ion collisions with Tsallis statistics in a blast-wave description. Phys Rev C (2009) 79:051901. doi:10.1103/PhysRevC.79.051901

CrossRef Full Text | Google Scholar

46. Waqas M, Peng G, Ajaz M, Ismail AH, Dawi E. Analyses of the collective properties of hadronic matter in Au-Au collisions at 54.4 GeV. Phys Rev D (2022) 106(7):075009. doi:10.1103/PhysRevD.106.075009

CrossRef Full Text | Google Scholar

47. Khandai PK, Sett P, Shukla P, Singh V. System size dependence of hadron pT spectra in p+p and Au+Au collisions at √sNN = 200 GeV. J Phys G (2014) 41:025105. doi:10.1088/0954-3899/41/2/025105

CrossRef Full Text | Google Scholar

48. Petrovici M, Andrei C, Berceanu I, Bercuci A, Herghelegiu A, Pop A. Recent results and open questions on collective type phenomena from A-A to pp collisions. AIP Conf Proc (2015) 1645(1):52–60. doi:10.1063/1.4909559

CrossRef Full Text | Google Scholar

49. Olimov KK, Kanokova SZ, Olimov K, Gulamov KG, Yuldashev BS, Lutpullaev SL, et al. Average transverse expansion velocities and global freeze-out temperatures in central Cu + Cu, Au + Au, and Pb + Pb collisions at high energies at RHIC and LHC. Phys Lett A (2020) 35(14):2050115. doi:10.1142/S0217732320501151

CrossRef Full Text | Google Scholar

50. Waqas M, Peng GX, Ajaz M, Haj Ismail A, Dawi EA. Analyses of the collective properties of hadronic matter in Au-Au collisions at 54.4 GeV. Phys Rev D (2022) 106(7):075009. doi:10.1103/PhysRevD.106.075009

CrossRef Full Text | Google Scholar

51. Wei HR, Liu FH, Lacey RA. Kinetic freeze-out temperature and flow velocity extracted from transverse momentum spectra of final-state light flavor particles produced in collisions at RHIC and LHC. Eur Phys J A (2016) 52(4):102. doi:10.1140/epja/i2016-16102-6

CrossRef Full Text | Google Scholar

52. Liu FH, Wei HR, Lacey RA. Transverse momentum and pseudorapidity distributions of final-state particles and spatial structure pictures of an interacting system in p-Pb collisions at √sNN = 5.02 TeV. Eur Phys J A (2015) 51(4):43. doi:10.1140/epja/i2015-15043-x

CrossRef Full Text | Google Scholar

53. Chatterjee S, Das S, Kumar L, Mishra D, Mohanty B, Sahoo R, et al. Adv High Energy Phys. (2015) 2015:349013. doi:10.1155/2015/349013

CrossRef Full Text | Google Scholar

54. Chatterjee S, Mohanty B, Singh R. Freezeout hypersurface at energies available at the CERN Large Hadron Collider from particle spectra: flavor and centrality dependence. Phys Rev C (2015) 92(2):024917. doi:10.1103/PhysRevC.92.024917

CrossRef Full Text | Google Scholar