Hyperboloidal approach to quasinormal modes

Oscillations of black hole spacetimes exhibit divergent behavior near the bifurcation sphere and spatial infinity. In contrast, these oscillations remain regular when evaluated near the event horizon and null infinity. The hyperboloidal approach provides a natural framework to bridge these regions smoothly, resulting in a geometric regularization of time-harmonic oscillations, known as quasinormal modes (QNMs). This review traces the development of the hyperboloidal approach to QNMs in asymptotically flat spacetimes, emphasizing both the physical motivation and recent advancements in the field. By providing a geometric perspective, the hyperboloidal approach offers an elegant framework for understanding black hole oscillations, with implications for improving numerical simulations, stability analysis, and the interpretation of gravitational wave signals.

1 Introduction

When a black hole (BH) spacetime is perturbed, gravitational waves (GW) carry the energy of the perturbation towards the BH horizon and to infinity. These perturbations show oscillations that decay exponentially at characteristic frequencies and are called quasinormal modes (QNM) [1–4]. Studying these QNMs is central to the black hole spectroscopy program [5–7], which aims to measure the oscillation frequencies from GW detections and thereby probe the BH geometry and its surrounding environment [1, 3, 4, 8]. The dominant quadrupole QNMs have already been measured in gravitational wave signals [9–11], while the detection of higher modes remains under debate [12–25].

Mathematically, the QNM problem is often formulated as an eigenvalue problem, where QNM frequencies appear as the eigenvalues of a second-order differential operator. However, in their traditional representation, the corresponding QNM eigenfunctions grow exponentially near the black hole and at spatial infinity, which does not seem physically acceptable for small perturbations of a background spacetime [26]. Reformulating the problem using hyperboloidal surfaces—regular spacelike surfaces that extend smoothly from the black hole event horizon to null infinity—reveals that QNMs are globally regular [27, 28]. This geometric regularization¹ of time-harmonic black hole perturbations has found many recent applications, which we review in this paper.

2 The traditional approach to QNMs

The Schwarzschild solution, the simplest black-hole (BH) solution to Einstein’s equations, is given by

$d{s}^2=-f\left(r\right)d{t}^2+\frac{1}{f\left(r\right)}d{r}^2+r^{2}d{\varpi }^2,\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}f\left(r\right)=1-\frac{2M}{r},$

where $d{\varpi }^2=d{\theta }^2+{\sin }^2\theta d{\varphi }^2$ is the metric on the unit sphere, and $M$ the black-hole’s mass. Perturbations of this solution are described by the Regge-Wheeler-Zerilli type wave equation:

$\left(-{\partial }_t^2+{\partial }_{r_{*}}^2-V\left(r_{*}\right)\right)u\left(t,r_{*}\right)=0,(1)$

where $r_{*}\in (-\infty ,\infty )$ is the tortoise coordinate and $V(r_{*})$ is the effective potential that behaves as $V\sim f(r)$ near the black-hole horizon and as $V\sim 1/r^2$ toward spatial infinity.

Solutions to (Equation 1) evolve through a transient phase, followed by a ringdown characterized by exponentially damped vibrations (QNMs) [34], and eventually a polynomial, non-oscillatory decay known as the tail [35, 36].

To analyze the QNM phase, one typically considers time-harmonic solutions

$u\left(t,r_{*}\right)=e^{-i\omega t}R\left(r_{*}\right),(2)$

that reduce the wave equation to a Helmholtz equation,

$\left(\frac{d^2}{d{r}_{*}^2}+{\omega }^2-V\left(r_{*}\right)\right)R\left(r_{*}\right)=0.(3)$

Sommerfeld recognized in 1912 that the Helmholtz equation, in stark contrast to the elliptic case, does not admit unique solutions even when we require that the solution vanishes at infinity [37, 38]. To ensure uniqueness, an outgoing radiation condition must be imposed. In the BH context, a Sommerfeld condition applies also near the BH. We therefore impose

$\underset{r_{*}\to \pm \infty }{\lim }\left(\frac{d}{d{r}_{*}}\mp i\omega \right)R\left(r_{*}\right)=0\iff R\left(r_{*}\right)\sim e^{\pm i\omega r_{*}}\mathrm{a}\mathrm{s}{r}_{*}\to \pm \infty .(4)$

It turns out, however, that the boundary conditions (Equation 4) are not sufficient [2, 39] and a more precise notion of purely outgoing solution is needed to uniquely define the QNMs [40]. The formal definition of QNMs followed a different route than the intuitive notion of QNMs as the eigenvalues of a given differential operator.

The time-harmonic Ansatz (Equation 2), closely related to a Fourier transformation, provides a general formalism oblivious to the specific form of initial data causing the perturbation. To define QNMs formally, one considers an initial value problem. Then, a Laplace transformation [2, 39, 41, 42] leads to a inhomogeneous spatial differential equation, with a source term accounting for the initial data. One must then ensure that the spacetime solution $u(t,r_{\ast })$ remains bounded as $t\to \infty$ [43]. In the Laplace formalism, the solution $u(t,r_{\ast })$ results from the convolution of the Green’s functions with the source term carrying information from the initial data. The inverse Laplace transformation requires an integration along a frequency values ${\omega }_I>0$, and there is only one possible choice of homogenous solutions $R_{\pm }(r_{\ast };\omega )$ to construct the correct Green’s function: they must satisfy the boundary conditions (Equation 4) at both ends $r_{\ast }\to \pm \infty$. Once the Green’s functions are fixed in the complex half-plane ${\omega }_I>0$, one analytically extends them into the region ${\omega }_I<0$. The QNMs are then uniquely defined as the poles of Green’s functions, or equivalently in the one-dimensional case, the roots of the Wronskian.

The Laplace approach uniquely defines QNMs via Green’s functions, bypassing the notions of eigenvalues and eigenfunctions. Such definition via this Green’s functions is also understood under the Lax-Phillips approach [44, 45]. However, this definition still allows QNM functions to blow up asymptotically, creating a puzzle: while black hole stability demands that linearized perturbations decay over time, the associated time-harmonic perturbations remain singular in the asymptotic regions.

The resolution lies in the global structure of spacetime. The QNM behavior at asymptotic boundaries results from the singular properties of the coordinates used in Equation 3. In Schwarzschild coordinates, as $r_{\ast }\to \pm \infty$, the limits correspond to spatial infinity $i^0$ and the bifurcation sphere $\mathcal{B}$. These loci connect to future and past null infinity at $i^0$ and white and black hole horizon at $\mathcal{B}$, and the blow-up of QNM eigenfunctions is a coordinate effect due to the accumulation of infinitely many time surfaces thereon.

When QNMs are represented on regular, hyperboloidal time slices, they do not exhibit this unbounded growth¹ [27, 28, 33], as we discuss in the next section.

3 The hyperboloidal approach to QNMs

The singularity of Schwarzschild time slices at the bifurcation sphere is well-known today, but understanding its causal structure took over four decades [46–49]. Given this singularity, it is not surprising that QNMs blow up near the black hole, but they also blow up near spatial infinity. Thus, switching to regular coordinates at the bifurcation sphere does not resolve the issue.

Part of the historical confusion about BHs was that it takes infinite Schwarzschild time for radiation to fall into a BH. The same statement is true concerning spatial infinity: it takes infinite Schwarzschild time for outgoing radiation to reach spatial infinity. Because this is “reasonable” from a physical point of view, it has been widely accepted that QNMs have a singular representation at both asymptotic regions.

The first suggestion that outgoing perturbations are regular in the frequency domain toward null infinity was made by Friedman and Schutz in a 1975 paper on the stability of relativistic stars [50]. Friedman and Schutz recognize the problem with standard time slices where outgoing modes behave asymptotically like $r^k{e}^{i\omega (t-r)}$ implying that stable modes with ${\omega }_I<0$ grow exponentially as $r\to \infty$. To make the representation finite, they recommend to use null hypersurfaces. In a footnote, they comment that the representation is regular also “if one uses a spacelike hypersurface that is only asymptotically null.”

Schmidt picked up this idea in a 1993-essay for the Gravity Research Foundation on relativistic stellar oscillations [26] arguing that QNMs on hyperboloids “are represented by proper eigenvalues and eigenfunctions.” However, the presentation includes no details beyond the 1975 paper.

To understand why it took almost 20 years from Schmidt’s essay [26] to the construction of a regular geometric framework to describe QNMs in asymptotically flat spacetimes¹ [27, 28, 33], we provide a short historical review of hyperboloidal coordinates.

3.1 A brief history of hyperboloidal coordinates

The central role of spacetime hyperbolas in relativity was recognized already by Minkowski in 1908 [51]. The Milne model from 1933 [52] or Dirac’s point-form of quantum field theory from 1949 are hyperboloidal [53]. In the 1970s, hyperboloidal studies were performed for the analysis of wave equations [54–56] and quantum field theory [57–60]. However, these early studies use a time-dependent formulation in which time freezes at null infinity.

The first hyperboloidal coordinates foliating null infinity are implicit in Penrose’s work on the global causal structure of spacetimes via conformal compactification [61, 62]. Indeed, one can obtain a hyperboloidal surface from any textbook discussing the Penrose diagram simply by looking at the level sets of Penrose time [63]. In the context of numerical relativity, it was recognized that hyperboloidal time functions that asymptotically approach the retarded time should be beneficial for the computation of gravitational waves [64, 65]. Explicit hyperboloidal coordinates in black-hole spacetimes were constructed in the context of the analysis of constant mean curvature foliations [66]. A remarkable but largely ignored paper by Gowdy in 1981 includes many key elements of the hyperboloidal approach used today in black-hole perturbation theory [67], including the height function approach to preserve time-translation symmetry, compactification fixing null infinity (scri-fixing), hyperboloidal solutions to the wave equation, and the structure of time-harmonic solutions relevant for the frequency domain. These ideas were not picked up by the community at the time.

The first systematic study of the hyperboloidal initial value problem for Einstein equations was initiated by Friedrich in 1983 [68]. Friedrich devised a reformulation of the Einstein equations with respect to a conformally rescaled metric that is regular across null infinity. The conformal field equations are well-suited for the analysis of the asymptotic behavior of Einstein’s equations and have led to seminal results such as the nonlinear, semi-global stability of de Sitter-type and Minkowski-type spacetimes [69, 70]. The developments around conformal field equations and attempts to use them numerically are reviewed in [71, 72].

Twenty years after Gowdy’s paper, Moncrief presented the hyperboloidal compactification of Minkowski spacetime using time-shifted hyperboloids in an unpublished talk [73] leading to the first numerical studies using hyperboloidal foliations in Minkowski spacetime [74–77]. Around this time, various suggestions for hyperboloidal coordinates and numerical simulations in black-hole spacetimes were made [78–83].

The construction widely used today in black-hole perturbation theory is based on scri-fixing coordinates with time-shifted hyperboloids presented in 2008 [84]. The idea is to combine the height function technique that preserves the time-symmetry of the underlying spacetime with an explicit radial compactification whose singular Jacobian at infinity is proportional to a prescribed conformal factor. In the following years, this method was used primarily in the time domain for solving wave-propagation problems [85–97].

The translation of the hyperboloidal method to the frequency domain was presented in [27], where it was demonstrated that hyperboloidal time functions regularize the QNM eigenfunctions in the asymptotic domains. Warnick used a related idea in [31] for AdS spacetimes in which spatial slices are naturally hyperbolic (see also [29, 30]). The first detailed analysis of QNMs in asymptotically flat black-hole spacetimes using the hyperboloidal approach was presented in [28]. We summarize the basic ideas of the hyperboloidal approach below.

3.2 A geometric framework

The construction of globally regular coordinates consists of a time transformation respecting the time symmetry of the background, a suitable spatial compactification, and conformal rescaling [84]. We first introduce the time function $\tau$ via [67, 82, 84].

$\tau =t+h\left(r\right).(5)$

The time transformation implies an exponential scaling in frequency domain [27]. Writing the time-harmonic ansatz in Equation 2 with respect to the new time coordinate in Equation 5, we get

$u\left(t,r_{*}\right)=e^{-i\omega t}R\left(r_{*}\right)=e^{-i\omega \tau }{e}^{i\omega h}R\left(r_{*}\right)=e^{-i\omega \tau }\bar{R}\left(r_{*}\right).$

The rescaled radial function $\bar{R}(r_{*})=e^{i\omega h}R(r_{*})$ is regular both near the event horizon and toward null infinity. To see this in an explicit example, consider the height function for the so-called minimal gauge [98–100]

$h_{\text{MG}}\left(r\right)=-r+2M\log \left|\frac{r}{2M}-1\right|-4M\log \left(\frac{r}{2M}\right)=-r_{*}-4M\log \left(\frac{r}{2M}\right).$

The minimal gauge height function has the following asymptotic behavior

$h_{\text{MG}}\sim -r_{*}\mathrm{f}\mathrm{o}\mathrm{r}r\to \infty ,h_{\text{MG}}\sim +r_{*}\mathrm{f}\mathrm{o}\mathrm{r}r\to 2M.$

The height function regularizes the QNM eigenfunctions in the asymptotic domains. The regularity of the QNM eigenfunctions is directly related to the regularity of the minimal gauge at the asymptotic boundaries near the horizon and near infinity (see Figure 1). The minimal gauge is unique in its simplicity and appears in different setups as a natural construction [101, 102]. Surprisingly, the minimal gauge was implicitly used by Leaver in his papers on QNMs in BH spacetime [103, 104]. Related hyperboloidal regularization procedures have been suggested over the years by various authors without an explicit recognition of the geometric background of their construction [105–111].

Figure 1

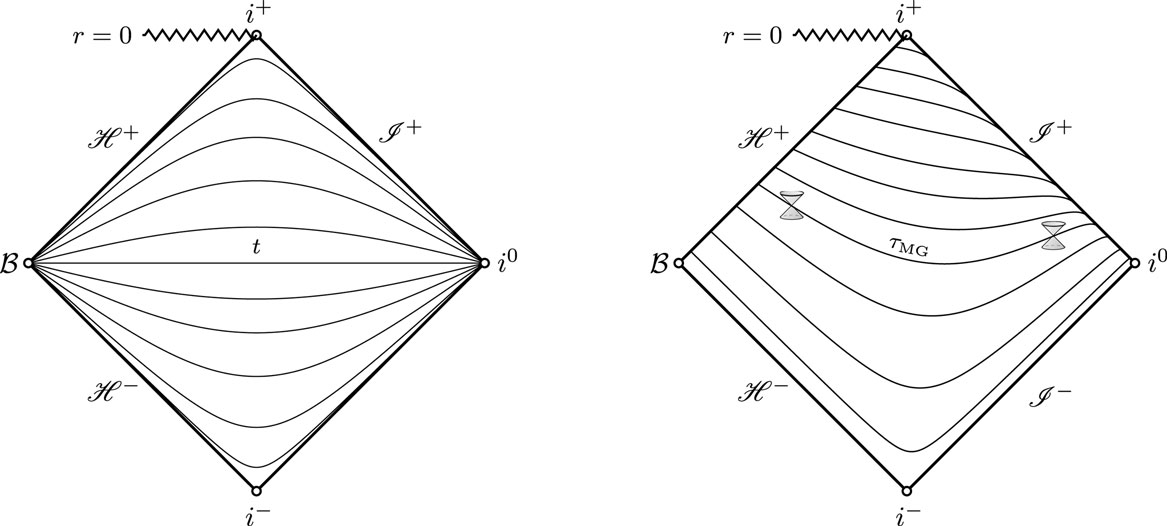
Figure 1. Penrose diagrams of the exterior domain in Schwarzschild spacetime contrasts the level sets of the standard Schwarzschild time (left panel) and the hyperboloidal minimal gauge (right panel). Schwarzschild time slices intersect at the bifurcation sphere, $\mathcal{B}$, and spatial infinity, $i^0$. Minimal gauge slices provide a smooth foliation of the future event horizon, $\mathcal{H^+}$, and future null infinity, ${\mathcal{I}}^{+}$.

In [27], it was shown that the time translation must be combined with a suitable rescaling to arrive at a regular representation of QNMs. The rescaling takes into account the asymptotic fall-off behavior of the QNM eigenfunctions toward the BH and toward infinity. The resulting equations have short-range potentials suitable for compactification of the exterior black region from the radial coordinate $r\in \left[\left.r_h,\infty \right)\right.$ — or equivalently, $r_{\ast }\in (-\infty ,+\infty )$ — into a compact domain $\sigma \in [{\sigma }_h,{\sigma }_{{\mathcal{I}}^{+}}]$. This rescaling is related to the conformal compactification of black-hole spacetimes.

The external boundary conditions (Equation 4) are automatically satisfied in terms of a radially compact hyperboloidal coordinates $(\tau ,\sigma )$[27, 100], when the underlying function $\bar{R}(\sigma )$ is regular at the black-hole horizon $({\sigma }_h)$ and future null infinity $({\sigma }_{{\mathcal{I}}^{+}})$. Thus, we no longer need to impose boundary conditions to the wave equation by hand. The boundary condition is replaced by a regularity condition on the underlying solution $\bar{R}(\sigma )$ in the entire domain $\sigma \in [{\sigma }_h,{\sigma }_{{\mathcal{I}}^{+}}]$. In practical terms, one derives the regularity condition at the boundary directly from the hyperboloidal differential equation. When formulating the frequency-domain problem in coordinates $(\tau ,\sigma )$, the resulting differential equation equivalent to Helmoltz Equation 3 assumes a generic form [28, 99, 100].

$\left({\alpha }_2\left(\sigma \right)\frac{d^2}{d{\sigma }^2}+{\alpha }_1\left(\sigma \right)\frac{d}{d\sigma }+{\alpha }_0\left(\sigma \right)\right)\bar{R}\left(\sigma \right)=0,(6)$

with coefficients ${\alpha }_2$, ${\alpha }_1$ and ${\alpha }_0$ depending on the particular choice for the hyperboloidal height function. The most important property of the above equation is that it is a singular ordinary differential equation, i. e., its principal part behaves as ${\alpha }_2\sim {(\sigma -{\sigma }_{{\mathcal{I}}^{+}})}^2(\sigma -{\sigma }_h)$ and therefore ${\alpha }_2({\sigma }_h)={\alpha }_2({\sigma }_{{\mathcal{I}}^{+}})=0$. Hence, at the boundaries, Equation 6 provides us directly with the relation between the field and its first $\sigma$-derivatives serving as boundary data ensuring a bounded solution. From the spacetime perspective, and the resulting wave equation, the same condition ${\alpha }_2({\sigma }_h)={\alpha }_2({\sigma }_{{\mathcal{I}}^{+}})=0$ ensures that, at the boundaries, the light cones point outwards the numerical domain, or equivalently, that the characteristic speeds of incoming modes vanish [27, 100].

The finite behaviour of the function $\bar{R}(\sigma )$ is one of the most important aspects in the hyperboloidal approach. As we discuss below, this feature allows us to unveil new properties of the QNM eigenfunctions, develop novel numerical algorithms and attack new problems relevant to black-hole physics and gravitational wave astronomy.

3.3 From geometry to analysis

The hyperboloidal framework regularizes solutions to the Helmholtz problem Equation 3. In fact, any bounded solution satisfying the singular ordinary differential Equation 6 automatically fulfills the Sommerfeld conditions (Equation 4). One would naively think that bounded solutions exist only at the QNMs frequencies. However, we saw in Section 2 that the conditions (Equation 4) are necessary, but not sufficient to specify the QNM problem uniquely. In the traditional formulation, the QNM eigenfunctions grow asymptotically. The complex plane spanned by the frequency $\omega$ might contain regions with solution satisfying (Equation 4), but contaminated by unwanted solutions that decrease at the boundaries. Removing the asymptotic blow-up allows us to peek directly into these unphysical solutions, which exist in the entire half-plane $\mathrm{I}\mathrm{m}(\omega )<0$ [28, 31].

The left panel of Figure 2 shows two solutions to Equation 6 which are bounded in the entire exterior BH domain, from $\sigma =0$ representing future null infinity and $\sigma =1$ the BH horizon: the solution in blue is obtained at a given QNM frequency ${\omega }_{\text{QNM}}$, whereas the solution in red corresponds to a given frequency in the half-plane $\mathrm{I}\mathrm{m}(\omega )<0$, but with $\omega \ne {\omega }_{\text{QNM}}$. These solutions are obtained with two different numerical approaches: the solid line results from solving the ODE with a Chebyshev collocation point spectral method [112], whereas the dotted points arise when using Leaver’s Taylor expansion, which corresponds to a frequency domain hyperboloidal formulation in the minimal gauge [28, 99, 113]. Both strategies yield the same results. At first glance, there is nothing special in the behavior of the solutions that allows us to distinguish a QNM from a non-QNM eigenfunction. Indeed, it is even possible to specify a hyperboloidal initial data such that the corresponding time evolution has an arbitrary exponentially damped oscillation [28].

Figure 2

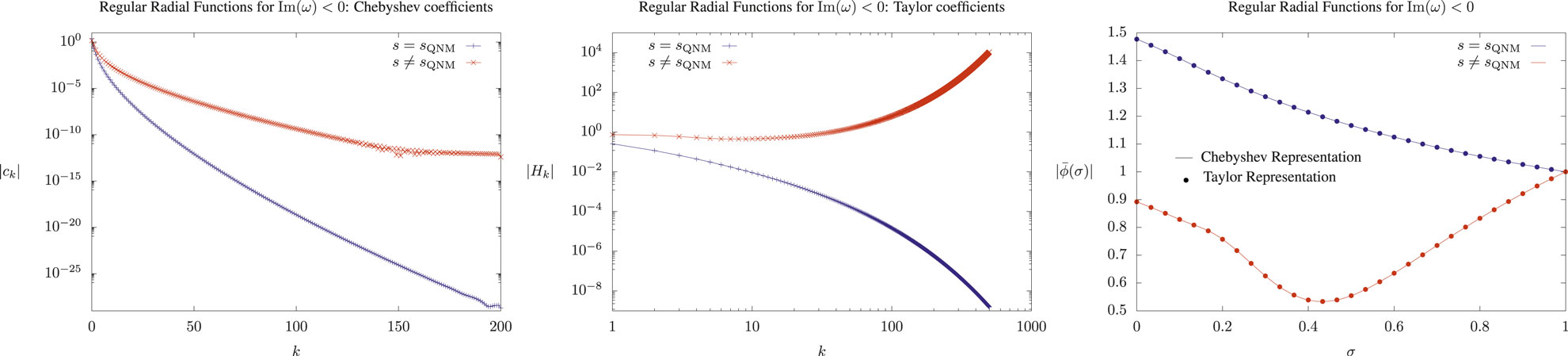
Figure 2. Solutions to hyperboloidal radial equation (left panel). Bounded solutions exist in the entire half-plane for $\mathrm{I}\mathrm{m}(\omega )<0$, regardless whether $\omega$ is a QNM or not. The continuous lines were obtained with a spectral method code based on a Chebyshev representation of the solution. Independently, the dots result from a Taylor representation of the solution as power series around the horizon (Leaver’s strategy). The QNM eigenfunctions are characterised by the solutions with a higher degree of regularity, heuristically verified via the faster decay of the corresponding Chebyshev coefficients $|c_k|$ (middle panel) or the asymptotic decay of the Taylor coefficients $|a_k|$.

What distinguishes a QNM from a non-QNM solution is their regularity class. By studying the convergence rate of their discrete numerical representation, one can infer that these functions belong to different regularity classes. The middle panel of Figure 2 shows the Chebyshev coefficients from the Chebyshev collocation point spectral method. These coefficients decay exponentially for $C^{\mathrm{\Omega }}$ analytic functions or algebraically for $C^k$ singular functions. We observe an intermediary decay, suggesting the regularity class of these functions is between $C^k$ and $C^{\mathrm{\Omega }}$. The Chebyshev coefficients for QNM eigenfunctions decay faster than for non-QNM eigenfunctions, indicating QNM eigenfunctions belong to a better regularity class. A similar conclusion arises from the Taylor expansion coefficients (right panel 2). For QNM eigenfunctions, $|a_k|$ decays asymptotically. For non-QNM functions, $|a_k|$ grows asymptotically. Even though the series does not converge absolutely, it converges conditionally due to oscillations in $\mathrm{I}\mathrm{m}(a_k)$ (left panel of Figure 2). These conclusions are formalized by interpreting QNM as a formal eigenvalue problem of the generator of time translations for a null foliation, acting on an appropriate Hilbert space [29–33, 114–116], where QNM eigenfunctions belong to the Gevrey-2 regularity class.

4 Applications

The QNM problem plays a fundamental role in the era of gravitational wave astronomy. The BH spectroscopy program faces three main challenges: (i) the measurability of the QNMs frequencies, limited by the GW detection signal-to-noise ratios; (ii) the relevance of nonlinear effects to the ringdown dynamics; and (iii) the QNMs spectral instability. As discussed in the previous sections, hyperboloidal formalism provides crucial theoretical tools to tackle different aspects of these challenges.

4.1 QNM excitation factors and tail decay

Even though challenge (i) mainly concerns the GW detection’s signal-to-noise ratio, it heavily relies on accurate predictions for the expected QNM excitations [117]. The excitation of each QNM depends on the particular initial perturbation triggering the dynamics. This perturbation also excites the late-time power-law tail decay. Determining these excitation factors has always been challenging due to the blow-up of the underlying modes at the bifurcation sphere and spatial infinity [118]. A common approach to avoid the infinities at the bifurcation sphere when calculating integrals along the physical coordinate $r_{\ast }\in (-\infty ,\infty )$ is to deform the integration path into the complex plane [119–121].

The hyperboloidal formalism offers an alternative strategy to determine such excitation factors due to the globally regular behavior of the QNM eigenfunctions. The direct identification of Leaver’s continued fraction strategy with spacetime solutions defined on hyperboloidal hypersurfaces allows the further development of the Leaver method to calculate QNMs (and tail decay) excitation factors for problems formulated on hyperboloidal slices [28, 99]. While Leaver’s method relies on a Taylor expansion around the horizon for the underlying hyperboloidal functions, the strategy can be adapted to directly solve a linear partial differential equation having the QNM excitation amplitude as an unknown parameter in the equation [122], or alternatively via the so-called Keldysh scheme [123]. The hyperboloidal formalism is also essential for recent advances in the understanding of the role played by the tail decay in BH spectroscopy [124–126].

4.2 Quadratic QNMs

Since GR is a nonlinear theory, challenge (ii) emphasizes that BH spectroscopy must also account for second-order, quadratic perturbations [21, 127–136]. The quadratic coupling of first-order solutions dictates the dynamics at second order in perturbation theory [137–139]. When formulated in the standard $t$ slices, the blow-up of QNM eigenfunctions at the bifurcation sphere and spatial infinity imposes severe restrictions for second-order studies, both at theoretical and numerical levels. The hyperboloidal framework for black-hole perturbations beyond the linear order becomes indispensable for regular evolutions [23, 132, 140], as well as for studies in the frequency domain [134, 141].

4.3 QNM instability and the pseudospectrum

Apart from his groundbreaking work in QNM [34], Vishveshwara also highlighted that the QNM spectra is very sensitive to small modifications in the black-hole potential [142, 143]. At the same time, the QNM spectra destabilisation was also observed by Nollter and Price [144, 145], but the phenomenon’s impact in the BH spectroscopy programme has been largely overlooked over the past decades. Only recently has the challenge (iii) gained a greater attention [112, 146–155].

Small modifications in oscillatory frequencies for wave equations result in minor spectral responses only if the wave operators are self-adjoint. However, the flow of GWs into the BH and out into the wave zone places BH perturbation theory within the framework of non-self-adjoint operators. The successful application of non-self-adjoint operator theory to gravitational systems was only made possible by the hyperboloidal approach to black-hole perturbations [112] (see also Ref. [156] for an alternative approach akin to “complex scaling”). In this approach, one can use the mathematical formalism of pseudospectra [157] to study the QNM spectral instability [112] and perform a non-modal analysis [151] that a traditional mode analysis might overlook. Since the breakthrough offered by the hyperboloidal framework, the analysis of QNM pseudospectra has been performed in several different contexts, from astrophysically relevant scenarios to applications in the gauge-gravity duality [158–167].

5 Discussion

The hyperboloidal approach to QNMs offers a geometric regularization of black-hole perturbations. By connecting the regular oscillations near BHs with those observed far away, this method bypasses the problematic divergences inherent in the traditional approach at the bifurcation sphere and spatial infinity.

With hindsight, the hyperboloidal approach relies on a simple coordinate transformation that resolves the asymptotic singularity of the standard time [84]. It is astonishing that it took decades for relativists to adopt regular coordinates to describe black-hole perturbations. We suspect that part of the confusion arose from the asymptotic behavior of time functions. It is not widely appreciated that the standard time coordinate in flat spacetime is singular at infinity with respect to the causal structure. Large-scale wave phenomena demand coordinates tailored to wave propagation—characteristic or hyperboloidal. This approach is critical not only for gravitational waves but also for addressing general wave propagation problems.

In recent years, the hyperboloidal approach has led to significant breakthroughs in the study of black-hole perturbations. As discussed, the regularity of the QNM eigenfunctions in the frequency domain enables a direct identification of the QNM excitation factors and tail decay 4.1, facilitates the efficient computation of second-order perturbations 4.2, and supports the analysis of the QNM pseudospectrum 4.3. Moreover, recent work has demonstrated that the hyperboloidal method can be extended to non-relativistic operators [168], further broadening its scope and applicability.

From a numerical perspective, finding the optimal choices among the many ways to construct hyperboloidal coordinates, particularly for high-precision and large-scale simulations, remains a challenge. Exploring gauge conditions and optimizing numerical algorithms to leverage advanced computational resources will be essential for practical applications, going beyond linear perturbations and including the numerical solution of the full Einstein equations along hyperboloidal surfaces [169, 170].

Much of the current work has focused on asymptotically flat, vacuum spacetimes. The formalism for black hole perturbation theory is fully developed for spherically symmetric spacetimes, but the same concepts are also valid for the Kerr solution [102, 113]. The hyperboloidal approach is versatile and extendable to more general settings, including those with different asymptotic structures, and nonvaccum spacetimes. Developing these extensions will be crucial for applying this framework to a broader range of physical scenarios.

Author contributions

RP: Writing–original draft, Writing–review and editing. AZ: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. RPM acknowledges support from the Villum Investigator program supported by the VILLUM Foundation (grant no. VIL37766) and the DNRF Chair program (grant no. DNRF162) by the Danish National Research Foundation and the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 101131233. AZ is supported by the National Science Foundation under Grant No. 2309084.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Note that we focus here on the geometric developments around the hyperboloidal framework in asymptotically flat spacetimes. The analytic aspects of QNM regularity beyond the mere coordinate singularity of standard time slices were clarified in a series of papers [29–33], discussed in Section 3.3.

References

1. Kokkotas KD, Schmidt BG. Quasi-normal modes of stars and black holes. Living Rev Relativity (1999) 2:2–72. doi:10.12942/lrr-1999-2

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Nollert HP. Quasinormal modes: the characteristic ‘sound’ of black holes and neutron stars. Classical Quan Gravity (1999) 16:R159–216. doi:10.1088/0264-9381/16/12/201

CrossRef Full Text | Google Scholar

3. Berti E, Cardoso V, Starinets AO. Quasinormal modes of black holes and black branes. Classical Quan Gravity (2009) 26:163001. doi:10.1088/0264-9381/26/16/163001

CrossRef Full Text | Google Scholar

4. Konoplya RA, Zhidenko A. Quasinormal modes of black holes: from astrophysics to string theory. Rev Mod Phys (2011) 83:793–836. doi:10.1103/RevModPhys.83.793

CrossRef Full Text | Google Scholar

5. Dreyer O, Kelly BJ, Krishnan B, Finn LS, Garrison D, Lopez-Aleman R. Black hole spectroscopy: testing general relativity through gravitational wave observations. Class Quant Grav (2004) 21:787–803. doi:10.1088/0264-9381/21/4/003

CrossRef Full Text | Google Scholar

6. Berti E, Cardoso V, Will CM. Gravitational-wave spectroscopy of massive black holes with the space interferometer LISA. Phys Rev D (2006) 73:064030. doi:10.1103/PhysRevD.73.064030

CrossRef Full Text | Google Scholar

7. Berti E, Sesana A, Barausse E, Cardoso V, Belczynski K. Spectroscopy of Kerr black holes with Earth- and space-based interferometers. Phys Rev Lett (2016) 117:101102. doi:10.1103/PhysRevLett.117.101102

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Franchini N, Völkel SH. Testing general relativity with black hole quasi-normal modes. arXiv:2305.01696 (2023). doi:10.1007/978-981-97-2871-8_9

CrossRef Full Text | Google Scholar

9. Abbott BP, Abbott R, Abbott T, Abernathy M, Acernese F, Ackley K, et al. Observation of gravitational waves from a binary black hole merger. Phys Rev Lett (2016) 116:061102. doi:10.1103/PhysRevLett.116.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Abbott R, Abbott T, Abraham S, Acernese F, Ackley K, Adams A, et al. Tests of general relativity with binary black holes from the second LIGO-Virgo gravitational-wave transient catalog. Phys Rev D (2021) 103:122002. doi:10.1103/PhysRevD.103.122002

CrossRef Full Text | Google Scholar

11. The LIGO Scientific Collaboration, the Virgo Collaboration, the KAGRA Collaboration, Abbott R, Abe H, Acernese F, et al. Tests of general relativity with GWTC-3 (2021) arXiv:2112.06861.

Google Scholar

12. Isi M, Giesler M, Farr WM, Scheel MA, Teukolsky SA. Testing the no-hair theorem with GW150914. Phys Rev Lett (2019) 123:111102. doi:10.1103/PhysRevLett.123.111102

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Capano CD, Nitz AH. Binary black hole spectroscopy: a no-hair test of GW190814 and GW190412. Phys Rev D (2020) 102:124070. doi:10.1103/PhysRevD.102.124070

CrossRef Full Text | Google Scholar

14. Capano CD, Cabero M, Westerweck J, Abedi J, Kastha S, Nitz AH, et al. Multimode quasinormal spectrum from a perturbed black hole. Phys Rev Lett (2023) 131:221402. doi:10.1103/PhysRevLett.131.221402

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Cotesta R, Carullo G, Berti E, Cardoso V. Analysis of ringdown overtones in GW150914. Phys Rev Lett (2022) 129:111102. doi:10.1103/PhysRevLett.129.111102

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Capano CD, Abedi J, Kastha S, Nitz AH, Westerweck J, Wang YF, et al. Estimating false alarm rates of sub-dominant quasi-normal modes in GW190521 class. Quantum Grav (2024) 41:245009. doi:10.1088/1361-6382/ad84ae

CrossRef Full Text | Google Scholar

17. Forteza XJ, Bhagwat S, Kumar S, Pani P. Novel ringdown amplitude-phase consistency test. Phys Rev Lett (2023) 130:021001. doi:10.1103/PhysRevLett.130.021001

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Finch E, Moore CJ. Searching for a ringdown overtone in GW150914. Phys Rev D (2022) 106:043005. doi:10.1103/PhysRevD.106.043005

CrossRef Full Text | Google Scholar

19. Abedi J, Capano CD, Kastha S, Nitz AH, Wang YF, Westerweck J, et al. Spectroscopy for asymmetric binary black hole mergers. Phys Rev D (2023) 108:104009. doi:10.1103/PhysRevD.108.104009

CrossRef Full Text | Google Scholar

20. Carullo G, Cotesta R, Berti E, Cardoso V, Carullo , et al. Reply:. Phys Rev Lett (2023) 131:169002. doi:10.1103/PhysRevLett.131.169002

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Baibhav V, Cheung MHY, Berti E, Cardoso V, Carullo G, Cotesta R, et al. Agnostic black hole spectroscopy: quasinormal mode content of numerical relativity waveforms and limits of validity of linear perturbation theory. Phys Rev D (2023) 108:104020. doi:10.1103/PhysRevD.108.104020

CrossRef Full Text | Google Scholar

22. Nee PJ, Völkel SH, Pfeiffer HP. Role of black hole quasinormal mode overtones for ringdown analysis. Phys Rev D (2023) 108:044032. doi:10.1103/PhysRevD.108.044032

CrossRef Full Text | Google Scholar

23. Zhu H, Ripley JL, Cárdenas-Avendaño A, Pretorius F. Challenges in quasinormal mode extraction: perspectives from numerical solutions to the Teukolsky equation. Phys Rev D (2024) 109:044010. doi:10.1103/PhysRevD.109.044010

CrossRef Full Text | Google Scholar

24. Siegel H, Isi M, Farr WM. Ringdown of GW190521: hints of multiple quasinormal modes with a precessional interpretation. Phys Rev D (2023) 108:064008. doi:10.1103/PhysRevD.108.064008

CrossRef Full Text | Google Scholar

25. Gennari V, Carullo G, Del Pozzo W. Searching for ringdown higher modes with a numerical relativity-informed post-merger model. Eur Phys J C (2024) 84:233. doi:10.1140/epjc/s10052-024-12550-x

CrossRef Full Text | Google Scholar

26. Schmidt BG. On relativistic stellar oscillations. Massachusetts, United States: Gravity Research Foundation essay (1993).

Google Scholar

27. Zenginoğlu A. A geometric framework for black hole perturbations. Phys Rev D (2011) 83:127502. doi:10.1103/PhysRevD.83.127502

CrossRef Full Text | Google Scholar

28. Ansorg M, Macedo RP. Spectral decomposition of black-hole perturbations on hyperboloidal slices. Phys Rev D (2016) 93:124016. doi:10.1103/PhysRevD.93.124016

CrossRef Full Text | Google Scholar

29. Horowitz GT, Hubeny VE. Quasinormal modes of ads black holes and the approach to thermal equilibrium. Phys Rev D (2000) 62:024027. doi:10.1103/physrevd.62.024027

CrossRef Full Text | Google Scholar

30. Vasy A. Microlocal analysis of asymptotically hyperbolic and kerr-de sitter spaces (with an appendix by semyon dyatlov). Inventiones mathematicae (2013) 194:381–513. doi:10.1007/s00222-012-0446-8

CrossRef Full Text | Google Scholar

31. Warnick CM. On quasinormal modes of asymptotically anti-de Sitter black holes. Commun Math Phys (2015) 333:959–1035. doi:10.1007/s00220-014-2171-1

CrossRef Full Text | Google Scholar

32. Gajic D, Warnick C. A model problem for quasinormal ringdown of asymptotically flat or extremal black holes. J Math Phys (2020) 61:102501. doi:10.1063/5.0024699

CrossRef Full Text | Google Scholar

33. Gajic D, Warnick CM. Quasinormal modes on Kerr spacetimes. arXiv preprint gr-qc:2407 (2024):04098. Available at: https://arxiv.org/abs/2407.04098.

Google Scholar

34. Vishveshwara CV. Scattering of gravitational radiation by a schwarzschild black-hole. Nature (1970) 227:936–8. doi:10.1038/227936a0

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Price RH. Nonspherical perturbations of relativistic gravitational collapse. i. scalar and gravitational perturbations. Phys Rev D (1972) 5:2419–38. doi:10.1103/PhysRevD.5.2419

CrossRef Full Text | Google Scholar

36. Gundlach C, Price RH, Pullin J. Late-time behavior of stellar collapse and explosions. i. linearized perturbations. Phys Rev D (1994) 49:883–9. doi:10.1103/PhysRevD.49.883

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Sommerfeld A. Die greensche funktion der schwingungsgleichung. J.-Ber Deutsch Math.-Verein (1912) 21:309–53. Available at: https://eudml.org/doc/145344.

Google Scholar

38. Schot SH. Eighty years of Sommerfeld’s radiation condition. Historia Mathematica (1992) 19:385–401. doi:10.1016/0315-0860(92)90004-U

CrossRef Full Text | Google Scholar

39. Nollert HP, Schmidt BG. Quasinormal modes of schwarzschild black holes: defined and calculated via laplace transformation. Phys Rev D (1992) 45:2617–27. doi:10.1103/PhysRevD.45.2617

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Bachelot A, Motet-Bachelot A. Les résonances d’un trou noir de schwarzschild. Ann de l’IHP Physique théorique (1993) 59:3–68. Available at: http://www.numdam.org/item/AIHPA_1993__59_1_3_0/.

Google Scholar

41. Leaver EW. Spectral decomposition of the perturbation response of the schwarzschild geometry. Phys Rev D (1986) 34:384–408. doi:10.1103/PhysRevD.34.384

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Sun Y, Price RH. Excitation of quasinormal ringing of a schwarzschild black hole. Phys Rev D (1988) 38:1040–52. doi:10.1103/PhysRevD.38.1040

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Kay BS, Wald RM. Linear stability of Schwarzschild under perturbations which are non-vanishing on the bifurcation 2-sphere. Class Quan Gravity (1987) 4:893–8. doi:10.1088/0264-9381/4/4/022

CrossRef Full Text | Google Scholar

44. Zworski M. Mathematical study of scattering resonances. Bull Math Sci (2017) 7:1–85. doi:10.1007/s13373-017-0099-4

CrossRef Full Text | Google Scholar

45. Dyatlov S, Zworski M. Mathematical theory of scattering resonances. American Mathematical Society (2019) Graduate Studies in Mathematics.

CrossRef Full Text | Google Scholar

46. Israel W. Dark stars: the evolution of an idea. Cambridge, United Kingdom: Three hundred years of gravitation (1987) p. 199–276.

Google Scholar

47. Senovilla JMM, Garfinkle D. The 1965 Penrose singularity theorem. Classical Quan Gravity (2015) 32:124008. doi:10.1088/0264-9381/32/12/124008

CrossRef Full Text | Google Scholar

48. Nielsen N. On the origin of the Gullstrand–Painlevé coordinates. The Eur Phys J H (2022) 47:6. doi:10.1140/epjh/s13129-022-00038-9

CrossRef Full Text | Google Scholar

49. Landsman K. Penrose’s 1965 singularity theorem: from geodesic incompleteness to cosmic censorship. Gen Relativity Gravitation (2022) 54:115. doi:10.1007/s10714-022-02973-w

CrossRef Full Text | Google Scholar

50. Friedman JL, Schutz BF. On the stability of relativistic systems. The Astrophysical J (1975) 200:204–20. doi:10.1086/153778

CrossRef Full Text | Google Scholar

51. Minkowski H. Raum und Zeit (Jahresbericht der Deutschen Mathematiker-Vereinigung) (1908) p. 75–88.

Google Scholar

52. Milne EA. Relativity, gravitation, and world-structure. Philosophy (1936) 11. Available at: https://archive.org/details/dli.ernet.7948/page/n3/mode/2up.

Google Scholar

53. Dirac PA. Forms of relativistic dynamics. Rev Mod Phys (1949) 21:392–9. doi:10.1103/revmodphys.21.392

CrossRef Full Text | Google Scholar

54. Chen YW, Lewy H. Solutions of the n-dimensional wave equation in the exterior of the characteristic cones (I). Indiana Univ Mathematics J (1970) 20:33–55. doi:10.1512/iumj.1971.20.20003

CrossRef Full Text | Google Scholar

55. Chen YW, Lewy H. On the hyperboloidal means and the wave equation. Indiana Univ Mathematics J (1971) 21:437–47. Available at: https://www.jstor.org/stable/24890372.

Google Scholar

56. Strichartz RS. Harmonic analysis on hyperboloids. J Funct Anal (1973) 12:341–83. doi:10.1016/0022-1236(73)90001-3

CrossRef Full Text | Google Scholar

57. Fubini S, Hanson AJ, Jackiw R. New approach to field theory. Phys Rev D (1973) 7:1732–60. doi:10.1103/physrevd.7.1732

CrossRef Full Text | Google Scholar

58. DiSessa A. Quantization on hyperboloids and full space-time field expansion. J Math Phys (1974) 15:1892–900. doi:10.1063/1.1666554

CrossRef Full Text | Google Scholar

59. Sommerfield CM. Quantization on spacetime hyperboloids. Ann Phys (1974) 84:285–302. doi:10.1016/0003-4916(74)90304-2

CrossRef Full Text | Google Scholar

60. Hostler L. Coulomb-like quantization of the electromagnetic field on spacelike hyperboloids. J Math Phys (1978) 19:2094–9. doi:10.1063/1.523565

CrossRef Full Text | Google Scholar

61. Penrose R. Zero rest-mass fields including gravitation: asymptotic behaviour. Proc R Soc Lond Ser A. Math Phys Sci (1965) 284:159–203. doi:10.1098/rspa.1965.0058

CrossRef Full Text | Google Scholar

62. Penrose R. Asymptotic properties of fields and space-times. Phys Rev Lett (1963) 10:66–8. doi:10.1103/PhysRevLett.10.66

CrossRef Full Text | Google Scholar

63. Zenginoğlu A. Hyperbolic times in Minkowski space. Am J Phys (2024) 92:965–74. doi:10.1119/5.0214271

CrossRef Full Text | Google Scholar

64. Smarr L, York JW. Kinematical conditions in the construction of spacetime. Phys Rev D (1978) 17:2529–51. doi:10.1103/PhysRevD.17.2529

CrossRef Full Text | Google Scholar

65. Eardley DM, Smarr L. Time functions in numerical relativity: marginally bound dust collapse. Phys Rev D (1979) 19:2239–59. doi:10.1103/PhysRevD.19.2239

CrossRef Full Text | Google Scholar

66. Brill DR, Cavallo JM, Isenberg JA. K -surfaces in the Schwarzschild space-time and the construction of lattice cosmologies. J Math Phys (1980) 21:2789–96. doi:10.1063/1.524400

CrossRef Full Text | Google Scholar

67. Gowdy RH. The wave equation in asymptotically retarded time coordinates: waves as simple, regular functions on a compact manifold. J Math Phys (1981) 22:675–8. doi:10.1063/1.524975

CrossRef Full Text | Google Scholar

68. Friedrich H. Cauchy problems for the conformal vacuum field equations in general relativity. Commun Math Phys (1983) 91:445–72. doi:10.1007/bf01206015

CrossRef Full Text | Google Scholar

69. Friedrich H. Existence and structure of past asymptotically simple solutions of einstein’s field equations with positive cosmological constant. J Geometry Phys (1986) 3:101–17. doi:10.1016/0393-0440(86)90004-5

CrossRef Full Text | Google Scholar

70. Friedrich H. On the existence of n-geodesically complete or future complete solutions of einstein’s field equations with smooth asymptotic structure. Commun Math Phys (1986) 107:587–609. doi:10.1007/bf01205488

CrossRef Full Text | Google Scholar

71. Frauendiener J. Conformal infinity. Living Rev Relativity (2004) 7:1. doi:10.12942/lrr-2004-1

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Kroon JAV. Conformal methods in general relativity. Cambridge: Cambridge University Press (2016).

Google Scholar

73. Moncrief V. Conformally regular ADM evolution equations (2000) Available from: Http://online.itp.ucsb.edu/online/numrel00/moncrief (Accessed December 27, 2024).

Google Scholar

74. Husa S. Numerical relativity with the conformal field equations. In: Current trends in relativistic astrophysics: theoretical, numerical, observational. Springer (2003) p. 159–92.

Google Scholar

75. Fodor G, Racz I. What does a strongly excited ’t Hooft-Polyakov magnetic monopole do? Phys Rev Lett (2004) 92:151801. doi:10.1103/physrevlett.92.151801

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Fodor G, Racz I. Numerical investigation of highly excited magnetic monopoles in su (2) yang-mills-higgs theory. Phys Rev D—Particles, Fields, Gravitation, Cosmology (2008) 77:025019. doi:10.1103/physrevd.77.025019

CrossRef Full Text | Google Scholar

77. Bizoń P, Zenginoğlu A. Universality of global dynamics for the cubic wave equation. Nonlinearity (2009) 22:2473–85. doi:10.1088/0951-7715/22/10/009

CrossRef Full Text | Google Scholar

78. Gentle AP, Holz DE, Kheyfets A, Laguna P, Miller WA, Shoemaker DM. Constant crunch coordinates for black hole simulations. Phys Rev D (2001) 63:064024. doi:10.1103/PhysRevD.63.064024

CrossRef Full Text | Google Scholar

79. Gowdy RH. The compactification of initial data on constant mean curvature time slices in spherically symmetric spacetimes. arXiv:gr-qc/0107016 (2001). Available at: https://arxiv.org/abs/gr-qc/0107016.

Google Scholar

80. Schmidt BG. Data for the numerical calculation of the kruskal space-time. In: R Beig, BG Englert, U Frisch, P Hänggi, K Hepp, W Hillebrandt, and et al., editors. The conformal structure of space-time, 604. Berlin, Heidelberg: Springer Berlin Heidelberg (2002) p. 283–95. doi:10.1007/3-540-45818-2_14

CrossRef Full Text | Google Scholar

81. Pareja MJ, Frauendiener J. Constant scalar curvature hypersurfaces in extended Schwarzschild space-time. Phys Rev D (2006) 74:044026. doi:10.1103/PhysRevD.74.044026

CrossRef Full Text | Google Scholar

82. Calabrese G, Gundlach C, Hilditch D. Asymptotically null slices in numerical relativity: mathematical analysis and spherical wave equation tests. Classical Quan Gravity (2006) 23:4829–45. doi:10.1088/0264-9381/23/15/004

CrossRef Full Text | Google Scholar

83. Misner CW, van Meter JR, Fiske DR. Excising das All: Evolving Maxwell waves beyond scri. Phys Rev D—Particles, Fields, Gravitation, Cosmology (2006) 74:064003. doi:10.1103/physrevd.74.064003

CrossRef Full Text | Google Scholar

84. Zenginoğlu A. Hyperboloidal foliations and scri-fixing. Classical Quan Gravity (2008) 25:145002. doi:10.1088/0264-9381/25/14/145002

CrossRef Full Text | Google Scholar

85. Zenginoğlu A. A hyperboloidal study of tail decay rates for scalar and Yang–Mills fields. Classical Quan gravity (2008) 25:175013. doi:10.1088/0264-9381/25/17/175013

CrossRef Full Text | Google Scholar

86. Zenginoğlu A, Nunez D, Husa S. Gravitational perturbations of schwarzschild spacetime at null infinity and the hyperboloidal initial value problem. Classical Quan Gravity (2009) 26:035009. doi:10.1088/0264-9381/26/3/035009

CrossRef Full Text | Google Scholar

87. Zenginoğlu A, Tiglio M. Spacelike matching to null infinity. Phys Rev D (2009) 80:024044. doi:10.1103/PhysRevD.80.024044

CrossRef Full Text | Google Scholar

88. Zenginoğlu A. Asymptotics of Schwarzschild black hole perturbations. Classical Quan Gravity (2010) 27:045015. doi:10.1088/0264-9381/27/4/045015

CrossRef Full Text | Google Scholar

89. Zenginoğlu A, Kidder LE. Hyperboloidal evolution of test fields in three spatial dimensions. Phys Rev D (2010) 81:124010. doi:10.1103/physrevd.81.124010

CrossRef Full Text | Google Scholar

90. Bizoń P, Rostworowski A, Zenginoğlu A. Saddle-point dynamics of a Yang–Mills field on the exterior Schwarzschild spacetime. Classical Quan Gravity (2010) 27:175003. doi:10.1088/0264-9381/27/17/175003

CrossRef Full Text | Google Scholar

91. Lora-Clavijo F, Cruz-Osorio A, Guzmán F. Evolution of a massless test scalar field on boson star space-times. Phys Rev D (2010) 82:023005. doi:10.1103/physrevd.82.023005

CrossRef Full Text | Google Scholar

92. Jasiulek M. Hyperboloidal slices for the wave equation of kerr–schild metrics and numerical applications. Classical Quan gravity (2011) 29:015008. doi:10.1088/0264-9381/29/1/015008

CrossRef Full Text | Google Scholar

93. Racz I, Tóth GZ. Numerical investigation of the late-time Kerr tails. Classical Quan Gravity (2011) 28:195003. doi:10.1088/0264-9381/28/19/195003

CrossRef Full Text | Google Scholar

94. Vega I, Wardell B, Diener P. Effective source approach to self-force calculations. Classical Quan Gravity (2011) 28:134010. doi:10.1088/0264-9381/28/13/134010

CrossRef Full Text | Google Scholar

95. Bernuzzi S, Nagar A, Zenginoğlu A. Binary black hole coalescence in the extreme-mass-ratio limit: testing and improving the effective-one-body multipolar waveform. Phys Rev D (2011) 83:064010. doi:10.1103/PhysRevD.83.064010

CrossRef Full Text | Google Scholar

96. Bernuzzi S, Nagar A, Zenginoğlu A. Binary black hole coalescence in the large-mass-ratio limit: the hyperboloidal layer method and waveforms at null infinity. Phys Rev D (2011) 84:084026. doi:10.1103/PhysRevD.84.084026

CrossRef Full Text | Google Scholar

97. Zenginoğlu A, Khanna G. Null infinity waveforms from extreme-mass-ratio inspirals in kerr spacetime. Phys Rev X (2011) 1:021017. doi:10.1103/physrevx.1.021017

CrossRef Full Text | Google Scholar

98. Schinkel D, Ansorg M, Macedo RP. Initial data for perturbed Kerr black holes on hyperboloidal slices. Classical Quan Gravity (2014) 31:165001. doi:10.1088/0264-9381/31/16/165001

CrossRef Full Text | Google Scholar

99. Panosso Macedo R, Jaramillo JL, Ansorg M. Hyperboloidal slicing approach to quasi-normal mode expansions: the Reissner-Nordström case. Phys Rev D (2018) 98:124005. doi:10.1103/PhysRevD.98.124005

CrossRef Full Text | Google Scholar

100. Panosso Macedo R. Hyperboloidal approach for static spherically symmetric spacetimes: a didactical introduction and applications in black-hole physics. Phil Trans Roy Soc Lond A (2024) 382:20230046. doi:10.1098/rsta.2023.0046

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Aimer JWA. Quasinormal modes of black holes (2023). New Zealand: University of Canterbury Christchurch. Doctoral dissertation. doi:10.26021/14994

CrossRef Full Text | Google Scholar

102. Ripley JL. Computing the quasinormal modes and eigenfunctions for the Teukolsky equation using horizon penetrating, hyperboloidally compactified coordinates. Class Quant Grav (2022) 39:145009. doi:10.1088/1361-6382/ac776d

CrossRef Full Text | Google Scholar

103. Leaver EW. An analytic representation for the quasi-normal modes of kerr black holes. Proc R Soc Lond A. Math Phys Sci (1985) 402:285–98. doi:10.1098/rspa.1985.0119

CrossRef Full Text | Google Scholar

104. Leaver EW. Quasinormal modes of Reissner-Nordström black holes. prd (1990) 41:2986–97. doi:10.1103/PhysRevD.41.2986

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Dolan SR, Ottewill AC. On an expansion method for black hole quasinormal modes and Regge Poles. Classical Quan Gravity (2009) 26:225003. doi:10.1088/0264-9381/26/22/225003

CrossRef Full Text | Google Scholar

106. Dolan SR. Quasinormal mode spectrum of a Kerr black hole in the eikonal limit. Phys Rev D (2010) 82:104003. doi:10.1103/PhysRevD.82.104003

CrossRef Full Text | Google Scholar

107. Jansen A. Overdamped modes in Schwarzschild-de Sitter and a Mathematica package for the numerical computation of quasinormal modes. The Eur Phys J Plus (2017) 132:546. doi:10.1140/epjp/i2017-11825-9

CrossRef Full Text | Google Scholar

108. Langlois D, Noui K, Roussille H. Black hole perturbations in modified gravity. Phys Rev D (2021) 104:124044. doi:10.1103/PhysRevD.104.124044

CrossRef Full Text | Google Scholar

109. Langlois D, Noui K, Roussille H. Asymptotics of linear differential systems and application to quasinormal modes of nonrotating black holes. Phys Rev D (2021) 104:124043. doi:10.1103/PhysRevD.104.124043

CrossRef Full Text | Google Scholar

110. Chung AKW, Wagle P, Yunes N. Spectral method for the gravitational perturbations of black holes: schwarzschild background case. Phys Rev D (2023) 107:124032. doi:10.1103/PhysRevD.107.124032

CrossRef Full Text | Google Scholar

111. Chung AKW, Wagle P, Yunes N. Spectral method for metric perturbations of black holes: kerr background case in general relativity (2023) doi:10.48550/arXiv.2312.08435

CrossRef Full Text | Google Scholar

112. Jaramillo JL, Panosso Macedo R, Al Sheikh L. Pseudospectrum and black hole quasinormal mode instability. Phys Rev X (2021) 11:031003. doi:10.1103/PhysRevX.11.031003

CrossRef Full Text | Google Scholar

113. Panosso Macedo R. Hyperboloidal framework for the Kerr spacetime. Class Quant Grav (2020) 37:065019. doi:10.1088/1361-6382/ab6e3e

CrossRef Full Text | Google Scholar

114. Gajic D, Warnick C. Quasinormal modes in extremal reissner–nordström spacetimes. Commun Math Phys (2021) 385:1395–498. doi:10.1007/s00220-021-04137-4

CrossRef Full Text | Google Scholar

115. Bizoń P, Chmaj T, Mach P. A toy model of hyperboloidal approach to quasinormal modes. Acta Physica Pol B (2020) 51:1007. doi:10.5506/APhysPolB.51.1007

CrossRef Full Text | Google Scholar

116. Warnick C. (In)completeness of quasinormal modes. Acta Physica Pol B Proc Suppl (2022) 15:1. doi:10.5506/APhysPolBSupp.15.1-A13

CrossRef Full Text | Google Scholar

117. Carullo G. Ringdown amplitudes of nonspinning eccentric binaries. arXiv preprint gr-qc:2406 (2024) 19442. doi:10.1088/1475-7516/2024/10/061

CrossRef Full Text | Google Scholar

118. Berti E, Cardoso V. Quasinormal ringing of Kerr black holes: the excitation factors. Phys Rev D (2006) 74:104020. doi:10.1103/PhysRevD.74.104020

CrossRef Full Text | Google Scholar

119. Zimmerman A, Yang H, Mark Z, Chen Y, Lehner L. Quasinormal modes beyond kerr. Astrophys Space Sci Proc (2015) 40:217–23. doi:10.1007/978-3-319-10488-1_19

CrossRef Full Text | Google Scholar

120. Green SR, Hollands S, Sberna L, Toomani V, Zimmerman P. Conserved currents for a Kerr black hole and orthogonality of quasinormal modes. Phys Rev D (2023) 107:064030. doi:10.1103/PhysRevD.107.064030

CrossRef Full Text | Google Scholar

121. London LT. A radial scalar product for Kerr quasinormal modes. ArXiv: 2312.17678 (2023). Available at: https://arxiv.org/abs/2312.17678.

Google Scholar

122. Ammon M, Grieninger S, Jimenez-Alba A, Macedo RP, Melgar L. Holographic quenches and anomalous transport. JHEP (2016) 09:131. doi:10.1007/JHEP09(2016)131

CrossRef Full Text | Google Scholar

123. Besson J, Jaramillo JL. Quasi-normal mode expansions of black hole perturbations: a hyperboloidal Keldysh’s approach. arXiv preprint gr-qc:2412 (2024):02793. Available at: https://arxiv.org/abs/2412.02793.

Google Scholar

124. Zenginoğlu A, Khanna G, Burko LM. Intermediate behavior of Kerr tails. Gen Rel Grav (2014) 46:1672. doi:10.1007/s10714-014-1672-8

CrossRef Full Text | Google Scholar

125. Cardoso V, Carullo G, De Amicis M, Duque F, Katagiri T, Pereniguez D, et al. Hushing black holes: tails in dynamical spacetimes. Phys Rev D (2024) 109:L121502. doi:10.1103/PhysRevD.109.L121502

CrossRef Full Text | Google Scholar

126. De Amicis M, Albanesi S, Carullo G. Inspiral-inherited ringdown tails. arXiv preprint gr-qc:2406 (2024) 17018. Available at: https://arxiv.org/abs/2406.17018.

Google Scholar

127. London L, Shoemaker D, Healy J. Modeling ringdown: beyond the fundamental quasinormal modes. Phys Rev D (2014) 90:124032. Erratum: Phys.Rev.D 94, 069902 (2016). doi:10.1103/PhysRevD.90.124032

CrossRef Full Text | Google Scholar

128. Cheung MHY, Baibhav V, Berti E, Cardoso V, Carullo G, Cotesta R, et al. Nonlinear effects in black hole ringdown. Phys Rev Lett (2023) 130:081401. doi:10.1103/PhysRevLett.130.081401

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Mitman K, Lagos M, Stein LC, Ma S, Hui L, Chen Y, et al. Nonlinearities in black hole ringdowns. Phys Rev Lett (2023) 130:081402. doi:10.1103/PhysRevLett.130.081402

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Zlochower Y, Gomez R, Husa S, Lehner L, Winicour J. Mode coupling in the nonlinear response of black holes. Phys Rev D (2003) 68:084014. doi:10.1103/PhysRevD.68.084014

CrossRef Full Text | Google Scholar

131. Sberna L, Bosch P, East WE, Green SR, Lehner L. Nonlinear effects in the black hole ringdown: absorption-induced mode excitation. Phys Rev D (2022) 105:064046. doi:10.1103/PhysRevD.105.064046

CrossRef Full Text | Google Scholar

132. Redondo-Yuste J, Carullo G, Ripley JL, Berti E, Cardoso V. Spin dependence of black hole ringdown nonlinearities. Phys Rev D (2024) 109:L101503. doi:10.1103/PhysRevD.109.L101503

CrossRef Full Text | Google Scholar

133. Cheung MHY, Berti E, Baibhav V, Cotesta R. Extracting linear and nonlinear quasinormal modes from black hole merger simulations. arXiv preprint gr-qc:2310.04489 (2023). Available at: https://arxiv.org/abs/2310.04489.

Google Scholar

134. Ma S, Yang H. Excitation of quadratic quasinormal modes for Kerr black holes. Phys Rev D (2024) 109:104070. doi:10.1103/PhysRevD.109.104070

CrossRef Full Text | Google Scholar

135. Zhu H, Ripley JL, Pretorius F, Ma S, Mitman K, Owen R, et al. Nonlinear effects in black hole ringdown from scattering experiments: spin and initial data dependence of quadratic mode coupling. Phys Rev D (2024) 109:104050. doi:10.1103/PhysRevD.109.104050

CrossRef Full Text | Google Scholar

136. Bucciotti B, Juliano L, Kuntz A, Trincherini E. Quadratic quasi-normal modes of a schwarzschild black hole. arXiv preprint gr-qc:2405 (2024):06012. doi:10.1007/JHEP09(2024)119

CrossRef Full Text | Google Scholar

137. Brizuela D, Martin-Garcia JM, Tiglio M. Complete gauge-invariant formalism for arbitrary second-order perturbations of a Schwarzschild black hole. Phys Rev D (2009) 80:024021. doi:10.1103/PhysRevD.80.024021

CrossRef Full Text | Google Scholar

138. Loutrel N, Ripley JL, Giorgi E, Pretorius F. Second-order perturbations of Kerr black holes: formalism and reconstruction of the first-order metric. Phys Rev D (2021) 103:104017. doi:10.1103/PhysRevD.103.104017

CrossRef Full Text | Google Scholar

139. Spiers A, Pound A, Moxon J. Second-order Teukolsky formalism in Kerr spacetime: formulation and nonlinear source. Phys Rev D (2023) 108:064002. doi:10.1103/PhysRevD.108.064002

CrossRef Full Text | Google Scholar

140. May T, Ma S, Ripley JL, East WE. Nonlinear effect of absorption on the ringdown of a spinning black hole. arXiv preprint gr-qc:2405 (2024):18303. doi:10.1103/PhysRevD.110.084034

CrossRef Full Text | Google Scholar

141. Bourg P, Panosso Macedo R, Spiers A, Leather B, Bonga B, Pound A. Quadratic quasi-normal mode dependence on linear mode parity. In preparation (2024). Available at: https://arxiv.org/abs/2405.10270.

Google Scholar

142. Vishveshwara CV. On the black hole trail.: a personal journey. Curr Sci (1996) 71:824–30.

Google Scholar

143. Aguirregabiria JM, Vishveshwara CV. Scattering by black holes: a Simulated potential approach. Phys Lett A (1996) 210:251–4. doi:10.1016/0375-9601(95)00937-X

CrossRef Full Text | Google Scholar

144. Nollert HP. About the significance of quasinormal modes of black holes. Phys Rev D (1996) 53:4397–402. doi:10.1103/PhysRevD.53.4397

PubMed Abstract | CrossRef Full Text | Google Scholar

145. Nollert HP, Price RH. Quantifying excitations of quasinormal mode systems. J Math Phys (1999) 40:980–1010. doi:10.1063/1.532698

CrossRef Full Text | Google Scholar

146. Jaramillo JL, Panosso Macedo R, Sheikh LA. Gravitational wave signatures of black hole quasinormal mode instability. Phys Rev Lett (2022) 128:211102. doi:10.1103/PhysRevLett.128.211102

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Gasperin E, Jaramillo JL. Energy scales and black hole pseudospectra: the structural role of the scalar product. Class Quant Grav (2022) 39:115010. doi:10.1088/1361-6382/ac5054

CrossRef Full Text | Google Scholar

148. Cheung MHY, Destounis K, Macedo RP, Berti E, Cardoso V. Destabilizing the fundamental mode of black holes: the elephant and the flea. Phys Rev Lett (2022) 128:111103. doi:10.1103/PhysRevLett.128.111103

PubMed Abstract | CrossRef Full Text | Google Scholar

149. Al Sheikh L. Scattering resonances and Pseudospectrum: stability and completeness aspects in optical and gravitational systems. Besançon, France: Université Bourgogne Franche-Comté (2022). Theses.

Google Scholar

150. Berti E, Cardoso V, Cheung MHY, Di Filippo F, Duque F, Martens P, et al. Stability of the fundamental quasinormal mode in time-domain observations against small perturbations. Phys Rev D (2022) 106:084011. doi:10.1103/PhysRevD.106.084011

CrossRef Full Text | Google Scholar

151. Jaramillo JL. Pseudospectrum and binary black hole merger transients. Class Quant Grav (2022) 39:217002. doi:10.1088/1361-6382/ac8ddc

CrossRef Full Text | Google Scholar

152. Cardoso V, Kastha S, Panosso Macedo R. Physical significance of the black hole quasinormal mode spectra instability. Phys Rev D (2024) 110:024016. doi:10.1103/PhysRevD.110.024016

CrossRef Full Text | Google Scholar

153. Hirano S, Kimura M, Yamaguchi M, Zhang J. Parametrized black hole quasinormal ringdown formalism for higher overtones. Phys Rev D (2024) 110:024015. doi:10.1103/PhysRevD.110.024015

CrossRef Full Text | Google Scholar

154. Warnick C. (In)stability of de Sitter quasinormal mode spectra. Front Appl Mathematics Stat (2024) 10:1472401. doi:10.3389/fams.2024.1472401

CrossRef Full Text | Google Scholar

155. Boyanov V. On destabilising quasi-normal modes with a radially concentrated perturbation. arXiv preprint gr-qc:2410 (2024) 11547. Available at: https://arxiv.org/abs/2410.11547.

Google Scholar

156. Galkowski J, Zworski M. Outgoing solutions via gevrey-2 properties. arXiv preprint math.AP:2004 (2020) 07868. doi:10.1007/s40818-021-00094-2

CrossRef Full Text | Google Scholar

157. Trefethen L, Embree M. Spectra and pseudospectra: the behavior of nonnormal matrices and operators. Princeton University Press (2005).

Google Scholar

158. Destounis K, Macedo RP, Berti E, Cardoso V, Jaramillo JL. Pseudospectrum of Reissner-Nordström black holes: quasinormal mode instability and universality. Phys Rev D (2021) 104:084091. doi:10.1103/PhysRevD.104.084091

CrossRef Full Text | Google Scholar

159. Boyanov V, Destounis K, Panosso Macedo R, Cardoso V, Jaramillo JL. Pseudospectrum of horizonless compact objects: a bootstrap instability mechanism. Phys Rev D (2023) 107:064012. doi:10.1103/PhysRevD.107.064012

CrossRef Full Text | Google Scholar

160. Areán D, Fariña DG, Landsteiner K. Pseudospectra of holographic quasinormal modes. JHEP (2023) 12:187. doi:10.1007/JHEP12(2023)187

CrossRef Full Text | Google Scholar

161. Sarkar S, Rahman M, Chakraborty S. Perturbing the perturbed: stability of quasinormal modes in presence of a positive cosmological constant. Phys Rev D (2023) 108:104002. doi:10.1103/PhysRevD.108.104002

CrossRef Full Text | Google Scholar

162. Destounis K, Boyanov V, Panosso Macedo R. Pseudospectrum of de Sitter black holes. Phys Rev D (2024) 109:044023. doi:10.1103/PhysRevD.109.044023

CrossRef Full Text | Google Scholar

163. Boyanov V, Cardoso V, Destounis K, Jaramillo JL, Panosso Macedo R. Structural aspects of the anti–de Sitter black hole pseudospectrum. Phys Rev D (2024) 109:064068. doi:10.1103/PhysRevD.109.064068

CrossRef Full Text | Google Scholar

164. Cownden B, Pantelidou C, Zilhão M. The pseudospectra of black holes in AdS. JHEP (2024) 05:202. doi:10.1007/JHEP05(2024)202

CrossRef Full Text | Google Scholar

165. Chen JN, Wu LB, Guo ZK. The pseudospectrum and transient of Kaluza-Klein black holes in Einstein-Gauss-Bonnet gravity (2024).

Google Scholar

166. Carballo J, Withers B. Transient dynamics of quasinormal mode sums. arXiv preprint hep-th:2406 (2024):06685. doi:10.1007/JHEP10(2024)084

CrossRef Full Text | Google Scholar

167. Garcia-Fariña D, Landsteiner K, Romeu PG, Saura-Bastida P. Pseudospectra of complex momentum modes. arXiv preprint hep-th:2407 (2024):06104. Available at: https://arxiv.org/abs/2407.06104.

Google Scholar

168. Burgess C, König F. Hyperboloidal method for quasinormal modes of non-relativistic operators. Front Phys (2024) 12:1457543. doi:10.3389/fphy.2024.1457543

CrossRef Full Text | Google Scholar

169. Peterson C, Gautam S, Vañó-Viñuales A, Hilditch D. Spherical evolution of the generalized harmonic gauge formulation of general relativity on compactified hyperboloidal slices. arXiv preprint gr-qc:2409 (2024):02994. Available at: https://arxiv.org/abs/2409.02994.

Google Scholar

170. Vañó-Viñuales A, Valente T. Height-function-based 4d reference metrics for hyperboloidal evolution. arXiv preprint gr-qc:2408 (2024):08952. doi:10.1007/s10714-024-03323-8

PubMed Abstract | CrossRef Full Text | Google Scholar