Unveiling radii and neutron skins of unstable atomic nuclei via nuclear collisions

Total reaction, interaction, and charge-changing cross sections, which are kinds of cross sections standing for total nuclear collision probability in medium-to high-energy region from a few to several hundred MeV, have been extensively utilized to probe nuclear sizes especially for unstable nuclei. In this mini review, experimental techniques and recent findings from these cross sections are briefly overviewed. Additionally, two new methods to extract neutron skin thickness solely from the above cross sections are explained: One is utilizing the energy and isospin dependence of the total reaction cross sections, and the other is the combination of the total reaction and charge-changing cross section measurements.

1 Introduction

In neutron-rich nuclei, a thick neutron skin forms, reflecting both the nuclear structure and the bulk properties of nuclear matter. The neutron skin thickness $\mathrm{\Delta }{r}_{\text{np}}$, which is defined as the difference between the root-mean-square (RMS) radii of the point-neutron and point-proton density distributions, $r_{\text{n}}$ and $r_{\text{p}}$:

$\mathrm{\Delta }{r}_{\text{np}}=r_{\text{n}}-r_{\text{p}}.(1)$

This quantity is particularly anticipated as a promising observable to determine the slope parameter, $L$, of the symmetry energy $c_{\text{sym}}(\rho )$ at the saturation density ${\rho }_0$ in the equation of state (EoS) of nuclear matter [1], where $\rho$ is the density. This parameter is defined as $L\equiv 3{\rho }_0\times {\left.\frac{d{c}_{\text{sym}}}{d\rho }\right|}_{{\rho }_0}$ playing a crucial role in extrapolating the EOS for symmetric nuclear matter to that for asymmetric nuclear matter. Although significant efforts have been made to determine the neutron skin thickness, $\mathrm{\Delta }{r}_{\text{np}}$, in neutron-rich stable nuclei using various experimental techniques [2–16], a consistent value for $L$ has not yet been determined. Recent compilations report the range of $L$ values as $58.9\pm 16.5$ MeV [17], $58.7\pm 28.1$ MeV [18], and 40–60 MeV [19].

Determining $\mathrm{\Delta }{r}_{\text{np}}$ of neutron-rich unstable nuclei has the advantage of constraining the parameter $L$, as a thicker neutron skin is expected [20–23]. There are some $\mathrm{\Delta }{r}_{\text{np}}$ measurements in neutron-rich unstable nuclei using the low-lying dipole resonance [24] and electric dipole polarizability [25–27]. Compared to the above experimental methods, the total reaction $({\sigma }_{\text{R}})$, interaction $({\sigma }_{\text{I}})$, and charge-changing cross sections $({\sigma }_{\text{CC}})$, which will be focused in this paper are powerful tools for determining the size properties and $\mathrm{\Delta }{r}_{\text{np}}$ of neutron-rich unstable nuclei far from the stability line. The ${\sigma }_{\text{R}}$ and ${\sigma }_{\text{I}}$ are sensitive to the matter radius $(r_{\text{m}})$, which is the RMS radius of the nucleon density distribution, ${\rho }_{\text{m}}(r)$. Therefore, if $r_{\text{m}}$ is precisely obtained via ${\sigma }_{\text{R}}$ or ${\sigma }_{\text{I}}$, one can determine $\mathrm{\Delta }{r}_{\text{np}}$ by combining with $r_{\text{p}}$ from another method, such as isotope shift measurements [28, 29], using Equation 1 together with the relation of $A{r}_{\text{m}}^2=Z{r}_{\text{p}}^2+N{r}_{\text{n}}^2$, where $A$, $Z$, and $N$ are the mass, atomic, and neutron numbers of the nucleus of interest.

Furthermore, recent developments using ${\sigma }_{\text{R}}$ and/or ${\sigma }_{\text{CC}}$, mentioned in Section 5, offer new ways to determine $\mathrm{\Delta }{r}_{\text{np}}$ solely from these total cross sections. Compared to other major nuclear reaction measurement techniques using RI beams [30], these total cross sections can be measured even with extremely low radioactive-isotope (RI) beam intensities of, e.g., around 0.1 particles/sec, making it possible to extract $\mathrm{\Delta }{r}_{\text{np}}$ of very neutron-rich nuclei. In this paper, we briefly review recent studies regarding these total cross sections, with a particular focus on advances related to the neutron skin.

2 Overview of experimental techniques

The ${\sigma }_{\text{R}}$ and ${\sigma }_{\text{I}}$ are defined as the total cross sections for all inelastic reactions and all reactions that change the nuclides, respectively. At energies above approximately 200 MeV/nucleon, ${\sigma }_{\text{I}}\approx {\sigma }_{\text{R}}$ is generally assumed in Glauber-model analyses (Section 3) because the inelastic scattering where the projectile nucleus remains in the ground state hardly occurs. Theoretical studies have indicated that the ratio of this inelastic scatteing cross section $({\sigma }_{\text{inel}})$ to ${\sigma }_{\text{R}}$, ${\sigma }_{\text{inel}}/{\sigma }_{\text{R}}$, is typically 2%–3% at energies above 200 MeV/nucleon, increasing to around 5% as energy decreases to several tens MeV/nucleon [31, 32]. The ${\sigma }_{\text{inel}}/{\sigma }_{\text{R}}$ values for Mg isotopes on ¹²$\mathrm{C}$ at 240 MeV/nucleon were experimentally estimated to be around 2% [33].

The ${\sigma }_{\text{R}\left(\text{I}\right)}$ is often measured using the transmission method [34] represented by

${\sigma }_{\text{R}\left(\text{I}\right)}=-\frac{1}{N_t}\ln \left(\frac{\gamma }{{\gamma }_0}\right),(2)$

where $N_t$ is the number of target nuclei per unit area, $\gamma$ and ${\gamma }_0$ are the nonreaction rates for measurements with and without the target. The $\gamma$ and ${\gamma }_0$ in Equation 2 are obtained by counting the number of incident particles and that of outgoing nonreaction ones, respectively. This method has lower experimental uncertainty compared to the associate-$\gamma$ method [35], which assumes that all inelastic scatterings necessarily emit $\gamma$ rays.

At energies above 200 MeV/nucleon, ${\sigma }_{\text{I}}$ is often measured instead of ${\sigma }_{\text{R}}$. This is because the “nonreaction particle” for ${\sigma }_{\text{I}}$ represents the particle that has not changed nuclide species, which is easier to identify experimentally. Conversely, at energies below around 100 MeV/nucleon, where ${\sigma }_{\text{inel}}$ cannot be ignored, ${\sigma }_{\text{R}}$ are often measured. The definition of “nonreaction particle” of ${\sigma }_{\text{R}}$ includes the “elastically scattered particle.” Therefore, in addition to the identification of nuclide species, energy or momentum measurements are required downstream of the target. The ${\sigma }_{\text{inel}}$ are practically estimated from the tail of the energy or momentum distribution [33, 36], while that peculiarly from the inelastic excitations to bound states is sometimes estimated from counting de-exciting $\gamma$ rays [37, 38].

The charge-changing cross section, ${\sigma }_{\text{CC}}$, mentioned in Section 5.2, is also measured by the transmission method. This is the total cross section of atomic-number-changing reactions of the projectile nucleus, so that particles with the same $Z$ number as the projectile ones downstream of the target are counted as “nonreaction particles.” Note that some studies treated products with a larger $Z$ than projectile nuclei as nonreaction particles because an increase in $Z$ is not considered to result from the fragmentation reaction [39–41]. For example, in C isotopes [39, 42], that contribution was comparable or less to the experimental uncertainty of ${\sigma }_{\text{CC}}$ (around 1%).

3 Glauber model

There are several approaches to theoretically describe the relationship between ${\sigma }_{\text{R}}$ (or ${\sigma }_{\text{I}}$) and the RMS radii of colliding nuclei, such as the black sphere model [31, 43–45] and the folding model with optical potentials [46–55]. Among these, the Glauber theory [56] has frequently been used. In the Glauber formalism, ${\sigma }_{\text{R}}$ is expressed as

${\sigma }_{\text{R}}=\int d\mathit{b}\left(1-{\left|e^{i\chi \left(\mathit{b}\right)}\right|}^2\right),(3)$

where $\mathit{b}$ is the impact parameter vector, $\chi (\mathit{b})$ is the phase-shift function for the elastic scattering between the projectile and target nuclei. The $\chi (\mathit{b})$ in Equation 3 is given by the ground-state wave functions of the projectile and target nuclei, ${\mathrm{\Psi }}_0^{\text{P}}$ and ${\mathrm{\Psi }}_0^{\text{T}}$, respectively:

$e^{i\chi \left(\mathit{b}\right)}=⟨{\mathrm{\Psi }}_0^{\text{P}}{\mathrm{\Psi }}_0^{\text{T}}\left|{\displaystyle \prod _{i\in \mathrm{p},\mathrm{n}}}{\displaystyle \prod _{j\in \mathrm{p},\mathrm{n}}}{\displaystyle \prod _{k\in \mathrm{P}}}{\displaystyle \prod _{l\in \mathrm{T}}}\left[1-{\mathrm{\Gamma }}_{ij}\left(E,{\mathit{s}}_k^{\text{P}}-{\mathit{s}}_l^{\text{T}}+\mathit{b}\right)\right]\right|{\mathrm{\Psi }}_0^{\text{P}}{\mathrm{\Psi }}_0^{\text{T}}⟩,(4)$

where the subscripts “$i$” and “$j$” denote the isospin of nucleons of the projectile and target nuclei, the superscripts “P” and “T” the projectile and target nuclei, respectively, $E$ is the incident energy per nucleon, and ${\mathit{s}}_k^{\text{P}}$ $({\mathit{s}}_l^{\text{T}})$ are the two-dimensional vectors of the $k$($l$)-th nucleon’s cordinates ($\mathit{r}$) in the plane perpendicular to the beam axis. The nucleon-nucleon profile function ${\mathrm{\Gamma }}_{ij}$, obtained by a Fourier transform of the nucleon-nucleon scattering amplitude, is typically parameterized as [57].

${\mathrm{\Gamma }}_{ij}\left(E,\mathit{b}\right)=\frac{1-i{\alpha }_{ij}\left(E\right)}{4\pi {\beta }_{ij}\left(E\right)}{\sigma }_{ij}\left(E\right)\exp \left(-\frac{{\mathit{b}}^2}{2{\beta }_{ij}\left(E\right)}\right),(5)$

where ${\sigma }_{ij}$ is the nucleon-nucleon total cross section [58] (Figure 1A), ${\alpha }_{ij}$ the ratio of the real to the imaginary part of the nucleon-nucleon scattering amplitude, and ${\beta }_{ij}$ the slope parameter of the nucleon-nucleon elastic differential cross section representing the range of nucleon-nucleon interaction.

Figure 1

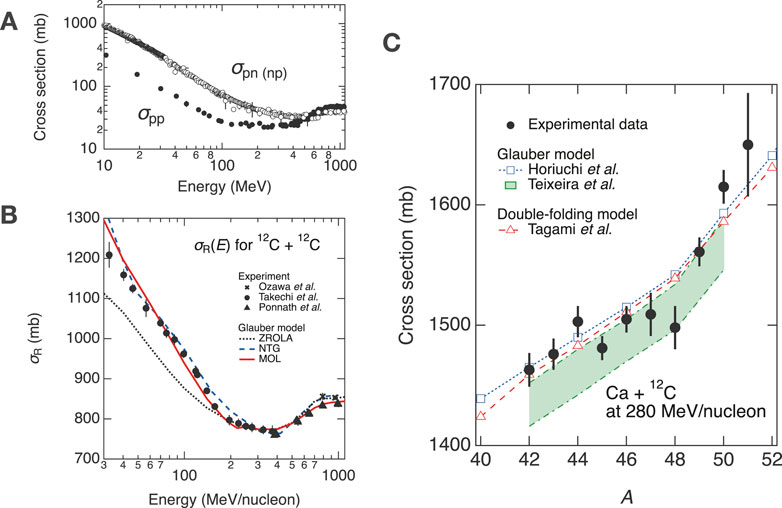
Figure 1. Properties regarding total-reaction cross sections ${\sigma }_{\text{R}}$ or interaction cross sections ${\sigma }_{\text{I}}$ (A) Energy dependence of proton–proton and proton–neutron (or neutron–proton) total cross sections, ${\sigma }_{\text{pp}}$ (closed circles) and ${\sigma }_{\text{pn\hspace{0.17em}}\left(\text{np}\right)}$ (open circles), which are fundamental inputs of the Glauber-model calculations. The experimental values are taken from Ref. [58]. (B) Energy dependence of reaction cross section ${\sigma }_{\text{R}}(E)$. Crosses [78], closed circles [64], and closed triangles [72] show experimental data, and the dotted black, dashed blue, and solid red lines represent the Glauber-model calculations under the zero-range OLA, NTG [63], and MOL [64] formalisms. (C) Comparison between experimental data [70] and theoretical calculations of ${\sigma }_{\text{I}}$ for Ca isotopes on ¹²$\mathrm{C}$ at 280 MeV/nucleon. Open blue squares connected by a dotted line represent the Glauber-model calculation under the NTG approximation with density distributions of Ca isotopes obtained from the Hartree–Fock calculation using the SLy4 interaction [71], dot-dashed green lines with the shaded band the Glauber-model calculations considering several effects with the density distributions obtained from the Hartree–Fock–Bogoliubov (HFB) or relativistic mean field calculations using 31 different interactions [69], respectively. For comparison, the double-folding-model calculation with the Gogny-D1S HFB with the angular momentum projection (GHFB + AMP) is also shown by open red triangles connected by a dashed line [50].

To calculate $\chi (\mathit{b})$ in Equation 4, multiple integrals of the wave functions of the projectile and target nuclei are required, which can be performed using the Monte Carlo integration technique [59, 60]. However, approximations are generally applied to avoid the complexity of the calculations. One of the simplest and most frequently used approximations is the optical-limit approximation (OLA):

$e^{i{\chi }_{\text{OLA}}\left(\mathit{b}\right)}={\displaystyle \prod _{i\in \mathrm{p},\mathrm{n}}}{\displaystyle \prod _{j\in \mathrm{p},\mathrm{n}}}\exp \left[-\iint d{\mathit{r}}^{\text{P}}d{\mathit{r}}^{\text{T}}{\rho }_i^{\text{P}}\left({\mathit{r}}^{\text{P}}\right){\rho }_j^{\text{T}}\left({\mathit{r}}^{\text{T}}\right){\mathrm{\Gamma }}_{ij}\left(E,{\mathit{s}}^{\text{P}}-{\mathit{s}}^{\text{T}}+\mathit{b}\right)\right],(6)$

Here, ${\rho }^{\text{P}}$ $({\rho }^{\text{T}})$ represents the density distribution of the projectile (target) nucleus. Using the OLA, ${\sigma }_{\text{R}}$ can be calculated given the density distributions of projectile and target nuclei and ${\mathrm{\Gamma }}_{ij}$. However, this approximation does not account for various possible multiple-scattering effects. To incorporate them effectively, ${\mathrm{\Gamma }}_{ij}$ is extended to the nucleon-target profile function, ${\mathrm{\Gamma }}_{\text{NT}}$ [61, 62], which is called the “nucleon-target formalism in the Glauber model” (NTG) [63] or “modified OLA” (MOL) [64]:

$e^{i{\chi }_{\text{NTG}}\left(\mathit{b}\right)}=\exp \left[-\int d{\mathit{r}}^{\text{P}}{\rho }^{\text{P}}\left({\mathit{r}}^{\text{P}}\right)\times \left\{1-\exp \left[-\int d{\mathit{r}}^{\text{T}}{\rho }^{\text{T}}\left({\mathit{r}}^{\text{T}}\right)\mathrm{\Gamma }\left(E,{\mathit{s}}^{\text{P}}-{\mathit{s}}^{\text{T}}+\mathit{b}\right)\right]\right\}\right].(7)$

Here, although Equation 7 also incorporate the isospin dependence $i$ and $j$ similar to those in Equation 6, these isospin notations are omitted for the sake of simplicity. Note that a modified version of this equation that satisfies symmetry regarding the exchange between projectile and target components is usually used [61, 62]. Other various effects have been also considered: the energy dependendent parameters of ${\alpha }_{ij}$ and ${\beta }_{ij}$ in ${\mathrm{\Gamma }}_{ij}$ [63, 65–68], Fermi-motion effect [64], and Pauli blocking [69]. Although these frameworks have minor differences, each is constructed to effectively reproduce the benchmark dataset (e.g., the energy dependence of ${\sigma }_{\text{R}}$ for ¹²$\mathrm{C}$ on ¹²$\mathrm{C}$ shown in Figure 1B). Then, measured ${\sigma }_{\text{R}\left(\text{I}\right)}$ results are analyzed based on these evaluated theoretical framework. As an example, Figure 1C shows ${\sigma }_{\text{I}}$ for Ca isotopes on ¹²$\mathrm{C}$ at 280 MeV/nucleon [70] together with the calculations using the Glauber model [69, 71] as well as the double-folding model [50] employing theoretical density distributions. To improve the Glauber formalism much more, there are recent experimental contributions, such as high-precision ${\sigma }_{\text{I}}$ data for ¹²$\mathrm{C}$ on ¹²$\mathrm{C}$ at energies of 400–1,000 MeV/nucleon [72] and ${\sigma }_{\text{R}\left(\text{I}\right)}$ for ¹⁷$\mathrm{F}$ and ¹⁷$\mathrm{N}\mathrm{e}$ on a solid hydrogen target [73] at energies of 50–450 MeV/nucleon [74, 75].

4 Progress of total-reaction and interaction cross section studies

4.1 Progress in recent 20 years

After the pioneering work of ${\sigma }_{\text{I}}$ measurements by Tanihata et al. [76, 77], ${\sigma }_{\text{R}}$ and ${\sigma }_{\text{I}}$ have been extensively measured at the RI-beam facilities. Here, the progress of studies related to ${\sigma }_{\text{R}}$ and ${\sigma }_{\text{I}}$ achieved after the 2001 review paper [78] is outlined.

Regarding nuclei near the neutron dripline, ²²C [38, 79] and ²⁹F [80] were newly identified as halo nuclei through ${\sigma }_{\text{R}\left(\text{I}\right)}$ measurements, and the structure of these nuclei and neighboring ³¹$\mathrm{F}$ were also investigated theoretically [60, 81–84]. The ${\sigma }_{\text{I}}$ measurements for ^22,23$\mathrm{O}$ found that the structure of ²³$\mathrm{O}$ can be understood within the model consisting of a ²²$\mathrm{O}$ core and a $2s_{1/2}$ valence neutron [85]. Systematic ${\sigma }_{\text{I}\left(\text{R}\right)}$ measurements for F [86], Ne [87], Na [88], and Mg [33] isotopes at RIBF, which accessed more neutron-rich ones compared to previous measurements at GSI [89, 90], have significantly contributed to revealing the area consisting of islands of inversion around $N=20$ and 28. Additionally, these systematic data showed that ^29,31$\mathrm{N}\mathrm{e}$ and ³⁷$\mathrm{M}\mathrm{g}$ were found to have the halo structure induced by the strong deformation [91, 92]. The mechanisms of these phenomena were further investigated by various theoretical studies [46–48, 93–95]. The ${\sigma }_{\text{R}}$ measurements, especially below 100 MeV/nucleon, have been extensively conducted to probe the details of density profiles near the nuclear surface [74, 96–109] because ${\sigma }_{\text{R}}$ at lower energy than 200 MeV/nucleon are more sensitive to the dilute density of nuclei due to the large ${\sigma }_{ij}$ values [36, 110–113] (Figure 1A).

In the heavier region, other halo nuclei and islands of inversion have been predicted theoretically [114–116]. Regarding experimental progress in this region, ${\sigma }_{\text{I}}$ measurements for Cl and Ar [37], Ca [70], and Kr isotopes [117] have been conducted mainly to discuss the evolution of neutron (proton) skins, which are reviewed separately below.

4.2 Studies on neutron skins

After revealing thick neutron skins in ^6,8$\mathrm{H}\mathrm{e}$ from ${\sigma }_{\text{I}}$ and neutron-removal cross sections [118], the first direct observation of neutron-skin growth along a long chain including unstable nuclei was conducted in Na isotopes by combining ${\sigma }_{\text{I}}$ results [119] with the $r_{\text{p}}$ from the isotope-shift measurements [120]. The deduced $\mathrm{\Delta }{r}_{\text{np}}$ of Na isotopes, as well as those of Cl and Ar isotopes [37], show a monotonic dependence on the difference between one-neutron and one-proton separation energies, $S_{\text{n}}-S_{\text{p}}$ [119]. In contrast to these isotopes, the trend of $\mathrm{\Delta }{r}_{\text{np}}$ in Kr isotopes was different, implying that only the valence nucleons are responsible for the trend [117].

Recent ${\sigma }_{\text{I}}$ measurements revealed a substantial growth of neutron skin in Ca isotopes across the neutron magic number $N=28$ [70], which is different from the isotopes mentioned above. It has been known that the trend of $r_{\text{p}}$ (charge radii) shows a sudden slope change against $N$ globally at the neutron magic numbers, which is called a “kink” [28, 29]. The experimental $r_{\text{m}}$ values determined from ${\sigma }_{\text{I}}$ for ^42–51$\mathrm{C}\mathrm{a}$ [70] (Figure 1C) also show a kink structure at $N=28$ similar to that of $r_{\text{p}}$ [121]. Interestingly, the magnitude of the kink in $r_{\text{m}}$ is much larger than that in $r_{\text{p}}$, resulting in the emergence of the kink also in the $\mathrm{\Delta }{r}_{\text{np}}$ evolution. Various mechanisms have been proposed for the possible origins behind the kink structure in $r_{\text{p}}$ (e.g., see Ref. [122]).

The evolution of neutron skin in Ca isotopes provides new insight also into the bulk properties of nuclear matter. The Hartree–Fock calculations have pointed out that the kink structure occurs depending on the properties of the occupying valence single-neutron states to minimize the energy loss resulting from the saturation of the densities in the internal region of the nucleus [71, 116]. Evaluating the contribution of $\mathrm{\Delta }{r}_{\text{np}}$ caused by the surface difference between ${\rho }_{\text{n}}(r)$ and ${\rho }_{\text{p}}(r)$ is also important for determining the EOS parameter $L$. Decomposing $\mathrm{\Delta }{r}_{\text{np}}$ into the bulk part $(\mathrm{\Delta }{r}_{\text{np}}^{\text{bulk}})$, which is sensitive to $L$, and the surface part $(\mathrm{\Delta }{r}_{\text{np}}^{\text{surface}})$ within the incompressible droplet model has clarified that the neutron-skin kink appears when the trend of $\mathrm{\Delta }{r}_{\text{np}}^{\text{surface}}$ changes [23, 123–126]. Thus, while the neutron skin is sensitive to the parameter $L$ as mentioned in the introduction, the neutron-skin kink itself plays a different role in identifying the effect of $\mathrm{\Delta }{r}_{\text{np}}^{\text{surface}}$ on determining $L$.

In addition to the approach with the total collision cross sections described above and below, methods only using nucleon removal cross sections have been proposed [127].

5 Extraction of neutron skin thickness solely from collision cross sections

Recently, two novel methods have been developed to derive $\mathrm{\Delta }{r}_{\text{np}}$ solely from nuclear collision cross sections. One method utilizes the energy and target dependence of ${\sigma }_{\text{R}}$ (Section 5.1), and the other combines ${\sigma }_{\text{CC}}$ and ${\sigma }_{\text{R}}$ (Section 5.2) [128–131].

5.1 Total reaction cross sections utilizing its energy and isospin dependence

This method [126, 132] utilizes the isospin and energy dependence of nucleon-nucleon total cross sections, ${\sigma }_{ij}(E)$ [58]. As shown in Equation 5, the ${\sigma }_{ij}(E)$ shown in Figure 1A is a fundamental input for Glauber model calculations, leading to the energy dependence of ${\sigma }_{\text{R}}$. The ratio of the proton-neutron $({\sigma }_{\text{pn}})$ to proton-proton (or neutron-neutron) total cross sections $({\sigma }_{\text{pp}\left(\text{nn}\right)})$ is ${\sigma }_{\text{pn}}/{\sigma }_{\text{pp}}\sim 3$ at $E\le \sim$100 MeV/nucleon, and ${\sigma }_{\text{pn}}/{\sigma }_{\text{pp}}$ decreases as the energy increases, then reaches unity at around 600 MeV/nucleon. At higher incident energies, although ${\sigma }_{\text{pp}}$ becomes slightly larger than ${\sigma }_{\text{pn}}$, ${\sigma }_{\text{pn}}/{\sigma }_{\text{pp}}$ remains around unity. Therefore, proton targets and nuclear targets such as ¹²C, which contain equal numbers of protons and neutrons, are expected to have a different sensitivity to $\mathrm{\Delta }{r}_{\text{np}}$.

Horiuchi et al. analyzed the correlation between ${\sigma }_{\text{R}}(E)$ and $\mathrm{\Delta }{r}_{\text{np}}$ through the Glauber-model calculation using the density distributions obtained from Skyrme-Hartree-Fock (SHF) theory [126]. In this analysis, the “reaction radius” $a_{\text{R}}$ was introduced in regard to ${\sigma }_{\text{R}}$, namely, $a_{\text{R}}(N,Z,E,T)\equiv \sqrt{{\sigma }_{\text{R}}(N,Z,E,T)/\pi }$, where $N$ and $Z$ are the neutron and atomic numbers of the projectile nucleus, $E$ is the reaction energy, and $T$ is the label of the target species. The correlation between $\mathrm{\Delta }{r}_{\text{np}}$ and the difference in $a_{\text{R}}$ obtained from ${\sigma }_{\text{R}}$ at different energies, $\mathrm{\Delta }{a}_{\text{R}}(E,E^{\prime })=a_{\text{R}}(N,Z,E^{\prime },T)-a_{\text{R}}(N,Z,E,T)$, shows global consistency over all isotopes of O, Ne, Mg, Si, S, Ca, and Ni isotopes examined here. For carbon targets, $\mathrm{\Delta }{a}_{\text{R}}(E,E^{\prime })$ is almost independent of $\mathrm{\Delta }{r}_{\text{np}}$, whereas for proton targets, the plot of $\mathrm{\Delta }{r}_{\text{np}}$ versus $\mathrm{\Delta }{a}_{\text{R}}(E,E^{\prime })$ shows a clear non-zero slope. Especially, the $\mathrm{\Delta }{a}_{\text{R}}(E,E^{\prime })$ trends including 100 MeV/nucleon data have a higher sensitivity to $\mathrm{\Delta }{r}_{\text{np}}$. To further investigate the effectiveness of ${\sigma }_{\text{R}}(E)$ on $\mathrm{\Delta }{r}_{\text{np}}$, $a_{\text{R}}$ was parameterized as the empirical formula of

$a_{\text{R}}\left(N,Z,E,T\right)\equiv \alpha \left(E,T\right)r_{\text{m}}\left(N,Z\right)+\beta \left(E,T\right)\mathrm{\Delta }{r}_{\text{np}}\left(N,Z\right)+\gamma \left(E,T\right),$

where $\alpha (E,T)$, $\beta (E,T)$, and $\gamma (E,T)$ are energy- and target-dependent parameters. The parameter $\beta (E,T)$, representing the effect of $\mathrm{\Delta }{r}_{\text{np}}$, shows prominent energy and target (isospin) dependence: $\beta (E,T)$ is independent of energy for carbon targets, whereas strongly dependent for proton targets. Therefore, it is possible to extract $\mathrm{\Delta }{r}_{\text{np}}$ by measuring ${\sigma }_{\text{R}}$ at multiple energies and/or targets having different $\beta (E,T)$. Furthermore, to enhance sensitivity to $\mathrm{\Delta }{r}_{\text{np}}$, it is desirable to use a combination of proton and neutron targets that are completely isospin asymmetric pair. The use of deuteron targets has been proposed as an alternative to a neutron target [133].

The sensitivity of ${\sigma }_{\text{R}}(E)$ for separating density distributions of proton and neutron, ${\rho }_{\text{p}}(r)$ and ${\rho }_{\text{n}}(r)$, using these properties was demonstrated experimentally in halo nuclei. The experimental ${\sigma }_{\text{R}}$ values for ¹¹Be and ⁸B on proton targets at 50–120 MeV/nucleon were consistent only with calculations assuming neutron and proton tails, respectively [134]. The ${\rho }_{\text{p}}(r)$ and ${\rho }_{\text{n}}(r)$ of ¹¹Li were determined solely from the energy dependence of the experimental ${\sigma }_{\text{R}}$ values on proton and carbon targets [103].

5.2 Charge-changing cross sections

The ${\sigma }_{\text{CC}}$ measurements aiming to derive $r_{\text{p}}$ have been conducted for isotopes up to Fe, particularly since 2010 [39, 40, 65, 135–147]. By analogy with the relationship between ${\sigma }_{\text{R}}$ and $r_{\text{m}}$, ${\sigma }_{\text{CC}}$ is expected to be sensitive to $r_{\text{p}}$. The relationship between ${\sigma }_{\text{CC}}$ and $r_{\text{p}}$ is usually treated in the following Glauber-model-like formalism [65, 135, 136]:

${\tilde{\sigma }}_{\text{CC}}=\int \left[1-{\left|e^{i{\chi }_{\text{p}}\left(\mathit{b}\right)}\right|}^2\right]d\mathit{b},(8)$

where ${\chi }_{\text{p}}(\mathit{b})$ is obtained from Equation 6 by omitting ${\rho }_{\text{n}}(r)$ of the projectile nucleus, that is, only $i=\mathrm{p}$ is adopted for Equation 6 [148]. In the case of ${\sigma }_{\text{CC}}$, the situation appears to be less straightforward than that of ${\sigma }_{\text{R}\left(\text{I}\right)}$ due to the potential influence of neutrons in the incident nucleus. Here, for the sake of subsequent expressions, the calculated value from this equation is denoted as ${\tilde{\sigma }}_{\text{CC}}$. There are several treatments to depict ${\sigma }_{\text{CC}}$ based on Equation 8. First, Yamaguchi et al. introduced an energy-dependent phenomenological correction factor $\epsilon (E)$ into Equation 8 with the zero-range optical-limit approximation (ZROLA) to reproduce ${\sigma }_{\text{CC}}$ data for ²⁸$\mathrm{S}\mathrm{i}$ on ¹²$\mathrm{C}$ at energies of 100–600 MeV/nucleon [135], as shown in Figure 2A. It has been shown that this calculation with $\epsilon (E)$ explains the experimental values for Be to O isotopes on ¹²$\mathrm{C}$ at 300 MeV/nucleon with 3% standard deviation [136]. Second, the experimental ${\sigma }_{\text{CC}}$ of stable B, C, N, and O isotopes on ¹²$\mathrm{C}$ at around 900 MeV/nucleon were well reproduced by the finite-range optical-limit approximation (FROLA) calculations without $\epsilon (E)$ [39–41, 141]. For ^10,11B, the ratio of the experimental values to the calculated ones is 1.01(2) [141]. Third, Tran et al. determined profile-function parameters with the FROLA calculation common to reproduce both ${\sigma }_{\text{R}}(E)$ and ${\sigma }_{\text{CC}}(E)$ for ¹²$\mathrm{C}$ on ¹²$\mathrm{C}$ over the range of 10–2,100 MeV/nucleon [65]. However, this calculation still underestimates at around 300 MeV/nucleon. Thus, although the consistency over respective treatments is not necessarily guaranteed, the reliability is ensured by locally normalizing with well-known ${\sigma }_{\text{CC}}$ data.

Figure 2

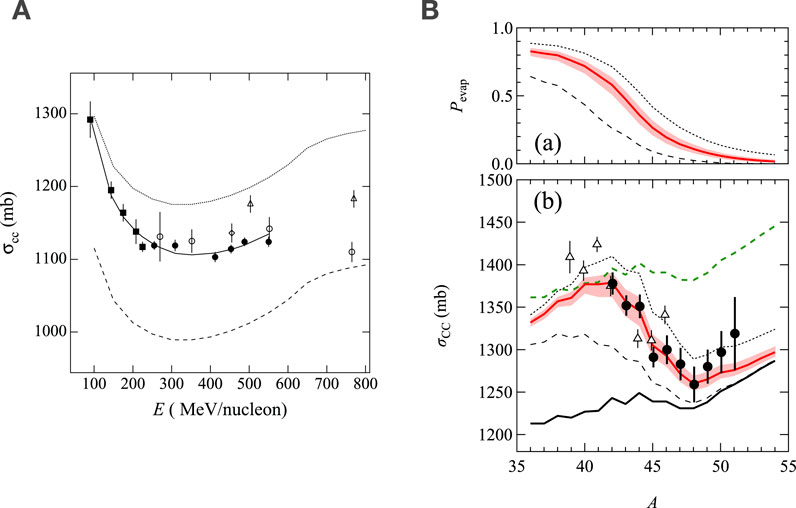
Figure 2. (A)Energy dependence of ${\sigma }_{\text{CC}}$ for ²⁸$\mathrm{S}\mathrm{i}$ on a carbon target [135]. The dashed and dotted lines represent the ZROLA calculations of ${\tilde{\sigma }}_{\text{CC}}$ (Equation 8) and ${\sigma }_{\text{R}}$, respectively. The solid line shows the ZROLA calculation of ${\sigma }_{\text{CC}}$ with the empirical correction factor $\epsilon (E)$. (B) $A$ dependence of ${\sigma }_{\text{CC}}$ for Ca isotopes on a carbon target at around 280 MeV/nucleon (bottom figure), and the corresponding $P_{\text{evap}}$ values (top figure). The black solid and green dashed lines represent ${\tilde{\sigma }}_{\text{CC}}$ calculations using Equation 8 with and without the empirical correction factor $\epsilon (E)$, respectively. The thin-dashed lines, red-solid lines with shaded bands, and dotted lines show ${\sigma }_{\text{CC}}$ calculations from Equation 9 with different $E_{\text{max}}$ values of 20, $45\pm 8$, and 70 MeV, respectively. Figures in (A, B) were reprinted from Ref. [135] and Ref. [144], respectively.

Contrary to the description by Equation 8, it has been suggested that considering the contribution of ${\rho }_{\text{n}}(r)$ of the projectile nucleus is crucial to describe ${\sigma }_{\text{CC}}$ [148–151]. Tanaka et al. demonstrated that the trend of the experimental ${\sigma }_{\text{CC}}$ data can be explained by explicitly incorporating the contribution of ${\rho }_{\text{n}}(r)$ of the projectile nucleus [144] based on the abrasion-ablation model [152, 153]. In this framework, the contribution of the cross section ${\sigma }_{\text{evap}}$, which accounts for the charge-changing process of the projectile nucleus caused by the evaporation of charged particles following neutron removal reactions, was introduced in addition to the ZROLA calculation of Equation 8:

${\sigma }_{\text{CC}}={\tilde{\sigma }}_{\text{CC}}+{\sigma }_{\text{evap}}.(9)$

The ${\sigma }_{\text{evap}}$ is calculated using the contribution probability of the neutron-removal reaction to ${\sigma }_{\text{CC}}$, $P_{\text{evap}}$. The $P_{\text{evap}}$ depends on the applied value of the parameter $E_{\text{max}}$, which represents the maximum excitation energy of the prefragment produced after a one-nucleon removal reaction (Figure 2B). Using $E_{\text{max}}=45$ MeV, this calculation consistently explains existing ${\sigma }_{\text{CC}}$ data on ¹²$\mathrm{C}$ at around 300 MeV/nucleon over a wide mass region from C to Fe isotopes, with 1.6% standard deviation [144]. Figure 2B represents measured ${\sigma }_{\text{CC}}$ results for Ca isotopes on ¹²$\mathrm{C}$ together with several caluculated cross sections explained in this subsection (see caption). This framework also reproduces new experimental results for C, N, and O isotopes on ¹²$\mathrm{C}$ at 300 MeV/nucleon [146] as well as one of two datasets of ${\sigma }_{\text{CC}}$ for N isotopes on ¹²$\mathrm{C}$ at around 900 MeV/nucleon [40]. The framework of Equation 9; Figure 2B indicates that the majority of ${\sigma }_{\text{CC}}$ provides information on ${\rho }_{\text{p}}(r)$ of the projectile nucleus and the contribution of ${\sigma }_{\text{evap}}$ decreases as $N$ of the projectile nucleus increases. Thus, in very neutron-rich region, the assumption of Equation 8 works well. The sensitivity of ${\sigma }_{\text{CC}}$ to $r_{\text{p}}$ becomes much larger.

A proton target has been adopted in ${\sigma }_{\text{CC}}$ measurements, as in the cases of ³⁰$\mathrm{N}\mathrm{e}$, ^32,33$\mathrm{N}\mathrm{a}$ [139], and ^34–36$\mathrm{A}\mathrm{r}$ [142]. Suzuki et al. emphasized the necessity of considering the contribution of ${\rho }_{\text{n}}(r)$ of the projectile nucleus peculiarly in ${\sigma }_{\text{CC}}$ on a proton target [154]. The FROLA calculation of Equation 8 underestimates the experimental ${\sigma }_{\text{CC}}$ values by 10%–20% for C isotopes on a proton target at around 900 MeV/nucleon. They found that this discrepancy can be explained by introducing the “p-n exchange” effect, in which a part of the proton flux of the target is converted to the neutron flux by neutrons of the projectile, contributing to ${\sigma }_{\text{CC}}$.

To derive the EOS parameter $L$, the difference in the charge radii of mirror nuclei, $\mathrm{\Delta }{r}_{\text{p}}^{\text{mirr}}$, has been used [155–160]. Similarly, the relationship between $L$ and the difference in ${\sigma }_{\text{CC}}$ of mirror nuclei, $\mathrm{\Delta }{\sigma }_{\text{CC}}^{\text{mirr}}$, was demonstrated to show a good linear correlation [161]. The degree of this linear correlation is equivalent to the ones between $L$ and $\mathrm{\Delta }{r}_{\text{np}}$ or $\mathrm{\Delta }{r}_{\text{p}}^{\text{mirr}}$.

6 Summary

This paper has reviewed recent advancements in the total reaction $({\sigma }_{\text{R}})$, interaction $({\sigma }_{\text{I}})$, and charge-changing cross sections $({\sigma }_{\text{CC}})$, with a special emphasis on the neutron skin and corresponding nuclear radii. The framework describing the relationship between these cross sections and the size properties of atomic nuclei has been well investigated, providing the advantage to probe nuclear sizes of neutron-rich unstable nuclei, where a thick neutron skin is expected. The review has also highlighted two novel methods for extracting $\mathrm{\Delta }{r}_{\text{np}}$ from the total collision cross sections: one utilizing the energy and isospin dependence of ${\sigma }_{\text{R}}$, and the other combining ${\sigma }_{\text{CC}}$ with ${\sigma }_{\text{R}}$. These advancements lead to more accurate constraining the slope parameter $(L)$ in the symmetry energy term of the EoS of nuclear matter through $\mathrm{\Delta }{r}_{\text{np}}$ of unstable nuclei in very neutron-rich region.

Author contributions

MT: Writing–original draft, Writing–review and editing. WH: Writing–review and editing. MF: Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Brown BA. Neutron radii in nuclei and the neutron equation of state. Phys Rev Lett (2000) 85:5296–9. doi:10.1103/PhysRevLett.85.5296

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Tsang MB, Stone JR, Camera F, Danielewicz P, Gandolfi S, Hebeler K, et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys Rev C (2012) 86:015803. doi:10.1103/physrevc.86.015803

CrossRef Full Text | Google Scholar

3. Trzcińska A, Jastrzȩbski J, Lubiński P, Hartmann FJ, Schmidt R, von Egidy T, et al. Neutron density distributions deduced from antiprotonic atoms. Phys Rev Lett (2001) 87:082501. doi:10.1103/physrevlett.87.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Klos B, Trzcinska A, Jastrzebski J, Czosnyka T, Kisielinski M, Lubinski P, et al. Neutron density distributions from antiprotonic ²⁰⁸Pb and ²⁰⁹Bi atoms. Phys Rev C (2007) 76:014311. doi:10.1103/physrevc.76.014311

CrossRef Full Text | Google Scholar

5. Terashima S, Sakaguchi H, Takeda H, Ishikawa T, Itoh M, Kawabata T, et al. Proton elastic scattering from tin isotopes at 295 MeV and systematic change of neutron density distributions. Phys Rev C (2008) 77:024317. doi:10.1103/physrevc.77.024317

CrossRef Full Text | Google Scholar

6. Zenihiro J, Sakaguchi H, Murakami T, Yosoi M, Yasuda Y, Terashima S, et al. Neutron density distributions of ^204,206,208Pb deduced via proton elastic scattering at = 295 MeV. Phys Rev C (2010) 82:044611. doi:10.1103/physrevc.82.044611

CrossRef Full Text | Google Scholar

7. Zenihiro J, Uesaka T, Sagawa H, Yoshida S. Proton density polarization of the doubly magic ⁴⁰Ca core in ⁴⁸Ca and EoS parameters. Prog Theor Exp Phys (2021) 2021. 023D05. doi:10.1093/ptep/ptab001

CrossRef Full Text | Google Scholar

8. Krasznahorkay A, Bacelar J, Bordewijk JA, Brandenburg S, Buda A, van ’t HG, et al. Excitation of the isovector giant dipole resonance by inelastic alpha scattering and the neutron skin of nuclei. Phys Rev Lett (1991) 66:1287–90. doi:10.1103/PhysRevLett.66.1287

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Krasznahorkay A, Fujiwara M, van Aarle P, Akimune H, Daito I, Fujimura H, et al. Excitation of isovector spin-dipole resonances and neutron skin of nuclei. Phys Rev Lett (1999) 82:3216–9. doi:10.1103/physrevlett.82.3216

CrossRef Full Text | Google Scholar

10. Tamii A, Poltoratska I, von Neumann-Cosel P, Fujita Y, Adachi T, Bertulani CA, et al. Complete electric dipole response and the neutron skin in ²⁰⁸Pb. Phys Rev Lett (2011) 107:062502. doi:10.1103/PhysRevLett.107.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hashimoto T, Krumbholz AM, Reinhard PG, Tamii A, von Neumann-Cosel P, Adachi T, et al. Dipole polarizability of ¹²⁰Sn and nuclear energy density functionals. Phys Rev C (2015) 92:031305. doi:10.1103/physrevc.92.031305

CrossRef Full Text | Google Scholar

12. Birkhan J, Miorelli M, Bacca S, Bassauer S, Bertulani CA, Hagen G, et al. Electric dipole polarizability of ⁴⁸Ca and implications for the neutron skin. Phys Rev Lett (2017) 118:252501. doi:10.1103/physrevlett.118.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Fearick RW, von Neumann-Cosel P, Bacca S, Birkhan J, Bonaiti F, Brandherm I, et al. Electric dipole polarizability of ⁴⁰Ca. Phys Rev Res (2023) 5:L022044. doi:10.1103/PhysRevResearch.5.L022044

CrossRef Full Text | Google Scholar

14. Abrahamyan S, Ahmed Z, Albataineh H, Aniol K, Armstrong DS, Armstrong W, et al. Measurement of the neutron radius of ²⁰⁸Pb through parity violation in electron scattering. Phys Rev Lett (2012) 108:112502. doi:10.1103/PhysRevLett.108.112502

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Adhikari D, Albataineh H, Androic D, Aniol K, Armstrong DS, Averett T, et al. Accurate determination of the neutron skin thickness of ²⁰⁸Pb through parity-violation in electron scattering. Phys Rev Lett (2021) 126:172502. doi:10.1103/PhysRevLett.126.172502

PubMed Abstract | CrossRef Full Text | Google Scholar

16. CREX Collaboration Adhikari D, Albataineh H, Androic D, Aniol KA, Armstrong DS, Averett T, et al. Precision determination of the neutral weak form factor of ⁴⁸Ca. Phys Rev Lett (2022) 129:042501. doi:10.1103/PhysRevLett.129.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Li BA, Han X. Constraining the neutron–proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density. Phys Lett B (2013) 727:276–81. doi:10.1016/j.physletb.2013.10.006

CrossRef Full Text | Google Scholar

18. Oertel M, Hempel M, Klähn T, Typel S. Equations of state for supernovae and compact stars. Rev Mod Phys (2017) 89:015007. doi:10.1103/revmodphys.89.015007

CrossRef Full Text | Google Scholar

19. Tews I, Lattimer JM, Ohnishi A, Kolomeitsev EE. Symmetry parameter constraints from a lower bound on neutron-matter energy. Astrophys J (2017) 848:105. doi:10.3847/1538-4357/aa8db9

CrossRef Full Text | Google Scholar

20. Oyamatsu K, Iida K. Saturation of nuclear matter and radii of unstable nuclei. Progr Theoret Phys (2003) 109:631–50. doi:10.1143/ptp.109.631

CrossRef Full Text | Google Scholar

21. Chen LW, Ko CM, Li BA, Xu J. Density slope of the nuclear symmetry energy from the neutron skin thickness of heavy nuclei. Phys Rev C (2010) 82:024321. doi:10.1103/physrevc.82.024321

CrossRef Full Text | Google Scholar

22. Iida K, Oyamatsu K. Symmetry energy, unstable nuclei and neutron star crusts. Eur Phys J (2014) 50:42. doi:10.1140/epja/i2014-14042-9

CrossRef Full Text | Google Scholar

23. Horiuchi W, Ebata S, Iida K. Neutron-skin thickness determines the surface tension of a compressible nuclear droplet. Phys Rev C (2017) 96:035804. doi:10.1103/physrevc.96.035804

CrossRef Full Text | Google Scholar

24. Rossi DM, Adrich P, Aksouh F, Alvarez-Pol H, Aumann T, Benlliure J, et al. Measurement of the dipole polarizability of the unstable neutron-rich nucleus ⁶⁸Ni. Phys Rev Lett (2013) 111:242503. doi:10.1103/physrevlett.111.242503

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Adrich P, Klimkiewicz A, Fallot M, Boretzky K, Aumann T, Cortina-Gil D, et al. Evidence for pygmy and giant dipole resonances in ¹³⁰Sn and ¹³²Sn. Phys Rev Lett (2005) 95:132501. doi:10.1103/physrevlett.95.132501

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Collaboration LAND, Klimkiewicz A, Paar N, Adrich P, Fallot M, Boretzky K, et al. Nuclear symmetry energy and neutron skins derived from pygmy dipole resonances. Phys Rev C (2007) 76:051603. doi:10.1103/physrevc.76.051603

CrossRef Full Text | Google Scholar

27. Wieland O, Bracco A, Camera F, Benzoni G, Blasi N, Brambilla S, et al. Search for the pygmy dipole resonance in ⁶⁸Ni at 600 MeV/nucleon. Phys Rev Lett (2009) 102:092502. doi:10.1103/physrevlett.102.092502

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Angeli I, Marinova KP. Table of experimental nuclear ground state charge radii: an update. At. Data Nucl Data Tables (2013) 99:69–95. doi:10.1016/j.adt.2011.12.006

CrossRef Full Text | Google Scholar

29. Li T, Luo Y, Wang N. Compilation of recent nuclear ground state charge radius measurements and tests for models. At. Data Nucl Data Tables (2021) 140:101440. doi:10.1016/j.adt.2021.101440

CrossRef Full Text | Google Scholar

30. Nakamura T, Sakurai H, Watanabe H. Exotic nuclei explored at in-flight separators. Prog Part Nucl Phys (2017) 97:53–122. doi:10.1016/j.ppnp.2017.05.001

CrossRef Full Text | Google Scholar

31. Kohama A, Iida K, Oyamatsu K. Difference between interaction cross sections and reaction cross sections. Phys Rev C (2008) 78:061601. doi:10.1103/physrevc.78.061601

CrossRef Full Text | Google Scholar

32. Hatakeyama S, Horiuchi W. Complete Glauber calculations for proton–nucleus inelastic cross sections. Nucl Phys A (2019) 985:20–37. doi:10.1016/j.nuclphysa.2019.02.004

CrossRef Full Text | Google Scholar

33. Takechi M, Suzuki S, Nishimura D, Fukuda M, Ohtsubo T, Nagashima M, et al. Evidence of halo structure in ³⁷Mg observed via reaction cross sections and intruder orbitals beyond the island of inversion. Phys Rev C (2014) 90:061305. doi:10.1103/physrevc.90.061305

CrossRef Full Text | Google Scholar

34. Kox S, Gamp A, Perrin C, Arvieux J, Bertholet R, Bruandet JF, et al. Trends of total reaction cross sections for heavy ion collisions in the intermediate energy range. Phys Rev C (1987) 35:1678–91. doi:10.1103/physrevc.35.1678

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Mittig W, Chouvel JM, Long ZW, Bianchi L, Cunsolo A, Fernandez B, et al. Measurement of total reaction cross sections of exotic neutron-rich nuclei. Phys Rev Lett (1987) 59:1889–91. doi:10.1103/physrevlett.59.1889

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Fukuda M, Mihara M, Fukao T, Fukuda S, Ishihara M, Ito S, et al. Density distribution of ⁸B studied via reaction cross sections. Nucl Phys A (1999) 656:209–28. doi:10.1016/s0375-9474(99)00308-5

CrossRef Full Text | Google Scholar

37. Ozawa A, Baumann T, Chulkov L, Cortina D, Datta U, Fernandez J, et al. Measurements of the interaction cross sections for Ar and Cl isotopes. Nucl Phys A (2002) 709:60–72. doi:10.1016/s0375-9474(02)01071-0

CrossRef Full Text | Google Scholar

38. Togano Y, Nakamura T, Kondo Y, Tostevin JA, Saito AT, Gibelin J, et al. Interaction cross section study of the two-neutron halo nucleus ²²C. Phys Lett B (2016) 761:412–8. doi:10.1016/j.physletb.2016.08.062

CrossRef Full Text | Google Scholar

39. Kanungo R, Horiuchi W, Hagen G, Jansen GR, Navratil P, Ameil F, et al. Proton distribution radii of ^12-19C illuminate features of neutron halos. Phys Rev Lett (2016) 117:102501. doi:10.1103/physrevlett.117.102501

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Bagchi S, Kanungo R, Horiuchi W, Hagen G, Morris TD, Stroberg SR, et al. Neutron skin and signature of the shell gap found from measured proton radii of ^17-22N. Phys Lett B (2019) 790:251–6. doi:10.1016/j.physletb.2019.01.024

CrossRef Full Text | Google Scholar

41. Kaur S, Kanungo R, Horiuchi W, Hagen G, Holt JD, Hu BS, et al. Proton distribution radii of ^16–24O: signatures of new shell closures and neutron skin. Phys Rev Lett (2022) 129:142502. doi:10.1103/physrevlett.129.142502

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Tanihata I, Terashima S, Kanungo R, Ameil F, Atkinson J, Ayyad Y, et al. Observation of large enhancements of charge exchange cross sections with neutron-rich carbon isotopes. Prog Theor Exp Phys (2016) 2016:043D05. doi:10.1093/ptep/ptw034

CrossRef Full Text | Google Scholar

43. Kohama A, Iida K, Oyamatsu K. Reaction cross section described by a black sphere approximation of nuclei. Phys Rev C (2005) 72:024602. doi:10.1103/physrevc.72.024602

CrossRef Full Text | Google Scholar

44. Iida K, Kohama A, Oyamatsu K. Formula for proton–nucleus reaction cross section at intermediate energies and its application. J Phys Soc Jpn (2007) 76:044201. doi:10.1143/jpsj.76.044201

CrossRef Full Text | Google Scholar

45. Sihver L, Kohama A, Iida K, Oyamatsu K, Hashimoto S, Iwase H, et al. Current status of the “hybrid kurotama model†for total reaction cross sections. Nucl Instrum Methods Phys Res B (2014) 334:34–9. doi:10.1016/j.nimb.2014.04.021

CrossRef Full Text | Google Scholar

46. Minomo K, Sumi T, Kimura M, Ogata K, Shimizu YR, Yahiro M. Deformation effect on total reaction cross sections for neutron-rich ne isotopes. Phys Rev C (2011) 84:034602. doi:10.1103/physrevc.84.034602

CrossRef Full Text | Google Scholar

47. Minomo K, Sumi T, Kimura M, Ogata K, Shimizu YR, Yahiro M. Determination of the structure of ³¹Ne by a fully microscopic framework. Phys Rev Lett (2012) 108:052503. doi:10.1103/physrevlett.108.052503

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Watanabe S, Minomo K, Shimada M, Tagami S, Kimura M, Takechi M, et al. Ground-state properties of neutron-rich Mg isotopes. Phys Rev C (2014) 89:044610. doi:10.1103/physrevc.89.044610

CrossRef Full Text | Google Scholar

49. Bonaccorso A, Carstoiu F, Charity RJ. Imaginary part of the ⁹C–⁹Be single-folded optical potential. Phys Rev C (2016) 94:034604. doi:10.1103/physrevc.94.034604

CrossRef Full Text | Google Scholar

50. Tagami S, Tanaka M, Takechi M, Fukuda M, Yahiro M. Chiral matrix folding-model approach to reaction cross sections for scattering of Ca isotopes on a C target. Phys Rev C (2020) 101:014620. doi:10.1103/physrevc.101.014620

CrossRef Full Text | Google Scholar

51. Moumene I, Bonaccorso A. Localization of peripheral reactions and sensitivity to the imaginary potential. Nucl Phys (2021) 1006:122109. doi:10.1016/j.nuclphysa.2020.122109

CrossRef Full Text | Google Scholar

52. Tagami S, Wakasa T, Matsui J, Yahiro M, Takechi M. Neutron skin thickness of ²⁰⁸Pb determined from the reaction cross section for proton scattering. Phys Rev C (2021) 104:024606. doi:10.1103/physrevc.104.024606

CrossRef Full Text | Google Scholar

53. Matsuzaki M, Tagami S, Yahiro M. Neutron skin thickness of ²⁰⁸Pb, ^116,120,124Sn, and ⁴⁰Ca determined from reaction cross sections of ⁴He scattering. Phys Rev C (2021) 104:054613. doi:10.1103/physrevc.104.054613

CrossRef Full Text | Google Scholar

54. Moumene I, Bonaccorso A. Optical potentials and nuclear reaction cross sections for n C and N C scattering. Phys Rev C (2023) 108:044609. doi:10.1103/physrevc.108.044609

CrossRef Full Text | Google Scholar

55. Wakasa T, Tagami S, Matsui J, Takechi M, Yahiro M. Neutron-skin values and matter and neutron radii determined from reaction cross sections of proton scattering on ¹²C, ^40,48Ca, ⁵⁸Ni, and ²⁰⁸Pb. Phys Rev C (2023) 107:024608. doi:10.1103/PhysRevC.107.024608

CrossRef Full Text | Google Scholar

56. Glauber RJ, Brittin WE, Dunham LG (1959) Lectures in theoretical physics, 1. Interscience.

Google Scholar

57. Ray L. Proton-nucleus total cross sections in the intermediate energy range. Phys Rev C (1979) 20:1857–72. doi:10.1103/physrevc.20.1857

CrossRef Full Text | Google Scholar

58. Particle Data Group Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F, et al. Review of particle physics. Phys Rev D (2018) 98:030001. doi:10.1103/PhysRevD.98.030001

CrossRef Full Text | Google Scholar

59. Varga K, Pieper SC, Suzuki Y, Wiringa RB. Monte Carlo integration in Glauber model analysis of reactions of halo nuclei. Phys Rev C (2002) 66:034611. doi:10.1103/physrevc.66.034611

CrossRef Full Text | Google Scholar

60. Nagahisa T, Horiuchi W. Examination of the ²²C radius determination with interaction cross sections. Phys Rev C (2018) 97:054614. doi:10.1103/physrevc.97.054614

CrossRef Full Text | Google Scholar

61. Abu-Ibrahim B, Suzuki Y. Utility of nucleon-target profile function in cross section calculations. Phys Rev C (2000) 61:051601. doi:10.1103/physrevc.61.051601

CrossRef Full Text | Google Scholar

62. Abu-Ibrahim B, Suzuki Y. Scatterings of complex nuclei in the Glauber model. Phys Rev C (2000) 62:034608. doi:10.1103/physrevc.62.034608

CrossRef Full Text | Google Scholar

63. Horiuchi W, Suzuki Y, Abu-Ibrahim B, Kohama A. Systematic analysis of reaction cross sections of carbon isotopes. Phys Rev C (2007) 75:044607. doi:10.1103/physrevc.75.044607

CrossRef Full Text | Google Scholar

64. Takechi M, Fukuda M, Mihara M, Tanaka K, Chinda T, Matsumasa T, et al. Reaction cross sections at intermediate energies and fermi-motion effect. Phys Rev C (2009) 79:061601. doi:10.1103/physrevc.79.061601

CrossRef Full Text | Google Scholar

65. Tran DT, Ong HJ, Nguyen TT, Tanihata I, Aoi N, Ayyad Y, et al. Charge-changing cross-section measurements of ^12-16C at around MeV and development of a Glauber model for incident energies MeV. Phys Rev C (2016) 94:064604. doi:10.1103/physrevc.94.064604

CrossRef Full Text | Google Scholar

66. Abu-Ibrahim B, Horiuchi W, Kohama A, Suzuki Y. Reaction cross sections of carbon isotopes incident on a proton. Phys Rev C (2008) 77:034607. doi:10.1103/physrevc.77.034607

CrossRef Full Text | Google Scholar

67. Abu-Ibrahim B, Horiuchi W, Kohama A, Suzuki Y. Erratum: reaction cross sections of carbon isotopes incident on a proton [Phys. Rev. C 77, 034607 (2008)]. Phys Rev C (2009) 80:029903. doi:10.1103/physrevc.80.029903

CrossRef Full Text | Google Scholar

68. Abu-Ibrahim B, Horiuchi W, Kohama A, Suzuki Y. Publisher’s Note: reaction cross sections of carbon isotopes incident on a proton [Phys. Rev. C77, 034607 (2008)]. Phys Rev C (2010) 81:019901. doi:10.1103/physrevc.81.019901

CrossRef Full Text | Google Scholar

69. Teixeira EA, Aumann T, Bertulani CA, Carlson BV. Nuclear fragmentation reactions as a probe of neutron skins in nuclei. The Eur Phys J A (2022) 58:205. doi:10.1140/epja/s10050-022-00849-w

CrossRef Full Text | Google Scholar

70. Tanaka M, Takechi M, Homma A, Fukuda M, Nishimura D, Suzuki T, et al. Swelling of doubly magic ⁴⁸Ca core in Ca isotopes beyond. Phys Rev Lett (2020) 124:102501. doi:10.1103/physrevlett.124.102501

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Horiuchi W, Inakura T. Core swelling in spherical nuclei: an indication of the saturation of nuclear density. Phys Rev C (2020) 101:061301. doi:10.1103/physrevc.101.061301

CrossRef Full Text | Google Scholar

72. Ponnath L, Aumann T, Bertulani CA, Gernhäuser R, Heil M, Almusidi T, et al. Measurement of nuclear interaction cross sections towards neutron-skin thickness determination. Phys Lett B (2024) 855:138780. doi:10.1016/j.physletb.2024.138780

CrossRef Full Text | Google Scholar

73. Moriguchi T, Ishimoto S, Igarashi S, Ozawa A, Abe Y, Ishibashi Y, et al. Developments of a thick and large solid hydrogen target for radioisotope beams. Nucl Instrum Methods Phys Res A (2010) 624:27–32. doi:10.1016/j.nima.2010.09.005

CrossRef Full Text | Google Scholar

74. Moriguchi T, Amano M, Ozawa A, Horiuchi W, Abe Y, Fujii T, et al. Energy dependence of total reaction cross sections for ¹⁷Ne on a proton target. Nucl Phys A (2020) 994:121663. doi:10.1016/j.nuclphysa.2019.121663

CrossRef Full Text | Google Scholar

75. Moriguchi T, Kagesawa R, Ozawa A, Horiuchi W, Abe Y, Amano M, et al. Investigation of total reaction cross sections for proton-dripline nuclei ¹⁷F and ¹⁷Ne on a proton target. Phys Rev C (2024) 110:014607. doi:10.1103/physrevc.110.014607

CrossRef Full Text | Google Scholar

76. Tanihata I, Hamagaki H, Hashimoto O, Nagamiya S, Shida Y, Yoshikawa N, et al. Measurements of interaction cross sections and radii of He isotopes. Phys Lett B (1985) 160:380–4. doi:10.1016/0370-2693(85)90005-x

CrossRef Full Text | Google Scholar

77. Tanihata I, Hamagaki H, Hashimoto O, Shida Y, Yoshikawa N, Sugimoto K, et al. Measurements of interaction cross sections and nuclear radii in the light p-shell region. Phys Rev Lett (1985) 55:2676–9. doi:10.1103/physrevlett.55.2676

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Ozawa A, Suzuki T, Tanihata I. Nuclear size and related topics. Nucl Phys A (2001) 693:32–62. doi:10.1016/s0375-9474(01)01152-6

CrossRef Full Text | Google Scholar

79. Tanaka K, Yamaguchi T, Suzuki T, Ohtsubo T, Fukuda M, Nishimura D, et al. Observation of a large reaction cross section in the drip-line nucleus ²²C. Phys Rev Lett (2010) 104:062701. doi:10.1103/physrevlett.104.062701

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Bagchi S, Kanungo R, Tanaka YK, Geissel H, Doornenbal P, Horiuchi W, et al. Two-neutron halo is unveiled in ²⁹F. Phys Rev Lett (2020) 124:222504. doi:10.1103/physrevlett.124.222504

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Horiuchi W, Suzuki Y. ²²C: an s-wave two-neutron halo nucleus. Phys Rev C (2006) 74:034311. doi:10.1103/physrevc.74.034311

CrossRef Full Text | Google Scholar

82. Singh J, Casal J, Horiuchi W, Fortunato L, Vitturi A. Exploring two-neutron halo formation in the ground state of ²⁹F within a three-body model. Phys Rev C (2020) 101:024310. doi:10.1103/physrevc.101.024310

CrossRef Full Text | Google Scholar

83. Fortunato L, Casal J, Horiuchi W, Singh J, Vitturi A. The ²⁹F nucleus as a lighthouse on the coast of the island of inversion. Commun Phys (2020) 3:132–5. doi:10.1038/s42005-020-00402-5

CrossRef Full Text | Google Scholar

84. Masui H, Horiuchi W, Kimura M. Two-neutron halo structure of ³¹F and a novel pairing antihalo effect. Phys Rev C (2020) 101:041303. doi:10.1103/physrevc.101.041303

CrossRef Full Text | Google Scholar

85. Kanungo R, Prochazka A, Uchida M, Horiuchi W, Hagen G, Papenbrock T, et al. Exploring the anomaly in the interaction cross section and matter radius of ²³O. Phys Rev C (2011) 84:061304. doi:10.1103/physrevc.84.061304

CrossRef Full Text | Google Scholar

86. Homma A, Takechi M, Ohtsubo T, Nishimura D, Fukuda M, Suzuki T, et al. Measurements of interaction cross sections for ^19-27F isotopes. JPS Conf Proc (2017) 14:021010. doi:10.7566/jpscp.14.021010

CrossRef Full Text | Google Scholar

87. Takechi M, Ohtsubo T, Fukuda M, Nishimura D, Kuboki T, Suzuki T, et al. Interaction cross sections for Ne isotopes towards the island of inversion and halo structures of ²⁹Ne and ³¹Ne. Phys Lett B (2012) 707:357–61. doi:10.1016/j.physletb.2011.12.028

CrossRef Full Text | Google Scholar

88. Suzuki S, Takechi M, Ohtsubo T, Nishimura D, Fukuda M, Kuboki T, et al. Measurements of interaction cross sections for ^22-35Na isotopes. EPJ Web of Conferences (2014) 66:03084. doi:10.1051/epjconf/20146603084

CrossRef Full Text | Google Scholar

89. Suzuki T, Geissel H, Bochkarev O, Chulkov L, Golovkov M, Fukunishi N, et al. Nuclear radii of Na and Mg isotopes. Nucl Phys A (1998) 630:661–77. doi:10.1016/s0375-9474(98)00799-4

CrossRef Full Text | Google Scholar

90. Kanungo R, Prochazka A, Horiuchi W, Nociforo C, Aumann T, Boutin D, et al. Matter radii of ^32-35Mg. Phys Rev C (2011) 83:021302. doi:10.1103/physrevc.83.021302

CrossRef Full Text | Google Scholar

91. Nakamura T, Kobayashi N, Kondo Y, Satou Y, Aoi N, Baba H, et al. Halo structure of the island of inversion nucleus ³¹Ne. Phys Rev Lett (2009) 103:262501. doi:10.1103/physrevlett.103.262501

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Kobayashi N, Nakamura T, Kondo Y, Tostevin JA, Utsuno Y, Aoi N, et al. Observation of a p-wave one-neutron halo configuration in ³⁷Mg. Phys Rev Lett (2014) 112:242501. doi:10.1103/physrevlett.112.242501

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Horiuchi W, Suzuki Y, Capel P, Baye D. Probing the weakly-bound neutron orbit of ³¹Ne with total reaction and one-neutron removal cross sections. Phys Rev C (2010) 81:024606. doi:10.1103/physrevc.81.024606

CrossRef Full Text | Google Scholar

94. Horiuchi W, Inakura T, Nakatsukasa T, Suzuki Y. Glauber-model analysis of total reaction cross sections for Ne, Mg, Si, and S isotopes with Skyrme-Hartree-Fock densities. Phys Rev C (2012) 86:024614. doi:10.1103/physrevc.86.024614

CrossRef Full Text | Google Scholar

95. Takatsu R, Suzuki Y, Horiuchi W, Kimura M. Microscopic study of the deformed neutron halo of ³¹Ne. Phys Rev C (2023) 107:024314. doi:10.1103/physrevc.107.024314

CrossRef Full Text | Google Scholar

96. Zhang HY, Shen WQ, Ren ZZ, Ma YG, Jiang WZ, Zhu ZY, et al. Measurement of reaction cross section for proton-rich nuclei at intermediate energies. Nucl Phys A (2002) 707:303–24. doi:10.1016/S0375-9474(02)01007-2

CrossRef Full Text | Google Scholar

97. Zheng T, Yamaguchi T, Ozawa A, Chiba M, Kanungo R, Kato T, et al. Study of halo structure of ¹⁶C from reaction cross section measurement. Nucl Phys A (2002) 709:103–18. doi:10.1016/S0375-9474(02)01043-6

CrossRef Full Text | Google Scholar

98. Fang DQ, Yamaguchi T, Zheng T, Ozawa A, Chiba M, Kanungo R, et al. One-neutron halo structure in ¹⁵C. Phys Rev C (2004) 69:034613. doi:10.1103/physrevc.69.034613

CrossRef Full Text | Google Scholar

99. Yamaguchi Y, Wu C, Suzuki T, Ozawa A, Fang DQ, Fukuda M, et al. Density distribution of ¹⁷B from a reaction cross-section measurement. Phys Rev C (2004) 70:054320. doi:10.1103/physrevc.70.054320

CrossRef Full Text | Google Scholar

100. Ozawa A, Cai YZ, Chen ZQ, Chiba M, Fang DQ, Guo ZG, et al. Measurements of the interaction cross-sections for ¹⁴Be and ^14,15B as projectiles with a new scheme at RIBLL. Nucl Instrum Methods Phys Res B (2006) 247:155–60. doi:10.1016/j.nimb.2006.01.054

CrossRef Full Text | Google Scholar

101. Tanaka K, Fukuda M, Mihara M, Takechi M, Nishimura D, Chinda T, et al. Density distribution of ¹⁷Ne and possible shell-structure change in the proton-rich sd-shell nuclei. Phys Rev C (2010) 82:044309. doi:10.1103/physrevc.82.044309

CrossRef Full Text | Google Scholar

102. Yamaguchi T, Tanaka K, Suzuki T, Ozawa A, Ohtsubo T, Aiba T, et al. Nuclear reactions of ^19,20C on a liquid hydrogen target measured with the superconducting TOF spectrometer. Nucl Phys A (2011) 864:1–37. doi:10.1016/j.nuclphysa.2011.05.095

CrossRef Full Text | Google Scholar

103. Moriguchi T, Ozawa A, Ishimoto S, Abe Y, Fukuda M, Hachiuma I, et al. Density distributions of ¹¹Li deduced from reaction cross-section measurements. Phys Rev C (2013) 88:024610. doi:10.1103/physrevc.88.024610

CrossRef Full Text | Google Scholar

104. Moriguchi T, Ozawa A, Ishimoto S, Abe Y, Fukuda M, Hachiuma I, et al. Density distribution of ¹⁴Be from reaction cross-section measurements. Nucl Phys A (2014) 929:83–93. doi:10.1016/j.nuclphysa.2014.06.003

CrossRef Full Text | Google Scholar

105. Fan GW, Fukuda M, Nishimura D, Cai XL, Fukuda S, Hachiuma I, et al. Structure of ⁸Li from a reaction cross-section measurement. Phys Rev C (2014) 90:044321. doi:10.1103/physrevc.90.044321

CrossRef Full Text | Google Scholar

106. Fukuda M, Morita Y, Nishimura D, Takechi M, Iwamoto K, Wakabayashi M, et al. Nucleon density distribution of the proton drip-line nucleus ¹²N studied via reaction cross sections. JPS Conf Proc (2015) 6:030103. doi:10.7566/jpscp.6.030103

CrossRef Full Text | Google Scholar

107. Tanaka M, Fukuda M, Nishimura D, Suzuki S, Takechi M, Mihara M, et al. Reaction cross sections for ⁸He and ¹⁴B on proton target for the separation of proton and neutron density distributions. JPS Conf Proc (2015) 6:020026. doi:10.7566/JPSCP.6.020026

CrossRef Full Text | Google Scholar

108. Nishizuka K, Takechi M, Ohtsubo T, Nishimura D, Fukuda M, Aoki K, et al. Measurements of reaction cross sections for ^9-11C. JPS Conf Proc (2017) 14:021015. doi:10.7566/JPSCP.14.021015

CrossRef Full Text | Google Scholar

109. Tanaka M, Fukuda M, Nishimura D, Takechi M, Suzuki S, Du H, et al. Reaction cross sections for ^13-15B and one-neutron halo in ¹⁴B. Acta Phys Pol B (2017) 48:461. doi:10.5506/aphyspolb.48.461

CrossRef Full Text | Google Scholar

110. Fukuda M, Ichihara T, Inabe N, Kubo T, Kumagai H, Nakagawa T, et al. Neutron halo in ¹¹Be studied via reaction cross sections. Phys Lett B (1991) 268:339–44. doi:10.1016/0370-2693(91)91587-l

CrossRef Full Text | Google Scholar

111. Tanihata I, Kobayashi T, Suzuki T, Yoshida K, Shimoura S, Sugimoto K, et al. Determination of the density distribution and the correlation of halo neutrons in ¹¹Li. Phys Lett B (1992) 287:307–11. doi:10.1016/0370-2693(92)90988-g

CrossRef Full Text | Google Scholar

112. Negoita F, Borcea C, Carstoiu F, Lewitowicz M, Saint-Laurent MG, Anne R, et al. ⁸B proton halo via reaction and breakup cross section measurements. Phys Rev C (1996) 54:1787–97. doi:10.1103/physrevc.54.1787

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Takechi M, Fukuda M, Mihara M, Chinda T, Matsumasa T, Matsubara H, et al. Reaction cross-sections for stable nuclei and nucleon density distribution of proton drip-line nucleus ⁸B. Eur Phys J (2005) 25:217–9. doi:10.1140/epjad/i2005-06-078-0

CrossRef Full Text | Google Scholar

114. Horiuchi W, Inakura T, Michimasa S. Large enhancement of total reaction cross sections at the edge of the island of inversion in ti, cr, and fe isotopes. Phys Rev C (2022) 105:014316. doi:10.1103/physrevc.105.014316

CrossRef Full Text | Google Scholar

115. Horiuchi W, Suzuki Y, Shalchi MA, Tomio L. Possible halo structure of ^62,72Ca by forbidden-state-free locally peaked Gaussians. Phys Rev C (2022) 105:024310. doi:10.1103/physrevc.105.024310

CrossRef Full Text | Google Scholar

116. Horiuchi W, Inakura T. Pairing core swelling effect in Pb isotopes at. Phys Rev C (2022) 105:044303. doi:10.1103/physrevc.105.044303

CrossRef Full Text | Google Scholar

117. Yamaguchi T, Suzuki T, Ohnishi T, Becker F, Fukuda M, Geissel H, et al. Nuclear matter radii of neutron-deficient Kr isotopes. Phys Rev C (2008) 77:034315. doi:10.1103/physrevc.77.034315

CrossRef Full Text | Google Scholar

118. Tanihata I, Hirata D, Kobayashi T, Shimoura S, Sugimoto K, Toki H. Revelation of thick neutron skins in nuclei. Phys Lett B (1992) 289:261–6. doi:10.1016/0370-2693(92)91216-v

CrossRef Full Text | Google Scholar

119. Suzuki T, Geissel H, Bochkarev O, Chulkov L, Golovkov M, Hirata D, et al. Neutron skin of Na isotopes studied via their interaction cross sections. Phys Rev Lett (1995) 75:3241–4. doi:10.1103/physrevlett.75.3241

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Huber G, Touchard F, Büttgenbach S, Thibault C, Klapisch R, Duong HT, et al. Spins, magnetic moments, and isotope shifts of ^21-31Na by high resolution laser spectroscopy of the atomic line. Phys Rev C (1978) 18:2342–54. doi:10.1103/physrevc.18.2342

CrossRef Full Text | Google Scholar

121. Garcia Ruiz RF, Bissell ML, Blaum K, Ekström A, Frömmgen N, Hagen G, et al. Unexpectedly large charge radii of neutron-rich calcium isotopes. Nat Phys (2016) 12:594–8. doi:10.1038/nphys3645

CrossRef Full Text | Google Scholar

122. Minamisono K, Rossi DM, Beerwerth R, Fritzsche S, Garand D, Klose A, et al. Charge radii of neutron deficient ^52,53Fe produced by projectile fragmentation. Phys Rev Lett (2016) 117:252501. doi:10.1103/physrevlett.117.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Iida K, Oyamatsu K. Surface tension in a compressible liquid-drop model: effects on nuclear density and neutron skin thickness. Phys Rev C (2004) 69:037301. doi:10.1103/physrevc.69.037301

CrossRef Full Text | Google Scholar

124. Warda M, Vinas X, Roca-Maza X, Centelles M. Neutron skin thickness in the droplet model with surface width dependence: indications of softness of the nuclear symmetry energy. Phys Rev C (2009) 80:024316. doi:10.1103/physrevc.80.024316

CrossRef Full Text | Google Scholar

125. Warda M, Centelles M, Vinas X, Roca-Maza X. Influence of the single-particle structure on the nuclear surface and the neutron skin. Phys Rev C (2014) 89:064302. doi:10.1103/physrevc.89.064302

CrossRef Full Text | Google Scholar

126. Horiuchi W, Suzuki Y, Inakura T. Probing neutron-skin thickness with total reaction cross sections. Phys Rev C (2014) 89:011601. doi:10.1103/physrevc.89.011601

CrossRef Full Text | Google Scholar

127. Fang DQ, Ma YG, Cai XZ, Tian WD, Wang HW. Effects of neutron skin thickness in peripheral nuclear reactions. Chin Phys. Lett. (2011) 28:102102. doi:10.1088/0256-307x/28/10/102102

CrossRef Full Text | Google Scholar

128. Fang DQ, Ma YG, Cai XZ, Tian WD, Wang HW. Neutron removal cross section as a measure of neutron skin. Phys Rev C (2010) 81:047603. doi:10.1103/physrevc.81.047603

CrossRef Full Text | Google Scholar

129. Ma CW, Wei HL, Yu M. Reexamination of the neutron skin thickness using neutron removal cross sections. Phys Rev C (2010) 82:057602. doi:10.1103/physrevc.82.057602

CrossRef Full Text | Google Scholar

130. Aumann T, Bertulani CA, Schindler F, Typel S. Peeling off neutron skins from neutron-rich nuclei: constraints on the symmetry energy from neutron-removal cross sections. Phys Rev Lett (2017) 119:262501. doi:10.1103/physrevlett.119.262501

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Bertulani CA, Valencia J. Neutron skins as laboratory constraints on properties of neutron stars and on what we can learn from heavy ion fragmentation reactions. Phys Rev C (2019) 100:015802. doi:10.1103/physrevc.100.015802

CrossRef Full Text | Google Scholar

132. Horiuchi W, Hatakeyama S, Ebata S, Suzuki Y. Extracting nuclear sizes of medium to heavy nuclei from total reaction cross sections. Phys Rev C (2016) 93:044611. doi:10.1103/physrevc.93.044611

CrossRef Full Text | Google Scholar

133. Horiuchi W, Suzuki Y, Uesaka T, Miwa M. Total reaction cross section on a deuteron target and the eclipse effect of the constituent neutron and proton. Phys Rev C (2020) 102:054601. doi:10.1103/physrevc.102.054601

CrossRef Full Text | Google Scholar

134. Nishimura D, Fukuda M, Takechi M, Mihara M, Ishikawa D, Komurasaki J, et al. Distinction between proton-neutron density distribution of halo nuclei at the nuclear surface via reaction cross sections. Nucl Phys A (2010) 834:470c–2c. doi:10.1016/j.nuclphysa.2010.01.067

CrossRef Full Text | Google Scholar

135. Yamaguchi T, Fukuda M, Fukuda S, Fan GW, Hachiuma I, Kanazawa M, et al. Energy-dependent charge-changing cross sections and proton distribution of si 28. Phys Rev C (2010) 82:014609. doi:10.1103/physrevc.82.014609

CrossRef Full Text | Google Scholar

136. Yamaguchi T, Hachiuma I, Kitagawa A, Namihira K, Sato S, Suzuki T, et al. Scaling of charge-changing interaction cross sections and point-proton radii of neutron-rich carbon isotopes. Phys Rev Lett (2011) 107:032502. doi:10.1103/physrevlett.107.032502

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Yamaki S, Yamaguchi T, Kouno J, Sato K, Ichihashi N, Suzuki T, et al. Systematic study of individual charge-changing cross sections of intermediate-energy secondary beams. Nucl Instrum Methods Phys Res B (2013) 317:774–8. doi:10.1016/j.nimb.2013.05.057

CrossRef Full Text | Google Scholar

138. Yamaki S, Kouno J, Nishimura D, Nagashima M, Takechi M, Sato K, et al. Charge-changing interactions probing point-proton radii of nuclei. EPJ Web of Conferences (2014) 66:03099. doi:10.1051/epjconf/20146603099

CrossRef Full Text | Google Scholar

139. Ozawa A, Moriguchi T, Ohtsubo T, Aoi N, Fang DQ, Fukuda N, et al. Charge-changing cross sections of ³⁰Ne, ^32,33Na with a proton target. Phys Rev C (2014) 89:044602. doi:10.1103/physrevc.89.044602

CrossRef Full Text | Google Scholar

140. Terashima S, Tanihata I, Kanungo R, Estrade A, Horiuchi W, Ameil F, et al. Proton radius of ¹⁴Be from measurement of charge-changing cross sections. Prog Theor Exp Phys (2014) 2014:101D02. doi:10.1093/ptep/ptu134

CrossRef Full Text | Google Scholar

141. Estradé A, Kanungo R, Horiuchi W, Ameil F, Atkinson J, Ayyad Y, et al. Proton radii of ^12–17B define a thick neutron surface in ¹⁷B. Phys Rev Lett (2014) 113:132501. doi:10.1103/physrevlett.113.132501

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Sawahata K, Ozawa A, Saito Y, Abe Y, Ichikawa Y, Inaba N, et al. Investigations of charge-changing processes for light proton-rich nuclei on carbon and solid-hydrogen targets. Nucl Phys A (2017) 961:142–53. doi:10.1016/j.nuclphysa.2017.02.012

CrossRef Full Text | Google Scholar

143. Tran DT, Ong HJ, Hagen G, Morris TD, Aoi N, Suzuki T, et al. Evidence for prevalent Z = 6 magic number in neutron-rich carbon isotopes. Nat Commun (2018) 9:1594. doi:10.1038/s41467-018-04024-y

PubMed Abstract | CrossRef Full Text | Google Scholar

144. Tanaka M, Takechi M, Homma A, Prochazka A, Fukuda M, Nishimura D, et al. Charge-changing cross sections for ^42–51Ca and effect of charged-particle evaporation induced by neutron-removal reactions. Phys Rev C (2022) 106:014617. doi:10.1103/physrevc.106.014617

CrossRef Full Text | Google Scholar

145. Wang CJ, Guo G, Ong HJ, Song YN, Sun BH, Tanihata I, et al. Charge-changing cross section measurements of 300 MeV/nucleon ²⁸Si on carbon and data analysis. Chin Phys C (2023) 47:084001. doi:10.1088/1674-1137/acd366

CrossRef Full Text | Google Scholar

146. Zhao JW, Sun BH, Tanihata I, Terashima S, Prochazka A, Xu JY, et al. Isospin-dependence of the charge-changing cross-section shaped by the charged-particle evaporation process. Phys Lett B (2023) 847:138269. doi:10.1016/j.physletb.2023.138269

CrossRef Full Text | Google Scholar

147. Zhao JW, Sun BH, Tanihata I, Xu JY, Zhang KY, Prochazka A, et al. Charge radii of ^11–16C, ^13–17N and ^15–18O determined from their charge-changing cross-sections and the mirror-difference charge radii. Phys Lett B (2024) 858:139082. doi:10.1016/j.physletb.2024.139082

CrossRef Full Text | Google Scholar

148. Bhagwat A, Gambhir YK. Microscopic investigations of mass and charge changing cross sections. Phys Rev C (2004) 69:014315. doi:10.1103/physrevc.69.014315

CrossRef Full Text | Google Scholar

149. Akaishi T, Hagino K. Analysis of charge changing cross sections with the Glauber-Abrasion-Ablation model. JPS Conf Proc (2015) 6:030097. doi:10.7566/JPSCP.6.030097

CrossRef Full Text | Google Scholar

150. Fan GW, Zhan X. Influence of neutrons on charge-changing cross-sections. Int J Mod Phys E (2019) 28:1950070. doi:10.1142/s0218301319500708

CrossRef Full Text | Google Scholar

151. Abdul-Magead IAM, Abu-Ibrahim B. Contribution of the projectile neutrons to the total charge-changing cross sections. Nucl Phys (2020) 1000:121804. doi:10.1016/j.nuclphysa.2020.121804

CrossRef Full Text | Google Scholar

152. Gaimard JJ, Schmidt KH. A reexamination of the abrasion-ablation model for the description of the nuclear fragmentation reaction. Nucl Phys A (1991) 531:709–45. doi:10.1016/0375-9474(91)90748-u

CrossRef Full Text | Google Scholar

153. Scheidenberger C, Pshenichnov IA, Sümmere K, Ventura A, Bondorf JP, Botvina AS, et al. Charge-changing interactions of ultrarelativistic Pb nuclei. Phys Rev C (2004) 70:014902. doi:10.1103/physrevc.70.014902

CrossRef Full Text | Google Scholar

154. Suzuki Y, Horiuchi W, Terashima S, Kanungo R, Ameil F, Atkinson J, et al. Parameter-free calculation of charge-changing cross sections at high energy. Phys Rev C (2016) 94:011602. doi:10.1103/physrevc.94.011602

CrossRef Full Text | Google Scholar

155. Wang N, Li T. Shell and isospin effects in nuclear charge radii. Phys Rev C (2013) 88:011301. doi:10.1103/physrevc.88.011301

CrossRef Full Text | Google Scholar

156. Brown BA. Mirror charge radii and the neutron equation of state. Phys Rev Lett (2017) 119:122502. doi:10.1103/physrevlett.119.122502

PubMed Abstract | CrossRef Full Text | Google Scholar

157. Yang J, Piekarewicz J. Difference in proton radii of mirror nuclei as a possible surrogate for the neutron skin. Phys Rev C (2018) 97:014314. doi:10.1103/physrevc.97.014314

CrossRef Full Text | Google Scholar

158. Gaidarov MK, Moumene I, Antonov AN, Kadrev DN, Sarriguren P, Moya de Guerra E. Proton and neutron skins and symmetry energy of mirror nuclei. Nucl Phys A (2020) 1004:122061. doi:10.1016/j.nuclphysa.2020.122061

CrossRef Full Text | Google Scholar

159. Brown BA, Minamisono K, Piekarewicz J, Hergert H, Garand D, Klose A, et al. Implications of the ³⁶Ca–³⁶S and ³⁸Ca–³⁸Ar difference in mirror charge radii on the neutron matter equation of state. Phys Rev Res (2020) 2:022035. doi:10.1103/physrevresearch.2.022035

CrossRef Full Text | Google Scholar

160. Pineda SV, König K, Rossi DM, Brown BA, Incorvati A, Lantis J, et al. Charge radius of neutron-deficient ⁵⁴Ni and symmetry energy constraints using the difference in mirror pair charge radii. Phys Rev Lett (2021) 127:182503. doi:10.1103/PhysRevLett.127.182503

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Xu JY, Li ZZ, Sun BH, Niu YF, Roca-Maza X, Sagawa H, et al. Constraining equation of state of nuclear matter by charge-changing cross section measurements of mirror nuclei. Phys Lett B (2022) 833:137333. doi:10.1016/j.physletb.2022.137333

CrossRef Full Text | Google Scholar