Feature analysis of 5G traffic data based on visibility graph

Introduction: As 5G networks become widespread and their application scenarios expand, massive amounts of traffic data are continuously generated. Properly analyzing this data is crucial for enhancing 5G services.

Methods: This paper uses the visibility graph method to convert 5G traffic data into a visibility graph network, conducting a feature analysis of the 5G traffic data. Using the AfreecaTV dataset as the research object, this paper constructs visibility networks at different scales and observes the evolution of degree distribution with varying data volumes. The paper employs the Hurst index to evaluate the 5G traffic network and uses community detection to study the networks converted from 5G traffic data of different applications.

Results: Experimental results reveal significant differences in node degree distribution and topological structures of 5G traffic data across different application scenarios, such as star structures and multiple subnetwork structures. It is found that the node degree distribution of 5G traffic networks exhibits heterogeneity, reflecting the uneven growth of node degrees during network expansion. The Hurst index analysis discovers that the 5G traffic network retains the long-term dependence and trends of the original data. Through community detection, it is observed that networks converted from 5G traffic data of different applications exhibit diverse community structures, such as high centrality nodes, star-like community structures, modularity, and multilayer characteristics.

Discussion: These findings indicate that 5G traffic networks in different application scenarios exhibit complex and diverse characteristics. The heterogeneity of node degree distribution and differences in topological structures reflect the imbalance in node connection methods during network expansion. The results of the Hurst index show that the 5G traffic network inherits the long-term dependence of the original data, providing a basis for analyzing the dynamic characteristics of the network. The diverse community structures reveal the inherent modularity and hierarchy of the network, which helps to understand the performance and optimization directions of 5G networks in different applications.

1 Introduction

With the proliferation of 5G networks and the continuous expansion of their application scenarios, massive traffic data is being generated. Efficient utilization of this data is crucial for enhancing 5G technology and services [1]. Analyzing 5G traffic data helps understand the bandwidth requirements of different applications, providing theoretical guidance for optimizing network resources. Classifying different applications not only aids in delivering differentiated services to improve Quality of Service (QoS) [2–4] but also helps in identifying abnormal traffic and potential security threats, allowing for effective protective measures to ensure network security [5].

As a method of time series analysis, visibility graph (VG) has gained significant attention in recent years [6]. VG transforms time series data into complex networks using visibility rules, making it possible to reveal the inherent dynamic characteristics of the time series data more intuitively. The core idea is to map data points in the time series to network nodes and connect relevant nodes based on visibility rules, forming a complex network structure. The VG method not only captures the characteristics of time series but also uncovers hidden spatiotemporal features and dynamic behaviors through network analysis.

Introducing VG to 5G traffic data analysis provides a new perspective. By integrating VG methods with 5G traffic analysis, the depth and breadth of data analysis can be enhanced, providing scientific evidence for the optimization of 5G networks and promoting further applications of 5G technology. Specifically, the VG algorithm can construct a 5G traffic network, analyzing the characteristics of 5G traffic data in different application scenarios. Observing the evolution characteristics of the visibility network helps understand the spatiotemporal distribution patterns of 5G traffic data, thereby better serving the applications of 5G networks.

This paper adopts a new time series network construction method—the VG algorithm—to establish a VG network for 5G traffic and analyzes the characteristics of 5G traffic data in different application scenarios using complex network theory. The main structure of the paper is as follows: In the first section, we introduce the necessity of this study; in the second section, we present related work; the third section provides the model used in this paper; the fourth section includes simulations and discussions; finally, we conclude the study.

2 Related work

The VG, as a method of transforming time series into complex networks, offers a new perspective for nonlinear time series analysis [7]. Its basic idea is to map data points in a time series to nodes in a complex network and determine the edges between nodes based on specific visibility criteria, embedding the time series into a network structure. Through this transformation, the topological structure of the network can intuitively reflect the dynamic changes and inherent relational characteristics of the time series. In recent years, VG has been widely applied in various fields, such as economics, finance, and biomedicine, demonstrating its powerful analytical capabilities and versatility.

In the economic and financial fields, VG is widely used for analyzing financial time series, such as stock prices and exchange rates [8, 9]. Researchers use VG rules to transform financial time series data into complex networks, utilizing complex network metrics such as degree, degree distribution, and betweenness to identify key nodes in financial markets, thus revealing the underlying dynamic mechanisms of the market. For example, researchers can use complex network analysis methods to identify critical junctions, thereby uncovering fluctuation patterns in stock prices and identifying key factors influencing stock price changes [10, 11].

In the biomedical field, VG has demonstrated its unique advantages, particularly in analyzing biomedical signals such as electrocardiograms (ECG) [12, 13] and electroencephalograms (EEG) [14, 15]. For instance, researchers [14] can use the VG method to convert EEG signals into complex networks, employing complex network research methods to analyze the differences between seizure stages and pre-seizure stages. Additionally, researchers can use the VG method to analyze ECG variations [16], aiding in the detection of heart disease and providing significant support for early diagnosis and prevention.

In earth sciences, the VG method is used to analyze complex characteristics of earth systems, such as climate change [17] and seismic activity [18]. For example, the VG method can transform temperature variations into complex networks, using community mining methods to study the intrinsic logical relationships between temperature changes [17]. Some researchers utilize the VG method to study seismic data, uncovering correlations between earthquake data [18].

In summary, VG, as a novel method connecting nonlinear signal analysis and complex networks, offers new perspectives for time series data analysis with its effective, stable, and easy-to-implement advantages. Therefore, it is necessary to introduce VG to analyze 5G traffic data. This approach not only provides a new perspective for 5G traffic data analysis but also effectively alleviates some limitations of current deep learning methods in analyzing 5G traffic data.

Compared to commonly used deep learning methods, VG has advantages in the following aspects: Firstly, VG effectively avoids the problem of data scarcity [19, 20]. Deep learning models typically rely on a large amount of high-quality training data [21, 22], but acquiring traffic data that comprehensively reflects the complexity of 5G networks is challenging [23]. VG can construct networks without requiring large-scale datasets, revealing spatiotemporal patterns and dynamic features in time series. Secondly, VG offers better interpretability. Deep learning models are often seen as “black boxes” [24], with their internal decision-making processes difficult to explain. By mapping time series data to complex networks, VG intuitively reflects the structural characteristics of the data, providing strong interpretability. Thirdly, VG excels in handling large-scale data. In a 5G network environment, the volume of traffic data is enormous and rapidly changing, requiring efficient analysis and processing methods. VG can quickly construct complex networks, offering high real-time performance. Lastly, the widespread application of VG in various fields has verified its applicability and effectiveness. VG has achieved success in multiple fields [25–30], showcasing its powerful analytical capabilities and broad adaptability, providing rich references and insights for 5G traffic data analysis.

For the above reasons, this paper employs the VG algorithm to convert 5G time series data into complex networks, analyzing the evolutionary characteristics of visibility networks using metrics such as network topology, degree distribution, Hurst index, and community division, to understand the features of 5G traffic data in different application scenarios.

3 Modelling

3.1 Complex networks

A complex network is a network structure composed of nodes and the relationships between nodes, which can be represented as a graph $G=\left[V,E\right]$. In graph $G$ , $V$ represents the set of nodes, indicating elements or time points in the system (as in this paper, where nodes correspond to time points of collected data); $E$ represents the set of edges, indicating the relationships between the individual elements (as in this paper, where edges indicate the visibility between nodes). Through the graph structure, complex networks can visually describe the intricate interactions within the system, providing a theoretical basis for analyzing complex systems. In the process of studying complex networks, researchers introduce an adjacency matrix $A$ to describe the connection relationships between nodes $i$ and $j$, defining it as an $N\times N$ matrix, where $N$ is the number of nodes. In this representation, the connection relationships between each pair of nodes can be directly reflected through matrix elements $A_{ij}$, thus providing a tool for analyzing the structural characteristics and dynamic evolution rules of the network. The mathematical expression of the adjacency matrix is shown in Equation 1.

$A_{ij}=\left\{\begin{array}{cc}1,& \text{if there is an edge between nodes }i\text{ and }j\\ 0,& \text{if there is no edge between nodes }i\text{ and }j\end{array}\right.(1)$

In complex network analysis, the degree of a node and the degree distribution are two fundamental and important concepts that reveal the structural characteristics of the network. The degree $k_i$ of a node $i$ is defined as the number of edges connected to it, and the mathematical expression is shown in Equation 2.

$k_i={\displaystyle \sum _{j=1}^N}{A}_{ij}(2)$

The degree distribution $P\left(k\right)$ is defined as the fraction of nodes in the network that have degree $k$, and the mathematical expression is shown in Equation 3.

$P\left(k\right)=\frac{N_k}{N}(3)$

Where $N_k$ is the number of nodes with degree $k$, and $N$ is the total number of nodes in the network. The degree distribution $P\left(k\right)$ describes the distribution of node degrees in the network and is an important indicator for measuring the structural characteristics of the network. In a scale-free network, the degree distribution follows a power-law distribution. An important feature of the power-law distribution is the long-tail effect, meaning that there are a few nodes with very high degrees, while the majority of nodes have relatively low degrees [31], and the mathematical expression is shown in Equation 4.

$P\left(k\right)\sim k^{-\gamma }(4)$

Where $\gamma$ is a constant, typically ranging between 2 and 3.

3.2 Louvain algorithm

Community detection is a significant issue in complex network research, as it reveals the modular structure of the network, dividing the network into several communities. This results in tighter connections within the community nodes and sparser connections between communities. To explore the community structure of 5G traffic data, this paper uses the Louvain algorithm [32]. The Louvain algorithm is an efficient community detection method that aims to optimize modularity. It identifies the community structure in the network through a hierarchical clustering method. Modularity is a critical measure for evaluating the quality of network partitioning, comparing the density of connections within communities to a random network of the same size. The definition of modularity is shown in Equation 5.

$Q=\frac{1}{2m}{\displaystyle \sum _{ij}}\left[W_{ij}-\frac{k_i{k}_j}{2m}\right]\delta \left(c_i,c_j\right)(5)$

Where $W_{ij}$ represents the weight of the edge between node $i$ and node $j$, $k_i$ and $k_j$ are the degrees of node $i$ and node $j$ respectively, $m$ is the number of edges in the network, and $\delta \left(c_i,c_j\right)$ is an indicator function that equals one if node $i$ and node $j$ belong to the same community, and 0 otherwise.

The Louvain algorithm optimizes modularity in two main steps: modularity optimization and community aggregation. During the modularity optimization phase, the algorithm iteratively moves each node to the community where it achieves the highest modularity increase, thereby locally optimizing modularity. In the community aggregation phase, the communities obtained from the previous phase are treated as super-nodes, constructing a new network and performing the modularity optimization phase again on this new network. Through this hierarchical clustering method, the Louvain algorithm can effectively detect the multi-level community structure in complex networks.

3.3 Visibility graph

The VG [6] is an important method for transforming time series data into complex networks and has been widely applied in various fields in recent years. The basic steps of the VG method are as follows:

Firstly, each data point in the time series is represented as a node in the VG. For example, for a time series $\left\{x_t\right\}$, where $t=1,2,\dots ,N$, each data point $x_t$ corresponds to a node $v_t$. Through this method, the dynamic information of the time series is converted into the nodes in the network.

Secondly, the connection between nodes $v_i$ and $v_j$ is determined based on the visibility criteria. Specifically, a link between nodes $v_i$ and $v_j$ exists if and only if for any node $v_k$ (where $i<k<j$) the following condition is satisfied in Equation 6.

$x_k<x_i+\frac{k-i}{j-i}\left(x_j-x_i\right)(6)$

This criterion ensures that the connection between nodes $v_i$ and $v_j$ is not obscured by any intermediate nodes in the graphical representation of the time series.

Finally, the adjacency matrix $A$ of the VG is constructed. Here, $A_{ij}=1$ indicates an edge exists between nodes $v_i$ and $v_j$, while $A_{ij}=0$ indicates no edge exists between them.

By following these steps, the time series data are successfully transformed into a VG, allowing the use of complex network theory and techniques to analyze the characteristics of the time series. Figure 1 demonstrates the process of converting 5G traffic data into a complex network.

Figure 1

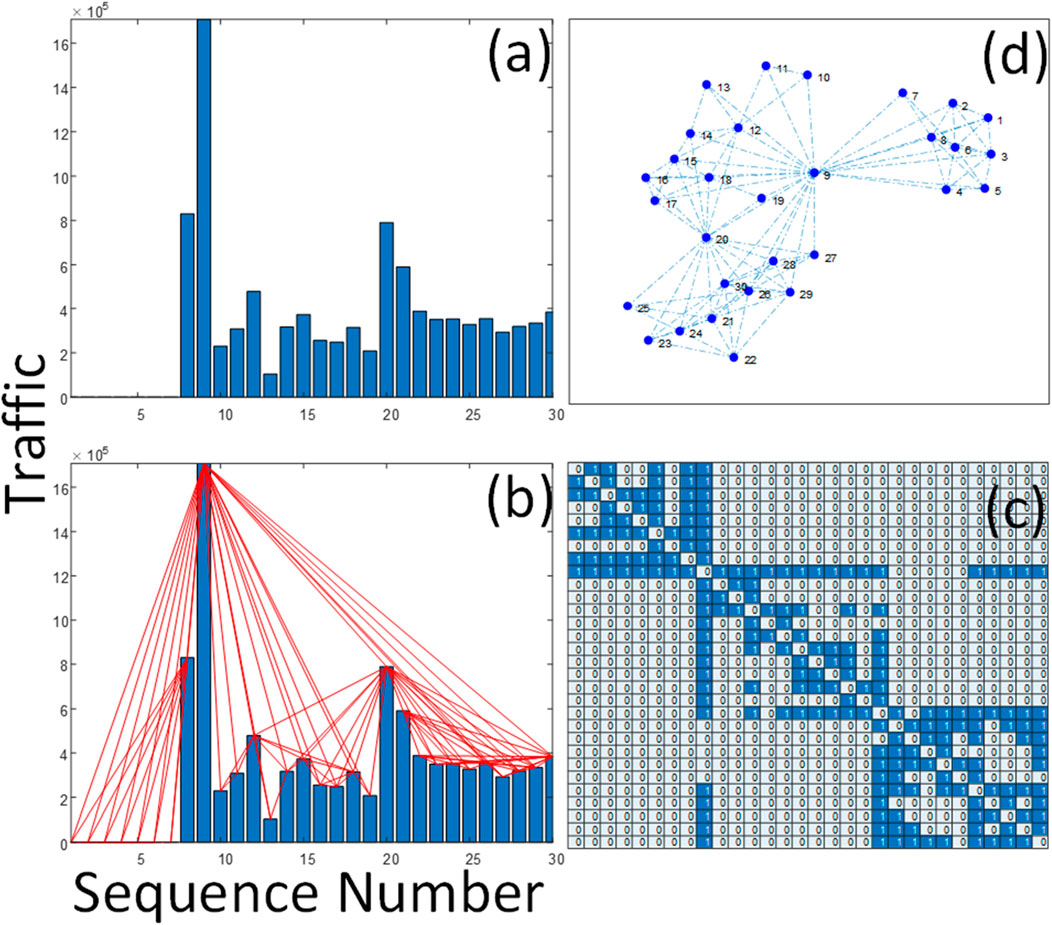
Figure 1. The process of transforming 5G traffic data into a complex network using the Visibility Graph method. (A) shows the first 32 data points from the AfreecaTV dataset, with the horizontal axis representing the data sequence number and the vertical axis representing the traffic volume. The data in (A) are converted into a visibility graph according to the VG criteria, resulting in the nodes connected by blue lines in (B). (C) is the adjacency matrix $A$ obtained from (B), where dark cells represent $A_{ij}=1$ and light cells represent $A_{ij}=0$. (D) shows the complex network derived from the adjacency matrix $A.$

4 Numerical simulations

4.1 Dataset

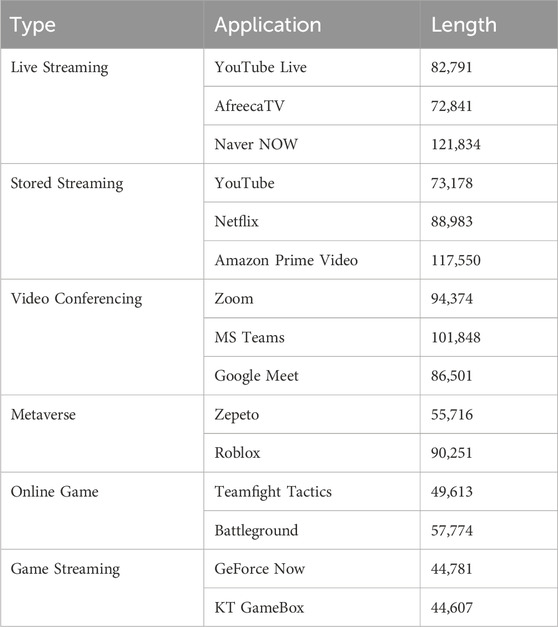
The 5G traffic data used in this paper are sourced from the literature [23]. The dataset has a total duration of 328 h and includes six main categories such as Live Streaming, Stored Streaming, and Video Conferencing, and 15 subcategories including YouTube Live and AfreecaTV. The complete dataset contains complex information such as source addresses and destination addresses. However, this study only uses traffic data (the 5G data used in the paper are shown in Table 1).

Table 1

Table 1. 5G traffic data.

4.2 Analysis of the visibility network structure

To comparatively analyze the characteristics of 5G traffic data under different applications, we constructed a localized 5G traffic network. We selected the first 200 data points from each dataset to establish a complex network, with the results shown in Figure 2. Due to significant noise in the first 465 data points of the GeForce Now dataset, which greatly affected data validity, we chose data points 502 to 701 from the GeForce Now dataset for analysis, and established the corresponding complex network, keeping other datasets unchanged.

Figure 2

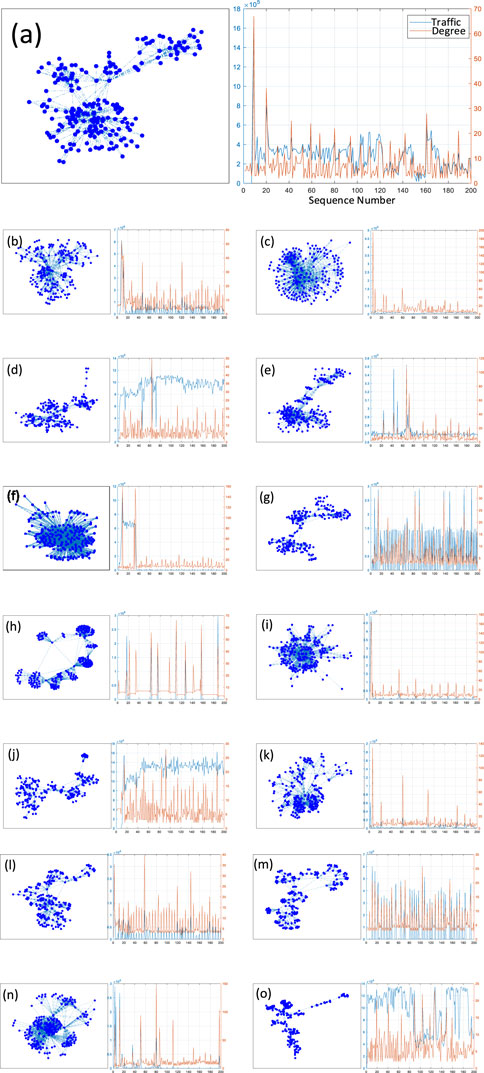
Figure 2. 5G Traffic Network and Node Degree. To analyze the topological characteristics of 5G traffic data, we constructed local networks using 5G traffic data and investigated the relationship between the traffic data and the node degrees. (A–O) correspond to the datasets AfreecaTV, Amazon Prime Video, Battleground, GeForce Now, Google Meet, KT GameBox, MS Teams, Naver NOW, Netflix, Roblox, Teamfight Tactics, YouTube, YouTube Live, Zepeto, and Zoom, respectively. In each figure, the left side shows a 5G traffic network with 200 nodes, while the right side displays a dual y-axis plot. For consistent comparative analysis, a force layout algorithm was applied to uniformly arrange the complex networks. In the dual y-axis plot, the x-axis represents the data index, the left y-axis blue curve indicates the downlink bitrate (DL_bitrate), and the right y-axis orange curve shows the degree of the data index (node) within the complex network.

The construction of localized 5G traffic networks is advantageous for visualization. Firstly, an excessive amount of data leads to dense graphs, reducing visualization effectiveness and making it difficult to discern data characteristics. Secondly, although long data sequences provide more information, they involve high computational costs, increased noise, and obscure main features, which are seldom used in practical applications. Finally, selecting 200 data points effectively represents some characteristics of 5G traffic data, ensuring the accuracy of the analysis.

As shown in Figure 2, the 15 sets of images can be divided into four distinctly different topological structures. Figures 2A, D, E, K exhibit a single-center dense structure; Figures 2B, N display multi-center characteristics; Figures 2C, F, I reveal star-like network structures; and Figures 2G, H, O demonstrate multiple branching phenomena. Figures 2J, L, M show relatively uniform network structures.

From the network structures on the left side of Figures 2A, D, E, K, it is evident that the connections between nodes are dense, indicating high traffic demand during specific periods. These networks feature a significant central node that connects many peripheral nodes, with most nodes having low degrees, fitting the characteristics of a power-law distribution. By observing the corresponding 5G traffic data and node degrees, it is found that significant traffic peaks correspond to central nodes. For example, in Figure 2A, the node with the highest degree in the entire network is node 9, with a degree of 66, followed by a node with a degree of 38, and most nodes have degrees between 2 and 5. Although Figures 2A, D, E, K all exhibit single-center dense structures, their specific network topologies and node distributions differ. The central nodes in Figures 2A, E are more concentrated, while the peripheral nodes in Figures 2D, K are slightly more dispersed.

The network structures in Figures 2B, N show multi-center characteristics. That is, central nodes connect with many peripheral nodes, forming several local dense areas. Compared to single-center dense structures, each central node in a multi-center network forms high-density connections within its local area, indicating multiple significant traffic peaks in the 5G traffic data reflected in Figures 2B, N. Analyzing the traffic data and node degree trends on the right, the multiple central nodes in Figures 2B, N have significantly higher traffic than other nodes, resulting in multiple central nodes in the network. In the multi-center network structure of Figure 2B, the central nodes are relatively dispersed, with loose connections between central nodes, forming several relatively independent local dense areas. Conversely, in Figure 2N, the central nodes are relatively concentrated, with tight connections between central nodes, forming an interconnected node cluster. For example, in Figure 2B, there are four central nodes numbered 8, 12, 47, and 121, with degrees of 52, 42, 37, and 37, respectively. In Figure 2N, there are six significant central nodes numbered 3, 12, 51, 80, 111, and 197, with degrees of 78, 107, 94, 147, 86, and 104, respectively.

In Figures 2C, F, I, the network structures exhibit star-like structures. This topological structure is characterized by a prominent central node connected to numerous peripheral nodes, forming a star-shaped layout. The central node plays a core role in the entire network, connecting almost all peripheral nodes and becoming the focal point for traffic and degree. The traffic data and degree trends in the right-side figures clearly show that the traffic peaks of the central node closely correspond to its degree. Although Figures 2C, F, I all exhibit star-like structures, their specific network topologies and node distributions differ. For instance, the central nodes in Figures 2C, I are more concentrated, with a larger number of connected peripheral nodes, showing a more pronounced center-periphery structure. In contrast, the central node in Figure 2F is relatively dispersed, forming several local dense areas.

In Figures 2G, H, O, the network structures show clear multiple sub-network phenomena. The connections between nodes are more dispersed, with multiple branches in the network forming a complex structure of multiple sub-networks. This network topology reflects the diversity and heterogeneity among different nodes in the 5G traffic data, indicating significant fluctuations in data traffic demand. However, each dataset differs significantly. For example, in Figure 2G, there are three obvious sub-networks around nodes 14, 83, and 137. In Figure 2H, there are eight sub-networks around nodes 22, 34, 63, 75, 110, 127, 157, and 188. In Figure 2O, there are five highly cohesive sub-networks around nodes 19, 41, 89, 104, and 127.

In Figures 2J, L, M, the network structures show relatively uniform characteristics. In these networks, connections between nodes are more evenly distributed, with no significant central nodes, making the entire network appear relatively balanced, indicating stable traffic demand in the corresponding application scenarios. The 5G traffic data represented by the blue line on the right show a uniform distribution of traffic demand, while the degree represented by the orange curve also shows a uniform variation trend. However, there are differences between each network. Specifically, the network structure in Figure 2J is more dispersed, with relatively loose connections between nodes. The network structure in Figure 2L shows a few nodes with higher degrees on the basis of uniform distribution but still maintains an overall uniform characteristic. The network structure in Figure 2M is tighter, with slightly more connections between nodes.

In summary, the network structures converted from 5G traffic data using the VG exhibit significant differences, providing new perspectives for a deeper understanding of the characteristics of 5G traffic data. Specifically, complex network models constructed using the VG technique reveal notable differences in node degree and topology under different application scenarios of 5G traffic data. For example, when there is a single significant traffic peak, the network shows a central node, forming a distinct star-shaped structure. When there are multiple traffic peaks, the network presents a multiple sub-network structure. These findings help reveal the traffic characteristics and demand differences of 5G networks in various application scenarios.

4.3 The degree distribution in 5G traffic networks

To analyze the characteristics of 5G traffic time series, we constructed visibility networks of 5G traffic data at different scales. Specifically, this paper uses the AfreecaTV dataset as the research subject, establishing VGs using the first 500, 1,000, 2000, 4,000, 6,000, 8,000, and 10,000 data points. By visualizing these visibility networks at different scales (as shown in Figure 3), we can intuitively observe the topological evolution of network structures under varying data volumes.

Figure 3

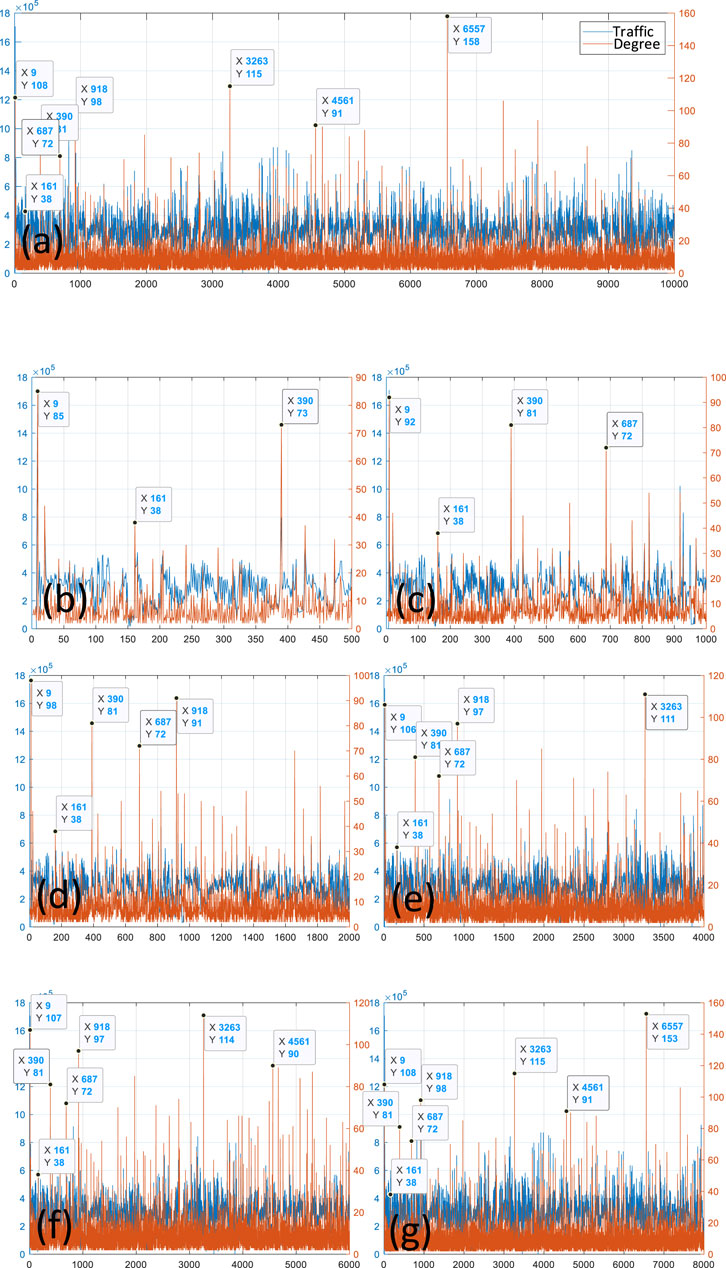
Figure 3. Node Degree Variation at Different Scales. Figure 3 illustrates the variation in node degrees at different scales. The data for (A) consists of 10,000 points, while (B–G) correspond to datasets with 500, 1,000, 2,000, 4,000, 6,000, and 8,000 points, respectively. We focus on the changes of the same nodes across these different figures.

In these networks, we focused on the changes in high-degree nodes (i.e., nodes with large degrees). High-degree nodes typically play significant structural roles in complex networks and represent traffic peaks in 5G traffic data. By analysing the degree changes of these nodes at different data scales, we can uncover the structural characteristics of 5G traffic data at various scales. Table 2 presents the variations of high-degree nodes at different scales.

Table 2

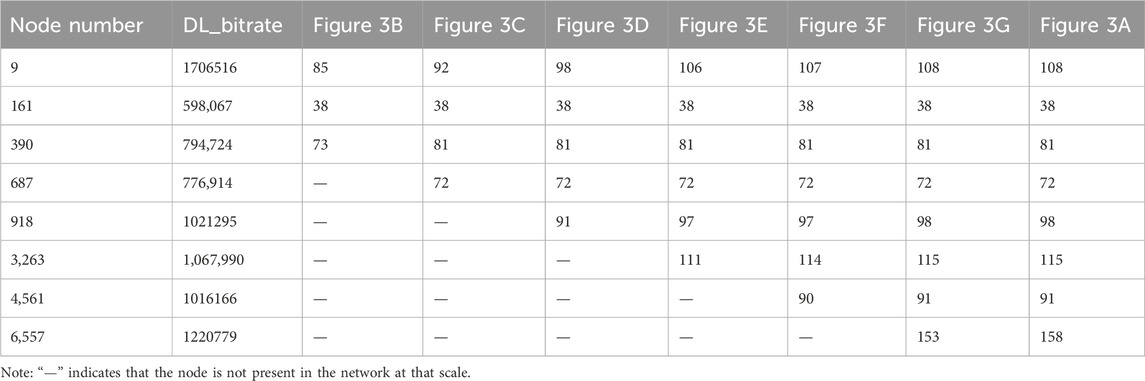
Table 2. Changes in Node Degree at Different Scales for the Same Nodes. In selecting the nodes, we chose those with relatively high degrees, i.e., nodes with higher DL_bitrate.

From the analysis of Table 2, it can be observed that as the scale increases, the degrees of high-degree nodes show a significant increase, while the degrees of low-degree nodes remain relatively unchanged.

Firstly, with the increase in data length, the degrees of high-degree nodes consistently rise. This indicates that in longer data sequences, these nodes gradually accumulate more connections, exhibiting higher degrees. This phenomenon can be explained by the fact that during the expansion of the dataset, nodes with higher visibility attract more connections, thereby significantly increasing their degrees. This also reflects the “rich-get-richer” effect within the network, where nodes with more connections are more likely to attract new ones. For instance, the degree of node 9 increases from 85 to 108 with increasing data length, directly illustrating this phenomenon.

Secondly, the degrees of low-degree nodes remain relatively unchanged as the data volume increases, indicating that the number of connections for these nodes does not significantly vary with the increase in data length. Low-degree nodes have lower visibility, their number of connections is fewer and more stable, and they are less affected by the increase in data length. For example, the degree of node 161 consistently stays at 38, and node 687, though initially absent in smaller scales, stabilizes at a degree of 72 in subsequent data points.

Lastly, apart from extreme degree nodes, certain nodes exhibit stability across different data scales. For instance, the degree of node 390 remains between 73 and 81 as the data length increases, demonstrating a stable connection structure.

In summary, we observe a heterogeneity in the degree distribution of the 5G traffic network, reflecting the uneven growth of node degrees during network expansion. Specifically, high-degree nodes significantly increase their connections with the growing data volume, while low-degree nodes remain relatively stable. This heterogeneity phenomenon is prevalent in many complex networks, especially those with power-law distribution characteristics. To investigate whether the 5G traffic network exhibits a power-law distribution, we performed a power-law function fitting on its degree distribution, resulting in Figure 4; Table 3.

Figure 4

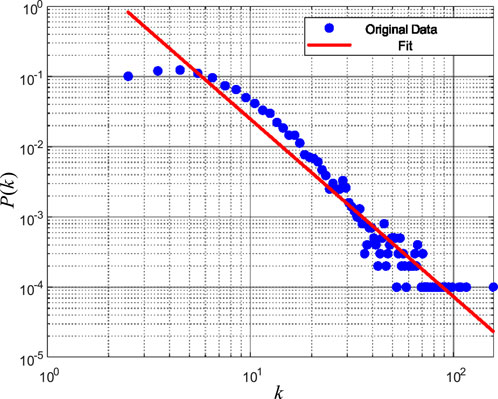
Figure 4. Power-law Distribution Fitting Results. Figure 4 presents the results of the power-law distribution fitting. The figure shows data consisting of 10,000 points (the same dataset as used in Figure 3A), fitted using the power-law distribution $P\left(k\right)\sim k^{-\gamma }$. The blue dots represent the original degree distribution $P\left(k\right)$, and the red line indicates the fitting curve of the power-law distribution. Both axes use logarithmic scales, with $P\left(k\right)$ on the y-axis and $k$ on the x-axis, to more clearly illustrate the characteristics of the power-law distribution.

Table 3

Table 3. Fitted power-law distribution parameters $\gamma$ and adjusted R² at different scales.

Figure 4 presents the results of the power-law distribution fitting for the degree distribution, using 10,000 data points and fitting the degree distribution to a power-law distribution $P\left(k\right)\sim k^{-\gamma }$. Table 3 provides the parameters $\gamma$ and the adjusted R-squared values (Adj. R²) from the power-law distribution fitting across different scales.

From Figure 4, it can be observed that the blue dots in the log-log scale clearly demonstrate the characteristics of the degree distribution. The majority of nodes have relatively low degrees, but their corresponding probability $P\left(k\right)$ is relatively high, as shown in the upper left part of the figure. Conversely, a few nodes have relatively high degrees, and their corresponding probability $P\left(k\right)$ is relatively low, as shown in the lower right part of the figure. This uneven distribution reveals the presence of the long-tail effect, where a small number of nodes have very high degrees. That is, the blue dots in the lower right part of the figure are fewer in number but have very high degrees, and the probability of these nodes extends far, forming a long tail.

The red fitting line accurately captures the trend of the blue dots, especially in the mid-to-high degree regions. The slope of the fitting line reflects the steepness of the tail; a steeper slope indicates a more pronounced long-tail effect. The adjusted R² value of 0.78 indicates that the power-law distribution model explains the degree distribution well, further confirming the existence of the long-tail effect.

Table 3 lists the power-law distribution fitting parameters and adjusted R-squared values (Adj. R²) for different data scales. With changes in data scale, the value of $\gamma$ fluctuates between 1.56 and 2.57, indicating differences in the power-law characteristics of the network structure across various data scales. Overall, a larger $\gamma$ (as in Figures 3A, F) implies a faster drop-off rate in the degree distribution and a relatively smaller number of high-degree nodes.

From Table 3, it can be seen that the Adj. R² values for different data scales vary significantly, ranging from 0.49 to 0.96. Notably, the adjusted R-squared value (Adj. R²) in Figure 3E is only 0.49, indicating a poorer fit compared to other data scales. Further analysis reveals that the addition of node 3,263, which connects to numerous other nodes, results in an anomaly in the network structure, causing the overall degree distribution to deviate from the predicted power-law distribution characteristics. Similar phenomena are also observed in Figure 3G.

These results indicate that when studying and optimizing 5G traffic networks, special attention should be paid to these anomalous nodes and their impact on the network structure. By identifying and managing these key nodes, the dynamic nature of the network can be better understood, and the network structure can be optimized.

4.4 Hurst analysis

In the analysis of 5G traffic data, the long-term dependency and self-similarity of time series are important characteristics, and the Hurst exponent is a crucial metric to describe these features [33, 34]. In this study, by calculating the Hurst exponent for both the time series and its VG network, we can reveal the long-term dependency and self-similarity in the node degree distribution, thereby gaining a deeper understanding of the network’s evolutionary patterns. To evaluate the long-term dependency of the 5G traffic time series, this paper employs the Rescaled Range Analysis (R/S) method [35] to calculate the Hurst exponent, with the results presented in Table 3.

The Hurst exponent (H) ranges from 0 to 1, with different values reflecting different characteristics of the time series. When $0.5<H<1$, it indicates that the time series exhibits long-term positive correlation (persistence), meaning that if the traffic increases over a period, it is likely to continue increasing in the future, and vice versa. This characteristic suggests that 5G traffic has a trend influenced by certain stable factors. When $H=0.5$, it implies that the time series behaves like a random walk, with no clear trend, and the traffic changes are random. This characteristic typically indicates that 5G traffic is influenced by many random factors, lacking significant long-term dependency structure. When $0<H<0.5$, it indicates that the time series exhibits long-term negative correlation (anti-persistence), meaning that if the traffic increases over a period, it is likely to decrease in the future, and vice versa.

From Table 4, it can be observed that the Hurst exponent of the original data ranges between 0.55 and 0.62, all greater than 0.5, indicating long-term positive correlation (persistence) in the original data. This means that the 5G traffic data at these scales exhibit significant trend continuity; the fluctuations in traffic are self-similar, and future fluctuations in the time series resemble those in the past. This reflects the stability and consistency of 5G traffic data across different time scales.

Table 4

Table 4. Hurst exponents at different scales.

Simultaneously, the Hurst exponent of the degree in the VG network ranges between 0.54 and 0.60, indicating that the VG network also exhibits persistence, self-similarity, and stability. Firstly, the Hurst exponent of the 5G traffic data generally exceeds 0.5, suggesting that the data series has long-term positive correlation, meaning future traffic fluctuations are likely to be similar to those in the past. This characteristic reflects the trend continuity in the time series, indicating that 5G traffic data exhibit relatively stable variation patterns over a certain period. Secondly, the fluctuations in the 5G traffic VG exhibit self-similarity, meaning that the characteristics of traffic fluctuations remain consistent across different time scales. Specifically, future fluctuations in the time series are likely to resemble those in the past, a notable feature of fractal time series. Lastly, the Hurst exponent of the degree in the 5G traffic VG remains relatively stable across different data scales. The degree of the VG network maintains a high Hurst exponent across all time scales, demonstrating the temporal stability and high connectivity of high-degree nodes in the network. This stability reflects the structural consistency of the complex network constructed from 5G traffic data across different time scales.

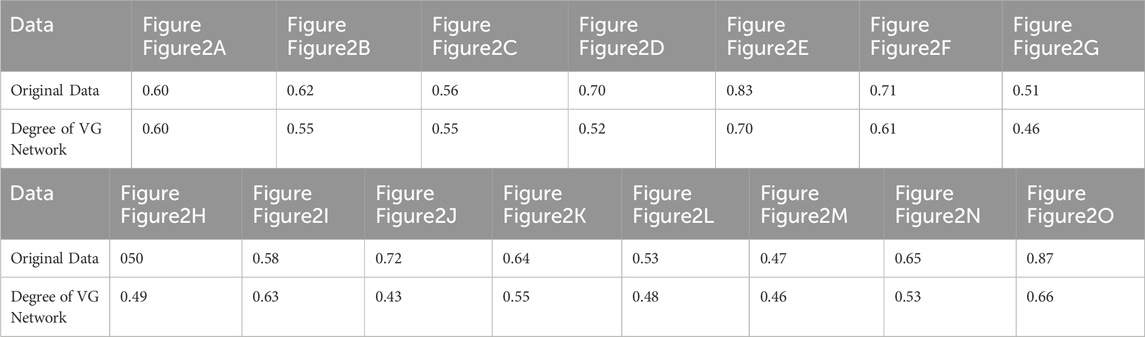
The Hurst exponents in Table 5 analyze the long-term dependence and self-similarity of 5G traffic data across different application scenarios, calculated for both the original data and the degree of the Visibility Graph (VG) network. The Hurst exponent ranges from 0 to one and is used to measure the long-term memory and trend of a time series. The data numbering in Table 5 corresponds to that in Figure 2, with 2000 data points used.

Table 5

Table 5. Hurst exponents for different applications.

As observed in Table 5, the Hurst exponent for the VG network’s degree is generally lower than that of the original data (e.g., Figures 2B, E, G, etc.), indicating that the volatility of node degrees is reduced in the VG network, which suggests that the network structure somewhat diminishes the long-term dependence of the original data. Conversely, in other cases (e.g., Figure 2I), the Hurst exponent for the VG network’s degree is higher than that of the original data, indicating that in these scenarios, the degree of nodes in the VG network better retains the trend of the original data. Moreover, in most application scenarios, the Hurst exponent for the VG network’s degree is lower than that of the corresponding original data. This suggests that after transforming the data into a complex network using the VG method, the structural characteristics of the network may somewhat reduce the trend and self-similarity of the sequence.

The study results indicate that the Hurst exponent of the 5G traffic time series and its VG network node degree effectively evaluates the long-term dependency and trend of traffic, providing a significant theoretical basis for performance analysis and optimization of 5G networks.

4.5 Community analysis

To uncover the intrinsic structure and dynamic behavior of 5G traffic data, we employ community detection methods to analyze the community structure of the VG network. Community detection is a technique that partitions network nodes into several subsets such that the connections within each subset are as dense as possible, while connections between different subsets are as sparse as possible.

In the context of 5G traffic data, traffic connections are relatively tight within a fluctuation cycle, while connections between different cycles are less frequent. Specifically, community detection methods can help reveal the intrinsic structure of the time series and identify the dynamic characteristics of the data. Firstly, by transforming the time series data into a network, community detection methods can identify the underlying structure of the data, such as periodic fluctuations and abrupt changes. This is significant for understanding the behavior of 5G traffic data over different periods. Secondly, 5G traffic data exhibit different dynamic behaviors under various application scenarios. Through community detection, we can identify these dynamic behaviors, providing valuable insights for the study of 5G traffic data. Figure 5 shows the community detection results of the 5G traffic network.

Figure 5

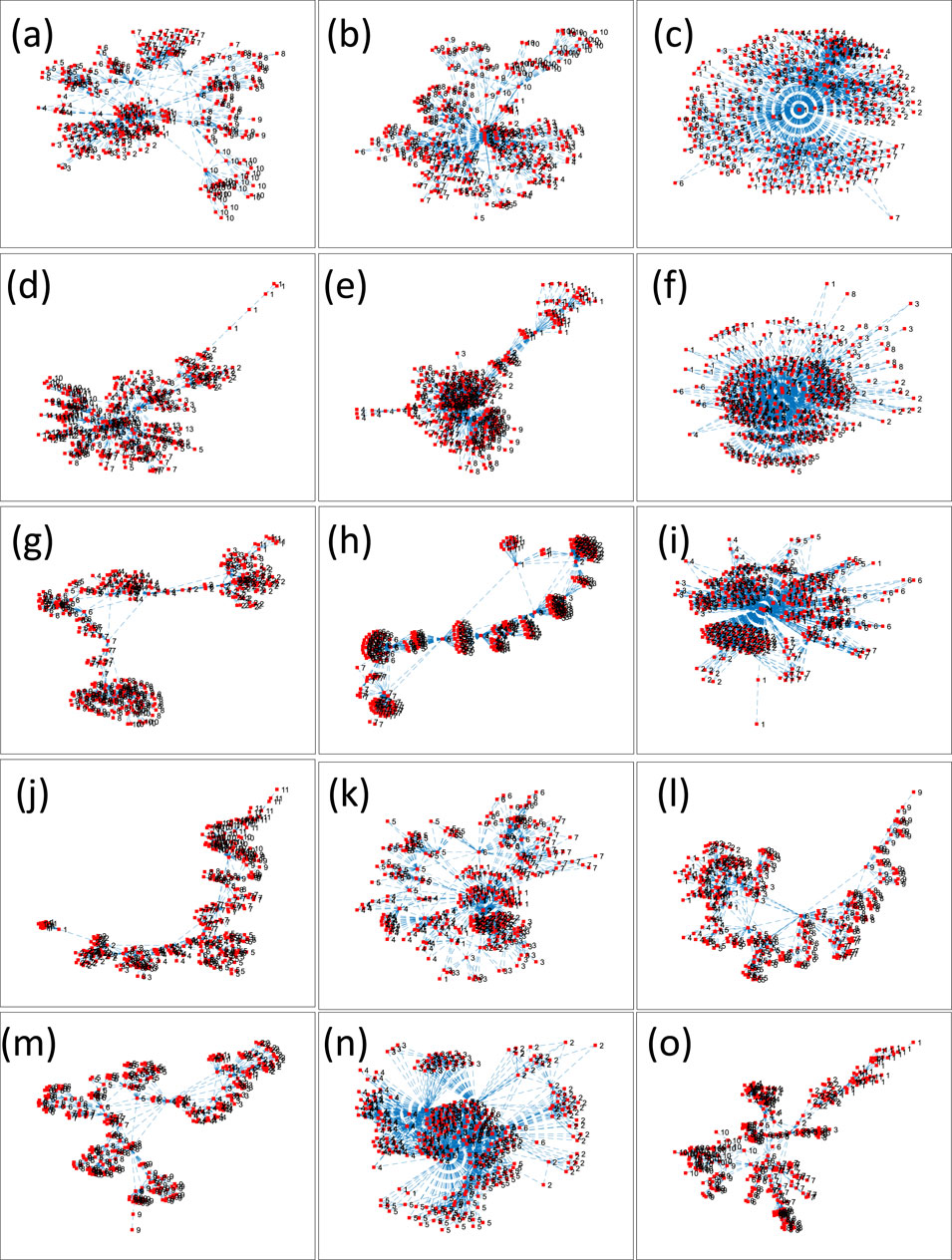
Figure 5. Community Detection Results of 5G Traffic Networks. Figure 5 presents the community detection results of 5G traffic networks. (A–O) correspond to the different datasets set in Figure 2, with 300 data points selected for analysis from each dataset. Notably, for the GeForce Now dataset, data points from 502 to 801 were selected for analysis. The Louvain algorithm was used for community detection; each red dot represents a node in the network, and the node numbers indicate the community to which the nodes belong. This visualization method allows us to intuitively observe the community structures of different datasets.

As shown in Figures 5A, B, K display more complex community structures. The boundaries between communities are blurred due to the significant number of inter-community links, indicating high visibility among the traffic data in these datasets. Figures 5C, F, I, N exhibit typical “star-shaped” community structures, suggesting that 5G traffic data have significant peaks with traffic concentrated on key nodes. Figures 5G, H, J, L, M show distinct community structures, reflecting clear periodic characteristics of traffic data in these scenarios. Figures 5D, E, O present both blurred and distinct community structures, highlighting the diversity and complexity of 5G traffic data in these contexts.

Figures 5A, B, K illustrate complex community structures with blurred boundaries and no clear edges, indicating numerous connections between different communities. For example, in Figure 5A, community node one is tightly connected not only with its internal nodes but also with nodes from other communities. Community node nine is connected to communities 1, 7, 8, and 10. This blurred boundary characteristic reflects the complex visibility and diversity in 5G traffic data. These visibility networks contain key nodes with high degree centrality. Central nodes are located at the core of communities and act as bridges between nodes within or between communities. In 5G traffic data, high centrality nodes typically correspond to traffic peaks, transforming into high centrality nodes through visibility rules. These nodes, as key connecting nodes in the VG, characterize the spatiotemporal features and peak phenomena of 5G traffic data.

Figures 5C, F, I, N display “star-shaped” community structures. In these figures, the network presents a distinct star-shaped structure where there are few or no direct connections between communities, instead connected indirectly through central nodes. For example, in Figure 5C, community seven is not directly connected to communities 2, 3, 4, or 5, but rather through community 1, forming a star-shaped community structure. The high connectivity and centrality of these central nodes reflect the absolute peaks in 5G traffic data. There are significant differences between the figures; for instance, Figure 5C has one central node, Figures 5F,I have two, and Figure 5N has three central nodes.

Figures 5G, H, J, L, M exhibit networks with clear community structures. There are distinct boundaries between communities, with most communities having no direct connections with each other. For instance, in Figure 5H, community seven is not directly connected to communities 2, 3, and 4, and even needs to connect indirectly through communities 1, 2, 5, and four to link with community 3. This feature indicates that nodes within each community are tightly connected, forming high-density networks, with clear boundaries reflecting the independence and complementarity of different functional modules within the network. This modular characteristic shows that the network can be divided into several communities with dense internal connections and sparse inter-community connections. Observing the 5G traffic data corresponding to Figures 5G, H, J, L, M, it is evident that the distinct community structures are due to the presence of multiple similar traffic peaks, i.e., periodic traffic peaks. These periodic peaks lead to high-density internal connections within communities and sparse connections between communities, forming distinct community structures. For example, this phenomenon can be clearly observed from the degree variation curve in Figure 2H.

Figures 5D, E, O demonstrate diversified community structures. These figures include both overlapping and distinct communities, reflecting the presence of multifunctional nodes and the multilayer nature of the network. For example, in Figures 5D, E, O, community one connects directly only to community 2, showing clear community structures. From the 5G traffic data corresponding to Figures 5D, E, O, it can be seen that there is a primary traffic peak with several smaller peaks, a phenomenon clearly visible in Figure 2D.

In conclusion, the community detection analysis of 5G traffic data reveals the spatiotemporal characteristics and peak phenomena under different applications, showcasing the relationships and independence among various traffic patterns. Different applications of 5G traffic data networks exhibit various community structures, such as high centrality nodes, star-shaped communities, modular characteristics, and multilayered networks.

5 Conclusion

This paper analyzes 5G traffic data using VG method based on complex network theory. The findings reveal significant differences in the dynamic characteristics and intrinsic structures of 5G traffic data across various application scenarios, showcasing the advantages and potential applications of VG method in traffic data analysis.

Firstly, by converting 5G traffic data into VGs, this study successfully constructed 5G traffic visibility networks. The research found notable differences in node degree distribution and topological structure among 5G traffic data from different application scenarios. Specifically, some scenarios exhibited a clear single-center dense structure, while others presented multi-center or star-shaped network structures. Analysis of node degree distribution and topological characteristics revealed the nonlinear features and hidden patterns of 5G traffic data. These discoveries provide new perspectives for understanding the spatiotemporal distribution patterns of 5G traffic and offer scientific bases for 5G network optimization and resource scheduling.

Secondly, this paper employed community detection methods to analyze the community structures within 5G traffic data. The study found diverse community structures across different application scenarios. For instance, in some scenarios, traffic data formed distinct community structures where nodes within each community were tightly connected, while connections between different communities were relatively sparse. This structure reflects the volatility and periodicity of 5G traffic data over different time periods. Additionally, the study discovered complex multifunctional node structures and multilayer network structures in some application scenarios. These findings contribute to a deeper understanding of the dynamic behavior and change patterns of 5G traffic data, providing important references for optimizing 5G networks and improving service quality.

Finally, the research results demonstrate that VG method offers high interpretability and real-time capabilities in analyzing 5G traffic data. Compared to traditional deep learning methods, VG method effectively avoids issues of data scarcity and intuitively reflects the structural characteristics of data through network topologies. Furthermore, VG method excels in handling large-scale and real-time data, quickly constructing complex networks and capturing the dynamic behavior of traffic data. These advantages highlight the broad application prospects of VG method in 5G traffic data analysis, potentially offering new solutions for 5G network optimization, traffic prediction, and anomaly detection.

In conclusion, this paper systematically analyzes 5G traffic data from the perspective of complex networks by introducing VG technology. The research results not only deepen the understanding of the dynamic characteristics of 5G traffic data but also provide theoretical support for optimizing 5G networks and resource management. In the future, with the continuous development of 5G technology, the application of VG method in traffic data analysis will become more widespread, contributing to the construction of efficient and stable 5G networks.

In future research, more advanced community detection methods could be employed. While this study utilizes the Louvain algorithm for community detection in 5G traffic data, this approach may not fully capture all potential community structures. Future studies could explore additional community detection algorithms, such as the Leiden algorithm, graph neural network-based methods, or other machine learning techniques, to achieve a more in-depth analysis of the community structure and dynamic behavior of the data. Simultaneously, it is important to recognize that degree distribution alone does not comprehensively reflect all structural characteristics of a network. As highlighted in the literature [36], even networks with the same degree distribution may exhibit significant differences in other key topological properties, such as clustering coefficient and characteristic path length. Therefore, future research should incorporate these topological features for a more comprehensive network analysis, leading to a deeper understanding of the network’s dynamics.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/0913ktg/5G-Traffic-Generator.

Ethics statement

Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

KS: Conceptualization, Data curation, Investigation, Methodology, Project administration, Software, Supervision, Writing–original draft, Writing–review and editing. JX: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by Natural Science Basic Research Program of Shaanxi (Program No. 2023-JC-YB-575).

Conflict of interest

Author JX was employed by Bull Group Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chergui H, Verikoukis C. Big data for 5G intelligent network slicing management. IEEE Netw (2020) 34(4):56–61. doi:10.1109/mnet.011.1900437

CrossRef Full Text | Google Scholar

2. Wang X, Hu J, Lin H, Garg S, Kaddoum G, Piran MJ, et al. QoS and privacy-aware routing for 5G-enabled industrial Internet of Things: a federated reinforcement learning approach. IEEE Trans Ind Inform (2021) 18(6):4189–97. doi:10.1109/tii.2021.3124848

CrossRef Full Text | Google Scholar

3. Kousaridas A, Manjunath RP, Perdomo J, Zhou C, Zielinski E, Schmitz S, et al. QoS prediction for 5G connected and automated driving. IEEE Commun Mag (2021) 59(9):58–64. doi:10.1109/mcom.110.2100042

CrossRef Full Text | Google Scholar

4. Buyakar TVK, Agarwal H, Tamma BR, Franklin AA Resource allocation with admission control for GBR and delay QoS in 5G network slices[C]//2020 International Conference on Communication Systems and NETworkS (COMSNETS). IEEE (2020). p. 213–220.

CrossRef Full Text | Google Scholar

5. Lilhore UK, Dalal S, Simaiya S. A cognitive security framework for detecting intrusions in IoT and 5G utilizing deep learning. Comput and Security (2024) 136:103560. doi:10.1016/j.cose.2023.103560

CrossRef Full Text | Google Scholar

6. Lacasa L, Luque B, Ballesteros F, Luque J, Nuño JC. From time series to complex networks: the visibility graph. Proc Natl Acad Sci (2008) 105(13):4972–5. doi:10.1073/pnas.0709247105

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zou Y, Donner RV, Marwan N, Donges JF, Kurths J. Complex network approaches to nonlinear time series analysis. Phys Rep (2019) 787:1–97. doi:10.1016/j.physrep.2018.10.005

CrossRef Full Text | Google Scholar

8. Mao S, Zeng XJ. Learning visibility attention graph representation for time series forecasting[C]. In: Proceedings of the 32nd ACM international conference on information and knowledge management (2023). p. 4180–4.

CrossRef Full Text | Google Scholar

9. Zhu J, Wei D. Analysis of stock market based on visibility graph and structure entropy. Physica A: Stat Mech its Appl (2021) 576:126036. doi:10.1016/j.physa.2021.126036

CrossRef Full Text | Google Scholar

10. Huang Y, Mao X, Deng Y. Natural visibility encoding for time series and its application in stock trend prediction. Knowledge-Based Syst (2021) 232:107478. doi:10.1016/j.knosys.2021.107478

CrossRef Full Text | Google Scholar

11. Akgüller Ö, Balcı MA, Batrancea LM, Gaban L. Path-based visibility graph kernel and application for the borsa istanbul stock network. Mathematics (2023) 11(6):1528. doi:10.3390/math11061528

CrossRef Full Text | Google Scholar

12. Kutluana G, Türker İ. Classification of cardiac disorders using weighted visibility graph features from ECG signals. Biomed Signal Process Control (2024) 87:105420. doi:10.1016/j.bspc.2023.105420

CrossRef Full Text | Google Scholar

13. Koka T, Muma M. Fast and sample accurate R-peak detection for noisy ECG using visibility graphs[C]. In: 2022 44th annual international conference of the IEEE engineering in medicine and biology society (EMBC). IEEE (2022). p. 121–6.

Google Scholar

14. Olamat A, Ozel P, Akan A. Synchronization analysis in epileptic EEG signals via state transfer networks based on visibility graph technique. Int J Neural Syst (2022) 32(02):2150041. doi:10.1142/s0129065721500416

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Mohammadpoory Z, Nasrolahzadeh M, Amiri SA. Classification of healthy and epileptic seizure EEG signals based on different visibility graph algorithms and EEG time series. Multimedia Tools Appl (2024) 83(1):2703–24. doi:10.1007/s11042-023-15681-7

CrossRef Full Text | Google Scholar

16. Kirichenko L, Radivilova T, Ryzhanov V. Applying visibility graphs to classify time series[C]//Lecture notes in computational intelligence and decision making: 2021 international scientific conference intellectual systems of decision-making and problems of computational intelligence. In: Proceedings. Springer International Publishing (2022). p. 397–409.

CrossRef Full Text | Google Scholar

17. Zhang P, Ning P, Cao R, Xu J. Analysis of climate change characteristics in Xi’an based on the visibility graph. Front Phys (2021) 9:702064. doi:10.3389/fphy.2021.702064

CrossRef Full Text | Google Scholar

18. Kundu S, Opris A, Yukutake Y, Hatano T. Extracting correlations in earthquake time series using visibility graph analysis. Front Phys (2021) 9:656310. doi:10.3389/fphy.2021.656310

CrossRef Full Text | Google Scholar

19. Liu X, Sun Q, Lu W, Wu C, Ding H. Big-data-based intelligent spectrum sensing for heterogeneous spectrum communications in 5G. IEEE Wireless Commun (2020) 27(5):67–73. doi:10.1109/mwc.001.1900493

CrossRef Full Text | Google Scholar

20. Kaur J, Khan MA, Iftikhar M, Imran M, Emad Ul Haq Q. Machine learning techniques for 5G and beyond. IEEE Access (2021) 9:23472–88. doi:10.1109/access.2021.3051557

CrossRef Full Text | Google Scholar

21. Chen XW, Lin X. Big data deep learning: challenges and perspectives. IEEE Access (2014) 2:514–25. doi:10.1109/ACCESS.2014.2325029

CrossRef Full Text | Google Scholar

22. Najafabadi MM, Villanustre F, Khoshgoftaar TM, Seliya N, Wald R, Muharemagic E. Deep learning applications and challenges in big data analytics. J Big Data (2015) 2:1–21. doi:10.1186/s40537-014-0007-7

CrossRef Full Text | Google Scholar

23. Choi Y-H, Kim D, Ko M, Cheon K-Y, Park S, Kim Y Ml-based 5g traffic generation for practical simulations using open datasets. IEEE Commun Mag (2023) 61(9):130–136. doi:10.1109/mcom.001.2200679

CrossRef Full Text | Google Scholar

24. Hassija V, Chamola V, Mahapatra A, Singal A, Goel D, Huang K, et al. Interpreting black-box models: a review on explainable artificial intelligence. Cogn Comput (2024) 16(1):45–74. doi:10.1007/s12559-023-10179-8

CrossRef Full Text | Google Scholar

25. Hu J, Zhang Y, Wu P, Li H. An analysis of the global fuel-trading market based on the visibility graph approach. Chaos, Solitons and Fractals (2022) 154:111613. doi:10.1016/j.chaos.2021.111613

CrossRef Full Text | Google Scholar

26. Cheng L, Zhu P, Sun W, Han Z, Tang K, Cui X. Time series classification by Euclidean distance-based visibility graph. Physica A: Stat Mech its Appl (2023) 625:129010. doi:10.1016/j.physa.2023.129010

CrossRef Full Text | Google Scholar

27. Hu J, Chu C, Zhu P, Yuan M. Visibility graph-based segmentation of multivariate time series data and its application. Chaos (Woodbury, NY) (2023) 33(9):093123. doi:10.1063/5.0152881

CrossRef Full Text | Google Scholar

28. Li H, Cao H, Feng Y, Li X, Pei J. Optimization of graph clustering inspired by dynamic belief systems. IEEE Trans Knowledge and Data Eng (2023)(01) 1–14. doi:10.1109/tkde.2023.3274547

CrossRef Full Text | Google Scholar

29. Li HJ, Feng Y, Xia C, Cao J. Overlapping graph clustering in attributed networks via generalized cluster potential game. ACM Trans Knowledge Discov Data (2024) 18(1):1–26. doi:10.1145/3597436

CrossRef Full Text | Google Scholar

30. Ma J, Li M, Li HJ. Traffic dynamics on multilayer networks with different speeds. IEEE Trans Circuits Syst Express Briefs (2021) 69(3):1697–701. doi:10.1109/tcsii.2021.3102577

CrossRef Full Text | Google Scholar

31. Barabási AL, Albert R. Emergence of scaling in random networks. Science (1999) 286(5439):509–12. doi:10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Traag VA, Waltman L, Van Eck NJ. From Louvain to Leiden: guaranteeing well-connected communities. Scientific Rep (2019) 9(1):5233–12. doi:10.1038/s41598-019-41695-z

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Bui Q, Ślepaczuk R. Applying Hurst Exponent in pair trading strategies on Nasdaq 100 index. Physica A: Stat Mech its Appl (2022) 592:126784. doi:10.1016/j.physa.2021.126784

CrossRef Full Text | Google Scholar

34. Ślęzak J, Metzler R. Minimal model of diffusion with time changing Hurst exponent. J Phys A: Math Theor (2023) 56(35):35LT01. doi:10.1088/1751-8121/acecc7

CrossRef Full Text | Google Scholar

35. Meraz M, Alvarez-Ramirez J, Rodriguez E. Multivariate rescaled range analysis. Physica A: Stat Mech its Appl (2022) 589:126631. doi:10.1016/j.physa.2021.126631

CrossRef Full Text | Google Scholar

36. Shang Y. Distinct clusterings and characteristic path lengths in dynamic small-world networks with identical limit degree distribution. J Stat Phys (2012) 149:505–18. doi:10.1007/s10955-012-0605-8

CrossRef Full Text | Google Scholar