- 1State Key Laboratory of Efficient Production of Forest Resources, Key Laboratory of National Forestry and Grassland Administration on Forestry Equipment and Automation, School of Technology, Beijing Forestry University, Beijing, China
- 2School of Artificial Intelligence, Optics and Electronics, Northwestern Polytechnical University, Xi’an, China
- 3School of Mathematics, Southeast University - Nanjing, Nanjing, China
To better understand the pattern phase transition of both physical and biological systems, we investigate a two-dimensional spin particle lattice system using statistical mechanics methods together with XY model governed by Hamiltonian equations of motion. By tweaking the coupling strength and the intensity of the generalization field, we observe phase transitions among four patterns of spin particles, i.e., vortex, ferromagnet, worm and anti-ferromagnet. In addition, we analyze the effect of space boundaries on the formations of vortex and worm. Considering the inherent dynamics of individual particles, we revealed the forming mechanism of such phase transitions, which provides a new perspective for understanding the emergence of phase transition of spin particles systems.
1 Introduction
Various types of phase transition are appealing features of both physical and biological particle systems, which have been extensively studied during recent decades. In general, pattern phase transition means a system composed of a large number of interacting particles undergoes a transition from one pattern phase to another responding to the change of one or more external parameters. There are abundant pattern phase transitions in natural, biological, chemical and physical systems, such as bird flocks [1–4], insects [5–7], bacterial colonies [8–10], fish schools and shoals [11–13], groups of mammals and crowds [14–16], crystals and superfluids [17, 18], etc. Researchers in the fields of physics, control engineering, system science, artificial intelligence and computer science recently have become more and more interested in the appealing pattern phase transition for such abundant particle systems.
Revealing the mechanism of phase transition is fairly helpful to understand complex physical and biological collective behaviors. The various pattern phase inspired by self-propelled particle systems are highly dependent on the interaction between particles, but the interaction mechanism of the phase transition is unknown, and one of the difficulties is the lack of the ability to predict the final equilibrium state and its stability only through the interaction between self-driven particles. In biological, physical and engineering multi-agent systems, researchers have discovered a large number of phase transitions between different modes. Among these investigations, Carrillo et al [19] researched the formation conditions of single and double rotating mills. Single-vortex configurations can be observed under generally random initial conditions, however, double-vortex configurations (i.e., half of the particles rotating clockwise and the other half counterclockwise) are only possible under carefully chosen initial conditions. Birnir [20] found the circling and flocking solutions of ordinary differential equations derived from the Vicsek model. Building on the work of Gautrais et al. [21], Calovi et al. [22] showed a switched phase diagram between the circular (milling) patterns and migratory patterns of fish schools by varying the weights of two control terms in the model. Cheng et al. [23] discovered pattern transitions among gaseous, liquid, and crystalline flocks by slightly varying the zero crossing slope of the inter-particle interaction function.
Analogous to kinetic systems, study of structure and phase transitions like lattices has drawn increasing attentions in recent years. The well-known statistical-mechanical models of particles like XY model and Ising model have intrinsic phase transitions for regular and irregular lattices [24]. From the perspective of statistical physics, the XY model with Hamiltonian equations of motion is probably one of the most concise models which have continuous degrees of freedom. In the field of condensed matter physics, it is a model which realized the phase transition of superfluid
With the pioneer efforts devoted to the collective motions on XY model, quite a few fascinating collective motion patterns are observed with the XY model, like flocking and torus. In this letter, we seek to refine the kinetic description of XY model which helps reveal the phase transition principles of XY model with Hamiltonian equations of motion. Following the dynamics of the XY model, we have meticulously described the role of model parameters in governing the state of the system so as to figure out the actual physical meaning of the parameters. By tweaking model parameters, a series of phase transitions emerge among vortex, ferromagnet, worm and anti-ferromagnet patterns.
2 Methods and results
The XY model has been widely applied to a large volume of physical systems like superfluids, nematic liquid crystals, electron nematics, planar magnets, and among others [25–28]. In this letter, we study an XY model considering an external field effects with Hamiltonian equations of motion and focus on the statistical properties from the perspective of particles dynamics. In the presence of a
where
Consider the
where
Let
the parallel state order quantifying the parallel tendency
and the vortex state order quantifying the vortex tendency
where
Apparently,
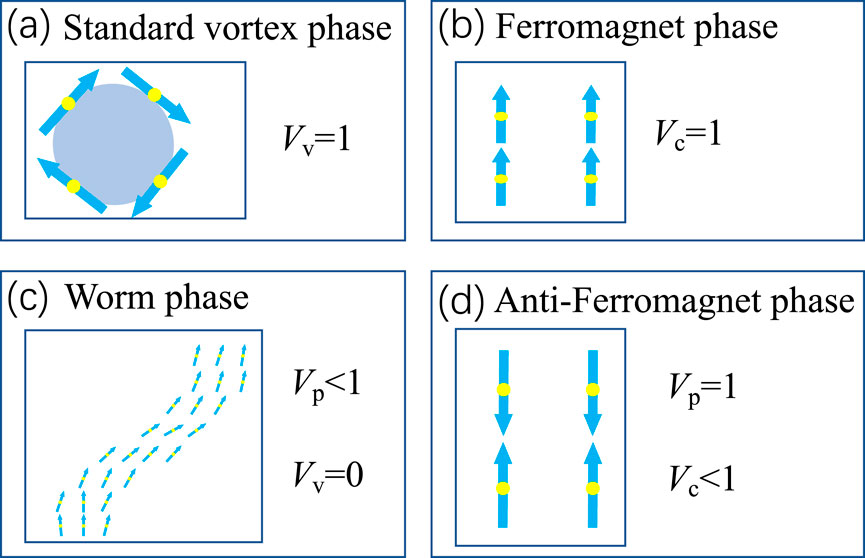
Figure 1. The order parameter characteristics of the four phases, i.e., vortex (A), ferromagnet (B), worm (C), and anti-ferromagnet (D), respectively.
In the numerical simulations,
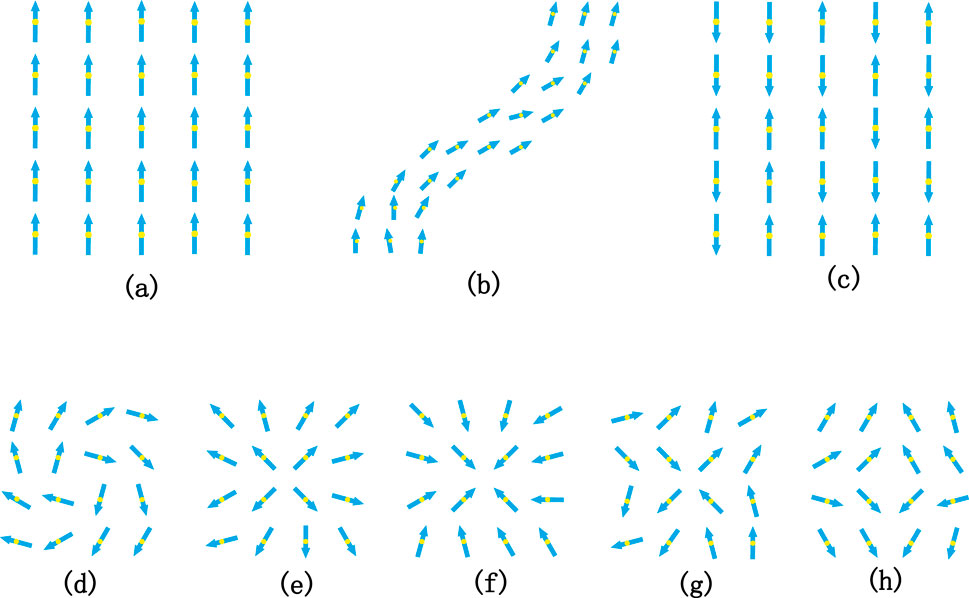
Figure 2. Ferromagnet (A), worm (B), anti-ferromagnet (C), and vortex in different forms (D–H). Dots represent the locations of the particles whereas arrows the spin directions. The particles are arranged with equal distances similar to crystals. Patterns (D–H) are rotational vortex, positive vortex, cross vortex, relative vortex and anti-vortex, respectively. Similar patterns [35] universally exist in superfluid, planar magnets, superconductors and electron nematics, etc. The XY dynamics system of spin particles undergoes phase transition among patterns (A–H) simply by tweaking a few model parameters.
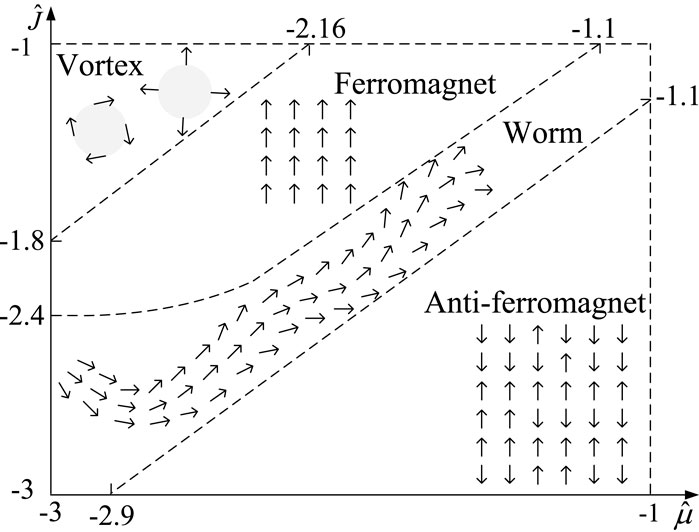
Figure 3 demonstrates the phase transitions among vortex, ferromagnet, worm and anti-ferromagnet patterns. At the top-left corner of the
In order to investigate more deeply into the principles governing the pattern phase transitions, we present three heat maps of
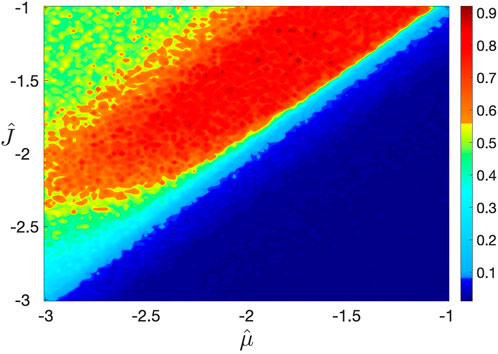
Figure 4. Heat map of the consensus state order parameter

Figure 5. Heat map of the parallel state order parameter
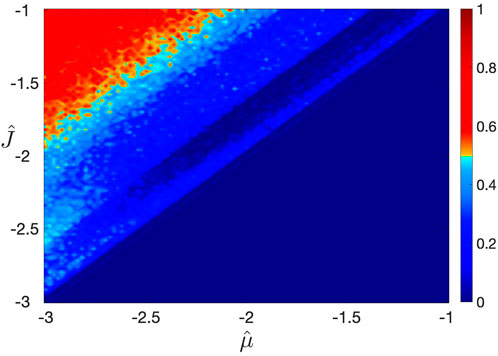
Figure 6. Heat map of the vortex state order parameter
Significantly, the order parameter
To investigate more deeply into the phase transition mechanism, we conduct the effects of the side length parameter

Figure 7. Evolution of the occurrence frequencies of the ferromagnet and vortex phases (A), the vortex state order parameter
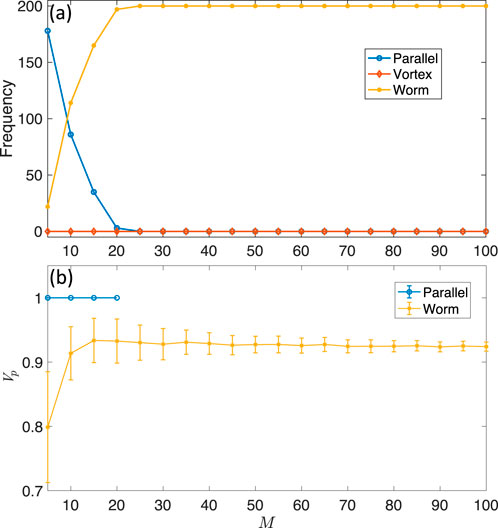
Figure 8. Evolution of the occurrence frequencies of the two parallel patterns (i.e., ferromagnet and anti-ferromagnet phases), vortex and worm phases (A), the parallel state order parameter
So far, the phases and their transitions discussed above are noise-free, i.e.,
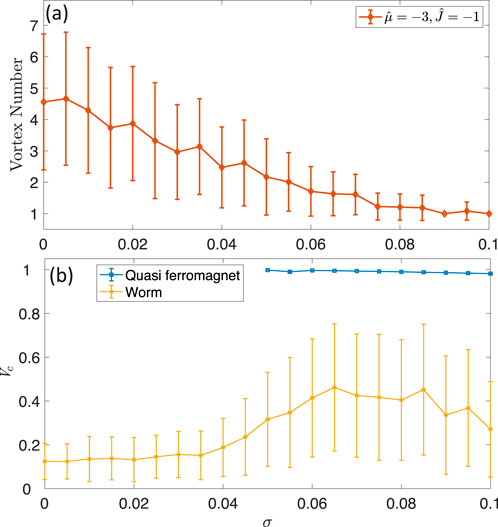
Figure 9. Evolution of the vortex number (A) and the consensus state order parameter
3 Conclusion
This letter investigates the pattern phase transition mechanism for a class of the XY model with Hamiltonian equations of motion. Three phase transitions among four patterns, i.e., vortex, ferromagnet, worm and anti-ferromagnet, are revealed simply by tweaking two parameters
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: http://imds.aia.hust.edu.cn/info/1247/2403.htm.
Author contributions
YW: Writing–original draft, Writing–review and editing. JY: Writing–original draft. BX: Writing–review and editing. YZ: Writing–review and editing. DC: Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China under Grant. 62273053, Fundamental Research Funds for the Central Universities of China (BLX202128), China Postdoctoral Science Foundation under Grant No. 2024M754222, and the Natural Science Foundation of Shanxi Province under Grant No. 2024JC-YBQN-0663.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Flack A, Nagy M, Fiedler W, Couzin ID, Wikelski M. From local collective behavior to global migratory patterns in white storks. Science (2018) 360:911–4. doi:10.1126/science.aap7781
2. Chen D, Vicsek T, Liu X, Zhou T, Zhang H-T. Switching hierarchical leadership mechanism in homing flight of pigeon flocks. Europhysics Lett (2016) 114:60008. doi:10.1209/0295-5075/114/60008
3. Lukeman R, Li Y-X, Edelstein-Keshet L. Inferring individual rules from collective behavior. Proc Natl Acad Sci (2010) 107:12576–80. doi:10.1073/pnas.1001763107
4. Attanasi A, Cavagna A, Castello LD, Giardina I, Grigera TS, Jelić A, et al. Information transfer and behavioural inertia in starling flocks. Nat Phys (2014) 10:691–6. doi:10.1038/nphys3035
5. Buhl J, Sumpter D, Couzin I, Hale JJ, Despland E, Miller ER, et al. From disorder to order in marching locusts. Science (2006) 312:1402–6. doi:10.1126/science.1125142
6. Franks NR, Pratt SC, Mallon EB, Britton NF, Sumpter DJT. Information flow, opinion polling and collective intelligence in house–hunting social insects. Philosophical Trans R Soc Lond Ser B: Biol Sci (2002) 357:1567–83. doi:10.1098/rstb.2002.1066
7. Bazazi S, Buhl J, Hale JJ, Anstey ML, Sword GA, Simpson SJ, et al. Collective motion and cannibalism in locust migratory bands. Curr Biol (2008) 18:735–9. doi:10.1016/j.cub.2008.04.035
8. Curatolo A, Zhou N, Zhao Y, Liu C, Daerr A, Tailleur J, et al. Cooperative pattern formation in multi-component bacterial systems through reciprocal motility regulation. Nat Phys (2020) 16:1152–7. doi:10.1038/s41567-020-0964-z
9. Szabo B, Szollosi GJ, Gönci B, Jurányi Z, Selmeczi D, Vicsek T. Phase transition in the collective migration of tissue cells: experiment and model. Phys Rev E—Statistical, Nonlinear, Soft Matter Phys (2006) 74:061908. doi:10.1103/PhysRevE.74.061908
10. Deisboeck TS, Couzin ID. Collective behavior in cancer cell populations. Bioessays (2009) 31:190–7. doi:10.1002/bies.200800084
11. Ward AJW, Sumpter DJT, Couzin ID, Hart PJB, Krause J. Quorum decision-making facilitates information transfer in fish shoals. Proc Natl Acad Sci (2008) 105:6948–53. doi:10.1073/pnas.0710344105
12. Hein AM, Gil MA, Twomey CR, Couzin ID, Levin SA. Conserved behavioral circuits govern high-speed decision-making in wild fish shoals. Proc Natl Acad Sci (2018) 115:12224–8. doi:10.1073/pnas.1809140115
13. Hoare D, Couzin ID, Godin J-GJ, Krause J. Context-dependent group size choice in fish. Anim Behav (2004) 67:155–64. doi:10.1016/j.anbehav.2003.04.004
14. Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic. Nature (2000) 407:487–90. doi:10.1038/35035023
15. Fischhoff I, Sundaresan SR, Cordingley J, Larkin HM, Sellier MJ, Rubenstein DI. Social relationships and reproductive state influence leadership roles in movements of plains zebra, equus burchellii. Anim Behav (2007) 73:825–31. doi:10.1016/j.anbehav.2006.10.012
16. Sarova R, Spinka M, Panamá J, Simecek P (2010). Graded leadership by dominant animals in a herd of female beef cattle on pasture. Anim Behav 79, 1037–45. doi:10.1016/j.anbehav.2010.01.019
17. Liu H, Lv J, Chen Q. Ising-like phase transition in the fully frustrated xyz model with weak disorder. Europhysics Lett (2008) 84:66004. doi:10.1209/0295-5075/84/66004
18. Jesariew D, Ilczyszyn MM, Pietraszko A. The crystal structure and the phase transitions of pyridinium trifluoromethanesulfonate. Mater Res Express (2014) 1:015705. doi:10.1088/2053-1591/1/1/015705
19. Carrillo JA, D’Orsogna M, Panferov V. Double milling in self-propelled swarms from kinetic theory. Kinetic Relat Models (2009) 2:363–78. doi:10.3934/krm.2009.2.363
20. Birnir B. An ode model of the motion of pelagic fish. J Stat Phys (2007) 128:535–68. doi:10.1007/s10955-007-9292-2
21. Gautrais J, Ginelli F, Fournier R, Blanco S, Soria M, Chaté H, et al. Deciphering interactions in moving animal groups. PLoS Comput Biol (2012) 8:e1002678. doi:10.1371/journal.pcbi.1002678
22. Calovi DS, Lopez U, Ngo S, Sire C, Chaté H, Theraulaz G. Swarming, schooling, milling: phase diagram of a data-driven fish school model. New J Phys (2014) 16:015026. doi:10.1088/1367-2630/16/1/015026
23. Cheng Z-X, Sun B, Wang S-J, Gao Y, Zhang YM, Zhou HX, et al. Nuclear factor-κb–dependent epithelial to mesenchymal transition induced by HIF-1α activation in pancreatic cancer cells under hypoxic Conditionsα activation in pancreatic cancer cells under hypoxic conditions. PLoS One (2011) 6:e23752. doi:10.1371/journal.pone.0023752
24. Baek SK, Minnhagen P, Kim BJ. Phase transition of xyz model in heptagonal lattice. Europhysics Lett (2007) 79:26002. doi:10.1209/0295-5075/79/26002
25. de Souza LC, de Souza AJF, Lyra ML. Hamiltonian short-time critical dynamics of the three-dimensional xyz model. Phys Rev E (2019) 99:052104. doi:10.1103/PhysRevE.99.052104
26. Mon K, Teitel S. Phase coherence and nonequilibrium behavior in josephs junction arrays. Phys Rev Lett (1989) 62:673–6. doi:10.1103/PhysRevLett.62.673
27. Kosterlitz JM. The critical properties of the two-dimensional xyz model. J Phys C: Solid State Phys (1974) 7:1046–60. doi:10.1088/0022-3719/7/6/005
28. Li Y-H, Teitel S. Finite-size scaling study of the three-dimensional classical xyz model. Phys Rev B (1989) 40:9122–5. doi:10.1103/PhysRevB.40.9122
29. Vicsek T, Zafeiris A. Collective motion. Phys Rep (2012) 517:71–140. doi:10.1016/j.physrep.2012.03.004
30. Cheng Z, Chen Z, Vicsek T, Chen D, Zhang HT. Pattern phase transitions of self-propelled particles: gases, crystals, liquids, and mills. New J Phys (2016) 18:103005. doi:10.1088/1367-2630/18/10/103005
31. Minchau BJ, Pelcovits RA. Two-dimensional xyz model in a random uniaxial field. Phys Rev B (1985) 32:3081–7. doi:10.1103/PhysRevB.32.3081
32. Asad A, Zheng B. Non-equilibrium critical dynamics of the two-dimensional xyz model with Hamiltonian equations of motion. J Phys A: Math Theor (2007) 40:9957–68. doi:10.1088/1751-8113/40/33/001
33. Leoncini X, Verga AD, Ruffo S. Hamiltonian dynamics and the phase transition of the xyz model. Phys Rev E (1998) 57:6377–89. doi:10.1103/PhysRevE.57.6377
34. Matteo P, Marconi UMB, Maggi C. Effective equilibrium picture in the xyz model with exponentially correlated noise. Phys Rev E (2018) 97:022605. doi:10.1103/PhysRevE.97.022605
Keywords: collective motions, pattern phase transition, spin particle, Hamiltonian equations, complex networks
Citation: Wu Y, Yan J, Xu B, Zheng Y and Chen D (2024) Pattern phase transition of spin particle lattice system. Front. Phys. 12:1472564. doi: 10.3389/fphy.2024.1472564
Received: 29 July 2024; Accepted: 21 October 2024;
Published: 08 November 2024.
Edited by:
Sanja Janicevic, University of Kragujevac, SerbiaReviewed by:
Tapas Bar, Catalan Institute of Nanoscience and Nanotechnology (CIN2), SpainDiana Thongjaomayum, Tezpur University, India
Copyright © 2024 Wu, Yan, Xu, Zheng and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yili Zheng, emhlbmd5aWxpQGJqZnUuZWR1LmNu; Duxin Chen, Y2hlbmR4QHNldS5lZHUuY24=
 Yue Wu
Yue Wu Jingnan Yan1
Jingnan Yan1 Bowen Xu
Bowen Xu Yili Zheng
Yili Zheng Duxin Chen
Duxin Chen