- 1Physikalisch-Technische Bundesanstalt, Braunschweig, Germany
- 2Biophysics Department, GSI Helmholtzzentrum für Schwerionenforschung GmbH, Darmstadt, Germany
The goal of this work is to characterize the secondary neutron spectra produced by 1 GeV/u56Fe beam colliding with a thick cylindric aluminum target and to perform a quantitative comparison with simulated results obtained with Monte Carlo codes. The measurements were performed using extended-range Bonner sphere spectrometers at two positions (15° and 40°) with respect to the beam direction. The secondary radiation field was simulated using four Monte Carlo codes (FLUKA, MCNP6, Geant4 and PHITS) and several physical models of nuclei transport and interaction. Neutron and proton energy distributions were simulated for the experimental measurement positions. The simulated neutron spectra, together with data measured with Bonner sphere spectrometers, after carrying out the correction of the contributions induced by the secondary protons, were used as input for the MAXED spectrum unfolding code to obtain the measured neutron spectra. Unfolded neutron spectra were compared with simulated ones to carry out a quantitative analysis of the performance of the chosen Monte Carlo codes and their corresponding physical models. This comparison showed that, because of experimental uncertainties and physical models, there are no unique solutions for each measurement location, but a range of solutions where the true experimental neutron spectra probably lie. The results showed deviations between 4.23% and 8.42% for some simulated spectra. Regarding the total integral values of neutron fluence and ambient equivalent dose, the unfolded neutron spectra showed deviations lower than 2%.
1 Introduction
Space exploration with semi-permanent and/or permanent settlements represents one of humanity’s greatest and most ambitious challenges. One of the main risks for missions beyond Low Earth Orbit (LEO), without the protection of the Earth’s atmosphere and its magnetic field, is related to acute and prolonged exposure to radiation [1]. Galactic cosmic radiation (GCR), consisting of a spectrum of highly energetic (up to several TeV/u) particles ranging from protons to heavy ions (up to 58Ni), is a very important category of radiation to consider because of its isotropic and ubiquitous distribution which is highly penetrating and modulated only by the solar activity [2]. GCRs interact with spacecraft shielding material (aluminum alloys) by producing, through nuclear spallation or fragmentation reactions, high energy secondary particles such as light charged fragments and neutrons. Consequently, during the spacecraft and habitat design, it is crucial to consider not only the primary GCR, but also the secondary radiation field [3]. Neutrons especially, being neutral particles, can penetrate thick shields and deep into organic tissues before interacting with nuclei inducing the production of ionizing secondary radiation which would induce direct biological damage. The quality factor of neutrons, which is a measure of their harmfulness for radiation protection purposes, is strongly energy dependent [4, 5]. Recent studies have shown that neutrons contribute significantly to the ambient dose equivalent of the crew on the International Space Station (ISS) in different locations [6, 7].
Many studies on the impact of the thickness of spacecraft aluminum alloys for GCR shielding, have shown that secondary neutrons and light ions are major contributors to the total equivalent dose inside the scoring area protected by the shielding material [8–11]. However, these comparative studies show large discrepancies because nuclear fragmentation processes are simulated using semi-empirical physical models. These large uncertainties have a negative impact on both the design phase of spacecraft, shelters on the Moon and Mars, and on predictions of possible biological damage. To overcome these problems, simulation codes must take advantage of experimental reaction cross sections to correctly reproduce the secondary radiation field. However, the information of energy-dependent reaction cross sections is partial and in many cases absent [12–14]. The scarcity of experimental data is due to the small number of facilities where ground-based experiments can be performed to measure the secondary radiation field induced by high energy (up to 1 GeV/u) heavy ion beams. Such facilitates are for instance the Heavy Ion Medical Accelerator in Chiba (HIMAC) of the National Institute of Radiological Sciences in Japan, NASA Space Radiation Lab (NSRL) of Brookhaven National Laboratory in United States and Helmholtzzentrum für Schwerionenforschung GmbH (GSI) in Germany. Recent studies have compared experimental neutron yields from thick target with simulated ones, the results showed that no physical model implemented in the various Monte Carlo codes fit perfectly for all energies and measurement angles [15–18].
The work presented in this paper is part of a larger multidisciplinary study funded by the ESA-IBER-2021 program with the aim of studying the physical characteristics and radiobiological effects of the secondary radiation field produced by a 1 GeV/u 56Fe ion beam bombarding a cylindrical aluminum target [19–21]. 56Fe was chosen for this study because among the various high charge (Z) and energy (E) (HZE) nuclei, it is one of the most abundant [22]. The 1 GeV/u energy was chosen because at that energy the iron beam is considered a reasonable approximation for the GCR, making the largest contribution to the equivalent dose, and near the solar cycle maximum, about half of the iron flux is found at energies of 1 GeV/u and above [23]. In addition, most radiobiological experiments on cells, tissues and animals have been performed at this energy [24]. Finally, only the 1 GeV/u energy was chosen because of experimental limitations.
Different from previous works [19–21], which focused only on neutron dosimetry, this work focuses on spectrometry with the complete characterization of the secondary neutron spectra measured with the Bonner Sphere-based system of the Physikalisch-Technische Bundesanstalt (PTB), called NEMUS, measured in the Cave A of the GSI for two representative measurement angles and on the comparison and validation of the simulations obtained with four Monte Carlo codes commonly used int the field of radiation protection in space. The first part of the article describes the working principle of the NEMUS system for neutron measurement, the experimental setup used in Cave A and finally the four Monte Carlo codes and corresponding physical models considered for the simulation of the secondary radiation field. The second part presents the simulation results of the secondary radiation field, the comparison between measured and simulated NEMUS readings. Finally, the simulated neutron experimental spectra are compared with the experimental spectra obtained through the MAXED unfolding code, analyzing the deviations of the integral quantities of fluence and ambient equivalent dose.
2 Materials and methods
2.1 Multiple bonner sphere spectrometer system
Bonner sphere spectrometers (BSS) are the most commonly used method for neutron field characterization in the broad energy range between thermal up to GeV. A BSS consists of central thermal neutron sensors (CTNS) placed in the center of a spheres of moderating material (typically high-density polyethylene) with a variable diameter [25]. Neutrons entering the sphere undergo various elastic scattering reactions with the hydrogen nuclei contained in the polyethylene. They can either escape from the sphere, undergo capture or thermalize and reach the thermal sensor allowing in this last case the neutron detection. The probability of one of these reactions occurring depends mainly on the energy of the incident neutron and the size of the sphere [26]. When a Bonner sphere of diameter (or type) d is subjected to a given neutron flux, for this study produced by a 56Fe particle beam, with an energy spectrum
where
In this work, the PTB Neutron Multisphere Spectrometer (NEMUS) was used for neutron spectrum measurements [29], see Figure 1. It consists of a set of ten polyethylene spheres with diameters from 3 inch (7.62 cm) to 12 inch (30.48 cm) and four modified spheres with polyethylene and lead or copper inlets. Three sets of CTNSs were used. The first two are spherical 3He-filled proportional counters (type SP-9, manufactured by Centronic Ltd., UK) with an approximate gas pressure of 200 kPa (2.0 bar) and 20 kPa (0.2 bar). The third thermal neutron sensor consists of a 235U-coated fission chamber (type 307719, manufactured by LND Inc., United States). For the last thermal sensor, there are no modified sphere response functions because such spheres have not yet been developed.

Figure 1. Photo of some Bonner spheres from NEMUS (photo taken and modified from [30]). Behind, there are five polyethylene spheres, in front on the right side is a modified open sphere with the metal shell of copper, in front on the left side is a modified open sphere with the metal shell of lead. Front in the center, there are three SP-9 counters with the various polyethylene components to assemble the sphere.
Figure 2 shows the neutron response functions of the bare, full polyethylene and modified sphere for the 0.2 bar (A), 2.0 bar (B) 3He-filled proportional counters. The neutron responses of the various detector configurations show that in order to detect neutrons having higher and higher energy, it is necessary to increase the diameter of the polyethylene spheres, because neutrons need more scattering events in order to thermalize and be detected by the CTNS. While for detecting neutrons with energy higher than 30 MeV, modified Bonner spheres need to be used. In addition, the two figures show that the 2.0 bar proportional counter, for the same type of Bonner Sphere, has a higher neutron sensitivity than the 0.2 bar counter. Regarding the data acquisition system used for this work, see reference [31] for more details.
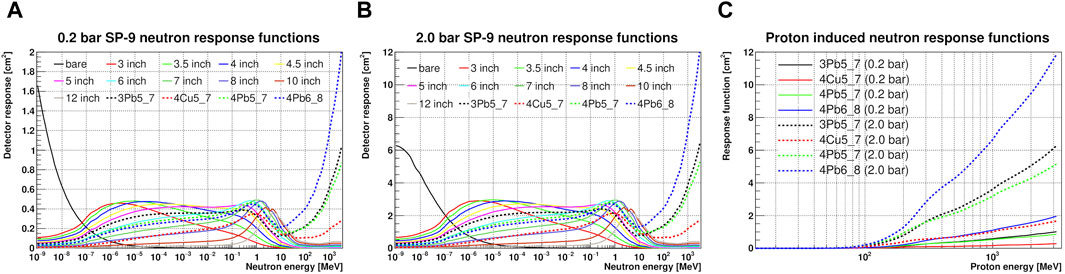
Figure 2. Neutron response functions of the NEMUS system of the (A) 0.2 bar, (B) 2.0 bar SP-9 and (C) proton induced for the modified spheres. The detector response functions with diameters between 3 and 12 inch indicate the neutron response functions for full polyethylene spheres (solid lines). The acronyms of the modified sphere response functions (dashed lines) indicate the various combinations of polyethylene inner sphere diameter (ISp), metal shell material and diameter (MeSh) and polyethylene outer shell diameter (OuSh), e.g., for 3Pb5_7, ISp = 3 inch, MeSh = lead (Pb) of 5 inch, OuSh = 7 inch.
An issue with modified Bonner spheres, in measurement conditions where high-energy charged particles (e.g., protons) are present, is that when these charged particles interact with the metal shell, they induce the production of further neutrons which by thermalizing can be detected by the neutron sensor. Consequently, these contributions must be subtracted from the total sphere reading
2.2 GSI cave A and experimental setup
The NEMUS system was used to carry out neutron measurements in GSI Cave A. The secondary radiation field was produced by a 1 GeV/u 56Fe beam, interacting with a cylindrical aluminum target 20 cm in diameter and 20 cm high at 30 cm from the beam window. The ion beam was delivered into Cave A by the SIS18 synchrotron [33] in the form of pencil beam with a Gaussian shape (with a full-width-half-maximum of 1.2 cm) and spills of duration of ≈2.5 s. For constant monitoring of the ion beam, an Ionization Chamber (IC), placed in front of the beam exit window, produces signals as the particles pass through. Then, these signals are converted into digital pulses by a current-to-frequency converter (IFC) and collected by the NEMUS acquisition system. Each pulse corresponds to a certain number of primary 56Fe particles (≈87 56Fe particle/IFC); this information was fundamental for obtaining absolute neutron yields in addition to the spectral information by the Bonner Spheres (see Section 3.2). For more information on the IC calibration procedure, see [34].
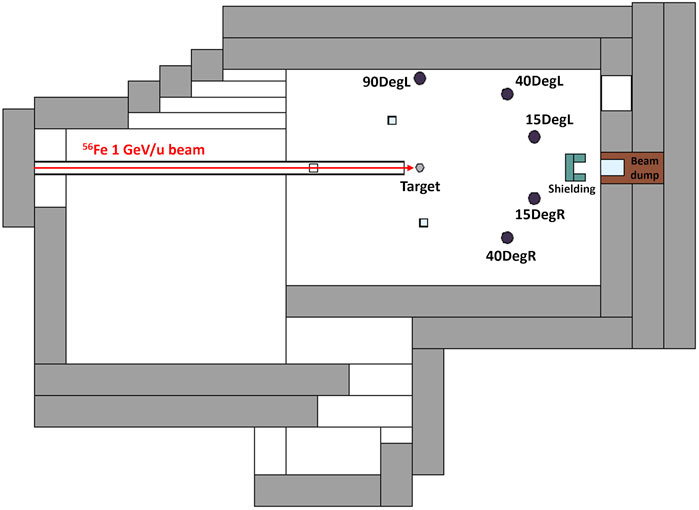
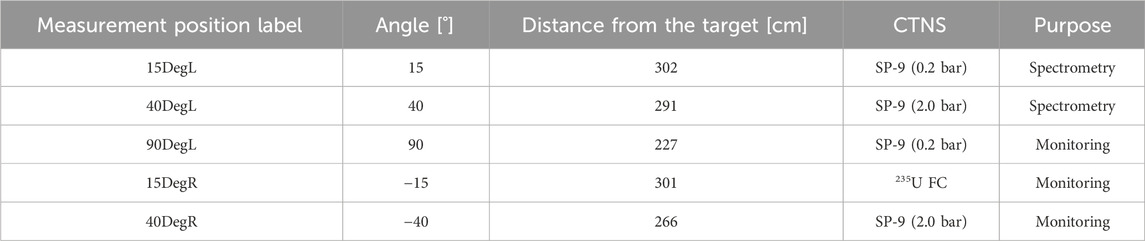
The experimental setup chosen in this work is similar to the one adopted by Boscolo et al. [19] and Sokolov et al. [20], Figure 3 shows a sketch of the implemented experiment with the labelled measurements positions for the Bonner Spheres; information concerning the angle and distance from the target, type of thermal sensor, and purpose are summarized in Table 1. For the 15DegL (Deg = degree, L = left) and 40DegL positions, neutron spectrometry measurements were performed by collecting the count rates produced by the various spheres, while the 15DegR (R = right), 90DegL and 40DegR positions were used only for neutron monitoring. For the measurement position at 15DegL, where the intensity of neutron and proton fluence is higher, the SP-9 0.2 bar thermal sensor was chosen because of its low neutron sensitivity which limits the count rate in the sensor so that there is no need to apply dead time correction.
2.3 Monte Carlo simulation codes
In this work, the simulation of the secondary radiation field measured in the GSI Cave A was done using the Monte Carlo codes FLUKA, MCNP, Geant4, and PHITS.
2.3.1 FLUKA
FLUKA (FLUktuierende KAskade in German, i.e., fluctuating cascade) version 4.2.2 [35, 36] is a general multipurpose Monte Carlo code for the calculation of particle transport and interaction with matter, it is used combined with the graphical user interface FLAIR (FLUKA Advanced Interface) version 3.2 [37]. The RQMD (Relativistic Quantum Molecular Dynamic) model [38] is used to simulate the nucleus-nucleus interactions in the energy range between 0.125 GeV/u and 5 GeV/u, for lower energies the Boltzmann Master Equation (BME) model is used. The neutron cross sections of the materials defined in FLUKA come from various data libraries (see the reference manual for more information). FLUKA has been used for the study of the secondary radiation field induced by proton beam [39–42], heavy ions [19, 20, 33, 40, 43–45] and by GCR [11, 46–48] with different material targets.
The Cave A geometric model takes into account the dimensions and material compositions of both the shielding elements that define the experimental room (such as the concrete walls and roof) and the materials inside the experimental room itself (experimental table where the target is placed, beam dump, etc.). Table 2 lists the properties of materials implemented in the geometric model of Cave A for all Monte Carlo simulations. This geometric model has already been widely used for previous studies to simulate the secondary radiation field produced by the interaction of various ion beams with different targets [19, 20, 33, 49]. The geometric model was modified to be consistent with the experimental setup described in Section 2.2. For the scoring of neutrons and protons at the measurement points, the USRTRACK card was used; it allows the extraction in the selected regions of the differential distribution of fluence in energy [dΦ/dE (particle/cm2 GeV∙56Fe particle)] using a logarithmic binning from 100 GeV down to 0.1 meV.
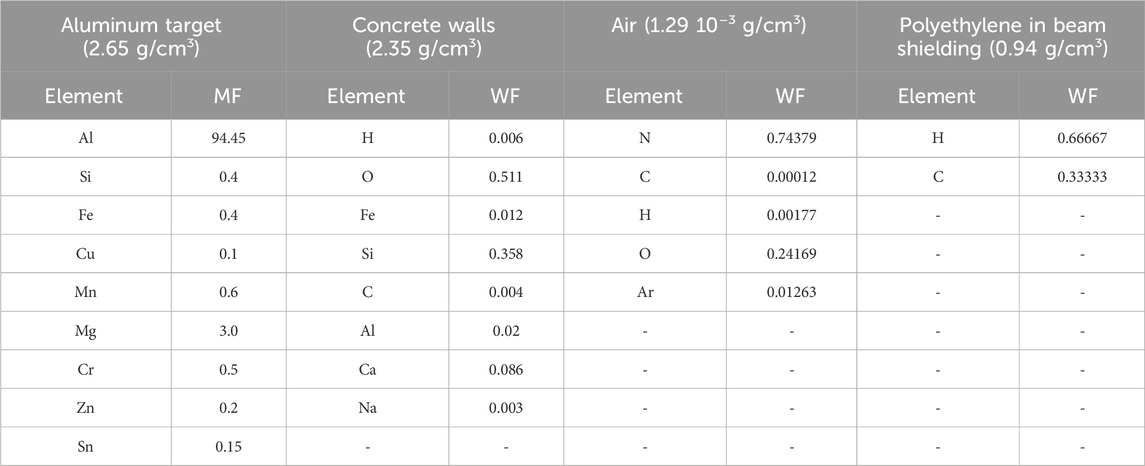
Table 2. GSI Cave A material proprieties implemented in Monte Carlo calculations using element Mass Fractions (MF) or Weight Fractions (WF). (Other components such as the Beam tube and the Beam dump were defined as pure iron).
2.3.2 MCNP 6.1
MCNP6 (Monte Carlo N-Particle) version 6.1 [50], is a general multipurpose Monte Carlo radiation transport code developed by Los Alamos National Laboratory (LANL) which resulted from the fusion of MCNPX and MCNP5 codes. The Cave A geometric model used for the simulations with the FLUKA code was exported into a format readable and executable by MCNP using the FLAIR interface. In the input file, it is possible to set the importance of the particles in the cells that define the geometry of the problem. For this study, all particles were considered (and not just heavy ions, neutrons, and protons) because light ions and other particles could trigger further nuclear reactions by inducing in turn the production of further neutrons [51]. The simulation of neutron transport having energies up to 20 MeV was done using the ENDF/B-VII (Evaluated Nuclear Data File) [52] cross section library, while for protons the selected library was ENDF70prot [53]. For proper thermal neutron transport, below 4 eV, the S (α,β) library was used. For energy ranges where there are no cross-section data libraries, particle transport is calculated by the use of nuclear models. These models, for neutron and proton transport, are based on the combination of intra-nuclear cascade (INC) models and evaporation (EV) models. In this work, the Cascade-Exciton Model (CEM3.03) was chosen, which includes both INC and EV models. For the transport of all other particles, the Los Alamos Quark-Gluon String model (LAQGSM) was used. MCNP has been used for the study of the secondary radiation field induced by proton beam [39, 51], heavy ions [15, 54–56] and cosmic radiation [57–59] with different material targets. The energy distribution of the neutron and proton fluence [Φ (particle/cm2 56Fe particle)] in the measurement points was scored using the averaged cell fluence tally F4.
2.3.3 GEANT4
Geant4 (GEometry ANd Tracking 4) version 11.0 [60] is a toolkit to simulate the passage and interaction of particles with the matter. The FLUKA geometric model of the Cave A experimental room was converted into a GDML (Geometry Description Markup Language) file, readable by Geant4, using the python library PyG4ometry [61]. Material neutron properties are defined by the G4NDL4.6 neutron library, based on the data library JEFF-3.3 [62]. For the hadron inelastic physics, the predefined QGSP_BIC_HP physics list was considered, where the acronym “HP” refers to the data driven high precision neutron package (NeutronHP), this option enables the use of neutron cross sections for energies below 20 MeV. In order to take into account thermal neutron scattering events (below 0.4 eV), the G4NeutronHPThermalScattering option was enabled. In addition to this option, certain materials were defined with the labels “TS_H_Water” or “TS_C_of_Graphite” to properly activate the scattering cross sections in the thermal energy range and thus the thermal neutron scattering events. In Geant4 we focused on physical models that simulate nuclear fragmentation of ions. All three available sets of physical models were chosen [58, 63, 64]. The first one is the Binary Intra-Nuclear cascade (BIC), the second one is the Quantum Molecular Dynamics (QMD) and the last is the Liege Intranuclear Cascade (INCLXX). Geant4 has been used for the study of the secondary radiation field induced by proton beam [42, 44, 65–67], heavy ions [18, 44, 54] and cosmic radiation [48, 58, 68, 69] with different material targets. Within the code, geometric volumes indicating the measurement points were set as Sensitive Detectors. In this way it is possible to choose and extract the type of information within the selected cell such as the nature of the particle, its energy and its track length. The data were processed to extract the energy distributions of neutron and proton fluences [Φ (particle/cm2 56Fe particle)] like how it is done by MCNP6 F4 tally, recording the particle track length (in particle cm/56Fe particle) entering the Sensitive Detector and dividing its value by the volume of the Sensitive Detector (in cm3).
2.3.4 PHITS
PHITS (Particle and Heavy Ion Transport code System) version 3.32 [70, 71] is a general-purpose Monte Carlo particle transport simulation code developed by the Japan Atomic Energy Agency (JAEA). The language adopted by PHITS to describe the geometric model of Cave A experimental room and the definition of material properties is the same as that used in MCNP6. For neutron energies between 20 MeV down to thermal energies, the JENDL-4.0 [72] cross section library was used. For energies between 20 MeV and 200 MeV, the JENDL-4/HE [73] data library was used which contains the cross sections for neutron and proton induced reactions for some materials. For neutron energies above 200 MeV or in the absence of the cross sections, the INCL4.6 physics model combined with the generalized evaporation model (GEM) was used. This model was also used for reactions induced by protons, deuterons, tritium, 3He and alpha particles. For the simulation of nuclear fragmentation processes of heavy ions, the JQMD2.0 (Quantum Molecular Dynamics version 2) model was chosen and coupled with Kurotama model for calculating the total cross sections of nucleus-nucleus reaction. PHITS has been used extensively for the simulation of the secondary neutron field produced by protons [39, 55], heavy ions [15, 45, 55, 74, 75] and cosmic radiation [76–79] with different material targets. The energy distribution of the neutron and proton fluence [Φ (particle/cm2 56Fe particle)] in the measurement points was scored using the cell fluence tally T-Track.
For all simulations, no variance reduction techniques were employed and the number of primary particles simulated was 107, so that the relative error was of the order of 0.09% for the measurement positions at 15DegL and 40DegL. Geant4 and PHITS simulations were run using a computing cluster which uses two 14-core Intel Xeon E5-2690v4 2.6 GHz and two 14-cores Intel Xeon Gold 6,132 2.6 GHz processors. MCNP6 simulations were run with a desktop PC with 8-core AMD Ryzen 7 Pro 5750G 3.8 GHz, while FLUKA simulations were run with a desktop PC with 8-core Intel Core i7-3770 3.4 GHz.
All results calculated with the four Monte Carlo codes considered as well as all other results obtained in this work were processed and analyzed using the ROOT (version 6.26) framework [80].
3 Results and discussion
3.1 Calculated secondary radiation field
The first information extracted through Monte Carlo codes is the spatial distribution of neutron and proton fluence within the Cave A experimental room. Figure 4 shows the bidimensional (xz plane) distribution of the total neutron (A), photon (B) and proton (C) fluence obtained with MCNP using the CEM3.03 physical model. Like the FLUKA USRBIN card, these distributions were obtained using MCNP TMESH and RMESH tallies. The results showed that for the measurement positions at 15DegL, 40DegL and 90DegL, neutrons represent an important contribution of the total fluence with fractions ranging between ≈43% and ≈45%. While photons exhibit fractions relative to the total fluence for the 15DegL, 40DegL and 90DegL measurement positions of ≈37%, ≈44%, and ≈51%, respectively. These photons can result from various processes, such as neutron capture and de-excitation of excited nuclei generated by both the primary beam or the target nuclear fragments [81]. Despite their ubiquitous presence during the processes of heavy ion interaction with a target, secondary gamma rays will not be further investigated, as they are beyond the scope of this work. Finally, protons have fractions relative to the total fluence at the 15DegL, 40DegL, and 90DegL measurement points of ≈11%, ≈3%, and ≈0.3%, respectively. As mentioned in Section 2.1, high-energy protons can interact with the metal shells of the modified Bonner spheres and induce the production of spallation neutrons that would be added to the primary neutrons. Consequently, such parasitic contributions must be eliminated especially for small scattering angles relative to the beam direction where proton contributions are more significant. It is possible to experimentally characterize the protons and/or other products of nuclear fragmentation induced by the iron beam with the target, through the use of ∆E-E telescopes [82–84]. In a previous IBPER-17 campaign, such detectors were used and data analysis is still in progress. In this work, the proton contributions are obtained from Monte Carlo simulations, however these predictions are also biased by uncertainties of the nuclear models.
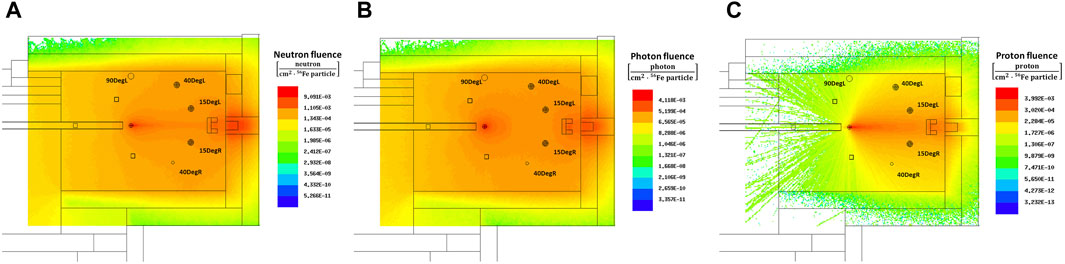
Figure 4. 2D neutron (A) gamma ray (B), and proton (C) fluence distribution in the Cave A experimental room obtained with MCNP6.1 using the CEM3.03 model.
Another study concerns the shape and contributions of the energy distributions of the simulated neutron and proton fluences. Figure 5A shows the comparison of neutron (A) and proton (B) fluences extracted from the 15DegL position by MCNP-CEM3.03 considering only the aluminum target (blue solid line) and defining all material properties present in Cave A (red solid line). From the ideal case, the direct peak, having a mean energy of (558.5 ± 3.1) MeV, is produced by the fragmentation interactions of the ion beam with the target [85], while the tail of the neutron spectrum for energies below 30 MeV should be induced by inelastic collisions of fragmentation products and other secondary particles interacting with the target. In the case where the material properties of Cave A are defined, the spectrum is divided into four specific zones, the direct peak (energies above 20 MeV), evaporation peak (energies between 100 keV and 20 MeV), the epithermal zone (energies between 0.4 eV and 100 keV) and the thermal peak (energies below 0.4 eV). The evaporation peaks are produced by excited fragment of heavy ions and by the excitation of nuclei induced by high-energy protons and neutrons; the excited nuclei subsequently produce isotropic evaporation neutrons [86]. The structure of the evaporation peak depends mainly on the nuclear resonances of the nuclei which define the Cave A material composition. In the epithermal zone, neutrons interact mainly though elastic scattering with hydrogen nuclei in the concrete walls. During these collisions, neutrons gradually lose their energies until they reach thermal equilibrium (≈25 meV) with the surrounding nuclei and are finally absorbed [87]. This comparison showed how the geometric model implemented in the simulations affects the shape of the neutron energy spectrum, underscoring the need to have a sufficiently accurate geometric model to compare simulated results with experimental ones.
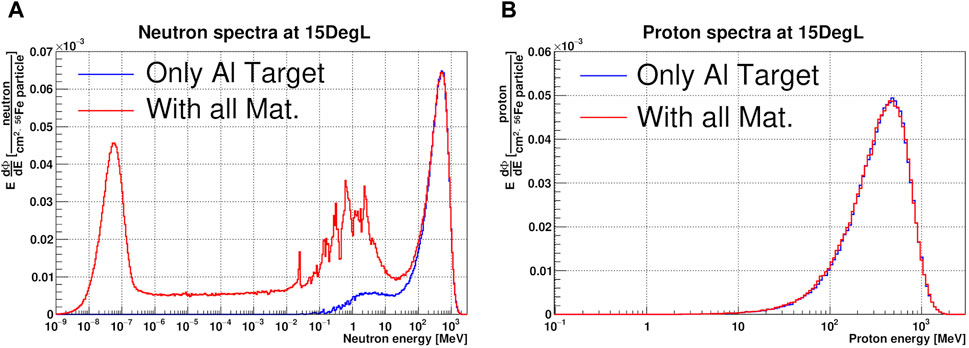
Figure 5. Comparison between neutron (A) and proton (B) fluences in lethargy units and normalized per 56Fe particle at the 15DegL measurement point obtained with MCNP- CEM3.03 by defining only the material properties of the aluminum target (blue solid line) and all materials in Cave A (red solid line).
Concerning the proton spectrum, see Figure 5B, no significant differences are seen between the two configurations, both spectra have a mean energy of (490 ± 3) MeV. This means that the proton contributions are exclusively related to the direct production of the collision reactions of 56Fe ions with the aluminum target.
Figure 6 shows the comparison between calculated neutron and proton spectra in lethargy units at the 15DegL (A,B), 40DegL (C,D) and 90DegL (E,F) measurement points obtained with all four Monte Carlo codes and physical models described in Section 2.3. The integral values of total fluence and as a function of the energy range are summarized in Table 3 for neutrons and Table 4 for protons. Globally, both FLUKA neutron and proton spectra are consistent with those obtained by Boscolo et al [19] and Sokolov et al. [20]. As for the simulated results obtained on the right side with respect to the beam line, they will not be shown in this paper because they are symmetrical to those obtained in the left side with deviations of less than 2%.
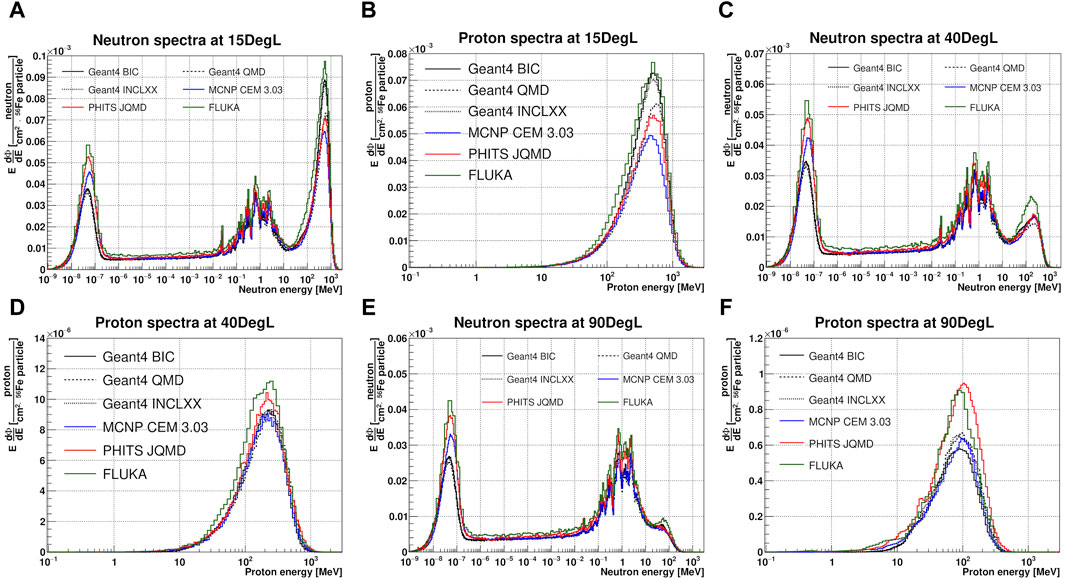
Figure 6. Comparison between calculated neutron and proton spectra in lethargy units and normalized per 56Fe particle at the 15DegL (A, B), 40DegL (C, D) and 90DegL (E, F) measurement points obtained with four Monte Carlo codes and physical models.
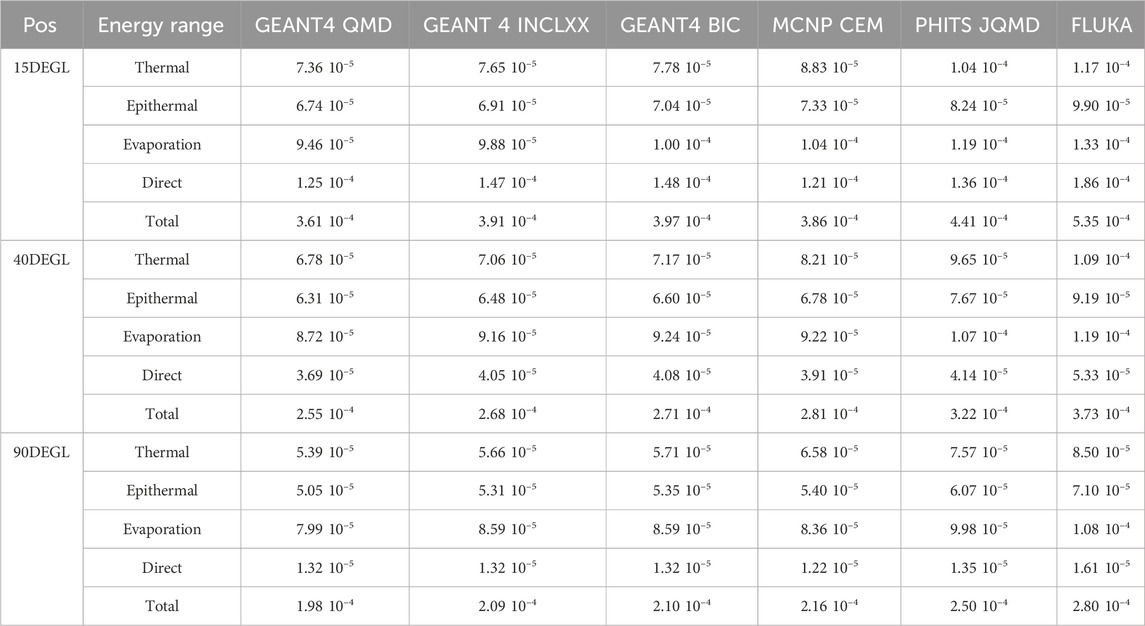
Table 3. Calculated neutron fluences [neutron/cm2 56Fe particle] extracted from the 15DegL, 40DegL and 90DegL measurement points as a function of the neutron energy range (Thermal: E < 0.4 eV, Epithermal: 0.4 eV < E < 100 keV, Evaporation: 100 keV < E < 20 MeV and Direct: E > 20 MeV).

Table 4. Calculated total proton fluences [proton/cm2 56Fe particle] extracted from the 15DegL, 40DegL and 90DegL measurement points.
Neutron spectra at the 15DegL position, show a direct peak with average energy of 559.4 ± 6.5 MeV. FLUKA shows the highest integral fluence in the energy range of the direct peak followed by Geant4-BIC and Geant4-INCLXX, while for MCNP-CEM it is the lowest. The total integral neutron fluence is highest for FLUKA and lowest for Geant4-QMD. While the proton spectra show a direct peak with average energy of (488.2 ± 8.5) MeV, the total fluence is highest for FLUKA and lowest for MCNP-CEM simulations.
Neutron spectra at the 40DegL position show a direct peak with average energy of (252.2 ± 2.4) MeV. The highest value of integral fluence on the direct peak is obtained by FLUKA followed by PHITS-JQMD, while the lowest value is obtained with Geant4-QMD. FLUKA and PHITS-JQMD have the highest total neutron fluence integral value, while the lowest value was found with Geant4-QMD. The proton spectra show a direct peak with average energy of (217.1 ± 18.6) MeV, the total fluence is highest for FLUKA followed by PHITS-JQMD, while the other simulations are equivalent. Neutron spectra at the 90DegL position show a direct peak with average energy of (60.3 ± 14.5) MeV. The trend of the fluence integrals is similar to that found at the 40DegL position except in the range of the direct peak where the fluence integral is minimal with MCNP-CEM. The proton spectra show a direct peak with average energy of (101.4 ± 22.3) MeV, the total fluence is highest for PHITS-JQMD and lowest for Geant4-BIC.
3.2 Measured NEMUS readings
As mentioned in Section 2.2, the various readings of the NEMUS system are obtained by repeating the measurements and changing the sphere diameter and type. Each reading consists of a number that is equivalent to the number of neutrons detected by the thermal sensor, normalized by dividing by the total number of primary 56Fe particles generated by the accelerator. Table 5 lists the normalized readings for the measurement positions at 15DegL and 40DegL as a function of the sphere dimension and type. Table 5 also lists the relative uncertainties of the various readings associated with the statistical uncertainty of the experimental data. Readings of the 3Pb5_7 and 4Pb6_8 spheres for the 15DegL and 40DegL measurement positions, respectively, are missing due to the instability of the ion beam, which made the experimental data unusable. In addition, there are the readings of the modified spheres with and without the proton contributions correction. Since protons generate neutrons rather uniformly inside the spheres [19], Equation 1 can be used to estimate the amount of proton-induced neutron contributions. Depending on the sphere type and the physical model of the Monte Carlo simulation, it has been estimated that protons contribute between 11% and 26% of the total reading with a standard deviation of ≈2% for the 15DegL position, while for the 40DegL position, they contribute between 2% and 5% with a standard deviation of ≈0.24%.
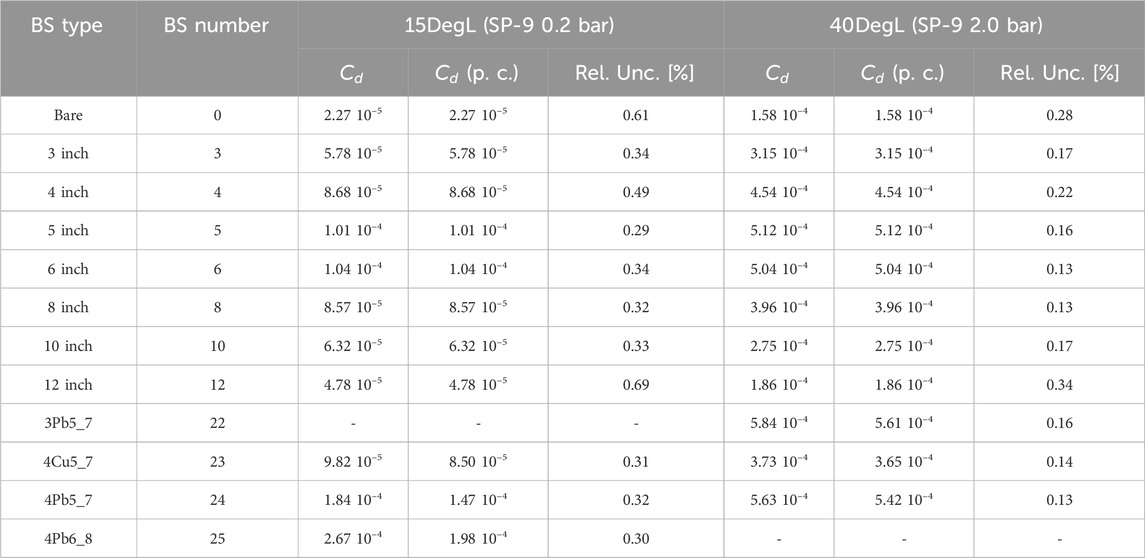
Table 5. Experimental NEMUS readings
Figure 7 shows the comparison between experimental readings measured with NEMUS and those calculated with Monte Carlo codes using Equation 1 for the 15DegL measurement position. The comparison shows that for the bare detector all simulations are higher suggesting that the thermal neutron peak in the simulations is overestimated. For spheres between 4″ and 12″, the calculated readings are underestimated suggesting that the real neutron spectrum in the energy range between the epithermal and evaporative zones has a higher fluence that caused by the oversimplified geometric model of GSI Cave A used for the simulations. Finally, for the modified spheres (BS number between 22 and 25) the calculated readings are underestimated compared with the experimental ones. However, it is difficult to estimate the impact of the neutron direct peak since the modified sphere response functions also includes the evaporation and epithermal energy ranges (see Figures 2A, B). The only way to estimate the real deviations is to reconstruct the measured neutron spectrum; an unfolding procedure is thus required to achieve this goal.
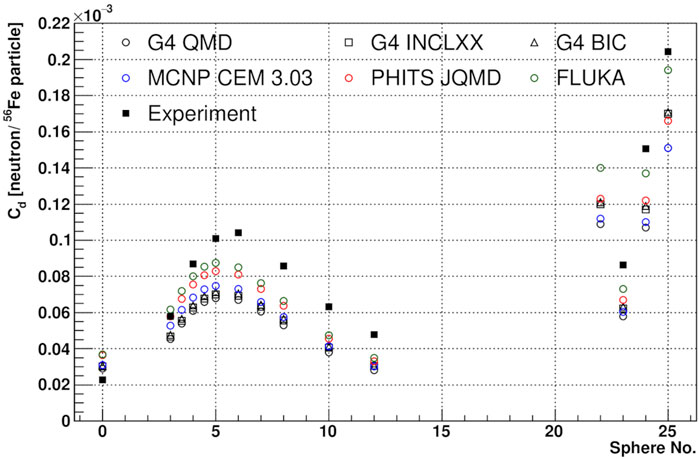
Figure 7. Comparison between measured and simulated NEMUS readings at position 15DegL as a function of the BS sphere number, both data sets are normalized per 56Fe particle.
3.3 Neutron spectra unfolding and ambient dose equivalent analysis
The unfolding, or deconvolution, procedure consists of solving the inverse problem associated with Equation 1 in order to estimate the neutron spectrum
where
To be initialized MAXED needs the measured readings of the Bonner Spheres with uncertainties, the matrix with the neutron response functions, a default energy spectrum and a χ2 target value for the unfolded readings. Estimated uncertainties from external sources were added by quadrature to the experimental uncertainties, such as the uncertainty of the NEMUS response functions, the uncertainty of the Monte Carlo simulations, and finally the uncertainty related to the correction of proton contributions (the latter was added only for the readings of the modified spheres). The main purpose of unfolding with MAXED is to have an estimate of the neutron spectrum that is consistent with the experimental data, which can be used to qualitatively evaluate the physical models implemented in the Monte Carlo simulations by comparing the unfolded spectra with those obtained by simulation.
Figure 8 shows the comparison between simulated (dashed line) spectra used as input default spectra and their corresponding unfolded (solid line) output neutron spectra, using G4-QMD (blue lines) and MCNP-CEM (red lines) for the 15DegL (A) and 40DegL (B) measurement position. The comparison shows that the two unfolded spectra are similar but not coincident over the entire energy range and this could be caused by the experimental and external statistical uncertainties introduced in MAXED. On the direct peak, the differences in the two unfolded spectra could also be caused by correction of the proton contributions (only on the direct peak), which are different for different Monte Carlo codes (see Section 3.1).
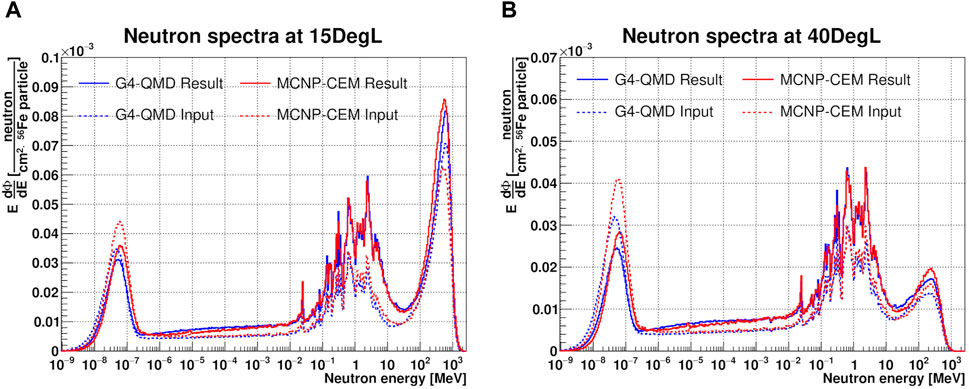
Figure 8. Comparison between unfolded (solid line) and corresponding simulated (dashed line) neutron spectra in lethargy units and normalized per 56Fe particle using G4-QMD (blue lines) and MCNP-CEM (red lines) for the 15DegL (A) and 40DegL (B) measurement positions.
Figure 9 shows the comparison between simulated neutron spectra (lines) used as input default spectra and the range of MAXED solutions for the 15DegL (A,B) and 40DegL (C,D) measurement positions. The shaded area of MAXED was obtained by considering, bin by bin, the range between the minimum and maximum value among the different unfolding results. The results show that there are large deviations for all energy ranges. For the range between thermal and evaporation neutrons, the deviations are mainly due to the overly simplistic geometric model used for the simulations. In fact, the geometric model does not take into account the correct amount of water contained in the concrete walls and their heterogeneity, which explains the deviations between the evaporation and thermal energy ranges [96]. Further deviations in the evaporation energy range could be caused by the absence in the geometric model of materials that would induce the production of additional evaporation neutrons. Concerning the direct peaks, no major shift of the mean peak energy was found. For the 15DegL measurement position, the simulated spectra with smallest deviations for the direct peak (i.e., that are closest to the unfolded solution) are those given by Geant4-BIC and INCLXX, with deviations of 4% and 5%, respectively. Largest deviations have been found with Geant4-QMD, FLUKA and MCNP-CEM with deviations of the order of 20%. On the 40DegL position, FLUKA shows the lowest deviation of 8.4% followed by PHITS-JQMD with a deviation of 15.7%.
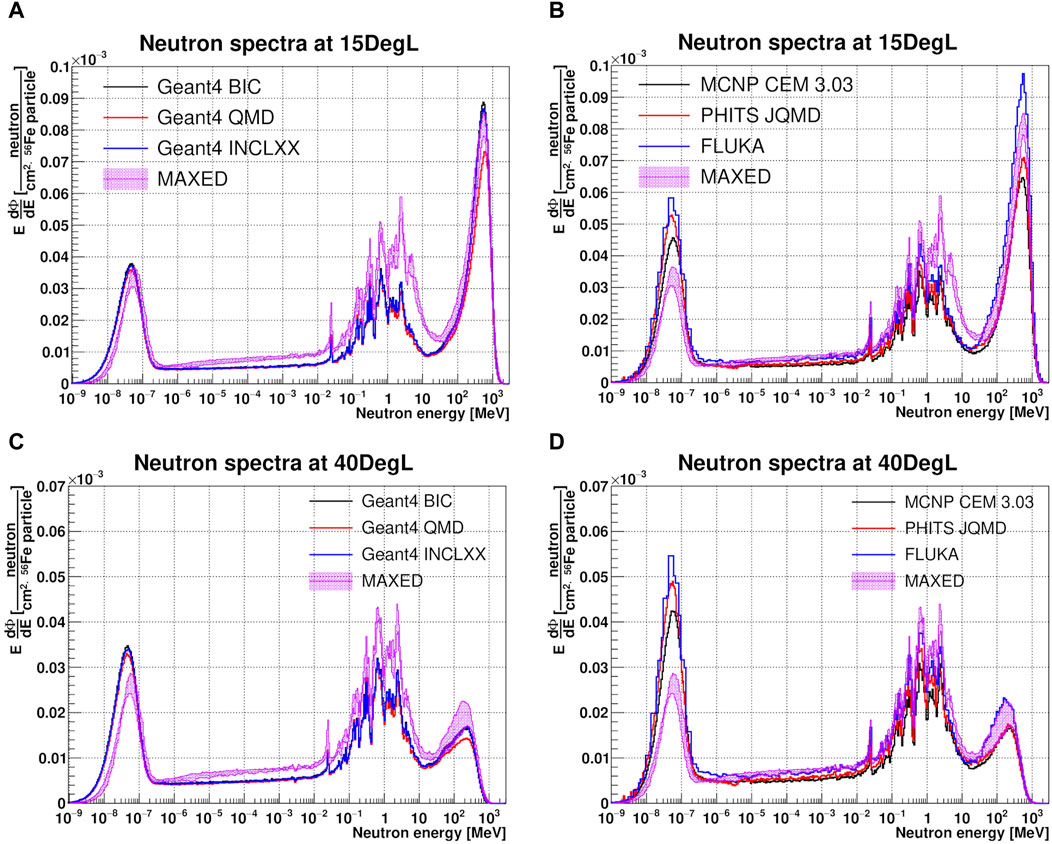
Figure 9. Comparison between simulated (lines) neutron spectra and MAXED solution set (purple shadow) of the unfolded neutron spectrum in lethargy units and normalized per 56Fe particle for the 15DegL (A, B) and 40DegL (C, D) measurement positions.
Figure 10 shows the integral neutron fluence quantities for simulated (filled bar chart) and unfolded (semi-transparent bar chart) results according to neutron energy ranges for the 15DegL (A) and 40DegL (B) measurement positions. The results show that all unfolded spectra have approximately the same total neutron fluence, with small standard deviations of the order of 2% and 1% for the 15DegL and 40DegL measurement positions, respectively. The mean fluence values of the unfolded spectra and the corresponding deviations from the Monte Carlo results are summarized in Table 6.
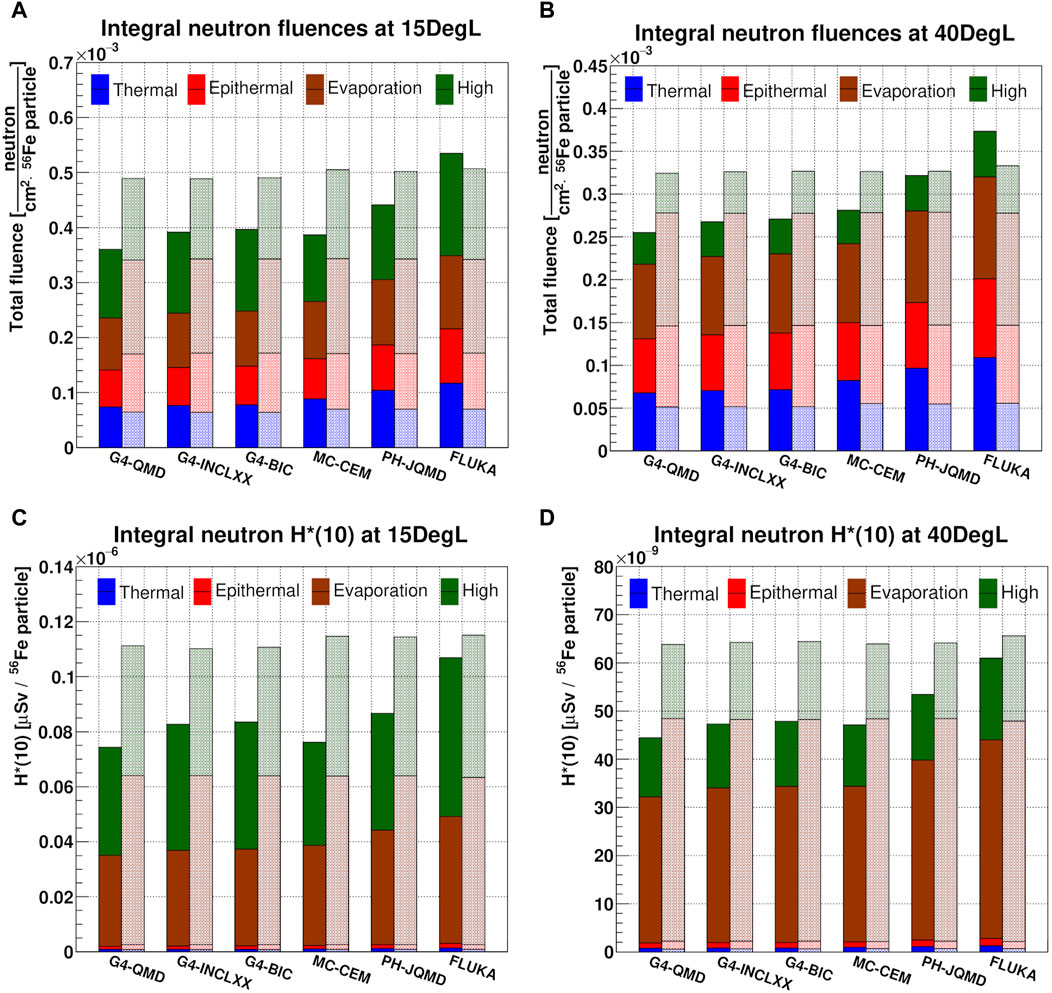
Figure 10. Integral neutron fluence and H* (10) quantities between simulated (filled bar chart) and unfolded (semi-transparent bar chart) results according neutron energy ranges for the 15DegL (A, C) and 40DegL (B, D) measurement positions. Both pairs of data are normalized per 56Fe particle.
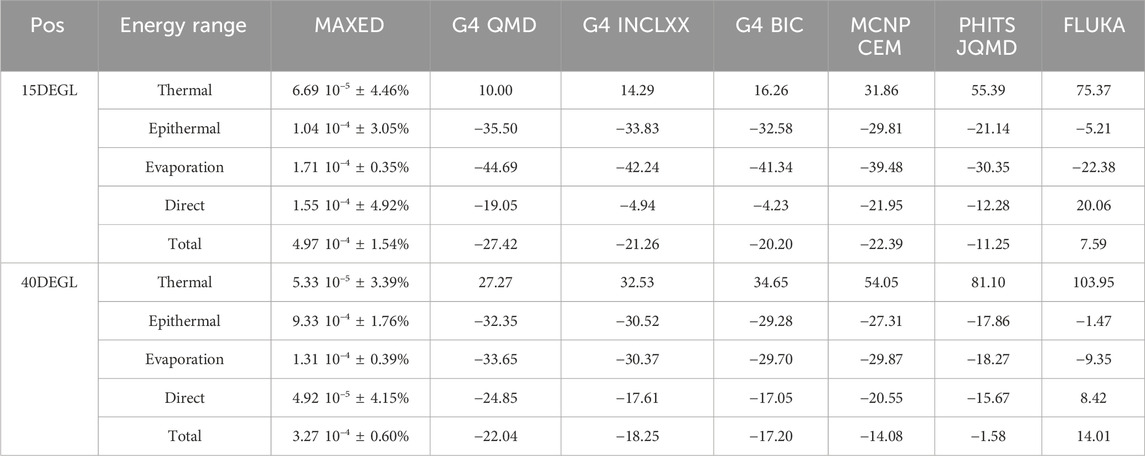
Table 6. Estimated mean neutron fluences [neutron/cm2 56Fe particle] with MAXED extracted from the 15DegL and 40DegL measurement positions and corresponding deviations [%] from the Monte Carlo results (Thermal: E < 0.4 eV, Epithermal: 0.4 eV < E < 100 keV, Evaporation: 100 keV < E < 20 MeV and Direct: E > 20 MeV).
Neutron ambient dose equivalent H* (10) distributions were obtained by multiplying neutron spectra with fluence-to-dose conversion coefficients [97, 98], and subsequently the integral values were calculated as a function of the energy range of the neutrons. This operation was done for both simulated and unfolded neutron spectra with MAXED. Figure 10 shows the integral neutron H* (10) quantities for simulated (filled bar chart) and unfolded (semi-transparent bar chart) results according to neutron energy ranges for the 15DegL (C) and 40DegL (D) measurement positions. Table 7 lists the mean integral neutron H* (10) values from the unfolded spectra and the corresponding deviations from the Monte Carlo results. The results show that for the 15DegL measurement position, evaporation neutrons and direct peak neutrons contribute to the H* (10) with weights of 54% and 43%, respectively. While for the 40DegL measurement position, evaporation neutrons and direct peak neutrons contribute to the H* (10) with weights of 72% and 25%, respectively. This is because the 252 MeV direct peak at the 40DegL position has both a lower fluence than the peak at 15DegL and the average energy of the peak is approximately at the minimum point (≈251.23.pSv cm2) of the fluence-to-ambient dose equivalent conversion function for neutrons between 100 MeV and 1 GeV [98].
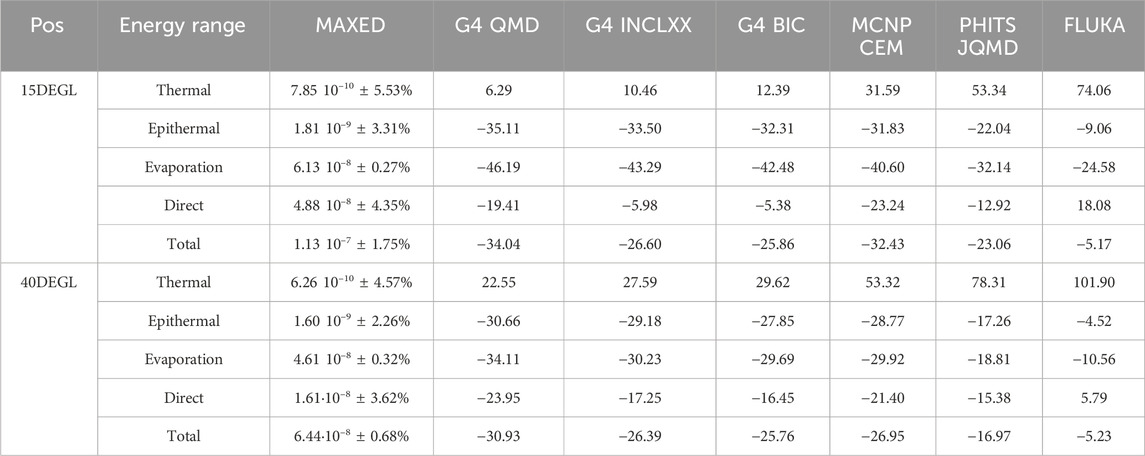
Table 7. Estimated mean neutron H* (10) [µSv/56Fe particle] with MAXED extracted from the 15DegL and 40DegL measurement points and corresponding deviations [%] from the Monte Carlo results (Thermal: E < 0.4 eV, Epithermal: 0.4 eV < E < 100 keV, Evaporation: 100 keV < E < 20 MeV and Direct: E > 20 MeV).
4 Conclusion
Manned space travel to the Moon and Mars will become more and more tangible in the near future. Spectroscopic knowledge of the secondary radiation field generated by GCRs interacting with spacecraft shielding materials are critical for both the design phase and the evaluation of possible biological risks to astronauts during the journey. In this study, we measured the secondary neutron field generated by a 1 GeV/u 56Fe ion beam interacting with a cylindrical aluminum target in order to simulate a specific energy portion of the secondary radiation field that would be generated inside a spacecraft. The PTB’s NEMUS system was used with three different thermal neutron sensors inside the GSI Cave A to perform neutron spectrometry measurements at three measurement angles with respect to the direction of the ion beam. Four Monte Carlo codes with different physical models were used both to estimate the neutron and proton energy spectra and to use these spectra as a priori information to initialize the unfolding process of neutron spectra using the MAXED code.
Before unfolding, the experimental data were corrected to exclude parasitic neutron contributions induced by the interaction of secondary protons with the metal shells of the modified Bonner spheres. The results showed that with the various unfolded spectra with MAXED, based on different simulations, a range of spectra was obtained. The unfolded spectra confirmed the average energies of the two direct peaks at 560 MeV and 230.MeV and showed that Geant4 with its BIC and INCLXX models, PHITS and FLUKA have the lowest deviations on direct peak intensities. The largest deviations were found with MCNP-CEM and Geant4-QMD.
The results showed that the total integral quantities of neutron fluence and equivalent ambient dose had standard deviations of less than 2%, regardless of the Monte Carlo code and physical model chosen. These results confirmed the validity of the NEMUS system with the MAXED unfolding code to perform characterization studies of wide energy range neutron spectra for energies above 500 MeV. Another important aspect of the capability of NEMUS other than that of satisfactory retrieving the full neutron spectrum is that of being able to calculate the total or energy-range-dependent neutron ambient dose equivalent quantities and so being used as neutron dosimeter.
Future data analysis will focus on the comparison of the experimental results obtained in this work and those obtained in previous experimental campaigns in which Thermoluminescent Dosimeters (TLDs) and Tissue Equivalent Proportional Counters (TEPCs) were used in the same secondary radiation field to carry out neutron dosimetry and microdosimentry studies. In addition, future studies will focus on experimental correction of neutron contributions induced by secondary protons by ∆E-E telescopes. Finally, the NEMUS system will be used in the future to characterize the secondary neutron field produced with other space shielding materials such as a Moon regolith simulant or polyethylene.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
AD: Writing–review and editing, Writing–original draft, Visualization, Software, Formal Analysis, Conceptualization. FH: Writing–review and editing, Software, Investigation, Conceptualization. DB: Writing–review and editing, Software, Investigation, Conceptualization. CS: Writing–review and editing, Investigation, Conceptualization. UW: Writing–review and editing, Supervision, Investigation, Conceptualization. MZ: Writing–review and editing, Supervision, Investigation, Funding acquisition, Data curation, Conceptualization.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The results presented here are based on the experiment AO-2017-IBER_010, which was performed in Cave A at the GSI Helmholtzzentrum fuer Schwerionenforschung, Darmstadt (Germany) in the frame of FAIR Phase-0. AO-2017-IBER_010 is supported by the European Space Agency (ESA) – IBER program and by the German Aerospace Center (DLR) under the funding number 50WB2125.
Acknowledgments
The authors would like to thank the whole GSI and PTB technical team, for their collaboration and valuable assistance during the experiments.
Conflict of interest
Authors FH, DB, CS, and UW were employed by company GSI Helmholtzzentrum für Schwerionenforschung GmbH.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Durante M, Cucinotta FA. Physical basis of radiation protection in space travel. Rev Mod Phys (2011) 83:1245–81. doi:10.1103/revmodphys.83.1245
2. George JS, Lave KA, Wiedenbeck ME, Binns WR, Cummings AC, Davis AJ, et al. Elemental composition and energy spectra of galactic cosmic rays during solar cycle 23. Astrophys J (2009) 698(2):1666–81. doi:10.1088/0004-637x/698/2/1666
3. Norbury JW, Slaba TC. Space radiation accelerator experiments – the role of neutrons and light ions. Life Sci Space Res (2014) 3:90–4. doi:10.1016/j.lssr.2014.09.006
4. Veinot KG, Hertel NE. Effective quality factors for neutrons based on the revised ICRP/ICRU recommendations. Radiat Prot Dosimetry (2005) 115(1–4):536–41. doi:10.1093/rpd/nci004
5. Baiocco G, Barbieri S, Babini G, Morini J, Alloni D, Friedland W, et al. The origin of neutron biological effectiveness as a function of energy. Sci Rep (2016) 6(1):34033. doi:10.1038/srep34033
6. Zeitlin C, Castro AJ, Beard KB, Abdelmelek M, Hayes BM, Johnson AS, et al. Results from the radiation assessment detector on the international space station, Part 2: the fast neutron detector. Life Sci Space Res (2023) 39:76–85. doi:10.1016/j.lssr.2023.03
7. Zeitlin C, Castro AJ, Beard KB, Hayes BM, Abdelmelek M, Laramore D, et al. Results from the radiation assessment detector on the international space station: Part 3, combined results from the CPD and FND. Life Sci Space Res (2023) 39:86–94. doi:10.1016/j.lssr.2023.06.002
8. Walker SA, Townsend LW, Norbury JW. Heavy ion contributions to organ dose equivalent for the 1977 galactic cosmic ray spectrum. Adv Space Res (2013) 51(9):1792–9. doi:10.1016/j.asr.2012.12.011
9. Slaba TC, Bahadori AA, Reddell BD, Singleterry RC, Clowdsley MS, Blattnig SR. Optimal shielding thickness for galactic cosmic ray environments. Life Sci Space Res (2017) 12:1–15. doi:10.1016/j.lssr.2016.12.003
10. Barthel J, Sarigul-Klijn N. Radiation production and absorption in human spacecraft shielding systems under high charge and energy Galactic Cosmic Rays: material medium, shielding depth, and byproduct aspects. Acta Astronaut. (2018) 144:254–62. doi:10.1016/j.actaastro.2017.12.040
11. Horst F, Boscolo D, Durante M, Luoni F, Schuy C, Weber U. Thick shielding against galactic cosmic radiation: a Monte Carlo study with focus on the role of secondary neutrons. Life Sci Space Res (2022) 33:58–68. doi:10.1016/j.lssr.2022.03.003
12. Nakamura T. Overview of experimental works on secondary particle production and transport by high-energy particle beams. Radiat Prot Environ (2012) 35(3):111. doi:10.4103/0972-0464.117665
13. Norbury JW, Battistoni G, Besuglow J, Bocchini L, Boscolo D, Botvina A, et al. Are further cross section measurements necessary for space radiation protection or ion therapy applications? Helium Projectiles Front Phys (2020) 8. doi:10.3389/fphy.2020.565954
14. Luoni F, Horst F, Reidel CA, Quarz A, Bagnale L, Sihver L, et al. Total nuclear reaction cross-section database for radiation protection in space and heavy-ion therapy applications. New J Phys (2021) 23(10):101201. doi:10.1088/1367-2630/ac27e1
15. McGirl N, Castellanos L, Srikrishna A, Heilbronn L. Secondary neutron yields produced by thick-target aluminum interactions (2016). Available from: https://ttu-ir.tdl.org/handle/2346/67707 (Accessed August 19, 2022).
16. Castellanos LA, McGirl NA, Srikrishna AP, Heilbronn L, La Tessa C, Rusek A, et al. Thick-target yields of secondary ions and neutrons for validation of radiation transport codes. In: 2017 IEEE Aerospace Conference; 4-11 March 2017; China (2017). p. 1–10.
17. Tsai PE, Lai BL, Heilbronn LH, Sheu RJ. Benchmark of neutron production cross sections with Monte Carlo codes. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater At (2018) 416:16–29. doi:10.1016/j.nimb.2017.11.029
18. Chen J, Yun S, Dong T, Ren Z, Zhang X. Validation of Geant4 physics models for nuclear beams in extended media. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater At (2018) 434:113–9. doi:10.1016/j.nimb.2018.08.022
19. Boscolo D, Scognamiglio D, Horst F, Weber U, Schuy C, Durante M, et al. Characterization of the secondary neutron field produced in a thick aluminum shield by 1 GeV/u 56Fe ions using TLD-based ambient dosimeters. Front Phys (2020) 8. doi:10.3389/fphy.2020.00365
20. Sokolov A, Kozlova E, Boscolo D, Durante M, Horst F, Radon T, et al. Neutron spectra at a high energy heavy ion accelerator measured with a TLD-based Bonner spectrometer. J Instrum (2021) 16(10):P10022. doi:10.1088/1748-0221/16/10/p10022
21. Horst F, Boscolo D, Cartechini G, Durante M, Hartel C, Kozlova E, et al. A multi-detector experimental setup for the study of space radiation shielding materials: measurement of secondary radiation behind thick shielding and assessment of its radiobiological effect. EPJ Web Conf (2022) 261:03002. doi:10.1051/epjconf/202226103002
22. Durante M, Cucinotta FA. Heavy ion carcinogenesis and human space exploration. Nat Rev Cancer (2008) 8(6):465–72. doi:10.1038/nrc2391
23. Zeitlin C, Guetersloh SB, Heilbronn LH, Miller J. Measurements of materials shielding properties with 1GeV/nuc 56Fe. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater At. (2006) 252(2):308–18. doi:10.1016/j.nimb.2006.08.011
24. Durante M, Golubev A, Park WY, Trautmann C. Applied nuclear physics at the new high-energy particle accelerator facilities. Phys Rep (2019) 800:1–37. doi:10.1016/j.physrep.2019.01.004
25. Bramblett RL, Ewing RI, Bonner TW. A new type of neutron spectrometer. Nucl Instrum Methods (1960) 9(1):1–12. doi:10.1016/0029-554x(60)90043-4
26. Thomas DJ, Alevra AV. Bonner sphere spectrometers—a critical review. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (2002) 476(1):12–20. doi:10.1016/s0168-9002(01)01379-1
27. Alevra AV, Thomas DJ. Neutron spectrometry in mixed fields: multisphere spectrometers. Radiat Prot Dosimetry (2003) 107(1–3):37–72. doi:10.1093/oxfordjournals.rpd.a006388
28. Mares V, Schraube H. High energy neutron spectrometry with Bonner spheres. China: Czech Republic (1998). p. 671.
29. Wiegel B, Alevra AV. NEMUS—the PTB neutron multisphere spectrometer: bonner spheres and more. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (2002) 476(1):36–41. doi:10.1016/s0168-9002(01)01385-7
30. fachabteilungen. Dep. 6 W. Neutron spektrometer NEMUS (neutron multisphere spectrometer) (2016). Available from: https://www.ptb.de/cms/en/ptb/fachabteilungen/abt6/fb-64/643-neutron-spectrometry/nemus/neutron-spektrometer-nemus-neutron-multisphere-spectrometer.html.
31. Dommert M, Reginatto M, Zbořil M, Lutz B. Dead time corrections for Bonner sphere measurements of secondary neutrons at a proton therapy facility. J Instrum (2021) 16(03):P03038. doi:10.1088/1748-0221/16/03/p03038
32. Goldhagen P, Reginatto M, Kniss T, Wilson JW, Singleterry RC, Jones IW, et al. Measurement of the energy spectrum of cosmic-ray induced neutrons aboard an ER-2 high-altitude airplane. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (2002) 476(1):42–51. doi:10.1016/s0168-9002(01)01386-9
33. Rollet S, Agosteo S, Fehrenbacher G, Hranitzky C, Radon T, Wind M. Intercomparison of radiation protection devices in a high-energy stray neutron field, Part I: Monte Carlo simulations. Radiat Meas (2009) 44(7):649–59. doi:10.1016/j.radmeas.2009.03.029
34. Luoni F, Weber U, Boscolo D, Durante M, Reidel CA, Schuy C, et al. Beam monitor calibration for radiobiological experiments with scanned high energy heavy ion beams at FAIR. Front Phys (2020) 8. doi:10.3389/fphy.2020.568145
35. Battistoni G, Boehlen T, Cerutti F, Chin PW, Esposito LS, Fassò A, et al. Overview of the FLUKA code. Ann Nucl Energy (2015) 82:10–8. doi:10.1016/j.anucene.2014.11.007
36. Ahdida C, Bozzato D, Calzolari D, Cerutti F, Charitonidis N, Cimmino A, et al. New capabilities of the FLUKA multi-purpose code. Front Phys (2022) 9. doi:10.3389/fphy.2021.788253
38. Sorge H, Stöcker H, Greiner W. Poincaré invariant Hamiltonian dynamics: modelling multi-hadronic interactions in a phase space approach. Ann Phys (1989) 192(2):266–306. doi:10.1016/0003-4916(89)90136-x
39. Oh J, Lee HS, Park S, Kim M, Hong S, Ko S, et al. Comparison of the FLUKA, MCNPX, and PHITS codes in yield calculation of secondary particles produced by intermediate energy proton beam. Prog Nucl Sci Technol (2011) 25:85–8. doi:10.15669/pnst.1.85
40. Agosteo S, Mereghetti A, Sagia E, Silari M. Shielding data for hadron-therapy ion accelerators: attenuation of secondary radiation in concrete. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater At. (2014) 319:154–67. doi:10.1016/j.nimb.2013.10.015
41. Nakao N, Kajimoto T, Sanami T, Froeschl R, Iliopoulou E, Infantino A, et al. Measurements and Monte Carlo simulations of high-energy neutron streaming through the access maze using activation detectors at 24 GeV/c proton beam facility of CERN/CHARM. J Nucl Sci Technol (2021) 58(8):899–907. doi:10.1080/00223131.2021.1887003
42. De Saint-Hubert M, Farah J, Klodowska M, Romero-Exposito MT, Tyminska K, Mares V, et al. The influence of nuclear models and Monte Carlo radiation transport codes on stray neutron dose estimations in proton therapy. Radiat Meas (2022) 150:106693. doi:10.1016/j.radmeas.2021.106693
43. Beskrovnaia L, Florko B, Paraipan M, Sobolevsky N, Timoshenko G. Verification of Monte Carlo transport codes FLUKA, GEANT4 and SHIELD for radiation protection purposes at relativistic heavy ion accelerators. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater At. (2008) 266(18):4058–60. doi:10.1016/j.nimb.2008.07.003
44. Robert C, Dedes G, Battistoni G, Böhlen TT, Buvat I, Cerutti F, et al. Distributions of secondary particles in proton and carbon-ion therapy: a comparison between GATE/Geant4 and FLUKA Monte Carlo codes. Phys Med Biol (2013) 58(9):2879–99. doi:10.1088/0031-9155/58/9/2879
45. Kim DH, Oh JH, Jung NS, Lee HS, Shin YS, Kwon DY, et al. A benchmarking study of high energy carbon ion induced neutron using several Monte Carlo codes. 2014 Available from: https://www.osti.gov/etdeweb/biblio/22355632.
46. Chen WL, Jiang SH, Sheu RJ. Cosmic-ray neutron simulations and measurements in Taiwan. Radiat Prot Dosimetry (2014) 161(1–4):303–6. doi:10.1093/rpd/ncu030
47. Lee KW, Sheu RJ. Comparing two measurements of the same cosmic-ray neutron spectrum using standard bonner spheres and high-sensitivity bonner cylinders. Radiat Prot Dosimetry (2017) 177(4):450–7. doi:10.1093/rpd/ncx063
48. Norbury JW, Slaba TC, Sobolevsky N, Reddell B. Comparing HZETRN, SHIELD, FLUKA and GEANT transport codes. Life Sci Space Res (2017) 14:64–73. doi:10.1016/j.lssr.2017.04.001
49. Wiegel B, Agosteo S, Bedogni R, Caresana M, Esposito A, Fehrenbacher G, et al. Intercomparison of radiation protection devices in a high-energy stray neutron field, Part II: bonner sphere spectrometry. Radiat Meas (2009) 44(7):660–72. doi:10.1016/j.radmeas.2009.03.026
50. Goorley JT, James MR, Booth TE, Brown FB, Bull JS, Cox LJ, et al. Initial MCNP6 release overview - MCNP6 version 1.0. Los Alamos, NM (United States): Los Alamos National Lab. LANL (2013). Available from: https://www.osti.gov/biblio/1086758.
51. Amgarou K, Bedogni R, Domingo C, Esposito A, Gentile A, Carinci G, et al. Measurement of the neutron fields produced by a 62MeV proton beam on a PMMA phantom using extended range Bonner sphere spectrometers. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (2011) 654(1):399–405. doi:10.1016/j.nima.2011.07.027
52. Chadwick MB, Herman M, Obložinský P, Dunn ME, Danon Y, Kahler AC, et al. ENDF/B-VII.1 nuclear data for science and technology: cross sections, covariances, fission product yields and decay data. Nucl Data Sheets (2011) 112(12):2887–996. doi:10.1016/j.nds.2011.11.002
53. Chadwick MB, Obložinský P, Herman M, Greene NM, McKnight RD, Smith DL, et al. ENDF/B-VII.0: next generation evaluated nuclear data library for nuclear science and technology. Nucl Data Sheets (2006) 107(12):2931–3060. doi:10.1016/j.nds.2006.11.001
54. Krylov A, Paraipan M, Sobolevsky N, Timoshenko G, Tret’yakov V. GEANT4, MCNPX, and SHIELD code comparison concerning relativistic heavy ion interaction with matter. Phys Part Nucl Lett (2014) 11(4):549–51. doi:10.1134/s1547477114040232
55. Lee A, Kim D, Jung NS, Oh JH, Oranj LM, Lee HS. Comparison of physics model for 600 MeV protons and 290 MeV·n-1 oxygen ions on carbon in MCNPX. J Radiat Prot Res (2016) 41(2):123–31. doi:10.14407/jrpr.2016.41.2.123
56. Lapins J, Guilliard N, Bernnat W, Buck A. Simulation of irradiation exposure of electronic devices due to heavy ion therapy with Monte Carlo Code MCNP6. EPJ Web Conf (2017) 153:04015. doi:10.1051/epjconf/201715304015
57. Wilson WH, Johnson CM, Lowrey JD, Biegalski SR, Haas DA. Cosmic-ray induced production of radioactive noble gases in the atmosphere, ground, and seawater. J Radioanal Nucl Chem (2015) 305(1):183–92. doi:10.1007/s10967-015-4181-7
58. Mesick KE, Feldman WC, Coupland DDS, Stonehill LC. Benchmarking Geant4 for simulating galactic cosmic ray interactions within planetary bodies. Earth Space Sci (2018) 5(7):324–38. doi:10.1029/2018ea000400
59. Lee JH, Kim HN, Jeong HY, Cho SO. Optimization of shielding to reduce cosmic radiation damage to packaged semiconductors during air transport using Monte Carlo simulation. Nucl Eng Technol (2020) 52(8):1817–25. doi:10.1016/j.net.2020.01.016
60. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. Geant4—a simulation toolkit. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (2003) 506(3):250–303. doi:10.1016/s0168-9002(03)01368-8
61. Walker SD, Abramov A, Nevay LJ, Shields W, Boogert ST. Pyg4ometry: a Python library for the creation of Monte Carlo radiation transport physical geometries. Comput Phys Commun (2022) 272:108228. doi:10.1016/j.cpc.2021.108228
62. Plompen AJM, Cabellos O, De Saint Jean C, Fleming M, Algora A, Angelone M, et al. The joint evaluated fission and fusion nuclear data library, JEFF-3.3. Eur Phys J A (2020) 56(7):181. doi:10.1140/epja/s10050-020-00141-9
63. Dudouet J, Cussol D, Durand D, Labalme M. Benchmarking GEANT4 nuclear models for hadron therapy with 95 MeV/nucleon carbon ions. Phys Rev C (2014) 89(5):054616. doi:10.1103/physrevc.89.054616
64. Bolst D, Cirrone GAP, Cuttone G, Folger G, Incerti S, Ivanchenko V, et al. Validation of Geant4 fragmentation for heavy ion therapy. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (2017) 869:68–75. doi:10.1016/j.nima.2017.06.046
65. Ivanchenko V, Dondero P, Fioretti V, Ivantchenko A, Lei F, Lotti S, et al. Validation of Geant4 10.3 simulation of proton interaction for space radiation effects. Exp Astron (2017) 44(3):437–50. doi:10.1007/s10686-017-9556-z
66. Lamrabet A, Maghnouj A, Tajmouati J, Bencheikh M. GEANT4 characterization of the neutronic behavior of the active zone of the MEGAPIE spallation target. Nucl Eng Technol (2021) 53(10):3164–70. doi:10.1016/j.net.2021.05.002
67. Domingo C, Lagares JI, Romero-Expósito M, Sánchez-Nieto B, Nieto-Camero JJ, Terrón JA, et al. Peripheral organ equivalent dose estimation procedure in proton therapy. Front Oncol (2022) 12:882476. doi:10.3389/fonc.2022.882476
68. Brall T, Mares V, Bütikofer R, Rühm W. Assessment of neutrons from secondary cosmic rays at mountain altitudes – Geant4 simulations of environmental parameters including soil moisture and snow cover. The Cryosphere (2021) 15(10):4769–80. doi:10.5194/tc-15-4769-2021
69. Brall T, Mares V, Bütikofer R, Rühm W. Assessment of secondary neutrons from galactic cosmic rays at mountain altitudes – Geant4 simulations and ground-based measurements of neutron energy spectra. Radiat Meas (2021) 144:106592. doi:10.1016/j.radmeas.2021.106592
70. Sato T, Niita K, Matsuda N, Hashimoto S, Iwamoto Y, Noda S, et al. Particle and heavy ion transport code system, PHITS, version 2.52. J Nucl Sci Technol (2013) 50(9):913–23. doi:10.1080/00223131.2013.814553
71. Sato T, Iwamoto Y, Hashimoto S, Ogawa T, Furuta T, ichiro AS, et al. Features of particle and heavy ion transport code system (PHITS) version 3.02. J Nucl Sci Technol (2018) 55(6):684–90. doi:10.1080/00223131.2017.1419890
72. Shibata K, Iwamoto O, Nakagawa T, Iwamoto N, Ichihara A, Kunieda S, et al. JENDL-4.0: a new library for nuclear science and engineering. J Nucl Sci Technol (2011) 48(1):1–30. doi:10.3327/jnst.48.1
73. Matsuda N, Kunieda S, Okamoto T, Tada K, Konno C. ACE library of JENDL-4.0/HE. Prog Nucl Sci Technol (2019) 6(0):225–9. doi:10.15669/pnst.6.225
74. Heilbronn L, Nakamura T, Iwata Y, Kurosawa T, Iwase H, Townsend LW. Overview of secondary neutron production relevant to shielding in space. Radiat Prot Dosimetry (2005) 116(1–4):140–3. doi:10.1093/rpd/nci033
75. Yonai S, Matsumoto S. Monte Carlo study toward the development of a radiation field to simulate secondary neutrons produced in carbon-ion radiotherapy. Radiat Phys Chem (2020) 172:108787. doi:10.1016/j.radphyschem.2020.108787
76. Matthiä D, Ehresmann B, Lohf H, Köhler J, Zeitlin C, Appel J, et al. The Martian surface radiation environment – a comparison of models and MSL/RAD measurements. J Space Weather Space Clim (2016) 6:A13. doi:10.1051/swsc/2016008
77. Naito M, Hasebe N, Shikishima M, Amano Y, Haruyama J, Matias-Lopes JA, et al. Radiation dose and its protection in the Moon from galactic cosmic rays and solar energetic particles: at the lunar surface and in a lava tube. J Radiol Prot (2020) 40(4):947–61. doi:10.1088/1361-6498/abb120
78. Zaman FA, Townsend LW, de Wet WC, Burahmah NT. The lunar radiation environment: comparisons between PHITS, HETC-HEDS, and the CRaTER instrument. Aerospace (2021) 8(7):182. doi:10.3390/aerospace8070182
79. Zaman FA, Townsend LW, de Wet WC, Looper MD, Brittingham JM, Burahmah NT, et al. Modeling the lunar radiation environment: a comparison among FLUKA, Geant4, HETC-HEDS, MCNP6, and PHITS. Space Weather (2022) 20(8):e2021SW002895. doi:10.1029/2021sw002895
80. Brun R, Rademakers F. ROOT — an object oriented data analysis framework. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (1997) 389(1):81–6. doi:10.1016/s0168-9002(97)00048-x
81. Nandy M. Secondary radiation in ion therapy and theranostics: a review. Front Phys (2021) 8. doi:10.3389/fphy.2020.598257
82. Gunzert-Marx K, Iwase H, Schardt D, Simon RS. Secondary beam fragments produced by 200 MeV u−1 12C ions in water and their dose contributions in carbon ion radiotherapy. New J Phys (2008) 10(7):075003. doi:10.1088/1367-2630/10/7/075003
83. Haettner E, Iwase H, Krämer M, Kraft G, Schardt D. Experimental study of nuclear fragmentation of 200 and 400 MeV/u12C ions in water for applications in particle therapy. Phys Med Biol (2013) 58(23):8265–79. doi:10.1088/0031-9155/58/23/8265
84. Rovituso M, Schuy C, Weber U, Brons S, Cortés-Giraldo MA, Tessa CL, et al. Fragmentation of 120 and 200 MeV u−1 4He ions in water and PMMA targets. Phys Med Biol (2017) 62(4):1310–26. doi:10.1088/1361-6560/aa5302
85. Nakamura T, Heilbronn L. Overview of secondary particle production and transport by high-energy heavy ions. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (2006) 562(2):706–9. doi:10.1016/j.nima.2006.02.027
86. Shrestha S, Newhauser WD, Donahue WP, Pérez-Andújar A. Stray neutron radiation exposures from proton therapy: physics-based analytical models of neutron spectral fluence, kerma and absorbed dose. Phys Med Biol (2022) 67(12):125019. doi:10.1088/1361-6560/ac7377
87. Piotrowski T, Mazgaj M, Żak A, Skubalski J. Importance of atomic composition and moisture content of cement based composites in neutron radiation shielding. Proced Eng (2015) 108:616–23. doi:10.1016/j.proeng.2015.06.188
88. Reginatto M, Goldhagen P, Neumann S. Spectrum unfolding, sensitivity analysis and propagation of uncertainties with the maximum entropy deconvolution code MAXED. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (2002) 476(1):242–6. doi:10.1016/s0168-9002(01)01439-5
89. Reginatto M. What can we learn about the spectrum of high-energy stray neutron fields from Bonner sphere measurements? Radiat Meas (2009) 44(7):692–9. doi:10.1016/j.radmeas.2009.04.005
90. Wiegel B, Alevra AV, Matzke M, Schrewe UJ, Wittstock J. Spectrometry using the PTB neutron multisphere spectrometer (NEMUS) at flight altitudes and at ground level. Nucl Instrum Methods Phys Res Sect Accel Spectrometers Detect Assoc Equip (2002) 476(1):52–7. doi:10.1016/s0168-9002(01)01387-0
91. Goldhagen P, Clem JM, Wilson JW. The energy spectrum of cosmic-ray induced neutrons measured on an airplane over a wide range of altitude and latitude. Radiat Prot Dosimetry (2004) 110(1–4):387–92. doi:10.1093/rpd/nch216
92. Howell RM, Burgett EA. Secondary neutron spectrum from 250-MeV passively scattered proton therapy: measurement with an extended-range Bonner sphere system. Med Phys (2014) 41(9):092104. doi:10.1118/1.4892929
93. Dommert M, Reginatto M, Zboril M, Fiedler F, Helmbrecht S, Enghardt W, et al. Measurement of the energy spectrum of secondary neutrons in a proton therapy environment. Curr Dir Biomed Eng (2017) 3(2):83–6. doi:10.1515/cdbme-2017-0018
94. Dommert M, Reginatto M, Zbořil M, Fiedler F, Helmbrecht S, Enghardt W, et al. A bayesian approach for measurements of stray neutrons at proton therapy facilities: quantifying neutron dose uncertainty. Radiat Prot Dosimetry (2018) 180(1–4):319–23. doi:10.1093/rpd/ncx264
95. Gómez-Ros JM, Bedogni R, Domingo C, Eakins JS, Roberts N, Tanner RJ. Results of the EURADOS international comparison exercise on neutron spectra unfolding in Bonner spheres spectrometry. Radiat Meas (2022) 153:106755. doi:10.1016/j.radmeas.2022.106755
96. Petit M. Concrete modeling for neutron transport and associated sensitivity studies performed at the AMANDE-MIRCOM facility. Nucl Sci Eng (2021) 195(8):864–76. doi:10.1080/00295639.2020.1867436
97. ICRP. Conversion coefficients for use in radiological protection against external radiation. 1996. Report No.: 74.
Keywords: space radiation shielding, nuclear fragmentation, neutron spectrum, Monte Carlo, bonner sphere, spectra unfolding, MAXED
Citation: Di Chicco A, Horst F, Boscolo D, Schuy C, Weber U and Zboril M (2024) Bonner sphere measurements of high-energy neutron spectra from a 1 GeV/u 56Fe ion beam on an aluminum target and comparison to spectra obtained by Monte Carlo simulations. Front. Phys. 12:1456472. doi: 10.3389/fphy.2024.1456472
Received: 28 June 2024; Accepted: 30 August 2024;
Published: 18 September 2024.
Edited by:
Alessandro Bartoloni, National Institute of Nuclear Physics of Rome, ItalyReviewed by:
Canel Eke, Akdeniz University, TürkiyeMustafa Mohammad Rafiei, Shahid Bahonar University of Kerman, Iran
Copyright © 2024 Di Chicco, Horst, Boscolo, Schuy, Weber and Zboril. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Augusto Di Chicco, YXVndXN0by5kaS1jaGljY29AcHRiLmRl
†Present address: Felix Horst, OncoRay—National Center for Radiation Research in Oncology, Faculty of Medicine, Dresden, Germany.
 Augusto Di Chicco
Augusto Di Chicco Felix Horst
Felix Horst Daria Boscolo
Daria Boscolo Christoph Schuy
Christoph Schuy Uli Weber
Uli Weber Miroslav Zboril
Miroslav Zboril