Dynamical analysis and soliton solutions of a variety of quantum nonlinear Zakharov–Kuznetsov models via three analytical techniques

Some new types of truncated M-fractional exact soliton solutions of the two important quantum plasma physics models, extended quantum Zakharov–Kuznetsov and extended quantum nonlinear Zakharov–Kuznetsov, are successfully achieved by applying the ${\exp }_a$ function technique, the improved $(G^{\prime }/G)$-expansion technique, and the Sardar sub-equation technique. These two models have many useful applications when explaining the waves in the quantum electron-positron-ion magnetoplasmas as well as weakly nonlinear ion-acoustic waves in plasma. The obtained results are in the form of dark, bright, periodic, and other soliton solutions. The results are verified and represented by two-dimensional, three-dimensional, and contour graphs. The results are newer than the existing results in the literature due to the use of fractional derivatives. Hence, the solutions will be fruitful in future studies on these models. The solutions obtained are useful in the areas of applied physics, applied mathematics, dynamical systems, and nonlinear waves in plasmas and in dense space plasma. The applied techniques are simple, fruitful, and reliable for solving other models in mathematical physics.

1 Introduction

Many naturally occurring phenomena in various areas of science and engineering, like plasma, acoustics, chemistry, biology, and many others, are expressed in the form of fractional nonlinear partial differential models (FNLPDMs). Both exact and approximate results have been obtained by applying different techniques in the literature. For example, the efficient $(G^{\prime }/G)$-expansion method [1], the new auxiliary equation technique [2], the new direct extended algebraic scheme [3], the new form of modified Kudryashov technique [4], the modified $(G^{\prime }/G)$-expansion method [5], the generalized algebra scheme [6], etc. Exact soliton solutions of many nonlinear partial differential models (NLPDMs) have been reported in the literature, such as the fractional Biswas–Arshed model [7], fractional-order Burger’s model [8], fractional new Hamiltonian amplitude model [9], the attraction-repulsion model [10], the negative order KdV–Calogero-Bogoyavlenskii–Schiff model [11], the coupled Solow–Swan model [12], the stochastic Sasa–Satsuma model [13], etc.

Currently, exact solutions, especially soliton-like solutions, have gained much importance because this has become a special topic in nonlinear science. Soliton theory has gained importance because of the exceptional properties of soliton. A soliton maintains its shape and velocity after interaction and stability. Solitons have different forms, like dark, periodic, singular, bright, dark-bright, kink, antikink, and many others.

We utilize three distinct techniques to obtain the exact soliton solutions in our research: the ${\exp }_a$ function technique, the improved $(G^{\prime }/G)$-expansion technique, and the Sardar sub-equation technique. Various applications of these techniques are mentioned in the literature. For example, optical solitons of the Sasa–Satsuma model are attained by utilizing the ${\exp }_a$ function method [14], various optical solitons of the perturbed Gerdjikov–Ivanov model are obtained with the use of the ${\exp }_a$ function method [15], the dark soliton, bright soliton and combo optical solitons of three coupled Maccari’s model are attained [16], and periodic-singular, singular solitons, and kink solitons of (1 + 1)-dimensional Mikhailov Novikov–Wang integrable equation are obtained [17]. Various exact wave solutions of extended shallow water wave models are gained by using the improved $(G^{\prime }/G)$-expansion technique [18], some exact traveling wave solutions of the Calogero–Bogoyavlenskii–Schiff model are attained with the help of the improved $(G^{\prime }/G)$-expansion technique [19], and singular-periodic, periodic, singular, M-shaped soliton solutions of the Hirota–Ramani equation are obtained [20]. The Sardar sub-equation approach has led to the discovery of new solitons for the (2 + 1)-dimensional Sawada–Kotera (SK) equation [21]. Optical wave solutions of the Fokas–Lenells model are obtained by utilizing the Sardar sub-equation technique in [22], and some exact traveling wave solutions of the Newton–Schrödinger system are obtained in [23].

Our research models are the extended quantum nonlinear Zakharov–Kuznetsov model and the modified quantum nonlinear Zakharov–Kuznetsov model, along with a truncated M-fractional derivative. These are the important models in mathematical physics, quantum physics, and plasma physics. Both models are used to explain the ion-acoustic waves in magnetized plasma with cold ions and hot isothermal electrons, as well as in electron-positron-ion magnetoplasmas in the presence of a uniform magnetic field.

Consider the (3 + 1)-dimensional truncated M-fractional extended quantum nonlinear Zakharov–Kuznetsov model [24].

$D_{M,t}^{\alpha ,\mathrm{\Upsilon }}f+\left({\theta }_{1}f+{\theta }_2{f}^2\right)D_{M,z}^{\alpha ,\mathrm{\Upsilon }}f+{\theta }_3{D}_{M,3z}^{3\alpha ,\mathrm{\Upsilon }}f+{\theta }_4{D}_{M,z}^{\alpha ,\mathrm{\Upsilon }}\left(D_{M,2x}^{2\alpha ,\mathrm{\Upsilon }}+D_{M,2y}^{2\alpha ,\mathrm{\Upsilon }}\right)f=0.(1)$

This model is used for ion-acoustic waves in a magnetized plasma containing cold ions and hot isothermal electrons. Different techniques have been used for Equation 1 without fractional derivatives to obtain the exact wave solutions, such as soliton solutions, and some other wave solutions have been achieved by applying the extended simplest equation technique [25]. Periodic and traveling wave solutions have been attained by using bifurcation theory [26]. Many exact wave solutions have been gained by utilizing the sine-Gordon expansion technique and the $1/G^{\prime }$ expansion technique in [27]. Different types of soliton solutions have been achieved by applying the ansatz techniques in [28], and periodic, dark, and kink-type soliton solutions have been gained by using the generalized Kudryashov and modified Khater methods in [29].

Consider the (3 + 1)-dimensional truncated M-fractional modified quantum nonlinear Zakharov–Kuznetsov model [24]:

$16\left(D_{M,t}^{\alpha ,\mathrm{\Upsilon }}f-\tau D_{M,x}^{\alpha ,\mathrm{\Upsilon }}f\right)+30\sqrt{f}{D}_{M,x}^{\alpha ,\mathrm{\Upsilon }}f+D_{M,3x}^{3\alpha ,\mathrm{\Upsilon }}f+D_{M,x}^{\alpha ,\mathrm{\Upsilon }}\left(D_{M,y}^{2\alpha ,\mathrm{\Upsilon }}+D_{M,z}^{2\alpha ,\mathrm{\Upsilon }}\right)f=0.(2)$

Equation 2 has been solved by different techniques in the literature: various soliton wave solutions have been gained by using the modified Sardar sub-equation method [30], and new kinds of soliton solutions, including the 1-soliton solution, have been obtained by applying the improved $\tan (\varphi /2)$-expansion technique and generalized $(G^{\prime }/G)$-expansion technique [31], dark and dark-bright optical wave solutions have been attained with the help of modified $\exp (-\vartheta (\sigma ))$-expansion technique [32], and quasiperiodic and multi-periodic traveling wave solutions are obtained by first and second simple methods [33].

The basic purpose of our research work is to determine the novel exact soliton solutions to the truncated M-fractional extended quantum nonlinear Zakharov–Kuznetsov model and the truncated M-fractional modified quantum nonlinear Zakharov–Kuznetsov model by applying the ${\exp }_a$ function technique, the improved $(G^{\prime }/G)$-expansion technique, and the Sardar sub-equation technique.

The motivation of this paper is to determine the new types of exact soliton solutions of the extended quantum nonlinear Zakharov–Kuznetsov model and the modified quantum nonlinear Zakharov–Kuznetsov model, along with a truncated M-fractional derivative. The effect of this derivative is also explained. Truncated M-fractional derivatives fulfill the characteristics of both integer and fractional derivatives. This definition of derivative provides more valuable results than other definitions. In addition, this definition of a fractional derivative provides results that are close to the numerical results. The obtained solutions are useful in the many areas of mathematical physics, especially quantum physics and plasma physics, to explain the ion-acoustic waves in magnetized plasma having cold ions and hot isothermal electrons, as well as in electron-positron-ion magnetoplasmas in the presence of a uniform magnetic field.

First, all three utilized techniques convert the nonlinear fractional partial differential equations into nonlinear ordinary differential equations (ODEs) and then solve the obtained ODEs. The methods explore the different types of solutions. The ${\exp }_a$ function technique provides the dark-singular, dark solitary wave, and others. The improved $(G^{\prime }/G)$-expansion technique explores the trigonometric and hyperbolic function solutions, and the Sardar sub-equation technique also exhibits the trigonometric and hyperbolic functions, but this method provides the solutions of different varieties. The first two methods are applicable for all types of fractional partial differential equations, but the Sardar sub-equation technique is not applicable for those ODEs in which the first derivative of function appears with a single power and as a product. All three techniques are useful for our models. These methods can be easily used to solve other nonlinear fractional partial differential equations.

The paper consists of the following sections:

Section 2 provides a complete description of the utilized techniques.

Section 3 addresses the mathematical treatments of our concerned models.

Section 4 addresses the applications of the techniques to obtain the exact soliton solutions of the extended quantum nonlinear Zakharov–Kuznetsov model.

Section 5 addresses the applications of the techniques to obtain the exact soliton solutions of the modified quantum nonlinear Zakharov–Kuznetsov model.

Section 6 provides graphical representations of some of the solutions.

Section 7 provides the physical analysis of the solutions.

Section 8 discusses the results.

Section 9 is the conclusion of our research work.

1.1 Truncated M-fractional derivative (TMFD)

Definition: consider $v(x):[0,\infty )\to \mathfrak{R}$; therefore, a truncated M-fractional derivative of $v$ of order $ϵ$ [34]

$D_{M,x}^{\alpha ,\mathrm{\Upsilon }}v\left(x\right)=\underset{\tau \to 0}{\lim }\frac{v\left(x{E}_{\mathrm{\Upsilon }}\left(\tau x^{1-\alpha }\right)\right)-v\left(x\right)}{\tau },\alpha \in \left(\mathrm{0,1}\right],\mathrm{\Upsilon }>0,$

here, $E_{\alpha }(.)$ represents a truncated Mittag–Leffler function [35]:

$E_{\mathrm{\Upsilon }}\left(z\right)={\displaystyle \sum _{j=0}^i}\frac{z^j}{\mathrm{\Gamma }\left(\mathrm{\Upsilon }j+1\right)},\mathrm{\Upsilon }>0\text{\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}}z\in \mathbf{C}.$

Properties: Consider that a, b $\in \mathfrak{R}$, and $g,f$ are $\alpha -$ differentiable at a point $x>0$, according to [34]:

$\left(c\right)\left(a\right)D_{M,x}^{\alpha ,\mathrm{\Upsilon }}\left(ag\left(x\right)+bf\left(x\right)\right)=a{D}_{M,x}^{\alpha ,\mathrm{\Upsilon }}g\left(x\right)+b{D}_{M,x}^{ϵ,\mathrm{\Upsilon }}f\left(x\right),$

$\left(b\right)D_{M,x}^{\alpha ,\mathrm{\Upsilon }}\left(g\left(x\right).f\left(x\right)\right)=g\left(x\right)D_{M,x}^{\alpha ,\mathrm{\Upsilon }}f\left(x\right)+f\left(x\right)D_{M,x}^{\alpha ,\mathrm{\Upsilon }}g\left(x\right),$

$\left(c\right)D_{M,x}^{\alpha ,\mathrm{\Upsilon }}\left(\frac{g\left(x\right)}{f\left(x\right)}\right)=\frac{f\left(x\right)D_{M,x}^{\alpha ,\mathrm{\Upsilon }}g\left(x\right)-g\left(x\right)D_{M,x}^{\alpha ,\mathrm{\Upsilon }}f\left(x\right)}{{\left(f\left(x\right)\right)}^2},$

$\left(d\right)D_{M,x}^{\alpha ,\mathrm{\Upsilon }}\left(B\right)=0,\text{\hspace{0.17em}\hspace{0.17em}where\hspace{0.17em}}B\text{\hspace{0.17em}is\hspace{0.17em}a\hspace{0.17em}constant},$

$\left(e\right)D_{M,x}^{\alpha ,\mathrm{\Upsilon }}g\left(x\right)=\frac{x^{1-\alpha }}{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}\frac{dg\left(x\right)}{dx}.$

The truncated M-fractional derivative (TMD) is a fractional derivative that was introduced by Sousa and de Oliveira [36]. This derivative has expunged the obstacles with the existing derivatives. This definition of derivative is used for various models, such as the Shynaray-IIA equation [37], the Cahn–Allen equation [38], and many more.

2 Techniques

2.1 ${\exp }_a$ function technique

Some of the main points of this method are given as:

Considering a nonlinear PDE:

$S\left(h,h^2{h}_x,h_t,h_{xx},h_{tt},h_{xt},\dots \right)=0.(3)$

Equation 3 reduces into a nonlinear ODE:

$T\left(H,\delta H^2{H}^{\prime },\delta H^{\prime },\dots ,\right)=0.(4)$

By applying the given wave transformations:

$h\left(x,t\right)=H\left(\xi \right),\xi =\delta x+\lambda t.$

Assuming the results for Equation 4 are [39–42]:

$H\left(\xi \right)=\frac{{\alpha }_0+{\alpha }_1{d}^{\xi }+\dots +{\alpha }_m{d}^{m\xi }}{{\beta }_0+{\beta }_1{d}^{\xi }+\cdots +{\beta }_m{d}^{m\xi }},d\ne \mathrm{0,1}.(5)$

Here, ${\alpha }_j$ and ${\beta }_j(0\le j\le m)$ are undetermined. The positive integer $m$ is found by using the homogenous balance approach in Equation 4. Substituting Equation 5 into Equation 4 yields:

$\wp \left(d^{\xi }\right)={\ell }_0+{\ell }_1{d}^{\xi }+\cdots +{\ell }_t{d}^{t\xi }=0.(6)$

Inserting ${\ell }_j(0\le j\le t)$ into Equation 6 and taking zero, a set of equations is attained:

${\ell }_j=0,herej=0,\dots ,t.$

After obtaining solutions, one can get exact solitons for Equation 3.

2.2 Improved $(G^{\prime }/G)-$expansion technique

We provide the main steps of this technique here [43].

Step 1. Let’s take a nonlinear fractional PDE.

$G\left(q,D_{M,t}^{\alpha ,\beta }q,q^2{q}_{\gamma },q_{\theta },q_{\theta \theta },q_{\gamma \gamma },q_{\gamma \theta },\dots \right)=0.(7)$

Step 2. Consider the following transformation:

$q\left(\gamma ,\theta ,t\right)=Q\left(\eta \right),\eta =\gamma -\upsilon \theta +\frac{\mathrm{\Gamma }\left(\beta +1\right)}{\alpha }\left(\kappa t^{\alpha }\right).(8)$

where $\nu$ and $\kappa$ represent the parameters. Inserting Equation 8 into Equation 7 yields the nonlinear ODE:

$H\left(Q,Q^2{Q}^{\prime },Q^{″},\dots \right)=0.(9)$

Step 3. Consider the solutions of Equation 9 shown as

$Q\left(\eta \right)={\displaystyle \sum _{j=0}^m}{\alpha }_j{\left(\frac{G^{\prime }\left(\eta \right)}{G\left(\eta \right)}\right)}^j.(10)$

In Equation 10, ${\alpha }_0$ and ${\alpha }_j,(j=\mathrm{1,2,3},\dots ,m)$ are undetermined. By using a homogenous balance scheme in Equation (9), we gain $m$.

The function $G=G(\eta )$ satisfies the equation:

$G{G}^{″}-{\kappa }_1{G}^2-{\kappa }_{2}G{G}^{\prime }-{\kappa }_3{\left(G^{\prime }\right)}^2=0.(11)$

where ${\kappa }_1$, ${\kappa }_2$, and ${\kappa }_3$ are constants.

Step 4. Assume Equation (11), we have solutions shown as:

Case 1: if ${\kappa }_2\ne 0$ and $\pi ={\kappa }_2^2+4{\kappa }_1-4{\kappa }_1{\kappa }_3>0$, we have

$\frac{G^{\prime }\left(\eta \right)}{G\left(\eta \right)}=\frac{{\kappa }_2\sqrt{\pi }\left(C_1\exp \left(\frac{1}{2}\eta \sqrt{\pi }\right)+C_2\exp \left(\frac{1}{2}\eta \left(-\sqrt{\pi }\right)\right)\right)}{\left(2\left(1-{\kappa }_3\right)\right)\left(C_1\exp \left(\frac{1}{2}\eta \sqrt{\pi }\right)-C_2\exp \left(\frac{1}{2}\eta \left(-\sqrt{\pi }\right)\right)\right)}+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}.$

Case 2: if ${\kappa }_2\ne 0$ and $\pi ={\kappa }_2^2+4{\kappa }_1-4{\kappa }_1{\kappa }_3<0$, we have

$\frac{G^{\prime }\left(\eta \right)}{G\left(\eta \right)}=\frac{{\kappa }_2\sqrt{-\left(\pi \right)}\left(C_1\iota \cos \left(\frac{1}{2}\eta \sqrt{-\left(\pi \right)}\right)-C_2\sin \left(\frac{1}{2}\eta \sqrt{-\left(\pi \right)}\right)\right)}{\left(2\left(1-{\kappa }_3\right)\right)\left(C_1\iota \sin \left(\frac{1}{2}\eta \sqrt{-\left(\pi \right)}\right)+C_2\cos \left(\frac{1}{2}\eta \sqrt{-\left(\pi \right)}\right)\right)}+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}.$

Case 3: if ${\kappa }_2=0$ and ${\kappa }_1-{\kappa }_1{\kappa }_3\ge 0$, we have

$\frac{G^{\prime }\left(\eta \right)}{G\left(\eta \right)}=\frac{\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\left(C_2\sin \left(\eta \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\right)+C_1\cos \left(\eta \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\right)\right)}{\left(1-{\kappa }_3\right)\left(C_1\sin \left(\eta \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\right)-C_2\cos \left(\eta \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\right)\right)}.$

Case 4: if ${\kappa }_2=0$ and ${\kappa }_1-{\kappa }_1{\kappa }_3<0$, we have

$\frac{G^{\prime }\left(\eta \right)}{G\left(\eta \right)}=\frac{\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\left(C_1\iota \cosh \left(\eta \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\right)-C_2\sinh \left(\eta \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\right)\right)}{\left(1-{\kappa }_3\right)\left(C_1\iota \sinh \left(\eta \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\right)-C_2\cosh \left(\eta \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\right)\right)}.$

Here, $\iota =\sqrt{-1}$, where ${\kappa }_1$, ${\kappa }_2$, ${\kappa }_3$, $C_1$, and $C_2$ are the constants.

Step 5. Substitute Equation 10 and Equation 11 into Equation 9 and collect the coefficients of every order of $\left(\frac{G^{\prime }(\eta )}{G(\eta )}\right)$. By setting each coefficient equal to zero, we obtain the system of algebraic equations involving $\nu$, $\kappa$, ${\alpha }_j,(j=\mathrm{0,1,2},\dots ,m)$, and other parameters.

Step 6. Solve the above system of algebraic equations with the Mathematica tool.

Step 7. By putting the solutions obtained above into Equation 10, we get the trigonometric, hyperbolic trigonometric, and rational function soliton type results of the nonlinear partial differential (NLPD) equation shown in Equation 7.

2.3 Sardar sub-equation technique

This technique [44] considers the nonlinear fractional PDE:

$J\left(g,g_z,g_{zz},g_{zt},g{g}_{tt},g_{\mathit{zzt}},\dots \right)=0,$

where $g=g(z,t)$ is a wave profile. Substituting a wave transformation of the form

$g\left(z,t\right)=G\left(\zeta \right),\zeta =\lambda z+\mu t$

yields the following form of a nonlinear ordinary differential equation (NLODE):

$Y\left(G,G^{″},G{G}^{″},G^{\prime }{G}^2,\dots \right)=0.(12)$

Consider a solution of Equation 12 in the form:

$G\left(\zeta \right)={\displaystyle \sum _{i=0}^m}{b}_i{\psi }^i\left(\zeta \right),(13)$

where $\psi (\zeta )$ satisfies the ODE given by

${\psi }^{\prime }\left(\zeta \right)=\sqrt{\sigma +\kappa {\psi }^2\left(\zeta \right)+{\psi }^4\left(\zeta \right)},(14)$

in which $\sigma$ and $\kappa$ are parameters.

Next, we proceed by first substituting Equations 13 and 14 into Equation 12 and sum the ${\psi }^i$ term. Then, we set the coefficients of similar powers equal to zero to deduce a system of equations in $b_i$, $\lambda$, and $\mu$. By manipulating this system, we can determine the unknown parameters.

Case 1: if $\kappa >0$ and $\sigma =0$, we have

${\psi }_1^{\pm }=\pm \sqrt{-\kappa rs}{\text{sech}}_{rs}\left(\sqrt{\kappa }\zeta \right),$

${\psi }_2^{\pm }=\pm \sqrt{\kappa rs}{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}_{rs}\left(\sqrt{\kappa }\zeta \right),$

where $sec{h}_{rs}(\zeta )=\frac{2}{r{e}^{\zeta }+s{e}^{-\zeta }}$, ${\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}_{rs}(\zeta )=\frac{2}{r{e}^{\zeta }-s{e}^{-\zeta }}$.

Case 2: if $\kappa <0$ and $\sigma =0$, we have

${\psi }_3^{\pm }=\pm \sqrt{-\kappa rs}{\sec }_{rs}\left(\sqrt{-\kappa }\zeta \right),$

${\psi }_4^{\pm }=\pm \sqrt{-\kappa rs}{\csc }_{rs}\left(\sqrt{-\kappa }\zeta \right),$

where ${\sec }_{rs}(\zeta )=\frac{2}{r{e}^{\iota \zeta }+s{e}^{-\iota \zeta }}$, ${\csc }_{rs}(\zeta )=\frac{2\iota }{r{e}^{\iota \zeta }-s{e}^{-\iota \zeta }}$.

Case 3: if $\kappa <0$ and $\sigma =\frac{{\kappa }^2}{4}$, we have

${\psi }_5^{\pm }=\pm \sqrt{-\frac{\kappa }{2}}{\tanh }_{rs}\left(\sqrt{-\frac{\kappa }{2}}\zeta \right),$

${\psi }_6^{\pm }=\pm \sqrt{-\frac{\kappa }{2}}{\coth }_{rs}\left(\sqrt{-\frac{\kappa }{2}}\zeta \right),$

${\psi }_7^{\pm }=\pm \sqrt{-\frac{\kappa }{2}}\left({\tanh }_{rs}\left(\sqrt{-2\kappa }\zeta \right)\pm \iota \sqrt{rs}{\text{sech}}_{rs}\left(\sqrt{-2\kappa }\zeta \right)\right),$

${\psi }_8^{\pm }=\pm \sqrt{-\frac{\kappa }{2}}\left({\coth }_{rs}\left(\sqrt{-2\kappa }\zeta \right)\pm \sqrt{ab}{\text{csch}}_{rs}\left(\sqrt{-2\kappa }\zeta \right)\right),$

${\psi }_9^{\pm }=\pm \sqrt{-\frac{\kappa }{8}}\left({\tanh }_{rs}\left(\sqrt{-\frac{\kappa }{8}}\zeta \right)+{\coth }_{rs}\left(\sqrt{-\frac{\kappa }{8}}\zeta \right)\right),$

where ${\tanh }_{rs}(\zeta )=\frac{r{e}^{\zeta }-s{e}^{-\zeta }}{r{e}^{\zeta }+s{e}^{-\zeta }}$, ${\coth }_{rs}(\zeta )=\frac{r{e}^{\zeta }+s{e}^{-\zeta }}{r{e}^{\zeta }-s{e}^{-\zeta }}$.

Case 4: if $\kappa >0$ and $\sigma =\frac{{\kappa }^2}{4}$, we have

${\psi }_{10}^{\pm }=\pm \sqrt{\frac{\kappa }{2}}{\tan }_{rs}\left(\sqrt{\frac{\kappa }{2}}\zeta \right),$

${\psi }_{11}^{\pm }=\pm \sqrt{\frac{\kappa }{2}}{\cot }_{rs}\left(\sqrt{\frac{\kappa }{2}}\zeta \right),$

${\psi }_{12}^{\pm }=\pm \sqrt{\frac{\kappa }{2}}\left({\tan }_{rs}\left(\sqrt{2\kappa }\zeta \right)\pm \sqrt{rs}{\sec }_{rs}\left(\sqrt{2\kappa }\zeta \right)\right),$

${\psi }_{13}^{\pm }=\pm \sqrt{\frac{\kappa }{2}}\left({\cot }_{rs}\left(\sqrt{2\kappa }\zeta \right)\pm \sqrt{rs}{\csc }_{rs}\left(\sqrt{2\kappa }\zeta \right)\right),$

${\psi }_{14}^{\pm }=\pm \sqrt{\frac{\kappa }{8}}\left({\tan }_{rs}\left(\sqrt{\frac{\kappa }{8}}\zeta \right)+{\cot }_{rs}\left(\sqrt{\frac{\kappa }{8}}\zeta \right)\right),$

where ${\tan }_{rs}(\zeta )=-\iota \frac{r{e}^{\iota \zeta }-s{e}^{-\iota \zeta }}{r{e}^{\iota \zeta }+s{e}^{-\iota \zeta }}$, ${\cot }_{rs}(\zeta )=\iota \frac{r{e}^{\iota \zeta }+s{e}^{-\iota \zeta }}{r{e}^{\iota \zeta }-s{e}^{-\iota \zeta }}$.

The advantage of this technique is that it provides many different kinds of solitons, such as dark, bright, singular, periodic singular, combined dark-singular, and combined dark-bright solitons. This method has simple calculations, high accuracy, and low computational effort and provides a variety of solution forms.

3 Mathematical analysis of concerning models

3.1 Extended QNLZK model

Considering the following wave transformation:

$f\left(x,y,z,t\right)=F\left(\xi \right),\xi =\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right),(15)$

where a, b, c, and $\lambda$ are the real constants. Using Equation 15 in Equation 1, we attain a nonlinear ODE after one-time integration and neglecting the integration constant:

$6F^{″}\left(c{\theta }_4\left(a^2+b^2\right)+c^3{\theta }_3\right)+2c{F}^3{\theta }_2+3c{F}^2{\theta }_1-6F\lambda =0.(16)$

By applying the homogenous balance technique to Equation 16, we get $m=1$.

3.2 Modified QNLZK model

By applying the transformation given in Equation 15 to Equation 2, we attain the following nonlinear ODE after one-time integration and neglecting the integration constant:

$30a{F}^{\frac{3}{2}}+a\left(a^2+b^2+c^2\right)F^{″}-16F\left(\tau a+\lambda \right)=0.(17)$

Consider the new transformation to retrieve the closed-form solutions:

$G=\sqrt{F}.(18)$

By using Equation 18 in Equation 17, we gain

$a\left(a^2+b^2+c^2\right)\left(G{G}^{″}+{\left(G^{\prime }\right)}^2\right)+10a{G}^3-8G^2\left(a\tau +\lambda \right)=0.(19)$

By balancing the ${(G^{\prime })}^2$ and $G^3$, we attain $m=2$. Now, we will solve Equation 16 and Equation 19 using the three aforementioned techniques.

4 Exact soliton solutions of the extended QNLZK model

4.1 By the ${\exp }_a$ function method

Equation 5 transforms into given form for $m=1$:

$H\left(\xi \right)=\frac{{\alpha }_0+{\alpha }_1{d}^{\xi }}{{\beta }_0+{\beta }_1{d}^{\xi }},(20)$

where ${\alpha }_0$, ${\alpha }_1$, ${\beta }_0$, and ${\beta }_1$ are unknowns. A set of equations is acquired by entering Equation 20 into Equation 16 and setting the coefficients of each power and constant term to 0. Using Mathematica, we discover:

Set 1.

$\left\{{\alpha }_0=-\frac{{\beta }_0{\theta }_1}{{\theta }_2},{\alpha }_1=0,\lambda =-\frac{c{\theta }_1^2}{6{\theta }_2},a=\mp \frac{\sqrt{-6{\theta }_2{\log }^2\left(d\right)\left(b^2{\theta }_4+c^2{\theta }_3\right)-{\theta }_1^2}}{\sqrt{6}\sqrt{{\theta }_2}\sqrt{{\theta }_4}\log \left(d\right)}\right\}.(21)$

$f\left(x,y,z,t\right)=-\frac{{\beta }_0{\theta }_1}{{\theta }_2\left({\beta }_0+{\beta }_1{d}^{\left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }+\frac{c{\theta }_1^2}{6{\theta }_2}{t}^{\alpha }\right)\right)}\right)},(22)$

where “a” is given in Equation 21.

Set 2.

$\left\{{\alpha }_0=0,{\alpha }_1=-\frac{{\beta }_1{\theta }_1}{{\theta }_2},\lambda =-\frac{c{\theta }_1^2}{6{\theta }_2},a=\mp \frac{\sqrt{-6{\theta }_2{\log }^2\left(d\right)\left(b^2{\theta }_4+c^2{\theta }_3\right)-{\theta }_1^2}}{\sqrt{6}\sqrt{{\theta }_2}\sqrt{{\theta }_4}\log \left(d\right)}\right\},$

$f\left(x,y,z,t\right)=-\frac{{\beta }_1{\theta }_1{d}^{\left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }+\frac{c{\theta }_1^2}{6{\theta }_2}{t}^{\alpha }\right)\right)}}{{\theta }_2\left({\beta }_0+{\beta }_1{d}^{\left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }+\frac{c{\theta }_1^2}{6{\theta }_2}{t}^{\alpha }\right)\right)}\right)},$

where “a” is given in Equation 21.

4.2 By the improved $(G^{\prime }/G)$-expansion technique

For $m=1$, Equation 10 reduces to:

$F\left(\xi \right)={\alpha }_0+{\alpha }_1\left(\frac{G^{\prime }\left(\xi \right)}{G\left(\xi \right)}\right).(23)$

Here, ${\alpha }_0$ and ${\alpha }_1$ are unknowns.

By substituting Equation 23 and Equation 11 into Equation 16, we can collect the coefficients of each power of $(\frac{G^{\prime }(\xi )}{G(\xi )})$. We obtain a system of equations by setting them equal to 0. By solving the obtained system using Mathematica software, we obtain the following solution sets:

Set 1.

$\begin{array}{l}\hfill \left\{{\alpha }_0=\frac{\sqrt{{\theta }_1^2{\kappa }_2^2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+{\theta }_1\left(4{\kappa }_1\left({\kappa }_3-1\right)-{\kappa }_2^2\right)}{2{\theta }_2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)},{\alpha }_1=\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{{\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)}},\right.\\ \hfill \left.\lambda =-\frac{c{\theta }_1^2}{6{\theta }_2},a=\mp \frac{\sqrt{6{\theta }_2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)\left(b^2{\theta }_4+c^2{\theta }_3\right)+{\theta }_1^2}}{\sqrt{6}\sqrt{{\theta }_2{\theta }_4\left(4{\kappa }_1\left({\kappa }_3-1\right)-{\kappa }_2^2\right)}}\right\},\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\frac{\sqrt{{\theta }_1^2{\kappa }_2^2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+{\theta }_1\left(4{\kappa }_1\left({\kappa }_3-1\right)-{\kappa }_2^2\right)}{2{\theta }_2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+\left(\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{{\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)}}\right)\\ \hfill \left(\left({\kappa }_2\sqrt{\pi }\left(C_1\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\pi }\right)+C_2\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left.\lambda t^{\alpha }\right)\left(-\sqrt{\pi }\right)\right)\right)\right)/\left(\left(2\left(1-{\kappa }_3\right)\right)\left(C_1\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\pi }\right)-C_2\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\right.\right.\right.\\ \hfill \left.\left.\left.\left.\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\left(-\sqrt{\pi }\right)\right)\right)\right)+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\frac{\sqrt{{\theta }_1^2{\kappa }_2^2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+{\theta }_1\left(4{\kappa }_1\left({\kappa }_3-1\right)-{\kappa }_2^2\right)}{2{\theta }_2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+\left(\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{{\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)}}\right)\\ \hfill \left(\left({\kappa }_2\sqrt{-\pi }\left(C_1\iota \cos \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)-C_2\sin \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left.-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)\right)\right)/\left(\left(2\left(1-{\kappa }_3\right)\right)\left(C_1\iota \sin \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)+\right.\right.\\ \hfill \left.\left.\left.C_2\cos \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)\right)\right)+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}\right),\end{array}$

where “a” and $\lambda$ are given in Equation 23.

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\frac{{\theta }_1\left(4{\kappa }_1{\kappa }_3-1\right)}{2{\theta }_2\left(-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+\left(\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{-4{\kappa }_1\left({\kappa }_3-1\right)}}\right)\left(\left(\sqrt{\mathrm{\Theta }}\left(C_2\sin \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left.b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)+C_1\cos \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)\right)\right)/\left(\left(1-\right.\right.\\ \hfill \left.{\kappa }_3\right)\times \left(C_1\sin \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)-C_2\cos \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+\right.\right.\right.\\ \hfill \left.\left.\left.\left.\left.c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)\right)\right)\right),\end{array}(24)$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\frac{{\theta }_{1}4{\kappa }_1\left({\kappa }_3-1\right)}{2{\theta }_2\left(-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+\left(\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{-4{\kappa }_1\left({\kappa }_3-1\right)}}\right)\left(\left(\sqrt{-\mathrm{\Theta }}\left(C_1\iota \cosh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left.b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\mathrm{\Theta }}\right)-C_2\sinh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\mathrm{\Theta }}\right)\right)\right)/\left(\left(1-\right.\right.\\ \hfill {\kappa }_3)\times \left(C_1\iota \sinh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\mathrm{\Theta }}\right)-C_2\cosh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+\right.\right.\right.\\ \hfill \left.\left.\left.\left.\left.c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\mathrm{\Theta }}\right)\right)\right)\right),\end{array}$

where $a=\mp \frac{\sqrt{6{\theta }_2\left(-4{\kappa }_1\left({\kappa }_3-1\right)\right)\left(b^2{\theta }_4+c^2{\theta }_3\right)+{\theta }_1^2}}{\sqrt{6}\sqrt{{\theta }_2{\theta }_4\left(4{\kappa }_1\left({\kappa }_3-1\right)\right)}}$ and $\lambda$ are given in Equation 23 and $\mathrm{\Theta }={\kappa }_1(1-{\kappa }_3)$.

Set 2.

$\begin{array}{l}\hfill \left\{{\alpha }_0=\frac{\sqrt{{\theta }_1^2{\kappa }_2^2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+{\theta }_1\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}{2{\theta }_2\left(4{\kappa }_1\left({\kappa }_3-1\right)-{\kappa }_2^2\right)},{\alpha }_1=-\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{{\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)}},\right.\\ \hfill \lambda \left.=-\frac{c{\theta }_1^2}{6{\theta }_2},a=\mp \frac{\sqrt{6{\theta }_2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)\left(b^2{\theta }_4+c^2{\theta }_3\right)+{\theta }_1^2}}{\sqrt{6}\sqrt{{\theta }_2{\theta }_4\left(4{\kappa }_1\left({\kappa }_3-1\right)-{\kappa }_2^2\right)}}\right\},\end{array}(25)$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\frac{\sqrt{{\theta }_1^2{\kappa }_2^2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+{\theta }_1\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}{2{\theta }_2\left(4{\kappa }_1\left({\kappa }_3-1\right)-{\kappa }_2^2\right)}-\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{{\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)}}\\ \hfill \times \left(\left({\kappa }_2\sqrt{\pi }\left(C_1\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\pi }\right)+C_2\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left.c{z}^{\alpha }-\lambda t^{\alpha }\right)\left(-\sqrt{\pi }\right)\right)\right)\right)/\times \left(\left(2\left(1-{\kappa }_3\right)\right)\left(C_1\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\pi }\right)-\right.\right.\\ \hfill \left.\left.\left.C_2\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\left(-\sqrt{\pi }\right)\right)\right)\right)+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\frac{\sqrt{{\theta }_1^2{\kappa }_2^2\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}+{\theta }_1\left({\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)\right)}{2{\theta }_2\left(4{\kappa }_1\left({\kappa }_3-1\right)-{\kappa }_2^2\right)}-\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{{\kappa }_2^2-4{\kappa }_1\left({\kappa }_3-1\right)}}\\ \hfill \times \left(\left({\kappa }_2\sqrt{-\pi }\left(C_1\iota \cos \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)-C_2\sin \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left.c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)\right)\right)/\times \left(\left(2\left(1-{\kappa }_3\right)\right)\left(C_1\iota \sin \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)\right.\right.\\ \hfill +\left.\left.\left.C_2\cos \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)\right)\right)+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}\right),\end{array}$

where “a” and $\lambda$ are given in Equation 25.

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{-4{\kappa }_1\left({\kappa }_3-1\right)}}\left(\left(\sqrt{\mathrm{\Theta }}\left(C_2\sin \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)\right.\right.\right.\\ \hfill \left.\left.+C_1\cos \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)\right)\right)/\left(\left(1-{\kappa }_3\right)\left(C_1\sin \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left.\left.\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)-C_2\cos \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)\right)\right)\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{{\theta }_1\left({\kappa }_3-1\right)}{{\theta }_2\sqrt{-4{\kappa }_1\left({\kappa }_3-1\right)}}\left(\left(\sqrt{-\mathrm{\Theta }}\left(C_1\iota \cosh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left.\lambda t^{\alpha }\right)\sqrt{-\mathrm{\Theta }}\right)-C_2\sinh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\mathrm{\Theta }}\right)\right)\right)/\left(\left(1-{\kappa }_3\right)\left(C_1\iota \sinh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\right.\right.\right.\\ \hfill \left.\left.\left.\left.\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\mathrm{\Theta }}\right)-C_2\cosh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\mathrm{\Theta }}\right)\right)\right)\right),\end{array}$

where $a=\mp \frac{\sqrt{6{\theta }_2\left(-4{\kappa }_1\left({\kappa }_3-1\right)\right)\left(b^2{\theta }_4+c^2{\theta }_3\right)+{\theta }_1^2}}{\sqrt{6}\sqrt{{\theta }_2{\theta }_4\left(4{\kappa }_1\left({\kappa }_3-1\right)\right)}}$ and $\lambda$ are given in Equation 23 and $\mathrm{\Theta }={\kappa }_1(1-{\kappa }_3)$.

4.3 By the Sardar sub-equation technique

For $m=1$, Equation 13 reduces to the form:

$F\left(\xi \right)=b_0+b_1\psi \left(\xi \right).(26)$

Here, $b_0$ and $b_1$ are the unknowns. Inserting Equation 26 into Equation 16 by using Equation 14, we can collect the coefficients of each power of $\psi (\xi )$. We get a system of equations after setting them equal to 0. By solving the gained system with the help of Mathematica software, we obtain the solution:

Set 1.

$\left\{b_0=-\frac{{\theta }_1}{2{\theta }_2},b_1=-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }},\lambda =-\frac{c{\theta }_1^2}{6{\theta }_2},a=\mp \frac{\sqrt{{\theta }_1^2-12{\theta }_2\kappa \left(b^2{\theta }_4+c^2{\theta }_3\right)}}{2\sqrt{3}\sqrt{{\theta }_2}\sqrt{{\theta }_4}\sqrt{\kappa }}\right\}.$

Case 1:

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\kappa rs}sec{h}_{rs}\left(\sqrt{\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),(27)$

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\kappa rs}{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}_{rs}\left(\sqrt{\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right).$

Case 2:

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\kappa rs}{\sec }_{rs}\left(\sqrt{-\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\kappa rs}{\csc }_{rs}\left(\sqrt{-\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right).$

Case 3:

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{2}}{\tanh }_{rs}\left(\sqrt{-\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{2}}{\coth }_{rs}\left(\sqrt{-\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{2}}\left({\tanh }_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.\pm \iota \sqrt{rs}sec{h}_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{2}}\left({\coth }_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.\pm \sqrt{rs}csc{h}_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{8}}\left({\tanh }_{rs}\left(\sqrt{-\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.+{\coth }_{rs}\left(\sqrt{-\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right).\end{array}$

Case 4:

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{2}}{\tan }_{rs}\left(\sqrt{\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{2}}{\cot }_{rs}\left(\sqrt{\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{2}}\left({\tan }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.\pm \sqrt{rs}{\sec }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{2}}\left({\cot }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.\pm \sqrt{ab}{\csc }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}-\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{8}}\left({\tan }_{rs}\left(\sqrt{\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.+{\cot }_{rs}\left(\sqrt{\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right).\end{array}$

Set 2.

$\left\{b_0=-\frac{{\theta }_1}{2{\theta }_2},b_1=\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }},\lambda =-\frac{c{\theta }_1^2}{6{\theta }_2},a=\mp \frac{\sqrt{{\theta }_1^2-12{\theta }_2\kappa \left(b^2{\theta }_4+c^2{\theta }_3\right)}}{2\sqrt{3}\sqrt{{\theta }_2}\sqrt{{\theta }_4}\sqrt{\kappa }}\right\}.$

Case 1:

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\kappa rs}sec{h}_{rs}\left(\sqrt{\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\kappa rs}{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}_{rs}\left(\sqrt{\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right).$

Case 2:

$f\left(x,y,y,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\kappa rs}{\sec }_{rs}\left(\sqrt{-\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\kappa rs}{\csc }_{rs}\left(\sqrt{-\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right).$

Case 3:

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{2}}{\tanh }_{rs}\left(\sqrt{-\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{2}}{\coth }_{rs}\left(\sqrt{-\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{2}}\left({\tanh }_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.\pm \iota \sqrt{rs}sec{h}_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{2}}\left({\coth }_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.\pm \sqrt{rs}csc{h}_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{-\frac{\kappa }{8}}\left({\tanh }_{rs}\left(\sqrt{-\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.+{\coth }_{rs}\left(\sqrt{-\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right).\end{array}$

Case 4:

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{2}}{\tan }_{rs}\left(\sqrt{\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{2}}{\cot }_{rs}\left(\sqrt{\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right),$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{2}}\left({\tan }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.\pm \sqrt{rs}{\sec }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{2}}\left({\cot }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.\pm \sqrt{rs}{\csc }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right),\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=-\frac{{\theta }_1}{2{\theta }_2}+\frac{i{\theta }_1}{\sqrt{2}{\theta }_2\sqrt{\kappa }}\left(\pm \sqrt{\frac{\kappa }{8}}\left({\tan }_{rs}\left(\sqrt{\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right.\right.\\ \hfill \left.\left.+{\cot }_{rs}\left(\sqrt{\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right).\end{array}$

5 Exact soliton solutions of the modified QNLZK model

5.1 By ${\exp }_a$ function method

Equation 5 transforms into the given form for $m=2$:

$F\left(\xi \right)=\frac{{\alpha }_0+{\alpha }_1{d}^{\xi }+{\alpha }_2{d}^{2\xi }}{{\beta }_0+{\beta }_1{d}^{\xi }+{\beta }_2{d}^{2\xi }},(28)$

where ${\alpha }_0$, ${\alpha }_1$,${\alpha }_2$, ${\beta }_0$, ${\beta }_1$, and ${\beta }_2$ are unknowns. A set of equations is acquired by entering Equation 28 into Equation 19 and setting the coefficients of each power and constant term to 0. Using Mathematica, we discover:

Set

$\begin{array}{l}\hfill \left\{{\alpha }_0=0,{\alpha }_2=0,{\beta }_1=\frac{2{\alpha }_1}{{\log }^2\left(d\right)\left(a^2+b^2+c^2\right)},{\beta }_2=\frac{{\alpha }_1^2}{{\beta }_0{\log }^4\left(d\right){\left(a^2+b^2+c^2\right)}^2},\right.\\ \hfill \left.\lambda =\frac{a}{4}\left({\log }^2\left(d\right)\left(a^2+b^2+c^2\right)-4\tau \right)\right\},\end{array}$

$f\left(x,y,z,t\right)={\left(\frac{{\alpha }_1{\beta }_0{\log }^4\left(d\right){\left(a^2+b^2+c^2\right)}^2{d}^{\left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)}}{{\left({\beta }_0{\log }^2\left(d\right)\left(a^2+b^2+c^2\right)+{\alpha }_1{d}^{\left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)}\right)}^2}\right)}^2.(29)$

5.2 By improved $(G^{\prime }/G)$-expansion technique

For $m=2$, Equation 10 reduces to:

$F\left(\xi \right)={\alpha }_0+{\alpha }_1\left(\frac{G^{\prime }\left(\xi \right)}{G\left(\xi \right)}\right)+{\alpha }_2{\left(\frac{G^{\prime }\left(\xi \right)}{G\left(\xi \right)}\right)}^2.(30)$

Here, ${\alpha }_0$, ${\alpha }_1$, and ${\alpha }_2$ are unknowns.

Substitute Equation 30 and Equation 11 into Equation 19 and collect the coefficients of each power of $(\frac{G^{\prime }(\xi )}{G(\xi )})$. We get a series of equations by setting them equal to 0. After solving the system using the Mathematica tool, we obtain the following solution set:

Set

$\begin{array}{l}\hfill \left\{{\alpha }_0=-{\kappa }_1\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right),{\alpha }_1=-{\kappa }_2\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right),{\alpha }_2=-{\left({\kappa }_3-1\right)}^2\left(a^2+b^2+c^2\right),\right.\\ \hfill \left.\lambda =\frac{1}{4}a\left({\kappa }_2^2\left(a^2+b^2+c^2\right)-4{\kappa }_1\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right)-4\tau \right)\right\},\end{array}(31)$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-{\kappa }_1\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right)-{\kappa }_2\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right)\left(\left({\kappa }_2\sqrt{\pi }\left(C_1\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\pi }\right)+C_2\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\left(-\sqrt{\pi }\right)\right)\right)\right)/\left(\left(2\left(1-{\kappa }_3\right)\right)\right.\\ \hfill \left(C_1\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\pi }\right)-C_2\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }\right.\right.\right.\\ \hfill \left.\left.\left.\left.\left.-\lambda t^{\alpha }\right)\left(-\sqrt{\pi }\right)\right)\right)\right)+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}\right)-{\left({\kappa }_3-1\right)}^2\left(a^2+b^2+c^2\right)\times \left(\left({\kappa }_2\sqrt{\pi }\left(C_1\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.-\lambda t^{\alpha }\right)\sqrt{\pi })+C_2\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\left(-\sqrt{\pi }\right)\right)\right)\right)/\left(\left(2\left(1-{\kappa }_3\right)\right)\left(C_1\right.\right.\\ \hfill \exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\pi }\right)-C_2\exp \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\right.\right.\\ \hfill {\left.{\left.\left.\left.\left.\left.\lambda t^{\alpha }\right)\left(-\sqrt{\pi }\right)\right)\right)\right)+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}\right)}^2\right)}^2,\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-{\kappa }_1\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right)-{\kappa }_2\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right)\left(\left({\kappa }_2\sqrt{-\pi }\left(C_1\iota \right.\right.\right.\right.\\ \hfill \left.\left.\cos \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)-C_2\sin \left(\frac{1}{2}\eta \sqrt{-\left(\pi \right)}\right)\right)\right)/\left(\left(2\left(1-{\kappa }_3\right)\right)\right.\\ \hfill \left(C_1\iota \sin \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)+C_2\cos \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }\right.\right.\right.\\ \hfill \left.\left.\left.\left.\left.-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)\right)\right)+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}\right)-{\left({\kappa }_3-1\right)}^2\left(a^2+b^2+c^2\right)\times \left(\left({\kappa }_2\sqrt{-\pi }\left(C_1\iota \cos \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+\right.\right.\right.\right.\right.\\ \hfill \left.\left.\left.\left.c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)-C_2\sin \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)\right)\right)/\left(\left(2\left(1-{\kappa }_3\right)\right)\left(C_1\right.\right.\\ \hfill \iota \sin \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{-\pi }\right)+C_2\cos \left(\frac{1}{2}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\right.\right.\\ \hfill {\left.{\left.\left.\left.\left.\left.\lambda t^{\alpha }\right)\sqrt{-\pi }\right)\right)\right)+\frac{{\kappa }_2}{2\left(1-{\kappa }_3\right)}\right)}^2\right)}^2,\end{array}$

where $\lambda$ is given in Equation 31.

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-{\kappa }_1\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right)-{\left({\kappa }_3-1\right)}^2\left(a^2+b^2+c^2\right)\left(\left(\sqrt{\mathrm{\Theta }}\left(C_2\right.\right.\right.\right.\\ \hfill \sin \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)+C_1\cos \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }\right.\right.\\ \hfill \left.\left.\left.\left.-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)\right)\right)/\left(\left(1-{\kappa }_3\right)\left(C_1\sin \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)-C_2\right.\right.\\ \hfill {\left.{\left.\left.\left.\cos \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)\right)\right)\right)}^2\right)}^2,\end{array}(32)$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-{\kappa }_1\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right)-{\left({\kappa }_3-1\right)}^2\left(a^2+b^2+c^2\right)\left(\left(\sqrt{\mathrm{\Theta }}\left(C_1\iota \right.\right.\right.\right.\\ \hfill \cosh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)-C_2\sinh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }\right.\right.\\ \hfill \left.\left.\left.\left.-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)\right)\right)/\left(\left(1-{\kappa }_3\right)\left(C_1\iota \sinh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)-C_2\right.\right.\\ \hfill {\left.{\left.\left.\left.\cosh \left(\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\sqrt{\mathrm{\Theta }}\right)\right)\right)\right)}^2\right)}^2,\end{array}(33)$

where $\lambda =\frac{1}{4}a\left(-4{\kappa }_1\left({\kappa }_3-1\right)\left(a^2+b^2+c^2\right)-4\tau \right)$ and $\mathrm{\Theta }=-{\kappa }_1+{\kappa }_1{\kappa }_3$.

5.3 By the Sardar sub-equation technique

For $m=2$, Equation 13 reduces to the form:

$F\left(\xi \right)=b_0+b_1\psi \left(\xi \right)+b_2\psi {\left(\xi \right)}^2,(33)$

where $b_0$, $b_1$, and $b_2$ are the unknowns. Equation 33 is inserted into Equation 19 by using Equation 14, and the coefficients of each power of $\psi (\xi )$ are summed up. After setting them equal to 0, we obtain a system of equations. We obtain the solution by solving the system with the help of Mathematica software.

Set 1.

$\left\{b_0=0,b_1=0,b_2=-\left(a^2+b^2+c^2\right),\lambda =a\left(a^2\kappa +b^2\kappa +c^2\kappa -\tau \right),\sigma =0\right\}.(34)$

Case 1:

$f\left(x,y,z,t\right)={\left(-\left(a^2+b^2+c^2\right){\left(\pm \sqrt{-\kappa rs}sec{h}_{rs}\left(\sqrt{\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)}^2\right)}^2,(35)$

$f\left(x,y,z,t\right)={\left(-\left(a^2+b^2+c^2\right){\left(\pm \sqrt{\kappa rs}{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}_{rs}\left(\sqrt{\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)}^2\right)}^2.$

Case 2:

$f\left(x,y,z,t\right)={\left(-\left(a^2+b^2+c^2\right){\left(\pm \sqrt{-\kappa rs}{\sec }_{rs}\left(\sqrt{-\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)}^2\right)}^2,$

$f\left(x,y,z,t\right)={\left(-\left(a^2+b^2+c^2\right){\left(\pm \sqrt{-\kappa rs}{\csc }_{rs}\left(\sqrt{-\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)}^2\right)}^2,$

where $\lambda$ is given in Equation 34.

Set 2.

$\left\{b_0=-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right),b_1=0,b_2=-\left(a^2+b^2+c^2\right),\lambda =-\frac{1}{2}a\left(a^2\kappa +b^2\kappa +c^2\kappa +2\tau \right),\sigma =\frac{{\kappa }^2}{4}\right\}.(36)$

Case 3:

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{-\frac{\kappa }{2}}{\tanh }_{rs}\left(\sqrt{-\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\right.\right.\right.\\ \hfill {\left.{\left.\left.\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)}^2\right)}^2,\end{array}(37)$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{-\frac{\kappa }{2}}{\coth }_{rs}\left(\sqrt{-\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\right.\right.\right.\\ \hfill {\left.{\left.\left.\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)}^2\right)}^2,\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{-\frac{\kappa }{2}}\left({\tanh }_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }\right.\right.\right.\right.\right.\left.\left.+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\\ \hfill {\left.{\left.\left.\pm \iota \sqrt{rs}sec{h}_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right)}^2\right)}^2,\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{-\frac{\kappa }{2}}\left({\coth }_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }\right.\right.\right.\right.\right.\left.\left.+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\\ \hfill {\left.{\left.\left.\pm \sqrt{rs}csc{h}_{rs}\left(\sqrt{-2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right)}^2\right)}^2,\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{-\frac{\kappa }{8}}\left({\tanh }_{rs}\left(\sqrt{-\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }\right.\right.\right.\right.\right.\left.\left.+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\\ \hfill {\left.{\left.\left.+{\coth }_{rs}\left(\sqrt{-\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right)}^2\right)}^2.\end{array}$

Case 4:

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{\frac{\kappa }{2}}{\tan }_{rs}\left(\sqrt{\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }\right.\right.\right.\right.\\ \hfill {\left.{\left.\left.\left.+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)}^2\right)}^2,\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{\frac{\kappa }{2}}{\cot }_{rs}\left(\sqrt{\frac{\kappa }{2}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }\right.\right.\right.\right.\\ \hfill {\left.{\left.\left.\left.+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)}^2\right)}^2,\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{\frac{\kappa }{2}}\left({\tan }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }\right.\right.\right.\right.\right.\left.\left.+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\\ \hfill {\left.{\left.\left.\pm \sqrt{rs}{\sec }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right)}^2\right)}^2,\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{\frac{\kappa }{2}}\left({\cot }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }\right.\right.\right.\right.\right.\left.\left.+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\\ \hfill {\left.{\left.\left.\pm \sqrt{rs}{\csc }_{rs}\left(\sqrt{2\kappa }\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right)}^2\right)}^2,\end{array}$

$\begin{array}{l}\hfill f\left(x,y,z,t\right)=\left(-\frac{1}{2}\kappa \left(a^2+b^2+c^2\right)-\left(a^2+b^2+c^2\right)\left(\pm \sqrt{\frac{\kappa }{8}}\left({\tan }_{rs}\left(\sqrt{\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }\right.\right.\right.\right.\right.\left.\left.+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\\ \hfill {\left.{\left.\left.+{\cot }_{rs}\left(\sqrt{\frac{\kappa }{8}}\frac{\mathrm{\Gamma }\left(\mathrm{\Upsilon }+1\right)}{\alpha }\left(a{x}^{\alpha }+b{y}^{\alpha }+c{z}^{\alpha }-\lambda t^{\alpha }\right)\right)\right)\right)}^2\right)}^2,\end{array}$

where $\lambda$ is given in Equation 36.

6 Graphical representation

Here, we represent some of our solutions with two-dimensional, three-dimensional, and contour graphs. The effect of the fractional derivative is also shown by graphs for $\alpha =0.6$, $\alpha =0.8$, and $\alpha =1$.

7 Physical explanation

Here, we present the physical significance of the abovementioned solutions to the truncated M-fractional extended nonlinear quantum Zakharov–Kuznetsov model (ENLQZKE) and the modified nonlinear quantum Zakharov–Kuznetsov model (MNLQZKE) by plotting these solutions in 2-D at different time levels and different values of $\alpha$, 3-D, and contour. We found interesting behaviors depending on the values of the free constants in the solutions, as shown in the figures. Figure 1 represents the dark-singular soliton solution for the values $d=3$, ${\beta }_0=-0.3$, ${\beta }_0=-0.05$, $\mathrm{\Upsilon }=1$, ${\theta }_1=-1$, ${\theta }_2=2$, ${\theta }_3=1$, ${\theta }_4=3$, $b=1$, $c=1$, $y=1$, $z=1$, and $-10<x<10$. Figure 2 represents the periodic wave solution for the values ${\kappa }_1=2$, ${\kappa }_3=0.5$, $\mathrm{\Upsilon }=1$, ${\theta }_1=1$, ${\theta }_2=2$, ${\theta }_3=1$, ${\theta }_4=3$, $b=1$, $c=1$, $y=1$, $z=1,C_1=1$, $C_2=1$, and $-3<x<3$. Figure 3 represents the bright wave solution for the values $\kappa =1$, $\mathrm{\Upsilon }=1$, ${\theta }_1=1$, ${\theta }_2=1$, ${\theta }_3=1$, ${\theta }_4=3$, $b=1$, $c=0.5$, $y=1$, $z=1$, and $-7<x<7$. Figure 4 represents the dark solitary wave solution for the values $d=3$, $\tau =0.8$, ${\alpha }_1=1$, ${\beta }_0=1$, $\mathrm{\Upsilon }=1$, $a=1$, $b=1$, $c=1$, $y=1$, $z=1$, and $-4<x<4$. Figure 5 represents the periodic wave solution for the values $\tau =1$, ${\kappa }_1=0.05$, ${\kappa }_3=0.1$, $\mathrm{\Upsilon }=1$, $a=1$, $b=1$, $c=1$, $y=1$, $z=1$, $C_1=1$, $C_2=-1.01$, and $-1<x<1$. Figure 6 represents the bright wave solution for the values $\tau =-0.01$, $\kappa =1$, $\mathrm{\Upsilon }=1$, $a=0.5$, $b=-0.01$, $c=0.05$, $y=1$, $z=1$, and $-2<x<2$. Figure 7 represents the dark wave solution for the values $\tau =0.1$, $\kappa =-1$, $\mathrm{\Upsilon }=1$, $a=-0.4$, $b=-0.01$, $c=0.01$, $y=1$, $z=1$, and $-1<x<1$.

Figure 1

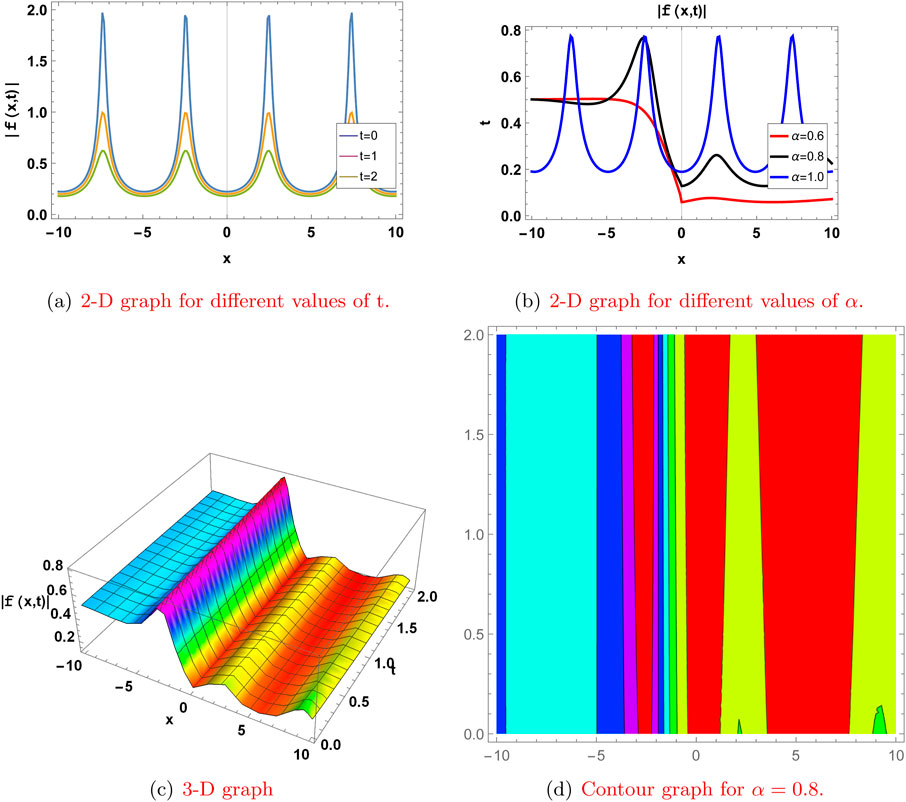
Figure 1. Graph for $|f(x,y,z,t)|$ function represents Equation 22 in two-dimensional, three-dimensional, and contour graphs at $d=3$, ${\beta }_0=-0.3$, ${\beta }_0=-0.05$, $\mathrm{\Upsilon }=1$, ${\theta }_1=-1$, ${\theta }_2=2$, ${\theta }_3=1$, ${\theta }_4=3$, $b=1$, $c=1$, $y=1$, $z=1$, and $-10<x<10$. (A) 2-D graph for different values of t. (B) 2-D graph for different values of $\alpha$. (C) 3-D graph. (D) Contour graph for $\alpha =0.8$.

Figure 2

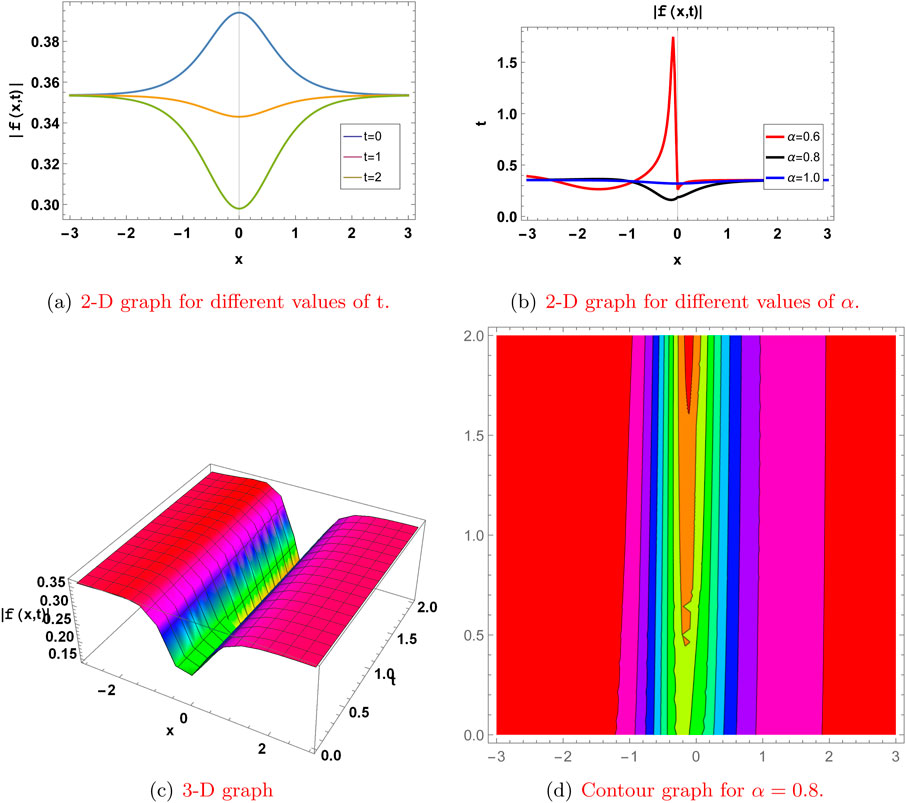
Figure 2. Graph for the $|f(x,y,z,t)|$ function represents Equation 24 in two-dimensional, three-dimensional, and contour graphs at ${\kappa }_1=2$, ${\kappa }_3=0.5$, $\mathrm{\Upsilon }=1$, ${\theta }_1=1$, ${\theta }_2=2$, ${\theta }_3=1$, ${\theta }_4=3$, $b=1$, $c=1$, $y=1$, $z=1,C_1=1$, $C_2=1$, and $-3<x<3$. (A) 2-D graph for different values of t. (B) 2-D graph for different values of $\alpha$. (C) 3-D graph. (D) Contour graph for $\alpha =0.8$.

Figure 3

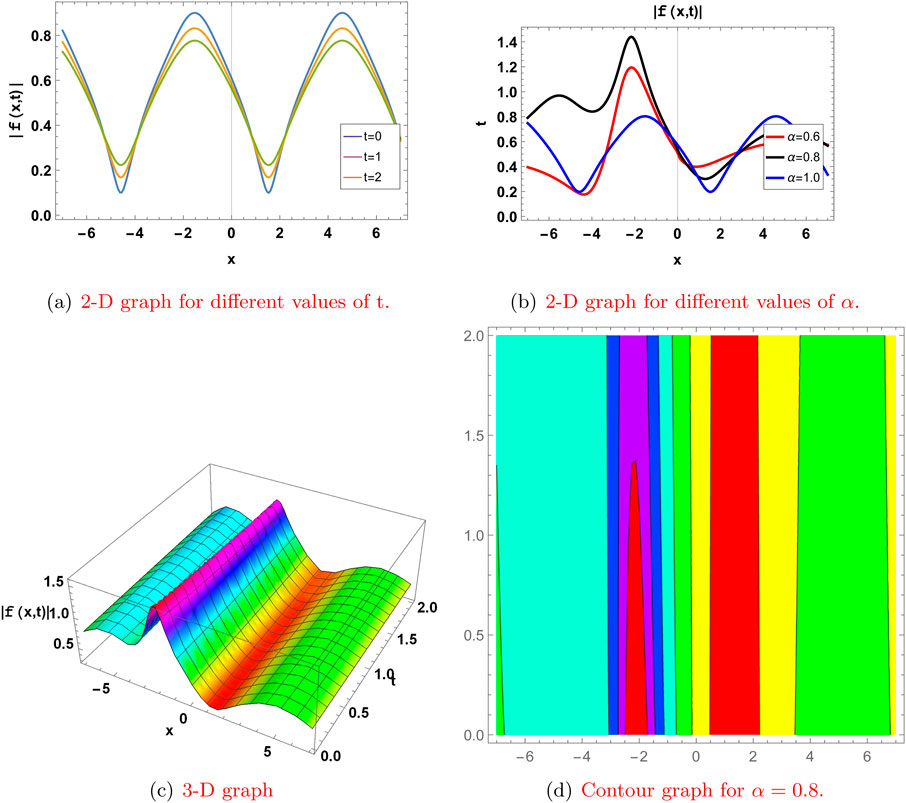
Figure 3. Graph for $|f(x,y,z,t)|$ function represents Equation 27 in two-dimensional, three-dimensional, and contour graphs at $\kappa =1$, $\mathrm{\Upsilon }=1$, ${\theta }_1=1$, ${\theta }_2=1$, ${\theta }_3=1$, ${\theta }_4=3$, $b=1$, $c=0.5$, $y=1$, $z=1$, and $-7<x<7$. (A) 2-D graph for different values of t. (B) 2-D graph for different values of $\alpha$. (C) 3-D graph. (D) Contour graph for $\alpha =0.8$.

Figure 4

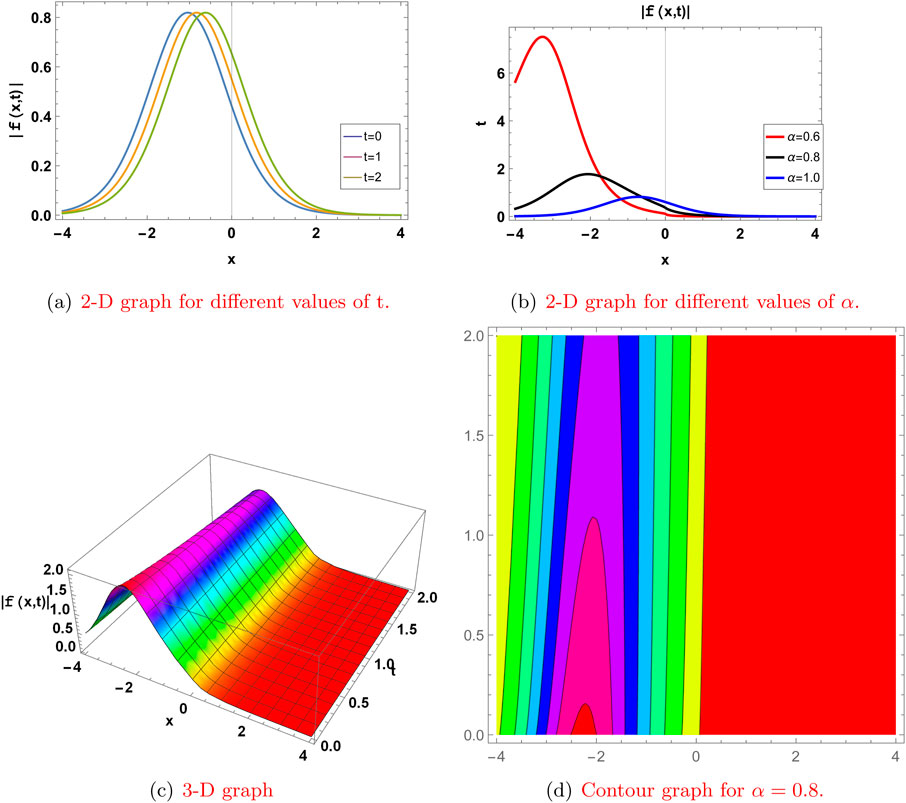
Figure 4. Graph for the $|f(x,y,z,t)|$ function represents Equation 29 in two-dimensional, three-dimensional, and contour graphs at $d=3$, $\tau =0.8$, ${\alpha }_1=1$, ${\beta }_0=1$, $\mathrm{\Upsilon }=1$, $a=1$, $b=1$, $c=1$, $y=1$, $z=1$, and $-4<x<4$. (A) 2-D graph for different values of t. (B) 2-D graph for different values of $\alpha$. (C) 3-D graph. (D) Contour graph for $\alpha =0.8$.

Figure 5

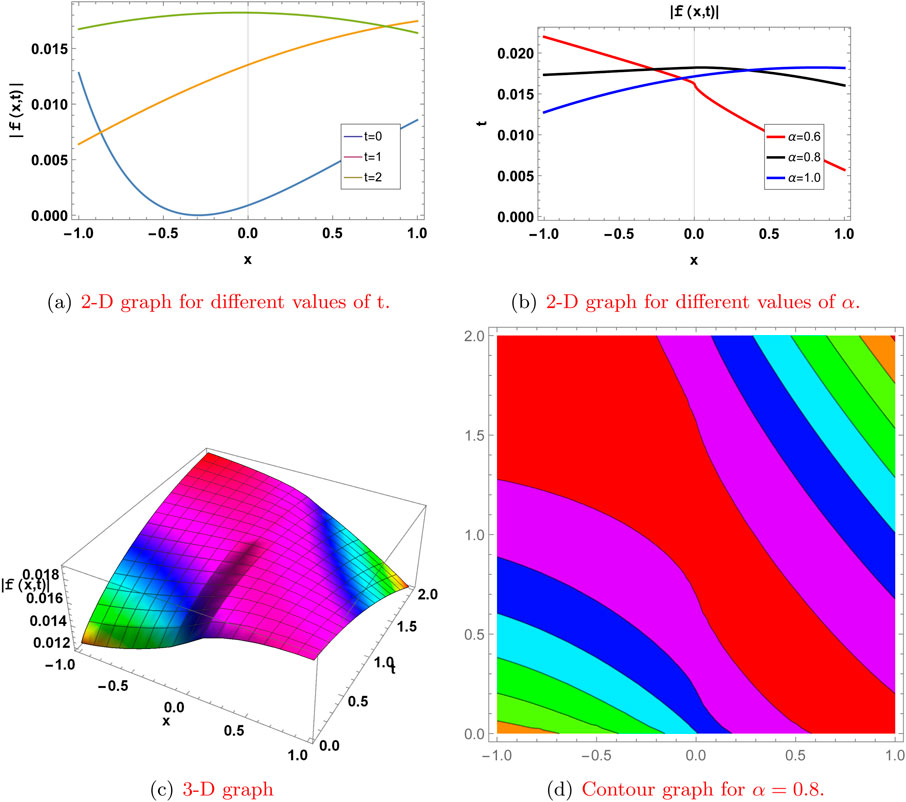
Figure 5. Graph for $|f(x,y,z,t)|$ function represents Equation 32 in two-dimensional, three-dimensional, and contour graphs at $\tau =1$, ${\kappa }_1=0.05$, ${\kappa }_3=0.1$, $\mathrm{\Upsilon }=1$, $a=1$, $b=1$, $c=1$, $y=1$, $z=1$, $C_1=1$, $C_2=-1.01$, and $-1<x<1$. (A) 2-D graph for different values of t. (B) 2-D graph for different values of $\alpha$. (C) 3-D graph. (D) Contour graph for $\alpha =0.8$.

Figure 6

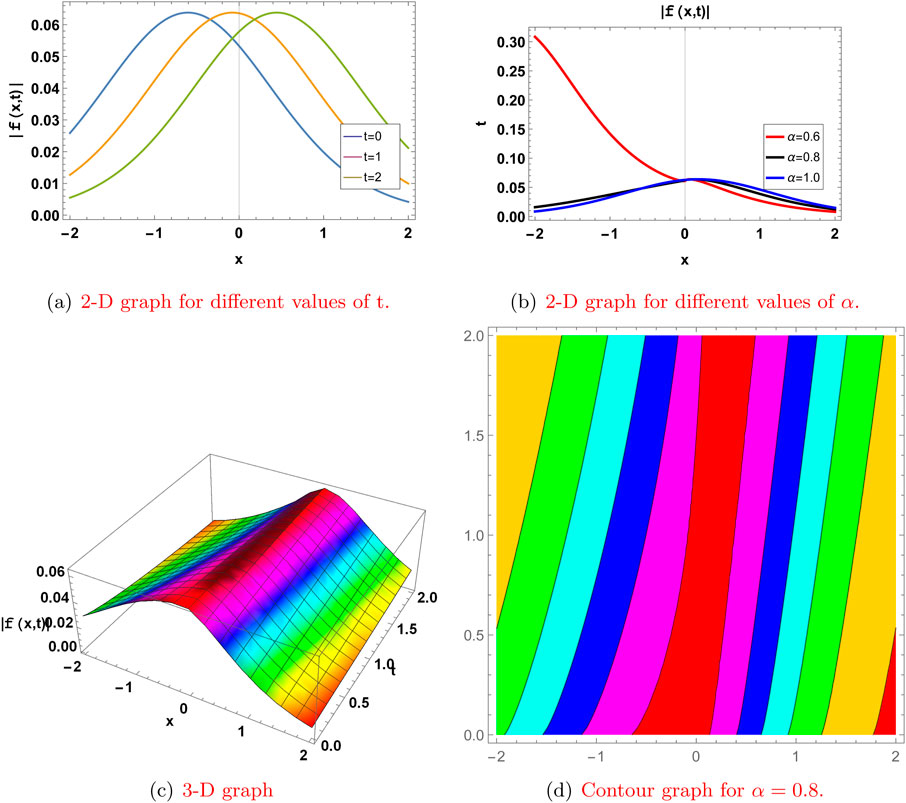
Figure 6. Graph for $|f(x,y,z,t)|$ function represents Equation (35) in two-dimensional, three-dimensional, and contour graphs at $\tau =-0.01$, $\kappa =1$, $\mathrm{\Upsilon }=1$, $a=0.5$, $b=-0.01$, $c=0.05$, $y=1$, $z=1$, and $-2<x<2$. (A) 2-D graph for different values of t. (B) 2-D graph for different values of $\alpha$. (C) 3-D graph. (D) Contour graph for $\alpha =0.8$.

Figure 7

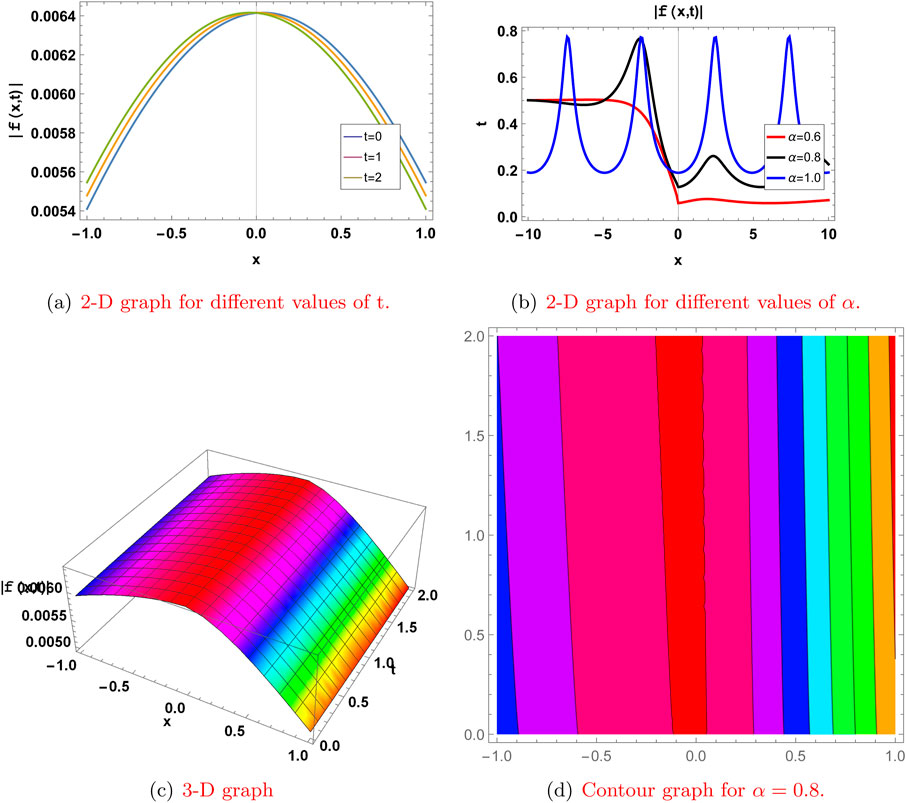
Figure 7. Graph for the $|f(x,y,z,t)|$ function represents Equation 37 in two-dimensional, three-dimensional, and contour graphs at $\tau =0.1$, $\kappa =-1$, $\mathrm{\Upsilon }=1$, $a=-0.4$, $b=-0.01$, $c=0.01$, $y=1$, $z=1$, and $-1<x<1$. (A) 2-D graph for different values of t. (B) 2-D graph for different values of α. (C) 3-D graph. (D) Contour graph for α = 0.8.

The results of this work encourage further future discussion in various branches of science, especially in quantum plasma physics.

8 Results and discussion

Here, we will compare the existing results and the results we obtained from the concerned model. Different techniques have been used for nonlinear extended and modified quantum Zakharov–Kuznetsov equations without fractional derivatives to obtain the exact wave solutions. Some solitary wave solutions are obtained in [24]; soliton and some other wave solutions have been achieved by applying the extended simplest equation technique [25]; periodic and traveling wave solutions have been attained by using bifurcation theory [26]. Many exact wave solutions have been gained by utilizing the sine-Gordon expansion technique and the $1/G^{\prime }$ expansion technique in [27]. Kink-antikink soliton, traveling wave, solitary wave, periodic wave, and dark-bright soliton solutions are obtained by using the extended modified rational expansion method in [45]. Soliton solutions in different forms, such as bell and anti-bell periodic, dark soliton, bright soliton, bright and dark solitary wave in periodic form, are obtained by applying the modified extended direct algebraic technique in [46]. Distinct exact solutions are obtained by utilizing the $(G^{\prime }/G^2)$-expansion method and the modified Kudryashov method in [47]. However, we consider the model in the truncated M-fractional derivative that has not been used previously in the literature. Furthermore, we utilize the ${\exp }_a$ function technique to obtain the rational wave solutions. The improved $(G^{\prime }/G)$-expansion technique is utilized to obtain the periodic and kink soliton solutions, while the Sardar sub-equation technique is used to gain the singular, dark, bright, dark-bright, and many other exact soliton solutions of the model. The obtained solutions have many applications in different branches of physics and other applied sciences.

9 Conclusion

We have succeeded in attaining novel exact soliton solutions to the extended nonlinear quantum Zakharov–Kuznetsov model (ENLQZKE) and the modified nonlinear quantum Zakharov–Kuznetsov model (MNLQZKE) with a truncated M-fractional derivative. For this purpose, we utilize the ${\exp }_a$ functional, improved $(G^{\prime }/G)$-expansion, and Sardar sub-equation techniques. The solutions contained the trigonometric, hyperbolic trigonometric, and exponential functions. The achieved solutions are verified using Mathematica software by putting the solutions back into the concerned equation. Our results are newer and closer to the numerical solutions than the existing solutions of the models in the literature. Some of the obtained solutions are also represented by two-dimensional, three-dimensional, and contour graphs. The obtained solutions are useful in the areas of applied physics, applied mathematics, dynamical systems, nonlinear waves in plasmas [48], and dense space plasma [49]. The methods applied are simple and useful for nonlinear fractional partial differential equations. This work may be helpful for future research on the concerned model and other related models. Nonlinear fractional partial differential equations are a good way to represent any naturally occurring phenomenon in applied science and engineering.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

AZ: investigation, methodology, validation, and writing–original draft. AA: conceptualization, formal analysis, funding acquisition, software, and writing–original draft. AB: formal analysis, investigation, project administration, supervision, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2024/01/921063).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Aniqa A, Ahmad J. Soliton solution of fractional Sharma-Tasso-Olever equation via an efficient (G′/G)-expansion method. Ain Shams Eng J (2022) 13(1):101528. doi:10.1016/j.asej.2021.06.014

CrossRef Full Text | Google Scholar

2. Riaz MB, Wojciechowski A, Oros GI, Rahman RU. Soliton solutions and sensitive analysis of modified equal-width equation using fractional operators. Symmetry (2022) 14(8):1731. doi:10.3390/sym14081731

CrossRef Full Text | Google Scholar

3. Faridi WA, Bakar MA, Akgül A, El-Rahman A, Din E, Sayed M. Exact fractional soliton solutions of thin-film ferroelectric material equation by analytical approaches. Alexandria Eng J (2023) 78:483–97. doi:10.1016/j.aej.2023.07.049

CrossRef Full Text | Google Scholar

4. Roshid MM, Rahman MM, Bashar MH, Hossain MM, Mannaf MA, Roshid HO. Dynamical simulation of wave solutions for the M-fractional Lonngren-wave equation using two distinct methods. Alexandria Eng J (2023) 81:460–8. doi:10.1016/j.aej.2023.09.045

CrossRef Full Text | Google Scholar

5. Alam MN, Aktar SHAMIMA, Tunç C. New solitary wave structures to time fractional biological population model. J Math Anal (2020) 11(3):59–70.

Google Scholar

6. Yu J. Some new exact wave solutions for the ZK-BBM equation. J Appl Sci Eng (2022) 26(7):981–8.

Google Scholar

7. Akbulut A, Islam SMR. Study on the Biswas–Arshed equation with the beta time derivative. Int J Appl Comput Mathematics (2022) 8(4):167. doi:10.1007/s40819-022-01350-0

CrossRef Full Text | Google Scholar

8. Uddin M, Arefin MA, Akbar MA, Inc M. New explicit solutions to the fractional-order burgers’ equation. Math Probl Eng (2021) 2021:1–11. doi:10.1155/2021/6698028

CrossRef Full Text | Google Scholar

9. Raheel M, Zafar A, Cevikel A, Rezazadeh H, Bekir A. Exact wave solutions of truncated M-fractional new Hamiltonian amplitude equation through two analytical techniques. Int J Mod Phys B (2023) 37(01):2350003. doi:10.1142/s0217979223500030

CrossRef Full Text | Google Scholar

10. Wu J, Huang Y. Boundedness of solutions for an attraction–repulsion model with indirect signal production. Mathematics (2024) 12(8):1143. doi:10.3390/math12081143

CrossRef Full Text | Google Scholar

11. Gu M, Peng C, Li Z. Traveling wave solution of (3+ 1)-dimensional negative-order KdV-Calogero-Bogoyavlenskii-Schiff equation. AIMS Mathematics (2024) 9(3):6699–708. doi:10.3934/math.2024326

CrossRef Full Text | Google Scholar

12. Wu J, Yang Z. Global existence and boundedness of chemotaxis-fluid equations to the coupled Solow-Swan model. AIMS Mathematics (2023) 8(8):17914–42. doi:10.3934/math.2023912

CrossRef Full Text | Google Scholar

13. Liu C, Li Z. The dynamical behavior analysis and the traveling wave solutions of the stochastic sasa–satsuma equation. Qual Theor Dynamical Syst (2024) 23(4):157. doi:10.1007/s12346-024-01022-y

CrossRef Full Text | Google Scholar

14. Raheel M, Zafar A, Tala-Tebue E. Optical solitons to time-fractional Sasa-Satsuma higher-order non-linear Schrödinger equation via three analytical techniques. Opt Quan Electronics (2023) 55(4):307. doi:10.1007/s11082-023-04565-7

CrossRef Full Text | Google Scholar

15. Zafar A, Ali KK, Raheel M, Sooppy K, Bekir A, Abundant M. fractional optical solitons to the pertubed Gerdjikov–Ivanov equation treating the mathematical nonlinear optics. Opt Quan Electronics (2022) 54(1):25. doi:10.1007/s11082-021-03394-w

CrossRef Full Text | Google Scholar

16. Chen Z, Manafian J, Raheel M, Zafar A, Alsaikhan F, Abotaleb M. Extracting the exact solitons of time-fractional three coupled nonlinear Maccari’s system with complex form via four different methods. Results Phys (2022) 36:105400. doi:10.1016/j.rinp.2022.105400

CrossRef Full Text | Google Scholar

17. Eslami M, Matinfar M, Asghari Y, Rezazadeh H, Abduridha SAJ. Diverse exact soliton solutions for three distinct equations with conformable derivatives via $$exp_{a}$$ function technique. Opt Quan Electronics (2024) 56(5):846. doi:10.1007/s11082-024-06518-0

CrossRef Full Text | Google Scholar

18. Hawlader F, Kumar D. A variety of exact analytical solutions of extended shallow water wave equations via improved (G′/G)-expansion method. Int J Phys Res (2017) 5(1):21–7.

CrossRef Full Text | Google Scholar

19. Shakeel M, Mohyud-Din ST, Tauseef S. Improved (G′/G)-expansion and extended tanh methods for (2+ 1)-dimensional Calogero–Bogoyavlenskii–Schiff equation. Alexandria Eng J (2015) 54(1):27–33. doi:10.1016/j.aej.2014.11.003

CrossRef Full Text | Google Scholar

20. Behera S. Optical solitons for the Hirota–Ramani equation via improved (G′/G)-expansion method. Mod Phys Lett B (2024):2450403. doi:10.1142/S0217984924504037

CrossRef Full Text | Google Scholar

21. Debin K, Rezazadeh H, Ullah N, Vahidi J, Tariq KU, Akinyemi L. New soliton wave solutions of a (2+ 1)-dimensional Sawada-Kotera equation. J Ocean Eng Sci (2022) 8:527–32. doi:10.1016/j.joes.2022.03.007

CrossRef Full Text | Google Scholar

22. Cinar M, Secer A, Ozisik M, Bayram M. Derivation of optical solitons of dimensionless Fokas-Lenells equation with perturbation term using Sardar sub-equation method. Opt Quan Electronics (2022) 54(7):402. doi:10.1007/s11082-022-03819-0

CrossRef Full Text | Google Scholar

23. Chahlaoui Y, Butt AR, Abbas H, Bekir A. Novel exact traveling wave solutions of Newton-Schrödinger system using Nucci reduction and Sardar sub-equation methods. Physica Scripta (2024) 99(8):085227. doi:10.1088/1402-4896/ad604c

CrossRef Full Text | Google Scholar

24. Areshi M, Seadawy AR, Ali A, AlJohani AF, Alharbi W, Alharbi AF. Construction of solitary wave solutions to the (3+ 1)-dimensional nonlinear extended and modified quantum Zakharov–Kuznetsov equations arising in quantum plasma physics. Symmetry (2023) 15(1):248. doi:10.3390/sym15010248

CrossRef Full Text | Google Scholar

25. Zayed EME, Shohib RMA, Al-Nowehy A-G. On solving the (3+ 1)-dimensional NLEQZK equation and the (3+ 1)-dimensional NLmZK equation using the extended simplest equation method. Comput and Mathematics Appl (2019) 78(10):3390–407. doi:10.1016/j.camwa.2019.05.007

CrossRef Full Text | Google Scholar

26. El-Taibany WF, El-Labany SK, Behery EE, Abdelghany AM. Nonlinear dust acoustic waves in a self-gravitating and opposite-polarity complex plasma medium. The Eur Phys J Plus (2019) 134(9):457. doi:10.1140/epjp/i2019-12827-3

CrossRef Full Text | Google Scholar

27. Ali KK, Yilmazer R, Yokus A, Bulut H. Analytical solutions for the (3+1)-dimensional nonlinear extended quantum Zakharov–Kuznetsov equation in plasma physics. Physica A: Stat Mech its Appl (2020) 548:124327. doi:10.1016/j.physa.2020.124327

CrossRef Full Text | Google Scholar

28. Humbu I, Muatjetjeja B, Motsumi TG, Adem AR. Solitary waves solutions and local conserved vectors for extended quantum Zakharov–Kuznetsov equation. The Eur Phys J Plus (2023) 138(9):873. doi:10.1140/epjp/s13360-023-04470-8

CrossRef Full Text | Google Scholar

29. Arshed S, Akram G, Sadaf M, Khan A. Solutions of (3+ 1)-dimensional extended quantum nonlinear Zakharov–Kuznetsov equation using the generalized Kudryashov method and the modified Khater method. Opt Quan Electronics (2023) 55(10):922. doi:10.1007/s11082-023-05137-5

CrossRef Full Text | Google Scholar

30. Saliou Y, Abbagari S, Houwe A, Osman MS, Yamigno DS, Crépin KT, et al. W-shape bright and several other solutions to the (3+ 1)-dimensional nonlinear evolution equations. Mod Phys Lett B (2021) 35(30):2150468. doi:10.1142/s0217984921504686

CrossRef Full Text | Google Scholar

31. Sindi CT, Manafian J. Soliton solutions of the quantum Zakharov-Kuznetsov equation which arises in quantum magneto-plasmas. The Eur Phys J Plus (2017) 132:67–23. doi:10.1140/epjp/i2017-11354-7

CrossRef Full Text | Google Scholar

32. Demiray ST, Kastal S, Demiray ST, Kastal S. Dark-Bright optical soliton solutions of (3+ 1)-dimensional modified quantum Zakharov-Kuznetsov equation. Turkish J Mathematics Computer Sci (2019) 11:90–4.

Google Scholar

33. Saha A, Karakoç BG, Ali KK. New exact soliton solutions, bifurcation and multistability behaviors of traveling waves for the (3+ 1)-dimensional modified Zakharov-Kuznetsov equation with higher order dispersion. Math. Sci. Appl. E-Notes (2023) 11(4):226–240.

CrossRef Full Text | Google Scholar

34. Sulaiman TA, Yel G, Bulut H. M-fractional solitons and periodic wave solutions to the Hirota–Maccari system. Mod Phys Lett B (2019) 33(05):1950052. doi:10.1142/s0217984919500520

CrossRef Full Text | Google Scholar

35. Sousa JVDAC, Capelas D E Oliveira E. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int J Anal Appl (2018) 16(1):83–96.

Google Scholar

36. Sousa JVDC, Oliveira de, Capelas E. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. arXiv preprint arXiv:1704.08187 (2017).

Google Scholar

37. Altalbe A, Taishiyeva A, Myrzakulov R, Bekir A, Zaagan AA. Effect of truncated M-fractional derivative on the new exact solitons to the Shynaray-IIA equation and stability analysis. Results Phys (2024) 57:107422. doi:10.1016/j.rinp.2024.107422

CrossRef Full Text | Google Scholar

38. Yao S-W, Manzoor R, Zafar A, Inc M, Abbagari S, Houwe A. Exact soliton solutions to the Cahn–Allen equation and Predator–Prey model with truncated M-fractional derivative. Results Phys (2022) 37:105455. doi:10.1016/j.rinp.2022.105455

CrossRef Full Text | Google Scholar

39. Ali AT, Hassan ER. General exp_a-function method for nonlinear evolution equations. Appl Mathematics Comput (2010) 217(2):451–9. doi:10.1016/j.amc.2010.06.025

CrossRef Full Text | Google Scholar

40. Zayed EME, Al-Nowehy AG. Generalized kudryashov method and general exp_a function method for solving a high order nonlinear Schrödinger equation. J Space Explor (2017) 6:1–26.

Google Scholar

41. Hosseini K, Ayati Z, Ansari R. New exact solutions of the Tzitzéica-type equations in non-linear optics using the exp_a function method. J Mod Opt (2018) 65(7):847–51. doi:10.1080/09500340.2017.1407002

CrossRef Full Text | Google Scholar

42. Zafar A. The exp_a function method and the conformable time-fractional KdV equations. Nonlinear Eng (2019) 8:728–32. doi:10.1515/nleng-2018-0094

CrossRef Full Text | Google Scholar

43. Sahoo S, Saha Ray S, Abdou MA. New exact solutions for time-fractional Kaup-Kupershmidt equation using improved exp_a expansion and extended (G′/G)-expansion methods. Alexandria Eng J (2020) 59:3105–10. doi:10.1016/j.aej.2020.06.043

CrossRef Full Text | Google Scholar

44. Ullah N, Asjad MI, Awrejcewicz J, Muhammad T, Baleanu D. On soliton solutions of fractional-order nonlinear model appears in physical sciences. AIMS Mathematics (2022) 7(5):7421–40. doi:10.3934/math.2022415

CrossRef Full Text | Google Scholar

45. Seadawy AR, Iqbal M, Althobaiti S, Sayed S. Wave propagation for the nonlinear modified Kortewege–de Vries Zakharov–Kuznetsov and extended Zakharov–Kuznetsov dynamical equations arising in nonlinear wave media. Opt Quan Electronics (2021) 53:85–20. doi:10.1007/s11082-020-02719-5

CrossRef Full Text | Google Scholar

46. Lu D, Seadawy AR, Arshad M, Wang J. New solitary wave solutions of (3+ 1)-dimensional nonlinear extended Zakharov-Kuznetsov and modified KdV-Zakharov-Kuznetsov equations and their applications. Results Phys (2017) 7:899–909. doi:10.1016/j.rinp.2017.02.002

CrossRef Full Text | Google Scholar

47. Ali MN, Osman MS, Husnine SM. On the analytical solutions of conformable time-fractional extended Zakharov–Kuznetsov equation through (G′/G²) expansion method and the modified Kudryashov method. SeMA J (2019) 76:15–25. doi:10.1007/s40324-018-0152-6

CrossRef Full Text | Google Scholar

48. Saha A, Banerjee S; Dynamical systems and nonlinear waves in plasmas, (2021).

CrossRef Full Text | Google Scholar

49. Kumar SU, Saha A, Chatterjee P. Bifurcations of nonlinear ion acoustic travelling waves in the frame of a Zakharov-Kuznetsov equation in magnetized plasma with a kappa distributed electron. Phys Plasmas (2013) 20(5). doi:10.1063/1.4804347

CrossRef Full Text | Google Scholar