
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 26 June 2024
Sec. Social Physics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1410089
This article is part of the Research TopicNetwork Learning and Propagation Dynamics AnalysisView all 14 articles
Within the context of contemporary society, the propagation of information is often subject to the influence of inter-individual connectivity, and individuals may exhibit divergent receptive attitudes towards identical information, a phenomenon denoted as the Hesitant-Common (HECO) trait. In light of this, the present study initially constructs a propagation network model devoid of correlation configurations to investigate the HECO characteristics within weighted social networks. Subsequently, the study employs a theoretical framework for edge partitioning, predicated on edge weights and HECO traits, to quantitatively analyze the mechanisms of individual information dissemination. Theoretical analyses and simulation outcomes consistently demonstrate that an augmentation in the proportion of common individuals facilitates both the diffusion and adoption of information. Concurrently, a phase transition crossover is observed, wherein the growth pattern of the ultimate adoption range, denoted as R(∞), transitions from a first-order discontinuous phase transition to a second-order continuous phase transition as the proportion of common individuals increases. An escalation in the weight distribution exponent is found to enhance information propagation. Furthermore, a reduction in the heterogeneity of degree distribution is conducive to the spread of information. Conversely, an increase in degree distribution heterogeneity and a diminution in the collective decision-making capacity can both exert inhibitory effects on the propagation of information.
With the rapid development of social media platforms such as TikTok, WeChat, and Twitter, social networks have increasingly become integral to human life. These media facilitate the swift reception and dissemination of diverse information, greatly enhancing the convenience of people’s work and daily activities. The communication pathways within social media constitute a vast network for information dissemination, with the world’s largest social media platform, Facebook, boasting billions of active monthly users, and the monthly volume of information flow is incalculable [1]. However, this complexity of information interweaving also presents challenges: once harmful information spreads within the network, it can cause significant damage. Beyond the challenges of information dissemination, social networks also play a crucial role in various fields such as healthcare [2, 3], cultural education [4, 5], and commercial marketing [6, 7]. They are utilized for analyzing information, signals, and financial communication patterns, demonstrating their multifunctionality in modern society. Therefore, an in-depth analysis of the information dissemination patterns within social networks is of significant importance for understanding their impact, optimizing information management, preventing risks, and promoting development in various sectors.
In recent years, numerous scholars have conducted research on information propagation models, including those based on the Internet of Things with layered structures [8], models grounded in game theory [9], and models inspired by heat transfer [10]. Among these, game theory-based models are capable of simulating decision-making processes of individuals aimed at maximizing their self-interest. However, these models are predicated on the assumption of rationality of the individuals, which may not be applicable to all social network contexts. Meanwhile, research on information propagation based on complex network theory and topological structures has emerged as a significant topic within the field of complex network studies [11–14]. There is an extensive body of research on the spread of epidemics across complex networks, and the modes of information propagation within social networks bear certain similarities to the spread of diseases in physically complex networks. Adopting and expanding the foundational models of epidemic propagation in complex networks can facilitate a better understanding of information dissemination in social networks. For instance, a modified Sub-Health-Healthy-Infection- Recovery (SHIR) model with time delays and nonlinear incidence rates has been established for two susceptible populations across different topological networks [15]. Guirui Liu and others developed the SIS-UAU model to describe the dynamics of epidemic and information propagation within overlay networks [16], by constructing a dual-layer network consisting of an epidemic dynamic evolution layer and an information propagation layer to study the dynamics of information and disease spread in superimposed networks. Furthermore, some scholars have described information propagation in complex networks using more refined models. Guan Gui and others formulated a SIR model with time delays, forced silence functions, and forgetting mechanisms in both homogeneous and heterogeneous networks to describe the dynamic mechanisms of rumor propagation [17]. To investigate the propagation trends of network rumors, the authors in [18] detailed the dynamic behavior of a delayed S2IS rumor propagation model with a saturation conversion function. Rumor propagation, as a hot topic in information propagation research [19–21], is also a category within social network dissemination, and such research aids various researchers in uncovering the underlying mechanisms of information propagation in social networks.
One of the primary mechanisms for information dissemination within social networks is through the interconnections among users [22]. Upon the inception of a piece of information, the originator initiates its propagation. It is possible that during the initial dissemination, multiple recipients receive the information simultaneously. Should a recipient successfully adopt the information, they then assume the role of a subsequent disseminator. Concurrently, this process may yield adopters who do not further propagate the information, as well as non-adopters. Ultimately, however, the information evolves into a shared resource among a majority of the network’s participants.
Taking into account the various factors that influence information propagation, user behavior on social networks exhibits diversity and heterogeneity, thereby giving rise to distinct patterns of information dissemination. In real-world social networks, interactions are more likely to occur among individuals with similar interests or preferences, and generally, individuals prefer to receive and share information that aligns with their interests and preferences. Temporal thematic analysis of mobile communication systems has revealed homophily characteristics in social interactions, where communication between individuals with similar attributes (such as gender and age) tends to be more frequent [23]. Bakshy et al., based on Facebook data, observed ideological homophily within friendship networks, where both conservatives and liberals are more likely to associate with friends of similar political affiliations [24].
Numerous systems within contemporary society can be characterized as networks, where the constituent elements are represented as nodes. If the interactions between nodes are quantifiable, the interconnecting edges can be assigned weights, thus forming a weighted network. Consequently, the edge weights within a weighted network typically serve to denote the individual relationships between nodes. For instance, in transaction networks, these weights can signify the proportion of transactions between financial institutions [25], while in transportation networks, they may represent the percentage of tourists utilizing different travel routes [26]. Social networks exhibit complex topological structures with significant heterogeneity in connection strength and capacity. Constructing the inter-individual connections as edges with heterogeneous weight distributions is conducive to uncovering the impact of edge weight heterogeneity on information propagation.
Existing research has demonstrated that individual heterogeneity in adoption manifests as varying receptive attitudes towards the same information, and individuals’ attitudes may change as they acquire different amounts of information [27, 28]. In their research presented in Ref. [29], Iyengar R. examined the propagation of obesity through social networking platforms, emphasizing the significance of group heterogeneity in the dissemination of health-related information. Golub B. investigated the learning processes predicated on individual heterogeneity within these networks and the subsequent influence on the collective intelligence of the group [30]. Furthermore, Lerman K. conducted empirical analyses on the dissemination of news across social media platforms, including Digg and Twitter, with a particular focus on the heterogeneity of user behaviors [31]. However, studies on information propagation in complex networks that consider group adoption heterogeneity are relatively scarce. Due to the distinct personalities of each individual in real-world social networks, the degree of information adoption varies. Based on the psychology of information adoption, this study categorizes the population within social networks into two types: common individuals and hesitant individuals, collectively referred to as the Hesitant-Common (HECO) model. Common individuals maintain a liberal attitude towards received information or behaviors and can adopt them at varying speeds, with an increased willingness to adopt as more information is received. In contrast, hesitant individuals experience a period of deliberation regarding whether to adopt, repeatedly verifying the information before reaching a decision to adopt, facilitated by the acquisition of more information. For example, when a trending piece of information emerges on the internet, common individuals are more likely to discover and disseminate it. Among similar common individuals, the adoption rate is higher, leading to faster propagation of the trending information and a quicker approach to relative saturation in the adoption range. On the other hand, hesitant individuals often receive trending information through common individuals, adopt it after thorough verification, and thus propagate it more slowly, with the adoption range reaching relative saturation after a period of time. Therefore, categorizing the population in social networks based on adoption heterogeneity can contribute to a deeper understanding of the propagation mechanisms within social networks.
In consideration of the factors previously discussed, this study investigates the influence of group adoption heterogeneity on information dissemination within social networks on weighted networks and explores the HECO characteristics in the context of information propagation. A model of the information adoption function is proposed to explain the HECO characteristics. Subsequently, a set of partitioning principles based on edge weight and HECO characteristics is formulated to quantify and analyze the mechanisms of individual information propagation. The impact of information propagation on group heterogeneity is validated through simulation results, which are consistent with theoretical analysis. The structure of the remainder of this paper is as follows: In the second section, an information propagation model based on group heterogeneity is established on weighted networks. The third section presents a theoretical analysis of edge partitioning based on edge weight and HECO characteristics. The fourth section examines the simulation results, confirming the propagation process of individual information in line with theoretical analysis. Finally, a summary is provided in the fifth section.
This section aims to construct a two-layer propagation network model based on an uncorrelated configuration model to investigate the impact of differences in HECO characteristics among populations on information dissemination within weighted social networks. In this model, the network consists of N nodes with a degree distribution P(k), and the propagation model follows the susceptible-adopted-recovered (SAR) paradigm. At any given moment, each node is in one of three states: susceptible state (S), adopted state (A), or recovered state (R). S-state nodes have not yet adopted the information and can receive information from neighboring nodes. A-state nodes have adopted the information and will pass it on to neighboring nodes. R-state nodes have lost interest in the information and no longer participate in the subsequent propagation process (i.e., they will neither adopt nor disseminate the information). The propagation mechanism is depicted in Figure 1A. In the weighted social network model presented in this study, an edge weight distribution is introduced to represent the degree of interaction between individuals, with different weight distributions reflecting the heterogeneity in information reception and dissemination among node connections. The edge weight between adjacent nodes
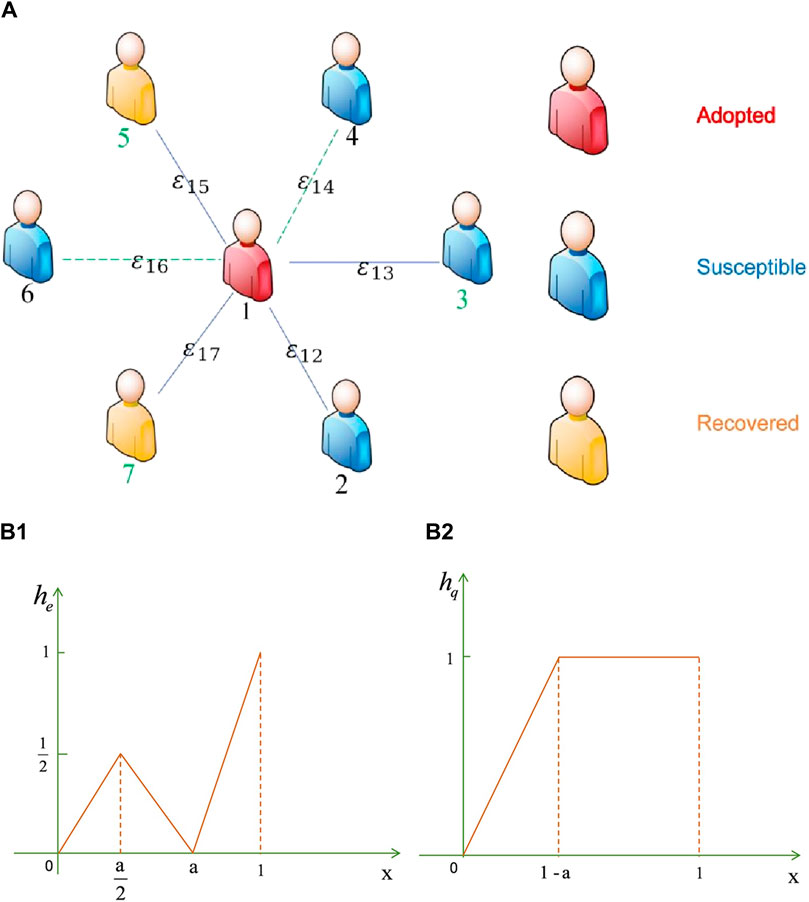
Figure 1. Subfigure (A) illustrates the schematic of the weighted social network propagation model. Different numerical labels with colors represent various types of populations, with black denoting the common population, such as 1, 2, 4, and 6. Green represents the hesitant population, such as 3, 5, and 7. The symbol
Where
Let
To characterize the decision-making capacity of a population, this study introduces a hesitancy parameter, denoted as
For the general population, there exists a normative reception and assimilation of information, wherein an increase in the quantity of information acquired further enhances the adoption of information by this demographic. Eq. 3 delineates the information adoption function of the general population:
In the aforementioned equations,
The simulation of information propagation in a weighted social network is depicted in Figure 2: A complex network with N nodes is constructed, where the edges between nodes are randomly generated according to the predefined network model, and all nodes are initially set to the S-state. A proportion
Building upon the literature [14, 32], this study examines the propagation of non-redundant information with group adoption heterogeneity on weighted networks. On this foundation, the paper proposes a theory of edge partitioning based on edge weight and HECO characteristics, thereby analyzing the information propagation mechanisms of the model. The study introduces nodes in a cavity state [33], which are capable of receiving information from neighbors but are unable to transmit information to other nodes. Assuming that edge weights are randomly distributed, the probability that a node has not received information from its neighbors by time t is characterized by Eq. 4:
Where
By time
Based on group heterogeneity, differences in HECO characteristics, and the information adoption function, if node
Similarly, when the received information
Then, for any hesitant node in state S, Eq. 9 can represent the probability that such nodes have not yet adopted the information by time
Similarly, if node
For any common node in state S, the probability of not adopting the information at the cut-off time
Consequently, the probability that node
Then, in this weighted network, the proportion of S-state nodes at time
Due to the three states in the SAR model, this study introduces the term
Where
Initially, the cavity node theory is introduced to calculate
Based on the differences in HECO characteristics and the information adoption function of the population, if node
Similarly, when the received information
When node
Consequently, the probability that a node
The probability that a node
Where
Subsequently, analyze
In addition, a node in state A may lose interest in information transmission with probability
By combining the initial conditions
By substituting Eqs 17, 20 into Eq. 12, one arrives at Eq. 27:
Substituting Eq. 21 into Eq. 18,
In the whole network, the density changes of each state can be represented by Eqs 29, 30:
Therefore, the formula 11, 23, 24 can be iterated together to obtain each state density
When
By combining the formula 11 and 25, the combinatorial iteration results in
Next, focus on the analysis of critical propagation probability, leading to the introduction of Eq. 32:
To validate the theoretical analysis mentioned above, we conducted numerical simulations and theoretical analysis based on weighted Erdos-Renyi (ER) networks [34] and weighted Scale-Free (SF) networks [35].
Firstly, a more comprehensive introduction to the Erdos-Renyi (ER) network and the Scale-Free (SF) network is provided. The ER network model is one of the most fundamental models in the study of complex network theory and holds significant importance for understanding randomness in networks and stochastic phenomena within networks. The construction rules are as follows: (1) There is a fixed number of nodes within the network; (2) Each pair of nodes is randomly connected with the same probability p, meaning that the existence of an edge (link) between any two nodes is independent, and this probability is identical for all node pairs; (3) The ER network model typically refers to an undirected graph, where edges have no direction; (4) The network contains no self-loops (nodes connecting to themselves) and multiple edges (more than one edge between the same pair of nodes) [36]. The ER network has practical applications, including: the ER model can be used to simulate random friendship formation in social networks [37], in bioinformatics, it is utilized to model the randomness of gene regulatory networks or protein interaction networks [38], and it can also be applied in transportation networks to simulate random route selection in urban traffic networks [39].
The SF network is a network model characterized by a power-law distribution in the connectivity degree of its nodes. The basic steps for constructing an SF network are as follows: (1) Initial Network: Start with a small network, typically consisting of a few nodes and the connections between them; (2) Growth: Over time, the network grows by adding new nodes. Each new node comes with several edges that connect to certain nodes in the existing network; (3) Preferential Attachment: The probability that a new node connects to an existing node is proportional to its degree (i.e., the number of connections of the existing node). This means that the more connections a node has, the higher the likelihood it will attract new connections; (4) Network Topology: In this manner, the network’s topology evolves over time, developing a special degree distribution known as a power-law distribution, which is one of the characteristics of SF networks; (5) No Self-Loops and Multiple Edges: Self-loops (nodes connecting to themselves) and multiple edges (more than one edge between two nodes) are generally not allowed during the construction process; (6) Network Size: Nodes and edges can continue to be added until the network reaches the desired scale [40]. Related instances of SF networks include: Protein interaction networks and metabolic networks in biological systems are often modeled as SF networks [41]. Certain parts of power transmission networks can be modeled as SF networks to study their robustness and vulnerability [42]. In financial markets, the network of transaction relationships between companies also exhibits characteristics of SF networks [43].
In the weighted ER network and SF network, 10,000 independent nodes are set in the network, the average degree of the network
In this paper, the relative variance X is used to illustrate the critical unit propagation probability and critical conditions in the simulation, and is articulated by Eq. 34 as follows:
Where
The analysis of information dissemination models within this study relies on the thermodynamic classification of phase transitions. Phase transitions are categorized based on the mathematical characteristics—continuous or discontinuous—of the partial derivatives of free energy with respect to temperature and pressure at the transition point. This categorization includes first-order, second-order, and higher-order phase transitions, with the focus of this study being on the first two types. In the context of thermodynamics, a first-order phase transition is characterized by equal chemical potentials between the new and old phases, yet differing first-order partial derivatives. This type of transition is associated with a discontinuous change in both entropy and volume. A second-order phase transition is distinguished by equal chemical potentials and first-order partial derivatives between phases, but with second-order partial derivatives that are not equal, resulting in no change in entropy or volume. The phase transition model is employed to describe the growth rate of the dissemination range during the process of information dissemination. A rapid growth in the dissemination range with the unit dissemination probability, marked by a discontinuous change, is classified as a first-order discontinuous phase transition. In contrast, a slow growth exhibiting a continuous change is classified as a second-order continuous phase transition.
In this section, to conduct a more nuanced examination of the influence of the HECO characteristic on the propagation of information within social networks, we focus on two parameters that are most representative of the HECO trait: the proportion of the common population
In this paper, the propagation of information on weighted ER network is discussed first. The nodes in ER network obey Poisson distribution, that is,
Figure 3 describes the impact of the unitary propagation probability
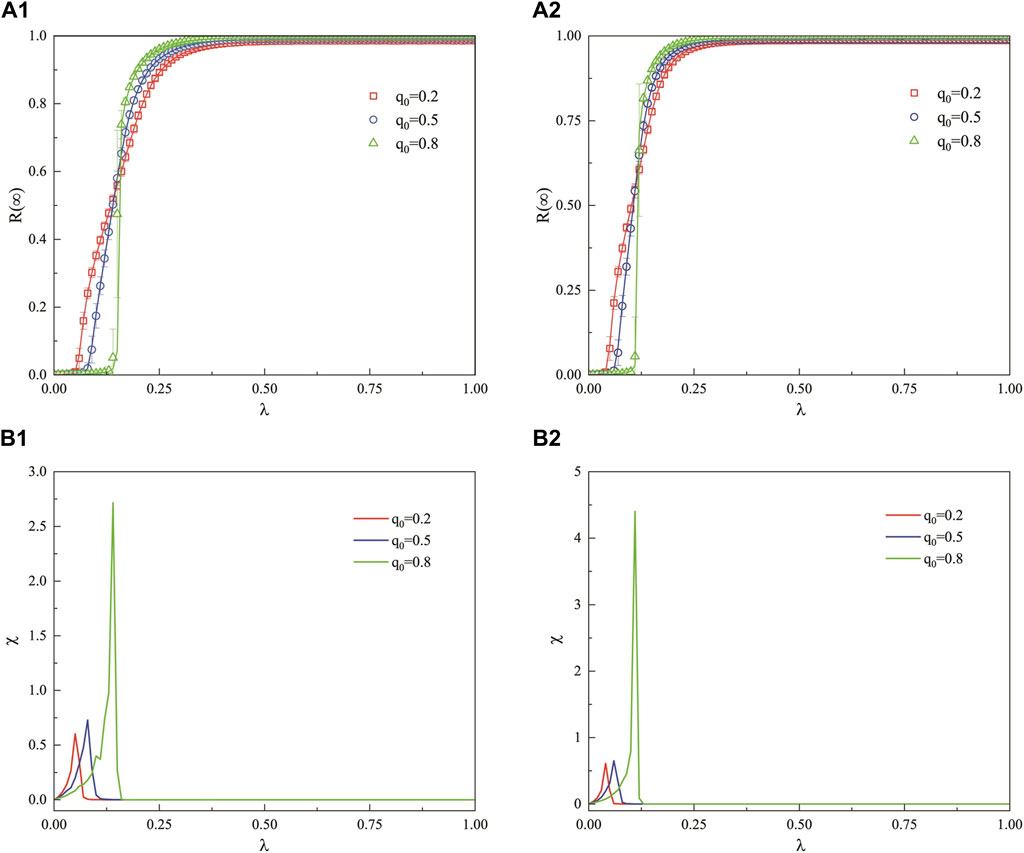
Figure 3. In the weighted ER network, when the decision-making ability of the hesitant population is relatively strong, the variation of the final propagation range for both adopting populations under different proportions
Figure 4 illustrates the impact of the unit propagation probability
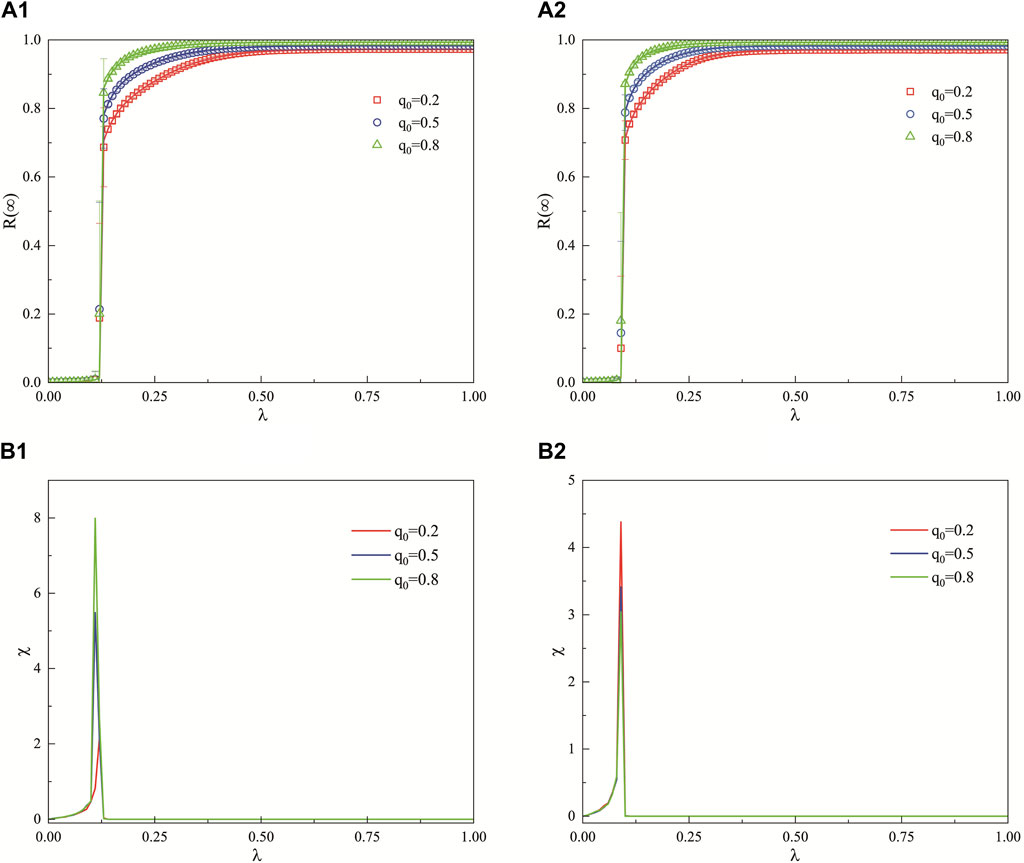
Figure 4. In the context of a weighted ER network, where the decision-making capacity of the hesitant population is moderate, this figure examines the effect of the unit propagation probability
From Figures 5A1, B1, it can be observed that as the unit propagation probability
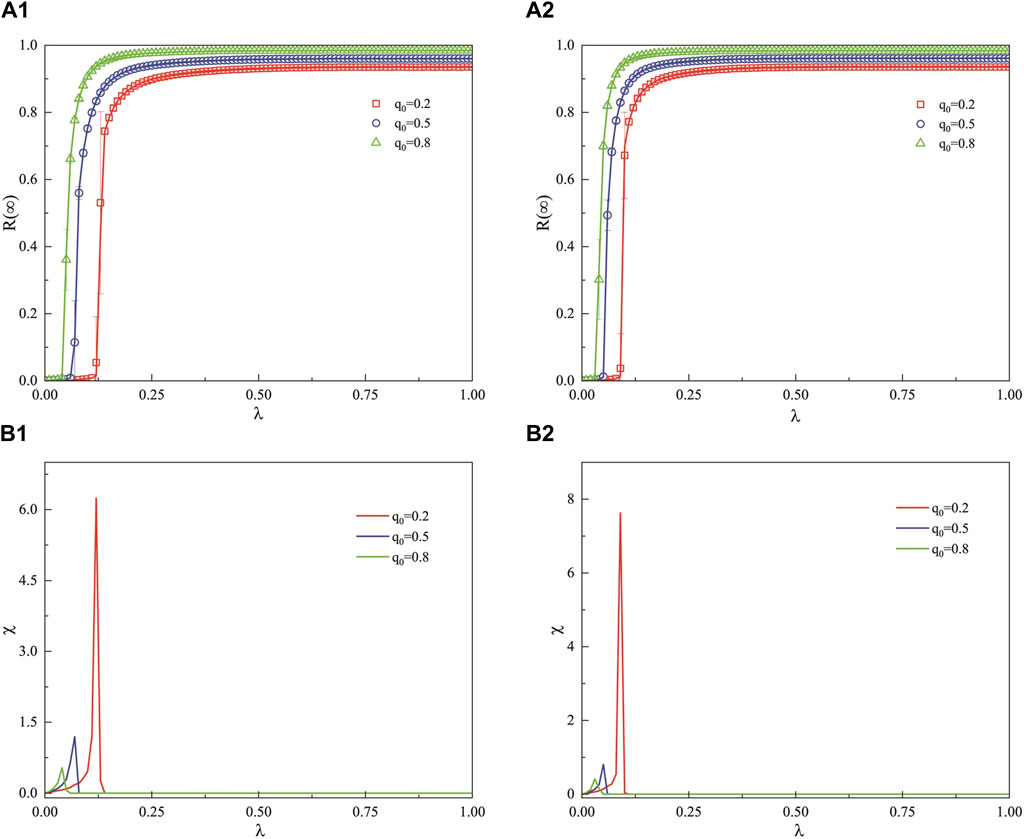
Figure 5. Under the weighted ER network, this figure presents the influence of the unit propagation probability
Figure 6 describes the joint effect of the unit propagation probability
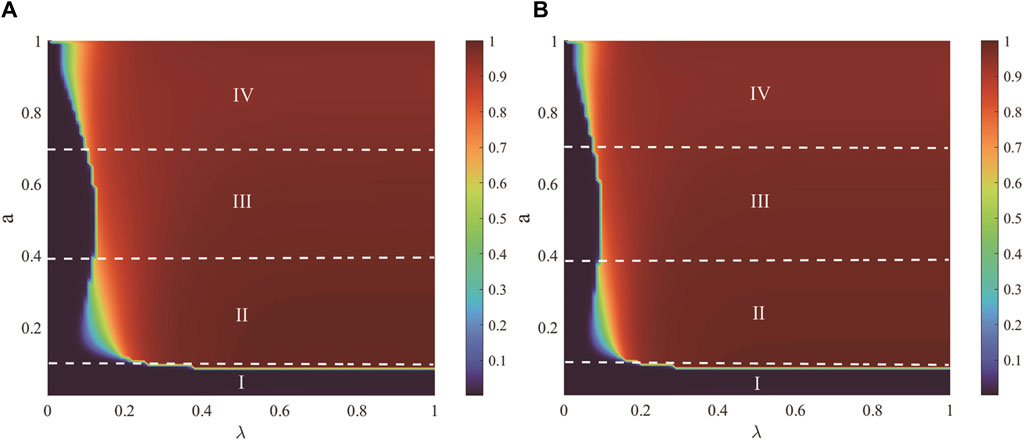
Figure 6. The joint effect of the unit propagation probability
Figure 7 illustrates the joint effect of the unit propagation probability
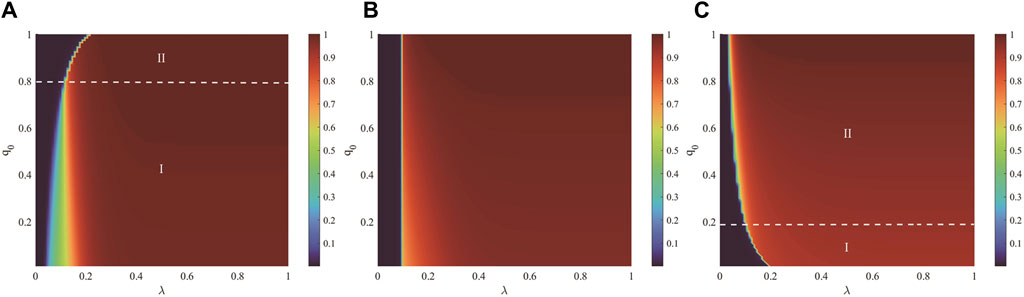
Figure 7. The joint effect of the unit propagation probability
In the weighted SF network, the degree distribution heterogeneity of nodes is negatively correlated with the degree index
Figure 8 demonstrates the impact of the unit propagation probability
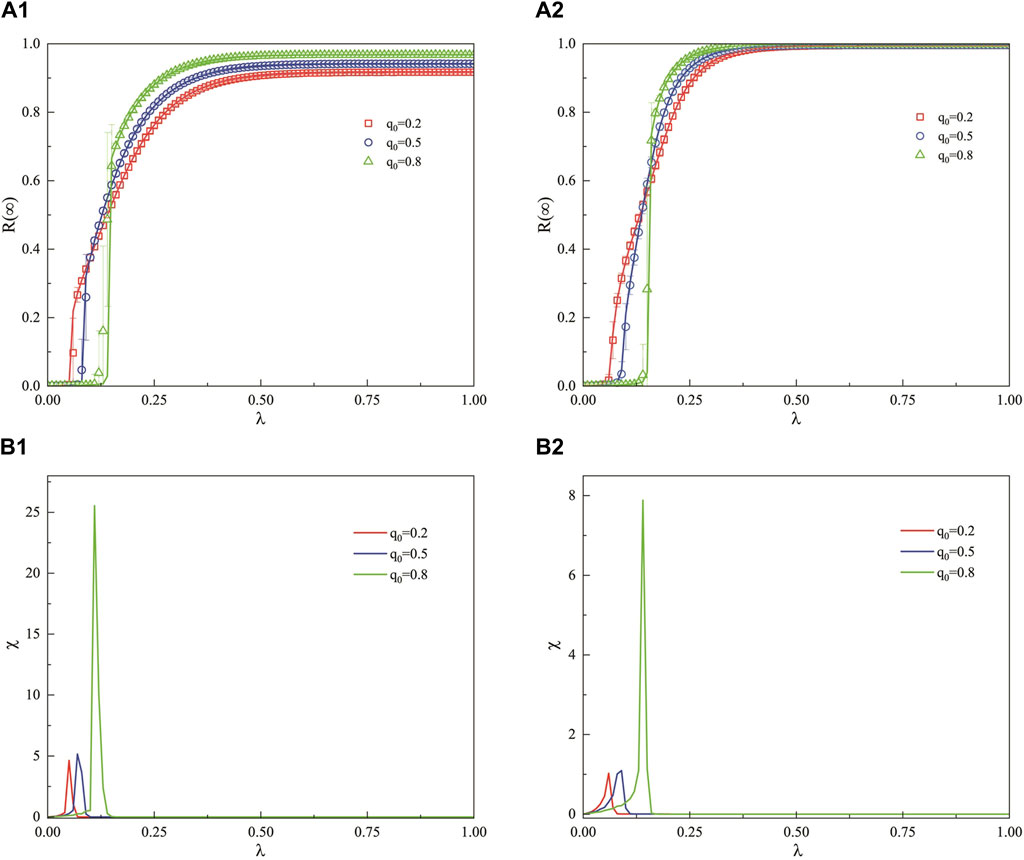
Figure 8. In a weighted SF network, when the decision-making ability of the hesitant population is relatively strong, this figure illustrates the impact of the unit propagation probability
Figure 9 depicts the influence of the unit propagation probability
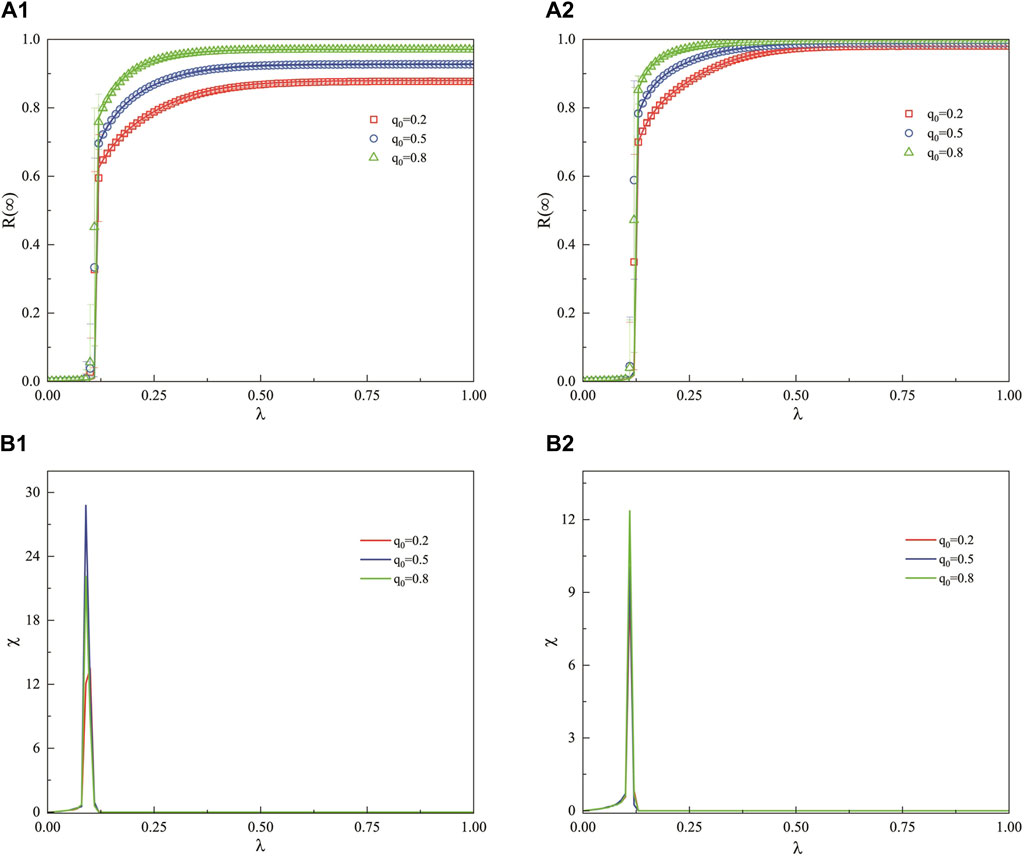
Figure 9. In a weighted SF network, this figure examines the influence of the unit propagation probability
Figures 10A1, B1 present the influence of different degree indices (
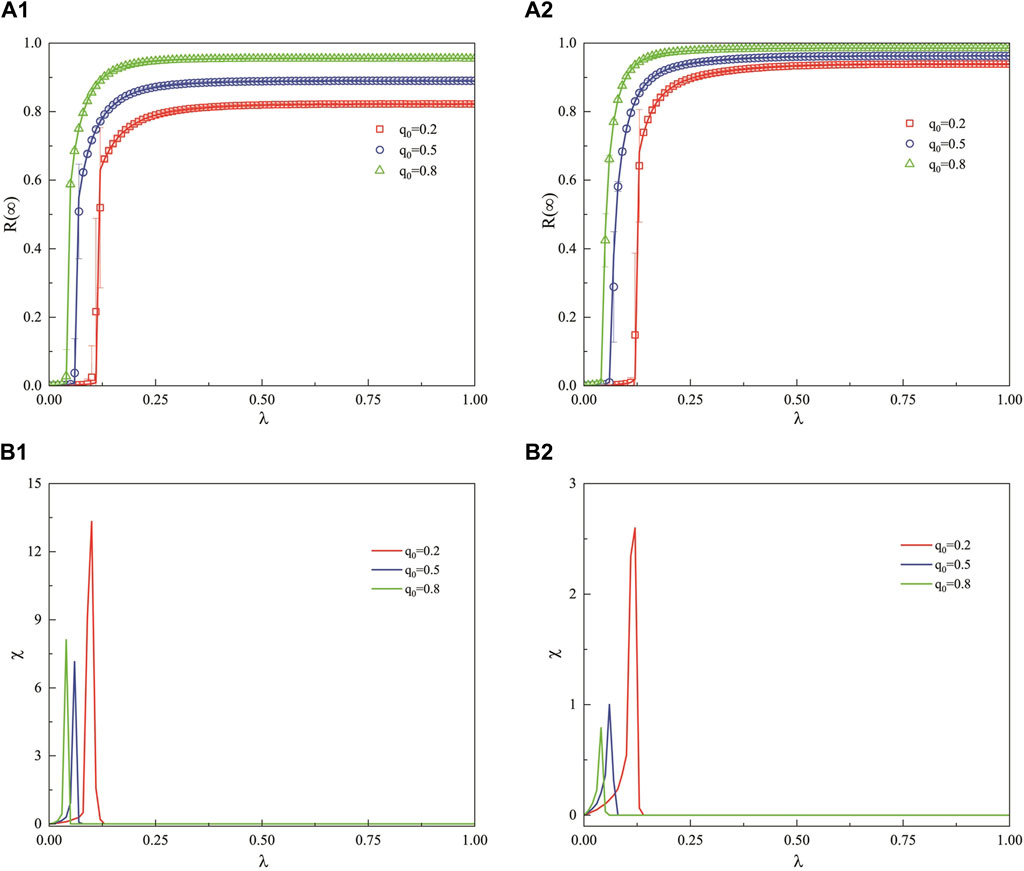
Figure 10. In a weighted SF network, this figure examines the impact of the unit propagation probability
Figure 11 illustrates the combined effect of the unit propagation probability
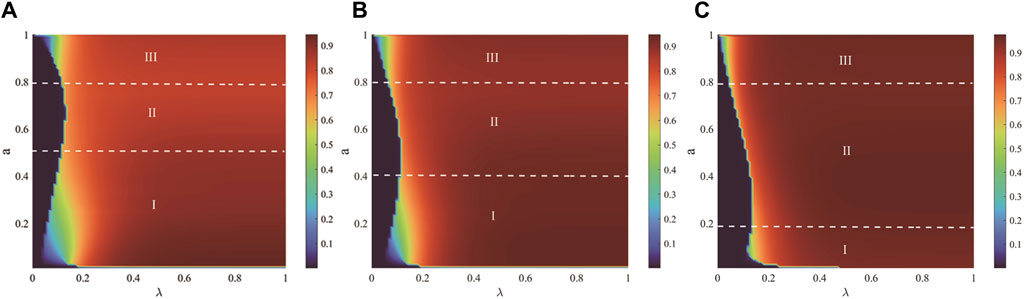
Figure 11. This figure illustrates the combined effect of the unit propagation probability
Figure 12: This figure represents the combined effect of the unit propagation probability
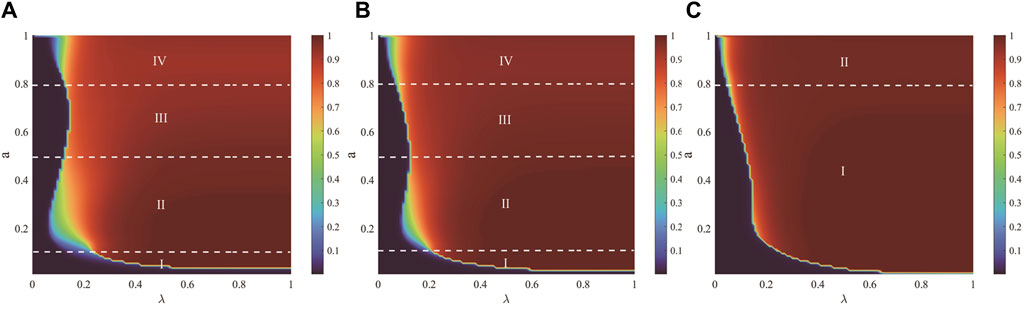
Figure 12. The joint effect of the unit propagation probability
Figure 13 illustrates the combined effect of the unit propagation probability
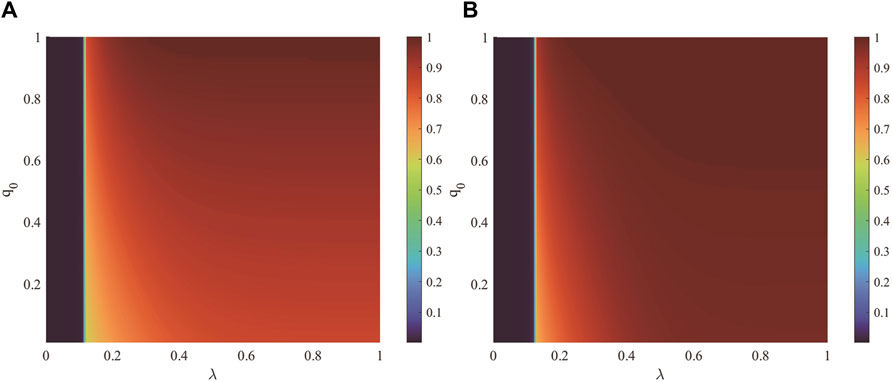
Figure 13. This figure delineates the joint impact of the unit propagation probability
This study investigates the propagation of information in social networks within weighted networks, considering the heterogeneity in group adoption characteristics. The heterogeneity is characterized by distinct Hesitant-Common (HECO) traits in information adoption across different populations. The paper proposes two information adoption functions to elucidate the impact of group heterogeneity on information propagation. For common individuals, their adoption probability increases with the accumulation of received information. However, for hesitant individuals, the adoption probability initially increases similarly to that of common individuals but then declines as more information is received, eventually stabilizing and no longer changing once the optimal decision-making capacity is reached. The study randomly selects a proportion
Through simulation analysis, this study explores the information adoption behaviors of different types of individuals (hesitant and common), and investigates how these behaviors impact the speed and extent of information dissemination. It also observes phase transition phenomena during the information propagation process, particularly the correlation between the pattern of change in the ultimate adoption range and the proportion of common individuals. The study examines the impact of variations in the weight distribution index on the speed and efficiency of information propagation. It discusses how the heterogeneity in the degree distribution of nodes within the network affects information dissemination and how this heterogeneity interacts with the phase transition patterns of information propagation. The influence of decision-making ability on propagation is a focal point of consideration. Findings align with theoretical analysis, indicating that common individuals facilitate the spread and adoption of information. Furthermore, a phase transition crossover phenomenon is observed, where the growth pattern of
The heterogeneity of groups within social networks plays a pivotal role in the propagation of information, yet there is a paucity of related research. This paper, through rigorous modeling and analysis, reveals the significant impact of the Hesitant-Common (HECO) attributes based on group heterogeneity on information dissemination. Furthermore, the HECO characteristics hold notable potential in practical applications, particularly in understanding and forecasting the dynamics of information propagation within social networks. Below are some potential applications of the HECO model across various domains: (1) Social Media Marketing: By understanding the extent to which users accept advertisements or trending information, the HECO model can assist marketers in designing more effective social media strategies to enhance the velocity and reach of information dissemination; (2) Public Health Campaigns: When promoting health information or awareness of vaccination initiatives, the model can predict the rate at which different demographic groups will accept health-related messages, thereby aiding health organizations in more accurately targeting their promotional resources; (3) Crisis Management: In emergency situations, comprehending the rapid spread of information is essential for an effective crisis response. The HECO model can forecast the speed and breadth of information propagation, assisting in the development of more robust emergency communication strategies; (4) Online Sentiment Analysis: Governments and corporations can utilize the HECO model to monitor and analyze the genesis and evolution of public opinion, thereby gaining a more profound understanding of the needs and reactions of the populace; (5) Product Promotion: Businesses can apply the HECO model to refine their strategies for new product promotion by identifying consumer groups most likely to rapidly accept and disseminate information, thus accelerating the market penetration of their products; (6) Information Security: Within the realm of cybersecurity, the HECO model can aid in the anticipation and prevention of the spread of misinformation or rumors by pinpointing key nodes in the propagation of information to bolster network defenses; (7) Traffic Planning: In the analysis of traffic networks, the conceptual framework of the HECO model can be employed to comprehend and optimize the flow of information, such as real-time traffic updates, to alleviate congestion and enhance traffic efficiency. By applying the HECO model in these domains, a deeper understanding and more effective utilization of the mechanisms of information propagation within social networks can be achieved, leading to improved quality and efficiency in decision-making processes. The research presented herein also offers a new direction for the study of information propagation in heterogeneous networks. However, this study only considers the propagation of group heterogeneity under basic scenarios and does not account for propagation within multi-layer networks. Additionally, the influence of parameters such as limited contact capacity is not considered. It is hoped that future research will have the opportunity to further explore this field.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
JJ: Methodology, Project administration, Supervision, Writing–review and editing. YH: Data curation, Formal Analysis, Methodology, Writing–original draft. WZ: Methodology, Writing–review and editing. YC: Validation, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by Education Department of Inner Mongolia Autonomous Region (NJZZ23074), Funds for basic scientific research of universities directly under the Autonomous region (ZTY2024065), Natural Science Foundation project of Inner Mongolia Autonomous Region (2024QN05046) and Research fund project of Inner Mongolia University of Technology.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Houghton D, Pressey A, Istanbulluoglu D. Who needs social networking? An empirical enquiry into the capability of Facebook to meet human needs and satisfaction with life. Comput Hum Behav (2020) 104:106153. doi:10.1016/j.chb.2019.09.029
2. Khan S, Saravanan V, Lakshmi TJ, Deb N, Othman NA. Privacy protection of healthcare data over social networks using machine learning algorithms. Comput Intelligence Neurosci (2022) 2022:9985933–8. doi:10.1155/2022/9985933
3. Kolowitz B, Lauro GR, Venturella J, Georgiev Y, Barone M, Deible C, et al. Clinical social networking--a new revolution in provider communication and delivery of clinical information across providers of care? J digital Imaging (2014) 27(2):192–9. doi:10.1007/s10278-013-9653-0
4. Gil-Fernández R, Calderón-Garrido D, León-Gómez A, Martin-Piñol C. Comparativa del uso educativo de las redes sociales en los grados de Maestro: universidades presenciales y online. Aloma (2019) 37(2):75–81. doi:10.51698/aloma.2019.37.2.75-81
5. bt Yahya SMSA, Ahmad SB Preliminary study on educational user interface architecture for social network. Int J Eng Technol (2018) 7(4):457–62. doi:10.14419/ijet.v7i4.36.23916
6. Liu T, He X, Guo X, Zhao Y. The influence of the network evolutionary game model of user information behavior on enterprise innovation product promotion based on mobile social network marketing perspective. Math Probl Eng (2022) 2022.
7. Lee S, Park H. A study on the effect of social networking marketing on the purchase intention in the airline. East Asian J Business Econ (2021) 9(2):55–73.
8. Zhang Y, Pan D, Fan S. Analysis of layered information dissemination model and caching strategy in Social Internet of Things. Nonlinear Dyn (2023) 111(15):14379–94. doi:10.1007/s11071-023-08594-5
9. He J, Li Y, Zhu N. A game theory-based model for the dissemination of privacy information in online social networks. Future Internet (2023) 15(3):92–412. doi:10.3390/fi15030092
10. Chen J, Huang J, Xin C, Liu M. Research on information dissemination model based on heat transfer in online social network. The J Supercomputing (2022) 79(7):7717–35.
11. Zhu X, Wang W, Cai S, Stanley HE. Optimal imitation capacity and crossover phenomenon in the dynamics of social contagions. J Stat Mech (2018) 2018.
12. Pan D, Zhang Y. Analysis of information propagation and control of a layered SITR model in complex networks. Front Phys (2022) 10:985517. doi:10.3389/fphy.2022.985517
13. He L, Zhu L, Zhang Z. Turing instability induced by complex networks in a reaction–diffusion information propagation model. Inf Sci (2021) 578:762–94. doi:10.1016/j.ins.2021.08.037
14. Wang W, Tang M, Zhang H, Gao H, Do Y, Liu Z. Epidemic spreading on complex networks with general degree and weight distributions. Phys Rev E, Stat nonlinear, soft matter Phys (2014) 90(4):042803. doi:10.1103/physreve.90.042803
15. Guan G, Guo Z. Stability behavior of a two-susceptibility SHIR epidemic model with time delay in complex networks. Nonlinear Dyn (2021) 106(1):1083–110. doi:10.1007/s11071-021-06804-6
16. Liu G, Liu Z, Jin Z. Dynamics analysis of epidemic and information spreading in overlay networks. J Theor Biol (2018) 444:28–37. doi:10.1016/j.jtbi.2018.02.010
17. Cao B, Guan G, Shen S, Zhu L. Dynamical behaviors of a delayed SIR information propagation model with forced silence function and control measures in complex networks. The Eur Phys J Plus (2023) 138(5):402. doi:10.1140/epjp/s13360-023-04005-1
18. Ding N, Guan G, Shen S, Zhu L. Dynamical behaviors and optimal control of delayed S2IS rumor propagation model with saturated conversion function over complex networks. Commun Nonlinear Sci Numer Simulation (2024) 128:107603. doi:10.1016/j.cnsns.2023.107603
19. Zhu L, Yang F, Guan G, Zhang Z. Modeling the dynamics of rumor diffusion over complex networks. Inf Sci (2021) 562:240–58. doi:10.1016/j.ins.2020.12.071
20. Zhu L, Wang X, Zhang Z, Lei C. Spatial dynamics and optimization method for a rumor propagation model in both homogeneous and heterogeneous environment. Nonlinear Dyn (2021) 105(4):3791–817. doi:10.1007/s11071-021-06782-9
21. Zhu X, Ma J, Su X, Tian H, Wang W, Cai S. Information spreading on weighted multiplex social network. Complexity (2019) 2019:1–15. doi:10.1155/2019/5920187
22. Chen X, Zhang S. An SEIR model for information propagation with a hot search effect in complex networks. Math biosciences Eng : MBE (2023) 20(1):1251–73. doi:10.3934/mbe.2023057
23. Kovanen L, Kaski K, Kertész J, Saramäki J. Temporal motifs reveal homophily, gender-specific patterns, and group talk in call sequences. Proc Natl Acad Sci USA (2013) 110(45):18070–5. doi:10.1073/pnas.1307941110
24. Bakshy E, Messing S, Adamic LA. Political science. Exposure to ideologically diverse news and opinion on Facebook. Science (2015) 348(6289):1130–2. doi:10.1126/science.aaa1160
25. Gandy A, Veraart LAM. Adjustable network reconstruction with applications to CDS exposures. J Multivariate Anal (2019) 172:193–209. doi:10.1016/j.jmva.2018.08.011
26. Barrat A, Barthelemy M, Pastor-Satorras R, Vespignani A. The architecture of complex weighted networks. Proc Natl Acad Sci USA (2004) 101(11):3747–52. doi:10.1073/pnas.0400087101
27. Chen T, Li Q, Yang J, Cong G, Li G. Modeling of the public opinion polarization process with the considerations of individual heterogeneity and dynamic conformity. Mathematics (2019) 7(10):917. doi:10.3390/math7100917
28. Zhu X, Yang Q, Tian H, Ma J, Wang W. Contagion of information on two-layered weighted complex network. IEEE Access (2019) 7:155064–74. doi:10.1109/access.2019.2948941
29. Iyengar R, Van den Bulte C, Valente TW. Opinion leadership and social contagion in new product diffusion. Marketing Sci (2011) 30(2):195–212. doi:10.1287/mksc.1100.0566
30. Golub B, Jackson MO. Naive learning in social networks and the wisdom of crowds. Am Econ J Microeconomics (2010) 2(1):112–49. doi:10.1257/mic.2.1.112
31. Lerman K, Ghosh R. Information contagion: an empirical study of the spread of news on digg and twitter social networks. Proc Int AAAI Conf Web Soc Media (2010) 4(1):90–7. doi:10.1609/icwsm.v4i1.14021
32. Wang W, Tang M, Zhang H, Lai Y. Dynamics of social contagions with memory of nonredundant information. Phys Rev E, Stat nonlinear, soft matter Phys (2015) 92(1):012820. doi:10.1103/physreve.92.012820
33. Yuan X, Hu Y, Stanley HE, Havlin S. Eradicating catastrophic collapse in interdependent networks via reinforced nodes. Proc Natl Acad Sci USA (2017) 114(13):3311–5. doi:10.1073/pnas.1621369114
34. Arratia R, Gordon L, Waterman MS. The erdos-renyi law in distribution, for coin tossing and sequence matching. Ann Stat (1990) 18(2):539–70. doi:10.1214/aos/1176347615
35. Wang S, Cheng W. Novel method for spreading information with fewer resources in scale-free networks. Physica A: Stat Mech its Appl (2019) 524:15–29. doi:10.1016/j.physa.2019.03.018
37. McPherson M, Smith-Lovin L, Cook JM. Birds of a feather: homophily in social networks. Annu Rev Sociol (2001) 27(1):415–44. doi:10.1146/annurev.soc.27.1.415
38. Barabasi AL, Oltvai ZN. Network biology: understanding the cell's functional organization. Nat Rev Genet (2004) 5(2):101–13. doi:10.1038/nrg1272
39. Louf R, Barthélemy M. How congestion causes long waiting times: a statistical physics approach to traffic instability. Phys Rev E (2013) 88(6):062814.
40. Barabási AL, Albert R. Emergence of scaling in random networks. science (1999) 286(5439):509–12. doi:10.1126/science.286.5439.509
41. Jeong H, Tombor B, Albert R, Oltvai ZN, Barabási AL. The large-scale organization of metabolic networks. Nature (2000) 407(6804):651–4. doi:10.1038/35036627
42. Dobson I, Carreras BA, Lynch VE, Newman DE. Complex systems analysis of series of blackouts: cascading failure, critical points, and self-organization. Chaos: Interdiscip J Nonlinear Sci (2007) 17(2):026103. doi:10.1063/1.2737822
Keywords: complex networks, weighted network, information propagation, individual hesitant-common characteristics, heterogeneous information adoption model
Citation: Jia J, Huang Y, Zhang W and Chen Y (2024) Information propagation characteristic by individual hesitant-common trend on weighted network. Front. Phys. 12:1410089. doi: 10.3389/fphy.2024.1410089
Received: 31 March 2024; Accepted: 17 May 2024;
Published: 26 June 2024.
Edited by:
Xuzhen Zhu, Beijing University of Posts and Telecommunications (BUPT), ChinaReviewed by:
Wenjie Dong, Nanjing University of Aeronautics and Astronautics, ChinaCopyright © 2024 Jia, Huang, Zhang and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianlin Jia, ampsQGltdXQuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.