The closed-form solution by the exponential rational function method for the nonlinear variable-order fractional differential equations

The symmetry features of fractional differential equations allow effective explanation of physical and biological phenomena in nature. The generalized form of the fractional differential equations is the variable-order fractional differential equations that describe the physical and biological applications. This paper discusses the closed-form traveling wave solutions for the nonlinear space–time variable-order fractional modified Kawahara and (2 + 1)-dimensional Burger hierarchy equations. The variable-order fractional differential equation has a derivative operator in the Caputo sense that is converted into the integer-order ordinary differential equation (ODE) by fractional transformation. The obtained ODE is solved by the exponential rational function method, and as a result, new exact solutions are constructed. Two problems are proposed to confirm the solutions of the space-time variable-order fractional differential equations.

1 Introduction

The non-linear fractional differential equations (NFDEs) have broad acceptability across numerous fields, such as control theory, signal processing, system identification, medicine, and probability [1, 4]. For the first time, the soliton theory was described by the Scottish scientist Jon Scott Russel [2]. This study received the attention of researchers, who found the soliton solution for various types of nonlinear partial differential equations. [3] considered the improved Bernoulli sub-equation function for the well-known nonlinear Schrödinger equation. They obtained trigonometric, exponential, and hyperbolic-type solutions with differential shapes of solitons. [4] studied three effective methods for the system of ion sound and Langmuir waves. They constructed seven sets of traveling wave solutions in kink bright solitary, periodic solitary, and dark solitary solitons. [5] explored the new exact traveling wave solutions for the simplified modified Camassa–Holm equation by the new auxiliary equation method. They discussed the stability analysis and presented the solutions in trigonometric, hyperbolic, exponential, and rational functions. They also compared their results with those of the existing literature. The (2 + 1)-dimensional Vakhnenko–Parkes equation is solved by the three high potential techniques by [6]. They constructed a variety of new exact solutions expressed by the exponential, hyperbolic, trigonometric, tanh, coth, sech, cosh, cot, cosech, tan, and their combinations. The obtained solutions are presented in 2D and 3D with their physical behavior. In another survey, [7] investigated the high-dimensional Boiti–Leon–Manna–Pempinelli equation by the generalized exponential function and Kudryashov method. They reported that the proposed methods are highly recommended in this field of research. [8] considered the Boussinesq equation and formulated their solutions by the Sardar subequation method. The results are plotted to demonstrate the efficiency and effectiveness of the method for such types of mathematical problems. [9] produced the shock-type traveling waves for the schema Burger’s equation by using the two analytical methods. The proposed problem confirms the shock dynamical structure. [10] used the modified exp-function method for the nonlinear strain wave equations. They reported new exact solutions in the form of hyperbolic and complex functions. [11] implemented the improved exponential expansion method on the Novikov–Veselov equation. They discussed the stability and accuracy and confirmed that the solution was convenient. [12] studied three different techniques: Adomian’s decomposition method, the modified extended tanh function method, and the improved F-expansion method for the nonlinear Benjamin–Bona–Mahony equation. They compared their results with those of the existing literature, discussed the stability, and plotted the result graphically, which demonstrated the efficiency of the methods. The Lonngren wave equation, which describes the electrical signals in a semiconductor, was solved analytically by [13]. They explained the results and compared with the existing results in the literature. Many other related literatures can be studied in [14–18].

In the above-cited literature, the researchers have found the exact traveling wave solutions for the nonlinear partial differential equations. However, in the last decade, researchers have focused on nonlinear fractional-order differential equations obtained by replacing fractional-order $\alpha \in \left(0,1\right)$ and have successfully found the exact traveling wave solutions by various methods because such problems describe real-world phenomena. Some of them are as [19], who found the closed-form solution for the fractional-order evaluation equations by the two analytical techniques; reported different shapes of solitons including bell-shaped, multi-soliton, single soliton, anti-bell-shaped, and periodic solitons; and demonstrated that the said methods are more efficient and straightforward for investigating the complex phenomena. [20] produced a generalized $\left(D_{\xi }^{\alpha }G/G\right)$-expansion method and implemented it on different evolution equations successfully. They are converting the fractional-order evolution equations into fractional-order ordinary differential equations, and the derivative operator is in the conformable fractional derivative sense. The generated results described the importance of the complex phenomena. [21] discussed two fractional-order models in the manuscript and implemented the extended tanh-function method. They discovered various new soliton solutions in the form of kink, bell, and other shapes and proved that the proposed method is more trustworthy. [22] formulated the closed-form solution for the nonlinear fractional-order $\left(2+1\right)$-dimensional breaking soliton equations. The fractional-order derivative is in the local fractional derivative sense. They formulated the new exact solution by the Khater method, and the results are plotted in 3D and 2D graphs, which showed that the method is more convenient. The tanh–coth method is considered for the three different fractional-order equations as fractional-order Burger’s, regularized long wave, and Boussinesq involving Riemann–Liouville fractional derivatives [23]. The method has provided abundant numbers of new solutions. [24] found many soliton solutions as kink, singular, and dark of the governing equation through the generalized projective Riccati equation method. The considered method is very concise and straightforward. [25] worked on the ansatz method and found the solution for the complex fractional Kundu–Eckhaus equation. The fractional derivative is in the sense of a truncated M-fractional derivative. They obtained new types of solutions as kink and solitary waves through the proposed method, which is more reliable. Local fractional derivative theory has been used in the bidirectional wave equation and proved that it describes the interaction of the fractal wave [26]. [27] contributed a new technique and found the new closed-form optical solutions for the Ginzburg–Landau equation, and they claim that the said method is very simple and reliable. [28] investigated the symmetric soliton solution for the fractional-order PDEs known as the coupled Konno–Onno system by the two modified forms of the extended direct algebraic method. The proposed method confirmed a symmetric soliton solution for such types of complex models. In another survey, [29] worked on the perturbed Gerdjikov–Ivanov equation, which discussed the optical pulses during propagation. They utilized the Riccati–Bernoulli sub-ODE method with the Backlund transform. The obtained results are in the form of trigonometric and rational functions that confirm the efficiency and feasibility of the proposed method. [30] introduced the optimal auxiliary function method and found out the system of coupled Schrödinger–KdV equations. They obtained the approximate solution of the coupled system of equations that clarifies the theoretical foundations, investigates its benefits, and provides information about its real-world implementation. [31] worked on an important mathematical model known as the conformable stochastic Kraenkel–Manna–Merle system and used the modified version of the extended direct algebraic method. The obtained soliton solution describes the magnetic field phenomena in zero conductivity ferromagnets and successfully plots the solution in 2D and 3D graphs. Many techniques have been used by different researchers for the nonlinear fractional-order evolution equations, such as the exp-function method [32], the exp $\left(-\mathrm{\Phi }\left(\xi \right)\right)$ method [33], the extended F-expansion [34], the new Kudryashov technique [35], the $G^{\prime }/G$-expansion method [36], $\left(G^{\prime }/G,1/G\right)$-expansion method [37], the extended tanh technique [38], the ${\varphi }^6$-expansion technique [39], and sine–cosine method [40]. The more comprehensive studies can be found in [41–46].

The fractional-order derivatives sometimes vary with time, and in that case, it is more suitable to describe the complex phenomena as in the porous medium or medium in structure [47, 48]. In a variable-order operator, the order may vary with time or space or space–time. [49] explained the real-world phenomenon, which shows that fractional-order behavior may vary with time and space. In the review paper, [50] discussed the details of the memory characteristics of variable-order operators such as memory property, fading memory, order memory, and non-local property. The variable-order fractional derivative can be defined as $\alpha \left(x,t\right)$, which is the function of the independent variables $x$ and $t$. Most of the researchers have worked on variable-order fractional differential equations numerically, and no one has worked on analytical methods. Furthermore, the comprehensive study can be found in [51–54]. This study focused on finding the closed-form traveling wave solution of the nonlinear variable-order fractional partial differential equations to cover the abovementioned gap. The considered equations are the nonlinear variable-order fractional modified Kawahara equation and $\left(2+1\right)$-dimensional variable-order fractional Burger’s hierarchy equation solved by the exponential rational function method. The constructed new closed-form solutions are plotted in 3D form, which confirms that the closed-form traveling wave solutions can also be found successfully for the nonlinear variable-order fractional partial differential equations.

The rest of the paper is organized as follows; Section 2 explains the basic Caputo fractional formula of variable order and discusses the methodology of the exponential rational function method. Similarly, Section 4 implements the proposed method to the VOF-MKE and VOF-BHE. Section 5 consists of results and discussion. Section 6 presents the conclusion.

2 Caputo fractional derivative

This section presents Caputo’s fractional derivative of variable order and their properties. Let the function $u\left(x,y,\dots ,t\right)$ of variable-order derivative be $\gamma \left(x,y,\dots t\right)$ and their values varying between 0 and 1 are defined as follows (Eq. 1): [50].

${{}_0^{c}D}_t^{\gamma \left(x,y,\dots t\right)}u\left(x,y,\dots ,t\right)=\left\{\begin{array}{c}\frac{1}{\mathrm{\Gamma }\left(1+\gamma \left(x,y,\dots t\right)\right)}{\int }_0^t\frac{u^{\prime }\left(x,y,..,t\right)}{\mathrm{\Gamma }{\left(t-\xi \right)}^{\gamma \left(x,y,\dots t\right)}}d\xi ,0<\gamma \left(x,y,\dots t\right)<1,\\ u^{\prime }\left(x,y,\dots ,t\right),\gamma \left(x,y,\dots t\right)=1.\end{array}\right.(1)$

The properties are as follows (Eq. 2):

${{}_0^{c}D}_t^{\gamma \left(x,y,\dots t\right)}{t}^{\beta }=\frac{\mathrm{\Gamma }\left(1-\beta \right)}{\mathrm{\Gamma }\left(1-\beta +\gamma \left(x,y,\dots t\right)\right)}{t}^{\beta -\gamma \left(x,y,\dots t\right)},0<\gamma \left(x,y,\dots t\right)<1.(2)$

3 Exponential rational function method

Consider that the following nonlinear VO-FDE of variable-order $\gamma \left(x,y,\dots ,t\right)$ is given as

$F\left(u,D_t^{\gamma \left(x,y,\dots t\right)}u,D_x^{2\gamma \left(x,y,\dots t\right)}u,D_t^{\gamma \left(x,y,\dots t\right)}{D}_x^{\gamma \left(x,y,\dots t\right)}u,D_y^{2\gamma \left(x,y,\dots t\right)}u,\dots \right)=0.(3)$

Here, $F$ is a polynomial in $u$ and $\gamma \left(x,y,\dots t\right)$ represents the fractional variable order. Moreover, the variable-order fractional transformation is as follows [17]:

$u\left(x,y,\dots ,t\right)=U\left(\xi \right),\xi =\frac{k{x}^{\gamma \left(x,y,\dots ,t\right)}+{ly}^{\gamma \left(x,y,\dots ,t\right)}+\dots -\omega t^{\gamma \left(x,y,\dots ,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,y,\dots ,t\right)\right)}.(4)$

Reduce Eq. 3 into the nonlinear ODE as follows:

$F\left(U,{\omega U}^{\prime },k^2{U}^{″},\omega k{U}^{″},{\omega }^2{U}^{″}\dots \right)=0.(5)$

Here, $l,\omega$, and $k$ are the constants, and let the solution for the above equation be in the form of

$U\left(\xi \right)={\displaystyle {\sum }_{k=0}^M}\frac{a_k}{{\left(1+{\mathrm{e}}^{\left(\xi \right)}\right)}^k}.(6)$

Here, M can be calculated by equating the highest-order linear term with the highest-order nonlinear term.

By substituting Eq. 6 into Eq. 5, the obtained result is an exponential function. The similar power of the exponential term is equated, and the obtained system of equations is solved simultaneously. The values of the unknown parameters in Eq. 6 are substituted and then Eq. 6 is put into Eq. 5. The obtained equation is put into Eq. 4, and the resultant equations are the series of the exact solution for Eq. 3.

4 Applications

In this section, the nonlinear space-time VO-FDEs, namely, the modified Kawahara equation and (2 + 1)-D VOF-BHE, is solved using the exponential rational function method as follows.

4.1 The variable-order fractional modified Kawahara equation

Consider the nonlinear space-time VOF-MKE as

$D_t^{\gamma \left(x,t\right)}u+6u^2{D}_x^{\gamma \left(x,t\right)}u+D_x^{3\gamma \left(x,t\right)}u-D_x^{5\gamma \left(x,t\right)}u=0,t>0,0<\gamma \left(x,t\right)<1.(7)$

The variable-order transformation $\xi =\frac{k{x}^{\gamma \left(x,t\right)}-\omega t^{\gamma \left(x,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,t\right)\right)}$ is used to reduce Eq. 7 into the ODE [17], as follows

$-\omega U+2k{U}^3+k^3{U}^{″}-k^5{U}^{\left(iv\right)}.(8)$

The high-order linear term with the nonlinear term was balanced to find the value of $M$ as

$M+4=3M,$

and $M=2.$

Substituting the value of $M$ in Eq. 6, we obtained the trial solution for Eq. 8.

$U=a_0+\frac{a_1}{\left(1+e^{\left(\xi \right)}\right)}+\frac{a_2}{{\left(1+e^{\left(\xi \right)}\right)}^2},(9)$

By substituting Eq. 9 into Eq. 8, the algebraic equation is obtained in terms of ${\left(e^{\xi }\right)}^{m}where\left(m=0,1,2,\dots .\right)$, and by separating the same power of ${\left(\exp \left(\xi \right)\right)}^n$, we obtain

${\left(e^{\xi }\right)}^0:12k{a}_0{a}_1{a}_2-\omega \left(a_0+a_1+a_2\right)+2k\left(a_0^3+a_1^3+a_2^3\right)+6k{a}_0\left(a_0{a}_1+a_1^2+a_2^2\right)+6k{a}_2\left(a_0^2+a_1^2+a_2^2\right)=0,$

$\begin{array}{l}{\left(e^{\xi }\right)}^1:24k{a}_0\left(a_1^2+a_0{a}_2\right)+30k{a}_0^2{a}_1+12k{a}_2\left(a_0{a}_2+a_2\right)+6k{a}_1{a}_2^2-k^3\left(a_1+2a_2-k^2{a}_1-2k^2{a}_2\right)\\ +36k{a}_0{a}_1{a}_2-\omega \left(6a_0+5a_1\right)-4\omega a_2+6k\left(2a_0^3+a_1^3\right)=0,\end{array}$

${\left(e^{\xi }\right)}^2:36k{a}_0\left(a_1^2+a_0{a}_2+a_1{a}_2\right)+60k{a}_1{a}_0^2+6k\left(a_0{a}_2^2+a_1^2{a}_2+a_1^3\right)-2k^3\left(a_1+5k^2{a}_1+18k^2{a}_2\right)-3\omega \left(5a_0+2a_2\right)-10\left(\omega a_1-3k{a}_0^3\right)=0,$

${\left(e^{\xi }\right)}^3:60k{a}_0^2{a}_1+24k{a}_0\left(a_1^2+a_0{a}_2\right)+2k{a}_1^3+6k{a}_2\left(k^2+11k^4+2a_0{a}_1\right)+40k{a}_0^3-2\omega \left(10a_0+5a_1+2a_2\right)=0,$

${\left(e^{\xi }\right)}^4:6k{a}_0\left(a_1^2+a_0{a}_2\right)+2k^3\left(a_1+2a_2\right)+2k^5\left(5a_1-8a_2\right)-15a_0\left(\omega -2k{a}_0^2\right)-\omega \left(a_2+5a_1\right)+30k{a}_0^2{a}_1=0,$

${\left(e^{\xi }\right)}^5:6k{a}_0^2\left(a_1+2a_0\right)+k^3{a}_1\left(1-k^2\right)-\omega \left(6a_0+a_1\right)=0,$

${\left(e^{\xi }\right)}^6:2k{a}_0^3-\omega a_0=0.$

The above system of equations is solved simultaneously, and the obtained values are given as follows:

Set. 1: $a_0=0,a_1=\frac{2\sqrt{3}}{\sqrt{5}},a_2=-\frac{2\sqrt{3}}{\sqrt{5}},\omega =\frac{4}{25\sqrt{5}},k=\frac{1}{\sqrt{5}}.$

Set. 2: $\begin{array}{l}{a}_0=\sqrt{\frac{11-3i\sqrt{15}}{40}},a_1=5\sqrt{\frac{11-3i\sqrt{15}}{40}}\left(\frac{-5+i\sqrt{15}}{20}-\frac{5}{2}\right),a_2=-5\sqrt{\frac{11-3i\sqrt{15}}{40}}\left(\frac{-5+i\sqrt{15}}{20}-\frac{5}{2}\right),\\ \omega =-\frac{1}{200}\left(\frac{-11+3i\sqrt{15}}{4}\right)\sqrt{-25+5i\sqrt{15}},k=\frac{1}{10}\sqrt{-25+5i\sqrt{15}}.\end{array}$

Case. 1: $u_1\left(x,t\right)=\frac{2\sqrt{3}{e}^{\left(\frac{k{x}^{\gamma \left(x,t\right)}-\omega t^{\gamma \left(x,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,t\right)\right)}\right)}}{\sqrt{5}{\left(1+e^{\left(\frac{k{x}^{\gamma \left(x,t\right)}-\omega t^{\gamma \left(x,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,t\right)\right)}\right)}\right)}^2}.$

Case. 2: $\begin{array}{l}{u}_2\left(x,t\right)=-\frac{1}{80{\left(1+e^{\left(\frac{k{x}^{\gamma \left(x,t\right)}-\omega t^{\gamma \left(x,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,t\right)\right)}\right)}\right)}^2}\\ \left(\left(5i-3\sqrt{15}\right)\left(2-11e^{\left(\frac{k{x}^{\gamma \left(x,t\right)}-\omega t^{\gamma \left(x,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,t\right)\right)}\right)}+2e^{2\left(\frac{k{x}^{\gamma \left(x,t\right)}-\omega t^{\gamma \left(x,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,t\right)\right)}\right)}+i\sqrt{15}{e}^{\left(\frac{k{x}^{\gamma \left(x,t\right)}-\omega t^{\gamma \left(x,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,t\right)\right)}\right)}\right)\right).\end{array}$

4.2 The variable-order fractional $\left(\mathrm{2}+\mathrm{1}\right)$-dimensional Burger hierarchy equation

Consider the nonlinear $\left(2+1\right)$-D VOF-BHE to study the traveling wave solution using the exponential function method.

$D_t^{\gamma \left(x,y,t\right)}u+\mathrm{\Psi }{D}_x^{2\gamma \left(x,y,t\right)}u+2\mathrm{\Psi }u{D}_x^{\gamma \left(x,y,t\right)}u+\mathrm{\Omega }\left(D_x^{\gamma \left(x,y,t\right)}u+D_y^{\gamma \left(x,y,t\right)}u\right)=0,$

$0<\gamma \left(x,y,t\right)<1.(10)$

The variable-order transformation $\xi =\frac{k{x}^{\gamma \left(x,y,t\right)}+\rho y^{\gamma \left(x,y,t\right)}-\omega t^{\gamma \left(x,y,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,y,t\right)\right)}$ is used to reduce Eq. 10 into the ODE [17] as follows:

$-\omega U+\mathrm{\Psi }{k}^2{U}^{\prime }+\mathrm{\Psi }k{U}^2+\mathrm{\Omega }\left(kU+\rho U\right)=0.(11)$

The high-order linear term with the highest-order nonlinear term is balanced to find the value of $M.$ as follows:

$M+1=2M,$

and $M=1.$

By substituting the value of $M$ in Eq. 6, we obtained the trial solution for Eq. 11.

$U=a_0+\frac{a_1}{\left(1+e^{\left(\xi \right)}\right)},(12)$

By substituting Eqs 12 into Eq. 11, the algebraic equation was obtained in terms of $\left({\mathrm{e}}^{\left(\xi \right)}\right)$, and by separating the same power of $\left(\exp \left(-\varphi \left(\xi \right)\right)\right)$, we obtain

${\left({\mathrm{e}}^{\left(\xi \right)}\right)}^0=-\omega a_0-\omega a_1+\mathrm{\Psi }k{a}_0^2+2\mathrm{\Psi }k{a}_0{a}_1+\mathrm{\Omega }{a}_{0}k+\mathrm{\Omega }{a}_0\rho +\mathrm{\Omega }{a}_{1}k+\mathrm{\Omega }{a}_1\rho =0,$

${\left({\mathrm{e}}^{\left(\xi \right)}\right)}^1=-2\omega a_0-\omega a_1-\mathrm{\Psi }{k}^2{a}_1+2\mathrm{\Psi }k{a}_0^2+2\mathrm{\Psi }{k\mathrm{a}}_0{\mathrm{a}}_1+2\mathrm{\Omega }{a}_{0}k+2\mathrm{\Omega }{a}_0\rho +\mathrm{\Omega }{a}_{1}k+\mathrm{\Omega }{a}_1\rho =0,$

${\left({\mathrm{e}}^{\left(\xi \right)}\right)}^2=-\omega a_0+\lambda k{a}_0^2+\mathrm{\Omega }{a}_{0}k+\mathrm{\Omega }{a}_0\rho =0.$

The above system of equations is solved simultaneously, and the obtained values are given as follows:

Set 1. $a_0=-a_1,\omega =\mathrm{\Psi }{\mathrm{a}}_1-\mathrm{\Omega }{\mathrm{a}}_1+\mathrm{\Omega }\rho ,k=-a_1.$

Set 2. $a_0=0,a_1=-k,\omega =-\mathrm{\Psi }{\mathrm{k}}^2+\mathrm{\Omega }k+\mathrm{\Omega }\rho .$

Substituting values from sets 1 and 2 in Eq. 12, we obtained the following solutions:

$u_1\left(x,y,t\right)=-\frac{a_1{e}^{\frac{k{x}^{\gamma \left(x,y,t\right)}+\rho y^{\gamma \left(x,y,t\right)}-\omega t^{\gamma \left(x,y,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,y,t\right)\right)}}}{1+e^{\frac{k{x}^{\gamma \left(x,y,t\right)}+\rho y^{\gamma \left(x,y,t\right)}-\omega t^{\gamma \left(x,y,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,y,t\right)\right)}}}.$

and

$u_2\left(x,y,t\right)=-\frac{k}{1+e^{\frac{k{x}^{\gamma \left(x,y,t\right)}+\rho y^{\gamma \left(x,y,t\right)}-\omega t^{\gamma \left(x,y,t\right)}}{\mathrm{\Gamma }\left(1+\gamma \left(x,y,t\right)\right)}}}.$

5 Discussion

In this segment, the graphical representation of various kinds of exact traveling wave solutions was discussed for the proposed VO-FDEs solved by the exponential rational function method. Some closed-form traveling wave solutions are generated to the recommended equations as variable-order fractional modified Kawahara and variable-order fractional (2 + 1)-dimensional Burger hierarchy equations. Figures 1, 2 represent the 3D graphical solution for the space–time variable-order fractional modified Kawahara equation. Figure 1 shows the periodic soliton solution for the fixed values of the parameters as $\omega =-\frac{1}{2},k=2,a_0=-\frac{1}{3},a_1=-\frac{1}{4},L=-\frac{1}{3},a_2=5,$ and the variable-order as $\gamma \left(x,t\right)=\cos \left(xt+\frac{1}{100}\right).$ Figure 2 shows the shape of the soliton solution at $\omega =-\frac{1}{2},k=2,a_0=-\frac{1}{3},a_1=-\frac{1}{4},L=-\frac{1}{3},a_2=5,\gamma \left(x,t\right)=\frac{\left(xt\right)-{\left(xt\right)}^3}{120}.$ Figures 3–5 represent the 3D plots for the nonlinear space–time variable-order fractional (2 + 1)-dimensional Burger hierarchy equation. Figure 4 shows the periodic shape soliton at $\omega =-\frac{1}{2},k=2,a_0=-\frac{1}{3},a_1=1,\gamma \left(x,y,t\right)={\cos }^2\left(xt+\frac{1}{100}\right),\mathrm{\Psi }=2,\mathrm{\Omega }=2,\mathrm{\rho }=3,\mathrm{y}=5$. Figures 3, 5 represent other shapes of solitons at $\omega =-0.5,k=2,a_0=-\frac{1}{3},a_1=-\frac{1}{4},\gamma \left(x,y,t\right)=\frac{{\left(xt\right)}^3-xt}{120},\mathrm{\Psi }=5,\mathrm{\Omega }=2,\mathrm{\rho }=2,\mathrm{y}=1$ for the closed-form solution $u_1\left(x,y,t\right)$ and at $\omega =-1,k=2,a_0=5,a_1=-1,\gamma \left(x,y,t\right)=\left(\frac{xt}{50}+\frac{2\mathrm{\pi }}{5}\right),\mathrm{\Psi }=5,\mathrm{\Omega }=2,\mathrm{\rho }=2,\mathrm{y}=0.5$ for the closed-form solution $u_2\left(x,y,t\right)$, respectively. The discussion confirmed that the closed-form traveling wave solution can be found for any type of nonlinear space–time variable-order fractional evolution equations.

Figure 1

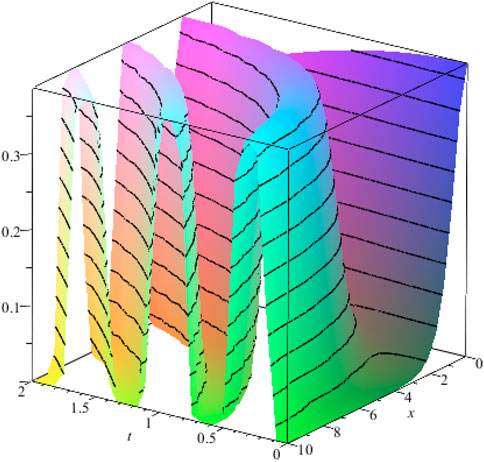
Figure 1. Graph for the solution $u_1\left(x,t\right)$ at $\omega =-\frac{1}{2},k=2,a_0=-\frac{1}{3},a_1=-\frac{1}{4},$ $L=-\frac{1}{3},a_2=5,\gamma \left(x,t\right)=\cos \left(xt+\frac{1}{100}\right).$

Figure 2

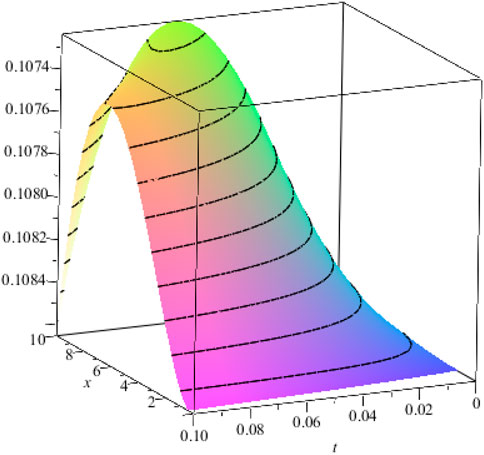
Figure 2. Graph for the solution $u_1\left(x,t\right)$ at $\omega =-\frac{1}{2},k=2,a_0=-\frac{1}{3},a_1=-\frac{1}{4},$ $L=-\frac{1}{3},a_2=5,\gamma \left(x,t\right)=\frac{\left(xt\right)-{\left(xt\right)}^3}{120}.$

Figure 3

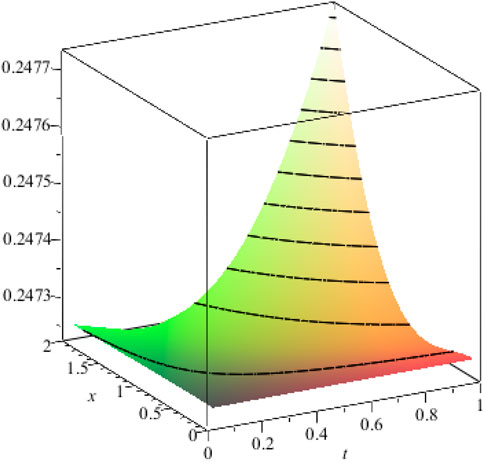
Figure 3. Graph for the solution $u_1\left(x,y,t\right)$ at $\omega =-0.5,k=2,a_0=-\frac{1}{3},a_1=-\frac{1}{4},$ $\gamma \left(x,y,t\right)=\frac{{\left(xt\right)}^3-xt}{120},\mathrm{\Psi }=5,\mathrm{\Omega }=2,\mathrm{\rho }=2,\mathrm{y}=1.$

Figure 4

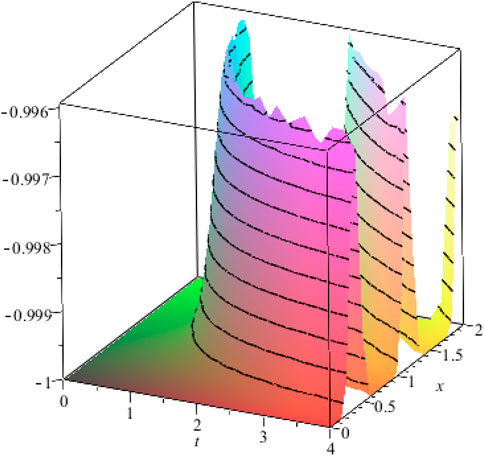
Figure 4. Graph for the solution $u_1\left(x,y,t\right)$ at $\omega =-\frac{1}{2},k=2,a_0=-\frac{1}{3},a_1=1,$ $\gamma \left(x,y,t\right)={\cos }^2\left(xt+\frac{1}{100}\right),\mathrm{\Psi }=2,\mathrm{\Omega }=2,\mathrm{\rho }=3,\mathrm{y}=5.$

Figure 5

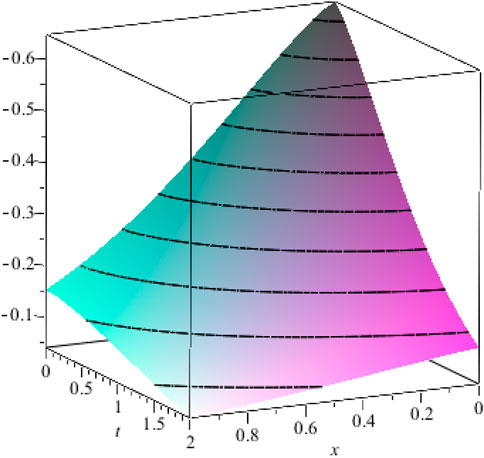
Figure 5. Graph for the solution $u_2\left(x,y,t\right)$ at $\omega =-1,k=2,a_0=5,a_1=-1,$ $\gamma \left(x,y,t\right)=\left(\frac{xt}{50}+\frac{2\mathrm{\pi }}{5}\right),\mathrm{\Psi }=5,\mathrm{\Omega }=2,\mathrm{\rho }=2,\mathrm{y}=0.5.$

6 Conclusion

In this article, we studied the closed-form solution for the nonlinear variable-order fractional evolution equation. The exponential rational function method is considered for VOF-MKE and VOF-BHE, and various new exact traveling wave solutions are successfully obtained for the arbitrary values of the parameters. The closed-form traveling wave solutions are in the form of periodic and other shapes of solitons. The obtained solution might be further beneficial and more achievable on the contrivances of the complex physical phenomena that occur in different fields. The result confirms that the variable-order FDEs are more efficient and feasible. Finally, the considered approach is a more powerful tool to obtain the closed-form traveling wave solutions to VOF-DEs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

MA: writing–review and editing, investigation, conceptualization, and funding acquisition. UA: writing–original draft, supervision, software, methodology, and investigation. AG: writing–review and editing, validation, resources, methodology, and formal analysis.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study is supported via funding from Prince Sattam Bin Abdulaziz University project number (PSAU/2024/R/1445).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bilal M, Ren J, Younas U. Stability analysis and optical soliton solutions to the nonlinear Schrödinger model with efficient computational techniques. Opt Quant Electron (2021) 53(7):406–19. doi:10.1007/s11082-021-03040-5

CrossRef Full Text | Google Scholar

2. Russell JS. Report on waves: made to the meetings of the British Association (1845). p. 1842–3.

Google Scholar

3. Haque MM, Akbar MA, Rezazadeh H, Bekir A. A variety of optical soliton solutions in closed-form of the nonlinear cubic quintic Schrödinger equations with beta derivative. Opt Quan Elect (2023) 55(13):1144. doi:10.1007/s11082-023-05470-9

CrossRef Full Text | Google Scholar

4. Wang KJ, Wang GD. Exact traveling wave solutions for the system of the ion sound and Langmuir waves by using three effective methods. Results Phys (2022) 35:105390. doi:10.1016/j.rinp.2022.105390

CrossRef Full Text | Google Scholar

5. Islam SR, Arafat SY, Wang H. Abundant closed-form wave solutions to the simplified modified Camassa-Holm equation. J Ocean Eng Sci (2023) 8(3):238–45. doi:10.1016/j.joes.2022.01.012

CrossRef Full Text | Google Scholar

6. Kumar S, Mann N. Abundant closed-form solutions of the (3+ 1)-dimensional Vakhnenko-Parkes equation describing the dynamics of various solitary waves in ocean engineering. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.04.007

CrossRef Full Text | Google Scholar

7. Kumar S, Kumar A. Abundant closed-form wave solutions and dynamical structures of soliton solutions to the (3+ 1)-dimensional BLMP equation in mathematical physics. J Ocean Eng Sci (2022) 7(2):178–87. doi:10.1016/j.joes.2021.08.001

CrossRef Full Text | Google Scholar

8. Muhammad T, Hamoud AA, Emadifar H, Hamasalh FK, Azizi H, Khademi M. Traveling wave solutions to the Boussinesq equation via Sardar sub-equation technique. AIMS Math (2022) 7(6):11134–49. doi:10.3934/math.2022623

CrossRef Full Text | Google Scholar

9. Mohanty SK, Kravchenko OV, Dev AN. Exact traveling wave solutions of the Schamel Burgers’ equation by using generalized-improved and generalized. Results Phys (2022) 33:105124. doi:10.1016/j.rinp.2021.105124

CrossRef Full Text | Google Scholar

10. Shakeel M, Shah NA, Chung JD. Application of modified exp-function method for strain wave equation for finding analytical solutions. Ain Shams Eng J (2023) 14(3):101883. doi:10.1016/j.asej.2022.101883

CrossRef Full Text | Google Scholar

11. Almatrafi MB. Abundant traveling waves and numerical solutions for the Novikov-Veselov system with their stability and accuracy. Applicable Anal (2023) 102(8):2389–402. doi:10.1080/00036811.2022.2027381

CrossRef Full Text | Google Scholar

12. Yao SW, Tariq KU, Inc M, Tufail RN. Modulation instability analysis and soliton solutions of the modified BBM model arising in dispersive medium. Results Phys (2023) 46:106274. doi:10.1016/j.rinp.2023.106274

CrossRef Full Text | Google Scholar

13. Zhang R, Shakeel M, Turki NB, Shah NA, Tag SM. Novel analytical technique for mathematical model representing communication signals: a new travelling wave solutions. Results Phys (2023) 51:106576. doi:10.1016/j.rinp.2023.106576

CrossRef Full Text | Google Scholar

14. Hussain A, Usman M, Zaman FD, Ibrahim TF, Dawood AA. Symmetry analysis, closed-form invariant solutions and dynamical wave structures of the Benney-Luke equation using optimal system of Lie subalgebras. Chin J Phys (2023) 84:66–88. doi:10.1016/j.cjph.2023.04.019

CrossRef Full Text | Google Scholar

15. AlBaidani MM, Ali U, Ganie AH. Nonlinear fractional-order differential equations: new closed-form traveling-wave solutions. Open Phys (2024) 22(1):20230192. doi:10.1515/phys-2023-0192

CrossRef Full Text | Google Scholar

16. Ali U, Naeem M, Alahmadi R, Abdullah FA, Khan MA, Ganie AH. An investigation of a closed-form solution for non-linear variable-order fractional evolution equations via the fractional Caputo derivative. Front Phys (2023) 11:1114319. doi:10.3389/fphy.2023.1114319

CrossRef Full Text | Google Scholar

17. Ali U, Ahmad H, Abu-Zinadah H. Soliton solutions for nonlinear variable-order fractional Korteweg–de Vries (KdV) equation arising in shallow water waves. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.06.011

CrossRef Full Text | Google Scholar

18. Akbar MA, Abdullah FA, Islam MT, Al Sharif MA, Osman MS. New solutions of the soliton type of shallow water waves and superconductivity models. Results Phys (2023) 44:106180. doi:10.1016/j.rinp.2022.106180

CrossRef Full Text | Google Scholar

19. Zaman UHM, Arefin MA, Akbar MA, Uddin MH. Solitary wave solution to the space-time fractional modified Equal Width equation in plasma and optical fiber systems. Results Phys (2023) 52:106903. doi:10.1016/j.rinp.2023.106903

CrossRef Full Text | Google Scholar

20. Islam MT, Akbar MA, Azad MAK. Traveling wave solutions in closed form for some nonlinear fractional evolution equations related to conformable fractional derivative. AIMS Math (2018) 3(4):625–46. doi:10.3934/math.2018.4.625

CrossRef Full Text | Google Scholar

21. Zaman UHM, Arefin MA, Akbar MA, Uddin MH. Stable and effective traveling wave solutions to the non-linear fractional Gardner and Zakharov–Kuznetsov–Benjamin–Bona–Mahony equations. Partial Differential Equations Appl Math (2023) 7:100509. doi:10.1016/j.padiff.2023.100509

CrossRef Full Text | Google Scholar

22. Ali U, Ganie AH, Khan I, Alotaibi F, Kamran K, Muhammad S, et al. Traveling wave solutions to a mathematical model of fractional order (2+ 1)-dimensional breaking soliton equation. Fractals (2022) 30(05):2240124. doi:10.1142/s0218348x22401247

CrossRef Full Text | Google Scholar

23. Behera S, Mohanty S, Virdi JPS. Analytical solutions and mathematical simulation of traveling wave solutions to fractional order nonlinear equations. Partial Differential Equations Appl Math (2023) 8:100535. doi:10.1016/j.padiff.2023.100535

CrossRef Full Text | Google Scholar

24. Das N, Ray SS. Exact traveling wave solutions and soliton solutions of conformable M-fractional modified nonlinear Schrödinger model. Optik (2023) 287:171060. doi:10.1016/j.ijleo.2023.171060

CrossRef Full Text | Google Scholar

25. Alabedalhadi M, Shqair M, Al-Omari S, Al-Smadi M. Traveling wave solutions for complex space-time fractional kundu-eckhaus equation. Mathematics (2023) 11(2):404. doi:10.3390/math11020404

CrossRef Full Text | Google Scholar

26. Sang X, Zhang Z, Yang H, Han X. Exact traveling wave solutions of the local fractional bidirectional propagation system equations. Fractal and Fractional (2022) 6(11):653. doi:10.3390/fractalfract6110653

CrossRef Full Text | Google Scholar

27. Bekir A, Güner Ö. Exact solutions of nonlinear fractional differential equations by (G′/G)-expansion method. Chin Phys B (2013) 22(11):110202. doi:10.1088/1674-1056/22/11/110202

CrossRef Full Text | Google Scholar

28. Yasmin H, Aljahdaly NH, Saeed AM, Shah R. Investigating symmetric soliton solutions for the fractional coupled konno–onno system using improved versions of a novel analytical technique. Mathematics (2023) 11(12):2686. doi:10.3390/math11122686

CrossRef Full Text | Google Scholar

29. Yasmin H, Alshehry AS, Ganie AH, Mahnashi AM, Shah R. Perturbed gerdjikov–ivanov equation: soliton solutions via backlund transformation. Optik (2024) 298:171576. doi:10.1016/j.ijleo.2023.171576

CrossRef Full Text | Google Scholar

30. Alshehry AS, Yasmin H, Ganie AH, Ahmad MW, Shah R. Optimal auxiliary function method for analyzing nonlinear system of coupled Schrödinger–KdV equation with Caputo operator. Open Phys (2023) 21(1):20230127. doi:10.1515/phys-2023-0127

CrossRef Full Text | Google Scholar

31. Yasmin H, Alshehry AS, Ganie AH, Shafee A, Shah R. Noise effect on soliton phenomena in fractional stochastic Kraenkel-Manna-Merle system arising in ferromagnetic materials. Scientific Rep (2024) 14(1):1810. doi:10.1038/s41598-024-52211-3

CrossRef Full Text | Google Scholar

32. Bekir A, Güner Ö, Cevikel AC. Fractional complex transform and exp-function methods for fractional differential equations. Abstract Appl Anal (2013) 2013:1–8. Hindawi. doi:10.1155/2013/426462

CrossRef Full Text | Google Scholar

33. Ali U, Mastoi S, Othman WA, Khater MM, Sohail M. Computation of traveling wave solution for a nonlinear variable-order fractional model of modified equal width equation. AIMS Math (2021) 6(9):10055–69. doi:10.3934/math.2021584

CrossRef Full Text | Google Scholar

34. Tariq KU, Javed R. Some traveling wave solutions to the generalized 3+1-dimensional Korteweg–de Vries–Zakharov–Kuznetsov equation in plasma physics. Math Methods Appl Sci (2023) 46(12):12200–16. doi:10.1002/mma.8596

CrossRef Full Text | Google Scholar

35. Rezazadeh H, Ullah N, Akinyemi L, Shah A, Mirhosseini-Alizamin SM, Chu YM, et al. Optical soliton solutions of the generalized non-autonomous nonlinear Schrödinger equations by the new Kudryashov's method. Results Phys (2021) 24:104179. doi:10.1016/j.rinp.2021.104179

CrossRef Full Text | Google Scholar

36. Shahoot AM, Alurrfi KA, Elmrid MO, Almsiri AM, Arwiniya AM. The (G′/G)-expansion method for solving a nonlinear PDE describing the nonlinear low-pass electrical lines. J Taibah Univ Sci (2019) 13(1):63–70. doi:10.1080/16583655.2018.1528663

CrossRef Full Text | Google Scholar

37. Miah MM, Ali HS, Akbar MA, Seadawy AR. New applications of the two variable (G′/G, 1/G)-expansion method for closed-form traveling wave solutions of integro-differential equations. J Ocean Eng Sci (2019) 4(2):132–43. doi:10.1016/j.joes.2019.03.001

CrossRef Full Text | Google Scholar

38. Zahran Emad HM, Khater Mostafa MA. Modified extended tanh-function method and its applications to the Bogoyavlenskii equation. Appl Math Model (2016) 40(3):1769–75. doi:10.1016/j.apm.2015.08.018

CrossRef Full Text | Google Scholar

39. Seadawy AR, Bilal M, Younis M, Rizvi STR, Althobaiti S, Makhlouf MM. Analytical mathematical approaches for the double-chain model of DNA by a novel computational technique. Chaos Solitons Fractals (2021) 144:110669. doi:10.1016/j.chaos.2021.110669

CrossRef Full Text | Google Scholar

40. Muhammad UA, Salisu A. Exact solutions of the (3+1) generalized fractional nonlinear wave equation with gas bubbles. Int J Sci Res Math Stat Sci (2022) 9(6).

Google Scholar

41. Alam MN, Seadawy AR, Baleanu D. Closed-form wave structures of the space-time fractional Hirota–Satsuma coupled KdV equation with nonlinear physical phenomena. Open Phys (2020) 18(1):555–65. doi:10.1515/phys-2020-0179

CrossRef Full Text | Google Scholar

42. Habib MA, Ali HS, Miah MM, Akbar MA. The generalized Kudryashov method for new closed-form traveling wave solutions to some NLEEs. Aims Math (2019) 4(3):896–909. doi:10.3934/math.2019.3.896

CrossRef Full Text | Google Scholar

43. Rafiq MN, Majeed A, Inc M, Kamran M. New traveling wave solutions for space-time fractional modified equal width equation with beta derivative. Phys Lett A (2022) 446:128281. doi:10.1016/j.physleta.2022.128281

CrossRef Full Text | Google Scholar

44. Khatun MA, Arefin MA, Uddin MH, İnç M, Akbar MA. An analytical approach to the solution of fractional-coupled modified equal width and fractional-coupled Burgers equations. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.03.016

CrossRef Full Text | Google Scholar

45. Babajanov B, Abdikarimov F. New exact soliton and periodic wave solutions of the nonlinear fractional evolution equations with additional term. Partial Differential Equations Appl Math (2023) 8:100567. doi:10.1016/j.padiff.2023.100567

CrossRef Full Text | Google Scholar

46. Ali HS, Habib MA, Miah MM, Miah MM, Akbar MA. Diverse solitary wave solutions of fractional order Hirota-Satsuma coupled KdV system using two expansion methods. Alexandria Eng J (2023) 66:1001–14. doi:10.1016/j.aej.2022.12.021

CrossRef Full Text | Google Scholar

47. Cao J, Qiu Y, Song G. A compact finite difference scheme for variable order sub-diffusion equation. Commun Nonlinear Sci Numer Simul (2017) 48:140–9. doi:10.1016/j.cnsns.2016.12.022

CrossRef Full Text | Google Scholar

48. Sun H, Chen W, Li C, Chen Y. Finite difference schemes for variable-order time-fractional diffusion equation. Int J Bifurc Chaos (2012) 22:1250085. doi:10.1142/s021812741250085x

CrossRef Full Text | Google Scholar

49. Lorenzo CF, Hartley TT. Variable order and distributed order fractional operators. Nonlinear Dyn (2002) 29:57–98. doi:10.1023/a:1016586905654

CrossRef Full Text | Google Scholar

50. Patnaik S, Hollkamp JP, Semperlotti F. Applications of variable-order fractional operators: a review. Proc R Soc A (2020) 476(2234):20190498. doi:10.1098/rspa.2019.0498

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Mohapatra SN, Mishra SR, Jena P. Time-fractional differential equations with variable order using RDTM and ADM: application to infectious-disease model. Int J Appl Comput Math (2022) 8(3):138. doi:10.1007/s40819-022-01332-2

CrossRef Full Text | Google Scholar

52. Rittmann BE, McCarty PL. Variable-order model of bacterial-film kinetics. J Environ Eng Division (1978) 104(5):889–900. doi:10.1061/jeegav.0000825

CrossRef Full Text | Google Scholar

53. Sweilam NH, Al-Mekhlafi SM, Albalawi AO, Machado JT. Optimal control of variable-order fractional model for delay cancer treatments. Appl Math Model (2021) 89:1557–74. doi:10.1016/j.apm.2020.08.012

CrossRef Full Text | Google Scholar

54. Salama FM, Ali U, Ali A. Numerical solution of two-dimensional time fractional mobile/immobile equation using explicit group methods. Int J Appl Comput Math (2022) 8(4):188. doi:10.1007/s40819-022-01408-z

PubMed Abstract | CrossRef Full Text | Google Scholar