- School of Physics, Harbin Institute of Technology, Harbin, China
The measurement of the rotational velocity using the rotational Doppler effect (RDE) of a vortex beam is easily affected by atmospheric turbulence, leading to dispersed orbital angular momentum (OAM), and reduced measurement accuracy. This study investigates the optimal ability of the Gerchberg-Saxton (GS) phase retrieval algorithm to compensate for the optical field and enhance the velocity measurement accuracy within the optimal range of intrinsic parameters, such as the number of GS iterations, and extrinsic parameters, such as the atmospheric turbulence intensity and beam properties. Through detailed theoretical and simulation analyses, we demonstrate the outstanding effectiveness of the GS algorithm in improving the velocity measurement accuracy. Simulations conducted for a system-target distance of zS-T = 500 m show a 29.88% improvement in the velocity measurement accuracy and a 1.03-fold increase in the spectral signal-to-noise ratio (SSNR) within the optimal range. It showcases advantages that set it apart from other methods. This study reveals the threshold of the ability of GS algorithm to significantly enhance the rotational velocity measurement accuracy, providing valuable insights to precision measurements of rotational velocities in free-space applications.
1 Introduction
The vortex beam is characterized by its spiral wavefront structure with an orbital angular momentum (OAM) and a phase factor of exp(ilθ) [1]. When irradiated onto the surface of a rotating object, the vortex beam induces a rotational Doppler shift (RDS) related to the angular velocity of the object, which is known as the rotational Doppler effect (RDE) of the vortex beam [2]. Recent research has extensively explored the RDE, focusing on its intrinsic mechanism, expanding application scenarios, and optimizing rotational velocity measurements [3–9].
Although vortex beam detection offers high sensitivity in sensing applications, the beam is susceptible to the influence of random atmospheric turbulence in practical remote-sensing scenarios [10]. This causes a OAM spectrum dispersion [11], leading to a decrease in the spectral signal-to-noise ratio (SSNR) and rotational velocity measurement accuracy. In previous studies, Li et al. investigated the mode crosstalk phenomenon of vortex beams in atmospheric turbulence utilizing Monte Carlo phase screens and Fresnel diffraction methods [12]. Ren conducted experiments to investigate channel impairments caused by atmospheric turbulence, which affect interchannel multimode crosstalk, and system power loss in OAM multiplexed free-space optical links over distances exceeding 120 m [13]. Numerous other studies have examined the influence of atmospheric turbulence on the optical fields, crosstalk, system power loss, and bit error rate (BER), among other factors [14, 15]. Adaptive optics (AO) algorithms, such as the Shack-Hartmann (SH) wavefront correction method [16–18], stochastic parallel gradient descent (SPGD) [19], and the Wirtinger flow (WF) algorithm [20], and others [21–23], play a crucial role in mitigating the beam distortion caused by atmospheric turbulence. Among these methods, the Gerchberg-Saxton (GS) algorithm, a phase retrieval AO algorithm, utilizes the distorted wavefront to compensate for the received beam and has a wide range of applications [24–26]. However, the ability of phase retrieval algorithms to improve the rotational velocity measurement accuracy of vortex beam has not been widely discussed.
Through theoretical and simulation analyses, this study investigates the ability of the GS phase retrieval algorithm to compensate for the optical field and enhance the velocity measurement accuracy within the optimal range of intrinsic parameters, such as the number of GS iterations, and extrinsic parameters, such as the atmospheric turbulence intensity and beam property. Additionally, this study further broadens the scope of the phase retrieval algorithm in practical applications, providing a significant assistance for enhancing the precise measurement of remote rotational velocity in vortex beams application.
2 Simulation principles
2.1 RDE and velocity measurement accuracy
The Laguerre-Gaussian (LG) beam is most used for RDE measurements. Its complex amplitude can be represented as
The RDE occurs due to the deviation angle γ between the motion direction of photons in the vortex beam and the optical axis [28]. It can be effectively described using the velocity projection model [29], where
In Eq. 1, τ denotes the accumulation time of the Avalanche photodiode (APD). The SSNR is given by
The standard deviation of the angular velocity measurement can be obtained from the error transfer equation as follows.
According to Eq. 2, the rotational velocity measurement error depends on three factors:
(a) Detector accumulation time
APD with reasonably long accumulation time can increase the number of detected photons, provide stable and reliable results, and improve the statistical accuracy of the signal, thereby reducing the velocimetry error.
(b) SSNR
Detector system factors such as the grain noise, dark counts, and thermal noise can reduce the SSNR, leading to a decrease in the measurement accuracy. Therefore, a higher SSNR results in smaller rotational velocity measurement errors.
(c) Topological charge
As shown in the formula
2.2 GS phase retrieval algorithm
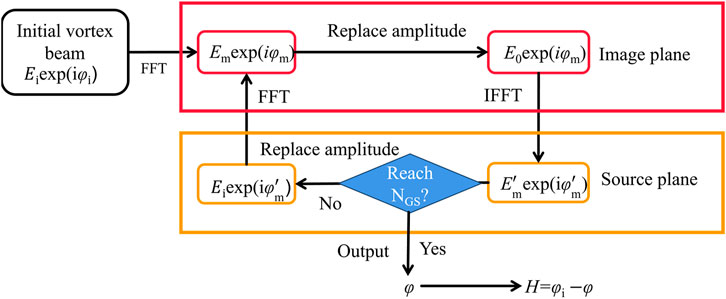
The basic principle of the GS algorithm is to iterate the optical intensity information according to the initial and distorted optical field, and obtain the pre-compensated phase screen through the algorithm calculation [32–34]. The distorted optical field achieves phase compensation through the correction of the pre-compensated phase screen. The flowchart of the GS algorithm is shown in Figure 1. Specifically, the complex amplitude of vortex beam Ei exp(i
2.3 Simulation design for rotational velocity extraction
The simulation was designed for rotational velocity extraction based on the following steps:
(a) The vortex beam, generated in the grating diffraction method, passes through a random phase screen to simulate atmospheric turbulence. The modal expansion method [2] is used to analyze the received optical field carrying the RDS after interacting with the rotating object. Barring any specialized treatment applied to the target, the different modes of scattered light are approximately uniformly distributed. Angular spectrum analysis is then performed on the received optical field. The expression is simplified and represented in the following form:
where
(b) The distorted beam is utilized to recovery the optical field using the GS algorithm, which iterates the light intensity information several times to obtain a pre-compensated phase screen.
(c) The recovered optical field is subjected to angular spectrum and spectral analyses based on Eq. 3. The RDS peak is extracted, and the rotational velocity and measurement accuracy of the object are obtained.
3 Velocimetry system design
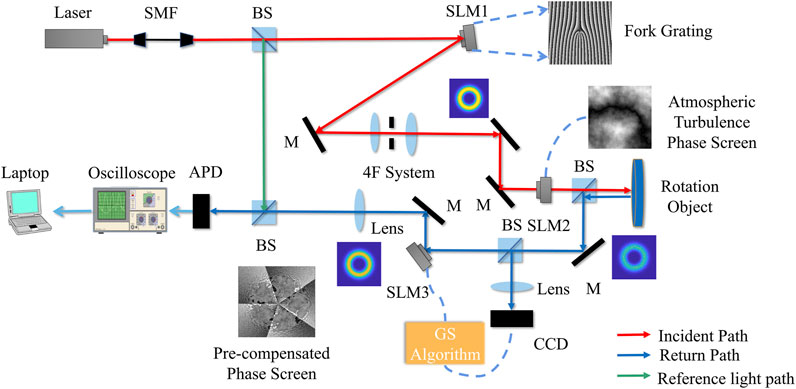
The schematic of the system design is displayed in Figure 2. The laser output a Gaussian mode beam at λ = 532 nm. The laser beam was coupled to a single-mode optical fiber (SMF) for collimation. The beam passed through spatial light modulator 1 (SLM1), loaded with a fork grating pattern, and generated a vortex beam. The vortex beam was obtained using a 4F system with an aperture that filtered the first-order diffraction modulation signal from the incident beam. The beam underwent distortion through SLM2, which loaded a random phase screen to simulate atmospheric turbulence using the power spectrum inversion method. The modified Von Karman spectrum [35] was used, and a subharmonic compensation method was adopted for the lack of low-frequency components present in the phase screen [36], with a compensation level of p = 3. The beam, after undergoing distortion, illuminated the rotating target surface. After passing through the beam splitter, the reflected echo beam was focused onto a Charge coupled device (CCD) to record the spot intensity. The distorted beam intensity was used as the iteration information for the GS algorithm to generate the pre-compensated phase screen, which was loaded onto SLM3. The transmitted echo beam passed through SLM3 to undergo phase compensation. After interfering with the reference light, an APD received and collected the photon signals, generating a temporal signal of the light intensity, which was Fourier-transformed to extract the RDS. The results were detected using an oscilloscope, and the data were processed to calculate the rotational velocity of the target. Figure 2 displays the intensity distribution of the selected vortex beam after passing through 4F system, and the SLM-loaded fork grating pattern. It also shows the atmospheric turbulence phase screen and the pre-compensated phase screen.
4 Results and analysis
4.1 GS algorithm to improve velocity measurement accuracy
First, we conducted a simulation analysis to assess the enhancement of velocity measurement accuracy for the distorted vortex beam utilizing the GS algorithm. The reversal of topological charges, resulting from the reflection of the dispersed OAM modes by the target and mirrors, was considered. The simulation parameters are listed in Table 1, unless specified otherwise. As shown in Figure 3, the phase compensation applied by the GS algorithm has notably smoothed the annular light intensity structure of the vortex beam, which originally became rough due to turbulence. The distorted phase distribution was substantially restored, which enabled a clear interpretation of the phase structure. The helical spectrum relative power (purity) of the reflected −5 mode increased significantly from 0.036 to 0.635, indicating a remarkable 16.64-fold improvement. In the spectrum shown in Figure 4, a RDS peak at f1 = 40 Hz (marked with a red circle) is discernible, which differs from the theoretical value by only 0.48%, and the spectral amplitude improved 1.05-fold. The SSNR increased from 9.9 dB to 15.76 dB, indicating a 59.2% SSNR improvement factor (SSNRIF). The velocity measurement accuracy improved from 1.56 rad/s to 1.23 rad/s, reflecting a 21.15% velocity measurement accuracy improvement factor (σIF). These results show that the optical field and angular spectral purity of the vortex beam, which are distorted by atmospheric turbulence, are significantly improved by the compensation of the GS algorithm. This improvement highlights the amplitude distinction between the RDS peak and noise, thus improving the SSNR and consequently increasing the velocity measurement accuracy.
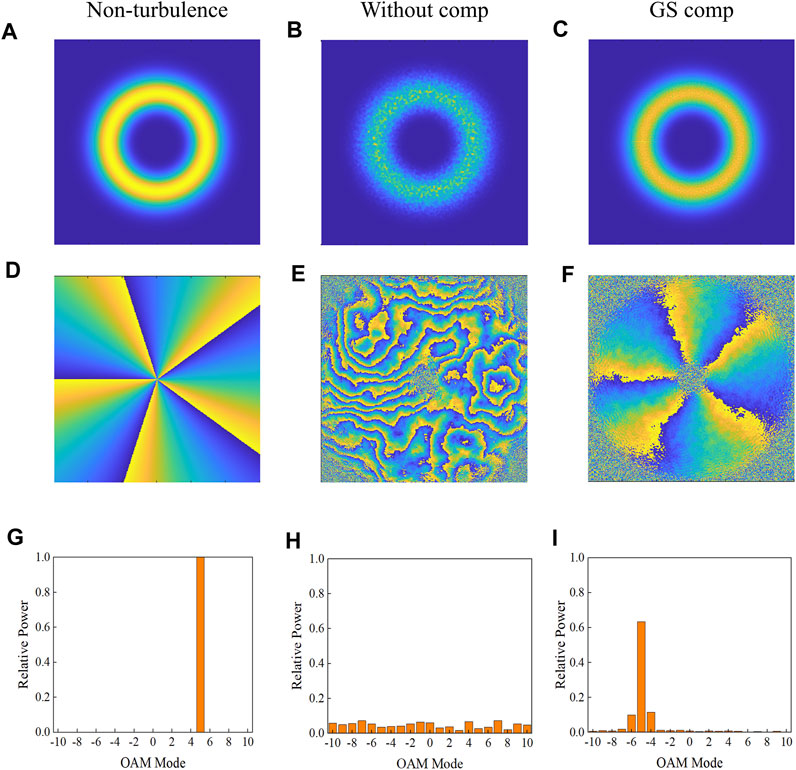
FIGURE 3. (A–C) Light intensity, (D–F) phase, and (G–I) OAM spectra of the vortex beam under non-turbulence, without compensation, and with GS compensation.
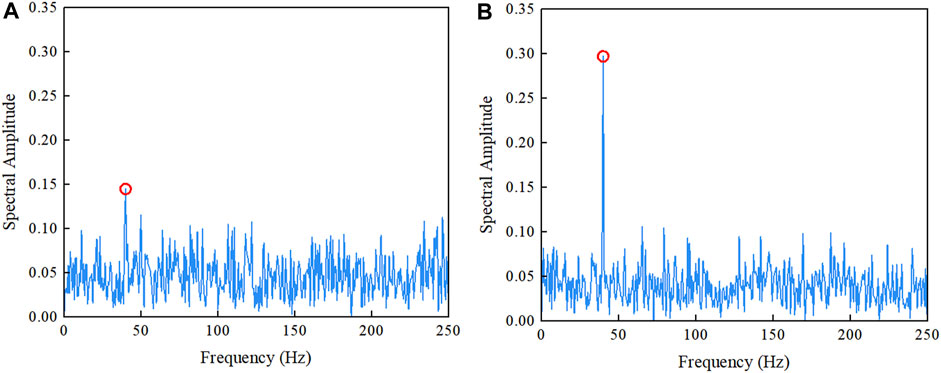
FIGURE 4. Spectrum of the vortex beam (A) without compensated, and (B) compensated with the GS algorithm. Red circles indicate the RDS peak.
Afterwards, the effectiveness of the GS algorithm in improving the distorted optical field and enhancing the velocimetry accuracy is discussed through experiments. By loading turbulence screen on the SLM to simulate atmospheric turbulence, and employing a rotating motor as a rotating target, we set up the experimental optical path and achieved the velocimetry experiment of l = 4 vortex beam at a rotation velocity of 1,000 r/min (16.67 r/s). The experimental results include intensity and spectrum of the vortex beam under non-turbulence, without GS compensation, and with GS compensation, as illustrated in Supplementary Figures S1, S2. Following the compensation with the GS algorithm, there is a noticeable improvement in the light intensity. In the spectrum, it can be observed that there is a frequency interval of Ω/2π between prominent peaks (Ω is measured in rad/s). This phenomenon is attributed to slight misalignment between the rotating target and the beam, as well as the scattering effect from rough target. Specifically, the power amplitude of the first characteristic peak (marked by a red circle) increases from −27.77 dB to −20.57 dB, representing a 25.93% improvement. In this case, this is a better choice for comparison than the RDS peak. The GS algorithm compensation in the experiment enhances the velocity accuracy by 14.19%, slightly lower than the simulated value of 0.8%. However, due to the reasons mentioned above, the velocity accuracy of the recovered beam is 10.5% lower compared to the simulation. We plan to address this issue in upcoming experiments by incorporating additional equipment for fine-tuning target positioning, refining the target, and optimizing the optical path. It underscores the importance of precise alignment and careful selection of target, which should be a focal point for the improvement of velocity accuracy in subsequent experiments.
4.2 Influence of beam properties on the GS algorithm to enhance velocimetry accuracy
The velocity measurement accuracy of vortex beams with topological charges l from 1 to 8 at zS−T = 500 m are shown in Figure 5A. The velocity measurement accuracy curve of recovered beam, obtained through 20 sets of repetitive calculations, exhibit a significant decrease, with reduction rates of 49.38% and 34.28% in the 1st and 2nd modes, respectively. After an average reduction rate of 17.08%, the curve stabilizes at l = 7, where the reduction rate is only 5.33% and the velocity measurement error reaches its minimum at 0.93 rad/s. Overall, the GS algorithm has an average velocity measurement accuracy improvement (velocimetry accuracy average improvement factor, σAIF) of 15.91% on the 1st to 8th OAM mode with a standard deviation of 3.28%. The reason for the deviations lies in the disparate ability of the GS algorithm to enhance the velocity measurement accuracy at low modes (1st–5th modes, σAIF = 17.9%) and high modes (6th–8th modes, σAIF = 12.5%). This is because the higher-mode vortex beams are more significantly affected by atmospheric turbulence, resulting in limited improvements in the velocity measurement accuracy. The negative topological charge has a similar property.
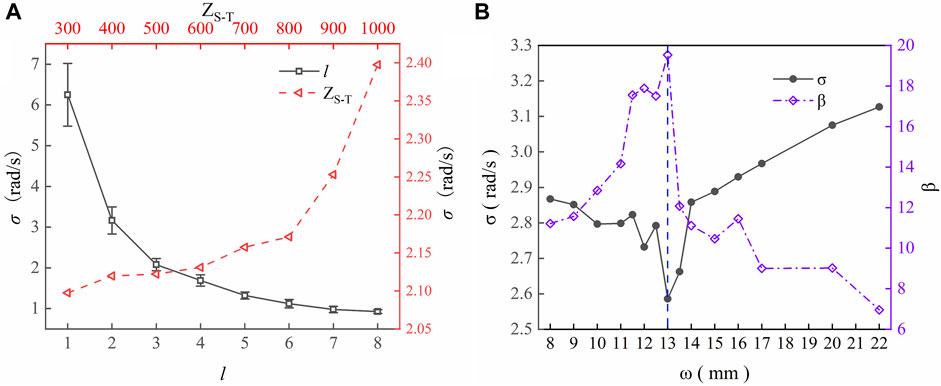
FIGURE 5. σ as a relationship of (A) l and zS-T, and (B) ω and OAM purity enhancement factor β. The dashed vertical line in (B) indicates the beam waist beyond which the ability of the GS algorithm to improve the OAM purity and velocimetry accuracy decreases rapidly.
Furthermore, we analyzed the enhancement in the average velocimetry accuracy of 1st to 8th modes at different zS-T using the GS algorithm. Within the zS-T range of 300 m to 800 m, the inhibitory effect of the transmission distance on the enhancement ability of the GS algorithm was relatively small (with an average reduction rate of 0.7%). Starting from zS-T = 800 m, the inhibitory effect of the transmission distance increased sharply, reaching a maximum value of 6.4%. σAIF at different transmission distances was 17.14% with a standard deviation of 2.72%. Although the GS algorithm improved the optical field through phase compensation, the velocimetry accuracy decreased owing to the cumulative effects of turbulence with increasing distance. As the transmission distance increased, the inhibitory effect gradually intensified. Similarly, the atmospheric coherence length r0 decreased with increasing transmission distance, as described by r0 = 0.185
We additionally observed a strong dependence of the algorithm’s compensation ability on the beam waist radius ω, as displayed in Figure 5B. The dispersion effect of atmospheric turbulence was minimized for a beam waist radius corresponding to the minimum spot size at a given transmission distance. Within the Rayleigh range zR, the beam propagated approximately in parallel across the propagation distance. When z = zR, the waist radius of the beam increased to
At the optimal beam waist radius, the GS phase retrieval algorithm can maximize the recovery of the OAM purity, reduce the amplitude of spurious frequency peaks, and thus improve the velocimetry accuracy. However, this was not evident in the higher-mode vortex beams, possibly because they are more affected by atmospheric turbulence. The GS algorithm is constrained in its ability to recover the distortions in excess spots beyond the optimal waist radius through phase compensation, limiting its effectiveness in enhancing the velocimetry accuracy.
4.3 Effect of atmospheric turbulence intensity on the GS algorithm to enhance the velocimetry accuracy
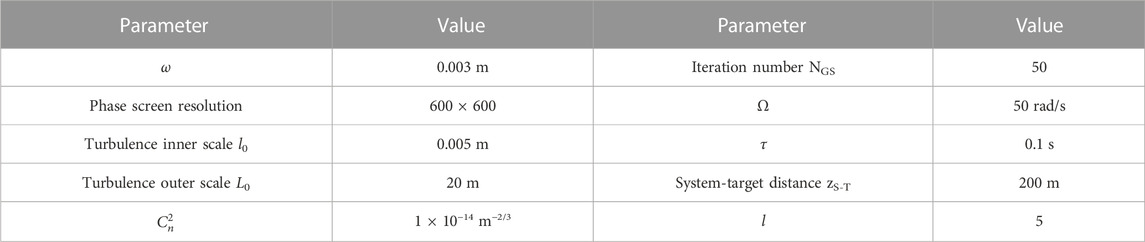
Table 2 lists the results for the velocity accuracy enhancement ability of the GS algorithm, which was simulated and analyzed under three relatively strong, moderate, and weak turbulence intensities of the 1st–8th mode vortex beams in the range of zS-T = 300–1,000 m.

TABLE 2. Average velocity accuracy without and with GS compensation σ, σGS, as well as σAIF, and σAVIF for 1st-to 8th-mode vortex beams in the range of zS-T = 300–1,000 m for three relatively strong, moderate, and weak turbulence intensities.
Compared to
In Figure 6, when
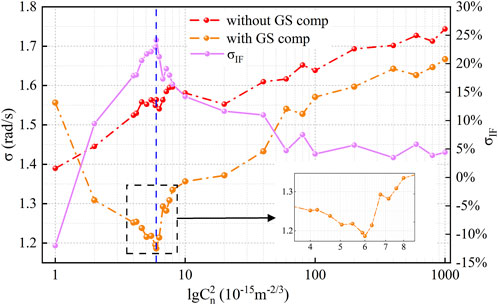
FIGURE 6. Relationships among σ, σIF, and
4.4 Effect of the number of GS algorithm iterations to enhance the velocimetry accuracy
Then, we discussed a crucial parameter in the GS algorithm, the number of GS algorithm iterations NGS, and its impact on velocity measurement accuracy and SSNR at zS-T = 500 m and
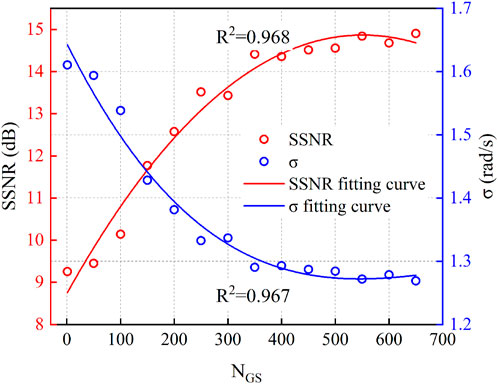
FIGURE 7. Relationships among σ, SSNR, and NGS for the l = 5 vortex beam at zS-T = 500 m and
We attribute the deviations of the data points from the curves to the random phase fluctuations of the atmospheric turbulence phase screen. This does not have a significantly impact on the overall trend. In the plateau range, the velocity accuracy and SSNR show improved average values of 20.41% and 57.88%, respectively, compared to the values obtained with only one GS iteration. We conclude that the compensation ability of the GS algorithm tends to stabilize when NGS is increased to the point where the SSNR and velocity accuracy enter a smooth phase. This indicates that a further increase in iteration number of the GS algorithm beyond 350 have a limited impact on improving the SSNR and σ of the optical field.
Based on the comprehensive simulation analysis, further investigations were conducted for zS-T = 500 m with the reported optimal parameters. The velocity accuracy increased from 1.64 rad/s to 1.15 rad/s, representing a 29.88% improvement. The SSNR increased 1.03-fold, rising from 8.92 dB to 18.14 dB.
Finally, we evaluate the distorted field compensation ability of the GS algorithm within the optimal parameters range and compare it with two other typical algorithms, as summarized in Table 3. Ref. [20] introduced an adaptive optics compensation approach based on the Wirtinger flow algorithm. It can be considered as a gradient descent method with initialization and iteration, effectively preventing convergence to local optimal solutions. Another notable approach, discussed in Ref. [37], involves incorporating Fourier-domain information as input information to the hybrid input–output algorithm (HIOA) to adjust the compensation phase screen. This additional information, combined with distorted light intensity, results in a substantial enhancement in OAM purity (∼20% → < 70%). Both algorithms enhance phase compensation ability through the optimization of iterative processes or the introduction of supplementary compensation information. However, neither discusses the optimal range for the algorithm’s application. Compared to other algorithms, a highlight of our work is the outstanding performance of the GS algorithm within the parameter range where it can achieve the optimal improvement in velocity accuracy. The GS algorithm demonstrates a remarkable 20.41% enhancement in velocity accuracy and a substantial 60% improvement in OAM purity. This underscores the significance of our algorithm in achieving optimal improvements in both velocity accuracy and OAM purity, setting it apart from other existing methods.
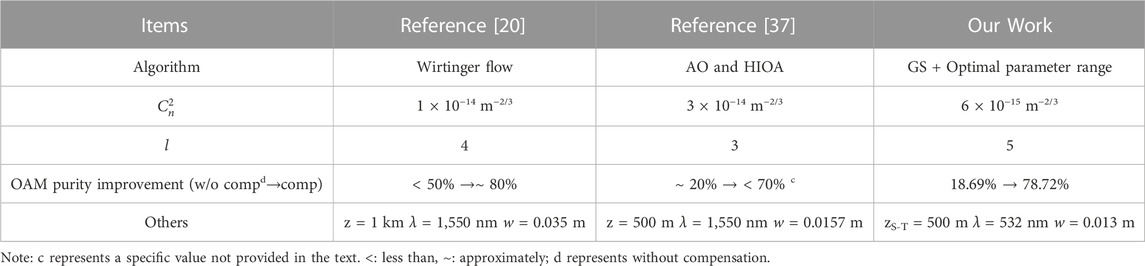
TABLE 3. Comparison of previously published works with this work on the OAM purity enhancement in atmospheric turbulence.
5 Conclusion
This paper demonstrates the outstanding performance of the GS phase retrieval algorithm to enhance the rotational velocimetry accuracy of distorted vortex beams within an optimal range of intrinsic and extrinsic parameters, as determined through simulation analysis. However, the algorithm’s deactivation beyond this range hampers its optimal compensation performance. Despite limitations observed in the simulation results, optimal parameters led to a 29.88% improvement in velocity accuracy and a 1.03-fold improvement in the SSNR. Unlike traditional metrics focusing solely on OAM purity, our study emphasizes SSNR for better distinguishing RDS peak from noise. Our work offers insights applicable to remote precision detection applications in free space. This research contributes to enhancing rotational velocimetry accuracy, with potential implications for diverse remote sensing scenarios.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
HW: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Writing–original draft, Investigation. ZZ: Funding acquisition, Project administration, Supervision, Writing–review and editing. HY: Methodology, Investigation, Writing–review and editing. HL: Methodology, Investigation, Writing–review and editing. YZ: Validation, Visualization, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foun-dation of China (Grant No. 62075049) and the Fundamental Re-search Funds for the Central Universities (FRFCU5710050-722; FRFCU5770500522; FRFCU9803502223; FRFCU5770600723) and the Industry-University Research Cooperation Fund of the Eighth Research Institute of China Aerospace Science and Technology Corporation.
Acknowledgments
The authors are grateful to the editors and referees for their valuable suggestions and comments, which greatly improved the presentation of this article. Additionally, HW thanked his girlfriend Ruiyang Yin and colleague Chengshuai Cui for their support.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1333427/full#supplementary-material
References
1. Allen L, Beijersbergen MW, Spreeuw R, Woerdman J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45(11):8185–9. doi:10.1103/physreva.45.8185
2. Lavery MP, Speirits FC, Barnett SM, Padgett MJ. Detection of a spinning object using light’s orbital angular momentum. Science (2013) 341(6145):537–40. doi:10.1126/science.1239936
3. Zhai Y, Fu S, Yin C, Zhou H, Gao C. Detection of angular acceleration based on optical rotational Doppler effect. Opt Express (2019) 27(11):15518–27. doi:10.1364/oe.27.015518
4. Courtial J, Robertson D, Dholakia K, Allen L, Padgett M. Rotational frequency shift of a light beam. Phys Rev Lett (1998) 81(22):4828–30. doi:10.1103/physrevlett.81.4828
5. Zhou H-L, Fu D-Z, Dong J-J, Zhang P, Chen D-X, Cai X-L, et al. Orbital angular momentum complex spectrum analyzer for vortex light based on the rotational Doppler effect. Light: Sci Appl (2017) 6(4):e16251–e. doi:10.1038/lsa.2016.251
6. Zhao M, Gao X, Xie M, Zhai W, Xu W, Huang S, et al. Measurement of the rotational Doppler frequency shift of a spinning object using a radio frequency orbital angular momentum beam. Opt Lett (2016) 41(11):2549–52. doi:10.1364/ol.41.002549
7. Qiu S, Liu T, Ren Y, Li Z, Wang C, Shao Q. Detection of spinning objects at oblique light incidence using the optical rotational Doppler effect. Opt Express (2019) 27(17):24781–92. doi:10.1364/oe.27.024781
8. Zhang Z, Cen L, Zhang J, Hu J, Wang F, Zhao Y. Rotation velocity detection with orbital angular momentum light spot completely deviated out of the rotation center. Opt Express (2020) 28(5):6859–67. doi:10.1364/oe.380324
9. Deng J, Li KF, Liu W, Li G. Cascaded rotational Doppler effect. Opt Lett (2019) 44(9):2346–9. doi:10.1364/ol.44.002346
10. Qiu S, Liu T, Li Z, Wang C, Ren Y, Shao Q, et al. Influence of lateral misalignment on the optical rotational Doppler effect. Appl Opt (2019) 58(10):2650–5. doi:10.1364/ao.58.002650
11. Ren Y, Huang H, Xie G, Ahmed N, Yan Y, Erkmen BI, et al. Atmospheric turbulence effects on the performance of a free space optical link employing orbital angular momentum multiplexing. Opt Lett (2013) 38(20):4062–5. doi:10.1364/ol.38.004062
12. Qilian L, Jiasong M, Min J, Wei W, Xuhong F, Baoju Z. Crosstalk among OAM modes through air channel: a simulation perspective. Communications, signal processing, and systems. In: Proceedings of the 2017 International Conference on Communications, Signal Processing, and Systems; July, 2017; Harbin, China (2017).
13. Ren Y, Wang Z, Liao P, Li L, Xie G, Huang H, et al. Experimental characterization of a 400 Gbit/s orbital angular momentum multiplexed free-space optical link over 120 m. Opt Lett (2016) 41(3):622–5. doi:10.1364/ol.41.000622
14. Anguita JA, Neifeld MA, Vasic BV. Turbulence-induced channel crosstalk in an orbital angular momentum-multiplexed free-space optical link. Appl Opt (2008) 47(13):2414–29. doi:10.1364/ao.47.002414
15. Zhao Y, Liu J, Du J, Li S, Luo Y, Wang A, et al. Experimental demonstration of 260-meter security free-space optical data transmission using 16-QAM carrying orbital angular momentum (OAM) beams multiplexing. In: Optical fiber communication conference; March, 2016; Anaheim, CA, USA (2016).
16. Aftab M, Choi H, Liang R, Kim DW. Adaptive Shack-Hartmann wavefront sensor accommodating large wavefront variations. Opt Express (2018) 26(26):34428–41. doi:10.1364/oe.26.034428
17. Kishimoto H, Sakashita N, Kishikawa H, Goto N, Liaw S-K. Reference beam-assisted broadband adaptive optics compensation for atmospheric turbulence on orbital angular momentum beams. In: Signal Processing in Photonic Communications; July, 2020; Washington, DC United States (2020).
18. Liu C, Pang K, Ren Y, Zhao J, Xie G, Cao Y, et al. Demonstration of adaptive optics compensation for emulated atmospheric turbulence in a two-orbital-angular-momentum encoded free-space quantum link at 10 Mbits/s. In: 2018 Conference on Lasers and Electro-Optics (CLEO); May, 2018; San Jose, CA, USA (2018).
19. Xie G, Ren Y, Huang H, Lavery MP, Ahmed N, Yan Y, et al. Phase correction for a distorted orbital angular momentum beam using a Zernike polynomials-based stochastic-parallel-gradient-descent algorithm. Opt Lett (2015) 40(7):1197–200. doi:10.1364/ol.40.001197
20. Zhou S, Zhang Q, Gao R, Chang H, Xin X, Li S, et al. High-accuracy atmospheric turbulence compensation based on a Wirtinger flow algorithm in an orbital angular momentum-free space optical communication system. Opt Commun (2020) 477:126322. doi:10.1016/j.optcom.2020.126322
21. Kumar N, Khandelwal V. Compensation of wavefront aberration using oppositional-breeding artificial fish swarm algorithm in free space optical communication. J Opt (2022) 52:1370–80. doi:10.1007/s12596-022-00947-4
22. Li Z, Cao J, Zhao X, Liu W. Atmospheric compensation in free space optical communication with simulated annealing algorithm. Opt Commun (2015) 338:11–21. doi:10.1016/j.optcom.2014.10.028
23. Wang H, Zhang Z, Wang Q, Feng R, Zhao Y. Enhanced measurement of vortex beam rotation using polarization-assisted particle swarm optimization for phase retrieval. Photonics (2023) 10(12):1293. doi:10.3390/photonics10121293
24. Fu S, Zhang S, Wang T, Gao C. Pre-turbulence compensation of orbital angular momentum beams based on a probe and the Gerchberg–Saxton algorithm. Opt Lett (2016) 41(14):3185–8. doi:10.1364/ol.41.003185
25. Li M, Li Y, Han J. Gerchberg–Saxton algorithm based phase correction in optical wireless communication. Phys Commun (2017) 25:323–7. doi:10.1016/j.phycom.2017.02.008
26. Dedo MI, Wang Z, Guo K, Guo Z. OAM mode recognition based on joint scheme of combining the Gerchberg–Saxton (GS) algorithm and convolutional neural network (CNN). Opt Commun (2020) 456:124696. doi:10.1016/j.optcom.2019.124696
27. Arlt J, Dholakia K, Allen L, Padgett M. The production of multiringed Laguerre–Gaussian modes by computer-generated holograms. J Mod Opt (1998) 45(6):1231–7. doi:10.1080/09500349808230913
28. Padgett M, Allen L. The Poynting vector in Laguerre-Gaussian laser modes. Opt Commun (1995) 121(1-3):36–40. doi:10.1016/0030-4018(95)00455-h
29. Ding Y, Ding Y, Qiu S, Liu T, Ren Y. Rotational frequency detection of spinning objects at general incidence using vortex beam (Invited). Infrared Laser Eng (2021) 50(9):1–7. doi:10.3788/IRLA20210451
30. Belmonte A, Torres JP. Optical Doppler shift with structured light. Opt Lett (2011) 36(22):4437–9. doi:10.1364/ol.36.004437
31. Jelalian AV. Laser radar systems. EASCON'80. In: Electronics and Aerospace Systems Conference; September, 1980; Arlington, VA, USA (1980).
32. Hongyan W, Yuejiao F, Chenyin S, Han Z, Qianqian D. Detection of topological charge for composite perfect vortex beams in atmospheric turbulence. Optik (2023) 291:171291. doi:10.1016/j.ijleo.2023.171291
33. Fu S, Wang T, Zhang S, Zhang Z, Zhai Y, Gao C. Non-probe compensation of optical vortices carrying orbital angular momentum. Photon Res (2017) 5(3):251–5. doi:10.1364/prj.5.000251
34. Dedo MI, Wang Z, Guo K, Sun Y, Shen F, Zhou H, et al. Retrieving performances of vortex beams with GS algorithm after transmitting in different types of turbulences. Appl Sci (2019) 9(11):2269. doi:10.3390/app9112269
35. Tatarski VI. Wave propagation in a turbulent medium. Mineola, New York, United States: Courier Dover Publications (2016).
36. Lane R, Glindemann A, Dainty J. Simulation of a Kolmogorov phase screen. Waves in Random Media (1992) 2(3):209–24. doi:10.1088/0959-7174/2/3/003
Keywords: the rotational Doppler effects, velocity measurement accuracy, orbital angular momentum, phase retrieval algorithm, atmospheric turbulence
Citation: Wang H, Zhang Z, Yun H, Liu H and Zhao Y (2024) Enhancing the accuracy of rotational velocity measurement for vortex beams within the optimal ability of phase retrieval algorithm. Front. Phys. 11:1333427. doi: 10.3389/fphy.2023.1333427
Received: 05 November 2023; Accepted: 11 December 2023;
Published: 03 January 2024.
Edited by:
Xinzhong LI, Henan University of Science and Technology, ChinaReviewed by:
Hehe Li, Henan University of Science and Technology, ChinaChaoliang Ding, Luoyang Normal University, China
Qian Yixian, Zhejiang Normal University, China
Copyright © 2024 Wang, Zhang, Yun, Liu and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zijing Zhang, emhhbmd6amhpdF9waHlAMTI2LmNvbQ==
 Hongyang Wang
Hongyang Wang Zijing Zhang*
Zijing Zhang*