Advancing clinical translation of cardiac biomechanics models: a comprehensive review, applications and future pathways

Cardiac mechanics models are developed to represent a high level of detail, including refined anatomies, accurate cell mechanics models, and platforms to link microscale physiology to whole-organ function. However, cardiac biomechanics models still have limited clinical translation. In this review, we provide a picture of cardiac mechanics models, focusing on their clinical translation. We review the main experimental and clinical data used in cardiac models, as well as the steps followed in the literature to generate anatomical meshes ready for simulations. We describe the main models in active and passive mechanics and the different lumped parameter models to represent the circulatory system. Lastly, we provide a summary of the state-of-the-art in terms of ventricular, atrial, and four-chamber cardiac biomechanics models. We discuss the steps that may facilitate clinical translation of the biomechanics models we describe. A well-established software to simulate cardiac biomechanics is lacking, with all available platforms involving different levels of documentation, learning curves, accessibility, and cost. Furthermore, there is no regulatory framework that clearly outlines the verification and validation requirements a model has to satisfy in order to be reliably used in applications. Finally, better integration with increasingly rich clinical and/or experimental datasets as well as machine learning techniques to reduce computational costs might increase model reliability at feasible resources. Cardiac biomechanics models provide excellent opportunities to be integrated into clinical workflows, but more refinement and careful validation against clinical data are needed to improve their credibility. In addition, in each context of use, model complexity must be balanced with the associated high computational cost of running these models.

1 Introduction

1.1 Cardiac physiology and pathophysiology

Cardiac biomechanics consists of the study of one or more of the processes involved in cardiac function. By studying the biomechanics of a patient’s heart and how it is different depending on the patient’s demographics and health state, we can optimise therapies, help planning procedures, or learn about pathophysiology. Historically, this study has been conducted clinically and experimentally, but more recently computer models have helped in this task [1]. Computational biomechanical modelling tools can aid in this effort, providing information that is inaccessible, too invasive, or unethical to obtain clinically. These tools must also be sufficiently robust to work with typically sparse clinical data and their associated uncertainty. Mathematical representations of fundamental mechanisms can provide the basis for a bottom-up reconstitution of whole-heart function in silico. Using this framework, cellular mechanisms such as ion exchange and cellular force generation can be linked to changes in the macroscopic behaviour, affecting clinical, measurable biomarkers such as ejection fraction.

In Figure 1, we outline the coupling between a typical clinical and experimental pipeline with the computationally modelling approach. Briefly, the clinical application dictates the type of cardiac biomechanics model to employ: passive, circulatory system, cell or three-dimensional electromechanics multiscale model. In-vivo clinical data collected from patients (top left of Figure 1) or ex-vivo experimental data (top right of Figure 1) are used to fit the model parameters and/or to validate model predictions. Once validated, the model can be used to provide mechanistic insight into processes underlying cardiac function, understand disease mechanisms, perform patient stratification, and test and/or compare different treatments (bottom of Figure 1). The continuous development and refinement of cardiac mechanical models witnessed over the past half century, together with increase in computational power, make this goal increasingly realistic.

FIGURE 1

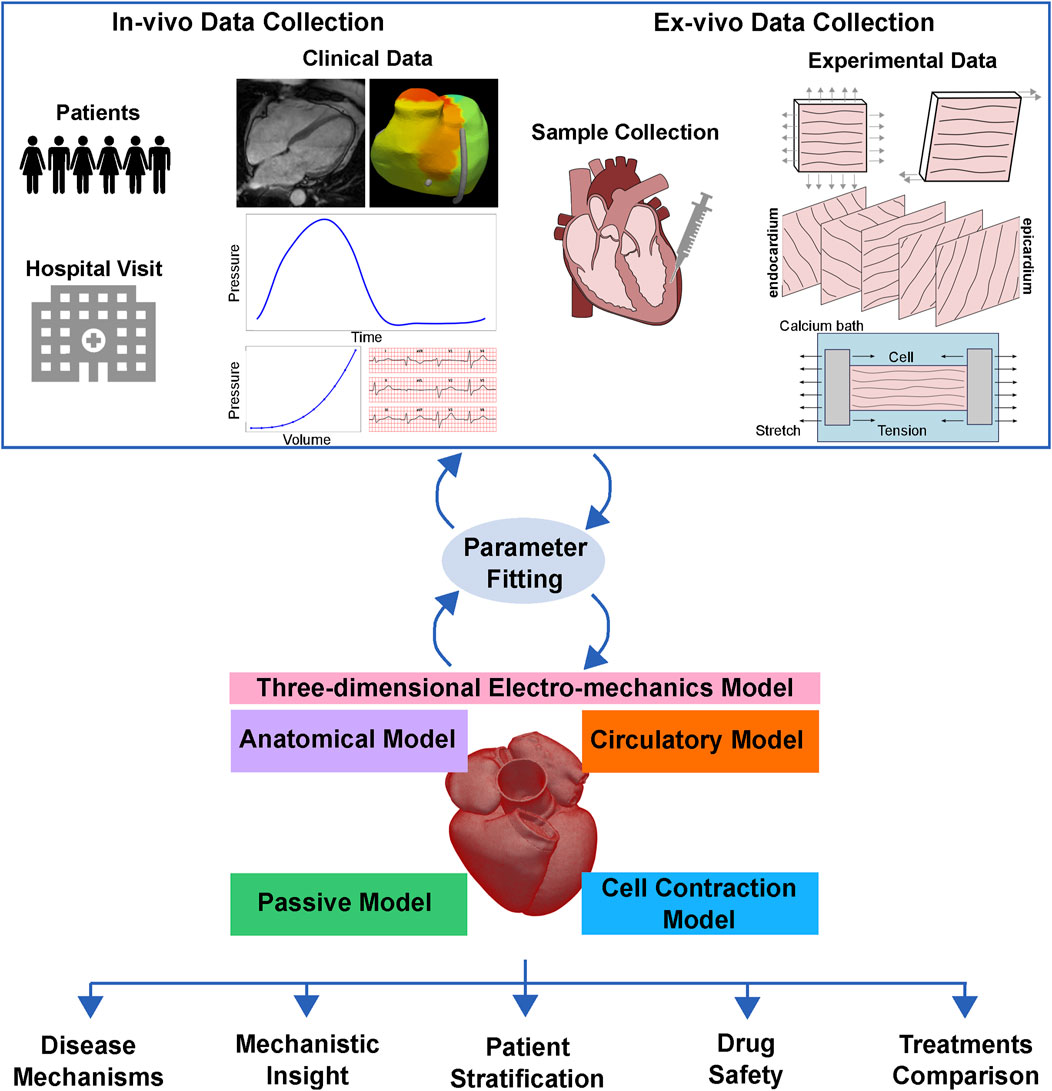
FIGURE 1. Clinical translation of cardiac biomechanics models. The clinical application dictates the type of cardiac biomechanics model to employ: passive, circulatory system, cell or three-dimensional multiscale model. In-vivo clinical data collected from patients or ex-vivo experimental data are used to fit the model parameters and/or to validate model predictions. Once validated, the model can be used to provide mechanistic insight into processes underlying cardiac function, understand disease mechanisms, perform patient stratification, and test and compare different treatments.

In this review, a mechanics model refers to a mathematical or computational representation of the physical properties and behaviours of cardiac tissues, cells (cell models), or the circulatory system (circulatory system models). To improve readability, when not explicitly specified (for example, with the term ‘whole-heart modelling’), we mean both anatomical and functional modelling. When only the geometry is replicated, we use the term ‘anatomical model’. We use the term ‘simulation’ to denote the computational processes that aim to replicate cardiac biomechanical phenomena. Unless stated otherwise, when we refer to techniques such as parameter estimation, it refers to in-vivo parameter estimation for patient-specific parameters, typically via inverse modelling.

1.2 Previous reviews of cardiac mechanics computational models

Cardiac mechanics models are developed to represent a high level of detail, including refined anatomies, accurate cell mechanics models, and to account for mechanisms of interaction between different chambers such as the pericardium, and the circulatory system, and between different physics through mechanoelectric feedback [1]. In recent years, multiple reviews have been published on cardiac biomechanical modelling. In [2], Wang et al. discussed some of the main articles on cardiac biomechanical models, with an emphasis on the images from which the anatomical data were extracted (for an introductory overview of image-based anatomical and mechanical modelling, see [3]). The focus was mainly on (left) ventricular properties and mechanics modelling, while mentioning several studies in which left ventricle (LV) modelling helped improve our understanding of the mechanisms underlying cardiac diseases. In 2019, Avazmohammadi et al. [4] summarised the last 30 years of myocardial biomechanics modelling focusing on constitutive equations, highlighting the need for better integration between clinical and experimental data with computational methods. This integration was the focus of the review by Bracamonte et al. [5], that is, on patient-specific inverse modelling. Several authors have summarised the main challenges of modelling cardiovascular mechanics, restricting their reviews to specific aspects of cardiac biomechanics, such as multiscale modelling [6] or computational models of specific pathologies [7–9].

Models of cardiac mechanics have been formulated for almost a century [1]. However, only recently did these models start to generate compelling evidence of their clinical relevance, paving the way for their clinical translation. In [10], Lesage et al. conducted a survey asking 163 clinicians about their familiarity with modelling and found that computational modelling-related terms such as patient-specific modelling are becoming well known. More than half of the responders had already used computer modelling and simulations to plan procedures, 57.4% of them in the cardiovascular field. Despite some potential sampling bias, this study indicates that clinical translation of cardiac computational modelling is already happening. However, none of the reviews mentioned above provided a summary of the state-of-the-art of the clinical translation of cardiac mechanics models.

In this review, we provide a picture of some of the main developments towards the clinical translation of cardiac mechanics models. In Section 2, we describe the main clinical and experimental data and methods used by the anatomical models and the simulations. In Section 3, we describe the processes of anatomical model generation and the incorporation of the fibre orientation and scar. We then describe the state-of-the-art of cellular contraction models in Section 4 and passive mechanics in Section 5. We review circulatory system models in Section 6 and ventricular, atrial, and four-chamber electromechanics models in Section 7. In Section 8 we briefly discuss how machine learning is influencing model translation. Lastly, in Section 9 we discuss the clinical applications of all the discussed models and the challenges that currently hinder the clinical translation of cardiac mechanics models. The final remarks of this review are given in Section 10.

2 Experimental and clinical data used in anatomical and mechanics models

There is a plethora of clinical tools and equipment available for collecting a wide range of data from a patient’s heart, including detailed anatomical, structural, and functional data. However, even given all this information, the clinical decision-making process remains challenging, as there is no tool capable of combining all this information into a unified framework. Computational electromechanics models have the potential to fulfil this purpose by unifying all clinical information into a multiscale, multiphysics and physics-constrained platform. In this section, we summarise the clinical and experimental data available to modellers to constrain and validate electromechanics models.

2.1 Anatomical and structure measurements

Anatomical information can be recovered from in-vivo or ex-vivo data. Histology can be used to obtain slices of hearts from different species, obtaining sparse shape information. Explanted hearts can also be imaged to obtain high-resolution images of the heart and surrounding tissues. However, ex-vivo imaging cannot be used for longitudinal or diagnostic studies. In-vivo imaging, on the other hand, allows one to collect longitudinal data for the same patients. Both ex-vivo and in-vivo hearts can be imaged by techniques such as computed tomography (CT) or magnetic resonance imaging (MRI). In contrast to CT, MRI does not require any ionising radiation and can therefore be used to image healthy subjects for multiple acquisitions over a short period of time while avoiding radiation exposure. However, MRI requires long acquisition times, which requires multiple breath holds from the patients and may be difficult for patients with cardiac disease. Moreover, it is not always suitable for patients with devices implanted and has low long-axis resolution. In these cases, CT provides submillimetre isotropic resolution, but involves ionising radiation. Echocardiography provides a rapid and inexpensive option to assess basic anatomical measurement using ultrasounds at the expense of accuracy.

Diffusion tensor MRI (DT-MRI) and histology can also be used to recover information about cell alignment within the myocardium. In the heart, myocytes are organised into fibre bundles. Although histology measurements are often used as a ground truth for the estimation of fibre direction [11], they are sparse and time consuming and are associated with an uncertainty of about 10° [11]. DT-MRI is a technique that allows to map the predominant direction of water molecules diffusion within the tissue, providing essential insights into the underlying fibre structures. When applied ex-vivo, this provides high-resolution data about fibre distribution in the whole heart. Although in-vivo DT-MRI is limited by cardiac motion and long acquisition times, it has been used to detect fibre disarray and remodelling in patients with hypertrophic [12] and dilated [13] cardiomyopathies, showing its potential for future clinical applications.

Scarring and fibrosis occur when cardiac tissue dies due to a lack of blood supply. Scar tissue constitutes a substrate for a wide range of pathologies, such as atrial fibrillation (AF) or ventricular tachycardia, and its distribution is used to identify potential ablation targets to prevent life-threatening arrhythmias. This makes scar estimation in cardiac patients crucial. Late gadolinium enhancement MRI can be used to quantify the extent, transmurality, and mass of the myocardial scar, which appears as a bright area on cardiac images. However, late gadolinium enhancement techniques are currently unable to detect diffuse myocardial fibrosis, which is an earlier form of fibrosis preceding replacement fibrosis that may be reversible. T1 mapping refers to information derived from MRI images to measure a mathematical constant, called T1 relaxation time. The main advantage over late gadolinium enhancement is that T1 mapping MRI does not require contrast and allows a quantitative measurement of features such as diffuse fibrosis, a reason why it has recently been used to detect this type of fibrosis [14]. Scar can also be quantified with electroanatomical mapping, as low-voltage areas have been shown to correlate with scar in both ventricles [15] and atria [16], although transmurality information is limited. Finally, the quantification of thin areas of the ventricular wall on CT with delayed enhancement has been correlated with areas with low voltage on electroanatomical mapping, but this is not widely used in clinical practise to identify scar tissue [17]. For a more thorough review on the link between anatomical and functional modelling and imaging, we refer the reader to [3].

2.2 Tissue and cell measurements

Passive tissue measurements have advanced our understanding of the mechanical properties of the myocardium. Initial evaluation of passive properties of the myocardium was carried out through uniaxial tests (e.g., stretching the sample in the longitudinal direction) in rabbit papillary muscle samples, showing the nonlinear behaviour of cardiac tissue [18]. Later, biaxial tests on canine myocardial strips excised from the subepicardium of the LV free wall, carried out by stretching the sample in the fibre and cross-fibre directions, showed increased stiffness in the fibre direction, indicating that the myocardium behaves as a transversely isotropic material rather than an isotropic material [19, 20]. Finally, more complex shear tests were used to investigate the shear properties of the myocardium. Using these types of measurements on tissue samples from the LV lateral wall, Dokos et al. [21] concluded that cardiac tissue is actually orthotropic. Most tissue measurements are performed on ventricular samples, leaving the properties of the atrial tissue poorly characterised. Bellini et al. [22] provided the first and only experimental dataset that characterises the passive properties of the healthy human myocardium of the left atrium (LA) and the right atrium (RA) by performing biaxial tests on samples collected from five different areas of the atria.

A substantial proportion of experiments investigating the active properties of the cardiac muscle are carried out in skinned muscle preparations, where the sarcolemmal membrane has been dissolved [23]. The benefits of these experiments include 1) the ability to tailor the biochemical environment of the sarcomere components; 2) the isolation of the contraction mechanisms from other cellular subsystems, such as the sarcolemmal membrane; and 3) the ability to preserve the system for several months (particularly useful for human samples, which are naturally scarce) [24]. The underlying assumption of skinned muscle measurements is that the structural and molecular features of the myofilament system are sufficiently preserved to reproduce the essential functional properties and behaviour of the original system. However, in reality, there are notable discrepancies between the skinned and intact systems, which make the translation of the measurements of the skinned system into their physiological context challenging [25]. Nonetheless, skinned muscle preparations are widely used to provide quantitative information about active tension properties and cardiac cell kinetics.

Force-calcium (F-Ca) relationships provide a conventional basic characterisation of steady-state force generation at the sarcomere level [26]. Typically measured using skinned preparations (although they have also been measured in intact myocytes [27]), the F-Ca relationships are used to measure the force generated by muscle fibres at different levels of calcium concentration and under different conditions, for example, sarcomere length [28]. More precise measurements have identified an asymmetry in the F-Ca curves [29].

More complex experiments carried out on both skinned and intact muscle preparations have been used to provide in-depth information about the system kinetics and to quantify the force generated by cellular contraction. Dominant processes can be observed by applying small length perturbations [28] or by measuring dynamic stiffness through a strain of varying frequency [30]. These experiments provide an intuitive framework for interpreting kinetics-modifying interventions, such as the application of the contraction inhibitor mavacamten [31]. Tension-recovery experiments, also performed in skinned preparations, probe the cross-bridge turnover dynamics. These experiments involve rapidly slackening the muscle fibre to zero tension, followed by rapid restretching, assumed to cause cross-bridge dissociation [32]. Therefore, the observed tension recovery reflects the dynamic reforming of the cross-bridges. Controlling calcium concentrations precisely in skinned muscle preparations on short time scales poses a challenge. Consequently, experiments that measure muscle twitches are conducted on intact cells, rather than skinned muscle preparations, to study dynamic force generation in response to calcium transients [33]. The experimental data described above are based on complex procedures and setups, making data collection time consuming and challenging. Furthermore, these experiments allow one to observe only very specific processes and, therefore, lack the link to other mechanisms affecting cardiac function as a whole.

2.3 Organ-scale measurements

Measurements carried out in myocardial tissue samples are fundamental to investigate tissue properties, both active (e.g., force generation), and passive, (e.g., material stiffness). However, in some cases, in-vivo measurements might be needed instead. In this section, we provide a brief summary of the main types of data and their collection techniques used to validate mechanics simulations.

Time-volume traces can be non-invasively derived from cine MRI. However, in some cases, MRI is not indicated, for example, due to the presence of a device. In such cases, if ionising radiation is not a concern, time-volume traces can be derived from retrospective gated cardiac CT. Cine MRI suffers from lower long-axis resolution compared to CT, but retrospective gated cardiac CT has a poorer temporal resolution than cine MRI. Echocardiography constitutes a non-invasive, inexpensive and widely available measurement of volumes, ejection fraction, and local longitudinal strains for all cardiac chambers. Tagged MRI and retrospective gated cardiac CT can also be used to measure local strains, but interpreting these data requires more advanced analysis, such as motion tracking and deep learning.

In addition to imaging, cardiac biomechanics can be characterised clinically using a range of diagnostic measurements. In-vivo end-diastolic pressure-volume relationships (EDPVRs) can be invasively measured using pressure-conductance catheters, providing simultaneous recordings of pressure and chamber volumes [34]. Invasive catheter measurements of LV pressure over time can be used to quantify the efficiency of myocardial contraction and relaxation using peak pressure and maximum and minimum pressure time derivatives. For cases where time traces of volume and/or pressure measurements are not available, [35] proposed a law (the so-called Klotz curve) to estimate EDPVR for a specific patient based on a single pressure-volume measurement. Clinically, EDPVR is used to assess the passive mechanical behaviour of a patient’s heart and can be used to identify the presence of fibrosis, remodelling, or hypertrophy [36].

Although they do not provide direct information on cardiac function, electrical measurements are widely used in the clinic in combination with functional mechanical measurements described above, and can be used to validate the electrical activation simulated in a multi-scale electromechanics model. Twelve-lead electrocardiograms (ECGs) are routinely used to identify myocardial scar, dyssynchrony, and other electrical disturbances. Body surface potential maps and electrocardiographic imaging are an extension of standard ECGs, with more recording electrodes located on the patient’s torso, and can provide more detailed information about the electrical activity of the heart. However, these techniques are not intended for routine clinical use and are restricted to specific use cases, such as response to cardiac resynchronisation therapy (CRT) [37, 38] or different types of arrhythmias [39].

All the data mentioned above can be used to validate the heart’s mechanical behaviour simulated by different types of computational biomechanics models of the heart. In the following section, we describe how anatomical models of the heart are built, mainly using three-dimensional imaging techniques such as CT or MRI.

3 Anatomical model generation

The first animal [40] and human [41] anatomical models of the heart were based on the LV, partially due to its regular shape, well approximated by a truncated ellipsoid. Increased availability of experimental data have made the realisation of more detailed anatomical models possible. Biventricular anatomical models of mammals have been generated using digital images of short-axis histological slices [42], ex-vivo MRI images of histological samples [43–45], and ex-vivo whole heart MRI [46–48]. The growing interest in the effect of the atria on cardiac function has led to increasingly anatomically detailed models generated from histological slices of the sheep atria [49], the human atria [50, 51] and the whole human heart [52]. Advances in in-vivo imaging allow one to acquire highly detailed anatomical datasets. Both MRI and CT have been used to generate patient-specific anatomical models of the ventricles [53–57], the LA [58–60], the atria [61], and the whole heart [56, 62, 63], as shown in the first row of Figure 2.

FIGURE 2

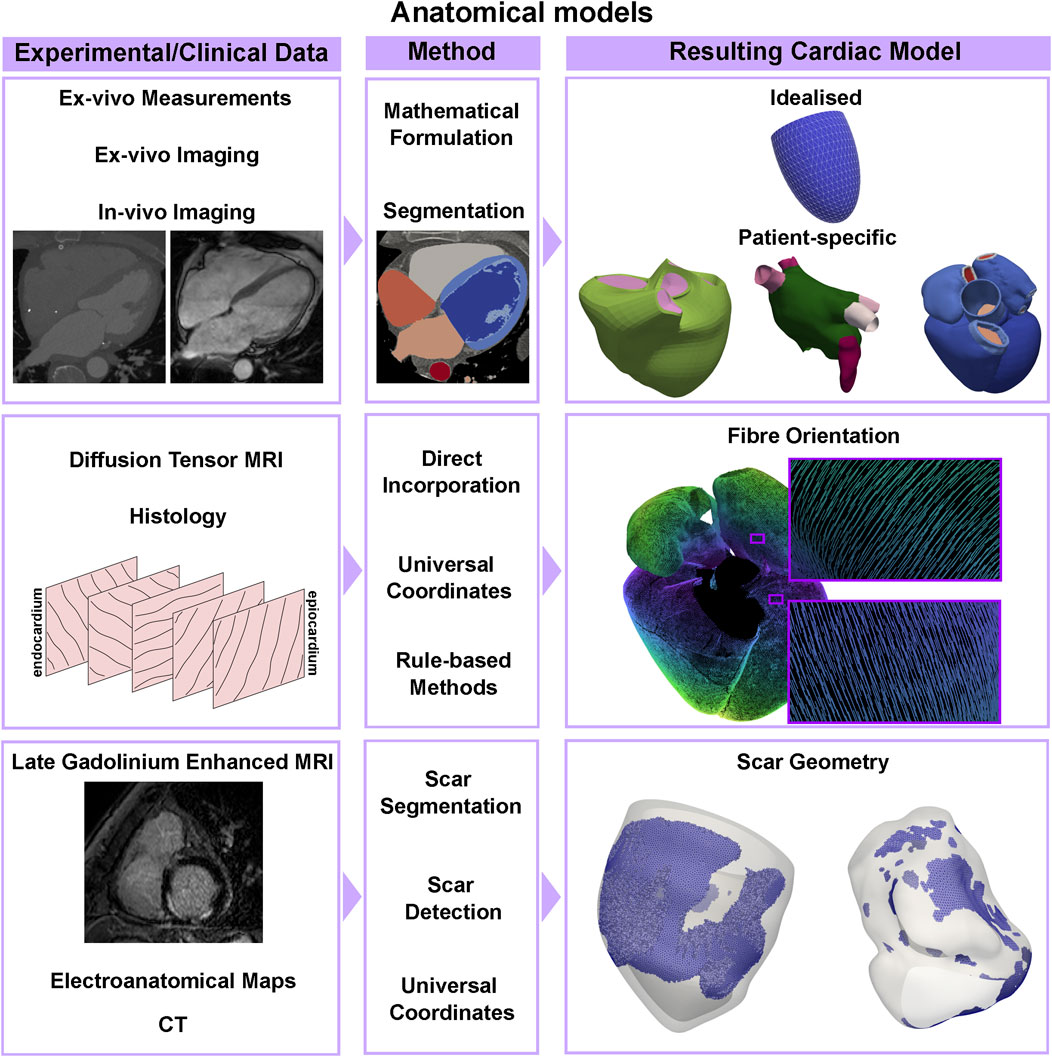
FIGURE 2. Anatomical models pipeline. An idealised geometry can be built using measurements from ex-vivo hearts and a mathematical formulation for a truncated ellipsoid, while patient-specific anatomies of ventricles, the atria, or the whole heart can be segmented from CT or MRI imaging data. Atrial and ventricular fibre orientations can be directly incorporated or mapped from ex-vivo DT-MRI datasets, or by using rule-based methods based on sparse histology data. Scarred tissue can be detected using late gadolinium enhanced MRI, thresholding electroanatomical voltage maps or by applying machine learning methods to CT datasets.

Fibre orientation in the ventricles has been directly incorporated from high-resolution ex-vivo DT-MRI datasets [43, 46, 64–66] or by registering histological data in a computational geometry [42], see the second row, left, of Figure 2. Although these methods provide measurement-based fibre architectures, they can be considerably difficult to apply in-vivo. For this reason, rule-based methods [67] remain popular. Essentially, these methods establish a series of rules for describing fibres in the myocardium based on (typically canine) histological data. Several rule-based methods have been developed for the ventricles [68–73] and atria [58, 71, 73–79]. Ventricular fibres can also be mapped from a geometry with a known fibre orientation using universal ventricular coordinates [80], a set of coordinates that uniquely define a point within a biventricular anatomy independently of the geometry. Similarly, universal atrial coordinates have been used to map ex-vivo DT-MRI fibres from an atlas onto patient-specific biatrial anatomies [59, 60, 81]. An example is shown in the right side of the second row of Figure 2. Due to the challenges of acquiring high-resolution in-vivo DT-MRI datasets, patient-specific fibre orientation is not yet achievable in cardiac anatomical models.

Depending on the application, tissue heterogeneity might play a role in the dynamics of interest. For example, accounting for the scar and border zone (the region usually surrounding the scar with abnormal conduction properties) in the anatomical and mechanics model is important when trying to detect the optimal location for leads in pacemaker implantation, to understand the strain and work distributions in different pathological conditions, or to reproduce reentrant waves during arrhythmias. More recently, machine learning techniques have been used to identify scar areas on delayed enhancement CT imaging [82] and CT angiography [83]. Electroanatomical voltage mapping can also be used to detect fibrotic areas by thresholding the voltage in the atria [84, 85] and in the ventricles [86, 87] to detect low-voltage areas, which can be surrogates for the scar. The typical data and methods can be seen in the bottom row of Figure 2, as well as an example of scar geometry in two ventricular meshes. However, in the ventricles, it can be hard to discern whether this scar is endocardial or transmural. When clinical data are not available, universal atrial and ventricular coordinates can also be used to map segmented scar areas from one geometry to another.

Once the anatomical model is built, functional properties must be assigned to the tissue. These can be classified as active or passive depending on whether the tissue generates force or not, respectively. In the following sections, we summarise the state-of-the-art for the active mechanics at the cellular level and the passive mechanics at the tissue level.

4 Active cell mechanics

Single-cell experiments have provided essential insight into myocyte biomechanics. However, these experiments typically focus on measuring specific effects in isolation and do not always capture the interactions between different mechanisms that occur simultaneously. In this context, the biomechanical modelling of cell contraction potentially provides a theoretical framework for integrating experimental measurements into a unified picture [4, 88].

Various paradigms of biomechanical models of force generation at the cell level have been proposed over the years. A depiction of the main ones can be seen in Figure 3. The Hill model of 1938 [89] was designed to reproduce careful measurements of the relationship between force and muscle velocity on a phenomenological basis, without invoking specific mechanisms of force production within the muscle. This simplified representation reduces the computational load and facilitates large multiscale analysis pipelines [53]. These multiscale pipelines include the integration of cardiac anatomy, electrophysiology, biomechanics, and hemodynamics in a patient-specific model of heart failure (HF) [55, 90]. In this context, the phenomenological nature of the cell model may well suffice in some data analysis pipelines designed for therapy planning, e.g., personalised cardiac CRT in a large cohort of patients [90].

FIGURE 3

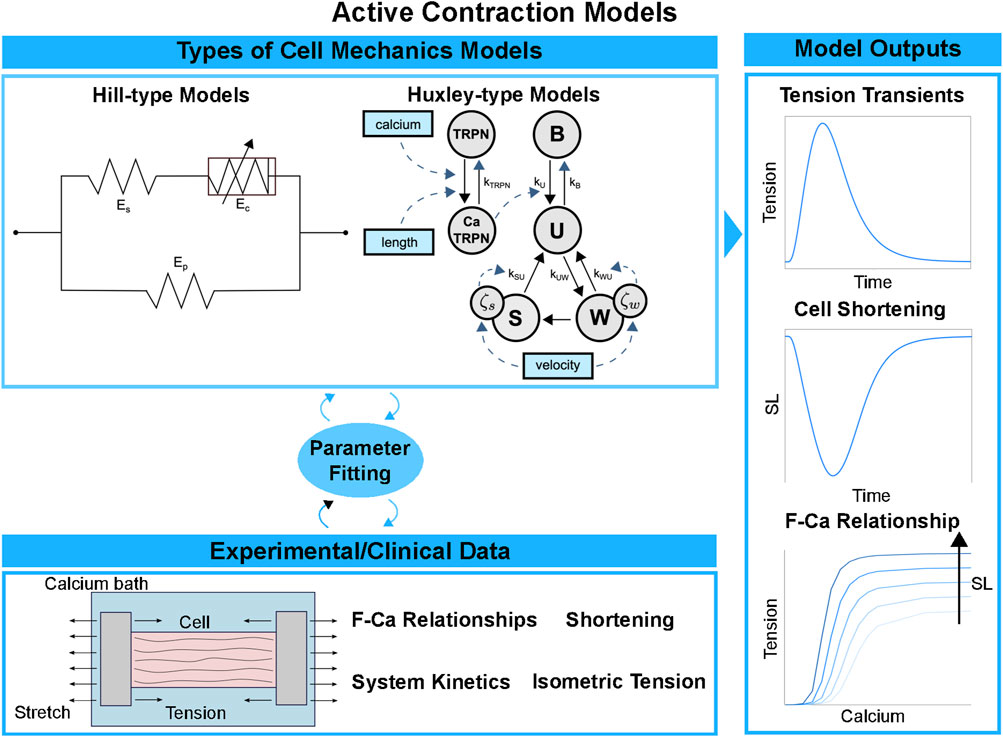
FIGURE 3. Cell contraction models pipeline. Simplified cell models directly computing the active tension transient can be used to save computational cost and discard the kinetic processes underlying active force generation. More complex cell models explicitly represent the molecular processes of the cross-bridge cycle, discretising it into a finite number of states. Different types of experimental data are used to fit the parameters and validate the cell model outputs: isometric tension transients, cell shortening and F-Ca relationships under different sarcomere length conditions.

In contrast, the Huxley model of 1957 [91, 92] sought to reproduce muscular function by starting from a more explicit representation of molecular interactions at the sarcomere level. In this framework, the force is generated from the strain of an elastic “spring” associated with the bound cross-bridge. Many subsequent Huxley-inspired models vary in their degree of sophistication. The cross-bridge cycle is represented in terms of transitions within a kinetic system comprising two [93], three [94, 95], four [28, 96], or more (e.g., [97–99]) states. In the hybrid approach by Gusseva et al. [100], a Hill-type model is used where the active behaviour of the myocardium is modelled within Huxley’s filament theory. In general, the computational cost increases with complexity and is typically much higher with Huxley-type models compared to Hill-type models. Force predictions in cellular biomechanical models are typically validated using measurements of F-Ca relationships, tension-recovery curves, or dynamic stiffness measurements and twitch dynamics in intact fibres, as seen in the bottom and on the right of Figure 3. In-vitro solution-kinetic data may also provide kinetic rate estimates of specific state transitions in contraction models. Constraining parameter values in complex mechanics models inevitably involves some degree of “inheritance”, that is, using experimental data from disparate existing sources that were sometimes obtained under inconsistent measurement conditions, which constitutes a source of uncertainty.

Alternative modelling approaches use a more abstract perspective based on the mass-action principle. They express biochemical transitions as “probability fluxes” between system states that may formally amalgamate ensembles of actual molecular states. Essential experimentally observed dynamic features can be reproduced, often requiring fewer ad hoc assumptions [101, 102]. The relative simplicity of such cell models arguably facilitates parameter calibration using more limited and more consistent datasets, unlike recent state-of-the-art platforms for simulating contraction [98, 103–105] that rely on calibrations derived from a wide set of experimental sources.

Spatially explicit cell models can extend the investigation of cross-bridge dynamics to filament interactions on the scale of the half-sarcomere. Fenwick et al. [106] suggested a mechanistic explanation of the sarcomere length dependence of force production. The status and location of individual myosin heads and actin binding sites can also be dynamically tracked to allow the exploration of the biophysical interactions of sarcomere components [103]. Cell models with resolution at the protein level provide a framework to investigate drug action pathways [107]. In particular, genetic mutations with a role in cardiomyopathies can serve as therapeutic targets [108]. Such effects, in principle, can at best be included only phenomenologically in spatially implicit cell models.

Modelling can provide insight into the impact of genetic variants of sarcomeric proteins and their manifestation under pathological conditions. In [109], the authors constructed an electromechanical cardiomyocyte model to reproduce phenotypes in hypertrophic cardiomyopathy, linking alterations in model parameters with mutations in myosin heavy chain and troponin genes. When the cell model is coupled with in-vitro measurements, they carried out an in silico clinical trial of the drug mavacamten, a contraction inhibitor used to treat hypertrophic cardiomyopathy. Similarly, in [105], Tomasevic et al. projected single-cell contraction onto the organ level using a finite element simulation to estimate the impact of drug interaction within cardiac cells. Therefore, this approach provides a clinical tool for tailoring drug administration to patients and altering myocardial contraction.

Coupling simulations with experimental measurements can help to elucidate the mechanism of action of drugs. Omecamtiv mecarbil (OM) was designed to directly target the cell contraction mechanism by selectively accelerating the formation of the force-generating state of the cross-bridges [110]. At the whole-heart level, it increases the duration of blood ejection without changing the contraction rate [111]. To improve understanding of the mechanism of action of OM, in [112] the authors combined a biomechanical model with machine learning to infer the model parameters from experimental data from rats. Recent modelling studies have further investigated the action of OM by simulating its impact on failing muscle. Using a cell model within a three-dimensional finite element analysis, in [113], van Herck et al. confirmed an increase in myocardial contraction driven by OM in the failing system. However, other discrepancies with experimental measurements highlight the need to further refine the cell model to fully understand the drug’s mechanism. Using Bayesian inference methods, in [114], Longobardi et al. fitted a cellular biomechanical model to in-vivo and in-vitro measurements of OM in rats. Combined with purely clinical studies of the drug, the model can assist in the development and improvement of clinical treatment.

Only myocytes activated by an action potential wave (a change in electric charge due to the exchange of ions) generate force in that instant. Nonactive tissue deforms as a result of passive forces. In the following section, we describe the main mechanics models that define how tissue deforms depending on its anisotropy and (hyper)elastic properties.

5 Passive mechanics

The passive behaviour of the myocardium is typically represented with a hyperelastic formulation, where stresses within the tissue are represented by a strain energy function [115]. The first material laws were developed for the LV myocardium, based on samples collected from the canine LV free wall [20]. Initially, the myocardium was represented as exponential and isotropic [116], to represent the nonlinear behaviour of cardiac tissue. Following biaxial experiments in canine myocardium samples [117], transversely isotropic laws were developed [19, 118–123], in order to represent the increased stiffness in the fibre direction compared to the transverse plane. More complex orthotropic laws [33, 115, 124–126] have been developed after the shear data published by [21]. Orthotropic material laws provide a more accurate representation of the passive properties of the ventricular myocardium, and, as shown by [127], transversely isotropic laws can reproduce only three of the six deformation modes from the Dokos dataset. However, more complex orthotropic formulations have more material parameters than simpler transversely isotropic laws, leading to concerns about reliability, uniqueness, and computational cost of parameter identification. For this reason, transversely isotropic material laws are still widely used in clinical applications of mechanics models.

Myocardial stiffness provides information about chamber filling and can be used as an indicator for various cardiac pathologies, but it is difficult to quantify in-vivo. In this context, cardiac mechanics models can provide a platform to measure passive filling properties of the patient’s heart non-invasively. A typical pipeline to show how anatomical models and material laws are coupled with experimental/clinical data is show in the left side of Figure 4. This coupling provides an estimation of multiple biomarkers, such as the patient’s heart estimated motion, stress and strain distributions and passive stiffness estimations. We depicted examples on a univentricular mesh in the left of Figure 4. Cardiac mechanics models were first applied to measure passive stiffness in-vivo in healthy animals [128–130] and patients [131–134] using cine-MRI data, passive pressure-volume relationships or, alternatively, the Klotz curve. Mojsejenko et al. [135] used diastolic cine-MRI and invasive LV pressure data collected from porcine hearts 1 week after infarction to estimate myocardium and scar stiffness, as well as changes in fibre orientation within the scar. Using cine-MRI patient data, transversely isotropic laws were used to quantify passive stiffness in patients with aortic coarctation and aortic valve stenosis [136], myocardial infarction [137], and to compare the passive stiffness of healthy controls and patients with dilated cardiomyopathy [138], HF [139], and tetralogy of Fallot [140]. Similar works have also been done using 3D printed phantoms [141]. All these applications made use of transversely isotropic laws and, in many cases, the number of estimated parameters was reduced either by using prior relationship between parameters or by fixing a subset of them. This highlights the need for more sophisticated fitting techniques allowing to fit more parameters at a time, or better curated and complete clinical datasets to help constrain a large number of parameters. This will ultimately allow orthotropic material laws to be used in clinical applications.

FIGURE 4

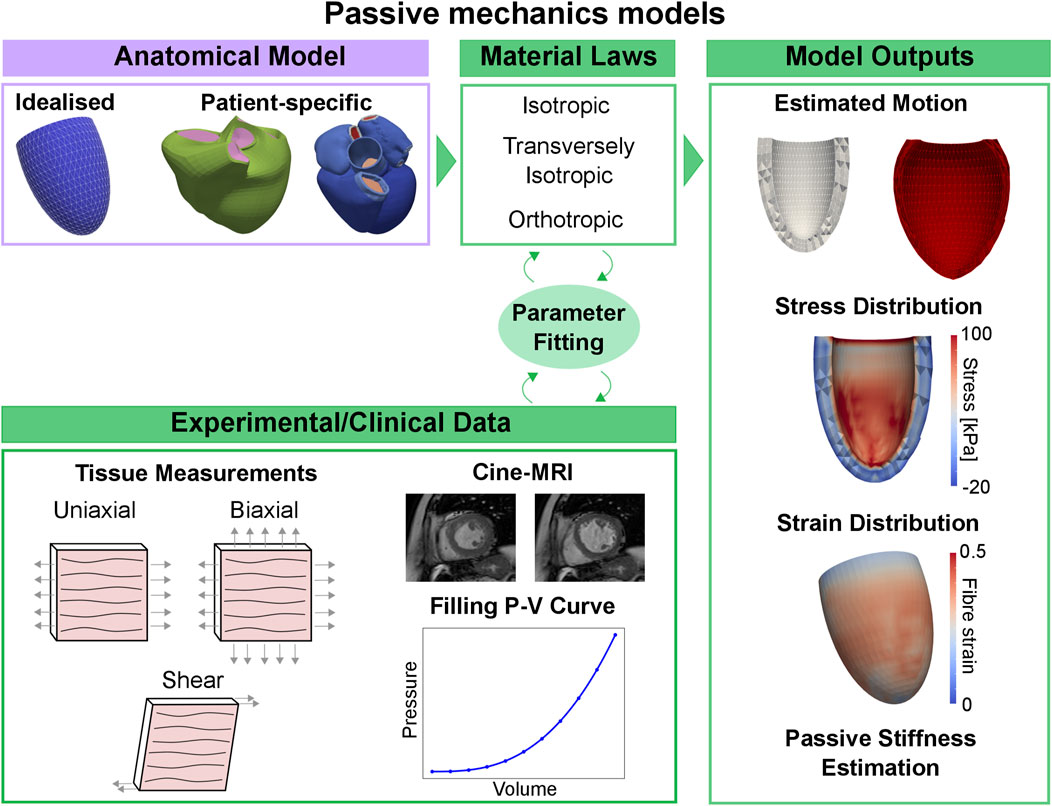
FIGURE 4. Passive mechanics models pipeline. Using an idealised or patient-specific geometry and a material law representing passive properties of the myocardium, the material parameters can be fitted to match stress-strain relationships derived from tissue measurements, or in-vivo cine-MRI data and pressure-volume relationships measured during the diastolic phase. Passive mechanics models can provide an estimation of the patient’s heart diastolic motion, stress and strain distribution and passive stiffness.

The material laws and applications described above were designed and performed in the ventricles and were based on experimental data collected from samples of the ventricular myocardium. Only relatively recently, due to the increased interest in atrial dynamics and modelling, existing linear elastic [142], nonlinear isotropic [143] and transversely isotropic [144–146] material laws have been adapted to represent the atrial myocardium. Other groups have proposed atrial-specific and transversely isotropic material laws [147, 148] and fitted the material parameters to the available experimental data from Bellini et al. [22]. Finite element analysis of the atria using a linear elastic model has been used to correlate low-voltage areas and areas with high stresses in the LA in patients with AF [142]. More complex nonlinear, isotropic, and transversely isotropic models have been used to approximate and investigate in-vivo stress distribution in porcine biatrial [149] and human LA [147] geometries, showing the potential of atrial modelling to improve our understanding of the mechanical behaviour of the complex anatomy of the atria.

Once active and passive mechanics of the myocardium are represented in a cardiac mechanics model, a representation of the circulatory system can be included to be able to track changes of pressures and volumes inside the cavities. Due to the computational cost, the circulatory system is commonly simulated with lumped parameter models. In the following section, we provide a summary of the state-of-the-art of lumped parameter models to represent the circulatory system.

6 Lumped parameter models for the circulatory system

Lumped parameter or zero-dimensional models represent the circulatory system as a combination of resistors, capacitors, and inductors, representing the resistance the blood encounters while flowing through different compartments, the energy stored by the vessels’ compliance, and blood inertia, respectively (see Figure 5, top left). The periodic activity of the heart is normally modelled using a varying elastance model. Although lumped parameter models discard spatial information, they constitute an appealing option for clinical applications due to the computational speed, compatible with clinical timescales, and their flexibility, with modules or compartments normally easily replaced by a more complex representation if required by the application of interest. The versatility of lumped parameter models makes them useful in a wide range of applications. Zero-dimensional models of the whole heart, systemic and pulmonary circulations have been applied to investigate diseases such as aortic stenosis and aortic valve regurgitation; and to simulate pulmonary hypertension to better understand the underlying causes of the disease and improve treatment [150]. They have also been used to test, using simulations, different types of ventricular assisted devices in peadiatric [151] and adult patients with HF [152]. An even simpler setup, including only the left side of the heart and the circulatory system, has been used to match the pressure-volume relationships measured from different stages of HF, in order to provide a visual representation of the stages of HF from the American Heart Association [153]. An example of these pressure-volume curves can be seen in the bottom of Figure 5. Other indices such as ejection fraction, cardiac output or flow transients can be obtained from such circulatory system models, see bottom right of Figure 5.

FIGURE 5

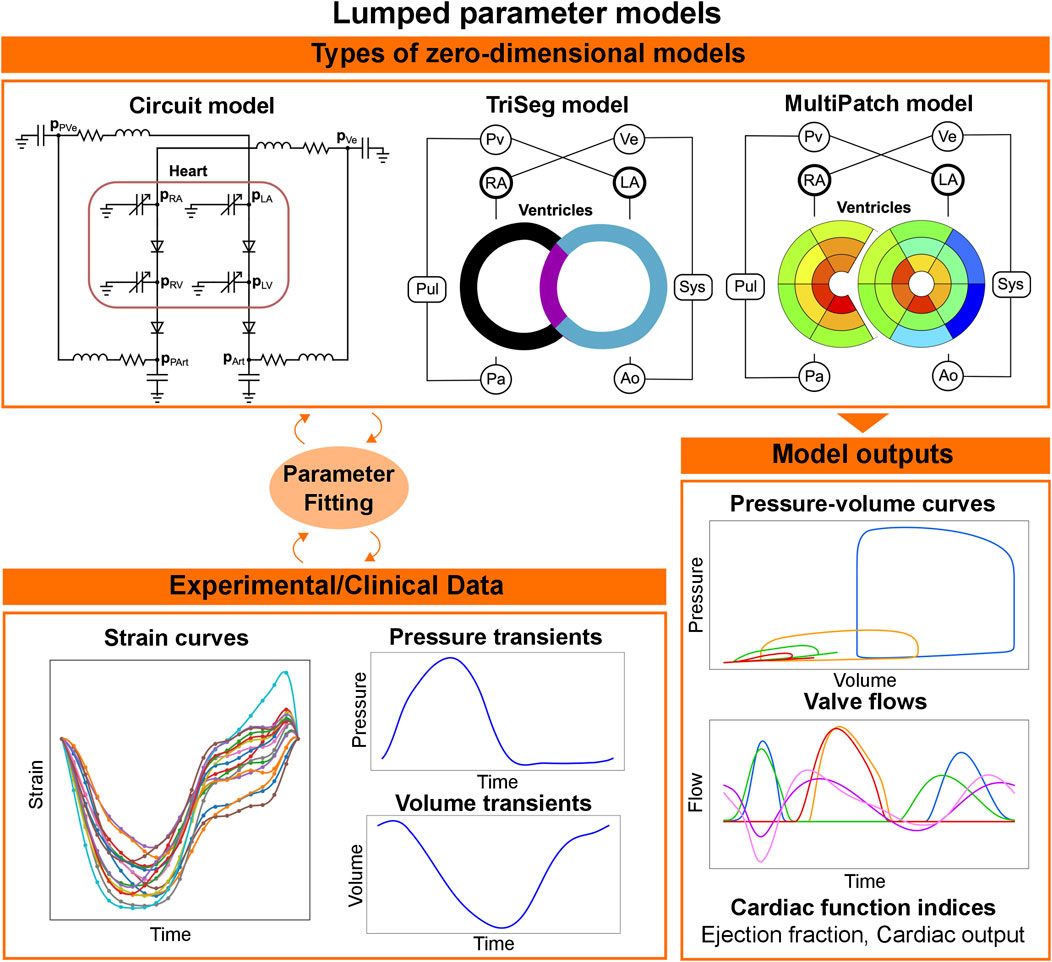
FIGURE 5. Workflow for lumped parameter models. In lumped parameter models, the circulatory system is modelled as an electric circuit (top left). The cardiac chambers and the other components of the circulatory system are simulated with varying elastance models and a combination of resistance, inductance and capacitance, respectively. To represent local dynamics, the heart can be represented with more sophisticated circulatory system models (TriSeg and MultiPatch). The parameters of the circulatory system can be fitted to available pressure and volume clinical data, or regional strains. Lumped-parameter models are then capable of simulating pressure curves, valve flows and global indices for cardiac function, such as cardiac output and ejection fraction.

Although lumped parameter models can be used for clinical applications because of their low computational demand and flexibility, some of their parameters do not necessarily have a physiological meaning, which makes it difficult to estimate their values from clinical or experimental data. To improve parameter identifiability and reduce the number of unknown parameters, Arts et al. developed CircAdapt [154], a lumped parameter model for the heart and circulatory system that includes adaptation rules capable of updating geometry parameters such as the wall volumes of the chambers and the wall areas of the vessels depending on the load they experience. Subsequent developments of CircAdapt were able to account for the mechanical interaction between the LV free wall, the right ventricle (RV) free wall and the septum (TriSeg model) [155], and for heterogeneity of cardiac tissue properties (MultiPatch model) [156], see top of Figure 5. In contrast to other lumped parameter models, which discard spatial information, these versions of CircAdapt provide local as well as global dynamics of the heart. This makes CircAdapt suitable for studying diseases or treatments in which LV-RV interaction and/or spatial heterogeneity are important. The TriSeg model has been used in combination with echocardiography strain data to investigate different substrates in RV arrhythmogenesis cardiomyopathy, and was able to link RV deformation abnormalities to changes in RV contractility and compliance [157, 158], to identify potential causes of abnormal septal motion in patients with pulmonary hypertension [159] and to link cellular contractile properties to CRT response [160]. The MultiPatch model has been used to investigate local work heterogeneity during different pacing modalities to compare various CRT delivery methods [161]. Depending on the application, CircAdapt and its extensions constitute a valuable tool for in silico investigations. Furthermore, thanks to its modular structure, CircAdapt can also be coupled with three-dimensional mechanics models to have a more sophisticated representation of the electromechanical function of the heart. In the following section, we provide a summary of the state-of-the-art of tissue- and organ-level cardiac electromechanics modelling, showing their integration with active and passive mechanics and the incorporation of lumped parameter models.

7 Three-dimensional electromechanics models

In order to simulate the electromechanical activation of the heart at the tissue level, an electrophysiology simulation is often needed, see Figure 6, top-centre. Before focusing on three-dimensional electromechanics models, we briefly explain electrophysiology simulations, as these are an essential building block of an electromechanics model. In essence, an ionic model is coupled with a tissue-level electrophysiology model and computes transmembrane potentials and/or other variables of interest, such as cytosolic calcium concentration. These variables (activation times, transmembrane potential, etc.) are then passed to the active stress model to trigger active tension development, represented with an active cell mechanics model. Electrophysiology and mechanics models can be coupled in multiple ways. We talk about phenomenological coupling if the tension development in the cell model is triggered with an activation time, discarding the cross-bridge cycle and the calcium transient. A detailed ionic model can otherwise provide a calcium transient that can be passed to the cell model (weak coupling). Both phenomenological and weak coupling neglect the effect of mechanical deformation on electrophysiology. Strong electromechanical coupling instead accounts for bidirectional coupling through stretch-activated channels and length-dependence calcium buffering of troponin C [162]. Although strong coupling is often not used due to its high computational cost and complexity, accounting for such mechanisms can be important for some applications, such as arrhythmias, where stretch-induced activation can serve as a trigger for ectopic beats. A review of the different ionic and tissue-level electrophysiology models is beyond the present scope. For more information, we refer the reader to [163].

FIGURE 6

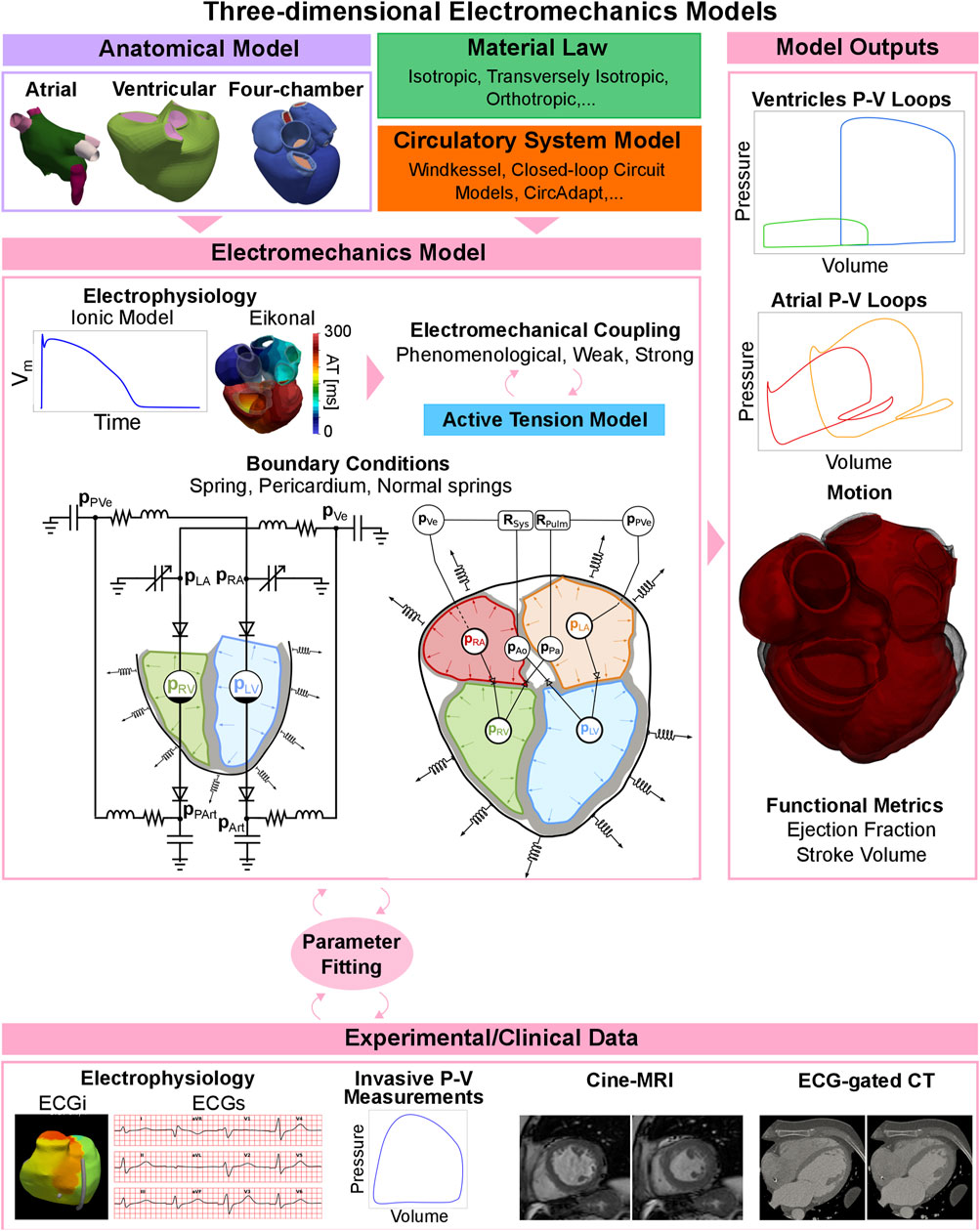
FIGURE 6. Three-dimensional electromechanics models pipeline. Depending on the application, tissue-level mechanics models can include to one chamber, two chambers, or the whole heart. A material law and a circulatory system model are needed to represent passive behaviour of the myocardium and the preload and the afterload of the chambers. The electrophysiology model is coupled with an active tension model to simulate active contraction, and the parameters are fitted to available clinical data. The electromechanics model can output pressure-volume loops for the chamber(s) of interest, the motion of the anatomy and functional metrics such as ejection fraction and stroke volume.

In Figure 6 we show a schematic representation of all the different components of three-dimensional electromechanics models. The electrophysiology output, together with boundary conditions such as springs, the pericardium, or normal springs constrain the mechanics model, both at the initial step of the simulation (initial conditions) and at each timestep (boundary conditions), as shown in the centre of Figure 6. Multiple outputs such as pressure and volume curves, motion, ejection fraction or stroke volume are produced, see left column of Figure 6. These results can be fitted to experimental or clinical data for validation (Figure 6, bottom row). Depending on the application, tissue-level mechanics models can include one chamber, two chambers (usually the ventricles or atria), or the whole heart. In this section we review the research done with electromechanics simulations, depending on whether they are done with ventricular, atrial, or four-chamber models. We use the terminology ‘tissue-level’ here to denote cases when not the whole organ is modelled, but only specific chambers. We refer to ‘tissue-level’ simulations to denote studies where only specific chambers rather than the whole heart was modelled.

7.1 Ventricular models

Ventricular mechanics models were the first cardiac models to be formulated at the tissue level mainly due to data availability and geometric simplicity. As early as 1892, Woods applied Laplace’s theorem to the LV assuming it to be a sphere [164]. Since then, multiple ventricular models have been used, from truncated ellipsoids to patient-specific anatomies.

Simplified ventricular geometries have been used to link subcellular simulations with simulation of the entire chamber [105] in patients with dilated and hypertrophic cardiomyopathies. Despite using a simplified LV geometry, this approach allows to link protein unction to observable clinical biomarkers after administering antiarrhymtic drugs, using a Huxley-based cell model. This simplification of the ventricular geometry makes it more manageable to investigate how changes at the subcellular level, such as the effects of drugs or alterations in proteins, influence the behaviour at the organ scale. Similarly, to translate mechanical behaviour from the cellular to the anatomical level, in [165, 166] the authors coupled the mechanical model of MyoSim to a simple hemispherical representation of the LV. In [100], Gusseva et al. combined a hybrid Hill-Huxley model with a spherical representation of the RV in a cohort of Tetralogy of Fallot patients after pulmonary valve replacement, to assess the predictive value of the mechanics models before and after replacement using a transversely isotropic material law.

Biomechanics ventricular models have been widely used to study therapies such as CRT. In [55], Sermesant et al. simulated the transversely isotropic mechanical behaviour of a biventricular mesh from a patient undergoing CRT using MRI and pressure catheters. In [53], Niederer et al. formulated a new active tension law in combination with a transversely isotropic material law to assess the influence of length dependence on failing hearts undergoing CRT. This law was later used by the same group to assess the distribution of work in CRT patients [56]. In [56], the authors used biventricular mechanics simulations to find the optimal location of the LV pacing lead based on the acute hemodynamic response. Gerach et al. [167] performed a CRT study using simplified LV geometries in a cohort of patients. These were combined with patient-specific electrophysiological measurements to quantify mechanical torsion in HF patients.

Mechanics models can be used to integrate electrophysiology models, which might lack sufficient data for certain diseases or applications, and computational fluid dynamics models, which may have demanding technical needs and high computational expenses. For example, multiple mechanics models have been used to study how physiological and pathological electrophysiology are impacted by cardiac mechanics. In [168], Salvador et al. modelled LV tachycardia using electromechanic simulations. They used a patient-specific geometry, scar location, pressure, and volume biomarkers. One of the main findings was that, due to the mechanoelectric feedback, tissue deformation affects the activation pattern of ventricular tachycardia. The authors extended this study in [169] to investigate the role of stretch-activated channels on the arrhythmia dynamics, finding that tissue deformation could affect the basic cycle length of tachycardia but not its stability. A transversely isotropic law and a Hill-based cellular model were used. The role of the mechanoelectric feedback was previously studied by Hermeling et al. [170], where, using lumped parameter models, Huxley-based cell models, and a simplified geometry, the authors found that the mechanoelectric feedback could partially explain electrophysiological characteristics such as T-wave memory in ventricular pacing. Finally, in [171] Adeniran et al. studied the effect of adding stretch-activated channels to ventricular models using a Huxley-based cell model, finding that it can be an essential feature to adequately model short QT syndrome.

Studies where a computational fluid dynamics model might have been adequate but was too prohibitive due to computational cost and complexity have also used ventricular mechanics models. This will depend on the context, as in some cases analysing the motion, pressures or stress, for instance, is enough and the specific blood flow patterns are not needed. In [172], Bakir et al. simulated ventricular assist devices for patients with dilated cardiomyopathy on idealised biventricular meshes, combining a simplified biventricular geometry and using an orthotropic material law with high-fidelity blood flow simulation in the cavities. This device was also modelled by Sack et al. in [173], where the authors focused on the effects of the device on septum deformation. An orthotropic material law was also used with a Hill-type active tension model. In [54], the authors compared biomarkers such as myofibre stress and strain in a patient with pulmonary hypertension with a healthy control using personalised biventricular models anatomically (from MRI) and functionally (through pressure catheters), while using a transversely isotropic material law. Therapies for complex and rare diseases such as Tetralogy of Fallot were modelled in [174], where Tang et al. simulated patch modelling for RV reconstruction comparing stress and strain distributions for different transversely isotropic patch designs [174] using delayed enhancement MRI to locate the patches and valves. In [175], Cutrì et al. modelled the ventricle of a patient with hypoplastic left heart syndrome. The authors used an orthotropic material law and a Hill-based cell model and simulated the effects of surgery.

Alternatively, ventricular mechanics models have also been used to achieve clinical translation mainly through two ways: conducting in silico trials and reducing the burden of expensive and not readily available imaging technologies such as CT and MRI. We use the definition of in silico trial used before in [176]: a research study that uses computer models of cells, tissues, organs, or systems of human subjects, assigned to one or more interventions (which may include some form of control group) to evaluate the effects of those interventions on health-related biomedical or behavioural outcomes. In [109] Margara et al. performed a set of in silico trials using ventricular mechanics to investigate the effect of specific mutations in hypertrophic cardiomyopathy. This setup was based on the one presented by Wang et al. [177]. In [177], Wang et al. presented a framework to simulate electromechanic simulations on a patient-specific biventricular mesh. Parameters were chosen from the literature or tuned to achieve physiological pressures and volumes, and a Hill-based model for active tension and an orthotropic material law were used. The purpose was to demonstrate the feasibility of such a framework. The clinical availability of imaging technologies can heavily influence the development of anatomical and functional models. In [178], Krishnamurthy et al. presented a pipeline that combines multimodal data (CT, catheter data, echocardiography) and integrates them into closed-loop biventricular mechanical simulations using a Hill-type cell model in patients with HF. Instead of using CT or MRI images, Aguado-Sierra et al. [179] created biventricular meshes from echocardiography images and ran mechanics simulations on HF patients using an orthotropic material law. Although this technique has lower resolution than CT or MRI, it might allow greater translation in environments where costly scans are not available. Additionally, models can be used to reduce the imaging burden using more accessible and readily available imaging technologies to provide insights into the patient’s heart, that otherwise would require more complex and time-consuming image acquisition protocols. In [180], Peña et al. also used echocardiography to create ventricular models but in foetuses at different stages and assess which properties (such as active tension) change over time. The authors used a transversely isotropic material law with a Hill-based active tension model.

7.2 Atrial models

The development of three-dimensional atrial models has lagged behind that of ventricular models, as the atria were long believed to contribute little to overall heart function. However, in recent years, the importance of atrial function and its role as an indicator of cardiac health have been increasingly recognised, triggering the development of atrial models. Typically, three-dimensional atrial models fall into two types: LA-only models and biatrial models, including both LA and RA. In terms of clinical applications, most atrial models have been used to investigate AF and the response to catheter ablation procedures. However, the vast majority of these atrial models focus only on atrial electrophysiology and neglect biomechanics.

Although the number of existing atrial biomechanics models in the literature is limited, they can have significant clinical value. Adeniran et al. [144] used a multiscale, transversely isotropic biatrial model to investigate how electrical remodelling induced by persistent AF affected atrial mechanics and leads to loss of atrial contraction commonly associated with persistent AF. A remodelled state was created by modifying a family of electromechanically coupled single cell models, previously validated against the F-Ca relationship of human atrial myocytes [181]. It has also been possible to create an AF pathological state in atrial models through tissue- and organ-level modifications, without considering cellular remodelling. Feng et al. created an AF state in their LA-mitral valve model [182], without considering cell-level characteristics, but simply by removing atrial contraction. Feng’s atrial model of healthy individuals included a transversely isotropic material model and used a phenomenological approach with a simplified active stress to model active contraction. In the AF case, the active stress was set to zero and represented only an advanced AF case where the atrial booster function is completely lost.

Given the number of remodelling mechanisms associated with AF, mechanics models can benefit from including more information. In the atrial model by Moyer et al. [183], the authors included information about changes in material properties, size, shape, pressure, and conduction. The authors used a transversely isotropic LA model with a Huxley-based cell model coupled to a hydraulic circuit model of the LV and pulmonary circulation to examine how AF-related remodelling could affect mechanics [183]. In this study, the baseline configuration was created from the average MRI-measured geometry of a cohort of healthy patients and loaded using scaled pressure-time curves measured from patients with paroxysmal AF prior to an ablation procedure. The mechanics model incorporated the contact between the LA and surrounding structures by applying inward pressures to the LA septum, anterior wall, and roof. Furthermore, a representation of the LV contraction force acting on the LA was included by applying a downward force driven by the displacement of the mitral valve measured along the pulmonary vein-mitral valve axis of the patient’s MRI. The baseline atrial model was modified to investigate the effect of common factors related to AF on atrial function. Modified factors included size - changing the geometry of the anatomical model so that the end-diastolic endocardial volume matched the average value measured from a cohort of AF patients; shape–modifying the geometry of the anatomical model to match the average geometry measured from patients with AF but scaled to match healthy atrial volumes; pressure - increasing the measured healthy pressure load curves; and fibrosis burden - increasing the isotropic stiffness terms in the myocardium material model. With pathological state atrial models, the global LA function could be examined with reference to the healthy case, illustrating the effect of the AF-related factor using simulated pressure-volume loops.

The baseline Moyer et al. atrial model [183] was further built upon in the paper by Phung et al., where three common scar tissue patterns created during catheter ablation procedures were added, to investigate the effect of scar on mechanical function [146]. Here, scar tissue was modelled in the atrium for the first time by stiffening the isotropic material parameter in the myocardial material model to an even greater extent compared to the increase made when modelling fibrosis, along with the elimination of anisotropy and active contraction [146]. Regional and global functions were assessed using the regional motion of the atrial wall segments and the pressure-volume loops, respectively. With these functional metrics, the effect of each ablation pattern on atrial function was examined with respect to the baseline atrial model. Here, the authors highlight the value of this type of investigation in planning and guiding ablation strategies to correct arrhythmia while having minimal effect on normal atrial function. The pressure-volume loops generated with this mechanics model, however, did not reproduce the characteristic figure-8 shape observed clinically. This could be due to issues surrounding the boundary conditions applied to the LA or to the tuning of the lumped parameter model used to represent the LV and pulmonary circulation. Although the characteristic atrial pressure-volume loop is difficult to achieve in silico, the simulated pressure-volume loops still provide valuable information on how the atrial function is affected under various conditions.

Atrial model output, including simulated motion, volume, and pressure data, is rarely validated in the literature (only in [183], Moyer et al. validated their mechanics model), due to lack of patient data. Additionally, the lack of patient data affects the construction of mechanical models of the atria. Many atrial models assume a constant pressure based on literature values [142, 144] due to difficulty in obtaining patient pressure trace data. Another issue related to atrial model construction is that none of the existing human atrial models mentioned the incorporation of a pericardium. However, the importance of the pericardium for cardiac biomechanics has recently been highlighted by computational studies [62, 184, 185]. Limitations of existing imaging methods have also affected the construction of atrial models. In the literature, many atrial models assume a uniform wall thickness [142, 144, 146], while physiologically, the atria have a heterogeneous wall thickness, ranging between 0.5 and 6.5 mm [186–188]. This limitation persists because the thin walls of the atria require high-resolution imaging to be captured. However, the study by Feng et al. [182] showed a difference in mechanical behaviour when a uniform wall thickness was assumed compared to a patient-specific wall thickness. In a study by Augustin et al. [147], the authors suggested a correlation between heterogeneous wall thickness and LA mechanical behaviour. As such, in the future, to derive the most clinical realism, it may be necessary to include patient-specific wall thickness in 3D atrial models when atrial mechanics is of interest. It should be mentioned, however, that the thin walls of the atria present some difficulties with respect to stability and convergence of the mechanical solver. Augustin et al. highlighted challenges in estimating the unloaded configuration [147] of the atria due to their thin walls. Simulated pressures might then be limited to values lower than physiological ranges, or myocardial stiffness may be increased in an attempt to avoid over-inflating the atria [147].

Atrial mechanics models are in their infancy compared to ventricular models and, as highlighted above, present significant challenges. However, due to the now widely recognised role that atria play in overall cardiac function, atrial models are rapidly developing, alongside novel atrial-specific imaging and functional data collection methods to capture the thin atrial walls and to better understand atrial physiology. The integration of richer clinical datasets from the atria into mechanics models will make atrial computational mechanical models more suitable for clinical applications.

7.3 Four-chamber models

Electromechanical models of the whole heart are increasingly being used to provide mechanistic insight into cardiac pathologies and predict clinical output metrics on the organ scale [189–192]. Although they suffer from higher computational cost and stability issues, four-chamber models imply significant advantages compared to biventricular models: they avoid the need for an unphysiological spatial boundary condition on the base or apex of a biventricular mesh, and incorporating the atria in combination with a closed-loop circulatory system also provides physiological preload and afterload to the ventricles. In addition to improved boundary conditions, four-chamber models are able to capture the complex atrioventricular interaction, which are critical in the study of cardiac pathologies affecting the whole organ. Despite the relative novelty of four-chamber biomechanics, there have already been successful applications for investigating pharmaceutical effects [189], evaluating surgical treatment strategies [190], and questioning the validity of computationally-derived clinical metrics [191].

Some applications, traditionally investigated through electrophysiological studies only, would benefit from the inclusion of biomechanics. An example of this is the use of four-chamber models to investigate cardiac arrhythmias. Peirlinck et al. [189] used a four-chamber electromechanical model coupled to a closed-loop circulatory system to investigate the proarrhythmic potential of pharmaceutical therapy. The mechanics model used a transversely isotropic hyperelastic material and implemented a Huxley-based law for the active stress modelling, including the active stress interaction between adjacent muscle fibres along the sheet direction. By blocking the pharmacologically affected ion channels, the mechanics model was used to link the effect of antiarrhythmic drugs on a single ion channel to the effect on the whole heart and system function.

The clinical application of four-chamber modelling to surgical planning for cardiac arrhythmias is also becoming increasingly feasible. Electromechanical models generated from healthy patients have been modified to include radiofrequency ablation scars typical of a surgical treatment strategy for AF [193]. Gerach et al. developed a four-chamber model using an orthotropic material law and a Huxley-based model for active tension. This model was embedded in an explicit representation of the pericardium, as in [185] and coupled to a closed-loop representation of the circulatory system. By defining the scar regions as non-conducting and simulating multiple heart beats, Gerach et al. found that the efficiency of ventricular pumping was not significantly affected by the atrial scar. This work was extended to include the increased mechanical stiffness of scar tissue and the new configuration was used to analyse combinations of five commonly used ablation scar patterns [190]. The authors concluded that the position and extent of ablation scars have implications not only for atrial pressures and stroke volumes but also for ventricular performance. These in silico experiments represent a promising step towards using four-chamber heart models to optimise choice of ablation strategy in a specific patient.

The four-chamber model of [193] was also extended by embedding the heart in a torso to investigate the influence of contraction on ECG [191]. With a conclusion similar to that from [194] but in a four-chamber heart, the model suggested that some features of the T-wave are significantly affected by cardiac motion. This has implications for the clinical translation of purely electrophysiological models, as some ECG features may not be accurately predicted without a full electromechanical approach.

Whole-heart models have also been used to study myocardial infarction [192]. Jafari et al. developed a four-chamber model using a transversely isotropic, hyperelastic material law for passive mechanics and implemented the active mechanics using a Huxley-based model accounting for sarcomere length and mechanical activation. This model was coupled to a lumped parameter representation of the circulatory system. An infarcted region was defined in the LV wall and the contractility of this region was reduced to simulate acute tissue damage after MI. A comparison of cardiac motion and pressure-volume loops for the healthy and infarcted heart indicated a reduction in cardiac work immediately after MI. The use of a four-chamber geometry removes the need for nonphysiological boundary conditions that require extensive parameter tuning to match the simulated motion with data acquired from the participant.

Four-chamber electromechanical models have also been used to investigate cardiac remodelling and its effect on cardiac function. Strocchi et al. [195] varied the orientation of the ventricular fibres and studied the effect on the displacement of the atrioventricular plane, atrial pressures, and venous return. Land et al. [196] used a four-chamber model to investigate AF-induced electrophysiological remodelling of the atria considering changes in calcium dynamics after restoration of sinus rhythm. The authors concluded that remodelling led to a lower peak atrial pressure and reduced atrial relaxation, as well as a small reduction in ventricular filling. Finally, Genet et al. created a four-chamber model for cardiac growth and remodelling during chronic HF by simulating parallel and serial deposition of sarcomere [197]. In addition to predicting wall thickness, chamber volume, and cardiac geometry, the four-chamber model can predict papillary muscle dislocation, annular dilation, and other clinically relevant outcomes. This work highlights the potential four-chamber models have for predicting the progression of HF in specific patients and promises to aid in personalised treatment planning for HF in the future.

8 Machine learning to reduce computational burden

One of the main barriers to the clinical translation of cardiac biomechanics models is the computational cost, as simulations usually require several hours of hundreds of cores in high-performance computing facilities [198].

Recently, a new approach has been presented to accelerate ventricular mechanics simulations: combining them with neural networks to reduce the computational burden. In [199] Motiwale et al. tested this approach with an idealised LV represented as a truncated ellipsoid. The neural network was trained by minimising certain residual force vectors obtained from the weak form of the partial differential equations that drive a simulation, achieving a speedup of 4 orders of magnitude.

Two of the main bottlenecks when running cardiac mechanics models are in parameter fitting and in sensitivity analysis. In both cases, multiple combinations of parameters must be chosen to run simulations and analyse the output. Although the different techniques of parameter fitting and sensitivity analysis are beyond the scope of this review, machine learning techniques such as Gaussian process emulators are being used to alleviate the computational cost [200]. In [200], Strocchi et al. ran multiple mechanics simulations to then train a set of Gaussian process emulators. These emulators were then used to rapidly and finely sample the parameter space and find the most influential simulation parameters. Similarly, in [201], Salvador et al. used latent neural ordinary differential equations to perform a global sensitivity analysis and parameter estimation, learning not scalar values, but temporal traces. Trained with 400 multiscale mechanics simulations, this approach allowed for simulations 300 times faster than real time on a single processor of a standard laptop.

9 Discussion

One of the end-goals of cardiac biomechanics models is clinical translation: to improve the clinical decision-making process, to improve and/or optimise a therapy outcome, and to gain more knowledge about a disease. Although this field is not new, there is still a gap before biomechanics models can fulfil this purpose.

In most of the papers discussed in this review that describe tissue-level simulations, only a few virtual patients were analysed (n < 20). Although a few patients might suffice for a pilot study, if we want to make general statements that will be true throughout the wider population, more virtual patients are needed. The main reasons for this shortcoming are 1) the time-consuming, expert-requiring pipelines to generate patient-specific anatomical models from imaging data and 2) the computational cost of simulations. For the former problem, reliable, validated, up-to-date and ideally open-source software tools are needed to accelerate simulation pipelines. For the latter, machine learning-based solutions can be used to reduce computational cost.

9.1 Enabling clinical translation through simulation software

At present, there are multiple software platforms to simulate cardiac mechanics, possibly due to the complexity of the systems considered, their multiscale and multiphysics nature, and the ever-evolving field in terms of solvers, physiological findings, and user-specific needs.

Cell models, such as the one used in [98], can be run in the MyoSim (or MATMyoSim) software¹. MyoSim, able to simulate half or full sarcomeres, monitors the distribution of cross-bridge strains at individual binding sites over time, dynamically adjusting these distributions as the cross-bridges undergo the power stroke or as the filaments slide past one another. This explicit representation of cross-bridge strain, while increasing the computational load relative to the mean-distortion approach, allows for a finer characterisation of strain-related effects, including cooperativity between near-neighbouring cross-bridges. MyoSim simulations have been included in finite-element simulations [202]. The FiberSim² platform, developed by the Campbell Muscle Lab, extends the MyoSim modelling approach to provide more flexibility to simulate spatially explicit phenomena [103]. Another option for cell simulations is MUSICO³ [104], a simulator developed by the Mijailovich Lab, based on Monte-Carlo modelling. Although not explicit, this approach exploits experimental measurements to predict contraction properties via sarcomere-level regulation pathways.

In some cases, simulation software platforms that initially focused purely on electrophysiology have broadened their scope to include mechanics, for example, the Cancer, Heart and Soft Tissue Environment (CHASTE)⁴ and the Cardiac Arrhythmia Research Package (CARP)⁵. In both cases, a cell dynamics-electrophysiology-mechanics coupling is possible from the microscale to the macroscale, although the electrophysiology is more established, with Cardiac CHASTE⁶ and OpenCARP⁷, respectively, compared to mechanics.

Some research groups have followed a top-to-bottom approach for software development. Instead of developing a tool specifically for cardiac mechanics simulations, general-purpose software (usually finite element-based) has been used for cardiac simulations. Some examples include SimCardEMS⁸, from the Simula Laboratory based on FEniCS, Ansys⁹, FEBio¹⁰ or Abaqus¹¹, from Dassault Systemes.

To allow clinical translation, thorough benchmark tests should be performed on the simulator, serving as a verification step before focussing on specific applications. Benchmark studies such as the one provided by Land et al. [203] are essential to achieve this goal. These recommendations were also described in the Food and Drug Administration (FDA) draft on the credibility of simulations in medical device submissions [204]. Although focused on medical devices and not encompassing only mechanics modelling, these recommendations are easily applicable to facilitate clinical translation of cardiac biomechanics models.

9.2 Learning from the existing regulatory framework

Clinical decisions are traditionally built on evidence from bench, animal studies, and clinical trials. All this information is usually collected in guidelines and recommendation guides. Recently, some guidelines have contained digital evidence, either from in silico studies or even in silico clinical trials. One of the most recent is the FDA draft on credibility for simulation and modelling of clinical devices [204], built on their previous report from 2016 [205]. Even if a study is not intended for an FDA submission of a medical device, practises such as code verification, validation, and uncertainty quantification are necessary steps to increase trust in mechanics models. However, these steps are rarely performed, even in in silico clinical trials [176].

Although lacking specific regulatory guidelines for best practise, mechanics modelling studies are already being used to support regulatory submissions at different stages [206], allowing them to complement clinical trials in aspects such as predicting performance beyond instructions for use, cost and time. In the United Kingdom, a recent report highlighted success stories of modelling and simulations in healthcare [207]. However, these cases do not yet include cardiac biomechanics, but cardiac electrophysiology or noncardiac biomechanics.

9.3 The gap between experimental data and models

The challenge of reliably calibrating and validating simulations with experimental data also increases with model complexity. For example, an important source of experimental data for these purposes is derived from skinned muscle preparations. This experimental system allows for a more direct characterisation and control of sarcomere biomechanical reactions than can be inferred from intact cells. However, the interpretation of these measurements in the context of intact cells faces significant challenges [25]. To a large extent, the interpretation of the measurements themselves often necessarily rests on model-based assumptions. Variations in measurements can be the result of experimental uncertainty, but also variability inherent in muscle samples. Unless addressed, these challenges will only increase in the future with novel techniques, such as experiments with engineered heart tissue [208]. Consequently, the expectation of achieving an ultimate model that is suitable for all purposes might be unreasonable. Therefore, the specific context of use should be established beforehand, as recommended by the FDA [204].

The lack of biophysical mechanisms of cell-scale contraction has yet to be fully clarified. Previously unconsidered phenomena are being established, for example, the tension-dependent regulation of thick-filament activation involving the myosin “off” state. Another issue that needs further investigation is that of tissue heterogeneity in cellular properties within a tissue [209–211]. This effect, unrepresented by the assumption of homogeneity in most existing models, can affect simulated cardiac muscle performance [212, 213].

On the experimental side, novel findings, including tissue staining [214] and proteomics [215] can provide novel tools to characterise tissue heterogeneity and find changes in response to disease. In [215], Linscheid et al. provided the largest dataset of cardiac protein expression from human samples collected in-vivo, classified by chamber-specific expression. Cardiac conexins (a class of proteins) have also been linked to specific tissue, for example, conexins Cx43 are expressed mainly in atrial and ventricular myocytes and less expressed in the conduction system such as Purkinje fibres, where conexins such as Cx40 are more ubiquitous [214]. These findings provide a potential bridge between the microstructure and the whole-organ level. However, it can be difficult to identify how specific changes in proteins affect cardiac function in-vivo or in bench studies. Multiscale modelling can bridge this gap using techniques such as global sensitivity analyses [200].

9.4 Future directions

Cardiac anatomy is highly variable depending on sex, subject size, and from healthy to diseased state, and adjusting for this variability is often important. Cardiac atlases built from a collection of patient-specific anatomical and mechanics models provide a statistical representation of the anatomy of a cohort. Multiple datasets of CT and MRI have been used to create biventricular [216–218], LA [81], biatrial [219], and whole heart atlases [198]. Statistical shape models have been used to investigate the LV shape induced by preterm birth in adults [220], obesity in adults [221] and children [222]; to identify potentially favourable remodelling as a response to CRT in patients with HF [223] and to quantify LA anatomical remodelling in patients with AF [224]. Although complex and computationally demanding, accounting for shape variability in cardiac mechanics models would make in silico mechanics models more relevant for clinical applications.

A different approach to account for patient intervariability would be to include genomic information. Currently, mechanics models include genetic effects mainly in the shape of expressed proteins, for example, with changes in ion channel properties. Including the vast amount of genetic information that can now be collected routinely would improve the personalisation level of patient-specific cardiac mechanics models.

Although multiple cardiac mechanics models used are already multiscale, there are still several relevant processes that are not being routinely included in these studies, namely, the link to other organs, perfusion, and energetics. In this regard, the recent work by Sharifi et al. [225] is notable, where the authors were able to mimic important features of the physiological baroreflex, one of the body’s homeostatic mechanisms that helps to maintain blood pressure at nearly constant levels. Regarding perfusion, the process linking the circulatory system with the myocardium, Zingaro et al. [226] recently presented a mechanics model linking cardiac mechanics with perfusion. However, this is just the first step to achieve clinical translation of this type of cardiac model. Lastly, modelling energetics can be useful, for instance, in some cases of HF, where there are abnormalities in how heart cells produce energy. Works such as that by Randall et al. [227] show how to model cardiac energetics, but there is a missing link with whole-organ cardiac mechanics. With all these advances, we could better model representations of physiological conditions, including exercise.

Models of cardiac growth and remodelling focusses on how heart structure changes after different stimuli. Changes are usually driven by a mechanical stimulus such as a pressure overload. This type of modelling is not routinely integrated with biomechanics modelling, due to several reasons. Firstly, the interplay between the growth law and the mechanics simulation is not clearly established. The meshes where growth and remodelling models are tested are mainly ventricular or biventricular and mostly very regular or ideal ellipsoids. This simplification hinders clinical translation and integration with patient-specific biomechanics models. Lastly, multiple growth laws are formulated with different advantages and disadvantages. Although it is unlikely (as happened with the passive material laws) that a single law becomes the only one used, more research is needed to understand the limitations of the available growth laws and the implications in the study, potentially requiring integration with clinical and/or experimental data. For a review of the existing growth and remodelling cardiac models, we refer the reader to [228]. These models would also benefit from adopting a multiscale approach, linking down to subcellular growth and remodelling models similar to those used in system modelling [229].

10 Conclusion

The clinical translation of cardiac biomechanics models is essential to have a societal impact by improving the lives of patients. Cardiac biomechanics models provide an excellent framework for integration into the clinical pipeline, but more refinement is needed. In particular, the context of use must be adequate to the high computational cost of biomechanics models, with a focus on better validation against clinical data.

Author contributions

CR: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. TB: Data curation, Investigation, Writing–original draft. RB: Data curation, Investigation, Writing–original draft. AL: Data curation, Investigation, Writing–original draft. SN: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Writing–review and editing. MS: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Supervision, Visualization, Writing–original draft, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. CR and MS receive funding from the British Heart Foundation (RG/20/4/34803). TB is funded by the Leverhulme Trust Mechanics of Life Doctoral Scholarship Programme. RB receives funding from EPSRC DTP (EP/T517963/1). AL is funded by the British Heart Foundation project grant PG/21/10534. SN is supported by the Wellcome/EPSRC Centre for Medical Engineering (WT 203148/Z/16/Z), NIH R01-HL152256, ERC PREDICT-HF 453 (864055), BHF (RG/20/4/34803), EPSRC (EP/X012603/1, EP/P01268X/1) and by the Technology Missions Fund under the EPSRC Grant EP/X03870X/1 and The Alan Turing Institute.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://campbell-muscle-lab.github.io/MATMyoSim/

²https://campbell-muscle-lab.github.io/FiberSim/

³https://www.solindies.com/musico

⁴https://www.cs.ox.ac.uk/chaste/

⁵https://carpentry.medunigraz.at/

⁶https://www.cs.ox.ac.uk/chaste/cardiac_index.html

⁷https://opencarp.org/

⁸https://computationalphysiology.github.io/simcardems/

⁹https://www.ansys.com/en-gb/applications/cardiovascular

¹⁰https://febio.org/knowledgebase/case-studies/structural-mechanics/cardiac-mechanics-benchmark-problems/

¹¹https://www.3ds.com/products-services/simulia/products/abaqus/

References

1. Niederer SA, Campbell KS, Campbell SG. A short history of the development of mathematical models of cardiac mechanics. J Mol Cell Cardiol (2019) 127:11–9. doi:10.1016/J.YJMCC.2018.11.015

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Wang VY, Nielsen PM, Nash MP. Image-based predictive modeling of heart mechanics. Annu Rev Biomed Eng (2015) 17:351–83. doi:10.1146/ANNUREV-BIOENG-071114-040609

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Nguyen TD, Kadri OE, Voronov RS. An introductory overview of image-based computational modeling in personalized cardiovascular medicine. Front Bioeng Biotechnol (2020) 8:529365. doi:10.3389/fbioe.2020.529365

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Avazmohammadi R, Soares JS, Li DS, Raut SS, Gorman RC, Sacks MS. A contemporary look at biomechanical models of myocardium. Annu Rev Biomed Eng (2019) 21:417–42. doi:10.1146/annurev-bioeng-062117-121129

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bracamonte JH, Saunders SK, Wilson JS, Truong UT, Soares JS. Patient-specific inverse modeling of in vivo cardiovascular mechanics with medical image-derived kinematics as input data: concepts, methods, and applications. Appl Sci (Basel, Switzerland) (2022) 12:3954. doi:10.3390/APP12083954

CrossRef Full Text | Google Scholar

6. Li W. Biomechanics of infarcted left ventricle: a review of modelling. Biomed Eng Lett (2020) 10:387–417. doi:10.1007/S13534-020-00159-4

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yoshida K, Holmes JW. Computational models of cardiac hypertrophy. Prog Biophys Mol Biol (2021) 159:75–85. doi:10.1016/J.PBIOMOLBIO.2020.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Rufaihah AJ, Chen CK, Yap CH, Mattar CN. Mending a broken heart: in vitro, in vivo and in silico models of congenital heart disease. Dis models Mech (2021) 14:dmm047522. doi:10.1242/DMM.047522

CrossRef Full Text | Google Scholar

9. Odeigah OO, Valdez-Jasso D, Wall ST, Sundnes J. Computational models of ventricular mechanics and adaptation in response to right-ventricular pressure overload. Front Physiol (2022) 13:948936. doi:10.3389/fphys.2022.948936

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lesage R, Van Oudheusden M, Schievano S, Van Hoyweghen I, Geris L, Capelli C. Mapping the use of computational modelling and simulation in clinics: a survey. Front Med Tech (2023) 5:1125524. doi:10.3389/FMEDT.2023.1125524

CrossRef Full Text | Google Scholar

11. Scollan DF, Holmes A, Winslow R, Forder J. Histological validation of myocardial microstructure obtained from diffusion tensor magnetic resonance imaging. Am J Physiol - Heart Circulatory Physiol (1998) 275:H2308–18. doi:10.1152/ajpheart.1998.275.6.h2308

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Tseng WYI, Dou J, Reese TG, Van Wedeen J. Imaging myocardial fiber disarray and intramural strain hypokinesis in hypertrophic cardiomyopathy with MRI. J Magn Reson Imaging (2006) 23:1–8. doi:10.1002/jmri.20473

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Von Deuster C, Sammut E, Asner L, Nordsletten D, Lamata P, Stoeck CT, et al. Studying dynamic myofiber aggregate reorientation in dilated cardiomyopathy using in vivo magnetic resonance diffusion tensor imaging. Circ Cardiovasc Imaging (2016) 9:e005018. doi:10.1161/CIRCIMAGING.116.005018

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Everett RJ, Stirrat CG, Semple SI, Newby DE, Dweck MR, Mirsadraee S. Assessment of myocardial fibrosis with T1 mapping MRI. Clin Radiol (2016) 71:768–78. doi:10.1016/j.crad.2016.02.013

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Kucukseymen S, Yavin H, Barkagan M, Jang J, Shapira-Daniels A, Rodriguez J, et al. Discordance in scar detection between electroanatomical mapping and cardiac MRI in an infarct swine model. JACC: Clin Electrophysiol (2020) 6:1452–64. doi:10.1016/j.jacep.2020.08.033

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bijvoet GP, Nies HM, Holtackers RJ, Linz D, Adriaans BP, Nijveldt R, et al. Correlation between cardiac MRI and voltage mapping in evaluating atrial fibrosis: a systematic review. Radiol Cardiothorac Imaging (2022) 4:e220061. doi:10.1148/ryct.220061

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Esposito A, Palmisano A, Antunes S, Maccabelli G, Colantoni C, Rancoita PMV, et al. Cardiac CT with delayed enhancement in the characterization of ventricular tachycardia structural substrate: relationship between CT-segmented scar and electro-anatomic mapping. JACC: Cardiovasc Imaging (2016) 9:822–32. doi:10.1016/j.jcmg.2015.10.024

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Pinto JG, Fung YC. Mechanical properties of the heart muscle in the passive state. J Biomech (1973) 6:597–616. doi:10.1016/0021-9290(73)90017-1

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Horowitz A, Lanir Y, Yin FC, Perl M, Sheinman I, Strumpf RK. Structural three-dimensional constitutive law for the passive myocardium. J Biomechanical Eng (1988) 110:200–7. doi:10.1115/1.3108431

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Demer LL, Yin FC. Passive biaxial mechanical properties of isolated canine myocardium. J Physiol (1983) 339:615–30. doi:10.1113/jphysiol.1983.sp014738

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Dokos S, Smaill BH, Young AA, LeGrice IJ. Shear properties of passive ventricular myocardium. Am J Physiol - Heart Circulatory Physiol (2002) 283:H2650–9. doi:10.1152/ajpheart.00111.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Bellini C, Di Martino ES, Federico S. Mechanical behaviour of the human atria. Ann Biomed Eng (2013) 41:1478–90. doi:10.1007/s10439-012-0699-9

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Solaro RJ, Pang DC, Briggs FN. The purification of cardiac myofibrils with Triton X-100. BBA - Bioenerg (1971) 245:259–62. doi:10.1016/0005-2728(71)90033-8

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Mosqueira D, Smith JG, Bhagwan JR, Denning C. Modeling hypertrophic cardiomyopathy: mechanistic insights and pharmacological intervention. Trends Mol Med (2019) 25:775–90. doi:10.1016/j.molmed.2019.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lewalle A, Campbell KS, Campbell SG, Milburn GN, Niederer SA. Functional and structural differences between skinned and intact muscle preparations. J Gen Physiol (2022) 154:e202112990–18. doi:10.1085/jgp.202112990

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sun YB, Irving M. The molecular basis of the steep force-calcium relation in heart muscle. J Mol Cell Cardiol (2010) 48:859–65. doi:10.1016/j.yjmcc.2009.11.019

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Dobrunz LE, Backx PH, Yue DT. Steady-state [Ca2+]i-force relationship in intact twitching cardiac muscle: direct evidence for modulation by isoproterenol and EMD 53998. Biophysical J (1995) 69:189–201. doi:10.1016/S0006-3495(95)79889-7

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Land S, Park-Holohan SJ, Smith NP, dos Remedios CG, Kentish JC, Niederer SA. A model of cardiac contraction based on novel measurements of tension development in human cardiomyocytes. J Mol Cell Cardiol (2017) 106:68–83. doi:10.1016/j.yjmcc.2017.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Dobesh D, Konhilas JP, de Tombe PP. Cooperative activation in cardiac muscle: impact of sarcomere length. Am J Physiol - Heart Circulatory Physiol (2002) 282:1055–62. doi:10.1152/ajpheart.00667.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kawai M, Brandt PW. Sinusoidal analysis: a high resolution method for correlating biochemical reactions with physiological processes in activated skeletal muscles of rabbit, frog and crayfish. J Muscle Res Cel Motil (1980) 1:279–303. doi:10.1007/BF00711932

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Awinda PO, Bishaw Y, Watanabe M, Guglin MA, Campbell KS, Tanner BC. Effects of mavacamten on Ca2+ sensitivity of contraction as sarcomere length varied in human myocardium. Br J Pharmacol (2020) 177:5609–21. doi:10.1111/bph.15271

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Brenner B. Effect of Ca2+ on cross-bridge turnover kinetics in skinned single rabbit psoas fibers: implications for regulation of muscle contraction. Proc Natl Acad Sci USA (1988) 85:3265–9. doi:10.1073/pnas.85.9.3265

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Hunter PJ, McCulloch AD, Ter Keurs HE. Modelling the mechanical properties of cardiac muscle. Prog Biophys Mol Biol (1998) 69:289–331. doi:10.1016/S0079-6107(98)00013-3

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Steendijk P, Tulner SA, Wiemer M, Bleasdale RA, Bax JJ, Van Der Wall EE, et al. Pressure-volume measurements by conductance catheter during cardiac resynchronization therapy. Eur Heart J Supplements (2004) 6:D35–D42. doi:10.1016/j.ehjsup.2004.05.012

CrossRef Full Text | Google Scholar

35. Klotz S, Hay I, Dickstein ML, Yi GH, Wang J, Maurer MS, et al. Single-beat estimation of end-diastolic pressure-volume relationship: a novel method with potential for noninvasive application. Am J Physiology-Heart Circulatory Physiol (2006) 291:H403–12. doi:10.1152/ajpheart.01240.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Bastos MB, Burkhoff D, Maly J, Daemen J, Den Uil CA, Ameloot K, et al. Invasive left ventricle pressure-volume analysis: overview and practical clinical implications. Eur Heart J (2020) 41:1286–97. doi:10.1093/eurheartj/ehz552

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Elliott MK, Mehta V, Sidhu BS, Niederer S, Rinaldi CA. Electrocardiographic imaging of His bundle, left bundle branch, epicardial, and endocardial left ventricular pacing to achieve cardiac resynchronization therapy. HeartRhythm Case Rep (2020) 6:460–3. doi:10.1016/j.hrcr.2020.04.012

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Arnold AD, Shun-Shin MJ, Keene D, Howard JP, Afzal Sohaib SM, Wright IJ, et al. His resynchronization therapy vs. biventricular pacing for heart failure with LBBB: a within-patient comparison of effects on acute haemodynamic function and ventricular activation. Europace (2018) 20. doi:10.1016/j.jacc.2018.09.073

CrossRef Full Text | Google Scholar

39. Rudy Y. Noninvasive electrocardiographic imaging of arrhythmogenic substrates in humans. Circ Res (2013) 112:863–74. doi:10.1161/CIRCRESAHA.112.279315

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Koushanpour E, Collings WD. Validation and dynamic applications of an ellipsoid model of the left ventricle. J Appl Physiol (1966) 21:1655–61. doi:10.1152/jappl.1966.21.5.1655

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Ghista DN, Sandler H. An analytic elastic-viscoelastic model for the shape and the forces in the left ventricle. J Biomech (1969) 2:35–47. doi:10.1016/0021-9290(69)90040-2

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Vetter FJ, McCulloch AD. Three-dimensional analysis of regional cardiac function: a model of rabbit ventricular anatomy. Prog Biophys Mol Biol (1998) 69:157–83. doi:10.1016/S0079-6107(98)00006-6

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Arevalo HJ, Helm PA, Trayanova NA. Development of a model of the infarcted canine heart that predicts arrhythmia generation from specific cardiac geometry and scar distribution. Comput Cardiol (2008) 35:497–500. doi:10.1109/CIC.2008.4749087

CrossRef Full Text | Google Scholar

44. Gurev V, Lee T, Constantino J, Arevalo H, Trayanova NA. Models of cardiac electromechanics based on individual hearts imaging data: image-based electromechanical models of the heart. Biomech Model Mechanobiology (2011) 10:295–306. doi:10.1007/s10237-010-0235-5

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Plank G, Burton RA, Hales P, Bishop M, Mansoori T, Bernabeu MO, et al. Generation of histo-anatomically representative models of the individual heart: tools and application. Phil Trans R Soc A: Math Phys Eng Sci (2009) 367:2257–92. doi:10.1098/rsta.2009.0056

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Bishop MJ, Hales P, Plank G, Gavaghan DJ, Scheider J, Grau V. Comparison of rule-based and dtmri-derived fibre architecture in a whole rat ventricular computational model. Lecture Notes Comp Sci (including subseries Lecture Notes Artif Intelligence Lecture Notes Bioinformatics) (2009) 5528:87–96. doi:10.1007/978-3-642-01932-6_10

CrossRef Full Text | Google Scholar

47. Bishop MJ, Plank G, Burton RA, Schneider JE, Gavaghan DJ, Grau V, et al. Development of an anatomically detailed MRI-derived rabbit ventricular model and assessment of its impact on simulations of electrophysiological function. Am J Physiol - Heart Circulatory Physiol (2010) 298:H699–718. doi:10.1152/ajpheart.00606.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Aslanidi OV, Nikolaidou T, Zhao J, Smaill BH, Gilbert SH, Holden AV, et al. Application of micro-computed tomography with iodine staining to cardiac imaging, segmentation, and computational model development. IEEE Trans Med Imaging (2013) 32:8–17. doi:10.1109/TMI.2012.2209183

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Zhao J, Butters TD, Zhang H, Legrice IJ, Sands GB, Smaill BH. Image-based model of atrial anatomy and electrical activation: a computational platform for investigating atrial arrhythmia. IEEE Trans Med Imaging (2013) 32:18–27. doi:10.1109/TMI.2012.2227776

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Zemlin CW, Herzel H, Panfilov AV, Zemlin CW, Herzel H, Ho SY, et al. A realistic and efficient model of excitation propagation in the human atria. Comp simulation Exp Assess Card Electrophysiol (2001).

Google Scholar

51. Seemann G, Höper C, Sachse FB, Dössel O, Holden AV, Zhang H. Heterogeneous three-dimensional anatomical and electrophysiological model of human atria. Phil Trans R Soc A: Math Phys Eng Sci (2006) 364:1465–81. doi:10.1098/rsta.2006.1781

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Freudenberg J, Schiemann T, Tiede U, Höhne K. Simulation of cardiac excitation patterns in a three-dimensional anatomical heart atlas. Comput Biol Med (2000) 30:191–205. doi:10.1016/S0010-4825(00)00005-6

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Niederer SA, Plank G, Chinchapatnam P, Ginks M, Lamata P, Rhode KS, et al. Length-dependent tension in the failing heart and the efficacy of cardiac resynchronization therapy. Cardiovasc Res (2011) 89:336–43. doi:10.1093/cvr/cvq318

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Xi C, Latnie C, Zhao X, Tan JL, Wall ST, Genet M, et al. Patient-specific computational analysis of ventricular mechanics in pulmonary arterial hypertension. J Biomechanical Eng (2016) 138. doi:10.1115/1.4034559

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Sermesant M, Chabiniok R, Chinchapatnam P, Mansi T, Billet F, Moireau P, et al. Patient-specific electromechanical models of the heart for the prediction of pacing acute effects in CRT: a preliminary clinical validation. Med Image Anal (2012) 16:201–15. doi:10.1016/J.MEDIA.2011.07.003

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Crozier A, Blazevic B, Lamata P, Plank G, Ginks M, Duckett S, et al. Analysis of lead placement optimization metrics in cardiac resynchronization therapy with computational modelling. Europace (2016) 18:iv113–20. doi:10.1093/europace/euw366

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Lamata P, Niederer S, Nordsletten D, Barber DC, Roy I, Hose DR, et al. An accurate, fast and robust method to generate patient-specific cubic Hermite meshes. Med Image Anal (2011) 15:801–13. doi:10.1016/j.media.2011.06.010

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Fastl TE, Tobon-Gomez C, Crozier A, Whitaker J, Rajani R, McCarthy KP, et al. Personalized computational modeling of left atrial geometry and transmural myofiber architecture. Med Image Anal (2018) 47:180–90. doi:10.1016/j.media.2018.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Solís-Lemus JA, Baptiste T, Barrows R, Sillett C, Gharaviri A, Raffaele G, et al. Evaluation of an open-source pipeline to create patient-specific left atrial models: a reproducibility study. Comput Biol Med (2023) 162:107009. doi:10.1016/j.compbiomed.2023.107009

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Roney CH, Pashaei A, Meo M, Dubois R, Boyle PM, Trayanova NA, et al. Universal atrial coordinates applied to visualisation, registration and construction of patient specific meshes. Med Image Anal (2019) 55:65–75. doi:10.1016/j.media.2019.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Roy A, Varela M, Aslanidi O. Image-based computational evaluation of the effects of atrial wall thickness and fibrosis on re-entrant drivers for atrial fibrillation. Front Physiol (2018) 9:1352. doi:10.3389/fphys.2018.01352

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Pfaller MR, Hörmann JM, Weigl M, Nagler A, Chabiniok R, Bertoglio C, et al. The importance of the pericardium for cardiac biomechanics: from physiology to computational modeling. Biomech Model Mechanobiology (2019) 18:503–29. doi:10.1007/s10237-018-1098-4

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Strocchi M, Augustin CM, Gsell MAF, Karabelas E, Neic A, Gillette K, et al. A publicly available virtual cohort of four-chamber heart meshes for cardiac electro-mechanics simulations. PLOS ONE (2020) 15:–:e0235145. doi:10.1371/journal.pone.0235145

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Guan D, Yao J, Luo X, Gao H. Effect of myofibre architecture on ventricular pump function by using a neonatal porcine heart model: from DT-MRI to rule-based methods. R Soc Open Sci (2020) 7:191655. doi:10.1098/rsos.191655

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Deng D, Jiao P, Ye X, Xia L. An image-based model of the whole human heart with detailed anatomical structure and fiber orientation. Comput Math Methods Med (2012) 2012:1–16. doi:10.1155/2012/891070

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Gonzalez-Tendero A, Zhang C, Balicevic V, Cardenes R, Loncaric S, Butakoff C, et al. Whole heart detailed and quantitative anatomy,myofibre structure and vasculature from X-ray phase-contrast synchrotron radiation-basedmicro computed tomography. Eur Heart J Cardiovasc Imaging (2017) 18:732–41. doi:10.1093/ehjci/jew314

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Streeter DD, Spotnitz HM, Patel DP, Ross J, Sonnenblick EH. Fiber orientation in the canine left ventricle during diastole and systole. Circ Res (1969) 24:339–47. doi:10.1161/01.RES.24.3.339

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Potse M, Dubé B, Richer J, Vinet A, Gulrajani RM. A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans Biomed Eng (2006) 53:2425–35. doi:10.1109/TBME.2006.880875

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Bayer JD, Blake RC, Plank G, Trayanova NA. A novel rule-based algorithm for assigning myocardial fiber orientation to computational heart models. Ann Biomed Eng (2012) 40:2243–54. doi:10.1007/s10439-012-0593-5

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Wong J, Kuhl E. Generating fibre orientation maps in human heart models using Poisson interpolation. Comp Methods Biomech Biomed Eng (2014) 17:1217–26. doi:10.1080/10255842.2012.739167

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Piersanti R, Africa PC, Fedele M, Vergara C, Dedè L, Corno AF, et al. Modeling cardiac muscle fibers in ventricular and atrial electrophysiology simulations. Comp Methods Appl Mech Eng (2021) 373:113468. doi:10.1016/j.cma.2020.113468

CrossRef Full Text | Google Scholar

72. Doste R, Soto-Iglesias D, Bernardino G, Alcaine A, Sebastian R, Giffard-Roisin S, et al. A rule-based method to model myocardial fiber orientation in cardiac biventricular geometries with outflow tracts. Int J Numer Methods Biomed Eng (2019) 35:e3185. doi:10.1002/cnm.3185

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Mountris KA, Pueyo E. A meshless fragile points method for rule-based definition of myocardial fiber orientation. Comp Methods Programs Biomed (2022) 226:107164. doi:10.1016/j.cmpb.2022.107164

CrossRef Full Text | Google Scholar

74. Krueger MW, Schmidt V, Tobón C, Weber FM, Lorenz C, Keller DU, et al. Modeling atrial fiber orientation in patient-specific geometries: a semi-automatic rule-based approach. Lecture Notes Comp Sci (including subseries Lecture Notes Artif Intelligence Lecture Notes Bioinformatics) (2011) 6666:223–32. doi:10.1007/978-3-642-21028-0{_}28

CrossRef Full Text | Google Scholar

75. Tobón C, Ruiz-Villa CA, Heidenreich E, Romero L, Hornero F, Saiz J. A three-dimensional human atrial model with fiber orientation. Electrograms and arrhythmic activation patterns relationship. PLoS ONE (2013) 8:e50883. doi:10.1371/journal.pone.0050883

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Ferrer A, Sebastián R, Sánchez-Quintana D, Rodríguez JF, Godoy EJ, Martínez L, et al. Detailed anatomical and electrophysiological models of human atria and torso for the simulation of atrial activation. PLoS ONE (2015) 10:e0141573. doi:10.1371/journal.pone.0141573

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Wachter A, Loewe A, Krueger MW, Dössel O, Seemann G. Mesh structure-independent modeling of patient-specific atrial fiber orientation. Curr Dir Biomed Eng (2015) 1:409–12. doi:10.1515/cdbme-2015-0099

CrossRef Full Text | Google Scholar

78. Zheng T, Azzolin L, Sánchez J, Dössel O, Loewe A. An automate pipeline for generating fiber orientation and region annotation in patient specific atrial models. Curr Dir Biomed Eng (2021) 7:136–9. doi:10.1515/cdbme-2021-2035

CrossRef Full Text | Google Scholar

79. Labarthe S, Bayer J, Coudière Y, Henry J, Cochet H, Jaïs P, et al. A bilayermodel of human atria:mathematical background, construction, and assessment. Europace (2014) 16:iv21–9. doi:10.1093/europace/euu256

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Bayer J, Prassl AJ, Pashaei A, Gomez JF, Frontera A, Neic A, et al. Universal ventricular coordinates: a generic framework for describing position within the heart and transferring data. Med Image Anal (2018) 45:83–93. doi:10.1016/j.media.2018.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Roney CH, Bendikas R, Pashakhanloo F, Corrado C, Vigmond EJ, McVeigh ER, et al. Constructing a human atrial fibre atlas. Ann Biomed Eng (2021) 49:233–50. doi:10.1007/s10439-020-02525-w

PubMed Abstract | CrossRef Full Text | Google Scholar

82. O’Brien H, Williams MC, Rajani R, Niederer S. Radiomics and machine learning for detecting scar tissue on CT delayed enhancement imaging. Front Cardiovasc Med (2022) 9:847825. doi:10.3389/fcvm.2022.847825

PubMed Abstract | CrossRef Full Text | Google Scholar

83. O’Brien H, Whitaker J, Singh Sidhu B, Gould J, Kurzendorfer T, O’Neill MD, et al. Automated left ventricle ischemic scar detection in CT using deep neural networks. Front Cardiovasc Med (2021) 8:655252. doi:10.3389/fcvm.2021.655252

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Kottkamp H, Schreiber D, Moser F, Rieger A. Therapeutic approaches to atrial fibrillation ablation targeting atrial fibrosis. JACC Clin Electrophysiol (2017) 3:643–53. doi:10.1016/j.jacep.2017.05.009

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Lahuerta AA, Roberto C, Saiz FJ, Cano Ó, Martinez-Mateu L, Alonso P, et al. Atrial low voltage areas: a comparison between atrial fibrillation and sinus rhythm. Cardiol J (2022) 29:252–62. doi:10.5603/CJ.a2021.0125

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Mukherjee RK, Costa CM, Neji R, Harrison JL, Sim I, Williams SE, et al. Evaluation of a real-time magnetic resonance imaging-guided electrophysiology system for structural and electrophysiological ventricular tachycardia substrate assessment. Europace (2019) 21:1432–41. doi:10.1093/europace/euz165

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Hutchinson MD, Gerstenfeld EP, Desjardins B, Bala R, Riley MP, Garcia FC, et al. Endocardial unipolar voltage mapping to detect epicardial ventricular tachycardia substrate in patients with nonischemic left ventricular cardiomyopathy. Circ Arrhythmia Electrophysiol (2011) 4:49–55. doi:10.1161/CIRCEP.110.959957

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Wakeling JM, Febrer-Nafría M, De Groote F. A review of the efforts to develop muscle and musculoskeletal models for biomechanics in the last 50 years. J Biomech (2023) 155:111657. doi:10.1016/j.jbiomech.2023.111657

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Hill A. The heat of shortening and the dynamic constants of muscle. Proc R Soc Lond Ser B - Biol Sci (1938) 126:136–95. doi:10.1098/rspb.1938.0050

CrossRef Full Text | Google Scholar

90. Kayvanpour E, Mansi T, Sedaghat-Hamedani F, Amr A, Neumann D, Georgescu B, et al. Towards personalized cardiology: multi-scale modeling of the failing heart. PLoS ONE (2015) 10:e0134869–18. doi:10.1371/journal.pone.0134869

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Huxley AF. Muscle structure and theories of contraction. Prog Biophys biophysical Chem (1957) 7:255–318. doi:10.1016/s0096-4174(18)30128-8

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Cadova M, Vilimek M, Daniel M. A comparative study of muscle force estimates using Huxley’s and Hill’s muscle model. Comput Methods Biomech Biomed Engin (2014) 17:311–7. doi:10.1080/10255842.2012.683426

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Haselgrove JC, Huxley HE. X-ray evidence for radial cross-bridge movement and for the sliding filament model in actively contracting skeletal muscle. J Mol Biol (1973) 77:549–68. doi:10.1016/0022-2836(73)90222-2

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Huxley AF, Simmons RM. Proposed mechanism of force generation in striated muscle. Nature (1971) 233:533–8. doi:10.1038/233533a0

PubMed Abstract | CrossRef Full Text | Google Scholar

95. McKillop DF, Geeves MA. Regulation of the interaction between actin and myosin subfragment 1: evidence for three states of the thin filament. Biophysical J (1993) 65:693–701. doi:10.1016/S0006-3495(93)81110-X

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Smith DA. A strain-dependent ratchet model for [phosphate]- and [ATP]-dependent muscle contraction. J Muscle Res Cel Motil (1998) 19:189–211. doi:10.1023/A:1005316830289

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Lombardi V, Piazzesi G. The contractile response during steady lengthening of stimulated frog muscle fibres. J Physiol (1990) 431:141–71. doi:10.1113/jphysiol.1990.sp018324

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Campbell KS. Dynamic coupling of regulated binding sites and cycling myosin heads in striated muscle. J Gen Physiol (2014) 143:387–99. doi:10.1085/jgp.201311078

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Mijailovich SM, Prodanovic M, Poggesi C, Geeves MA, Regnier M. Multiscale modeling of twitch contractions in cardiac trabeculae. J Gen Physiol (2021) 153:e202012604. doi:10.1085/JGP.202012604

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Gusseva M, Hussain T, Hancock Friesen C, Greil G, Chapelle D, Chabiniok R. Prediction of ventricular mechanics after pulmonary valve replacement in tetralogy of Fallot by biomechanical modeling: a step towards precision healthcare. Ann Biomed Eng (2021) 49:3339–48. doi:10.1007/s10439-021-02895-9

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Razumova MV, Bukatina AE, Campbell KB. Stiffness-distortion sarcomere model for muscle simulation. J Appl Physiol (1999) 87:1861–76. doi:10.1152/jappl.1999.87.5.1861

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Rice JJ, Wang F, Bers DM, de Tombe PP. Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophysical J (2008) 95:2368–90. doi:10.1529/biophysj.107.119487

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Kosta S, Colli D, Ye Q, Campbell KS. FiberSim: a flexible open-source model of myofilament-level contraction. Biophysical J (2022) 121:175–82. doi:10.1016/j.bpj.2021.12.021

CrossRef Full Text | Google Scholar

104. Mijailovich SM, Kayser-Herold O, Stojanovic B, Nedic D, Irving TC, Geeves MA. Three-dimensional stochastic model of actin-myosin binding in the sarcomere lattice. J Gen Physiol (2016) 148:459–88. doi:10.1085/jgp.201611608

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Tomasevic S, Milosevic M, Milicevic B, Simic V, Prodanovic M, Mijailovich SM, et al. Computational modeling on drugs effects for left ventricle in cardiomyopathy disease. Pharmaceutics (2023) 15:793–18. doi:10.3390/pharmaceutics15030793

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Fenwick AJ, Wood AM, Tanner BC. The spatial distribution of thin filament activation influences force development and myosin activity in computational models of muscle contraction. Arch Biochem Biophys (2021) 703:108855. doi:10.1016/j.abb.2021.108855

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Campbell KS, Yengo CM, Lee LC, Kotter J, Sorrell VL, Guglin M, et al. Closing the therapeutic loop. Arch Biochem Biophys (2019) 663:129–31. doi:10.1016/j.abb.2019.01.006

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Varian K, Tang WH. Therapeutic strategies targeting inherited cardiomyopathies. Curr Heart Fail Rep (2017) 14:321–30. doi:10.1007/s11897-017-0346-8

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Margara F, Psaras Y, Wang ZJ, Schmid M, Doste R, Garfinkel AC, et al. Mechanism based therapies enable personalised treatment of hypertrophic cardiomyopathy. Scientific Rep (2022) 12:1–17. doi:10.1038/s41598-022-26889-2

CrossRef Full Text | Google Scholar

110. Hwang PM, Sykes BD. Targeting the sarcomere to correct muscle function. Nat Rev Drug Discov (2015) 14:313–28. doi:10.1038/nrd4554

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Malik F, Harman J, Elias K, Morgan B, Rodriguez H, Brejc K, et al. Cardiac myosin activation: a potential therapeutic approach for systolic heart failure. Science (2011) 331:1439–43. doi:10.1126/science.1200113

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Parikh J, Rumbell T, Butova X, Myachina T, Acero JC, Khamzin S, et al. Generative adversarial networks for construction of virtual populations of mechanistic models: simulations to study Omecamtiv Mecarbil action. J Pharmacokinet Pharmacodynamics (2022) 49:51–64. doi:10.1007/s10928-021-09787-4

CrossRef Full Text | Google Scholar

113. Van Herck I, Mora MT, Llopis-Lorente J, Finsberg H, Daversin-Catty C, Saiz J, et al. Omecamtiv mecarbil improves contraction behaviour in a 3D electromechanical tissue model of heart failure. Comput Cardiol (2022) 3–6. doi:10.22489/CinC.2022.033

CrossRef Full Text | Google Scholar

114. Longobardi S, Sher AA, Niederer SA. In silico mapping of the omecamtiv mecarbil effects from the sarcomere to the whole-heart and back again. In: DB Ennis, LE Perotti, and VY Wang, editors. Functional imaging and modeling of the heart. FIMH 2021. Lecture notes in computer science, 12738. Springer International Publishing (2021). p. 406–15. doi:10.1007/978-3-030-78710-3_39

CrossRef Full Text | Google Scholar

115. Holzapfel GA, Ogden RW. Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Phil Trans R Soc A: Math Phys Eng Sci (2009) 367:3445–75. doi:10.1098/rsta.2009.0091

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Demiray H. Stresses in ventricular wall. J Appl Mech Trans ASME (1976) 43:194–7. doi:10.1115/1.3423806

CrossRef Full Text | Google Scholar

117. Novak VP, Yin FC, Humphrey JD. Regional mechanical properties of passive myocardium. J Biomech (1994) 27:403–12. doi:10.1016/0021-9290(94)90016-7

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Humphrey JD, Strumpf RK, Yin FC. Determination of a constitutive relation for passive myocardium: II. -Parameter estimation. J Biomechanical Eng (1990) 112:340–6. doi:10.1115/1.2891194

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Huyghe JM, van Campen DH, Arts T, Heethaar RM. The constitutive behaviour of passive heart muscle tissue: a quasi-linear viscoelastic formulation. J Biomech (1991) 24:841–9. doi:10.1016/0021-9290(91)90309-B

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Humphrey JD, Yin FC. On constitutive relations and finite deformations of passive cardiac tissue: I. A pseudostrain-energy function. J Biomechanical Eng (1987) 109:298–304. doi:10.1115/1.3138684

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Guccione JM, McCulloch AD, Waldman LK. Passive material properties of intact ventricular myocardium determined from a cylindrical model. J Biomechanical Eng (1991) 113:42–55. doi:10.1115/1.2894084

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Kerckhoffs RC, Bovendeerd PH, Kotte JC, Prinzen FW, Smits K, Arts T. Homogeneity of cardiac contraction despite physiological asynchrony of depolarization: a model study. Ann Biomed Eng (2003) 31:536–47. doi:10.1114/1.1566447

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Costa KD, Hunter PJ, Rogers JM, Guccione JM, Waldman LK, McCulloch AD. A three-dimensional finite element method for large elastic deformations of ventricular myocardium: II—prolate spheroidal coordinates. J Biomechanical Eng (1996) 118:464–72. doi:10.1115/1.2796032

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Costa KD, Holmes JW, McCulloch AD. Modelling cardiac mechanical properties in three dimensions. Phil Trans R Soc B Biol Sci (2001) 359:1233–50. doi:10.1098/rsta.2001.0828

CrossRef Full Text | Google Scholar

125. Schmid H, Nash MP, Young AA, Hunter PJ. Myocardial material parameter estimation - a comparative study for simple shear. J Biomechanical Eng (2006) 128:742–50. doi:10.1115/1.2244576

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Usyk TP, Mazhari R, McCulloch AD. Effect of laminar orthotropic myofiber architecture on regional stress and strain in the canine left ventricle. J Elasticity (2000) 61:143–64. doi:10.1023/A:1010883920374

CrossRef Full Text | Google Scholar

127. Schmid H, O’Callaghan P, Nash MP, Lin W, LeGrice IJ, Smaill BH, et al. Myocardial material parameter estimation: a non-homogeneous finite element study from simple shear tests. Biomech Model Mechanobiology (2008) 7:161–73. doi:10.1007/s10237-007-0083-0

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Moulton MJ, Creswell LL, Downing SW, Actis RL, Szabó BA, Pasque MK. Myocardial material property determination in the in vivo heart using magnetic resonance imaging. Int J Card Imaging (1996) 12:153–67. doi:10.1007/BF01806218

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Remme EW, Hunter PJ, Smiseth O, Stevens C, Rabben SI, Skulstad H, et al. Development of an in vivo method for determining material properties of passive myocardium. J Biomech (2004) 37:669–78. doi:10.1016/j.jbiomech.2003.09.023

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Wang VY, Lam HI, Ennis DB, Young AA, Nash MP. Passive ventricular mechanics modelling using MRI of structure and function. Medical image computing and computer-assisted intervention: MICCAI. Int Conf Med Image Comput Computer-Assisted Intervention (2008) 11:814–21. doi:10.1007/978-3-540-85990-1_98

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Palit A, Bhudia SK, Arvanitis TN, Turley GA, Williams MA. In vivo estimation of passive biomechanical properties of human myocardium. Med Biol Eng Comput (2018) 56:1615–31. doi:10.1007/s11517-017-1768-x

PubMed Abstract | CrossRef Full Text | Google Scholar

132. Gao H, Li WG, Cai L, Berry C, Luo XY. Parameter estimation in a Holzapfel–Ogden law for healthy myocardium. J Eng Math (2015) 95:231–48. doi:10.1007/s10665-014-9740-3

PubMed Abstract | CrossRef Full Text | Google Scholar

133. Xi J, Lamata P, Niederer S, Land S, Shi W, Zhuang X, et al. The estimation of patient-specific cardiac diastolic functions from clinical measurements. Med Image Anal (2013) 17:133–46. doi:10.1016/j.media.2012.08.001

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Kovacheva E, Baron L, Schuler S, Gerach T, Dössel O, Loewe A. Optimization framework to identify constitutive law parameters of the human heart. Curr Dir Biomed Eng (2020) 6:95–8. doi:10.1515/cdbme-2020-3025

CrossRef Full Text | Google Scholar

135. Mojsejenko D, McGarvey JR, Dorsey SM, Gorman JH, Burdick JA, Pilla JJ, et al. Estimating passive mechanical properties in a myocardial infarction using MRI and finite element simulations. Biomech Model Mechanobiology (2015) 14:633–47. doi:10.1007/s10237-014-0627-z

PubMed Abstract | CrossRef Full Text | Google Scholar

136. Marx L, Niestrawska JA, Gsell MA, Caforio F, Plank G, Augustin CM. Robust and efficient fixed-point algorithm for the inverse elastostatic problem to identify myocardial passive material parameters and the unloaded reference configuration. J Comput Phys (2022) 463:111266. doi:10.1016/j.jcp.2022.111266

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Balaban G, Finsberg H, Funke S, Håland TF, Hopp E, Sundnes J, et al. In vivo estimation of elastic heterogeneity in an infarcted human heart. Biomech Model Mechanobiology (2018) 17:1317–29. doi:10.1007/s10237-018-1028-5

PubMed Abstract | CrossRef Full Text | Google Scholar

138. Hadjicharalambous M, Asner L, Chabiniok R, Sammut E, Wong J, Peressutti D, et al. Non-invasive model-based assessment of passive left-ventricular myocardial stiffness in healthy subjects and in patients with non-ischemic dilated cardiomyopathy. Ann Biomed Eng (2017) 45:605–18. doi:10.1007/s10439-016-1721-4

PubMed Abstract | CrossRef Full Text | Google Scholar

139. Nasopoulou A, Shetty A, Lee J, Nordsletten D, Rinaldi CA, Lamata P, et al. Improved identifiability of myocardial material parameters by an energy-based cost function. Biomech Model Mechanobiology (2017) 16:971–88. doi:10.1007/s10237-016-0865-3

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Yu H, del Nido PJ, Geva T, Yang C, Tang A, Wu Z, et al. Patient-specific in vivo right ventricle material parameter estimation for patients with tetralogy of Fallot using MRI-based models with different zero-load diastole and systole morphologies. Int J Cardiol (2019) 276:93–9. doi:10.1016/j.ijcard.2018.09.030

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Kolawole FO, Peirlinck M, Cork TE, Levenston M, Kuhl E, Ennis DB. Validating MRI-derived myocardial stiffness estimates using in vitro synthetic heart models. Ann Biomed Eng (2023) 51:1574–87. doi:10.1007/s10439-023-03164-7

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Hunter RJ, Liu Y, Lu Y, Wang W, Schilling RJ. Left atrial wall stress distribution and its relationship to electrophysiologic remodeling in persistent atrial fibrillation. Circ Arrhythmia Electrophysiol (2012) 5:351–60. doi:10.1161/CIRCEP.111.965541

PubMed Abstract | CrossRef Full Text | Google Scholar

143. Di Martino ES, Bellini C, Schwartzman DS. In vivo porcine left atrial wall stress: computational model. J Biomech (2011) 44:2589–94. doi:10.1016/j.jbiomech.2011.08.023

PubMed Abstract | CrossRef Full Text | Google Scholar

144. Adeniran I, Maciver DH, Garratt CJ, Ye J, Hancox JC, Zhang H. Effects of persistent atrial fibrillation-induced electrical remodeling on atrial electro-mechanics - insights from a 3D model of the human atria. PLoS ONE (2015) 10:e0142397. doi:10.1371/journal.pone.0142397

PubMed Abstract | CrossRef Full Text | Google Scholar

145. Fritz T, Dössel O, Krueger M. Electromechanical modeling of the human atria. Biomed Eng/Biomedizinische Technik (2013) 58. doi:10.1515/bmt-2013-4321

CrossRef Full Text | Google Scholar

146. Phung TKN, Moyer CB, Norton PT, Ferguson JD, Holmes JW. Effect of ablation pattern on mechanical function in the atrium. PACE - Pacing Clin Electrophysiol (2017) 40:648–54. doi:10.1111/pace.13086

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Augustin CM, Fastl TE, Neic A, Bellini C, Whitaker J, Rajani R, et al. The impact of wall thickness and curvature on wall stress in patient-specific electromechanical models of the left atrium. Biomech Model Mechanobiology (2020) 19:1015–34. doi:10.1007/s10237-019-01268-5

PubMed Abstract | CrossRef Full Text | Google Scholar

148. Satriano A, Bellini C, Vigmond EJ, Di Martino ES. A feature-based morphing methodology for computationally modeled biological structures applied to left atrial fiber directions. J Biomechanical Eng (2013) 135:31001. doi:10.1115/1.4023369

PubMed Abstract | CrossRef Full Text | Google Scholar

149. Di Martino ES, Bellini C, Schwartzman DS. In vivo porcine left atrial wall stress: effect of ventricular tachypacing on spatial and temporal stress distribution. J Biomech (2011) 44:2755–60. doi:10.1016/j.jbiomech.2011.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Tang H, Dai Z, Wang M, Guo B, Wang S, Wen J, et al. Lumped-parameter circuit platform for simulating typical cases of pulmonary hypertensions from point of hemodynamics. J Cardiovasc Translational Res (2020) 13:826–52. doi:10.1007/s12265-020-09953-y

CrossRef Full Text | Google Scholar

151. Di Molfetta A, Ferrari G, Iacobelli R, Filippelli S, Fresiello L, Guccione P, et al. Application of a lumped parameter model to study the feasibility of simultaneous implantation of a continuous flow ventricular assist device (VAD) and a pulsatile flow VAD in BIVAD patients. Artif Organs (2017) 41:242–52. doi:10.1111/aor.12911

PubMed Abstract | CrossRef Full Text | Google Scholar

152. Capoccia M, Marconi S, Singh SA, Pisanelli DM, De Lazzari C. Simulation as a preoperative planning approach in advanced heart failure patients. A retrospective clinical analysis. BioMedical Eng Online (2018) 17:52. doi:10.1186/s12938-018-0491-7

PubMed Abstract | CrossRef Full Text | Google Scholar

153. Warriner DR, Brown AG, Varma S, Sheridan PJ, Lawford P, Hose DR, et al. Closing the loop: modelling of heart failure progression from health to end-stage using a meta-analysis of left ventricular pressure-volume loops. PLoS ONE (2014) 9:e114153. doi:10.1371/journal.pone.0114153

PubMed Abstract | CrossRef Full Text | Google Scholar

154. Arts T, Delhaas T, Bovendeerd P, Verbeek X, Prinzen FW. Adaptation to mechanical load determines shape and properties of heart and circulation: the CircAdapt model. Am J Physiol - Heart Circulatory Physiol (2005) 288:H1943–54. doi:10.1152/ajpheart.00444.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

155. Lumens J, Delhaas T, Kirn B, Arts T. Three-wall segment (TriSeg) model describing mechanics and hemodynamics of ventricular interaction. Ann Biomed Eng (2009) 37:2234–55. doi:10.1007/s10439-009-9774-2

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Walmsley J, Arts T, Derval N, Bordachar P, Cochet H, Ploux S, et al. Fast simulation of mechanical heterogeneity in the electrically asynchronous heart using the MultiPatch module. PLoS Comput Biol (2015) 11:e1004284. doi:10.1371/journal.pcbi.1004284

PubMed Abstract | CrossRef Full Text | Google Scholar

157. Van Osta N, Kirkels F, Lyon A, Koopsen T, Van Loon T, Cramer MJ, et al. Electromechanical substrate characterization in arrhythmogenic cardiomyopathy using imaging-based patient-specific computer simulations. Europace (2021) 23:i153–60. doi:10.1093/europace/euaa407

PubMed Abstract | CrossRef Full Text | Google Scholar

158. Mast TP, Teske AJ, Walmsley J, van der Heijden JF, van Es R, Prinzen FW, et al. Right ventricular imaging and computer simulation for electromechanical substrate characterization in arrhythmogenic right ventricular cardiomyopathy. J Am Coll Cardiol (2016) 68:2185–97. doi:10.1016/j.jacc.2016.08.061

PubMed Abstract | CrossRef Full Text | Google Scholar

159. Palau-Caballero G, Walmsley J, Van Empel V, Lumens J, Delhaas T. Why septal motion is a marker of right ventricular failure in pulmonary arterial hypertension: mechanistic analysis using a computer model. Am J Physiol - Heart Circulatory Physiol (2017) 312:H691–700. doi:10.1152/ajpheart.00596.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

160. Dupuis LJ, Arts T, Prinzen FW, Delhaas T, Lumens J. Linking cross-bridge cycling kinetics to response to cardiac resynchronization therapy: a multiscale modelling study. Europace (2018) 20:iii87–93. doi:10.1093/europace/euy230

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Meiburg R, Rijks JHJ, Beela AS, Bressi E, Grieco D, Delhaas T, et al. Comparison of novel ventricular pacing strategies using an electro-mechanical simulation platform. Europace (2023) 25:euad144. doi:10.1093/europace/euad144

PubMed Abstract | CrossRef Full Text | Google Scholar

162. Limbu S, Prosser BL, Lederer WJ, Ward CW, Jafri MS. X-ROS signaling depends on length-dependent calcium buffering by troponin. Cells (2021) 10:1189. doi:10.3390/CELLS10051189

PubMed Abstract | CrossRef Full Text | Google Scholar

163. Beheshti M, Umapathy K, Krishnan S. Electrophysiological cardiac modeling: a review. Crit Reviews™ Biomed Eng (2016) 44:99–122. doi:10.1615/CRITREVBIOMEDENG.2016016454

CrossRef Full Text | Google Scholar

164. Woods RH. A few applications of a physical theorem to membranes in the human body in a state of tension. J Anat Physiol (1892) 26:362–70.

PubMed Abstract | CrossRef Full Text | Google Scholar

165. Campbell KS, Chrisman BS, Campbell SG. Multiscale modeling of cardiovascular function predicts that the end-systolic pressure volume relationship can Be targeted via multiple therapeutic strategies. Front Physiol (2020) 11:1043–12. doi:10.3389/fphys.2020.01043

PubMed Abstract | CrossRef Full Text | Google Scholar

166. Campbell KB, Simpson AM, Campbell SG, Granzier HL, Slinker BK. Dynamic left ventricular elastance: a model for integrating cardiac muscle contraction into ventricular pressure-volume relationships. J Appl Physiol (2008) 104:958–75. doi:10.1152/japplphysiol.00912.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

167. Gerach T, Appel S, Wilczek J, Golba KS, Jadczyk T, Loewe A. Dyssynchronous left ventricular activation is insufficient for the breakdown of wringing rotation. Front Physiol (2022) 13:838038. doi:10.3389/FPHYS.2022.838038

PubMed Abstract | CrossRef Full Text | Google Scholar

168. Salvador M, Fedele M, Africa PC, Sung E, Dede’ L, Prakosa A, et al. Electromechanical modeling of human ventricles with ischemic cardiomyopathy: numerical simulations in sinus rhythm and under arrhythmia. Comput Biol Med (2021) 136:104674. doi:10.1016/J.COMPBIOMED.2021.104674

PubMed Abstract | CrossRef Full Text | Google Scholar

169. Salvador M, Regazzoni F, Pagani S, Dede’ L, Trayanova N, Quarteroni A. The role of mechano-electric feedbacks and hemodynamic coupling in scar-related ventricular tachycardia. Comput Biol Med (2022) 142:105203. doi:10.1016/J.COMPBIOMED.2021.105203

PubMed Abstract | CrossRef Full Text | Google Scholar

170. Hermeling E, Delhaas T, Prinzen FW, Kuijpers NH. Mechano-electrical feedback explains T-wave morphology and optimizes cardiac pump function: insight from a multi-scale model. Prog Biophys Mol Biol (2012) 110:359–71. doi:10.1016/J.PBIOMOLBIO.2012.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

171. Adeniran I, Hancox JC, Zhang H. In silico investigation of the short QT syndrome, using human ventricle models incorporating electromechanical coupling. Front Physiol (2013) 4:166. doi:10.3389/fphys.2013.00166

PubMed Abstract | CrossRef Full Text | Google Scholar

172. Bakir AA, Al Abed A, Stevens MC, Lovell NH, Dokos S. A multiphysics biventricular cardiac model: simulations with a left-ventricular assist device. Front Physiol (2018) 9:391479. doi:10.3389/fphys.2018.01259

CrossRef Full Text | Google Scholar

173. Sack KL, Dabiri Y, Franz T, Solomon SD, Burkhoff D, Guccione JM. Investigating the role of interventricular interdependence in development of right heart dysfunction during LVAD support: a patient-specific methods-based approach. Front Physiol (2018) 9:520. doi:10.3389/fphys.2018.00520

PubMed Abstract | CrossRef Full Text | Google Scholar

174. Tang D, Yang C, Geva T, Gaudette G, Nido PJ. Effect of patch mechanical properties on right ventricle function using MRI-based two-layer anisotropic models of human right and left ventricles. Computer Model Eng Sci : CMES (2010) 56:113–30.

Google Scholar

175. Cutrì E, Meoli A, Dubini G, Migliavacca F, Hsia TY, Pennati G. Patient-specific biomechanical model of hypoplastic left heart to predict post-operative cardio-circulatory behaviour. Med Eng Phys (2017) 47:85–92. doi:10.1016/J.MEDENGPHY.2017.06.024

PubMed Abstract | CrossRef Full Text | Google Scholar

176. Rodero C, Baptiste TMG, Barrows RK, Keramati H, Sillett CP, Strocchi M, et al. A systematic review of cardiac in-silico clinical trials. Prog Biomed Eng (2023) 5:032004. doi:10.1088/2516-1091/ACDC71

PubMed Abstract | CrossRef Full Text | Google Scholar

177. Wang ZJ, Santiago A, Zhou X, Wang L, Margara F, Levrero-Florencio F, et al. Human biventricular electromechanical simulations on the progression of electrocardiographic and mechanical abnormalities in post-myocardial infarction. EP Europace (2021) 23:i143–52. doi:10.1093/EUROPACE/EUAA405

CrossRef Full Text | Google Scholar

178. Krishnamurthy A, Villongco CT, Chuang J, Frank LR, Nigam V, Belezzuoli E, et al. Patient-specific models of cardiac biomechanics. J Comput Phys (2013) 244:4–21. doi:10.1016/J.JCP.2012.09.015

PubMed Abstract | CrossRef Full Text | Google Scholar

179. Aguado-Sierra J, Krishnamurthy A, Villongco C, Chuang J, Howard E, Gonzales MJ, et al. Patient-specific modeling of dyssynchronous heart failure: a case study. Prog Biophys Mol Biol (2011) 107:147–55. doi:10.1016/J.PBIOMOLBIO.2011.06.014

PubMed Abstract | CrossRef Full Text | Google Scholar

180. Peña E, Tracqui P, Azancot A, Doblare M, Ohayon J. Unraveling changes in myocardial contractility during human fetal growth: a finite element analysis based on in vivo ultrasound measurements. Ann Biomed Eng (2010) 38:2702–15. doi:10.1007/s10439-010-0010-x

PubMed Abstract | CrossRef Full Text | Google Scholar

181. Narolska NA, Eiras S, Van Loon RB, Boontje NM, Zaremba R, Spiegelen Berg SR, et al. Myosin heavy chain composition and the economy of contraction in healthy and diseased human myocardium. J Muscle Res Cel Motil (2005) 26:39–48. doi:10.1007/s10974-005-9005-x

PubMed Abstract | CrossRef Full Text | Google Scholar

182. Feng L, Gao H, Griffith B, Niederer S, Luo X. Analysis of a coupled fluid-structure interaction model of the left atrium and mitral valve. Int J Numer Methods Biomed Eng (2019) 35:e3254. doi:10.1002/cnm.3254

PubMed Abstract | CrossRef Full Text | Google Scholar

183. Moyer CB, Norton PT, Ferguson JD, Holmes JW. Changes in global and regional mechanics due to atrial fibrillation: insights from a coupled finite-element and circulation model. Ann Biomed Eng (2015) 43:1600–13. doi:10.1007/S10439-015-1256-0

PubMed Abstract | CrossRef Full Text | Google Scholar

184. Strocchi M, Gsell MAF, Augustin CM, Razeghi O, Roney CH, Prassl AJ, et al. Simulating ventricular systolic motion in a four-chamber heart model with spatially varying robin boundary conditions to model the effect of the pericardium. J Biomech (2020) 101:109645. doi:10.1016/j.jbiomech.2020.109645

PubMed Abstract | CrossRef Full Text | Google Scholar

185. Fritz T, Wieners C, Seemann G, Steen H, Dössel O. Simulation of the contraction of the ventricles in a human heart model including atria and pericardium. Biomech Model Mechanobiology (2014) 13:627–41. doi:10.1007/s10237-013-0523-y

PubMed Abstract | CrossRef Full Text | Google Scholar

186. Bishop M, Rajani R, Plank G, Gaddum N, Carr-White G, Wright M, et al. Three-dimensional atrial wall thickness maps to inform catheter ablation procedures for atrial fibrillation. Europace (2016) 18:376–83. doi:10.1093/europace/euv073

PubMed Abstract | CrossRef Full Text | Google Scholar

187. Ho SY, Sanchez-Quintana D, Cabrera JA, Anderson RH. Anatomy of the left atrium: implications for radiofrequency ablation of atrial fibrillation. J Cardiovasc Electrophysiol (1999) 10:1525–33. doi:10.1111/J.1540-8167.1999.TB00211.X

PubMed Abstract | CrossRef Full Text | Google Scholar

188. Whitaker J, Karády J, Karim R, Tobon-Gomez C, Fastl T, Razeghi O, et al. Standardised computed tomographic assessment of left atrial morphology and tissue thickness in humans. Int J Cardiol Heart Vasculature (2021) 32:100694. doi:10.1016/J.IJCHA.2020.100694

CrossRef Full Text | Google Scholar

189. Peirlinck M, Yao J, Sahli Costabal F, Kuhl E. How drugs modulate the performance of the human heart. Comput Mech (2022) 69:1397–411. doi:10.1007/s00466-022-02146-1

CrossRef Full Text | Google Scholar

190. Gerach T, Schuler S, Wachter A, Loewe A. The impact of standard ablation strategies for atrial fibrillation on cardiovascular performance in a four-chamber heart model. Cardiovasc Eng Tech (2023) 14:296–314. doi:10.1007/s13239-022-00651-1

CrossRef Full Text | Google Scholar

191. Moss R, Wülfers EM, Schuler S, Loewe A, Seemann G. A fully-coupled electro-mechanical whole-heart computational model: influence of cardiac contraction on the ECG. Front Physiol (2021) 12:778872. doi:10.3389/fphys.2021.778872

PubMed Abstract | CrossRef Full Text | Google Scholar

192. Jafari A, Pszczolkowski E, Krishnamurthy A. A framework for biomechanics simulations using four-chamber cardiac models. J Biomech (2019) 91:92–101. doi:10.1016/j.jbiomech.2019.05.019

PubMed Abstract | CrossRef Full Text | Google Scholar

193. Gerach T, Schuler S, Fröhlich J, Lindner L, Kovacheva E, Moss R, et al. Electro-mechanical whole-heart digital twins: a fully coupled multi-physics approach. Mathematics (2021) 9:1247. doi:10.3390/math9111247

CrossRef Full Text | Google Scholar

194. Smith NP, Buist ML, Pullan AJ. Altered T wave dynamics in a contracting cardiac model. J Cardiovasc Electrophysiol (2003) 14:S203–9. doi:10.1046/J.1540.8167.90312.X

PubMed Abstract | CrossRef Full Text | Google Scholar

195. Strocchi M, Augustin CM, Gsell MAF, Karabelas E, Neic A, Gillette K, et al. The effect of ventricular myofibre orientation on atrial dynamics. In: DB Ennis, LE Perotti, and VY Wang, editors. Functional imaging and modeling of the heart. Cham: Springer International Publishing (2021). p. 659–70.

CrossRef Full Text | Google Scholar

196. Land S, Niederer SA. Influence of atrial contraction dynamics on cardiac function. Int J Numer Methods Biomed Eng (2018) 34:e2931. doi:10.1002/cnm.2931

PubMed Abstract | CrossRef Full Text | Google Scholar

197. Genet M, Lee LC, Baillargeon B, Guccione JM, Kuhl E. Modeling pathologies of diastolic and systolic heart failure. Ann Biomed Eng (2016) 44:112–27. doi:10.1007/s10439-015-1351-2

PubMed Abstract | CrossRef Full Text | Google Scholar

198. Rodero C, Strocchi M, Marciniak M, Longobardi S, Whitaker J, O’Neill MD, et al. Linking statistical shape models and simulated function in the healthy adult human heart. PLOS Comput Biol (2021) 17:e1008851. doi:10.1371/journal.pcbi.1008851

PubMed Abstract | CrossRef Full Text | Google Scholar

199. Motiwale S, Zhang W, Sacks MS. High-speed high-fidelity cardiac simulations using a neural network finite element approach. Funct Imaging Model Heart (Springer, Cham) (2023) 537–44. doi:10.1007/978-3-031-35302-4{_}55

CrossRef Full Text | Google Scholar

200. Strocchi M, Longobardi S, Augustin CM, Gsell MAF, Petras A, Rinaldi CA, et al. Cell to whole organ global sensitivity analysis on a four-chamber heart electromechanics model using Gaussian processes emulators. PLOS Comput Biol (2023) 19:e1011257. doi:10.1371/JOURNAL.PCBI.1011257

PubMed Abstract | CrossRef Full Text | Google Scholar

201. Salvador M, Strocchi M, Regazzoni F, Dede’ L, Niederer SA, Quarteroni A. Real-time whole-heart electromechanical simulations using latent neural ordinary differential equations. ArXiV (2023).

Google Scholar

202. Zhang X, Liu ZQ, Campbell KS, Wenk JF. Evaluation of a novel finite element model of active contraction in the heart. Front Physiol (2018) 9:425–10. doi:10.3389/fphys.2018.00425

PubMed Abstract | CrossRef Full Text | Google Scholar

203. Land S, Gurev V, Arens S, Augustin CM, Baron L, Blake R, et al. Verification of cardiac mechanics software: benchmark problems and solutions for testing active and passive material behaviour. Proc R Soc A: Math Phys Eng Sci (2015) 471:20150641. doi:10.1098/RSPA.2015.0641

PubMed Abstract | CrossRef Full Text | Google Scholar

204. Food and Drug Administration (FDA). Assessing the credibility of computational modeling and simulation in medical device submissions. Tech. rep. Silver Spring, MD: Food and Drug Administration (2021). 31 Center for Devices and Radiological Health.

Google Scholar

205. Food and Drug Administration (FDA). Reporting of computational modeling studies in medical device submissions - guidance for industry and Food and drug administration staff. Tech. rep. U.S. Department of Health and Human Services (2016). Silver Spring, MD: Food and Drug Administration. 31 Center for Devices and Radiological Health.

Google Scholar

206. Morrison TM, Dreher ML, Nagaraja S, Angelone LM, Kainz W. The role of computational modeling and simulation in the total product life cycle of peripheral vascular devices. J Med Devices, Trans ASME (2017) 11:024503. doi:10.1115/1.4035866

PubMed Abstract | CrossRef Full Text | Google Scholar

207. Frangi A, Denison T, Myles P, Ordish J, Brown P, Turpin R, et al. Unlocking the power of computational modelling and simulation across the product lifecycle in life sciences: a UK Landscape Report. Tech. rep. InSilicoUK Pro-Innovation Regulations Network (2023). doi:10.5281/ZENODO.7723230

CrossRef Full Text | Google Scholar

208. Schwan J, Kwaczala AT, Ryan TJ, Bartulos O, Ren Y, Sewanan LR, et al. Anisotropic engineered heart tissue made from laser-cut decellularized myocardium. Scientific Rep 2016 (2016) 6:1–12. doi:10.1038/srep32068

PubMed Abstract | CrossRef Full Text | Google Scholar

209. Landesberg A, Beyar R, Sideman S, Markhasln VS. Effects of cardiac inhomogeneity in fiber activity on interfiber interaction and mechanical performance. IFAC Proc Volumes (1994) 27:139–40. doi:10.1016/s1474-6670(17)46183-0

CrossRef Full Text | Google Scholar

210. Landesberg A, Markhasin VS, Beyar R, Sideman S. Effect of cellular inhomogeneity on cardiac tissue mechanics based on intracellular control mechanisms. Am J Physiol - Heart Circulatory Physiol (1996) 270:H1101–14. doi:10.1152/ajpheart.1996.270.3.h1101

PubMed Abstract | CrossRef Full Text | Google Scholar

211. Solovyova O, Katsnelson L, Guriev S, Nikitina L, Protsenko Y, Routkevitch S, et al. Mechanical inhomogeneity of myocardium studied in parallel and serial cardiac muscle duplexes: experiments and models. Chaos, Solitons and Fractals (2002) 13:1685–711. doi:10.1016/S0960-0779(01)00175-8

CrossRef Full Text | Google Scholar

212. Campbell SG, Hatfield PC, Campbell KS. A mathematical model of muscle containing heterogeneous half-sarcomeres exhibits residual force enhancement. PLoS Comput Biol (2011) 7:e1002156. doi:10.1371/journal.pcbi.1002156

PubMed Abstract | CrossRef Full Text | Google Scholar

213. Maron BJ, Maron MS, Maron BA, Loscalzo J. Moving beyond the sarcomere to explain heterogeneity in hypertrophic cardiomyopathy: JACC review topic of the week. J Am Coll Cardiol (2019) 73:1978–86. doi:10.1016/j.jacc.2019.01.061

PubMed Abstract | CrossRef Full Text | Google Scholar

214. Boyden PA. Purkinje physiology and pathophysiology. J Interv Card Electrophysiol (2018) 52:255–62. doi:10.1007/s10840-018-0414-3

PubMed Abstract | CrossRef Full Text | Google Scholar

215. Linscheid N, Poulsen PC, Pedersen ID, Gregers E, Svendsen JH, Olesen MS, et al. Quantitative proteomics of human heart samples collected in vivo reveal the remodeled protein landscape of dilated left atrium without atrial fibrillation. Mol Cell Proteomics : MCP (2020) 19:1132–44. doi:10.1074/mcp.RA119.001878

CrossRef Full Text | Google Scholar

216. Romero D, Sebastian R, Bijnens BH, Zimmerman V, Boyle PM, Vigmond EJ, et al. Effects of the purkinje system and cardiac geometry on biventricular pacing: a model study. Ann Biomed Eng (2010) 38:1388–98. doi:10.1007/s10439-010-9926-4

PubMed Abstract | CrossRef Full Text | Google Scholar

217. Fonseca CG, Backhaus M, Bluemke DA, Britten RD, Chung JD, Cowan BR, et al. The cardiac Atlas Project-an imaging database for computational modeling and statistical atlases of the heart. Bioinformatics (2011) 27:2288–95. doi:10.1093/bioinformatics/btr360

PubMed Abstract | CrossRef Full Text | Google Scholar

218. Frangi AF, Rueckert D, Schnabel JA, Niessen WJ. Automatic construction of multiple-object three-dimensional statistical shape models: application to cardiac modeling. IEEE Trans Med Imaging (2002) 21:1151–66. doi:10.1109/TMI.2002.804426

PubMed Abstract | CrossRef Full Text | Google Scholar

219. Nagel C, Schuler S, Dössel O, Loewe A. A bi-atrial statistical shape model for large-scale in silico studies of human atria: model development and application to ECG simulations. Med Image Anal (2021) 74:102210. doi:10.1016/j.media.2021.102210

PubMed Abstract | CrossRef Full Text | Google Scholar

220. Lewandowski AJ, Augustine D, Lamata P, Davis EF, Lazdam M, Francis J, et al. Preterm heart in adult life: cardiovascular magnetic resonance reveals distinct differences in left ventricular mass, geometry, and function. Circulation (2013) 127:197–206. doi:10.1161/CIRCULATIONAHA.112.126920

PubMed Abstract | CrossRef Full Text | Google Scholar

221. Corden B, De Marvao A, Dawes TJ, Shi W, Rueckert D, Cook SA, et al. Relationship between body composition and left ventricular geometry using three dimensional cardiovascular magnetic resonance. J Cardiovasc Magn Reson (2016) 18:32. doi:10.1186/s12968-016-0251-4

PubMed Abstract | CrossRef Full Text | Google Scholar

222. Marciniak M, van Deutekom AW, Toemen L, Lewandowski AJ, Gaillard R, Young AA, et al. A three-dimensional atlas of child’s cardiac anatomy and the unique morphological alterations associated with obesity. Eur Heart J - Cardiovasc Imaging (2022) 23:1645–53. doi:10.1093/ehjci/jeab271

PubMed Abstract | CrossRef Full Text | Google Scholar

223. Warriner DR, Jackson T, Zacur E, Sammut E, Sheridan P, Hose DR, et al. An asymmetric wall-thickening pattern predicts response to cardiac resynchronization therapy. JACC Cardiovasc Imaging (2018) 11(10):1545–6. doi:10.1016/j.jcmg.2018.01.022

PubMed Abstract | CrossRef Full Text | Google Scholar

224. Cates J, Bieging E, Morris A, Gardner G, Akoum N, Kholmovski E, et al. Computational shape models characterize shape change of the left atrium in atrial fibrillation. Clin Med Insights: Cardiol (2015) 8:CMC.S15710. doi:10.4137/CMC.S15710

PubMed Abstract | CrossRef Full Text | Google Scholar

225. Sharifi H, Mann CK, Wenk JF, Campbell KS. A multiscale model of the cardiovascular system that regulates arterial pressure via closed loop baroreflex control of chronotropism, cell-level contractility, and vascular tone. Biomech Model mechanobiology (2022) 21:1903–17. doi:10.1007/S10237-022-01628-8

CrossRef Full Text | Google Scholar

226. Zingaro A, Vergara C, Dede’ L, Regazzoni F, Quarteroni A. A comprehensive mathematical model for cardiac perfusion. Scientific Rep (2023) 13:14220. doi:10.1038/S41598-023-41312-0

CrossRef Full Text | Google Scholar

227. Randall EB, Hock M, Lopez R, Marzban B, Marshall C, Beard DA. Quantitative analysis of mitochondrial ATP synthesis. Math Biosciences (2021) 340:108646. doi:10.1016/J.MBS.2021.108646

CrossRef Full Text | Google Scholar

228. Niestrawska JA, Augustin CM, Plank G. Computational modeling of cardiac growth and remodeling in pressure overloaded hearts—linking microstructure to organ phenotype. Acta Biomater (2020) 106:34–53. doi:10.1016/J.ACTBIO.2020.02.010

PubMed Abstract | CrossRef Full Text | Google Scholar

229. Saucerman JJ, Tan PM, Buchholz KS, McCulloch AD, Omens JH. Mechanical regulation of gene expression in cardiac myocytes and fibroblasts. Nat Rev Cardiol (2019) 16:361–78. doi:10.1038/S41569-019-0155-8

PubMed Abstract | CrossRef Full Text | Google Scholar