The influence of rotation and viscosity on generalized conformable fractional micropolar thermoelasticity with two temperatures

This research paper presents the generalized micropolar thermo-visco-elasticity model in an isotropic elastic medium that has two temperatures with conformable fractional order theory. The whole elastic medium rotates at a constant angular velocity. The generalized theory of thermoelasticity with one relaxation time is used to describe this model. We aim to study the effect of conformable fractional derivative, effect of rotation, and the two-temperature coefficients. The normal mode analysis is used to acquire the specific articulations for each component under consideration. Moreover, some specific cases are discussed with regarding to the problem. Numerical findings are gathered and displayed graphically for the variables under consideration. The outcomes were analyzed in terms of the presence or absence of rotation, viscosity, conformable fractional parameter and two temperatures for various values.

1 Introduction

The study of fractional calculus, a subject that has garnered significant attention from mathematicians, engineers, and physicians, involves the investigation of mathematical analysis utilizing differential operators of any order. The fractional calculus has extended the usual definitions of integer order integrals and derivatives in ordinary differential calculus by transforming them into real-order operators [1–6].

Over the past 40 years, there has been a lot of focus on Theories of thermoelasticity that permit for restricted heat wave speed. These theories, known as general thermo-elasticity theories, are hyperbolic and differ from the traditional combined thermo-elasticity (C-T) theory [7], This predicts an infinite pace of heat propagation and is based on a parabolic heat equation. Lord and Shulman (L-S) [8] were the first to alter the usual Fourier law by including a unique heat conduction law, resulting in a wave type heat equation, on the other hand Green and Lindsay (G-L) [9], introduced the temperature-rate hypothesis of thermoelasticity. Green and Naghdi (G-N) [10], proposed a theory of thermo-elasticity without energy dissipation, this, unlike earlier models, does not account for thermal energy loss. Chandrasekharaia proposed two theories of dual-phase lag thermo-elasticity [11, 12] and Tzou [13]. Eringen developed the general theory of micropolar elasticity [14, 15]. In this form of solid, the vector of displacement and micro-rotation is fully defined, whereas the displacement vector alone defines motion in the case of classical elasticity [16]. The essential equations of the theory of micropolar thermoelasticity linearly get by Tauchert et al. [17] and Boschi [18]. Ciarletta [19] proposed a thermoelasticity with micropolar energy dissipation. A Lord-Shulman model of micropolar thermoelasticity dependent linear theory was proposed by Sherief et al. [20]. Othman is to blame for various issues with thermoelastic spinning media [21].

Many authors have made significant contributions to resolving the boundary value problem for thermoelasticity [22–27].

Chen and Gurtin discussed two types of temperatures: thermodynamic temperature and conductive temperature [28]. In time-independent settings, the connection between these two temperatures is linked to the heat supply. The two temperatures are similar in the absence of a heat supply and often differ in the presence of a heat supply. The two temperatures and strain are shown to have inputs in the form of a travelling wave and an instantaneous reaction that happens during the body. The waves in the two-temperature thermoelasticity theory were investigated by Warren [29], but no study in the sense of a generalised thermoelasticity theory has been carried out so far. So, along with two temperatures, the theory of two-temperature-generalized thermo-visco-elasticity will be constructed in this work.

Many authors have made significant contributions to resolving the boundary value problem for linear viscoelastic thermal materials [30–33].

The current study seeks to determine the physical quantities, such as viscosity, rotation, conformable fractional parameter, and two-temperatures, in a homogeneous, isotropic, micropolar thermo-elastic material [1, 34–40].

2 Field equations and constitutive relations

We put a system in a generalized micropolar thermo-viscoelastic medium under five theories, two temperatures and rotation as [41, 42]:

(i) The constitutive relations

${\sigma }_{ij}=2{\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)e_{ij}+{\lambda }_e\left(1+{\alpha }_0\frac{\partial }{\partial t}\right)e{\delta }_{ij}-{\gamma }_e{T}_0\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)T{\delta }_{ij},(1)$

$m_{ij}=\alpha {\varphi }_{r,r}{\delta }_{ij}+\epsilon {\varphi }_{j,i}+\beta {\varphi }_{i,j}.(2)$

(ii) Stress equation of motion

$\begin{array}{l}\left[{\lambda }_e\left(1+{\alpha }_o\frac{\partial }{\partial t}\right)+{\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)\right]\nabla \left(\nabla \cdot \overline{u}\right)+\left[{\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+\upsilon \right]{\nabla }^2\overline{u}+\upsilon \left(\nabla \times \overline{\varphi }\right)\\ -{\gamma }_e\left(1+{\gamma }_o\frac{\partial }{\partial t}\right)\nabla T=\rho \left[\ddot{\overline{u}}+\overline{\mathrm{\Omega }}\times \left(\overline{\mathrm{\Omega }}\times \overline{u}\right)+2\overline{\mathrm{\Omega }}\times \dot{\overline{u}}\right].\end{array}(3)$

(iii) Couple stress equation of motion [43, 44]

$\left(\alpha +\beta +\epsilon \right)\nabla \left(\nabla \cdot \overline{\varphi }\right)-\epsilon \nabla \times \left(\nabla \times \overline{\varphi }\right)+\upsilon \left(\nabla \times \overline{u}\right)-2\upsilon \overline{\varphi }=\rho j\left(\ddot{\overline{\varphi }}+\overline{\mathrm{\Omega }}\times \dot{\overline{\varphi }}\right).(4)$

(iv) Heat conduction equation with five theories

$k{\theta }_{,ii}=\rho C_E\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{t}^{1-\alpha }\frac{\partial }{\partial t}\right)\dot{T}+{\gamma }_e{T}_0\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{t}^{1-\alpha }\frac{\partial }{\partial t}\right)\dot{e},(5)$

With,

$T=\theta -a{\theta }_{,ii}.(6)$

3 Problem formulation

Take a homogenous, isotropic, micropolar-viscoelastic generalised medium with rotation and two temperatures with Cartesian rectangular system of coordinates $\left(x,y,z\right)$ , getting half-space surface like the plane $z=0$. Two more terminology for the displacement equation in the rotating frame: the centripetal acceleration $\overline{\mathrm{\Omega }}\times \left(\overline{\mathrm{\Omega }}\times \overline{u}\right)$ just because of the time change and the Coriolis acceleration $2\overline{\mathrm{\Omega }}\times \dot{\overline{u}}$ because of the moving frame of reference.

Our study was restricted to $x-z$ plane. Then $\overline{u}$, $\overline{\mathrm{\Omega }}$ and $\overline{\varphi }$ will have the components:

$\overline{u}=\left(u,0,w\right),\overline{\mathrm{\Omega }}=\left(0,\mathrm{\Omega },0\right)\text{ and }\overline{\varphi }=\left(0,\varphi ,0\right)(7)$

Combination of (3), (4) and (7) provides:

$\begin{array}{l}\rho \left(\ddot{u}+2\mathrm{\Omega }\dot{w}-{\mathrm{\Omega }}^{2}u\right)={\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right){\nabla }^{2}u+\left(\left(1+{\alpha }_1\frac{\partial }{\partial t}\right){\mu }_e+\left(1+{\alpha }_0\frac{\partial }{\partial t}\right){\lambda }_e\right)e_{,x}\\ -\upsilon {\varphi }_{,z}-{\gamma }_e\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)T_{,x},\end{array}(8)$

$\begin{array}{l}\rho \left(\ddot{w}-{\mathrm{\Omega }}^{2}w-2\mathrm{\Omega }\dot{u}\right)=\left({\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+\upsilon \right){\nabla }^{2}w+\\ \left({\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+{\lambda }_e\left(1+{\alpha }_0\frac{\partial }{\partial t}\right)\right)e_{,z}+\upsilon {\varphi }_{,z}-{\gamma }_e\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)T_{,z},\end{array}(9)$

$\epsilon {\nabla }^2\varphi +\upsilon \left(u_{,z}-w_{,x}\right)-2\upsilon \varphi =\rho j\ddot{\varphi }.(10)$

From Eqs 1, 2, 7 the stresses can be formulated as follow:

${\sigma }_{xx}=\left(2{\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+\upsilon \right)u_{,x}+{\lambda }_e\left(1+{\alpha }_0\frac{\partial }{\partial t}\right)e-{\gamma }_e\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)T,(11)$

${\sigma }_{zz}=\left(2{\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+\upsilon \right)w_{,z}+{\lambda }_e\left(1+{\alpha }_0\frac{\partial }{\partial t}\right)e-{\gamma }_e\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)T,(12)$

${\sigma }_{xz}=\left({\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+\upsilon \right)w_{,x}+{\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)u_{,z}+\upsilon \varphi ,(13)$

${\sigma }_{zx}=\left({\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+\upsilon \right)u_{,z}+{\mu }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)w_{,x}-\upsilon \varphi ,(14)$

$m_{xy}=\epsilon {\varphi }_{,x},(15)$

$m_{zy}=\epsilon {\varphi }_{,z}.(16)$

For simplification, we take the non-dimensional variables:

$\left\{x^{\prime },z^{\prime }\right\}=\frac{\varpi }{c_o}\left\{x_i,z_i\right\},\left\{t^{\prime },{\tau }_0^{\prime },{\alpha }_0^{\prime },{\alpha }_1^{\prime },{\gamma }_0^{\prime }\right\}=\varpi \left\{t,{\tau }_0,{\alpha }_0,{\alpha }_1,{\gamma }_0\right\},$

$\begin{array}{l}\left\{T^{\prime },{\theta }^{\prime }\right\}=\frac{\left\{T,\theta \right\}}{T_0},{\sigma }_{ij}^{\prime }=\frac{{\sigma }_{ij}}{{\gamma }_e{T}_0},{\mathrm{\Omega }}^{\prime }=\frac{\mathrm{\Omega }}{c_0^2\eta },\left\{u^{\prime },w^{\prime }\right\}=\frac{\rho c_o\varpi }{{\gamma }_e{T}_o}\left\{u,w\right\},m_{ij}^{\prime }=\frac{\varpi }{{\gamma }_e{T}_o{c}_o}{m}_{ij},{\varphi }^{\prime }=\frac{\rho c_o^2}{{\gamma }_e{T}_o}\varphi .\end{array}(17)$

Where, $c_0^2=\frac{{\lambda }_e+2{\mu }_e+\upsilon }{\rho },\varpi =\frac{\rho c_o^2{C}_E}{k}.$

With regard to the non-dimensional quantities set out in (17), Eqs 8–10, Eqs 5, 6 take the form:

$\begin{array}{l}\ddot{u}-{\mathrm{\Omega }}^{2}u+2\mathrm{\Omega }\dot{w}=\left(a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+{\upsilon }_1\right){\nabla }^{2}u+\left[a_2\left(1+{\alpha }_o\frac{\partial }{\partial t}\right)+a_3\left(1+{\alpha }_o\frac{\partial }{\partial t}\right)\right]e_{,x}\\ -{\upsilon }_1{\varphi }_{,z}-\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)T_{,x},\end{array}(18)$

$\begin{array}{l}\ddot{w}-{\mathrm{\Omega }}^{2}w-2\mathrm{\Omega }\dot{u}=\left(a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+{\upsilon }_1\right){\nabla }^{2}w+\left[a_2\left(1+{\alpha }_o\frac{\partial }{\partial t}\right)+a_3\left(1+{\alpha }_o\frac{\partial }{\partial t}\right)\right]e_{,z}\\ +{\upsilon }_1{\varphi }_{,x}-\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)\left(1+{\upsilon }_0\frac{\partial }{\partial t}\right)T_{,z},\end{array}(19)$

${\nabla }^2\varphi +a_4\left(u_{,z}-w_{,x}\right)-2a_4\varphi =a_5\ddot{\varphi },(20)$

${\nabla }^2\theta =\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{t}^{1-\alpha }\frac{\partial }{\partial t}\right)\dot{T}+{\epsilon }_o\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{t}^{1-\alpha }\frac{\partial }{\partial t}\right)\dot{e},(21)$

$T=\left(1-a^{*}{\nabla }^2\right)\theta .(22)$

Also, the constitutive relations (11)–(16) reduce to

${\sigma }_{xx}=\left(2a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+{\upsilon }_1\right)u_{,x}+a_2\left(1+{\alpha }_0\frac{\partial }{\partial t}\right)e-\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)T,(23)$

${\sigma }_{zz}=\left(2a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+{\upsilon }_1\right)w_{,z}+a_2\left(1+{\alpha }_0\frac{\partial }{\partial t}\right)e-\left(1+{\gamma }_0\frac{\partial }{\partial t}\right)T,(24)$

${\sigma }_{xz}=\left(a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+{\upsilon }_1\right)w_{,x}+a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)u_{,z}+{\upsilon }_1\varphi ,(25)$

${\sigma }_{zx}=\left(a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+{\upsilon }_1\right)u_{,z}+a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)w_{,x}-{\upsilon }_1\varphi ,(26)$

$m_{xy}=a_6{\varphi }_{,x},(27)$

$m_{zy}=a_6{\varphi }_{,z},(28)$

Where,

$\begin{array}{l}{a}_1=\frac{{\mu }_e}{\rho c_0^2},a_2=\frac{{\lambda }_e}{{\gamma }_e{T}_o},a_3=\frac{{\mu }_e}{{\gamma }_e{T}_o},a_4=\frac{\upsilon c_o^2}{\epsilon {\varpi }^2},a_5=\frac{\rho j{c}_o^2}{\epsilon },{\mathrm{a}}_6=\frac{\epsilon {\varpi }^2}{\rho c_o^4},{\epsilon }_o=\frac{{\gamma }_e}{\rho C_E},a^{*}=\frac{a{\varpi }^2}{c_o^2},{\upsilon }_1=\frac{\upsilon }{\rho c_o^2}.\end{array}(29)$

We define $e\left(x,z,t\right)$ and $\psi \left(x,z,t\right)$ as the displacement potentials recount to $u$ and $w$

$e=u_{,x}+w_{,z},\psi =u_{,z}-w_{,x}.(30)$

4 Normal mode analysis

In terms of normal modes, the solution of the considered variables can be written as:

$\left[u,w,e,\psi ,T,\theta ,\varphi ,m_{ij},{\sigma }_{ij}\right]\left(x,z,t\right)=\left[\overline{u},\overline{w},\overline{e},\overline{\psi },\overline{T},\overline{\theta },\overline{\varphi },{\overline{m}}_{ij},{\overline{\sigma }}_{ij}\right]\left(z\right)\exp \left(\omega t+ibx\right).(31)$

Where, $\left[\overline{u},\overline{w},\overline{e},\overline{\psi },\overline{T},\overline{\theta },\overline{\varphi },{\overline{m}}_{ij},{\overline{\sigma }}_{ij}\right]\left(z\right)$ are the amplitudes of the variables, $\omega$ is the complex angular frequency, $b$ is the wave number in the $z$-direction and $=\sqrt{-1}$ .

From Eqs 18, 19 we get

$\begin{array}{l}\ddot{e}-{\mathrm{\Omega }}^{2}e-2\mathrm{\Omega }\dot{\psi }=\left(a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+a_2\left(1+{\alpha }_o\frac{\partial }{\partial t}\right)+a_3\left(1+{\alpha }_o\frac{\partial }{\partial t}\right)+{\upsilon }_1\right){\nabla }^{2}e\\ -\left(1+{\gamma }_0\frac{\partial }{\partial t}\right){\nabla }^{2}T,\end{array}(32)$

$\ddot{\psi }-{\mathrm{\Omega }}^2\psi +2\mathrm{\Omega }\dot{e}=\left(a_1\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+{\upsilon }_1\right){\nabla }^2\psi -{\upsilon }_1{\nabla }^2\varphi .(33)$

Using Eqs 22, 30, 31, Eqs 20, 21, 31 and 32 lead to

$\left[b_1\left({\mathrm{D}}^2-b^2\right)-b_2\right]\overline{\theta }=b_3\overline{e},(34)$

$\left[b_4-b_5\left({\mathrm{D}}^2-b^2\right)\right]\overline{e}-b_6\overline{\psi }=-b_7\left({\mathrm{D}}^2-b^2\right)\left[1-a^{*}\left({\mathrm{D}}^2-b^2\right)\right]\overline{\theta },(35)$

$\left[b_4-b_8\left({\mathrm{D}}^2-b^2\right)\right]\overline{\psi }=-b_6\overline{e}-{\upsilon }_1\left({\mathrm{D}}^2-b^2\right)\overline{\varphi },(36)$

$\left(D^2-b^2\right)\overline{\varphi }+a_4\overline{\psi }-2a_4\overline{\varphi }={\omega }^2{a}_5\overline{\varphi }.(37)$

Also, the constitutive relations (18)–(21) become

${\overline{\sigma }}_{xx}=\left(2a_1\left(1+{\alpha }_1\omega \right)+{\upsilon }_1\right)ib\overline{u}+a_2\left(1+{\alpha }_o\omega \right)\overline{e}-\left(1+{\gamma }_o\omega \right)\overline{T},(38)$

${\overline{\sigma }}_{zz}=\left(2a_1\left(1+{\alpha }_1\omega \right)+{\upsilon }_1\right)D\overline{w}+a_2\left(1+{\alpha }_o\omega \right)\overline{e}-\left(1+{\gamma }_o\omega \right)\overline{T},(39)$

${\overline{\sigma }}_{xz}=\left(a_1\left(1+{\alpha }_1\omega \right)+{\upsilon }_1\right)ib\overline{w}+a_1\left(1+{\alpha }_o\omega \right)D\overline{u}+{\upsilon }_1\overline{\varphi },(40)$

${\overline{\sigma }}_{zx}=\left(a_1\left(1+{\alpha }_1\omega \right)+{\upsilon }_1\right)D\overline{u}+a_1\left(1+{\alpha }_o\omega \right)ib\overline{w}-{\upsilon }_1\overline{\varphi },(41)$

${\overline{m}}_{xy}=ib{a}_6\overline{\varphi },(42)$

${\overline{m}}_{zy}=a_{6}D\overline{\varphi }.(43)$

Where,

$\mathrm{D}=\frac{d}{dz},b_1=a^{*}\omega \left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{t}^{1-\alpha }\omega \right),b_2={\epsilon }_o\omega \left(1+{\gamma }_0\omega \right)\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{t}^{1-\alpha }\omega \right),$

$\begin{array}{l}{b}_3={\epsilon }_o\omega \left(1+{\gamma }_0\omega \right)\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{t}^{1-\alpha }\omega \right),b_4={\omega }^2-{\mathrm{\Omega }}^2,\\ b_5=\left(1+{\alpha }_1\omega \right)a_1+\left(1+{\alpha }_0\omega \right)a_2+\left(1+{\alpha }_1\omega \right)a_3+{\upsilon }_1,b_6=2\mathrm{\Omega }\omega ,\\ b_7=\left(1+{\gamma }_o\omega \right),b_8={\upsilon }_1+a_1\left(1+{\alpha }_1\omega \right),b_9={\omega }^2{a}_5+2a_4.\end{array}$

Eliminating $\overline{\psi }\left(z\right)$, $\overline{\theta }\left(z\right)$ and $\overline{\varphi }\left(z\right)$ between Eqs 34–37, we get the following eighth order ordinary differential equation satisfied with $\overline{e}\left(z\right)$

$\left[{\mathrm{D}}^8-A{\mathrm{D}}^6+B{\mathrm{D}}^4-C{D}^2+E\right]\overline{e}\left(z\right)=0.(44)$

Where,

$A=\frac{\left(b_1{b}_5+{\mathrm{a}}^{*}{b}_3{b}_7\right)\left(a_4{\upsilon }_1-b_4-b_8{b}_9-2b^2{b}_8\right)-b_8\left(b_1{b}_4+2b^2{b}_1{b}_5+b_2{b}_5+b_3{b}_7+2a^{*}{b}^2{b}_3{b}_7\right)}{-b_1{b}_5{b}_8-a^{*}{b}_3{b}_7{b}_8},$

$B=\frac{\begin{array}{l}\left(-b_1{b}_5-a^{*}{b}_3{b}_7\right)\left(b_4{b}_9+b^2{b}_4+b^2{b}_8{b}_9+b^4{b}_8-b^2{a}_4{\upsilon }_1\right)-b_8\left(b^2{b}_1{b}_4+b^4{b}_1{b}_5+b_2{b}_4+b^2{b}_2{b}_5\right)\\ +\left(a_4{\upsilon }_1-b_4-b_8{b}_9-2b^2{b}_8\right)\left(b_1{b}_4+2b^2{b}_1{b}_5+b_2{b}_5+b_3{b}_7+2a^{*}{b}^2{b}_3{b}_7\right)-a^{*}{b}^4{b}_3{b}_7{b}_8\\ -b^2{b}_3{b}_7{b}_8-b_1{b}_6^2\end{array}}{-b_1{b}_5{b}_8-a^{*}{b}_3{b}_7{b}_8},$

$C=\frac{\begin{array}{l}-\left(b_4{b}_9+b^2{b}_4+b^2{b}_8{b}_9+b^4{b}_8-b^2{a}_4{\upsilon }_1\right)\left(b_1{b}_4+2b^2{b}_1{b}_5+b_2{b}_5+b_3{b}_7+2a^{*}{b}^2{b}_3{b}_7\right)\\ +\left(a_4{\upsilon }_1-b_4-b_8{b}_9-2b^2{b}_8\right)\left(a^{*}{b}^4{b}_3{b}_7+b^2{b}_3{b}_7+b^2{b}_1{b}_4+b^4{b}_1{b}_5+b_2{b}_4+b^2{b}_2{b}_5\right)\\ -{\mathrm{b}}_6^2\left(b_1{b}_9+2b^2{b}_1+b_2\right)\end{array}}{-b_1{b}_5{b}_8-a^{*}{b}_3{b}_7{b}_8},$

$E=\frac{\begin{array}{l}-\left(b_4{b}_9+b^2{b}_4+b^2{b}_8{b}_9+b^4{b}_8-b^2{a}_4{\upsilon }_1\right)\left(a^{*}{b}^4{b}_3{b}_7+b^2{b}_3{b}_7+b^2{b}_1{b}_4+b^4{b}_1{b}_5+b_2{b}_4+b^2{b}_2{b}_5\right)\\ -b_6^2\left(b^2{b}_1{b}_9+b^4{b}_1+b_2{b}_9+b^2{b}_2\right)\end{array}}{-b_1{b}_5{b}_8-a^{*}{b}_3{b}_7{b}_8}.$

By rewriting Eq. 44, we get

$\left({\mathrm{D}}^2-k_1^2\right)\left({\mathrm{D}}^2-k_2^2\right)\left({\mathrm{D}}^2-k_3^2\right)\left({\mathrm{D}}^2-k_4^2\right)\overline{e}\left(z\right)=0.(45)$

Where, the roots of the characteristic Eq. 44

$k_n^2\left(n=\mathrm{1,2,3,4}\right).$

The solution of Eq. 44, which bounded as $x\to \infty$, is given by

$\overline{e}\left(z\right)={\displaystyle \sum _{n=1}^4}{M}_n{e}^{-k_{n}z}.(46)$

In a similar manner,

$\overline{\theta }\left(x\right)={\displaystyle \sum _{n=1}^4}{H}_{1n}{M}_n{e}^{-k_{n}z},(47)$

$\overline{\psi }\left(z\right)={\displaystyle \sum _{n=1}^4}{H}_{3n}{M}_n{e}^{-k_{n}z}.(48)$

Substituting from Eqs 46 to Eq. 48 and (31) in Eqs 30, 22 and Eqs 38–43, the thermodynamic temperature, micro-rotation, the displacement, force stresses and the couple stresses components take the form

$\overline{T}\left(z\right)={\displaystyle \sum _{n=1}^4}{H}_{2n}{M}_n{e}^{-k_{n}z},(49)$

$\overline{\varphi }\left(z\right)={\displaystyle \sum _{n=1}^4}{H}_{4n}{M}_n{e}^{-k_{n}z},(50)$

$\overline{w}\left(z\right)={\displaystyle \sum _{n=1}^4}{H}_{5n}{M}_n{e}^{-k_{n}z},(51)$

$\overline{u}\left(z\right)={\displaystyle \sum _{n=1}^4}{H}_{6n}{M}_n{e}^{-k_{n}z},(52)$

${\overline{\sigma }}_{xx}\left(z\right)={\displaystyle \sum _{n=1}^4}{H}_{7n}{M}_n{e}^{-k_{n}z},(53)$

${\overline{\sigma }}_{zz}\left(z\right)={\displaystyle \sum _{n=1}^4}{H}_{8n}{M}_n{e}^{-k_{n}z},(54)$

${\overline{\sigma }}_{xz}\left(z\right)={\displaystyle \sum _{n=1}^4}{H}_{9n}{M}_n{e}^{-k_{n}z},(55)$

${\overline{\sigma }}_{zx}\left(z\right)={\displaystyle \sum _{n=1}^4}{G}_{1n}{M}_n{e}^{-k_{n}z},(56)$

${\overline{m}}_{xy}\left(z\right)={\displaystyle \sum _{n=1}^4}{G}_{2n}{M}_n{e}^{-k_{n}z},(57)$

${\overline{m}}_{zy}\left(x\right)={\displaystyle \sum _{n=1}^4}{G}_{3n}{M}_n{e}^{-k_{n}z}.(58)$

Where,

$\begin{array}{l}{H}_{1n}=\frac{b_3}{b_1\left(k_n^2-b^2\right)-b_2},H_{2n}=\left[1-a^{*}\left(k_n^2-b^2\right)\right]H_{1n},\\ H_{3n}=\frac{\left(b_4-b_5\left(k_n^2-b^2\right)\right)+H_{2n}\left(b_7\left(k_n^2-b^2\right)\right)}{b_6},\\ H_{4n}=\frac{a_4{H}_{3n}}{b_9-\left(k_n^2-b^2\right)},H_{5n}=\frac{-k_n-ib{H}_{3n}}{k_n^2-b^2},H_{6n}=\frac{-i\left(1+k_n{H}_{5n}\right)}{b},\\ H_{7n}=ib{H}_{6n}\left(2a_1\left(1+{\alpha }_1\omega \right)+{\upsilon }_1\right)+{\mathrm{a}}_2\left(1+{\alpha }_o\omega \right)-H_{2n}\left(1+{\gamma }_o\omega \right)\\ H_{8n}=-k_n{H}_{5n}\left(2a_1\left(1+{\alpha }_1\omega \right)+{\upsilon }_1\right)+a_2\left(1+{\alpha }_o\omega \right)-H_{2n}\left(1+{\gamma }_o\omega \right),\\ H_{9n}=ib{H}_{5n}\left(a_1\left(1+{\alpha }_1\omega \right)+{\upsilon }_1\right)+{\upsilon }_1{H}_{4n}-a_1{k}_n{H}_{6n}\left(1+{\alpha }_1\omega \right),\\ G_{1n}=-k_n{H}_{6n}\left(a_1\left(1+{\alpha }_1\omega \right)+{\upsilon }_1\right)+ib{a}_1{H}_{5n}\left(1+{\alpha }_1\omega \right)-{\upsilon }_1{H}_{4n},\\ G_{2n}=ib{a}_6{H}_{4n},G_{3n}=-a_6{k}_n{H}_{4n}.\end{array}$

$M_n\left(n=\mathrm{1,2,3,4}\right)$, some coefficients can be calculated based on the boundary conditions

5 The boundary conditions

To obtain the coefficients $M_n\left(n=\mathrm{1,2,3,4}\right)$, we use the surface’s boundary conditions on the surface $z=0$ as

$T\left(x,0,t\right)=f\left(x,0,t\right)=f^{*}\exp \left(\omega t+ibx\right),(59)$

${\sigma }_{zz}\left(x,0,t\right)=0,(60)$

${\sigma }_{zx}\left(x,0,t\right)=0,(61)$

$m_{zy}\left(x,0,t\right)=0.(62)$

Where, $f\left(x,t\right)$ is an arbitrary function of $x,t$ and $f^{*}$ is the magnitude of the constant temperature applied to the boundary.

Using Eqs 59–62, the following equations satisfied by the coefficient $M_n\left(n=\mathrm{1,2,3,4}\right)$ can be obtained

${\displaystyle \sum _{n=1}^4}{H}_{2n}{M}_n=f^{*},(63)$

${\displaystyle \sum _{n=1}^4}{H}_{8n}{M}_n=0,(64)$

${\displaystyle \sum _{n=1}^4}{G}_{1n}{M}_n=0,(65)$

${\displaystyle \sum _{n=1}^4}{G}_{3n}{M}_n=0.(66)$

We complete the solution of the problem by solving the system of Eqs 63–66.

6 Numerical results and disccusion

To perform numerical calculations [45] the magnesium crystal value of the related parameters is taken at

$T_o=23{}^{o}C$

$\begin{array}{l}{\lambda }_e=9.4\times {10}^{10}kg{m}^{-1}{s}^{-2},\epsilon =0.779\times {10}^{-9}kgm{s}^{-2},,k=2.510w.m^{-1}.k^{-1},{\alpha }_t=2.36\times {10}^{-5}{k}^{-1},\\ \rho =1.74\times {10}^{3}kg.m^{-3},C_E=9.623J.k{g}^{-1}.k^{-1},\upsilon ={10}^{10}kg{m}^{-1}{s}^{-2},{\mu }_e=4\times {10}^{10}kg{m}^{-1}{s}^{-2},\\ j=0.2\times {10}^{-19}{m}^2.\end{array}$

The comparison was performed for

$\begin{array}{l}x=0.01,f^{*}=1,\omega ={\omega }_0+i\xi ,{\omega }_0=-2,\xi =1,b=0.5,{\tau }_0=0.08,\alpha =0.1\\ a=0.5,\mathrm{\Omega }=0.1,{\alpha }_0=0.6,{\alpha }_1=0.9.\end{array}$

The numerical data given above were used to determine the real part distribution of the displacement component, force stress components, conductive temperature, thermo-dynamic temperature, micro-rotation, and couple stress components in relation to the problem under consideration. Figures 1–25 show the results.

FIGURE 1

FIGURE 1. Thermodynamic temperature $T$ for various values of rotation.

FIGURE 2

FIGURE 2. Conductive temperature $\theta$ for various values of rotation.

FIGURE 3

FIGURE 3. Horizontal displacement $u$ for various values of rotation.

FIGURE 4

FIGURE 4. Force stress components ${\sigma }_{zx}$ for various values of rotation.

FIGURE 5

FIGURE 5. Force stress components ${\sigma }_{zz}$ for various values of rotation.

FIGURE 6

FIGURE 6. Couple stress components $m_{zy}$ for various values of rotation.

FIGURE 7

FIGURE 7. Micro-rotation $\phi$ for various values of rotation.

FIGURE 8

FIGURE 8. Thermodynamic temperature $T$ for two various values of two-temperature parameter.

FIGURE 9

FIGURE 9. Conductive temperature $\theta$ for two various values of two - temperature parameter.

FIGURE 10

FIGURE 10. Horizontal displacement $u$ for two various values of two-temperature parameter.

FIGURE 11

FIGURE 11. Force stress components ${\sigma }_{zx}$ for two various values of two-temperature parameter.

FIGURE 12

FIGURE 12. Force stress components ${\sigma }_{zz}$ for two various values of two-temperature parameter.

FIGURE 13

FIGURE 13. Couple stress components $m_{zy}$ for two various values of two-temperature parameter.

FIGURE 14

FIGURE 14. Micro-rotation $\varphi$ for two various values of two-temperature parameter.

FIGURE 15

FIGURE 15. Thermodynamic temperature distribution $T$ in the nonexistence and existence of viscosity.

FIGURE 16

FIGURE 16. Conductive temperature distribution $\theta$ in the nonexistence and existence of viscosity.

FIGURE 17

FIGURE 17. Horizontal displacement distribution $u$ in the nonexistence and existence of viscosity.

FIGURE 18

FIGURE 18. Distribution of force stress components ${\sigma }_{zx}$ in the nonexistence and existence of viscosity.

FIGURE 19

FIGURE 19. Distribution of force stress components ${\sigma }_{zz}$ in the nonexistence and existence of viscosity.

FIGURE 20

FIGURE 20. Distribution of couple stress components $m_{zy}$ in the nonexistence and existence of viscosity.

FIGURE 21

FIGURE 21. Distribution of micro-rotation $\varphi$ in the nonexistence and existence of viscosity.

FIGURE 22

FIGURE 22. Distribution of the temperature $T$ for various values of $\alpha$.

FIGURE 23

FIGURE 23. Distribution of the temperature $\theta$ for various values of $\alpha$.

FIGURE 24

FIGURE 24. Distribution of the horizontal displacement $u$ for various values of $\alpha .$

FIGURE 25

FIGURE 25. Distribution of the stress component ${\sigma }_{zx}$ for various values of $\alpha$.

From an implementation standpoint, we divided the schematics into four components.

(i) For different values of rotation, the micropolar thermo-visco-elasticity theory with conformable fractional order theory and two-temperatures is concerned. Figures 1–7 i.e.., $\left(\mathrm{\Omega }=\mathrm{0.1,0.01}\right).$

(ii) For different values of $a\left(a=0,\mathrm{a}=0.5\right)$, the micropolar thermo-visco-elasticity theory with rotation and conformable fractional order theory is concerned. Figures 8–14, where $a=0$ indicates one-type temperature and $a=0.5$ indicates two-types of temperature.

(iii) Concerned are micropolar thermoelasticity with rotation, conformable fractional order theory, and two temperatures. Figures 15–21 show variable comparisons for various values of ${\alpha }_0$ and ${\alpha }_1$ where, ${\alpha }_0={\alpha }_1=0$ indicates a generalized theory of micropolar thermo-elasticity (TE) and ${\alpha }_0=0.6,$ ${\alpha }_1=0.9$ indicates generalized theory of micropolar thermo-visco-elasticity (TVE).

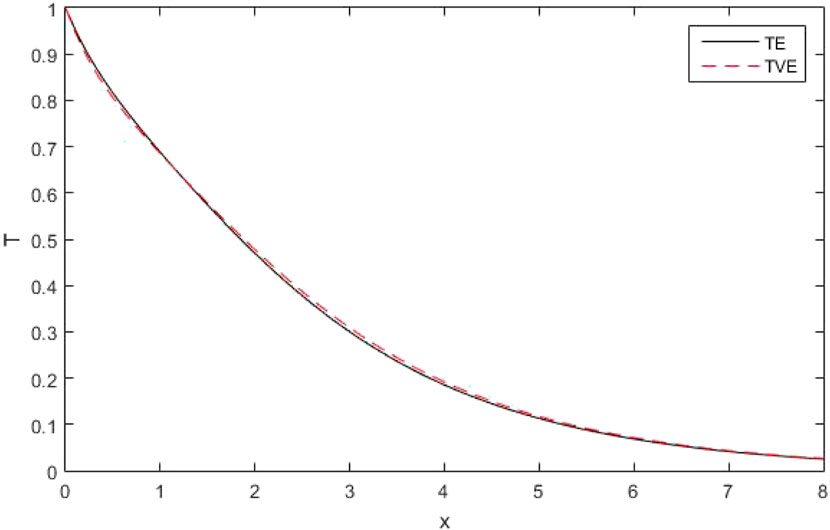
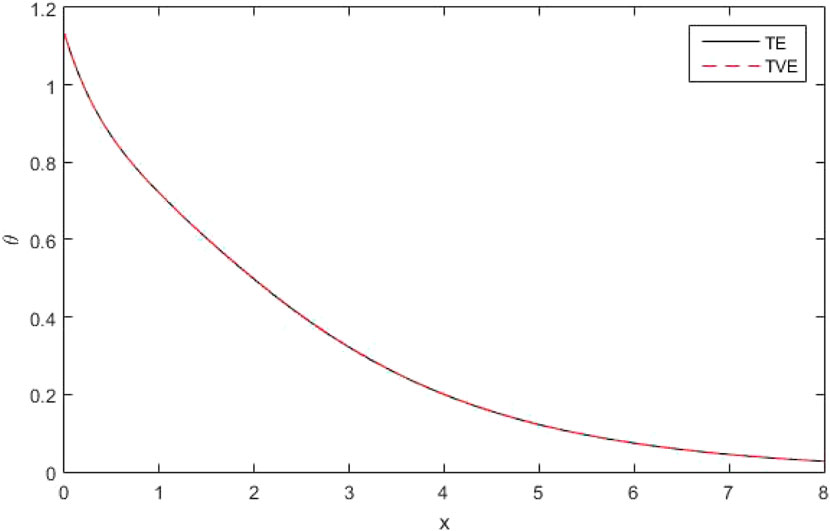
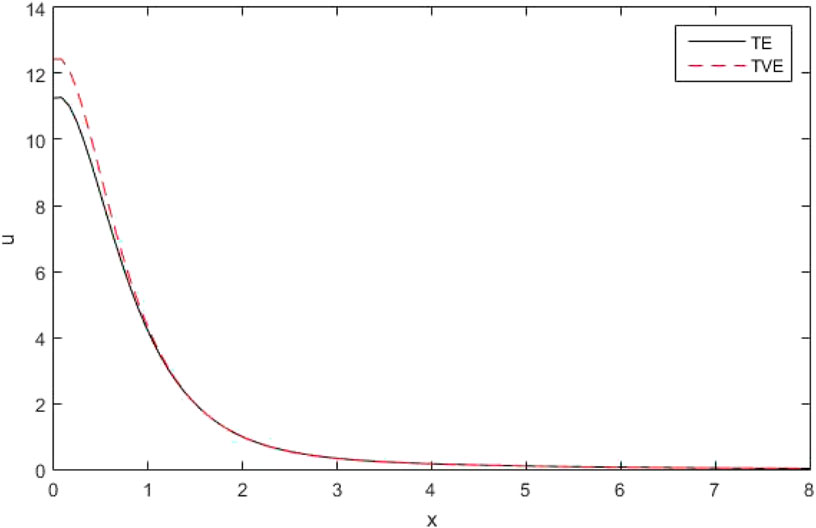
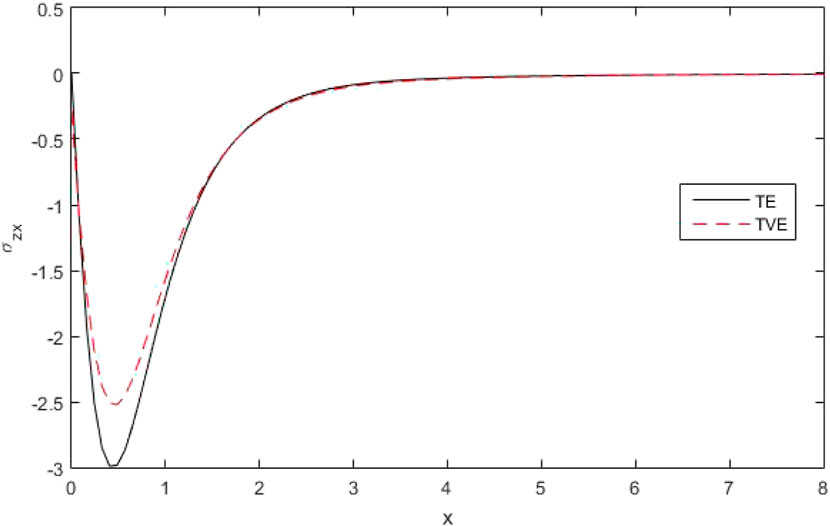
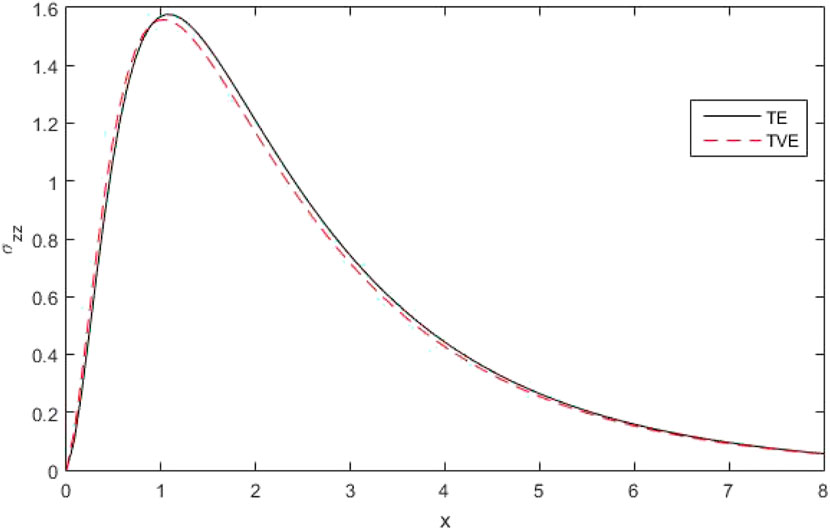
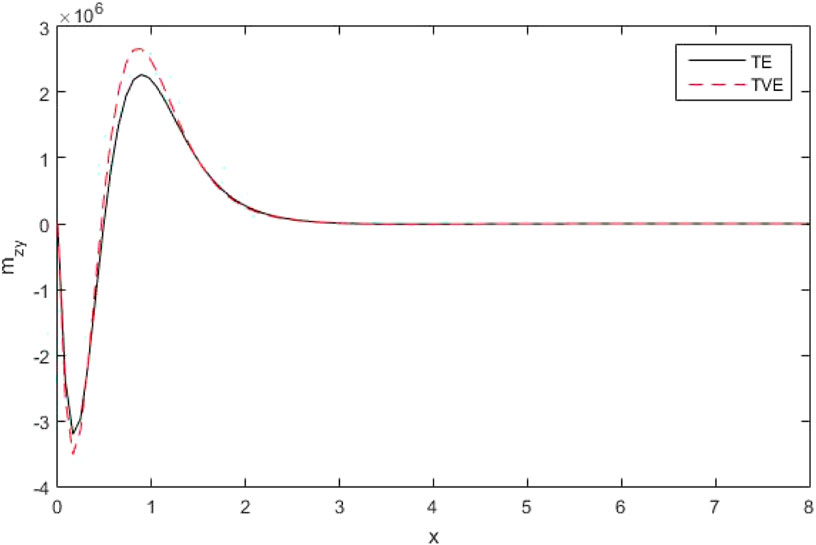
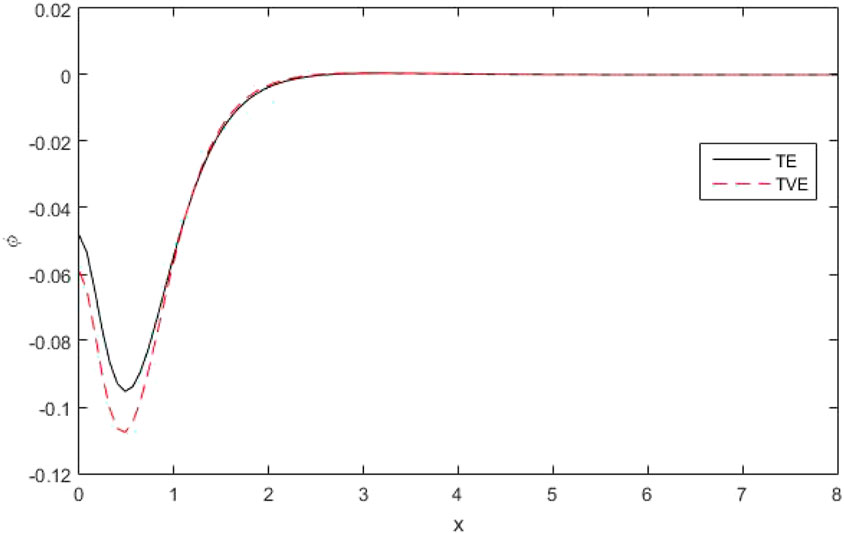
(v)The Figures 22–25 clarified four curves predicted by the different theories of thermo-elasticity, such that

• $\alpha =1,$ indicates the generalized micropolar thermoelastic theory with one relaxation time [8].

• $t=0,$ indicates the coupled theory of micropolar thermoelasticity [46].

• $0<\alpha <1,$ indicates the generalized conformable fractional order theory of micropolar thermo-elasticity.

(i) (Effect of rotation)

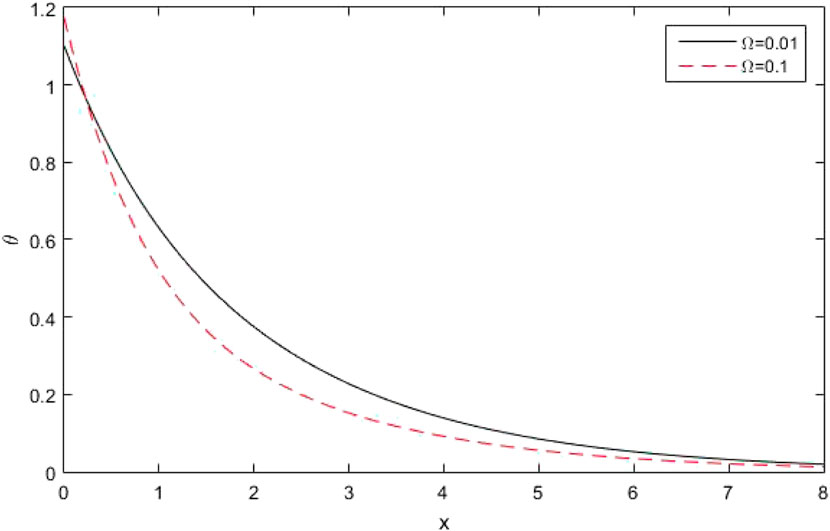
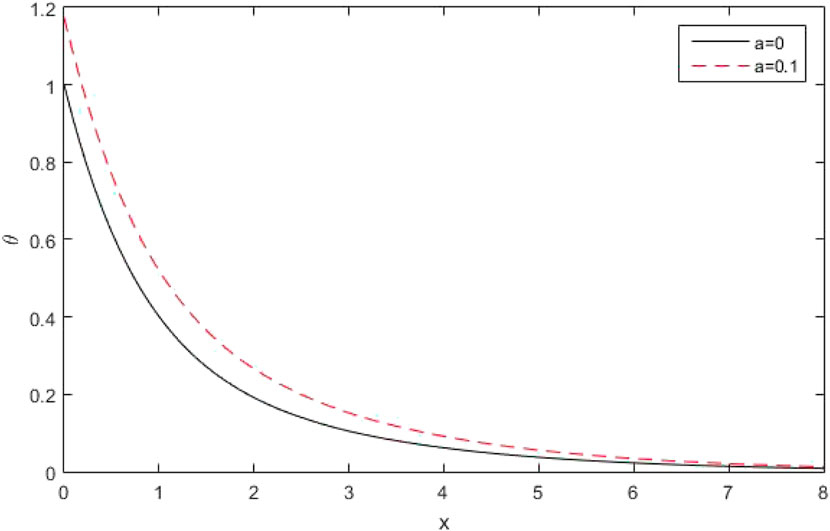
Figures 1, 2 depict the distribution of $\theta$ and $T$ with distance $x$ with two-temperatures for varying rotational values. It is noticed that curves of $\theta$ and $T$ begin from a positive value. Then, it then reduces to zero indefinitely.

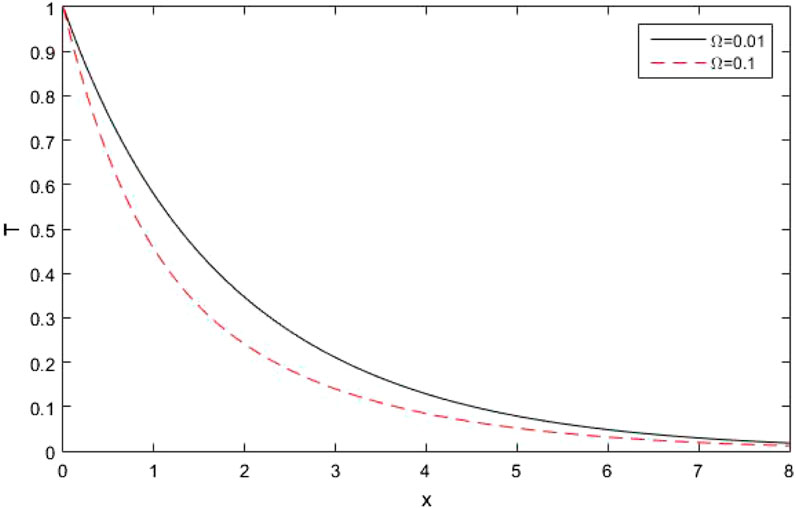
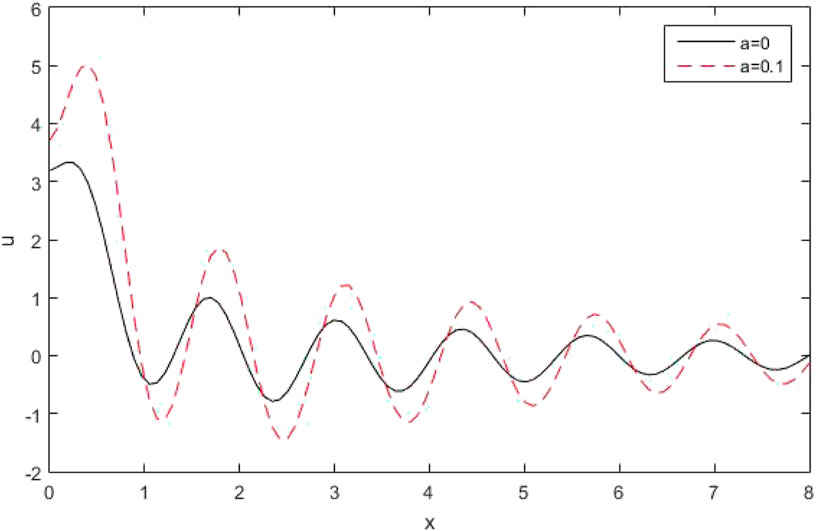
Figure 3 shows the variations of $u$ with distance $x$ with two-temperatures for different values of rotation. The rotation has a decreasing influence.

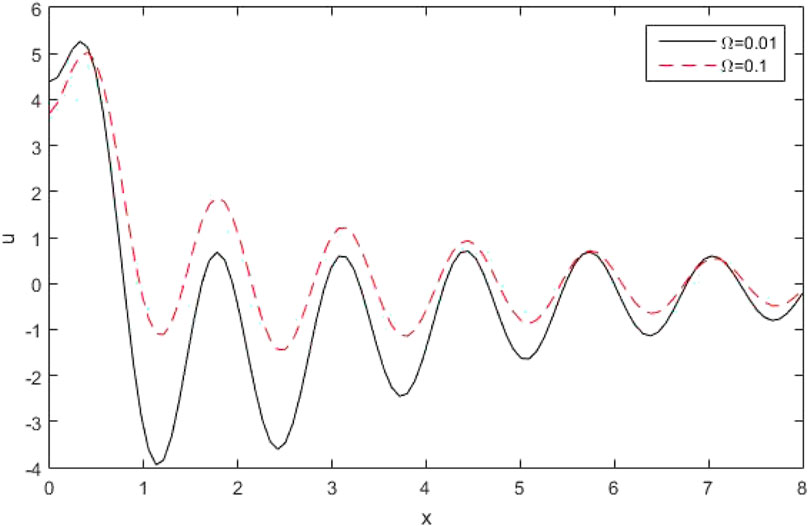
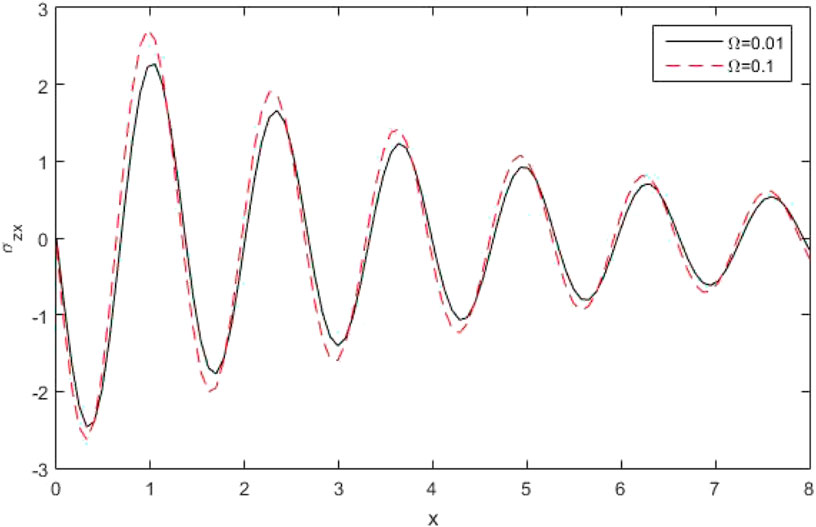
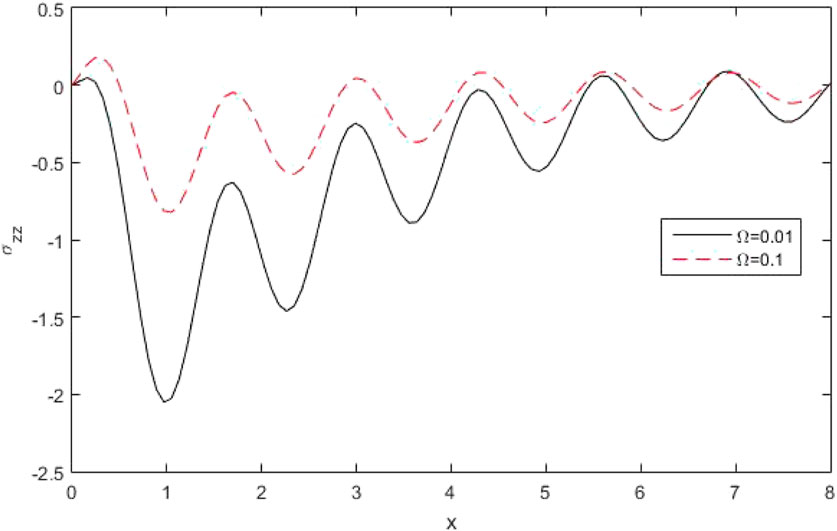
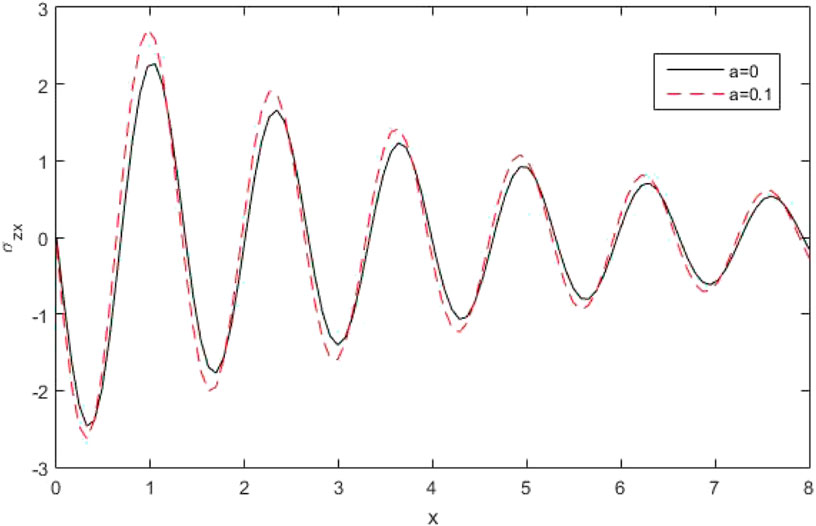
Figures 4, 5 represent the profile of force stress components ${\sigma }_{zx},{\sigma }_{zz}$ based for various values of rotation with two-temperature. They start with a zero value that is completely compatible with the limits. The value of ${\sigma }_{zx},{\sigma }_{zz}$ for $\mathrm{\Omega }=0.1$ is less as compared to $\mathrm{\Omega }=0.01,$ the values of ${\sigma }_{zx},{\sigma }_{zz}$ tending to zero.

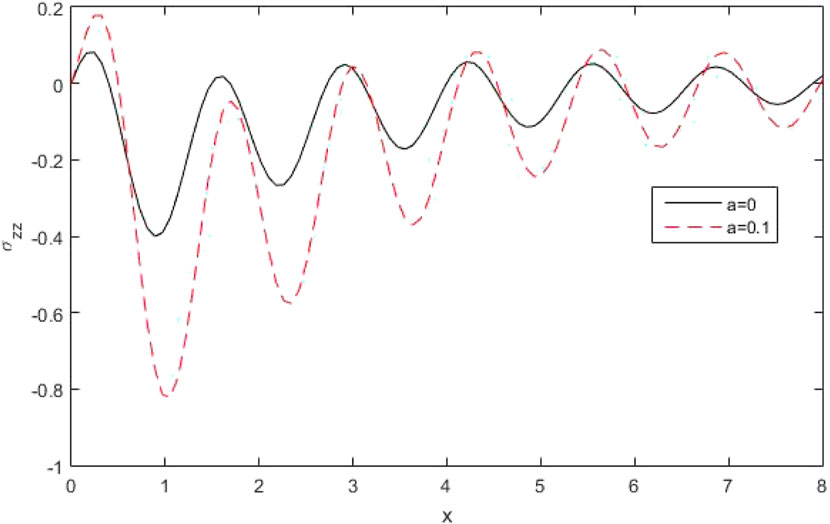
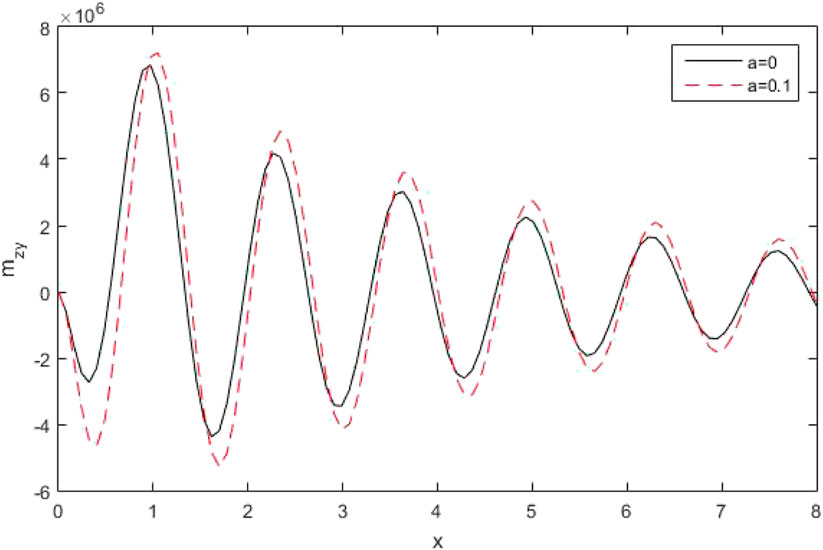
Figure 6 displays the disparity of the couple stress component $m_{zy}$ with distance $x$ for two-temperatures for varying rotational values. It begins with a zero value entirely consistent with the limit conditions. We notice that the value of $m_{zy}$ for $\mathrm{\Omega }=0.1$ is less as compared to $\mathrm{\Omega }=0.01$, the values of $m_{zy}$ tending to zero.

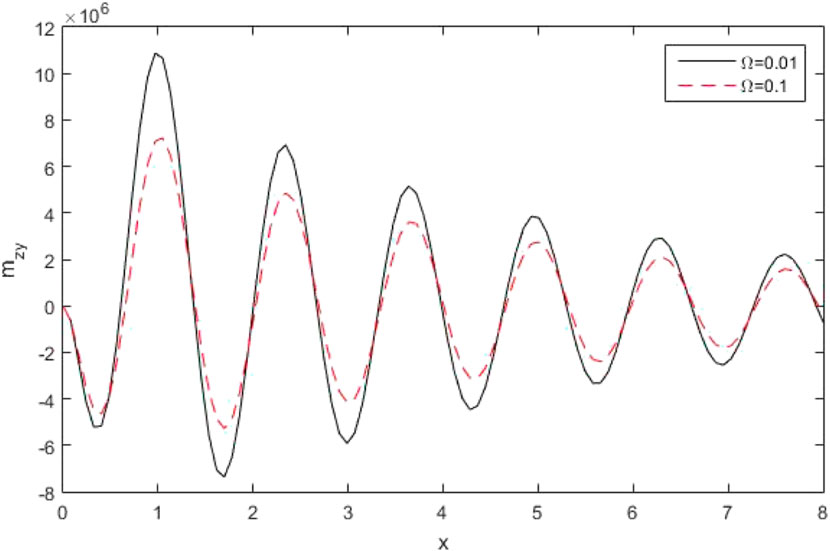
Figure 7 shows the variation of the micro-rotation $\varphi$ with distance $x$, with two-temperatures for different values of rotation. The rotation has a decreasing influence.

(ii) Effect of two temperatures

Figure 8 illuminates the supply of the thermodynamic temperature $T$ with distance $x$ for different $a=0,a=0.1.$ values under the influence of rotation. It begins with $T=1$ that fully complies with the limit conditions, subsequently decreases continually to zero value. We noticed that the parameter $a$ has an increasing effect

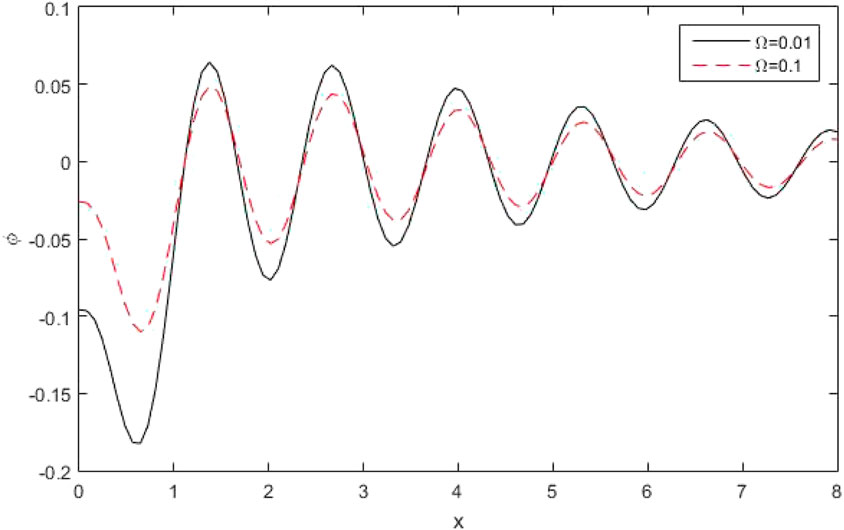
Figure 9 shows the conductive temperature $\theta$ with distance $x$ with the effect of rotation. We noticed that the curve of $\theta$ begins from a positive value. It then, reduces constantly to zero. We notice that the parameter $a$ has an increasing effect.

Figure 10 displays the variations of $u$ with distance $z$ under the influence of rotation for different values of $a=0,a=0.5$. The parameter $a$ is seen to have an increasing impact.

Figures 11, 12 denote the outline of the force stress component ${\sigma }_{zx},{\sigma }_{zz}$ under the effect of rotation for changed values of $a=0,a=0.5$. It begins with a zero value that is fully consistent with the limits. In this figure, we can see that the values of ${\sigma }_{zx},{\sigma }_{zz}$ for $a=0$ is greater than that at $=0.5$ .

Figure 13 shows the profile of the couple stress component $m_{zy}$ under the influence of rotation for the values of $a=0,a=0.5$. This begins with a zero value that is totally compatible with the limits. In this figure, we can see that the value of $m_{zy}$ for $a=0.5$ is greater than that at as $a=0$ It is observed that the influence is rising in parameter.

Figure 14 represents the variation of the micro-rotation with distance under the influence of rotation for different values of $=0,$ $a=0.5$. In the figure the value of $\varphi$ for $a=0.5$ is greater than that at $a=0$. The $a$ parameter is seen to have a growing effect.

(iii) Effect of viscosity

Figures 15, 16 depict $\theta$ and $T$ in two-temperature under the influence of rotation with and without of viscosity. It has been observed that the curves of $\theta$ and $T$ begin from a positive value, Then it decreases constantly to zero.

Figure 17 shows the deviation of the horizontal displacement distribution $u$ with distance $x$ under the influence of rotation and two-temperatures with and without viscosity. It can be seen that $\text{TE}>\text{TVE}$

Figures 18, 19 represent the profile of stress components ${\sigma }_{zx},$ ${\sigma }_{zz}$ under the influence of rotation and two-temperature for $\text{TE}$ and $\text{TVE}$.They begin with a zero value that is fully in line with the limit conditions. The value of ${\sigma }_{zx}$ for $\text{TVE}$ is greater than that for $\text{TE}.$ the value of ${\sigma }_{zz}$ for TE is greater than that for TVE.

Figure 20 depicts the disparity of the couple stress $m_{zy}$ with distance $x$ under the influence of rotation and two-temperatures for $\text{TE}$ and $\text{TVE}$.We observe that the value of $m_{zy}$ for $\text{TVE}$ is greater than that for $\text{TE}.$

Figure 21 depicts the variation of the micro-rotation $\varphi$ with distance $x$ under the influence of rotation and two-temperature for $\text{TE}$ and $\text{TVE}$. We observe that the value of $\varphi$ for $\text{TVE}$ is greater than that for $\text{TE}.$

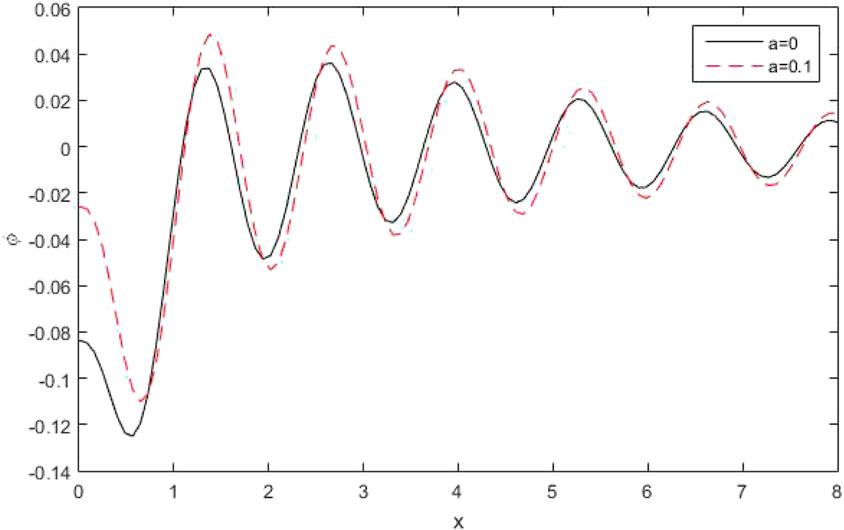
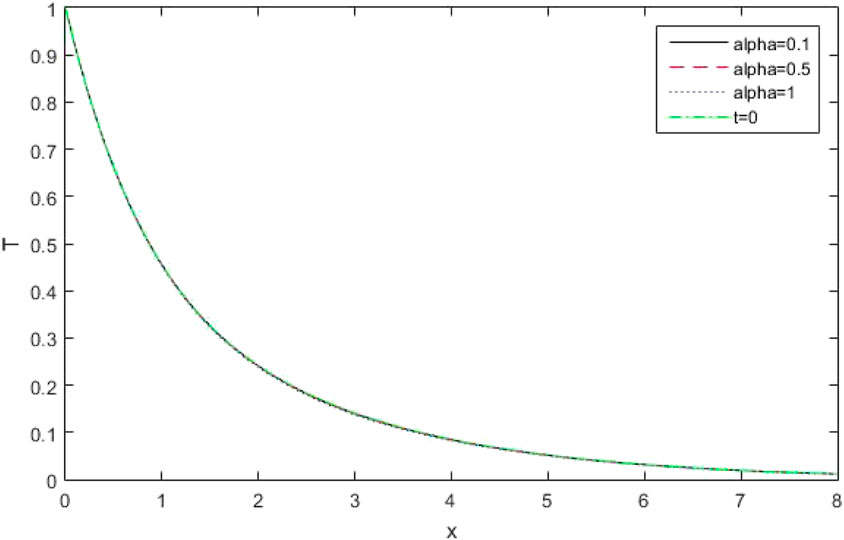
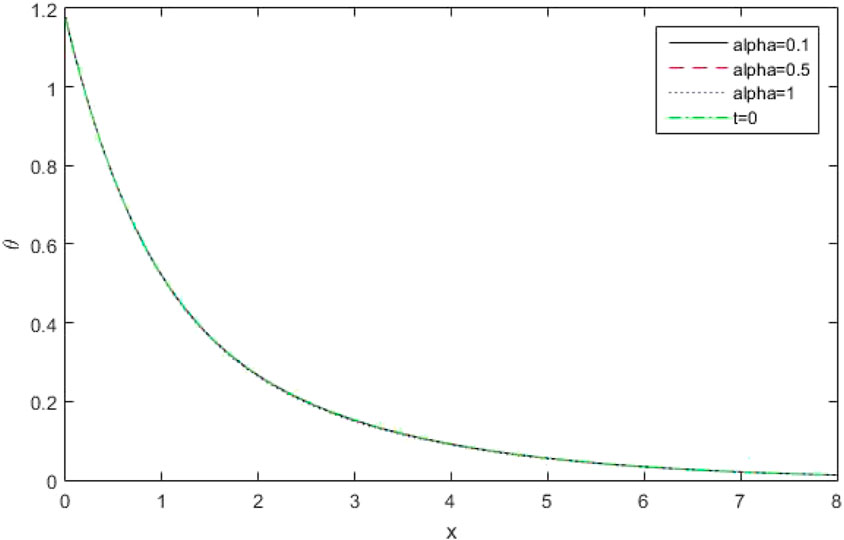
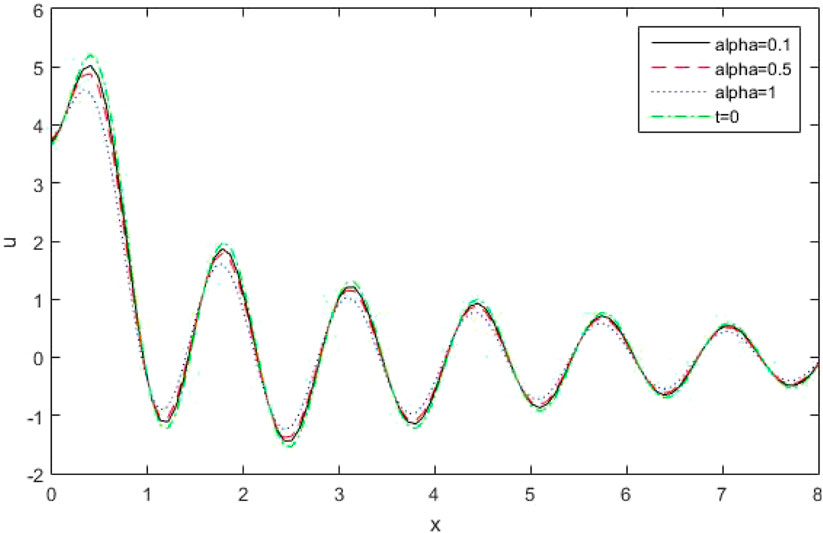
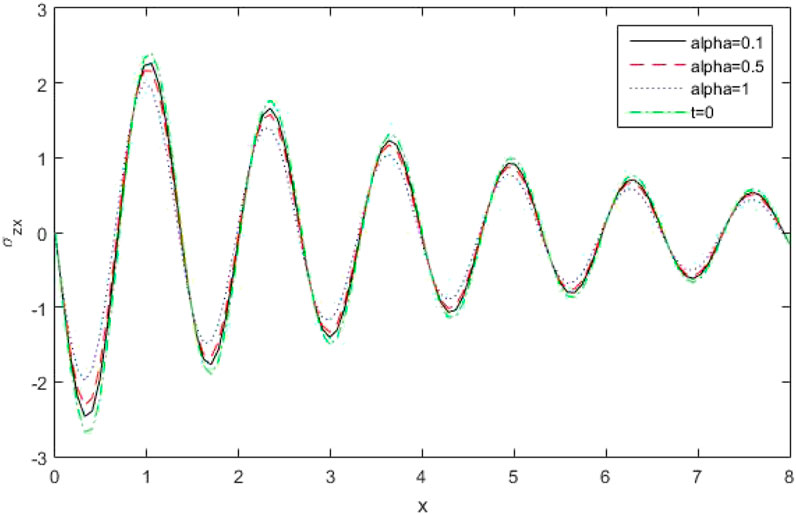
(v) Effect of Conformable fractional parameter

The figures [22–24] clarified four curves predicted by the different theories of thermo-elasticity, such that

• $\alpha =1,$ indicates the generalized thermoelastic theory with one relaxation time [10].

• $t=0,$ indicates the coupled theory of thermoelasticity [9].

• $0<\alpha <1,$ indicates the generalized conformable fractional order theory of thermo-elasticity.

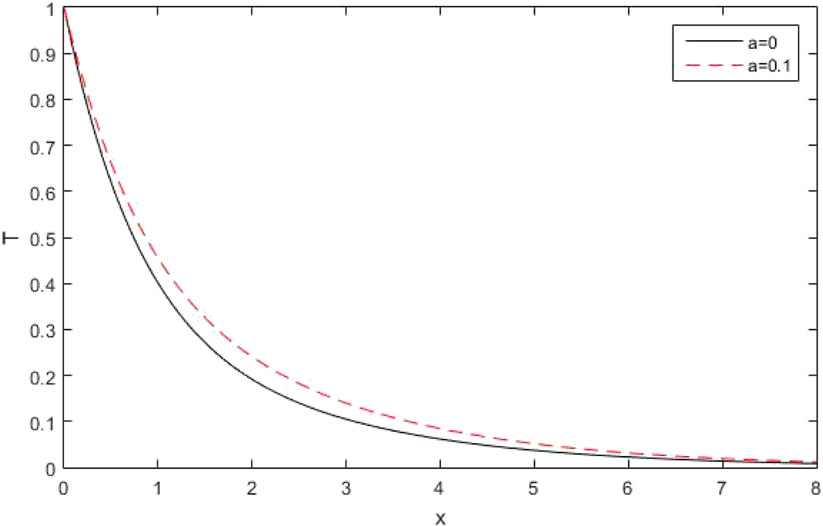
Figures 22, 23 depict the distribution of the thermo-dynamic temperature $T$ and conductive temperature $\theta$ with distance $x,$ under the influence of rotation and two-temperature for various values of $\alpha$ and for $t=0$. It is observed that the variation of $\theta$ starts from a positive value, then decreases continually to zero. It is also visible that for $\alpha =1,$ the result coincides with all results of applications that are taken in the context of the generalized thermoelasticity with one relaxation time, for $t=0,$ the result coincides with all results of applications that are taken in the case of the coupled theory, for $\alpha =0.1$ and $\alpha =0.5$ gives new results for the generalized conformable fractional order theory of thermoelasticity From this figure it is spotted that as fractional parameter $\alpha$ increase the measure of the temperature $\theta$ rise.

Figure 24 shows the variations of $u$ via distance $x$ under the influence of rotation and two-temperature for various values of $\alpha$ and $t=0.$ For $\alpha =1,$ the result to agree with all results of applications that are taken in the context of the generalized thermoelasticity with one relaxation time, for $t=0,$ the result agree with all results of applications that are taken in the context of the coupled theory, for $\alpha =1$ and $\alpha =0.5$ gives new results for the generalized conformable fractional order theory of thermoelasticity.

Figure 25 explains the variations of stress components ${\sigma }_{zx}$ with distance $x$ under the influence of rotation and two-temperature for various values of $\alpha$ and for $t=0$. It can be visible that they beginning with zero value that fully agrees with the boundary conditions.

7 Conclusion

Normal mode analysis was employed to investigate the behavior of the conductive temperature, the thermodynamic temperature, the component of horizontal displacement, the component of force stress, the couple stresses, and the micro-rotation under the effect of rotation, conformable fractional order theory, viscosity, and two-temperatures in a homogeneous, isotropic, generalized micropolar thermo-viscoelastic medium. We aim to study the effect of conformable fractional derivative, effect of rotation, and the two-temperature coefficients. The above analysis leads us to the following conclusions:

• Variations in various fields are clearly constrained to a certain zone in all of the data, and the values vanish outside of the region, which is consistent with the perspective of generalized micropolar thermo-visco- elasticity theory.

• All of the physical values fulfill the boundary criteria.

• The thermodynamic and conductive temperature nature of all models $\text{TE}$ and $\text{TVE}$ is same.

• The angular velocity and two-temperature parameters have a significant impact on the horizontal displacement component, the force stress components, the couple stresses components, and the micro-rotation. However, there are minor impacts on the conductive temperature and the thermodynamic temperature.

• For two temperature parameter values, $\theta$ and $T$ show a virtually identical pattern, and increasing the value of the two-temperature parameter leads the values of those functions to grow. While increasing the two-temperature parameter value leads the values of the horizontal displacement and stress components to drop, increasing the two-temperature parameter value causes the values of these functions to rise, as shown in the figures.

The given model will be valuable for scientists working on micropolar thermoelasticity in understanding the viscoelastic characteristics of human soft tissue and may lead to enhanced diagnostic applications. The findings may be used to both theoretical and empirical wave propagation.

• The fractional parameter $\alpha$ highly influences all variables.

• According to this work, we can treat the theory of conformable fractional order generalized micropolar thermoelasticity as an improvement in studying thermoelastic materials, we have to construct a new ranking for materials according to their fractional parameter $\alpha$, where this parameter becomes a new conductor of its ability to conduct heat under the effect of thermoelastic properties, we use these properties in the factory of glasses and ceramic.

Author contributions

SE-S: Software, Writing–review and editing. AE-B: Methodology, Writing–original draft. HA: Writing–original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

Authors extend their appreciation to Princess Nourah Bint Abdulrahman University for funding this research under researchers supporting project number PNURSP2023R154, Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Abo-Dahab MS, Lotfy KH. Generalized magneto-thermoelasticity with fractional derivative heat transfer for a rotation of a fibre-reinforced thermoelastic. J Comput Theor Nanosci (2015) 12:1869–81. doi:10.1166/jctn.2015.3972

CrossRef Full Text | Google Scholar

2. Youssef HM. Theory of generalized thermoelasticity with fractional order strain. JVC/Journal Vib Control (2016) 22:3840–57. doi:10.1177/1077546314566837

CrossRef Full Text | Google Scholar

3. Kumar R, Singh K, Pathania D. Effects of Hall current and rotation in a fractional ordered magneto-micropolar thermoviscoelastic half-space due to ramp-type heat. Int J Appl Comput Math (2020) 6:23–0. doi:10.1007/s40819-020-0773-1

CrossRef Full Text | Google Scholar

4. El-Bary AA, Atef HM. Modified approach for stress strain equation in the linear kelvin-voigt solid based on fractional order. J Comput Theor Nanosci (2016) 13:579–83. doi:10.1166/jctn.2016.4843

CrossRef Full Text | Google Scholar

5. Sherief HH, El-Sayed AMA, Abd El-Latief AM. Fractional order theory of thermoelasticity. Int J Sol Struct (2010) 47:269–75. doi:10.1016/j.ijsolstr.2009.09.034

CrossRef Full Text | Google Scholar

6. Ezzat MA, Karamany ASE. Fractional order heat conduction law in magneto-thermoelasticity involving two temperatures. Z Angew Math Phys (2011) 62:937–52. doi:10.1007/s00033-011-0126-3

CrossRef Full Text | Google Scholar

7. Biot MA. Thermoelasticity and irreversible thermodynamics. J Appl Phys (1956) 27:240–53. doi:10.1063/1.1722351

CrossRef Full Text | Google Scholar

8. Lord HW, Shulman Y. A generalized dynamical theory of thermoelasticity. J Mech Phys Sol (1967) 15:299–309. doi:10.1016/0022-5096(67)90024-5

CrossRef Full Text | Google Scholar

9. Green AE, Lindsay KA. Thermoelasticity. J Elast (1972) 2:1–7. doi:10.1007/BF00045689

CrossRef Full Text | Google Scholar

10. Green AE, Naghdi PM. Thermoelasticity without energy dissipation. J Elast (1993) 31:189–208. doi:10.1007/BF00044969

CrossRef Full Text | Google Scholar

11. Chandrasekharalah DS. Thermoelasticity with second sound: a rewiew. Appl Mech Rev (1986) 39:355–76. doi:10.1115/1.3143705

CrossRef Full Text | Google Scholar

12. Chandrasekharaiah DS. Hyperbolic thermoelasticity: a review of recent literature. Appl Mech Rev (1998) 51:705–29. doi:10.1115/1.3098984

CrossRef Full Text | Google Scholar

13. Tzou DY. A unified field approach for heat conduction from macro-to micro-scales. J Heat Transfer (1995) 117:8–16. doi:10.1115/1.2822329

CrossRef Full Text | Google Scholar

14. Eringen AC, Suhubi ES. Nonlinear theory of simple micro-elastic solids-I. Int J Eng Sci (1964) 2:189–203. doi:10.1016/0020-7225(64)90004-7

CrossRef Full Text | Google Scholar

15. Shubi ES, Eringen AC. Nonlinear theory of micro-elastic solids—II E. Int J Eng Sci (1964) 2:389–404. doi:10.1016/0020-7225(64)90017-5

CrossRef Full Text | Google Scholar

16. Nowacki W, Ins . Thermal Stresses in anisotropic bodies (1974).

Google Scholar

17. Tauchert TR, Claus WD, Ariman T. The linear theory of micropolar thermoelasticity. Int J Eng Sci (1968) 6:37–47. doi:10.1016/0020-7225(68)90037-2

CrossRef Full Text | Google Scholar

18. Boschi E, Iesan D. A generalized theory of linear micropolar thermoelasticity. Rev Mod Phys (1948) 20:35–9. doi:10.1103/RevModPhys.20.35

CrossRef Full Text | Google Scholar

19. Ciarletta M. A theory of micropolar thermoelasticity without energy dissipation. J Therm Stress (1999) 22:581–94. doi:10.1080/014957399280760

CrossRef Full Text | Google Scholar

20. Sherief H, Hamza A, Amany M. Theory of generalized micropolar thermoelasticity and an axisymmetric half-space problem. J Therm Stress (2005) 28:409–37. doi:10.1080/01495730590916641

CrossRef Full Text | Google Scholar

21. Othman MIA. Effect of rotation and relaxation time on a thermal shock problem for a half-space in generalized thermo-viscoelasticity. Acta Mech (2005) 174:129–43. doi:10.1007/s00707-004-0190-2

CrossRef Full Text | Google Scholar

22. Awad E. On the generalized thermal lagging behavior: refined aspects. J Therm Stress (2012) 35:293–325. doi:10.1080/01495739.2012.663682

CrossRef Full Text | Google Scholar

23. Ezzat MA, Awad ES. Constitutive relations, uniqueness of solution, and thermal shock application in the linear theory of micropolar generalized thermoelasticity involving two temperatures. J Therm Stress (2010) 33:226–50. doi:10.1080/01495730903542829

CrossRef Full Text | Google Scholar

24. Marin M, Abbas IA, Vlase S, Craciun EM. Some backward in time results for thermoelastic dipolar structures. Front Phys (2020) 8. doi:10.3389/fphy.2020.00041

CrossRef Full Text | Google Scholar

25. Marin M, Öchsner A, Craciun EM. A generalization of the Saint-Venant ’ s principle for an elastic body with dipolar structure. Contin Mech Thermodyn (2019) 32:269–78. doi:10.1007/s00161-019-00827-6

CrossRef Full Text | Google Scholar

26. Marin M, Öchsner A, Craciun EM. A generalization of the Gurtin ’ s variational principle in thermoelasticity without energy dissipation of dipolar bodies. Contin Mech Thermodyn (2020) 32:1685–94. doi:10.1007/s00161-020-00873-5

CrossRef Full Text | Google Scholar

27. Awad E, Alhazmi SE, Abdou MA. Anomalous thermally induced deformation in kelvin – voigt plate with ultrafast double-strip surface heating (2023). p. 1–23.

Google Scholar

28. Chen PJ, Gurtin ME. On a theory of heat conduction involving two temperatures. Z für Angew Math Phys ZAMP (1968) 19:614–27. doi:10.1007/BF01594969

CrossRef Full Text | Google Scholar

29. Warren WE, Chen PJ. Wave propagation in the two temperature theory of thermoelasticity. Acta Mech (1973) 16:21–33. doi:10.1007/BF01177123

CrossRef Full Text | Google Scholar

30. Othman MIA, Atef HM, El-Bary AA. A novel model of multi-temperatures theory in generalized thermo-viscoelasticity. Waves in Random and Complex Media (2021) 1–18. doi:10.1080/17455030.2021.1962019

CrossRef Full Text | Google Scholar

31. Alharbi AM, Othman MIA, Atef HM. Effect of viscosity and rotation on a generalized two-temperature thermoelasticity under five theories. Struct Eng Mech (2021) 78:755–64. doi:10.12989/sem.2021.78.6.755

CrossRef Full Text | Google Scholar

32. Alharbi AM, Atef HM, Othman MIA. Thermal effects and initial stress on magneto-thermo-viscoelastic medium with two temperature under five theories. ZAMM Z Angew Math Mech (2022) 102:1–18. doi:10.1002/zamm.202000392

CrossRef Full Text | Google Scholar

33. Alharbi AM, Othman MIA, Atef HM. Thomson effect with hyperbolic two-temperature on magneto-thermo-visco-elasticity. Appl Math Mech (English Ed (2021) 42:1311–26. doi:10.1007/s10483-021-2763-7

CrossRef Full Text | Google Scholar

34. Mahdy AMS, Lotfy K, Ahmed MH, El-Bary A, Ismail EA. Electromagnetic Hall current effect and fractional heat order for microtemperature photo-excited semiconductor medium with laser pulses. Results Phys (2020) 17:103161. doi:10.1016/j.rinp.2020.103161

CrossRef Full Text | Google Scholar

35. Lotfy K, Tantawy R, Anwar N. Thermomechanical response model on a reflection photothermal diffusion waves (RPTD) for semiconductor medium (2019).

Google Scholar

36. Lotfy K. A novel model of magneto photothermal diffusion (MPD) on polymer nano-composite semiconductor with initial stress. Waves in Random and Complex Media (2021) 31:83–100. doi:10.1080/17455030.2019.1566680

CrossRef Full Text | Google Scholar

37. Khamis AK, El-Bary AA, Lotfy K, Bakali A. Photothermal excitation processes with refined multi dual phase-lags theory for semiconductor elastic medium. Alexandria Eng J (2020) 59:1–9. doi:10.1016/j.aej.2019.11.016

CrossRef Full Text | Google Scholar

38. Lotfy K, Hassan W, El-Bary AA, Kadry MA. Response of electromagnetic and Thomson effect of semiconductor medium due to laser pulses and thermal memories during photothermal excitation. Results Phys (2020) 16:102877. doi:10.1016/j.rinp.2019.102877

CrossRef Full Text | Google Scholar

39. Lotfy K. Effect of variable thermal conductivity during the photothermal diffusion process of semiconductor medium. Silicon (2019) 11:1863–73. doi:10.1007/s12633-018-0005-z

CrossRef Full Text | Google Scholar

40. Othman MIA, Farouk RM. Transient disturbance in a half-space under generalized magneto- thermoelasticity with internal heat source transient disturbance in a half-space under generalized magneto-thermoelasticity with internal heat source (2009). doi:10.12693/APhysPolA.116.185

CrossRef Full Text | Google Scholar

41. Othman MIA, Singh B. The effect of rotation on generalized micropolar thermoelasticity for a half-space under five theories. Int J Sol Struct (2007) 44:2748–62. doi:10.1016/j.ijsolstr.2006.08.016

CrossRef Full Text | Google Scholar

42. Othman MIA, Fekry M. Effect of magnetic field on generalized thermo-viscoelastic diffusion medium with voids. Int J Struct Stab Dyn (2016) 16:1550033–21. doi:10.1142/S0219455415500339

CrossRef Full Text | Google Scholar

43. Othman MIA, Tantawi RS, Hilal MIM. Effect of initial stress and the gravity field on micropolar thermoelastic solid with microtemperatures. J Theor Appl Mech (2016) 54:847–57. doi:10.15632/jtam-pl.54.3.847

CrossRef Full Text | Google Scholar

44. Othman MIA, Hasona WM, Abd-Elaziz EM. Effect of rotation and initial stress on generalized micropolar thermoelastic medium with three-phase-lag. J Comput Theor Nanosci (2015) 12:2030–40. doi:10.1166/jctn.2015.3983

CrossRef Full Text | Google Scholar

45. Eringen C. Foundations of micropolar thermoelasticity (1970). doi:10.1007/978-3-7091-2904-3

CrossRef Full Text | Google Scholar

46. Boley BA, Tolins IS. Transient coupled thermoelastic boundary value problems in the half-space. J Appl Mech Trans ASME (1960) 29:637–46. doi:10.1115/1.3640647

CrossRef Full Text | Google Scholar

47. Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Math (2014) 264:65–70. doi:10.1016/j.cam.2014.01.002

CrossRef Full Text | Google Scholar

48. Shaw S, Othman MIA. On the concept of a conformable fractional differential equation. J Eng Therm Sci (2021) 1:17–29. doi:10.21595/jets.2021.22072

CrossRef Full Text | Google Scholar

Nomenclature

Appendix

Researchers in the field of thermoelasticity have all employed fractional derivatives to develop the heat conduction equation based on these derivatives

$k{\theta }_{,ii}=\rho c_E\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right){\theta }_{,t}+\gamma T_0\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)e_{,t}-\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)Q(\mathrm{A1})$

They arrived at this equation through the utilization of the following definitions:

(i) Riemann-Liouville definition. For $\alpha \in \left[n-1\right.,\left.n\right),$ the $\alpha$ derivatives of $f$ is

$D_a^{\alpha }\left(f\right)\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(n-\alpha \right)}\frac{d^n}{d{t}^n}{\displaystyle \underset{a}{\overset{t}{\int }}}\frac{f\left(x\right)}{{\left(t-x\right)}^{\alpha -n+1}}dx.(\mathrm{A2})$

(ii) Caputo definition. For $\alpha \in \left[n-1\right.,\left.n\right),$ the $\alpha$ derivatives of $f$ is

$D_a^{\alpha }\left(f\right)\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(n-\alpha \right)}{\displaystyle \underset{a}{\overset{t}{\int }}}\frac{f^{\left(n\right)}\left(x\right)}{{\left(t-x\right)}^{\alpha -n+1}}dx.(\mathrm{A3})$

Nevertheless, these two definitions possess certain limitations that can be summarized as follows:

(i) The Riemann-Liouville derivatives do not hold true for

$D_a^{\alpha }\left(1\right)=0\left(D_a^{\alpha }\left(1\right)=0\text{ for the caputo derivative}\right),\text{if\hspace{0.17em}}\alpha \text{\hspace{0.17em}is\hspace{0.17em}not\hspace{0.17em}natural}.(\mathrm{A4})$

(ii) None of the fractional derivatives fulfill the well-known formula for the derivative of the product of two functions:

$D_a^{\alpha }\left(fg\right)=f{D}_a^{\alpha }\left(g\right)+g{D}_a^{\alpha }\left(f\right).(\mathrm{A5})$

(iii) None of the fractional derivatives comply with the established formula for the derivative of the division of two functions:

$D_a^{\alpha }\left(f/g\right)\left(t\right)=\frac{g{D}_a^{\alpha }\left(f\right)-f{D}_a^{\alpha }\left(g\right)}{g^2}.(\mathrm{A6})$

(iv) None of the fractional derivatives abide by the chain rule.

$D_a^{\alpha }\left(fog\right)\left(t\right)=f^{\left(\alpha \right)}\left(g\left(t\right)\right)g^{\left(\alpha \right)}\left(t\right).(\mathrm{A7})$

(v) Fractional derivatives do not abide by the general rule $D^{\alpha }{D}^{\beta }f=D^{\alpha +\beta }f$ It was necessary to adopt another definition of fractional derivatives, which is the "Conformable fractional derivatives," in order to overcome the limitations discussed above [47, 48].

The fractional derivatives of the order $\alpha \in \left(0\right.,\left.1\right]$ of the absolutely continuous function $f\left(t\right)$ is

$\frac{d^{\alpha }f\left(t\right)}{d{t}^{\alpha }}=t^{1-\alpha }\frac{df\left(t\right)}{dt}(\mathrm{A8})$