Special concepts of edge regularity in the cubic fuzzy graph structure environment with an application

The cubic fuzzy graph structure is a tool for modeling problems, in which there are two fuzzy values for each variable and the relationships between them that cannot be expressed as a single fuzzy number. Inducing the same relationship among different subjects has an important effect on the understanding of uncertain problems. This is especially ambiguous and complicated when we are dealing with two different fuzzy values. With the aim of explaining edge regular in relationships among vertices, the current research has introduced this concept in the cubic fuzzy graph structure and expressed some of its characteristics. The edge regular and the total edge regularity are described in relation to several relationships. This concept has been applied in some special types such as the complete cubic fuzzy graph structure, and its results have been reviewed. Moreover, the vertex regular and its relationship with the edge regularity have been discussed. This study showed that the degree of vertices is effective in the edge adjustment process. In the end, an application of the topic under discussion is presented.

1 Introduction

In today’s world, a graph is a well-known mathematical model for a set whose members are related in some way. Mathematicians are particularly interested in understanding how many vertices and edges a graph can have before various substructures appear. They eagerly look for a set of vertices that are all connected by edges of the same color after certain coloring procedures. In social networks, edges that do not belong to any cluster or that connect different clusters are important in detecting anomalies. In similar cases, especially in weighted graphs, the idea of regularity of vertices and edges in a graph was gradually proposed.

In dealing with some events, classical graphs showed that they are not able to accurately describe and model uncertain problems. The theory of fuzzy set (FS) proposed by Zadeh [1] tried to model human reasoning, and in this process, it used approximate information and inaccurate data to make decisions under uncertain conditions. Actually, these systems mathematically model the existing inaccuracy and provide a suitable tool for real problems. With the introduction of the fuzzy graph (FG) based on fuzzy sets by Rosenfeld [2], a new perspective in the field of weighted graphs was opened to researchers. Gradually, different types of FGs were proposed by researchers. Talebi [3] studied the Cayley fuzzy graph. A generalization of fuzzy sets called the intuitionistic fuzzy set (IFS) was explained by Atanassov [4]. Borzooei et al. [5] presented properties of the product on the intuitionistic fuzzy graph (IFG). In 2011, Akram and Dudek [6] proposed an interval of fuzzy numbers instead of a fuzzy number by introducing the interval-valued fuzzy graph (IVFG). Concepts of the interval-valued intuitionistic fuzzy graph (IVIFG) were introduced by Talebi et al. [7, 8]. Rashmanlou et al. [9] explained some concepts of the bipolar fuzzy graph. Some properties of the single-valued neutrosophic graph were studied by Zeng et al. [10]. Certain concepts of vague graphs were studied by Kosari et al. [11–13]. Akram et al. [14–16] investigated concepts of connectivity in the m-polar fuzzy network model. The connectivity index in a directed rough fuzzy graph was studied by Ahmad et al. [17]. An extension of the fuzzy competition graph and its applications was presented by Pramanik et al. [18].

In 2006, Sampathkumar [19] established a new concept of graphs called the graph structure (GS) by generalizing signed or colored graphs. Since uncertainty and ambiguity in many phenomena often occur in the form of two or more separate relationships, therefore, a large part of problems can be modeled with the fuzzy graph structure (FGS). The idea of the FGS was first presented by Dinesh [20]. This concept was later developed by Ramakrishnan and Dinesh [21]. The progress of the FGS was further completed by the introduction of the intuitionistic fuzzy graph structure (IFGS) and m-polar FGS by Akram et al. [22, 23]. Kou et al. [24] researched the vague graph structure. Some decision-making based on the FGS was presented by Akram et al. [25, 26].

In general, in all types of FGs, most of the membership values of vertices and edges are in the form of one or more fuzzy numbers or one or more interval-valued fuzzy numbers. In fuzzy research studies, it was found that it was not possible to assign a fuzzy number to all graph vertices, especially when the membership value cannot be expressed with a fuzzy number. Jun et al. [27] tried to use two fuzzy values and interval fuzzy values in assigning the membership of graph vertices. By introducing the cubic fuzzy set (CFS), they were able to label the vertices of an FG with two fuzzy and interval values by combining FS and IVFS. With the flexibility of this concept, various problems arising from uncertainties can be solved. June et al. [28] also combined the neutrosophic set with CFS and presented a new set called neutrosophic CFS. Novel neutrosophic cubic graph structures were introduced by Gulistan et al. [29]. Muhiuddin et al. [30] studied graphs based on m-polar cubic structures. New types of CFGs and their applications are categorized in the studies of Rashid et al. [31]. Muhiuddin et al. [32] presented a new definition of CFG. Rashmanlou et al. [33] explained some of the concepts of the CFG.

The concept of the regular FG was first mentioned in the research by Ghani and Radha [34]. Pal et al. [35, 36] introduced the concept of the irregular and regular FGs. The irregularity concept, total irregularity, and total degree in an FG were defined by Gani and Lathi [37]. The degree and the total degree of an edge were introduced by Radha and Kumaravel [38]. Cary [39] initiated the idea of perfectly regular and perfectly edge regular FGs. Karunambigai et al. [40] introduced the concept of edge regular IFGs. Kumar et al. [41] investigated the regularity concept in CFGs.

As a combination of FGS and CFG, the cubic fuzzy graph structure (CFGS) is considered a more developed CFG model. Maximal product concepts in CFGS were reviewed by Rao et al. [42]. Some concepts of connectivity in CFGS were described by Shi et al. [43]. It is important to study the regularity in CFGS that supports multiple relationships. The necessity of examining the regularity in a CFGS is because in most cases, we face more than one relationship among objects for modeling. Li et al. [44] investigated the concept of vertex regularity in a CFGS.

This paper investigates the edge regularity in a CFGS. We examined some related features by defining the edge degree and total edge degree. In the following, by introducing the order and size in the CFGS, some related results were investigated. Moreover, a study on the edge regular in the complete CFGS is carried out. Vertex regularity and its relationship with an edge regular were discussed. At the end, an application of a CFGS in the field of goods and passenger transportation was presented.

2 Preliminaries

At the beginning of the discussion, we have to go over some basic definitions to enter the main concepts.

A graph in the form of G = (V, E) is a set of vertices V surrounded by a set of relations E. A graph structure (GS) X = (V, E₁, E₂, …, E_k) is introduced from the set V with a set of mutual relationship of E₁, E₂, …, E_k on V that every E_i is non-reflective and symmetric for 1 ≤ i ≤ k [19].

A fuzzy graph (FG) on V is a pair G = (ς, ϑ), where ς is a fuzzy subset (FS) of V and ϑ is a fuzzy relation on ς, so that ϑ(x, y) ≤ ς(x) ∧ ς(y) and ∀x, y ∈ V.

A cubic fuzzy set (CFS) of $\mathcal{A}$ on V is considered

$\mathcal{A}=\left\{⟨\left[\mu \left(z\right),\nu \left(z\right)\right],\eta \left(z\right)⟩\mid z\in V\right\},$

where [μ(z), ν(z)] is an interval-valued fuzzy number and η(z) is a fuzzy number as the membership value of z, so that μ, ν, η: V → [0, 1] [29].

Definition 2.1. [21] Consider Z = (V, E₁, E₂, …, E_k) as a GS. Then, $\mathcal{Z}=(\varsigma ,{\psi }_1,{\psi }_2,\dots ,{\psi }_k)$ is known as the FGS if ς, ψ₁, ψ₂, …, ψ_k are FSs on V, E₁, E₂, …, E_k, respectively, so that

${\psi }_i\left(ab\right)\le \varsigma \left(a\right)\wedge \varsigma \left(b\right),\forall a,b\in V,1\le i\le k.$

Definition 2.2. [32] The pair $\mathcal{G}=(\mathcal{A},\mathcal{B})$ is named a cubic fuzzy graph (CFG) on V if $\mathcal{A}=\{⟨[\alpha (z),\beta (z)],\gamma (z)⟩\mid z\in V\}$ is a CFS on V, and $\mathcal{B}=\{⟨[\alpha (wz),\beta (wz)],\gamma (wz)⟩\mid wz\in E\}$ is a CFS on V × V so that for all wz ∈ E,

$\begin{array}{ll}\hfill & {\alpha }_{\mathcal{B}}\left(wz\right)\le {\alpha }_{\mathcal{A}}\left(w\right)\wedge {\alpha }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill & {\beta }_{\mathcal{B}}\left(wz\right)\le {\beta }_{\mathcal{A}}\left(w\right)\wedge {\beta }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill & {\gamma }_{\mathcal{B}}\left(wz\right)\le {\gamma }_{\mathcal{A}}\left(w\right)\wedge {\gamma }_{\mathcal{A}}\left(z\right).\hfill \end{array}$

Definition 2.3. [42] Consider ${\mathcal{G}}^{*}=(V,E_1,E_2,\dots ,E_k)$ as a GS. Then, $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is known as a CFGS on ${\mathcal{G}}^{*}$ if $\mathcal{A}=\{⟨[\alpha (z),\beta (z)],\gamma (z)⟩\mid z\in V\}$ is a CFS on V, and ${\mathcal{B}}_i=\{⟨[{\alpha }_{{\mathcal{B}}_i}(wz),{\beta }_{{\mathcal{B}}_i}(wz)],{\gamma }_{{\mathcal{B}}_i}(wz)⟩\mid wz\in E_i\}$ is a CFS on E_i so that

$\begin{array}{ccc}\hfill {\alpha }_{{\mathcal{B}}_i}\left(wz\right)& \le \hfill & {\alpha }_{\mathcal{A}}\left(w\right)\wedge {\alpha }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill {\beta }_{{\mathcal{B}}_i}\left(wz\right)& \le \hfill & {\beta }_{\mathcal{A}}\left(w\right)\wedge {\beta }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill {\gamma }_{{\mathcal{B}}_i}\left(wz\right)& \le \hfill & {\gamma }_{\mathcal{A}}\left(w\right)\wedge {\gamma }_{\mathcal{A}}\left(z\right),\forall wz\in E_{i}and1\le i\le k.\hfill \end{array}$

Definition 2.4. [42] A CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is named a complete CFGS if

$\begin{array}{ccc}\hfill {\alpha }_{{\mathcal{B}}_i}\left(wz\right)& =\hfill & {\alpha }_{\mathcal{A}}\left(w\right)\wedge {\alpha }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill {\beta }_{{\mathcal{B}}_i}\left(wz\right)& =\hfill & {\beta }_{\mathcal{A}}\left(w\right)\wedge {\beta }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill {\gamma }_{{\mathcal{B}}_i}\left(wz\right)& =\hfill & {\gamma }_{\mathcal{A}}\left(w\right)\wedge {\gamma }_{\mathcal{A}}\left(z\right),\forall w,z\in Vand1\le i\le k.\hfill \end{array}$

Example 2.5. The CFGS of $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,{\mathcal{B}}_3)$ drawn in Figure 1 is a complete CFGS.

$\begin{array}{ll}\hfill & \mathcal{A}=\left\{\langle z_1,\left[0.7,0.9\right],1\rangle ,\langle z_2,\left[0.5,0.6\right],0.6\rangle ,\langle z_3,\left[0.6,0.8\right],1\rangle ,\langle z_4,\left[0.4,0.5\right],0.6\rangle \right\},\hfill \\ \hfill & {\mathcal{B}}_1=\left\{\langle z_1{z}_2,\left[0.5,0.6\right],0.6\rangle ,\langle z_3{z}_4,\left[0.4,0.5\right],0.6\rangle \right\},\hfill \\ \hfill & {\mathcal{B}}_2=\left\{\langle z_1{z}_4,\left[0.4,0.5\right],0.6\rangle ,\langle z_2{z}_3,\left[0.5,0.6\right],0.6\rangle \right\},\hfill \\ \hfill & {\mathcal{B}}_3=\left\{\langle z_1{z}_3,\left[0.6,0.8\right],1\rangle ,\langle z_2{z}_4,\left[0.4,0.5\right],0.6\rangle \right\}.\hfill \end{array}$

FIGURE 1

FIGURE 1. Complete CFGS, $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,{\mathcal{B}}_3)$.

Definition 2.6. [44] Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ to be a CFGS. The ${\mathcal{B}}_i$-degree of vertex z is considered to be ${\mathfrak{D}}_{{\mathcal{B}}_i}(z)=⟨[{\mathfrak{D}}_{{\alpha }_i}(z),{\mathfrak{D}}_{{\beta }_i}(z)],{\mathfrak{D}}_{{\gamma }_i}(z)⟩$, and it is defined as follows:

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\alpha }_i}\left(z\right)={\displaystyle \sum _{wz\in E_i,z\ne w}}{\alpha }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & {\mathfrak{D}}_{{\beta }_i}\left(z\right)={\displaystyle \sum _{wz\in E_i,z\ne w}}{\beta }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & {\mathfrak{D}}_{{\gamma }_i}\left(z\right)={\displaystyle \sum _{wz\in E_i,z\ne w}}{\gamma }_{{\mathcal{B}}_i}\left(wz\right).\hfill \end{array}$

Definition 2.7. [44] Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ to be a CFGS. The total ${\mathcal{B}}_i$-degree of vertex z is denoted by $\mathfrak{T}{\mathfrak{D}}_{{\mathcal{B}}_i}(z)=⟨[\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}(z),\mathfrak{T}{\mathfrak{D}}_{{\beta }_i}(z)],\mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}(z)⟩$, where

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(z\right)={\displaystyle \sum _{wz\in E_i,z\ne w}}{\alpha }_{{\mathcal{B}}_i}\left(wz\right)+{\alpha }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(z\right)={\displaystyle \sum _{wz\in E_i,z\ne w}}{\beta }_{{\mathcal{B}}_i}\left(wz\right)+{\beta }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(z\right)={\displaystyle \sum _{wz\in E_i,z\ne w}}{\gamma }_{{\mathcal{B}}_i}\left(wz\right)+{\gamma }_{\mathcal{A}}\left(z\right).\hfill \end{array}$

Table 1 shows some abbreviations in this article.

TABLE 1

TABLE 1. Some abbreviations.

3 The edge regularity in cubic fuzzy graph structures

In this section, we introduce the edge regularity in a CFGS and examine some of its properties.

Definition 3.1. Let $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ be a CFGS. The ${\mathcal{B}}_i$-edge degree of wz in $\mathcal{G}$ is denoted by ${\mathfrak{D}}_{{\mathcal{B}}_i}(wz)=⟨[{\mathfrak{D}}_{{\alpha }_i}(wz),{\mathfrak{D}}_{{\beta }_i}(wz)],{\mathfrak{D}}_{{\gamma }_i}(wz)⟩$ and defined as

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(w\right)+{\mathfrak{D}}_{{\alpha }_i}\left(z\right)-2{\alpha }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & {\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(w\right)+{\mathfrak{D}}_{{\beta }_i}\left(z\right)-2{\beta }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & {\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(w\right)+{\mathfrak{D}}_{{\gamma }_i}\left(z\right)-2{\gamma }_{{\mathcal{B}}_i}\left(wz\right).\hfill \end{array}$

This definition is equivalent to

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\displaystyle \sum _{t\ne z}}{\alpha }_{{\mathcal{B}}_i}\left(wt\right)+{\displaystyle \sum _{t\ne w}}{\alpha }_{{\mathcal{B}}_i}\left(zt\right),\hfill \\ \hfill & {\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\displaystyle \sum _{t\ne z}}{\beta }_{{\mathcal{B}}_i}\left(wt\right)+{\displaystyle \sum _{t\ne w}}{\beta }_{{\mathcal{B}}_i}\left(zt\right),\hfill \\ \hfill & {\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\displaystyle \sum _{t\ne z}}{\gamma }_{{\mathcal{B}}_i}\left(wt\right)+{\displaystyle \sum _{t\ne w}}{\gamma }_{{\mathcal{B}}_i}\left(zt\right).\hfill \end{array}$

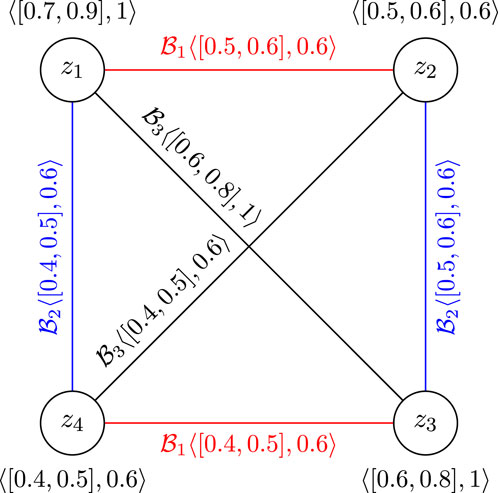
Example 3.2. Consider CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2)$, which is shown in Figure 2, where

$\begin{array}{ll}\hfill & \mathcal{A}=\left\{\langle z_1,\left[0.7,0.8\right],0.9\rangle ,\langle z_2,\left[0.5,0.7\right],0.8\rangle ,\langle z_3,\left[0.4,0.5\right],0.6\rangle ,\right.\hfill \\ \hfill & \left.\langle ,z_4,\left[0.6,0.7\right],0.9,\rangle ,,\langle ,z_5,\left[0.3,0.4\right],0.5,\rangle ,,\langle ,z_6,\left[0.8,0.9\right],0.7,\rangle \right\},\hfill \\ \hfill & {\mathcal{B}}_1=\left\{\langle z_1{z}_2,\left[0.3,0.4\right],0.5\rangle ,\langle z_3{z}_4,\left[0.4,0.5\right],0.6\rangle ,\langle z_3{z}_6,\left[0.3,0.4\right],0.5\rangle \right\},\hfill \\ \hfill & {\mathcal{B}}_2=\left\{\langle z_1{z}_3,\left[0.1,0.2\right],0.3\rangle ,\langle z_2{z}_4,\left[0.5,0.6\right],0.7\rangle ,\langle z_3{z}_5,\left[0.2,0.3\right],0.4\rangle \right\}.\hfill \end{array}$

The ${\mathcal{B}}_2$-edge degree z₁z₃ in $\mathcal{G}$ is calculated as follows:

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\alpha }_2}\left(z_1{z}_3\right)={\mathfrak{D}}_{{\alpha }_2}\left(z_1\right)+{\mathfrak{D}}_{{\alpha }_2}\left(z_3\right)-2{\alpha }_{{\mathcal{B}}_2}\left(z_1{z}_3\right)=0.1+0.3-2\left(0.1\right)=0.2,\hfill \\ \hfill & {\mathfrak{D}}_{{\beta }_2}\left(z_1{z}_3\right)={\mathfrak{D}}_{{\beta }_2}\left(z_1\right)+{\mathfrak{D}}_{{\beta }_2}\left(z_3\right)-2{\beta }_{{\mathcal{B}}_2}\left(z_1{z}_3\right)=0.2+0.5-2\left(0.2\right)=0.3,\hfill \\ \hfill & {\mathfrak{D}}_{{\gamma }_2}\left(z_1{z}_3\right)={\mathfrak{D}}_{{\gamma }_2}\left(z_1\right)+{\mathfrak{D}}_{{\gamma }_2}\left(z_3\right)-2{\gamma }_{{\mathcal{B}}_2}\left(z_1{z}_3\right)=0.3+0.7-2\left(0.3\right)=0.4.\hfill \end{array}$

Therefore, ${\mathfrak{D}}_{{\mathcal{B}}_2}(z_1{z}_3)=⟨[0.2,0.3],0.4⟩$.

FIGURE 2

FIGURE 2. A CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2)$.

Remark 3.3. For any CFGS of $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$, the following relationship for degrees of vertices of $\mathcal{G}$ is held:

$\begin{array}{ll}\hfill & {\displaystyle \sum _{j=1}^n}{\mathfrak{D}}_{{\alpha }_i}\left(z_j\right)=2{\displaystyle \sum _{j=1,l>j}^{n-1}}{\alpha }_{{\mathcal{B}}_i}\left(z_j{z}_l\right),\hfill \\ \hfill & {\displaystyle \sum _{j=1}^n}{\mathfrak{D}}_{{\beta }_i}\left(z_j\right)=2\sum _{j=1,l>j}^{n-1}{\beta }_{{\mathcal{B}}_i}\left(z_j{z}_l\right),\hfill \\ \hfill & {\displaystyle \sum _{j=1}^n}{\mathfrak{D}}_{{\gamma }_i}\left(z_j\right)=2{\displaystyle \sum _{j=1,l>j}^{n-1}}{\gamma }_{{\mathcal{B}}_i}\left(z_j{z}_l\right),\forall 1\le i\le kand1\le l\le n.\hfill \end{array}$

Definition 3.4. Let $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ be a CFGS. The total degree of ${\mathcal{B}}_i$-edge wz is determined as $\mathfrak{T}{\mathfrak{D}}_{{\mathcal{B}}_i}(wz)=⟨[\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}(wz),\mathfrak{T}{\mathfrak{D}}_{{\beta }_i}(wz)],\mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}(wz)⟩$, where

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(wz\right)+{\alpha }_{{\mathcal{B}}_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(w\right)+{\mathfrak{D}}_{{\alpha }_i}\left(z\right)-{\alpha }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(wz\right)+{\beta }_{{\mathcal{B}}_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(w\right)+{\mathfrak{D}}_{{\beta }_i}\left(z\right)-{\beta }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(wz\right)+{\gamma }_{{\mathcal{B}}_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(w\right)+{\mathfrak{D}}_{{\gamma }_i}\left(z\right)-{\gamma }_{{\mathcal{B}}_i}\left(wz\right).\hfill \end{array}$

This is equivalent to

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\displaystyle \sum _{t\ne z}}{\alpha }_{{\mathcal{B}}_i}\left(wt\right)+{\displaystyle \sum _{t\ne w}}{\alpha }_{{\mathcal{B}}_i}\left(zt\right)+{\alpha }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\displaystyle \sum _{t\ne z}}{\beta }_{{\mathcal{B}}_i}\left(wt\right)+{\displaystyle \sum _{t\ne w}}{\beta }_{{\mathcal{B}}_i}\left(zt\right)+{\beta }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\displaystyle \sum _{t\ne z}}{\gamma }_{{\mathcal{B}}_i}\left(wt\right)+{\displaystyle \sum _{t\ne w}}{\gamma }_{{\mathcal{B}}_i}\left(zt\right)+{\gamma }_{{\mathcal{B}}_i}\left(wz\right).\hfill \end{array}$

Example 3.5. Consider CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2)$, as shown in Figure 2. The total degree of ${\mathcal{B}}_2$-edge z₁z₃ in $\mathcal{G}$ can be computed as follows:

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_2}\left(z_1{z}_3\right)={\mathfrak{D}}_{{\alpha }_2}\left(z_1\right)+{\mathfrak{D}}_{{\alpha }_2}\left(z_3\right)-{\alpha }_{{\mathcal{B}}_2}\left(z_1{z}_3\right)=0.1+0.3-0.1=0.3,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\beta }_2}\left(z_1{z}_3\right)={\mathfrak{D}}_{{\beta }_2}\left(z_1\right)+{\mathfrak{D}}_{{\beta }_2}\left(z_3\right)-{\beta }_{{\mathcal{B}}_2}\left(z_1{z}_3\right)=0.2+0.5-0.2=0.5,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\gamma }_2}\left(z_1{z}_3\right)={\mathfrak{D}}_{{\gamma }_2}\left(z_1\right)+{\mathfrak{D}}_{{\gamma }_2}\left(z_3\right)-{\gamma }_{{\mathcal{B}}_2}\left(z_1{z}_3\right)=0.3+0.7-0.3=0.7.\hfill \end{array}$

Therefore, $\mathfrak{T}{\mathfrak{D}}_{{\mathcal{B}}_2}(z_1{z}_3)=⟨[0.3,0.5],0.7⟩$.

Definition 3.6. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ as a CFGS. If all edges have the same ${\mathcal{B}}_i$-edge degree ⟨[a, b], c⟩, then, $\mathcal{G}$ is said to be the ⟨[a, b], c⟩- ${\mathcal{B}}_i$-edge regular. Moreover, If all edges have the same total ${\mathcal{B}}_i$-edge degree ⟨[a, b], c⟩, then, $\mathcal{G}$ is said to be the ⟨[a, b], c⟩-total ${\mathcal{B}}_i$-edge regular.

Definition 3.7. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ as a CFGS. The minimum ${\mathcal{B}}_i$-edge degree of $\mathcal{G}$ is shown as ${\delta }_{{\mathcal{B}}_i}(\mathcal{G})=⟨[{\delta }_{{\alpha }_i}(\mathcal{G}),{\delta }_{{\beta }_i}(\mathcal{G})],{\delta }_{{\gamma }_i}(\mathcal{G})⟩$, where

$\begin{array}{ll}\hfill & {\delta }_{{\alpha }_i}\left(\mathcal{G}\right)=\bigwedge \left\{{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\},\hfill \\ \hfill & {\delta }_{{\beta }_i}\left(\mathcal{G}\right)=\bigwedge \left\{{\mathfrak{D}}_{{\beta }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\},\hfill \\ \hfill & {\delta }_{{\gamma }_i}\left(\mathcal{G}\right)=\bigwedge \left\{{\mathfrak{D}}_{{\gamma }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\}.\hfill \end{array}$

Furthermore, the minimum total ${\mathcal{B}}_i$-edge degree of $\mathcal{G}$ is shown as ${\delta }_{{\mathcal{B}}_i}^t(\mathcal{G})=⟨[{\delta }_{{\alpha }_i}^t(\mathcal{G}),{\delta }_{{\beta }_i}^t(\mathcal{G})],{\delta }_{{\gamma }_i}^t(\mathcal{G})⟩$, where

$\begin{array}{ll}\hfill & {\delta }_{{\alpha }_i}^t\left(\mathcal{G}\right)=\bigwedge \left\{\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\},\hfill \\ \hfill & {\delta }_{{\beta }_i}^t\left(\mathcal{G}\right)=\bigwedge \left\{\mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\},\hfill \\ \hfill & {\delta }_{{\gamma }_i}^t\left(\mathcal{G}\right)=\bigwedge \left\{\mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\}.\hfill \end{array}$

Definition 3.8. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ as a CFGS. The maximum ${\mathcal{B}}_i$-edge degree of $\mathcal{G}$ is shown as ${\mathrm{\Delta }}_{{\mathcal{B}}_i}(\mathcal{G})=⟨[{\mathrm{\Delta }}_{{\alpha }_i}(\mathcal{G}),{\mathrm{\Delta }}_{{\beta }_i}(\mathcal{G})],{\mathrm{\Delta }}_{{\gamma }_i}(\mathcal{G})⟩$, where

$\begin{array}{ll}\hfill & {\mathrm{\Delta }}_{{\alpha }_i}\left(\mathcal{G}\right)=\bigvee \left\{{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\},\hfill \\ \hfill & {\mathrm{\Delta }}_{{\beta }_i}\left(\mathcal{G}\right)=\bigvee \left\{{\mathfrak{D}}_{{\beta }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\},\hfill \\ \hfill & {\mathrm{\Delta }}_{{\gamma }_i}\left(\mathcal{G}\right)=\bigvee \left\{{\mathfrak{D}}_{{\gamma }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\}.\hfill \end{array}$

Furthermore, the maximum total ${\mathcal{B}}_i$-edge degree of $\mathcal{G}$ is shown as ${\mathrm{\Delta }}_{{\mathcal{B}}_i}^t(\mathcal{G})=⟨[{\mathrm{\Delta }}_{{\alpha }_i}^t(\mathcal{G}),{\mathrm{\Delta }}_{{\beta }_i}^t(\mathcal{G})],{\mathrm{\Delta }}_{{\gamma }_i}^t(\mathcal{G})⟩$, where

$\begin{array}{ll}\hfill & {\mathrm{\Delta }}_{{\alpha }_i}^t\left(\mathcal{G}\right)=\bigvee \left\{\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\},\hfill \\ \hfill & {\mathrm{\Delta }}_{{\beta }_i}^t\left(\mathcal{G}\right)=\bigvee \left\{\mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\},\hfill \\ \hfill & {\mathrm{\Delta }}_{{\gamma }_i}^t\left(\mathcal{G}\right)=\bigvee \left\{\mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right),wz\in {\mathcal{B}}_i\right\}.\hfill \end{array}$

Remark 3.9. A CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is called the ⟨[a, b], c⟩-${\mathcal{B}}_i$-edge regular if

${\delta }_{{\mathcal{B}}_i}\left(\mathcal{G}\right)={\mathrm{\Delta }}_{{\mathcal{B}}_i}\left(\mathcal{G}\right)=⟨\left[a,b\right],c⟩.$

Moreover, $\mathcal{G}$ is called the ⟨[a, b], c⟩-total ${\mathcal{B}}_i$-edge regular if

${\delta }_{{\mathcal{B}}_i}^t\left(\mathcal{G}\right)={\mathrm{\Delta }}_{{\mathcal{B}}_i}^t\left(\mathcal{G}\right)=⟨\left[a,b\right],c⟩.$

Example 3.10. Consider CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2)$, as shown in Figure 3, where

$\begin{array}{ll}\hfill & \mathcal{A}=\left\{⟨z_1,\left[0.7,0.9\right],1⟩,⟨z_2,\left[0.5,0.6\right],0.6⟩,⟨z_3,\left[0.6,0.8\right],1⟩,⟨z_4,\left[0.4,0.5\right],0.6⟩\right\},\hfill \\ \hfill & {\mathcal{B}}_1=\left\{⟨z_1{z}_2,\left[0.2,0.3\right],0.4⟩,⟨z_3{z}_4,\left[0.2,0.3\right],0.4⟩\right\},\hfill \\ \hfill & {\mathcal{B}}_2=\left\{⟨z_1{z}_4,\left[0.3,0.4\right],0.5⟩,⟨z_1{z}_3,\left[0.1,0.2\right],0.3⟩,⟨z_2{z}_3,\left[0.4,0.5\right],0.6⟩\right\}.\hfill \end{array}$

The total degree of ${\mathcal{B}}_1$-edges is equal to ⟨[0.2, 0.3], 0.4⟩. Therefore, $\mathcal{G}$ is a ⟨[0.2, 0.3], 0.4⟩-total ${\mathcal{B}}_1$-edge regular. As it is seen

${\delta }_{{\mathcal{B}}_1}^t\left(\mathcal{G}\right)={\mathrm{\Delta }}_{{\mathcal{B}}_1}^t\left(\mathcal{G}\right)=⟨\left[0.2,0.3\right],0.4⟩.$

FIGURE 3

FIGURE 3. ⟨[0.2, 0.3], 0.4⟩-total ${\mathcal{B}}_1$-edge regular CFGS, $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2)$.

Theorem 3.11. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ as a CFGS which is both an ${\mathcal{B}}_i$-edge regular and a total ${\mathcal{B}}_i$-edge regular, then ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant.

Proof. Suppose that $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ be the ⟨[a, b], c⟩-${\mathcal{B}}_i$-edge regular and the ⟨[a′, b′], c′⟩-total ${\mathcal{B}}_i$-edge regular. Then, for all $wz\in {\mathcal{B}}_i$

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\mathcal{B}}_i}\left(wz\right)=\langle \left[{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),{\mathfrak{D}}_{{\beta }_i}\left(wz\right)\right],{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)\rangle =\langle \left[a,b\right],c\rangle ,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\mathcal{B}}_i}\left(wz\right)=\langle \left[\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),\mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)\right],\mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)\rangle =\langle \left[a^{\prime },b^{\prime }\right],c^{\prime }\rangle .\hfill \end{array}$

Thus, by definition

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(wz\right)+{\alpha }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(wz\right)+{\beta }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(wz\right)+{\gamma }_{{\mathcal{B}}_i}\left(wz\right).\hfill \end{array}$

Therefore,

${\alpha }_{{\mathcal{B}}_i}\left(wz\right)=a^{\prime }-a,{\beta }_{{\mathcal{B}}_i}\left(wz\right)=b^{\prime }-b,{\gamma }_{{\mathcal{B}}_i}\left(wz\right)=c^{\prime }-c,forallwz\in {\mathcal{B}}_i.$

Hence, ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant.

Remark 3.12. The total ${\mathcal{B}}_i$-edge regular does not imply the ${\mathcal{B}}_i$-edge regularity for a CFGS and vice versa.

Example 3.13. Consider the CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2)$, as shown in Figure 3. $\mathcal{G}$ is a total ${\mathcal{B}}_i$-edge regular, but it is not a ${\mathcal{B}}_i$-edge regular.

Theorem 3.14. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ as a CFGS. Then, ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant functions on ${\mathcal{B}}_i$ if and only if the following are equivalent:

(i) $\mathcal{G}$ is a ${\mathcal{B}}_i$-edge regular.

(ii) $\mathcal{G}$ is a total ${\mathcal{B}}_i$-edge regular.

Proof. Suppose $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is a CFGS and ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant functions on ${\mathcal{B}}_i$, i.e.,

${\alpha }_{{\mathcal{B}}_i}\left(wz\right)=k,{\beta }_{{\mathcal{B}}_i}\left(wz\right)=m,{\gamma }_{{\mathcal{B}}_i}\left(wz\right)=n,forsomek,m,n\in \left[\mathrm{0,1}\right]andallwz\in {\mathcal{B}}_i.$

(i) ⇒ (ii) Consider $\mathcal{G}$ as a ⟨[a, b], c⟩-${\mathcal{B}}_i$-edge regular. Then, for all $wz\in {\mathcal{B}}_i$

${\mathfrak{D}}_{{\mathcal{B}}_i}\left(wz\right)=\langle \left[{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),{\mathfrak{D}}_{{\beta }_i}\left(wz\right)\right],{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)\rangle =\langle \left[a,b\right],c\rangle .$

On the other hand, we have

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(wz\right)+{\alpha }_{{\mathcal{B}}_i}\left(wz\right)=a+k,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(wz\right)+{\beta }_{{\mathcal{B}}_i}\left(wz\right)=b+m,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(wz\right)+{\gamma }_{{\mathcal{B}}_i}\left(wz\right)=c+n.\hfill \end{array}$

Thus, $\mathcal{G}$ is a ⟨[a + k, b + m], c + n⟩-total ${\mathcal{B}}_i$-edge regular.(ii) ⇒ (i) Consider $\mathcal{G}$ as a ⟨[a′, b′], c′⟩-total ${\mathcal{B}}_i$-edge regular, a′, b′, c′ ∈ [0, 1]. Then,

$\mathfrak{T}{\mathfrak{D}}_{{\mathcal{B}}_i}\left(wz\right)=\langle \left[\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),\mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)\right],\mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)\rangle =\langle \left[a^{\prime },b^{\prime }\right],c^{\prime }\rangle .$

Therefore,

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\alpha }_i}\left(wz\right)=\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right)-{\alpha }_{{\mathcal{B}}_i}\left(wz\right)=a^{\prime }-k,\hfill \\ \hfill & {\mathfrak{D}}_{{\beta }_i}\left(wz\right)=\mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)-{\beta }_{{\mathcal{B}}_i}\left(wz\right)=b^{\prime }-m,\hfill \\ \hfill & {\mathfrak{D}}_{{\gamma }_i}\left(wz\right)=\mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)-{\gamma }_{{\mathcal{B}}_i}\left(wz\right)=c^{\prime }-n.\hfill \end{array}$

Then, $\mathcal{G}$ is a ⟨[a′ − k, b′ − m], c′ − n⟩-${\mathcal{B}}_i$-edge regular.Conversely, suppose that (i) ⇔ (ii). We prove that ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant functions. Suppose ${\alpha }_{{\mathcal{B}}_i}$ not to be a constant function. Then, there exists $xy,wz\in {\mathcal{B}}_i$ so that ${\alpha }_{{\mathcal{B}}_i}(xy)\ne {\alpha }_{{\mathcal{B}}_i}(wz)$. Since $\mathcal{G}$ is a ⟨[a, b], c⟩-${\mathcal{B}}_i$-edge regular, then ${\alpha }_{{\mathcal{B}}_i}(xy)={\alpha }_{{\mathcal{B}}_i}(wz)=a$. On the other hand, by definition

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(xy\right)={\mathfrak{D}}_{{\alpha }_i}\left(xy\right)+{\alpha }_{{\mathcal{B}}_i}\left(xy\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(wz\right)+{\alpha }_{{\mathcal{B}}_i}\left(wz\right).\hfill \end{array}$

Since ${\alpha }_{{\mathcal{B}}_i}(xy)\ne {\alpha }_{{\mathcal{B}}_i}(wz)$, then, $\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}(xy)\ne \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}(wz)$. Therefore, $\mathcal{G}$ is not a total ${\mathcal{B}}_i$-edge regular. Now, suppose that $\mathcal{G}$ be a total ${\mathcal{B}}_i$-edge regular. Then, $\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}(xy)=\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}(wz)$. It follows that ${\mathfrak{D}}_{{\alpha }_i}(xy)-{\mathfrak{D}}_{{\alpha }_i}(wz)={\alpha }_{{\mathcal{B}}_i}(xy)-{\alpha }_{{\mathcal{B}}_i}(wz)\ne 0$. Therefore, ${\mathfrak{D}}_{{\alpha }_i}(xy)\ne {\mathfrak{D}}_{{\alpha }_i}(wz)$. Then, $\mathcal{G}$ is not a ${\mathcal{B}}_i$-edge regular. This result is in contradiction with the assumption. Therefore, ${\alpha }_{{\mathcal{B}}_i}$ is a constant function. In the same way, it is proved that ${\beta }_{{\mathcal{B}}_i}$ and ${\gamma }_{{\mathcal{B}}_i}$ are also constant functions.

Theorem 3.15. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ to be a complete CFGS, and ${\alpha }_{\mathcal{A}}$, ${\beta }_{\mathcal{A}}$, and ${\gamma }_{\mathcal{A}}$ are constant functions. Then, $\mathcal{G}$ is a ${\mathcal{B}}_i$-edge regular.

Proof. Let $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ be a complete CFGS. Then, for all w, z ∈ V and 1 ≤ i ≤ k, we have

$\begin{array}{ccc}\hfill {\alpha }_{{\mathcal{B}}_i}\left(wz\right)& =\hfill & {\alpha }_{\mathcal{A}}\left(w\right)\wedge {\alpha }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill {\beta }_{{\mathcal{B}}_i}\left(wz\right)& =\hfill & {\beta }_{\mathcal{A}}\left(w\right)\wedge {\beta }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill {\gamma }_{{\mathcal{B}}_i}\left(wz\right)& =\hfill & {\gamma }_{\mathcal{A}}\left(w\right)\wedge {\gamma }_{\mathcal{A}}\left(z\right).\hfill \end{array}$

Suppose that ${\alpha }_{\mathcal{A}}(z)=a$, ${\beta }_{\mathcal{A}}(z)=b$ and ${\gamma }_{\mathcal{A}}(z)=c$, ∀z ∈ V. Therefore, ${\alpha }_{{\mathcal{B}}_i}(wz)=a$, ${\beta }_{{\mathcal{B}}_i}(wz)=b$, and ${\gamma }_{{\mathcal{B}}_i}(wz)=c$, ∀wz ∈ E_i, and 1 ≤ i ≤ k. Since $\mathcal{G}$ is a complete CFGS, then, every vertex in $\mathcal{G}$ is connected to n − 1 vertices by ${\mathcal{B}}_i$-edges having the same membership values. Thus, the degree of each vertex z ∈ V can be written as ${\mathfrak{D}}_{{\mathcal{B}}_i}(z)=⟨[(n-1)a,(n-1)b],(n-1)c⟩$. Then,

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(w\right)+{\mathfrak{D}}_{{\alpha }_i}\left(z\right)-2{\alpha }_{{\mathcal{B}}_i}\left(wz\right)=\left(n-1\right)a+\left(n-1\right)a-2a=2\left(n-2\right)a,\hfill \\ \hfill & {\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(w\right)+{\mathfrak{D}}_{{\beta }_i}\left(z\right)-2{\beta }_{{\mathcal{B}}_i}\left(wz\right)=\left(n-1\right)b+\left(n-1\right)b-2b=2\left(n-2\right)b,\hfill \\ \hfill & {\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(w\right)+{\mathfrak{D}}_{{\gamma }_i}\left(z\right)-2{\gamma }_{{\mathcal{B}}_i}\left(wz\right)=\left(n-1\right)c+\left(n-1\right)c-2c=2\left(n-2\right)c,\hfill \end{array}$

for all wz ∈ E_i. Then, $\mathcal{G}$ is a ${\mathcal{B}}_i$-edge regular CFGS.

Theorem 3.16. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ to be a complete CFGS, and ${\alpha }_{\mathcal{A}}$, ${\beta }_{\mathcal{A}}$, and ${\gamma }_{\mathcal{A}}$ are constant functions. Then, $\mathcal{G}$ is a total ${\mathcal{B}}_i$-edge regular.

Proof. The proof is the same as the previous theorem, except that

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(w\right)+{\mathfrak{D}}_{{\alpha }_i}\left(z\right)-{\alpha }_{{\mathcal{B}}_i}\left(wz\right)=\left(n-1\right)a+\left(n-1\right)a-a=\left(2n-3\right)a,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(w\right)+{\mathfrak{D}}_{{\beta }_i}\left(z\right)-{\beta }_{{\mathcal{B}}_i}\left(wz\right)=\left(n-1\right)b+\left(n-1\right)b-b=\left(2n-3\right)b,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(w\right)+{\mathfrak{D}}_{{\gamma }_i}\left(z\right)-{\gamma }_{{\mathcal{B}}_i}\left(wz\right)=\left(n-1\right)c+\left(n-1\right)c-c=\left(2n-3\right)c,\hfill \end{array}$

for all wz ∈ E_i and 1 ≤ i ≤ k. Therefore, $\mathcal{G}$ is a total ${\mathcal{B}}_i$-edge regular CFGS.

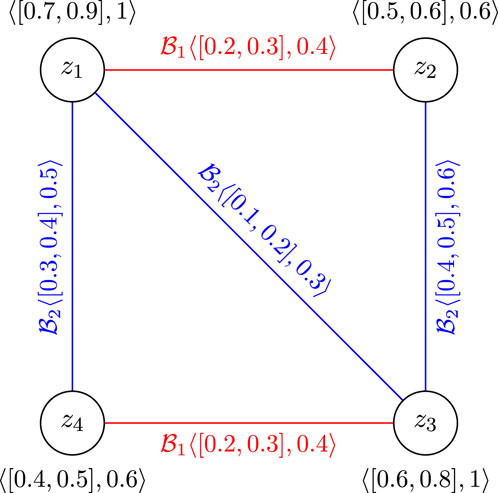
Example 3.17. Consider the complete CFGS of $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,{\mathcal{B}}_3)$, as shown in Figure 4, where

$\begin{array}{ll}\hfill & {\alpha }_{\mathcal{A}}\left(z\right)=0.5,{\beta }_{\mathcal{A}}\left(z\right)=0.6and{\gamma }_{\mathcal{A}}\left(z\right)=0.7,forallz\in V,\hfill \\ \hfill & {\mathcal{B}}_1=\left\{\langle z_1{z}_2,\left[0.5,0.6\right],0.7\rangle ,\langle z_3{z}_4,\left[0.5,0.6\right],0.7\rangle \right\},\hfill \\ \hfill & {\mathcal{B}}_2=\left\{\langle z_1{z}_4,\left[0.5,0.6\right],0.7\rangle ,\langle z_2{z}_3,\left[0.5,0.6\right],0.7\rangle \right\},\hfill \\ \hfill & {\mathcal{B}}_3=\left\{\langle z_1{z}_3,\left[0.5,0.6\right],0.7\rangle ,\langle z_2{z}_4,\left[0.5,0.6\right],0.7\rangle \right\}.\hfill \end{array}$

FIGURE 4

FIGURE 4. ${\mathcal{B}}_i$-edge regular complete CFGS, $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,{\mathcal{B}}_3)$.

Definition 3.18. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ a CFGS. Then, $\mathcal{G}$ is called the perfect ${\mathcal{B}}_i$-edge regular if $\mathcal{G}$ is a ${\mathcal{B}}_i$-edge regular and also is a total ${\mathcal{B}}_i$-edge regular.

Example 3.19. The CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,{\mathcal{B}}_3)$ shown in Figure 4 is a ${\mathcal{B}}_i$-edge regular and also is a total ${\mathcal{B}}_i$-edge regular, so it is a perfect ${\mathcal{B}}_i$-edge regular CFGS.

Theorem 3.20. If $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is a perfect ${\mathcal{B}}_i$-edge regular CFGS, then, ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant functions, for i = 1, 2, …, k.

Proof. Suppose that $\mathcal{G}$ be a perfect ${\mathcal{B}}_i$-edge regular CFGS. In such a case, $\mathcal{G}$ must be a ${\mathcal{B}}_i$-edge regular CFGS and a total ${\mathcal{B}}_i$-edge regular CFGS, i.e., for all wz ∈ E_i,

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\mathcal{B}}_i}\left(wz\right)=\langle \left[{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),{\mathfrak{D}}_{{\beta }_i}\left(wz\right)\right],{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)\rangle =\langle \left[a,b\right],c\rangle ,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\mathcal{B}}_i}\left(wz\right)=\langle \left[\mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right),\mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)\right],\mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)\rangle =\langle \left[a^{\prime },b^{\prime }\right],c^{\prime }\rangle .\hfill \end{array}$

According to the definition of the total ${\mathcal{B}}_i$-edge degree,

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(wz\right)+{\alpha }_{{\mathcal{B}}_i}\left(wz\right)\Rightarrow a^{\prime }=a+{\alpha }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(wz\right)+{\beta }_{{\mathcal{B}}_i}\left(wz\right)\Rightarrow b^{\prime }=b+{\beta }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(wz\right)+{\gamma }_{{\mathcal{B}}_i}\left(wz\right)\Rightarrow c^{\prime }+c+{\gamma }_{{\mathcal{B}}_i}\left(wz\right).\hfill \end{array}$

Therefore,

$\begin{array}{ll}\hfill & {\alpha }_{{\mathcal{B}}_i}\left(wz\right)=a^{\prime }-a,\hfill \\ \hfill & {\alpha }_{{\mathcal{B}}_i}\left(wz\right)=b^{\prime }-b,\hfill \\ \hfill & {\alpha }_{{\mathcal{B}}_i}\left(wz\right)=c^{\prime }-c.\hfill \end{array}$

Hence, ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant functions.

Definition 3.21. The order of a CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is determined as $\mathfrak{P}(\mathcal{G})=⟨[{\mathfrak{P}}_{\alpha }(\mathcal{G}),{\mathfrak{P}}_{\beta }(\mathcal{G})],{\mathfrak{P}}_{\gamma }(\mathcal{G})⟩$, where

$\begin{array}{ll}\hfill & {\mathfrak{P}}_{\alpha }\left(\mathcal{G}\right)={\displaystyle \sum _{z\in V}}{\alpha }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill & {\mathfrak{P}}_{\beta }\left(\mathcal{G}\right)={\displaystyle \sum _{z\in V}}{\beta }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill & {\mathfrak{P}}_{\gamma }\left(\mathcal{G}\right)={\displaystyle \sum _{z\in V}}{\gamma }_{\mathcal{A}}\left(z\right).\hfill \end{array}$

The ${\mathcal{B}}_i$-size of a CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is defined as ${\mathfrak{Q}}_{{\mathcal{B}}_i}(\mathcal{G})=⟨[{\mathfrak{Q}}_{{\alpha }_i}(\mathcal{G}),{\mathfrak{Q}}_{{\beta }_i}(\mathcal{G})],{\mathfrak{Q}}_{{\gamma }_i}(\mathcal{G})⟩$, where

$\begin{array}{ll}\hfill & {\mathfrak{Q}}_{{\alpha }_i}\left(\mathcal{G}\right)={\displaystyle \sum _{wz\in E_i}}{\alpha }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & {\mathfrak{Q}}_{{\beta }_i}\left(\mathcal{G}\right)={\displaystyle \sum _{wz\in E_i}}{\beta }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & {\mathfrak{Q}}_{{\gamma }_i}\left(\mathcal{G}\right)={\displaystyle \sum _{wz\in E_i}}{\gamma }_{{\mathcal{B}}_i}\left(wz\right).\hfill \end{array}$

The size of a CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is defined as $\mathfrak{Q}(\mathcal{G})=⟨[{\mathfrak{Q}}_{\alpha }(\mathcal{G}),{\mathfrak{Q}}_{\beta }(\mathcal{G})],{\mathfrak{Q}}_{\gamma }(\mathcal{G})⟩$, where

$\begin{array}{ll}\hfill & {\mathfrak{Q}}_{\alpha }\left(\mathcal{G}\right)={\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{wz\in E_i}}{\alpha }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & {\mathfrak{Q}}_{\beta }\left(\mathcal{G}\right)=\sum _{i=1}^k{\displaystyle \sum _{wz\in E_i}}{\beta }_{{\mathcal{B}}_i}\left(wz\right),\hfill \\ \hfill & {\mathfrak{Q}}_{\gamma }\left(\mathcal{G}\right)={\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{wz\in E_i}}{\gamma }_{{\mathcal{B}}_i}\left(wz\right).\hfill \end{array}$

Theorem 3.22. If $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is a perfect ${\mathcal{B}}_i$-edge regular CFGS, then

$\begin{array}{ll}\hfill & {\mathfrak{P}}_{\alpha }\left(\mathcal{G}\right)\ge {\displaystyle \sum _{z\in V}}\underset{w\ne z}{\max }\left\{{\alpha }_{{\mathcal{B}}_i}\left(wz\right)\right\},\hfill \\ \hfill & {\mathfrak{P}}_{\beta }\left(\mathcal{G}\right)\ge {\displaystyle \sum _{z\in V}}\underset{w\ne z}{\max }\left\{{\beta }_{{\mathcal{B}}_i}\left(wz\right)\right\},\hfill \\ \hfill & {\mathfrak{P}}_{\gamma }\left(\mathcal{G}\right)\ge {\displaystyle \sum _{z\in V}}\underset{w\ne z}{\max }\left\{{\gamma }_{{\mathcal{B}}_i}\left(wz\right)\right\}.\hfill \end{array}$

Proof. According to the definition of CFGS,

$\begin{array}{ccc}\hfill {\alpha }_{{\mathcal{B}}_i}\left(wz\right)& \le \hfill & {\alpha }_{\mathcal{A}}\left(w\right)\wedge {\alpha }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill {\beta }_{{\mathcal{B}}_i}\left(wz\right)& \le \hfill & {\beta }_{\mathcal{A}}\left(w\right)\wedge {\beta }_{\mathcal{A}}\left(z\right),\hfill \\ \hfill {\gamma }_{{\mathcal{B}}_i}\left(wz\right)& \le \hfill & {\gamma }_{\mathcal{A}}\left(w\right)\wedge {\gamma }_{\mathcal{A}}\left(z\right),forallwz\in E_{i}and1\le i\le k.\hfill \end{array}$

Thus, we have

$\begin{array}{ll}\hfill & {\alpha }_{\mathcal{A}}\left(z\right)\ge \underset{w\ne z}{\max }\left\{{\alpha }_{{\mathcal{B}}_i}\left(wz\right)\right\},\hfill \\ \hfill & {\beta }_{\mathcal{A}}\left(z\right)\ge \underset{w\ne z}{\max }\left\{{\beta }_{{\mathcal{B}}_i}\left(wz\right)\right\},\hfill \\ \hfill & {\gamma }_{\mathcal{A}}\left(z\right)\ge \underset{w\ne z}{\max }\left\{{\gamma }_{{\mathcal{B}}_i}\left(wz\right)\right\}.\hfill \end{array}$

Therefore,

$\begin{array}{ll}\hfill & {\mathfrak{P}}_{\alpha }\left(\mathcal{G}\right)={\displaystyle \sum _{zinV}}{\alpha }_{\mathcal{A}}\left(z\right)\ge {\displaystyle \sum _{z\in V}}\underset{w\ne z}{\max }\left\{{\alpha }_{{\mathcal{B}}_i}\left(wz\right)\right\},\hfill \\ \hfill & {\mathfrak{P}}_{\beta }\left(\mathcal{G}\right)={\displaystyle \sum _{zinV}}{\beta }_{\mathcal{A}}\left(z\right)\ge {\displaystyle \sum _{z\in V}}\underset{w\ne z}{\max }\left\{{\beta }_{{\mathcal{B}}_i}\left(wz\right)\right\},\hfill \\ \hfill & {\mathfrak{P}}_{\gamma }\left(\mathcal{G}\right)={\displaystyle \sum _{zinV}}{\gamma }_{\mathcal{A}}\left(z\right)\ge {\displaystyle \sum _{z\in V}}\underset{w\ne z}{\max }\left\{{\gamma }_{{\mathcal{B}}_i}\left(wz\right)\right\}.\hfill \end{array}$

Theorem 3.23. If $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ is a ⟨[a_i, b_i], c_i⟩-${\mathcal{B}}_i$-edge regular CFGS, for 1 ≤ i ≤ k, then

$\begin{array}{ll}\hfill & {\mathfrak{Q}}_{\alpha }\left(\mathcal{G}\right)={\displaystyle \sum _{i=1}^k}|E_i|a_i,\hfill \\ \hfill & {\mathfrak{Q}}_{\beta }\left(\mathcal{G}\right)={\displaystyle \sum _{i=1}^k}|E_i|b_i,\hfill \\ \hfill & {\mathfrak{Q}}_{\gamma }\left(\mathcal{G}\right)={\displaystyle \sum _{i=1}^k}|E_i|c_i.\hfill \end{array}$

Proof. The proof is obvious.

In the following theorem, we examine the relationship between a ${\mathcal{B}}_i$-vertex regular and a ${\mathcal{B}}_i$-edge regular in CFGS.

Theorem 3.24. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ to be a CFGS and ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant functions, for i = 1, 2, …, k. If $\mathcal{G}$ is a ${\mathcal{B}}_i$-vertex regular, then, $\mathcal{G}$ is a perfect ${\mathcal{B}}_i$-edge regular.

Proof. Suppose that $\mathcal{G}$ be a ⟨[a, b], c⟩-${\mathcal{B}}_i$-vertex regular CFGS so that ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant functions. Let ${\alpha }_{{\mathcal{B}}_i}(wz)=k$, ${\beta }_{{\mathcal{B}}_i}(wz)=m$, and ${\gamma }_{{\mathcal{B}}_i}(wz)=n$ for 1 ≤ i ≤ k. Then,

${\mathfrak{D}}_{{\mathcal{B}}_i}\left(z\right)=\langle \left[{\mathfrak{D}}_{{\alpha }_i}\left(z\right),{\mathfrak{D}}_{{\beta }_i}\left(z\right)\right],{\mathfrak{D}}_{{\gamma }_i}\left(z\right)\rangle =\langle \left[a,b\right],c\rangle ,forallz\in V.$

On the other hand, for all wz ∈ E_i,

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(w\right)+{\mathfrak{D}}_{{\alpha }_i}\left(z\right)-2{\alpha }_{{\mathcal{B}}_i}\left(wz\right)=a+a-2k=2\left(a-k\right),\hfill \\ \hfill & {\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(w\right)+{\mathfrak{D}}_{{\beta }_i}\left(z\right)-2{\beta }_{{\mathcal{B}}_i}\left(wz\right)=b+b-2m=2\left(b-m\right),\hfill \\ \hfill & {\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(w\right)+{\mathfrak{D}}_{{\gamma }_i}\left(z\right)-2{\gamma }_{{\mathcal{B}}_i}\left(wz\right)=c+c-2n=2\left(c-n\right).\hfill \end{array}$

Moreover, by the definition of total ${\mathcal{B}}_i$-edge degree,

$\begin{array}{ll}\hfill & \mathfrak{T}{\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(w\right)+{\mathfrak{D}}_{{\alpha }_i}\left(z\right)-{\alpha }_{{\mathcal{B}}_i}\left(wz\right)=a+a-k=2a-k,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(w\right)+{\mathfrak{D}}_{{\beta }_i}\left(z\right)-{\beta }_{{\mathcal{B}}_i}\left(wz\right)=b+b-m=2b-m,\hfill \\ \hfill & \mathfrak{T}{\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(w\right)+{\mathfrak{D}}_{{\gamma }_i}\left(z\right)-{\gamma }_{{\mathcal{B}}_i}\left(wz\right)=c+c-n=2c-n.\hfill \end{array}$

Then, $\mathcal{G}$ is a perfect ${\mathcal{B}}_i$-edge regular.

Theorem 3.25. Consider $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,\dots ,{\mathcal{B}}_k)$ to be a ${\mathcal{B}}_i$-vertex regular CFGS. If $\mathcal{G}$ is a ${\mathcal{B}}_i$-edge regular, then, ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant functions.

Proof. Suppose that $\mathcal{G}$ be a ⟨[k, m], n⟩-${\mathcal{B}}_i$-edge regular CFGS. So, ${\mathfrak{D}}_{{\alpha }_i}(wz)=k$, ${\mathfrak{D}}_{{\beta }_i}(wz)=m$, and ${\mathfrak{D}}_{{\gamma }_i}(wz)=n$, for 1 ≤ i ≤ k. According to the definition of ${\mathcal{B}}_i$-edge degree, for all wz ∈ E_i,

$\begin{array}{ll}\hfill & {\mathfrak{D}}_{{\alpha }_i}\left(wz\right)={\mathfrak{D}}_{{\alpha }_i}\left(w\right)+{\mathfrak{D}}_{{\alpha }_i}\left(z\right)-2{\alpha }_{{\mathcal{B}}_i}\left(wz\right)\Rightarrow k=2a-2{\alpha }_{{\mathcal{B}}_i}\left(wz\right)\Rightarrow {\alpha }_{{\mathcal{B}}_i}\left(wz\right)=\frac{2a-k}{2},\hfill \\ \hfill & {\mathfrak{D}}_{{\beta }_i}\left(wz\right)={\mathfrak{D}}_{{\beta }_i}\left(w\right)+{\mathfrak{D}}_{{\beta }_i}\left(z\right)-2{\beta }_{{\mathcal{B}}_i}\left(wz\right)\Rightarrow m=2b-2{\beta }_{{\mathcal{B}}_i}\left(wz\right)\Rightarrow {\beta }_{{\mathcal{B}}_i}\left(wz\right)=\frac{2b-m}{2},\hfill \\ \hfill & {\mathfrak{D}}_{{\gamma }_i}\left(wz\right)={\mathfrak{D}}_{{\gamma }_i}\left(w\right)+{\mathfrak{D}}_{{\gamma }_i}\left(z\right)-2{\gamma }_{{\mathcal{B}}_i}\left(wz\right)\Rightarrow n=2c-2{\gamma }_{{\mathcal{B}}_i}\left(wz\right)\Rightarrow {\gamma }_{{\mathcal{B}}_i}\left(wz\right)=\frac{2c-n}{2}.\hfill \end{array}$

Therefore, ${\alpha }_{{\mathcal{B}}_i}$, ${\beta }_{{\mathcal{B}}_i}$, and ${\gamma }_{{\mathcal{B}}_i}$ are constant functions.

4 Application

The transportation sector has its own importance in the economy of every country, which is well felt with the expansion of economic activities, the increase in national production, and the need to develop and improve transportation networks. Transportation in today’s human life is responsible for the safe, fast, economic movement of cargo, passengers, or information according to the environmental model. Transportation is one of the inevitable necessities of every human society, which causes the dynamics of economic and social development. The transportation component can and should be presented as a tool to achieve sustainable development. The transportation network importance in the social, economic, and even political and military structure of today’s societies is so urgent that experts consider it the foundation of sustainable development of any society. The transportation system is a set of devices, facilities, routes, rules, and regulations that are used to move people and goods.

All kinds of daily transportation methods are progressing, and their safety and comfort are improving. As you know, there are three methods of transportation including land, air, and sea, and the land-based transportation is divided into two branches of rail and road. Usually, most people use road transport to travel or move their cargo because it is both more economical and safer, but it takes more time than other methods.

Air-based transportation is a fast approach to move cargo and passengers that can make transfers in less than a few hours. However, the air-based transportation is less secure than other types of transportation methods and costs more. In the sea-based transportation that we often deal with ships and vessels, the security is well provided and the costs are reasonable, but the speed of the arrival of passengers or goods is very long. Usually, most people use the land and air to transfer cargo or travel.

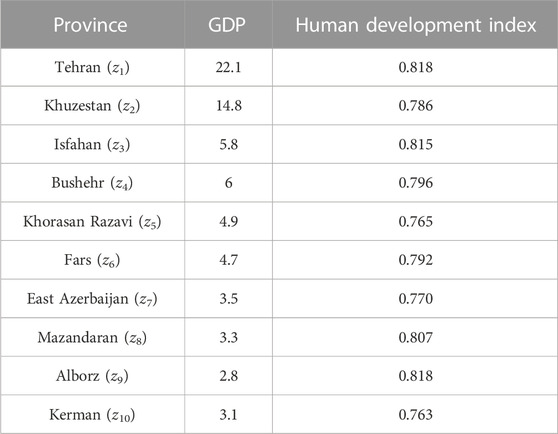
According to the data by Iran’s Statistics Center in 2018, more than 70% of the gross domestic product (GDP) was produced in the provinces of Tehran, Khuzestan, Isfahan, Bushehr, Khorasan Razavi, Fars, East Azerbaijan, Mazandaran, Alborz, and Kerman. The GDP and human development indexes are two factors that can determine the power of provinces in terms of capacity to accept goods and passengers. Table 2 shows the percentage of GDP and human development indexes in the mentioned provinces.

TABLE 2

TABLE 2. GDP and human development indexes of each province.

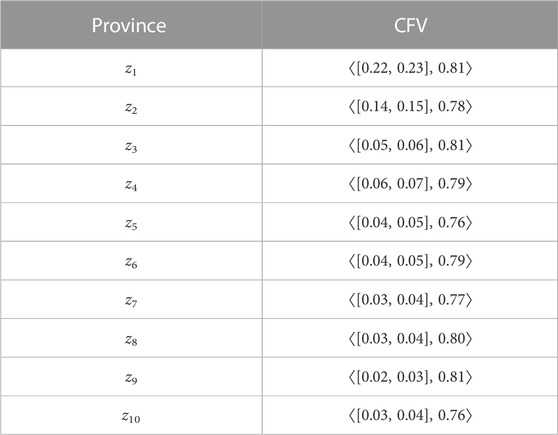
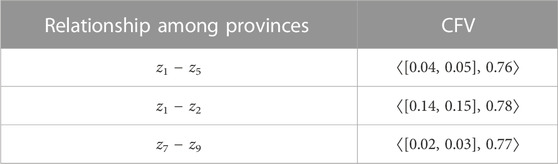
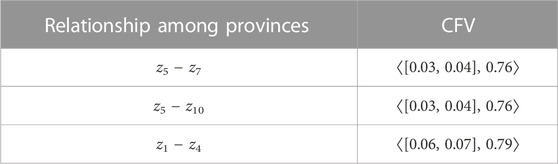
Table 3 shows the cubic fuzzy values (CFVs) of the mentioned provinces, which are expressed in the GDP with an interval-valued fuzzy number and the human development index with a fuzzy number.

TABLE 3

TABLE 3. CFVs of provinces.

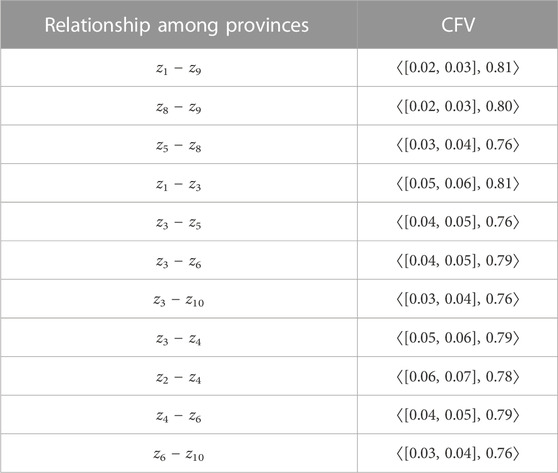
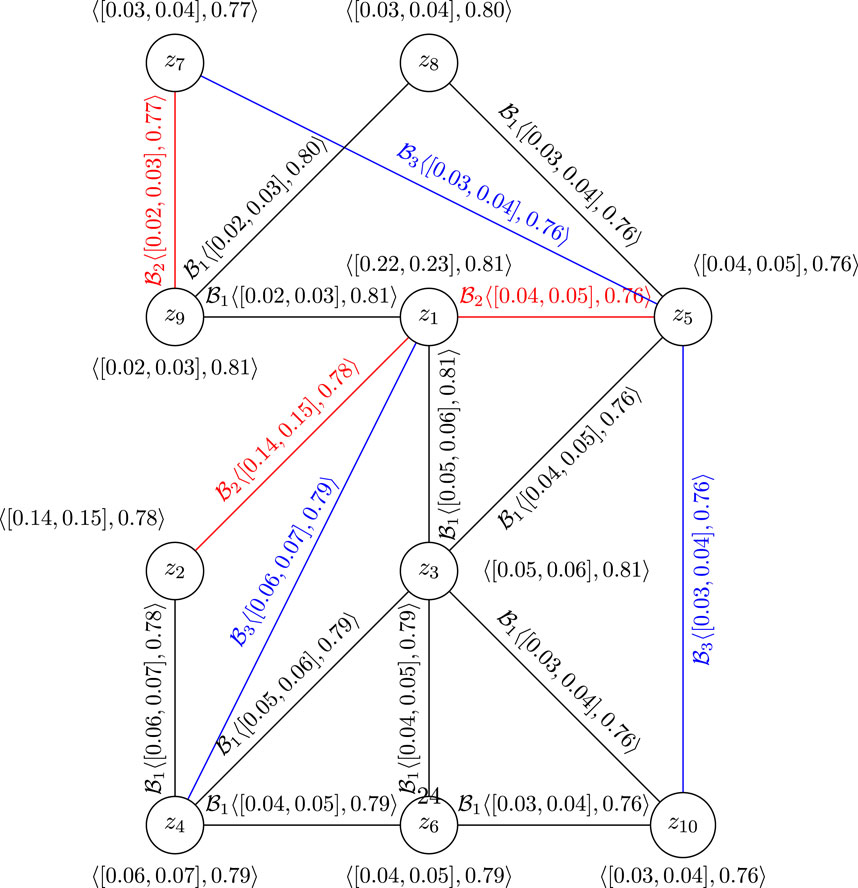
Considering the provinces as the vertices of a graph, we define the relationships between the vertices as follows:${\mathcal{B}}_1=$ provinces that often exchange goods and passengers by road.${\mathcal{B}}_2=$ provinces that often exchange goods and passengers by rail.${\mathcal{B}}_3=$ provinces that often exchange goods and passengers by air.

The CFVs of the connection between provinces corresponding to ${\mathcal{B}}_1$, ${\mathcal{B}}_2$, and ${\mathcal{B}}_3$ are calculated in Tables 4–6. Since there are usually different routes among provinces, in this study, the route that has the most exchange of passengers and goods is considered. With this assumption, it is clear that these paths are all strong.

TABLE 4

TABLE 4. CFVs attributed to the ${\mathcal{B}}_1$ relation.

TABLE 5

TABLE 5. CFVs attributed to the ${\mathcal{B}}_2$ relation.

TABLE 6

TABLE 6. CFVs attributed to the ${\mathcal{B}}_3$ relation.

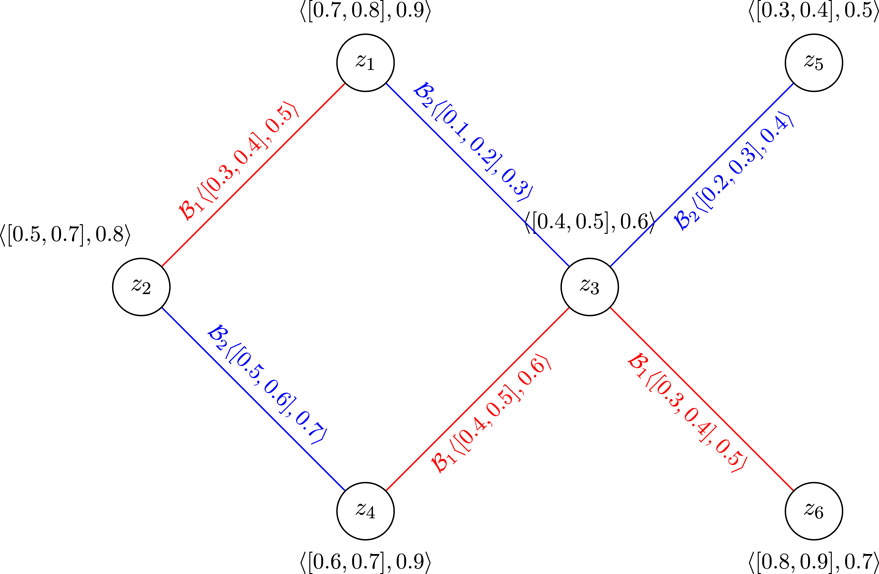
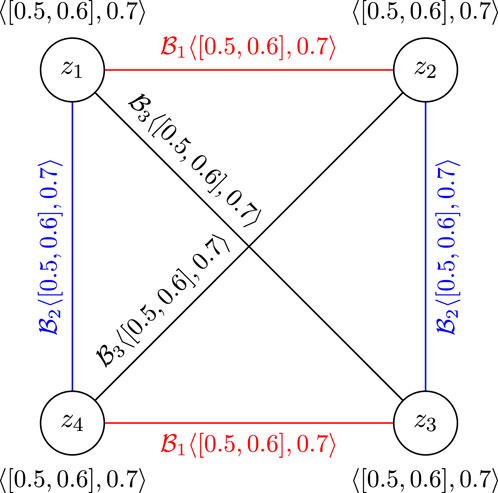
Now, we can explain the situation of passenger and goods transportation among the mentioned provinces by a CFGS, as shown in Figure 5.

FIGURE 5

FIGURE 5. CFGS $\mathcal{G}=(\mathcal{A},{\mathcal{B}}_1,{\mathcal{B}}_2,{\mathcal{B}}_3)$.

In Figure 5, by removing the z₁z₄ edge, we will have a ${\mathcal{B}}_3$-edge regular CFGS. As can be seen, most of the transportation routes of goods and passengers are by road. In general, the elements of security, price, and speed are mostly different among the transportation methods. It is usually suggested to use the land-based transportation method, which consists of rail and road, because they are more economical and safer. It is better to use air for travel or quick transfer of goods, and the sea route for security and access to impossible places.

5 Conclusion

The cubic fuzzy graph structure (CFGS) is an opportunity to model problems that have two values of the fuzzy and interval membership in uncertain issues and have a variety of relationships among them. The lack of research on the concepts of edge regularity in graphs led us to investigate the edge regularity in the CFGS and to study some of its properties. In this context, a comparative study between edge regular and total edge regularity in a CFGS with necessary and sufficient conditions is provided. All the results are expressed in the form of a cubic fuzzy number in order to provide the possibility of comparison to different degrees. The results show that there is a direct relationship between the regularity of the edges and the membership value of the vertices. The observations indicate a direct relationship between the edge membership functions and edge regularity. The obtained results show that the constancy of the membership functions of the edge results in the edge regularity of the CFGS and vice versa. Meanwhile, some properties are not always true. In the presented application, it was found that a ${\mathcal{B}}_i$-edge regular CFGS was obtained by removing some ${\mathcal{B}}_i$-edges. In our future work, we will further categorize product operations in CFGS.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

XS and SK conceived and designed the experiments; AT performed the experiments; SS and AT analyzed the data; SK and SS contributed reagents/materials/analysis tools; XS wrote the paper. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Key R&D Program of China (grant no. 2019YFA0706402) and the National Natural Science Foundation of China under grant nos 62172302, 62072129, and 61876047.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zadeh LA. Fuzzy sets. Inf Control (1965) 8:338–53. doi:10.1016/S0019-9958(65)90241-X

CrossRef Full Text | Google Scholar

2. Rosenfeld A. Fuzzy graphs, fuzzy sets and their applications. New York, NY, USA: Academic Press (1975). p. 77–95.

CrossRef Full Text | Google Scholar

3. Talebi AA. Cayley fuzzy graphs on the fuzzy groups. Comput Appl Math (2018) 37(4):4611–32. doi:10.1007/s40314-018-0587-5

CrossRef Full Text | Google Scholar

4. Atanassov K. Intuitionistic fuzzy sets. Fuzzy Sets Syst (1986) 20:87–96. doi:10.1016/s0165-0114(86)80034-3

CrossRef Full Text | Google Scholar

5. Borzooei RA, Rashmanlou H. Ring sum in product intuitionistic fuzzy graphs. J Adv Res Pure Math (2015) 7(1):16–31. doi:10.5373/jarpm.1971.021614

CrossRef Full Text | Google Scholar

6. Akram M, Dudek WA. Interval-valued fuzzy graphs. Comput Math Appl (2011) 61(2):289–99. doi:10.1016/j.camwa.2010.11.004

CrossRef Full Text | Google Scholar

7. Talebi AA, Rashmanlou H, Sadati SH. New concepts on m-polar interval-valued intuitionistic fuzzy graph. TWMS J Appl Eng Math (2020) 10(3):808–16.

Google Scholar

8. Talebi AA, Rashmanlou H, Sadati SH. Interval-valued intuitionistic fuzzy competition graph. J Multiple-Valued Logic Soft Comput (2020) 34:335–64.

Google Scholar

9. Rashmanlou H, Jun YB, Borzooei RA. More results on highly irregular bipolar fuzzy graphs. Ann Fuzzy Math Inform (2014) 8(1):149–68.

Google Scholar

10. Zeng S, Shoaib M, Ali S, Smarandache F, Rashmanlou H, Mofidnakhaei F. Certain properties of single-valued neutrosophic graph with application in food and agriculture organization. Int J Comput Intell Syst (2021) 14(1):1516–40. doi:10.2991/ijcis.d.210413.001

CrossRef Full Text | Google Scholar

11. Kosari S, Rao Y, Jiang H, Liu X, Wu P, Shao Z. Vague graph structure with application in medical diagnosis. Symmetry (2020) 12(10):1582. doi:10.3390/sym12101582

CrossRef Full Text | Google Scholar

12. Rao Y, Kosari S, Shao Z. Certain properties of vague graphs with a novel application. Mathematics (2020) 8(10):1647. doi:10.3390/math8101647

CrossRef Full Text | Google Scholar

13. Shi X, Kosari S. Certain properties of domination in product vague graphs with an application in medicine. Front Phys (2021) 9:680634. doi:10.3389/fphy.2021.680634

CrossRef Full Text | Google Scholar

14. Akram M, Siddique S, Alcantud JCR. Connectivity indices of m-polar fuzzy network model, with an application to a product manufacturing problem. Artif Intelligence Rev (2022) 1–44. doi:10.1007/s10462-022-10360-9

CrossRef Full Text | Google Scholar

15. Akram M, Siddique S, Alharbi MG. Clustering algorithm with strength of connectedness for m-polar fuzzy network models. Math Biosciences Eng (2022) 19(1):420–55. doi:10.3934/mbe.2022021

CrossRef Full Text | Google Scholar

16. Akram M, Zafar F. A new approach to compute measures of connectivity in rough fuzzy network models. J Intell Fuzzy Syst (2019) 36(1):449–65. doi:10.3233/jifs-181751

CrossRef Full Text | Google Scholar

17. Ahmad U, Nawaz I, Broumi S. Connectivity index of directed rough fuzzy graphs and its application in traffic flow network. Granular Comput (2023) 1–22. doi:10.1007/s41066-023-00384-z

CrossRef Full Text | Google Scholar

18. Pramanik T, Muhiuddin G, Alanazi AM, Pal M. An extension of fuzzy competition graph and its uses in manufacturing industries. Mathematics (2020) 8(6):1008. doi:10.3390/math8061008

CrossRef Full Text | Google Scholar

19. Sampathkumar E. Generalized graph structures. Bull Kerala Math Assoc (2006) 3(2):65–123.

Google Scholar

20. Dinesh T. A study on graph structures, incidence algebras and their fuzzy analogues (2011).

Google Scholar

21. Dinesh T, Ramakrishnan T. On generalised fuzzy graph structures. Appl Math Sci (2011) 5(4):173–80.

Google Scholar

22. Akram M, Akram M. m–Polar fuzzy graph structures. In: M– polar fuzzy graphs: Theory, methods and applications (2019). p. 209–33.

CrossRef Full Text | Google Scholar

23. Akram M, Akmal R. Intuitionistic fuzzy graph structures. Kragujevac J Math (2017) 41(2):219–37. doi:10.5937/kgjmath1702219a

CrossRef Full Text | Google Scholar

24. Kou Z, Akhoundi M, Chen X, Omidi S. A study on vague graph structures with an application. Adv Math Phys (2022) 2022, 1–14. doi:10.1155/2022/3182116

CrossRef Full Text | Google Scholar

25. Akram M, Sitara M. Decision-making with q-rung orthopair fuzzy graph structures. Granular Comput (2022) 7(3):505–26. doi:10.1007/s41066-021-00281-3

CrossRef Full Text | Google Scholar

26. Koam AN, Akram M, Liu P. Decision-making analysis based on fuzzy graph structures. Math Probl Eng (2020) 2020:1–30. doi:10.1155/2020/6846257

CrossRef Full Text | Google Scholar

27. Jun YB, Kim CS, Yang KO. Cubic sets. Ann Fuzzy Math Inform (2012) 4(1):83–98.

Google Scholar

28. Jun YB, Smarandache F, Kim CS. Neutrosophic cubic sets. New Math Nat Comput (2017) 13(01):41–54. doi:10.1142/s1793005717500041

CrossRef Full Text | Google Scholar

29. Gulistan M, Ali M, Azhar M, Rho S, Kadry S. Novel neutrosophic cubic graphs structures with application in decision making problems. IEEE access (2019) 7:94757–78. doi:10.1109/access.2019.2925040

CrossRef Full Text | Google Scholar

30. Muhiuddin G, Alanazi AM, Mahboob A, Alkhaldi AH, Alatwai W. A Novel Study of Graphs Based on -Polar Cubic Structures. J Funct Spaces (2022) 2022, 1–12. doi:10.1155/2022/2643575

CrossRef Full Text | Google Scholar

31. Rashid S, Yaqoob N, Akram M, Gulistan M. Cubic graphs with application. Int J Anal Appl (2018) 16(5):733–50.

Google Scholar

32. Muhiuddin G, Takallo MM, Jun YB, Borzooei RA. Cubic graphs and their application to a traffic flow problem. Int J Comput Intelligence Syst (2020) 13(1):1265–80. doi:10.2991/ijcis.d.200730.002

CrossRef Full Text | Google Scholar

33. Rashmanlou H, Muhiuddin G, Amanathulla SK, Mofidnakhaei F, Pal M. A study on cubic graphs with novel application. J Intell Fuzzy Syst (2021) 40(1):89–101. doi:10.3233/jifs-182929

CrossRef Full Text | Google Scholar

34. Gani AN, Radha K. On regular fuzzy graphs. J Phys Sci (2008) 12:33–40.

Google Scholar

35. Samanta S, Pal M. Irregular bipolar fuzzy graphs (2012). p. 1682. ArXiv, (1209).

Google Scholar

36. Borzooei RA, Rashmanlou H, Samanta S, Pal M. Regularity of vague graphs. J Intell Fuzzy Syst (2016) 30(6):3681–9. doi:10.3233/ifs-162114

CrossRef Full Text | Google Scholar

37. Nagooani A, Latha SR. Isomorphism on irregular fuzzy graphs. Int J Math Sci Eng Appl (2012) 6(3):193–208.

Google Scholar

38. Radha K, Kumaravel N. On edge regular fuzzy graphs. Int J Math Arch (2004) 5:100–12.

Google Scholar

39. Cary M. Perfectly regular and perfectly edge-regular fuzzy graphs. Ann Pure Appl Math (2018) 16(2):461–9. doi:10.22457/apam.v16n2a24

CrossRef Full Text | Google Scholar

40. Karunambigai MG, Sivasankar S, Palanivel K. Some properties of a regular intuitionistic fuzzy graph. Int J Math Comput (2015) 26(4):53–61.

Google Scholar

41. Krishna KK, Rashmanlou H, Talebi AA, Mofidnakhaei F. Regularity of cubic graph with application. J Indonesian Math Soc (2019) 1–15. doi:10.22342/jims.25.1.607.1-15

CrossRef Full Text | Google Scholar

42. Rao Y, Akhoundi M, Talebi AA, Sadati SH. The maximal product in cubic fuzzy graph structures with an application. Int J Comput Intelligence Syst (2023) 16(1):18. doi:10.1007/s44196-023-00193-x

CrossRef Full Text | Google Scholar

43. Shi X, Akhoundi M, Talebi AA, Sadati SH. Some properties of cubic fuzzy graphs with an application. Symmetry (2022) 14(12):2623. doi:10.3390/sym14122623

CrossRef Full Text | Google Scholar

44. Li L, Kosari S, Sadati SH, Talebi AA. Concepts of vertex regularity in cubic fuzzy graph structures with an application. Front Phys (2023) 10:1324. doi:10.3389/fphy.2022.1087225

CrossRef Full Text | Google Scholar