- 1College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, China
- 2Collaborative Innovation Center of Novel Software Technology and Industrialization, Nanjing, China
- 3School of Computer Science and Engineering, Southeast University, Nanjing, China
- 4Key Laboratory of Computer Network and Information Integration, Ministry of Education, Southeast University, Nanjing, China
Quantum secret sharing (QSS) protocols without entanglement have showed high security by virtue of the characteristics of quantum mechanics. However, it is still a challenge to compare the security of such protocols depending on quantitative security analysis. Based on our previous security analysis work on protocols using single qubits and two-level unitary operations, QSS protocols with single qutrits and three-level unitary operations are considered in this paper. Under the Bell-state attack we propose, the quantitative security analyses according to different three-level unitary operations are provided respectively in the one-step and two-step situations. Finally, important conclusions are drawn for designing and implementing such QSS protocols. The method and results may also contribute to analyze the security of other high-level quantum cryptography schemes based on unitary operations.
1 Introduction
Quantum secret sharing (QSS) is an important branch of quantum cryptography, whose security is based on the fundamental principle of quantum mechanics. It can share both the classical message [1–11] and quantum information [12–22]. Taking QSS protocols for classical message sharing into account, it is observed that it is a more efficient and lower cost way to use single particles instead of entangled particles. In addition, to achieve the unconditional security (in theory) and the ability of detecting eavesdropping, unitary operations are always used in such protocols. The classical secret message is encoded into quanta and/or scrambles the particles by unitary operations so that the eavesdropper cannot reliably identify each quantum state by appropriate measurement.
The quantitative security analysis of such protocols can be transformed into a quantitative calculation of unitary operation security. The feasibility of this idea has been proven by our pioneering work [23]. In [23], we proposed the substitute-Bell-state attack and the definition of minimum failure probability for the attack. Thus, the quantitative security analysis can be conducted according to the different selection methods of unitary operations. Several cases of two-level unitary operations were analyzed in [23] and more two-level cases are considered in our recent research [24].
However, these works on the security analysis of QSS are focused on the qubit system. In many scenarios, quantum communication protocols using high-dimensional states demonstrate larger capacity and better performance than the qubit system. Thus, it is worth studying the security of QSS protocols beyond the two-level system. Quantitative security analysis of QSS protocols remains a tough problem, and our pioneering idea is worth recommending. However, the research work based on this idea is not sufficient. In this paper, the security of QSS protocols using three-level unitary operations is analyzed quantitatively, and some comparisons between two-level and three-level situations are made. Finally, valuable conclusions are obtained, which can guide the designing and implementation of QSS protocols with single qutrits.
2 The security of unitary operations in quantum secret sharing protocols based on qutrits
2.1 Three-level Bell states and unitary operations
In a three-level quantum system, we call a single quantum state as a qutrit. The Z-basis of a three-level quantum system is
where
where
To analyze the security of QSS protocols based on qutrits quantitatively, we design the Bell-state attack, which uses three-level Bell states and unitary operations. In a
where
Without loss of generality, the first Bell state
where
A unitary operation is a bounded linear operation
Without the loss of generality, we select the first situation as an example for research.
Next, to measure the security of different unitary operations, we first provide a general QSS protocol based on qutrits, and then propose the so-called Bell-state attack and state the minimum failure probability for this attack. The quantitative computing results show how to select appropriate three-level unitary operations to protect the QSS protocols against a Bell-state attack.
2.2 A general quantum secret sharing protocol based on qutrits
A generic QSS protocol based on qutrits is shown in Figure 1 (it is supposed to be a (n, n) secret sharing threshold protocol). The procedure is as follows:
(1) First, Alice prepares qutrits all in
(2) After that, the qutrit sequence, denoted as
(3) Bob 1 to Bob n perform local three-level unitary operations according to the values of
(4) Bob n sends the qutrits back to Alice. Then, Bob 1 to Bob n declare the information about individual unitary operations (not unitary operations themselves) via classical communication.
(5) Alice measures the qutrits using proper bases according to the information and publishes the result.
(6) Only when all the Bobs collaborate together, the secret can be revealed. Sample detection can be implemented by classical communication to judge if there is a wiretap.
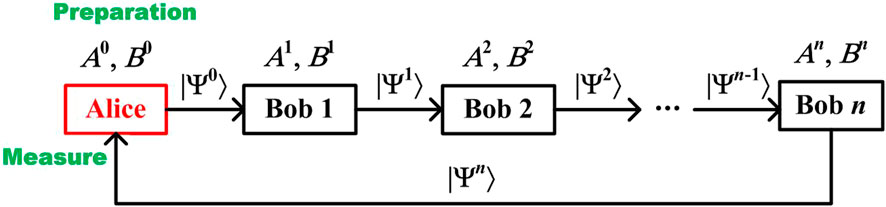
FIGURE 1. A general QSS protocol based on single states. Binary string
In addition, unitary operations can be executed in one or two steps, which were defined in our previous work, shown as follows [23].
Definition 1. (one-step unitary operation): Bob i performs once a random local unitary operation on each quantum state before sending. All possible options are put into “{}”, called a unitary operation set.
Definition 2. (two-step unitary operation): Bob i performs twice a random local unitary operation on each quantum state before sending, and the probability of the first and second operations being the same is zero. The symbol “{; }” is used to indicate the two-step unitary operation, while the first possible options are listed before the semicolon, and the subsequent options, after the semicolon.
2.3 Bell-state attack in a three-level quantum system
Bob i is supposed to be dishonest during the execution of the three-level QSS protocol. He aims to generate a Bell-state attack to obtain the integrated encoded information from Bob i+1 to Bob j. The schematic diagram of the Bell-state attack is illustrated in Figure 2 (which is a variant of the substitute-Bell-state attack [23]), and the procedure of the attack is as follows:
(1) Bob
(2) Bob
(3) Bob
(4) The particle sequences
(5) When samples are tested, Bob
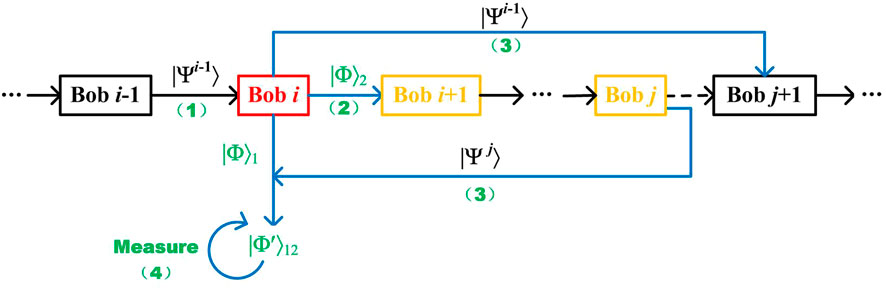
FIGURE 2. Schematic diagram of Bell-state attack from Bob i for the integrated encoding information from Bob i+1 to Bob j.
It should be noted that Bob j can also be Bob i+1, and in this situation, Bob i aims only to obtain the unitary operations that Bob
Now, the key question is how to measure the effect of the Bell-state attack? To determine this, we pick up the minimum failure probability formula that we put forward previously [23, 24].
Definition 3. (minimum failure probability): Assume that a QSS protocol based on single qutrits is under a Bell-state attack. The attacker has acquired N new two-qutrit states
Apparently,
2.4 The security of one-step three-level unitary operations
To research the security of three-level unitary operations under a Bell-state attack, we first provide the nine unitary operations corresponding to nine Bell states (shown in Formula 4) in Formula 8. In other words, the nine Bell states can be obtained when the second qutrit of the initial state
where
Moreover, without the loss of generality,
It should be noted that
Here is the explanation of why
Finally, there are seven sets of one-step three-level unitary operations corresponding to the aforementioned matrices, and the minimum failure probability
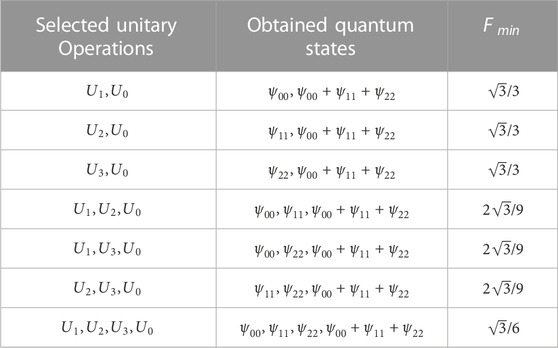
TABLE 1. The minimum failure probability of Bell-state attack under one-step three-level unitary operations. The quantum states are obtained from the different transformations of initial state
From Table 1, we can conclude the following:
(1) If the four unitary operations of
(2) Based on the aforementioned analysis, the minimum failure probability formula in a three-level quantum system can be simplified as follows:
where N denotes the number of selected unitary operations. For the six situations listed in Formula 6, if we choose the other five situations and corresponding
2.5 The security of two-step three-level unitary operations
The one-step unitary operation case is mentioned previously. We try the similar analysis in a two-step unitary operation instance.
First of all, according to the definition of a two-step unitary operation and the selected four unitary operations
1.
2.
3.
4.
Here, the first possible unitary operations are listed before the semicolon, and the subsequent operations, after the semicolon; the symbol “
Second, we provide the states after continuous action of two unitary operations (shown in Table 2), supposing the initial state is
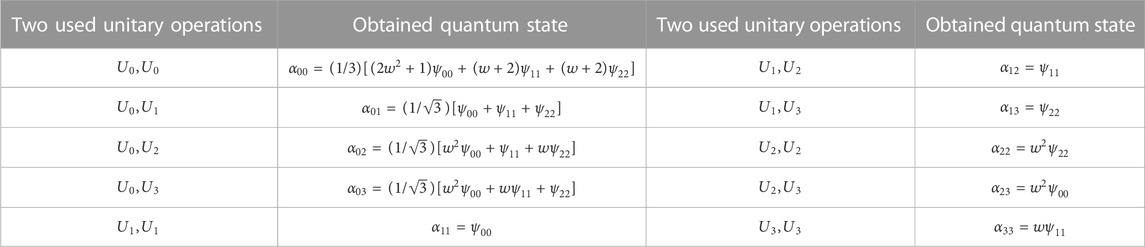
TABLE 2. The states after continuous action of two unitary operations. The two subscripts of
Third, to calculate
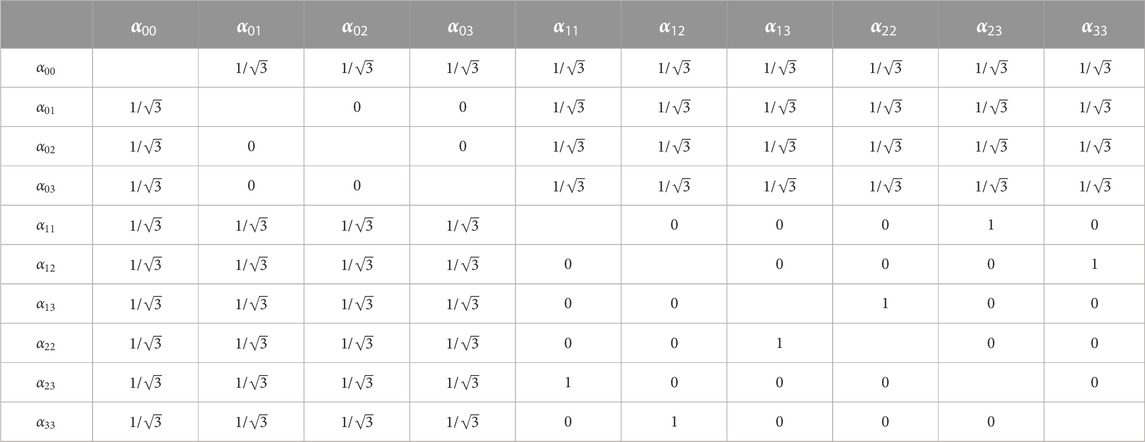
TABLE 3. The norm of inner product of the two quantum states. The inner product values are symmetric about the diagonal.
From Table 3 we can see that the inner product values are symmetric about the diagonal and the inner product values between
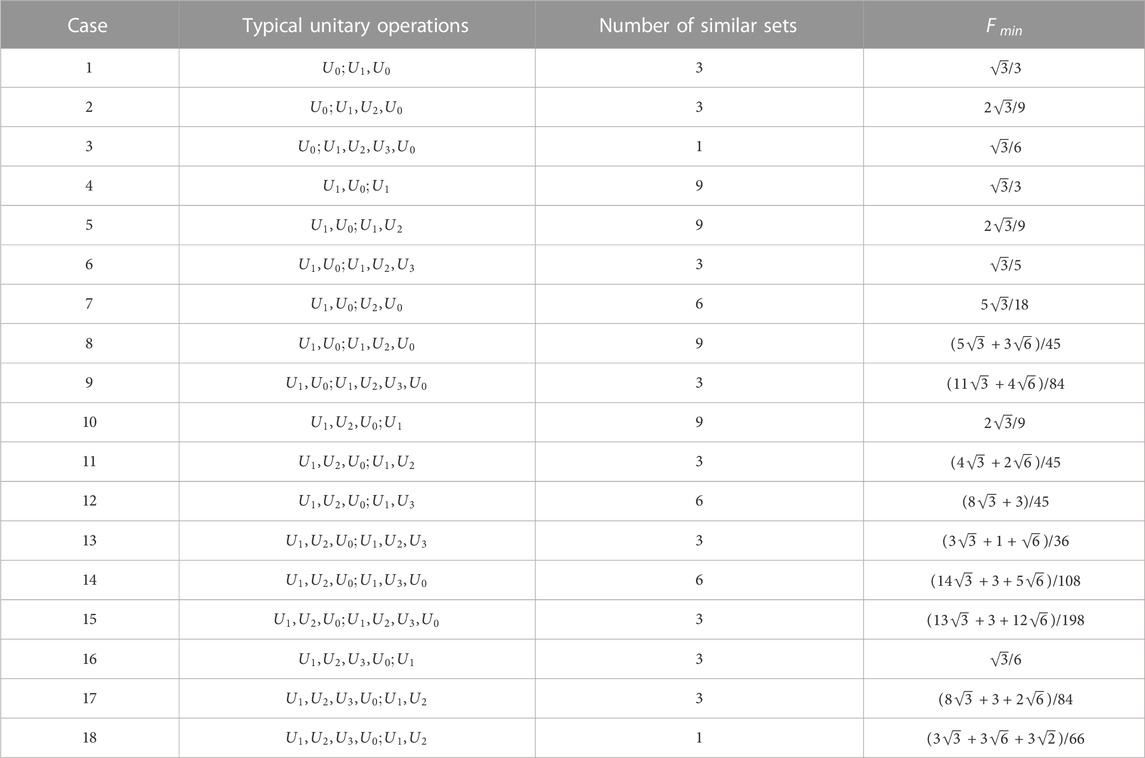
TABLE 4. The values of
From Table 4, it can be seen that the values of
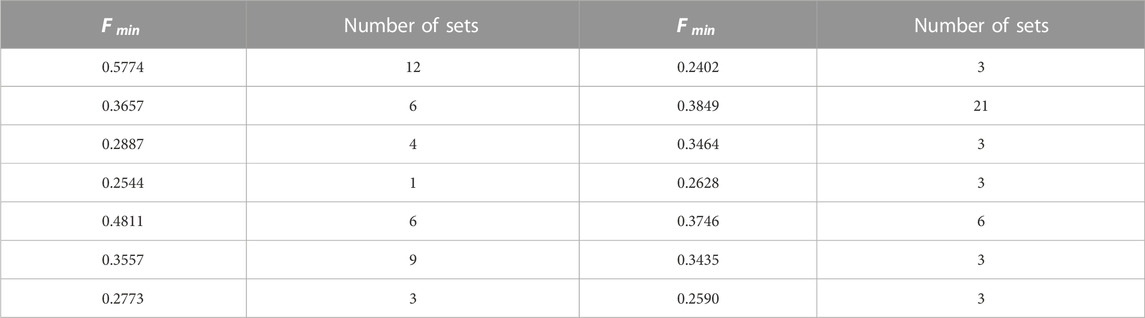
TABLE 5. The values of
The results in Table 5 are also illustrated in Figure 3 for clarity. Then, some conclusions can be drawn based on the results.
(1) Among the two-step three-level unitary operations, the minimum failure probability of the Bell-state attack densely distributed between [0.34, 0.39], totally 48 sets, and there are 17 sets between [0.24, 0.29]. Furthermore, 12 sets have the highest value of
(2) The sets that have the highest value of
(3) Among the six situations shown in Formula 6, if another situation is selected, that is, another Bell-state combination and corresponding
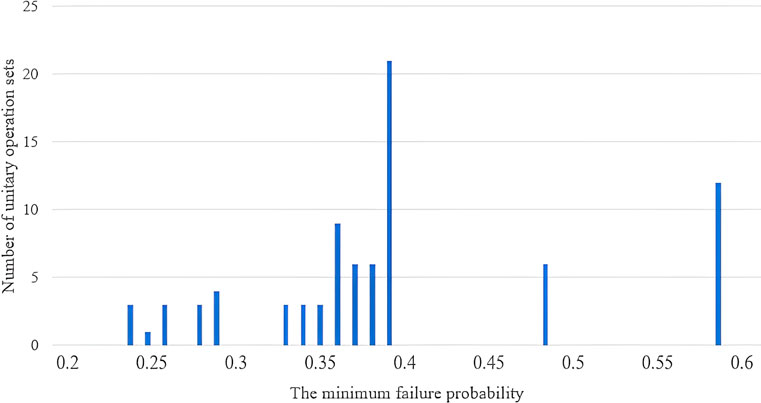
FIGURE 3. The minimum failure probability of two-step three-level unitary operations. The values of
2.6 The selection of three-level unitary operations
Based on the quantitative computing results and analysis on one-step and two-step unitary operations in a three-level system, the selection rules of unitary operations are summarized as follows:
(1) The unitary operations in QSS protocols based on qutrits should be chosen carefully. First, the unitary operations whose
(2) More complex unitary operations cannot be counted on to generate higher security. In a one-step unitary operation, Max [
(3) When the same unitary operations are selected, the security of two-step unitary operations is not necessarily higher than that of one-step unitary operations. There exist possibilities. For example,
(4) The maximum of
In brief, we should choose the unitary operation sets that have a higher value of
3 Conclusion
In this paper, we first present a general QSS protocol based on single qutrits, and then propose the Bell-state attack and the definition of minimum failure probability for the attack. In this way, QSS protocols based on single qutrits and three-level unitary operations are considered, and the quantitative security analysis is performed corresponding to different sets of four three-level unitary operations. The results show that the selection of unitary operations will significantly affect the security of such QSS protocols. As a result, some crucial rules for choosing unitary operations are given to ensure the security or achieve a higher security. This work can serve as an important guidance in designing and implementing QSS protocols based on single qutrits and three-level unitary operations. The method and results may also contribute to analyze the security of other high-level quantum cryptography protocols based on unitary operations, such as secure computation [25], quantum secure direct communication [26], quantum key agreement [27], quantum private query [28], and quantum oblivious transfer [29]. Furthermore, unitary operations are also used in other quantum algorithms, for example, the quantum blockchain algorithm [30] and quantum artificial intelligence algorithm [31], and it will be interesting in attempting to analyze their security using our method.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
JX, XL, and ZL conceived the presented idea. YH and YZ verified the methods and developed the analyses. ZZ and YS completed the calculation. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by the National Natural Science Foundation of China (Grant nos 62201252 and 62071240), the Innovation Program for Quantum Science and Technology (Grant no. 2021ZD0302900), and the Natural Science Foundation of Jiangsu Province, China (Grant no. BK20220804).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Matsumoto R. Message randomization and strong security in quantum stabilizer-based secret sharing for classical secrets. Des Code Cryptogr (2020) 88:1893–907. doi:10.1007/s10623-020-00751-w
2. Zhang Z, Li Y, Man Z. Multiparty quantum secret sharing. Phys Rev A (2005) 71:044301. doi:10.1103/physreva.71.044301
3. Tavakoli A, Herbauts I, Zukowski M, Bourennane M. Secret sharing with a single d-level quantum system. Phys Rev A (2015) 92:030302. doi:10.1103/PhysRevA.92.030302
4. Karimipour V, Asoudeh M. Quantum secret sharing and random hopping: Using single states instead of entanglement. Phys Rev A (2015) 92:030301. doi:10.1103/PhysRevA.92.030301
5. Lin SS, Guo G, Xu Y, Sun Y, Liu X. Cryptanalysis of quantum secret sharing with d-level single particles. Phys Rev A (2016) 93:062343. doi:10.1103/PhysRevA.93.062343
6. Li Z, Li Q, Liu C, Peng Y, Chan WH. Limited resource semiquantum secret sharing. Quan Inf Process (2018) 17(10):285. doi:10.1007/s11128-018-2058-8
7. Tsai C, Chang Y, Lai Y, Yang CW. Cryptanalysis of limited resource semi-quantum secret sharing. Quan Inf Process (2020) 19(8):224–8. doi:10.1007/s11128-020-02690-w
8. Hu Z, Chen C, Zhang Z, Zhang H. Secure cooperative transmission for mixed RF/FSO spectrum sharing networks. IEEE Trans Commun (2020) 68(5):3010–23. doi:10.1109/tcomm.2020.2971483
9. Hu WW, Zhou RG, Li X, Fan P, Tan C. A novel dynamic quantum secret sharing in high-dimensional quantum system. Quan Inf Process (2021) 20:159–28. doi:10.1007/s11128-021-03103-2
10. Tian Y, Li J, Chen XB, Ye CQ, Li HJ. An efficient semi-quantum secret sharing protocol of specific bits. Quan Inf Process (2021) 20(6):217. doi:10.1007/s11128-021-03157-2
11. Tsai CW, Yang CW, Lin J. Multiparty mediated quantum secret sharing protocol. Quan Inf Process (2022) 21(2):63. doi:10.1007/s11128-021-03402-8
12. Dou Z, Xu G, Chen XB, Liu X, Yang YX. A secure rational quantum state sharing protocol. Sci China Inf Sci (2018) 61:022501. doi:10.1007/s11432-016-9151-x
13. Zha X, Jiang R, Wang M. Two schemes of multiparty quantum direct secret sharing via a six-particle GHZ state. Commun Theor Phys (2020) 72(2):025102. doi:10.1088/1572-9494/ab5d01
14. Wang J, Li L, Peng H, Yang Y. Quantum-secret-sharing scheme based on local distinguishability of orthogonal multiqudit entangled states. Phys Rev A (2017) 95:022320. doi:10.1103/physreva.95.022320
15. Lipinska V, Murta G, Ribeiro J, Wehner S. Verifiable hybrid secret sharing with few qubits. Phys Rev A (2020) 101(3):032332. doi:10.1103/physreva.101.032332
16. Zhang K, Zhang X, Jia H, Zhang L. A new n-party quantum secret sharing model based on multiparty entangled states. Quan Inf Process (2019) 18(3):81. doi:10.1007/s11128-019-2201-1
17. Shi R. Useful equations about Bell states and their applications to quantum secret sharing. IEEE Commun Lett (2019) 24(2):386–90. doi:10.1109/lcomm.2019.2954134
18. Qin H, Wallace T, Raylin T. Hierarchical quantum secret sharing based on special high-dimensional entangled state. IEEE J Sel Top Quant (2020) 26(3):6600106. doi:10.1007/s11128-019-2571-4
19. Sutradhar K, Om H. Efficient quantum secret sharing without a trusted player. Quan Inf Process (2020) 19(2):73. doi:10.1007/s11128-019-2571-4
20. Habibidavijani M, Barry S. Continuous-variable ramp quantum secret sharing with Gaussian states and operations. New J Phys (2019) 21(11):113023. doi:10.1088/1367-2630/ab4d9c
21. Yang Y, Ga S, Li D, Zhou YH, Shi WM. Three-party quantum secret sharing against collective noise. Quan Inf Process (2019) 18(7):215. doi:10.1007/s11128-019-2319-1
22. Wang Y, Lou X, Fan Z, Wang S, Huang G. Verifiable multi-dimensional (t,n) threshold quantum secret sharing based on quantum walk. Int J Theor Phys (2022) 61(2):24.doi:10.1007/s10773-022-05009-w
23. Xu J, Chen H, Liu W, Liu Z. Selection of unitary operations in quantum secret sharing without entanglement. Sci China Inf Sci (2011) 54:1837–42. doi:10.1007/s11432-011-4240-9
24. Xu J, Xi L, Liu Z, Zhou Y, Han Y, Chen D, et al. Quantitative security analysis of two-level unitary operations in quantum secret sharing protocols based on single qubits (2023).
25. Tan X, Zhang X, Song T. Verifiable delegated quantum computation with χ-type entangled states. Comput Stand Inter (2017) 54:36–40. doi:10.1016/j.csi.2016.09.008
26. Zou Z, Zhou L, Zhong W, Sheng Y. Measurement-device-independent quantum secure direct communication of multiple degree of freedom of a single photon. Sci China Phys Mech (2020) 63:230362. doi:10.1007/s11433-019-1450-8
27. Li L, Li Z. A multi-party quantum key agreement protocol based on Shamir’s secret sharing. Intj Theor Phys (2019) 58:3081–90. doi:10.1007/s10773-019-04187-4
28. Yang Y, Gao S, Li D, Zhou Y, Shi W. Three-party quantum secret sharing against collective noise. Quan Inf Process (2019) 18:215. doi:10.1007/s11128-019-2319-1
29. Zhang X, Wei C, Qin S, Gao F, Wen Q. Practical efficient 1-out-of-n quantum oblivious transfer protocol. Quan Inf Process (2023) 22(2):99. doi:10.1007/s11128-022-03817-x
30. Gao XX, Xu J, Fan JH. A novel quantum byzantine consensus protocol based on malicious node prevention mechanism. In: 2022 International Conference on Blockchain Technology and Information Security; July 15-17, 2022; Huaihua (2022).
Keywords: quantum cryptography, quantum secret sharing, three-level unitary operation, quantitative security analysis, qutrit
Citation: Xu J, Li X, Han Y, Zhou Y, Liu Z, Zhang Z and Song Y (2023) Quantitative security analysis of three-level unitary operations in quantum secret sharing without entanglement. Front. Phys. 11:1213153. doi: 10.3389/fphy.2023.1213153
Received: 27 April 2023; Accepted: 23 May 2023;
Published: 19 June 2023.
Edited by:
Weibin Li, University of Nottingham, United KingdomReviewed by:
Lihua Gong, Nanchang University, ChinaSu-Juan Qin, Beijing University of Posts and Telecommunications (BUPT), China
Copyright © 2023 Xu, Li, Han, Zhou, Liu, Zhang and Song. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Juan Xu, anVhbnh1QG51YWEuZWR1LmNu
 Juan Xu
Juan Xu Xi Li3
Xi Li3 Yunguang Han
Yunguang Han Zhihao Liu
Zhihao Liu Zhengye Zhang
Zhengye Zhang