- 1Department of Mechanical Engineering, School of Mechanical and Manufacturing Engineering (SMME), National University of Sciences and Technology (NUST), Islamabad, Pakistan
- 2Department of Mathematics and Statistics, Riphah International University, Islamabad, Pakistan
- 3Department of Intelligent Mechatronics Engineering, Sejong University, Seoul, Republic of Korea
- 4Department of Scientific Computing, Pukyong National University, Busan, Republic of Korea
- 5Interdisciplinary Biology Laboratory (iBLab), Division of Biological Science, Graduate School of Science, Nagoya University, Nagoya, Japan
- 6Department of Mathematics and Institute of Mathematical Science, Pusan National University, Busan, Republic of Korea
- 7Finance Fishery Manufacture Industrial Mathematics Center on BigData, Pusan National University, Busan, Republic of Korea
The dependent or independent variables of differential equations may be reduced by applying its associated Lie point symmetries. Seven-dimensional Lie point symmetry algebra exists for differential equations representing heat transfer in a boundary layer flow in the presence of radiation. The linear combinations of these seven Lie symmetries are used first to deduce the invariants and then derive the Lie similarity transformations for the original set of partial differential equations (PDEs). This procedure is repeated for the set of transformed equations to further reduce the system of PDEs into the system of ordinary differential equations (ODEs). Multiple exact similarity transformations are obtained using this procedure. All these transformations map the system of three PDEs with three independent variables of flow and heat transfer under the specified set of conditions into two-dimensional systems of equations with only one independent variable, the system of ODEs. Approximate solutions for these reduced systems are established using the finite difference method to illustrate the effects of unsteadiness, Prandtl number, and radiation on the boundary layer thickness, flow, and heat transfer. This type of study was conducted under the effect of these parameters previously with a different set of similarity transformations. However, the Lie similarity transformations deduced in this work, which have not been employed, lead to different types of reduced systems of ODEs, thereby providing different velocities and temperature profiles and providing valid solutions for previously unexplored regions for unsteadiness in the fluid flow and heat transfer. Some of these transformations and their resulting systems provide results that contradict the flow and heat transfer in real fluids.
1 Introduction
Heat transfer in thin films has garnered significant attention in various manufacturing processes. For example, the process of cooling thin films during the extrusion of polymer sheets, metal sheets, wire coatings, painting, polishing, and many other processes involves heat transfer in thin liquid films. Moreover, some industrial processes, such as surface paint and heat treatments on ceramics, involve radiation treatment to control the temperature of the fluid and boundary layer thickness without affecting the temperature of the surface. In many of these applications, the final product requires a smooth surface finish, which is attained by controlling the rate of heat transfer in these films. With advancements in manufacturing techniques and processes, more accurate methods are required to predict the physics of heat transfer in these types of fluid flows. In some industries, radiation treatments are performed to control the temperature, unsteadiness, and rate of heat transfer in the fluid by altering the surface temperature, such as surface paints on metal sheets in the automobile industry, surface polishing on ceramic products, and thin-walled solar water heaters. These applications require applying thermal radiation effects in energy equations while modeling fundamental boundary layer flows.
Crane [1] investigated the fluid flow driven on a semi-infinite linearly stretching surface, which Wang [2] extended to include the unsteady effects of hydrodynamics in thin-film stretching sheets. Andersson et al. [3] modeled the non-Newtonian fluid flow in a thin film on an unsteady stretching sheet using a power law. Andersson et al. [4] studied this phenomenon further by incorporating heat transfer. Moreover, on an unsteady stretching surface, Chen [5] studied non-Newtonian fluid flow; Dandapat et al. [6] included thermocapillary effects; Chen [7] illustrated viscous dissipation effects on heat transfer in a thin-film flow of a non-Newtonian fluid; Wang [8] obtained analytical solutions for the problem considered in [4] using the homotopy analysis method (HAM); and Dandapat et al. [9] explored the heat transfer in thin films with variable thermal conductivity, viscosity, and thermocapillarity. Several other authors [10–15] developed numerical and analytical solutions to similar problems with additional physical conditions and constraints. Liu and Megahed [16] illustrated the effects of thermal radiation, variable thermal conductivity, and viscosity on heat transfer and fluid flow in a thin film on an unsteady stretching sheet. Furthermore, Kumar [17] scrutinized the 3D flow and non-linear radiative heat transfer of non-Newtonian nanoparticles over an exponentially stretching sheet. Kumar [18] analyzed the flow and heat transfer of non-Newtonian nanofluid over a stretching sheet by considering the slip factor. Reddy et al. [19] demonstrated the transverse magnetic flow over a Reiner–Philippoff nanofluid by considering solar radiation. Kumar [20] studied the ferromagnetic hybrid nanofluid effects on heat transfer under solar radiation. Azam et al. [21] examined the transient bioconvection and activation energy impacts on Casson nanofluid with gyrotactic microorganisms and non-linear radiation. Puneeth et al. [22] considered a 3D flow of a nanofluid with non-linear thermal radiation and multi-slip conditions. Sudharani et al. [23] analyzed the influence of slip flow and linear radiation on a hybrid and tri-hybrid nanofluid. Naik et al. [24] investigated heat transfer under the influence of magnetic dipole. In all these studies, the similarity transformations remained the same. In such boundary layer problems, the flow originates from the origin, and the stretching of the elastic sheet causes it to flow in a plane parallel to its motion. Restriction of the stretching sheet velocity and temperature, namely, when
In this study, we used the Lie symmetry method [25–27] to derive similarity transformations. Safdar et al. [28] proposed Lie similarity transformations for an unsteady flow in a thin film over a stretching sheet and constructed analytic solutions using Lie point symmetries. In their work, instead of using
Previous studies on flow and heat transfer have primarily focused on the solution method(s) or analysis with additional parameters by utilizing the pre-existing basic similarity transformations given by [2,8]. Single reductions of systems of differential equations representing steady flows are performed using such similarity transformations, whereas double reductions through these transformations are performed for unsteady fluid flows. In these transformations, the velocity of the elastic sheet is considered
Bilal et al. [30] recently conducted a detailed heat transfer analysis of boundary layer flow in the presence of radiation using two different types of transformations. It was observed that the valid transformation obtained using Lie point symmetries yields results in the different regions compared with the existing transformations. The comparison showed that the previously existing transformation is valid only for steady and marginally accelerating fluid (unsteadiness). However, the Lie transformations provide a valid solution for any range of unsteadiness in the fluid. In addition, the previous transformations are valid for a specific time interval, which depends on a range of unsteadiness parameters. However, the Lie similarity transformations provide valid solutions at any given time. This motivates the author to derive all the Lie point similarity transformations associated with the system of PDEs representing the flow and heat transfer in the boundary layer in the presence of radiation.
The remainder of this study is organized as follows: Section 2 describes the mathematical formulation and Lie point symmetry transformations/generators of the flow. The numerical solutions are presented in Section 3. The results and discussion based on the velocity and temperature profiles are presented in Section 4, and conclusions are presented in Section 5.
2 Mathematical formulation and construction of similarity transformations
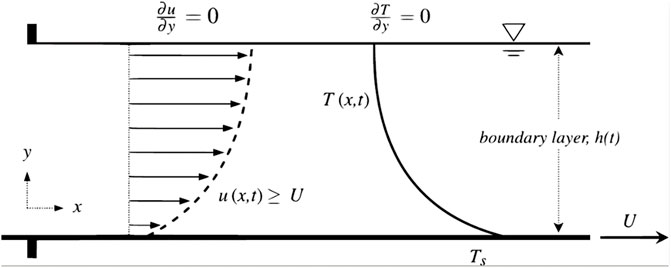
Consider a fully developed, viscous, nonvolatile, unsteady, incompressible, two-dimensional fluid flowing on a thin horizontal elastic surface and emerging from a hole (shown in Figure 1) that emerges from the origin of the
such that
In the aforementioned equations, the
According to [4], the surface temperature
According to the Rosseland approximation [31],
In Eqs 3, 4,
The formulas of
where
Likewise, the boundary conditions (Eq. 2) are transformed to
where
The aforementioned approach serves as a reference procedure for converting a system of PDEs into a system of ODEs. The transformed system (8) is valid only when
2.1 Lie symmetries and symmetry transformations
Lie developed an algebraic approach for constructing Lie point symmetries associated with differential equations [25–27]. These point transformations map the dependent and independent variables of a differential equation into new dependent and independent variables. These mappings leave the differential equations form-invariant such that their properties (e.g., linearity/non-linearity, order, and type) remain unaltered. Here, for the system of PDEs considered (1), we followed the procedure described by [28] for such systems and their associated conditions (2). The Lie point symmetry associated with system (1) in the general form can be written as
where
The coefficients in these extensions are obtained from
where
The subscript in
where
This criterion is evaluated using the continuity equation of system (1). The partial derivatives and coefficients of
where
MAPLE offers a built-in code, “Infinitesimals,” for computing Lie point symmetries in its package “PDEtools.” We use the same method to obtain the symmetry transformations for system (1), which form a Lie algebra. These symmetry generators
To obtain similarity transformations using symmetry generators, condition (2) must remain form-invariant when operated by generators. Both velocity and temperature are functions of the time
2.2 Double reductions with similarity transformations
In this subsection, successive double reductions of DEs were used to construct similarity transformations using Lie point symmetry generators. We allowed the symmetry procedure to determine the form of the surface velocity using boundary condition (2). We demonstrate the process of reduction considering the symmetries
By substituting generators and expanding them at
Solving the aforementioned linear PDEs, we obtain
To derive invariants, we apply
whose solution provides the invariants
and new dependent variables:
System (1) in these new variables is transformed into
whereas the boundary conditions (2) become
For the second successive reduction, the following symmetry generators for Eq. 24 are derived, which admits a three-dimensional Lie algebra:
The combination of
The invariants obtained using
whereas the new dependent variables are
The second reduction is obtained by substituting the variables in (24) and the associated conditions in (25). The transformed system can now be expressed as
and
The prime here denotes a derivative with respect to
This yields
Transformations (33) map the first equation of (1) into
and the second transformed equation of (1) under (33) is presented in Table 2.
All conditions (2) are transformed to
By employing these symmetries or their linear combinations, which are again Lie point symmetries, we reduce system (1) twice, using the invariants of these symmetries and their linear combinations. These reductions are in the independent variables of the system, and such double reductions enable the construction of the Lie similarity transformation, as presented in Table 2. This table presents the second transformed equation of (1) obtained through the Lie similarity transformations mentioned previously. The first transformed equation of (1) under all similarity transformations is (34), which is the same for all the systems in Table 2.
3 Numerical solution
The difference equations for a non-linear coupled system of ODEs in (8) are constructed using forward finite difference schemes. We now solve the resulting non-linear algebraic equations obtained along with (9) using the Newton–Raphson method. The boundary conditions at
Forward difference:
Backward difference:
The resulting non-linear algebraic equations are solved implicitly. If the dimensionless film thickness
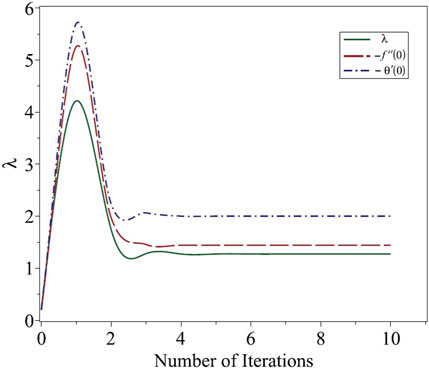
3.1 Convergence and grid independence
Newton’s method was used because of its quadratic convergence rate; however, its convergence strongly depended on the initial guess. We performed iterations with an initial guess of
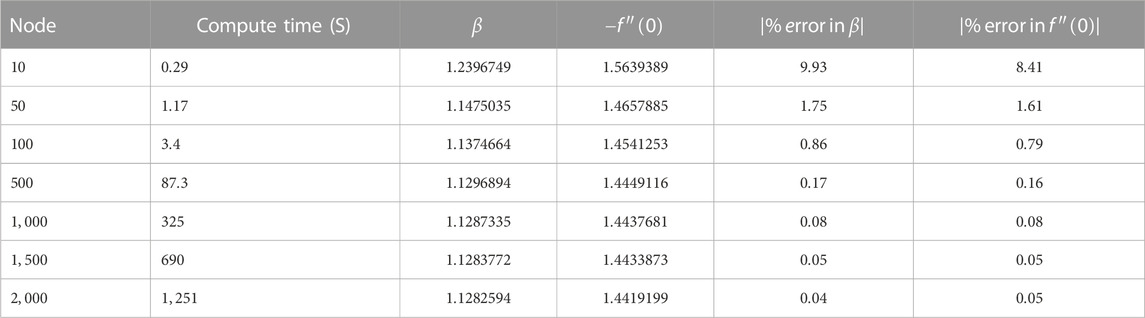
In addition, for all finite-difference-based approximation methods, the truncation error decreased with an increase in the number of nodes. The grid independence was assessed, and a comparison was made with the analytical solution, as shown in Table 3. As the number of nodes exceeds
3.2 Validation of the numerical solution method
The numerical results obtained using
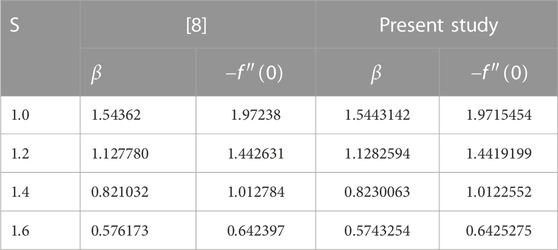
TABLE 4. Validation of the numerical solution using 2,000 nodes with the analytical solution provided by [8].
4 Results and discussion
Five similarity transformations exist for the system of PDEs (1), given in Table 2. The first step is to obtain the approximate solution of the reduced system of ODEs to classify the transformations based on the trends. In this section, we studied the effect of variation of different parameters of flow and heat transfer in the boundary layer. Table 2 indicates that the first equation in all systems (1)–(5) is the same, namely, an uncoupled non-linear ODE with
4.1 Similarity transformations
A major limitation of the previous similarity transformations for similar types of systems is that they are only valid when
However, the similarity solutions for all the systems in the current study obtained using the Lie symmetry transformation and presented in Table 2 have no such limitations. Mathematically, they are all valid at any time (i.e.,
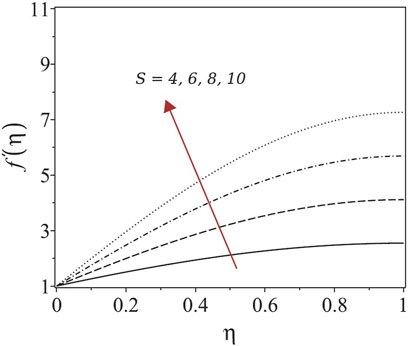
4.2 Effects of unsteadiness
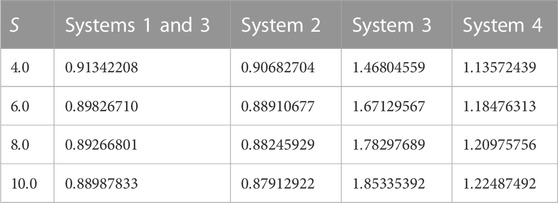
Table 5 presents the variation in the dimensionless film thickness
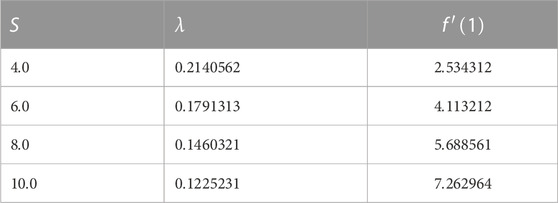
TABLE 5. Variation of the surface velocity and dimensionless film thickness with the unsteadiness parameter.
Figure 4A; Figure 5A; Figure 6A; Figure 7A show the effects of variation in temperature distribution
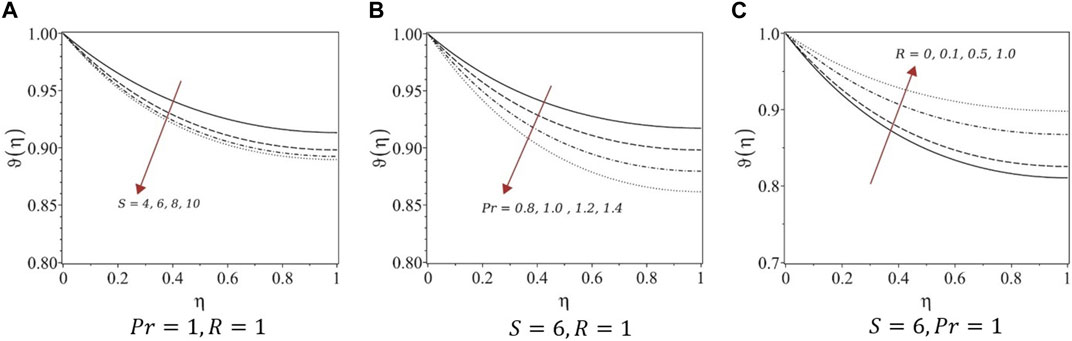
FIGURE 4. Temperature profiles of systems (1) and (3). (A) Pr = 1, R = 1, (B) S = 6, R = 1, and (C) S = 6, Pr = 1.
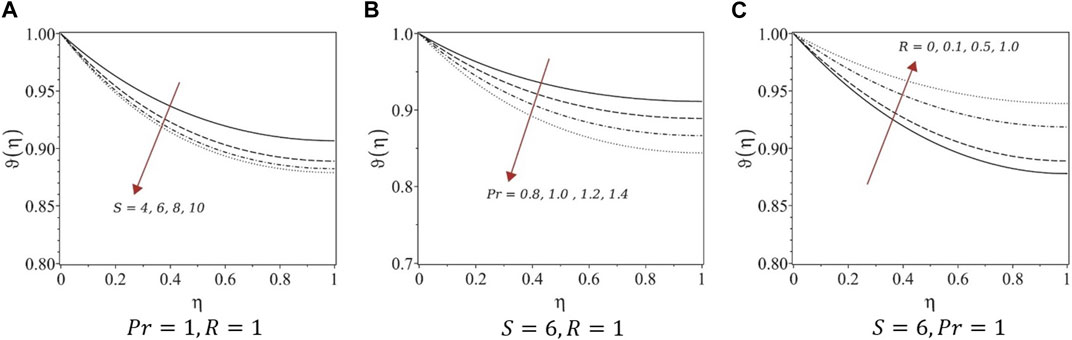
FIGURE 5. Temperature profiles of systems (2). (A) Pr = 1, R = 1, (B) S = 6, R = 1, and (C) S = 6, Pr = 1.
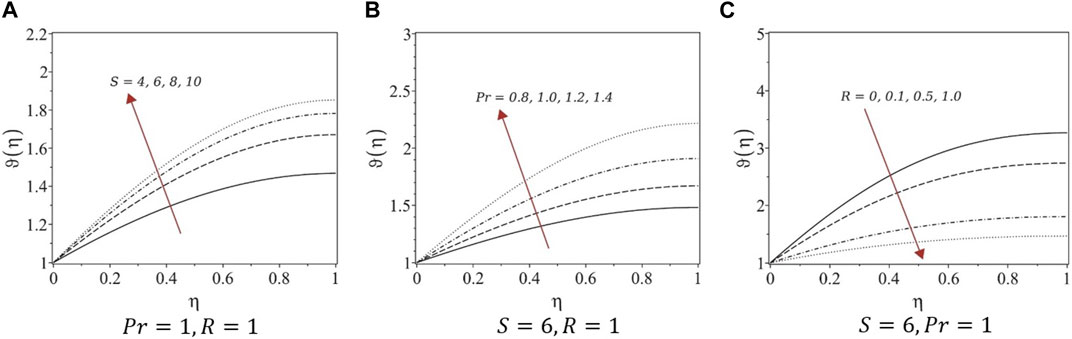
FIGURE 6. Temperature profiles of systems (4). (A) Pr = 1, R = 1, (B) S = 6, R = 1, and (C) S = 6, Pr = 1.
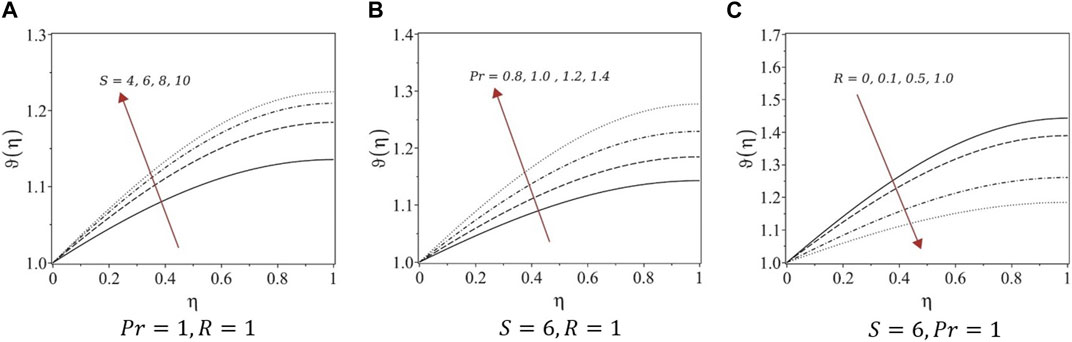
FIGURE 7. Temperature profiles of systems (5). (A) Pr = 1, R = 1, (B) S = 6, R = 1, and (C) S = 6, Pr = 1.
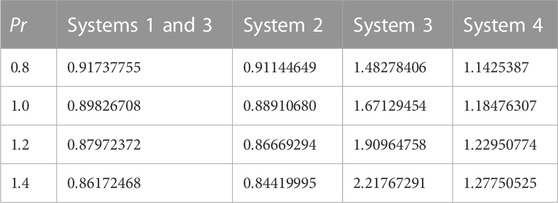
4.3 Effects of the Prandtl number
Figure 4B; Figure 5B; Figure 6B; Figure 7B show the effects of the variation of the Prandtl number
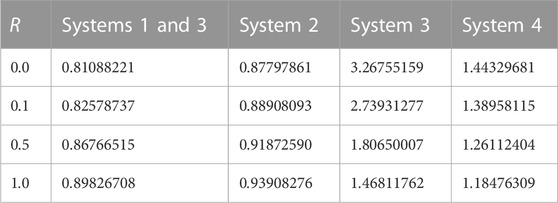
4.4 Effects of radiation
The effects of the radiation
5 Conclusion
We transformed the system of PDEs representing the flow and heat transfer in the boundary layer in the presence of radiation into a system of ODEs using Lie similarity transformations. The Lie similarity transformations presented in this study are different from the existing ones in terms of validity and applicability. These similarity transformations were obtained through invariants associated with linear combinations of Lie symmetry generators, which were used to perform double reductions of the flow model. Four distinct classes of systems of ODEs were revealed with five deduced Lie similarity transformations.
Numerical solutions for the obtained systems of ODEs were determined using finite-difference approximations to eliminate unphysical cases. The first equations in all five systems are the same; hence, the velocity profiles are similar under variations in the unsteadiness parameter. For fully developed flows, the film thickness decreased, whereas the velocity increased with growing unsteadiness. Similar trends were observed for the velocity profiles constructed in this study. For systems (1) and (3), the temperature decreased with increasing unsteadiness and Prandtl number, whereas the temperature increased with increasing radiation parameters. However, for systems (4) and (5), the temperature increased with the unsteadiness parameter and Prandtl number and decreased with increasing the radiation, which is not the case with real fluids. Therefore, we suggest avoiding the similarity transformation of systems (4) and (5) to study similar types of problems.
Overall, the valid similarity solutions determined using an extensive mathematical procedure allowed us to obtain solutions for unsteady fluid flow and heat transfer in the boundary layer. The HAM or homotopy perturbation method can be used to obtain the analytic solutions for the transformed system, providing valid results. The analytic solutions for fully resolved laminar boundary layer flow and heat transfer at any given time can be obtained by inserting the values for appropriate boundary conditions.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material. Further inquiries can be directed to the corresponding authors.
Author contributions
Conceptualization: MS; data curation: MB; formal analysis: MB, SA, MS, MA, and AZ; software: MB and MS; validation: MB, SA, MS, MA, and AZ; visualization: MB, MS, KK, KK, and JH; writing—original draft preparation: MS and MB; writing—review and editing: SA, KK, MA, AZ, KK, and JH; funding: KK and JH. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (2022R1C1C2003637 to KK and RS-2023-00210403 to JH).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Crane LJ. Flow past a stretching plate. Z für Angew Mathematik Physik ZAMP (1970) 21(4):645–7. doi:10.1007/bf01587695
2. Wang C. Liquid film on an unsteady stretching surface. Q Appl Math (1990) 48(4):601–10. doi:10.1090/qam/1079908
3. Andersson HI, Aarseth JB, Braud N, Dandapat BS. Flow of a power-law fluid film on an unsteady stretching surface. J Non-Newtonian Fluid Mech (1996) 62(1):1–8. doi:10.1016/0377-0257(95)01392-x
4. Andersson HI, Aarseth JB, Dandapat BS. Heat transfer in a liquid film on an unsteady stretching surface. Int J Heat Mass Transfer (2000) 43(1):69–74. doi:10.1016/s0017-9310(99)00123-4
5. Chen CH. Heat transfer in a power-law fluid film over a unsteady stretching sheet. Heat Mass Transfer (2003) 39(8):791–6. doi:10.1007/s00231-002-0363-2
6. Dandapat BS, Santra B, Andersson HI. Thermocapillarity in a liquid film on an unsteady stretching surface. Int J Heat Mass Transfer (2003) 46(16):3009–15. doi:10.1016/s0017-9310(03)00078-4
7. Chen CH. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. J Non-Newtonian Fluid Mech (2006) 135(2-3):128–35. doi:10.1016/j.jnnfm.2006.01.009
8. Wang C. Analytic solutions for a liquid film on an unsteady stretching surface. Heat Mass Transfer (2006) 42(8):759–66. doi:10.1007/s00231-005-0027-0
9. Dandapat B, Santra B, Vajravelu K. The effects of variable fluid properties and thermocapillarity on the flow of a thin film on an unsteady stretching sheet. Int J Heat Mass Transfer (2007) 50(5-6):991–6. doi:10.1016/j.ijheatmasstransfer.2006.08.007
10. Liu IC, Andersson HI. Heat transfer in a liquid film on an unsteady stretching sheet. Int J Therm Sci (2008) 47(6):766–72. doi:10.1016/j.ijthermalsci.2007.06.001
11. Abel MS, Tawade J, Nandeppanavar MM. Effect of non-uniform heat source on MHD heat transfer in a liquid film over an unsteady stretching sheet. Int J Non-Linear Mech (2009) 44(9):990–8. doi:10.1016/j.ijnonlinmec.2009.07.004
12. Aziz RC, Hashim I. Liquid film on unsteady stretching sheet with general surface temperature and viscous dissipation. Chin Phys Lett (2010) 27(11):110202. doi:10.1088/0256-307X/27/11/110202
13. Noor NFM, Hashim I. Thermocapillarity and magnetic field effects in a thin liquid film on an unsteady stretching surface. Int J Heat Mass Transfer (2010) 53(9-10):2044–51. doi:10.1016/j.ijheatmasstransfer.2009.12.052
14. Aziz RC, Hashim I, Alomari AK. Thin film flow and heat transfer on an unsteady stretching sheet with internal heating. Meccanica (2011) 46(2):349–57. doi:10.1007/s11012-010-9313-0
15. Aziz RC, Hashim I, Abbasbandy S. Effects of thermocapillarity and thermal radiation on flow and heat transfer in a thin liquid film on an unsteady stretching sheet. Math Probl Eng (2012) 2012:1–14. doi:10.1155/2012/127320
16. Liu IC, Megahed A. Numerical study for the flow and heat transfer in a thin liquid film over an unsteady stretching sheet with variable fluid properties in the presence of thermal radiation. J Mech (2012) 28(2):291–7. doi:10.1017/jmech.2012.32
17. Kumar KG. Scrutinization of 3D flow and non-linear radiative heat transfer of non-Newtonian nanoparticles over an exponentially sheet. Int J Numer Methods Heat Fluid Flow (2019) 30:2051–62. doi:10.1108/hff-12-2018-0741
18. Kumar KG. Exploration of flow and heat transfer of non-Newtonian nanofluid over a stretching sheet by considering slip factor. Int J Numer Methods Heat Fluid Flow (2019) 30(4):1991–2001. doi:10.1108/hff-11-2018-0687
19. Reddy MG, Rani S, Kumar KG, Seikh A, Rahimi-Gorji M, Sherif M. Transverse magnetic flow over a Reiner–Philippoff nanofluid by considering solar radiation. Mod Phys Lett (2019) 33(36):1950449. doi:10.1142/s0217984919504499
20. Kumar KG, Hani EH, Assad ME, Rahimi-Gorji M, Nadeem S. A novel approach for investigation of heat transfer enhancement with ferromagnetic hybrid nanofluid by considering solar radiation. Microsystem Tech (2021) 27:97–104. doi:10.1007/s00542-020-04920-8
21. Azam M, Abbas N, Ganesh Kumar K, Wali S. Transient bioconvection and activation energy impacts on Casson nanofluid with gyrotactic microorganisms and non-linear radiation. Waves in Random and Complex Media (2022) 1–20. doi:10.1080/17455030.2022.2078014
22. Puneeth V, Manjunatha S, Kumar KG, Reddy MG. Perspective of multiple slips on 3D flow of Al<sub>2</sub>O<sub>3</sub>–TiO<sub>2</sub>–CuO/H<sub>2</sub>O ternary nanofluid past an extending surface due to non-linear thermal radiation. Waves in Random and Complex Media (2022) 1–19. doi:10.1080/17455030.2022.2041766
23. Sudharani MVVNL, Prakasha DG, Kumar KG, Chamkha AJ. Computational assessment of hybrid and tri hybrid nanofluid influenced by slip flow and linear radiation. The Eur Phys J Plus (2023) 138(3):257. doi:10.1140/epjp/s13360-023-03852-2
24. Naik LS, Prakasha DG, Praveena MM, Krishnamurthy MR, Kumar KG. Stratification flow and variable heat transfer over different non-Newtonian fluids under the consideration of magnetic dipole. Int J Mod Phys B (2023) 13:2450071. doi:10.1142/s0217979224500711
25. Olver PJ. Applications of Lie groups to differential equations. Berlin: Springer Science & Business Media (1993).
26. Ibragimov NH, Ibragimov NK. Elementary Lie group analysis and ordinary differential equations. New York: Wiley (1999).
27. Hydon PE. Symmetry methods for differential equations: A beginner's guide. Cambridge, UK: Cambridge University Press (2000).
28. Safdar M, Khan MI, Taj S, Malik M, Shi QH. Construction of similarity transformations and analytic solutions for a liquid film on an unsteady stretching sheet using lie point symmetries. Chaos, Solitons and Fractals (2021) 150:111115. doi:10.1016/j.chaos.2021.111115
29. Bilal M, Safdar M, Taj S, Zafar A, Ali MU, Lee SW. Reduce-order modeling and higher order numerical solutions for unsteady flow and heat transfer in boundary layer with internal heating. Mathematics (2022) 10(24):4640. doi:10.3390/math10244640
30. Bilal M, Safdar M, Ahmed S, Riaz AK. Analytic similarity solutions for fully resolved unsteady laminar boundary layer flow and heat transfer in the presence of radiation. Heliyon (2023) 9(4):e14765. doi:10.1016/j.heliyon.2023.e14765
31. Raptis A. Flow of a micropolar fluid past a continuously moving plate by the presence of radiation. Int J Heat Mass Transfer (1998) 18(41):2865–6. doi:10.1016/s0017-9310(98)00006-4
Keywords: boundary layer, radiation, Lie transformations, Lie similarity transformation, numerical solutions
Citation: Bilal M, Safdar M, Ahmed S, Kallu KD, Ali MU, Zafar A, Kim KS and Hyuk Byun J (2023) Numerical approximations for fluid flow and heat transfer in the boundary layer with radiation through multiple Lie similarity transformations. Front. Phys. 11:1210827. doi: 10.3389/fphy.2023.1210827
Received: 23 April 2023; Accepted: 05 July 2023;
Published: 24 July 2023.
Edited by:
Francisco Vega Reyes, University of Extremadura, SpainReviewed by:
Mahmoud Abdelrahman, Mansoura University, EgyptK. Ganesh Kumar, S.J.M. Institute of Technology, India
Copyright © 2023 Bilal, Safdar, Ahmed, Kallu, Ali, Zafar, Kim and Hyuk Byun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Umair Ali, dW1haXJAc2Vqb25nLmFjLmty; Kwang Su Kim, a3dhbmdzdWtpbUBwa251LmFjLmty; Jong Hyuk Byun, bWF0aWNheEBwdXNhbi5hYy5rcg==
 Muhammad Bilal
Muhammad Bilal Muhammad Safdar1
Muhammad Safdar1 Shoaib Ahmed
Shoaib Ahmed Karam Dad Kallu
Karam Dad Kallu Muhammad Umair Ali
Muhammad Umair Ali Amad Zafar
Amad Zafar Jong Hyuk Byun
Jong Hyuk Byun