- 1Institute of Modern Physics, Chinese Academy of Sciences, Lanzhou, China
- 2Institute for Theoretical Physics I, Heinrich-Heine-Universität Düsseldorf, Universitätsstrasse 1, Düsseldorf, Germany
We investigate the fragmentation of the helium dimer, 4He2, into He2+ + He+ and He2+ + He2+ ions in collisions with fast highly charged projectiles. We discuss the main physical mechanisms driving these processes. We explore the energy and angular distributions of the ionic fragments produced during collisions of the dimer with 1 GeV/u U92+ and 11.37 MeV/u S14+ projectiles and also present the total fragmentation cross-sections. According to our results, the fragmentation in these collisions is fully dominated by the direct removal of three or four electrons from the dimer by the projectile in a single collision. Our results also suggest that the total fragmentation cross-sections depend on the binding energy
1 Introduction
The He2 dimer is a spectacular quantum system. The interaction between two (ground-state) helium atoms in this dimer is extremely weak supporting just one bound state with a tiny binding energy of ≃ 10–7 eV [1]. The dimer represents the largest known ground-state diatomic molecule having the average bond length of
When the He2 dimer is bombarded by charged projectiles, it can be fragmented into helium ions. These ions repeal each other, resulting in a Coulomb explosion of the system. The kinetic energy of the ionic fragments, which is released in this explosion, depends on their charges and the initial distance between them. The study of the spectra of the kinetic energy release may yield valuable information about the structure of the He2 dimer and the fragmentation mechanisms.
The process of He2 fragmentation into singly charged ions in collisions with 150 keV/u alpha particles and 11.37 MeV/u S14+ projectiles was explored in Ref. 3 and Refs. 4, 5, respectively. Lately, the process of He2 fragmentation into singly charged ions by relativistic highly charged projectiles was considered in Refs. 6, 7.
The fragmentation of the He2 dimer into singly charged helium ions caused by photo absorption was explored as well [8–10], [11].
However, to our knowledge, there have been no studies on the processes of the fragmentation of the He2 dimer proceeding with the emission of more than two electrons. One can expect that such processes possess new and interesting features, which make them qualitatively different compared to the fragmentation into singly charged ions. Therefore, in the present paper, we shall theoretically explore the fragmentation reactions
occurring in very energetic collisions of highly charged projectiles with the He2 dimer.
Here, we will consider collisions with two projectiles, 1 GeV/u U92+ and 11.37 MeV/u S14+, respectively. The first of them has the highest charge and impact velocity which—to our knowledge—can be currently reached at the GSI (Darmstadt, Germany). The second was already used in an experiment [4] on the collisional fragmentation of the He2 dimers into singly charged helium ions.
The paper is organized as follows. The next (very short) section contains some preliminary remarks. In Sections 3, 4, we explore the fragmentation reactions (1) and (2), respectively. In Section 5, we consider the total fragmentation cross-sections, and Section 6 summarizes the main conclusions.
Atomic units (ℏ = |e| = me = 1) are used throughout unless otherwise is stated.
2 Preliminary remarks
Let the He2 target collide with a bare projectile, which has a charge Zp ≫ 1 and moves with a high velocity v, 1 ≪v < c where c ≈ 137 a. u. is the speed of light.
We shall assume that the ratio η = Zp/v (η = Zpe2/ℏv), which characterizes the effective strength of the projectile–target interaction in the collision is well below 1. In such a case, the field of the projectile in the collision is overall weak rather than strong. Consequently, the breakup of the He2 will occur with a non-negligible probability only provided the number of “steps” in the interaction of the projectile with the constituents of the dimer is reduced to a necessary minimum.
In high-energy collisions between a bare projectile-nucleus and a target-atom, three basic atomic processes can occur: 1) atomic ionization (or excitation), 2) an atomic electron can be captured by the projectile, and 3) electron–positron pair production becomes possible in relativistic collisions. However, in high-energy collisions with light atoms, the latter two are much weaker than ionization (excitation) [12–15]. This point (together with the condition of a minimum interaction steps) very significantly restricts the number of the main fragmentation mechanisms, which governs the breakup reactions (1) and (2) of the He2 dimer by high-energy charged projectiles.
3 Fragmentation with the emission of three electrons
3.1 The fragmentation mechanisms for the reaction Zp + He2 → Zp + He+ + He2+ + 3 e−
It is rather evident that under the conditions mentioned previously, the minimum number of the interactions necessary for triple ionization of the He2 dimer (which involve both the interaction(s) between the projectile and the dimer and the interaction(s) between the constituents of the dimer) is equal to three. The analysis shows that there are the following fragmentation mechanisms involving basically three interactions which drive the reaction (1).
1. In the first mechanism, the projectile—in a single collision—knocks out two electrons from one site of the dimer and one electron from the other site. The three electrons quickly fly away, and the residual system He+ + He2+ undergoes an explosion due to the repulsive Coulomb force acting between the ions. Since the size of the He2 is very large, the interactions between the constituents of the dimer play no noticeable role in this mechanism. We shall call this mechanism direct fragmentation and abbreviate it as DF-3.
2. In the second mechanism, the projectile interacts with just one site of the dimer. As a result of this interaction, the site becomes doubly ionized. There is a certain probability that one of the emitted electrons will move toward the other site, singly ionizing it. This mechanism is a combination of double ionization of the helium atom by a high-energy projectile and the so-called e2e process on helium (single ionization by electron impact). In what follows, we shall refer to this mechanism as double ionization—e2e (DI-e2e).
3. In the next—third—mechanism, the projectile in a single collision with the dimer interacts with both its sites. As a result of these interactions, two singly charged helium ions are formed. Then, an electron emitted from one of the sites of the dimer moves toward the other site and, by knocking out its remaining bound electron, produces a doubly charged helium ion. This mechanism is a combination of two single ionization events by the projectile and the e2e process on a singly charged helium ion. We shall denote this mechanism as single ionization—single ionization—e2e (SI-SI-e2e).
4. In the fourth mechanism, the projectile interacts just with one site of the dimer singly ionizing it. The emitted electron moves toward the remaining neutral helium atom and doubly ionizes it. This mechanism is a combination of single ionization caused by the interaction with the projectile and the so-called e3e process on helium (helium double ionization by electron impact). This mechanism will be referred to as single ionization—e3e (SI-e3e).
It will be seen in the following section (Section 3.4) that the main contribution to the (final) kinetic energy of the helium ions is given by the Coulomb explosion and that this energy does not significantly exceed 10 eV (20 eV for the fragmentation into two He2+ ions). The kinetic energies of the transitory He2+–He and He+–He systems, which—within the DF-3 mechanism—are formed after the interaction of the projectile with the first atom of the dimer, are even smaller (
The mechanisms 2–4 involve ionization of one site of the dimer by an electron, which was emitted from the other site by the projectile impact. The kinetic energy of an electron, capable of knocking out electron(s) from a helium atom or ion, has to be larger than the corresponding ionization potential. The velocity of such an electron exceeds, by orders of magnitude, the typical velocities of the nuclei in the transitory He2+–He (DI-e2e), He+–He+ (SI-SI-e2e), and He+–He (SI-e3e) systems. Thus, within these mechanisms, the transformation of the He2 dimer into the He2+–He+ system also occurs at “frozen” positions of the helium nuclei.
3.2 The relative efficiency of the fragmentation mechanisms involving electron impact ionization
The DI-e2e, SI-SI-e2e, and SI-e3e mechanisms involve the ionization of a He atom (or electron removal from He+) by electron impact. Let us qualitatively compare their relative efficiency.
Comparing the DI-e2e and the SI-SI-e2e for collisions with 1 GeV/u U92+ projectiles, we first note that according to our calculations, the total cross-section
Furthermore, in Figure 1, we have presented the results of our calculations for the energy distributions of electrons emitted from helium atoms in collisions with 1 GeV/u U92+ [16] together with experimental data from Ref. 17, focusing on the so called soft electron peak which is known to strongly dominate the total electron emission from very light atoms, like He [18].
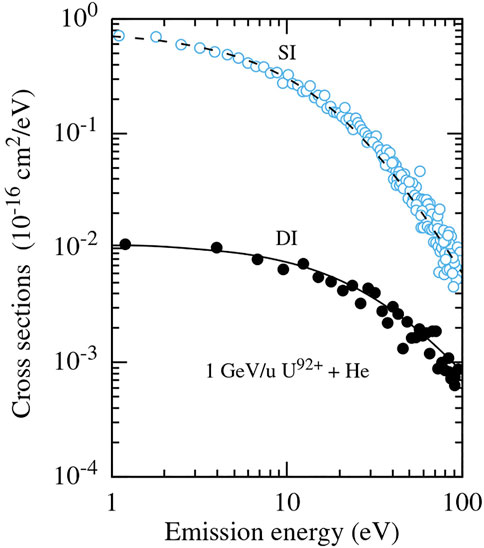
FIGURE 1. Energy spectra of electrons emitted in the processes of single (SI) and double (DI) ionization of the helium atom in collision with 1 GeV/u U92+ projectiles. Dash and solid curves: results of our calculations. Open and solid circles are the experimental data from Ref. 17 normalized to the calculated results.
It can be deduced from these results that the electrons with energies
Taking also into account that in collisions with electrons, the cross-sections for single ionization of a neutral helium atom [19, 20] are by one order of magnitude larger than the cross-section for electron removal from He+ [21], we may conclude that the DI-e2e mechanism is so much more efficient than the SI-SI-e2e mechanism and that the latter can simply be neglected.
Using the results of our calculations shown in Figure 2, the same conclusion can also be drawn for collisions with 11.37 MeV/u S14+.
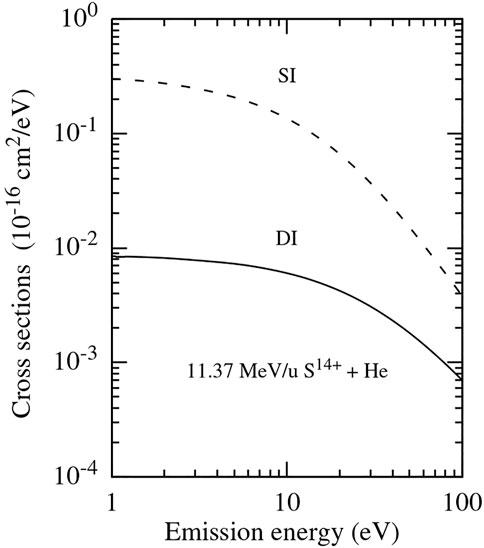
FIGURE 2. Energy spectra of electrons emitted in the processes of single (SI) and double (DI) ionization of the helium atom in collisions with 11.37 MeV/u S14+ projectiles. Dash and solid curves: results of our calculations.
Let us now compare the DI-e2e and the SI-e3e mechanisms. For collisions with 1 GeV/u U92+ projectiles, the cross-section for single ionization of a helium atom of the He2 dimer is
We have already seen that the energy spectrum of electrons emitted in single ionization decreases with the increase in the emission energy much more rapidly than the energy spectrum of electrons produced in helium double ionization. For instance, it can be inferred from Figures 1, 2 that the number of electrons emitted in single ionization with energies
Therefore, taking into account that in collisions with electrons, the cross-section for helium double ionization is at least two orders of magnitude smaller than the cross-section for helium single ionization (both cross sections are given, e.g., in Ref. 19), we conclude that the SI-e3e mechanism is much less efficient than DI-e2e and can be neglected.
3.3 The main fragmentation mechanisms
Thus, summarizing the aforementioned discussion, we see that among the mechanisms involving ionization by electron impact, the DI-e2e is by far the main one. Taking also into account that in fast collisions with highly charged projectiles, the direct mechanism (DF-2) for the fragmentation into two He+ ions turned out to be very efficient and anticipating a similar relative efficiency for the DF-3, we may expect that the fragmentation reaction (1) is essentially driven by just two mechanisms, the DF-3 and the DI-e2e, and in what follows only will be considered.
3.4 The direct fragmentation mechanism
It is convenient to begin the consideration of collisions between the He2 dimer and the projectile using the semi-classical approach. Within it, the motion of the heavy particles (the projectile and the nuclei of the dimer) is treated classically, while the electrons are described quantum mechanically.
As our reference frame, we take the frame where the dimer is at rest and the origin is at the position of the nucleus of one of the dimer atoms. We shall refer to this atom as atom A, whereas the other will be denoted by B. In this reference frame, the projectile moves along a classical straight-line trajectory Rp(t) = b + vt, where b = (bx, by, 0) is the impact parameter with respect to the nucleus of atom A, and v = (0, 0, v) is the collision velocity. The coordinates of the nucleus of atom B in this frame are given by the inter-nuclear vector R of the dimer.
The He2 dimer is very large and, therefore, the ionization of atoms A and B by the projectile occurs practically independently of each other and can be treated using the independent electron approximation. Within this approximation, the probabilities
Here,
The independent electron approximation yields good results for ionization of a helium atom in collisions with fast highly charged projectiles, i.e. it can also be applied to the electrons of the same atom. Within this approximation the probabilities for single and double ionization of helium atoms A and B read
where w (bX) is the probability to remove one electron from the Xth helium atom (X = A, B) in the collision with a projectile at an impact parameter bX (bX = b, b′).
The cross-section for the formation of the He2+–He+ system via the DF-3 mechanism at a given inter-nuclear vector R of the He2 dimer is then given by
The ionization probabilities (4) depend just on the absolute value of the impact parameters b and b′. Therefore, the cross-section (5) depends only on the absolute value R⊥ of the two-dimensional vector R⊥:
In the present study, we calculate the single-electron probabilities w(b) using the (relativistic) symmetric eikonal approximation [23]. The initial and final states of the undistorted helium atom are computed regarding the atom as an effective single-electron system, where the “active” electron moves in the effective field created by the “frozen” atomic core consisting of the atomic nucleus and the “passive” electron. The interaction of the active electron with this effective field was described by the potential
where r is the distance between the active electron and the atomic nucleus, α = 3.36 and β = 1.665 [24].
The usage of the probability w(b), obtained in the aforementioned described way, gives very good results for helium single ionization. In the case of double ionization, it yields a good agreement in the shape of the energy distribution of the emitted electrons, however, overestimating the total cross-section. Indeed, comparing results of the present calculations for helium double ionization with those of Ref. 25 one can conclude that the present approach overestimates the total cross-section by about 30%. We, therefore, expect that the cross-sections for the DF-3 and DI-e2e mechanisms, reported in this paper, are also overestimated by about 30%.
The cross-section (5) describes the triple ionization of the He2 dimer at a fixed inter-nuclear vector R and, thus, cannot be directly measured during the experiment. In order to transform the cross-section (5) into quantities which can be measured, we begin with the expression
where Ψi(R) is the wave function of the relative motion of the atoms in the ground state of the He2 dimer (normalized according to ∫d3R |Ψi(R)|2 = 1).
We recall that in the reference frame, which we have chosen, before the collision with the projectile, the He2 dimer is at rest. Let
Here, EK = K2/2μ is the final kinetic energy of the relative motion of the ionic fragments,
We shall now assume that the absolute value of the relative momentum Krec of the fragments caused by the recoil effect is significantly smaller than that of their final relative momentum K. In such fragmentation events, momentum K will be directed essentially along the inter-nuclear vector R of the initial He2 dimer. In addition, we can neglect the first term on the right hand side of Eq. 7, obtaining
Taking these two points into account, we can express d3R according to
where ΘK and φK are the polar and azimuthal angles of K, respectively (with the z-axis being along the projectile velocity v).
With the help of Eqs 6, 8, 9, we finally obtain that the fragmentation cross-section differential in energy EK and angle ΘK is given by
3.5 The DI-e2e fragmentation mechanism
Let us now consider the breakup of the helium dimer via the DI-e2e fragmentation mechanism. The size R of the dimer is very large on the atomic scale. In addition, one has k R ≫ 1 where k is the momentum of the electron, which has sufficient energy to ionize a helium atom. Therefore, this mechanism can be split into two consecutive steps: double ionization of one of the atoms by the projectile and single ionization of the other atom by the electron emitted from the first atom (and vice versa).
Let
The cross-section σDI-e2e for the formation of the He2+–He+ system in collisions with the He2 dimer having a fixed inter-nuclear vector R can be evaluated according to
where
and, similarly,
Here,
The quantity
where
Let σe2e (ɛk) be the total cross-section for single ionization of a helium atom from the ground state by the impact of an electron incident with energy ɛk. The effective solid angle ΔΩX for electron impact ionization can be estimated as ΔΩX = σe2e (ɛk)/R2, where R is the distance between the atoms in the He2 dimer. Since the magnitude of the cross-section σe2e (ɛk) remains always well below 4 × 10−17 cm2 ≈ 1.43 a. u. (see e.g.[20]) and, hence, is much smaller than R2, ΔΩX is very small and the integration over the solid angle in Eqs 12, 13 can be performed assuming that the cross-section
The process of double ionization of helium atoms in collisions with highly charged ions is driven predominantly by the independent interactions between the projectile and each of the atomic electrons. In high-energy collisions, this leads to the formation of a characteristic dipole pattern for the emitted electrons with their angular distribution being proportional to sin2ϑk [26], where ϑk = arccos (k ⋅v/k v) is the polar emission angle of the electron with respect to the projectile velocity. Taking this into account, we get
Here,
where the integration runs over the full 4π solid angle, is the cross-section for helium double ionization by the projectile differential in energy of one of the emitted electrons. We note that the angular dependence
Using Eq. 15, we perform in Eqs. 12, 13, the integration over dΩk (keeping in mind that the solid angles ΔΩA and ΔΩB are very small such that
Here, ϑk is the polar emission angle of the electrons which moves from one site of the dimer to the other inside the cone, determined by the solid angle ΔΩA (or ΔΩB).
In order for an electron, which was emitted from one atom of the dimer, to hit the other atom, it must move almost in parallel/antiparallel to the inter-nuclear vector R of the dimer. Therefore, one has sin2ϑk ≈ sin2ϑR, where ϑR = arccos (R ⋅v/R v) is the polar angle of the orientation of the dimer.
Starting with the expression
where σDI-e2e(R) ∼ sin2ϑR/R2 (see Eq. 17 and the previous paragraph), and performing essentially the same steps as in the derivation of the cross-section (10), we obtain the cross-section for the dimer fragmentation via the DI-e2e mechanism differential in the kinetic energy release EK and the polar fragmentation angle ΘK:
3.6 Numerical results and discussion
3.6.1 Preliminary remarks
In our derivation of the cross-sections (10) and (19), we have assumed that the absolute value of the final relative momentum K of the helium ions is significantly larger than that of their relative recoil momentum
In single ionization of helium atoms by very high-energy projectiles, when the parameter η is well below 1, the typical recoil momenta of the He+ ions do not exceed 1 a. u. [17, 23]. For the process of helium double ionization in such collisions, for which the data on the recoil momenta seem to be absent, one can expect that they do not significantly exceed 2 a. u.
Then, the range of the typical values of Krec can be estimated as Krec ≲ 3/2 a. u. and the corresponding recoil energy
One has to stress that the condition that the vector K is (almost) parallel/antiparallel to the inter-nuclear vector R at the collision instant, which enables one to derive the doubly differential cross-sections (10) and (19), is not necessary for calculating the energy distribution of the ionic fragments. Indeed, the latter merely requires the relation between the kinetic energy release EK and the size of the dimer R at the collision instant given by Eq. 8 that holds if EK ≫ Erec ≃ 10 meV and, hence, is well fulfilled already at EK ≳ 100 meV.
It will be seen in the following that the breakup of the He2 dimer occurring with the emission of three electrons is strongly dominated by events with the kinetic energy release EK ≥ 1 eV. This corresponds to K > 16 a. u., and thus, our assumption used to derive the cross-sections (10) and (19) is well fulfilled for the overwhelming majority of the fragmentation events.
3.6.2 Fragmentation via the DF-3 mechanism
Figure 3 shows the contribution,
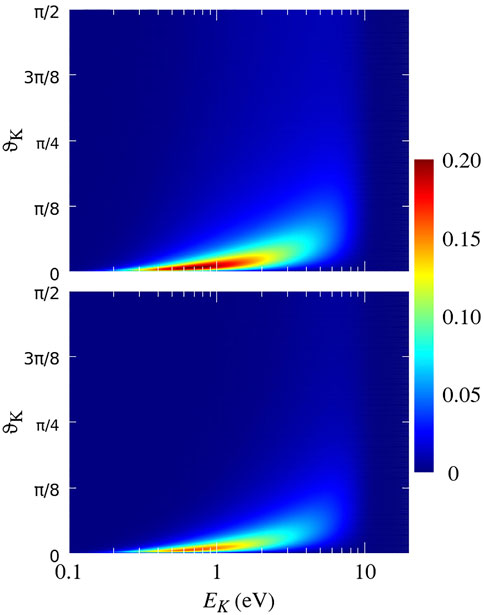
FIGURE 3. Cross-section
It follows from Figure 3 (see also Figures 4, 5) that the spectrum of the helium ions produced via DF-3 is mainly localized at kinetic energies 0.4 eV ≲ EK ≲ 10 eV and fragmentation angles ΘK ≲ π/8 and that there is a correlation between the energy and angle: at smaller EK the spectrum is restricted to smaller ΘK, and with increasing energy, the spectrum shifts to noticeably larger ΘK.
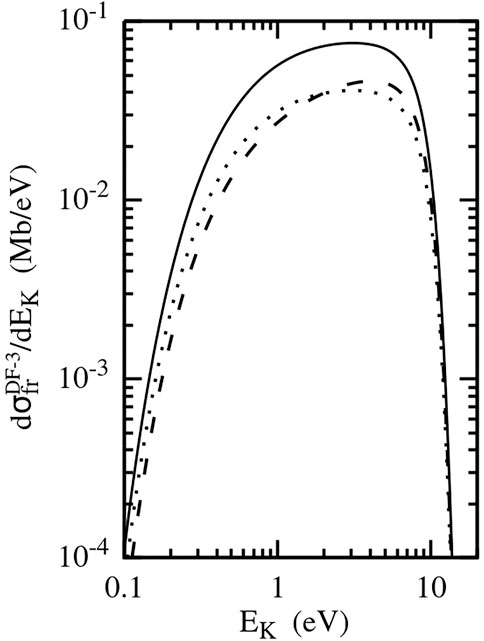
FIGURE 4. Cross-section
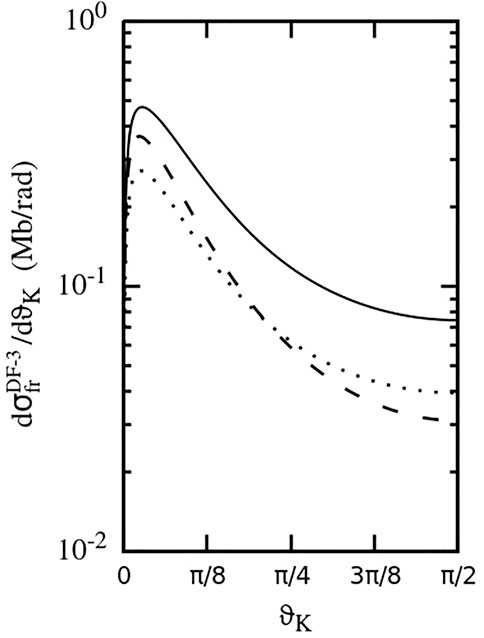
FIGURE 5. Cross-section
Using the relation EK = Q1Q2/R = 2/R we find that the kinetic energies 0.4 eV ≲ EK ≲ 10 eV correspond to the instantaneous size R of the He2 dimer in the range 5.44 a. u. ≲ R ≲ 136 a. u. The probability of finding the He2 dimer in this range is very large
At energies ≳ 12–14 eV, the spectrum essentially vanishes since these energies correspond to the inter-nuclear distances R ≲ 4 a. u., where the probability of finding the He2 dimer is negligibly small. Very weak spectrum intensities at EK ≲ 0.4 eV have a different reason. These energies correspond to the distances of R ≳ 136 a. u., where the probability of finding the He2 dimer is substantial
The cross-section
Figure 4 presents the energy spectrum, given by the cross section
Figure 4 also indicates that the increase in the impact energy enhances (in relative terms) the lower-energy part of the fragmentation spectrum. This is especially clearly seen by comparing the calculated energy spectra in collisions with 11.37 MeV/u S14+ and 7 GeV/u U92+ (the collision velocity v = 136 a.u.). By replacing the former projectile with the latter, we essentially do not vary the effective perturbation strength η = Zp/v (
Figure 5 presents the angular distribution, given by the cross-section
A comparison of the angular distribution in collisions with 11.37 MeV/u S14+ and 7 GeV/u U92+ shows that for a fixed η = Zp/v, the geometric opening of these cones increases when the impact energy grows. This is consistent with a larger effective interaction range of a higher-energy projectile which, therefore, can fragment the He2 dimer at larger values of its transverse size R⊥ that results in broader angular distributions of the fragments.
However, we note that—according to Figure 5—the magnitude of η also influences the shape of angular distribution: in this figure, it is the broadest for the fragmentation by 1 GeV/u U92+ where η ≈ 0.77. Since the cross-sections for the DF-3 mechanism roughly scale as
3.6.3 Fragmentation via the DI-e2e mechanism
Figure 6 shows the cross-section
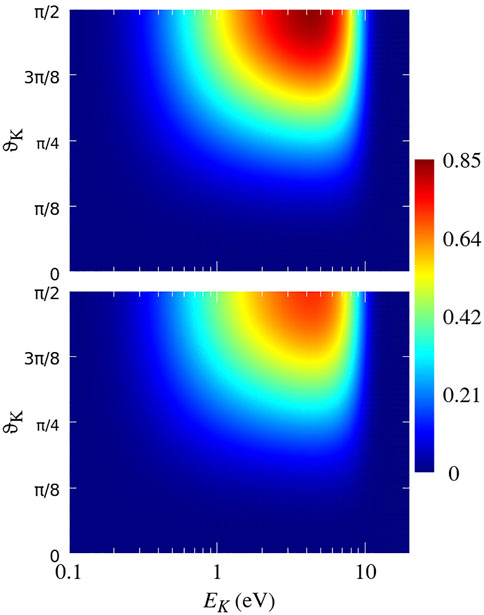
FIGURE 6. Cross-section
The position of the maximum in the spectrum in Figure 6 at ΘK ≈ π/2 follows from Eq. 19, where the angular dependence of the cross-section is given by the factor sin3ΘK = sin ΘK sin2ΘK. The part sin ΘK of this factor is purely geometrical and the origin of sin2ΘK can be traced back to arise in the dipole-like dependence (∼ sin2ϑk) of the electron emission from helium atoms in collisions with very fast highly charged projectiles.
The shift of the maximum of the spectra in Figure 6 to larger energies (compared to that in Figure 3) also lies in the shape of the emission pattern of the electrons ejected from helium atoms by the projectiles.
The cross-section (17) is proportional to factor 1/R2 which reflects the decrease in the probability for the emitted electron to hit the other atom with an increasing R. This factor is inherent to e2e step of the fragmentation processes on large dimers ([6, 27]) and does not depend on the shape of the angular distribution of electrons emitted by the projectile impact. The dependence 1/R2 shows that the DI-e2e mechanism possesses a large action range being able to produce the He2+-He+ system even if the distance R is much larger than 1 a. u.
Because of the sin2ϑk dependence of the electron emission, this mechanism is most efficient in collisions where the polar orientation angle of the dimer is large. In contrast, the most “comfortable” geometry for the DF-3 mechanism is where the angle ΘR ≈ ΘK between the dimer orientation vector R and the collision velocity v is small. At small ΘR the transverse distance R⊥, whose value determines the efficiency of the DF-3 mechanism, can remain not very large even at large R. This is why the maximum in the spectra in Figure 3 is located at smaller energies compared to that in Figure 6.
In Figure 7 we show the energy spectrum of the helium ions. The abrupt fall of the spectrum intensity at EK > 10 eV is due to an extreme rapid decrease of the probability to find the He2 dimer with the decreasing distance R in the range of R ≲ 5–6 a. u.
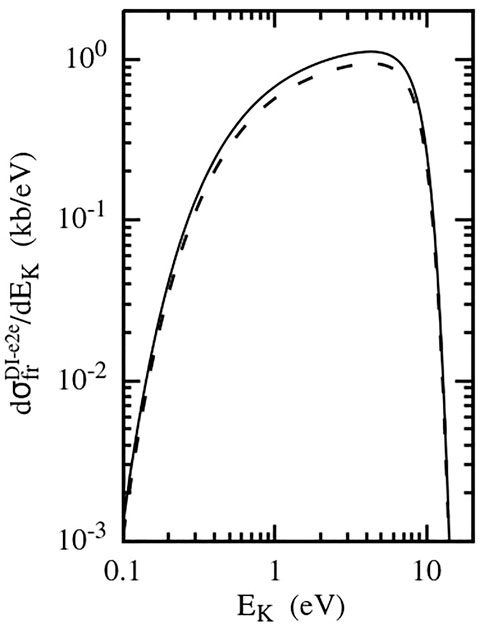
FIGURE 7. Cross-section
The shape of the energy spectra in Figures 4, 7 is rather similar. However, the dependence of their intensity on parameter η = Zp/v is much stronger for the DF-3 mechanism since it involves more interactions with the projectile.
The angular spectra in Figure 8 qualitatively differ from those in Figure 5 since the DI-e2e and DF-3 mechanisms favor very different collision geometries. In addition, the shape of the angular distribution in Figure 8 is very similar for collisions with both projectiles, whereas in Figure 5 this shape significantly varies reflecting not only the different values of the parameter η but also different effective interaction ranges.
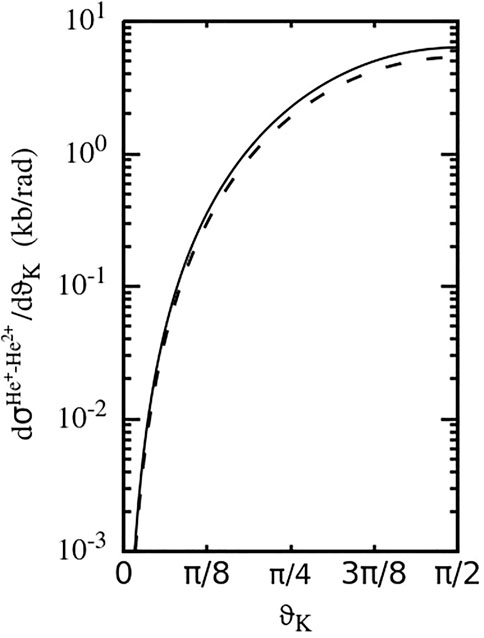
FIGURE 8. Cross-section
As it follows from Figures 3 - 8 (see also Table 1), the absolute values of the DF-3 and DI-e2e cross-sections in very fast collisions with highly charged projectiles at η = Zp/v ∼ 1 differ by two orders of magnitude. Thus, in such collisions, the DF-3 mechanism fully dominates the fragmentation of the He2 into He2+-He+ ions and our discussion of the DI-e2e mechanism might seem to be just of academic interest.
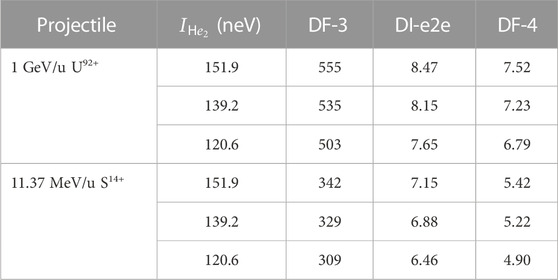
TABLE 1. Total cross-sections (in kb) for the He2 fragmentation via the DF-3, DI-e2e, and DF-4 mechanisms in collisions with 1 GeV/u U92+ and 11.37 MeV/u S14+ projectiles calculated for three different values of the dimer binding energy
However, this is not the case since the shape of the spectra of ionic fragments produced via the DI-e2e mechanism remains essentially the same when the parameter η decreases. The DF-3 and DI-e2e cross-sections scale roughly as ∼ η6 and ∼ η4, respectively. Therefore, in very fast collisions with highly charged ions, for which η is significantly less than 1, the relative importance of the DI-e2e mechanism greatly increases and can have a noticeable impact on the fragmentation process. Indeed, our preliminary calculations for the breakup of the He2 dimer by 1 GeV/u Ca20+ projectiles (η ≈ 0.16) indicate that in such collisions the DI-e2e mechanism is already clearly seen in the energy-angular and angular distributions of the ionic fragments.
4 Fragmentation with the emission of four electrons
4.1 The fragmentation mechanisms for the reaction Zp + He2 → Zp + He2+ + He2+ + 4 e−
As in triple ionization, quadruple ionization of the He2 dimer in collisions with fast projectiles may proceed both via the interaction(s) between the projectile and the electrons of the dimer and the interaction(s) between the electrons. The minimum number of such interactions is equal to four. The analysis shows that the reaction (2) can occur via the following fragmentation mechanisms with all of them involving basically four interactions.
1. First, the projectile—in a single collision—knocks out all four electrons of the dimer. The electrons quickly escape and the bare helium nuclei, repealing each other, gain kinetic energy. We shall refer to this mechanism as direct (DF-4).
2. Second, the projectile also interacts with both sites of the dimer in a single collision. This leads to the “instantaneous” formation of the triply charged system, He2+ + He+. Then, one of the electrons emitted from the doubly ionized site of the dimer moves toward the He+ and knocks out the remaining bound electron producing the second doubly charged helium ion. This mechanism is, thus, a combination of double and single ionization events caused by the (direct) interaction with the projectile and the e2e process on a helium ion. We shall denote this mechanism as double ionization–single ionization—e2e (DI-SI-e2e).
3. Third, the projectile interacts with just one site of the dimer. As a result of this interaction, the site becomes doubly ionized. One of the emitted electrons moves toward the other site and doubly ionizes it. This mechanism is a combination of double ionization of the helium atom by a high-energy projectile and the e3e process on helium. This mechanism can be referred to as double ionization—e3e (DI-e3e).
4. Fourth, in this mechanism, the first step is exactly the same as in the DI-e3e. Now, however, both electrons emitted from one site of the dimer directly by the projectile participate in double ionization of the other site. This mechanism is a combination of double ionization of the helium atom by a high-energy projectile and double ionization by the impact of two electrons. This mechanism can be denoted as double ionization—2e4e (DI-2e4e).
5. In the last—fifth—mechanism, the projectile singly ionizes both sites of the dimer. Each of the emitted electrons moves toward the “foreign” helium ion, knocking out the remaining electron there. This mechanism is a combination of two single ionization events due to the direct interactions with the projectile and two e2e processes on singly charged helium ions. This mechanism can be denoted as single ionization—single ionization—e2e—e2e (SI-SI-e2e-e2e).
We have not yet performed a detailed analysis of all five fragmentation mechanisms which result in He2 breakup into He2+ ions. However, it is quite evident that all of them are “instantaneous” on the time scale, characterizing the motion of the helium ions.
Furthermore, one can expect that among the mechanisms involving the electron–electron interaction, the last two are less efficient. Moreover, keeping in mind our results for the fragmentation with emission of three electrons, it becomes rather evident that in collisions with highly charged projectiles at η ≲ 1 the process of fragmentation into two He2+ ions will be strongly dominated by the DF-4 mechanism, and in what follows, we shall fully concentrate on it.
4.2 The direct fragmentation mechanism
Our consideration of the DF-4 mechanism largely follows that of the DF-3. We shall again use the semi-classical approach and the independent electron approximation.
The probability of
Here,
The cross-section for the formation of the He2+–He2+ system in collisions between the He2 dimer with a given inter-nuclear vector R and the projectile reads
Since the ionization probability
Using the cross-section (21), which describes the quadruple ionization of the He2 dimer that has a fixed inter-nuclear vector R at the collision instant, we found that the fragmentation cross-section differential in the kinetic energy release EK and the fragmentation angle ΘK is given by
where Q = 2 is the charge of the ionic fragments.
4.3 Numerical results and discussion
Our numerical results for the cross-sections
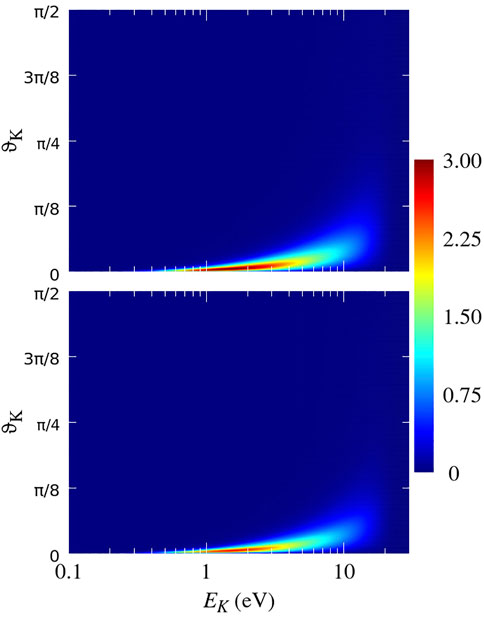
FIGURE 9. Cross-section
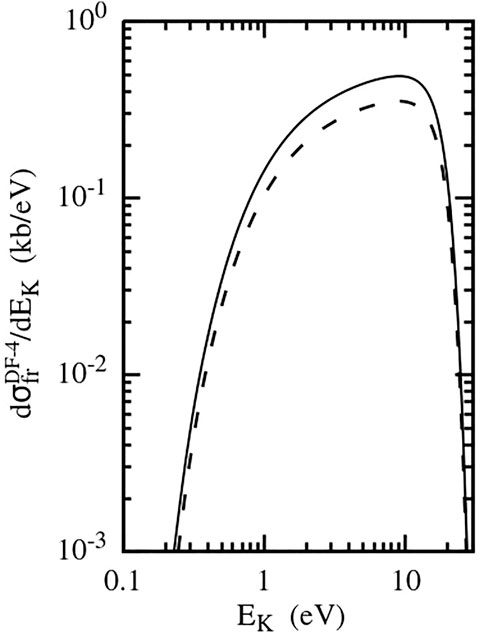
FIGURE 10. Cross-section
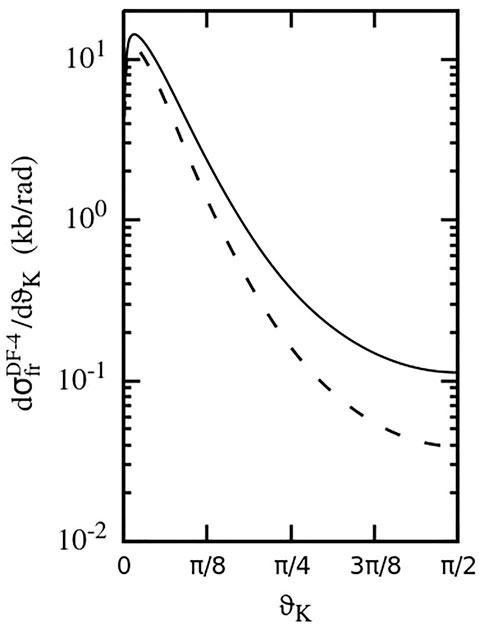
FIGURE 11. Cross-section
The maximal values of the transverse dimer size R⊥, at which the DF-4 mechanism can still be efficient, are significantly smaller than those for the DF-3. As a result, the process of fragmentation into two He2+ ions is characterized by an even much narrower angular distribution than that driven by DF-3 (compare Figures 9, 11 with Figures 3, 5).
The energies typical for the DF-4 are about two times larger than those for the DF-3 (compare Figures 9, 10 with Figures 3, 4). Since in the breakup into two He2+ ions, the product of the charges of the fragments is twice as large, the aforementioned difference in typical energies is an indication that the main contribution to the DF-4 and DF-3 is given by roughly the same range of the inter-nuclear distances R of the He2 dimer.
5 The total fragmentation cross-sections
Table 1 shows the results for the total cross-sections for the breakup of the He2 dimer into He2+ + He+ ionic fragments and into two α particles caused by collisions with 1 GeV/u U92+ and 11.37 MeV/u S14+ projectiles. The contributions of the DF-3 and DI-e2e mechanisms to the production of He2+ + He+ ions are given separately.
A few conclusions can be drawn from these results. First, fragmentation occurring with the emission of three electrons is strongly dominated by the DF-3 mechanism whose cross-sections exceed by almost two orders of magnitude those for the DI-e2e. Second, comparing the results for collisions with 1 GeV/u U92+ and 11.37 MeV/u S14+ we see that, as expected, the decrease in the parameter η = Zp/v results in a relative enhancement of the DI-e2e mechanism. Third, the cross-section for the fragmentation into the He2+–He+ pair is by two orders of magnitude larger than the cross section for the breakup into two bare helium nuclei. However, it is interesting to note that at η ∼ 1 the field of a projectile is so efficient in ionizing the sites of the dimer that the cross-section for the DF-4 mechanism, which involves (at least) four interactions (all with the projectile), can be about the same as that for the DI-e2e, where the minimal number of interactions is smaller (3) but the e2e process is involved.
The results of our calculations for differential cross-sections shown in Figures 3, 4, 5, 6, 7, 8, 9, 10, 11 were obtained by describing the ground state of the He2 dimer by a wave function Ψi corresponding to the dimer binding energy
The inspection of the table suggests that the cross-sections for all three mechanisms depend on
The origin of this dependence can be understood as follows. The He2 dimer is a very weakly bound system which spends most of the time in the classically forbidden region. Suppose that in the range of the inter-nuclear distances Rmin ≲ R ≲ Rmax , which yields the main contribution to the fragmentation events, the wave function Ψi(R) of the dimer can be approximated by a wave function of a system bound by a zero-range force, which has the form
6 Conclusion
In conclusion, we have theoretically explored the fragmentation of the He2 dimer into He2+–He+ and He2+–He2+ ionic pairs by fast highly charged projectiles in collisions, where the parameter η = Zp/v remains well below 1. In particular, calculations performed in this study were carried out for 1 GeV/u U92+ and 11.37 MeV/u S14+ projectiles, where η ≈ 0.77 and η ≈ 0.67, respectively.
We have described the main fragmentation mechanisms which drive these processes and shown that they all are essentially instantaneous on the time scale of the motion of the helium ions. At η ≲ 1 the most important are the direct mechanisms, in which the projectile produces the He2+–He+ and He2+–He2+ fragments by directly removing three and four electrons, respectively, from the He2 dimer in a single collision event. The interaction between the electrons during the fragmentation process in these mechanisms essentially plays no role.
The other fragmentation mechanisms, in addition to the interaction with the projectile, also involve the interaction between the electrons. Here, the projectile directly removes only a part of the necessary amount of electrons and the rest of them are ejected via the e2e or e3e processes in which an electron emitted from one site of the dimer by the projectile moves toward the other site, knocking out one or two electrons present there. At η ≲ 1 these mechanisms contribute very little to the total fragmentation. However, compared to the direct mechanisms, their cross-sections have a different dependence on η, becoming relatively more important when η decreases. In particular, our preliminary estimates show that in fast collisions at η ≲ 0.2 the mechanism for fragmentation into He2+–He+ ions, which involves double ionization of one site of the dimer and e2e process on the other site, already yields a significant contribution.
We have shown that in fast collisions with highly charged projectiles, the fragmentation into He2+–He+ ions is driven by the direct DF-3 mechanism, where the projectile removes three electrons from the dimer and the DI-e2e mechanisms, which involves double ionization of one site of the dimer by the projectile and the e2e process on the other site. They lead to a qualitatively different pattern in the angular distribution of the helium ions. At η ≲ 1 the DF-3 mechanism strongly dominates; however, at η ≲ 0.2 the DI-e2e mechanism already yields a significant contribution.
For the fragmentation into two He2+ ions, we have calculated only the contribution of the direct fragmentation mechanism (DF-4), which is expected to be highly dominant at η ≲ 1. This mechanism is characterized by the angular distribution of the He2+ ions, which is strongly aligned along the projectile velocity and the energy distribution extending to more than 20 eV.
In collisions with 1 GeV/u U92+ and 11.37 MeV/u S14+ projectiles, the total cross-sections for the fragmentation into He2+–He+ ions are about 0.5 and 0.3 Mb, respectively. The cross-section for the breakup into He2+ ions is about two orders of magnitude smaller. We have found that the total cross-sections depend on the binding energy
Finally, it is interesting to note that at η ∼ 1, the field of a projectile is so efficient in ionizing the dimer sites that the cross-section for the direct fragmentation (DF-4) into He2+, which necessitates (minimum) four interactions with the projectile, is about as strong as the fragmentation via the DI-e2e mechanism, where the minimal number of interactions is smaller (3)but the e2e process is involved.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Acknowledgments
BN, SZ, and XM gratefully acknowledge the support from the “National Key Research and Development Program of China” (Grant No. 2017YFA0402300) and the CAS President’s Fellowship Initiative. Our numerical results were obtained using the facilities of the Supercomputer Center HIRFL at the Institute of Modern Physics of the Chinese Academy of Sciences (Lanzhou, China).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Grisenti RE, Schöllkopf W, Toennies JP, Hegerfeldt GC, Köhler T, Stoll M. Determination of the bond length and binding energy of the helium dimer by diffraction from a transmission grating. Phys Rev Lett (2000) 85:2284–7. doi:10.1103/physrevlett.85.2284
2. Friedrich BA. A fragile union between Li and He atoms. Physics (2013) 6:42. doi:10.1103/physics.6.42
3. Titze J, Schöffler MS, Kim H-K, Trinter F, Waitz M, Voigtsberger J, et al. Ionization dynamics of helium dimers in fast collisions with He++. Phys Rev Lett (2011) 106:033201. doi:10.1103/PhysRevLett.106.033201
4. Kim H-K, Gassert H, Titze JN, Waitz M, Voigtsberger J, Trinter F, et al. Orientation dependence in multiple ionization of He2 and Ne2 induced by fast, highly charged ions: Probing the impact-parameter-dependent ionization probability in 11.37-MeV/u S14+ collisions with He and Ne. Phys Rev A (2014) 89:022704. doi:10.1103/PhysRevA.89.022704
6. Najjari B, Wang Z, Voitkiv AB. Probing the helium dimer by relativistic highly charged projectiles. Phys Rev Lett (2021) 127:203401. doi:10.1103/PhysRevLett.127.203401
7. Najjari B, Zhang SF, Ma X, Voitkiv AB. Fragmentation of the 4He2 dimer by relativistic highly charged projectiles in collisions with small kinetic energy release. Phys Rev A (2022) 105:062807. doi:10.1103/PhysRevA.105.062807
8. Havermeier T, Jahnke T, Kreidi K, Wallauer R, Voss S, Schoffler M, et al. Single photon double ionization of the helium dimer. Phys Rev Lett (2010) 104:153401. doi:10.1103/physrevlett.104.153401
9. Havermeier T, Jahnke T, Kreidi K, Wallauer R, Voss S, Schoffler M, et al. Interatomic coulombic decay following photoionization of the helium dimer: Observation of vibrational structure. Phys Rev Lett (2010) 104:133401. doi:10.1103/physrevlett.104.133401
10. Sisourat N, Kryzhevoi NV, Kolorenč P, Scheit S, Jahnke T, Cederbaum LS. Ultralong-range energy transfer by interatomic Coulombic decay in an extreme quantum system. Nat Phys (2010) 6:508–11. doi:10.1038/nphys1685
11. Zeller S, Kunitski M, Voigtsberger J, Kalinin A, Schottelius A, Schober C, et al. Imaging the He2 quantum halo state using a free electron laser. Proc Natl Acad Sci U S A (2016) 113:14651–5. doi:10.1073/pnas.1610688113
12.For example, in collisions of 1 GeV/u U92+ with He the radiative electron capture cross section σrec ≃ 10−23 cm2 (see e.g. results for radiative recombination on p. 272 of [13]) is about 8 orders of magnitude smaller than the cross section for single ionization of He σi ≈ 10−15 cm2 (see e.g. [15]). The process of nonradiative electron capture is characterized by even much weaker cross sections.
14. Voitkiv AB, Koval AV. Cross sections for hydrogen and helium ionization by impacts of fast highly charged ions. J Phys B (1998) 31:499–513. doi:10.1088/0953-4075/31/3/017
15. Voitkiv AB, Najjari B, Moshammer R, Ullrich J. Helium single ionization in relativistic collisions with highly charged ions. Phys Rev A (2002) 65:032707. doi:10.1103/physreva.65.032707
16.The calculations were performed by using Eqs. (4) and the symmetric eikonal approximation (see Subsection III.D).
17. Moshammer R, Schmitt W, Ullrich J, Kollmus H, Cassimi A, Dörner R, et al. Ionization of helium in the attosecond equivalent light pulse of 1 GeV/nucleon U92+ projectiles. Phys Rev Lett (1997) 79:3621. doi:10.1103/PhysRevLett.79.3621
18. Stolterfoht N., DuBois R. D., Rivarola R. D. Electron emission in heavy ion-atom collisions (1997). Springer handbook of atomic, molecular, and optical Physics. Editor G. W. F. Drake (Springer, Berlin: Springer Nature Switzerland AG). Chapter 57 (2023).
19. Shah MB, Elliott DS, McCallion P, Gilbody HB. Single and double ionisation of helium by electron impact. J Phys B (1988) 21:2751–61. doi:10.1088/0953-4075/21/15/019
21. Dolder KT, Harrison MFA, Thonemann PC. A measurement of the ionization cross-section of helium ions by electron impact. Proc R Soc Lond Ser A Math Phys Sci (1961) 264:367. doi:10.1098/rspa.1961.0205
22.The integration of the energy spectra over the relevant energy intervals shows that the corresponding ratio is 1:1.
23. Voitkiv AB, Najjari B. Ionization of helium by relativistic highly charged ions within the symmetric eikonal approximation. J Phys B (2004) 37:4831–48. doi:10.1088/0953-4075/37/24/009
24. Martin F, Salin A. Accurate evaluation of multiple-excitation cross sections from one-electron amplitudes. Phys Rev A (1997) 55:2004–8. doi:10.1103/physreva.55.2004
25. Voitkiv AB, Najjari B, Ullrich J. Four-body quantum dynamics of helium double ionization by relativistic highly charged ion impact. J Phys B (2005) 38:L107–14. doi:10.1088/0953-4075/38/7/l01
26. Voitkiv AB, Grün N, Scheid W. Hydrogen and helium ionization by relativistic projectiles in collisions with small momentum transfer. J Phys B (1999) 32:3923–37. doi:10.1088/0953-4075/32/15/321
27. Najjari B, Voitkiv AB. Photofragmentation of large dimers into singly charged ions via the knockout mechanism. Phys Rev A (2021) 104:033104. doi:10.1103/physreva.104.033104
28. Feltgen R, Kirst H, Köhler KA, Pauly H, Torello F. Unique determination of the He2ground state potential from experiment by use of a reliable potential model. J Chem Phys (1982) 76(5):2360–78. doi:10.1063/1.443264
29. Janzen AR, Aziz RA. An accurate potential energy curve for helium based on ab initio calculations. J Chem Phys (1997) 107(3):914–9. doi:10.1063/1.474444
Keywords: helium dimer, fragmentation, fast highly charged ions, three-electron emission, four electron emission, (e, 2e) collisions
Citation: Najjari B, Zhang SF, Ma X and Voitkiv AB (2023) Fragmentation of the 4He2 dimer with the emission of three or four electrons by fast highly charged projectiles. Front. Phys. 11:1145511. doi: 10.3389/fphy.2023.1145511
Received: 16 January 2023; Accepted: 02 March 2023;
Published: 30 March 2023.
Edited by:
Michael Charlton, Swansea University, United KingdomReviewed by:
Roberto Rivarola, Instituto de Física Rosario, ArgentinaIlya Fabrikant, University of Nebraska-Lincoln, United States
Copyright © 2023 Najjari, Zhang, Ma and Voitkiv. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. B. Voitkiv, dm9pdGtpdkB0cDEudW5pLWR1ZXNzZWxkb3JmLmRl
 B. Najjari
B. Najjari S. F. Zhang1
S. F. Zhang1 X. Ma
X. Ma