Transportation of Fe3O4-SiO2-Al2O3/EO and SiO2-Al2O3/EO nanoparticles in magnetized Reiner–Philippoff liquid, including modified fluxes via Galerkin algorithm: Significance of EMHD

This developing study is focused on mass diffusion and thermal energy enhancement in Reiner–Philippoff martial across a vertical-surface under an exposed Lorentz force. Characterization of the thermal energy and mass diffusion are modified utilizing non-Fourier’s theory in the presence of a heat source. Three types of nanoparticles—${Al}_2{O}_3$, titanium dioxide, and ${TiO}_2$—in engine oil are inserted for production of heat energy. Darcy’s Forchheimer theory is used to analyze behavior flow and heat energy. Moreover, effects related to Dufour and Soret are added. A transformed system of ODEs is achieved regarding the developed model using similarity variables. Numerically developing models in the form of ODEs are handled with the aid of the finite element method (FEM). Fluidic thermal energy is augmented against upshot values of time relaxation number. Fluidic concentration declines against changes in Schmidt number and chemical reaction number.

1 Introduction

Non-Newtonian fluids have numerous applications and are used extensively in many materials. This investigation deals with Sutterby nanofluid boundary-layer flow in a stretched cylinder by including updated models for mass and heat transfers and applying the Cattaneo–Christov theory. Boundary-layer analysis leads to the creation of a mathematical model. By utilizing conservation principles, the physical phenomena are first generated in terms of PDEs. The penetrating medium is influenced by the advanced Darcy’s law. The suggested model’s non-linear equations are optimally and dynamically investigated. By establishing the conservation rules for mass, momentum, energy, and concentration, non-linear partial differential equations (PDEs) are created. The OHAM is adopted and aims to develop numerical solutions for non-linear systems, as previously discussed [1]. Nanofluids are the newest category of fluids, and Choi first described them at the beginning of 1995. Akbar et al. [2] formulated a model of peristaltic transport in the presence of thermal conductive using variable viscosity-based temperature with carbon nanoparticles; the authors found the exact solution of the developed model. Akram et al. [3] utilized curved microchannels to investigate heat transfer and flow behavior in the presence of titanium dioxide in Carneau fluid rheology; the authors estimated the motion of nanoparticles using mechanisms of thermophoretic and Brownian motion via an exact solution technique. Maraj et al. [4] discovered the consequences of Lorentz force, including CNTs and thermal deposition in the channel, utilizing exact closed-form solutions involving radiation and magnetic field. Akram et al. [5] studied thermal features of peristaltic transport involving Lorentz force and electroosmosis with SWCNTs in aqueous diagrams. Multiple industrial and technological implications, including wire drawing, glass fiber production, assembly of particularly elastic sheets, and cooling of concerning metallic plates are among the pertinent themes investigated previously [6] regarding the study of fluid attributes in multiple mathematical models. When a fixed magnetic field was supplied, Bhandari and Husain carefully examined the combined impacts particularly of rotating viscosity and magnetized force subjected to a 2D Ferro hydrodynamic non-conductor nanoliquid flow across a stretched surface. To explore the hybrid nanomaterials’ flow demeanor when subjected to a stretched sheet, Gul et al. presented a computer model. Fractional calculus ideas have been widely used in different areas in recent years. This topic has recently expanded in several different directions, including fractional-order multipoles influenced by electromagnetism and in the field of electrochemistry. Moreover, tracer is used within the fluid flow demeanor, the neuron model in the field of biology, finance, and signal processing. The Riemann–Liouville and Caputo fractional derivatives are the most popular applications discussed by Shah and Khan [7]. Biomedical engineering and medical care greatly benefit from the radiation and magnetic field impacts appertaining to nanofluids. Khan et al. [8] examined gold particle performance toward the blood flow demeanor (Sisko fluid flow) through a penetrating, slick, curvy surface. Partial slip impacts were considered in thoroughly analyzing the properties referring to nanofluidic flow. After Choi’s original study, a significant advancement in this field was made. In an experimental study, Eastman et al. examined heat transfer in the presence of Al₂O₃ and CuO particles, synthesized using ethylene glycol and water, respectively. Investigation based on blood flow demeanor in small arteries involves many variable features. Understanding the rheological behavior of blood and other biological fluids, namely urine, spermatozoa, and eye drops, requires accounting for heat conductivity and viscosity change. In the current work, which was motivated by these applications, we describe the peristaltic flow demeanor—particularly Ree–Eyring liquid via a uniform compliant channel—while accounting for the influence of varying thermal conductivity and viscosity, as described previously [9]. Recent studies have shown a particular interest in dusty fluid model flows due to their two-phase nature. This effect occurs when solid particles are dispersed in fluid (gas or liquid) flows. As an example, consider the chemical process that results in droplet formation when relatively small dust particles agglomerate, leading to high dusty-air velocity. Cosmic dust, a mixture of gas and dust particles, is the essential precursor for planetary systems, as expressed previously [10]. In tabular and graphical formats, Khan and Pop [11] examined fluctuation in declining Nusselt and reduced Sherwood numbers. Falkner–Skan flow is one of the most well-known motives for investigating magnetohydrodynamics, on account of its applications in the field of fluid dynamics and heat transfer. In the scientific community, conventional flow behavior, specifically Newtonian and non-Newtonian fluids subjected to a moving wedge, is very popular right now. Lin et al. investigated the properties of heat transmission within the static wedge flow demeanor. The authors examined the model particularly for every conceivable finite Prandtl number value. Watanabe and Watanabe and Pop, respectively, researched forced and free-convection Falkner–Skan flow. Akbar et al. [12] discussed investigations into shape factors associated with SiO₂/MoS₂ nanoparticles in a base fluid in a channel including a temperature gradient (oscillatory). Convection may occur in three different ways in heat transfer flows: naturally, forcibly, and mixed. The last of these has uses in a variety of industrial and natural phenomena, including nuclear reactor cooling, electronic systems, and heat exchangers used to heat or cool fluids in the food industry and in compact heat exchangers, as studied previously [13]. In numerous systems pertaining to heating and cooling, fluids including water and kerosene oil, ethylene, and glycol are frequently utilized. Most of these fluids, which are sometimes referred to as the basic fluids, are poor heat conductors. We must address the issues caused by these systems' weak conductivities in order to improve their performance. Nowadays, a relatively novel approach is being used to increase thermal conductivity and other thermal characteristics. Habib et al. [14] discussed a new discovery regarding nanofluid behavior in clinical isolates of Staphylococcus aureus using gold nanoparticles. Alghamdi et al. [15] favored adopting non-linear stretching sheets. These crucial industrial applications drove researchers to carefully examine boundary-layer flow demeanor over linear and non-linear prolonged sheets of a range of geometric thicknesses. Micropolar nanofluidic flow demeanor embedded with buoyancy force, along with magnetic field subjected to an enclosure, has been studied for its heat and mass transmission mechanism. The proposed mathematical model needed to assess effectiveness, particularly nanoparticle thermal efficiency, must be built using mass and energy and must be within the momentum equations. This study aims to increase the effectiveness of heat and mass transmission within the heat transport machinery and heat-ameliorated units used in engineering and industrial operations. The proposed dimensionless 2D model given the significance of dimensional analysis analyzed previously [16]. The substandard thermal conductivity of operating liquids, which constrains high solidity and performance appertaining to thermal production within heat exchanges, is currently a serious worldwide problem. Most frequently, ethanol and water, as well as an acetone and an ethylene–glycol combination, are used as working fluids, as discussed previously [17]. Additionally, in response to this issue, numerous scientists and engineers have demonstrated the essential principles of improving thermal properties, specifically for energy-transported liquids, and efficiency, particularly of heat transfer in industrial appliances.

Examining entropy production in catalytic and non-linear thermal radiative impacts involves assessing the hydromagnetic stagnation point flow demeanor of a micropolar nanofluid. A water nanofluid is created by mixing in the magnetite nanoparticles. The time-independent, significant 2D flow demeanor is supposed to start with a vertically stretchable sheet. When creating the governing equations for the relevant issue, the Joule heating and viscous dissipation impacts are considered, as described previously [18]. Using updated heat and mass flux models, the entropy production approach is subjected to Maxwell nanofluid incorporated with gyrotactic microorganisms influenced by homogeneous–heterogeneous processes. Amended models are provided using the dual diffusive theory and the generalized Fick’s equation. According to boundary-layer theory, derived equations that depict the flow situation under consideration are modeled as PDEs. An appropriate transformation is then applied to alter the resulting PDEs toward the transformed ODEs and is subsequently solved using a powerful technique called the optimal homotopy analysis approach. Special instances of certain previously published research are in close accordance with our findings. Graphs are used to describe the effects, specifically of physical factors within the velocity, as well as temperature, concentration, reaction rate, the concentration of motile bacteria, and entropy production, as examined in an earlier study [19]. Based on the three-dimensional and steady power-law for nanofluidic flow demeanor close to the stagnation point area, the MHD and non-linear thermal radiative impacts included in penetrable material are applied to conduct an entropy generation study. The heat transformation phenomena inside the boundary layer configured by the stretchy moving disc are investigated and accompanied by non-uniformly thermal radiative heat source/sink exposed to convective boundary circumstances. The basic fluid ethylene glycol (C₂H₆O₂) is combined with multi-wall carbon nanotubes (MWCNTs). The suggested fluid flow issue is analytically modeled, as discussed previously [20]. Incompressible viscous hybrid nanofluid flow is analyzed in three dimensions in a rotating frame. The basic liquid is ethylene glycol, and the nanoparticles are copper and silver. Fluid flows within the dual parallel surfaces, with the bottom surface extending linearly. Since fluid conducts, a consistent magnetic field is applied. We consider the viscous dissipation impacts and Joule heating and non-linear thermal radiations. The Nusselt number and surface drag force are addressed as interesting quantities. Xia et al. [21] examined the rate of entropy formation. Because of their significant industrial applications and high heat transfer rates, nanofluids are of great importance to scientists. Hybrid nanofluids, a brand-new form of nanofluid, have lately been employed to accelerate heat transfer even further. The current phenomena focus particularly on the investigation of SWCNT–MWCNT/water hybrid nanofluidic flow demeanor and on heat transmission subjected to a moving wedge. The flow demeanor in the porosity media is described by the Darcy–Forchheimer relationship. In addition, Ahmad et al. [22] covered in depth the effect of varying viscosity and velocity, as well as thermal slip, thermal radiation, and heat production. By performing a theoretical study, peculiarly viscous three-dimensional fluid flow demeanor incorporated with gyrotactic microorganisms across a non-linear stretchy surface, heat mechanisms, and mass transmission may be understood. To regulate the flow of fluid, the fluctuating magnetic field is thought to be normal toward the stretchy surface. The varying thermal conductivity prompts a discussion of thermal transportation. Mass transportation incorporates chemical processes and variable mass diffusion properties. The porous medium is defined using the Darcy–Forchheimer equation. To improve diffusion, Abdelsalam and Sohail [23] included Brownian motion and thermophoresis. The current study investigates viscous fluid flow in three dimensions when specific heat (PHF) and concentration (PCF) fluxes are present. Chemical reactions, viscosity dissipation, and Joule heating impacts are all considered when the mathematical formulation is being constructed. Fluid becomes electrically conductive when influenced by the applied magnetic field, whereas the non-linear system referring to ordinary differential equations is obtained by appropriate transformations. The resultant non-linear system determines the solution. To investigate the effects, particularly the physical factors, of the temperature and concentration distributions, graphs are plotted. Maraj et al. [24] estimated rotational flow and motion of hybrid nanoparticles with Hall currents in a vertical channel using conditions of thermal periodic and velocity slip via closed-form solutions. Saleem et al. [25] adopted FEM for statistical solutions, referring to a set of ODEs. Damaged arteries with stenosis have reduced blood flow; the accumulation of plaque within the artery walls, brought on by fats and oils, leads to the development of this stenosis. Multiple stenoses may exist in an artery that has severe stenosis. Multiple stenoses cause the artery to narrow, which restricts blood flow across it. Many academics have recently been interested in examining this particular kind of stenotic artery. Blood flows through tiny channels, with non-Newtonian behavior in big vessels and Newtonian behavior in smaller vessels. Owing to various peculiarities, particularly blood circulation along with the mechanical characteristics of the vessel walls, it is essential to examine the blood flow through a stenotic channel. Shahzad et al. [26] determined the location of stenosis on the vessel wall and the flow behavior through sick blood arteries by observing blood flow across a stenotic artery. In this investigation, the contributions of viscous dissipation and thermophoresis, as well as Brownian motion, gravitational effects, and stratification impacts, were examined. Physical events are derived as linked systems of partial differential equations. An appropriate transformation converts the model’s equation system into straightforward ordinary differential equations (ODEs). Naz et al. [27] used an ideal homotopy analysis approach and an improvised system that relies on coupled non-linear ODEs solved in Mathematica. Due to its use in several sectors, heat transfer is crucial. Hybrid nanofluidic flow, a novel manner of nanofluids with a greater heat exponent in comparison to the nanofluids, is being utilized to improve the ability of regular fluids to transport heat. In a base fluid, two-element nanoparticles are known as hybrid nanofluids (HNFs). Jamshed et al. [28] demonstrated the properties of steady hybrid nanofluidic flow and thermal transfer over a slippery surface. Convection, whether forced or natural, is more significant in the context of fluid dynamics than the other two well-known heat transfer processes, conduction and radiation. It happens because of differences in the thermal energy that is applied differently to various parts of the fluid under examination. Akram et al. [29] discussed theoretical investigations of thermal transfer based on Au and Ag hybrid water-based nanoparticles induced by electroosmotic pumping in a microchannel. Due to their poor heat conductivity, pure liquids like water and oil have proven to be problematic in this respect. To improve heat transmission and modify the carrier fluid’s thermal characteristics, nanoparticles with an approximate diameter of less than 100 nm, materials with intensified thermal conductivities, are mixed along with the fluid, as discussed previously [30]. This analysis emphasizes the importance of radiation and Joule heating effects, particularly for Casson liquid-boundary layer flow (BLF) configured by a linearly elongating surface, as well as the properties of momentum and entropy production. Likewise, species and thermal dissemination are also considered. Thermal conductivity and mass diffusion coefficient models that vary with temperature are used to provide thermal and species transportation. Emerging issues take the non-linear partial differential equations form, in opposition to the principles governing the movement of mass, momentum, heat, and species. The exhibited issue may be transformed into ordinary differential equations with the proper modification. Sohail et al. [31] used the optimal homotopy analysis method (OHAM) as a competent and dependable approach for obtaining numerical solutions, specifically for upgraded boundary-layer ordinary differential equations (ODEs). Due to its applicability, heat transfer analysis in two-dimensional flows has drawn the interest of several academics in recent years. Akram et al. [32] derived features of electroosmotic flow by inserting silver nanoparticles and solving using two various approaches. Applications like drawing wire, making plastic and rubber sheets, cooling electric plates enclosed by a bath, melt spinning, and hot rolling, among others, all benefit from fluid passage over elongating sheets. Because a plate expands at a specific rate, Sakiadis was the first to examine fluid flow. Crane then concentrated on the laminar flow demeanor, specifically two-dimensional, incompressible, and viscous fluid subjected to a stretching plate. There is a precise closed-form solution to this problem. Following the above-mentioned studies, many researchers (see, for instance, [33]) concentrated on fluid flow caused by stretched plates. These researchers investigated flow demeanor across an exponentially stretching sheet with the impacts of MHD and radiation, and discovered that the magnetic and radiation parameters are what reduce the heat transmission rate. The authors looked across the Eyring–Powell fluid boundary-layer fluid flow configured by a linearly stretching sheet and computed the findings for velocity profiles using the collocation method.

2 Mathematical analysis

Two-dimensional consequences of mass diffusion and thermal fields of a complex fluid (Reiner–Philippoff) were investigated under conditions of EMHD on a vertical plate. Three phases of hybrid nanomaterial are implemented in the presence of engine oil. Fields associated with mass diffusion and thermal conductivity are carried out by heat sink and non-Fourier’s theory, as well as variable properties pertaining to mass diffusion and thermal conductivity. A flow diagram with boundary conditions and suspension of ternary hybrid nanoparticles is shown in Figure 1. Conservation laws have been implemented to obtain distributions for motion, concentration, and thermal conductivity, as listed below. The thermophysical properties of different used materials are depicted in Table 1.

FIGURE 1

FIGURE 1. Physical configuration of the model.

TABLE 1

TABLE 1. Thermal properties of engine oil, silicon dioxide, and aluminum oxide [36, 37].

The reduced form of PDEs [34–36] is derived as

$\begin{array}{c}\frac{\partial v_1}{\partial x}+\frac{\partial v_2}{\partial y}=0,\\ v_1\frac{\partial v_1}{\partial x}+v_2\frac{\partial v_1}{\partial y}+\frac{{\nu }_{THnf}}{k^{*}}f{v}_1=\frac{1}{{\rho }_{Thnf}}\frac{\partial \mathit{\tau }}{\partial y}-{\frac{{\sigma }_{THnf}}{{\rho }_{Thnf}}B}_0^2{v}_1+\frac{B_0^2\left(x\right)}{{\rho }_{Thnf}}EB-G{\left({\beta }_1\right)}_{Thnf}\left(T-T_{\infty }\right),\end{array}(1)$

$-\frac{f}{{\left(k^{*}\right)}^{12}}{v_1}^2-G{\left({\beta }_2\right)}_{Thnf}\left(C-C_{\infty }\right),(2)$

$\begin{array}{c}{v}_1\frac{\partial T}{\partial x}+v_2\frac{\partial T}{\partial y}+{\gamma }_1\left[\begin{array}{c}{v_1}^2\frac{{\partial }^{2}T}{\partial x^2}+{v_2}^2\frac{{\partial }^{2}T}{\partial y^2}+2v_1{v}_2\frac{{\partial }^{2}T}{\partial x\partial y}+\left(v_1\frac{\partial v_1}{\partial x}+v_2\frac{\partial v_1}{\partial x}\right)\frac{\partial T}{\partial x}\\ +\left(v_1\frac{\partial v_2}{\partial x}+v_2\frac{\partial v_2}{\partial x}\right)\frac{\partial T}{\partial y}-\frac{Q_0}{{\left({\rho C}_p\right)}_{hnf}}\left(v_1\frac{\partial T}{\partial x}+v_2\frac{\partial T}{\partial y}\right)\end{array}\right]\\ =\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{\partial }{\partial y}\left(k_{Thnf}^T\frac{\partial T}{\partial y}\right)+\frac{Q_0}{{\left({\rho C}_p\right)}_{Thnf}}\left(T-T_{\infty }\right),\end{array}(3)$

$\begin{array}{c}{v}_1\frac{\partial C}{\partial x}+v_2\frac{\partial C}{\partial y}+{\gamma }_2\left[\begin{array}{c}{v_1}^2\frac{{\partial }^{2}C}{\partial x^2}+{v_2}^2\frac{{\partial }^{2}C}{\partial y^2}++2v_1{v}_2\frac{{\partial }^{2}C}{\partial x\partial y}+\left(v_1\frac{\partial v_1}{\partial x}+v_2\frac{\partial v_1}{\partial x}\right)\frac{\partial C}{\partial x}\\ +\left(v_1\frac{\partial v_2}{\partial x}+v_2\frac{\partial v_2}{\partial x}\right)\frac{\partial C}{\partial y}-K_M\left(v_1\frac{\partial C}{\partial x}+v_2\frac{\partial C}{\partial y}\right)\end{array}\right]\\ =K_M\left(C-C_{\infty }\right)+\frac{\partial }{\partial y}\left(D_{Thnf}\frac{\partial C}{\partial y}\right)\end{array}(4)$

and subjected to the desired boundary conditions

$v_1=a{x}^{\frac{1}{3}},C=C_w,v_2=0,T=T_w:y=0,{C\to C_{\infty },v}_1\to 0,T\to T_{\infty }:y\to \infty .(5)$

Similarity, the variables of temperature-dependent concentration and temperature-dependent thermal conductivity are defined as

$\mathrm{\phi }=\frac{C-C_w}{C_w-C_{\infty }},\eta =\frac{y}{x^{1/3}}{\left(\frac{a}{{\nu }_f}\right)}^{1/2},\mathrm{\psi }=x^{2/3}{\left(a{\nu }_f\right)}^{1/2},\mathrm{\tau }={\rho }_f{\left(a^3{\nu }_f\right)}^{1/2},\mathrm{\theta }=\frac{T-T_w}{T_w-T_{\infty }},(6)$

$k_{Thnf}^t=k_{Thnf}\left[1+{ϵ}_1\left(\frac{T-T_{\infty }}{T_w-T_{\infty }}\right)\right],(7)$

$D_{Thnf}^c=D_{Thnf}\left[1+{ϵ}_2\left(\frac{T-T_{\infty }}{T_w-T_{\infty }}\right)\right].(8)$

The system of ODEs [34] is formulated as

$D_{1}G-F^{″}\frac{G^2+\lambda {\mathrm{{\rm Y}}}^2}{G^2+{\mathrm{{\rm Y}}}^2}=0,(9)$

$G^{\prime }-D_1\frac{1}{3}{F^{\prime }}^2+D_1\frac{2}{3}F{F}^{″}-\frac{{\sigma }_{Thnf}}{{\sigma }_f}M{F}^{\prime }+D_1{\lambda }_1\theta -ϵF^{\prime }-D_1{F}_r{F^{\prime }}^2+D_1{\lambda }_2\phi +\frac{{\sigma }_{Thnf}}{{\sigma }_f}M{E}_1=0,(10)$

$\begin{array}{c}{\left(1+{ϵ}_1\theta \right)\theta }^{″}+{ϵ}_1{\left({\theta }^{\prime }\right)}^2+\mathit{Pr}\mathrm{\Gamma }\frac{k_f{\left(\rho C_p\right)}_{Thnf}}{k_{Thnf}{\left(\rho C_p\right)}_f}\left[F{F}^{\prime }{\theta }^{\prime }+\eta F^2{\theta }^{″}-H_{t}F{\theta }^{\prime }\right]\\ +\frac{k_f{\left(\rho C_p\right)}_{Thnf}}{k_{Thnf}{\left(\rho C_p\right)}_f}\frac{2}{3}PrF{\theta }^{\prime }+\frac{k_f}{k_{Thnf}}{H}_t\mathit{Pr}\theta =0,\end{array}(11)$

${\left(1+{ϵ}_2\phi \right)\phi }^{″}+{ϵ}_2{\phi }^{\prime }{\theta }^{\prime }+\frac{2}{3D_2}PrF{\phi }^{\prime }+\frac{Sc{\mathrm{\Gamma }}_1}{D_2}\left[F{F}^{\prime }{\phi }^{\prime }+\eta F^2{\phi }^{″}-K_{c}F{\phi }^{\prime }\right]-\frac{K_{c}Sc}{D_2}\phi =0.(12)$

Equation 5 in dimensionless form [34] is defined as

$F\left(0\right)=0,F^{\prime }\left(0\right)=1,\theta \left(0\right)=1,\phi \left(0\right)=1,F\left(\infty \right)\to 0,\theta \left(\infty \right)\to 0,\phi \left(\infty \right)\to 0.(13)$

The defined correlations associated with tri-hybrid nanoparticles [36] are

${\rho }_{Thnf}=\left(1-{\mathrm{\Phi }}_1\right)\left\{\left(1-{\mathrm{\Phi }}_2\right)\left[\left(1-{\mathrm{\Phi }}_3\right){\rho }_f+{\mathrm{\Phi }\mathrm{\Phi }}_3{\rho }_3\right]+{\mathrm{\Phi }}_2{\rho }_2\right\}+{\mathrm{\Phi }\mathrm{\Phi }}_1{\rho }_1,(14)$

$\frac{K_{hnf}}{K_{nf}}=\frac{K_2+2K_{nf}-2{\mathrm{\Phi }}_1\left(K_{nf}-K_2\right)}{K_2+2K_{nf}+{\mathrm{\Phi }}_2\left(K_{nf}-K_2\right)},D_2={\left(1-{\mathrm{\Phi }}_3\right)}^{1.5}{\left(1-{\mathrm{\Phi }}_1\right)}^{1.5}{\left(1-{\mathrm{\Phi }}_2\right)}^{1.5},(15)$

$\frac{K_{Thnf}}{K_{hnf}}=\frac{K_1+2K_{hnf}-2{\mathrm{\Phi }}_1\left(K_{hnf}-K_1\right)}{K_1+2K_{hnf}+{\mathrm{\Phi }}_1\left(K_{hnf}-K_1\right)},\frac{K_{nf}}{K_f}=\frac{K_3+2K_f-2{\mathrm{\Phi }}_3\left(K_f-K_3\right)}{K_3+2K_f+{\mathrm{\Phi }}_3\left(K_f-K_3\right)},(16)$

$\frac{{\sigma }_{Tnf}}{{\sigma }_{hnf}}=\frac{{\sigma }_1\left(1+2{\mathrm{\Phi }}_1\right)-{\mathrm{\Phi }}_{hnf}\left(1-2{\mathrm{\Phi }}_1\right)}{{\sigma }_1\left(1-{\mathrm{\Phi }}_1\right)+{\sigma }_{hnf}\left(1+{\mathrm{\Phi }}_1\right)},\frac{{\sigma }_{nf}}{{\sigma }_f}=\frac{{\sigma }_3\left(1+2{\mathrm{\Phi }}_3\right)+{\mathrm{\Phi }}_f\left(1-2{\mathrm{\Phi }}_3\right)}{{\sigma }_3\left(1-{\mathrm{\Phi }}_3\right)+{\sigma }_f\left(1+{\mathrm{\Phi }}_3\right)},{\mu }_{Thnf}=\frac{{\mu }_f}{{\left(1-{\mathrm{\Phi }}_3\right)}^{2.5}{\left(1-{\mathrm{\Phi }}_2\right)}^{2.5}{\left(1-{\mathrm{\Phi }}_1\right)}^{2.5}},(17)$

$D_1=\frac{\left[\left(1-{\mathrm{\Phi }}_2\right)\left\{\left(1-{\mathrm{\Phi }}_1\right)+{\mathrm{\Phi }}_1\frac{{{\rho }_s}_1}{{\rho }_f}\right\}\right]+{\mathrm{\Phi }}_2\frac{{{\rho }_s}_2}{{\rho }_f}}{{{\left(1-{\mathrm{\Phi }}_1\right)}^{-2.5}\left(1-{\mathrm{\Phi }}_2\right)}^{-2.5}},\frac{{\sigma }_{hnf}}{{\sigma }_{nf}}=\frac{{\sigma }_2\left(1+2{\mathrm{\Phi }}_2\right)+{\mathrm{\Phi }}_{nf}\left(1-2{\mathrm{\Phi }}_2\right)}{{\sigma }_2\left(1-{\mathrm{\Phi }}_2\right)+{\sigma }_{nf}\left(1+{\mathrm{\Phi }}_2\right)}.(18)$

The mathematical expressions of Sherwood number and temperature gradient [34] are

$Nu=\frac{-x{k}_{Thnf}\frac{\partial T}{\partial y}{|}_{y=0}}{{\left(T_w-T_{\infty }\right)k}_f},{\left(R_e\right)}^{-1/2}{N}^{*}u=-\frac{k_{Thnf}}{k_f}{\theta }^{\prime }\left(0\right),(20)$

$Sh=\frac{-x{Q}_t}{D_{Thnf}\left(C-C_{\infty }\right)},{\left(Re\right)}^{-1/2}{S}^{*}h=-\frac{1}{D_2}{\phi }^{\prime }\left(0\right),(21)$

where (Reynolds number) $Re\left(=\frac{U_{w}x}{{\nu }_f}\right).$

3 Numerical procedure

The current model in terms of ODEs is numerically handled by a finite element approach based on the following steps:

${\int }_{{\eta }_e}^{{\eta }_{e+1}}{wet}_1\left(F^{\prime }-T\right)d\eta =0,(22)$

${\int }_{{\eta }_e}^{{\eta }_{e+1}}{wet}_2\left[\begin{array}{c}{G}^{\prime }-D_1\frac{1}{3}{T}^2+D_1\frac{2}{3}F{T}^{\prime }-\frac{{\sigma }_{hnf}}{{\sigma }_f}MT+D_1{\lambda }_1\theta \\ -ϵT-D_1{F}_r{T}^2+D_1{\lambda }_2\phi +\frac{{\sigma }_{hnf}}{{\sigma }_f}M{E}_1\end{array}\right]d\eta =0,(23)$

${\int }_{{\eta }_e}^{{\eta }_{e+1}}{wet}_3\left[\begin{array}{c}\left(1+{ϵ}_1\theta \right){\theta }^{″}+{ϵ}_1{\left({\theta }^{\prime }\right)}^2++\frac{k_f{\left(\rho C_p\right)}_{Thnf}}{k_{Thnf}{\left(\rho C_p\right)}_f}\frac{2}{3}PrF{\theta }^{\prime }+\frac{k_f}{k_{hnf}}{H}_t\mathit{Pr}\theta \\ +\mathit{Pr}\mathrm{\Gamma }\frac{k_f{\left(\rho C_p\right)}_{Thnf}}{k_{hnf}{\left(\rho C_p\right)}_f}\left[FT\theta +\eta F^2{\theta }^{″}+H_{t}F\theta \right]\end{array}\right]d\eta =0,(24)$

${\int }_{{\eta }_e}^{{\eta }_{e+1}}{wet}_4\left[\begin{array}{c}\frac{Sc{\mathrm{\Gamma }}_1}{D_2}\left(FT{\phi }^{\prime }+\eta F^2{\phi }^{″}+K_{c}F{\phi }^{\prime }\right)-\frac{K_{c}Sc}{D_2}\phi \\ {\left(1+{ϵ}_2\phi \right)\phi }^{″}+{ϵ}_2\phi \theta \end{array}\right]d\eta =0.(25)$

3.1 Discretization

The computational form domain has been discretized into elements, and weighted residuals are derived as

${K_{ij}^{11}=0,K}_{ij}^{13}=0,{K_{ij}^{14}=0,K}_{ij}^{12}=-{{\displaystyle \int }}_{{\eta }_e}^{{\eta }_{e+1}}\left({\psi }_j{\psi }_i\right)d\eta ,B_i^1=0,(26)$

$K_{ij}^{22}={\int }_{{\eta }_e}^{{\eta }_{e+1}}\left[\begin{array}{c}-{\left(\frac{{\overline{G}}^2+\lambda {\mathrm{{\rm Y}}}^2}{{\overline{G}}^2+\lambda {\mathrm{{\rm Y}}}^2}\right)}^{\prime }\frac{d{\psi }_j}{d\eta }\frac{d{\psi }_j}{d\eta }-D_1\frac{1}{3}\overline{T}{\psi }_j{\psi }_i+D_1\frac{2}{3}\overline{F}{\psi }_i\frac{d{\psi }_j}{d\eta }-\frac{{\sigma }_{hnf}}{{\sigma }_f}M{\psi }_j{\psi }_i\\ -ϵ{\psi }_j{\psi }_i-D_1{F}_r\overline{H}{\psi }_i\frac{d{\psi }_j}{d\eta }\end{array}\right]d\eta ,(27)$

$K_{ij}^{23}={\int }_{{\eta }_e}^{{\eta }_{e+1}}\left[D_1{\lambda }_1{\psi }_j{\psi }_i\right]d\eta ,K_{ij}^{24}={\int }_{{\eta }_e}^{{\eta }_{e+1}}\left[D_1{\lambda }_2{\psi }_j{\psi }_i\right]d\eta ,B_i^2=\frac{{\sigma }_{hnf}}{{\sigma }_f}M{E}_1,K_{ij}^{21}=0,(28)$

$K_{ij}^{33}={\int }_{{\eta }_e}^{{\eta }_{e+1}}\left[\begin{array}{c}-\left(1+{ϵ}_1\theta +\mathit{Pr}\mathrm{\Gamma }\frac{k_f{\left(\rho C_p\right)}_{Thnf}}{k_{hnf}{\left(\rho C_p\right)}_f}\eta {\overline{F}}^2\right)\frac{d{\psi }_j}{d\eta }\frac{d{\psi }_j}{d\eta }+{ϵ}_1\overline{{\theta }^{\prime }}{\psi }_i\frac{d{\psi }_j}{d\eta }+\frac{k_f}{k_{hnf}}{H}_t\mathit{Pr}{\psi }_j{\psi }_i\\ \frac{k_f{\left(\rho C_p\right)}_{Thnf}}{k_{Thnf}{\left(\rho C_p\right)}_f}\frac{2}{3}\mathit{Pr}\overline{F}{\psi }_i\frac{d{\psi }_j}{d\eta }+r\mathrm{\Gamma }\frac{k_f{\left(\rho C_p\right)}_{Thnf}}{k_{hnf}{\left(\rho C_p\right)}_f}\left(\overline{F}\overline{T}{\psi }_i\frac{d{\psi }_j}{d\eta }+H_t\overline{F}{\psi }_i\frac{d{\psi }_j}{d\eta }\right)\end{array}\right]d\eta ,(29)$

$K_{ij}^{44}={\int }_{{\eta }_e}^{{\eta }_{e+1}}\left[\begin{array}{c}-\left(1+{ϵ}_2\overline{\phi }+\eta {\overline{F}}^2\right)\frac{d{\psi }_j}{d\eta }\frac{d{\psi }_j}{d\eta }+{ϵ}_2\overline{{\phi }^{\prime }}{\psi }_i\frac{d{\psi }_j}{d\eta }+\frac{2}{3}Sc\overline{F}{\psi }_i\frac{d{\psi }_j}{d\eta }-\frac{K_{c}Sc}{D_2}{\psi }_j{\psi }_i\\ \frac{Sc{\mathrm{\Gamma }}_1}{D_2}\left(\overline{F}\overline{T}{\psi }_i\frac{d{\psi }_j}{d\eta }+K_c\overline{F}{\psi }_i\frac{d{\psi }_j}{d\eta }\right)\end{array}\right]d\eta ,(30)$

$K_{ij}^{31}=0,K_{ij}^{41}=0,K_{ij}^{32}=0,K_{ij}^{42}=0,K_{ij}^{34}=0,K_{ij}^{43}=0,B_i^3=0,B_i^4=0.(31)$

3.2 Assembly process

The assembly process is implemented to derive a global stiffness matrix. In this step, the boundary vector, source vector, and stiffness matrix are obtained as.

3.3 Investigations of error and convergence

Error analysis is estimated as

$Er=\left|{\mathrm{\Omega }}^j-{\mathrm{\Omega }}^{j-1}\right|.(32)$

Table 2 shows mesh-free simulations and convergence analysis, while criteria regarding convergence are defined as

$\mathit{Max}\left|{\mathrm{\Omega }}^j-{\mathrm{\Omega }}^{j-1}\right|<{10}^{-8}.(33)$

TABLE 2

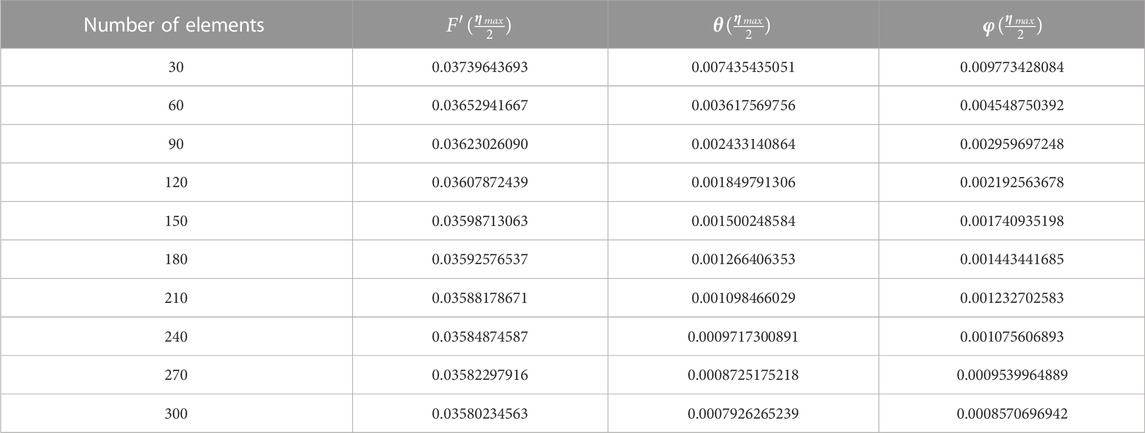
TABLE 2. Analysis of the grid-independent study carried out for 300 elements for concentration, velocity, and temperature profiles.

3.4 Validation of works

The code for FEM was designed in MAPLE 18. Table 3 illustrates the present validation in view of temperature gradient, with an already-published study [38] having different values of $\mathrm{{\rm Y}}$ in the absence of tri-hybrid nanoparticles, variable properties, heat sink, and non-Fourier’s law. It was noticed that the present results were obtained by the finite element method while the present simulations, obtained by the finite element method, are compared with a shooting approach termed the RK4-method (see Table 3).

TABLE 3

TABLE 3. Validation of present works for Nusselt number with different values of $\mathrm{{\rm Y}}$ when ${ϵ}_1=0,\mathrm{\Gamma }=0,{\mathrm{\Phi }}_1={\mathrm{\Phi }}_3={\mathrm{\Phi }}_2=0,H_t=0.$

4 Results and discussion

The development of a two-dimensional model is formulated in view of Reiner–Philippoff toward a surface involving buoyancy forces and electric field. Energy transfer and mass species are carried out in the presence. Dispersions of tiny nanoparticles are incorporated using generalized theory. Mass diffusion (variable) and thermal conductivity (variable) are inserted into the concentration and energy equations. A finite element scheme has been utilized to simulate numerical study of the present problem. Graphical explanations regarding flow, solute, and thermal energy versus various parameters are displayed in the following sections.

4.1 Study of fluidic motion

In this subsection, graphs related to velocity curves are plotted versus electric magnetic ($E_1$) number, Forchheimer number ($F_r$), and fluid parameter ($\gamma$). Comparative study of tri-hybrid nanofluid and hybrid nanoparticles on a velocity field is conducted versus parameters, shown in Figures 2–4. It is evident that solid curves are generated to represent the role of nanoparticles (tri-hybrid), and dash–dot lines are plotted to sketch the estimation of hybrid nanomaterials. Figure 2 predicts the behavior of $E_1$ on the velocity field. Here, $E_1$ is electric field number, and velocity increases versus enhancement in $E_1.$ Here, the parameter related to $E_1$ is known as the electric magnetic number; it is modeled using the electric magnetic number in the momentum equation. Mathematically, a parameter regarding $E_1$ is based on $\left(\frac{{\sigma }_{Thnf}}{{\sigma }_f}M{E}_1\right)$ and appears in the dimensionless momentum equation. Direct proportional relations have been estimated among velocity and $E_1.$ Therefore, velocity increases against $E_1>0.$ The physical reason behind this increasing trend is the appearance of a Lorentz force because forces (electromagnetic) behave in the same direction during the flow of nanoparticles. Furthermore, drag force declines when $E_1$ is enhanced. Thickness in view of momentum layers is increased against magnified values of $E_1.$ Figure 3 predicts the influence of $F_r$ on fluidic motion. Momentum layers are based on variation in $F_r.$ It is mentioned that a retardation motion is created in motion regarding particles, which creates a resistance force in fluidic particles. Momentum layers are also reduced using higher values of $F_r.$ Physical, numerous pores are placed at the surface. Therefore, velocity field is reduced when $F_r$ is increased. Moreover, $F_r$ is known as a Forchheimer porous medium, which is related to resistive force on the flow. It is a non-linear function versus velocity, while it experiences retardation force. Mathematically, the direct proportional relation among drag force and $F_r$ is increased when $F_r$ is enhanced. Thickness based on momentum layers declines versus enhancement of $F_r.$ This drag force reduces flow on the surface. Figure 4 shows the behavior of $\mathrm{{\rm Y}}$ on velocity curves. This is a dimensionless parameter that is modeled due to the appearance of Reiner–Philippoff liquid in the momentum. It is evident that fluidic motion is decreased when $\mathrm{{\rm Y}}$ increases. Moreover, thickness based on momentum layers declines with higher impacts of $\mathrm{{\rm Y}}.$ Mathematically, an inverse proportional relation has been observed among $\mathrm{{\rm Y}}$ and velocity. Therefore, an increase in $\mathrm{{\rm Y}}$ results in flow decreases on the surface. $\gamma$ is a dimensional parameter also called the Bingham number; it is a ratio among viscous stress and yield stress. Apparent viscosity has a direct proportional relation with increasing shear rate. Consequently, flow increases when shear rate is enhanced.

FIGURE 2

FIGURE 2. Effect of $E_1$ on velocity curves.

FIGURE 3

FIGURE 3. Effect of $F_r$ on velocity curves.

FIGURE 4

FIGURE 4. Effect of $\mathrm{{\rm Y}}$ on velocity curves.

4.2 Study of fluidic temperature

Figures 5–7 show the role of fluidic temperature against changes in $H_t$, ${ϵ}_1$, and ${\lambda }_1$. The solid lines are plotted to sketch the role of tri-hybrid nano-structures, while dash–dot lines are plotted to measure the role of hybrid nanoparticles. Figure 5 represents behavior among fluidic temperature and $H_t$. Fluidic temperature is increased by applying an external heat source at the wall. Mathematically, heat sink ($H_t$) is directly proportional to $\left(T-T_{\infty }\right)$, whereas temperature difference increases when $H_t$ is increased. In Figure 5, two types of heat transfer are experienced based on heat generation and heat absorption. Furthermore, heat absorption is numerically predicted by $H_t<0$, and heat generation is predicted by $H_t>0.$ Physically, the heat source (external) is implemented at the surface and is utilized to control thermal thickness. Thermal layer thickness for $H_t<0$ is higher than for $H_t>0.$ The characteristic of ${ϵ}_1$ on thermal layers is shown in Figure 6. The appearance ${ϵ}_1$ is created due to the appearance of variable thermal conductivity. In the current investigation, thermal conductivity is considered as a function of thermal energy. Mathematically, thermal conductivity is based on temperature, whereas ${ϵ}_1$ is based on $\left(T_w-T_{\infty }\right)$. An increase in ${ϵ}_1$ enhances the temperature difference. Mathematically, ${ϵ}_1$ is a function of temperature difference. Consequently, temperature difference is based on ${ϵ}_1.$ Hence, temperature increases against increases in thermal conductivity. Moreover, the thickness of thermal layers for ${ϵ}_1=0$ is less than the thickness (of thermal layers) for ${ϵ}_1\ne 0.$ Whether an involvement of the time relaxation parameter is created due to the appearance of a generalized mechanism of heat transmission is investigated. $\mathrm{\Gamma }$ denotes relaxation time number, and $\mathrm{\Gamma }$ reveals production regarding time related to migration of heat energy through a heated surface. Physically, fluid particles need more time in the case of transfer of thermal energy toward neighboring particles. This reason declines in thermal energy, as depicted in Figure 7.

FIGURE 5

FIGURE 5. Effect of $H_t$ on thermal energy curves.

FIGURE 6

FIGURE 6. Effect of ${ϵ}_1$ on thermal energy curves.

FIGURE 7

FIGURE 7. Effect of $\mathrm{\Gamma }$ on thermal energy curves.

4.3 Investigation of fluidic concentration

Figures 8–10 determine the characterizations of fluidic concentration versus impacts of $Sc,K_c$, and ${ϵ}_2$ upon inserting a tri-hybrid nanofluid. Solid lines are the sketched behavior of tri-hybrid nanofluid, while dash–dot lines are sketched for hybrid nanofluid. Figure 8 reveals the role of $Sc$ on fluidic concentration in the presence of hybrid and tri-hybrid nanofluids. Physically, it is the division of momentum and mass diffusion diffusivities. Hence, an inverse proportional relation of mass diffusion is found versus $Sc$. Therefore, an increase in $Sc$ resulting form higher mass diffusivity is observed. Moreover, mass diffusion for tri-hybrid nanofluids is higher than the amount of mass diffusion for hybrid nano-structures. This reduction of $\phi \left(\eta \right)$ occurs when mass diffusivity decreases against higher values of $Sc.$ Thickness related to concentration can be managed through numerical values of $Sc.$ Furthermore, the amount of mass diffusion for $Sc=0$ is less than the amount of mass diffusion for $Sc\ne 0.$ Figure 9 demonstrates the relationship between mass diffusion and variable mass diffusion number; it shows that the appearance of ${ϵ}_2$ on mass diffusion is created due to the implication of variable mass diffusion. Furthermore, variable mass diffusion is based on temperature difference. Therefore, mass diffusion declines when ${ϵ}_2$ is increased. From Eq. 8, it was shown that ${ϵ}_2$ is a function of temperature difference. Consequently, ${ϵ}_2$ is also based on concentration difference, while mass diffusion increases when ${ϵ}_2$ is increased. An illustration of the chemical reaction parameter on mass diffusion is shown in Figure 10. Two kinds of chemical reactions are generated for positive or negative numerical values of the chemical reaction parameters. For both cases, mass diffusion declines when $K_c$ is increased. Here, three cases of chemical reactions based on chemical parameters have been observed. It is estimated that $K_c<0$ when solute particles have been generated, while $K_c>0$ when solute particles are utilized in the chemical reaction and $K_c=0$ when no chemical reaction has occurred. As Figure 10 shows, increasing concentrations can be controlled by generative chemical reactions, whereas destructive chemical reactions are performed for increasing concentration tendency.

FIGURE 8

FIGURE 8. Effect of $Sc$ on concentration curves.

FIGURE 9

FIGURE 9. Effect of ${ϵ}_2$ on concentration curves.

FIGURE 10

FIGURE 10. Effect of $K_c$ on concentration curves.

4.4 Study of Sherwood number and Nusselt number

The impact of ${Al}_2{O}_3$-$Si{O}_2$-${Fe}_3{O}_4$/EO and $Si{O}_2$-${Fe}_3{O}_4$/EO on the Sherwood number and temperature gradient versus magnetic number, Schmidt number, $H_t$, and $K_c$ are observed. Numerical outcomes among ${Al}_2{O}_3$-$Si{O}_2$-${Fe}_3{O}_4$/EO and $Si{O}_2$-${Fe}_3{O}_4$/EO are recorded in Tables 4, 5. It was observed that temperature gradient and Sherwood number decline with various values of $H_t$ and $M.$ However, the opposite trend was estimated for Sherwood number and temperature gradient. Essentially, the thermal rate and Sherwood number are greater for ${Al}_2{O}_3$-$Si{O}_2$-${Fe}_3{O}_4$/EO than for $Si{O}_2$-${Fe}_3{O}_4$/EO (see Tables 4, 5).

TABLE 4

TABLE 4. Change in $H_t,M,Sc$, and $K_c$ on Sherwood and Nusselt numbers with ${Al}_2{O}_3$-$Si{O}_2$-${Fe}_3{O}_4$/EO.

TABLE 5

TABLE 5. Change in $H_t,M,Sc,$ and $K_c$ on Sherwood and Nusselt numbers with $Si{O}_2$-${Fe}_3{O}_4$/EO.

5 Conclusion

Features of fluidic motion, fluidic thermal energy, and fluidic concentration are determined in a two-dimensional model under non-Fourier’s law with variable properties. A heat source and chemical reactions are also taken out into a mixture of nanoparticles. A strong scheme, termed a finite element method, is utilized. The main findings of the problem are summarized as follows:

➢ Velocity field has been enhanced against changes in $H_t$, but the opposite behavior is observed versus $M$ and $F_r.$

➢ Heat energy increases against changes in relaxation number, heat source number, and variable thermal conductivity parameter.

➢ Fluidic concentration declines against changes in Schmidt number and chemical reaction parameter.

➢ The cooling process can be improved by adding ternary hybrid nano-structures rather than other nanoparticles.

➢ The highest production of thermal energy can be achieved utilizing tri-hybrid nanoparticles as compared with hybrid nanofluids and nanofluids.

➢ Thermal gradient and mass diffusion gradient are higher for ${Al}_2{O}_3$-$Si{O}_2$-${Fe}_3{O}_4$/EO than for $Si{O}_2$-${Fe}_3{O}_4$/EO.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This study was supported by funding from Prince Sattam bin Abdulaziz University (project number PSAU/2023/R/1444).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sohail M, Naz R. Modified heat and mass transmission models in the magnetohydrodynamic flow of Sutterby nanofluid in stretching cylinder. Physica A: Stat Mech its Appl (2020) 549:124088. doi:10.1016/j.physa.2019.124088

CrossRef Full Text | Google Scholar

2. Akbar NS, Maraj EN, Noor NFM, Habib MB. Exact solutions of an unsteady thermal conductive pressure driven peristaltic transport with temperature-dependent nanofluid viscosity. Case Stud Therm Eng (2022) 35:102124. doi:10.1016/j.csite.2022.102124

CrossRef Full Text | Google Scholar

3. Akram J, Akbar NS, Alansari M, Tripathi D. Electroosmotically modulated peristaltic propulsion of TiO2/10W40 nanofluid in curved microchannel. Int Commun Heat Mass Transfer (2022) 136:106208. doi:10.1016/j.icheatmasstransfer.2022.106208

CrossRef Full Text | Google Scholar

4. Maraj EN, Akbar NS, Iqbal Z, Azhar E. Framing the MHD mixed convective performance of CNTs in rotating vertical channel inspired by thermal deposition: Closed form solutions. J Mol Liquids (2017) 233:334–43. doi:10.1016/j.molliq.2017.03.041

CrossRef Full Text | Google Scholar

5. Akram J, Akbar NS, Tripathi D. Electroosmosis augmented MHD peristaltic transport of SWCNTs suspension in aqueous media. J Therm Anal Calorim (2022) 147(3):2509–26. doi:10.1007/s10973-021-10562-3

CrossRef Full Text | Google Scholar

6. Saeed A, Bilal M, Gul T, Kumam P, Khan A, Sohail M. Fractional order stagnation point flow of the hybrid nanofluid towards a stretching sheet. Scientific Rep (2021) 11(1):20429–15. doi:10.1038/s41598-021-00004-3

CrossRef Full Text | Google Scholar

7. Shah NA, Khan I. Heat transfer analysis in a second grade fluid over and oscillating vertical plate using fractional Caputo–Fabrizio derivatives. The Eur Phys J C (2016) 76(7):362–11. doi:10.1140/epjc/s10052-016-4209-3

CrossRef Full Text | Google Scholar

8. Khan U, Zaib A, Ishak A. Magnetic field effect on Sisko fluid flow containing gold nanoparticles through a porous curved surface in the presence of radiation and partial slip. Mathematics (2021) 9(9):921. doi:10.3390/math9090921

CrossRef Full Text | Google Scholar

9. Rajashekhar C, Mebarek-Oudina F, Vaidya H, Prasad KV, Manjunatha G, Balachandra H. Mass and heat transport impact on the peristaltic flow of a Ree–Eyring liquid through variable properties for hemodynamic flow. Heat Transfer (2021) 50(5):5106–22. doi:10.1002/htj.22117

CrossRef Full Text | Google Scholar

10. Rehman SU, Fatima N, Ali B, Imran M, Ali L, Shah NA, et al. The Casson dusty nanofluid: Significance of Darcy–forchheimer law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics (2022) 10(16):2877. doi:10.3390/math10162877

CrossRef Full Text | Google Scholar

11. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat mass transfer (2010) 53(11-12):2477–83. doi:10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

12. Akbar NS, Iqbal Z, Ahmad B, Maraj EN. Mechanistic investigation for shape factor analysis of SiO₂/MoS₂–ethylene glycol inside a vertical channel influenced by oscillatory temperature gradient. Can J Phys (2019) 97(9):950–8. doi:10.1139/cjp-2018-0717

CrossRef Full Text | Google Scholar

13. Laouira H, Mebarek-Oudina F, Hussein AK, Kolsi L, Merah A, Younis O. Heat transfer inside a horizontal channel with an open trapezoidal enclosure subjected to a heat source of different lengths. Heat Transfer—asian Res (2020) 49(1):406–23. doi:10.1002/htj.21618

CrossRef Full Text | Google Scholar

14. Habib MB, Akbar NS. New trends of nanofluids to combat Staphylococcus aureus in clinical isolates. J Therm Anal Calorim (2021) 143(3):1893–9. doi:10.1007/s10973-020-09502-4

CrossRef Full Text | Google Scholar

15. Alghamdi M, Wakif A, Thumma T, Khan U, Baleanu D, Rasool G. Significance of variability in magnetic field strength and heat source on the radiative-convective motion of sodium alginate-based nanofluid within a Darcy-Brinkman porous structure bounded vertically by an irregular slender surface. Case Stud Therm Eng (2021) 28:101428. doi:10.1016/j.csite.2021.101428

CrossRef Full Text | Google Scholar

16. Batool S, Rasool G, Alshammari N, Khan I, Kaneez H, Hamadneh N. Numerical analysis of heat and mass transfer in micropolar nanofluids flow through lid driven cavity: Finite volume approach. Case Stud Therm Eng (2022) 37:102233. doi:10.1016/j.csite.2022.102233

CrossRef Full Text | Google Scholar

17. Khan U, Zaib A, Shah Z, Baleanu D, Sherif ESM. Impact of magnetic field on boundary-layer flow of Sisko liquid comprising nanomaterials migration through radially shrinking/stretching surface with zero mass flux. J Mater Res Technol (2020) 9(3):3699–709. doi:10.1016/j.jmrt.2020.01.107

CrossRef Full Text | Google Scholar

18. Ishtiaq B, Zidan AM, Nadeem S, Alaoui MK. Analysis of entropy generation in the nonlinear thermal radiative micropolar nanofluid flow towards a stagnation point with catalytic effects. Physica Scripta (2022) 97(8):085204. doi:10.1088/1402-4896/ac79d7

CrossRef Full Text | Google Scholar

19. Sohail M, Naz R, Abdelsalam SI. On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Physica Scripta (2020) 95(4):045206. doi:10.1088/1402-4896/ab3c3f

CrossRef Full Text | Google Scholar

20. Ghaffari A, Mustafa I, Muhammad T, Altaf Y. Analysis of entropy generation in a power-law nanofluid flow over a stretchable rotatory porous disk. Case Stud Therm Eng (2021) 28:101370. doi:10.1016/j.csite.2021.101370

CrossRef Full Text | Google Scholar

21. Xia WF, Hafeez MU, Khan MI, Shah NA, Chung JD. Entropy optimized dissipative flow of hybrid nanofluid in the presence of non-linear thermal radiation and Joule heating. Scientific Rep (2021) 11(1):16067–16. doi:10.1038/s41598-021-95604-4

CrossRef Full Text | Google Scholar

22. Ahmad S, Nadeem S, Ullah N. Entropy generation and temperature-dependent viscosity in the study of SWCNT–MWCNT hybrid nanofluid. Appl Nanoscience (2020) 10(12):5107–19. doi:10.1007/s13204-020-01306-0

CrossRef Full Text | Google Scholar

23. Abdelsalam SI, Sohail M. Numerical approach of variable thermophysical features of dissipated viscous nanofluid comprising gyrotactic micro-organisms. Pramana (2020) 94(1):67–12. doi:10.1007/s12043-020-1933-x

CrossRef Full Text | Google Scholar

24. Maraj EN, Zehra I, SherAkbar N. Rotatory flow of MHD (MoS₂-SiO₂)/H₂O hybrid nanofluid in a vertical channel owing to velocity slip and thermal periodic conditions. Colloids Surf A: Physicochemical Eng Aspects (2022) 639:128383. doi:10.1016/j.colsurfa.2022.128383

CrossRef Full Text | Google Scholar

25. Saleem S, Gopal D, Shah NA, Feroz N, Kishan N, Chung JD, et al. Modelling entropy in magnetized flow of eyring–powell nanofluid through nonlinear stretching surface with chemical reaction: A finite element method approach. Nanomaterials (2022) 12(11):1811. doi:10.3390/nano12111811

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Shahzad MH, Awan AU, Akhtar S, Nadeem S. Entropy and stability analysis on blood flow with nanoparticles through a stenosed artery having permeable walls. Sci Prog (2022) 105(2):003685042210960. doi:10.1177/00368504221096000

CrossRef Full Text | Google Scholar

27. Naz R, Noor M, Shah Z, Sohail M, Kumam P, Thounthong P. Entropy generation optimization in MHD pseudoplastic fluid comprising motile microorganisms with stratification effect. Alexandria Eng J (2020) 59(1):485–96. doi:10.1016/j.aej.2020.01.018

CrossRef Full Text | Google Scholar

28. Jamshed W, Prakash M, Hussain SM, Eid MR, Nisar KS, Muhammad T, et al. Entropy amplified solitary phase relative probe on engine oil based hybrid nanofluid. Chin J Phys (2022) 77:1654–81. doi:10.1016/j.cjph.2021.11.009

CrossRef Full Text | Google Scholar

29. Akram J, Akbar NS, Tripathi D. A theoretical investigation on the heat transfer ability of water-based hybrid (Ag–Au) nanofluids and Ag nanofluids flow driven by electroosmotic pumping through a microchannel. Arabian J Sci Eng (2021) 46(3):2911–27. doi:10.1007/s13369-020-05265-0

CrossRef Full Text | Google Scholar

30. Alsabery AI, Hashim I, Hajjar A, Ghalambaz M, Nadeem S, Saffari Pour M. Entropy generation and natural convection flow of hybrid nanofluids in a partially divided wavy cavity including solid blocks. Energies (2020) 13(11):2942. doi:10.3390/en13112942

CrossRef Full Text | Google Scholar

31. Sohail M, Shah Z, Tassaddiq A, Kumam P, Roy P. Entropy generation in MHD Casson fluid flow with variable heat conductance and thermal conductivity over non-linear bi-directional stretching surface. Scientific Rep (2020) 10(1):12530–16. doi:10.1038/s41598-020-69411-2

CrossRef Full Text | Google Scholar

32. Akram J, Akbar NS, Tripathi D. Analysis of electroosmotic flow of silver-water nanofluid regulated by peristalsis using two different approaches for nanofluid. J Comput Sci (2022) 62:101696. doi:10.1016/j.jocs.2022.101696

CrossRef Full Text | Google Scholar

33. Sohail M, Ali U, Al-Mdallal Q, Thounthong P, Sherif ESM, Alrabaiah H, et al. Theoretical and numerical investigation of entropy for the variable thermophysical characteristics of couple stress material: Applications to optimization. Alexandria Eng J (2020) 59(6):4365–75. doi:10.1016/j.aej.2020.07.042

CrossRef Full Text | Google Scholar

34. Xiu W, Saleem S, Weera W, Nazir U. Cattaneo-Christove thermal flux in Reiner–Philippoff martial under action of variable Lorentz force employing tri-hybrid nanomaterial approach. Case Stud Therm Eng (2022) 38:102267. doi:10.1016/j.csite.2022.102267

CrossRef Full Text | Google Scholar

35. Hou E, Wang F, Nazir U, Sohail M, Jabbar N, Thounthong P. Dynamics of tri-hybrid nanoparticles in the rheology of pseudo-plastic liquid with dufour and soret effects. Micromachines (2022) 13(2):201. doi:10.3390/mi13020201

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Nazir U, Saleem S, Al-Zubaidi A, Shahzadi I, Feroz N. Thermal and mass species transportation in tri-hybridized Sisko martial with heat source over vertical heated cylinder. Int Commun Heat Mass Transfer (2022) 134:106003. doi:10.1016/j.icheatmasstransfer.2022.106003

CrossRef Full Text | Google Scholar

37. Nazir U, Mukdasai K. Combine influence of Hall effects and viscous dissipation on the motion of ethylene glycol conveying alumina, silica and titania nanoparticles using the non-Newtonian Casson model. AIMS Maths (2023) 8(2):4682–99. doi:10.3934/math.2023231

CrossRef Full Text | Google Scholar

38. Sajid T, Sagheer M, Hussain S. Impact of temperature-dependent heat source/sink and variable species diffusivity on radiative Reiner–Philippoff fluid. Math Probl Eng (2020) 2020:9701860. doi:10.1155/2020/9701860

CrossRef Full Text | Google Scholar

Nomenclature

$v_1\mathrm{a}\mathrm{n}\mathrm{d}{v}_2$ velocity components

$\nu$ dynamic viscosity

$\mathit{\tau }$ vector tensor

$G$ gravitational acceleration

$T$ fluidic temperature

$C$ concentration

$Q_0$ heat source

$C_p$ specific heat capacitance

$k$ thermal conductivity

${\gamma }_2\mathrm{a}\mathrm{n}\mathrm{d}{\gamma }_1$ time relaxation parameters

$C_w$ wall concentration

$\mathrm{\psi }$ stream function

PDEs partial differential equations

$\sigma$ electrical conductivity

$\mathit{Pr}$ Prandtl fluid

${\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2,{\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{\Phi }}_3$ volume fractions

$U_w$ wall difference

EO engine oil

$a$ stretching ratio number along the x-direction

$E_1$ electric field parameter

$ϵ$ porous number

$\theta$ dimensionless temperature

$\mathrm{\Gamma }\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{\Gamma }}_1$ time relaxation parameters

$nf$ nanofluid

$Nu$ Nusselt number

MHD magneto-hydrodynamics

FEM finite element method

$Sc$ Schmidt number

${wet}_4,{wet}_3,{wet}_1,{andwet}_2$ weight functions

$x\mathrm{a}\mathrm{n}\mathrm{d}y$ space coordinates

$f$ permeability

$B_0$ magnetic field

${\beta }_2\mathrm{a}\mathrm{n}\mathrm{d}{\beta }_1$ buoyancy parameters

$T_{\infty }$ ambient temperature

$C_{\infty }$ ambient concentration

$\rho$ density

$D$ mass diffusion

$K_M$ chemical reaction number

$T_w$ wall temperature

$\eta$ independent variable

${ϵ}_1\mathrm{a}\mathrm{n}\mathrm{d}{ϵ}_2$ very small numbers

$\lambda$ fluid number

$F_r$ Forchheimer number

$\phi$ concentration

$Re$ Reynolds number

ODEs ordinary differential equations

$H_t$ heat sink

$\mathrm{{\rm Y}}$ fluid number

$E$ electric field

$F\mathrm{a}\mathrm{n}\mathrm{d}G$ dimensionless velocity

EO engine oil

$Thnf$ tri-hybrid nanofluid

$s_1,s_3,\mathrm{a}\mathrm{n}\mathrm{d}{s}_2$ solid nanoparticles

$Sh$ Sherwood number

EMHD electric magneto-hydrodynamic

$K_c$ chemical reaction number

$Q_t$ wall flux