Studies of different kernel functions in nuclear mass predictions with kernel ridge regression

The kernel ridge regression (KRR) approach has been successfully applied in nuclear mass predictions. Kernel function plays an important role in the KRR approach. In this work, the performances of different kernel functions in nuclear mass predictions are carefully explored. The performances are illustrated by comparing the accuracies of describing experimentally known nuclei and the extrapolation abilities. It is found that the accuracies of describing experimentally known nuclei in the KRR approaches with most of the adopted kernels can reach the same level around 195 keV, and the performance of the Gaussian kernel is slightly better than other ones in the extrapolation validation for the whole range of the extrapolation distances.

1 Introduction

Nuclear mass is important for both nuclear physics [1] and astrophysics [2, 3]. During the past decades, great progress has been made in mass measurements of atomic nuclei, and about 2,500 nuclear masses have been measured to date [4]. Nevertheless, the masses of a large number of neutron-rich nuclei involved in the r-process remain unknown from experiments and cannot be measured even with the next-generation RIB facilities. Therefore, theoretical predictions for nuclear masses are imperative at the present time. Global mass model can be traced back to the von Weizsäcker mass formula based on the famous liquid drop model (LDM) [5]. Lots of efforts have been made in pursuing different possible extensions of the LDM, which are known as the macroscopic-microscopic models, such as the finite-range droplet model (FRDM) [6] and the Weizsäcker-Skyrme (WS) model [7]. The microscopic mass models based on the non-relativistic and relativistic density functional theories (DFTs) have also been developed [8–17]. The root-mean-square (rms) deviation between theoretical mass models and the available experimental data [4] range from about 3 MeV for the BW model [18] to about 300 keV for the WS ones [7], which is still not sufficient for accurate studies of exotic nuclear structure and astrophysical nucleosynthesis [19, 20]. What’s more, for neutron-rich nuclei far away from the experimentally known region, the differences among the predictions of different mass models can be as large as several tens MeV [6–11, 21–23].

Machine learning (ML) has been successfully applied in various fields of physics [24, 25]. For nuclear physics, ML applications can be traced back to early 1990s [26, 27], and recently, it has been widely adopted to nuclear masses [28–41], charge radii [36, 42–45], decays and reactions [46–53], ground and excited states [54–58], nuclear landscape [59, 60], fission yields [61–63], nuclear liquid-gas phase transition [64], variational calculations [65, 66], nuclear energy density functional [67], etc. In nuclear mass studies, ML approaches, such as the radial basis function (RBF) approach [28, 29, 68–71], the Bayesian neural network (BNN) approach [31–33, 72], and the kernel ridge regression (KRR) approach [36, 37, 41, 73], have been employed to further improve the accuracies of nuclear mass models. By training the machine learning network with the mass model residuals, i.e., deviations between experimental and calculated masses, machine learning approaches can significantly reduce the corresponding rms deviation to below 200 keV.

The KRR approach was employed to improve nuclear mass predictions for the first time in Ref. [36]. It is shown that the extrapolation behavior of the KRR approach is quite different with other approaches, e.g., the RBF approach. The RBF approach would worsen the mass descriptions for nuclei at large extrapolation distances, as the effects of the adopted linear kernel remain large at such distances. However, the KRR approach can automatically identify the limit of the extrapolation distance and avoid the risk of worsening the mass description for nuclei at large extrapolation distances, which is due to the decay behavior of the Gaussian kernel as the increase of extrapolation distance. This reflects the importance of kernel function in nuclear mass predictions with kernel-based machine learning approaches.

There are many commonly-used kernel functions in the KRR approach. The detail features of different kernels are different, which can affect the performances of the KRR approach in nuclear mass predictions. It is therefore necessary to study the effects of different kernel functions on the performances of the KRR approach in the practical applications of nuclear mass predictions.

In this work, the performances of the KRR approach for nuclear mass predictions with different kernel functions, including Gaussian, Laplacian, Matern, Cachy, Multiquadric, inverse Multiquadric, Logarithm, power, and inverse power kernels, are compared. The paper is organized as follows: In Section 2, the theoretical framework of the KRR approach is introduced. The numerical details are given in Section 3. In Section 4, the comparisons through the leave-one-out cross-validation and extrapolation validation are presented. Finally, a summary is given in Section 5.

2 Theoretical framework

The KRR approach is a powerful machine-learning approach for non-linear regression and has been successfully applied in nuclear mass predictions [36]. In this method, the KRR function is written as

$S\left({\mathit{x}}_j\right)={\displaystyle \sum _{i=1}^m}K\left({\mathit{x}}_j,{\mathit{x}}_i\right)w_i,(1)$

where x_i ≡ (N_i, Z_i) are locations of nuclei in the nuclear chart, m is the number of training nuclei, w_i are weight parameters to be determined, K (x_j, x_i) is the kernel function, which measures the correlations between nuclei. The weight parameters w_i are determined by minimizing the loss function defined as

$L\left(\mathit{w}\right)={\displaystyle \sum _{i=1}^m}{\left[S\left({\mathit{x}}_i\right)-y\left({\mathit{x}}_i\right)\right]}^2+\lambda \Vert \mathit{w}{\Vert }^2,(2)$

where w = (w₁, … , w_m). The first term of Eq. 2 is the variance between the data y (x_i) and the KRR prediction S(x_i), and the second is the penalty term that penalizes large weights to reduce the risk of overfitting. The hyperparameter λ determines the strength of penalty. Minimizing Eq. 2 yields

$\mathit{w}={\left(\mathit{K}+\lambda \mathit{I}\right)}^{-1}\mathit{y},(3)$

where K is the kernel matrix with elements K_ij = K (x_i, x_j), and I is the identity matrix.

Nine kernel functions are adopted in the present study, i.e., the Gaussian kernel K(r) = exp (−r²/2σ²), the Laplacian kernel K(r) = exp (−r/σ), the Matern kernel K(r) = (1 + 3r/5σ) exp (−3r/5σ), the Cachy kernel K(r) = 1/(1 + r²/σ), the Multiquadric (MQ) kernel $K(r)=\sqrt{r^2+{\sigma }^2}$, the inverse MQ kernel $K(r)=1/\sqrt{r^2+{\sigma }^2}$, the Logarithm kernel K(r) = ln (r^σ + 1), the power kernel K(r) = r^σ, and the inverse power kernel K(r) = 1/r^σ, where the Euclidean norm $r=\Vert {\mathit{x}}_i-{\mathit{x}}_j\Vert =\sqrt{{(N_i-N_j)}^2+{(Z_i-Z_j)}^2}$ is defined to be the distance between two nuclei. The adjustable hyperparameter σ ≥ 0 in each kernel plays an important role in the performance of the corresponding kernel, and should be carefully tuned according to the nuclear mass data.

3 Numerical details

The KRR function (1) is trained to reconstruct the mass residuals, i.e., the deviations M_res (N, Z) = M_exp (N, Z) − M_th(N, Z) between the experimental data M_exp and theoretical predictions M_th for a given mass model. Once the weights w_i are obtained, the reconstructed function S (N, Z) can be calculated with Eq. 1 for every nucleus (N, Z). The predicted mass for a nucleus (N, Z) is, thus, given by M_KRR = M_th(N, Z) + S(N, Z).

The experimental masses M_exp are taken from the AME2020 [4], while only those nuclei with Z, N ≥ 8 and experimental errors σ^exp < 100 keV are considered. There are totally 2340 data composing the entire data set. The theoretical masses M_th are taken from the mass table WS4 [7].

One of the hyperparameters, i.e., penalty strength λ, had been carefully validated to be 0.3 for the KRR study of nuclear masses in Ref. [36], which would be adopted in this study.

4 Results and discussion

The main purpose of this work is to compare the performances of different kernel functions in the KRR approach for nuclear mass predictions. The performances are illustrated by comparing the accuracies of describing experimentally known nuclei and the extrapolation abilities, through the leave-one-out cross-validation and the extrapolation validation.

4.1 Leave-one-out cross-validation

The leave-one-out cross-validation is adopted to evaluate the accuracy of the KRR approach with different given types of kernel functions. In the leave-one-out cross-validation, for a given set of hyperparameters (σ, λ), the mass prediction for each of the 2,340 nuclei is obtained by the KRR network trained on all other 2,339 nuclei. The rms deviation Δ_rms between experimental and predicted masses of the 2,340 nuclei is calculated and regarded as a measure of the accuracy.

There are mainly two advantages of the leave-one-out cross-validation. First, it avoids the randomness caused by the random sampling in the validation-set method. Second, it matches the idea that when one wants to predict the mass of an unknown nucleus, information of all the other nuclei with experimentally known masses would be considered to build the model.

In Figure 1, the Δ_rms between the KRR predictions with different kernels and the experimental data are shown as functions of the corresponding hyperparameter σ, respectively. The minima of the Δ_rms between the experimental data and the theoretical nuclear mass predictions, as shown in Figure 1 for every kernels, are listed in Table 1, together with the corresponding hyperparameters σ.

FIGURE 1

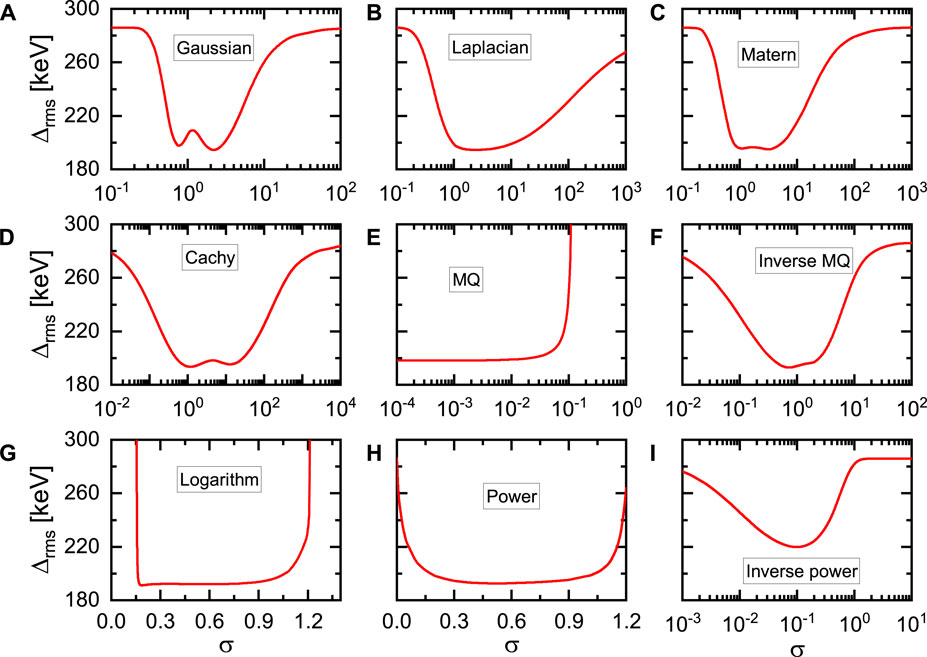
FIGURE 1. The Δ_rms between the KRR predictions with different kernels (A-I for nine different kernels) and the experimental data as functions of the corresponding hyperparameter σ.

TABLE 1

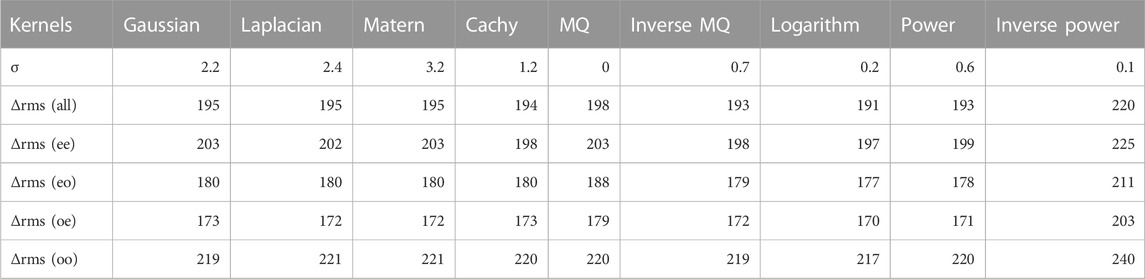
TABLE 1. The minima of the Δ_rms (in unit of keV) and the corresponding hyperparameters in the leave-one-out cross-validation for the KRR approach with different kernels.

As can be seen in both Figure 1; Table 1, if the hyperparameters σ are adjusted to proper values respectively, the KRR approach with most of the kernels can reduce the Δ_rms to similar level around 195 keV, except for the one with inverse power kernel, which reduces the Δ_rms to 220 keV. Note that for the MQ kernel $K(r)=\sqrt{r^2+{\sigma }^2}$, the predictions with smaller σ gives smaller Δ_rms, which indeed reduces to be the linear kernel K(r) = r when σ = 0. It is also noted that the Δ_rms increases rapidly as the decrease of the hyperparameter σ of the logarithm kernel approaching small values. This is because that the Logarithm kernel K(r) = ln (r^σ + 1) would approach to a constant ln (2) and lose the predicted power, when the σ is taken as a small value.

It is found that the predictions of the even-odd (eo) and odd-even (oe) nuclei are more accurate that the predictions of the even-even (ee) and odd-odd (oo) nuclei, which holds true for all the kernels. This is because the KRR prediction generates a smooth nuclear mass surface, which tends to average the predictions of all the nuclear masses. Generally speaking, the ee nuclei are most bound and the oo nuclei are least bound, while the eo and oe nuclei are in-between. Therefore, the smooth KRR prediction tends to have better descriptions of the eo and oe nuclei. If one want to well capture the odd-even effects and improve the nuclear mass predictions in the framework of KRR approach, the adopted kernel function should be remodulated to include the odd-even effects [37]. As is known, the shell effects commonly have an energy change of about 10 MeV between a magic nucleus and its mid-shell isotopes. Therefore, it is naturally believed that the shell effects can be captured by the KRR approach with precision of 195 keV.

The results from the leave-one-out cross-validation indicate that the KRR approach with different kernels can reach similar accuracies in interpolation or very short extrapolation, if proper values of hyperparameters are adopted. Therefore, in the applications of predicting nuclear masses for the nuclei that very close to the experimentally known region, the choices of different kernel functions may hardly affect the prediction accuracy.

4.2 Extrapolation validation

In order to examine the extrapolation abilities of the KRR approaches with different kernels, the set of nuclei with known masses is redivided as shown in Figure 2. For each isotopic chain of Z ≥ 26, the eight most neutron-rich nuclei are removed out from the training set, and they are classified into eight test sets respectively, corresponding to the different extrapolation distances from the remain training set in the neutron direction. This is the similar as the division in Refs. [36], but for Z ≥ 26. The rms deviations Δ_rms between the experimental and predicted masses of the eight test sets would be taken as a measure to compare the extrapolation abilities.

FIGURE 2

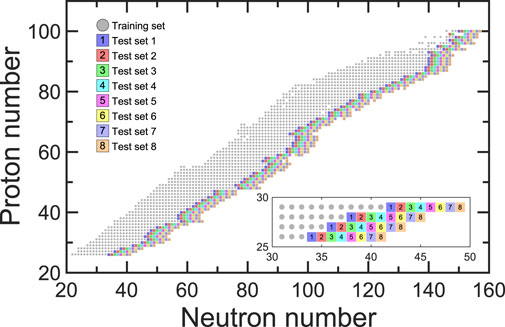
FIGURE 2. Nuclei in the training set (gray) and eight test sets (other colors) for examining the extrapolation power for the neutron-rich nuclei. The inset zoom in the region from Z = 26 to 29.

Figure 3 shows the Δ_rms of the eight test sets for the KRR approach with different kernels adopting the corresponding hyperparameters listed in Table 1, in comparison with the ones for the WS4 mass model. First of all, for the case of short extrapolation, i.e., extrapolation distance smaller than four, the KRR approach with all of the adopted kernels can reduce the Δ_rms obtained by the WS4 mass model. For the test sets with large extrapolation distances, i.e., extrapolation distance larger than four, the KRR approach with the MQ, logarithm, and power kernels obviously worsen the WS4 predictions. This is due to the fact that the corrections for the MQ, logarithm, and power kernels increase with the increasing of the Euclidean norm r. While, for the other six kernels, the corrections decrease with the increasing of the Euclidean norm r, which give them the abilities to reduce the risk of worsening the mass descriptions for nuclei at large extrapolation distances. The detail discussions can be seen in Ref. [36], where the Gaussian kernel is taken as an example.

FIGURE 3

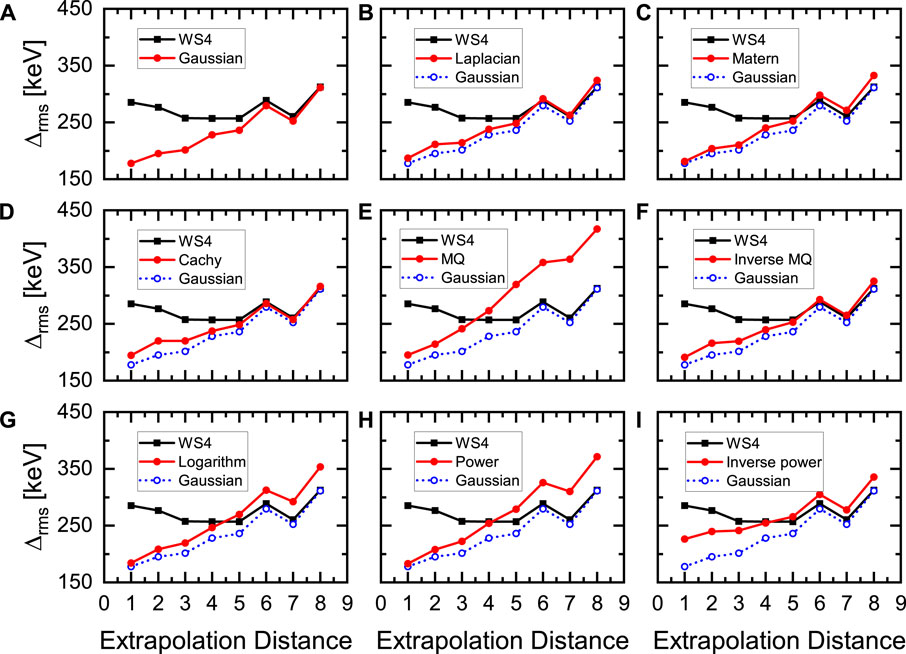
FIGURE 3. Comparison of the extrapolation power of the KRR approach with different kernels (A-I for nine different kernels) for eight test sets with different extrapolation distances.

The extrapolation performances of the KRR approach with the six kernels that the corrections decrease with the increasing of the Euclidean norm r are similar, except for the inverse power kernel. They can improve the mass predictions of the nuclei with extrapolation distance smaller than five, and reduce the risk of worsening mass predictions at large extrapolation distances. Among these adopted kernels, the performance of the Gaussian kernel is slightly better than other ones in the extrapolation validation for the whole range of the extrapolation distances. Therefore, the Gaussian kernel, which is commonly used in machine-learning, can be also taken as a default choice in the nuclear mass predictions.

5 Summary

The performances of different kernel functions, i.e., Gaussian, Laplacian, Matern, Cachy, Multiquadric, inverse Multiquadric, Logarithm, power, and inverse power kernels, in nuclear mass predictions with the KRR approach in describing experimentally known nuclei and extrapolating to neutron-rich nuclei are compared. The comparison is performed through the leave-one-out cross-validation and the extrapolation validation. From the leave-one-out cross-validation, it is found that the KRR approach with most of the kernels can reduce the Δ_rms to similar level around 195 keV. From the extrapolation validation, it is found that the performances of the kernel functions strongly depend on its increasing/decreasing behaviors with respect to the Euclidean norm r. For the case that the kernel functions decrease with the increasing of the Euclidean norm r, the corresponding KRR predictions can reduce the risk of worsening the mass predictions for nuclei at large extrapolation distances. Among these adopted kernels, the performance of the Gaussian kernel is slightly better than other ones in the extrapolation validation for the whole range of the extrapolation distances. Therefore, it is suggested to be taken as the default choice in the nuclear mass predictions.

In the present study, only the masses are considered as the outputs to train the ML models, and thus the obtained ML models are unable to predict other nuclear properties. However, the predictions of different nuclear properties by ML models at the same time can be achieved by the idea of multi-task learning. Multi-task learning (MTL) is a subfield of machine learning, in which multiple related learning tasks are solved at the same time by exploiting commonalities and differences across tasks. It has been successfully applied in nuclear physics, e.g., in the description of giant dipole resonance key parameters [58] and in the description of nuclear masses and separation energies [41]. It would be interesting to apply different kernels in the MTL framework in future works, in that case the performances and reliabilities of different kernels can be evaluated on additional nuclear properties.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www-nds.iaea.org/amdc/ame2020/mass_1.mas20.txt; http://www.imqmd.com/mass/WS4.txt.

Author contributions

XW conceived the idea, performed the calculations, and wrote the manuscript.

Funding

This work was partly supported by the National Key R&D Program of China (Contracts No. 2018YFA0404400 and No. 2017YFE0116700), the National Natural Science Foundation of China (Grants No. 11875075, No. 11935003, No. 11975031, No. 12141501, and No. 12070131001), the China Postdoctoral Science Foundation under Grant No. 2021M700256, and the High-performance Computing Platform of Peking University.

Acknowledgments

XW acknowledges P. W. Zhao and L. H. Guo for helpful discussions.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lunney D, Pearson JM, Thibault C. Recent trends in the determination of nuclear masses. Rev Mod Phys (2003) 75:1021–82. doi:10.1103/RevModPhys.75.1021

CrossRef Full Text | Google Scholar

2. Burbidge EM, Burbidge GR, Fowler WA, Hoyle F. Synthesis of the elements in stars. Rev Mod Phys (1957) 29:547–650. doi:10.1103/RevModPhys.29.547

CrossRef Full Text | Google Scholar

3. Mumpower M, Surman R, McLaughlin G, Aprahamian A. The impact of individual nuclear properties onr-process nucleosynthesis. Prog Part Nucl Phys (2016) 86:86–126. doi:10.1016/j.ppnp.2015.09.001

CrossRef Full Text | Google Scholar

4. Wang M, Huang W, Kondev F, Audi G, Naimi S. The AME 2020 atomic mass evaluation (II). tables, graphs and references. Chin Phys C (2021) 45:030003. doi:10.1088/1674-1137/abddaf

CrossRef Full Text | Google Scholar

5. Weizsäcker C. Zur theorie der kernmassen. Z Physik (1935) 96:431–58. doi:10.1007/BF01337700

CrossRef Full Text | Google Scholar

6. Möller P, Sierk A, Ichikawa T, Sagawa H. Nuclear ground-state masses and deformations: Frdm(2012). Atom Data Nucl Data Tables (2016) 109:1–204. doi:10.1016/j.adt.2015.10.002

CrossRef Full Text | Google Scholar

7. Wang N, Liu M, Wu X, Meng J. Surface diffuseness correction in global mass formula. Phys Lett B (2014) 734:215–9. doi:10.1016/j.physletb.2014.05.049

CrossRef Full Text | Google Scholar

8. Goriely S, Chamel N, Pearson JM. Further explorations of skyrme-Hartree-Fock-bogoliubov mass formulas. xiii. the 2012 atomic mass evaluation and the symmetry coefficient. Phys Rev C (2013) 88:024308. doi:10.1103/PhysRevC.88.024308

CrossRef Full Text | Google Scholar

9. Geng LS, Toki H, Meng J. Masses, deformations and charge radii—nuclear ground-state properties in the relativistic mean field model. Prog Theor Phys (2005) 113:785–800. doi:10.1143/PTP.113.785

CrossRef Full Text | Google Scholar

10. Xia X, Lim Y, Zhao P, Liang H, Qu X, Chen Y, et al. The limits of the nuclear landscape explored by the relativistic continuum hartree–bogoliubov theory. Atom Data Nucl Data Tables (2018) 121-122:1–215. doi:10.1016/j.adt.2017.09.001

CrossRef Full Text | Google Scholar

11. Goriely S, Chamel N, Pearson JM. Skyrme-Hartree-Fock-bogoliubov nuclear mass formulas: Crossing the 0.6 mev accuracy threshold with microscopically deduced pairing. Phys Rev Lett (2009) 102:152503. doi:10.1103/PhysRevLett.102.152503

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Erler J, Birge N, Kortelainen M, Nazarewicz W, Olsen E, Perhac AM, et al. The limits of the nuclear landscape. Nature (2012) 486:509–12. doi:10.1038/nature11188

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Afanasjev A, Agbemava S, Ray D, Ring P. Nuclear landscape in covariant density functional theory. Phys Lett B (2013) 726:680–4. doi:10.1016/j.physletb.2013.09.017

CrossRef Full Text | Google Scholar

14. Lu KQ, Li ZX, Li ZP, Yao JM, Meng J. Global study of beyond-mean-field correlation energies in covariant energy density functional theory using a collective Hamiltonian method. Phys Rev C (2015) 91:027304. doi:10.1103/PhysRevC.91.027304

CrossRef Full Text | Google Scholar

15. Yang YL, Wang YK, Zhao PW, Li ZP. Nuclear landscape in a mapped collective Hamiltonian from covariant density functional theory. Phys Rev C (2021) 104:054312. doi:10.1103/PhysRevC.104.054312

CrossRef Full Text | Google Scholar

16. Zhang K, Cheoun M-K, Choi Y-B, Chong PS, Dong J, Dong Z, et al. Nuclear mass table in deformed relativistic hartree–bogoliubov theory in continuum, i: Even–even nuclei. Atom Data Nucl Data Tables (2022) 144:101488. doi:10.1016/j.adt.2022.101488

CrossRef Full Text | Google Scholar

17. Pan C, Cheoun M-K, Choi Y-B, Dong J, Du X, Fan X-H, et al. Deformed relativistic hartree-bogoliubov theory in continuum with a point-coupling functional. ii. examples of odd nd isotopes. Phys Rev C (2022) 106:014316. doi:10.1103/PhysRevC.106.014316

CrossRef Full Text | Google Scholar

18. Kirson MW. Mutual influence of terms in a semi-empirical mass formula. Nucl Phys A (2008) 798:29–60. doi:10.1016/j.nuclphysa.2007.10.011

CrossRef Full Text | Google Scholar

19. Mumpower MR, Surman R, Fang D-L, Beard M, Möller P, Kawano T, et al. Impact of individual nuclear masses on r-process abundances. Phys Rev C (2015) 92:035807. doi:10.1103/PhysRevC.92.035807

CrossRef Full Text | Google Scholar

20. Jiang XF, Wu XH, Zhao PW. Sensitivity study of r-process abundances to nuclear masses. Astrophys J (2021) 915:29. doi:10.3847/1538-4357/ac042f

CrossRef Full Text | Google Scholar

21. Duflo J, Zuker A. Microscopic mass formulas. Phys Rev C (1995) 52:R23–7. doi:10.1103/PhysRevC.52.R23

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Pearson J, Nayak R, Goriely S. Nuclear mass formula with bogolyubov-enhanced shell-quenching: Application to r-process. Phys Lett B (1996) 387:455–9. doi:10.1016/0370-2693(96)01071-4

CrossRef Full Text | Google Scholar

23. Koura H, Tachibana T, Uno M, Yamada M. Nuclidic mass formula on a spherical basis with an improved even-odd term. Prog Theor Phys (2005) 113:305–25. doi:10.1143/PTP.113.305

CrossRef Full Text | Google Scholar

24. Carleo G, Cirac I, Cranmer K, Daudet L, Schuld M, Tishby N, et al. Machine learning and the physical sciences. Rev Mod Phys (2019) 91:045002. doi:10.1103/RevModPhys.91.045002

CrossRef Full Text | Google Scholar

25. Boehnlein A, Diefenthaler M, Sato N, Schram M, Ziegler V, Fanelli C, et al. Colloquium: Machine learning in nuclear physics. Rev Mod Phys (2022) 94:031003. doi:10.1103/RevModPhys.94.031003

CrossRef Full Text | Google Scholar

26. Gazula S, Clark J, Bohr H. Learning and prediction of nuclear stability by neural networks. Nucl Phys A (1992) 540:1–26. doi:10.1016/0375-9474(92)90191-L

CrossRef Full Text | Google Scholar

27. Gernoth K, Clark J, Prater J, Bohr H. Neural network models of nuclear systematics. Phys Lett B (1993) 300:1–7. doi:10.1016/0370-2693(93)90738-4

CrossRef Full Text | Google Scholar

28. Wang N, Liu M. Nuclear mass predictions with a radial basis function approach. Phys Rev C (2011) 84:051303. doi:10.1103/PhysRevC.84.051303

CrossRef Full Text | Google Scholar

29. Niu ZM, Zhu ZL, Niu YF, Sun BH, Heng TH, Guo JY. Radial basis function approach in nuclear mass predictions. Phys Rev C (2013) 88:024325. doi:10.1103/PhysRevC.88.024325

CrossRef Full Text | Google Scholar

30. Zhang HF, Wang LH, Yin JP, Chen PH, Zhang HF. Performance of the levenberg–marquardt neural network approach in nuclear mass prediction. J Phys G-nucl Part Phys (2017) 44:045110. doi:10.1088/1361-6471/aa5d78

CrossRef Full Text | Google Scholar

31. Utama R, Piekarewicz J, Prosper HB. Nuclear mass predictions for the crustal composition of neutron stars: A bayesian neural network approach. Phys Rev C (2016) 93:014311. doi:10.1103/PhysRevC.93.014311

CrossRef Full Text | Google Scholar

32. Niu ZM, Liang HZ. Nuclear mass predictions based on bayesian neural network approach with pairing and shell effects. Phys Lett B (2018) 778:48–53. doi:10.1016/j.physletb.2018.01.002

CrossRef Full Text | Google Scholar

33. Neufcourt L, Cao YC, Nazarewicz W, Viens F. Bayesian approach to model-based extrapolation of nuclear observables. Phys Rev C (2018) 98:034318. doi:10.1103/PhysRevC.98.034318

CrossRef Full Text | Google Scholar

34. Pastore A, Neill D, Powell H, Medler K, Barton C. Impact of statistical uncertainties on the composition of the outer crust of a neutron star. Phys Rev C (2020) 101:035804. doi:10.1103/PhysRevC.101.035804

CrossRef Full Text | Google Scholar

35. Idini A. Statistical learnability of nuclear masses. Phys Rev Res (2020) 2:043363. doi:10.1103/PhysRevResearch.2.043363

CrossRef Full Text | Google Scholar

36. Wu D, Bai CL, Sagawa H, Zhang HQ. Calculation of nuclear charge radii with a trained feed-forward neural network. Phys Rev C (2020) 102:054323. doi:10.1103/PhysRevC.102.054323

CrossRef Full Text | Google Scholar

37. Wu XH, Guo LH, Zhao PW. Nuclear masses in extended kernel ridge regression with odd-even effects. Phys Lett B (2021) 819:136387. doi:10.1016/j.physletb.2021.136387

CrossRef Full Text | Google Scholar

38. Shelley M, Pastore A. A new mass model for nuclear astrophysics: Crossing 200 kev accuracy. Universe (2021) 7:131. doi:10.3390/universe7050131

CrossRef Full Text | Google Scholar

39. Gao ZP, Wang YJ, Lü HL, Li QF, Shen CW, Liu L. Machine learning the nuclear mass. Nucl Sci Tech (2021) 32:109. doi:10.1007/s41365-021-00956-1

CrossRef Full Text | Google Scholar

40. Liu Y, Su C, Liu J, Danielewicz P, Xu C, Ren Z. Improved naive bayesian probability classifier in predictions of nuclear mass. Phys Rev C (2021) 104:014315. doi:10.1103/PhysRevC.104.014315

CrossRef Full Text | Google Scholar

41. Wu X, Lu Y, Zhao P. Multi-task learning on nuclear masses and separation energies with the kernel ridge regression. Phys Lett B (2022) 834:137394. doi:10.1016/j.physletb.2022.137394

CrossRef Full Text | Google Scholar

42. Akkoyun S, Bayram T, Kara SO, Sinan A. An artificial neural network application on nuclear charge radii. J Phys G-nucl Part Phys (2013) 40:055106. doi:10.1088/0954-3899/40/5/055106

CrossRef Full Text | Google Scholar

43. Utama R, Chen W-C, Piekarewicz J. Nuclear charge radii: Density functional theory meets bayesian neural networks. J Phys G-nucl Part Phys (2016) 43:114002. doi:10.1088/0954-3899/43/11/114002

CrossRef Full Text | Google Scholar

44. Ma Y, Su C, Liu J, Ren Z, Xu C, Gao Y. Predictions of nuclear charge radii and physical interpretations based on the naive bayesian probability classifier. Phys Rev C (2020) 101:014304. doi:10.1103/PhysRevC.101.014304

CrossRef Full Text | Google Scholar

45. Ma J-Q, Zhang Z-H. Improved phenomenological nuclear charge radius formulae with kernel ridge regression. Chin Phys C (2022) 46:074105. doi:10.1088/1674-1137/ac6154

CrossRef Full Text | Google Scholar

46. Niu ZM, Fang JY, Niu YF. Comparative study of radial basis function and bayesian neural network approaches in nuclear mass predictions. Phys Rev C (2019) 100:054311. doi:10.1103/PhysRevC.100.054311

CrossRef Full Text | Google Scholar

47. Lovell AE, Nunes FM, Catacora-Rios M, King GB. Recent advances in the quantification of uncertainties in reaction theory. J Phys G-nucl Part Phys (2020) 48:014001. doi:10.1088/1361-6471/abba72

CrossRef Full Text | Google Scholar

48. Ma C-W, Peng D, Wei H-L, Niu Z-M, Wang Y-T, Wada R. Isotopic cross-sections in proton induced spallation reactions based on the bayesian neural network method. Chin Phys C (2020) 44:014104. doi:10.1088/1674-1137/44/1/014104

CrossRef Full Text | Google Scholar

49. Wu D, Bai CL, Sagawa H, Nishimura S, Zhang HQ. β-delayed one-neutron emission probabilities within a neural network model. Phys Rev C (2021) 104:054303. doi:10.1103/PhysRevC.104.054303

CrossRef Full Text | Google Scholar

50. Saxena G, Sharma PK, Saxena P. Modified empirical formulas and machine learning for alpha-decay systematics. J Phys G-nucl Part Phys (2021) 48:055103. doi:10.1088/1361-6471/abcd1c

CrossRef Full Text | Google Scholar

51. Neudecker D, Cabellos O, Clark AR, Grosskopf MJ, Haeck W, Herman MW, et al. Informing nuclear physics via machine learning methods with differential and integral experiments. Phys Rev C (2021) 104:034611. doi:10.1103/PhysRevC.104.034611

CrossRef Full Text | Google Scholar

52. Wang X, Zhu L, Su J. Modeling complex networks of nuclear reaction data for probing their discovery processes. Chin Phys C (2021) 45:124103. doi:10.1088/1674-1137/ac23d5

CrossRef Full Text | Google Scholar

53. Huang TX, Wu XH, Zhao PW. Application of kernel ridge regression in predicting neutron-capture reaction cross-sections. Commun Theor Phys (2022) 74:095302. doi:10.1088/1572-9494/ac763b

CrossRef Full Text | Google Scholar

54. Jiang WG, Hagen G, Papenbrock T. Extrapolation of nuclear structure observables with artificial neural networks. Phys Rev C (2019) 100:054326. doi:10.1103/PhysRevC.100.054326

CrossRef Full Text | Google Scholar

55. Lasseri R-D, Regnier D, Ebran J-P, Penon A. Taming nuclear complexity with a committee of multilayer neural networks. Phys Rev Lett (2020) 124:162502. doi:10.1103/PhysRevLett.124.162502

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Yoshida S. Nonparametric bayesian approach to extrapolation problems in configuration interaction methods. Phys Rev C (2020) 102:024305. doi:10.1103/PhysRevC.102.024305

CrossRef Full Text | Google Scholar

57. Wang X, Zhu L, Su J. Providing physics guidance in bayesian neural networks from the input layer: The case of giant dipole resonance predictions. Phys Rev C (2021) 104:034317. doi:10.1103/PhysRevC.104.034317

CrossRef Full Text | Google Scholar

58. Bai J, Niu Z, Sun B, Niu Y. The description of giant dipole resonance key parameters with multitask neural networks. Phys Lett B (2021) 815:136147. doi:10.1016/j.physletb.2021.136147

CrossRef Full Text | Google Scholar

59. Neufcourt L, Cao Y, Nazarewicz W, Olsen E, Viens F. Neutron drip line in the ca region from bayesian model averaging. Phys Rev Lett (2019) 122:062502. doi:10.1103/PhysRevLett.122.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Neufcourt L, Cao Y, Giuliani SA, Nazarewicz W, Olsen E, Tarasov OB. Quantified limits of the nuclear landscape. Phys Rev C (2020) 101:044307. doi:10.1103/PhysRevC.101.044307

CrossRef Full Text | Google Scholar

61. Wang Z-A, Pei J, Liu Y, Qiang Y. Bayesian evaluation of incomplete fission yields. Phys Rev Lett (2019) 123:122501. doi:10.1103/PhysRevLett.123.122501

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Lovell AE, Mohan AT, Talou P. Quantifying uncertainties on fission fragment mass yields with mixture density networks. J Phys G-nucl Part Phys (2020) 47:114001. doi:10.1088/1361-6471/ab9f58

CrossRef Full Text | Google Scholar

63. Qiao CY, Pei JC, Wang ZA, Qiang Y, Chen YJ, Shu NC, et al. Bayesian evaluation of charge yields of fission fragments of ²³⁹U. Phys Rev C (2021) 103:034621. doi:10.1103/PhysRevC.103.034621

CrossRef Full Text | Google Scholar

64. Wang R, Ma Y-G, Wada R, Chen L-W, He W-B, Liu H-L, et al. Nuclear liquid-gas phase transition with machine learning. Phys Rev Res (2020) 2:043202. doi:10.1103/PhysRevResearch.2.043202

CrossRef Full Text | Google Scholar

65. Keeble J, Rios A. Machine learning the deuteron. Phys Lett B (2020) 809:135743. doi:10.1016/j.physletb.2020.135743

CrossRef Full Text | Google Scholar

66. Adams C, Carleo G, Lovato A, Rocco N. Variational Monte Carlo calculations of a ≤ 4 nuclei with an artificial neural-network correlator ansatz. Phys Rev Lett (2021) 127:022502. doi:10.1103/PhysRevLett.127.022502

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Wu XH, Ren ZX, Zhao PW. Nuclear energy density functionals from machine learning. Phys Rev C (2022) 105:L031303. doi:10.1103/PhysRevC.105.L031303

CrossRef Full Text | Google Scholar

68. Niu ZM, Sun BH, Liang HZ, Niu YF, Guo JY. Improved radial basis function approach with odd-even corrections. Phys Rev C (2016) 94:054315. doi:10.1103/PhysRevC.94.054315

CrossRef Full Text | Google Scholar

69. Ma NN, Zhang HF, Yin P, Bao XJ, Zhang HF. Weizsäcker-skyrme-type nuclear mass formula incorporating two combinatorial radial basis function prescriptions and their application. Phys Rev C (2017) 96:024302. doi:10.1103/PhysRevC.96.024302

CrossRef Full Text | Google Scholar

70. Niu ZM, Liang HZ, Sun BH, Niu YF, Guo JY, Meng J. High precision nuclear mass predictions towards a hundred kilo-electron-volt accuracy. Sci Bull (2018) 63:759–64. doi:10.1016/j.scib.2018.05.009

CrossRef Full Text | Google Scholar

71. Li T, Wei H, Liu M, Wang N. Ability of the radial basis function approach to extrapolate nuclear mass. Commun Theor Phys (2021) 73:095301. doi:10.1088/1572-9494/ac08fa

CrossRef Full Text | Google Scholar

72. Niu ZM, Liang HZ. Nuclear mass predictions with machine learning reaching the accuracy required by r-process studies. Phys Rev C (2022) 106:L021303. doi:10.1103/PhysRevC.106.L021303

CrossRef Full Text | Google Scholar

73. Guo L, Wu X, Zhao P. Nuclear mass predictions of the relativistic density functional theory with the kernel ridge regression and the application to r-process simulations. Symmetry (2022) 14:1078. doi:10.3390/sym14061078

CrossRef Full Text | Google Scholar