Enhancement of the two-photon blockade effect via Van der Waals interaction

We theoretically investigate the influence of the Van der Waals interaction on the two-photon blockade phenomenon with the corresponding photon correlation functions g⁽²⁾(0) > 1 and g⁽³⁾(0) < 1 in a two-atom cavity-QED system, where two three-level ladder-type atoms are coherently driven by a pumping field and a coupling field simultaneously. Choosing a specific frequency of the coupling field, we show the energy splitting phenomenon caused by electromagnetically induced transparency. Correspondingly, the two-photon blockade phenomenon can be achieved near the two-photon resonant frequency. Using the Van der Waals interaction between the Rydberg states of the two atoms, we also show that the two-photon blockade can be improved when two atoms radiate in-phase or out-of-phase. As a result, two photons leak from the cavity simultaneously, but the third photon is blockaded. These results presented in this study hold potential applications in manipulating photon states and generating nonclassical light sources.

1 Introduction

Creation and manipulation of single photons are pivotal requirements in quantum science and technology. Photon blockade (PB), proposed by Imamoḡlu et al. [1], is one of the effective methods for realizing single-photon sources. In the process of single PB, the absorption of the first photon blocks the absorption of the next photon until the previous photon is released from the system. As a consequence, the photons are emitted from the system one by one and antibunched photons with sub-Poissonian distribution can be observed [2].

To date, this single PB has been experimentally implemented in various quantum systems, such as the atom-cavity quantum electrodynamics (QED) system [3–6], semiconductor cavity-QED system [7], photonic crystal system [8], circuit cavity-QED system [9], and so on. Recently, the realization of two-photon blockade (two-PB) via the quantum interference effect has been proposed [10, 11] and demonstrated in quantum dot cavity-QED systems [12]. Moreover, the two-PB phenomenon also increases great research interest, where two photons go out of the cavity together, but the third photon is blockaded [13–15].

Two-PB can occur if the driving field frequency is equal to the two-photon dressed-state resonance frequency while far from one-photon resonance and three-photon absorption [16]. Thus, the observation of two-PB requires strong nonlinearities with respect to the decay rate of the system, e.g., Kerr nonlinearity magnitudes [1] or atom-cavity coupling strength [3] to be at least larger than the cavity mode linewidth. In the strong coupling regime, two-PB has been predicted in a few systems, such as a cavity with a Kerr-type medium coherently driven by a laser field [17] or a sequence of Gaussian pulses [18], and coupled nanomechanical resonator systems [19]. Recently, the two-PB phenomenon has been realized experimentally in an atom-driven cavity-QED system [20].

In this study, we study the two-PB behavior in a single-mode cavity-QED system with two three-level ladder-type atoms coupled via the Rydberg interaction. Unlike using an effective Kerr-type interaction to achieve two-PB in Ref. [19], we show that the Van der Waals interaction (Vdw) between two Rydberg states will significantly enhance the optical nonlinearity [21] in the cavity-QED system, leading to a significant improvement of the two-PB. Moreover, the mean photon number can also be enhanced in the presence of the Vdw interaction.

2 Physical model

As shown in Figure 1, two ladder-type three-level atoms are trapped inside a single model optical cavity with wavelength λ_cav, and the distance between the two atoms is ΔZ. The corresponding energy levels and energies of each atom are labeled by |i⟩ and ℏω_i (i = g, e, r), respectively. A weak probe field with the Rabi frequency Ω_p and angular frequency ω_p drives the |g⟩ ↔|e⟩ transition, and a strong coupling field with the Rabi frequency Ω_c and angular frequency ω_c drives the |e⟩ ↔|r⟩ transition. In our system, the atomic state |r⟩ is chosen as the Rydberg state so that the decay rate of state |r⟩ is much smaller than that of the state |e⟩. Assuming the cavity-mode frequency ω_cav is equal to ω_e for mathematical simplicity and using the electric dipole and rotating-wave approximations, the Hamiltonian of the system can be expressed as (setting ℏ = 1)

$\begin{array}{ll}\hfill H& ={\mathrm{\Delta }}_{\text{p}}{a}^{†}a+\sum _{j=1}^2\left[{\mathrm{\Delta }}_{\text{p}}{\sigma }_{ee}^{\left(j\right)}+{\mathrm{\Delta }}_r{\sigma }_{rr}^{\left(j\right)}\right]\hfill \\ \hfill & +\sum _{j=1}^2\left[g_j{a}^{†}{\sigma }_{ge}^{\left(j\right)}+{\mathrm{\Omega }}_{\text{c}}{\sigma }_{er}^{\left(j\right)}+{\mathrm{\Omega }}_{\text{p}}{\sigma }_{me}^{\left(j\right)}+\mathrm{H}.\mathrm{c}\right]+{\mathcal{V}}_{\text{vdw}}{\sigma }_{rr}^{\left(1\right)}{\sigma }_{rr}^{\left(2\right)},\hfill \end{array}(1)$

where Δ_p = ω_cav − ω_p and Δ_r = Δ_p + Δ_c with Δ_c = ω_r − ω_e − ω_c. Here, a (a^†) is the annihilation (creation) operator of the cavity mode, while ${\sigma }_{mn}^{(j)}=|m^{(j)}\rangle \langle n^{(j)}|$ (m, n = g, e, r and j = 1–2) with z_j is the atomic operator for the j-th atom. The position-dependent atom cavity coupling strength for the j-th atom is given by g_j = g₀ cos (2πz_j)/λ_cav being the position of the j-th atom [22], and $g_0={\mu }_{eg}\sqrt{{\omega }_{\text{cav}}/2\hslash {\epsilon }_{0}V}$ being the amplitude of the coupling strength. Assuming that one atom is located at the antinode of the cavity mode, then the coupling strengths can be expressed as g₁ = g₀ and g₂ = g₀ cos (Φ_z) with Φ_z = 2πΔZ/λ_cav and ΔZ = z₂ − z₁. The last term of Eq.1 describes the Vdw interaction between of two atoms with interaction strength ${\mathcal{V}}_{\text{vdw}}$, which results in an energy shift of state |rr⟩ and prevents the simultaneous excitation of two atoms.

FIGURE 1

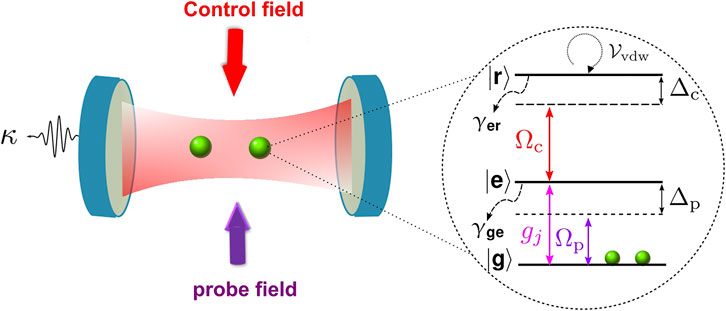
FIGURE 1. (Color online) Schematic diagram of a single-mode cavity coupled with two three-level ladder-type atoms. Levels |g⟩ and |e⟩ are coupled to the cavity field with the coupling strength g_j. Moreover, the control field of frequency ω_c with Rabi frequency Ω_C couples the transition |e⟩ to |r⟩ and a probe field with frequency ω_p and strength Ω_p coupled the state |g⟩ and |e⟩, respectively. γ_er and γ_ge are the spontaneous emission rates from states |r⟩ and |e⟩, respectively, and κ is the cavity decay. The two-atom system with Van der Waals potential between the Rydberg states creates an interaction ${\mathcal{V}}_{\text{vdw}}$ dependent on the atom separation.

The master equation for the density matrix operator of the system is then given by

$\frac{\partial \rho }{\partial t}=-\frac{i}{\hslash }\left[H,\rho \right]+\frac{\kappa }{2}\mathcal{L}\left[a\right]+\sum _{j=1}^2\left[\frac{{\gamma }_{ge}}{2}\mathcal{L}\left({\sigma }_{ge}^{\left(j\right)}\right)+\frac{{\gamma }_{er}}{2}\mathcal{L}\left({\sigma }_{er}^{\left(j\right)}\right)\right],(2)$

where $\mathcal{L}(O)=2O\rho O^{†}-O^{†}O\rho -\rho O^{†}O$ is the Lindblad superoperator with respect to the operate O. Here, κ and γ_ij are the cavity decay rate and the atomic decay rate, respectively, from state |j⟩ to state |i⟩.

Numerically solving Eq. 2, one can evaluate the equal-time second-order correlation function $g^{(2)}(0)=⟨a^{†}{a}^{†}aa⟩/{⟨a^{†}a⟩}^2$ and the equal-time third-order correlation function $g^{(3)}(0)=⟨a^{†}{a}^{†}{a}^{†}aaa⟩/{⟨a^{†}a⟩}^3$, which described the statistical properties of the photons leaking from the cavity. Generally, g⁽²⁾(0) < 1 represents the photon antibunching phenomenon, implying that photons leave the cavity one by one with sub-Poisson statistics. In this work, we focus on another case, where two photons leave the cavity together but the third photon is blockaded. Likewise, this phenomenon can also be described by exploring the photon correlation functions, which requires g⁽²⁾(0) > 1 and g⁽³⁾(0) < 1.

3 Two-PB for in phase radiations

First, we turn off the coupling field and consider the case of in-phase radiation, i.e., Φ_Z = 0, resulting in g₁ = g₂ = g₀. In this case, the dressed states in absence of the coupling field (equivalent Jaynes–Cummings model) are given in Figure 2A(see the blue states). In panel (b), there exist four peaks in the cavity excitation spectrum, where two large side peaks correspond to the single photon excitations with ${\mathrm{\Delta }}_{\text{p}}=\pm \sqrt{2}{g}_0$, while two small peaks correspond to the two-photon excitations with ${\mathrm{\Delta }}_{\text{p}}=\pm \sqrt{6}{g}_0/2$[see Figure 2B, blue arrow]. As shown in Ref. [13], it is difficult to observe the two-PB phenomenon by increasing the probe field intensity in this case, because the increasing of Ω_P will result in the broadening of the dressed states, which compensates the inharmonic energy splitting and prohibits the observation of the two-PB [20].

FIGURE 2

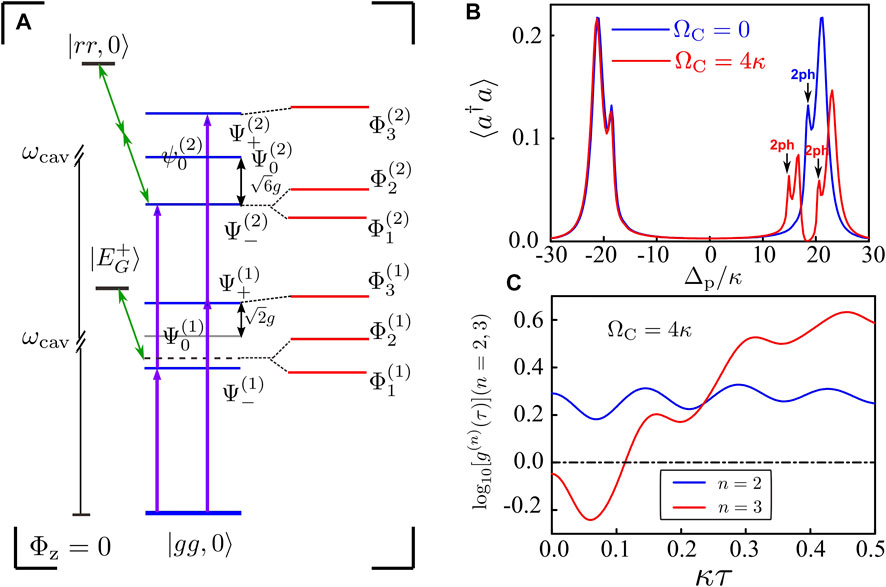
FIGURE 2. (Color online) (A) Schematic energy-level structure diagram explaining the energy splitting induced by Ω_C in the case of Φ_z = 0. (B) Mean photon number ⟨a^†a⟩ as a function of normalized detuning Δ_p/κ for the Ω_C = 0 (blue solid curve) and Ω_C = 4κ (pink solid curve). (C) Time-dependent field correlation functions log₁₀ [g⁽²⁾(τ)] and log₁₀ [g⁽³⁾(τ)] versus the normalized delay time κτ with Δ_p = 21.3κ. The strength of the probe field is Ω_p = 0.8κ in panel (B) and Ω_p = 1.5κ in panel (C). Other system parameters are chosen as g₀ = 15κ, γ_er = 1κ, and γ_ge = γ_er/200.

To overcome this energy broadening, we turn on the coupling field but neglect the Vdw interaction so that the physical mechanism can be clearly demonstrated. Choosing ${\mathrm{\Delta }}_c=-\sqrt{6}{g}_0/2$, the coupling field resonantly couples states |rr, 0⟩ and ${\mathrm{\Psi }}_{-}^{(2)}$ so that the state ${\mathrm{\Psi }}_{-}^{(2)}$ is split into a doublet [see Figure 2A, the red states], which is well known as the electromagnetically induced transparency (EIT) effect. Correspondingly, the right peaks in the cavity excitation spectrum are split into two doublets, where two large peaks originate from the one-photon excitations, but the other two small peaks result from the two-photon excitations [see Figure 2B, red curves].

In Figure 2C, we plot the time-dependent second-order correlation $g^{(2)}(\tau )=⟨a^{†}(t)a^{†}(t+\tau )a(t+\tau )a(t)⟩/{⟨a^{†}(t)\mathrm{a}(t)⟩}_{\text{ss}}^2$ and the third-order correlation $g^{(3)}(\tau )=⟨a^{†}(t)a^{†}(t)a^{†}(t+\tau )a(t+\tau )a(t)a(t)⟩/{⟨a^{†}(t)\mathrm{a}(t)⟩}_{\text{ss}}^3$ at two-photon resonance $|gg,0\rangle \to {\mathrm{\Phi }}_1^{(2)}$ frequency Δ_p = 21.3κ with Ω_p = 1.5κ. It is clear that the two-PB with g⁽²⁾(0) > 1 and g⁽³⁾(0) < 1 can be achieved under this condition, where two bunching photons leak from the cavity with the super Poissonian statistical distribution, but the third photon is blockaded due to the energy splitting induced by the coupling field.

Now, let us consider the influence of the Vdw interaction on the two-PB. As shown in Figure 3A, the g⁽²⁾(0) is always larger than unity, but the g⁽³⁾(0) decreases as the Vdw interaction [23–26] strength increases. Thus, the two-PB can be improved by increasing the Vdw interaction strength. At the same time, the mean photon number is also slightly increased (see blue dashed curve). This phenomenon can be explained by exploring the analytical expression of the photon correlation functions. It should be noted that the following analytical expressions are valid only for weak driving fields. Truncating the Hilbert space by the three-photon space, g⁽²⁾(0) and g⁽³⁾(0) can be expressed analytically as functions of the photon number distributions p_n under the weak probe field regime,

$g^{\left(2\right)}\left(0\right)=\frac{{\sum }_n\left(n-1\right)p_n}{{\left[{\sum }_{n}n{p}_n\right]}^2}\approx \frac{2p_2}{{\left(p_1+2p_2\right)}^2},(\mathrm{3a})$

$g^{\left(3\right)}\left(0\right)=\frac{{\sum }_{n}n\left(n-1\right)\left(n-2\right)p_n}{{\left[{\sum }_{n}n{p}_n\right]}^3}\approx \frac{6p_3}{{\left(p_1+2p_2\right)}^3},(\mathrm{3b})$

where $p_1\approx |C_{gg,1}{|}^2+|C_{+,1}{|}^2+|C_{{+}^{\prime },1}{|}^2$ and p₂ ≈ 2|C_gg,2|², and p₃ ≈ 3|C_gg,3|². Here, |C_α,n|² is the probability of the product state |α, n⟩, involving$|+,1\rangle =1/\sqrt{2}(|eg,1\rangle +|ge,1\rangle )[\left.\right(|{+}^{\prime },1\rangle =1/\sqrt{2}(|rg,1\rangle +|gr,1\rangle )]$. Due to the dressing of atoms by the Vdw interaction, the bare state |rr, 0⟩ is shifted so that the probability |C_rr,0|² drops quickly as shown in Figure 3B. On the other hand, the probability of one photon increases quickly since the Vdw interaction does not affect the states in one-photon space, resulting in the drops in the values of $p_2/{[p_1+2p_2]}^2$ and $p_3/{[p_1+2p_2]}^3$[the inset figure of Figure 3B]. Moreover, provided that only the lowest several photon states can be excited, the mean photon number can be approximately expressed as ⟨a^†a⟩ ≈ p₁ + 2p₂ ≈ p₁. Therefore, the increased Vdw interaction strength increases the mean photon number in the cavity.

FIGURE 3

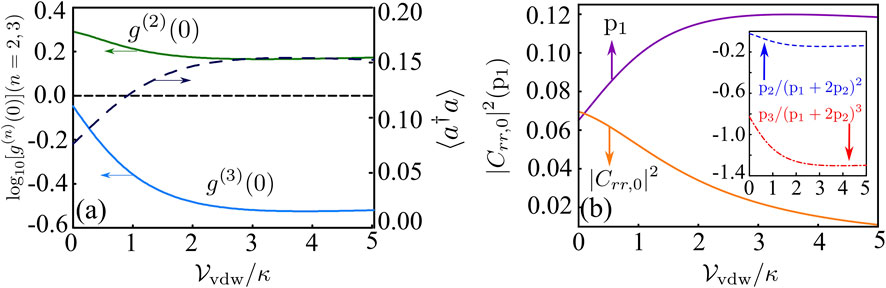
FIGURE 3. (Color online) (A) log₁₀ [⟨a^†a⟩] (blue-black dashed curve), log₁₀ [g⁽²⁾(0)] (green solid curve), and log₁₀ [g⁽³⁾(0)] (wathet blue solid curve) are plotted as functions of the Vdw interaction strength ${\mathcal{V}}_{\text{vdw}}/\kappa$ for Φ_z = 0. (B) Probability of the product state |rr, 0⟩ and one-photon distributions p₁ versus the ${\mathcal{V}}_{\text{vdw}}/\kappa$. The inset is the logarithmic plot (of base 10) of the proportional relationship which is described in Eq. 3. System parameters used here are the same as in Figure 2C.

4 Two-PB for out-of-phase radiations

Now, we study the out-of-phase configuration Φ_z = π, yielding g₁ = −g₂ = g₀. In the absence of the control field, one can easily obtain the dressed states of the system as shown in Figure 4A (see the blue states). Detailed expressions of the eigenvalues and eigenstates can be found in Ref. [13]. Contrary to the in-phase case, the $|gg,0\rangle \to {\mathrm{\Psi }}_{\pm }^{(1)}$ transitions are forbidden since the driving field only couples the symmetric state (i.e., | + ,n⟩ state). Thus, one can observe three peaks in the cavity excitation spectrum [see Figure 4A, blue curve]. Here, the large central peak corresponds to the multi-photon excitation process, i.e., $|gg,0\rangle \to {\mathrm{\Psi }}_0^{(1)}\to {\mathrm{\Psi }}_0^{(2)}\cdots \to {\mathrm{\Psi }}_0^{(n)}$ transition. The other two small side peaks correspond to the two-photon excitation processes, i.e., $|gg,0\rangle \to {\mathrm{\Psi }}_{\pm }^{(2)}$ transitions.

FIGURE 4

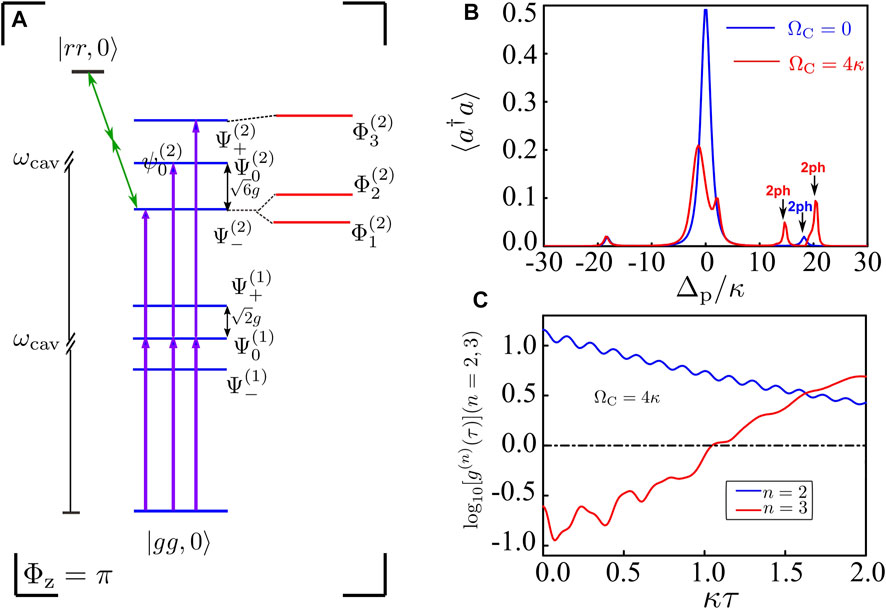
FIGURE 4. (Color online) (A) Schematic energy-level structure illustrating the energy splitting induced by Ω_C in the case of Φ_z = π. (B) Numerical results for ⟨a^†a⟩ as functions of normalized detuning Δ_p/κ with Ω_C = 0 (blue solid line) and Ω_C = 4κ (red solid line). (C) Time evolution of log₁₀ [g⁽²⁾(τ)] (reseda solid curve) and log₁₀ [g⁽³⁾(τ)] (wathet blue solid curve) with Δ_p = 21.3κ. In (b) Ω_P = 1.5κ and in (c) Ω_P = 2.0κ, other system parameters are the same as in Figure 2.

In the presence of the control field but without the Vdw interaction, the energy levels (blue lines in Figure 4A) will experience shifting and splitting due to the EIT effect. To improve the two-PB blockade, one requires that the state in two-photon space is resonantly coupled by the pump field via the two-photon process, but other states in N-photon (N > 3) states are far off-resonance. Thus, we choose the control field detuning ${\mathrm{\Delta }}_c=-\sqrt{6}{g}_0/2$ so that the control field resonantly couples state ${\mathrm{\Psi }}_{-}^{(2)}$ and state |rr, 0⟩. Then, the state ${\mathrm{\Psi }}_{-}^{(2)}$ is split into a doublet as shown in Figure 4A, and the states in high-order photon space are shifted. In Figure 4B, we demonstrate this energy splitting by plotting the mean photon number against the pump field detuning. Choosing the probe field frequency to Δ_p = 21.3κ, two-PB can be achieved and the time-dependent correlation functions g⁽²⁾(0) ≈ 15.3 and g⁽³⁾(0) ≈ 0.32 are shown in Figure 4C. Apparently, the two-PB phenomenon can be improved in the case of out-of-phase radiations.

Finally, we investigate the influence of the Vdw interaction on the two-PB when two atoms radiate out of phase. In Figure 5A, we show the dependence of the correlation functions log₁₀ [g⁽²⁾(0)], log₁₀ [g⁽³⁾(0)], and the mean photon number ⟨a^†a⟩ on the Vdw interaction strength. Here, we choose the system parameters as g = 15κ, γ_ge = κ, γ_er = γ_ge/200, Ω_p = 2.0κ, Δ_p = 21.3κ, ${\mathrm{\Delta }}_c=-\sqrt{6}{g}_0/2$, and Ω_C = 8κ. It is clear that the values of g⁽³⁾(0) decrease quickly with the increase of the Vdw interaction strength. Taking ${\mathcal{V}}_{\text{vdw}}=10\kappa$, we find g⁽³⁾(0) ≈ 0.01 , which is 25 times smaller than the value at ${\mathcal{V}}_{\text{vdw}}=0\kappa$. At the same time, the value of g⁽²⁾(0) is always larger than unity, and the mean photon number increases slightly. In Figure 5B, we show the deviations of photon number distribution p_n with respect to the Poisson distribution ${\mathcal{V}}_{\text{vdw}}/\kappa$, which is defined as $(p_n-{\mathcal{P}}_n)/{\mathcal{P}}_n$. It is clear that multi-photon transitions for ${\mathcal{V}}_{\text{vdw}}=10\kappa$ are suppressed compared with the case of ${\mathcal{V}}_{\text{vdw}}=0$. Thus, a significantly improved two-PB can be accomplished in the presence of the Vdw interaction.

FIGURE 5

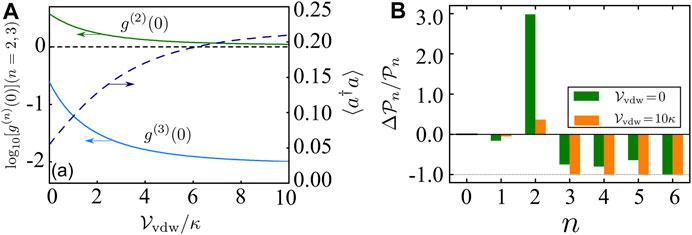
FIGURE 5. (Color online) (A) log₁₀ [⟨a^†a⟩] (blue-black dashed curve), log₁₀ [g⁽²⁾(0)] (green solid curve), and log₁₀ [g⁽³⁾(0)] (wathet blue solid curve) for different values of ${\mathcal{V}}_{\text{vdw}}/\kappa$ in the case of Φ_z = π with Ω_C = 8κ. (B) Relative deviations of photon number distribution with respect to the Poisson distribution. Other system parameters used here are the same as in Figure 4C.

5 Conclusion

In summary, we have proposed a model to realize strong two-PB (g⁽²⁾(0) > 1 and g⁽³⁾(0) < 0.01) by trapping two Rydberg atoms with EIT configuration inside an optical cavity. We show that the external control field can be used to effectively control the collective states of two atoms and the cavity mode, yielding two-PB for in-phase and out-of-phase radiations, respectively. Moreover, in the presence of the Vdw interaction, the mean photon number can be increased, and the two-PB phenomenon can be strongly improved in the case of out-of-phase radiations. With the development of atom trapping and cooling techniques, our scheme can be implemented not only in classical cavity-QED systems, as in experiments of Meschede [27] and Rempe groups [28], but also in a 1D topological photonics system involving an asymmetric edge mode [29]. Thus, our scheme has potential applications in manipulating photon states and generating nonclassical light, such as the two-photon source.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YY and CZ took the lead on the research work by running the simulations, performing most of the analysis, and producing all the figures. KH contributed to the code development. KH, ZZ, CZ, and YY wrote substantial parts of the manuscript. All authors contributed equally to the discussions, read the manuscript, and provided critical feedback.

Funding

KH acknowledges the support of the Natural Science Foundation of Anhui Provincial Education Department (Grant No. KJ2021A0632), the project of excellent young talents of universities in Anhui province (Grant No. gxyq2021194), and the Doctor Foundation of Anhui Jianzhu University (Grant No. 2020QDZ21). CZ and YY acknowledge the support of the National Nature Science Foundation (Grants No. 61975154 and 11874287) and the National Key Research and Development Program of China (Grants No. 2021YFA1400600 and 2021YFA1400602).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Imamoglu A, Schmidt H, Woods G, Deutsch M. Strongly interacting photons in a nonlinear cavity. Phys Rev Lett (1997) 78:1467–70. doi:10.1103/PhysRevLett.79.1467

CrossRef Full Text | Google Scholar

2. Agarwal GS. Quantum optics. New York: Cambridge University Press (2013).

Google Scholar

3. Birnbaum KM, Boca A, Miller R, Boozer AD, Northup TE, Kimble HJ. Photon blockade in an optical cavity with one trapped atom. Nature (2005) 436:87–90. doi:10.1038/nature03804

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Fink JM, Göppl M, Baur M, Bianchetti R, Leek PJ, Blais A, et al. Climbing the Jaynes-Cummings ladder and observing its nonlinearity in a cavity QED system. Nature (2008) 454:315–8. doi:10.1038/nature07112

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Souza JA, Figueroa E, Chibani H, Villas-Boas CJ, Rempe G. Coherent control of quantum fluctuations using cavity electromagnetically induced transparency. Phys Rev Lett (2013) 111:113602. doi:10.1103/PhysRevLett.111.113602

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zhou YH, Shen HZ, Zhang XY, Yi XX. Zero eigenvalues of a photon blockade induced by a non-Hermitian Hamiltonian with a gain cavity. Phys Rev A (2018) 97:043819. doi:10.1103/PhysRevA.97.043819

CrossRef Full Text | Google Scholar

7. Ulrich SM, Gies C, Ates S, Wiersig J, Reitzenstein S, Hofmann C, et al. Photon statistics of semiconductor microcavity lasers. Phys Rev Lett (2017) 98:043906. doi:10.1103/PhysRevLett.98.043906

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Faraon A, Fushman I, Englund D, Stoltz N, Petroff P, Vuckovic J. Coherent generation of non-classical light on a chip via photon-induced tunnelling and blockade. Nat Phys (2008) 4:859–63. doi:10.1038/nphys1078

CrossRef Full Text | Google Scholar

9. Liu YX, Xu XW, Miranowicz A, Nori F. From blockade to transparency: Controllable photon transmission through a circuit-QED system. Phys Rev A (2014) 89:043818. doi:10.1103/physreva.89.043818

CrossRef Full Text | Google Scholar

10. Liew TCH, Savona V. Single photons from coupled quantum modes. Phys Rev Lett (2011) 104:183601. doi:10.1103/PhysRevLett.104.183601

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Bamba M, Imamoglu A. Origin of strong photon antibunching in weakly nonlinear photonic molecules. Phys Rev A (2011) 83:021802. doi:10.1103/PhysRevA.83.021802

CrossRef Full Text | Google Scholar

12. Snijders HJ, Frey JA, Norman J, Flayac H, Savona V, Gossard A, et al. Observation of the unconventional photon blockade. Phys Rev Lett (2018) 121:043601. doi:10.1103/PhysRevLett.121.043601

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhu CJ, Yang YP, Agarwal GS. Collective multiphoton blockade in cavity quantum electrodynamics. Phys Rev A (2017) 95:063842. doi:10.1103/PhysRevA.95.063842

CrossRef Full Text | Google Scholar

14. Hou K, Zhu CJ, Yang YP, Agarwal GS. Interfering pathways for photon blockade in cavity QED with one and two qubits. Phys Rev A (2019) 100:063817. doi:10.1103/PhysRevA.100.063817

CrossRef Full Text | Google Scholar

15. Zhu CJ, Hou K, Yang YP, Deng L. Hybrid level anharmonicity and interference-induced photon blockade in a two-qubit cavity QED system with dipole–dipole interaction. Photon Res (2021) 9:1264–71. doi:10.1364/PRJ.421234

CrossRef Full Text | Google Scholar

16. Shamailov SS, Parkins AS, Collett MJ, Carmichael HJ. Multi-photon blockade and dressing of the dressed states. Opt Commun (2010) 283:766–72. doi:10.1016/j.optcom.2009.10.062

CrossRef Full Text | Google Scholar

17. Miranowicz A, Paprzycka M, Liu YX, Bajer J, Nori F. Two-photon and three-photon blockades in driven nonlinear systems. Phys Rev A (2013) 87:023809. doi:10.1103/PhysRevA.87.023809

CrossRef Full Text | Google Scholar

18. Hovsepyan GH, Shahinyan AR, Kryuchkyan GY. Multiphoton blockades in pulsed regimes beyond stationary limits. Phys Rev A (2014) 90:013839. doi:10.1103/PhysRevA.90.013839

CrossRef Full Text | Google Scholar

19. Miranowicz A, Bajer J, Lambert N, Liu YX, Nori F. Tunable multiphonon blockade in coupled nanomechanical resonators. Phys Rev A (2016) 93:013808. doi:10.1103/PhysRevA.93.013808

CrossRef Full Text | Google Scholar

20. Hamsen C, KNicolas T, Wilk T, Rempe G. Two-photon blockade in an atom-driven cavity QED system. Phys Rev Lett (2017) 118:133604. doi:10.1103/PhysRevLett.118.133604

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Peyronel T, Firstenberg O, Liang QY, Hofferberth S, Gorshkov AV, Pohl T, et al. Quantum nonlinear optics with single photons enabled by strongly interacting atoms. Nature (2012) 488:57–60. doi:10.1038/nature11361

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Pleinert MO, Zanthier JV, Agarwal GS. Hyperradiance from collective behavior of coherently driven atoms. Optica (2017) 4:779–85. doi:10.1364/OPTICA.4.000779

CrossRef Full Text | Google Scholar

23. Jaksch D, Cirac JI, Zoller P, Rolston SL, Cote R, Lukin MD. Fast quantum gates for neutral atoms. Phys Rev Lett (2010) 85:2208–11. doi:10.1103/PhysRevLett.85.2208

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Boddeda R, Usmani I, Bimbard E, Grankin A, Ourjoumtsev A, Brion E, et al. Rydberg-induced optical nonlinearities from a cold atomic ensemble trapped inside a cavity. J Phys B: Mol Opt Phys (2016) 49:084005. doi:10.1088/0953-4075/49/8/084005

CrossRef Full Text | Google Scholar

25. Grankin A, Brion E, Bimbard E, Boddeda R, Usmani I, Ourjoumtsev A, et al. Quantum statistics of light transmitted through an intracavity Rydberg medium. New J Phys (2014) 16:043020. doi:10.1088/1367-2630/16/4/043020

CrossRef Full Text | Google Scholar

26. Huang JF, Liao JQ, Sun CP. Photon blockade induced by atoms with Rydberg coupling. Phys Rev A (2013) 87:023822. doi:10.1103/PhysRevA.87.023822

CrossRef Full Text | Google Scholar

27. Reimann R, Alt W, Kampschulte T, Macha L, Ratschbacher L, Thau N, et al. Cavity-modified collective Rayleigh scattering of two atoms. Phys Rev Lett (2015) 114:023601. doi:10.1103/PhysRevLett.114.023601

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Neuzner A, Korber M, Rempe G. Interference and dynamics of light from a distance-controlled atom pair in an optical cavity. Nat Photon (2016) 10:303–6. doi:10.1038/nphoton.2016.19

CrossRef Full Text | Google Scholar

29. Yang FQ, Song J, Guo ZW, Xu X, Zhu K, Jiang J, et al. Actively controlled asymmetric edge states for directional wireless power transfer. Opt Express (2021) 29:7844–57. doi:10.1364/OE.417887

PubMed Abstract | CrossRef Full Text | Google Scholar