Design of Grid Multi-Wing Chaotic Attractors Based on Fractional-Order Differential Systems

In this article, a new method for generating grid multi-wing chaotic attractors from fractional-order linear differential systems is proposed. In order to generate grid multi-wing attractors, we extend the method of constructing heteroclinic loops from classical differential equations to fractional-order differential equations. Firstly, two basic fractional-order linear systems are obtained by linearization at two symmetric equilibrium points of the fractional-order Rucklidge system. Then a heteroclinic loop is constructed and all equilibrium points of the two basic fractional-order linear systems are connected by saturation function switching control. Secondly, the theoretical methods of switching control and construction of heteromorphic rings of fractal-order two-wing and multi-wing chaotic attractors are studied. Finally, the feasibility of the proposed method is verified by numerical simulation.

1 Introduction

At present, chaotic dynamics is gradually transitioning from the basic theoretical research of mathematics and physics to the practical engineering application field. For example, chaotic theory has been greatly developed in the fields of memristor [1–6], secure communication [7–11], image encryption [12–17], neural network [18–29], so chaotic dynamics has a wide application prospect. A key factor in the application of chaos in engineering is to improve the complex dynamic characteristics of chaos. In recent years, many scholars have deeply analysed and studied the complex dynamic characteristics of chaos, and found many chaotic attractors with complex dynamics. Some research results show that chaotic systems with multi-wing or multi-scroll attractors can show richer and more complex dynamic characteristics [30–35].

Fractional calculus has a history of more than 300 years, but its applications in engineering and physics have only aroused interest in recent decades [36–38]. With the deepening of scientific research, some researchers were surprised to find that these systems have complex chaos and bifurcation phenomena when studying fractional-order nonlinear differential systems [39–45]. In [42], the author designed a method to eliminate chaos in the system trajectory through state feedback controller. In order to form multi-scroll attractors, the potential nonlinearity of fractional-order chaotic systems is changed. In [43], it is proved that the fractional-order system coupled by two fractional Lorentz systems can produce four-wing chaotic attractors. In [44], a series method of saturation function is proposed, which can enable fractional-order differential systems to generate multi-spiral chaotic attractors, including multi-scroll chaotic attractors in three directions. In [45], a suitable nonlinear state feedback controller is designed by employing the four construction criteria of the basic fractional-order differential nominal linear system to generate multi-wing chaotic attractors for the controlled fractional-order differential system. However, these multi-wing chaotic systems all contain product terms, which makes their circuit implementation complicated. In [46], Petras proposed a fractional-order Chua’s model based on memristor. Through digital simulation, it is found that the fractional-order Chua’s circuit can also produce two-scroll chaotic attractors. However, it is still a very challenging problem to find how to generate grid multi-wing attractors in fractal-order chaotic systems.

In this article, a new design method of generating grid multi-wing chaotic attractors from fractional-order differential system is proposed by switching control of saturation function and constructing heteroclinic loops. Because the fractional-order derivative is a nonlocal operator with weak singular kernel, the multi-wing attractors generated in fractional-order differential system are very different from the multi-wing attractors generated in the classical differential system. In addition, it can be seen from [47–52] that shil’nikov theorem can be used to construct two-wing and multi-wing chaotic attractors in classical differential systems. In this paper, the classical differential system construction method is extended to the fractional-order differential system construction method based on shil’nikov theorem [47]. Firstly, the heteroclinic loops are constructed from the fractional-order piecewise linear differential system, and then a method to generate various grid multi-wing attractors through switching control is proposed. Two basic fractional-order linear systems are constructed by linearization at two symmetrical equilibrium points of fractional-order Rucklidge system [53]. After switching the control, in order to connect all the equilibrium points of the two basic fractional-order linear systems [54], we design a heteroclinic loop. Under appropriate conditions, according to shil’nikov theorem, a variety of grid multi-wing attractors can be obtained. We use a predictor-corrector numerical simulation algorithm to confirm the effectiveness of the proposed method [55].

The other parts of this paper are organized as follows. In Section 2, we first introduce some preliminary knowledge about fractional-order differential systems. Two fundamental fractional differential linear systems are deduced from Rucklidge system in Section 3. In Section 4, we study the theoretical method of designing fractional-order two-wing and multi-wing chaotic attractors by switching control and constructing heteroclinic loops. Finally, the conclusions of this paper are given in Section 5.

2 Fractional-Order Differential System

Unlike ordinary differential equations, due to the lack of appropriate mathematical methods, the research on the theoretical analysis and numerical solution of fractional-order calculation is still a difficult topic. In recent years, Caputo type fractional-order differential equations have aroused great interest. Under the promotion of Adams [56], we choose Caputo version of Adams prediction correction algorithm. Next, we will give a brief introduction to the fractional-order algorithm.

Fractional-order differential equation is generally expressed by the following formula:

$\{\begin{array}{l}{D}_t^{{\alpha }_1}x\left(t\right)=\frac{d^{{\alpha }_1}x\left(t\right)}{d{t}^{{\alpha }_1}}=f_1\left(x,y,z\right)\\ D_t^{{\alpha }_2}y\left(t\right)=\frac{d^{{\alpha }_2}y\left(t\right)}{d{t}^{{\alpha }_2}}=f_2\left(x,y,z\right)0\le t\ge T\\ D_t^{{\alpha }_3}z\left(t\right)=\frac{d^{{\alpha }_3}y\left(t\right)}{d{t}^{{\alpha }_3}}=f_3\left(x,y,z\right)\end{array}(1)$

When the initial values are chosen as $x\left(0\right)=x_0,y\left(0\right)=y_0,z\left(0\right)=z_0$, ${\alpha }_i\in \left(\mathrm{0,1}\right)$, $i=\mathrm{1,2,3}$, Eq. 1 forms the following Volterra integral equation:

$\{\begin{array}{l}x\left(t\right)=x\left(0\right)+\frac{1}{\mathrm{\Gamma }\left({\alpha }_1\right)}{\displaystyle {\int }_0^t{\left(t-\tau \right)}^{{\alpha }_1-1}{f}_1\left(x\left(\tau \right),y\left(\tau \right),z\left(\tau \right)\right)}d\tau \\ y\left(t\right)=y\left(0\right)+\frac{1}{\mathrm{\Gamma }\left({\alpha }_2\right)}{\displaystyle {\int }_0^t{\left(t-\tau \right)}^{{\alpha }_2-1}{f}_2\left(x\left(\tau \right),y\left(\tau \right),z\left(\tau \right)\right)}d\tau \\ z\left(t\right)=z\left(0\right)+\frac{1}{\mathrm{\Gamma }\left({\alpha }_3\right)}{\displaystyle {\int }_0^t{\left(t-\tau \right)}^{{\alpha }_3-1}{f}_3(x\left(\tau \right),y\left(\tau \right),z\left(\tau \right))}d\tau \end{array}(2)$

where $\Gamma \left({\alpha }_i\right)$ is the Gamma function, which can be defined as $\Gamma \left({\alpha }_i\right)={\displaystyle {\int }_0^{\infty }{e}^{-t}}{t}^{{\alpha }_i-1}dt$. Set $h=\frac{T}{N}$, $t_n=nh\left(n=\mathrm{0,1,2},\dots N\right)$, then Eq. 2 can take discretization as:

$\{\begin{array}{l}{x}_h\left(t_{n+1}\right)=x\left(0\right)+\frac{h^{{\alpha }_1}}{\mathrm{\Gamma }\left({\alpha }_1+2\right)}{f}_1\left(x_h^p\left(t_{n+1}\right),y_h^p\left(t_{n+1}\right),z_h^p\left(t_{n+1}\right)\right)+\frac{h^{{\alpha }_1}}{\mathrm{\Gamma }({\alpha }_1+2)}{\displaystyle \sum a_{1,j,n+1}}{f}_1\left(x\left(t_j\right),y\left(t_j\right),z\left(t_j\right)\right)\\ y_h\left(t_{n+1}\right)=y\left(0\right)+\frac{h^{{\alpha }_2}}{\mathrm{\Gamma }\left({\alpha }_2+2\right)}{f}_2\left(x_h^p\left(t_{n+1}\right),y_h^p\left(t_{n+1}\right),z_h^p\left(t_{n+1}\right)\right)+\frac{h^{{\alpha }_2}}{\mathrm{\Gamma }({\alpha }_2+2)}{\displaystyle \sum a_{2,j,n+1}}{f}_2\left(x\left(t_j\right),y\left(t_j\right),z\left(t_j\right)\right)\\ z_h\left(t_{n+1}\right)=z\left(0\right)+\frac{h^{{\alpha }_3}}{\mathrm{\Gamma }\left({\alpha }_3+2\right)}{f}_3\left(x_h^p\left(t_{n+1}\right),y_h^p\left(t_{n+1}\right),z_h^p\left(t_{n+1}\right)\right)+\frac{h^{{\alpha }_3}}{\mathrm{\Gamma }({\alpha }_3+2)}{\displaystyle \sum a_{3,j,n+1}}{f}_3\left(x\left(t_j\right),y\left(t_j\right),z\left(t_j\right)\right)\end{array}(3)$

where ${\alpha }_{i,j,n+1}$ is given by: ${\alpha }_{i,j,n+1}=\{\begin{array}{l}{n}^{{\alpha }_i+1}-\left(n-{\alpha }_i\right){\left(n+1\right)}^{{\alpha }_i},j=0,\\ {\left(n-j-2\right)}^{a_i+1}+{\left(n-j\right)}^{a_i+1}-2{\left(n-j+1\right)}^{a_i+1},1\le j\le n,\left(i=\mathrm{1,2,3}\right)\\ 1,j=n+1\end{array}$

, and the predicted value $x_h^p\left(t_{n+1}\right)$ is determined by:

$\{\begin{array}{l}{x}_h^p\left(t_{n+1}\right)=x\left(0\right)+\frac{1}{\mathrm{\Gamma }\left({\alpha }_1\right)}{\displaystyle \sum _{j=0}^n{b}_{1,j,n+1}{f}_1\left(x_h\left(t_j\right)\right)}\\ y_h^p\left(t_{n+1}\right)=y\left(0\right)+\frac{1}{\mathrm{\Gamma }\left({\alpha }_2\right)}{\displaystyle \sum _{j=0}^n{b}_{2,j,n+1}{f}_2\left(x_h\left(t_j\right)\right)}\\ z_h^p\left(t_{n+1}\right)=z\left(0\right)+\frac{1}{\mathrm{\Gamma }\left({\alpha }_3\right)}{\displaystyle \sum _{j=0}^n{b}_{3,j,n+1}{f}_3\left(x_h\left(t_j\right)\right)}\end{array}(4)$

In which $b_{i,j,n+1}=\frac{h{\alpha }_i}{{\alpha }_i}\left(\left(n-j+1\right){\alpha }_i-\left(n-j\right){\alpha }_i\right)\left(i=\mathrm{1,2,3}\right),0\le j\le n$. The estimation error in this method is $e=\max \left\{\max \left|x\left(t_j\right)-x_h\left(t_j\right)\right|,\max \left|y\left(t_j\right)-y_h\left(t_j\right)\right|,\max \left|z\left(t_j\right)-z_h\left(t_j\right)\right|\right\}=o\left(h^{\rho }\right)$, where $j=(\mathrm{0,1,2},\dots ,N),\rho =\min \left\{1+{\alpha }_1,1+{\alpha }_2,1+{\alpha }_3\right\}$. By using this method, we can determine the numerical solution of the fractional-order difference equation system.

3 Design of Two Fundamental Fractional-Order Linear Systems

Considering the fractional-order version of Rucklidge system, it can be expressed by the following formula:

$\{\begin{array}{l}{D}_t^{{\alpha }_1}x\left(t\right)=\frac{d^{{\alpha }_1}x\left(t\right)}{d{t}^{{\alpha }_1}}=-2\text{x}+6.7y-yz\\ D_t^{{\alpha }_2}y\left(t\right)=\frac{d^{{\alpha }_2}y\left(t\right)}{d{t}^{{\alpha }_2}}\left(t\right)=x\\ D_t^{{\alpha }_3}z\left(t\right)=\frac{d^{{\alpha }_3}y\left(t\right)}{d{t}^{{\alpha }_3}}=y^2-z\end{array}(5)$

where ${\alpha }_{\text{i}}(i=\mathrm{1,2,3})$ is the fractional-order satisfying $0<{\alpha }_i\le 1$. Clearly, system (Eq. 5) has three equilibria: $E_0=\left(\mathrm{0,0,0}\right),E_1=(0,\sqrt{6.7},6.7),E_2=(0,-\sqrt{6.7},6.7)$. Linearizing system (Eq. 5) at equilibrium point $E_1$, one gets the following fractional-order linear system:

$\left(\begin{array}{l}{D}_t^{{\alpha }_1}{x}_1\left(t\right)\\ D_t^{{\alpha }_2}{\text{y}}_1\left(t\right)\\ D_t^{{\alpha }_3}{z}_1\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-2& 0& -\sqrt{6.7}\\ 1& 0& 0\\ 0& 2\sqrt{6.7}& -1\end{array}\right)\left(\begin{array}{l}{\text{x}}_1\\ y_1\\ z_1\end{array}\right)=J_1{X}_1(6)$

In the same way, we linearize system (Eq. 5) at equilibrium point $E_2$, and the following fractional-order linear system can be obtained:

$\left(\begin{array}{l}{D}_t^{{\alpha }_1}{x}_2\left(t\right)\\ D_t^{{\alpha }_2}{\text{y}}_2\left(t\right)\\ D_t^{{\alpha }_3}{z}_2\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-2& 0& \sqrt{6.7}\\ 1& 0& 0\\ 0& 2\sqrt{6.7}& -1\end{array}\right)\left(\begin{array}{l}{\text{x}}_2\\ y_2\\ z_2\end{array}\right)=J_2{X}_2(7)$

Through the processing of the above method, systems (Eqs 6, 7) can be called basic fractional-order linear systems. Obviously, the only equilibrium point of systems Eqs 6, 7 is $O_0=O_1=\left(\mathrm{0,0,0}\right)$, and the corresponding eigenvalues are ${\lambda }_1=\gamma =-3.5145$ and ${\lambda }_{\mathrm{2,3}}=\sigma \pm j\omega =0.2577\pm j1.9353$. Therefore, equilibrium points $O_1$ and $O_2$ become saddle focus with index 2. Moreover, ${\lambda }_1<0$, $R_e\left({\lambda }_{\mathrm{2,3}}\right)>0$ and $\left|{\lambda }_1\right|>R_e\left({\lambda }_{\mathrm{2,3}}\right)$, satisfy the conditions of Shil’nikov Theorem [47]. If all eigenvalues of Jacobian matrix $A=\partial f/\partial x$ meet the following condition:

$\left|\arg \left(eig\left(A\right)\right)\right|>\alpha \pi /2(8)$

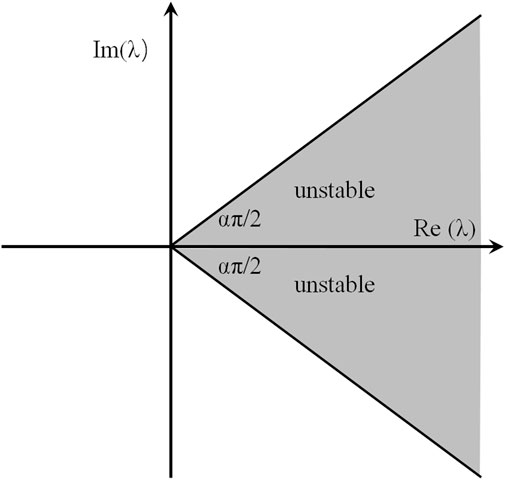
According to the analysis in [56], the equilibrium points in systems Eqs 6, 7 are locally asymptotically stable. If a system has more memory, the system is usually more stable than those systems with less memory [57]. It can be seen from inequality (Eq. 8) that due to the large memory of fractional-order differential equation systems, they are more stable than integer order equation systems. Through analysis, we conclude that the unstable regions are shown in Figure 1. It can be seen from the figure that except for the unstable regions, other regions are stable regions.

FIGURE 1

FIGURE 1. Stability region of fractional-order linear system when fractional-order is equal to $\alpha \pi /2$.

$\alpha \pi /2$When the values of ${\alpha }_i<1$ (i = 1, 2, 3) change, system Eqs 6, 7 do not always remain chaotic. According to inequality (Eq. 8), if the system (Eq. 6) wants to maintain a chaotic state, in the unstable regions, at each non original equilibrium point of the system (Eq. 6), the Jacobian matrix must have two conjugate eigenvalues [58]. According to this description, we have ${\alpha }_i>\frac{2}{\pi }\arctan \left(\frac{1.9353}{0.2577}\right)\approx 0.916$, for i = 1, 2, 3. Moreover, their corresponding eigenvectors are given as follows:

$\{\begin{array}{l}{\eta }_1=\left(\begin{array}{l}-0.4725\\ 0.1737\\ 0.7149\end{array}\right)\pm \text{j}\left(\begin{array}{l}0.4050\\ 0.2673\\ 0\end{array}\right)\\ {\mu }_1=\left(\begin{array}{l}-0.8381\\ 0.2384\\ -0.4907\end{array}\right)\end{array};\{\begin{array}{l}{\eta }_2=\left(\begin{array}{l}0.4725\\ -0.1737\\ 0.7149\end{array}\right)\pm \text{j}\left(\begin{array}{l}-0.4050\\ -0.2673\\ 0\end{array}\right)\\ {\mu }_2=\left(\begin{array}{l}-0.8381\\ 0.2384\\ 0.4907\end{array}\right)\end{array}$

Through analysis and calculation, one-dimensional stable eigenline $E^S\left(O_1\right)$ and two-dimensional unstable eigenplane $E^U\left(O_1\right)$ of system (Eq. 6) at $O_1$ can be obtained:

$\{\begin{array}{l}{E}^S\left(O_1\right):\frac{x}{l_1}=\frac{y}{m_1}=\frac{z}{n_1}\\ E^U\left(O_1\right):A_{1}x+B_{1}y+C_{1}z=0\end{array}(9)$

Here $l_1=-0.8381,m_1=0.2384,n_1=-0.4907$, $A_1=-0.1911$, $B_1=0.2895$, $C_1=-0.1966$. Similarly, one-dimensional stable eigenline $E^S\left(O_2\right)$ and two-dimensional unstable eigenplane $E^U\left(O_2\right)$ of system (Eq. 7) at $O_2$ can be obtained:

$\{\begin{array}{l}{E}^S\left(O_2\right):\frac{x}{l_2}=\frac{y}{m_2}=\frac{z}{n_2}\\ E^U\left(O_2\right):A_{2}x+B_{2}y+C_{2}z=0\end{array}(10)$

Here $l_2=-0.8381,m_2=0.2384,n_2=0.4907$, $A_2=0.1911,B_2=-0.2895,C_2=-0.1966$. Clearly, the stable manifolds $E^S\left(O_1\right)$ and $E^S\left(O_2\right)$ are symmetric to a certain extent, respectively, as are unstable manifolds $E^U\left(O_1\right)$ and $E^U\left(O_2\right)$. Based on this symmetry, we can construct a heteroclinic loop, and heteroclinic chaos can be generated from fractional-order multi piecewise Rucklidge system, just as heteroclinic chaos can be generated from integer multi piecewise linear system [53].

4 Design of Two-Wing and Multi-Wing Chaotic Attractors

In this section, we construct heteroclinic loops, and then use the switching control method to design two-wing and multi-wing chaotic attractors in the two basic fractional-order linear systems introduced earlier. Based on the fundamental fractional linear systems Eqs 6, 7, extend the heteroclinic Shil’nikov theorem [47], we can design a switch controller and then connect the heteroclinic track of systems Eqs 6, 7 to make the track form a heteroclinic loop. Set the switching controller to $\text{w}=F(x,y,z)$ and the switching plane to $S=\{\left(x,y,z\right)|y=0\}$. From systems Eqs 6, 7, the following switching systems can be constructed:

$\{\begin{array}{l}\left(\begin{array}{l}{D}_t^{{\alpha }_1}x\left(t\right)\\ D_t^{{\alpha }_2}\text{y}\left(t\right)\\ D_t^{{\alpha }_3}z\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-2& 0& -\sqrt{6.7}\\ 1& 0& 0\\ 0& 2\sqrt{6.7}& -1\end{array}\right)\left(\left(\begin{array}{l}\text{x}\\ y\\ z\end{array}\right)-w\right)=J_1\left(X-w\right)V\in V_1=\left\{\left(x,y,z\right)|y>0\right\}\\ \left(\begin{array}{l}{D}_t^{{\alpha }_1}x\left(t\right)\\ D_t^{{\alpha }_2}\text{y}\left(t\right)\\ D_t^{{\alpha }_3}z\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-2& 0& \sqrt{6.7}\\ 1& 0& 0\\ 0& -2\sqrt{6.7}& -1\end{array}\right)\left(\left(\begin{array}{l}\text{x}\\ y\\ z\end{array}\right)-w\right)=J_2\left(X-w\right)V\in V_2=\left\{\left(x,y,z\right)|y>0\right\}\end{array}(11)$

It should be noted here that according to Ref. [54], the existence condition of heteroclinic loop in system (Eq. 11) can determine the detailed mathematical expression of switching controller $w=F(x,y,z)={[f_1(x,y,z),f_2(x,y,z),f_3(x,y,z)]}^T$. It is obvious that the equilibrium points $P_2(x_2,y_2,z_2)\in V_2$ and $P_1(x_1,y_1,z_1)\in V_1$ of system Eq. 11 are located on either side of the switching plane $S=\{\left(x,y,z\right)|y=0\}$.

Here, $E^S\left(P_1\right)$ and $E^S\left(P_2\right)$ are the eigenlines systems Eqs 6, 7 at $P_1$ and $P_2$, $E^U\left(P_1\right)$ and $E^U\left(P_2\right)$ are the eigenplanes of systems Eqs 6, 7 at $P_1$ and $P_2$, respectively. Let:

$Q_1=E^S\left(P_1\right)\cap S=\left(x_1-\frac{l_1}{m_1}{y}_1,0,z_1-\frac{n_1}{m_1}{y}_1\right),$

$Q_2=E^S\left(P_2\right)\cap S=\left(x_2-\frac{l_2}{m_2}{y}_2,0,z_2-\frac{n_2}{m_2}{y}_2\right),$

$L_1=E^U\left(P_1\right)\cap S=A_1\left(x-x_1\right)+B_1\left(0-y_1\right)+C_1\left(z-z_1\right)=0,$

$L_2=E^U\left(P_2\right)\cap S=A_2(x-x_2)+B_2(0-y_2)+C_2(z-z_2)=0.$

If $Q_1$ is at $L_2$, there is heteroclinic orbital $H_1=E^U\left(P_2\right)\cup Q_1\cup E^S\left(P_1\right)$ between $P_2$ and $P_1$. Similarly, if $Q_2$ is at $L_1$, there is heteroclinic orbital $H_2=E^U\left(P_1\right)\cup Q_2\cup E^S\left(P_2\right)$ between $P_1$ and $P_2$. Thus, if $Q_1$ is located at $L_2$, $Q_2$ is located at $L_1$, then a heterotopic loop is formed by two heteroclinic orbitals $H_1$ and $H_2$, which join $P_1$ and $P_2$ together. According to heteroclinic Shil’nikov theory [47], if this situation exists, the system (6) has chaotic state in the sense of Smale’s horseshoe.

From the transformation (x, y, z) →(−x,−y, z), it can be seen that there is invariance of the system, so the switching plane $S=\{\left(x,y,z\right)|y=0\}$ satisfying $P_1(x_1,y_1,z_1)\in V_1$ and $P_2(x_2,y_2,z_2)\in V_2$ with $x_1=-x_2=x_0$, $y_1=-y_2=y_0>0$, and $z_1=z_2=z_0$ can be selected. Thus, one can deduce the necessary conditions of $Q_1\in L_2$ and $Q_2\in L_1$ as follows: $x_0=\frac{A_1{l}_2-B_1{m}_2+C_1{n}_2}{2A_1{m}_2}{y}_0=\frac{A_2{l}_1-B_2{m}_1+C_2{n}_1}{2A_2{m}_1}{y}_0$.

Which indicates that $y_0$ depending on $x_0$, and $z_0$ can be any values. In this case, let $y_0=y_1=-y_2=1$ and $z_1=z_2=z_0=0$, then one gets $x_0=x_1=-x_2=0.0585$, $P_1(x_1,y_1,z_1)=P_1(0.0585,\mathrm{1,0})$, and $P_2(x_2,y_2,z_2)=P_2(-0.0585,-\mathrm{1,0})$. Thus, the switching controller is $F\left(x,y,z\right)={\left({\text{x}}_{0}s\left(y\right),y_{0}s\left(y\right),z_{0}s\left(z\right)\right)}^T$ with $x_0=0.0585,y_0=1$, and $z_0=0$, where s(y) (or s(z))is the saturated function, is described by: $s\left(y\right)=\frac{1}{2\alpha }(\left|y+\alpha \right|-\left|y-\alpha \right|)$.Where $\alpha$ decides the slope of the saturated function, here we set $\alpha =0.01$.

According to the above theoretical analysis, switch controller $s_0=s\left(y\right)$, $w_0=F(x,y,z)={(x_{0}s\left(y\right),y_{0}s\left(y\right),z_{0}s\left(z\right))}^T$ can be designed, where $x_0=0.0585,y_0=1$, and $z_0=0$. From system (Eq. 11), one gets

$\left(\begin{array}{l}{D}_t^{{\alpha }_1}x\left(t\right)\\ D_t^{{\alpha }_2}\text{y}\left(t\right)\\ D_t^{{\alpha }_3}z\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-2& 0& -s\left(y\right)\sqrt{6.7}\\ 1& 0& 0\\ 0& s\left(y\right)2\sqrt{6.7}& -1\end{array}\right)\left(\left(\begin{array}{l}\text{x}\\ y\\ z\end{array}\right)-F\left(x,y,z\right)\right)(12)$

The simulation of various fractional-order double-wing buttery chaotic attractor can be obtained when ${\alpha }_i>0.916$, as shown in Figure 2 when ${\alpha }_i=0.92$.

FIGURE 2

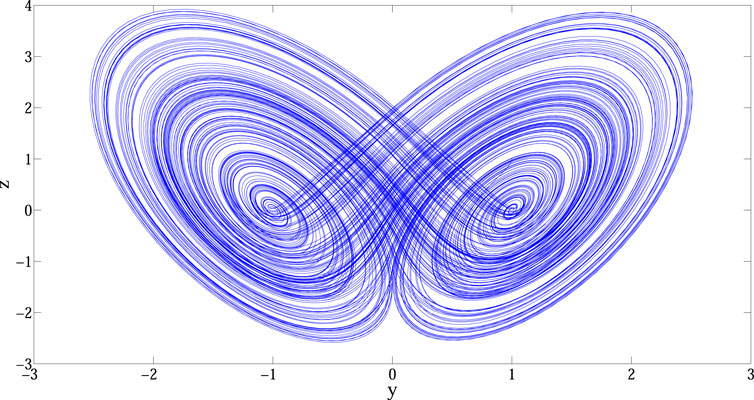
FIGURE 2. Double-wing buttery chaotic attractor of system (Eq. 12) When ${\alpha }_i=0.92$.

${\alpha }_i=0.92$In the same way, we can design the following systems according to systems (Eqs 6, 11):

$\left(\begin{array}{l}{D}_t^{{\alpha }_1}x\left(t\right)\\ D_t^{{\alpha }_2}\text{y}\left(t\right)\\ D_t^{{\alpha }_3}z\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-2& 0& -T\sqrt{6.7}\\ 1& 0& 0\\ 0& 2T\sqrt{6.7}& -1\end{array}\right)\left(\left(\begin{array}{l}\text{x}\\ y\\ z\end{array}\right)-F\left(x,y,z\right)\right)(13)$

where F(x, y, z) is the equilibrium switching controller, and $T=T(x,y,z)$ is the parameter switching controller. F(x, y, z) and T(x, y, z) are the sequence of saturation functions here, as shown below:

$T\left(x,y,z\right)=s\left(y\right)+{\displaystyle \sum _{m=1}^M{\left(-1\right)}^m\left[s\left(y+2m{y}_0\right)+s\left(y-2m{y}_0\right)\right]}(14)$

$F\left(x,y,z\right)=\left(\begin{array}{l}{f}_1\left(x,y,z\right)\\ f_2\left(x,y,z\right)\\ f_3\left(x,y,z\right)\end{array}\right)=\left(\begin{array}{l}{x}_{0}s\left(y\right)+{\displaystyle \sum _{m=1}^M{x}_0\left[s\left(y+2m{y}_0\right)+s\left(y-2m{y}_0\right)\right]}\\ y_{0}s\left(y\right)+{\displaystyle \sum _{m=1}^M{y}_0\left[s\left(y+2m{y}_0\right)+s\left(y-2m{y}_0\right)\right]}\\ z_{0}s\left(y\right)+{\displaystyle \sum _{n=1}^N{z}_0\left[s\left(z+2m{z}_0\right)+s\left(z-2m{z}_0\right)\right]}\end{array}\right)(15)$

where $s(y+2{\text{my}}_0)=\frac{1}{2\alpha }(\left|y+2m{y}_0+\alpha \right|-\left|y+2m{y}_0-\alpha \right|)$.

The prediction correction algorithm is used to solve the fractional-order differential system (Eq. 13), and the simulation results of the fractional-order 12-wing buttery chaotic attractor are obtained when ${\alpha }_i>0.916$, $x_0=0.0585,y_0=1$, $z_0=0$ $N=0$ and $M=5$, the multi-wing attractors are shown in Figure 3 when ${\alpha }_i=0.92$.

FIGURE 3

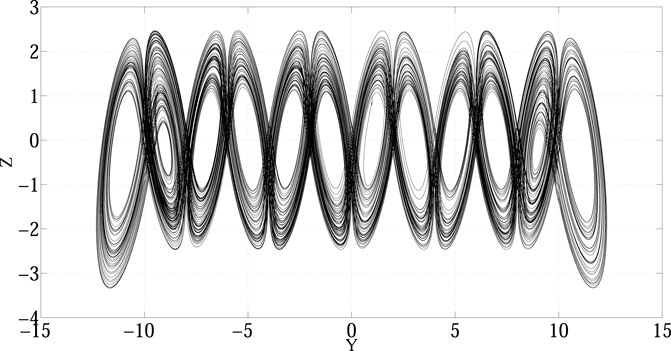
FIGURE 3. 12-wing chaotic attractor of system (Eq. 13) when ${\alpha }_i=0.92$.

A grid multi-wing buttery chaotic attractor with a grid of 2 × 2 is obtained when $x_0=0.0585$, $y_0=1$, $z_0=1$, $M=0$, $N=0$ and ${\alpha }_i=0.94$, as shown in Figure 4.

FIGURE 4

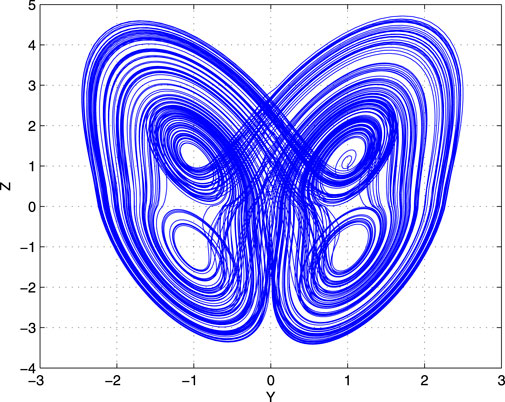
FIGURE 4. 2 × 2-wing chaotic attractor of system (Eq. 13) when ${\alpha }_i=0.94$

${\alpha }_i=0.94$A grid multi-wing buttery chaotic attractor with a grid of 6 × 4 is obtained when $x_0=0.0585,y_0=1$, $z_0=1.125$, $M=2$, $N=1$ and ${\alpha }_i=0.93$, as shown in Figure 5.

FIGURE 5

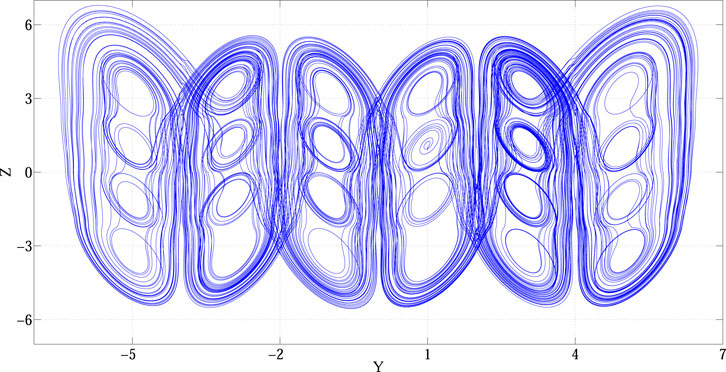
FIGURE 5. 6 × 4-wing chaotic attractor of system (Eq. 13) When ${\alpha }_i=0.93$

${\alpha }_i=0.93$Keeping other parameters unchanged, change the order to ${\alpha }_i=0.95$. The simulation results are shown in Figure 6, it can be seen that the system (Eq. 13) can also generate grid 6 × 4-wing chaotic attractors.

FIGURE 6

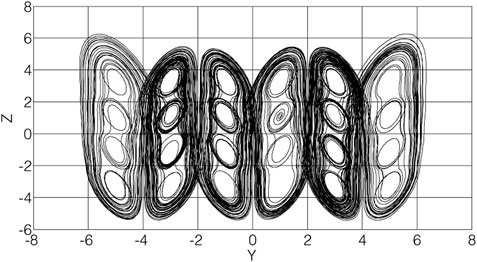
FIGURE 6. 6 × 4 -wing chaotic attractor of system (Eq. 13) When ${\alpha }_i=0.95$

From the above simulation results, it can be seen that if the appropriate parameters are set, when ${\alpha }_i>0.916$, the system can generate multi-wing and grid multi-wing chaotic attractors.

5 Conclusion

In this paper, based on fractional-order linear differential system, a novel grid multi-wing chaotic attractor is proposed by switching saturation function control and constructing heteroclinic loops. Firstly, the two symmetric equilibrium points of the fractional Rucklidge system are linearized to obtain two basic fractional-order linear systems. Then all the equilibrium points of the two basic fractional-order linear systems are connected by a saturation function switching control and a heteroclinic loop. Finally, the effectiveness of the proposed design method is verified by numerical simulation. Since the proposed fractional-order chaotic system can generate multi-wing chaotic attractors with complex dynamic characteristics, however, it does not contain product terms and is easy to implement in circuits, so the chaotic system proposed in this paper has abundant potential engineering applications. In the future, we will further design the circuit realization of the fractional-order multi-wing chaotic system.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YL, XZ, FY and YH contributed to conception and design of the study. JG and YH organized the database. YL and FY performed the statistical analysis. YL and FY wrote the first draft of the manuscript. YL, XZ, JG, and FY wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work is supported by the Hunan Provincial Natural Science Foundation of China under Grant 2019JJ60034, and the Scientific Research Fund of Hunan Provincial Education Department under Grants 19A106, 19B131, 21B0345 and 20k306, and by the Industry University Research Innovation Fund of Chinese Universities—a new generation of information technology innovation project under Grant 2020ITA07029.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Yu F, Kong X, Chen H. A 6D Fractional-Order Memristive Hopfield Neural Network and its Application in Image Encryption. Front Phys (2022) 10:847385. doi:10.3389/fphy.2022.847385

CrossRef Full Text | Google Scholar

2. Xu Q, Cheng S, Ju Z, Chen M, Wu H. Asymmetric Coexisting Bifurcations and Multi-Stability in an Asymmetric Memristive Diode-Bridge-Based Jerk Circuit. Chin J Phys (2021) 70:69–81. doi:10.1016/j.cjph.2020.11.007

CrossRef Full Text | Google Scholar

3. Xu C, Wang C, Jiang J, Sun J, Lin H. Memristive Circuit Implementation of Context-dependent Emotional Learning Network and its Application in Multi-Task. IEEE Trans Comput.-Aided Des Integr Circuits Syst (2021) 1. doi:10.1109/TCAD.2021.3116463

CrossRef Full Text | Google Scholar

4. Yao W, Wang C, Sun Y, Zhou C. Robust Multimode Function Synchronization of Memristive Neural Networks with Parameter Perturbations and Time-Varying Delays. IEEE Trans Syst Man Cybern: Syst (2022) 52(1):260–274. doi:10.1109/TSMC.2020.2997930

CrossRef Full Text | Google Scholar

5. Wan Q, Yan Z, Li F, Liu J, Chen S. Multistable Dynamics in a Hopfield Neural Network Under Electromagnetic Radiation and Dual Bias Currents. Nonlinear Dyn (2022). doi:10.1007/s11071-022-07544-x

CrossRef Full Text | Google Scholar

6. Ma M, Yang Y, Qiu Z, Peng Y, Sun Y, Li Z, et al. A Locally Active Discrete Memristor Model and its Application in a Hyperchaotic Map. Nonlinear Dyn (2022) 107:2935–49. doi:10.1007/s11071-021-07132-5

CrossRef Full Text | Google Scholar

7. Yu F, Qian S, Chen X, Huang Y, Liu L, Shi C, et al. A New 4D Four-Wing Memristive Hyperchaotic System: Dynamical Analysis, Electronic Circuit Design, Shape Synchronization and Secure Communication. Int J Bifurcation Chaos (2020) 30(10):2050147. doi:10.1142/S0218127420501473

CrossRef Full Text | Google Scholar

8. Zhou L, Tan F, Yu F. A Robust Synchronization-Based Chaotic Secure Communication Scheme with Double-Layered and Multiple Hybrid Networks. IEEE Syst J (2019) 14(2):2508–19. doi:10.1109/JSYST.2019.2927495

CrossRef Full Text | Google Scholar

9. Yu F, Zhang Z, Liu L, Shen H, Huang Y, Shi C, et al. Secure Communication Scheme Based on a New 5D Multistable Four-Wing Memristive Hyperchaotic System with Disturbance Inputs. Complexity (2020) 2020, 5859273. doi:10.1155/2020/5859273

CrossRef Full Text | Google Scholar

10. Li Y, Li Z, Ma M, Wang M. Generation of Grid Multi-Wing Chaotic Attractors and its Application in Video Secure Communication System. Multimed Tools Appl (2020) 79:29161–77. doi:10.1007/s11042-020-09448-7

CrossRef Full Text | Google Scholar

11. Yu F, Liu L, He B, Huang Y, Shi C, Cai S, et al. Analysis and FPGA Realization of a Novel 5D Hyperchaotic Four-Wing Memristive System, Active Control Synchronization, and Secure Communication Application. Complexity (2019) 2019, 4047957. doi:10.1155/2019/4047957

CrossRef Full Text | Google Scholar

12. Li X, Mou J, Banerjee S, Cao Y. An Optical Image Encryption Algorithm Based on Fractional-Order Laser Hyperchaotic System. Int J Bifurcation Chaos (2022) 32(03):2250035. doi:10.1142/s0218127422500353

CrossRef Full Text | Google Scholar

13. Fei Y, Zhang Z, Shen H. FPGA Implementation and Image Encryption Application of a New PRNG Based on a Memristive Hopfield Neural Network with a Special Activation Gradient. Chin Phys B (2022) 31(2):020505. doi:10.1088/1674-1056/ac3cb2

CrossRef Full Text | Google Scholar

14. Deng J, Zhou M, Wang C, Wang S, Xu C. Image Segmentation Encryption Algorithm with Chaotic Sequence Generation Participated by Cipher and Multi-Feedback Loops. Multimed Tools Appl (2021) 80:13821–40. doi:10.1007/s11042-020-10429-z

CrossRef Full Text | Google Scholar

15. Gao X, Mou J, Xiong L, Sha Y, Yan H, Cao Y. A Fast and Efficient Multiple Images Encryption Based on Single-Channel Encryption and Chaotic System. Nonlinear Dyn (2022) 108:613–36. doi:10.1007/s11071-021-07192-7

CrossRef Full Text | Google Scholar

16. Zeng J, Wang C. A Novel Hyperchaotic Image Encryption System Based on Particle Swarm Optimization Algorithm and Cellular Automata. Secur. Commun. Netw. (2021) 2021:6675565. doi:10.1155/2021/6675565

CrossRef Full Text | Google Scholar

17. Gao X, Mou J, Banerjee S, Cao Y, Xiong L, Chen X. An Effective Multiple-Image Encryption Algorithm Based on 3D Cube and Hyperchaotic Map. J King Saud Univ - Computer Inf Sci (2022) 34:1535–51. doi:10.1016/j.jksuci.2022.01.017

CrossRef Full Text | Google Scholar

18. Yu F, Liu L, Li K, Cai S. A Robust and Fixed-Time Zeroing Neural Dynamics for Computing Time-Variant Nonlinear Equation Using a Novel Nonlinear Activation Function. Neurocomputing (2019) 350:108–16. doi:10.1016/j.neucom.2019.03.053

CrossRef Full Text | Google Scholar

19. Yang L, Wang C. Emotion Model Of Associative Memory Possessing Variable Learning Rates With Time Delay. Neurocomputing (2021) 460(14):117–125. doi:10.1016/j.neucom.2021.07.011

CrossRef Full Text | Google Scholar

20. Xu C, Wang C, Sun Y, Hong Q, Deng Q, Chen H. Memristor-based Neural Network Circuit with Weighted Sum Simultaneous Perturbation Training and its Applications. Neurocomputing (2021) 462:581–90. doi:10.1016/j.neucom.2021.08.072

CrossRef Full Text | Google Scholar

21. Lin H, Wang C, Deng Q, Xu C, Deng Z, Zhou C. Review on Chaotic Dynamics of Memristive Neuron and Neural Network. Nonlinear Dyn (2021) 106(1):959–73. doi:10.1007/s11071-021-06853-x

CrossRef Full Text | Google Scholar

22. Xu Q, Ju Z, Ding S, Feng C, Chen M, Bao B. Electromagnetic Induction Effects on Electrical Activity within a Memristive Wilson Neuron Model. Cogn Neurodyn (2022). doi:10.1007/s11571-021-09764-0

CrossRef Full Text | Google Scholar

23. Zhou C, Wang C, Sun Y, Yao W. Weighted Sum Synchronization of Memristive Coupled Neural Networks. Neurocomputing (2020) 403, 211–223. doi:10.1016/j.neucom.2020.04.087

CrossRef Full Text | Google Scholar

24. Fei Y, Zhang Z, Shen H. Design and FPGA Implementation of a Pseudo-random Number Generator Based on a Hopfield Neural Network under Electromagnetic Radiation. Front Phys (2021) 9:690651. doi:10.3389/fphy.2021.690651

CrossRef Full Text | Google Scholar

25. Yao W, Wang C, Sun Y, Zhou C, Lin H, et al. Synchronization of Inertial Memristive Neural Networks With Time-Varying Delays via Static or Dynamic Event-Triggered Control. Neurocomputing (2020) 404:367–80. doi:10.1016/j.neucom.2020.04.099

CrossRef Full Text | Google Scholar

26. Xiong B, Yang K, Zhao J, Li K. Robust Dynamic Network Traffic Partitioning against Malicious Attacks. J Netw Computer Appl (2017) 87:20–31. doi:10.1016/j.jnca.2016.04.013

CrossRef Full Text | Google Scholar

27. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S. Dynamics Analysis, Hardware Implementation And Engineering Applications Of Novel Multi-Style Attractors In A Neural Network Under Electromagnetic Radiation. Chaos, Solitons & Fractals (2021) 152:111350. doi:10.1016/j.chaos.2021.111350

CrossRef Full Text | Google Scholar

28. Yao W, Wang C, Cao J, Sun Y, Zhou C. Hybrid Multisynchronization of Coupled Multistable Memristive Neural Networks With Time Delays. Neurocomputing (2019) 363:281–94. doi:10.1016/j.neucom.2019.07.014

CrossRef Full Text | Google Scholar

29. Long M, Zeng Y. Detecting Iris Liveness with Batch Normalized Convolutional Neural Network. CMC-Computers Mater Continua (2019) 58(2):493–504. doi:10.32604/cmc.2019.04378

CrossRef Full Text | Google Scholar

30. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S. A New Multi-Scroll Chua’s Circuit With Composite Hyperbolic Tangent-Cubic Nonlinearity: Complex Dynamics, Hardware Implementation and Image Encryption Application. Integration (2021) 81:71–83. doi:10.1016/j.vlsi.2021.05.011

CrossRef Full Text | Google Scholar

31. Zhang X, Wang C. A Novel Multi-Attractor Period Multi-Scroll Chaotic Integrated Circuit Based on CMOS Wide Adjustable CCCII. IEEE Access (2019) 7(1):16336–50. doi:10.1109/access.2019.2894853

CrossRef Full Text | Google Scholar

32. Yu F, Chen H, Kong X. Dynamic Analysis and Application in Medical Digital Image Watermarking of a New Multi-Scroll Neural Network with Quartic Nonlinear Memristor. Eur Phys J Plus (2022) 137:434. doi:10.1140/epjp/s13360-022-02652-4

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zhou L, Wang C, Zhou L. A Novel No-Equilibrium Hyperchaotic Multi-Wing System via Introducing Memristor. Int J Circ Theor Appl (2018) 46(1):84–98. doi:10.1002/cta.2339

CrossRef Full Text | Google Scholar

34. Zhou L, Wang C, Zhou L. Generating Hyperchaotic Multi-wing Attractor in a 4D Memristive Circuit. Nonlinear Dyn (2016) 85(4):2653–63. doi:10.1007/s11071-016-2852-8

CrossRef Full Text | Google Scholar

35. Cui L, Lu M, Ou Q, Duan H, Luo W. Analysis and Circuit Implementation of Fractional Order Multi-wing Hidden Attractors. Chaos, Solitons and Fractals (2020) 138:109894. doi:10.1016/j.chaos.2020.109894

CrossRef Full Text | Google Scholar

36. Podlubny I. Fractional Differential Equations. New York: Academic Press (1999):340–68.

Google Scholar

37. Hifer R. Applications of Fractional Calculus in Physics. World Scientific (2001) 120–75.

Google Scholar

38. Cafagna D, Grassi G. Bifurcation and Chaos in the Fractional-Order Chen System via a Time-Domain Approach. Int J Bifurcation Chaos (2008) 18:1845–63. doi:10.1142/s0218127408021415

CrossRef Full Text | Google Scholar

39. Yang F, Mou J, Liu J. Characteristic Analysis of the Fractional-Order Hyperchaotic Complex System and its Image Encryption Application. Signal Process. (2020) 169:107373. doi:10.1016/j.sigpro.2019.107373

CrossRef Full Text | Google Scholar

40. Xie W, Wang C, Lin H. A Fractional-Order Multistable Locally Active Memristor and its Chaotic System with Transient Transition, State Jump. Nonlinear Dyn (2021) 104:4523–41. doi:10.1007/s11071-021-06476-2

CrossRef Full Text | Google Scholar

41. Deng W, Li C. Synchronization of Chaotic Fractional Chen System. J Phys Soc Jpn (2005) 74:1645–8. doi:10.1143/jpsj.74.1645

CrossRef Full Text | Google Scholar

42. Ahmad WM. Generation and Control of Multi-Scroll Chaotic Attractors in Fractional Order Systems. Chaos, Solitons and Fractals (2005) 25:727–35. doi:10.1016/j.chaos.2004.11.073

CrossRef Full Text | Google Scholar

43. Cafagna D, Grassi G. Fractional-order Chaos: a Novel Four-wing Attractor in Coupled Lorenz Systems. Int J Bifurcation Chaos (2009) 19:3329–38. doi:10.1142/s0218127409024785

CrossRef Full Text | Google Scholar

44. Deng W, Lü J. Design of Multidirectional Multiscroll Chaotic Attractors Based on Fractional Differential Systems via Switching Control. Chaos (2006) 16:043120. doi:10.1063/1.2401061

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Zhang C, Yu S. Generation of Multi-wing Chaotic Attractor in Fractional Order System. Chaos, Solitons and Fractals (2011) 44:845–50. doi:10.1016/j.chaos.2011.06.017

CrossRef Full Text | Google Scholar

46. Petras I. Fractional-Order Memristor-Based Chua's Circuit. IEEE Trans Circuits Syst (2010) 57(12):975–9. doi:10.1109/tcsii.2010.2083150

CrossRef Full Text | Google Scholar

47. Silva CP. Shil'nikov's Theorem-A Tutorial. IEEE Trans Circuits Syst (1993) 40:675–82. doi:10.1109/81.246142

CrossRef Full Text | Google Scholar

48. Chua L, Komuro M, Matsumoto T. The Double Scroll Family. IEEE Trans Circuits Syst (1986) 33:1072–118. doi:10.1109/tcs.1986.1085869

CrossRef Full Text | Google Scholar

49. Shilnikov LP. Chuas Circuit: Rigorous Results and Future Problems. IEEE Trans Circuits Syst Fundam Theor Appl (1993) 40:784–6. doi:10.1109/81.246153

CrossRef Full Text | Google Scholar

50. Mees A, Chapman P. Homoclinic and Heteroclinic Orbits in the Double Scroll Attractor. IEEE Trans Circuits Syst (1987) 34:1115–20. doi:10.1109/tcs.1987.1086251

CrossRef Full Text | Google Scholar

51. Li Z, Chen G, Halang WA. Homoclinic and Heteroclinic Orbits in a Modified Lorenz System. Inf Sci (2004) 165:235–45. doi:10.1016/j.ins.2003.06.005

CrossRef Full Text | Google Scholar

52. Li G, Chen X. Constructing Piecewise Linear Chaotic System Based on the Heteroclinic Shil'nikov Theorem. Commun Nonlinear Sci Numer Simulation (2009) 14:194–203. doi:10.1016/j.cnsns.2007.07.007

CrossRef Full Text | Google Scholar

53. Rucklidge AM. Chaos in Models of Double Convection. J Fluid Mech (1992) 237:209–29. doi:10.1017/s0022112092003392

CrossRef Full Text | Google Scholar

54. Yu S, Lu J, Chen G, Yu X. Generating Grid Multiwing Chaotic Attractors by Constructing Heteroclinic Loops into Switching Systems. IEEE Trans Circuits Syst (2011) 58(5):314–8. doi:10.1109/tcsii.2011.2149090

CrossRef Full Text | Google Scholar

55. Vanĕc̆ek A, C̆elikovský S. Control Systems: From Linear Analysis to Synthesis of Chaos. Englewood Cliffs, NJ: Prentice-Hall (1996):433–60.

Google Scholar

56. Diethelm K, Ford NJ, Freed AD. A Predictor Corrector Approach for the Numerical Solution of Fractional Differential Equations. Nonlinear Dyn (2002) 29(1):3–22. doi:10.1023/a:1016592219341

CrossRef Full Text | Google Scholar

57. Ahmed E, El-Sayed AMA, El-Saka HAA. Equilibrium Points, Stability and Numerical Solutions of Fractional-Order Predator-Prey and Rabies Models. J Math Anal Appl (2007) 325(1):542–53. doi:10.1016/j.jmaa.2006.01.087

CrossRef Full Text | Google Scholar

58. Mohammad ST, Mohammad H. A Necessary Condition for Double Scroll Attractor Existence in Fractional-Order Systems. Phys Lett A (2007) 367(1):102–13. doi:10.1016/j.physleta.2007.05.081

CrossRef Full Text | Google Scholar