Correlation Optics, Coherence and Optical Singularities: Basic Concepts and Practical Applications

The main idea of this review is to trace the interrelations and inter-transitions between the basic concepts and approaches of the correlation optics (including the light coherence) and the singular optics dealing with networks of “exceptional” points of light fields. The principles and examples are described of formation of light fields with required structures (amplitude, phase and polarization distributions, spectral properties as well as the internal energy flows and energy gradients responsible for optical forces) via superpositions of model optical fields of simple standard configurations and under controllable correlation conditions. The theoretical and experimental results, obtained by the authors and other researchers, demonstrate possibilities of the general approach to the complex fields formation with spatial and polarization inhomogeneities. A special topic, considered in more detail, is the interaction of structured optical fields with the media containing suspended micro- and nanoparticles, their inhomogeneous heating by the laser radiation and the accompanying self-diffraction and self-focusing phenomena. Possible light-induced phase transitions and controllable generation of the gas-vapor microbubbles in the medium are discussed. Specific optical singularities in polychromatic light fields are analyzed in connection to the field coherence. Some experimental solutions for revealing the fine structure of optical fields by means of the interference schemes are presented. Practical applications for the micromanipulation techniques, optical diagnostics of remote and random objects, optical treatment and laboratory practice in biology and medicine are described and discussed.

1 Introduction

The term “correlation optics” was first introduced in the 60–70s of the past century in applications related to the development of holography. In particular, the referenceless holography employing the holographic associative memory (ghost-image holography) [1–8] was a hot topic at that time. Simultaneously, the ideas of correlation optics were developed within the framework of a broader concept – “pseudo-depolarization” of multiply scattered coherent radiation [9]. Apparently, the fields of this type were first described in Refs. 10, 11 (before the “emergence” of singular optics and, accordingly, without explicit recognition of the singular features). In these works, the fields were called pseudo-depolarized in the following sense. Locally (at each point), the field is fully polarized (e.g., the local intensity can be completely nullified at certain orientations of the quarter-wave plate and the linear analyzer), but the polarization state varies from point to point, and to extinguish the field at any other point one needs to change the orientations of the polarizer-analyzer pairs. Essentially, any integrated polarization analysis over a sufficiently large area of the beam cross section indicates the absence of a predominant state of polarization. Accordingly, the efficiency of holographic recording of objects generating pseudo-depolarized fields with deterministically (uniformly) polarized reference wave varies for different parts of the field and is, generally speaking, lower than for non-depolarizing objects. In the modern terminology, such fields are frequently characterized by the term “global depolarization”, which invokes the view of the Poincare sphere, as the “globe” of polarization states of light [12–15].

The correlation-optics concept is close to the Emile Wolf’s idea of “Optics of observable quantities” [16, 17]. It emphasizes that the parameters underlying classical wave optics (local values of the amplitude, phase and polarization of a light wave) are not directly measured and, consequently, cannot be directly controlled. However, these parameters can be available through certain correlation functions, describing the immediately observable features of the light field behavior. The correlation functions can be determined and realized experimentally by measuring and controlling the time-averaged values of the field intensity under proper experimental conditions, and this opens ways for the meaningful and consistent control of the optical-field parameters “in a whole”.

In this paradigm, the interference with controllable reference waves is the main instrument, and its fruitful application requires detailed and consistent allowance for the full set of the light-wave parameters. For example, the experimentally registered interference pattern gives access to the underlying parameters via the only channel of the pattern visibility. At the same time, its consistent interpretation requires the knowledge of the polarization properties and the degree of coherence of the superposing waves. In particular, even the explanation of the two-slit Young experiment is not fully determinate in the case of “completely unpolarized” light [14, 18].

In this context, let us start the correlation-optics analysis by a short inventory of the underlying light-field characteristics. As usual, the optical field is considered as an electromagnetic wave whose electric E(R, t) and magnetic H(R, t) vectors are space- and time-dependent, $\mathbf{R}={\left(x,y,z\right)}^T$ is the spatial radius-vector (superscript “T” denotes matrix transposition); t symbolizes time. In regions without free charges and currents, the field vectors satisfy the Maxwell’s equations [19]:

$\nabla \mathbf{H}=0,\frac{\partial \mathbf{H}}{\partial t}=-\frac{c}{\mu }\nabla \times \mathbf{E},\nabla \mathbf{E}=0,\frac{\partial \mathbf{E}}{\partial t}=\frac{c}{\epsilon }\nabla \times \mathbf{H},(1)$

where c is the speed of light in vacuum, ε and μ are the permittivity and permeability of the medium, respectively, and the Gaussian system of units is used. Eq. 1 show that the electric and magnetic fields in the light wave are interrelated, and the distribution of either one of them, E or H, is sufficient for the full electromagnetic wave characterization. In view of the most physical manifestations, it is suitable to consider characteristics of the vector E as the underlying parameters of an optical field.

As a rule, we consider quasi-monochromatic waves [19–22] which can be presented via the Fourier integral

$\mathit{E}\left(\mathbf{R},t\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\mathbf{E}\left(\mathbf{R},\nu \right)e^{-i\nu t}\frac{d\nu }{2\pi }}=\mathrm{Re}{\displaystyle \underset{0}{\overset{\infty }{\int }}\mathbf{E}\left(\mathbf{R},\nu \right)e^{-i\nu t}\frac{d\nu }{\pi }}(2)$

in which the spectral density $\mathbf{E}\left(\mathbf{R},\nu \right)$ differs from zero in a narrow interval with the central frequency ω so that

$\mathit{E}\left(\mathbf{R},t\right)=\mathrm{Re}\left[\left({\displaystyle \underset{0}{\overset{\infty }{\int }}\mathbf{E}\left(\mathbf{R},\nu \right)\frac{d\nu }{\pi }}\right)e^{-i\omega t}\right]\equiv \mathrm{Re}\left[\mathbf{E}\left(\mathbf{R},\tau \right)\exp \left(-i\omega t\right)\right](3)$

where $\mathbf{E}\left(\mathbf{R},\tau \right)$ characterizes the wave amplitude at the central frequency. Its dependence on time is slow with respect to the oscillation period 2π/ω, which is reflected by the “slow-time” argument τ. The slow-time complex function $\mathbf{E}\left(\mathbf{R},\tau \right)$ supplies a suitable instrument for description and analysis of such waves [23–25].

An important special class of light fields is the so called paraxial waves [23–25] where the physically selected longitudinal direction (propagation direction) z exists, and the rate of the field amplitude variations along z is much lower than that in the transverse (x, y) plane; in turn, the characteristic variations’ scale in the transverse plane is much higher than the vacuum wavelength $\lambda =2\pi /k$ ($k=\omega /c$ is the wave number). In such situations, the electric vector is nearly transverse and can be described by the complex amplitude distribution

$\mathbf{E}\left(\mathbf{R},\tau \right)={\mathbf{E}}_{\perp }+{\mathit{e}}_z{E}_z=\left[\mathbf{u}+\frac{i}{kn}{\mathit{e}}_z\left({\nabla }_{\perp }\cdot \mathbf{u}\right)\right]e^{iknz}.(4)$

Here, the subscript “⊥” denotes the transverse part of the vector, R_⊥ = r = (x, y)^T, e_z is the unit vector of the longitudinal direction z, $n=\sqrt{\epsilon \mu }$ is the medium refractive index, u(r, z, $\tau$) is the paraxial complex amplitude [23, 24]:

$\mathbf{u}={\mathit{e}}_{\perp }u={\mathit{e}}_x{u}_x+{\mathit{e}}_y{u}_y={\mathit{e}}_{+}{u}_{+}+{\mathit{e}}_{-}{u}_{-},(5)$

e_x, e_y being the unit vectors of the transverse coordinates, and

${\mathit{e}}_{+}=\frac{1}{\sqrt{2}}\left({\mathit{e}}_x+i{\mathit{e}}_y\right),{\mathit{e}}_{-}=\frac{1}{\sqrt{2}}\left({\mathit{e}}_x-i{\mathit{e}}_y\right),u_{+}=\frac{1}{\sqrt{2}}\left(u_x-i{u}_y\right),u_{-}=\frac{1}{\sqrt{2}}\left(u_x+i{u}_y\right)(6)$

are the complex unit vectors and the transverse field components in the circular-polarization basis. The transverse complex amplitude Eq. 4 satisfies the paraxial wave equation [23, 24]:

$i\frac{\partial u_{\sigma }}{\partial z}=-\frac{1}{2kn}{\nabla }_{\perp }^2{u}_{\sigma },(7)$

where ${\nabla }_{\perp }={\mathit{e}}_x\left(\frac{\partial }{\partial x}\right)+{\mathit{e}}_y\left(\frac{\partial }{\partial y}\right)$ is the transverse gradient, and σ = ±1 for the basis of circular polarizations or σ = x, y for the basis of linear polarization which are equally admissible in the paraxial approximation. The main (first) term of Eq. 4 describes the transverse field component, while the longitudinal component (second term) is of the relative order $\gamma ={\left(kb\right)}^{-1}$ in magnitude, with b being the characteristic transverse scale of the distribution u(r, z). The quantity $\gamma$ is the small parameter of the paraxial approximation; the longitudinal characteristic scale of the paraxial beam equals $z_R=k{b}^2$.

2 Foundations of the Correlation-Optics and Polarization-Optics Formalism

2.1 General Concepts and Relations

Correlation functions are determined as time-average values of the products of the field characteristics taken at different spatial points and different moments of time. In the paraxial case, main correlation functions are collected in the coherence matrix introduced by Wolf [16, 17, 26, 27].

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)=\begin{array}{c}\langle \left(\begin{array}{c}{E}_x^{\ast }\left({\mathbf{r}}_1,{\tau }_1\right)\\ E_y^{\ast }\left({\mathbf{r}}_1,{\tau }_1\right)\end{array}\right)\left(\begin{array}{cc}{E}_x\left({\mathbf{r}}_2,{\tau }_1+\mathrm{\Delta }\tau \right)& E_y\left({\mathbf{r}}_2,{\tau }_1+\mathrm{\Delta }\tau \right)\end{array}\right)\rangle \\ =\left[\begin{array}{cc}{W}_{xx}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)& W_{xy}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)\\ W_{yx}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)& W_{yy}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)\end{array}\right]. \end{array}(8)$

where $W_{ij}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)=\langle E_i^{\ast }\left({\mathbf{r}}_1,{\tau }_1\right)E_j\left({\mathbf{r}}_2,{\tau }_1+\mathrm{\Delta }\tau \right)\rangle$ (i, j = x, y) is the two-point correlation function (cross-correlation function), and ⟨…⟩ denotes an ensemble average (practically coincides with the time-average). Matrix (Eq. 8) performs a transition from the underlying field parameters to the immediately observable correlation (time-averaged) properties of light fields. Normally, the correlation functions tend to zero for large enough difference between ${\mathbf{r}}_1$ and ${\mathbf{r}}_2$ and $\text{Δ}\tau >{\tau }_c$ (coherence time). On the contrary, when ${\mathbf{r}}_1={\mathbf{r}}_2,\mathrm{\Delta }\tau =0$, the coherence matrix contains data on the correlation between the Cartesian components of the electric-field-vector fluctuations at a given spatial point at a given time and is directly related to the Stokes parameters:

$\begin{array}{l}{S}_0=\langle E_x{E}_x^{\ast }\rangle +\langle E_y{E}_y^{\ast }\rangle =I,S_1=\langle E_x{E}_x^{\ast }\rangle -\langle E_y{E}_y^{\ast }\rangle ,\\ S_2=\langle E_x{E}_y^{\ast }\rangle +\langle E_y{E}_x^{\ast }\rangle ,S_3=i(\langle E_x{E}_y^{\ast }\rangle -\langle E_y{E}_x^{\ast }\rangle )\end{array}(9)$

(S₀ coincides with the light intensity I). The Stokes parameters are local and do not describe variations of the state of polarization of a light beam upon its propagation.

In many cases, both fully and partially coherent paraxial beams can be suitably characterized by the Wigner distribution function, which “unites” the spatial distribution of the light energy in a fixed cross section with the angular distribution of the wave propagation in the far field [28–31]:

$U\left(\mathbf{r},\mathbf{p}\right)=\frac{1}{{\lambda }^2}{\displaystyle \int W\left(\mathbf{r},\mathbf{\rho }\right)\exp \left[-ik\left(\mathbf{p}\cdot \mathbf{\rho }\right)\right]d^2\mathbf{\rho }},$

where

$W\left(\mathbf{r},\mathbf{\rho }\right)=\langle u\left(\mathbf{r}+\frac{\mathbf{\rho }}{2}\right)u^{\ast }\left(\mathbf{r}-\frac{\mathit{\rho }}{2}\right)\rangle ,$

u is the scalar complex amplitude Eqs 5–7 of the paraxial field, and vector p = (p_x, p_y)^T determines the transverse components of the unit-vector (p_x, p_y, 1)^T specifying the far-field direction. Wigner function enables the suitable characterization of the beam propagation properties via the first- and second-order “intensity moments” [29–31]:

${\displaystyle \int \left(\begin{array}{c}\mathbf{r}\\ \mathbf{p}\end{array}\right)U\left(\mathbf{r},\mathbf{p}\right)d^{2}r{d}^{2}p},{\displaystyle \int \left(\begin{array}{c}\mathbf{r}\\ \mathbf{p}\end{array}\right){\left(\begin{array}{c}\mathbf{r}\\ \mathbf{p}\end{array}\right)}^{T}U\left(\mathbf{r},\mathbf{p}\right)d^{2}r{d}^{2}p}$

(here, the 4-column and 4-row are multiplied according to the matrix-product rule, like in Eq. 8). Remarkably, this formalism can be generalized to vector beams with inhomogeneous polarization [30], and it is directly applicable to description of the beams propagating in stochastic scattering media [32].

2.2 Non-Paraxial Fields and Genuine 3D Polarization States

The paraxial representations Eqs 4–9 are quite relevant in most applications. However, in highly structured light fields, their 3D (non-paraxial) versions are useful:

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)= \left[\begin{array}{ccc}{W}_{xx}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)& W_{xy}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)& W_{xz}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)\\ W_{yx}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)& W_{yy}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)& W_{yz}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)\\ W_{zx}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)& W_{zy}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)& W_{zz}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\mathrm{\Delta }\tau \right)\end{array}\right],(10)$

which differs from the paraxial prototype (Eq. 8) solely by addition of the third coordinate z. Accordingly, the 3D generalization of (Eq. 9) leads to the Stokes-Gell-Mann parameters [33].

$\begin{array}{c}{S}_0=\langle {\left|E_x\right|}^2+{\left|E_y\right|}^2\rangle ;S_{11}=\langle {\left|E_x\right|}^2\rangle -\langle {\left|E_y\right|}^2\rangle ;S_{12}=\sqrt{3}\frac{\langle {\left|E_x\right|}^2\rangle +\langle {\left|E_y\right|}^2\rangle -2\langle {\left|E_z\right|}^2\rangle }{2};\\ S_{12}=2\text{Re}\langle E_y^{\ast }{E}_z\rangle ;S_{22}=2\text{Re}\langle E_z^{\ast }{E}_x\rangle ;S_{23}=2\text{Re}\langle E_x^{\ast }{E}_y\rangle ;\\ S_{31}=2\text{Im}\langle E_y^{\ast }{E}_z\rangle ;S_{32}=2\text{Im}\langle E_z^{\ast }{E}_x\rangle ;S_{33}=2\text{Im}\langle E_x^{\ast }{E}_y\rangle .\end{array}(11)$

Note that for paraxial fields, where only the x- and y-components of the field are significant, the Stokes-Gell-Mann parameters S₀, S₁₁, S₂₃, S₃₃ reduce to the standard Stokes parameters (Eq. 10), while S₁₂ becomes the same as S₀, and the remaining ones vanish.

In the framework of the presented statistical-electrodynamic definition of the Stokes parameters (Eq. 11), these parameters appear as “single-point” second-order correlation functions of the orthogonal polarization components. In this case, the phase relations between the orthogonal components, which determine the state of polarization, are also taken into account.

Recent advances in the areas of nanophotonics and near-field optics stipulate growing interest to the polarimetric structure of 3D light fields [34–50]. An interesting fact is that any state of polarization of the 3D fields can be represented in terms of regular and irregular components [34–36]. In such cases, the regular component is formed by composition of a pure state (perfectly polarized), a 2D unpolarized state (for which the polarization ellipse behaves randomly in a fixed plane) and a 3D unpolarized state. The irregular component is determined by the coherent composition of two pure states with polarization ellipses lying in different planes, while any irregular distribution is a 3D optical field. The genuine 3D states of polarization demonstrate essential role of the (nominally) longitudinal polarization component and are characterized by fluctuations in the direction of propagation.

An extension of this approach involves the assessment of purity for partially polarized fields in three dimensions [37] with separation of the circularly- and linearly-polarized contributions, which is proposed to be described via the coherency-matrix elements parameterized in terms of polarization ellipticity, regarding the intrinsic polarization properties of the field. The similar concepts appear to be fruitful for purposeful formation of complex optical fields with inhomogeneous 3D polarization structures [38, 39]. Alternative highly efficient instruments for characterization of the partially-coherent 3D optical fields involve fruitful concepts of the polarimetric dimension, polarimetric purity and polarimetric regularity [35, 36, 49].

A well-developed 3D polarization can be formed upon tight focusing of partially coherent beams. Considering the example of a radially polarized Gaussian Schell-model beam [40] and partially polarized beams constructed by incoherent superposition of two orthogonally polarized plane-wave modes, it was revealed that there exists a nano-scale region near the focus where the field shows the expressed 3D polarization. The focal field in this case demonstrates a variety of polarization states from fully unpolarized to 3D polarized, which can be used for detection and optical manipulation of micro- and nanoparticles [41].

As is well known, the circularly polarized light is the source of the spin angular momentum (SAM) directed longitudinally (along the direction of propagation) [19, 24]. Accordingly, a complex inhomogeneous states of polarization are associated with the SAM whose local values and directions are dictated by the local 3D polarization [42–44]. For non-paraxial light, the transverse spin, orthogonal to the main direction of propagation, is rather typical, and its existence is largely independent on the state of polarization of the wave. As is shown in Refs. 45, 48, the transverse spin is independent of the 2D polarization and is preserved even in 3D fields generated by completely unpolarized paraxial light. This is in sharp contrast to the usual longitudinal SAM, which is directly related to the 2D polarization and vanishes in unpolarized fields. This shows the difference between the 2D and 3D descriptions of polarization: A completely unpolarized 2D field is, at the same time, half-polarized in a 3D sense.

Accordingly, 3D-structured light beams that are generated by a 2D source may also carry a sort of the azimuthal phase factor, i.e., acquire a nonzero contribution to the optical helicity density [45, 46], which does not depend on the state of polarization and can therefore originate from an unpolarized 2D light source. As a consequence, light generated by a completely unpolarized paraxial OV source can exhibit optical activity [46].

A characteristic feature of 3D fields is the existence of the longitudinal electric and/or magnetic components, commensurate to the usual transverse ones [23–25, 42–44]. In paraxial beams, this fact is responsible for a set of fine effects concerning the polarization-dependent deviations from the geometric-optics beam trajectory [51–53]. The physical relevance and especial role of the longitudinal field components have been confirmed with the model examples of fields formed by the interference of plane waves propagating in orthogonal directions [54]. In general, light fields with the longitudinal polarization naturally appear upon propagation through optically anisotropic crystals, due to strong focusing, in cases of or multiple scattering in dull media or at random phase objects and in optical waveguides as well as in the processes of optical heterodyning (mixtures of waves of various states of polarization). The longitudinal field components can be employed in sensitive optical diagnostics, in particular, for the confocal microscopy of isolated anisotropic molecules and in the nanorough-surface investigation [55]. Their presence is typical for electromagnetic localized waves that will be briefly discussed below in Section 6.

Noteworthy, the most complete characterization of the polarized light is available through estimating the measure of mutual coherence of the orthogonally polarized beam components. Thus, a combination of elements of the Wolf coherence matrix can be used to describe such characteristics of a light beam as intensity, coherence, and polarization [56]. In 2003, E. Wolf substantiated the fundamental role of interference for the analysis of partially polarized light on the basis of a unified theory of coherence and polarization of stochastic electromagnetic fields [16, 17, 26]. It should be noted that the most profound and fundamental definition of the polarization of light is just given in terms of mutual coherence of the orthogonal polarization components of the beam. Accordingly, the degree of polarization appears to be equal to the maximum value of the degree of coherence of the orthogonal polarization components, which is realized in the case of equal-intensity components.

2.3 Poincaré Sphere and Its Generalizations

A special place in the representation of polarized light is occupied by the approach proposed by Poincaré in 1892, which is based on the stereographic description of polarized light fields in the form of a Poincaré sphere. Its physical meaning is directly related to the set of normalized Stokes parameters [19, 20] which follows from (Eq. 9) in the form

$s_{\mathrm{1,2,3}}=S_{\mathrm{1,2,3}}/S_0.(12)$

and the sphere is determined by equation $s_1^2+s_2^3+s_3^2=1$. Its equator (see Figure 1) contains all states of linear polarization, and the north (south) pole represents right-handed (left-handed) circularly polarized light. Points on the northern (southern) hemisphere represent the right-handed (left-handed) elliptical states of polarization which are characterized by two angles: the polarization azimuth (with respect to the y-axis) $\psi =\frac{1}{2}\text{arctan}\left(s_2/s_1\right)$ and the angle of ellipticity $\chi =\frac{1}{2}\text{arcsin}\left(s_3\right)$ [57] such that $\text{tan}\chi$ equals to the ratio of the polarization ellipse’s axes, and the sign of $\chi$ determines the polarization handedness.

FIGURE 1

FIGURE 1. Poincaré sphere and its parameters.

If an ideal correlation exists between the two transverse electric-field components, and the state of polarization does not change in time, such a beam is totally (or perfectly) polarized. Oppositely, when the correlation between the transverse components is absent, the beam is unpolarized. In all other cases, the situation of partial polarization takes place. Naturally, it makes sense to talk about the constancy of the field amplitudes in time intervals much shorter than the coherence time of the radiation, which is related to the width of the source power spectrum (Eq. 2) [58]. For longer time intervals, these values change. Therefore, the interrelations between the absolute values of the field components, as well as their relative phases, can fluctuate, which is reflected in the change in the position of a point on the Poincaré sphere (Figure 2).

FIGURE 2

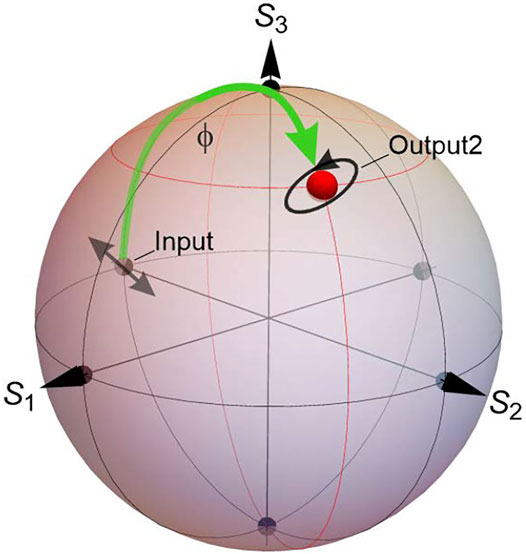
FIGURE 2. Demonstration of the phase shift ϕ in the course of the beam evolution (visualization with the help of the Poincaré sphere).

Evolution of the state of polarization during the beam propagation can be described by the curve on the Poincaré sphere. In Figure 2, the beam being initially in the “Input” state, after a proper evolution (propagation through an optical system or inhomogeneous medium), appears in the “Output2” state, and its phase is changed by ϕ. When the final state of polarization returns to the initial value (the point describes a closed loop on the Poincaré sphere), the phase shift ϕ, generally, differs from zero: the beam acquires an additional phase – the Pancharatnam–Berry geometric phase [59]. This phase is caused by the geometry of the curved polarization space and equals to half the solid angle subtended by the polarization trajectory.

In parallel to the coherency and polarization optics, the fruitful contributions to the correlation optics are associated with the study of optical singularities. At the beginning of its formation (1981–2001), singular optics [60] was based on the coherent approach. In the simplest case, the complex amplitude of scalar monochromatic and fully polarized electromagnetic fields was considered. The main attention was focused on the phase singularities where the phase of the field complex amplitude (Eq. 5) is indeterminate (phase uncertainty). Such points normally belong to specific lines or contours, closed within the observable regions or open (closed at infinity), where the field amplitude is zero. These objects demonstrate a complex of unique physical properties, due to which the same objects are referred to by various terms: phase singularities, wavefront dislocations, isolated amplitude zeros, optical vortices (OVs) [23–25, 60–61]. A common example of the circular light beams of this sort is the Laguerre–Gaussian mode of a laser resonator [60–62], which spectacularly illustrates the main physical attributes: the helical dependence of the phase near the singularity core

$\sim \exp \left(\pm il\phi \right)(13)$

where $\phi$ is the azimutal angle, the phase increment on a round-trip near the core 2lπ where l is an integer topological charge of the singularity, and the transverse energy circulation due to which the beam carries an orbital angular momentum (OAM) with respect to the propagation axis, with the numerical value lħ per photon. Importantly, all these properties are of the topological nature and are therefore stable to the field perturbations, except that the multicharged OV with |l| > 1 can split into a set of |l| “secondary” singularities with the unit topological charge.

The possibility of several singularities inside a “single” optical field invokes important questions relating their interactions and interrelations. Each singularity, in a certain way, “organizes” the field nearby, and interacts with the adjacent singularities according to distinct regularities dictated by the topological “unity” of the beam as a whole. As a result, a “singular skeleton” – a coherent and harmonious network of interrelated singularities – is formed, which enables efficient qualitative characterization of the whole field [63–66]. The locations and characteristics of separate phase singularities, considered in the framework of the “singular skeleton” regularities (for example, the sign principle [66]) contribute to deeper understanding of the singular field formation and lay the foundation for key applications of singular optics.

The phase singularities of scalar fields are prototypes for other singular networks, especially, of the polarization singularities in inhomogeneously polarized fields A specific feature of an inhomogeneously polarized optical field is the absence of scalar phase singularities. This is explained by the fact that the condition for obtaining the absolute zero of the field amplitude is the exact spatial coincidence (not proximity!) of the amplitude zeros for two orthogonally polarized field components, which is extremely improbable. However, the specific polarization singularities occur in points where the polarization azimuth angle ψ or the sign of the ellipticity angle χ is indeterminate.

For example, a linearly polarized resulting field is obtained due to superposition of two correlated linearly polarized components (preferably, but not obligatory, orthogonal) with the zero phase difference. The ratio of amplitudes determines the polarization azimuth. Then, for a weakly-structured pseudo-polarized light field, the existence of lines (so called L-lines) is expected in the transverse cross section, where the mentioned phase coincidence is preserved but the amplitudes change, which causes gradual variations of the polarization azimuth [62–64]. On the Poincare sphere, such lines are mapped to the equator (Figure 1), each point of which corresponds to the linear state of polarization with the certain azimuth.

For the circular polarization, a superposition of two orthogonal linearly-polarized mutually-coherent components is necessary, with simultaneous fulfilment of the two conditions: 1) the phase difference is $\pm \pi /2$ и 2) the amplitudes of the components are equal. This means that the condition for obtaining circular polarization is much stricter than the condition for obtaining linear polarization. Thus, it is necessary to look for isolated points where the pseudo-polarized field is circularly polarized. Such isolated points appear at the “north” and “south” poles of Poincare sphere, which correspond to the C-point polarization singularities [63–65], with opposite polarization handednesses. In these points, the directions of the electric field vector rotation (chirality) are clearly defined and are opposite at the upper and lower points of the sphere. In other words, the photon SAM in the states corresponding to the upper and lower poles are opposite.

As in the case of a scalar field, the system of polarization singularities is topologically stable and forms the singular skeleton of a vector field, thereby setting the behavior of the field at each point and determining the sign principle for reproducing singularities [66]. The relationship between the correlation optics and singular optics is demonstrated by the example of obtaining structured optical gratings by the interference of three linearly polarized plane waves with the creation of a structure of alternating polarization singularities. In this case, it is possible to control polarization singularities by complex interference methods performing the six- and eight-beam interference experiments [67]. In general, it can be noted that the modern development of singular optics is based on the general principles of correlation coherent optics, and is associated with the study of phase and polarization singularities, as well as the formation, on their basis, of networks of singularities as integral systems.

A clear connection between the principles of correlation and singular optics is persuasively demonstrated by the example of the Poincaré sphere, when the principles of mapping the polarization states are transferred to the formation of the higher-order Poincaré (HOP) sphere [68]. The HOP sphere concept unites the notions of the OV and vector beams (VB), which enables the pictorial representation of the state of polarization of spatially structured light [68–70]. In contrast to the traditional Poincare sphere, the HOP sphere describes simultaneously the state of polarization and the spatial state of the OV beam so that the poles of HOP sphere represent the orthogonally polarized circular OVs. These two eigen states are characterized by the screw phase dislocations described by the multipliers (Eq. 13) and carrying the corresponding OAM $l\hslash$ per photon [71, 72]. Each point of the HOP sphere represents their linear superposition. The HOP sphere equator is associated with the spatially-modified states with linear polarization [73, 74]. Therefore, the HOP sphere describes the light fields based on the more general orthogonal vector basis states which carry both the SAM and OAM. This sphere describes the higher-order states of polarization of generalized vortex VBs and reflects additional degrees of freedom for structured light beams [75].

The HOP sphere also makes it possible to reproduce complex polarization distributions, which are associated with the polarization representations of both Poincaré beams and full-Poincaré beams [76]. Such polarization distributions of optical VBs find their applications in the generation of optical forces to capture micro- and nano-particles, in laser cutting technologies, where the flat-top intensity distribution is used to realize a clean cut [77], for quantum communications [78], polarimetry measurements [79, 80], and in the studies of polarization speckles [81].

The superposition of beams with different states of polarization is the basis for generating other polarization states, from simple ones inherent in scalar fields to more complex ones inherent in VBs. Polarization states are represented by a set of positions on the Poincaré sphere, which provides a three-dimensional map that allows one to predict the resulting polarization state for a given set of optical polarization elements. The Poincaré sphere representation is sufficient for fully coherent radiation. At the same time, approaches employing the Poincaré sphere can be used to reproduce the polarization states of a partially coherent field by estimating the degree of coherence of the orthogonal field components [82–85].

The connection, established between the coherent scalar singular optics and the vector singularities in inhomogeneously polarized coherent fields, indicates the next step associated with extension of the singular-optics approaches to polychromatic light fields [86, 87]. In such situations, one can speak of the phase singularities in the form of OV for some separate spectral components. An important prerequisite for such manifestations is the spatial coherence of the light field, which, in case of the amplitude zero of a certain spectral component, means its “subtraction” from the “white” light field (usually accompanied by a significant, although incomplete, suppression of neighboring spectral components), and leads to additional image coloring.

As a result, the foundation is laid for understanding the regularities of the field formation, analysis of the key practical applications of singular optics, and determination of the relationship between the correlation optics and singular optics. These interrelations, their physical contents and practical prospects are demonstrated in the following sections of this review, which present mainly the results of studies conducted by its authors in close collaboration with other research groups.

3 Influence of the Correlation Parameters on Spatial and Polarization Properties of Optical Fields

3.1 Correlation Functions and Propagation Properties of Partially Coherent Beams

Important motivation of the correlation-optics approaches lies in the fact that the degree of coherence supplies an additional channel for the control and regulation of the main structural properties of propagating light fields. In particular, the beams with incomplete coherence demonstrate such unique properties as self-focusing, self-shifting, self-splitting and self-reconstruction during the free propagation [40, 88–90]. Especially interesting and rich of details patterns are available for beams with “non-conventional” correlation functions (NCCF) when the cross-spectral density differs from the “conventional” Gaussian form

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\propto \exp \left[-{\left({\mathbf{r}}_1-{\mathbf{r}}_2\right)}^2/{\delta }^2\right]$

(δ is the coherence length), and for partially coherent vortex beams (PCVBs) where

$W\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\propto \exp \left[-{\left({\mathbf{r}}_1-{\mathbf{r}}_2\right)}^2/{\delta }^2\right]\exp \left[il\left({\theta }_1-{\theta }_2\right)\right].(14)$

(θ₁ and θ₂ are the azimuthal coordinates of the points r₁ and r₂ in the proper polar frame). In such cases, paradoxical, at first glance, situations occur where a decrease of the source coherency leads to a lower focal spot size, better concentration of the transmitted radiation, higher homogeneity of illumination. A decrease in the spatial coherence of such light beams can, for example, increase the signal-to-noise ratio in optical communication systems operating under the influence of atmospheric turbulence. Partially coherent beams can effectively remove speckles of the illuminating radiation in presence of multiple random scattering, e.g., in problems of laser nuclear fusion. Such beams can be used to reduce noise when taking a photograph and to implement classical phantom interference.

Additionally, partially cohernt source beams contribute to formation of a desirable target intensity distribution, including flat-top or multi-lobe structures [40, 88, 89]. By controlling the spatial coherence of the input beam, one can control the symmetry of the target intensity distribution and, accordingly, of the cross-spectral density distributions [88, 91].

As a result, in some cases partially coherent beams offer essential advantages over coherent ones in such applications as remote sensing, laser ranging, free-space optical communications. optical manipulations, ultra-high resolution imaging, etc. In addition, partially coherent beams have advantages in particle capture, atomic cooling, second harmonic generation, optical scattering, and laser scanning.

Peculiar features of the focal spots produced by beams with NCCF are interesting for the selective light-matter interactions and for creation of special optical traps [90]. Proper regulation of the spatial coherence and the degree of polarization of a PCVB supplies new methods of the optical trap formation with special distribution of the target intensity and polarization distributions. Remarkably, a desirable focal-spot intensity pattern (with axial minimum, maximum, or of a multi-lobe structure, “optical cages” – 3D regions of low intensity surrounded by the high-intensity “walls”), can be adjusted solely by the spatial coherence length of the initial beam [40, 88, 89, 91]. Therefore, a single system employing, for example, a partially coherent elegant Laguerre–Gaussian beam [91] can be used for optical trapping of particles with refractive index larger or smaller than that of the ambient, and switching between the different regimes is performed by varying the spatial coherence length of the source beam.

It should be emphasized that in such optical-trapping schemes, the simplest type of partially coherent beam, for example, the Gaussian Shell-model beam [87], can produce the same trapping efficiency as a fully coherent laser beam, even if the peak intensity is much lower. This indicates a great advantage in applications associated with trapping biological objects sensitive to the high-intensity thermal heating. Additional possibilities for the optical trapping applications are supplied by the special types of PCVBs: cosine-Gaussian correlated Schell-model beam, multi-Gaussian and generalized multi-Gaussian correlated Schell-model beams, Laguerre–Gaussian correlated Schell-model beam, Bessel-Gaussian correlated Schell-model beam, vector Hermite-Gaussian correlated Schell-model beam, etc. [88, 89, 92, 93]. In cases of partially coherent vector beams, modulation of the correlation parameters not only changes the focal intensity distributions but also modifies the polarization distribution in the focal spot [93, 94].

An interesting class of beams with spatially inhomogeneous circular coherence distribution show efficient self-focusing even upon propagation in turbulent media [95, 96]. The self-focusing phenomenon disappears when the initial coherence is high enough or the turbulence is strong. Moreover, the partially coherent pulsed sources with circular spatial coherence distribution and “sinc” temporal coherence distribution [97] show a spatial-temporal self-focusing in a disperse medium depending on the beam and the medium characteristics. These phenomena may have potential applications in optical underwater communication and beam shaping, laser micromachining and laser filamentation.

3.2 Interrelations Between the Correlation and Polarization Parameters of Vector Optical Fields

In the following part of this section we describe an example clearly demonstrating the relationship between the degree of coherence of the interfering plane waves, linearly polarized in the plane formed by their wavevectors (plane of incidence), and the distribution of the intensity and polarization state observed in the resulting field [82–85] (Figure 3). In this situation, a new useful parameter of the interference field is proposed – the visibility modulation depth (VMD), which specifies an unambiguous relation between the degree of correlation between the orthogonal field components and the states of polarization that can be analyzed and evaluated. Here we deviate from the more traditional characteristics used for describing partially coherent and partially polarized beams, based on the correlation matrix (Eqs 8, 10), such as the degree of mutual coherence [88, 98], the degree of coherence in the electromagnetic approximation [99], the electromagnetic degree of coherence [100, 101], internal degrees of coherence [102], and employ the Poincaré sphere principles for visualizing the states of polarization and their mapping onto a plane using the stereographic projections.

FIGURE 3

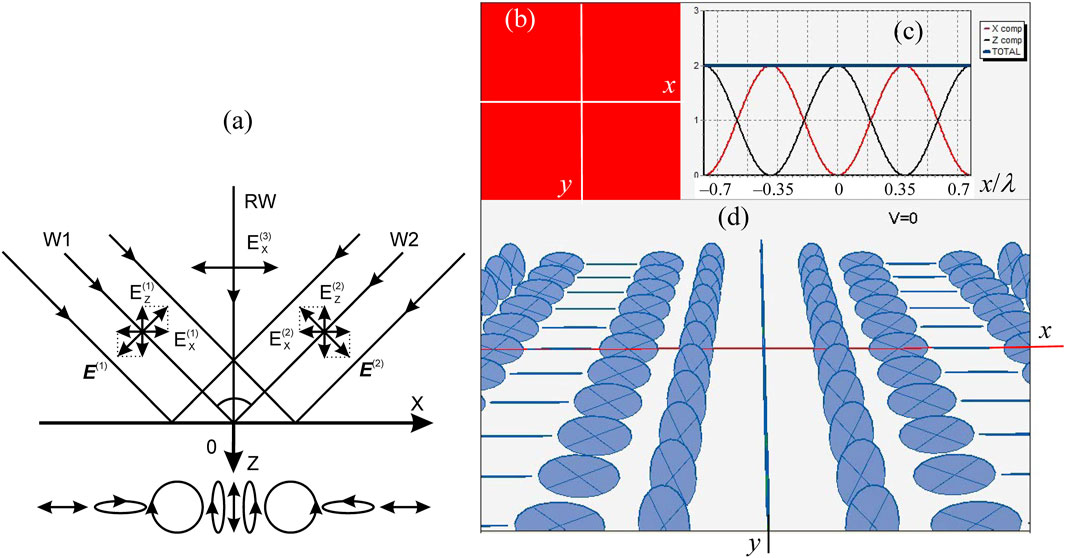
FIGURE 3. Polarization properties of the field formed by two orthogonal plane waves W1 and W2 with equal amplitudes, linearly polarized in the (x, z)-plane. (A) Geometric configuration of the waves; (B) intensity distribution in the (x, y)-plane (plane of observation); (C) partial intensities of the orthogonally polarized components and the resulting field (corresponding visibility of the interference pattern V = 0); (D) schematic view of the polarization ellipses in different points of the (x, y)-plane.

The situation is illustrated by the field formed due to interference of two identical plane waves with mutually orthogonal directions of propagation (Figure 3A). The resulting field is polarized inhomogeneously: with varying x, the state of polarization changes from the linear z-polarization (at $kx=0$) through ellipltic to the circular polarization (at $kx=\pm \pi /2\sqrt{2}$) and further to the linear x-polarization (at $kx=\pm \pi /\sqrt{2}$), and this pattern is periodically reproduced along the whole range of x. However, the intensity distribution is uniform (Figure 3B) because the periodic variations of the partial intensities of the orthogonal components exactly compensate each other (Figure 3C).

The scheme of Figures 3B–D corresponds to the “standard” situation where the waves are completely correlated: the degree of correlation |η^(1,2)| = 1. For the detailed study of the field properties in more general situations, we have suggested to use a reference wave – third linearly-polarized plane wave (RW in Figure 3A), correlated at least with one of the two superposing waves and directed along the middle line between the wavevectors of W1 and W2. In such a way, the spatially inhomogeneous polarization of the resulting field can be transformed into a periodic spatial intensity distribution [82, 83, 103]. Accordingly, in the three-wave interference experiment, the above-introduced VMD can be estimated as

$M=2{\displaystyle \sum _m{\displaystyle \sum _{ij}\frac{\sqrt{\mathrm{tr}\left[W^{\left(m\right)}\left(\mathit{r},\mathit{r},0\right)\right]\mathrm{tr}\left[W^{\left(3\right)}\left(\mathit{r},\mathit{r},0\right)\right]}}{W_{ij}^{\left(m\right)}\left(\mathit{r},\mathit{r},0\right)+W_{ij}^{\left(3\right)}\left(\mathit{r},\mathit{r},0\right)}{\eta }_{ij}^{\left(m,3\right)}}}(15)$

where m = 1, 2 is the number of the wave, and i, j = x, z; additionally $W_{ij}^{\left(m\right)}\left(\mathbf{r},\mathbf{r},0\right)$ is the correlation-matrix element (10) of the mth wave in the associated coordinate frame (Figure 3A), and $W_{ij}^{\left(3\right)}\left(\mathbf{r},\mathbf{r},0\right)$ corresponds to the RW.

According to Eq. 15, the physical meaning of the VMD can be interpreted in more detail. Let us suppose that we choose a RW that is completely correlated with one of the initial waves, for example, ${\eta }^{\left(\mathrm{1,3}\right)}=1$. The phase of the RW varies within (0, 2π). Then, by selecting the intensities of the three waves, we obtain that the VMD of the interference pattern M is proportional to the degree of mutual coherence between the RW and the second of the initial waves, i.e., $M=K\cdot {\eta }^{\left(\mathrm{2,3}\right)}$, where K is a constant, whose value depends on the ratio of the corresponding waves’ intensities.

The maximum intensity of the reconstructed field distribution corresponds to the case in which the electric vector of the RW lies in the plane of incidence, and the minimum intensity corresponds to the case in which the RW is polarized orthogonally to the plane of incidence. The maximum modulation of the resulting interference pattern occurs when the electric vectors of the RW and the two superimposed waves W1 and W2 lie in the pattern plane. A change in the polarization azimuth of the reference wave leads to a decrease in the interference pattern contrast.

This 3-wave interference approach not only reveals the contribution of a certain polarization component to the correlation of the fields, but also demonstrates the relationship between the degree of coherence and the degree of polarization (Figure 4).

FIGURE 4

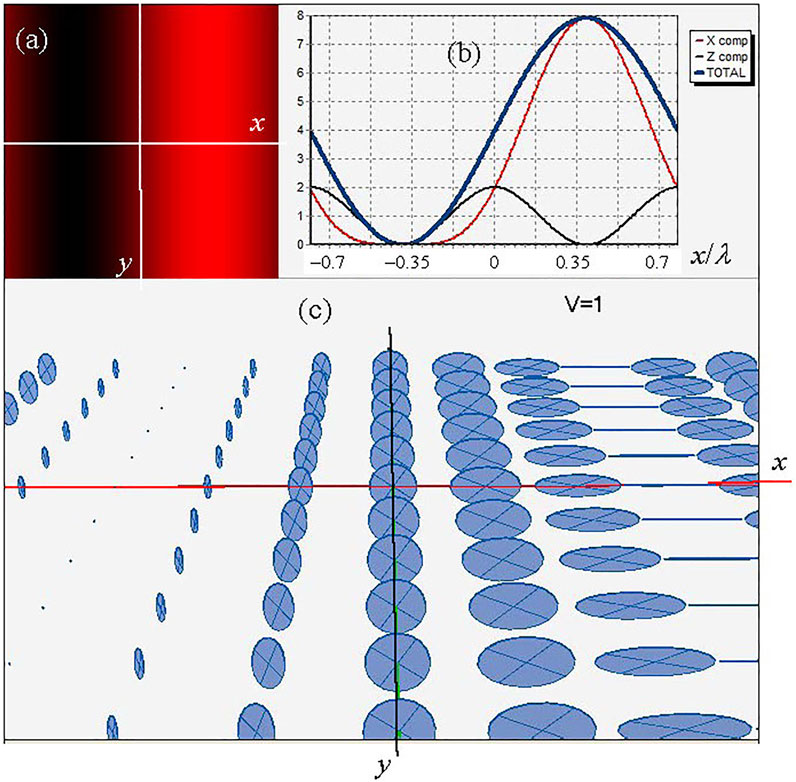
FIGURE 4. Change in the modulation depth of the resulting interference field with the RW phase variation. (A) 2D intensity distribution (cf. Figure 3B); (B) Intensities of the partial polarization components and the resulting field; (C) schematic view of the polarization ellipses in different points of the (x, y)-plane.

A change in the degree of coherence leads to a change in the spatial distribution of polarization (Figure 5). In this case, the coherent and incoherent components of the beam are considered separately. The incoherent component forms an intensity background with preserved polarization, and the coherent component forms a complex polarization distribution, which is visualized using the third – RW – beam.

FIGURE 5

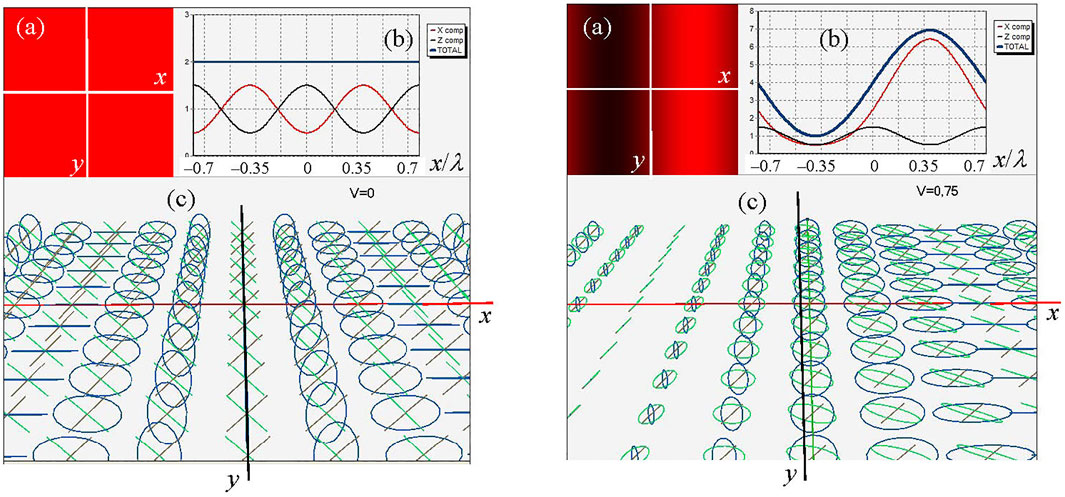
FIGURE 5. Modulation of the polarization and intensity distribution in case where the superposing waves W1 and W2 of Figure 1A are not completely coherent. (A) 2D intensity distribution (cf. Figure 3B); (B) Intensities of the partial polarization components and the resulting field; (C) schematic view of the polarization ellipses in different points of the (x, y)-plane (brown color shows the contribution of the incoherent component of W2, green color denotes the contribution of the “residual” coherent component of W1, blue illustrates the resulting polarization).

The situation discussed with the help of Figures 3–5 is, in fact, a simple example of the general approach to formation of the optical fields with controllable spatial and polarization structure, where the control is performed via the manipulation of the interfering beams’ phases, their degrees of polarization, and the degree of coherence. The VMB parameter, introduced in connection with the 3-wave interference, appears as an efficient instrument for the analysis of the degree of coherence of superposing elliptically polarized beams and the associated degree of polarization in arbitrary points of the observation plane.

In particular, such fields with observed modulation of the polarization demonstrate the corresponding modulations of the Poynting vector (PV) distribution [104, 105], sometimes accompanied by the appearance of the PV singularities in the plane of analysis (Figure 6). Together with the complex pattern of the energy density modulations, this fact can be used for the purposes of optical manipulation (trapping and deliberate transportation of micro- and nanoparticles). The character and the speed of their optically-induced motion depends on the size and properties of the particles, as well as on the ponderomotive factors of the optical field itself, which include the gradient force, light-pressure force and forces associated with the “spin”, “orbital” and “reactive” components of the internal energy flows [23, 24, 106, 107].

FIGURE 6

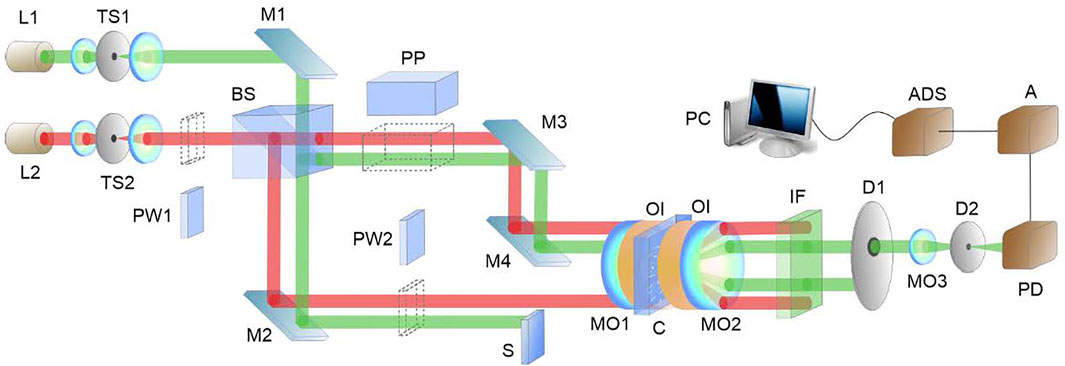
FIGURE 6. The experimental equipment layout: L1, L2, lasers; TS1, TS2, telescopic systems; М1, М2, М3, М4, mirrors; PW1, PW2, half-wave plates for λ = 635 nm; PP, plane-parallel plate; MO1, MO2, micro-objectives; С, cuvette with the Au hydrosol; IF, interference filter with maximum transmission at λ = 532 nm; D1, D2, diaphragms; S, opaque screen; PD, photodetector; А, amplifier; АDC, analog-digital converter; PC, computer.

The effects of the PV modulations are demonstrated in the arrangement shown in Figure 6 [104]. Here, these are manifested in the redistribution of the Au-hydrosol nanoparticles (size 20–40 nm) and their localization in the areas the energy density minima. A He-Ne laser with a power of 5 mW was used as a radiation source; the probing beam (λ = 532 nm) was used for the detection of the gold particles redistribution via the diffracted signal. The probing beam power did not exceed 0.5 mW in order to minimize the heating of the gold particles.

The mean velocity of ensemble of N particles with the radius r and the mass M suspended in the medium with the refractive index n and the viscosity η in the optical field with inhomogeneous energy and polarization can be determined by equation [108].

$\begin{array}{l}\overline{v}\left(t\right)=\frac{1}{M}\left[\exp \left(-\frac{6\pi \eta r}{M}t\right)-1\right]\{\frac{1}{N}{\displaystyle \sum _q\frac{2\pi n}{c}{\alpha }^{\prime }{K}_q{\eta }^{\left(\mathrm{1,2}\right)}\sqrt{{\left(\frac{1}{\mathrm{\Delta }{x}_q}\right)}^2+{\left(\frac{1}{\mathrm{\Delta }{z}_q}\right)}^2}}-\\ -\frac{1}{N}{\displaystyle \sum _q[\left(C_{abs}+C_{scatt}\right)\frac{n}{c}\frac{\sqrt{\epsilon {\epsilon }_0}}{\sqrt{\mu {\mu }_0}}} \\ \times {\displaystyle \sum _{i,j}\left\{W_{ij}^{\left(1\right)}\left(\mathbf{r},\mathbf{r},0\right)+W_{ij}^{\left(2\right)}\left(\mathbf{r},\mathbf{r},0\right)+2\sqrt{\mathrm{tr}\left[W^{\left(1\right)}\left(\mathbf{r},\mathbf{r},0\right)\right]\mathrm{tr}\left[W^{\left(2\right)}\left(\mathbf{r},\mathbf{r},0\right)\right]}\cdot {\eta }_{ij}^{\left(\mathrm{1,2}\right)}\cos {\delta }_q\right\}}]\}.\end{array}(16)$

This means that the velocity depends on the degree of correlation between the orthogonal field components and is determined by the degree of coherence ${\eta }_{ij}^{\left(\mathrm{1,2}\right)}$:

${\eta }_{ij}^{\left(m\right)}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\tau \right)=\frac{W_{ij}^{\left(m\right)}\left({\mathbf{r}}_1,{\mathbf{r}}_2,\tau \right)}{\sqrt{\mathrm{tr}\left[W^{\left(1\right)}\left(\mathbf{r},\mathbf{r},0\right)\right]}\cdot \sqrt{\mathrm{tr}\left[W^{\left(2\right)}\left(\mathbf{r},\mathbf{r},0\right)\right]}}$

where, as in Eq. 15, m = 1, 2; i, j = x, z.

In Eq. 16, $K_q=-2\frac{\sqrt{{\epsilon }_0}}{\sqrt{{\mu }_0}}\sqrt{\mathrm{tr}\left[W^{\left(1\right)}\left(\mathbf{r},\mathbf{r},0\right)\right]\mathrm{tr}\left[W^{\left(2\right)}\left(\mathbf{r},\mathbf{r},0\right)\right]}\cdot \left(1-\cos {\delta }_q\right)$ is a parameter that characterizes the energy density in a point where the qth particle is located. $K_q$ depends on the phase difference between the superposing waves in this point (${\delta }_q$ is the phase difference between the electric vectors of the superposing beams), $\text{Δ}{x}_q$ and $\text{Δ}{z}_q$ characterize the indeterminacy of the particle location with respect to the energy minimum (their lowest values are determined by the particle size), the quantities $C_{scatt}=\frac{k^4{\left|\alpha \right|}^2}{4\pi }$ and $C_{abs}=k\alpha "$ denote the scattering and absorption cross sections of the particle with polarizability absolute value $\left|\alpha \right|$ and the real and imaginary parts ${\alpha }^{\prime }, {\alpha }^{″}$, $k=2\pi /\lambda$ is the wave number.

To summarize the current Section, we should emphasize that nanoparticles with different special properties offer powerful means for investigation and diagnostics of complex optical fields. The particles’ redistribution under the influence of internal energy flows, the possibility of their localization in the regions of local minima or maxima of the energy density, etc., enable a comprehensive analysis of the optical speckle field, and, depending on the problem, give ways to recover the important inhomogeneities of the object field, to reconstruct the source of the speckle field, to build a phase map, thereby offering a solution to the inverse optical problem [109] (reconstruction of the total field from the observed intensity distribution). The specific advantages are associated with the luminescent nanoparticles. For example, the carbon particles with sizes of the order of 10 nm, showing a significant absorption in the long-wavelength spectral region and luminescence in the yellow-green band, enable to visualize the field singularities [109]. Invariance of the spatial map of the speckle-field singular skeleton, as a structure fixed in space and time, is the source of reliable information about the object, and demonstrates the deep connections between the correlation optics and singular optics [23, 60, 61].

4 Non-Linear Correlation-Optics Effects in Stochastic Media With Absorbing Micro- and Nanoparticles

4.1 Light-Induced Gratings and Self-Diffraction of Laser Radiation in Water Suspensions

The coherent superposition of two linearly polarized beams manifests itself in the formation of highly inhomogeneous field distributions, in particular, of the dynamic gratings, which are characterized by complex amplitude and phase patterns [110]. In media with suspended microparticles, optical forces induce the creation of specific “material” gratings which, in turn, influence the light propagation, inducing the self-diffraction phenomena. Characteristics of the optically-induced gratings depend on the medium physical properties, especially, the temperature distribution, thermal relaxation, Brownian motion of the suspended particles, etc. In many cases the balance is established between the redistribution of heat fluxes and internal flows of the light energy, so the generated gratings appear to be stable. The process of grating generation requires a rather high local energy absorption, which is provided by the highly absorbing particles but if their number and sizes are small enough, the total light absorption remains moderate.

In the scheme of Ref. 110 (Figure 7), an inhomogeneous field distribution is created due to the interference of two quasi-plane-wave beams in the medium with the effective refractive index n₀ and the absorption coefficient κ; the waves with amplitudes A1 and A2 approach the sample (medium) surface at angles θ₁ and −θ₂ with respect to axis z normal to the sample surface; further we will suppose that θ₁ = −θ₂ = θ. Under such conditions, the density of the energy absorbed in the medium during the time t is determined by equation

$q\left(x,z,t\right)=\frac{q_0\left(t\right)}{\cos \theta }\left(1+V\cos \mathrm{\Phi }\right)\exp \left(-\frac{\kappa z}{\cos \theta }\right),q_0\left(t\right)=\kappa \frac{c}{n_0}{I}_{0}t(17)$

where $I_0=g{n}_0^2\left(A_1^2+A_2^2\right)$ is the total incident field intensity, $V=\frac{2A_1{A}_2}{A_1^2+A_2^2}$, $g={\left(8\pi \right)}^{-1}$ in the Gaussian system of units, and $\text{Φ}={\text{Φ}}_1+{\phi }_1-{\text{Φ}}_2-{\phi }_2=2kx\sin \theta +\phi$, ${\text{Φ}}_1=k_0\left(x\text{sin}\theta +z\text{cos}\theta \right)$, ${\text{Φ}}_2=k_0\left(-x\text{sin}\theta +z\text{cos}\theta \right)$, $k_0=n_{0}k$, ${\phi }_1$ and ${\phi }_2$ are the initial phases of the beams approaching the sample.

FIGURE 7

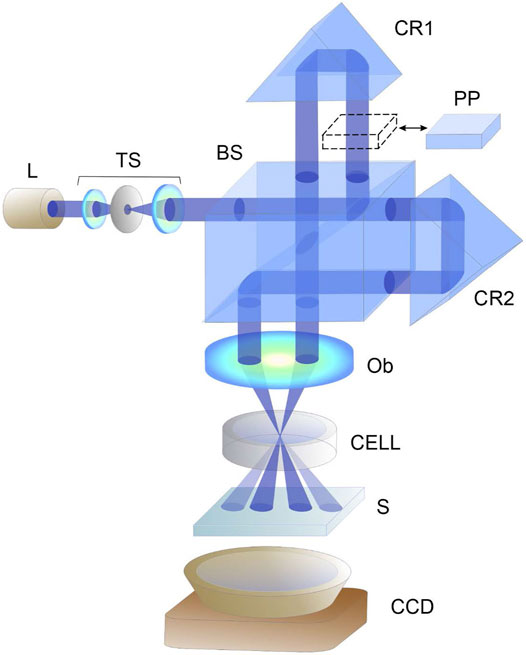
FIGURE 7. Optical arrangement for studying the effect of self-diffraction in the cell containing the medium with suspended microparticles: (L) CASIX LDS-1500 laser generating at λ = 445 nm and controllable power ≤ 0.3 W; BS, beam splitter; СR1, СR2, 90° angle reflectors; Ob, micro-objective; S, screen; ССD, registering camera.

One can estimate [110] the relative efficiency of the light diffraction into the 0th and 1st diffraction orders considering the sample as a thin layer of the width d with the refractive index inhomogeneity dictated by the light-induced grating generated according to (Eq. 17):

$D_0=\left\{1-\frac{1}{2}{\left[\frac{kd}{\cos \theta }\left(\frac{dn}{dT}\right)\frac{q_0}{C\rho }V\right]}^2\right\}\exp \left(-\frac{\kappa d}{\cos \theta }\right),(18)$

$D_1=\frac{1}{4}{\left[\frac{kd}{\cos \theta }\left(\frac{dn}{dT}\right)\frac{q_0}{C\rho }V\right]}^2\exp \left(-\frac{\kappa d}{\cos \theta }\right).(19)$

Inhomogeneity of absorption induces the spatial inhomogeneity of the refractive index, $n=n_0+\text{Δ}n$. Under conditions of Ref. 110, the medium properties are modulated mainly due to the thermal mechanism, i.e.

$\text{Δ}n=\text{Δ}n\left(x,z,t\right)=\left(\frac{dn}{dT}\right)\frac{q\left(x,z,t\right)}{C\rho }(20)$

where $\left(dn/dT\right)$ is the refractive index temperature coefficient, С is the heat capacity per unit mass of the medium, ρ is its mass density. Eq. 19 testifies that, at small angles of incidence θ, the first-order diffracted intensity grows with increasing θ; in the special conditions of Ref. 110, this factor was dominating.

At the same time, the particles’ redistribution in the inhomogeneous optical field enhance the effect of the dynamical grating generation. Each particle experiences a complex mechanical action caused by a complex of ponderomotive factors. In particular, the optical forces are associated with the optical field inhomogeneity and the internal energy flow (field momentum components) [23–25], which redistribute the particles to the regions of maximum light intensity. Additionally, there exists the photophoretic force associated with inhomogeneous heating of the absorbing particles [111–114], which moves the particles to the intensity minimum. The total optical force can be described as

${\mathbf{F}}_e=\frac{1}{4g{n}_0^2}\mathrm{Re}\left({\alpha }_e\right)\nabla I+\frac{\omega }{g}\mathrm{Im}\left({\alpha }_e\right){\mathbf{p}}_O^e(21)$

where $I\equiv I\left(x,z\right)$ is the local field intensity (energy flow density),

$I\left(x,z\right)=I_0\left(1+V\cos \Phi \right)\exp \left(-\frac{\alpha z}{\cos \theta }\right),$

and ${\mathbf{p}}_O^e$ is the electric part of the orbital momentum of the field [107]. The electric polarizability α_e is determined by the relations [106, 107].

${\alpha }_e=\frac{{\alpha }_e^0}{1-i\frac{2}{3\epsilon }{k}^3{\alpha }_e^0}\approx {\alpha }_e^0+i\frac{2}{3\epsilon }{k}^3{\left|{\alpha }_e^0\right|}^2,{\alpha }_e^0=\epsilon a^3\frac{{\epsilon }_p-\epsilon }{{\epsilon }_p+2\epsilon }(22)$

$\epsilon =n_0^2$ and ε_p are the permittivities of the medium and the particle, respectively. In the scheme of Ref. 110 (Figure 7), the orbital momentum ${\mathbf{p}}_O^e$ is directed along the axis z and, hence, does not influence the transverse motion of the particles. The latter is completely determined by the gradient optical force described by the first summand of Eq. 21.

Figures 8A,B illustrates the field distribution formed inside the sample – a cuvette (cell) with suspended ink particles in the form of polymer spheres 0.2 μm in diameter with a coating made of carbon-based absorptive resin. In case when the two waves are coherent, the distinct interference pattern is formed with the period of 2.5 µm.

FIGURE 8

FIGURE 8. The field pattern observed inside the cuvette: (A) when both beams are coherent and (B) when the beams are incoherent. Registered light intensity distributions in the screen plane (Figure 7): (C) the plane-parallel plate is placed instead of the sample, the self-diffraction is absent; (D–G) the self-diffraction patterns at different angles of the beams’ convergence.

The following images show the results of the self-diffraction at a distance 50 mm from the cuvette. For comparison, the image of Figure 8C represents a reference intensity distribution when a plane-parallel plate is placed instead of the sample. In contrast, the images of Figures 8D–G show clearly pronounced diffraction maxima with noticeable intensity, which confirm the light-induced grating formation. Expectedly, the thermal nature of the phase gratings should provide a number of observed diffraction orders but actually, only the zero- and first-order diffraction maxima are observed. This can be ascribed to the fact that the gratings cannot be considered thin. The contrast of a phase-modulated grating depends on the concentration of particles, on the temperature gradient, on the degree of coherence of the superposing beams, and on the angle of their convergence.

The results presented above demonstrate the specific manifestations of the coherence and correlations between the laser beams associated with their interaction with nonlinear media, which can be used for the deliberate field formation as well as in the optical data storage and optical diagnostics of the processes of particle interaction with a light-absorbing medium. The study of such processes supplies the background for new instruments of the light-induced trapping and manipulation of micro- and nanoparticles, which is also the subject of singular optics, but allowance for the stochastic and coherent properties of light opens additional channels for the control and subtle regulation of the processes.

Importantly, the self-diffraction phenomena described occur at relatively low and controllable power (≤0.3 W) whereas the usual conditions for observing the non-linear optical phenomena require much higher power, normally available in the pulse regime. This is a special advantage of the media with absorbing particles, in which a temperature gradient is formed under the action of optical radiation: here not only the conditions for self-diffraction, but also for self-focusing and generation of shock waves can be realized with the use of a continuous laser radiation of low power rather than by short laser pulses that, propagating in the medium, may cause its destruction. This fact is suitable for possible utilization of these effects in diagnostic purposes both in nanotechnologies and, e.g., for acoustic destruction of pathologically altered tissues in medicine [115].

4.2 Self-Focusing and Caustic Diffraction Pattern Manifestations

The classical non-linear effect – self-focusing of a light beam with an initially plane wavefront and a Gaussian intensity distribution – can also be realized in the disperse medium with suspended absorbing particles. Especially interesting self-focusing features, with specific and non-trivial radiation redistribution, take place when the incident beam is additionally focused by a cylindrical lens (CL) [116]. In this case, the output optical field demonstrates a complex structure including caustics in the intensity distributions and the phase singularities, typical for the Pearcey or Fraunhofer diffraction pattern [117, 118], depending on the beam aperture. The corresponding optical arrangement, enabling to study the mechanisms of transformations of the focused light in the medium with suspended particles, is shown in Figure 9.

FIGURE 9

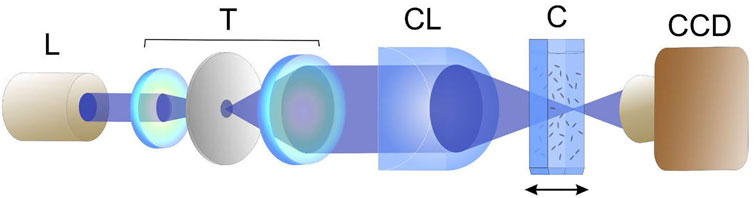
FIGURE 9. Optical scheme for demonstration of the laser beam self-focusing in the disperse medium: L, laser module; T, telescopic system; CL, cylindrical lens; C, quartz cuvette with the hydrosol medium; CCD, registering unit.

The radiation with λ = 445 nm and controllable power is generated by the laser module XJ-A140. The telescopic system forms the collimated beam of the diameter 10 mm. Further, the beam is focused by the cylindrical lens into the sample containing the water suspension of the absorbing particles similar to those used in the self-diffraction experiments (Figure 7). The cuvette walls are 0.5 mm thick, whereas the width of the suspension layer equals to 10 μm.

After passing the cuvette, the beam profile is registered, and the pattern differs for different positions of the cuvette with respect to the focal plane of the CL. As expected, the resulting intensity distribution is strongly inhomogeneous and depends on the refractive index modulation (Figure 10). When the sample is situated far from the focus, the intensity in the medium is moderate so that the absorbed power density (Eq. 17) and the corresponding refractive index modulation (Eq. 20) are insufficient for the light self-action. As a result, the phenomena of self-focusing and self-diffraction do not appear (Figures 10A,C). When the cuvette is close to the CL focus (Figure 10B), the high radiation density induces the refractive index modulation, accompanied by a redistribution of the field intensity. In this case, the self-focusing of the radiation occurs, which is accompanied by the self-diffraction at the inhomogeneous grating formed by the optically-trapped particles.

FIGURE 10

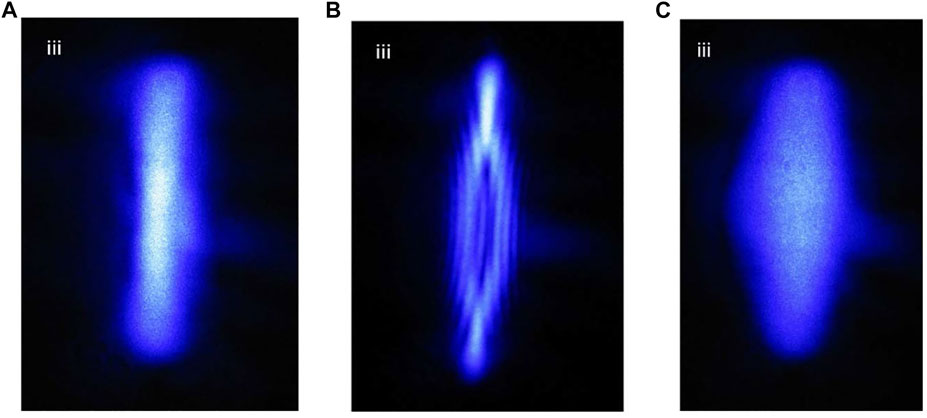
FIGURE 10. Views of the intensity distribution after passing the cuvette C with suspended particles, for different positions of the cuvette: (A) the cuvette is situated immediately behind the CL, (B) the cuvette is placed at 350 μm before the focal plane of the CL, (C) the cuvette is placed far behind the focal plane.

Actually, near the CL focus the particles in the sample are redistributed according to the Pearcey diffraction pattern. The whole picture of the radiation self-focusing can be interpreted as a result of the self-diffraction on this light-generated Pearcey-like grating.

4.3 Light-Stimulated Phase Transitions and Controllable Formation of Ordered Bubble Ensembles

Another group of interesting effects occurring in aqueous solutions with absorbing particles involves the heat-induced phase transitions in the matrix material (water) accompanied by the generation of gas and vapor bubbles of nano- and micrometer sizes [119]. The light energy, absorbed by such a particle, is transmitted to the medium environment and causes its heating which, upon certain conditions, takes on an explosive character: the medium (water solution) is locally evaporated, and the gas bubble is formed with growing volume. The bubble growth stops when the energy income from the absorbing particle is compensated by the energy outflow through the bubble surface.

In the system of Figure 11A, the moderately focused (focal spot size ∼ 100 μm) continuous laser beam (λ = 980 nm) is used, and the generation of microbubbles can be controlled by the radiation power. The creation and manipulation of bubbles is performed due to the macroscopic effects of heating a certain number of closely situated particles. The inhomogeneous temperature distribution is formed, and its character is regulated by the laser radiation power, particles’ concentration and the phase transition effects. The resulting bubbles and their ensembles are stable and can exist for a long time under favorable illumination conditions. By moving the laser spot, the spatial localization of microbubbles in the liquid volume moves accordingly due to the Marangoni effect [120]. The growth of bubbles up to submillimeter sizes, as well as the formation of spatially ordered systems of the bubbles with a certain size distribution can be observed and controlled by the power of input laser radiation.

FIGURE 11

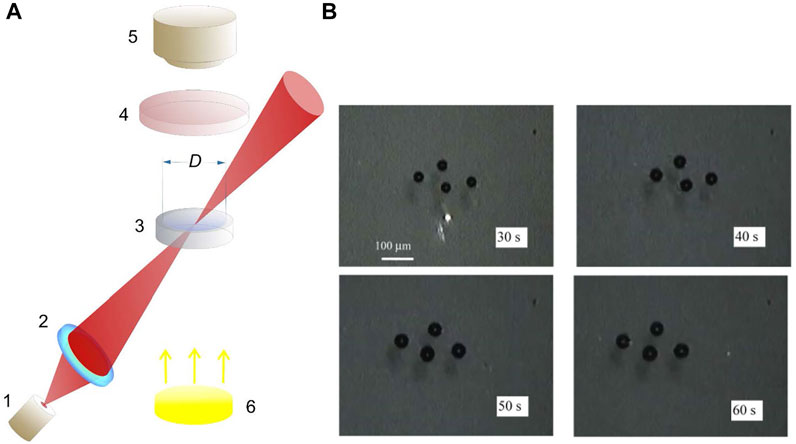
FIGURE 11. (A) The experimental setup for the bubbles generation and observation: (1) IR laser, (2) objective, (3) cuvette with the water suspension of absorbing nanoparticles, (4) spectral filter to stop the IR radiation, (5) CCD camera, (6) white-light source for visible illumination; (B) Illustration of the behavior of the four-bubble ensemble in different moments of time; a gradual increase of the bubbles’ sizes is seen.

In the literature [119–130], several regimes of the bubbles’ creation and development were described: 1) bubbles generation near the absorbing particles; 2) stable growth of the existing bubbles; 3) stationary existence of the bubbles upon the thermal and hydrodynamic equilibrium conditions, and 4) shrinkage and collapse of the bubbles when the illuminating power decreases.

The experimental arrangement performing the controllable generation and manipulation of microbubbles in the water suspension of the black pigment ink particles (InkTec Corporation) is presented in Figure 11A. The semiconductor laser (Wavespectrum, WSLD-980-004-C, the vacuum wavelength λ = 980 nm, maximum power 4 W) produces the radiation which is focused into the cuvette filled by the suspension. To avoid high levels of the recording unit 5 illumination, the bubble-generating laser beam was directed obliquely (at an angle of 15°), so that the camera recorded only the scattered radiation. The laser power was controlled within the range 0.1–3 W; the processes in the cuvette were visualized by illumination with white light and recorded by a CCD camera with a spectral filter protecting from IR radiation. This enabled to observe not only the bubbles illuminated by visible light, but also the track of the infrared laser beam inside the cuvette (Figure 11B).

Laser-generated microbubbles are widely used in special modern technologies [120, 121]: as micropumps [122], micromixers [123], microrobots [124] for cleaning solid surfaces [125, 126], for ink printers [127], etc. However, generation of such microbubbles under the action of the CW focused laser radiation requires a rather high energy level, which can be appropriate for technical applications but is inacceptable, for example, in biomedicine, where strong radiation can be harmful to tissues. A decrease in the threshold power is achieved by using pulsed lasers [128–130], and the required temperature inhomogeneity is achieved by using highly absorbing nanoparticles, such as gold nanoparticles.

In this case, the required mean laser power is significantly reduced. The controlled microbubbles in a biological environment perform unique mechanical and optical functions. Their collapse mechanically affects the surrounding area, which can be used for selective delivering of proper biologically active species to specific cells in cell surgery, for the deliberate cell destruction and transfection [128–130]. The ability of bubbles to scatter light makes them suitable micro-objects for imaging cells and tissues.

5 Correlation Optics and Optical Singularities

In this Section, we describe some correlation-optics approaches to formation and diagnostics of the polarization and phase singularities in optical fields. Let us start with mentioning that complex “non-generic” polarization and phase singularities can be generated in the course of superposition of regular and partially coherent vector fields with certain standard structures [130–132]. For example, a coherent coaxial mixture of weighted orthogonally polarized single-charged Laguerre–Gaussian modes with different radial indices produces unusual non-generic spatially stable polarization structures such as closed C-contours (2D manifolds of points with pure circular polarization) and L-contours [25] with a fixed azimuth of linear polarization [130]. In Refs. 131, 132, vector singularities are described in partially polarized combined fields formed by incoherent superposition of orthogonally polarized beams. It is shown that the vector singularities of special types arise at the transverse cross section of a paraxial combined beam instead of the common singularities, such as the OVs (inherent in scalar, i.e., homogeneously polarized, fields), C-points, where polarization is circular, and L-lines, along which polarization is linear [25]. These are U-lines (closed or closing at infinity) along which the degree of polarization equals to zero and the state of polarization is undetermined, and isolated P-points where the degree of polarization equals to 1 and the state of polarization is determined by the non-vanishing component of the combined beam. U and P singularities are adequately described in terms of the complex degree of polarization represented in the Stokes space, namely, on the surface and inside the Poincaré sphere. These singularities are topologically stable and form the “vector skeleton” of a combined beam.

Other interesting aspects of optical singularities in partially coherent fields manifest themselves in relations to the beams with NCCFs and to PCVBs [40, 133] previously discussed in Section 3.1. Importantly, the PCVBs are usually missing the main features of coherent OVs – their isolated axial amplitude zero and the ring-like intensity pattern. Due to randomization, the OV-associated amplitude zero normally disappears, and even the intensity minimum can transform into the axial intensity maximum [88, 89]. In many cases, the phase singularity of a PCVB is “hidden” [134, 135] and does not manifest in the visible beam pattern. Nevertheless, a PCVB demonstrates a lot of unique and interesting properties stipulated by the singular character of the correlation function. According to Eq. 14, this correlation function contains the “vortex” phase (screw phase dislocation) with the integer topological charge; respectively, the ring-like amplitude structure of the correlation function with corresponding ring-like linear phase dislocations is possible and rather typical [88, 89]. Moreover, a PCVB can carry OAM proportional to the topological charge [136]. The focal-spot (or far-field) intensity pattern sensitively depends on the correlation parameters of the input PCVB source, and the coherence-length modulation provides a convenient way to form a desirable target intensity pattern, which is useful, e.g., for laser materials processing and optical trapping. In addition, a PCVB shows an essential advantage over coherent beams or partially coherent beams without a vortex phase to reduce scintillation caused by turbulence, which is favorable in free-space or atmospheric optical communications [137].

For vector PCVBs, the resulting intensity distribution depends on the coherence length δ and is determined by the form of the NCCF, when δ is relatively small, and by the vortex phase, when δ is large [138]. The absolute value of the degree of coherence is determined by the NCCF form and, especially, by its vortex component (Eq. 14). A recent research [139] has demonstrated a special form of PCVB called controllable twisted Gaussian Schell-model beam, which provides the means for purposeful manipulation of the beam OAM. Such flexibility of the NCCF phase control and the OAM detection promises fruitful applications in the theory of coherence and for the OAM-based ghost imaging.

A specific example demonstrating the connections and interpenetrations of the correlation-optics and singular-optics concepts is the diagnostics and detection of singularities in “white” polychromatic radiation [86, 87]. In this case, the optical field singularities in the form of screw wavefront dislocation [23–25, 60, 61] (OV, see Eq. 13) were detected. The use of a reference wave provides an efficient experimental tool for diagnostics of OVs in “white” (polychromatic) light, by registering and analyzing the characteristic interference “forks” [23, 25, 60]. In the specific context of the correlation optics, the sensitive OV detection provides additional ways for revelation and high-resolution localization of the optical-field singularities, offering thus fruitful ways for studying the stochastic speckle-fields, reconstruction of the object fields, inhomogeneity diagnostics of rough surfaces, etc.

Noteworthy, the proposed technique for detecting singularities is based on the approaches of coherent optics developed for studying the irregular wave-front behavior. This method of analyzing the polychromatic radiation makes it possible to reveal the spatial coincidence of the amplitude zeros of separate spectral components in white light [86]. Since the coherence length of white light is rather low (of the order of several wavelengths), the diagnostics of singularities in this case strongly relies upon the accuracy of the interference experiment. This is ensured by a high degree of spatial coherence of the reference wave and a rather high mutual spectral purity in both channels of the interferometer to obtain reliable maxima and minima of the interference pattern (Figure 12).

FIGURE 12

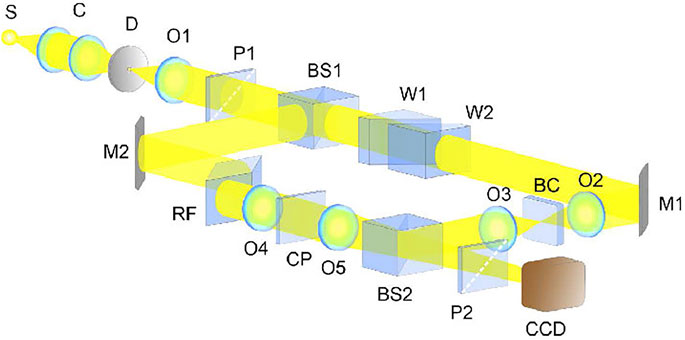
FIGURE 12. Experimental arrangement for the white-light OV analysis: S, white light source; C, condenser; D, diaphragm; O1, O2, O3 and O4, objectives; P1 and P2, polarizer and analyzer; BS1 and BS2, beam-splitting cubes; M1 and M2, mirrors; BC, singularity-generating object; CP, compensating plate; RF, Fresnel rhombus; W1 and W2, moving and stationary optical wedges; CCD, camera.

The OV cores (amplitude zeros) for all spectral components of the beam are reliably detected via the interference with a coherent wave (Figure 13). In this case, a white-light OV is observed, in which the amplitude zeros of all spectral components coincide, which leads to an achromatic interference “fork” (fringe bifurcation points well seen in Figure 13B correspond to the amplitude zeros in Figure 13A). The shape and orientation of the interference fork illustrate the possibility of determining both the OV charge and its sign.

FIGURE 13

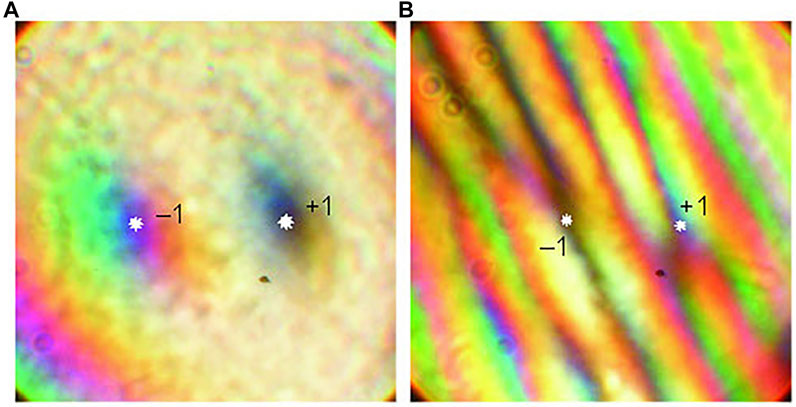
FIGURE 13. Singularities obtained in a white-light beam passing a double-axial crystal placed between matched polarizer P1 and analyzer P2 (Figure 12): (A) without reference wave; (B) with a reference wave (interference pattern). The topological charges are indicated of the two singularities with exact locations marked by the asterisks.

An example of possible practical application of this approach for diagnostics of the amplitude zeros in the polychromatic radiation is the method for controlling the thickness of growing films [140, 141]. The analysis of the interference between the polychromatic fields reflected by the reference substrate and by the inspected surface (for example, a surface of a film during its growth) enables one to determine the film thickness via the emergence of an OV in the resulting speckle field. This process provides a subwavelength resolution due to the ability to identify the spectral component for which zero amplitude occurs at a certain stage of the film growth process.

Another interesting example demonstrating the relationship between the coherence theory and the singular optics is the identification of nontraditional phase singularities [141, 142], which do not occur within the framework of classical coherent singular optics, but are detected when a polychromatic beam passes through a dielectric plate with the rough surface. The magnitude of the surface inhomogeneities should be such that, on the one hand, they would provide sufficient light scattering but, on the other hand, the surface should not be rough enough to destroy the regular (forward-scattered) component of the scattered radiation. In this situation, the coloring of the white beam, that has passed through the object, takes place. Such coloring can be interpreted as a manifestation of a certain sort of phase singularity. One can speak of the emergence of a zero amplitude of the complex transmittance for an individual spectral component of a beam with a wide spectral composition. The pronounced coloring of the surface and the change in the spectrum of a polychromatic beam can only be explained by the interference of partial components and the manifestation of the wavefront singularities formed in the individual spectral components. The presence of a regular component in the scattered radiation means that the heights of inhomogeneities are comparable with the wavelengths of all spectral components of the probing beam. Accordingly, the mutual coherence of partial scattered waves is preserved, and there is a need to take into account the phase relationships between such waves for both scattered (random) and specularly-reflected (regular) radiation, even if the spatial and temporal coherence of an extended source is rather low. The partial waves or, in other words, partial re-scatterers, mutually related by a common source field and separated by subwavelength distances, as a rule, radiate in the direction where the phase difference of these elementary emitters vanishes.

At the same time, when there is no regular component, i.e., the magnitude of the inhomogeneities is such that the stochastic light scattering prevails, then another peculiar optical effect of image coloring is observed. In the case of a small illumination area, a sufficiently high spatial coherence is achieved, and polychromatic (color) speckles and phase singularities in the spectral components appear in the scattered field.

6 Mechanical Manifestation of the Internal Energy Flows in the Interference Arrangements

An interesting example, demonstrating the interrelations and the transition from correlation optics to singular optics, is a widely presented model of generation of the pronounced “spin energy flow” (spin momentum) [23–25] in the superposition scheme of two circularly polarized Gaussian beams [143]. Importantly, this model convincingly reveals the spin-orbital decomposition and the mechanical action of the internal spin energy flows, or linear “spin momentum” [144] in light fields.

To demonstrate the mechanical action of the spin flow, an experiment was proposed in which latex microparticles (refractive index 1.48) suspended in water were used. The particles were chosen so that their shape was close to ellipsoidal with an approximate cross-section size of 1.5 µm × 1 µm. Such dimensions make it possible to observe individual particles within one fringe of the interference pattern formed in the focal region (Figure 14). The interference pattern is formed by superposition of two inclined Gaussian beams with controllable circular polarization.

FIGURE 14

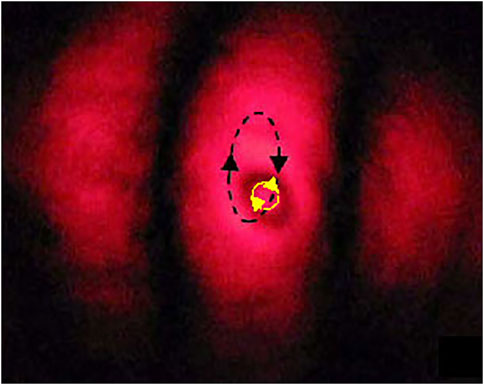
FIGURE 14. Position of the particle trapped within the central lobe of the interference pattern [143]. Black dashed line shows its center-of-mass trajectory; simultaneously, the particle spins near its center of mass (yellow contour).

It was shown in experiment that a trapped asymmetric particle rotates around its center of mass (yellow contour), which can be explained by partial absorption of incident light with circular polarization, which possesses an internal spin angular momentum. Simultaneously, the center of mass performs an orbital motion (black dashed contour in Figure 14) inspired by the mechanical action of the linear spin momentum [23–25, 144]. The linear spin momentum is a part of the mechanical momentum of light associated with its circular (elliptic) polarization, and it is able to perform a mechanical action similar to that of the usual light pressure [23–25]. In the experiments of Ref. 143, the “pure” spin-momentum action is well separated from the transverse light pressure that is balanced by the gradient force, so that the observed orbital motion of the particle is caused solely by the spin momentum. Remarkably, both spinning and the orbital rotation reverse if the circular polarization of the incident beam changes the sign. When the incident beam polarization is linear, both spinning and orbital rotation stop.

To finalize this Section, we describe the model experiment which illustrates the application of the correlation-optics ideas in the near-field optical-manipulation techniques. In particular, it shows how the interference mechanism enables to reveal the spin-flow action of the evanescent field – a strictly localized wave in the low-index medium formed during the total-reflection process.

The specific features of partially coherent evanescent waves are attracting growing interest, and a number of impressive results have been obtained in the last years [49, 145, 146]. Generally, such waves are typical genuine 3D fields with a complicated and controllable polarization structure. Random evanescent fields may exhibit subwavelength surface coherence lengths and their degree of polarization can change notably on distances equaling only a fraction of a wavelength. By combining several mutually incoherent exciting sources, wide possibilities for micro- and nanoengineering of electromagnetic fields were revealed; in particular, it is possible to tailor evanescent fields sharing polarization properties identical to those of universal blackbody radiation, yet with tunable coherence states [146]. Interesting and potentially useful field structures can be realized with employment of partially coherent surface plasmon-polariton (SPP) fields, in particular, SPP with vortices [145]. Such near-field structures with controllable coherence are generated by superposition of planar SPPs at the metal-air interface. Remarkably, the dynamical characteristics of such fields: energy density, energy flow density, orbital and spin angular momentum, as well as the state of polarization, can be widely tuned by adjusting the spatial coherence of the fields. These abilities can find applications ranging from controllable excitation of nanoantennas and manipulation of nanoparticles to near-field data storage and optical communication in advanced nanoplasmonic devices.

In Figure 15, a special near-field situation is illustrated where the elliptically-polarized evanescent wave is excited above the total-reflection prism surface (X = 0) by the incident wave with the linear 45°-polarization (with respect to the incidence plane) [147–149]. In this evanescent wave, the specific field momentum distribution is formed with both longitudinal (Z) and transverse (Y) components [150, 151]. These momentum components can be absorbed and/or reflected by the material object, which produces an optical force inspiring the correspondent motion of the object. The evanescent-wave conditions of [147–149] with moderate and low light intensities are especially favorable for optical diagnostics of the biological objects; Figure 15 shows the optical forces inducing the motion of a human erythrocyte (red blood cell).

FIGURE 15

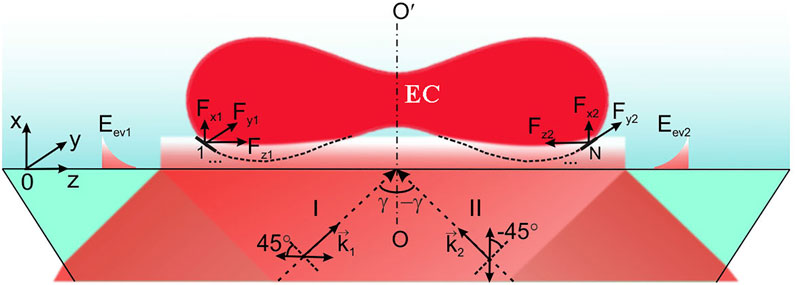
FIGURE 15. Superposition of the opposite evanescent waves formed by the total reflection of two beams linearly polarized at ±45° with respect to the plane of incidence and approaching the prism surface at an angle γ > arcsin(n_l/n_p) where n_l and n_p are the refractive indices of the liquid above the prism and of the prism material, correspondingly. Here $E_{ev1}$ and $E_{ev2}$ denote the separate evanescent waves formed from the incident beams with the wavevectors k₁ and k₂; F_x1, F_x2, F_y1, F_y2, F_z1, F_z2 are the optical-force components acting on small areas of the erythrocyte cell (EC) surface; $O{O}^{\prime }$ is the symmetry axis of the erythrocyte.

The experimental scheme proposed in order to observe the controlled transverse displacements of the erythrocyte in the YOZ plane under the evanescent-wave mechanical action, includes two oppositely directed evanescent waves of the same amplitude and frequency, formed above the glass prism in which the total internal reflection of waves with the wavevectors k₁ and k₂ takes place (angle γ exceeds the total-reflection value). In the model experiment, the prism surface was covered by a thin liquid layer where the biological cells can be placed. A proper localization of the object in the vertical (X) direction was ensured by the evanescent wave inhomogeneity due to which the gradient force makes the cell to float close to the prism surface. The longitudinal energy-flow components of the two evanescent waves cancel out, whereas the transverse components are added. Such an effect is achieved by using identical linearly polarized incident beams polarized at 45° with respect to the plane of incidence (inside the prism), and the formation of the same elliptical polarization for both oppositely-propagating evanescent waves above the prism surface.

A series of experiments [148, 149] has demonstrated the controlled motion of the erythrocytes under the action of the evanescent wave in the transversal direction. Importantly, the motion characteristics can be finely regulated by adjusting the incident beams’ parameters, and the same technique can be applied to other biological cells. Additionally, in the arrangement similar to that of Figure 15, the cell rotation near its own axis and, consequently, its contactless orientation in the YOZ plane can be realized due to the vertical spin of the evanescent wave [150, 151]. All these features can be favorable for the laboratory diagnostics, sorting and delivering of biological species.

7 Conclusion

The present review embraces main ideas and concepts of the correlation and singular optics with a special attention to the penetration of classical ideas of coherence and correlations into the modern area of singular optics. The degree of coherence and the correlation properties of superposing light beams open new channels for formation of light fields with prescribed complex distributions of the phase, amplitude, polarization, as well as the special patterns of the internal energy flows. An important step in understanding and analysis of such “combined” fields is the application of generalized stereographic projections based on the ideas of the Poincare sphere, from its classic realization to the higher-order Poincare sphere for representation of fields with complex and interrelated spatial and polarization distributions. Such optical fields offer a rich choice of spatial, spectral and polarization inhomogeneities, non-trivial and informative distributions of the energy flows, which supply additional possibilities for selective optical influences, complex optical diagnostics and analysis of various objects. Importantly, partially coherent beams offer essential advantages over the usual fully-coherent fields in various practical aspects. In many situations, they provide better concentration of light energy within the focal spot, reducing or eliminating the scintillation or speckle modulations, improving the signal-to-noise ratio in imaging and communication systems. Moreover, special sources with non-conventional correlation functions enable self-focusing, self-shifting and, generally, purposeful self-structuring of light beams propagating in homogeneous or scattering media, which opens new prospects for optical trapping, manipulation, micro- and nanoengineering.

In this view, the theory of partial coherence, which statistically describes the spatial and polarization degrees of freedom in complex optical fields, reveals additional features of the origins and meaning of the main concepts of singular optics. In particular, it generalizes the deep relations between the amplitude zeros and the wavefront dislocations (OVs) in stochastic polychromatic fields. The local intensity maxima and minima, including regions of intensity minimum with and without singularities, form a consistent interrelated network (“optical-field skeleton”), which is topologically stable against small perturbations associated with the light propagation in weakly inhomogeneous media or with the object evolution “as a whole”. Such features, inherent in the correlation-optics representation of optical fields, makes it possible to solve the “inverse phase problem” of restoring the phase distribution of the field (and, accordingly, the phase-determining parameters of the investigated object) from the known distribution of amplitude, including the points with singularities [109].

These features demonstrate the abilities of classical correlation-optics approaches, combined with the modern singular optics, for the representation and study of complex optical fields, extracting information about the properties of macro-, micro- and nanoobjects. Noteworthy, the qualitative recognition and differentiation of the meaningful “skeleton” points of the field becomes possible due to the explicit involvement of optical forces and corresponding mechanical actions of light fields. As sensitive markers, the probing bodies (carbon nanoparticles) with bright luminescence can be used [109, 152], whose motion and localization under the action of optical forces enables to indicate the intensity extrema and singular points of the field. Moreover, the regions of phase singularities can be distinguished from “regular” intensity minima by the difference in concentration of the trapped nanoparticles and their near-singularity motions.

The experimental approaches, schemes, arrangements, presented in the review and employing the probing particles of different nature and properties, are useful not only for the detection of optical flows and related optical forces, but can be expanded to solving insistent practical problems related to the creation of micromanipulators with different mechanisms of action, micromotors and micromachines [154, 156–158]. Particular efforts, made for the singularities’ identification in polychromatic radiation and their analysis by the interference methods [86, 87], promise fruitful applications for continuous monitoring the thickness of films during their growth or for the quality inspection of surfaces with roughness [141, 142].

The limited volume of the review inevitably restricts its practical contents to a few applications, which, in our opinion, spectacularly demonstrate the mutual influence and mutual reinforcement of the correlation-optics and singular-optics methods. However, there are much more examples [153] of penetration of such approaches into modern telecommunication systems, super-resolution microscopy, image recognition and processing, etc. To conclude, we can only briefly mention some prospective applications of the ideas and methods described in the present review, which could not be comprehensively characterized in the main text but may be of interest for readers in their further activity.

An instructive example concerns the analysis of the second-order spatial coherence distribution of a structured random light beam and its utilization for the information encryption [154]. The usual optical-encryption protocols employing the first-order field characteristics (light phase or intensity) are highly dependent on interference effects and are unstable when light interacts with matter. An alternative optical encryption protocol, by which information is encoded into a second-order spatial coherence distribution of a structured random light beam, has two key advantages over traditional counterparts. First, the complexity of measuring the spatial coherence distribution of light improves the security of the encryption protocol. The second is the relative insensitivity of the second-order statistics to the environmental noise, which makes the protocol robust to environmental fluctuations such as atmospheric turbulence. Such results open up promising opportunities for further research into optical encryption in complex environments.

On the other hand, the methods for generation of optical fields with desirable properties can be (and already are) widely used in biological and medical technologies [155–158] for transportation, controllable motion of micro- and nanoparticles through the use of a wide variety of controlled parameters (characteristics) of the field, including optical forces of different physical nature (gradient force, light pressure force, forces associated with the spin and orbital energy flows). Depending on their properties, such particles may serve as “agents” delivering the specific influences to prescribed zones of biological organisms, cells, etc., or as informative “markers”, or as “nano-antennas” sensitive to external influences and transmitting them to the biological environment. As a version of this application, the specially “constructed” light fields and specially localized particles can be used for inspiring specific local reactions, in particular, local phase transitions and creation of microbubbles [122–127]. The bubbles, in turn, may serve as “vehicles” for transportation of microdoses of medical species, for their delivery to specific areas in the cell surgery, etc., which can be made very accurately by the laser control of the direction and speed of the bubble’s motion [128–130]. In the laboratory diagnostics, useful prospects are associated with the controllable motion of biological cells in the liquid media based on the near-field optics, for example, regulation of the erythrocyte’s motion in the evanescent light fields [145–149].

As for the more traditional methods of optical diagnostics, based on the analysis of optical field scattered or reflected by an object, the interrelations between the polarization and correlation characteristics of optical fields, inherent in the correlation-optics approaches, form the basis of the polarization-holography approaches for information recording and restoring, for registration and recovery of phase maps and real-time investigation of distant moving objects, for the improved diagnostics of biological tissues of different types, etc.

Author Contributions

OA, CZ, and DI contributed conception and design of the study; CZ and JZ wrote the first draft of the manuscript; AB and JZ wrote Introduction and Conclusion; JZ, OA, and DI wrote Sections 2 and 3; AB, OA, and CZ wrote Sections 4 and 5, AB and DI wrote Section 6. All authors contributed to manuscript revision, read and approved the submitted version.

Funding

Research Institute of Zhejiang University–Taizhou, Center for Modern Optical Technology, China; Ministry of Education and Science of Ukraine (project 610/22, #0122U001830).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Pennington KS, Collier RJ. Hologram‐generated Ghost Image Experiments. Appl Phys Lett (1966) 8(1):14–6. doi:10.1063/1.1754407

CrossRef Full Text | Google Scholar

2. Collier RJ, Pennington KS. Ghost Imaging by Holograms Formed in the Near Field. Appl Phys Lett (1966) 8(2):44–6. doi:10.1063/1.1754474

CrossRef Full Text | Google Scholar

3. Van Heerden PJ. A New Optical Method of Storing and Retrieving Information. Appl Opt (1963) 2:387–92. doi:10.1364/AO.2.000387

CrossRef Full Text | Google Scholar

4. Aristov VV, Broude VL, Kovalskii LV, Polyanskii VK, Timofeev VB, Shekhtman VI. On Holography without Reference Beam. USSR Dokl Acad Sci (1967) 177(1):65–7. Available from: http://mi.mathnet.ru/dan33442.

Google Scholar

5. Mokhun II, Roslyakov SN, Yatsenko VV. Reconstruction of the Phase and Amplitude Components of the Diffraction Field Scattered by a fine-structure Object. Bulletin of the Russian Academy of Sciences. Physics (1992) 56(4):205–11.

Google Scholar

6. Mokhun II, Besaga RN, Yatsenko VV. Reconstruction of Optical fields by Referenceless Holograms. Opt Spectrosc (1994) 76(4):593–8.

Google Scholar

7. Polyanskiǐ PV. Associative Properties of Second-Order Holograms. J Opt Technol (1997) 64(4):300–7.

Google Scholar

8. Polyanskii PV. Associative Memory Using a Static Phase-Conjugating Mirror on the Basis of a Quadric Hologram. Opt Spectrosc (1998) 84(2):300–5.

Google Scholar

9. Sorensen CM. Polarized and Depolarized Light-Scattering Studies on Brownian Diffusional and Critical Fluid Systems: Theory and experiment. PhD thesis. Boulder, USA: Colorado Univ. (1976). doi:10.2172/7077162

CrossRef Full Text

10. Polyanskii VK, Kovalskii LV. Informative Contents of the Light Radiation Field. In: Materials of the Third All-Union School on Holography. Leningrad: LINP (1972). p. 53–72.

Google Scholar

11. Polyanskii VK, Kovalskii LV. On the Question about the “Thin” Structure of Scattered Radiation. Optika i spektroskopiya (1973) 35(2):345–50.

Google Scholar

12. DeBoo B, Sasian J, Chipman R. Degree of Polarization Surfaces and Maps for Analysis of Depolarization. Opt Express (2004) 12:4941–58. doi:10.1364/OPEX.12.004941

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ellis J, Dogariu A. Complex Degree of Mutual Polarization. Opt Lett (2004) 29:536–8. doi:10.1364/OL.29.000536

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ellis J, Dogariu A. Differentiation of Globally Unpolarized Complex Random fields. J Opt Soc Am A (2004) 21:988–93. doi:10.1364/JOSAA.21.000988

CrossRef Full Text | Google Scholar

15. Ellis J, Dogariu A. Discrimination of Globally Unpolarized fields through Stokes Vector Element Correlations. J Opt Soc Am A (2005) 22:491–6. doi:10.1364/JOSAA.22.000491

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Wolf E. Unified Theory of Coherence and Polarization of Random Electromagnetic Beams. Phys Lett A (2003) 312:263–7. doi:10.1016/S0375-9601(03)00684-4

CrossRef Full Text | Google Scholar

17. Wolf E. Correlation-induced Changes in the Degree of Polarization, the Degree of Coherence, and the Spectrum of Random Electromagnetic Beams on Propagation. Opt Lett (2003) 28:1078–80. doi:10.1364/OL.28.001078

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Ellis J, Dogariu A. Optical Polarimetry of Random fields. Phys Rev Lett (2005) 95:203905. doi:10.1103/PhysRevLett.95.203905

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Born M, Wolf E. Principles of Optics. 7th ed. Cambridge: Cambridge University Press (1999). p. 952.

Google Scholar

20. Azzam RMA, Bashara NM. Ellipsometry and Polarized Light. Amsterdam: North-Holland (1977).

Google Scholar

21. Perina J. Coherence of Light. Berlin, Heidelberg: Springer (1985).

Google Scholar

22. Goodman JW. Statistical Optics. Hoboken, NJ, USA: John Wiley & Sons (2015).

Google Scholar

23. Angelsky OV, Bekshaev AY, Hanson SG, Zenkova CY, Mokhun II, Jun Z. Structured Light: Ideas and Concepts. Front Phys (2020) 8:114. doi:10.3389/fphy.2020.00114

CrossRef Full Text | Google Scholar

24. Bekshaev A, Bliokh KY, Soskin M. Internal Flows and Energy Circulation in Light Beams. J Opt (2011) 13(5):053001. doi:10.1088/2040-8978/13/5/053001

CrossRef Full Text | Google Scholar

25. Angelsky OV, Bekshaev AY, Mokhun II, Vasnetsov MV, Zenkova CY, Hanson SG, et al. Review on the Structured Light Properties: Rotational Features and Singularities. Opto-Electronics Rev (2022) 30(2):e140860. doi:10.24425/opelre.2022.140860

CrossRef Full Text | Google Scholar

26. Korotkova O, Wolf E. Generalized Stokes Parameters of Random Electromagnetic Beams. Opt Lett (2005) 30:198–200. doi:10.1364/OL.30.000198

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Korotkova O, Wolf E. Changes in the State of Polarization of a Random Electromagnetic Beam on Propagation. Opt Commun (2005) 246:35–43. doi:10.1016/j.optcom.2004.10.078

CrossRef Full Text | Google Scholar

28. Bastiaans MJ. Application of the Wigner Distribution Function in Optics. In: W Mecklenbräuker, and F Hlawatsch, editors. The Wigner Distribution—Theory and Applications in Signal Processing. Amsterdam; New York: Elsevier (1997). p. 375–429. urn:nbn:nl:ui:25-f7c8c278-e2ef-4873-9eb0-b1a327f2ea25.

Google Scholar

29. Dragoman D. I: The Wigner Distribution Function in Optics and Optoelectronics. Prog Opt (1997) 37:1–56. doi:10.1016/S0079-6638(08)70336-6

CrossRef Full Text | Google Scholar

30. Mejıas PM, Martınez-Herrero R, Piquero G, Movilla JM. Parametric Characterization of the Spatial Structure of Non-uniformly Polarized Laser Beams. Prog Quant Electron (2002) 26(2):65–130. doi:10.1016/S0079-6727(02)00003-4

CrossRef Full Text | Google Scholar

31. Anan’ev YA, Bekshaev AY. Theory of Intensity Moments for Arbitrary Light Beams. Opt Spectrosc (1994) 76:558–68.

Google Scholar

32. Anan’ev YA, Bekshaev AY, Grimblatov VM. Spatial-angular Moments of Light Beam Intensity in a Lens-like Scattering Medium. Opt Spectrosc (1999) 87(1):105–10.

Google Scholar

33. Alonso MA. Geometric Descriptions for the Polarization for Nonparaxial Optical fields: A Tutorial (2020). arXiv [Preprint]. arXiv:2008.02720.

Google Scholar

34. Gil JJ, Norrman A, Friberg AT, Setälä T. Nonregularity of Three-Dimensional Polarization States. Opt Lett (2018) 43:4611–4. doi:10.1364/OL.43.004611

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Gil JJ, Friberg AT, Setälä T, San José I. Structure of Polarimetric Purity of Three-Dimensional Polarization States. Phys Rev A (2017) 95:053856. doi:10.1103/PhysRevA.95.053856

CrossRef Full Text | Google Scholar

36. Gil JJ, Norrman A, Setälä T, Friberg AT. Nonregular Three-Dimensional Polarization States. In: Frontiers in Optics/Laser Science 2018. OSA Technical Digest. Washington, DC, USA: Optica Publishing Group (2018). p. JW4A.12. doi:10.1364/FIO.2018.JW4A.12

CrossRef Full Text | Google Scholar

37. Sheppard CJR, Bendandi A, Le Gratiet A, Diaspro A. Purity of 3D Polarization. J Opt Soc Am A (2021) 39:6–16. doi:10.1364/JOSAA.444326

CrossRef Full Text | Google Scholar

38. Zenkova C, Gorsky M, Gorodynska N. About the Estimation of Degree of Coherence for Circularly Polarized Waves. Ukr J Phys Opt (2010) 11:127–37. doi:10.3116/16091833/11/3/127/2010

CrossRef Full Text | Google Scholar

39. Zenkova C, Gorsky M, Gorodynska N. Metrology of Degree of Coherence of Circularly Polarized Optical Waves. Opto-Electronics Rev (2011) 19(3):14–9. doi:10.2478/s11772-011-0022-6

CrossRef Full Text | Google Scholar

40. Cai Y, Chen Y, Wang F. Generation and Propagation of Partially Coherent Beams with Nonconventional Correlation Functions: a Review [Invited]. J Opt Soc Am A (2014) 31:2083–96. doi:10.1364/JOSAA.31.002083

CrossRef Full Text | Google Scholar

41. Chen Y, Wang F, Dong Z, Cai Y, Norrman A, Gil JJ, et al. Polarimetric Dimension and Nonregularity of Tightly Focused Light Beams. Phys Rev A (2020) 101:053825. doi:10.1103/PhysRevA.101.053825

CrossRef Full Text | Google Scholar

42. Aiello A, Banzer P. The Ubiquitous Photonic Wheel. J Opt (2016) 18:085605. doi:10.1088/2040-8978/18/8/085605

CrossRef Full Text | Google Scholar

43. Bekshaev AY, Bliokh KY, Nori F. Transverse Spin and Momentum in Two-Wave Interference. Phys Rev X (2015) 5:011039. doi:10.1103/PhysRevX.5.011039

CrossRef Full Text | Google Scholar

44. Bliokh KY, Nori F. Transverse and Longitudinal Angular Momenta of Light. Phys Rep (2015) 592:1–38. doi:10.1016/j.physrep.2015.06.003

CrossRef Full Text | Google Scholar

45. Eismann JS, Nicholls LH, Roth DJ, Alonso MA, Banzer P, Rodríguez-Fortuño FJ, et al. Transverse Spinning of Unpolarized Light. Nat Photon (2021) 15:156–61. doi:10.1038/s41566-020-00733-3

CrossRef Full Text | Google Scholar

46. Forbes KA. Optical Helicity of Unpolarized Light. Phys Rev A (2022) 105:023524. doi:10.1103/PhysRevA.105.023524

CrossRef Full Text | Google Scholar

47. Gil JJ, San José I, Norrman A, Friberg AT, Setälä T. Sets of Orthogonal Three-Dimensional Polarization States and Their Physical Interpretation. Phys Rev A (2019) 100:033824. doi:10.1103/PhysRevA.100.033824

CrossRef Full Text | Google Scholar

48. Chen Y, Wang F, Dong Z, Cai Y, Norrman A, Gil JJ, et al. Structure of Transverse Spin in Focused Random Light. Phys Rev A (2021) 104:013516. doi:10.1103/PhysRevA.104.013516

CrossRef Full Text | Google Scholar

49. ChenNorrman YA, Norrman A, Ponomarenko SA, Friberg AT. Optical Coherence and Electromagnetic Surface Waves. Prog Opt (2020) 65:105–72. doi:10.1016/bs.po.2019.11.001

CrossRef Full Text | Google Scholar

50. Bauer T, Banzer P, Karimi E, Orlov S, Rubano A, Marrucci L, et al. Observation of Optical Polarization Möbius Strips. Science (2015) 347:964–6. doi:10.1126/science.1260635

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Bekshaev A. Improved Theory for the Polarization-dependent Transverse Shift of a Paraxial Light Beam in Free Space. Ukr J Phys Opt (2011) 12:10–8. doi:10.3116/16091833/12/1/10/2011

CrossRef Full Text | Google Scholar

52. Bekshaev AY. Polarization-dependent Transformation of a Paraxial Beam upon Reflection and Refraction: A Real-Space Approach. Phys Rev A (2012) 85:023842. doi:10.1103/PhysRevA.85.023842

CrossRef Full Text | Google Scholar

53. Bliokh KY, Aiello A. Goos-Hänchen and Imbert-Fedorov Beam Shifts: an Overview. J Opt (2013) 15:014001. doi:10.1088/2040-8978/15/1/014001

CrossRef Full Text | Google Scholar

54. Angelsky OV, Dominikov NN, Maksimyak PP, Tudor T. Experimental Revealing of Polarization Waves. Appl Opt (1999) 38(14):3112–7. doi:10.1364/AO.38.003112

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Zenkova CY, Ivansky DI, Tkachuk VM, Zheng J. Structured Light in Applications Related to the Reconstruction of Three-Dimensional Landscape of Nanorough Surfaces. Opt Mem Neural Networks (2022) 31(1):22–35. doi:10.3103/S1060992X22010118

CrossRef Full Text | Google Scholar

56. Mandel L, Wolf E. Coherence Properties of Optical fields. Rev Mod Phys (1965) 37:231–87. doi:10.1103/RevModPhys.37.231

CrossRef Full Text | Google Scholar

57. Piquero G, Martínez-Herrero R, de Sande JCG, Santarsiero M. Synthesis and Characterization of Non-uniformly Totally Polarized Light Beams: Tutorial. J Opt Soc Am A (2020) 37:591–605. doi:10.1364/JOSAA.379439

CrossRef Full Text | Google Scholar

58. Wolf E. Introduction to the Theory of Coherence and Polarization of Light. Cambridge: Cambridge University (2007).

Google Scholar

59. Hannonen A, Saastamoinen K, Leppänen L-P, Koivurova M, Shevchenko A, Friberg AT, et al. Geometric Phase in Beating of Light Waves. New J Phys (2019) 21:083030. doi:10.1088/1367-2630/ab3740

CrossRef Full Text | Google Scholar

60. Soskin MS, Vasnetsov MV. Singular Optics. Prog Opt (2001) 42:219–76. doi:10.1016/S0079-6638(01)80018-4

CrossRef Full Text | Google Scholar

61. Bekshaev A, Soskin M, Vasnetsov M. Paraxial Light Beams with Angular Momentum. New York: Nova Science Publishers (2008). p. 112.

Google Scholar

62. Siegman AE. Lasers. Sausalito: University Science Books (1986).

Google Scholar

63. Mokhun II. Introduction to Linear Singular Optics. In: O Angelsky, editor. Optical Correlation: Techniques and Applications. Bellingham, Washington: SPIE Press (2007). p. 1–131. doi:10.1117/3.714999

CrossRef Full Text | Google Scholar

64. Angelsky OV, Besaha RN, Mokhun AI, Mokhun II, Sopin MO, Soskin MS, et al. Singularities in Vectoral fields. Proc SPIE (1999) 3904:40–54. doi:10.1117/12.370443

CrossRef Full Text | Google Scholar

65. Freund I, Mokhun AI, Soskin MS, Angelsky OV, Mokhun II. Stokes Singularity Relations. Opt Lett (2002) 27:545–7. doi:10.1364/OL.27.000545

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Freund I, Shvartsman N. Wave-field Phase Singularities: The Sign Principle. Phys Rev A (1994) 50:5164–72. doi:10.1103/PhysRevA.50.5164

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Pal SK, Gangwar KK, Senthilkumaran P. Tailoring Polarization Singularity Lattices by Phase Engineering of Three-Beam Interference. Optik (2022) 255:168680. doi:10.1016/j.ijleo.2022.168680

CrossRef Full Text | Google Scholar

68. Xu R, Chen P, Tang J, Duan W, Ge S-J, Ma L-L, et al. Perfect Higher-Order Poincaré Sphere Beams from Digitalized Geometric Phases. Phys Rev Appl (2018) 10:034061. doi:10.1103/PhysRevApplied.10.034061

CrossRef Full Text | Google Scholar

69. Milione G, Sztul HI, Nolan DA, Alfano RR. Higher-Order Poincaré Sphere, Stokes Parameters, and the Angular Momentum of Light. Phys Rev Lett (2011) 107:053601. doi:10.1103/PhysRevLett.107.053601

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Naidoo D, Roux FS, Dudley A, Litvin I, Piccirillo B, Marrucci L, et al. Controlled Generation of Higher-Order Poincaré Sphere Beams from a Laser. Nat Photon (2016) 10:327–32. doi:10.1038/nphoton.2016.37

CrossRef Full Text | Google Scholar

71. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Huang K, Liu H, Restuccia S, Mehmood MQ, Mei S-T, Giovannini D, et al. Spiniform Phase-Encoded Metagratings Entangling Arbitrary Rational-Order Orbital Angular Momentum. Light Sci Appl (2018) 7:17156. doi:10.1038/lsa.2017.156

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Zhan Q. Cylindrical Vector Beams: from Mathematical Concepts to Applications. Adv Opt Photon (2009) 1:1–57. doi:10.1364/AOP.1.000001

CrossRef Full Text | Google Scholar

74. Liu G-G, Lee Y-H, Huang Y, Zhu Z, Tan G, Cai M-Q, et al. Dielectric Broadband Meta-Vector-Polarizers Based on Nematic Liquid crystal. APL Photon (2017) 2:126102. doi:10.1063/1.5006016

CrossRef Full Text | Google Scholar

75. Fan J, Xiao N, Zhao J, Shi H, Liao R, Xie C, et al. Controlled Generation of Wavelength-Tunable Higher Order Poincaré Sphere Beams from a Femtosecond Optical Parametric Oscillator. IEEE J Select Top Quan Electron. (2020) 26(6):1–5. doi:10.1109/JSTQE.2020.2991769

CrossRef Full Text | Google Scholar

76. Lopez-Mago D. On the Overall Polarisation Properties of Poincaré Beams. J Opt (2019) 21:115605. doi:10.1088/2040-8986/ab4c25

CrossRef Full Text | Google Scholar

77. Han W, Cheng W, Zhan Q. Flattop Focusing with Full Poincaré Beams under Low Numerical Aperture Illumination. Opt Lett (2011) 36:1605–7. doi:10.1364/OL.36.001605

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Fickler R, Lapkiewicz R, Ramelow S, Zeilinger A. Quantum Entanglement of Complex Photon Polarization Patterns in Vector Beams. Phys Rev A (2014) 89:060301. doi:10.1103/PhysRevA.89.060301

CrossRef Full Text | Google Scholar

79. Sivankutty S, Andresen ER, Bouwmans G, Brown TG, Alonso MA, Rigneault H. Single-shot Polarimetry Imaging of Multicore Fiber. Opt Lett (2016) 41:2105–8. doi:10.1364/OL.41.002105

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Suárez-Bermejo JC, González de Sande JC, Santarsiero M, Piquero G. Mueller Matrix Polarimetry Using Full Poincaré Beams. Opt Lasers Eng (2019) 122:134–41. doi:10.1016/j.optlaseng.2019.05.030

CrossRef Full Text | Google Scholar

81. Salla GR, Kumar V, Miyamoto Y, Singh RP. Scattering of Poincaré Beams: Polarization Speckles. Opt Express (2017) 25:19886–93. doi:10.1364/OE.25.019886

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Angelsky OV, Hanson SG, Zenkova CY, Gorsky MP, Gorodyns’ka NV. On Polarization Metrology (Estimation) of the Degree of Coherence of Optical Waves. Opt Express (2009) 17:15623–34. doi:10.1364/OE.17.015623

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Angelsky OV, Zenkova CY, Gorsky MP, Gorodyns'ka NV. Feasibility of Estimating the Degree of Coherence of Waves at the Near Field. Appl Opt (2009) 48:2784–8. doi:10.1364/AO.48.002784

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Zenkova CY. Interconnection of Polarization Properties and Coherence of Optical fields. Appl Opt (2014) 53:B43–52. doi:10.1364/AO.53.000B43

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Zenkova C, Gorsky M, Gorodynska N. Metrology of Degree of Coherence of Circularly Polarized Optical Waves. Opto-Electronics Rev (2011) 19(3):14–9. doi:10.2478/s11772-011-0022-6

CrossRef Full Text | Google Scholar

86. Angelsky OV, Maksimyak AP, Maksimyak PP, Hanson SG. Interference Diagnostics of white-light Vortices. Opt Express (2005) 13:8179–83. doi:10.1364/OPEX.13.008179

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Angelsky OV, Hanson SG, Maksimyak AP, Maksimyak PP. On the Feasibility for Determining the Amplitude Zeroes in Polychromatic fields. Opt Express (2005) 13:4396–405. doi:10.1364/OPEX.13.004396

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Zeng J, Lin R, Liu X, Zhao C, Cai Y. Review on Partially Coherent Vortex Beams. Front Optoelectron (2019) 12(3):229–48. doi:10.1007/s12200-019-0901-x

CrossRef Full Text | Google Scholar

89. Liu X, Zeng J, Cai Y. Review on Vortex Beams with Low Spatial Coherence. Adv Phys X (2019) 4:1626766. doi:10.1080/23746149.2019.1626766

CrossRef Full Text | Google Scholar

90. Voelz D, Xiao X, Basu S, Hyde MW, Korotkova O. Modeling the Electromagnetic Gaussian Schell-Model Source. In: Imaging and Applied Optics 2015, OSA Technical Digest (Online). Washington, DC, USA: Optica Publishing Group (2015). p. PW3E.1. doi:10.1364/PCDVTAP.2015.PW3E.1

CrossRef Full Text | Google Scholar

91. Zhao C, Cai Y. Trapping Two Types of Particles Using a Focused Partially Coherent Elegant Laguerre-Gaussian Beam. Opt Lett (2011) 36:2251–3. doi:10.1364/OL.36.002251

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Chen Y, Wang F, Cai Y. Partially Coherent Light Beam Shaping via Complex Spatial Coherence Structure Engineering. Adv Phys X (2022) 7:2009742. doi:10.1080/23746149.2021.2009742

CrossRef Full Text | Google Scholar

93. Chen Y, Wang F, Zhao C, Cai Y. Experimental Demonstration of a Laguerre-Gaussian Correlated Schell-Model Vortex Beam. Opt Express (2014) 22:5826–38. doi:10.1364/OE.22.005826

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Chen Y, Wang F, Yu J, Liu L, Cai Y. Vector Hermite-Gaussian Correlated Schell-Model Beam. Opt Express (2016) 24:15232–50. doi:10.1364/OE.24.015232

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Ding C, Koivurova M, Turunen J, Pan L. Self-focusing of a Partially Coherent Beam with Circular Coherence. J Opt Soc Am A (2017) 34:1441–7. doi:10.1364/JOSAA.34.001441

CrossRef Full Text | Google Scholar

96. Santarsiero M, Martínez-Herrero R, Maluenda D, de Sande JCG, Piquero G, Gori F. Partially Coherent Sources with Circular Coherence. Opt Lett (2017) 42:1512–5. doi:10.1364/OL.42.001512

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Zhao Z, Ding C, Zhang Y, Pan L. Spatial-temporal Self-Focusing of Partially Coherent Pulsed Beams in Dispersive Medium. Appl Sci (2019) 9:3616. doi:10.3390/app9173616

CrossRef Full Text | Google Scholar

98. Tervo J. Coherence and Polarization in Stationary Random Electromagnetic fields. Opt Pure Appl (2005) 28(3):27–36.

Google Scholar

99. Tervo J, Setala T, Friberg A. Degree of Coherence for Electromagnetic fields. Opt Express (2003) 11:1137–43. doi:10.1364/OE.11.001137

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Réfrégier P, Goudail F. Invariant Degrees of Coherence of Partially Polarized Light. Opt Express (2005) 13(16):6051–60. doi:10.1364/OPEX.13.006051

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Setälä T, Tervo J, Friberg AT. Contrasts of Stokes Parameters in Young's Interference experiment and Electromagnetic Degree of Coherence. Opt Lett (2006) 31(18):2669–71. doi:10.1364/OL.31.002669

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Réfrégier P, Roueff A. Intrinsic Coherence: A New Concept in Polarization and Coherence Theory. Opt Photon News (2007) 18:30–5. doi:10.1364/OPN.18.2.000030

CrossRef Full Text | Google Scholar

103. Zenkova CY, Yermolenko SB, Angelskaya AO, Soltys IV. The Polarization Peculiarities of the Correlation (Intrinsic Coherence) of Optical fields. Opt Mem Neural Networks (2011) 20(4):247–54. doi:10.3103/S1060992X11040072

CrossRef Full Text | Google Scholar

104. Angelsky OV, Gorsky MP, Maksimyak PP, Maksimyak AP, Hanson SG, Zenkova CY. Investigation of Optical Currents in Coherent and Partially Coherent Vector fields. Opt Express (2011) 19:660–72. doi:10.1364/OE.19.000660

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Zenkova CY, Gorsky MP, Maksimyak PP, Maksimyak AP. Optical Currents in Vector fields. Appl Opt (2011) 50:1105–12. doi:10.1364/AO.50.001105

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Nieto-Vesperinas M, Sáenz JJ, Gómez-Medina R, Chantada L. Optical Forces on Small Magnetodielectric Particle. Opt Express (2010) 18(11):11428–43. doi:10.1364/OE.18.011428

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Bekshaev AY. Subwavelength Particles in an Inhomogeneous Light Field: Optical Forces Associated with the Spin and Orbital Energy Flows. J Opt (2013) 15:044004. doi:10.1088/2040-8978/15/4/044004

CrossRef Full Text | Google Scholar

108. Zenkova C, Soltys I, Angelsky P. The Use of Motion Peculiarities of Particles of the Rayleigh Light Scattering Mechanism for Defining the Coherence Properties of Optical fields. Optica Applicata (2013) 43:297–312. doi:10.5277/oa130210

CrossRef Full Text | Google Scholar

109. Angelsky OV, Zenkova CY, Hanson SG, Ivansky DI, Tkachuk VM, Zheng J. Random Object Optical Field Diagnostics by Using Carbon Nanoparticles. Opt Express (2021) 29:916–28. doi:10.1364/OE.411118

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Angelsky OV, Bekshaev AY, Maksimyak PP, Maksimyak AP, Hanson SG, Zenkova CY. Self-diffraction of Continuous Laser Radiation in a Disperse Medium with Absorbing Particles. Opt Express (2013) 21:8922–38. doi:10.1364/OE.21.008922

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Shvedov VG, Desyatnikov AS, Rode AV, Krolikowski W, Kivshar YS. Optical Guiding of Absorbing Nanoclusters in Air. Opt Express (2009) 17(7):5743–57. doi:10.1364/OE.17.005743

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Desyatnikov AS, Shvedov VG, Rode AV, Krolikowski W, Kivshar YS. Photophoretic Manipulation of Absorbing Aerosol Particles with Vortex Beams: Theory versus experiment. Opt Express (2009) 17(10):8201–11. doi:10.1364/OE.17.008201

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Malai NV. Effect of Motion of the Medium on the Photophoresis of Hot Hydrosol Particles. Fluid Dyn (2006) 41(6):984–91. doi:10.1007/s10697-006-0113-0

CrossRef Full Text | Google Scholar

114. Soong CY, Li WK, Liu CH, Tzeng PY. Theoretical Analysis for Photophoresis of a Microscale Hydrophobic Particle in Liquids. Opt Express (2010) 18(3):2168–82. doi:10.1364/OE.18.002168

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Blum NT, Yildirim A, Chattaraj R, Goodwin AP. Nanoparticles Formed by Acoustic Destruction of Microbubbles and Their Utilization for Imaging and Effects on Therapy by High Intensity Focused Ultrasound. Theranostics (2017) 7(3):694–702. doi:10.7150/thno.17522

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Angelsky OV, Bekshaev AY, Maksimyak PP, Maksimyak AP, Hanson SG, Zenkova CY. Self-action of Continuous Laser Radiation and Pearcey Diffraction in a Water Suspension with Light-Absorbing Particles. Opt Express (2014) 22:2267–77. doi:10.1364/OE.22.002267

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Nye JF. Evolution from a Fraunhofer to a Pearcey Diffraction Pattern. J Opt A: Pure Appl Opt (2003) 5(5):495–502. doi:10.1088/1464-4258/5/5/310

CrossRef Full Text | Google Scholar

118. Pearcey T. XXXI. The Structure of an Electromagnetic Field in the Neighbourhood of a Cusp of a Caustic. Lond Edinb Dublin Philos Mag J Sci (1946) 37:311–7. doi:10.1080/14786444608561335

CrossRef Full Text | Google Scholar

119. Angelsky OV, Bekshaev AY, Maksimyak PP, Maksimyak AP, Hanson SG, Kontush SM. Controllable Generation and Manipulation of Micro-bubbles in Water with Absorptive Colloid Particles by CW Laser Radiation. Opt Express (2017) 25:5232–43. doi:10.1364/OE.25.005232

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Ortega-Mendoza JG, Sarabia-Alonso JA, Zaca-Morán P, Padilla-Vivanco A, Toxqui-Quitl C, Rivas-Cambero I, et al. Marangoni Force-Driven Manipulation of Photothermally-Induced Microbubbles. Opt Express (2018) 26:6653–62. doi:10.1364/OE.26.006653

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Li J, Zhao F, Deng Y, Liu D, Chen C-H, Shih W-C. Photothermal Generation of Programmable Microbubble Array on Nanoporous Gold Disks. Opt Express (2018) 26:16893–902. doi:10.1364/OE.26.016893

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Dijkink R, Ohl C-D. Laser-induced Cavitation Based Micropump. Lab Chip (2008) 8(10):1676–81. doi:10.1039/B806912C

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Hellman AN, Rau KR, Yoon HH, Bae S, Palmer JF, Phillips KS, et al. Laser-induced Mixing in Microfluidic Channels. Anal Chem (2007) 79(12):4484–92. doi:10.1021/ac070081i

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Hu W, Ishii KS, Fan Q, Ohta AT. Hydrogel Microrobots Actuated by Optically Generated Vapour Bubbles. Lab Chip (2012) 12(19):3821–6. doi:10.1039/C2LC40483D

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Song WD, Hong MH, Lukyanchuk B, Chong TC. Laser-induced Cavitation Bubbles for Cleaning of Solid Surfaces. J Appl Phys (2004) 95(6):2952–6. doi:10.1063/1.1650531

CrossRef Full Text | Google Scholar

126. Ohl C-D, Arora M, Dijkink R, Janve V, Lohse D. Surface Cleaning from Laser-Induced Cavitation Bubbles. Appl Phys Lett (2006) 89(7):074102. doi:10.1063/1.2337506

CrossRef Full Text | Google Scholar

127. Takahashi K, Yoshino K, Hatano S, Nagayama K, Asano T. Novel Applications of Thermally Controlled Microbubble Driving System. In: Proceedings of IEEE Conference on Micro Electro Mechanical Systems. Interlaken, Switzerland: IEEE (2001). p. 286–9. doi:10.1109/MEMSYS.2001.906534

CrossRef Full Text | Google Scholar

128. Sarabia-Alonso JA, Ortega-Mendoza JG, Ramírez-San-Juan JC, Zaca-Morán P, Ramírez-Ramírez J, Padilla-Vivanco A, et al. Optothermal Generation, Trapping, and Manipulation of Microbubbles. Opt Express (2020) 28:17672–82. doi:10.1364/OE.389980

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Fales AM, Vogt WC, Wear KA, Pfefer TJ, Ilev IK. Experimental Investigation of Parameters Influencing Plasmonic Nanoparticle-Mediated Bubble Generation with Nanosecond Laser Pulses. J Biomed Opt (2019) 24(6):1. doi:10.1117/1.JBO.24.6.065003

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Bogatyryova GV, Felde KV, Polyanskii PV, Soskin MS. Nongeneric Polarization Singularities in Combined Vortex Beams. Opt Spectrosc (2004) 97(5):782–9. doi:10.1134/1.1828629

CrossRef Full Text | Google Scholar

131. Felde CV, Chernyshov AA, Bogatyryova GV, Polyanskii PV, Soskin MS. Polarization Singularities in Partially Coherent Combined Beams. Jetp Lett (2008) 88(7):418–22. doi:10.1134/S002136400819003X

CrossRef Full Text | Google Scholar

132. Chernyshov AA, Felde CV, Bogatyryova HV, Polyanskii PV, Soskin MS. Vector Singularities of the Combined Beams Assembled from Mutually Incoherent Orthogonally Polarized Components. J Opt A: Pure Appl Opt (2009) 11:094010. doi:10.1088/1464-4258/11/9/094010

CrossRef Full Text | Google Scholar

133. Chen Y, Wang F, Liu L, Zhao C, Cai Y, Korotkova O. Generation and Propagation of a Partially Coherent Vector Beam with Special Correlation Functions. Phys Rev A (2014) 89:013801. doi:10.1103/PhysRevA.89.013801

CrossRef Full Text | Google Scholar

134. Gbur G, Visser TD, Wolf E. Hidden Singularities in Partially Coherent Wavefields. J Opt A: Pure Appl Opt (2004) 6(5):S239–S242. doi:10.1088/1464-4258/6/5/017

CrossRef Full Text | Google Scholar

135. Gbur G, Visser TD. Coherence Vortices in Partially Coherent Beams. Opt Commun (2003) 222(1–6):117–25. doi:10.1364/fio.2003.thb5

CrossRef Full Text | Google Scholar

136. Peng X, Liu L, Wang F, Popov S, Cai Y. Twisted Laguerre-Gaussian Schell-Model Beam and its Orbital Angular Moment. Opt Express (2018) 26:33956–69. doi:10.1364/oe.26.033956

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Liu X, Liu L, Chen Y, Cai Y. Partially Coherent Vortex Beam: From Theory to experiment. In: H Perez-de-Tejada, editor. Vortex Dynamics and Optical Vortices. London, UK: IntechOpen (2017). p. 275–96. doi:10.5772/66323

CrossRef Full Text | Google Scholar

138. Peng X, Lu X, Liu X, Zhao C, Lin R, Liu L, et al. Generation and Propagation of a Hermite-Gaussian Correlated Schell-Model LG0l Beam. Appl Sci (2019) 9:610. doi:10.3390/app9030610

CrossRef Full Text | Google Scholar

139. Wang H, Peng X, Zhang H, Liu L, Chen Y, Wang F, et al. Experimental Synthesis of Partially Coherent Beam with Controllable Twist Phase and Measuring its Orbital Angular Momentum. Nanophotonics (2022) 11(4):689–96. doi:10.1515/nanoph-2021-0432

CrossRef Full Text | Google Scholar

140. Shakeri-Zadeh A, Zareyi H, Sheervalilou R, Laurent S, Ghaznavi H, Samadian H. Gold Nanoparticle-Mediated Bubbles in Cancer Nanotechnology. J Controlled Release (2021) 330:49–60. doi:10.1016/j.jconrel.2020.12.022

CrossRef Full Text | Google Scholar

141.OV Angelsky, editor. Introduction to Singular Correlation Optics. Bellingham: SPIE Press (2019). p. 252.

Google Scholar

142. Angelsky OV, Polyanskii PV, Hanson SG. Singular-optical Coloring of Regularly Scattered white Light. Opt Express (2006) 14:7579–86. doi:10.1364/OE.14.007579

PubMed Abstract | CrossRef Full Text | Google Scholar

143. Angelsky OV, Bekshaev AY, Maksimyak PP, Maksimyak AP, Hanson SG, Zenkova CY. Orbital Rotation without Orbital Angular Momentum: Mechanical Action of the Spin Part of the Internal Energy Flow in Light Beams. Opt Express (2012) 20:3563–71. doi:10.1364/OE.20.003563

PubMed Abstract | CrossRef Full Text | Google Scholar

144. Berry MV. Optical Currents. J Opt A: Pure Appl Opt (2009) 11:094001. doi:10.1088/1464-4258/11/9/094001

CrossRef Full Text | Google Scholar

145. Chen Y, Norrman A, Ponomarenko SA, Friberg AT. Partially Coherent Surface Plasmon Polariton Vortex fields. Phys Rev A (2019) 100:053833. doi:10.1103/PhysRevA.100.053833

CrossRef Full Text | Google Scholar

146. Norrman A, Setälä T, Friberg AT. Generation and Electromagnetic Coherence of Unpolarized Three-Component Light fields. Opt Lett (2015) 40(22):5216–9. doi:10.1364/OL.40.005216

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Angelsky OV, Maksymyak PP, Zenkova CY, Maksymyak AP, Hanson SG, Ivanskyi DI. Peculiarities of Control of Erythrocytes Moving in an Evanescent Field. J Biomed Opt (2019) 24(5):1. doi:10.1117/1.JBO.24.5.055002

PubMed Abstract | CrossRef Full Text | Google Scholar

148. Angelsky OV, Zenkova CY, Maksymyak PP, Maksymyak AP, Ivanskyi DI, Tkachuk VM. Peculiarities of Energy Circulation in Evanescent Field. Application for Red Blood Cells. Opt Mem Neural Networks (2019) 28(1):11–20. doi:10.3103/S1060992X19010028

CrossRef Full Text | Google Scholar

149. Angelsky OV, Zenkova CY, Hanson SG, Zheng J. Extraordinary Manifestation of Evanescent Wave in Biomedical Application. Front Phys (2020) 8:159. doi:10.3389/fphy.2020.00159

CrossRef Full Text | Google Scholar

150. Bekshaev AY. Dynamical Characteristics of an Electromagnetic Field under Conditions of Total Reflection. J Opt (2018) 20(4):045604. doi:10.1088/2040-8986/aab035

CrossRef Full Text | Google Scholar

151. Angelsky OV, Bekshaev AY, Dragan GS, Maksimyak PP, Zenkova CY, Zheng J. Structured Light Control and Diagnostics Using Optical Crystals. Front Phys (2021) 9:715045. doi:10.3389/fphy.2021.715045

CrossRef Full Text | Google Scholar

152. Angelsky OV, Zenkova CY, Ivansky DI, Tkachuk VM, Zheng J. Carbon Nanoparticles for Study Complex Optical fields. J Optoelectronics Adv Mater (2021) 23(5–6):209–15.

Google Scholar

153. Rubinsztein-Dunlop H, Forbes A, Berry MV, Dennis MR, Andrews DL, Mansuripur M, et al. Roadmap on Structured Light. J Opt (2017) 19:013001. doi:10.1088/2040-8978/19/1/013001

CrossRef Full Text | Google Scholar

154. Peng D, Huang Z, Liu Y, Chen Y, Wang F, Ponomarenko SA, et al. Optical Coherence Encryption with Structured Random Light. PhotoniX (2021) 2:6. doi:10.1186/s43074-021-00027-z

PubMed Abstract | CrossRef Full Text | Google Scholar

155. He C, He H, Chang J, Chen B, Ma H, Booth MJ. Polarisation Optics for Biomedical and Clinical Applications: a Review. Light Sci Appl (2021) 10:194. doi:10.1038/s41377-021-00639-x

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Alali S, Vitkin A. Polarized Light Imaging in Biomedicine: Emerging Mueller Matrix Methodologies for Bulk Tissue Assessment. J Biomed Opt (2015) 20(6):061104. doi:10.1117/1.JBO.20.6.061104

PubMed Abstract | CrossRef Full Text | Google Scholar

157. Song L, Feng Y, Guo X, Shen Y, Wu D, Wu Z, et al. Ultrafast Polarization Bio-Imaging Based on Coherent Detection and Time-Stretch Techniques. Biomed Opt Express (2018) 9:6556–68. doi:10.1364/BOE.9.006556

PubMed Abstract | CrossRef Full Text | Google Scholar

158. York T, Achilefu S, Lake SP, Raman B, Gruev V, Powell SB, et al. Bioinspired Polarization Imaging Sensors: From Circuits and Optics to Signal Processing Algorithms and Biomedical Applications. Proc IEEE (2014) 102(10):1450–69. doi:10.1109/JPROC.2014.2342537

PubMed Abstract | CrossRef Full Text | Google Scholar