Insightful Facts on Peristalsis Flow of Water Conveying Multi-Walled Carbon Nanoparticles Through Elliptical Ducts With Ciliated Walls

In this research, a mathematical model is disclosed that elucidates the peristaltic flow of carbon nanotubes in an elliptic duct with ciliated walls. This novel topic of nanofluid flow is addressed for an elliptic domain for the very first time. The practical applications of current analysis include the customization of the mechanical peristaltic pumps, artificial cilia and their role in flow control, drug delivery and prime biological applications etc. The dimensional mathematical problem is transformed into its non-dimensional form by utilizing appropriate transformations and dimensionless parameters. Exact mathematical solutions are computed over the elliptic domain for the partial differential equations appearing in this convection heat transfer problem. A thorough graphical assessment is performed to discuss the prime results. The graphical visualization of the flow in this elliptic duct is obtained by plotting streamlines. The viscous effects are playing a vital role in the heat enhancement as compared to the molecular conduction. Since the incrementing Brinkman number results in a declined conduction due to viscous dissipation that eventually results in an enhanced temperature profile. This research first time elucidates the impacts of nanofluid flow on the peristaltic pumping through an elliptic domain having ciliated walls. Considering water as base fluid with multi-wall Carbon nanotubes for this ciliated elliptic domain having sinusoidal boundaries.

Introduction

Peristalsis is concerned with fluid dynamics problems involving flow inside ducts with wavelike deformable walls. The flexible walls’ sinusoidal movement eventually aids in the development of flow along the duct’s axis. This fascinating subject has a wide range of functional, engineering, and medical applications, making it a hot research topic. Slurries, various heated mixtures, and chemicals are among its primary industrial applications; see Jaffrin and Shapiro [1]. These are some finest mathematical models furnished by different precise researchers that elucidate the peristaltic flow in distinct geometries like cylinders, Barton [2] had numerically examined the peristaltic flow inside a cylindrical conduit, Siddiqui and Schwarz [3] had conveyed the perturbation solution analysis on Peristaltic pumping of a non-Newtonian fluid, Nadeem et al. [4] had interpreted the Homotopy Analysis solutions on the peristaltic pumping of non-Newtonian Sisko fluid, curved channels, Nadeem and Maraj [5] had disclosed the Homotopy Perturbation solutions on the Peristaltic pumping of Hyperbolic Tangent non-Newtonian fluid thorough a curved domain, Rashid et al. [6] had also utilized the Homotopy Perturbation analysis to interpret the magnetohydrodynamics effects on the peristaltic pumping of Williamson fluid inside a curved domain, rectangular ducts, Nadeem and Akram [7] had provided exact solutions on Jeffrey fluid flow within a rectangular domain having sinusoidal wall fluctuations, Ellahi et al. [8] provided the Homotopy Perturbation analysis on the three dimensional flow inside a rectangular conduit working as a peristaltic pump, Akram and Saleem [9] had interpreted the Carreau fluid transportation inside a rectangular domain operating as a peristaltic pump, asymmetric geometry, Nadeem and Akram [10] had disclosed the peristaltic pumping activity for asymmetric domain by using the regular perturbation expansion method, Akbar et al. [11] had highlighted the impact of nanofluids on peristaltic pumping through asymmetric domain, Akbar [12] had also considered the magnetohydrodynamic effects on the peristaltic pumping through asymmetric domain and the peristaltic pumping through an elliptic duct via exact solutions was interpreted by Saleem et al. [13].

Nanofluids consist of small-scale (1–100 nm in size) nano particles that are scattered in the base fluid. Scientifically, experts prefer multi-walled carbon nanotubes (MWCNTs) been a special form of carbon nanoparticles because they are nested inside one another and possess elongated hollow cylindrical tiny molecules of sp2 carbon [14, 15]. These are useful in industrial problems where thermal conductivity is a prime factor [16]. Akbar and Nadeem [17] had reported a mathematical study that elucidates the combine analysis of peristaltic flow and nanofluids. Akbar and Butt [18] had mathematically elucidated the peristaltic flow of water as a base fluid with nano particles having distinct structures. Akbar [19] had numerically examined the nanofluid flow inside asymmetric domain via Runge-Kutta technique. Nadeem et al. [20, 21] had evaluated the nanofluids impact on the peristaltic pumping through an annular in addition to rectangular domain. Akbar et al. [22] evaluated the magnetohydrodynamic impacts on the nanofluid pumping through a vertically held asymmetric domain.

The consequence of ciliated walls on the peristalsis driven flow is also a subject of keen interest. Cilia are tiny structures (like human hair) that play a prime role in the flow development. The peristaltic flow mechanism is also studied for distinct geometries having ciliated boundaries like ciliated cylindrical tube, Butt et al. [23] had provided exact solutions on the Phan Thien Tanner non-Newtonian flow inside a ciliated cylindrical domain, Saleem et al. [24] had interpreted the effects of hybrid nanofluid on the peristaltic pumping through a ciliated curved domain, Akbar and Khan [25] highlighted the impacts of MHD on the peristaltic pumping via a ciliated asymmetric domain. Sadaf and Nadeem [26] had presented a mathematical model that relates the combine effects of ciliated walls and peristalsis with nanofluid flow. Akbar [27] had reported the mathematical investigation of peristaltic flow of CNT in a symmetric geometry having ciliated boundaries. Akbar and Butt [28] elucidated the impacts of MHD and entropy interpretation on the peristaltic pumping of water based nanofluids through a cylindrical ciliated domain. Nadeem and Sadaf [29] had investigated the trapping phenomenon of nanofluids flow via a ciliated annular domain. Vaidya et al. [30, 31] had highlighted the impacts of chemical reactions on the peristaltic pumping of Ree-Eyring non-Newtonian fluid passing through a permeable domain in addition to an asymmetric domain under MHD effects. Ashraf et al. [32] had examined the MHD impacts on nanofluid flow of Casson fluid through a cylindrical domain with sinusoidal wall fluctuations. Samuel et al. [33–35] had interpreted the effects of MHD, nanofluidic volume fraction with convection analysis through numerical techniques. Saleem et al. [36] highlighted the impacts of activation energy and magnetohydrodynamics on ciliary propelled flow of nanofluid. Ramesh et al. [37] modelled the cilia driven couple stress fluid flow under MHD effects. Farooq et al. [38] had analysed the micro polar flow developed due to cilia propelled rhythmic wave. Akbar et al. [39] modelled the pressure driven flow generated due to rhythmic activity of cilia.

A thorough and careful investigation of the available literature has disclosed that the peristaltic flow of carbon nanotubes in an elliptic duct with ciliated walls is not mathematically reported yet. Thus, the intent of the present mathematical computation is to elucidate this important topic for an elliptic domain for the first time. The base fluid considered in this mathematical study is water and multi-wall carbon nanotubes are taken into account. The viscous dissipation effect is also incorporated for a detailed study of convection heat transfer. Exact mathematical solutions are computed and the results are verified through graphical assessment. Streamlines depict the visualization of flow pattern.

Mathematical Model

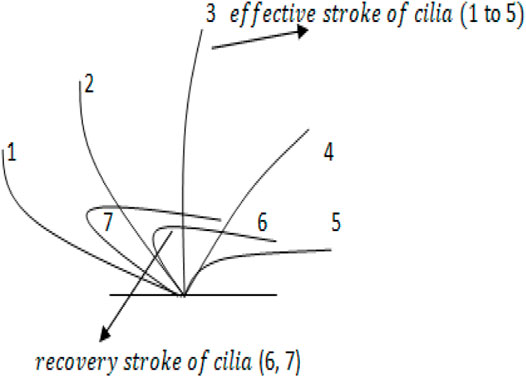
The peristaltic flow of carbon nanotubes in an elliptic duct with ciliated walls is mathematically investigated. A Cartesian coordinate system approach is utilized to interpret this mathematical study. The geometry of the problem is given by Figure 1 providing the model of elliptic domain having ciliated walls. The sinusoidal wall fluctuations are evident in Figure 1 and the ciliated wall are also mentioned. Figure 1 contains the front together with a side view of this geometry, the front view highlights the elliptic domain of this duct.

FIGURE 1

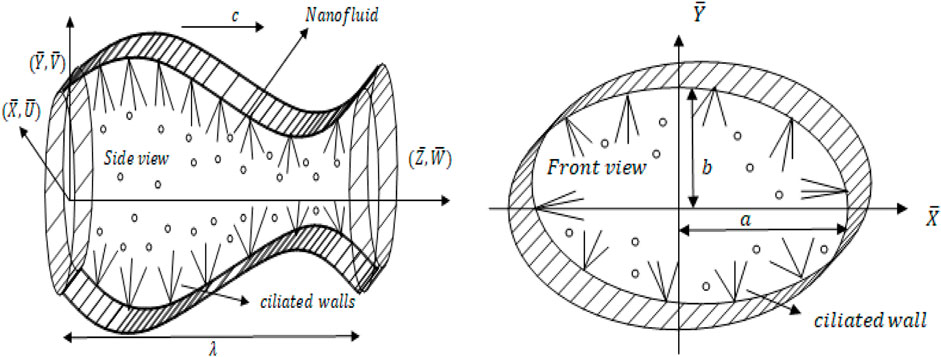
FIGURE 1. Geometrical model of the flow problem referred as [13].

The envelope model of cilia motion that considers the elliptical shape movements is taken into account. The equations considered for this model incorporates the sinusoidal metachronal wave movements generated due to rhythmic cilia motion. The computational equations that narrate this envelope model of cilia tips are referred as [40].

$\overline{Y}=b_0+b_0\varphi Cos(\frac{2\pi }{\lambda }(\overline{Z}-c\overline{t}))=\overline{f}\left(\overline{Z},\overline{t}\right),\overline{Z}={\overline{Z}}_0+b_0\varphi \alpha Sin(\frac{2\pi }{\lambda }(\overline{Z}-c\overline{t}))=\overline{g}\left(\overline{Z},{\overline{Z}}_0,\overline{t}\right),(1)$

The following computational equations are used to express the velocities of cilia tips (i.e. axial and radial velocity respectively).

$\overline{W}={\frac{\partial \overline{Z}}{\partial \overline{t}}|}_{{\overline{Z}}_0}=\frac{\partial \overline{g}}{\partial \overline{t}}+\frac{\partial \overline{g}}{\partial \overline{Z}}\frac{\partial \overline{Z}}{\partial \overline{t}}=\frac{\partial \overline{g}}{\partial \overline{t}}+\frac{\partial \overline{g}}{\partial \overline{Z}}\overline{W},\overline{V}={\frac{\partial \overline{Y}}{\partial \overline{t}}|}_{{\overline{Z}}_0}=\frac{\partial \overline{f}}{\partial \overline{t}}+\frac{\partial \overline{f}}{\partial \overline{Z}}\frac{\partial \overline{Z}}{\partial \overline{t}}=\frac{\partial \overline{f}}{\partial \overline{t}}+\frac{\partial \overline{f}}{\partial \overline{Z}}\overline{W},(2)$

The simplification of Eqs 1, 2 provides the following equations

$\overline{W}=\frac{-\left(\frac{2\pi }{\lambda }\right)\left[\varphi \alpha b_{0}cCos\left(\frac{2\pi }{\lambda }\left(\overline{Z}-c\overline{t}\right)\right)\right]}{\left[1-\left(\frac{2\pi }{\lambda }\right)\left\{\varphi \alpha b_{0}Cos\left(\frac{2\pi }{\lambda }\left(\overline{Z}-c\overline{t}\right)\right)\right\}\right]} ,\overline{V}=\frac{\left(\frac{2\pi }{\lambda }\right)\left[\varphi b_{0}cSin\left(\frac{2\pi }{\lambda }\left(\overline{Z}-c\overline{t}\right)\right)\right]}{\left[1-\left(\frac{2\pi }{\lambda }\right)\left\{\varphi \alpha b_{0}Cos\left(\frac{2\pi }{\lambda }\left(\overline{Z}-c\overline{t}\right)\right)\right\}\right]} ,(3)$

The above mentioned velocities $\overline{W}$ and $\overline{V}$ mainly differentiate between the two strokes of cilia motion, (i.e., effective and recovery strokes respectively). The cilia tips are assumed to circulate in an elliptical course, as revealed in Figure 2. Cilium remains inflexible and rigid during its effective stroke. On contrary, it shows flexibility during its recovery stroke and retreats loosely.

FIGURE 2

FIGURE 2. Cilia movement.

The mathematical modelling for the incompressible flow with carbon nanotubes and heat convection is provided in dimensional form as follows

$\frac{\partial \overline{U}}{\partial \overline{X}}+\frac{\partial \overline{V}}{\partial \overline{Y}}+\frac{\partial \overline{W}}{\partial \overline{Z}}=0,(4)$

${\rho }_{nf}\left(\frac{\partial \overline{U}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{U}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{U}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{U}}{\partial \overline{Z}}\right)=-\frac{\partial \overline{P}}{\partial \overline{X}}+{\mu }_{nf}\left(\frac{{\partial }^2\overline{U}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{U}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{U}}{\partial {\overline{Z}}^2}\right),(5)$

${\rho }_{nf}\left(\frac{\partial \overline{V}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{V}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{V}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{V}}{\partial \overline{Z}}\right)=-\frac{\partial \overline{P}}{\partial \overline{Y}}+{\mu }_{nf}\left(\frac{{\partial }^2\overline{V}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{V}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{V}}{\partial {\overline{Z}}^2}\right),(6)$

${\rho }_{nf}\left(\frac{\partial \overline{W}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{W}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{W}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{W}}{\partial \overline{Z}}\right)=-\frac{\partial \overline{P}}{\partial \overline{Z}}+{\mu }_{nf}\left(\frac{{\partial }^2\overline{W}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{W}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{W}}{\partial {\overline{Z}}^2}\right),(7)$

${\left(\rho C_p\right)}_{nf}\left(\frac{\partial \overline{T}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{T}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{T}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{T}}{\partial \overline{Z}}\right)=k_{nf}\left(\frac{{\partial }^2\overline{T}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{T}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{T}}{\partial {\overline{Z}}^2}\right)+{\mu }_{nf}\left[2\left\{{\left(\frac{\partial \overline{U}}{\partial \overline{X}}\right)}^2+{\left(\frac{\partial \overline{V}}{\partial \overline{Y}}\right)}^2+{\left(\frac{\partial \overline{W}}{\partial \overline{Z}}\right)}^2\right\}+{\left(\frac{\partial \overline{U}}{\partial \overline{Y}}+\frac{\partial \overline{V}}{\partial \overline{X}}\right)}^2+{\left(\frac{\partial \overline{V}}{\partial \overline{Z}}+\frac{\partial \overline{W}}{\partial \overline{Y}}\right)}^2+{\left(\frac{\partial \overline{W}}{\partial \overline{X}}+\frac{\partial \overline{U}}{\partial \overline{Z}}\right)}^2\right],(8)$

The respective dimensional form of boundary conditions for ciliated walls and elliptic domain are given as

$\overline{W}=\frac{-\left(\frac{2\pi }{\lambda }\right)\left[\varphi \alpha b_{0}cCos\left(\frac{2\pi }{\lambda }\left(\overline{Z}-c\overline{t}\right)\right)\right]}{\left[1-\left(\frac{2\pi }{\lambda }\right)\left\{\varphi \alpha b_{0}Cos\left(\frac{2\pi }{\lambda }\left(\overline{Z}-c\overline{t}\right)\right)\right\}\right]} ,\mathrm{f}\mathrm{o}\mathrm{r}\frac{{\overline{x}}^2}{{\overline{a}}^2}+\frac{{\overline{y}}^2}{{\overline{b}}^2}=1.\overline{T}={\overline{T}}_w\mathrm{f}\mathrm{o}\mathrm{r}\frac{{\overline{x}}^2}{{\overline{a}}^2}+\frac{{\overline{y}}^2}{{\overline{b}}^2}=1.(9)$

The unsteady and steady frames of reference are related by using the following equations

$\overline{x}=\overline{X}, \overline{y}=\overline{Y}, \overline{z}=\overline{Z}-c\overline{t}, \overline{p}=\overline{P}, \overline{u}=\overline{U}, \overline{v}=\overline{V}, \overline{w}=\overline{W}-c,(10)$

The non-dimensional variables that are incorporated in present analysis are given as

$x=\frac{\overline{x}}{D_h}, y=\frac{\overline{y}}{D_h}, z=\frac{\overline{z}}{\lambda }, t=\frac{c\overline{t}}{\lambda }, w=\frac{\overline{w}}{c}, p=\frac{D_h^2\overline{p}}{{\mu }_f\lambda c}, \theta =\frac{\overline{T}-{\overline{T}}_w}{{\overline{T}}_b-{\overline{T}}_w}, \delta =\frac{b_0}{a_0}, \varphi =\frac{d}{b_0},u=\frac{\lambda \overline{u}}{D_{h}c}, v=\frac{\lambda \overline{v}}{D_{h}c}, a=\frac{\overline{a}}{D_h}, b=\frac{\overline{b}}{D_h}, B_r=\frac{{\mu }_f{c}^2}{k_f\left({\overline{T}}_b-{\overline{T}}_w\right)}, \beta =\frac{b_0}{\lambda },(11)$

Whenever we deal with a non-circular domain then the concept of hydraulic diameter needs to be considered. It is considered as four times the cross-sectional area divided by the wetted perimeter of cross-section. The mathematical expression for the hydraulic diameter of elliptic duct is narrated as

$D_h=\frac{\pi b_0}{E\left(e\right)},(12)$

The computational equation that narrates the eccentricity of ellipse is $e=\sqrt{1-{\delta }^2}$, where $\delta$ is the aspect ratio and the second kind elliptical integral $E\left(e\right)$ is referred as Yang et al. [41].

$E\left(e\right)=\underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{{\displaystyle \int }}}\sqrt{1-e^{2}Si{n}^2{\alpha }_1}d{\alpha }_1,(13)$

The useful transformations provided in Eq. 10, the dimensionless variables given in Eq. 11 are used in Eqs 5–9 and the approximation $(\lambda \to \infty )$ is used to avail the following set of dimensionless equations

$\frac{\partial p}{\partial x}=0,(14)$

$\frac{\partial p}{\partial y}=0,(15)$

$\frac{dp}{dz}=\left(\frac{{\mu }_{nf}}{{\mu }_f}\right)\left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}\right),(16)$

$\left(\frac{k_{nf}}{k_f}\right)\left(\frac{{\partial }^2\theta }{\partial x^2}+\frac{{\partial }^2\theta }{\partial y^2}\right)+B_r\left(\frac{{\mu }_{nf}}{{\mu }_f}\right)\left[{\left(\frac{\partial w}{\partial x}\right)}^2+{\left(\frac{\partial w}{\partial y}\right)}^2\right]=0,(17)$

Eq. 17 contains the dimensionless brinkman number $B_r$ that is the product of two dimensionless numbers Prandtl ($P_r$) and Eckert ($E_r$), i.e., $B_r=$ $P_r{E}_r.$

The dimensionless boundary conditions over the elliptic domain are

$w=-1-\frac{2\pi \varphi \alpha \beta Cos\left(2\pi z\right)}{1-2\pi \varphi \alpha \beta Cos\left(2\pi z\right)},\mathrm{f}\mathrm{o}\mathrm{r}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.(18)$

$\theta =0,\mathrm{f}\mathrm{o}\mathrm{r}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(19)$

Where $a=\frac{E\left(e\right)}{\pi }\left[\frac{1}{\delta }+\varphi Sin\left(2\pi z\right)\right],$ $b=\frac{E\left(e\right)}{\pi }\left[1+\varphi Sin\left(2\pi z\right)\right].$ Where $a$ and $b$ provide the dimensionless form of wall functions that tackle the sinusoidal movement of travelling boundaries.

Table 1 Akbar [42], provides the thermophysical properties of base fluid water and nanofluid. Table 2 Akbar [27], shows the mathematical properties of nanofluid.

TABLE 1

TABLE 1. Thermophysical properties of nanofluid.

TABLE 2

TABLE 2. Mathematical expressions for nanofluid thermophysical properties.

Exact Solution

The dimensionless form of momentum equation is a non-homogeneous partial differential Eq. 16 subject to non-homogeneous boundary conditions (18). In order to solve this PDE, a polynomial solution method to solve PDE’s over elliptic domain is taken into account. Consider the solution in a six constants polynomial form for velocity profile as narrated below

$w(x,y)=C_1{x}^4+C_2{y}^4+C_3{x}^2{y}^2+C_4{x}^2+C_5{y}^2+C_6,(20)$

Substituting Eq. 20 into Eq. 16 and equating the coefficients of $x^2, y^2, x^0, y^0$ on both sides of equation, we get

$12C_1+2C_3=0,(\mathrm{i})$

$2C_3+12C_2=0,(\mathrm{ii})$

$2C_4+2C_5=\frac{\raisebox{1ex}{$dp$}\!\left/ \!\raisebox{-1ex}{$dz$}\right.}{\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.},(\mathrm{iii})$

Now using Eq. 20 in boundary condition (18) and equating the coefficients of $x^4, x^2, x^0$, we have following equations

$C_1{a}^4+C_2{b}^4-C_3{a}^2{b}^2=0,(\mathrm{iv})$

$-2C_2{b}^4+C_3{a}^2{b}^2+C_4{a}^2-C_5{b}^2=0,(\mathrm{v})$

$C_2{b}^4+C_5{b}^2+C_6=-1-\frac{2\pi \varphi \alpha \beta Cos\left(2\pi z\right)}{1-2\pi \varphi \alpha \beta Cos\left(2\pi z\right)},(\mathrm{vi})$

The simultaneous solution of above equations gives the following values of constants

$C_1=0, C_2=0, C_3=0, C_4=\frac{b^2\frac{dp}{dz}}{2(a^2+b^2)\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)}, C_5=\frac{a^2\frac{dp}{dz}}{2(a^2+b^2)\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)},C_6=-\frac{-a^2{b}^2\frac{dp}{dz}-2a^2\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)-2b^2\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)+2a^2{b}^2\frac{dp}{dz}\pi \alpha \beta \varphi Cos\left(2\pi z\right)}{2(a^2+b^2)\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)(-1+2\pi \varphi \alpha \beta Cos\left(2\pi z\right))},$

The values of these constants is inserted in Eq. 20 and exact mathematical solution is obtained for velocity as follows

$w\left(x,y\right)=\frac{\left(\raisebox{1ex}{$dp$}\!\left/ \!\raisebox{-1ex}{$dz$}\right.\right)a^2{b}^2\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\right)}{2(a^2+b^2)\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)}+\frac{1}{-1+2\pi \varphi \alpha \beta Cos\left(2\pi z\right)},(21)$

The non-dimensional mathematical expression for flow rate $q\left(z\right)$ is availed by integrating Eq. 21 over the elliptic domain.

$q\left(z\right)=-\frac{a^3{b}^3\frac{dp}{dz}\pi }{4(a^2+b^2)\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)}+\frac{ab\pi }{-1+2\pi \varphi \alpha \beta Cos\left(2\pi z\right)},(22)$

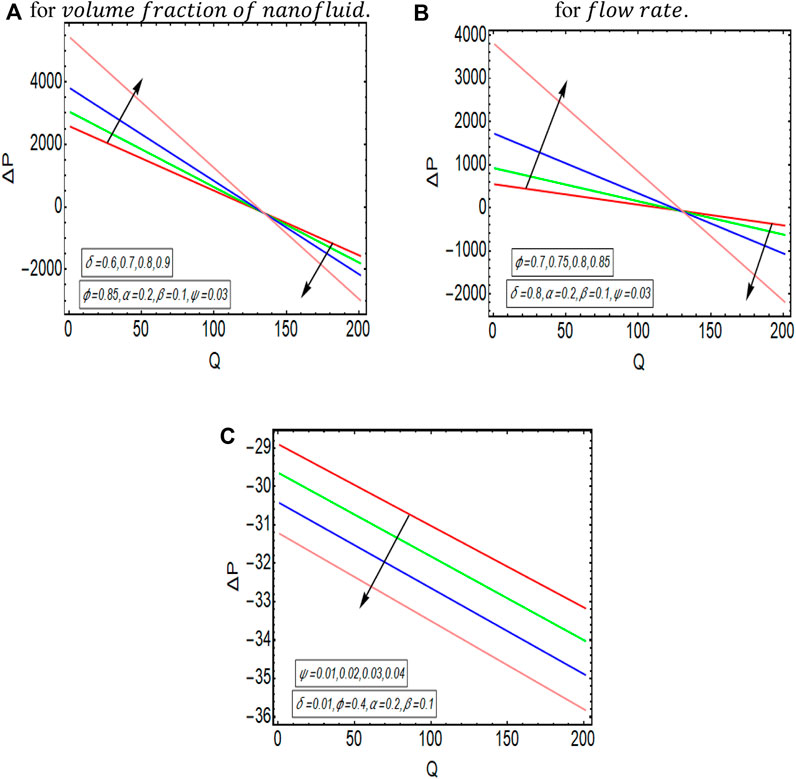
The pressure gradient is calculated by using Eq. 22 and given as

$\frac{dp}{dz}=\frac{4(a^2+b^2)\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)\left[\frac{{{\displaystyle \int }}_0^{1}abdz-Q}{\pi }+\frac{ab}{-1+2\pi \varphi \alpha \beta Cos\left(2\pi z\right)}\right]}{a^3{b}^3},(23)$

The pressure rise for a single wave-length is computed by using

$\mathrm{\Delta }P=\underset{0}{\overset{1}{{\displaystyle \int }}}\frac{\partial p}{\partial z}dz,(24)$

The technique that was utilized to get an exact velocity solution is employed again to get an exact temperature function given as

$\theta \left(x,y\right)=\frac{-B_r{\left(\frac{dp}{dz}\right)}^2{a}^2{b}^2\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\right)\left[b^6{x}^2+a^2{b}^4\left(b^2+6x^2-y^2\right)+a^6\left(b^2+y^2\right)+a^4{b}^2(4b^2-x^2+6y^2)\right]}{12{\left(a^2+b^2\right)}^2(a^4+6a^2{b}^2+b^4)\left(\frac{k_{nf}}{k_f}\right)\left(\frac{{\mu }_{nf}}{{\mu }_f}\right)}(25)$

Analysis of Results

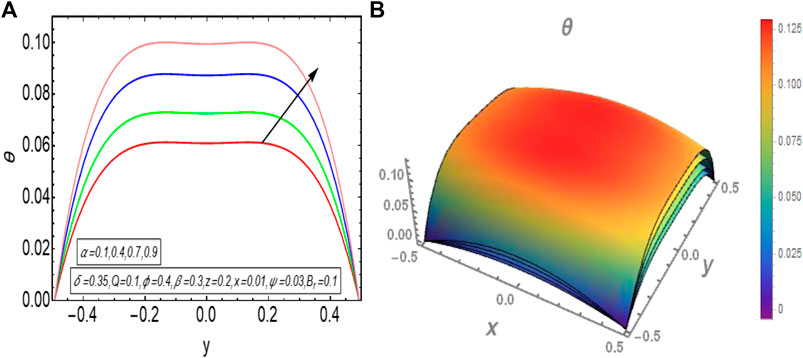
The results obtained in the exact solution section, that is exact solution of momentum equation given by Eq. 21 exactly satisfies the corresponding momentum Eq. 16 and boundary condition (18). Further, the exact solution of temperature profile given by Eq. 25 also satisfies the corresponding energy Eq. 17 with boundary condition (19). The validation of these solutions is also confirmed by using Mathematica software. According to the modelled problem and relevant boundary conditions, the flow profile in addition to the temperature profile should have a maximum value in the centre of elliptic domain and both the profiles should decline towards the walls of channel. Thus, it is evident from the graphical results that flow and temperature are maximum in the centre and reduces towards the boundaries. The temperature graphs show that temperature profile declines toward the boundaries and becomes zero as it was considered in the boundary condition (19). If $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is inserted in Eq. 21 then the reduced form gives the boundary condition (18). Further, if $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is inserted in Eq. 25 then the reduced form provides the boundary condition (19). This also validates the considered boundary conditions.

Discussion of Results

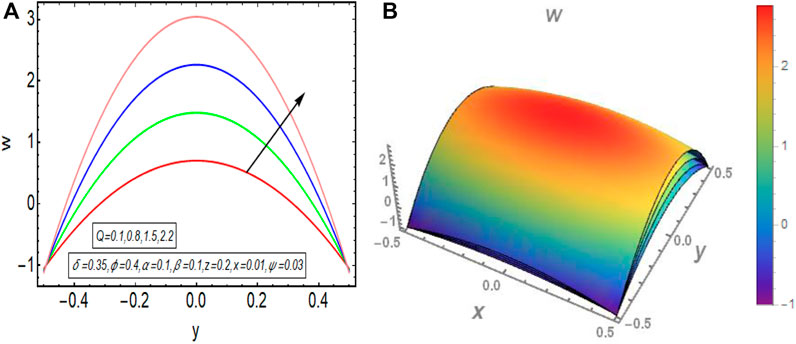
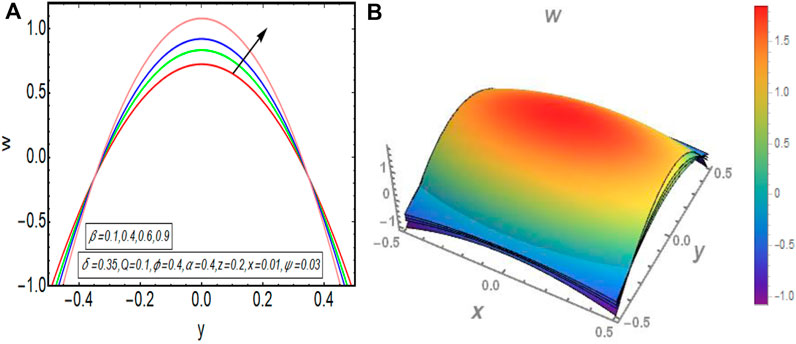
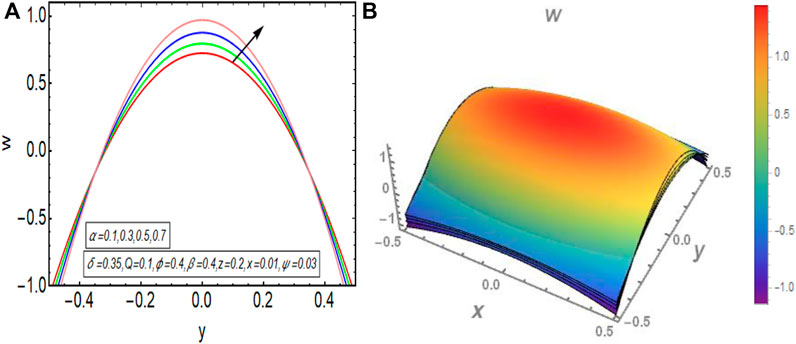
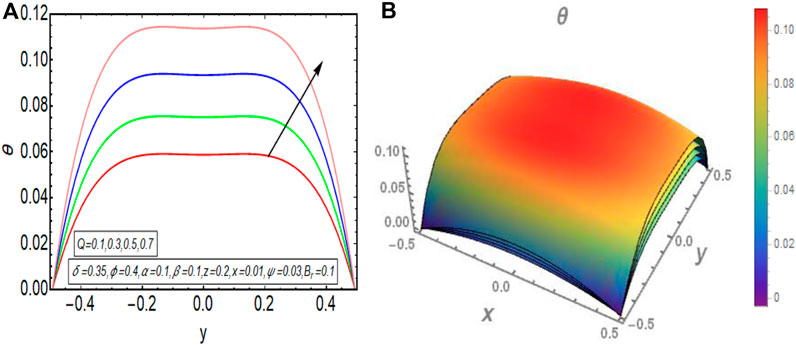
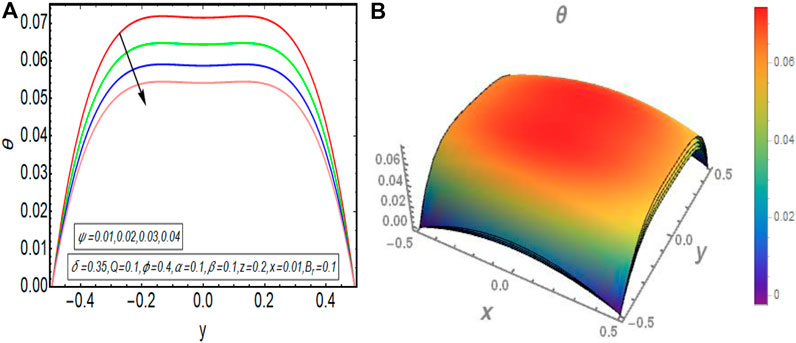
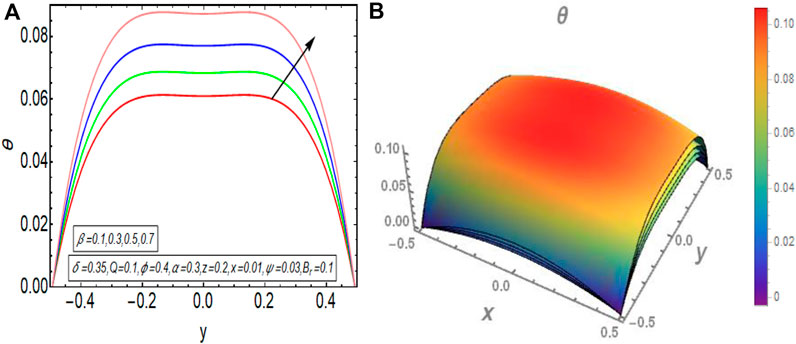
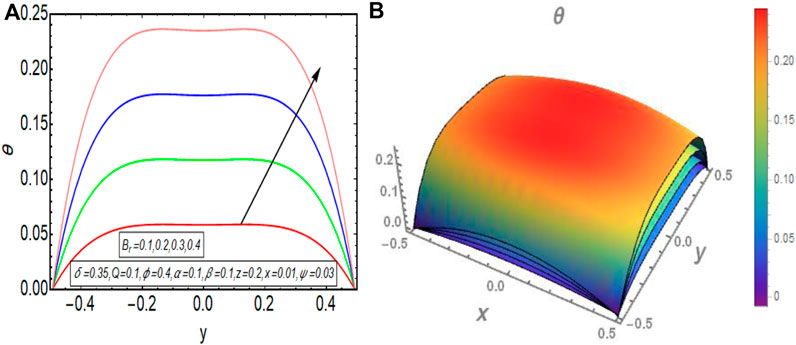
The graphical results that are incorporated in this section provide a comprehensive evaluation of the mathematical computations given in the exact solution segment. A thorough graphical evaluation is considered for velocity, temperature and various physical characteristics of peristalsis. Figures 3–5 unfold the effect of some important physical parameters on the velocity profile. Figure 3 (i.e., Figures 3A,B) provides the graphical outcome of velocity profile for increasing flow rate $Q$. Figure 3A reveals that velocity depicts an increasing behaviour for the escalating numerical values of parameter $Q$. Figure 3B shows the dependence of velocity on both the independent variables $x$ and $y$ and it is 3D-graphical plot of velocity for the escalating flow rate. An axial symmetry flow profile is noted here in this graph and maximum flow velocity is observed in the centre while it is diminishing towards duct walls. Figure 4 (i.e., Figures 4A,B) depicts the graphical result of velocity for the distinct escalating numerical values of wave number. Figure 4A unfolds that velocity shows an escalating behaviour for the distinct increasing numerical values of $\beta$ in the centre of elliptic duct while a converse behaviour is observed near walls. Figure 4B gives a 3D-graphical plot of velocity for distinct escalating values of $\beta$. Figure 5 (i.e., Figures 5A,B) gives the graphical assessment of velocity for the escalating numerical values of $\alpha$. Figure 5A discloses that velocity increases with the escalating numerical values of $\alpha$ in the centre of duct while a converse behaviour near the walls is noted also for escalating numerical values of $\alpha$. This converse behaviour of velocity at the ciliated walls is due to increasing eccentricity of elliptical motion of cilia movement. Figure 5B discloses the 3D-graphical result of velocity for distinct escalating values of $\alpha$. All these graphical outcomes of velocity reveal an axially symmetry flow that is a fully developed flow and velocity is diminishing towards walls of duct. Figures 6–10 unfold the graphical outcomes of temperature profile for distinct parameters of physical importance. Figure 6 (i.e., Figures 6A,B) reveals the graphical assessment of temperature for distinct escalating numerical values of $Q$. Figure 6A unfolds that the temperature depicts an escalating behaviour for distinct incrementing numerical values of $Q$. Figure 6B depicts the 3D-graphical plot of temperature for different escalating numerical values of $Q$. An axially symmetric behaviour is observed for temperature profile. Figure 7 (i.e., Figures 7A,B) reveals the graphical result of temperature profile for various escalating numerical values of $\psi$. The parameter $\psi$ is representing the concentration of carbon nanotubes in the base fluid. Figure 7A depicts a diminishing temperature profile with escalating concentration of carbon nanotubes in the base fluid (i.e., water). Since the increasing concentration of carbon nanotubes in the base fluid escalates the thermal conductivity of fluid and this eventually results in decline of temperature of base fluid. Further, it also verifies the inverse relation between the thermal conductivity of fluid and the temperature of fluid. Figure 7B is the 3D-graphical plot of temperature profile for escalating numerical values of $\psi$. Figure 8 (i.e., Figures 8A,B) is plotted to represent the effect of $\beta$ on temperature. Figure 8A discloses that the increment in the numerical value of wave number results in the escalation of temperature. Figure 8B is the 3D-graphical plot of temperature for distinct escalating numerical values of $\beta$. Figure 9 (i.e., Figures 9A,9B) is the graphical assessment of temperature profile for distinct escalating numerical values of $B_r$ Figure 9A unfolds that the temperature escalates rapidly with even a small increase in the numerical value of $B_r$ It reveals that the viscous effects are playing a vital role in the heat enhancement as compared to the molecular conduction. Figure 9B unfolds the 3D-graphical plot of temperature profile for escalating numerical values of $B_r$ This graph beautifully shows the dependence of temperature profile on the independent variables $x$ and $y$. Figure 10 (i.e., Figures 10A,B) is the graphical representation of temperature for escalating numerical values of $\alpha$. Figure 10A discloses an escalation in the temperature profile for distinct incrementing numerical values of $\alpha$. Figure 10B provides a 3D-graphical plot of temperature for enhancing numerical values of $\alpha$. All these temperature graphs reveal an axial symmetry profile of temperature. Further, temperature gains maximum escalation in the centre of duct and drops to zero at the duct walls. Figures 11A–D provide a graphical assessment of $\frac{dp}{dz}$ for different escalating numerical values of distinct parameters. Figure 11A reveals an escalation in the value of $\frac{dp}{dz}$ for different enhancing numerical values of $\delta$. Figure 11B depicts an escalation in the value of $\frac{dp}{dz}$ in the first half length of axial coordinate while a drop in the value of $\frac{dp}{dz}$ is noted in the next half length of axial coordinate for escalating numerical values of $\varphi$. Basically, the escalation is noted here for crest of peristaltic wave while the drop is noted for the trough. This drop in the pressure gradient for the trough of peristaltic wave eventually accelerates the flow in the axial direction. Figure 11C depicts a drop in the value of $\frac{dp}{dz}$ for distinct accelerating numerical values of $\psi$. Figure 11D reveals that the value of $\frac{dp}{dz}$ diminishes for the escalating numerical values of $Q$. Figures 12A–C provide the graphical results of $\Delta P$ plotted against the dimensionless flow rate $Q$. Figure 12A unfolds an escalation in the value of $\Delta P$ in the region $\Delta P>0$ while a converse behaviour is observed for the region $\Delta P<0$ with enhancing numerical values of $\delta$. Figure 12B reveals that $\Delta P$ escalates in the region $\Delta P>0$ and drops in the region $\Delta P<0$ with enhancing numerical values of $\varphi$. Figure 12C unfolds a decline in the value of $\Delta P$ with escalating concentration of carbon nanotubes $\psi$. Figures 13A–D provide the graphical visualization of flow in the elliptic duct. These graphical results are obtained for distinct escalating numerical values of flow rate. The escalation in the trapping size can be clearly seen in these graphs for incrementing $Q$. Streamlines disclose the behaviour of flow regime inside this ciliated elliptic duct.

FIGURE 3

FIGURE 3. (A) 2D-velocity plot for $flowrate$. (B) 3D-velocity plot for $flow rate$.

FIGURE 4

FIGURE 4. (A) 2D-velocity plot for $wavenumber$. (B) 3D-velocity plot for $wavenumber$.

FIGURE 5

FIGURE 5. (A) 2D-velocity plot for $ellipticalmotioneccentricity$. (B) 3D-velocity plot for $ellipticalmotioneccentricity$.

FIGURE 6

FIGURE 6. (A) 2D-Temperature plot for $flow rate$. (B) 3D-Temperature plot for $flow rate$.

FIGURE 7

FIGURE 7. (A) 2D-Temperature plot for $volumefractionofnanofluid$. (B) 3D-Temperature plot for $volumefractionofnanofluid$.

FIGURE 8

FIGURE 8. (A) 2D-Temperature plot for $wavenumber$. (B) 3D-Temperature plot for $wavenumber$.

FIGURE 9

FIGURE 9. (A) 2D-Temperature plot for $Brinkmannumber$. (B) 3D-Temperature plot for Brinkman number.

FIGURE 10

FIGURE 10. (A) 2D-Temperature plot for $ellipticalmotioneccentricity$. (B) 3D-Temperature plot for $ellipticalmotioneccentricity$.

FIGURE 11

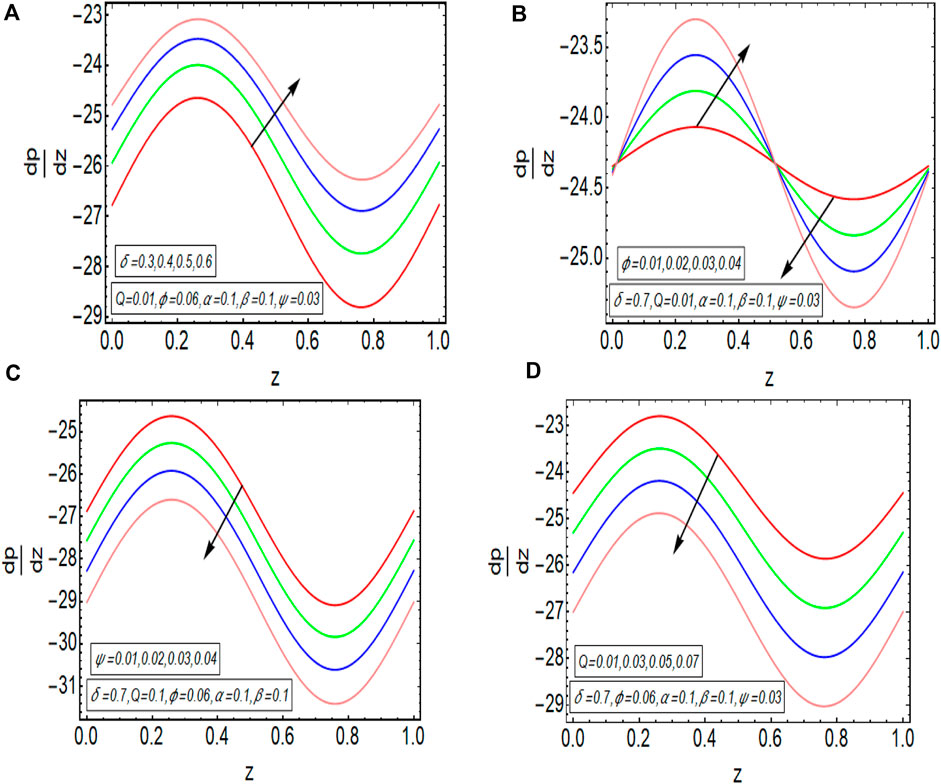
FIGURE 11. (A) $\frac{dp}{dz}$ plot against axial coordinate for $aspectratio$. (B) $\frac{dp}{dz}$ plot against axial coordinate for $occulsion$. (C) $\frac{dp}{dz}$ plot against axial coordinate for $volumefractionofnanofluid$. (D) $\frac{dp}{dz}$ plot against axial coordinate for $flow rate$.

FIGURE 12

FIGURE 12. (A) $\Delta P$ against $flow rate$ for $aspectratio$. (B) $\Delta P$ against $flow rate$ for $occulsion$. (C) $\Delta P$ against $flow rate$ for $volumefractionofnanofluid$.

FIGURE 13

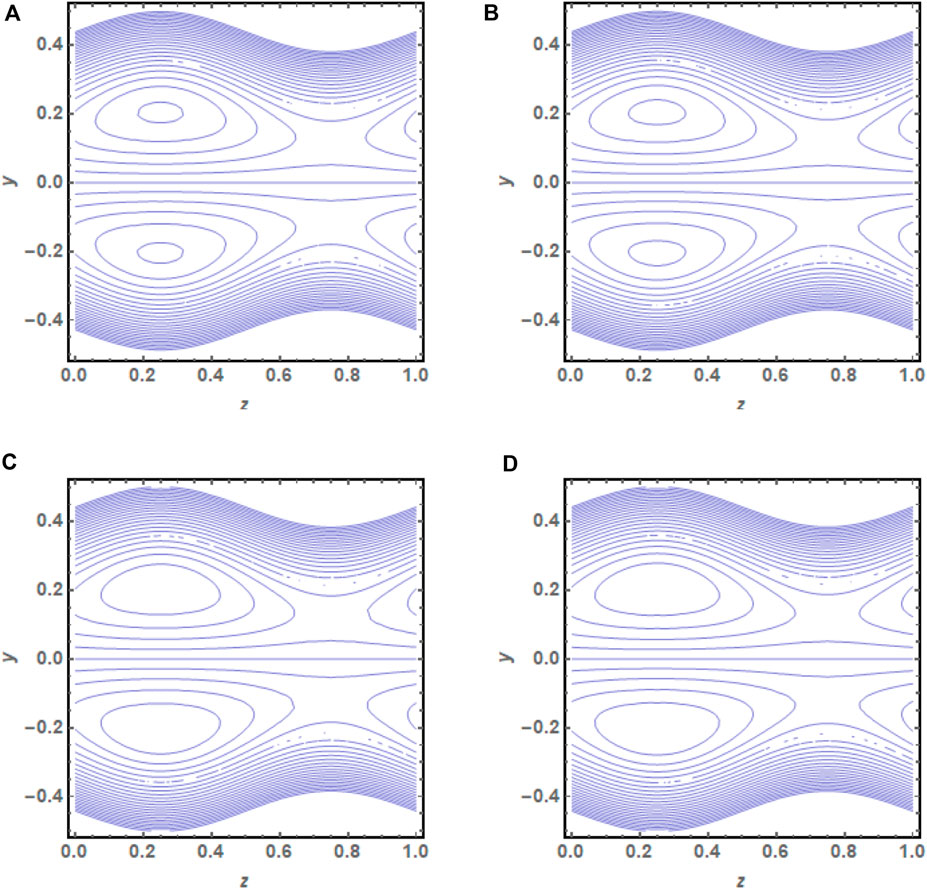
FIGURE 13. (A) Streamlines plot at flow rate $=0.01$. (B) Streamlines plot at flow rate $=0.03$. (C) Streamlines plot at flow rate $=0.05$. (D) Streamlines plot at flow rate $=0.07$.

Conclusions

The peristaltic flow of carbon nanotubes in an elliptic duct with ciliated walls is mathematically investigated. A Cartesian coordinate system approach is utilized to interpret this mathematical study. The prime outcomes are given below.

• All the graphical outcomes of velocity reveal an axially symmetry flow that is a fully developed flow and velocity is diminishing towards walls of duct.

• The increasing concentration of carbon nanotubes in the base fluid escalates the thermal conductivity of fluid and this eventually results in decline of temperature of base fluid.

• The inverse relation between the thermal conductivity of fluid and the temperature of fluid is noted.

• All the temperature graphs reveal an axial symmetry profile of temperature. Further, temperature gains maximum escalation in the centre of duct and drops to zero at the duct walls.

• The escalation in the trapping size can be clearly seen in these graphs for incrementing $Q$.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

SN and AS are group Heads and suggest the initial theme. SaA has done the mathematical and numerical part where as OM has done the drafting and proof reading.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Jaffrin MY, Shapiro AH. Peristaltic Pumping. Annu Rev Fluid Mech (1971) 3(1):13–37. doi:10.1146/annurev.fl.03.010171.000305

CrossRef Full Text | Google Scholar

2. Barton C, Raynor S. Peristaltic Flow in Tubes. Bull Math Biophys (1968) 30(4):663–80. doi:10.1007/bf02476682

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Siddiqui AM, Schwarz WH. Peristaltic Flow of a Second-Order Fluid in Tubes. J Non-Newtonian Fluid Mech (1994) 53:257–84. doi:10.1016/0377-0257(94)85052-6

CrossRef Full Text | Google Scholar

4. Nadeem S, Akbar NS. Peristaltic Flow of Sisko Fluid in a Uniform Inclined Tube. Acta Mech Sin (2010) 26(5):675–83. doi:10.1007/s10409-010-0356-1

CrossRef Full Text | Google Scholar

5. Nadeem S, Maraj EN. The Mathematical Analysis for Peristaltic Flow of Hyperbolic tangent Fluid in a Curved Channel. Commun Theor Phys (2013) 59(6):729–36. doi:10.1088/0253-6102/59/6/14

CrossRef Full Text | Google Scholar

6. Rashid M, Ansar K, Nadeem S. Effects of Induced Magnetic Field for Peristaltic Flow of Williamson Fluid in a Curved Channel. Physica A: Stat Mech its Appl (2020) 553:123979. doi:10.1016/j.physa.2019.123979

CrossRef Full Text | Google Scholar

7. Nadeem S, Akram S. Peristaltic Flow of a Jeffrey Fluid in a Rectangular Duct. Nonlinear Anal Real World Appl (2010) 11(5):4238–47. doi:10.1016/j.nonrwa.2010.05.010

CrossRef Full Text | Google Scholar

8. Ellahi R, Riaz A, Nadeem S. Three Dimensional Peristaltic Flow of Williamson Fluid in a Rectangular Duct. Indian J Phys (2013) 87(12):1275–81. doi:10.1007/s12648-013-0340-2

CrossRef Full Text | Google Scholar

9. Akram S, Saleem N. Analysis of Heating Effects and Different Wave Forms on Peristaltic Flow of Carreau Fluid in Rectangular Duct. Adv Math Phys 2020 (2020):1–14. doi:10.1155/2020/8294318

CrossRef Full Text | Google Scholar

10. Nadeem S, Akram S. Peristaltic Flow of a Williamson Fluid in an Asymmetric Channel. Commun Nonlinear Sci Numer Simul (2010) 15(7):1705–16. doi:10.1016/j.cnsns.2009.07.026

CrossRef Full Text | Google Scholar

11. Akbar NS, Raza M, Ellahi R. Interaction of Nanoparticles for the Peristaltic Flow in an Asymmetric Channel with the Induced Magnetic Field. Eur Phys J Plus (2014) 129(7):155. doi:10.1140/epjp/i2014-14155-6

CrossRef Full Text | Google Scholar

12. Sher Akbar N. Influence of Magnetic Field on Peristaltic Flow of a Casson Fluid in an Asymmetric Channel: Application in Crude Oil Refinement. J Magn Magn Mater (2015) 378:463–8. doi:10.1016/j.jmmm.2014.11.045

CrossRef Full Text | Google Scholar

13. Saleem A, Akhtar S, Nadeem S, Alharbi FM, Ghalambaz M, Issakhov A. Mathematical Computations for Peristaltic Flow of Heated Non-newtonian Fluid inside a Sinusoidal Elliptic Duct. Phys Scr (2020) 95(10):105009. doi:10.1088/1402-4896/abbaa3

CrossRef Full Text | Google Scholar

14. Animasaun IL, Shah NA, Wakif A, Mahanthesh B, Sivaraj R, Koriko OK. Ratio of Momentum Diffusivity to thermal Diffusivity: Introduction, Meta-Analysis, and Scrutinization (2022).

Google Scholar

15. Rasool G, Saeed AM, Lare AI, Abderrahmane A, Guedri K, Vaidya H, et al. Darcy-Forchheimer Flow of Water Conveying Multi-Walled Carbon Nanoparticles through a Vertical Cleveland Z-Staggered Cavity Subject to Entropy Generation. Micromachines (2022) 13(5):744. doi:10.3390/mi13050744

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Choi SU, Eastman JA. Enhancing thermal Conductivity of Fluids with Nanoparticles. IL (United States): Argonne National Lab. (1995). (No. ANL/MSD/CP-84938; CONF-951135-29).

Google Scholar

17. Akbar NS, Nadeem S. Endoscopic Effects on Peristaltic Flow of a Nanofluid. Commun Theor Phys (2011) 56(4):761–8. doi:10.1088/0253-6102/56/4/28

CrossRef Full Text | Google Scholar

18. Akbar NS, Butt AW. Ferromagnetic Effects for Peristaltic Flow of Cu-Water Nanofluid for Different Shapes of Nanosize Particles. Appl Nanosci (2016) 6(3):379–85. doi:10.1007/s13204-015-0430-x

CrossRef Full Text | Google Scholar

19. Akbar NS. Peristaltic Sisko Nano Fluid in an Asymmetric Channel. Appl Nanosci (2014) 4(6):663–73. doi:10.1007/s13204-013-0205-1

CrossRef Full Text | Google Scholar

20. Nadeem S, Riaz A, Ellahi R, Akbar NS. Effects of Heat and Mass Transfer on Peristaltic Flow of a Nanofluid between Eccentric Cylinders. Appl Nanosci (2014) 4(4):393–404. doi:10.1007/s13204-013-0225-x

CrossRef Full Text | Google Scholar

21. Nadeem S, Riaz A, Ellahi R, Akbar NS. Mathematical Model for the Peristaltic Flow of Jeffrey Fluid with Nanoparticles Phenomenon through a Rectangular Duct. Appl Nanosci (2014) 4(5):613–24. doi:10.1007/s13204-013-0238-5

CrossRef Full Text | Google Scholar

22. Akbar NS, Raza M, Ellahi R. Impulsion of Induced Magnetic Field for Brownian Motion of Nanoparticles in Peristalsis. Appl Nanosci (2016) 6(3):359–70. doi:10.1007/s13204-015-0447-1

CrossRef Full Text | Google Scholar

23. Butt AW, Akbar NS, Mir NA. Heat Transfer Analysis of Peristaltic Flow of a Phan-Thien-Tanner Fluid Model Due to Metachronal Wave of Cilia. Biomech Model Mechanobiol (2020) 19:1925–33. doi:10.1007/s10237-020-01317-4

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Saleem A, Akhtar S, Alharbi FM, Nadeem S, Ghalambaz M, Issakhov A. Physical Aspects of Peristaltic Flow of Hybrid Nano Fluid inside a Curved Tube Having Ciliated wall. Results Phys (2020) 19:103431. doi:10.1016/j.rinp.2020.103431

CrossRef Full Text | Google Scholar

25. Akbar NS, Khan ZH. Influence of Magnetic Field for Metachoronical Beating of Cilia for Nanofluid with Newtonian Heating. J Magn Magn Mater (2015) 381:235–42. doi:10.1016/j.jmmm.2014.12.086

CrossRef Full Text | Google Scholar

26. Sadaf H, Nadeem S. Influences of Slip and Cu-Blood Nanofluid in a Physiological Study of Cilia. Comp Methods Programs Biomed (2016) 131:169–80. doi:10.1016/j.cmpb.2016.04.008

CrossRef Full Text | Google Scholar

27. Sher Akbar N. Biomathematical Analysis of Carbon Nanotubes Due to Ciliary Motion. Int J Biomath (2015) 08(02):1550023. doi:10.1142/s1793524515500230

CrossRef Full Text | Google Scholar

28. Akbar NS, Butt AW. Entropy Generation Analysis for Metachronal Beating of Ciliated Cu-Water Nanofluid with Magnetic Field. Int. J. Exergy (2016) 19(1):41–54. doi:10.1504/ijex.2016.074266

CrossRef Full Text | Google Scholar

29. Nadeem S, Sadaf H. Trapping Study of Nanofluids in an Annulus with Cilia. AIP Adv (2015) 5(12):127204. doi:10.1063/1.4937474

CrossRef Full Text | Google Scholar

30. Vaidya H, Choudhari R, Mebarek-Oudina F, Animasaun IL, Prasad KV, Makinde OD. Combined Effects of Homogeneous and Heterogeneous Reactions on Peristalsis of Ree-Eyring Liquid: Application in Hemodynamic Flow. Heat Trans (2021) 50(3):2592–609. doi:10.1002/htj.21995

CrossRef Full Text | Google Scholar

31. Vaidya H, Rajashekhar C, Divya BB, Manjunatha G, Prasad KV, Animasaun IL. Influence of Transport Properties on the Peristaltic MHD Jeffrey Fluid Flow through a Porous Asymmetric Tapered Channel. Results Phys (2020) 18:103295. doi:10.1016/j.rinp.2020.103295

CrossRef Full Text | Google Scholar

32. Ashraf MU, Qasim M, Wakif A, Afridi MI, Animasaun IL. A Generalized Differential Quadrature Algorithm for Simulating Magnetohydrodynamic Peristaltic Flow of Blood-Based Nanofluid Containing Magnetite Nanoparticles: a Physiological Application. Numer Methods Partial Diff Equations (2020) 38(3): 666–692. doi:10.1002/num.22676

CrossRef Full Text | Google Scholar

33. Oke AS. Heat and Mass Transfer in 3d mhd Flow of eg-Based Ternary Hybrid Nanofluid Over a Rotating Surface. Arabian J Sci Eng 2022 (2022) 1–17. doi:10.1007/s13369-022-06838-x

CrossRef Full Text | Google Scholar

34. Kinyanjui Kigio J, Winifred Nduku M, Abayomi Samuel O. Analysis of Volume Fraction and Convective Heat Transfer on MHD Casson Nanofluid over a Vertical Plate. Fluid Mech (2021) 7(1):1. doi:10.11648/j.fm.20210701.11

CrossRef Full Text | Google Scholar

35. Oke AS, Animasaun IL, Mutuku WN, Kimathi M, Shah NA, Saleem S. Significance of Coriolis Force, Volume Fraction, and Heat Source/sink on the Dynamics of Water Conveying 47 Nm Alumina Nanoparticles over a Uniform Surface. Chin J Phys (2021) 71:716–27. doi:10.1016/j.cjph.2021.02.005

CrossRef Full Text | Google Scholar

36. Saleem N, Munawar S, Tripathi D. Entropy Analysis in Ciliary Transport of Radiated Hybrid Nanofluid in Presence of Electromagnetohydrodynamics and Activation Energy. Case Stud Therm Eng (2021) 28:101665. doi:10.1016/j.csite.2021.101665

CrossRef Full Text | Google Scholar

37. Ramesh K, Tripathi D, Anwar Bég O. Cilia-Assisted Hydromagnetic Pumping of Biorheological Couple Stress Fluids. Propul Power Res (2019) 8(3):221–33. doi:10.1016/j.jppr.2018.06.002

CrossRef Full Text | Google Scholar

38. Farooq AA, Tripathi D, Elnaqeeb T. On the Propulsion of Micropolar Fluid inside a Channel Due to Ciliary Induced Metachronal Wave. Appl Math Comput (2019) 347:225–35. doi:10.1016/j.amc.2018.10.021

CrossRef Full Text | Google Scholar

39. Akbar NS, Tripathi D, Khan ZH, Bég OA. Mathematical Modelling of Pressure-Driven Micropolar Biological Flow Due to Metachronal Wave Propulsion of Beating Cilia. Math Biosci (2018) 301:121–8. doi:10.1016/j.mbs.2018.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Sadaf H, Nadeem S. Fluid Flow Analysis of Cilia Beating in a Curved Channel in the Presence of Magnetic Field and Heat Transfer. Can J Phys (2020) 98(2):191–7. doi:10.1139/cjp-2018-0715

CrossRef Full Text | Google Scholar

41. Yang ZH, Chu YM, Zhang W. Monotonicity of the Ratio for the Complete Elliptic Integral and Stolarsky Mean. J Inequalities Appl (2016) 2016(1):1–10. doi:10.1186/s13660-016-1113-1

CrossRef Full Text | Google Scholar

42. Akbar N. Entropy Generation Analysis for a CNT Suspension Nanofluid in Plumb Ducts with Peristalsis. Entropy (2015) 17(3):1411–24. doi:10.3390/e17031411

CrossRef Full Text | Google Scholar

Nomenclature

$(\overline{U},\overline{V},\overline{W})$ Velocity components

$d$ Wave amplitude

${\overline{T}}_w$ Duct’s wall temperature

$D_h$ Hydraulic diameter of ellipse

$C_p$ Heat capacity

$\mu$ viscosity

$\varphi$ Occlusion (amplitude to radius ratio)

$e$ Eccentricity of ellipse

$\alpha$ Eccentricity of elliptical motion of cilia

$B_r$ Brinkman number

$\psi$ Volume fraction of MWCNT $(3\%)$

$nf$ Nanofluid

$(\overline{X, }\overline{Y},\overline{Z})$ Cartesian coordinate system

$a_0,b_0$ Ellipse half axes $(b_0<a_0)$

$\lambda$ wavelength

$c$ Velocity of propagation

${\overline{T}}_b$ Bulk temperature

$k$ Thermal conductivity

$\rho$ Density

$\delta$ Aspect ratio

$\beta$ Wave number for metachronal wave

$t$ time

MWCNT Multi wall carbon nanotubes

$p$ pressure