Dynamics of Non-Newtonian Tangent Hyperbolic Liquids Conveying Tiny Particles on Objects with Variable Thickness when Lorentz Force and Thermal Radiation are Significant

The flow via needle has prominent applications in the modern world such as nano-wires, microstructure electric gadgets, microsensors, surgical instruments and biological treatments. The present investigation focuses on boundary layer heat, flow, and mass transfer of MHD tangent hyperbolic fluid (conveying tiny particles) via a thin needle under the impacts of activation energy, non-constant thermal conductivity, heat source, and nonlinear thermal radiation. In the description of the Buongiorno model, the significant features of Brownian motion and thermophoresis have been included. Adopting appropriate transformations to the given problem specified by the set of partial differential equations yields the dimensionless form of ordinary differential equations After that, these obtained ODEs are solved numerically via MATLAB bvp4c. A comparative result with previous findings is conducted. Physical parameters’ impact on flow rate, heat, and concentration is exhibited and explained in depth. The main findings of this study are that flow patterns reduce as the magnetic parameter and the Weissenberg number grow. Higher values of Brownian motion, heat source/sink, nonlinear radiation, and thermophoretic parameter improve the thermal profile. Moreover, the rate of heat transfer for the variable property case is significantly improved. Concentration profiles reduce as the thermophoresis parameter and chemical reaction parameter grow but improve as the activation energy and Brownian motion parameter rise. The percentage increase in Sherwood number is 35.07 and 5.44 when the thermophoresis takes input in the range 0 ≤ Nt ≤ 0.2 and activation energy parameters 0 ≤ E ≤ 0.2. The Weissenberg number and power-law index parameters are all designed to boost the Sherwood number.

1 Introduction

Symmetrical boundary layer stream and heat transmission around an axis is crucial in industry. The slandering surface created by spinning a parabola around its axis is known as thin needle geometry. In such geometries, physical events occur in the vicinity of the slandering cylindrical tube with non-uniform stiffness. Such specific geometry was chosen because of its practical importance in a range of fields, such as blood flow problems, metal spinning, and cancer treatment. Many scientists and researchers have examined the heat transfer and flow via a moving thin needle. Numerous flow circumstances have been analyzed in this framework. Polymers, metals, hot wire for heat removal, boats, ceramics, microscale cooling devices, lubrication, and anemometers are just a few of the applications for heat transmission. The boundary layer flow for Newtonian fluid over a thin needle was first introduced by [1]. Later on, the dual solution on a thin needle was achieved by [2]. As a result, various academics and experts discussed heat transmission in their fields of study. [3] presented the scientific solution of the Casson nanofluid between two stretched discs, as well as the effect of entropy formation. The problem of a non-Newtonian nanofluid with thermophoresis and Brownian motion impacts was modelled by [4]. [5] employed an analytical approach to examine forced convective heat transfer in non-uniform incompressible flows over a nonisothermal thin needle. [6] explored the flow of BL nanofluid down a vertical thin needle. [7] demonstrated the effect of double diffusion and nonlinear heat radiation on Casson nanofluid flow over thin needle. The impact of Ohmic heating, viscid dissipation, and changing buoyancy force on nanofluids flow over a thin needle was then investigated by [8]. With thermal radiation and internal nanoparticle diffusion, [9] studied the influence of homogeneous–heterogeneous reactions on the thin needle. The fundamental studies on boundary layer flow of fluids via thin needle were provided by [10]. Other significant studies on the thin needle may be found in [11–20].

Nanofluids have piqued researchers’ interest because they can provide considerable heat transfer with little or no pressure decrease. Nanofluids consist of nanoparticles suspended in a base fluid. Nanofluids are made up of minuscule quantities of nano-meter-sized particles that are consistently and securely suspended in a fluid, and they have a crucial role in enhancing heat transfer. Nanofluid research can help improve the thermal conductivity of metals like copper, silver, and gold. In the pioneering work of [21], who has conducted numerous experiments in this sector, many analysts have worked on nanofluids. [22] concluded that nano-fluid has heat elimination and convective properties. [23] described the heat transmission properties of nano-liquids in microchannels. [24] demonstrated how nanofluid behaves when it flows over a porous stretched sheet. In this situation, a partial slip was also taken. Under a homogenous magnetic field, [25] deliberated on the dynamics of a hybrid nanofluid through a wavy cavity. Sequel to the prospect and usefulness of nanofluids, [26] explained the rising effects of Brownian motion and thermo-migration on the dynamics of water conveying three different shapes of nanoparticles. In the same approach, we recommend that you expatiate on [27–33].

Because of its vast range of uses and importance, chemical reaction research has exploded in the engineering and industrial zone. These applications contain for example fog generation, glass manufacturing, circulation, chemical, biological processing, and food preparation. A chemical reaction occurs in the flow system when there is external mass in the fluid that could be homogenous or diverse. When a single phase of the material, such as solid, liquid, or gas, is present, the former happens consistently, but the latter happens when two or more phases, for example solid, liquid and gas are present. [34] used permeable media for nanoparticles to explore the impression of chemical reactions on MHD flow. Mass and heat transmission, with the coefficient of skin friction all intensification, when the volume percentage of nanoparticles and magnetic field increases, according to this research. The irreversibility of nanofluid radiative flow through a moving thin needle was examined by [35]. It was discovered that shrinking the needle’s size reduces entropy while enhancing the heat radiation effect. [36] investigate the MHD, Hall current, and the radiative flow of nanofluid induced over a thin needle under the porous media. Some important investigations about chemical reactions are [37–39].

Numerous studies have analysed flow and temperature analyses in a moving thin needle with a variety of flow challenges due to the necessity of many applications such as Microstructure electronic devices, hot cable anemometers, medication, thermal deduction chilling devices and Electronic machinery in micro configuration. [40] used thermal radiation and chemical reaction on MHD Casson fluid flow on a vertically positioned thin needle. In this study, it was discovered that when the needle thickness increased, the heat transmission rate of nanofluid increased as well. For a persistent moving needle, [41] numerically examined the BL mixed convection flow in the MHD ferrofluid. To solve the modelled problem, the authors employed the Runge-Kutta method and discovered that increasing the needle size lowered the flow and heat profiles. In a similar and contradicting scenario, [42] scrutinized the flow of mixed convection over the thin needle. [43] evaluated the chemical reaction, heat source, and nanofluid flow across a slender needle.

Because of its industrial and engineering applications, non-Newtonian liquids are of tremendous interest. A single constitutive relationship cannot sufficiently capture the attributes of such fluids. Toothpaste, shaving creams, soup, china clay, blood, and mayonnaise are instances of non-Newtonian liquids with a low shear rate. Scholars have explored several models of non-Newtonian liquids in terms of their potential applications. The Tangent hyperbolic liquid model is the most essential because it can predict shear thinning with high accuracy. This model has been proposed by researchers and experts for use in industrial and laboratory sectors. Tangent hyperbolic fluid includes ketchup, whipped cream, blood, and melting cheese. Tangent hyperbolic fluid is a rate-type non-Newtonian fluid that applies to both strong and weak shear forces. The rate will take precedence over the shear stress in shear thinning, and vice versa in shear thickening. The Tangent hyperbolic fluid model, on the other hand, has an advantage over its contemporaneous equivalents because of its unique qualities of physical robustness, computational ease, and simplicity. To use the homotopy analysis method (HAM), [44] established an analytical expression for Tangent hyperbolic bio-convective nanomaterial flow containing motile microorganisms. Under mixed convection conditions, [45] explored the boundary layer flow of nanofluids across a microscopic thin needle. The velocity profile appears to be lowered in the presence of large magnetic forces. For increasing thermophoresis parameter, the opposite trend of temperature and concentration gradients is worth noticing. MHD Tangent hyperbolic nanomaterial flow with varying thickness was considered by [46]. According to the findings of this study, velocity falls as the Weissenberg number and magnetic parameter are increased. A tangent hyperbolic nanomaterial model is used to characterise the primary sliding mechanisms, Brownian and thermophoresis diffusions. [47] used a stretchy surface to represent the behaviour of a two-phase nanofluid model in the occurrence of chemical reaction impacts. [48] premeditated the thermal flow rate of nanofluid flowing on a thin needle. In this analysis, the modelled problem was handled by the bvp4c technique. In addition, increasing the number of nanoparticles and reducing the needle size enhanced skin friction along the needle’s surface, according to this study. [49] employed thermal dissipation to produce entropy for nanofluid flow on a thin needle. [50] demonstrated the heat and mass transfer via natural convection in a tiny needle. They discovered that the temperature scatterings were amplified by radiation conflicts. [51] came up with the numerical results. [52] scrutinized the flow of nanofluids through a thin needle that was constantly moving. Currently, [53] are investigating the effects of heat transmission on free convection down a vertical thin needle. Heat transfer has the same impact on thin needle and plate. Moreover, when the thin needle stops resisting the free stream, then get the dual solution. The current conclusion is insufficient to provide additional information on viscous dissipation, nonlinear radiation, and BL flow in a thin needle condition. As a result, we must focus more on the thin needle phenomena. The slandering thin needle’s boundary layer flow and radius are the same nevertheless, the slandering needle moves in a parabolic motion. Free, mixed, and forced convective boundary layers are the difficulties, and many academics have studied these ideas and offered some useful results [54–57].

When compared to variations in other transport parameters, the variation in thermal conductivity with temperature is quite significant. Thermal conductivity is well known to be extremely temperature-sensitive. Temperature-dependent thermal efficiency can be described as a linear function of temperature in a variety of scientific and technical activities. When there is a considerable temperature difference, the temperature-dependent thermal conductivity becomes significant, resulting in more/less energy transmission. Their nonlinear temperature dependence can take many different shapes, such as linear, constant, nonlinear, power law, and so on. [58] employed a computational method to investigate the upshot of radiation, variable thermal conductivity and MHD on the Williamson nanofluid across a stretching cylinder. Through horizontal plates, [59] attempted to inspect the non-constant thermal conductivity of the non-Newtonian slate-type fluid. [60] evaluated the impact of variable thermal conductivity in a mixed convective flow of viscous fluid over a rapidly expanded surface for heat transfer studies. Other notable studies on thin needles with non-constant thermal conductivity can be found in [61–65].

It is worthy of notice that there is little or no report on mass and heat transfer features of tangent hyperbolic fluid flow through a horizontal thin needle in the existence of activation energy. The variable thermal conductivity varies in temperature also considered. Heat sink/source and non-linear thermal radiation all have intriguing effects. The numerical solution was calculated using the Matlab tool bvp4c after it was transformed to dimensionless form. The following research questions are inspired by the motivations for doing this analysis:

1) What role does mass transfer play in viscous nanoparticles flowing horizontally in thin needles?

2) How do the thermal characteristics of nanoparticles vary when non-linear thermal radiation features are used?

3) How do different developing parameters affect heat and mass transfer rates and flow rates?

4) How do heat and mass transfer rates improve in the occurrence of heat source/sink and magnetic force implications?

5) Using the well-known Buongiorno model, the authors explored the impact of thermophoresis and Brownian motion on flow systems.

2 Formulation

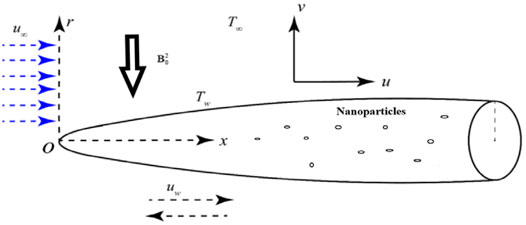
Deliberate the steady, incompressible, laminar, and 2D flow of tangent hyperbolic fluid with conveying tiny particles near the moving thin needle. As shown in Figure 1, the thin needle has a radius of $\sqrt{\frac{\chi x{\nu }_f}{U}}=r=R,$ where ${\nu }_f$ is the kinematic viscosity, $r$ is the radial coordinate, $\chi$ is the size or shape of the needle and x is the axial coordinate with a flow speed $u_w$ needle is moving horizontally. The thickness of the thin needle is less than the thickness of the temperature, concentration and momentum boundary layer. On the needle’s surface, the pressure gradient is negligible and the magnetic field strength ${\mathrm{{\rm B}}}_{\mathrm{0}}$ is applied in the radial direction. The thin needle boundary is heated (T) and concentrated (C) to the point where $T_w>T_{\infty }$ and $C_w>C_{\infty }.$ In addition, the temperature and concentration $\left(T_{\infty },C_{\infty }\right)$ of the free-stream zone are assumed to be constant. The energy equation also considers the impact of the heat sink/source, nonlinear radiation, and viscous dissipation impact. The flow is subjected to the influences of activation energy, which is chemically reactive.

FIGURE 1

FIGURE 1. Physical flow geometry.

The boundary layer equations using Buongiorno’s fluid model, such as continuity, momentum, thermal energy equations, and concentration can be represented in cylindrical coordinates using the above assumptions [4–6, 40, 66–69].

$\frac{\partial }{\partial r}\left(rv\right)+\frac{\partial }{\partial x}\left(ru\right)=0,(1)$

${\rho }_f\left(v\frac{\partial u}{\partial r}+u\frac{\partial u}{\partial x}\right)={\nu }_f\left[\left(1-m\right)\frac{{\partial }^{2}u}{\partial r^2}+\left(1-m\right)\frac{1}{r}\frac{\partial u}{\partial r}+m\sqrt{2}{\mathrm{\Gamma }}^{\ast }\frac{\partial u}{\partial r}\frac{{\partial }^{2}u}{\partial r^2}+\frac{m\mathrm{\Gamma }}{\sqrt{2}r}{\left(\frac{\partial u}{\partial r}\right)}^2\right]-{\delta }_f{B}_o^{2}u,(2)$

$\begin{array}{l}{\left(\rho Cp\right)}_f\left(v\frac{\partial T}{\partial r}+u\frac{\partial T}{\partial x}\right)=k\left(T\right)\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}\right)+{\left(\frac{\partial T}{\partial r}\right)}^2\frac{\partial k\left(T\right)}{\partial T}+\frac{{\left(\rho C_p\right)}_p}{{\left(\rho C_p\right)}_f}\left[\frac{D_T}{\mathrm{\Delta }C{T}_{\infty }}{\left(\frac{\partial T}{\partial r}\right)}^2+D_B\frac{\partial T}{\partial r}\frac{\partial C}{\partial r}\right]\\ +Q_o\left(T_w-T_{\infty }\right)-\frac{1}{r}\frac{\partial }{\partial r}\left(r{q}_r\right),\end{array}(3)$

$\left(v\frac{\partial C}{\partial r}+u\frac{\partial C}{\partial x}\right)=\frac{D_B}{r}\frac{\partial }{\partial r}\left(r\frac{\partial C}{\partial r}\right)+\frac{\mathrm{\Delta }C{D}_T}{T_{\infty }}\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial T}{\partial r}r\right)-k_r^2\left(C-C_{\infty }\right){\left(\frac{T}{T_{\infty }}\right)}^c\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-E_{\alpha }}{k_{B}T}\right),(4)$

with the suitable boundary condition offered as [20],

$\begin{array}{l}v=0,u-u_w=0,T-T_w=0,C-C_w=0,\text{at}r=R\left(x\right),\\ T\to 0,u\to u_{\infty },C\to 0,\text{at}r\to \infty .\end{array}(5)$

In Eqs. 2–4 ${\left(\rho Cp\right)}_f,$ ${\mu }_f,$ ${\rho }_f,$ $D_B,$ ${\delta }_f,$ $D_T,$ $k\left(T\right)$ and m are notations of Heat capacity, viscosity, density, effective diffusion coefficient, Electrical conductivity, Thermophoretic diffusions, variable thermal conductivity and power-law index of the nanofluid respectively. Also, it is worth noting here that the corrective coefficient $\mathrm{\Delta }C$ used in the conservation equations of nanoparticles’ concentration and energy has the dimension of molar concentration [66–68].

$k\left(T\right)=k_o\left[1+\frac{T-T_{\infty }}{T_w-T_{\infty }}{\delta }_k\right],(6)$

Now presenting the similarity transformations [20],

$\eta =\frac{U{r}^2}{{\nu }_{f}x},\psi ={\nu }_{f}xf\left(\eta \right)\mathrm{and}\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},(7)$

Where continuity equation satisfied by the stream function $\psi$ with $v=-\frac{1}{r}\frac{\partial \psi }{\partial x}\text{and}u=\frac{1}{r}\frac{\partial \psi }{\partial r}$ and remaining governing PDEs are reduced in ODEs

$\left(2-2m\right)\left(\eta f^{‴}+f^{″}\right)+f{f}^{″}-M{f}^{\prime }+5We\eta {\left(f^{″}\right)}^2+5We{\eta }^2{f}^{‴}{f}^{″}=0,(8)$

$\begin{array}{l}\left(1+{\delta }_k\theta \right)\left(2\eta {\theta }^{″}+2{\theta }^{\prime }\right)+2{\delta }_k\eta {{\theta }^{\prime }}^2+Nr\left(\eta {\theta }^{″}+\frac{{\theta }^{\prime }}{2}\right){\left(1+\left({\theta }_w-1\right)\theta \right)}^3+3\eta Nr{\left({\theta }^{\prime }\right)}^2\left({\theta }_w-1\right)\left({\left(\left({\theta }_w-1\right)\theta +1\right)}^2\right)\\ +\mathrm{Pr}H\theta +2\eta \left(Nt{{\theta }^{\prime }}^2+Nb{\theta }^{\prime }{\varphi }^{\prime }\right)=0,\end{array}(9)$

$\left(2\eta {\varphi }^{″}+2{\varphi }^{\prime }\right)+Scf{\varphi }^{\prime }+\frac{Nt}{Nb}\left(\eta {\theta }^{″}+{\theta }^{\prime }\right)+\frac{1}{2}{\mathrm{\Gamma }}^{\ast }Sc\varphi {\left(1+\delta \theta \right)}^c{e}^{\left(\raisebox{1ex}{$-E$}\!\left/ \!\raisebox{-1ex}{$1+\delta \theta $}\right.\right)}=0,(10)$

with boundary condition become,

$\begin{array}{l}{f}^{\prime }\left(\chi \right)=\frac{a}{2},f\left(\chi \right)=\frac{\chi a}{2},\theta \left(\chi \right)=1,\varphi \left(\chi \right)=1,\\ f^{\prime }\left(\infty \right)=\frac{1-a}{2},\theta \left(\infty \right)=0,\varphi \left(\infty \right)=0,\eta \to \infty .\end{array}(11)$

Furthermore, assume $\chi =\eta$ to represent the needle thickness or size also $a$ the velocity ratio parameter, the Weissenberg number $We,$ the elasticity parameter $\delta ,$ $M$ the magnetic parameter, $\mathrm{Re}$ the local Reynolds number, ${\theta }_w$ the temperature ratio parameter, $Nt$ the thermophoresis parameter, $N_r$ the thermal radiation, $H$ the heat generation parameter, $Nb$ Brownian motion parameter, $\Gamma$ chemical reaction parameter, Schmidt number $Sc,$ variable thermal conductivity parameter ${\delta }_k,$ activation energy $E,$ and the Prandtl number $\mathrm{Pr}$.

$\begin{array}{l}a=u_w/U,We=\frac{\sqrt{2}m{\mathrm{\Gamma }}^{\ast }}{r},\delta =\frac{\left(T_w-T_{\infty }\right)}{T_{\infty }},M=\frac{{\delta }_f{B}_o^2}{2{\rho }_{f}U},\mathrm{Re}=\frac{Ux}{{\nu }_f},{\theta }_w=\frac{T_w}{T_{\infty }},\\ Nt=\frac{{\left(\rho C_p\right)}_p}{{\left(\rho C_p\right)}_f}\frac{\left(T_w-T_{\infty }\right)D_T}{T_{\infty }{\nu }_f},N_r=\frac{16T_{\infty }^3{\delta }^{\ast \ast }}{k^{\ast \ast }{k}_f},H=\frac{Q_o}{2U{\left(\rho cp\right)}_f},Nb=\frac{{\left(\rho C_p\right)}_p}{{\left(\rho C_p\right)}_f}\frac{D_B\left(C_w-C_{\infty }\right)}{{\nu }_f\mathrm{\Delta }C},\\ \mathrm{\Gamma }=\frac{x{k}_r^2}{U},Sc=\frac{{\nu }_f}{D_B},{\delta }_k=\frac{\left(T_w-T_{\infty }\right)}{T_{\infty }},E=\frac{E_a}{T_{\infty }{k}_f},\mathrm{Pr}=\frac{{\alpha }_f}{k_f}\end{array}$

Physical quantities of interest by [18] for local surface drag force $\left(C{f}_x\right)$, local heat transfer rate $\left(N{u}_x\right)$ and local Sherwood number $\left(S{h}_x\right)$ are defined as

$C{f}_x=\frac{x{\tau }_w}{U^2{\rho }_f},N{u}_x=\frac{x{q}_w}{k_f\left(T_w-T_{\infty }\right)},\mathrm{and}S{h}_x=\frac{x{h}_w}{D_f\left(C_w-C_{\infty }\right)},(12)$

Where ${\tau }_w={\mu }_f{\left(\left(1-m\right)\frac{\partial u}{\partial r}+\frac{m\Gamma }{\sqrt{2}}{\left(\frac{\partial u}{\partial r}\right)}^2\right)}_{r=\chi },$ $q_w={\left(-k_f\frac{\partial T}{\partial r}-\frac{16{\delta }^{\ast \ast }{T}^3}{3k^{\ast \ast }}\frac{\partial T}{\partial r}\right)}_{r=\chi }$ an $h_w=-D_f{\left(\frac{\partial C}{\partial r}\right)}_{r=\chi }$ are known as the shear stress, heat-flux and mass flux respectively.

Utilizing Eq. 7, we get

$\begin{array}{l}{\left(\mathrm{Re}\right)}^{0.5}{C}_f=8\sqrt{\chi }\left(\left(1-m\right)+2\eta We{f}^{″}\left(\chi \right)\right)f^{″}\left(\chi \right),\\ {\left(\mathrm{Re}\right)}^{-0.5}N{u}_x=-2\sqrt{\chi }{\theta }^{\prime }\left(\chi \right)\left[1+Nr{\left(1+\theta \left(\chi \right)\left({\theta }_w-1\right)\right)}^3\right],\\ {\left(\mathrm{Re}\right)}^{-0.5}S{h}_x=-2\sqrt{\chi }{\varphi }^{\prime }\left(\chi \right).\end{array}(13)$

2.1 Solution Methodology

This subsection presents the nonlinearly generated ODEs Eqs. 8–10 and the boundary constraints Eq. 11, which is numerically solved using the bvp4c technique. Here, the step-size $\mathrm{\Delta }h=0.001$ is chosen to get the desired convergence criterion of ${10}^{-6}$ the problem. The regulatory Eqs. 8–10 are incorporated into a first-order methodology by introducing the new variable, as illustrated below, to bring out this numeric method,

$f=q_1,f^{\prime }=q_2,f^{″}=q_3,\theta =q_4,{\theta }^{\prime }=q_5,\varphi =q_6,{\varphi }^{\prime }=q_7,(14)$

$f^{‴}=\frac{-2\left(1-m\right)q_3-q_1{q}_3+M{q}_2-5We\eta {\left(q_3\right)}^2}{2\eta \left(1-m\right)+5We{\eta }^2{q}_3},(15)$

${\theta }^{″}=\frac{1}{1+{\delta }_k{q}_4+Nr\eta {\left(1+\left({\theta }_w-1\right)q_4\right)}^3}\left[\begin{array}{l}-2\left(1+{\delta }_k{q}_4\right)q_5-0.5Nr{q}_5{\left(1+\left({\theta }_w-1\right)q_4\right)}^3\\ -3Nr\left({\theta }_w-1\right){\left(q_5\right)}^2{\left(1+\left({\theta }_w-1\right)q_4\right)}^2-2{\delta }_k\eta {\left(q_5\right)}^2\\ -\mathrm{Pr}H{q}_4-2\eta \left(Nt{\left(q_5\right)}^2+Nb{q}_5{q}_7\right)\end{array}\right],(16)$

${\varphi }^{″}=\frac{-1}{2\eta }\left[2q_6+Sc{q}_1{q}_6+\frac{Nt}{Nb}\left(\eta {\theta }^{″}+q_5\right)+\frac{1}{2}{\mathrm{\Gamma }}^{\ast }Sc{q}_6{\left(1+\delta q_4\right)}^c{e}^{\left(\raisebox{1ex}{$-E$}\!\left/ \!\raisebox{-1ex}{$1+q_4\theta $}\right.\right)}\right],(17)$

with boundary conditions,

$\begin{array}{l}{q}_2\left(\chi \right)=\frac{a}{2},q_1\left(\chi \right)=\frac{\chi a}{2},q_4\left(\chi \right)=1,q_6\left(\chi \right)=1,\\ q_2\left(\infty \right)=\frac{1-a}{2},q_4\left(\infty \right)=0,q_6\left(\infty \right)=0,\eta \to \infty .\end{array}(18)$

3 Analysis and Discussion of Results

The main focus is on analyzing the heat and flow of tangent hyperbolic fluid by conveying tiny particles over a thin needle with activation energy using Buongiorno’s model. In the presence of a magnetic field, the incompressible liquid is electrically conducted.

3.1 Analysis of Results

For the analysis of results, the equations with appropriate variables govern the dimensionless form. The nonlinear ODEs are computed using the bvp4c numerical approach. The results are visually provided for associated profiles, as well as trends in Sherwood number skin friction coefficient, and Nusselt number, together with an explanation of the impression of several parameters such as $\mathrm{Pr}=9,$ $M=0.1,$ $Nr=0.3,$ $We=0.2,$ ${\theta }_w=1.2,$ $m=0.7,$ $H=0.1,$ $Nb=0.6,$ $Sc=0.5,$ $\gamma =0.7,$ $E=1.3,$ ${\delta }_k=1.5,$ $Nt=0.7,$ $\delta =0.2,$ $a=0.1,$ $\chi =0.2,$ and $c=0.7$ on a thin needle and free stream surface.

For the code validation, the present study and previous ones ([2], [5], [18], [40]) were compared see Table 1 and found to be in good agreement.

TABLE 1

TABLE 1. Comparative investigation for $f^{″}\left(\chi \right)$ when.$M=We=0.$

3.2 Discussion of Results

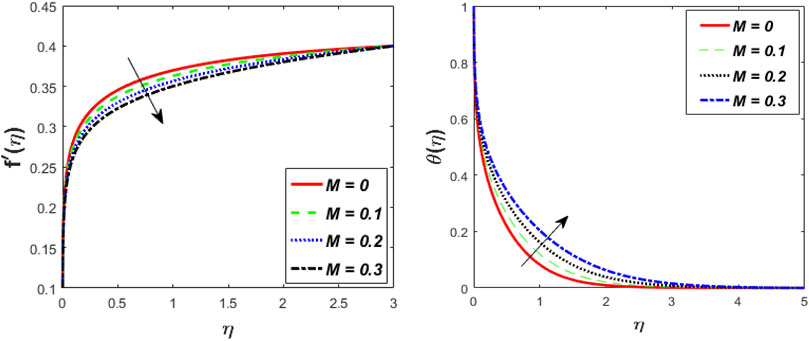
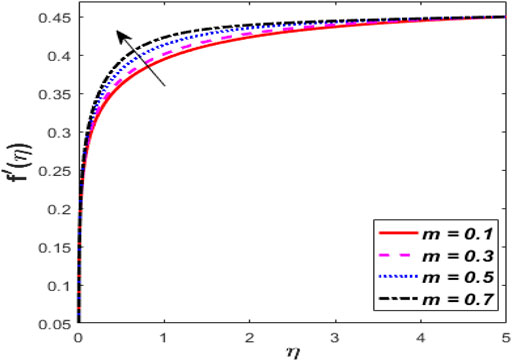
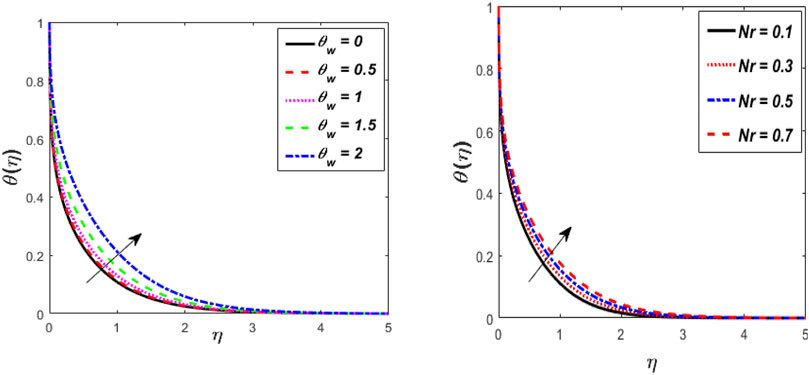
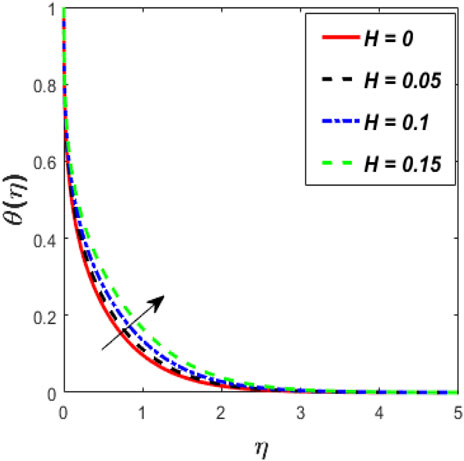
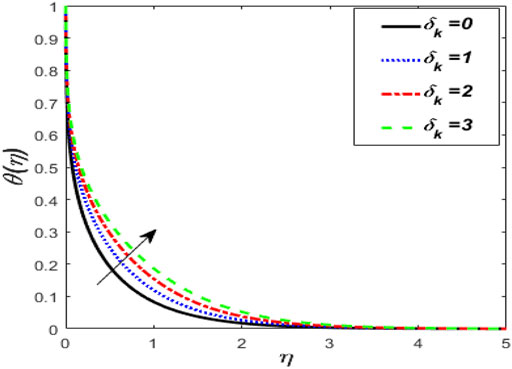
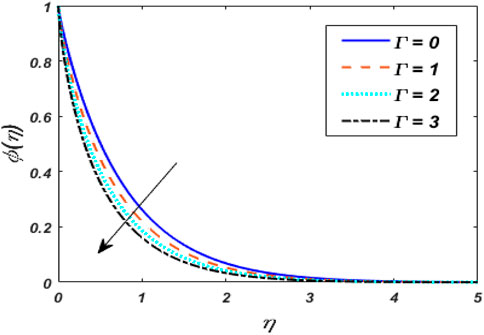
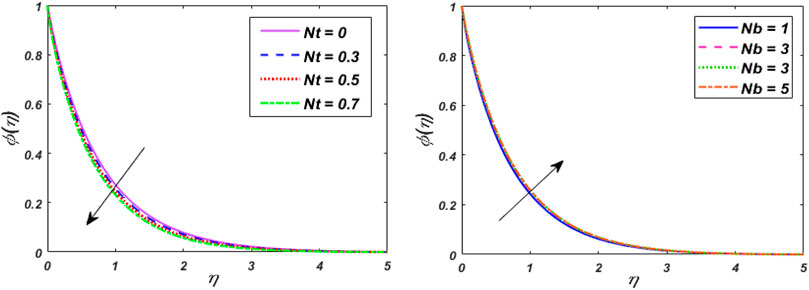
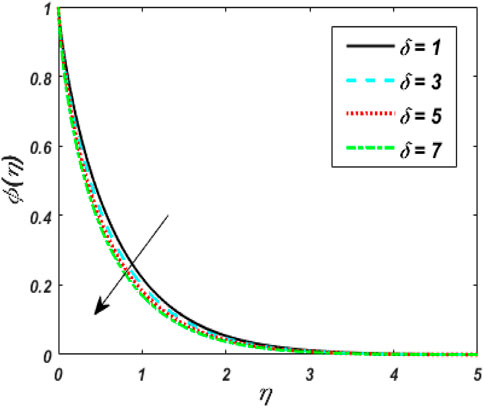
Figure 2 indicates the deviations of momentum and heat fields under strong magnetic (M) effects. It was discovered that raising the vitalities of the magnetic arena causes the momentum profile to shrink and intensifies the thermal field of tangent hyperbolic fluid with conveying tiny particles. Increasing the magnetic field does increase the Lorentz force. As a result of the flow degeneration and enhancement of the thermal field, Lorentz properties have detected it. The characteristics of the flow rate and thermal fields for shoot-up values of Weissenberg number (We) are plotted in Figure 3. The graph depicts the tangent hyperbolic fluid velocity falling while the thermal profile upsurges when We increased. The physical ratio of the liquid’s relaxation time to a certain process time is the We. It increases the fluid thickness, causing the velocity distribution to narrow. The relaxation time climbs as the value of We raises, resulting in higher flow resistance. Consequently, the temperature range and thickness of the fluid flow are improved. Figure 4 show the effect of the power-law index (m) versus the flow rate for classical and fractional order values, respectively. An increase in velocity profile is caused by bigger values of the m. Physically, increasing m increases non-linearity, which causes a friction force to rise radial velocity. Figure 5 shows the dominance of thermal radiation (Nr) and temperature ratio parameter (θ_w) on the temperature distribution. The temperature inclines for rising values of the Nr, according to the analysis. The fluid is heated as the Nr increases, and heat is transferred to the fluid. The ratio of θ_w is the temperature ratio of the ambient and wall temperature. Smaller or larger values of θ_w indicated that the wall temperature was more solid than the ambient temperature with a fixed value of variable thickness. The temperature of tangent hyperbolic fluid with conveying tiny particles increased when the value of θ_w was increased. The variation of the dimensionless temperature with the heat source/sink parameter (H) is depicted in Figure 6. With a rise in H, the temperature of the fluid escalates. The thermal boundary layer rises after the temperature distribution is improved via H. Because the heat source process produces more heat, the temperature goes up. The purpose of Figure 7 is to show how the thermal conductivity parameter $\left({\delta }_k\right)$ affects temperature. The graph shows that as ${\delta }_k$ increases, the temperature rises. As this is usually known, low thermal conductivity fluids have a low temperature while high thermal conductivity fluids have a high temperature. Fluids with higher thermal conductivity have a higher temperature, implying that kinetic energy is transformed into thermal energy more quickly, resulting in more heat loss. The temperature profile is depicted in Figure 8 for varied values of thermophoresis (Nt) and Brownian motion parameters (Nb). The temperature profile is inclined as the values of these parameters rise. Because an elevation in Nt indicates a quality that directly opposes tangent hyperbolic fluid by conveying tiny particles’ passage to the proper flow zone, this is the scenario. It is defined as a measure of thermophoretic dispersion caused by a heat gradient in conveying tiny particles’ momentum diffusion. The huge Nt has a lot of thermophoretic power. This causes the conveying tiny particles’ near the hot surface to be pushed into the surrounding liquid. As a result, the liquid’s speed slows near the moving slender needle’s surface, causing the temperature gradient to rise. As Nb rises, the random motion of conveying tiny particles upturns, which case an increase in collisions between these conveying tiny particles’. The kinetic energy of the conveying tiny particles’ is converted to heat energy and growths the thermal boundary layer of the tangent hyperbolic fluid. Figure 9 spectacles the impression of Schmidt number (Sc) on the concentration profile. The Sc is the ratio of momentum diffusivity to mass diffusivity, which is a dimensionless quantity. Flows with synchronous momentum and mass transmission are known as Schmidt numbers. Schmidt number will fall when the mass transfer is greater than momentum diffusivity, implying that the effect of momentum diffusivity will be greater for lower values of Sc during fluid flows. Temperature and associated boundary layer profiles rise when the Sc is increased, while the increase is minor. Finally, as the Schmidt number rises, the concentration profile decreases, leading to the shrinking of the boundary layer profiles. The Sc has an inverse relationship with the molecular diffusion coefficient, and the profiles for the concentration profile peak at the thin needle’s surface and drop away from it. The relaxation time $\left(\Gamma \right)$ via concentration distribution is perceived in Figure 10. The concentration profile reductions as the value of $\Gamma$ increases. Physically, as the value of $\Gamma$ growths, the diffusivity of chemical molecules declines and less diffusion occurs, resulting in a decrease in the concentration boundary layer of fluid. As a result, an intensification in $\Gamma$ destroys the concentration of fluid. Figure 11 demonstrates the concentration profile for various thermophoresis (Nt) and Brownian motion parameter (Nb) values. It is revealed that for several values of Nb, the increasing behaviour in the conveying tiny particles’ concentration profile is noticeable, however, the conveying tiny particles’ concentration profile for the Nt shows the reverse trend. Physically, higher amounts of Nb speed up collisions between the random motions of the fluid conveying tiny particles’, causing the temperature to rise, resulting in increased heat and mass transfer. For growing values of Nb, the concentration and solutal BL thickness display augmentation behaviour. When Brownian diffusivity falls, the fraction of conveying tiny particles’ concentration increases. The Nt improves as the heat conductivity of the conveying tiny particles rises, infiltrating deeper into nanoparticles and reducing the thickness of the concentration boundary layer. Consequently, growing Nt reduces the concentration profile of the conveying tiny particles’. The random mobility of the fluid particles is also reduced. As the activation energy parameter (E) increases, the concentration profile goes up, as shown in Figure 12. As E rises, the number of molecules with the least amount of energy increases, resulting in the maximum mass transfer of the flow system as it improved the concentration boundary layer of tangent hyperbolic fluid. As a result, larger values of E increase the concentration profile. Figure 13 depicts the concentration profile of conveying tiny particles’ as a function of the elasticity parameter $\left(\delta \right).$ It has been observed that as the elasticity parameter improves, the nanoparticle concentration profile decreases.

FIGURE 2

FIGURE 2. M against $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$.

FIGURE 3

FIGURE 3. We against $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$.

FIGURE 4

FIGURE 4. m against $f^{\prime }\left(\eta \right).$

FIGURE 5

FIGURE 5. ${\theta }_w$ and $Nr$ against $\theta \left(\eta \right).$

FIGURE 6

FIGURE 6. $H$ against $\theta \left(\eta \right).$

FIGURE 7

FIGURE 7. ${\delta }_k$ against $\theta \left(\eta \right).$

FIGURE 8

FIGURE 8. $Nt$ and $Nb$ against $\theta \left(\eta \right).$

FIGURE 9

FIGURE 9. $Sc$ against $\varphi \left(\eta \right).$

FIGURE 10

FIGURE 10. $\Gamma$ against $\varphi \left(\eta \right).$

FIGURE 11

FIGURE 11. $Nt$ and $Nb$ against $\varphi \left(\eta \right).$

FIGURE 12

FIGURE 12. $E$ against $\varphi \left(\eta \right).$

FIGURE 13

FIGURE 13. $\delta$ against $\varphi \left(\eta \right).$

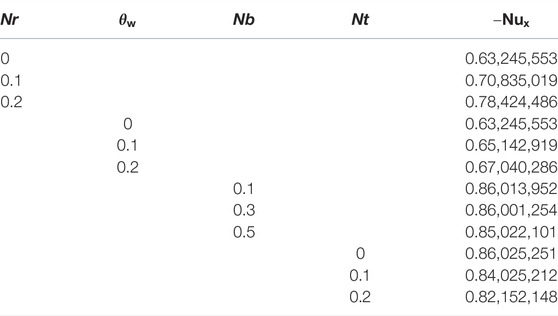
The numerical findings of local skin friction coefficients versus various parameters are exposed in Table 2. For higher M, m, and We, the local skin friction coefficient is amplified. Table 3 describes that the local Nusselt number is boosted up for Nr and ${\theta }_w$ while deteriorated for Nt and Nb. The local Sherwood number is raised for E, and Nt while declined for Nb, Sc, and $\Gamma$ as shown in Table 4.

TABLE 2

TABLE 2. Skin friction against several parameters.

TABLE 3

TABLE 3. Nusselt number against several parameters.

TABLE 4

TABLE 4. Sherwood number against several parameters.

4 Conclusion

The boundary layer flow, mass, and heat transfer of tangent hyperbolic conveying tiny particles across a thin needle implanted with activation energy are examined in this work. Brownian motion, nonlinear thermal, thermophoresis, source/sink and non-constant thermal conductivity are also included. Based on the outcome of the analysis and discussion of the results, it is worth concluding that:

1) Advanced M and We values, as well as a decelerating of fluid velocity and the thickness of its boundary layer while for increasing m the fluid velocity raise. For higher m, and We, the local skin friction coefficient is amplified.

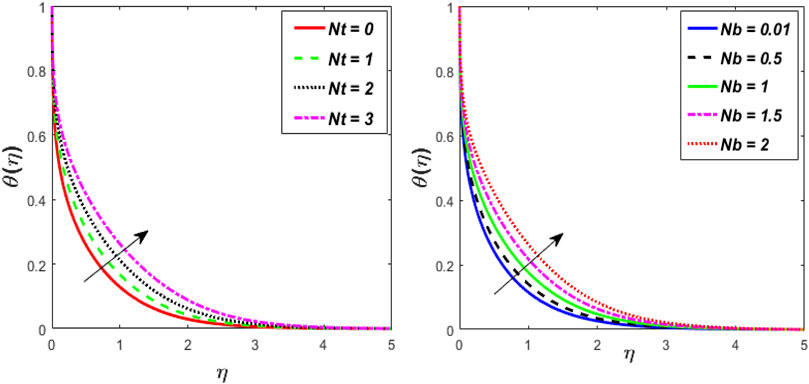
2) The thermal profile is improved as a result of improvements in We, Nt, Nb, ${\delta }_k$ and ${\theta }_w$ parameters. The local Nusselt number is heightened up for Nr and ${\theta }_w$ while declined for Nt and Nb.

3) The variable thermal conductivity is found to be significantly different from the constant fluid properties.

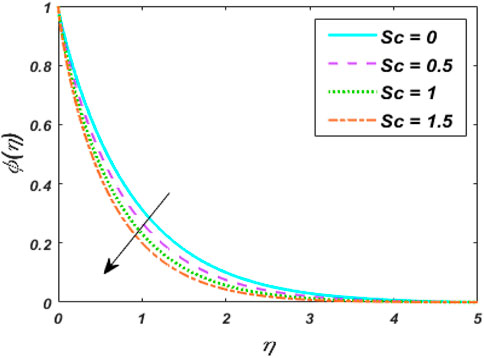
4) Increases in Nb improve the concentration gradient, but inclined values of Nt have the reverse effect. The local Sherwood number is raised for E, and Nt while declined for Nb, Sc, and $\Gamma .$

5) Higher values of the Sc and $\delta$ cause a delay in nanoparticle concentration. The acceleration in values of Nb and E improves the mass transfer rate.

Biomimetic, aerodynamics and metal spinning are a few important applications of this investigation. The preceding research can be expanded in the future by including the impact of non-linear mixed convection and variable viscosity. Furthermore, in the current study, the standard fluid could be substituted by a nanofluid or hybrid nanofluid.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

Conceptualization, IS, MN and IK; methodology, RA and IS; writing—original draft preparation, MN, HH and MA; writing—review and editing, IS; Formal analysis, RA and IK; Funding acquisition, IK; Investigation, HH and MN; supervision, IS All authors have read and agreed to the published version of the manuscript.

Funding

The authors extend their appreciation to Deanship of Scientific Research at King Khalid University, Saudi Arabia for funding this work through General Research Project under Grant No. GRP. 327/43.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lee LL. Boundary Layer over a Thin Needle. Phys Fluids (1967) 10:820–2. doi:10.1063/1.1762194

CrossRef Full Text | Google Scholar

2. Ishak A, Nazar R, Pop I. Boundary Layer Flow over a Continuously Moving Thin Needle in a Parallel Free Stream. Chin Phys. Lett. (2007) 24:2895–7. doi:10.1088/0256-307x/24/10/051

CrossRef Full Text | Google Scholar

3. Khan N, Riaz I, Hashmi MS, Musmar SA, Khan SU, Abdelmalek Z, Tlili I. Aspects of Chemical Entropy Generation in Flow of Casson Nanofluid between Radiative Stretching Disks. Entropy (2020) 22(5):495. doi:10.3390/e22050495

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ashraf K, Siddique I, Hussain A. Impact of Thermophoresis and Brownian Motion on Non-newtonian Nanofluid Flow with Viscous Dissipation Near Stagnation point. Phys Scr (2020) 95(5):055217. doi:10.1088/1402-4896/ab72c1

CrossRef Full Text | Google Scholar

5. Chen JLS, Smith TN. Forced Convection Heat Transfer from Nonisothermal Thin needles. ASME J Heat Trans (1978) 100:358–62. doi:10.1115/1.3450809

CrossRef Full Text | Google Scholar

6. Trimibitas R, Grosan T, Pop I. Mixed Convective Boundary Layer Flow along Vertical Thin Needle in Nanofluids. Int J Numeric Methods Heat Fluid Flow (2014) 24(3):579–94. doi:10.1108/HFF-05-2012-0098

CrossRef Full Text | Google Scholar

7. Souayeh B, Reddy MG, Sreenivasulu P, Poornima T, Rahimi-Gorji M, Alarifi IM. Comparative Analysis on Non-linear Radiative Heat Transfer on MHD Casson Nanofluid Past a Thin Needle. J Mol Liquids (2019) 284:163–74. doi:10.1016/j.molliq.2019.03.151

CrossRef Full Text | Google Scholar

8. Nayak MK, Mabood F, Makinde OD. Heat Transfer and Buoyancy‐driven Convective MHD Flow of Nanofluids Impinging over a Thin Needle Moving in a Parallel Stream Influenced by Prandtl Number. Heat Transfer (2020) 49(2):655–72. doi:10.1002/htj.21631

CrossRef Full Text | Google Scholar

9. Chu Y-M, Khan MI, Ur Rehman MI, Kadry S, Nayak MK. Flow and thermal Management of MHD Cross Nanofluids over a Thin Needle with Auto Catalysis Chemical Reactions. Int J Mod Phys B (2020) 34(30):2050287. doi:10.1142/s0217979220502872

CrossRef Full Text | Google Scholar

10. Lawrence LL. Boundary Layer over a Thin Needle. Phys Fluid (1967) 10(4):820–2.

Google Scholar

11. Mohan Krishna P, Sharma RP, Sandeep N. Boundary Layer Analysis of Persistent Moving Horizontal Needle in Blasius and Sakiadis Magnetohydrodynamic Radiative Nanofluid Flows. Nucl Eng Tech (2017) 49(8):1654–9. doi:10.1016/j.net.2017.07.023

CrossRef Full Text | Google Scholar

12. Khan I, Khan W, Qasim M, Afridi I, Alharbi S. Thermodynamic Analysis of Entropy Generation Minimization in Thermally Dissipating Flow over a Thin Needle Moving in a Parallel Free Stream of Two Newtonian Fluids. Entropy (2019) 21(1):74. doi:10.3390/e21010074

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ramesh GK, Shehzad SA, Izadi M. Thermal Transport of Hybrid Liquid over Thin Needle with Heat Sink/Source and Darcy-Forchheimer Porous Medium Aspects. Arab J Sci Eng (2020) 45:9569–78. doi:10.1007/s13369-020-04853-4

CrossRef Full Text | Google Scholar

14. Hamid A, Khan M. Thermo-physical Characteristics during the Flow and Heat Transfer Analysis of GO-Nanoparticles Adjacent to a Continuously Moving Thin Needle, Chin. J Phys (2020) 64:227–40.

Google Scholar

15. Salleh S, Bachok N, Arifin N, Ali F, Pop I. Magnetohydrodynamics Flow Past a Moving Vertical Thin Needle in a Nanofluid with Stability Analysis. Energies (2018) 11(12):3297. doi:10.3390/en11123297

CrossRef Full Text | Google Scholar

16. Waleed Ahmed Khan M, Ijaz Khan M, Hayat T, Alsaedi A. Entropy Generation Minimization (EGM) of Nanofluid Flow by a Thin Moving Needle with Nonlinear thermal Radiation. Physica B: Condensed Matter (2018) 534:113–9. doi:10.1016/j.physb.2018.01.023

CrossRef Full Text | Google Scholar

17. Mabood F, Nayak MK, Chamkha AJ. Heat Transfer on the Cross Flow of Micropolar Fluids over a Thin Needle Moving in a Parallel Stream Influenced by Binary Chemical Reaction and Arrhenius Activation Energy. Eur Phys J Plus (2019) 134(9):427. doi:10.1140/epjp/i2019-12716-9

CrossRef Full Text | Google Scholar

18. Song Y-Q, Hamid A, Khan MI, Gowda RJP, Kumar RN, Prasannakumara BC, Khan SU, Khan MI, Malik MY. Solar Energy Aspects of Gyrotactic Mixed Bioconvection Flow of Nanofluid Past a Vertical Thin Moving Needle Influenced by Variable Prandtl Number. Chaos, Solitons & Fractals (2021) 151:111244. doi:10.1016/j.chaos.2021.111244

CrossRef Full Text | Google Scholar

19. Tlili I, Nabwey HA, Reddy MG, Sandeep N, Pasupula M. Effect of Resistive Heating on the Incessantly Poignant Thin Needle in Magnetohydrodynamic Sakiadis Hybrid Nanofluid. Ain Shams Eng J (2020) 12(1):1025–32. doi:10.1016/j.asej.2020.09.009

CrossRef Full Text | Google Scholar

20. Bilal M, Urva Y. Analysis of Non-newtonian Fluid Flow over fine Rotating Thin Needle for Variable Viscosity and Activation Energy. Arch Appl Mech (2021) 91:1079–95. doi:10.1007/s00419-020-01811-2

CrossRef Full Text | Google Scholar

21. Choi SUS. Enhancing thermal Conductivity of Fluids with Nanoparticles. Usa, ASME FED (1995) 231:99–105.

Google Scholar

22. Kim J, Kang YT, Choi CK. Analysis of Convective Instability and Heat Transfer Characteristics of Nanofluids. Phys Fluids (2004) 16:2395–401. doi:10.1063/1.1739247

CrossRef Full Text | Google Scholar

23. Bowers J, Cao H, Qiao G, Li Q, Zhang G, Mura E, Ding Y. Flow and Heat Transfer Behaviour of Nanofluids in Microchannels. Prog Nat Sci Mater Int (2018) 28:225–34. doi:10.1016/j.pnsc.2018.03.005

CrossRef Full Text | Google Scholar

24. Das K. Nanofuid Flow over a Non-linear Permeable Stretching Sheet with Partial Slip. J Egypt Math Soc (2014) 23:451–6. doi:10.1016/j.joems.2014.06.014

CrossRef Full Text | Google Scholar

25. Ashorynejad HR, Shahriari A. MHD Natural Convection of Hybrid Nanofluid in an Open Wavy Cavity. Results Phys (2018) 9:440–55. doi:10.1016/j.rinp.2018.02.045

CrossRef Full Text | Google Scholar

26. Saleem S, Animasaun IL, Yook S-J, Al-Mdallal QM, Shah NA, Faisal M. Insight into the Motion of Water Conveying Three Kinds of Nanoparticles Shapes on a Horizontal Surface: Significance of Thermo-Migration and Brownian Motion. Surf Inter (2022) 30:101854. doi:10.1016/j.surfin.2022.101854

CrossRef Full Text | Google Scholar

27. Ahmad I, Faisal M, Javed T, Mustafa A, Kiyani MZ. Numerical Investigation for Mixed Convective 3D Radiative Flow of Chemically Reactive Williamson Nanofluid with Power Law Heat/mass Fluxes. Ain Shams Eng J (2022) 13(1):101508. doi:10.1016/j.asej.2021.05.022

CrossRef Full Text | Google Scholar

28. Ahmad I, Faisal M, Javed T, Animasaun IL. Insight into the Relationship between Unsteady Cattaneo-Christov Double Diffusion, Random Motion and Thermo-Migration of Tiny Particles. Ain Shams Eng J (2022) 13(1):101494. doi:10.1016/j.asej.2021.05.008

CrossRef Full Text | Google Scholar

29. Nadeem M, Elmoasry A, Siddique I, Jarad F, Zulqarnain RM, Alebraheem J, Elazab NS. Study of Triangular Fuzzy Hybrid Nanofluids on the Natural Convection Flow and Heat Transfer between Two Vertical Plates. Comput Intelligence Neurosci (2021) 2021:3678335. doi:10.1155/2021/3678335

CrossRef Full Text | Google Scholar

30. Siddique I, Zulqarnain RM, Nadeem M, Jarad F. Numerical Simulation of MHD Couette Flow of a Fuzzy Nanofluid through an Inclined Channel with thermal Radiation Effect. Comput Intelligence Neurosci (2021) 2021:1–16. doi:10.1155/2021/6608684

CrossRef Full Text | Google Scholar

31. Nadeem M, Siddique I, Ali R, Alshammari N, Jamil RN, Hamadneh N, Andualem M. Study of Third-Grade Fluid under the Fuzzy Environment with Couette and Poiseuille Flows. Math Probl Eng (2022) 2022:1–19. doi:10.1155/2022/2458253

CrossRef Full Text | Google Scholar

32. Nadeem M, Siddique I, Jarad F, Jamil RN. Numerical Study of MHD Third-Grade Fluid Flow through an Inclined Channel with Ohmic Heating under Fuzzy Environment. Math Probl Eng (2021) 2021:9137479. doi:10.1155/2021/9137479

CrossRef Full Text | Google Scholar

33. Siddique I, Jamil RN, Nadeem M, El-Wahed Khalifa HA, Alotaibi F, Khan I, Andualem M. Fuzzy Analysis for Thin-Film Flow of a Third-Grade Fluid Down an Inclined Plane. Math Probl Eng (2022) 16:3495228. doi:10.1155/2022/3495228

CrossRef Full Text | Google Scholar

34. Mabood F, Shateyi S, Rashidi MM, Momoniat E, Freidoonimehr N. MHD Stagnation point Flow Heat and Mass Transfer of Nanofluids in Porous Medium with Radiation, Viscous Dissipation and Chemical Reaction. Adv Powder Tech (2016) 27:742–9. doi:10.1016/j.apt.2016.02.033

CrossRef Full Text | Google Scholar

35. Afridi MI, Tlili I, Qasim M, Khan I. Nonlinear Rosseland thermal Radiation and Energy Dissipation Effects on Entropy Generation in CNTs Suspended Nanofluids Flow over a Thin Needle. Bound Value Probl (2018) 148:1–14. doi:10.1186/s13661-018-1062-3

CrossRef Full Text | Google Scholar

36. Tlili I, Ramzan M, Kadry S, Kim HW, Nam Y. Radiative MHD Nanofluid Flow over a Moving Thin Needle with Entropy Generation in a Porous Medium with Dust Particles and Hall Current. Entropy (2020) 22:354. doi:10.3390/e22030354

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Faisal M, Ahmad I, Javed T. Keller-Box Simulation for Nonzero and Zero Mass Fluxes of Nanofluid Flow Impinging over a Bi-directional Stretching Sheet: An Unsteady Mathematical Model. Int J Mod Phys C (2021) 32(04):2150052. doi:10.1142/s0129183121500522

CrossRef Full Text | Google Scholar

38. Javed T, Faisal M, Ahmad I. Dynamisms of Solar Radiation and Prescribed Heat Sources on Bidirectional Flow of Magnetized Eyring-Powell Nanofluid. Case Stud Therm Eng (2020) 21:100689. doi:10.1016/j.csite.2020.100689

CrossRef Full Text | Google Scholar

39. Faisal M, Ahmad I, Javed T. Radiative Nanofluid Flow Due to Unsteady Bi-directional Stretching Surface with Convective and Zero Mass Flux Boundary Conditions: Using Keller Box Scheme. Comput Therm Sci Int J (2020) 12(4):361–85. doi:10.1615/computthermalscien.2020033674

CrossRef Full Text | Google Scholar

40. Hamid A. Terrific Effects of Ohmic-Viscous Dissipation on Casson Nanofluid Flow over a Vertical Thin Needle: Buoyancy Assisting & Opposing Flow. J Mater Res Tech (2020) 9(5):11220–30. doi:10.1016/j.jmrt.2020.07.070

CrossRef Full Text | Google Scholar

41. Sulochana C, Ashwinkumar GP, Sandeep N. Boundary Layer Analysis of Persistent Moving Horizontal Needle in Magnetohydrodynamic Ferrofluid: A Numerical Study. Alexandria Eng J (2018) 57(4):2559–66. doi:10.1016/j.aej.2017.08.020

CrossRef Full Text | Google Scholar

42. Ahmad S, Arifin NM, Nazar R, Pop I. Mixed Convection Boundary Layer Flow along Vertical Thin needles: Assisting and Opposing Flows. Int Commun Heat Mass Trans (2007) 35(2):157–62.

Google Scholar

43. Afridi MI, Qasim M, Wakif A, Hussanain A. Numerical Analysis of Boundary Layer Flow Adjacent to a Thin Needle in Nanofluid with the Presence of Heat Source and Chemical Reaction. Symmetry (2019) 11:543. doi:10.3390/sym11040543

CrossRef Full Text | Google Scholar

44. Shafq A, Hammouch Z, Sindhu TN. Bioconvective MHD Flow of tangent Hyperbolic Nanofluid with Newtonian Heating. Int J Mech Sci (2017) 133:759–66.

Google Scholar

45. Trimbitas R, Grosan T, Pop I. Mixed Convection Boundary Layer Flow along Vertical Thin needles in Nanofluids. Int J Numer Methods Heat Fluid Flow (2014) 24(3):579–94. doi:10.1108/hff-05-2012-0098

CrossRef Full Text | Google Scholar

46. Hayat T, Waqas M, Alsaedi A, Bashir G, Alzahrani F. Magnetohydrodynamic (MHD) Stretched Flow of tangent Hyperbolic Nanoliquid with Variable Thickness. J Mol Liquids (2017) 229:178–84. doi:10.1016/j.molliq.2016.12.058

CrossRef Full Text | Google Scholar

47. Eid MR. Chemical Reaction Effect on MHD Boundary-Layer Flow of Two-phase Nanofluid Model over an Exponentially Stretching Sheet with a Heat Generation. J Mol Liquids (2016) 220:718–25. doi:10.1016/j.molliq.2016.05.005

CrossRef Full Text | Google Scholar

48. Waini I, Ishak A, Pop I. Hybrid Nanofluid Flow and Heat Transfer Past a Vertical Thin Needle with Prescribed Surface Heat Flux. Hff (2019) 29(12):4875–94. doi:10.1108/hff-04-2019-0277

CrossRef Full Text | Google Scholar

49. Afridi MI, Tlili I, Goodarzi M, Osman M, Khan NA. Irreversibility Analysis of Hybrid Nanofluid Flow over a Thin Needle with Effects of Energy Dissipation. Symmetry (2019) 11(5):663. doi:10.3390/sym11050663

CrossRef Full Text | Google Scholar

50. Singh BB. An Integral Treatment for Heat and Mass Transfer along a Vertical wall by Natural Convection in a Porous media. WIT Trans Engng Sci (2007) 56:143–51. doi:10.2495/mpf070141

CrossRef Full Text | Google Scholar

51. Putra N, Roetzel W, Das SK. Nat convection nano-fluids, Heat mass transfer (2003) 39(8):775–84. doi:10.1007/s00231-002-0382-z

CrossRef Full Text

52. Soid SK, Ishak A, Pop I. Boundary Layer Flow Past a Continuously Moving Thin Needle in a Nanofluid. Appl Therm Eng (2017) 114:58–64. doi:10.1016/j.applthermaleng.2016.11.165

CrossRef Full Text | Google Scholar

53. Narain JP, Uberoi MS. Combined Forced and Free-Convection over Thin needles. Int J Heat Mass Transfer (1973) 16(8):1505–12. doi:10.1016/0017-9310(73)90179-8

CrossRef Full Text | Google Scholar

54. Sulochana C, Samrat SP, Sandeep N. Boundary Layer Analysis of an Incessant Moving Needle in MHD Radiative Nanofluid with Joule Heating. Int J Mech Sci (2017) 128-129:326–31. doi:10.1016/j.ijmecsci.2017.05.006

CrossRef Full Text | Google Scholar

55. Afridi MI, Qasim M. Entropy Generation and Heat Transfer in Boundary Layer Flow over a Thin Needle Moving in a Parallel Stream in the Presence of Nonlinear Rosseland Radiation. Int J Therm Sci (2018) 123:117–28. doi:10.1016/j.ijthermalsci.2017.09.014

CrossRef Full Text | Google Scholar

56. Nieuwstadt FTM, Wolthers W, Leijdens H, Krishna Prasad K, Schwarz-van Manen A. The Reduction of Skin Friction by Riblets under the Influence of an Adverse Pressure Gradient. Experiments in fluids (1993) 15(1):17–26. doi:10.1007/bf00195591

CrossRef Full Text | Google Scholar

57. Faisal M, Ahmad I, Javed T. Dynamics of MHD tangent Hyperbolic Nanofluid with Prescribed thermal Conditions, Random Motion and Thermo-Migration of Nanoparticles. J Dispersion Sci Tech (2021) 1–15. doi:10.1080/01932691.2021.1931291

CrossRef Full Text | Google Scholar

58. Bilal M, Sagheer M, Hussain S. Numerical Study of Magnetohydrodynamics and thermal Radiation on Williamson Nanofluid Flow over a Stretching cylinder with Variable thermal Conductivity. Alexandria Eng J (2018) 57:3281–9. doi:10.1016/j.aej.2017.12.006

CrossRef Full Text | Google Scholar

59. Miao L, Massoudi M. Heat Transfer Analysis and Flow of a Slag-type Fluid: Effects of Variable thermal Conductivity and Viscosity. Int J Non-Linear Mech (2015) 76:8–19. doi:10.1016/j.ijnonlinmec.2015.05.001

CrossRef Full Text | Google Scholar

60. Hayat T, Khan MI, Farooq M, Gull N, Alsaedi A. Unsteady Three-Dimensional Mixed Convection Flow with Variable Viscosity and thermal Conductivity. J Mol Liquids (2016) 223:1297–310. doi:10.1016/j.molliq.2016.09.069

CrossRef Full Text | Google Scholar

61. Khan U, Zaib A, Ishak A, Bakar SA, Animasaun IL, Yook S-J. Insights into the Dynamics of Blood Conveying Gold Nanoparticles on a Curved Surface when Suction, thermal Radiation, and Lorentz Force Are Significant: The Case of Non-newtonian Williamson Fluid. Mathematics Comput Simulation (2022) 193:250–68. doi:10.1016/j.matcom.2021.10.014

CrossRef Full Text | Google Scholar

62. Khan U, Shafiq A, Zaib A, Baleanu D. Hybrid Nanofluid on Mixed Convective Radiative Flow from an Irregular Variably Thick Moving Surface with Convex and Concave Effects. Case Stud Therm Eng (2020) 21:100660. doi:10.1016/j.csite.2020.100660

CrossRef Full Text | Google Scholar

63. Khan U, Zaib A, Mebarek-Oudina F. Mixed Convective Magneto Flow of SiO2-MoS2/C2H6O2 Hybrid Nanoliquids through a Vertical Stretching/Shrinking Wedge: Stability Analysis. Arab J Sci Eng (2020) 45(11):9061–73. doi:10.1007/s13369-020-04680-7

CrossRef Full Text | Google Scholar

64. Khan U, Zaib A, Ishak A, Roy NC, Bakar SA, Muhammad T, Yahia IS. Exact Solutions for MHD Axisymmetric Hybrid Nanofluid Flow and Heat Transfer over a Permeable Non-linear Radially Shrinking/stretching Surface with Mutual Impacts of thermal Radiation. Eur Phys J Spec Top (2022) 1–10. doi:10.1140/epjs/s11734-022-00529-2

CrossRef Full Text | Google Scholar

65. Khan U, Waini I, Zaib A, Ishak A, Pop I. MHD Mixed Convection Hybrid Nanofluids Flow over a Permeable Moving Inclined Flat Plate in the Presence of Thermophoretic and Radiative Heat Flux Effects. Mathematics (2022) 10(7):1164. doi:10.3390/math10071164

CrossRef Full Text | Google Scholar

66. Dawar A, Wakif A, Thumma T, Shah NA. Towards a New MHD Non-homogeneous Convective Nanofluid Flow Model for Simulating a Rotating Inclined Thin Layer of Sodium Alginate-Based Iron Oxide Exposed to Incident Solar Energy. Int Commun Heat Mass Transfer (2022) 130:105800. doi:10.1016/j.icheatmasstransfer.2021.105800

CrossRef Full Text | Google Scholar

67. Song Y-Q, Obideyi BD, Shah NA, Animasaun IL, Mahrous YM, Chung JD. Significance of Haphazard Motion and thermal Migration of Alumina and Copper Nanoparticles across the Dynamics of Water and Ethylene Glycol on a Convectively Heated Surface. Case Stud Therm Eng (2021) 26:101050. doi:10.1016/j.csite.2021.101050

CrossRef Full Text | Google Scholar

68. Oke AS, Animasaun IL, Mutuku WN, Kimathi M, Shah NA, Saleem S. Significance of Coriolis Force, Volume Fraction, and Heat Source/sink on the Dynamics of Water Conveying 47 Nm Alumina Nanoparticles over a Uniform Surface. Chin J Phys (2021) 71:716–27. doi:10.1016/j.cjph.2021.02.005

CrossRef Full Text | Google Scholar

69. Faisal M, Ahmad I, Javed T. Numerical Assessments of Prescribed Heat Sources on Unsteady 3D Flow of Williamson Nanoliquid through Porous media. Spec Top Rev Porous Media: Int J (2021) 12(2):71. doi:10.1615/specialtopicsrevporousmedia.2021034104

CrossRef Full Text | Google Scholar