A Note on Resistance Distances of Graphs

Let G be a connected graph with vertex set V(G). The resistance distance between any two vertices u, v ∈ V(G) is the net effective resistance between them in the electric network constructed from G by replacing each edge with a unit resistor. Let S ⊂ V(G) be a set of vertices such that all the vertices in S have the same neighborhood in G − S, and let G[S] be the subgraph induced by S. In this note, by the {1}-inverse of the Laplacian matrix of G, formula for resistance distances between vertices in S is obtained. It turns out that resistance distances between vertices in S could be given in terms of elements in the inverse matrix of an auxiliary matrix of the Laplacian matrix of G[S], which derives the reduction principle obtained in [J. Phys. A: Math. Theor. 41 (2008) 445203] by algebraic method.

1 Introduction

The novel concept of resistance distance was introduced by Klein and Randić [8] in 1993. For a connected graph G with vertex set V(G) = {1, 2, …, n}, the resistance distance between u, v ∈ V(G), denoted by Ω_G (u, v), is defined to be the effective resistance between u and v in the corresponding electric network obtained from G by replacing each edge with a unit resistor. Since resistance distance is an intrinsic graph metric and an important component of circuit theory, with potential applications in chemistry, it has been extensively studied in mathematics, physics, and chemistry. For more information, we refer the readers to recent papers [2, 4, 6, 7, 10, 11, 15] and references therein.

Let G be a connected graph of order n. For any set of vertices U ⊂ V(G), we use G [U] to denote the subgraph induced by U, and G − U to denote the subgraph obtained from G by removing all the vertices in U as well as all the edges incident to vertices of U. The adjacency matrix A_G of G is an n × n matrix such that the (i, j)-th element of A_G is equal to 1 if vertices i and j are adjacent and 0 otherwise. The Laplacian matrix of G is L_G = D_G − A_G, where D_G is the diagonal matrix of vertex degrees of G. Clearly, L_G is real symmetric and singular.

Let M be an n × m real matrix. An m × n real matrix X is called a {1}-inverse of M and denoted by M⁽¹⁾, if X satisfies the following equation:

$MXM=M.$

If M is singular, then it has infinite {1}-inverses. It is well known that resistance distances in a connected graph G can be obtained from any {1}-inverse of L_G (see [1]). So far, there are many well-established results on this inverse. For example, in 2014, Bu et al [4] obtained the {1}-inverse of the Laplacian matrix for a class of connected graphs, and investigated resistance distances in subdivision-vertex join and subdivision-edge join of graphs. Then in 2015, an exact expression for the {1}-inverse of the Laplacian matrix of connected graphs was obtained by Sun et al. [13]. After that, Liu et al. [9] obtained the {1}-inverses for the Laplacian matrix of subdivision-vertex and subdivision-edge coronae networks. Recently, Cao et al. [5] also characterised the {1}-inverses for the Laplacian of corona and neighborhood corona networks. Sardar et al. [12] determined resistance distances of some classes of rooted product graphs via the Laplacian {1}-inverses method.

In this paper, some results on the {1}-inverses for Laplacian matrices of graphs with given special properties are established. As an application, for any given vertex set S ⊂ V(G) such that all the vertices in S have the same neighborhood N in G − S, explicit formula for resistance distances between vertices in S is obtained. It turns out that resistance distances between vertices in S could be given in terms of elements in the inverse matrix of an auxiliary matrix of the Laplacian matrix of G[S], which derives the reduction principle obtained in [J. Phys. A: Math. Theor. 41 (2008) 445203] by algebraic method.

2 Preliminary Results

In this section, we present some preliminary results. We first introduce the concept of group inverse and Moore-Penrose inverse of a matrix.

Definition 2.1. For a square matrix X, the group inverse of X, denoted by X^#, is the unique matrix H that satisfies matrix equations:

$XHX=X,HXH=H,XH=HX.$

Definition 2.2. Let M be an n × m matrix. An m × n matrix X is called the Moore-Penrose inverse of M, if X satisfies the following conditions:

$MXM=M,XMX=X,{\left(MX\right)}^H=MX,{\left(XM\right)}^H=XM.$

where X^H represents the conjugate transpose of the matrix X.If M is real symmetric, then there exists a unique M^# and M^# is the symmetric {1}-inverse of M. In particular, M^# is equal to the Moore-Penrose inverse of M because M is symmetric [3].Let (M)_ij denote the (i, j)-entry of M. It is well known that resistance distances in a connected graph G can be obtained from any {1}-inverse of L_G according to the following lemma.

Lemma 2.3. [3] Let G be a connected graph. Then for vertices i and j,

$\begin{array}{ll}\hfill {\mathrm{\Omega }}_G\left(i,j\right)& ={\left(L_G^{\left(1\right)}\right)}_{ii}+{\left(L_G^{\left(1\right)}\right)}_{jj}-{\left(L_G^{\left(1\right)}\right)}_{ij}-{\left(L_G^{\left(1\right)}\right)}_{ji}\hfill \\ \hfill & ={\left(L_G^{\#}\right)}_{ii}+{\left(L_G^{\#}\right)}_{jj}-2{\left(L_G^{\#}\right)}_{ij}.\hfill \end{array}$

Let 0 and e be all-zero and all-one column vectors, respectively. Let J_n×m be the n × m all-one matrix. The following result is due to Sun et al. [13] which characterizes the {1}-inverse of the Laplacian matrix.

Lemma 2.4. [13] Let $L_G=\left[\begin{array}{cc}\hfill L_1\hfill & \hfill L_2\hfill \\ \hfill L_2^T\hfill & \hfill L_3\hfill \end{array}\right]$ be the Laplacian matrix of a connected graph. If L₁ is nonsingular, then $X=\left[\begin{array}{cc}\hfill L_1^{-1}+L_1^{-1}{L}_2{S}^{\#}{L}_2^T{L}_1^{-1}\hfill & \hfill -L_1^{-1}{L}_2{S}^{\#}\hfill \\ \hfill -S^{\#}{L}_2^T{L}_1^{-1}\hfill & \hfill S^{\#}\hfill \end{array}\right]$ is a symmetric {1}-inverse of L_G, where $S=L_3-L_2^T{L}_1^{-1}{L}_2$.In particular, if each column vector of $L_2^T$ is − e or 0, then X can be further simplified. For convenience, in the rest of this section (see Lemmas 2.5, 2.6, 2.7), we always assume that $L_G=\left[\begin{array}{cc}\hfill L_1\hfill & \hfill L_2\hfill \\ \hfill L_2^T\hfill & \hfill L_3\hfill \end{array}\right]$, with the property that L₁ is nonsingular, and each column vector of $L_2^T$ is − e or 0.

Lemma 2.5. [4] Let L_G be defined as above. Then $X=\left[\begin{array}{cc}\hfill L_1^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill S^{\#}\hfill \end{array}\right]$ is a symmetric {1}-inverse of L_G, where $S=L_3-L_2^T{L}_1^{-1}{L}_2$.According to Lemma 2.4, we could get the following results.

Lemma 2.6. Let L_G be defined as above. If each row of L₁ sums to k, then each column vector of $-L_1^{-1}{L}_2{S}^{\#}$ is proportional to the all-one vector, where $S=L_3-L_2^T{L}_1^{-1}{L}_2$.

Proof. Suppose that the number of columns of L₂ is n₂ and let $L_2=\left[\begin{array}{cccc}\hfill {\mathbf{r}}_1\hfill & \hfill {\mathbf{r}}_2\hfill & \hfill \dots \hfill & \hfill {\mathbf{r}}_{n_2}\hfill \end{array}\right]$ with r_i being its i-th column vector, i = 1, 2, …, n₂. First we show that for any r_i, all the elements of $L_1^{-1}{\mathbf{r}}_i$ are the same. If r_i = 0, then the assertion holds since L₁r_i = 0. Otherwise, r_i = −e. Since L₁ is nonsingular with each row sum being k, it follows that each row of L⁻¹₁ sums to $\frac{1}{k}$. Thus $L_1^{-1}{\mathbf{r}}_i=L_1^{-1}(-\mathbf{e})=-\frac{1}{k}(\mathbf{e})$, which also implies that all the elements of $L_1^{-1}{\mathbf{r}}_i$ are the same. Hence, each column of $-L_1^{-1}{L}_2$ is proportional to the all-one vector, that is, all the row vectors of $-L_1^{-1}{L}_2$ are the same. It thus follows that each column of $-L_1^{-1}{L}_2{S}^{\#}$ is proportional to the all-one vector, i.e. all the elements in any given column of $-L_1^{-1}{L}_2{S}^{\#}$ are the same. □According to Lemma 2.6, we have the following result.

Lemma 2.7. Let L_G be defined as above. If each row of L₁ sums to k, then there exists a real number ξ such that $L_1^{-1}{L}_2{S}^{\#}{L}_2^T{L}_1^{-1}=\xi J_{n_1\times n_1}$, where $S=L_3-L_2^T{L}_1^{-1}{L}_2$.

Proof. Let $M_1=L_1^{-1}{L}_2{S}^{\#}$. According to the argument in the proof of Lemma 2.6, all the row vectors in M₁ are the same. On the other hand, since L₁ is real symmetric, it follows that

$L_2^T{L}_1^{-1}=L_2^T{\left(L_1^{-1}\right)}^T={\left(L_1^{-1}{L}_2\right)}^T.$

Let $M_2=L_2^T{L}_1^{-1}$. Then all the column vectors in M₂ are the same since all the row vectors in $-L_1^{-1}{L}_2$ are the same. Thus, we conclude that there exists a real number ξ such that

$L_1^{-1}{L}_2{S}^{\#}{L}_2^T{L}_1^{-1}=M_1{M}_2=\xi J_{n_1\times n_1}.$

This completes the proof. □

3 Main Results

In this section, we consider resistance distances between vertices in a specific subset S of V(G). Let S ⊂ V(G) such that all the vertices in S have the same neighborhood N in G − S. In the following, we give explicit formula for resistance distances between vertices in S. For simplicity, we use L_S to denote the Laplacian matrix of the subgraph induced by S. Suppose that the cardinalities of S and N are n₁ and k, respectively. Then the Laplacian matrix of G can be written as follows.

$L_G=\left[\begin{array}{cc}\hfill L_S+k{I}_{n_1}\hfill & \hfill L_2\hfill \\ \hfill L_2^T\hfill & \hfill L_3\hfill \end{array}\right],$

where $I_{n_1}$ is the identity matrix of order n₁.

Now we are ready to give formula for resistance distances between vertices in S.

Theorem 3.1. Let S ⊂ V(G) such that all the vertices in S have the same neighborhood N in G − S. Then for i, j ∈ S, we have

${\mathrm{\Omega }}_G\left(i,j\right)={\left(L_1^{-1}\right)}_{ii}+{\left(L_1^{-1}\right)}_{jj}-2{\left(L_1^{-1}\right)}_{ij}.$

where $L_1=L_S+k{I}_{n_1}$.

Proof. Let $L_1=L_S+k{I}_{n_1}$. Clearly, L₁ is nonsingular, and each row of L₁ sums to k and each column vector of L₂ is − e or 0. Then by Lemma 2.7, there exists a real number ξ such that $L_1^{-1}{L}_2{S}^{\#}{L}_2^T{L}_1^{-1}=\xi J_{n_1\times n_1}$, where $S=L_3-L_2^T{L}_1^{-1}{L}_2$. Then by Lemma 2.5, we can obtain the {1}-inverse of L_G as follows.

$X=\left[\begin{array}{cc}\hfill L_1^{-1}+\xi J_{n_1\times n_1}\hfill & \hfill -L_1^{-1}{L}_2{S}^{\#}\hfill \\ \hfill -S^{\#}{L}_2^T{L}_1^{-1}\hfill & \hfill S^{\#}\hfill \end{array}\right].$

Thus, for vertices i, j ∈ S, by Lemma 2.3, we have

$\begin{array}{ll}\hfill {\mathrm{\Omega }}_G\left(i,j\right)& ={\left(X\right)}_{ii}+{\left(X\right)}_{jj}-{\left(X\right)}_{ij}-{\left(X\right)}_{ji}\hfill \\ \hfill & ={\left(L_1^{-1}+\xi J_{n_1\times n_1}\right)}_{ii}+{\left(L_1^{-1}+\xi J_{n_1\times n_1}\right)}_{jj}-{\left(L_1^{-1}+\xi J_{n_1\times n_1}\right)}_{ij}-{\left(L_1^{-1}+\xi J_{n_1\times n_1}\right)}_{ji}\hfill \\ \hfill & ={\left(L_1^{-1}\right)}_{ii}+\xi +{\left(L_1^{-1}\right)}_{jj}+\xi -{\left(L_1^{-1}\right)}_{ij}-\xi -{\left(L_1^{-1}\right)}_{ji}-\xi \hfill \\ \hfill & ={\left(L_1^{-1}\right)}_{ii}+{\left(L_1^{-1}\right)}_{jj}-2{\left(L_1^{-1}\right)}_{ij}.\hfill \end{array}$

The proof is complete. □

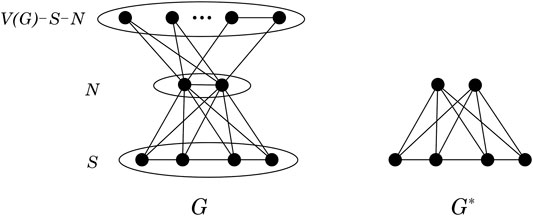
Theorem 3.1indicates that, if S ⊂ V(G) satisfies that all the vertices in S have the same neighborhood N in G − S, then resistance distances between vertices in S depends only on the subgraph G[S] and the cardinality of N. In other words, if we use G* to denote the subgraph obtained from G[S ∪ N] by deleting all the edges between vertices in N (see Figure 1), then resistance distances between vertices in S depends only on G*. In fact, for i, j ∈ S, ${\mathrm{\Omega }}_G(i,j)={\mathrm{\Omega }}_{G^{*}}(i,j)$, as shown in the following.

FIGURE 1

FIGURE 1. Illustration of graphs G and its subgraph G*.

Theorem 3.2. Let S ⊂ V(G) such that all the vertices in S have the same neighborhood N in G − S. Let G* the graph obtained from G[S ∪ N] by deleting all the edges between vertices in N. Then for i, j ∈ S, we have

${\mathrm{\Omega }}_{G^{*}}\left(i,j\right)={\left(L_1^{-1}\right)}_{ii}+{\left(L_1^{-1}\right)}_{jj}-2{\left(L_1^{-1}\right)}_{ij}.$

where $L_1=L_S+k{I}_{n_1}$.

Proof. According to the definition of G*, it is readily to see that the Laplacian matrix of G* is

$L_{G^{*}}=\left[\begin{array}{cc}\hfill L_1\hfill & \hfill -J_{n_1\times k}\hfill \\ \hfill -J_{k\times n_1}\hfill & \hfill k{I}_k\hfill \end{array}\right].$

Since each column vector of $-J_{k\times n_1}$ is − e, by Lemma 2.5, we can obtain the symmetric {1}-inverse of $L_{G^{*}}$ as follows:

$Y=\left[\begin{array}{cc}\hfill L_1^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill S^{\#}\hfill \end{array}\right],$

where $S=k{I}_k-J_{k\times n_1}{L}_1^{-1}{J}_{n_1\times k}$. Hence by Lemma 2.3, we have

${\mathrm{\Omega }}_{G^{*}}\left(i,j\right)={\left(L_1^{-1}\right)}_{ii}+{\left(L_1^{-1}\right)}_{jj}-2{\left(L_1^{-1}\right)}_{ij},$

as required. □

Remark 1. Combining Theorems 3.1 and 3.2, we could conclude that if S ⊂ V(G) satisfies that all the vertices in S have the same neighborhood N in G − S, then resistance distances between vertices in S can be computed as in the subgraph obtained from G[S ∪ N] by deleting all the edges between vertices in N. It should be mentioned that this fact, known as the reduction principle, was established in [14]. We confirm this result by algebraic method, rather than electric network method as used in [14]. Furthermore, we also give an exact formula for resistance distances between vertices in S. By Theorem 3.1, we are able to establish some interesting properties.

Theorem 3.3. Let S ⊂ V(G) such that all the vertices in S have the same neighborhood N in G − S. Then for i, j ∈ S and u ∈ G − S, we have

${\mathrm{\Omega }}_G\left(i,u\right)-{\mathrm{\Omega }}_G\left(j,u\right)={\left(L_1^{-1}\right)}_{ii}-{\left(L_1^{-1}\right)}_{jj}.$

where $L_1=L_S+k{I}_{n_1}$.

Proof. As given in the proof of Theorem 3.1, we know that the {1}-inverse of L_G is

$X=\left[\begin{array}{cc}\hfill L_1^{-1}+\xi J_{n_1\times n_1}\hfill & \hfill -L_1^{-1}{L}_2{S}^{\#}\hfill \\ \hfill -S^{\#}{L}_2^T{L}_1^{-1}\hfill & \hfill S^{\#}\hfill \end{array}\right].$

where ξ be a real number and $S=L_3-L_2^T{L}_1^{-1}{L}_2$. By Lemma 2.3, we have

${\mathrm{\Omega }}_G\left(i,u\right)-{\mathrm{\Omega }}_G\left(j,u\right)={\left(X\right)}_{ii}+{\left(X\right)}_{uu}-{\left(X\right)}_{iu}-{\left(X\right)}_{ui}-\left[{\left(X\right)}_{jj}+{\left(X\right)}_{uu}-{\left(X\right)}_{ju}-{\left(X\right)}_{uj}\right].$

Note that L₁ is nonsingular and every row sums to k and each column vector of L₂ is − e or a zero vector. So by Lemma 2.6, we know that each column of $-L_1^{-1}{L}_2{S}^{\#}$ is proportional to all-one vector, which implies that (X)_iu = (X)_ju. Since X is real symmetric, we also have (X)_ui = (X)_uj. It follows that

$\begin{array}{ll}\hfill {\mathrm{\Omega }}_G\left(i,u\right)-{\mathrm{\Omega }}_G\left(j,u\right)& ={\left(X\right)}_{ii}+{\left(X\right)}_{uu}-{\left(X\right)}_{jj}-{\left(X\right)}_{uu}\hfill \\ \hfill & ={\left(L_1^{-1}\right)}_{ii}+\xi +{\left(L_1^{-1}\right)}_{uu}+\xi -{\left(L_1^{-1}\right)}_{jj}-\xi -{\left(L_1^{-1}\right)}_{uu}-\xi \hfill \\ \hfill & ={\left(L_1^{-1}\right)}_{ii}-{\left(L_1^{-1}\right)}_{jj}.\hfill \end{array}$

This completes the proof. □It is interesting to note from Theorem 3.2 that the difference between Ω_G (i, u) and Ω_G (j, u) depends only on the subgraph G [S] and the cardinality of N, no matter the chosen of u. Then we have the following result.

Corollary 3.4. Let S ⊂ V(G) such that all the vertices in S have the same neighborhood N in G − S. Then for i, j ∈ S and u, v ∈ G − S, we have

${\mathrm{\Omega }}_G\left(i,u\right)-{\mathrm{\Omega }}_G\left(j,u\right)={\mathrm{\Omega }}_G\left(i,v\right)-{\mathrm{\Omega }}_G\left(j,v\right).$

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YY contributed to conception and design of the study. WS performed the theoretical analysis and wrote the first draft of the manuscript. YY revised the manuscript. Both authors read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank the anonymous referees for their helpful comments and suggestions. The support of the National Natural Science Foundation of China (through Grant No. 12171414) and Natural Science Foundation of Shandong Province (through no. ZR2019YQ02) is greatly acknowledged.

References

1. Bapat RB. Resistance Distance in Graphs. Math Stud (1999) 68(1-4):87–98.

Google Scholar

2. Bapat RB, Gupta S. Resistance Distance in Wheels and Fans. Indian J Pure Appl Math (2010) 41(1):1–13. doi:10.1007/s13226-010-0004-2

CrossRef Full Text | Google Scholar

3. Bu C, Sun L, Zhou J, Wei Y. A Note on Block Representations of the Group Inverse of Laplacian Matrices. Electron J Linear Algebra (2012) 23:866–76. doi:10.13001/1081-3810.1562

CrossRef Full Text | Google Scholar

4. Bu C, Yan B, Zhou X, Zhou J. Resistance Distance in Subdivision-Vertex Join and Subdivision-Edge Join of Graphs. Linear Algebra its Appl (2014) 458:454–62. doi:10.1016/j.laa.2014.06.018

CrossRef Full Text | Google Scholar

5. Cao J, Liu J, Wang S. Resistance Distances in corona and Neighborhood corona Networks Based on Laplacian Generalized Inverse Approach. J Algebra Appl (2019) 18(3):1950053. doi:10.1142/s0219498819500531

CrossRef Full Text | Google Scholar

6. Chen H, Zhang F. Resistance Distance and the Normalized Laplacian Spectrum. Discrete Appl Maths (2007) 155:654–61. doi:10.1016/j.dam.2006.09.008

CrossRef Full Text | Google Scholar

7. Fowler PW. Resistance Distances in Fullerene Graphs. Croat Chem Acta (2002) 75(2):401–8.

Google Scholar

8. Klein DJ, Randić M. Resistance Distance. J Math Chem (1993) 12:81–95. doi:10.1007/bf01164627

CrossRef Full Text | Google Scholar

9. Liu JB, Pan XF, Hu FT. The {1}-inverse of the Laplacian of Subdivision-Vertex and Subdivision-Edge Coronae with Applications. Linear and Multilinear Algebra (2017) 65(1):178–91. doi:10.1080/03081087.2016.1179249

CrossRef Full Text | Google Scholar

10. Liu JB, Wang WR, Zhang YM, Pan XF. On Degree Resistance Distance of Cacti. Discrete Appl Maths (2016) 203:217–25. doi:10.1016/j.dam.2015.09.006

CrossRef Full Text | Google Scholar

11. Palacios JL. Resistance Distance in Graphs and Random Walks. Int J Quant Chem (2001) 81(1):29–33. doi:10.1002/1097-461x(2001)81:1<29::aid-qua6>3.0.co;2-y

CrossRef Full Text | Google Scholar

12. Sardar MS, Alaeiyan M, Farahani MR, Cancan M, Ediz S. Resistance Distance in Some Classes of Rooted Product Graphs Obtained by Laplacian Generalized Inverse Method. J Inf Optimization Sci (2021) 42(7):1447–67. doi:10.1080/02522667.2021.1899210

CrossRef Full Text | Google Scholar

13. Sun L, Wang W, Zhou J, Bu C. Some Results on Resistance Distances and Resistance Matrices. Linear and Multilinear Algebra (2015) 63(3):523–33. doi:10.1080/03081087.2013.877011

CrossRef Full Text | Google Scholar

14. Yang Y, Zhang H. Some Rules on Resistance Distance with Applications. J Phys A: Math Theor (2008) 41(44):445203. doi:10.1088/1751-8113/41/44/445203

CrossRef Full Text | Google Scholar

15. Zhang H, Yang Y. Resistance Distance and Kirchhoff index in Circulant Graphs. Int J Quan Chem. (2007) 107(2):330–9. doi:10.1002/qua.21068

CrossRef Full Text | Google Scholar